1 Introduction

Determining exact and approximate solutions to nonlinear systems, even for simple systems governed by a single equation, continues to be an important contemporary endeavor in engineering science and applied mathematics [1–11]. This is in part due to the absence of a single analytical method capable of reliably finding all solutions (periodic, quasiperiodic, aperiodic, chaotic, etc.) to any given nonlinear system. It is reasonable to expect that such a panacea may never exist.

When seeking approximate solutions, the method of Multiple Scales (MS) is arguably among the most powerful and general perturbation techniques used in the engineering and applied mathematics communities [12]. It readily accommodates systems with dissipation, and its resulting evolution equations can be used to study stability of periodic solutions. Multiple scales have been used to solve nonlinear problems ranging from classical Duffing and van der Pol oscillators, to more recent explorations of quantum optical oscillators [13] and nonlinear wave propagation [14]. Extensive background on the method and its application to a wide range of nonlinear problems can be found in the monographs of Nayfeh and co-workers [12, 15, 16], and in texts by Jordan and Smith [17, 18], to name only a few. The major limitation of the method is its reliance on the existence, or appropriate introduction, of a small parameter. Thus, it belongs to a class of methods appropriate for studying weakly nonlinear systems.

In the search for more general analysis techniques (i.e., applicable to systems not necessarily weakly nonlinear), two homotopy-based analysis approaches have recently been presented for determining a wide variety of solutions to nonlinear problems encountered in physics and engineering. These techniques are notable for their ability to analyze weakly and strongly nonlinear systems since the presence of a small parameter is not required. They will be referred to herein as HAM and HPM. Both are outgrowths of homotopy techniques studied and developed in the field of mathematical topology [19]. The Homotopy Analysis Method (HAM) was first introduced by Liao [20–29] and has since been further developed and applied by many subsequent researchers to find solutions to a variety of nonlinear ordinary differential equations, both single equations and systems of equations. Most HAM papers analyze periodic and limit cycle solutions in a set of ordinary differential equation as per the original conception of the method, but others analyze wave-like solutions (including solitons) [30–34], solutions to boundary value problems [35–38], and even solutions to systems of differential algebraic equations (DAEs) [39]. The essential idea of the Homotopy Analysis Method is to introduce a continuation, or homotopy, of the original equation’s governing operator and field variable using an embedding parameter, say \(p\), such that the new operator varies continuously from a simple one (when \(p=0\)) to the original operator (when \(p=1\)). Further, the original field variable is obtained from the new one via a Taylor series with respect to \(p\), evaluated at \(p=1\). If the new operator is properly chosen, then the Taylor series is convergent. The goal is to then choose a homotopy which allows for straightforward solution and subsequent convergence of the Taylor series. Note that the approach typically yields only one possible solution, which has been proven to be one of the exact solutions [40].

The Homotopy Perturbation Method (HPM) is the second homotopy-based approach used in solving nonlinear equations. It was first introduced by He [41–45] and has also seen wide application and development by a number of other researchers. The method has been shown to accurately capture periodic, limit cycle, and other solution behavior in a diverse number of nonlinear systems, to include discontinuous nonlinear systems [44], nonlinear wave equations [45], reaction–diffusion equations [46], autonomous Duffing equations [47], integro-differential equations [48], and systems with boundary layers [49], to name just a few. Similar to HAM, the Homotopy Perturbation Method introduces a continuous homotopy whereby the original operator is replaced by one with an embedded homotopy parameter, say \(p\), such that the new operator varies continuously from a simple one (when \(p=0\)) to the original operator (when \(p=1\)). It differs from HAM, however, in that the original field variable is expanded asymptotically using polynomials of the homotopy parameter \(p\). Unlike typical perturbation approaches, a small parameter is not required since \(p\) serves the same purpose. Much like other perturbation approaches, separation of the equations by their dependence on the order of \(p\) yields a cascading of equations which are solved starting at order \(p^{0}\). Higher order equations see the lower order solutions on the right-hand side, resulting in secular and non-secular terms. Secular terms must be removed by appropriate choices, and then these ordered equations are solved to any desired degree; however, the asymptotic approach typically yields accurate results using only the first couple of orders.

To date, problems solved with either of the homotopy methods are almost exclusively autonomous. A few exceptions include a direct application of HAM [40] and HPM [50] to a forced Duffing equation. The study using HAM finds very accurate periodic solutions, even at larger values of the small parameter \(\varepsilon \), but requires a 10th-order approximation to get good results. The study using HPM is carried out to a significantly lower order, but does not consider large values of \(\varepsilon \). In both homotopy approaches, stability is not assessed within the method itself.

Considering both the advantages and weaknesses of existing Multiple Scales and homotopy methods, this paper presents a homotopy-enriched multiple scales approach for analyzing weakly and strongly nonlinear non-autonomous systems. An enrichment to Multiple Scales is pursued for several reasons. The first is that the method of Multiple Scales is highly flexible and can be tailored to capture a variety of forced solution types including periodic solutions at the forcing frequency, subharmonic and superharmonic solutions, quasiperiodic solutions, and others. It will be seen that the enriched method extends this flexibility beyond the conventional MS approach due to its introduction of a homotopy parameter. The second is that Multiple Scales have a strong standing in the engineering and applied mathematics communities, and thus an enrichment which leverages most of its existing machinery may be easily adopted by others. Finally, the method of Multiple Scales yields evolution equations which when combined with a local stability analysis yields stability information lacking in most other asymptotic approaches. The resulting technique shares many more similarities with the Multiple Scales technique than either of the homotopy techniques, and thus is most appropriately viewed as an enrichment to Multiple Scales rather than a homotopy variant.

The paper is organized as follows. Section 2 overviews the conventional Multiple Scales approach and its local stability analysis as applied to a forced Duffing system. Section 3 introduces the enriched technique as applied to the Duffing system, while Sect. 4 compares and contrasts results for the system generated using conventional MS, enriched MS, and numerical simulation. Section 5 applies the enriched technique to a forced van der Pol oscillator and discusses the flexibility of the enriched technique in terms of multiple possible homotopies and the resulting solutions uncovered. Section 6 concludes with remarks on the findings of the study.

2 The method of multiple scales—a brief review

The method of Multiple Scales (MS) has been widely used in finding periodic and other solutions to weakly nonlinear equations. An overview of the method and its application in a wide array of problems can be found in the text by Nayfeh and Mook [12]. The method is briefly reviewed next for a forced Duffing equation before developing the enriched technique. Note that this review follows precisely that presented by Nayfeh and Mook [12] in their Chapter 4.

The harmonically forced cubic Duffing equation considered herein is expressed as

$$\begin{aligned} \ddot{u}+\varepsilon 2 \mu \dot{u}+\omega _{0}^{2}u+\varepsilon \alpha u^{3}=\varepsilon k \cos (\varOmega \hbox {t}), \end{aligned}$$
(1)

where \(\varepsilon \) typically denotes a small parameter (not necessarily so herein), \(\mu \) denotes the damping coefficient, \(\omega _0 \) denotes the linear system’s natural frequency, \(\alpha \) denotes the cubic stiffness coefficient, \(k\) denotes the forcing amplitude, \(\varOmega \) denotes the forcing frequency, and an overdot denotes a time derivative. Equation (1) can be obtained from a physical system using any number of order reduction approaches (e.g., modal reduction), expansions about an equilibrium state, and/or assumptions on the size of the physical parameters. What is important is that for an analysis of primary resonance using Multiple Scales (and many other asymptotic approaches), the damping, nonlinearity, and the forcing must be ordered to appear with a leading term proportional to \(\varepsilon \) in order to remove secular terms. Any approximate solution technique then attempts to be as faithful to an exact solution to Eq. (1) as possible. Note that the exact solution should be expected to be a function of \(\varepsilon \) since this parameter does not appear in all terms—this point will be assessed in the conventional and enriched Multiple Scales approaches.

The conventional MS technique starts by introducing new time scales, \(T_i =\varepsilon ^{i}t, i=0,1,2,\ldots \) related to conventional time \(t\). Partial time derivatives are introduced such that \(D_i \) denotes \(\partial /\partial T_i , \mathrm{{d}}/\mathrm{{d}}t=D_0 +\varepsilon D_1 +\varepsilon ^{2}D_2 +\cdots \), and \(\mathrm{{d}}^{2}/\mathrm{{d}}t^{2}=D_0^2 +\varepsilon 2D_0 D_1 +\varepsilon ^{2}D_1^2 +\cdots \). Next, the displacement is expanded asymptotically with respect to \(\varepsilon \),

$$\begin{aligned} u\left( t,\varepsilon \right) =u_0 \left( T_0 ,T_1 ,\ldots \right) +\varepsilon u_1 \left( T_0 ,T_1 ,\ldots \right) +\cdots . \end{aligned}$$
(2)

Substituting Eq. (2) into (1) and separating orders of \(\varepsilon \) results in the first two ordered equations,

$$\begin{aligned}&\varepsilon ^{0}:D_0^2 u_0 +\omega _0^2 u_0 =0,\end{aligned}$$
(3a)
$$\begin{aligned}&\varepsilon ^{1}:D_0^2 u_1 +\omega _0^2 u_1 =-2D_0 D_1 u_0 -2\mu D_0 u_0 -\alpha u_0^3\nonumber \\&+kcos(\omega _0 T_0 +\sigma T_1 ), \end{aligned}$$
(3b)

where detuning \(\sigma \) has been introduced through the expression \(\varOmega =\omega _0 +\varepsilon \sigma \). Solving Eq. (3a) for \(u_0 \), substituting into Eq. (3b), and then removing secular terms leads to an approximation valid to first order,

$$\begin{aligned} u=\hbox {a}(T_1 )\hbox {cos}\left( \varOmega t-\gamma (T_1 )\right) +O(\varepsilon ), \end{aligned}$$
(4)

with amplitude \(\hbox {a}(T_1 )\) and phase \(\gamma (T_1 )\) governed by a set of evolution equations,

$$\begin{aligned}&a^{{\prime }}(T_1 )=-\mu a+\frac{1}{2}\frac{k}{\omega _0 }\hbox {sin}(\gamma ),\end{aligned}$$
(5)
$$\begin{aligned}&a\left( {T_1 } \right) \gamma ^{{\prime }}\left( {T_1 } \right) =\sigma a-\frac{3}{8}\frac{\alpha }{\omega _0 }a^{3}+\frac{1}{2}\frac{k}{\omega _0 }\hbox {cos}(\gamma ), \end{aligned}$$
(6)

where \(()^{{\prime }}\) denotes a derivative of \(()\) with respect to \(T_1 \). Fixed-point solutions to Eqs. (5)–(6) determine periodic solutions, which after some manipulation, yield the frequency response

$$\begin{aligned} \left[ \mu ^{2}+\left( \frac{3}{8}\frac{\alpha }{\omega _0 }a^{2}-\sigma \right) ^{2} \right] a^{2}=\frac{1}{4\omega _0^2 }k^{2}. \end{aligned}$$
(7)

Equation (7) yields three positive solutions for \(a(\sigma )\). It is important to observe that the conventional MS solution for amplitude as a function of detuning does not have an intrinsic dependence on \(\varepsilon \). This characteristic of the MS solution is not typically raised, but it does have important ramifications as the strength of the nonlinearity increases (as discussed further in Sect. 4).

The Multiple Scales approach also provides a convenient linear stability analysis for each of these solutions. This is in contrast to many other approximate solution techniques (e.g., Lindstedt Poincaré and harmonic balance) and thus makes the method very appealing. The basic idea is to perturb the fixed-point solutions for \(a\) and \(\gamma \), linearize the evolution equations about these perturbations, and assess stability from the resulting eigenvalue problem—full discussion can be found in the text by Nayfeh and Mook [12]. Such a stability approach will be detailed for the enriched Multiple Scales approach.

3 Enriched multiple scales—Duffing equation

The homotopy enrichment aims to extend the method of Multiple Scales such that it can analyze periodic solutions to strongly nonlinear systems and determine their stability. Thus, the governing equation considered is

$$\begin{aligned} \ddot{u}+2\hat{\mu }\dot{u}+\omega _{0}^{2}u+\hat{\alpha }u^{3}=\hat{k} \cos (\varOmega \hbox {t}), \end{aligned}$$
(8)

where \(\hat{\mu }, \hat{\alpha }\), and \(\hat{k}\) denote damping, cubic stiffness, and forcing coefficients, respectively. For the sake of comparison to the conventional MS approach, the parameter \(\varepsilon \) is re-introduced such that \(\hat{\mu }=\varepsilon \mu , \hat{\alpha } =\varepsilon \alpha \), and \(\hat{k}=\varepsilon k\), where the parameter \(\varepsilon \) is not necessarily small. Thus, Eq. (1) is again the starting point for the analysis with the understanding that \(\varepsilon \) can be either a small or large parameter.

The enriched Multiple Scales approach begins by seeking a homotopy with respect to a parameter \(p\) such that when \(p=0\) a linear equation results, and when \(p=1\) the nonlinear Duffing equation, Eq. (1), is recovered. We recognize that the forced solution should respond at the forcing frequency \(\varOmega \) and, hence, pose the following homotopy:

$$\begin{aligned}&\ddot{u}+\varOmega ^{2}u \nonumber \\&=p\left[ (\varOmega ^{2}-\omega _{0}^{2})u-2\varepsilon \mu \dot{u}-\varepsilon \alpha u^{3}+\varepsilon k \cos (\varOmega \hbox {t})\right] ,\nonumber \\ \end{aligned}$$
(9)

where, importantly, the linear natural frequency has been changed from \(\omega _0 \) appearing in Eq. (1) to \(\varOmega \) appearing in Eq. (9). Note, however, that Eq. (9) recovers Eq. (1) when \(p=1\), as required, and the desired linear equation when \(p=0\). Our starting point for the analysis of the Duffing system differs fundamentally from that presented in [50] in which the homotopy is defined such that the linear system responds at the forcing frequency, regardless of the strength of the nonlinearity. Thus, the solution at the lowest order is already close to the nonlinear solution, and hence only the first two terms will be required to effectively capture the response of weakly and strongly nonlinear systems.

Next, the displacement is expanded asymptotically with respect to \(p\),

$$\begin{aligned} u\left( t,\varepsilon \right) =u_0 \left( {T_0 ,T_1 ,\ldots } \right) +pu_1 \left( {T_0 ,T_1 ,\ldots } \right) +\cdots ,\nonumber \\ \end{aligned}$$
(10)

where displacements \(u_i , i=0,1,2,\ldots \) are assumed to depend on multiple time scales given by \(T_i =p^{i}t, i=0,1,2,\ldots \). Note the use of the homotopy parameter in definition of the new scales, which differs from the conventional MS approach. Partial time derivatives are also introduced such that \(D_i \) denotes \(\partial /\partial T_i \), \(\mathrm{{d}}/\mathrm{{d}}t=D_0 +pD_1 +p^{2}D_2 +\cdots \), and \(\mathrm{{d}}^{2}/\mathrm{{d}}t^{2}=D_0^2 +p2D_0 D_1 +p^{2}D_1^2 +\cdots \). Substitution of Eq. (10) into Eq. (9) and separating orders of \(p\) results in the first two ordered equations,

$$\begin{aligned}&p^{0}:D_0^2 u_0 +\varOmega ^{2}u_0 =0,\end{aligned}$$
(11a)
$$\begin{aligned}&p^{1}:D_0^2 u_1 +\varOmega ^{2}u_1 =-2D_0 D_1 u_0 +\left( \varOmega ^{2}-\omega _0^2 \right) u_0\nonumber \\&\qquad \quad -2\varepsilon \mu D_0 u_0 -\varepsilon \alpha u_0^3 +\varepsilon kcos\left( \varOmega t \right) . \end{aligned}$$
(11b)

The solution to Eq. (11a) is expressed in complex form as

$$\begin{aligned} u_0 =A(T_1 )e^{i\varOmega T_0 }+cc, \end{aligned}$$
(12)

where \(cc\) denotes the complex conjugate of all preceding terms. Next, the \(u_0 \) solution is substituted into Eq. (11b), and secular terms are removed from the right-hand side. Removal of these secular terms requires that

$$\begin{aligned}&-2i\varOmega A^{{\prime }}+\left( \varOmega ^{2}-\omega _0^2 \right) A\nonumber \\&\quad -2i\varepsilon \mu \varOmega A-\varepsilon \alpha 3A^{2}\overline{A}+\frac{1}{2}\varepsilon k=0, \end{aligned}$$
(13)

where an overbar denotes the complex conjugate and \(()^{{\prime }}\) denotes a derivative of \(()\) with respect to \(T_1 =pt\). Introducing the polar form \(A=\frac{1}{2}ae^{i\beta }\) where both the amplitude \(a(T_1 )\) and phase \(\beta (T_1 )\) are real functions of \(T_1 \), then separating real from imaginary parts, Eq. (13) yields the two evolution equations

$$\begin{aligned}&a\varOmega \beta ^{{\prime }}+\frac{1}{2}\left( \varOmega ^{2}-\omega _0^2 \right) a-\varepsilon \alpha \frac{3}{8}a^{3}+\frac{1}{2}\varepsilon k\cos \beta =0,\nonumber \\ \end{aligned}$$
(14a)
$$\begin{aligned}&-\varOmega a^{\prime }-\varepsilon \mu \varOmega a-\frac{1}{2}\varepsilon k\sin \beta =0. \end{aligned}$$
(14b)

Note that these evolution equations are already in autonomous form, unlike those that result from the conventional Multiple Scales technique, and thus may avoid solution difficulties in more complex systems.

3.1 Periodic solutions

Periodic solutions to Eq. (1) correspond to fixed-point solutions to Eqs. (14a)–(14b). Setting derivatives with respect to \(T_1 \) to zero and solving yields the frequency response (amplitude \(a_0 \) and phase \(\beta _0 \) versus forcing frequency \(\varOmega )\),

$$\begin{aligned}&\left( {\varepsilon \mu \varOmega a_0 } \right) ^{2}+\left( {\varepsilon \alpha \frac{3}{8}a_0 ^{3}-\frac{1}{2}\left( {\varOmega ^{2}-\omega _0^2 } \right) a_0 } \right) ^{2}\nonumber \\&\quad =\frac{1}{4}\varepsilon ^{2}k^{2},\end{aligned}$$
(15)
$$\begin{aligned}&\tan \beta _0 =\frac{8\varepsilon \mu \varOmega a_0 }{4\left( {\varOmega ^{2}-\omega _0^2 } \right) a_0 -3\varepsilon \alpha a_0 ^{3}}. \end{aligned}$$
(16)

Of note in these solutions is the explicit dependence on \(\varepsilon \), which is not the case in the conventional Multiple Scales approach. Although strictly not necessary, to facilitate comparison to conventional MS results, we introduce a detuning parameter [12] \(\sigma \) such that

$$\begin{aligned} \varOmega =\omega _0 +\varepsilon \sigma . \end{aligned}$$
(17)

As in all other presented equations, \(\varepsilon \) need not be small for the enriched Multiple Scales method. Note that the conventional MS approach exhibits dependence on \(\varepsilon \) only after reconstituting the frequency response via Eq. (17), whereas the enriched MS technique exhibits \(\varepsilon \) dependence in Eqs. (15) and (17).

3.2 Stability

Similar to conventional Multiple Scales, the evolution equations enable solution stability to be studied using a linear stability analysis. Letting \(a\left( {T_1 } \right) =a_0 +a_1 \left( {T_1 } \right) \) and \(\beta \left( {T_1 } \right) =\beta _0 +\beta _1 \left( {T_1 } \right) \) and linearizing with respect to \(a_1 \) and \(\beta _1 \), the solution stability can be determined from the eigenvalue problem,

$$\begin{aligned}&\left\{ \begin{array}{c} a_1 \\ \beta _1 \nonumber \\ \end{array} \right\} ^{{\prime }}\\&\quad =\left[ \begin{array}{ll} {-}\varepsilon \mu &{}\quad \left( {-}\frac{3}{8}\frac{\alpha \varepsilon }{\varOmega }a_0^3 {+}\frac{1}{2}\frac{\varOmega ^{2}{-}\omega _0^2 }{\varOmega }\right) a_0 \\ \frac{1}{a_0 }\left( \frac{9}{8}\frac{\alpha \varepsilon }{\varOmega }a_0^2 -\frac{1}{2}\frac{\varOmega ^{2}-\omega _0^2 }{\varOmega } \right) &{}\quad {-\varepsilon \mu } \\ \end{array} \right] \nonumber \\&\quad \left\{ \begin{array}{c} a_1 \\ \beta _1 \\ \end{array} \right\} , \end{aligned}$$
(18)

where the phase \(\beta _0 \) has been eliminated using the fixed-point solutions. This eigenvalue problem leads to a characteristic equation similar, but with small differences, to that obtained from the conventional MS approach [12],

$$\begin{aligned}&\lambda ^{2}+2\varepsilon \mu \lambda +\left( {-\frac{3}{8}\frac{\alpha \varepsilon }{\varOmega }a_0^2 +\frac{1}{2}\frac{\varOmega ^{2}-\omega _0^2 }{\varOmega }} \right) \nonumber \\&\quad \left( {-\frac{9}{8}\frac{\alpha \varepsilon }{\varOmega }a_0^2 +\frac{1}{2}\frac{\varOmega ^{2}-\omega _0^2 }{\varOmega }} \right) +\varepsilon ^{2}\mu ^{2}=0. \end{aligned}$$
(19)

From Eq. (19), the fixed-point solutions are unstable when

$$\begin{aligned}&\left( \!-\frac{3}{8}\frac{\alpha \varepsilon }{\varOmega }a_0^2 {+}\frac{1}{2}\frac{\varOmega ^{2}{-}\omega _0^2 }{\varOmega } \right) \left( {{-}\frac{9}{8}\frac{\alpha \varepsilon }{\varOmega }a_0^2 +\frac{1}{2}\frac{\varOmega ^{2}-\omega _0^2 }{\varOmega }} \right) \nonumber \\&\quad +\varepsilon ^{2}\mu ^{2}<0\quad . \end{aligned}$$
(20)

and are stable otherwise.

4 Nonlinear frequency response results—Duffing oscillator

Results are presented assessing the character and performance of the enriched Multiple Scales technique. The first results concern solution predictions using conventional Multiple Scales, enriched Multiple Scales, and numerical simulation as the parameter \(\varepsilon \) varies from a relatively small value of 0.1 up to a very large value of 100. This progression assesses the ability of the enriched Multiple Scales approach to correctly analyze periodic solutions for both weakly and strongly nonlinear systems. Next, the three solution approaches are used to study solution behavior for a weakly nonlinear system (\(\varepsilon =0.1\)) as either the forcing or the nonlinearity is increased beyond the weak limit. For these results, in particular, discussion centers on the accuracy advantages that the enriched approach may have over the conventional approach.

4.1 Solution behavior with increasing \(\varepsilon \)

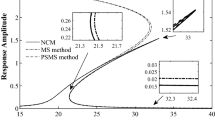
Figure 1 presents frequency response results generated using Eqs. (7) and (15) for an example parameter set \(\left\{ {\omega _0 =5,\mu =0.05, \alpha =2.0, k=2.0} \right\} \). Each subfigure corresponds to a point \(\varepsilon \) in the set \(\left\{ 0.1, 1.0, 10.0,\right. \) \( \left. 100.0 \right\} \). Varying this single parameter simultaneously changes the strength of the nonlinearity, forcing, and damping, which are typically ordered to appear together as inhomogeneous terms at higher orders. In addition to the frequency response solution from the enriched (solid lines) and conventional MS (dashed lines), results from numerical solutions appear in Fig. 1 as markers (red and blue). The incremental procedure for generating these points involves simulating the system starting at a detuning value of \(-1\), allowing steady state to be reached, and using the last steady-state solution to inform the starting condition for the next value of detuning. The amplitude of the arrived at periodic solution is then used to locate the red markers at each detuning. The procedure is also repeated in reverse starting at a detuning value of 3.0 (blue markers). The effect of doing this is that the numerical solution emulates forward and backward frequency sweeps, and captures well-known jump phenomena [12] in the solutions.

Fig. 1
figure 1

Frequency response predicted using enriched MS (solid lines), conventional MS (dashed), and numerical simulation (markers) for an example parameter set \(\left\{ {\omega _0 =5, \mu =0.05, \alpha =2.0, k=2.0} \right\} \) with a \(\varepsilon =0.1\), b \(\varepsilon =1\), c \(\varepsilon =10\), d \(\varepsilon =100\)

Full size image

Several qualitative and quantitative differences between the enriched and conventional Multiple Scales are evident in Fig. 1, even when the Duffing system can be considered weakly nonlinear (i.e., \(\varepsilon <1.0\)). Qualitatively, the enriched solution depends intrinsically on \(\varepsilon \) as evident by Eq. (15) and the progression of frequency responses provided in Fig. 1. The conventional solutions, on the other hand, are independent of \(\varepsilon \). This results further in several quantitative points of difference, which become more apparent as \(\varepsilon \) increases. At the lowest value of \(\varepsilon \) considered (see close-up in Fig. 2), the enriched approach predicts a maximum response amplitude \(a_{\max } =3.83\), while the conventional predicts \(a_{\max } =3.99\), resulting in a discrepancy of over 4 %. Similarly, the enriched approach predicts an upper branch bifurcation point at a detuning value \(\sigma =2.15\), while the conventional approach predicts this bifurcation point to be at \(\sigma =2.39\), amounting to a discrepancy of over 10 %. Note that numerical simulations more closely support the conclusions of the enriched approach. Although not shown, as \(\varepsilon \) is decreased below \(0.1\), the enriched and conventional solutions converge and the disagreement diminishes, as expected.

As the value \(\varepsilon \) increases still further to ranges where the conventional MS method is known to suffer breakdown, the enriched MS method continues to show very strong agreement with numerical simulations (see Fig. 1b–d). At \(\varepsilon =1\), a value sometimes employed in “bookkeeping” asymptotic approaches [15], where a small parameter does not arise physically, and it becomes evident that increasing \(\varepsilon \) results in a system with less hardening (less bending of the frequency response to the right) and lower maximum amplitude. At \(\varepsilon =10\), the total detuning \(\varepsilon \sigma \) is such that at small negative values of \(\sigma \), the forcing frequency \(\varOmega \) approaches the frequency \(-\omega _0 \), and thus a second resonance curve begins to appear (to the left) in Fig. 1c. Finally, at \(\varepsilon =100\), these two resonances coalesce and result in the two-peaked frequency response curve in Fig. 1d. Due to this coalescence, no jump behavior is observed, and the unstable solution branches disappear. Note that during this entire progression of \(\varepsilon \), numerical simulations track closely the changing frequency response curves predicted by the enriched MS.

Evaluation of the stability condition, Eq. (20), for the parameter sets and solutions plotted in Figs. 1 and 2 reveals that all periodic solutions along the top and bottom branches (blue and red curves) are stable, while all solutions along the middle branch (green curve) are unstable. For weakly nonlinear systems, this is well known and can be found using a conventional MS approach. Conventional MS would err if used to find the stability of the strongly nonlinear system. However, for \(\varepsilon =100\), the enriched MS stability analysis indicates that all solutions predicted are stable. These stability predictions are confirmed by stable numerical simulations and solution jumps in Fig. 1a–c (e.g., see red markers from the forward sweep).

Fig. 2
figure 2

Closer inspection of the frequency response predicted using enriched MS (solid lines), conventional MS (dashed), and numerical simulation (markers) for \(\varepsilon =0.1\) and an example parameter set \(\left\{ {\omega _0 =5, \mu =0.05, \alpha =2.0, k=2.0} \right\} \) near the upper branch bifurcation point

Full size image

4.2 Solution behavior with increasing nonlinearity at \(\varepsilon =0.1\)

Next, a weakly nonlinear system (\(\varepsilon =0.1)\) is studied as the nonlinearity is increased. All other parameters carry over from the previous parameter set \(\left\{ {\omega _0 =5, \mu =0.05, k=2.0} \right\} \). Figure 3 presents frequency response results for \(\alpha \in \left\{ {2, 20, 200} \right\} \). Similar to the study in which \(\varepsilon \) increases, the enriched Multiple Scales technique demonstrates clear advantages over the conventional technique as the strength of the nonlinearity increases, even though the problem is weakly nonlinear. For \(\alpha =2\), the two techniques exhibit close agreement. For a value \(\alpha =20\), the enriched method exhibits less bending of the frequency response (i.e., is less hardening), and the bifurcation point occurs at a much lower detuning than predicted by the conventional technique. Note that the numerical frequency sweeps and jump location clearly support the predictions of the enriched technique. This becomes further apparent when \(\alpha =200\).

Fig. 3
figure 3

Frequency response predicted using enriched MS (solid lines), conventional MS (dashed), and numerical simulation (markers) for an example parameter set \(\left\{ {\varepsilon =0.1,\omega _0 =5, \mu =0.05, k=2.0} \right\} \) with \(\alpha =2\) (top), \(\alpha =20\) (middle), \(\alpha =200\) (bottom)

Full size image

4.3 Solution behavior with increasing forcing at \(\varepsilon =0.1\)

Next, the same weakly nonlinear system (\(\varepsilon =0.1)\) is studied as the forcing amplitude is increased. All other parameters carry over from the original parameter set \(\left\{ {\omega _0 =5, \mu =0.05, \propto \, =\,2.0} \right\} \). Figure 4 presents frequency response results for \(k\in \left\{ {2, 20, 200} \right\} \). Much like the study on increasing nonlinearity, the increasing of forcing leads to less hardening behavior in the enriched results as opposed to the conventional results. This difference becomes exaggerated with larger values of \(k\), and the enriched results are more closely supported by the numerical simulations.

Fig. 4
figure 4

Frequency response predicted using enriched MS (solid lines), conventional MS (dashed), and numerical simulation (markers) for an example parameter set \(\left\{ \varepsilon \!=\!0.1,\omega _0 \!=\!5, \mu \!=\!0.05, \propto \!=\!2.0 \right\} \) with \(k=2\) (top), \(k=20\) (middle), \(k=200\) (bottom)

Full size image

5 Enriched multiple scales—van der Pol Oscillator

The harmonically forced van der Pol oscillator considered next takes the form

$$\begin{aligned} \ddot{u}+\varepsilon (u^{2}-1)\dot{u}+\omega _{0}^{2}u=K\cos (\varOmega \hbox {t}), \end{aligned}$$
(21)

where \(\varepsilon \) denotes a small parameter, \(\omega _0 \) denotes the linear system’s natural frequency, \(K\) denotes the forcing amplitude, \(\varOmega \) denotes the forcing frequency, and an overdot denotes a time derivative. At large values of \(\varepsilon \) or forcing amplitude, the response of the van der Pol oscillator is dominated by a relaxation-type limit cycle [18, 51] rich in frequency content; thus, asymptotic techniques predicated on solutions responding at linear combinations of \(\varOmega \) and \(\omega _0 \) are not appropriate. For this reason, only the weakly nonlinear response is studied using the enriched Multiple Scales technique. Nonresonant response is considered first in which the homotopy is selected such that when \(p=0\), the system appears to be a simple linear oscillator with natural frequency \(\omega _0 \) and forcing frequency \(\varOmega \). This is followed by an entirely different homotopy designed to capture system subharmonic response at twice and three times the forcing frequency. The multiple choices of homotopy demonstrate flexibility the enriched technique has that is not shared by the conventional approach.

5.1 Response away from \(\omega _0 \)

Consider first the forced response of the van der Pol equation when \(\varOmega \) is not near the system natural frequency \(\omega _0 \) (i.e., strong forcing). In this case, the homotopy parameter \(p\) is introduced such that a forced, linear system results when \(p=0\) and the full nonlinear system is recovered when \(p=1\),

$$\begin{aligned} \ddot{u}+p(\varepsilon (u^{2}-1)\dot{u})+\omega _{0}^{2}u=K \cos (\varOmega \hbox {t}). \end{aligned}$$
(22)

This is one choice for introducing the homotopy. Another would be to introduce \(p\) such that a linear equation is recovered with natural frequency \(\varOmega \), as per Sect. 3. However, the van der Pol equation does not have linear damping, and thus response at \(\omega _0 \) cannot be assumed to decay out for large time. Thus, the former homotopy is more appropriate. As in the Duffing system, \(u\) is expanded asymptotically with respect to \(p\),

$$\begin{aligned} u\left( {t,\varepsilon } \right) {=}u_0 \left( {T_0 ,T_1 ,\ldots } \right) +pu_1 \left( {T_0 ,T_1 ,\ldots } \right) {+}\cdots ,\nonumber \\ \end{aligned}$$
(23)

and partial time derivatives are also introduced such that \(\mathrm{{d}}/\mathrm{{d}}t=D_0 +pD_1 +p^{2}D_2 +\ldots \), and \(\mathrm{{d}}^{2}/\mathrm{{d}}t^{2}=D_0^2 +p2D_0 D_1 +p^{2}D_1^2 +\ldots \). Substitution of Eq. (22) into Eq. (23) and separating orders of \(p\) result in the first two ordered equations,

$$\begin{aligned}&p^{0}:D_0^2 u_0 +\omega _0^2 u_0 =\frac{K}{2}e^{i\varOmega \hbox {T}_0 }+cc,\end{aligned}$$
(24a)
$$\begin{aligned}&p^{1}:D_0^2 u_1 +\omega _0^2 u_1 =-2D_0 D_1 u_0 \nonumber \\&\quad +\varepsilon \left( {1-u_0^2 } \right) D_0 u_0 . \end{aligned}$$
(24b)

The solution to Eq. (24a) takes the form

$$\begin{aligned} u_0 =A\left( {T_1 } \right) e^{i\omega _0 T_0 }+\Lambda e^{i\varOmega T_0 }+cc, \end{aligned}$$
(25)

where \(\Lambda =\frac{K}{2}\frac{1}{\omega _0^2 -\varOmega ^{2}}\). Next, the solution for \(u_0 \) is substituted into Eq. (24b), and secular terms are identified and then removed from the right-hand side. The terms are numerous and not presented here in detail. Instead, it is remarked that they contain terms proportional to \(e^{i3\omega _0 T_0 }\!\!, e^{i2\omega _0 T_0 }\!, e^{i\omega _0 T_0 }\!, e^{i(2\varOmega +\omega _0 )T_0 }\!\!, e^{i(2\varOmega -\omega _0 )T_0 }\!,\) \(e^{i(\varOmega +2\omega _0 )T_0 }, e^{i(\varOmega -2\omega _0 )T_0 }, e^{i3\varOmega T_0 }, e^{i\varOmega T_0 }\),  and their complex conjugates. Based on these terms and the linear kernel, four sub-cases must be considered: (a) nonresonant response where \(\varOmega \) is not near 0, \(3\omega _0 \), and \(1/3\omega _0 \); (b) nonresonant response where \(\varOmega \) near 0; (c) subharmonic resonance where \(\varOmega \) is near \(3\omega _0 \); and (d) superharmonic resonance where \(3\varOmega \) is near \(\omega _0 \). When \(\varOmega \) is not near 0, \(3\omega _0 \), and \(1/3\omega _0 \), the secular terms are given strictly by \(e^{i\omega _0 T_0 }\) dependence. Setting the coefficient multiplying \(e^{i\omega _0 T_0 }\) to zero yields the evolution equation

$$\begin{aligned} A^{{\prime }}=\varepsilon \left[ {\frac{1}{2}\left( 1-A\bar{A}\right) A-\Lambda ^{2}A} \right] , \end{aligned}$$
(26)

where \(()^{{\prime }}\) denotes a derivative of \(()\) with respect to \(T_1 =pt\). Fixed-point solutions to Eq. (26) yield quasiperiodic response (due to \(\omega _0 \) and \(\varOmega \) appearing in Eq. (25)) and frequency response diagrams can be generated. Stability of the natural response can also be studied with a local approach, similar to that presented in Sect. 3. Frequency response results, however, are not presented since Eq. (26) will be shown to match results found by the conventional Multiple Scales approach.

When \(\varOmega \) is near 0, a detuning is introduced such that \(\varOmega =\varepsilon \hbox {p}\sigma \), where the introduction of p ensures that the frequency detuning appears at time scale \(T_1 \). The problem then has to be restated starting at Eq. (22) and working forward. The forcing term on the right-hand side of Eq. (22) takes the form \(\frac{K}{2}e^{i\varepsilon \sigma \hbox {T}_1} +cc\), and thus the solution for \(u_0 (T_0 ,T_1 )\) takes the form

$$\begin{aligned} u_0 (T_0 ,T_1 )=A\left( {T_1 } \right) e^{i\omega _0 T_0 }+\Lambda e^{i\varepsilon \sigma T_1 }+cc. \end{aligned}$$
(27)

Substituting Eq. (27) into Eq. (24b) and removing secular terms with time dependence \(e^{i\omega _0 T_0 }\) yields the evolution equation

$$\begin{aligned} A^{{\prime }}=\varepsilon \left[ \frac{1}{2}\left( 1-A\bar{A} \right) A-\Lambda ^{2}A-\Lambda ^{2}A\hbox {cos}(2\varepsilon \sigma T_1 ) \right] . \end{aligned}$$
(28)

When \(\varOmega \) is near \(3\omega _0 \), a detuning is introduced such that \(\varOmega =3\omega _0 +\varepsilon p\sigma \). Similarly, when \(3\varOmega \) is near \(\omega _0 \), a detuning is introduced such that \(\omega _0 =3\varOmega +\varepsilon p\sigma \). The forcing for these two cases takes the form \(\frac{K}{2}e^{i3\omega _0 T_0 }e^{i\varepsilon \sigma T_1}+cc\) and \(\frac{K}{2}e^{i\frac{1}{3}\omega _0 T_0 }e^{-\frac{1}{3}i\varepsilon \sigma {T}_{1}} +cc\), respectively. As before, secular terms with time dependence \(e^{i\omega _0 T_0 }\) are removed from Eq. (24) leading to the evolution equations,

$$\begin{aligned} A^{{\prime }}&= \varepsilon \left[ \frac{1}{2}\left( 1-A\bar{A} \right) A-\Lambda ^{2}A-\frac{1}{2}\bar{A}^{2}\Lambda \hbox {e}^{i\varepsilon \sigma T_1} \right] ,\nonumber \\ \end{aligned}$$
(29)
$$\begin{aligned} A^{{\prime }}&= \varepsilon \left[ \frac{1}{2}\left( 1-A\bar{A} \right) A-\Lambda ^{2}A-\frac{1}{6}\Lambda ^{3}\hbox {e}^{-i\varepsilon \sigma T_1} \right] , \nonumber \\ \end{aligned}$$
(30)

respectively.

For comparison purposes, the conventional Multiple Scales have been employed to solve the forced van der Pol equation when \(\varOmega \) is not near \(\omega _0 \) [12]. The reported evolution equations analogous to Eqs. (26), (28)–(30) are

$$\begin{aligned} A^{{\prime }}&= \frac{1}{2}\left( 1-A\bar{A}\right) A-\Lambda ^{2}A,\end{aligned}$$
(31a)
$$\begin{aligned} A^{{\prime }}&= \frac{1}{2}\left( 1-A\bar{A}\right) A-\Lambda ^{2}A\nonumber \\&-\Lambda ^{2}A\hbox {cos}(2\sigma T_1 ), \quad \varOmega =\varepsilon \sigma ,\end{aligned}$$
(31b)
$$\begin{aligned} A^{{\prime }}&= \frac{1}{2}\left( 1-A\bar{A} \right) A-\Lambda ^{2}A \nonumber \\&+\frac{1}{2}\left( {2-\frac{\varOmega }{\omega _0 }} \right) \bar{A} ^{2}\Lambda \hbox {e}^{i\sigma \mathrm{T}_1}, \quad \varOmega =3\omega _0 +\varepsilon \sigma , \nonumber \\ \end{aligned}$$
(31c)
$$\begin{aligned} A^{{\prime }}&= \frac{1}{2}\left( 1-A\bar{A} \right) A-\Lambda ^{2}A-\frac{1}{2}\frac{\varOmega }{\omega _0 }\Lambda ^{3}\hbox {e}^{-i\sigma \mathrm{T}_1 },\nonumber \\&\omega _0 =3\varOmega +\varepsilon \sigma , \end{aligned}$$
(31d)

where \(()^{{\prime }}\) in this context denotes a derivative of \(()\) with respect to time \(T_1 =\varepsilon t\). Comparing Eqs. (31a)–(31b) to Eqs. (26) and (28)–(30) with \(p\) set to 1, it can be seen that the same evolution equations are recovered due to the presence of a leading \(\varepsilon \) multiplier in the enriched evolution equations. Comparing Eqs. (31c)–(31d) to Eqs. (29)–(30), a small discrepancy exists, as follows. In Eq. (31c), using the detuning relationship provided in the equation, the final term on the right-hand side can be evaluated as \(-\frac{1}{2}\left( {1+\frac{\varepsilon \sigma }{\omega _0 }} \right) \bar{A}^{2}\Lambda \hbox {e}^{i\sigma \mathrm{T}_1 }\), which differs from the final term in the right-hand side of Eq. (29) by a term of order \(\varepsilon ^{1}\), which is negligible. Similarly, the appropriate detuning relationship substituted into the last term on the right-hand side of Eq. (31d) yields the same final term of Eq. (30) to order \(\varepsilon ^{1}\).

5.2 Period-2 subharmonic response

Next, we seek solutions and conditions for the existence of period-two subharmonic response to the forced van der Pol equation. Note that the conventional Multiple Scales treatment does not offer such an analysis method. With the enriched method, an alternative homotopy can be introduced in which the linear equation (\(p=0\)) responds at \(\varOmega /2\), in effect imposing a subharmonic response. The special case of \(\omega _0 =1\) with a period-two subharmonic solution is analyzed by Jordan and Smith [17] and will be used for the comparison purposes.

The analysis begins by proposing the alternative homotopy

$$\begin{aligned}&\ddot{u}+p(\varepsilon (u^{2}-1)\dot{u}+\omega _{0}^{2}u)\nonumber \\&\quad +(1-p)\left( \frac{\varOmega }{2}\right) ^{2} u=K \cos (\varOmega \hbox {t}). \end{aligned}$$
(32)

Following a similar procedure where an expansion for \(u\) is introduced with dependence on multiple time scales, the ordered equations for this case yield

$$\begin{aligned}&p^{0}:D_0^2 u_0 +\left( {\frac{\varOmega }{2}} \right) ^{2}u_0 =\frac{K}{2}e^{i\varOmega \hbox {T}_0 }+cc,\end{aligned}$$
(33a)
$$\begin{aligned}&p^{1}:D_0^2 u_1 +\left( {\frac{\varOmega }{2}} \right) ^{2}u_1 =-2D_0 D_1 u_0 \nonumber \\&+\varepsilon \left( {1-u_0^2 } \right) D_0 u_0 +\left( {\left( {\frac{\varOmega }{2}} \right) ^{2}-\omega _0^2 } \right) u_0 . \end{aligned}$$
(33b)

The solution to Eq. (33a) takes the form

$$\begin{aligned} u_0 =A\left( {T_1 } \right) e^{i\frac{\varOmega }{2}T_0 }+\Lambda e^{i\varOmega T_0 }+cc, \end{aligned}$$
(34)

where \(\Lambda =-\frac{2K}{3\varOmega ^{2}}\). Next, the solution for \(u_0 \) is substituted into Eq. (33b), and secular terms are identified and then removed from the right-hand side. The terms are again too numerous to be presented here in detail. Instead, it is remarked that they contain terms proportional to \(e^{i3\varOmega T_0}\), \(e^{i\frac{5}{2}\varOmega T_0 }, e^{i2\varOmega T_0}\!, e^{i\frac{3}{2}\varOmega T_0 }, e^{i\varOmega T_0}\!, e^{i\frac{1}{2}\varOmega T_0 }\), and their complex conjugates. Based on the linear kernel of Eq. (33b), secular terms are those terms with dependence on \(e^{i\frac{1}{2}\varOmega T_0 }\) and its complex conjugate. Removal of these terms yields

$$\begin{aligned}&-i\varOmega A^{{\prime }}-i\frac{\varepsilon \varOmega }{2}\left[ {A^{2}\bar{A} +\left( {\frac{8K^{2}}{9\varOmega ^{4}}-1} \right) A} \right] \nonumber \\&\quad +\left( \frac{\varOmega ^{2}}{4}-1 \right) A=0, \end{aligned}$$
(35)

where \(()^{{\prime }}\) denotes a derivative of \(()\) with respect to \(T_1 \). Introducing the polar form \(A=\frac{1}{2}ae^{i\beta }\) where both the amplitude \(a(T_1 )\) and phase \(\beta (T_1 )\) are real functions of \(T_1 \), then separating real from imaginary parts, Eq. (35) yields the two evolution equations:

$$\begin{aligned}&\left[ \frac{\varOmega }{2}\beta ^{{\prime }}+\frac{1}{2}\left( {\frac{\varOmega ^{2}}{4}-1} \right) \right] a=0 \quad \mathop \rightarrow \limits ^\mathrm{{yields}} \quad \frac{\varOmega }{2}\beta ^{{\prime }}\nonumber \\&\quad +\frac{1}{2}\left( \frac{\varOmega ^{2}}{4}-1 \right) =0,\end{aligned}$$
(36a)
$$\begin{aligned}&-\frac{\varOmega }{2}a^{{\prime }}-\frac{\varepsilon \varOmega }{2}\left[ {\frac{a^{3}}{8}-\frac{a}{2}} \right] -\frac{2}{9}\frac{\varepsilon \hbox {K}^{2}}{\varOmega ^{3}}a=0. \end{aligned}$$
(36b)

The evolution equations effectively decouple for \(a(T_1 )\) and phase \(\beta (T_1 )\). As previously, fixed-point solutions \(a_0 \) and \(\beta _0 \) are sought. Note that a fixed-point solution for \(\beta (T_1 )\) ensures capture of the period-2 solution sought, while any time-varying solution for \(\beta (T_1 )\) effectively destroys the period-2 subharmonic. Note further that Eq. (36b) appears in the normal form of a supercritical pitchfork bifurcation [16]. From Eq. (36), the fixed-point solutions require

$$\begin{aligned} \varOmega =\pm 2, \quad a_0 =0,\pm \sqrt{4-\frac{32K^{2}}{9\varOmega ^{4}}}. \end{aligned}$$
(37)

Inspection of the solution for both \(\varOmega \) and \(a_0 \) reveals that a bifurcation point exists at \(K^{*}=\sqrt{18}\) such that the period-2 subharmonic solution \(a_0 =\pm \sqrt{4-\frac{32K^{2}}{9\varOmega ^{4}}}\) exists for \(K<K^{*}\) and otherwise does not. Knowledge of the supercritical pitchfork bifurcation normal form [16] makes it clear that the trivial solution \(a_0 =0\) is unstable for \(K<K^{*}\) and stable when \(K>K^{*}\). Similarly, the solutions \(a_0 =\pm \sqrt{4-\frac{32K^{2}}{9\varOmega ^{4}}}\) are stable for \(K<K^{*}\) and unstable when \(K>K^{*}\).

Collecting results from the analysis, the final solutions for the period-2 response to order \(p^{0}\) are given as

$$\begin{aligned} u_0 =\left\{ {{\begin{array}{l} {\sqrt{4{-}\frac{2K^{2}}{9}}\cos \left( {t{+}\beta _0 } \right) {-}\frac{K}{3}\cos 2t, K{<}\sqrt{18}} \\ {-\frac{K}{3}\cos 2t, K>\sqrt{18}} \\ \end{array} }} \right\} , \end{aligned}$$
(38)

where \(\beta _0 \) is an arbitrary constant. Verification of this result is presented in Fig. 5 for choices of \(K=4\) (just below \(\sqrt{18})\) and \(K=4.5\) (just above \(\sqrt{18})\). Steady-state phase planes (left sub-figures) reveal a period-2 orbit when \(K=4\) and a period-1 orbit when \(K=4.5\), in agreement with the enriched Multiple Scales solution. Similarly, analysis of the frequency content of each solution (right sub-figures) demonstrates that the case \(K=4\) exhibits the forcing frequency (2 rad/sec) and the period-2 subharmonic (1 rad/sec), while the case \(K=4.5\) again exhibits only the forced solution.

Fig. 5
figure 5

Phase planes (left sub-figures) and frequency content (right sub-figures) for the van der Pol system with forcing frequency \(\varOmega =2\), system natural frequency \(\omega _0 =1\), and small parameter \(\varepsilon =0.1\). Results generated for forcing amplitude \(K=4\), sub-figures (a) and (b), and \(K=4.5\), sub-figures (c) and (d)

Full size image

The text by Jordan and Smith [17] offers a treatment of a system similar to Eq. (22) with the exception that \(\omega _0 \) is replaced by the constant 1. They showed that a period-2 subharmonic exists for this specific linear kernel by an assumed solution form similar to single-frequency harmonic balance, but with a perturbed frequency. Their solution technique also determines the existence of solutions for \(K<\sqrt{18}\). They do not, however, determine the condition \(\varOmega =\pm 2\) since \(\omega _0 \) is considered to be 1 at the onset, and they do not arrive at the pitchfork bifurcation normal form. A treatment of period-2 subharmonics of the van der Pol oscillator using a conventional Multiple Scales approach is not available, although it could be approached as excitation \(\varOmega \) near \(2\omega _0 \). This, however, is different from the spirit of the solution taken herein, which is to find a period-2 subharmonic regardless of the closeness of this subharmonic to \(\omega _0 \)—the fact that this subharmonic only exists when \(\varOmega =\pm 2\) (and thus \(\omega _0 =1)\) is borne out in the enriched Multiple Scales solution development as opposed to specified up front by specific selection of the system parameters.

5.3 Period-3 subharmonic response

We briefly discuss treatment of a period-3 subharmonic response using the enriched Multiple Scales analysis. Analysis of period-3 solutions does not appear in the monographs cited earlier and other monographs [12, 15–18, 52–54]. Much like the period-2 subharmonic analysis, a homotopy is proposed in which the van der Pol system responds at \(\varOmega /3\), in effect imposing a period-3 subharmonic response,

$$\begin{aligned}&\ddot{u}+p(\varepsilon (u^{2}-1)\dot{u}+\omega _{0}^{2}u)+(1-p)\left( \frac{\varOmega }{3}\right) ^{2}\nonumber \\&\quad u=K \cos (\varOmega \hbox {t}). \end{aligned}$$
(39)

Following a similar procedure where an expansion for \(u\) is introduced, ordered equations are identified, solutions are sought at order \(p^{0}\), and secular terms are removed at order \(p^{1}\), it is again found that a special case exists for period-3 subharmonics when \(\omega _0 =1\). The bifurcation point associated with the analogous supercritical pitchfork bifurcation is in this case \(K^{*}=\sqrt{1024/7}\) such that the period-3 subharmonic solution exists for \(K<K^{*}\), and otherwise does not. Verification of this result is presented in Fig. 6 for choices of \(K=\sqrt{1024/7}-1\) and \(K=\sqrt{1024/7}+1\). Steady-state phase planes (left sub-figures) and frequency content (right sub-figures) verify a period-3 orbit when \(K<K^{*}\) and a period-1 orbit when \({>}K^{*}\).

Fig. 6
figure 6

Phase planes (left sub-figures) and frequency content (right sub-figures) for the van der Pol system with forcing frequency \(\varOmega =3\), system natural frequency \(\omega _0 =1\), and small parameter \(\varepsilon =0.1\). Results generated for forcing amplitude \(K=\sqrt{1024/7}-1\), sub-figures (a) and (b), and \(K=\sqrt{1024/7}+1\), sub-figures (c) and (d)

Full size image

6 Concluding remarks

This article presented an enriched Multiple Scales method for analyzing weakly and strongly nonlinear systems. The technique follows closely the conventional Multiple Scales approach, but relies on the introduction of time scales and ordering dependent on a homotopy parameter as opposed to a small parameter. As in the conventional approach, a local stability analysis can be performed from the resulting evolution equations. In a Duffing system, results demonstrate that the enriched technique allows stronger system nonlinearities and forcing to be accurately analyzed. For a van der Pol system, the added flexibility of the enriched method has been demonstrated through the choice of multiple possible homotopies, and hence multiple analysis types (e.g., response at the forcing frequency or subharmonic response). Since the enriched method amounts to only a small procedural change to the popular Multiple Scales method, and since it demonstrates some accuracy and flexibility advantages, it may find applicability beyond the two prototypical nonlinear systems studied herein (e.g., other sources of nonlinearity and multi-degree of freedom nonlinear systems).