1 Introduction

Study on tethered satellite system (TSS) has become one central issue of concerns in spacecraft engineering, attracting the attention of researchers in a series of areas [1, 2]. Since the first proposal of TSS, it has been extensively applied in actual engineering, such as tethered space robot [3], tethered space harpoon [4], and tethered space net [5]. The first tethered satellite system mission TSS-1 was jointly proposed by the USA and Italy in 1992 [6]. Since then, many research institutions have carried out a large number of space experiments on tethered satellite systems [7] and made abundant achievements [8,9,10,11], but also caused several mission failures [6, 12, 13].

Based upon this, most researchers concentrated on mechanism design and accordingly the dynamics and control of space capture [14]. An analytical tether length rate control law for the deployment of a flexible TSS under the space perturbations was proposed [15]. Reference [16] proposed a novel adaptive dynamic sliding mode scheme for the deployment of the tethered satellite system. Although the input and command signals are limited based on the strictly bounded terms, the control tension force is discontinuous. Another controller was designed by utilizing small-gain theorem in Ref. [17], while the transversal thrust was considered to suppress the tethers’ oscillation. A feedback tension control law for the deployment of space tether with tension constraint and saturation function was proposed by in Ref. [18]. Sakawa [19] used the optimal control to solve the linearized nonlinear system. An input shaping scheme was proposed to generate reasonable planning of the control signal [20], and it is widely used to solve underactuated problem. An earth-oriented double-pyramid formation was investigated in Ref. [21] and discovered that the stable configuration was along the nadir direction, and the optimal control of a double-pyramid Earth-facing formation was discussed. A novel adaptive dynamic sliding mode scheme for the deployment of the TSS was proposed in Ref. [15]. Because of the Coriolis force and orbital motion, the research on the spin stability of TSS is essential for the realization of a fast and stable deployment/retrieval [22].

Stability analysis is a core research content in mechanism study of vibration behaviors of dynamic systems. Many stability analysis methods have been used to study nonlinear vibration behaviors of TSS. According to the variation demands of space missions, different satellite formations are often required to complete the missions together. For example, multi-point simultaneous measurements, as required in magnetospheric studies, can be conducted by a set of probes connected by tethers aligned along the local vertical. The potential application of multi-tethers systems is probably greatest in space interferometry both LEO and deep space [23]. Therefore, the study of n-star (or n-body) TSS is of great significance. Correa et al. [24] applied the one-dimensional stable configuration to the 4-body tether system, and pointed out that it can be extended to the tether system of N satellites. Pizarro-Chong et al. [25] studied the tethered formations of hub-and-spoke and closed-hub-and-spoke composed of N bodies, and simulated the system composed of \(3\sim 6\) satellites. The results show that the system composed of more than 4 satellites needs to provide initial spin angular velocity and tether tension to maintain configuration stability. Tragesser [26] proved that the n-star system with closed-loop configuration behaves very similar to a rigid body in the cylindrical equilibrium case when the spin rapid enough, based upon abundant simulation analysis. But there is still a lack of elaboration on the critical angular velocity of the stable spin for TSS with close-loop configuration.

The Floquet theory [27, 28] was used to solve a series of dynamic problems [29, 30], such as rotor dynamics [31, 32], while few researchers used it to study the stability and dynamic behaviors of TSS.

The motivation of this paper is to propose a method for the stable spin conditions of TSS with arbitrary parameter feature based upon a general model with closed-loop configuration. In Sect. 2, a general model of TSS with closed-loop configuration is established and a brief introduction to Floquet theory is also discussed. Section 3 proposes a general method for stability analysis based upon the Floquet theory of the TSS and discusses the numerical results of some examples based on 3-star system. Finally, conclusions and outlooks are drawn in Sect. 4.

2 Dynamic modeling of tethered satellite system

2.1 General tethered satellite system

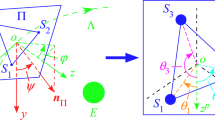
A general model of a TSS with n satellites \(S_1\), \(S_2\), \(\ldots \), \(S_n\) connected in a closed-loop configuration is considered. The mathematical model of the TSS can be approximated to the bead-spring-damping ring (BSDR) form shown in Fig. 1, no matter the masses of tethers are considered or not, by the following fixed steps.

  1. 1.

    Define \(m_i\) as the mass of the ith satellite \(S_i\);

  2. 2.

    The ith mass tether connecting satellite \(S_i\) and \(S_{i+1}\) is divided into finite segment (\(n_i\)) units consisting of concentrated mass, massless spring and damping, in which \(1\le i<n\);

  3. 3.

    The mass \(m_{i,j}\) of each unit at the ith segment is defined in which \(1\le j\le n_i\); and spring stiffness \(k_{i,j}\), damping coefficient \(C_{i,j}\), and equilibrium length of each spring \(L_{i,j}\) are defined in which \(0\le j\le n_i\), based upon the actual rope design parameters.

Fig. 1
figure 1

General tethered satellite system model

Full size image

In order to analyze the dynamic behavior of the system in space, the inertial coordinate system \(O-XYZ\) is established by connecting to the centroid of the earth fixedly, and the rotating coordinate system \(o-xyz\) is established by connected to the centroid of the tethered satellite system fixedly, respectively, shown in Fig. 2. The positive direction of X-axis is defined as the direction along the centroid of the earth to the ascending node; the Z-axis is perpendicular to the orbital plane of the TSS system with the positive direction of pointing to the north pole from the centroid of the earth; and the positive direction of Y-axis is determined by the right-hand rule, in the inertial coordinate system \(O-XYZ\). The positive directions of y-axis and z-axis are defined as the direction along the centroid of the earth to the centroid of the TSS and the same direction of the Z-axis, respectively, and the positive direction of x-axis is determined by the right-hand rule, in the rotating coordinate system \(o-xyz\). Assuming the revolution angular velocity of the \(o-xyz\) around the \(O-XYZ\) is \(\Omega \), and the positive direction of rotation is counterclockwise.

Fig. 2
figure 2

Schematic diagram of reference frame

Full size image

The motion equation of the ith bead of the BSDR system in the coordinate \(o-xyz\) can be expressed as follows

$$\begin{aligned} m_i\varvec{\ddot{r}_i}=\varvec{G_i}+\varvec{T_i}+\varvec{D_i}+\varvec{F_i^e}+\varvec{F_i^k}, \end{aligned}$$
(1)

in which \(1\le i\le n+m\) (including all the lumped mass of n satellites and \(m=\sum _{i=1}^{n-1}n_i\) tether units), and for the ith bread, \(m_i\): the mass, \(\varvec{r_i}=\left( x_i,y_i,z_i\right) ^\mathrm{T}\): the position vector in the \(o-xyz\), \(\varvec{G_i}\): the gravity, \(\varvec{T_i}\): the rope tension, \(\varvec{D_i}\): the damping force, \(\varvec{F_i^e}\): the convected inertial force, \(\varvec{F_i^k}\): the Coriolis inertial force, \(\varvec{\dot{r}_i}\) and \(\varvec{\ddot{r}_i}\): the first and second order derivative of the position vector \(\varvec{r_i}\) to the time t, respectively, without considering the perturbation factors such as \(J_2\) perturbation, thermal effect, and atmospheric resistance.

Firstly, the gravitational term in Eq. (1) can be obtained as follows

$$\begin{aligned} \varvec{G_i}=-\dfrac{m_i\mu _E\left( \varvec{r_i}-\varvec{r_E}\right) }{|\varvec{r_i}-\varvec{r_E}|^3}. \end{aligned}$$
(2)

where \(\mu _E\approx 3.986\times 10^5\mathrm{km^3/s^2}\) is the gravity parameter of the earth, \(\varvec{r_E}=\left( 0,-R,0\right) ^\mathrm{T}\) is the centroid position vector of the earth in \(o-xyz\), \(R=H+R_E\), in which H is the orbital height of the BSDR system, and \(R_E=6378\) km is the average radius of the earth.

Next, the tension term in Eq. (1) , which is determined by the sum of two adjacent tether tensions, can be obtained as follows

$$\begin{aligned} \varvec{T_i}= & {} -s_{i,j}E_{i,j}A_{i,j}\left( \dfrac{1}{L_{i,j}}-\dfrac{1}{r_{i,j}}\right) \left( \varvec{r_i}-\varvec{r_j}\right) \nonumber \\&-s_{i,k}E_{i,k}A_{i,k}\left( \dfrac{1}{L_{i,k}}-\dfrac{1}{r_{i,k}}\right) \left( \varvec{r_i}-\varvec{r_k}\right) , \end{aligned}$$
(3)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} j=2,k=n+m\mathrm{,\quad } i=1,\\ j=1,k=n+m-1\mathrm{,\quad } i=n+m,\\ j=i+1, k=i-1\mathrm{,\quad } \mathrm{else}, \end{array}\right. } \end{aligned}$$
(4)

\(r_{i,j}=|\varvec{r_i}-\varvec{r_j}|\) is the instantaneous distance between the ith and jth beads, and \(s_{i,j}\) satisfies the following relation

$$\begin{aligned} s_{i,j}= {\left\{ \begin{array}{ll} 1,\mathrm{\quad } r_{i,j}>L_{i,j},\\ 0,\mathrm{\quad } \mathrm{else}, \end{array}\right. } \end{aligned}$$
(5)

which control the effective of the tether tension.

The damping term in Eq. (1), which indicates the sum of two tether damping along each axis direction based on the linear damping model, can be obtained as the following expression

$$\begin{aligned} \varvec{D_i}= -s_{i,j}C_{i,j}\dfrac{\dot{r}_{i,j}}{r_{i,j}}\left( \varvec{r_i}-\varvec{r_{j}}\right) -s_{i,k}C_{i,k}\dfrac{\dot{r}_{i,k}}{r_{i,k}}\left( \varvec{r_i}-\varvec{r_{k}}\right) , \end{aligned}$$
(6)

where \(\dot{r}_{i,j}\) is the instantaneous relative speed between the ith and jth beads.

The convected inertial force term in Eq. (1) can be considered to be consisted with the translation convected inertial force and the centrifugal convected inertial force, which can be expressed as follows

$$\begin{aligned} \varvec{F_i^e}=-m_i\varvec{\dot{\omega }}\times \left( \varvec{r_i}-\varvec{r_E}\right) -m_i\varvec{\omega }\times \left( \varvec{\omega }\times \left( \varvec{r_i}-\varvec{r_E}\right) \right) , \end{aligned}$$
(7)

where \(\Omega \) is the value of spin angular velocity of the coordinate \(o-xyz\) which equals to its revolution angular velocity numerically, and \(\varvec{\omega }=\left( 0,0,\Omega \right) ^\mathrm{T}\) and \(\varvec{\dot{\omega }}\) represent the rotational angular velocity and angular acceleration of the \(o-xyz\), respectively. \(\varvec{\dot{\omega }}=0\) must be hold by supposing the orbit of revolution is circular, then the relation can be obtained as follows

$$\begin{aligned} -m_i\varvec{\omega }\times \left( \varvec{\omega }\times \left( \varvec{r_i}-\varvec{r_E}\right) \right)= & {} \left[ \begin{array}{ccc} \varvec{i} &{} \varvec{j} &{} \varvec{k} \\ 0 &{} 0 &{} \Omega \\ -\left( y_i+R\right) \Omega &{} x_i\Omega &{} 0 \end{array} \right] \nonumber \\= & {} \left[ \begin{array}{ccc} -x_i\Omega ^2\\ -\left( y_i+R\right) \Omega ^2\\ 0 \end{array} \right] , \end{aligned}$$
(8)

where \(\varvec{i}\), \(\varvec{j}\), and \(\varvec{k}\) represent the x, y, and z axes unit vectors in the \(o-xyz\). Furthermore, the convected inertial force can be repressed as

$$\begin{aligned} \varvec{F_i^e}=\left( m_ix_i\Omega ^2,m_i\left( y_i+R\right) \Omega ^2,0\right) ^\mathrm{T}. \end{aligned}$$
(9)

Finally, consider the Coriolis inertia force term in Eq. (1) can be obtained as

$$\begin{aligned} \varvec{F_i^k}=-2m_i\bar{\omega }\times \varvec{\dot{r}_i}, \end{aligned}$$
(10)

where \(\varvec{\bar{\omega }}=\varvec{\omega }\) is the spin angular velocity of the \(o-xyz\), then Eq. (10) can be rewritten as

$$\begin{aligned} \varvec{F_i^k}=\left( 2m_i\Omega \dot{y}_i,-2m_i\Omega \dot{x}_i,0\right) ^\mathrm{T}. \end{aligned}$$
(11)

2.2 Brief introduction to Floquet theory

Floquet theory is a stability theory for a periodic variable coefficient linear ordinary differential equation, which was put forward by G. Floquet in 1883 [33]. This section will discuss the general method for N dimensions equation. Consider a system of first-order differential equations

$$\begin{aligned} \varvec{\dot{p}}\left( t\right) =\varvec{A}\left( t\right) \varvec{p}\left( t\right) , \end{aligned}$$
(12)

where \(\varvec{A}\) is a matrix with period T. Supposing the system (12) has N linearly independent particular solutions

$$\begin{aligned} {\left\{ \begin{array}{ll} \varvec{p_1}\left( t\right) =\left( p_{11}\left( t\right) ,p_{12}\left( t\right) ,\ldots ,p_{1N}\left( t\right) \right) ^\mathrm{T}\\ \varvec{p_2}\left( t\right) =\left( p_{21}\left( t\right) ,p_{22}\left( t\right) ,\ldots ,p_{2N}\left( t\right) \right) ^\mathrm{T}\\ \vdots \\ \varvec{p_N}\left( t\right) =\left( p_{N1}\left( t\right) ,p_{N2}\left( t\right) ,\ldots ,p_{NN}\left( t\right) \right) ^\mathrm{T} \end{array}\right. }, \end{aligned}$$
(13)

and the initial conditions are satisfied

$$\begin{aligned} \left( \varvec{p_1}\left( 0\right) ,\varvec{p_2}\left( 0\right) ,\ldots ,\varvec{p_N}\left( 0\right) \right) =\varvec{I}. \end{aligned}$$
(14)

It is easy to prove that this set of particular solution is the fundamental solution system of system (12). Based on periodicity, if \(\varvec{P_i}\left( t\right) \left( 1\le i\le N\right) \) is one of the particular solution, then \(\varvec{P_i}\left( t+T\right) \left( 1\le i\le N\right) \) must be another particular solution, which can be expressed as

$$\begin{aligned} p_{ij}\left( t+T\right) =\sum _{k=1}^N a_{ik}p_{kj}\left( t\right) , \end{aligned}$$
(15)

in which (\(1\le i,j\le N\)). Substituting \(t=0\) and Eq. (14) into Eq. (15), the equation can be solved as follows

$$\begin{aligned} a_{ij}=p_{ij}\left( T\right) . \end{aligned}$$
(16)

In order to determine the stability of the periodic solution of the system (12), it is necessary to find a particular solution which satisfies the following conditions

$$\begin{aligned} \varvec{p^*}\left( t+T\right) =\rho \varvec{p^*}\left( t\right) , \end{aligned}$$
(17)

in which \(\varvec{p^*}\left( t\right) \) and \(\varvec{p^*}\left( t+T\right) \) can be expressed as the fundamental solution system (12)

$$\begin{aligned} \varvec{p^*}\left( t\right) =\left( \sum _{i=1}^N b_i p_{i1}\left( t\right) ,\sum _{i=1}^N b_i p_{i2}\left( t\right) ,\ldots ,\sum _{i=1}^N b_i p_{iN}\left( t\right) \right) ^\mathrm{T}, \end{aligned}$$
(18)

and

$$\begin{aligned} \varvec{p^*}\left( t+T\right)= & {} \left( \sum _{i=1}^N b_i p_{i1}\left( t+T\right) ,\sum _{i=1}^N b_i p_{i2}\left( t+T\right) ,\right. \nonumber \\&\left. \ldots ,\sum _{i=1}^N b_i p_{iN}\left( t+T\right) \right) ^\mathrm{T}, \end{aligned}$$
(19)

respectively. It can be obtained by utilizing Eqs. (15), (18), and (19) into Eq. (17) as follows

$$\begin{aligned} \rho \left[ \begin{array}{ccc} \sum _{i=1}^N b_i p_{i1}\left( t\right) \\ \sum _{i=1}^N b_i p_{i2}\left( t\right) \\ \vdots \\ \sum _{i=1}^N b_i p_{iN}\left( t\right) \end{array} \right]= & {} \left[ \begin{array}{ccc} \sum _{i=1}^N b_i p_{i1}\left( t+T\right) \\ \sum _{i=1}^N b_i p_{i2}\left( t+T\right) \\ \vdots \\ \sum _{i=1}^N b_i p_{iN}\left( t+T\right) \end{array} \right] \nonumber \\= & {} \left[ \begin{array}{ccc} \sum _{i=1}^N b_i \sum _{j=1}^N a_{ij}p_{j1}\left( t\right) \\ \sum _{i=1}^N b_i \sum _{j=1}^N a_{ij}p_{j2}\left( t\right) \\ \vdots \\ \sum _{i=1}^N b_i \sum _{j=1}^N a_{ij}p_{jN}\left( t\right) \end{array} \right] ,\nonumber \\ \end{aligned}$$
(20)

which is equivalent to

$$\begin{aligned} \varvec{P}\left( t\right) \cdot \varvec{M}\equiv \varvec{0}, \end{aligned}$$
(21)

by assuming

$$\begin{aligned} \varvec{P}\left( t\right) =\left( \varvec{p_1} \left( t\right) ,\varvec{p_2}\left( t\right) ,\ldots ,\varvec{p_N}\left( t\right) \right) , \end{aligned}$$
(22)

and

$$\begin{aligned} \varvec{M}= \left[ \begin{array}{ccc} \left( a_{11}-\rho \right) b_1+a_{21}b_2+\cdots +a_{N1}b_N\\ a_{12}b_1+\left( a_{22}-\rho \right) b_2+\cdots +a_{N2}b_N\\ \vdots \\ a_{1N}b_1+a_{2N}b_2+\cdots +\left( a_{NN}-\rho \right) b_N \end{array} \right] . \end{aligned}$$
(23)

It means that the following relation must be held

$$\begin{aligned} {\left\{ \begin{array}{ll} \left( a_{11}-\rho \right) b_1+a_{21}b_2+\cdots +a_{N1}b_N=0\\ a_{12}b_1+\left( a_{22}-\rho \right) b_2+\cdots +a_{N2}b_N=0\\ \vdots \\ a_{1N}b_1+a_{2N}b_2+\cdots +\left( a_{NN}-\rho \right) b_N=0 \end{array}\right. }. \end{aligned}$$
(24)

Ulteriorly, Eq. (24) can be rewritten as follows

$$\begin{aligned} \varvec{A_T}\cdot \left( \varvec{B}-\rho \varvec{I}\right) =\varvec{0}, \end{aligned}$$
(25)

by assuming

$$\begin{aligned} \varvec{A_T}= & {} \left[ \begin{array}{ccc} a_{11},a_{21},\ldots ,a_{N1}\\ a_{12},a_{22},\ldots ,a_{N2}\\ \vdots \\ a_{1N},a_{2N},\ldots ,a_{NN} \end{array} \right] \nonumber \\= & {} \left[ \begin{array}{ccc} p_{11}\left( T\right) ,p_{21}\left( T\right) ,\ldots ,p_{N1}\left( T\right) \\ p_{12}\left( T\right) ,p_{22}\left( T\right) ,\ldots ,p_{N2}\left( T\right) \\ \vdots \\ p_{1N}\left( T\right) ,p_{2N}\left( T\right) ,\ldots ,p_{NN}\left( T\right) \end{array} \right] , \end{aligned}$$
(26)

and

$$\begin{aligned} \varvec{B}=\left( b_1,b_2,\ldots ,b_N\right) ^\mathrm{T}, \end{aligned}$$
(27)

where \(\rho \) is the eigenvalue of the matrix \(\varvec{A_T}\), which means that the zero solution is asymptotically stable, if and only if all \(|\rho \vert <1\), otherwise the zero solution is unstable.

3 Dynamical analysis

3.1 General method for stability analysis of TSS

The motion Eq. (1) is rewritten into a first-order form, to analyze the periodic stability of TSS

$$\begin{aligned} \varvec{\dot{x}}=\varvec{F}, \end{aligned}$$
(28)

where

$$\begin{aligned}&\varvec{x}=\left( u_1,v_1,w_1,\ldots ,u_{n+m},v_{n+m},w_{n+m},\right. \nonumber \\&\qquad \left. x_1,y_1,z_1,\ldots ,x_{n+m},y_{n+m},z_{n+m}\right) ^\mathrm{T}, \end{aligned}$$
(29)
$$\begin{aligned}&\varvec{F}=\left( f_1^x,f_1^y,f_1^z,\ldots ,f_{n+m}^x,f_{n+m}^y,\right. \nonumber \\&\qquad \left. f_{n+m}^z,u_1,v_1,w_1,\ldots ,u_{n+m},v_{n+m},w_{n+m}\right) ^\mathrm{T},\nonumber \\ \end{aligned}$$
(30)
$$\begin{aligned}&\left( u_i,v_i,w_i\right) ^\mathrm{T}=\varvec{\dot{r}_i}, \end{aligned}$$
(31)

and

$$\begin{aligned} \left( f_i^x,f_i^y,f_i^z\right) ^\mathrm{T}=\varvec{G_i}+\varvec{T_i}+\varvec{D_i}+\varvec{F_i^e}+\varvec{F_i^k}, \end{aligned}$$
(32)

Assuming \(P_0:\left( \varvec{\bar{x}}\right) \) is a fixed point on the Poincare section, where

$$\begin{aligned} \varvec{\bar{x}}= & {} \left( \bar{u}_1,\bar{v}_1,\bar{w}_1,\ldots ,\bar{u}_{n+m},\bar{v}_{n+m},\bar{w}_{n+m},\right. \nonumber \\&\left. \bar{x}_1,\bar{y}_1,\bar{z}_1,\ldots ,\bar{x}_{n+m},\bar{y}_{n+m},\bar{z}_{n+m}\right) ^\mathrm{T}, \end{aligned}$$
(33)

\(\varvec{p}=\left( p_1,\ldots ,p_{6\left( n+m\right) }\right) ^\mathrm{T}\) consisted of \(2\left( n+m\right) \) small amounts, and \(P_1:\left( \varvec{\bar{x}}+\varvec{p}\right) \) is a point in the small neighborhood of \(P_0:\left( \varvec{\bar{x}}\right) \) that \(P_1\) can be regarded as a perturbation of \(P_0\). Therefore, \(P_1\) can be expanded into Taylor series form by retaining the linear terms based upon \(P_0\), which can be obtained as follows

$$\begin{aligned} \varvec{\dot{p}}=\varvec{J_0}\cdot \varvec{p}, \end{aligned}$$
(34)

where

$$\begin{aligned} \varvec{J_0}=\dfrac{\partial \varvec{F}}{\partial \varvec{x}^\mathrm{T}}\mid _{\varvec{x}=\varvec{\bar{x}}}. \end{aligned}$$
(35)

The system (36) with the initial conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} p_1\left( t_0\right) =1,p_2\left( t_0\right) =0,\ldots ,p_{6\left( n+m\right) }\left( t_0\right) =0\\ p_1\left( t_0\right) =0,p_2\left( t_0\right) =1,\ldots ,p_{6\left( n+m\right) }\left( t_0\right) =0\\ \vdots \\ p_1\left( t_0\right) =0,p_2\left( t_0\right) =0,\ldots ,p_{6\left( n+m\right) }\left( t_0\right) =1 \end{array}\right. }, \end{aligned}$$
(36)

can be solved by dividing into the following two cases, based on the ordinary differential equation theory.

  1. 1.

    When the matrix \(\varvec{J}\) has \(N=6\left( n+m\right) \) linearly independent eigenvectors \(\varvec{v_1}, \varvec{v_2}, \ldots , \varvec{v_N}\), and their corresponding eigenvalues are \(\varvec{\lambda _1}, \varvec{\lambda _2}, \ldots , \varvec{\lambda _N}\). Then a basis solution matrix of homogeneous linear differential equations with constant coefficients Eq. (28) can always be expressed as

    $$\begin{aligned} \varvec{P}\left( t\right)= & {} \left( \varvec{p_1}\left( t\right) ,\varvec{p_2}\left( t\right) , \ldots ,\varvec{p_N}\left( t\right) \right) \nonumber \\= & {} \left( e^{\lambda _1t}\varvec{v_1},e^{\lambda _2t}\varvec{v_2},\ldots ,e^{\lambda _Nt}\varvec{v_N}\right) \end{aligned}$$
    (37)

    the general solution can be expressed as

    $$\begin{aligned} \varvec{p}\left( t\right) =\varvec{P}\left( t\right) \cdot \varvec{C} \end{aligned}$$
    (38)

    where \(\varvec{C}=\left( C_1,C_2,\ldots ,C_N\right) ^\mathrm{T}\) is a matrix consisted of undetermined constants. Substituting the initial condition (36) into Eq. (38), the equation can be obtained as follows

    $$\begin{aligned} \varvec{I}=\varvec{V}\cdot \varvec{C} \end{aligned}$$
    (39)

    where

    $$\begin{aligned} \varvec{V}=\left( \varvec{v_1},\varvec{v_2},\ldots ,\varvec{v_N}\right) , \end{aligned}$$
    (40)

    is the eigen-matrix of \(J|_{\varvec{x}=\varvec{\bar{x}}}\), and the constant matrix satisfies the relation as follows

    $$\begin{aligned} \varvec{C}=\varvec{V}^{-1}. \end{aligned}$$
    (41)

    Thus, the general solution can be rewritten as

    $$\begin{aligned} \varvec{p}\left( t\right) =\varvec{P}\left( t\right) \cdot \varvec{V}^{-1}. \end{aligned}$$
    (42)
  2. 2.

    When the matrix \(\varvec{J}\) has less than N linearly independent eigenvectors, it is easy to prove the following conclusion. If \(\lambda _i\) is the \(N_i\)-fold eigenvalue of \(\varvec{J}\), then there must be \(N_i\) linearly independent solutions in the form of

    $$\begin{aligned} \varvec{p}\left( t\right) =e^{\lambda _i t}\sum _{j=0}^{N_i-1}\dfrac{t^j}{j!}\varvec{v_{i,j}}, \end{aligned}$$
    (43)

    in which \(\varvec{v}_{i,0}\) is a non-zero solution of

    $$\begin{aligned} \left( \varvec{J_0}-\lambda _i\varvec{I}\right) ^{N_i}\varvec{v}=\varvec{0}, \end{aligned}$$
    (44)

    and a recurrence relation can be obtained as follows

    $$\begin{aligned} \varvec{v}_{i,j}=\left( \varvec{J_0}-\lambda _i\varvec{I}\right) \varvec{v}_{i,j-1}, \end{aligned}$$
    (45)

    where \(1\le j\le N_i-1\). Define the matrices \(\varvec{P}\) and \(\varvec{V}\) are separately consisted of N linearly independent vectors \(\varvec{p_i}\) and \(\varvec{v_i}\), then the general solution of the system in this situation can be solved by substituting \(\varvec{P}\) and \(\varvec{V}\) into (42).

The eigenvalues of the matrix \(\varvec{p}\left( t\right) \) at the periodic sampling time \(\rho _1,\rho _2,\ldots ,\rho _N\) are the Floquet multiples, according to the Floquet theory in Subsect. 2.2. It is easy to prove that the Floquet multiplier of the system is the eigenvalue of the matrix

$$\begin{aligned} \varvec{A_T}=\varvec{p}\left( T\right) , \end{aligned}$$
(46)

by assuming \(t_0=0\), and the periodic solution must be asymptotically stable if and only if the following condition is satisfied

$$\begin{aligned} |\rho _i|_\mathrm{max}<1,\mathrm{\quad } 1\le i\le N. \end{aligned}$$
(47)

3.2 Verification based on a typical example

Taking a 3-star system connected by massless tethers as an example, the stability analysis is carried out based on the above general model and analysis method, by letting

$$\begin{aligned} {\left\{ \begin{array}{ll} n=3\\ m=0 \end{array}\right. }. \end{aligned}$$
(48)

The motion equation of the system can be obtained as follows

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} {\ddot{x}_1}=-&{}\dfrac{\mu _Ex_1}{\left( x_1^2+\left( y_1+R\right) ^2+z_1^2\right) ^{\frac{3}{2}}}+x_1\Omega ^2+2\Omega v_1\\ &{}-s_{1,2}\dfrac{EA}{M}\left( \dfrac{1}{L}-\dfrac{1}{\sqrt{\left( x_1-x_2\right) ^2+\left( y_1-y_2\right) ^2+\left( z_1-z_2\right) ^2}}\right) \left( x_1-x_2\right) \\ &{}-s_{1,2}\dfrac{C}{M}\dfrac{\left( x_1-x_2\right) \left( u_1-u_2\right) +\left( y_1-y_2\right) \left( v_1-v_2\right) +\left( z_1-z_2\right) \left( w_1-w_2\right) }{\left( x_1-x_2\right) ^2+\left( y_1-y_2\right) ^2+\left( z_1-z_2\right) ^2}\left( x_1-x_2\right) \\ &{}-s_{1,3}\dfrac{EA}{M}\left( \dfrac{1}{L}-\dfrac{1}{\sqrt{\left( x_1-x_3\right) ^2+\left( y_1-y_3\right) ^2+\left( z_1-z_3\right) ^2}}\right) \left( x_1-x_3\right) \\ &{}-s_{1,3}\dfrac{C}{M}\dfrac{\left( x_1-x_3\right) \left( u_1-u_3\right) +\left( y_1-y_3\right) \left( v_1-v_3\right) +\left( z_1-z_3\right) \left( w_1-w_3\right) }{\left( x_1-x_3\right) ^2+\left( y_1-y_3\right) ^2+\left( z_1-z_3\right) ^2}\left( x_1-x_3\right) \end{aligned}\\ \end{array}\right. } \end{aligned}$$
$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} {\ddot{y}_1}=-&{}\dfrac{\mu _E\left( y_1+R\right) }{\left( x_1^2+\left( y_1+R\right) ^2+z_1^2\right) ^{\frac{3}{2}}}+\left( y_1+R\right) \Omega ^2-2\Omega u_1\\ &{}-s_{1,2}\dfrac{EA}{M}\left( \dfrac{1}{L}-\dfrac{1}{\sqrt{\left( x_1-x_2\right) ^2+\left( y_1-y_2\right) ^2+\left( z_1-z_2\right) ^2}}\right) \left( y_1-y_2\right) \\ &{}-s_{1,2}\dfrac{C}{M}\dfrac{\left( x_1-x_2\right) \left( u_1-u_2\right) +\left( y_1-y_2\right) \left( v_1-v_2\right) +\left( z_1-z_2\right) \left( w_1-w_2\right) }{\left( x_1-x_2\right) ^2+\left( y_1-y_2\right) ^2+\left( z_1-z_2\right) ^2}\left( y_1-y_2\right) \\ &{}-s_{1,3}\dfrac{EA}{M}\left( \dfrac{1}{L}-\dfrac{1}{\sqrt{\left( x_1-x_3\right) ^2+\left( y_1-y_3\right) ^2+\left( z_1-z_3\right) ^2}}\right) \left( y_1-y_3\right) \\ &{}-s_{1,3}\dfrac{C}{M}\dfrac{\left( x_1-x_3\right) \left( u_1-u_3\right) +\left( y_1-y_3\right) \left( v_1-v_3\right) +\left( z_1-z_3\right) \left( w_1-w_3\right) }{\left( x_1-x_3\right) ^2+\left( y_1-y_3\right) ^2+\left( z_1-z_3\right) ^2}\left( y_1-y_3\right) \end{aligned}\\ \begin{aligned} {\ddot{z}_1}=-&{}\dfrac{\mu _Ez_1}{\left( x_1^2+\left( y_1+R\right) ^2+z_1^2\right) ^{\frac{3}{2}}}\\ &{}-s_{1,2}\dfrac{EA}{M}\left( \dfrac{1}{L}-\dfrac{1}{\sqrt{\left( x_1-x_2\right) ^2+\left( y_1-y_2\right) ^2+\left( z_1-z_2\right) ^2}}\right) \left( z_1-z_2\right) \\ &{}-s_{1,2}\dfrac{C}{M}\dfrac{\left( x_1-x_2\right) \left( u_1-u_2\right) +\left( y_1-y_2\right) \left( v_1-v_2\right) +\left( z_1-z_2\right) \left( w_1-w_2\right) }{\left( x_1-x_2\right) ^2+\left( y_1-y_2\right) ^2+\left( z_1-z_2\right) ^2}\left( z_1-z_2\right) \\ &{}-s_{1,3}\dfrac{EA}{M}\left( \dfrac{1}{L}-\dfrac{1}{\sqrt{\left( x_1-x_3\right) ^2+\left( y_1-y_3\right) ^2+\left( z_1-z_3\right) ^2}}\right) \left( z_1-z_3\right) \\ &{}-s_{1,3}\dfrac{C}{M}\dfrac{\left( x_1-x_3\right) \left( u_1-u_3\right) +\left( y_1-y_3\right) \left( v_1-v_3\right) +\left( z_1-z_3\right) \left( w_1-w_3\right) }{\left( x_1-x_3\right) ^2+\left( y_1-y_3\right) ^2+\left( z_1-z_3\right) ^2}\left( z_1-z_3\right) \end{aligned}\\ \begin{aligned} {\ddot{x}_2}=-&{}\dfrac{\mu _Ex_2}{\left( x_2^2+\left( y_2+R\right) ^2+z_2^2\right) ^{\frac{3}{2}}}+x_2\Omega ^2+2\Omega v_2\\ &{}-s_{2,3}\dfrac{EA}{M}\left( \dfrac{1}{L}-\dfrac{1}{\sqrt{\left( x_2-x_3\right) ^2+\left( y_2-y_3\right) ^2+\left( z_2-z_3\right) ^2}}\right) \left( x_2-x_3\right) \\ &{}-s_{2,3}\dfrac{C}{M}\dfrac{\left( x_2-x_3\right) \left( u_2-u_3\right) +\left( y_2-y_3\right) \left( v_2-v_3\right) +\left( z_2-z_3\right) \left( w_2-w_3\right) }{\left( x_2-x_3\right) ^2+\left( y_2-y_3\right) ^2+\left( z_2-z_3\right) ^2}\left( x_2-x_3\right) \\ &{}-s_{2,1}\dfrac{EA}{M}\left( \dfrac{1}{L}-\dfrac{1}{\sqrt{\left( x_2-x_1\right) ^2+\left( y_2-y_1\right) ^2+\left( z_2-z_1\right) ^2}}\right) \left( x_2-x_1\right) \\ &{}-s_{2,1}\dfrac{C}{M}\dfrac{\left( x_2-x_1\right) \left( u_2-u_1\right) +\left( y_2-y_1\right) \left( v_2-v_1\right) +\left( z_2-z_1\right) \left( w_2-w_1\right) }{\left( x_2-x_1\right) ^2+\left( y_2-y_1\right) ^2+\left( z_2-z_1\right) ^2}\left( x_2-x_1\right) \end{aligned}\\ \begin{aligned} {\ddot{y}_2}=-&{}\dfrac{\mu _E\left( y_2+R\right) }{\left( x_2^2+\left( y_2+R\right) ^2+z_2^2\right) ^{\frac{3}{2}}}+\left( y_2+R\right) \Omega ^2-2\Omega u_2\\ &{}-s_{2,3}\dfrac{EA}{M}\left( \dfrac{1}{L}-\dfrac{1}{\sqrt{\left( x_2-x_3\right) ^2+\left( y_2-y_3\right) ^2+\left( z_2-z_3\right) ^2}}\right) \left( y_2-y_3\right) \\ &{}-s_{2,3}\dfrac{C}{M}\dfrac{\left( x_2-x_3\right) \left( u_2-u_3\right) +\left( y_2-y_3\right) \left( v_2-v_3\right) +\left( z_2-z_3\right) \left( w_2-w_3\right) }{\left( x_2-x_3\right) ^2+\left( y_2-y_3\right) ^2+\left( z_2-z_3\right) ^2}\left( y_2-y_3\right) \\ &{}-s_{2,1}\dfrac{EA}{M}\left( \dfrac{1}{L}-\dfrac{1}{\sqrt{\left( x_2-x_1\right) ^2+\left( y_2-y_1\right) ^2+\left( z_2-z_1\right) ^2}}\right) \left( y_2-y_1\right) \\ &{}-s_{2,1}\dfrac{C}{M}\dfrac{\left( x_2-x_1\right) \left( u_2-u_1\right) +\left( y_2-y_1\right) \left( v_2-v_1\right) +\left( z_2-z_1\right) \left( w_2-w_1\right) }{\left( x_2-x_1\right) ^2+\left( y_2-y_1\right) ^2+\left( z_2-z_1\right) ^2}\left( y_2-y_1\right) \end{aligned}\\ \end{array}\right. } \end{aligned}$$
$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} {\ddot{z}_2}=-&{}\dfrac{\mu _Ez_2}{\left( x_2^2+\left( y_2+R\right) ^2+z_2^2\right) ^{\frac{3}{2}}}\\ &{}-s_{2,3}\dfrac{EA}{M}\left( \dfrac{1}{L}-\dfrac{1}{\sqrt{\left( x_2-x_3\right) ^2+\left( y_2-y_3\right) ^2+\left( z_2-z_3\right) ^2}}\right) \left( z_2-z_3\right) \\ &{}-s_{2,3}\dfrac{C}{M}\dfrac{\left( x_2-x_3\right) \left( u_2-u_3\right) +\left( y_2-y_3\right) \left( v_2-v_3\right) +\left( z_2-z_3\right) \left( w_2-w_3\right) }{\left( x_2-x_3\right) ^2+\left( y_2-y_3\right) ^2+\left( z_2-z_3\right) ^2}\left( z_2-z_3\right) \\ &{}-s_{2,1}\dfrac{EA}{M}\left( \dfrac{1}{L}-\dfrac{1}{\sqrt{\left( x_2-x_1\right) ^2+\left( y_2-y_1\right) ^2+\left( z_2-z_1\right) ^2}}\right) \left( z_2-z_1\right) \\ &{}-s_{2,1}\dfrac{C}{M}\dfrac{\left( x_2-x_1\right) \left( u_2-u_1\right) +\left( y_2-y_1\right) \left( v_2-v_1\right) +\left( z_2-z_1\right) \left( w_2-w_1\right) }{\left( x_2-x_1\right) ^2+\left( y_2-y_1\right) ^2+\left( z_2-z_1\right) ^2}\left( z_2-z_1\right) \end{aligned}\\ \begin{aligned} {\ddot{x}_3}=-&{}\dfrac{\mu _Ex_3}{\left( x_3^2+\left( y_3+R\right) ^2+z_3^2\right) ^{\frac{3}{2}}}+x_3\Omega ^2+2\Omega v_3\\ &{}-s_{3,1}\dfrac{EA}{M}\left( \dfrac{1}{L}-\dfrac{1}{\sqrt{\left( x_3-x_1\right) ^2+\left( y_3-y_1\right) ^2+\left( z_3-z_1\right) ^2}}\right) \left( x_3-x_1\right) \\ &{}-s_{3,1}\dfrac{C}{M}\dfrac{\left( x_3-x_1\right) \left( u_3-u_1\right) +\left( y_3-y_1\right) \left( v_3-v_1\right) +\left( z_3-z_1\right) \left( w_3-w_1\right) }{\left( x_3-x_1\right) ^2+\left( y_3-y_1\right) ^2+\left( z_3-z_1\right) ^2}\left( x_3-x_1\right) \\ &{}-s_{3,2}\dfrac{EA}{M}\left( \dfrac{1}{L}-\dfrac{1}{\sqrt{\left( x_3-x_2\right) ^2+\left( y_3-y_2\right) ^2+\left( z_3-z_2\right) ^2}}\right) \left( x_3-x_2\right) \\ &{}-s_{3,2}\dfrac{C}{M}\dfrac{\left( x_3-x_2\right) \left( u_3-u_2\right) +\left( y_3-y_2\right) \left( v_3-v_2\right) +\left( z_3-z_2\right) \left( w_3-w_2\right) }{\left( x_3-x_2\right) ^2+\left( y_3-y_2\right) ^2+\left( z_3-z_2\right) ^2}\left( x_3-x_2\right) \end{aligned}\\ \begin{aligned} {\ddot{y}_3}=-&{}\dfrac{\mu _E\left( y_3+R\right) }{\left( x_3^2+\left( y_3+R\right) ^2+z_3^2\right) ^{\frac{3}{2}}}+\left( y_3+R\right) \Omega ^2-2\Omega u_3\\ &{}-s_{3,1}\dfrac{EA}{M}\left( \dfrac{1}{L}-\dfrac{1}{\sqrt{\left( x_3-x_1\right) ^2+\left( y_3-y_1\right) ^2+\left( z_3-z_1\right) ^2}}\right) \left( y_3-y_1\right) \\ &{}-s_{3,1}\dfrac{C}{M}\dfrac{\left( x_3-x_1\right) \left( u_3-u_1\right) +\left( y_3-y_1\right) \left( v_3-v_1\right) +\left( z_3-z_1\right) \left( w_3-w_1\right) }{\left( x_3-x_1\right) ^2+\left( y_3-y_1\right) ^2+\left( z_3-z_1\right) ^2}\left( y_3-y_1\right) \\ &{}-s_{3,2}\dfrac{EA}{M}\left( \dfrac{1}{L}-\dfrac{1}{\sqrt{\left( x_3-x_2\right) ^2+\left( y_3-y_2\right) ^2+\left( z_3-z_2\right) ^2}}\right) \left( y_3-y_2\right) \\ &{}-s_{3,2}\dfrac{C}{M}\dfrac{\left( x_3-x_2\right) \left( u_3-u_2\right) +\left( y_3-y_2\right) \left( v_3-v_2\right) +\left( z_3-z_2\right) \left( w_3-w_2\right) }{\left( x_3-x_2\right) ^2+\left( y_3-y_2\right) ^2+\left( z_3-z_2\right) ^2}\left( y_3-y_2\right) \end{aligned}\\ \begin{aligned} {\ddot{z}_3}=-&{}\dfrac{\mu _E\left( y_2+R\right) }{\left( x_2^2+\left( y_2+R\right) ^2+z_2^2\right) ^{\frac{3}{2}}}+\left( y_2+R\right) \Omega ^2-2\Omega u_2\\ &{}-s_{3,1}\dfrac{EA}{M}\left( \dfrac{1}{L}-\dfrac{1}{\sqrt{\left( x_3-x_1\right) ^2+\left( y_3-y_1\right) ^2+\left( z_3-z_1\right) ^2}}\right) \left( z_3-z_1\right) \\ &{}-s_{3,1}\dfrac{C}{M}\dfrac{\left( x_3-x_1\right) \left( u_3-u_1\right) +\left( y_3-y_1\right) \left( v_3-v_1\right) +\left( z_3-z_1\right) \left( w_3-w_1\right) }{\left( x_3-x_1\right) ^2+\left( y_3-y_1\right) ^2+\left( z_3-z_1\right) ^2}\left( z_3-z_1\right) \\ &{}-s_{3,2}\dfrac{EA}{M}\left( \dfrac{1}{L}-\dfrac{1}{\sqrt{\left( x_3-x_2\right) ^2+\left( y_3-y_2\right) ^2+\left( z_3-z_2\right) ^2}}\right) \left( z_3-z_2\right) \\ &{}-s_{3,2}\dfrac{C}{M}\dfrac{\left( x_3-x_2\right) \left( u_3-u_2\right) +\left( y_3-y_2\right) \left( v_3-v_2\right) +\left( z_3-z_2\right) \left( w_3-w_2\right) }{\left( x_3-x_2\right) ^2+\left( y_3-y_2\right) ^2+\left( z_3-z_2\right) ^2}\left( z_3-z_2\right) \end{aligned}\\ \end{array}\right. } \end{aligned}$$
(49)
Fig. 3
figure 3

Clockwise spin angular velocity \(|\omega |=2.0\Omega \) of tether formation system, the numerical simulation results of the trajectories of each satellite

Full size image

where \(m_i=M\), \(E_{i,j}=E\), \(A_{i,j}=A\), \(C_{i,j}=C\), \(L_{i,j}=L\), and \(i=1,2,3\), by assuming the initial position and velocity are in the xoy plane. Considering that the system has an initial steady-state configuration of regular N-polygon, which may be assumed that the 1st satellite is located on the y-axis at the initial moment, the distance from the origin of the \(o-xyz\) is \(R_1\). Then the initial position of any satellite can be obtained as follows

$$\begin{aligned} {\left\{ \begin{array}{ll} \bar{x}_i=R_1\cos \left( \left( i-1\right) \delta \alpha +\dfrac{\pi }{2}\right) \\ \bar{y}_i=R_1\sin \left( \left( i-1\right) \delta \alpha +\dfrac{\pi }{2}\right) \\ \bar{z}_i=0\\ \bar{u}_i=-\omega R_1\sin \left( \left( i-1\right) \delta \alpha +\dfrac{\pi }{2}\right) \\ \bar{v}_i=\omega R_1\cos \left( \left( i-1\right) \delta \alpha +\dfrac{\pi }{2}\right) \\ \bar{w}_i=0 \end{array}\right. }, \end{aligned}$$
(50)

in which N is the number of satellites, and \(\delta \alpha =\dfrac{2\pi }{N}\) expresses the angle between two adjacent satellites. It is easy to prove that \(R_1\) satisfies the following relation

$$\begin{aligned} -\omega ^2R_1=\dot{v}_1\vert _{t=0}, \end{aligned}$$
(51)

in which \(\omega \) expresses the spin angular velocity of the TSS system. In order to verify the initial steady-state configuration of tethered satellite system, a simulation model was established. The trajectories of the 1st, 2nd, and 3rd satellites are shown in Figs. 3 and 4, which are represented by red, green, and blue dotted curves, respectively; and the black circles and the solid lines in black represent the satellites and the tethers connecting two adjacent satellites, under the spin angular velocity condition \(\vert \omega \vert =2.0\Omega \) and \(\vert \omega \vert =2.5\Omega \), separately.

Fig. 4
figure 4

Clockwise spin angular velocity \(|\omega |=2.5\Omega \) of tether formation system, the numerical simulation results of the trajectories of each satellite

Full size image

Based on the motion Eq. (49) and the initial conditions (50), the TSS can maintain the initial configuration depend on its spin under both conditions, which proves the correctness of the steady-state configuration and the solution of the initial conditions.

Fig. 5
figure 5

The Floquet multiplier of the system in clockwise spin, a for the curve of Floquet multiplier and spin angular velocity, b for the local enlargement of the curve

Full size image

Substituting the initial conditions into the motion Eq. (49), the Jacobian matrix can be solved as follows

$$\begin{aligned} \varvec{J_0}= \left[ \begin{array}{llll} \dfrac{\partial \dot{u}_1}{\partial u_1}, &{}\dfrac{\partial \dot{u}_1}{\partial v_1}, &{}\ldots , &{}\dfrac{\partial \dot{u}_1}{\partial z_3}\\ \dfrac{\partial \dot{v}_1}{\partial u_1}, &{}\dfrac{\partial \dot{v}_1}{\partial v_1}, &{}\ldots , &{}\dfrac{\partial \dot{v}_1}{\partial z_3}\\ \vdots , &{}\vdots , &{}\ddots , &{}\vdots \\ \dfrac{\partial \dot{z}_3}{\partial u_1}, &{}\dfrac{\partial \dot{z}_3}{\partial v_1}, &{}\ldots , &{}\dfrac{\partial \dot{z}_3}{\partial z_3}\\ \end{array} \right] |_{t=0} = \left[ \begin{array}{ll} \varvec{A}, &{}\varvec{B}\\ \varvec{I}, &{}\varvec{0} \end{array} \right] . \end{aligned}$$
(52)

The curve of Floquet multiplier depended on clockwise spin angular velocity of the TSS can be obtained based upon the method mentioned in Subsect. 3.1 with the parameters shown in Table 1.

Table 1 Parameters of the tethered satellite system
Full size table

It can be found from Fig. 5 that the configuration is stable when the spin angular velocity is higher than the critical angular velocity (about 2.17 times of the revolution angular velocity). The correctness of the critical angular velocity solved by the Floquet theory can be verified by introducing disturbances into the systems with different spin angular velocities which are shown in Figs. 3 and 4. The operation situations of the disturbed systems with the spin angular velocities of \(|\omega |=2.0\Omega \) and \(|\omega |=2.5\Omega \) are shown in Figs. 6 and 7, respectively. Obviously, the configuration of the disturbed system cannot be held when the spin angular velocity is lower than the critical angular velocity (\(|\dfrac{\omega }{\Omega }|=2.0<2.17\)), while the disturbed system will converge to the original configuration in about 2 periods, when the spin angular velocity satisfies \(|\dfrac{\omega }{\Omega }|=2.5>2.17\).

Fig. 6
figure 6

The orbit of each satellite, when the clockwise spin angular velocity of the system satisfies \(\vert \omega \vert =2.0\Omega \)

Full size image
Fig. 7
figure 7

The orbit of each satellite, when the clockwise spin angular velocity of the system satisfies \(|\omega |=2.5\Omega \)

Full size image
Fig. 8
figure 8

Relative deviation of the system, a for the situation of \(|\omega |=2.0\Omega \) and b for the situation of \(|\omega |=2.5\Omega \)

Full size image
Fig. 9
figure 9

The Floquet multiplier of the system with different masses of satellites in clockwise spin, a for the curve of Floquet multiplier and spin angular velocity with the satellite masses of \(50\,\mathrm{kg}\), b for the local enlargement of the curve shown in (a), (c) for the curve of Floquet multiplier and spin angular velocity with the satellite masses of \(1000\,\mathrm{kg}\), and d for the local enlargement of the curve shown in (c)

Full size image
Fig. 10
figure 10

The simulation results of the system with the satellite mass of \(50\,\mathrm{kg}\). a for the orbit of each satellite when the clockwise spin angular velocity of the system satisfies \(|\omega |=2.5\Omega \), b for the top view of (a), (c) for the relative deviation of the system satisfies \(|\omega |=2.5\Omega \), d for the orbit of each satellite when the clockwise spin angular velocity of the system satisfies \(|\omega |=2.9\Omega \), e for the top view of (d), and (f) for the relative deviation of the system satisfies \(|\omega |=2.9\Omega \)

Full size image
Fig. 11
figure 11

The simulation results of the system with the satellite mass of \(1000\,\mathrm{kg}\). a for the orbit of each satellite when the clockwise spin angular velocity of the system satisfies \(|\omega |=1.5\Omega \), b for the top view of (a), (c) for the relative deviation of the system satisfies \(|\omega |=1.5\Omega \), d for the orbit of each satellite when the clockwise spin angular velocity of the system satisfies \(|\omega |=2.2\Omega \), e for the top view of (d), and f for the relative deviation of the system satisfies \(|\omega |=2.2\Omega \)

Full size image

The relative deviation from the initial steady-state configuration is defined as follows

$$\begin{aligned} d_i=\dfrac{|\varvec{r_i}|}{R_0}-1, \end{aligned}$$
(53)

to analyze the convergence of each satellite to the initial configuration depends on time. The relative deviation curves of two operating modes with the two spin angular velocities of \(|\omega |=2.0\Omega \) and \(|\omega |=2.5\Omega \) are shown in Fig. 8. It is shown that the relative deviation of each satellite in the disturbed system cannot be attenuated to 0 when the spin angular velocity is less than critical angular velocity, shown in Fig. 8a; but the relative deviation of each satellite will gradually decay to 0 to restore the initial steady state configuration in a limited time, when the spin angular velocity satisfies \(|\dfrac{\omega }{\Omega }|=2.5>2.17\). Therefore, the solution of periodical stability obtained by the general method based upon the Floquet theory mentioned in Subsect. 3.1 has been proved that the configuration solved by (50) and (51) is stable when the clockwise spin angular velocity rapider than about 2.17 times the revolution angular velocity.

3.3 Sensitivity analysis of system parameters

The effects of the critical angular velocity caused by the variation of the system parameters are considered based upon the above 3-star system.

Firstly, two groups of 3-star system with different satellite masses are analyzed, in which the satellite masses in the first group are \(50\,\mathrm{kg}\) (less than the original system) and which in the other group are \(1000\,\mathrm{kg}\) (greater than original system), respectively. It can be found from Fig. 9 that the changing of satellite mass will significantly affect the critical angular velocity of the stable spin of the system, based upon the Floquet theory. The Floquet multiplier of the system with the satellite masses of 50 kg and \(1000\,\mathrm{kg}\) are shown in Fig. 9a, b, c, and d, respectively, and the critical angular velocities are separately about 2.79 and 2.07 times of the revolution angular velocity. This leads a conclusion that the critical angular velocity will decrease with the increase in satellite mass, which means that the increase in the system inertia caused by increasing satellite mass will reduce the stable spin condition. The critical angular velocities solved by the Floquet theory are verified by disturbed simulations. The configuration of the disturbed system with the satellite mass of \(50\,\mathrm{kg}\), shown in Fig. 10, can hold the original configuration in about 2 periods, if the spin angular velocity satisfies \(|\dfrac{\omega }{\Omega }|=2.9>2.79\). As shown in Fig. 11, the configuration of the disturbed system with the satellite mass of \(1000\,\mathrm{kg}\) can be converged to the original configuration in about 3 periods, if the spin angular velocity satisfies (\(|\dfrac{\omega }{\Omega }|=2.2>2.07\)). The relative deviation of each satellite in the disturbed system will gradually decay to 0 to restore the initial steady state configuration in a limited time when and only when the spin angular velocity is larger than the critical angular velocity, shown in Figs. 10c, f and 11c, f. Secondly, the applicability of the general model and its stability discrimination method for complex system with multi-body is demonstrate. Considering the 3-star system consisted of multi-beads (more than 3) with different masses, introduced by the mass effect of tethers. Assuming the tether connecting two satellites with the mass satisfies \(M=1000\,\mathrm{kg}\) can be divided into two segments with the center mass is \(m=10\,\mathrm{kg}\). Considering that each tether is divided into two segments, and the steady-state configuration of 3-star system with 6 beads is shown in Fig.12. The parameters \(R_1\) and \(R_2\) can be determined by the following equations

$$\begin{aligned} {\left\{ \begin{array}{ll} -\omega ^2R_1=\dot{v}_1|_{t=0},\\ -\omega ^2R_2=\cos \left( \alpha +\dfrac{\pi }{2}\right) \dot{u}_2|_{t=0}+\sin \left( \alpha +\dfrac{\pi }{2}\right) \dot{v}_2\vert _{t=0}. \end{array}\right. } \end{aligned}$$
(54)

The critical angular velocity of the 6-bead system can be determined by analyzing the Floquet multiplier in Fig. 13, which implies a conclusion similar to that shown in Fig. 9d, that is \(|\omega |\approx 2.08\Omega \). The simulation results of the stability of the disturbed 6-bead system under different spin angular velocities are shown in Fig. 14. It can be found that the simulation results verified the correctness of the stability condition implied by the results of the Floquet multiplier shown in Fig. 13. The trajectory of each bead of the disturbed system will gradually approach a circular orbit in about 10 periods in order to stabilize the system configuration, when the spin angular velocity is larger than the critical angular velocity (\(|\omega |\approx 2.08\Omega \)). On the contrary, the system cannot maintain configuration steadily when the spin angular velocity is not large enough. However, the 6-bead system cannot approach the initial stable configuration in a limited time even when the spin angular velocity is greater than the critical angular velocity. It is means that a rapid enough spin can keep the configuration stable but cannot completely suppress the vibration, for the system with more than 3 beads.

Fig. 12
figure 12

The steady-state configuration of 3-star system with 6 beads

Full size image
Fig. 13
figure 13

The Floquet multiplier of the 6-beads system

Full size image

In other words, it is obvious from Fig. 15a and c that the relative deviation of the center distance of each beads cannot approach to 0, whether or not the spin angular velocity is greater than the critical angular velocity; but the relative deviation of the tether length can approach to 0, only when the spin angular velocity is greater than the critical angular velocity. Considering there are multiple solutions of the geometry of the system with the constant tether length but different included angles, when the number of beads in the system exceeds 3. The kinetic energy causing the change of the included angle of adjacent tethers will not be dissipated, since there is no constraint on the rotational relationship between each bead and tether. Therefore, it can be concluded that although the spin stability conditions of the closed-loop system with more than 3-bead can be accurately analyzed by the general model and the method proposed in this paper, the periodic change of configuration caused by the variation of tether angle cannot be suppressed only by accelerating the spin angular velocity.

Fig. 14
figure 14

The simulation results of the 6-bead system. a for the orbit of each bead when the clockwise spin angular velocity of the system satisfies \(|\omega |=1.5\Omega \), b for the top view of a, c for the orbit of each bead when the clockwise spin angular velocity of the system satisfies \(|\omega |=2.2\Omega \), d for the top view of (c)

Full size image
Fig. 15
figure 15

Relative deviation of the system. a for the distance from each bead to the center of the system with the spin angular velocity of \(|\omega |=1.5\Omega \), b for the length of each tether with the spin angular velocity of \(|\omega |=1.5\Omega \), c for the distance from each bead to the center of the system with the spin angular velocity of \(|\omega |=2.2\Omega \), and (b) for the length of each tether with the spin angular velocity of \(|\omega |=2.2\Omega \)

Full size image

4 Conclusion and outlooks

In this paper, a general dynamic model of n-star tethered satellite system with closed-loop configuration has been proposed. An analytical method of periodic solution stability of the general dynamic model is provided based on Floquet theory, which proves that the periodic solution stability of the system depends on the maximum modulus of the eigenvalue for a matrix related to the Jacobian matrix of the system. On the basis of the general periodic solution stability analysis method, taking a 3-star system with the initial configuration of equilateral triangle, the critical stable clockwise spin angular velocity of the system is analyzed, and the numerical simulation is carried out to verify the results. The results show that the analytical method of periodic solution stability can solve the critical stable spin angular velocity of the TSS accurately. The system can guarantee stable spin when the value of its spin angular velocity is higher than the critical stable spin angular velocity; otherwise, the disturbed system will not be able to re-converge to the initial configuration in finite time. The periodic oscillation of the stable configuration consisted of more than 3 beads, caused by variation of the included angle of the tethers, cannot be suppressed only by accelerating the spin angular velocity. Therefore, the vibration suppression scheme except changing the spin angular velocity is of great significance for the multi-bead (more than 3) system, which is being actively studied by the authors.