Stable Deployment Control of a Multi-tethered Formation System Considering the Spinning Motion of Parent Satellite

Abstract

Tethered satellite formation systems have attracted significant attention in recent years, primarily because they offer potential advantages for certain space missions, such as space interferometry measurement. This work considers the stable deployment of a spinning multi-mass tethered system arranged in a hub-spoke configuration in the orbital plane. The system contains a parent satellite (hub) modeled as a rigid body, and several sub-satellites connected to the hub via inelastic tethers (spokes). The deployment dynamics are derived using Lagrange’s equations. The spinning motion of the parent satellite is controlled by active torque, while tether deployment is conducted by release mechanisms on the parent satellite and low-thrust engines installed on each sub-satellite. Considering the physical restraints of tether tension during the deployment process, an optimal controller is proposed using Bellman dynamic programming, based on a simplified dynamic model. Then, the obtained controller is employed in the complete model, where the coupling effect between the spinning of parent body and tether deployment are taken into account. Finally, numerical simulations are presented to illustrate the effectiveness of the proposed control strategy.

1 Introduction

Satellite formation flying [2] is seen as a promising technology for space exploration and in recent decades has aroused considerable research interest. Multiple small satellites are capable of completing missions like a conventional monolithic satellite, but with enhanced flexibility and reliability. Tethered satellite formation (TSF) is a new type of formation flying. The configuration of a TSF system in space is formed and maintained via tethers [5], which promises more accurate formation geometry and lower fuel consumption.

A TSF system can be arranged in various geometries depending on mission requirements. One of the basic geometries of multi-tethered constellations is the hub-spoke configuration [7], where the parent satellite is located at the center of configuration and peripheral satellites are connected to the central body via tethers. Due to the radial geometry of the hub-spoke configuration, this kind of formation is very suitable for use in certain new space missions, such as multi-point measurement and the space sail [4]. Usually, a hub-spoke TSF rotates around its center of mass to maintain stability, and the configuration has been found to spin stably whether in the orbital plane or in the plane normal to the orbital plane [8]. In addition, a relatively high spin rate is useful to improve the rotational stability of the system and maintain its initial configuration in the presence of external disturbances [1].

For a TSF system, stable deployment is the process of achieving an expected configuration, and therefore, is an essential prerequisite for carrying out space missions. In hub-spoke tethered formations, the rotational deployment strategy [10] has been widespreadly used, based on rotational stability of the configuration and the centrifugal stiffening effect provided by spinning of the parent body. However, controlling the deployment of hub-spoke TSF systems is no easy task, because there is a strong nonlinear coupling effect between the spinning motion of parent satellite, tether deployment, and tether vibrations, which results in complex dynamic behaviors.

Consequently, to make controller design more convenient, it has been common practice in previous works to treat the satellites as a set of mass points, that is, the attitude motions of satellites are assumed to be prescribed and remain stable during tether deployment [10]. These assumptions could make deployment controller design easier, and based on these assumptions, active deployment control has been proposed to release the tethers to desired lengths [6]. However, as the tethers are released out, the spin rate of parent satellite will decrease if its dimensions are simply ignored and no control torque is employed. In addition, it is also important to assess the interaction between tether deployment and the spinning of parent satellite to make sure that the tethers will not be entangled on the parent body during deployment.

The purpose of this work is to present an optimal deployment controller for a spinning multi-tethered formation system with a hub-spoke configuration. First of all, in Sect. 2, a complete coupled mathematical model of the system is developed using Lagrangian approach. Then, in Sect. 3, the simplified dynamic model is derived and the solution of the optimal problem is obtained based on Bellman dynamic programming. Finally, in Sect. 4, numerical simulations are presented to illustrate the performance of the proposed controller in the complete model of the system.

2 Mathematical Modeling

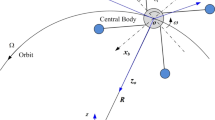
The multi-tethered system considered in this paper, shown in Fig. 1, comprises a parent satellite of mass ${\text{m}}_{\rm{c}}$ and ${\text{n}}$ sub-satellites of mass ${\text{m}}_{\rm{i}}$, ${\text{i}} = {1, 2, } \ldots , {\text{n}}$. The parent satellite is modeled by a symmetrical solid sphere of radius ${\text{r}}$, while the sub-satellites are treated as a set of point masses, for that the dimensions of sub-satellites are usually much smaller than the tether length. Furthermore, it is assumed that the tethers are of negligible mass, and are straight and inelastic during deployment.

Fig. 1

The multi-tethered satellite system

The dynamics of the multi-tethered system is represented using the Earth-centered inertial (ECI) coordinate frame ${\text{OXYZ}}$ and the orbital coordinate system ${\text{Cxyz}}$. The origin ${\text{O}}$ is at the center of the Earth, the ${\text{OX}}$ axis points to the vernal equinox, the ${\text{OZ}}$ axis is aligned with the Earth’s rotation axis, and the ${\text{OY}}$ axis is obtained by the right-hand rule. Define the unit vectors of the ECI frame as i, j, k and when the formation system is moving in a circular orbit, its orbital angular velocity can be expressed as: $\Omega = \Omega {\rm{k}}$. The origin of the moving frame Cxyz is located at the center of mass of the configuration, the Cx axis points along the local vertical, the Cy axis is in the orbital plane and points in the direction of the orbital velocity vector of the parent body, and the Cz axis completes the right-hand triad. The unit vectors of the orbital coordinate system are given by ${\text{i}}_{\text{c}} , {\text{j}}_{\text{c}} , {\text{k}}_{\text{c}}$.

The equations governing the planar deployment of the configuration are derived using Lagrangian approach, which requires the expressions of kinetic and potential energies of the system. In order to describe the spinning motion of parent satellite around the center of mass of the system, define ${\text{r}}_{\text{i}}$, ${\text{i}} = {1, 2, } \ldots , {\text{n}}$ as the radius vectors of the points, where the tethers are joined to the parent body, and $\alpha_i$ as the angles between ${\text{r}}_{\text{i}}$ and the Cx axis, as shown in Fig. 1. Then, the deployment of i-th tether can be characterized by its length $l_i$ and libration angle $\theta_i$ (also see Fig. 1), which represents the angle between the direction of the i-th tether and the direction of the radius vector ${\text{r}}_{\text{i}}$. Thus, considering the geometric relations between the parent satellite and sub-satellites, the position of the i-th peripheral satellite can be expressed in the orbital coordinate system as:

$$ {{\boldsymbol{p}}}_i = x_i \cdot {{\boldsymbol{i}}}_c + y_i \cdot {{\boldsymbol{j}}}_c + z_i \cdot {{\boldsymbol{k}}}_c $$

(1)

where the components are $x_i = r\cos \alpha_i + l_i \cos \left( {\alpha_i - \theta_i } \right)$, $y_i = r\sin \alpha_i + l_i \sin \left( {\alpha_i - \theta_i } \right)$, $z_i = 0$, respectively.

Then, the kinetic energy of the multi-tethered system can be written as [10]:

$$ T = \frac{1}{2}\left[ {J_c \left( {{\Omega } + \omega } \right)^2 + m_c {{\boldsymbol{v}}}_c^2 + \mathop \sum \limits_{i = 1}^n m_i \left( {{{\boldsymbol{v}}}_c + {{\boldsymbol{v}}}_i } \right)^2 } \right] $$

(2)

where $J_c$ is the rotational inertia of the parent satellite and $\omega = {\dot{\alpha }}_i$ represents its spin rate; ${{\boldsymbol{v}}}_c$ is the orbital velocity vector of the system and has the form ${{\boldsymbol{v}}}_c = {{\boldsymbol{\varOmega}}} \times {{\boldsymbol{R}}}_c$, where vector ${{\boldsymbol{R}}}_c$ goes from the center of the Earth to the center of the parent satellite; ${{\boldsymbol{v}}}_i$ represents the relative velocity vector of the i-th sub-satellite to the parent body and can be written in the form ${{\boldsymbol{v}}}_i = {\dot{\boldsymbol{p}}}_i + {{\boldsymbol{\varOmega}}} \times {{\boldsymbol{p}}}_i$.

The gravitational potential energy of the system can be expressed as:

$$ V = - \mu \left( {\frac{m_c }{{\left| {{{\boldsymbol{R}}}_c } \right|}} + \sum_{i = 1}^n {\frac{m_i }{{\left| {{{\boldsymbol{R}}}_c + {{\boldsymbol{p}}}_i } \right|}}} } \right) $$

(3)

where $\mu$ is the geocentric gravitational constant.

By substituting Eqs. (2) and (3) into Lagrange’s equations, one can obtain the equations of rotational deployment motion of the system in terms of generalized coordinates $\alpha_i$, $\theta_i$, $l_i$, which can be written in the following form by employing nondimensional time $\tau = \Omega t$:

$$ \begin{aligned} \left[ {J_c + \sum_{i = 1}^n {m_i } \left( {r^2 + l_i^2 + 2l_i rcos\theta_i } \right)} \right]\ddot \alpha _i - \sum_{i = 1}^n {m_i } \left( {l_i^2 + l_i rcos\theta_i } \right)\ddot \theta _i \\ & \quad \\- \sum_{i = 1}^n {m_i } rsin\theta_i \ddot l_i + \sum_{i = 1}^n {m_i } \left[ {2\dot{l}_i \left( {\dot{\alpha }_i - \dot{\theta }_i + 1} \right)\left( {l_i + rcos\theta_i } \right) - rl_i \dot{\theta }_i \left( {2\dot{\alpha }_i - \dot{\theta }_i + 2} \right)sin\theta_i } \right] \\ \ & \quad \\ + d_{\alpha_i } = \frac{{Q_{\alpha_i } }}{{{\Omega }^2 }} \\ \end{aligned} $$

(4-1)

$$ \ddot \theta _i - \left( {1 + \frac{r}{l_i }\cos \theta_i } \right)\ddot \alpha ^- 2\frac{{\dot{l}_i }}{l_i }\left( {\dot{\alpha }_i - \dot{\theta }_i + 1} \right) + \frac{r}{l_i }\sin \theta_i \left( {\dot{\alpha }_i^2 + 2\dot{\alpha }_i } \right) + d_{\theta_i } = \frac{{Q_{\theta_i } }}{{m_i {\Omega }^2 l_i^2 }} $$

(4-2)

$$ \ddot l_i - r\sin \theta_i \ddot {\alpha }_i - l_i \left[ {\left( {\dot{\alpha }_i - \dot{\theta }_i + 1} \right)^2 - 1} \right] - r\cos \theta_i \left( {\dot{\alpha }_i^2 + 2\dot{\alpha }_i } \right) + d_{l_i } = \frac{{Q_{l_i } }}{{m_i {\Omega }^2 }} $$

(4-3)

where $Q_{\alpha_i }$, $Q_{\theta_i }$, $Q_{l_i }$ are generalized forces; $d_{\alpha_i }$, $d_{\theta_i }$ and $d_{l_i }$ are periodic gravitational perturbation terms caused by the spinning of parent satellite and have the following forms:

$$ d_{\alpha_i } = 3\sum_{i = 1}^n {m_i } \left[ {\frac{1}{2}r^2 \sin 2\alpha_i + \frac{1}{2}l_i^2 \sin \left( {2\alpha_i - 2\theta_i } \right) + rl_i \sin \left( {2\alpha_i - \theta_i } \right)} \right] $$

(5-1)

$$ d_{\theta_i } = - 3\left[ {\frac{1}{2}\sin \left( {\alpha_i - \theta_i } \right) + \frac{r}{l_i }\cos \alpha_i \sin \left( {\alpha_i - \theta_i } \right)} \right] $$

(5-2)

$$ d_{l_i } = - 3\left[ {l_i {\text{cos}}^2 \left( {\alpha_i - \theta_i } \right) + r\cos \alpha_i \cos \left( {\alpha_i - \theta_i } \right)} \right] $$

(5-3)

3 Deployment Control

The main intention of this work is to employ effective control to make sure that the multi-tethered system can be successfully deployed and ends up in an expected stable hub-spoke configuration. In other words, when the tethers are fully deployed, the motion of the system at the final time $t_f$ should satisfy the following conditions: $\ddot{\alpha }_i \left( {t_f } \right) = 0$, $\dot{\alpha }_i \left( {t_f } \right) = const$, $\dot{\theta }_i \left( {t_f } \right) = 0$, $\theta_i \left( {t_f } \right) = const < {\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 2}}\right.\kern-0pt}\!\lower0.7ex\hbox{$2$}}$, $\ddot l_i \left( {t_f } \right) = \dot{l}_i \left( {t_f } \right) = 0$ and $l_i \left( {t_f } \right) = l_d$ (the desired length of tethers).

3.1 Problem Description

It is assumed that tether deployment begins from a stable initial state, that is, at the initial moment the sub-satellites are tightly connected to the parent body and the whole system spins stably in the orbital plane along the symmetry axis of the configuration. Later, the sub-satellites are arranged around the parent body as the tethers are released out, and it is expected that the spin rate of the fully deployed system remains the same as the initial spin rate, which may be achieved using tangential thrusters installed on the parent satellite. Therefore, to cope with the deployment control problem, the motion of the system can be divided into several steps:(i) maintain the initial spin rate of the parent satellite via active torque, while at the same time, tether deployment is seen as perturbations on the motion of the parent body; (ii) develop effective control upon tether deployment using tether tensions and thrusts, assuming that the spinning motion of parent satellite is known and stable; (iii) verify the validity of the proposed controllers in the complete coupled dynamic model shown in Eqs. (4).

Following the above concept of controller design, first of all, the control torque acting on the parent satellite is given by:

$$ F_c = r\left[ {k_\omega \left( {\dot{\alpha } - \omega_\alpha } \right) + k_\alpha \left( {\alpha - \omega_\alpha \cdot \tau } \right)} \right] $$

(6)

where $k_\omega$ and $k_\alpha$ are parameters of the control law; $\omega_\alpha$ denotes the initial spin rate of the parent satellite.

Then, the dominant effort could be shifted to the deployment controller design of the tethers, while both the orbital motion of the parent satellite and its spinning motion are considered stable under the proposed torque. Decoupling the spin acceleration of the parent satellite, Eqs. (4) can be simplified as:

$$ \ddot \theta _i - 2\frac{{\dot{l}_i }}{l_i }\left( {\omega_\alpha - \dot{\theta }_i + 1} \right) + \frac{r}{l_i }\sin \theta_i \left( {\omega_\alpha^2 + 2\omega_\alpha } \right) + d_{\theta_i } = \frac{{Q_{\theta_i } }}{{m_i {\Omega }^2 l_i^2 }} $$

(7-1)

$$ \ddot l_i - l_i \left[ {\left( {\omega_\alpha - \dot{\theta }_i + 1} \right)^2 - 1} \right] - r\cos \theta_i \left( {\omega_\alpha^2 + 2\omega_\alpha } \right) + d_{l_i } = \frac{{Q_{l_i } }}{{m_i {\Omega }^2 }} $$

(7-2)

Because the values of the perturbation terms $d_{\theta_i }$ and $d_{l_i }$ are always small, it is reasonable to neglect them in the following controller design procedure.

3.2 Optimal Controller Design

Tether deployment control is assumed to be achieved via tether tensions and thrust forces. The directions of the tether tensions ${{\boldsymbol{T}}}_i$ and thrust forces ${{\boldsymbol{F}}}_i$ acting on the sub-satellites are along and perpendicular to each tether, respectively, as shown in Fig. 1. Thus, the generalized forces $Q_{\theta_i }$, $Q_{l_i }$ in Eqs. (7) can be determined by the principle of virtual work: $Q_{\theta_i } = - F_i l_i$ and $Q_{l_i } = - T_i$. And the nominal values of tether tensions and thrusts can be calculated by substituting the conditions at the final time $t_f$ into Eqs. (7): $F_{{\text{nom}}} = 0$ and $T_{{\text{nom}}} = m_i {\Omega }^2 \left( {l_d + r} \right)\left( {\omega_\alpha^2 + 2\omega_\alpha } \right)$.

Notice that the nonlinear equations for each tether length and libration angle are in the same form. For the sake of brevity and without loss of generality, the subscript i may be omitted in the controller design. Define the system state vector as ${{\boldsymbol{x}}} = \left( {x_1 {, }x_2 {,} x_3 {,} x_4 } \right)^{\text{T}} = \left( {\theta {,} \dot{\theta }{, }l{,} \dot{l}} \right)^{\text{T}}$, Eqs. (7) can be rewritten as:

$$ \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\dot{x}_1 = x_2 } \\ {\dot{x}_2 = 2\frac{x_4 }{{x_3 }}\left( {\omega_\alpha - x_2 + 1} \right) - \frac{r}{x_3 }\sin x_1 \left( {\omega_\alpha^2 + 2\omega_\alpha } \right) - \frac{F}{{m{\Omega }^2 x_3 }}} \\ \end{array} } \\ {\begin{array}{*{20}c} {\dot{x}_3 = x_4 } \\ {\dot{x}_4 = x_3 \left[ {\left( {\omega_\alpha - x_2 + 1} \right)^2 - 1} \right] + r\cos x_1 \left( {\omega_\alpha^2 + 2\omega_\alpha } \right) - \frac{T}{{m{\Omega }^2 }}} \\ \end{array} } \\ \end{array} } \right. $$

(8)

Equation (8) can be expressed as a general form:

$$ \frac{{d{{\boldsymbol{x}}}}}{d\tau } = f\left( {{{\boldsymbol{x}}},{{\boldsymbol{u}}}\left( \tau \right)} \right) $$

(9)

where $f\left( {{{\boldsymbol{x}}},{{\boldsymbol{u}}}\left( \tau \right)} \right)$ is the dynamic function of the system and ${{\boldsymbol{u}}}\left( \tau \right)$ is the control function.

Then, the linearized system of Eq. (9) near the final state ${{\boldsymbol{x}}}_d = \left( {0{,} 0{,} l_d {,} 0} \right)^{\text{T}}$ is obtained as:

$$ \frac{{d{{\boldsymbol{y}}}}}{d\tau } = {{\boldsymbol{Ay}}} + {{\boldsymbol{B}}}{\Delta }{{\boldsymbol{u}}} $$

(10)

where ${{\boldsymbol{y}}} = {\Delta }{{\boldsymbol{x}}} = {{\boldsymbol{x}}} - {{\boldsymbol{x}}}_{{\boldsymbol{d}}}$; ${\Delta }{{\boldsymbol{u}}} = \left[ {{\Delta }F,{\Delta }T} \right]^{\text{T}}$ represent control amendments relative to the nominal values; ${{\boldsymbol{A}}}$ and ${{\boldsymbol{B}}}$ are parameter matrices of the linearized system and have the forms:

$$ {{\boldsymbol{A}}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & 1 \\ {A_{21} } & {A_{22} } \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 \\ {A_{23} } & {A_{24} } \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & 0 \\ {A_{41} } & {A_{42} } \\ \end{array} } & {\begin{array}{*{20}c} 0 & 1 \\ {A_{43} } & {A_{44} } \\ \end{array} } \\ \end{array} } \right]{,}{\boldsymbol{ B}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & 0 \\ { - \frac{1}{{m{\Omega }^2 x_3 }}} & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} { 0} & { 1} \\ { 0} & { - \frac{1}{{m{\Omega }^2 }}} \\ \end{array} } \\ \end{array} } \right] $$

(11)

where the components are: $A_{2j} = \frac{{\partial f_2 \left( {{\boldsymbol{x}}} \right)}}{\partial x_j }$ and $A_{4j} = \frac{{\partial f_4 \left( {{\boldsymbol{x}}} \right)}}{\partial x_j }$, $j = 1{,} 2{,} \ldots {,} 4$.

The optimal control problem of the linearized system can be solved based on the theory of Bellman dynamic programming [3]. The performance index is given by a quadratic function:

$$ J = \mathop \smallint \limits_0^{t_f } \left( {y^{\text{T}} {{\boldsymbol{E}}}y + c{\Delta }{{\boldsymbol{u}}}^2 } \right) $$

(12)

where ${{\boldsymbol{E}}}$ is a positive definite matrix, and $c > 0$ represents the weighting coefficient.

According to Eq. (10) and the optimal criterion shown in Eq. (12), the Hamilton–Jacobi-Bellman (HJB) equation can be written as:

$$ \mathop {\min }\limits_u \left[ {y^{\text{T}} {{\boldsymbol{E}}}y + c{\Delta }{{\boldsymbol{u}}}^2 + \frac{\partial v\left( y \right)}{{\partial y}}\left( {{{\boldsymbol{Ay}}} + {{\boldsymbol{B}}}{\Delta }{{\boldsymbol{u}}}} \right)} \right] = 0 $$

(13)

where $v\left( y \right)$ is a value function and can be represented by $v\left( y \right) = y^{\text{T}} {{\boldsymbol{P}}}y$, and ${{\boldsymbol{P}}}$ is a symmetric matrix. Then, the optimal solution of Eq. (13) can be expressed as:

$$ {\Delta }{{\boldsymbol{u}}}^* = - \frac{1}{c}{{\boldsymbol{B}}}^{\text{T}} {{\boldsymbol{Py}}} = - {{\boldsymbol{Ky}}} $$

(14)

where ${{\boldsymbol{K}}}$ is the parameter matrix of the optimal solution. After substituting the expression of ${\Delta }{{\boldsymbol{u}}}^*$ into the HJB equation, one obtains:

$$ {{\boldsymbol{PA}}} + {{\boldsymbol{A}}}^{\text{T}} {{\boldsymbol{P}}} - \frac{1}{c}{{\boldsymbol{PBB}}}^{\text{T}} {{\boldsymbol{P}}} + {{\boldsymbol{E}}} = 0 $$

(15)

Once the matrix ${{\boldsymbol{P}}}$ is determined by Eq. (15), the parameter matrix ${{\boldsymbol{K}}}$ of the optimal solution is then obtained. Eventually, the control input vector of the system is:

$$ {{\boldsymbol{u}}} = {{\boldsymbol{u}}}_{{\text{nom}}} + {\Delta }{{\boldsymbol{u}}}^* $$

(16)

where ${{\boldsymbol{u}}}_{{\text{nom}}} = \left[ {F_{{\text{nom}}} {,} T_{{\text{nom}}} } \right]^{\text{T}}$.

Considering the physical constraints of tether tensions, the control tension is modified as follows:

$$ T = \left\{ {\begin{array}{*{20}c} {T_{{\text{nom}}} + {\Delta }T{,}} & {{\text{if}} T_{{\text{nom}}} + {\Delta }T > T_{{\text{min}}} } \\ {T_{{\text{min}}} {,}} & {{\text{if}} T_{{\text{nom}}} + {\Delta }T \le T_{{\text{min}}} } \\ \end{array} } \right. $$

(17)

where $T_{{\text{min}}}$ is the minimum value of tether tension that keeps tethers taut.

4 Numerical Simulations and Discussions

Numerical simulations are performed in this section to validate the effectiveness of the optimal deployment controller using the complete dynamic model of the multi-tethered satellite system.

4.1 Simulation Parameters

The system parameters are shown in Table 1. The initial spin rate of the system is set to be 100 times faster than its orbital angular velocity. And the initial values of libration angle and tether length are: ${{\boldsymbol{x}}}_0 = \left( {\theta_0 {,} \dot{\theta }_0 {,} l_0 {,} \dot{l}_0 } \right)^{\text{T}} = \left[ {0{,} 0{,} 1{,} 0.1} \right]^{\text{T}}$.

Table 1 The system parameters

The parameters of the active torque that controls the spinning of parent satellite are: $k_\omega = 100$ and $k_\alpha = 1$. The matrix ${{\boldsymbol{E}}}$ for optimal criterion is chosen as: ${{\boldsymbol{E}}} = {\text{diag}}\left[ 100,1000,0.1,1 \right]$ and the weighting coefficient is $c = 1$. Knowing the parameters of optimal criterion and the system parameters listed in Table 1, the feedback parameters of the optimal deployment controller are calculated as:

$$ {{\boldsymbol{K}}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - 9.8990} & { - 31.6236} \\ { - 0.0403} & {0.1043} \\ \end{array} } & {\begin{array}{*{20}c} {0.0013} & {0.0010} \\ { - 0.4335} & { - 1.0000} \\ \end{array} } \\ \end{array} } \right] $$

4.2 Simulation Results

The simulation results are shown in the following figures. And it should be noted that the time scale in the simulation results is represented by true anomaly.

Figure 2 demonstrates the changes in the spin angle ($\alpha$) of the parent satellite, tether length ($l$) and libration angle ($\theta$) of the tether. The corresponding change rates of the variables are shown in Fig. 3.

Fig. 2

The changes in the system states

Fig. 3

The change rates of the system states

It can be seen that the spin angle of the parent satellite steadily increases during tether deployment. The spin rate of the parent body decreases slightly in the initial phase because of the release of tethers, and then the spin rate returns to its initial value and remains almost unchanged during the post-deployment process, which means that the spinning motion of the parent satellite is stable under the control torque. In addition, as shown in Figs. 2 and 3, the tether is successfully deployed to the desired final length (100 m), and during this process its libration angle is close to zero, which ensures that there is no risk of tether entanglement around the parent satellite.

The control torque acting on the parent satellite and the control forces on the sub-satellite are shown in Fig. 4. The control torque $F_c$ and thrust force $F$ eventually converge to zero, while the tether tension $T$ stabilizes at a constant (10.22 N), which is almost equal to the nominal value $T_{{\text{nom}}}$. However, it is worth noting that the curves of control torque and control forces fluctuate slightly in the post-deployment phase, which is due to the inherent periodic perturbance terms in the coupled dynamic model of the system.

Fig. 4

The control torque and control forces

Figure 5 depicts the deployment trajectory of the sub-satellite in Cxy plane of the orbital coordinate frame. It can be seen that the trajectory in the initial stage is sparser than that of the final stage, which suggests that the tether is deployed at a relatively faster speed in the initial stage, which is consistent with the change rate of tether length, as shown in Fig. 3.

Fig. 5

The trajectory of the sub-satellite

5 Conclusions

The present work studies the deployment control of a spinning multi-tethered satellite formation system in the orbital plane. Considering the dimensions of the parent satellite, an active control law is proposed to stabilize the spinning motion of parent body during tether deployment. Then, the optimal deployment controller is obtained by solving the HJB equation. Finally, numerical studies are presented to illustrate the effectiveness of the proposed control strategy in the complete coupled dynamic model. That is, the formation system ends up in a hub-spoke configuration, and during this process the spin rate of the parent satellite remains nearly constant, while the tethers are stably deployed to the desired final length without entangling with the parent satellite.