Nonsmooth modal analysis of an elastic bar subject to a unilateral contact constraint

Abstract

This contribution proposes a numerical procedure capable of performing nonsmooth modal analysis (mode shapes and corresponding frequencies) of the autonomous wave equation defined on a finite one-dimensional domain with one end subject to a Dirichlet condition and the other end subject to a frictionless time-independent unilateral contact condition. Nonsmooth modes of vibration are defined as one-parameter continuous families of nonsmooth periodic orbits satisfying the local equation together with the linear and nonlinear boundary conditions. The analysis is performed using the wave finite element method, which is a shock-capturing finite volume method. As opposed to the traditional finite element method with time-stepping schemes, potentially discontinuous deformation, stress and velocity wave fronts induced by the unilateral contact condition are here accurately described, which is critical for seeking periodic orbits. Additionally, the proposed strategy introduces neither numerical dispersion nor artificial dissipation of energy, as required for modal analysis. As a consequence of the mixed time–space discretization, no impact law is needed for the well-posedness of the problem in line with the continuous framework. The frequency–energy dependency nonlinear spectrum of vibration, shown in the form of backbone curves, provides valuable insight on the dynamics. In contrast to the linear system (without the unilateral contact condition) whose modes of vibration are standing harmonic waves, the nonsmooth modes of vibrations are traveling waves stemming from the unilateral contact condition. It is also shown that the vibratory resonances of the periodically driven system with light structural damping are well predicted by nonsmooth modal analysis. Furthermore, the initially unstressed and prestressed configurations exhibit stiffening and softening behaviors, respectively, as expected.

1 Introduction

Many industrial applications require the appropriate prediction of the dynamics of colliding elastic bodies in their design process [1]. Through unilateral contact forces preventing inter-penetration of matter, a collision initiates a disturbance in the form of a stress wave. Analytical solutions to the initial value problem are only known for simple cases such as longitudinal collision of rods or transverse contact of beams [2]. For more general configurations, the solution should be approximated numerically. However, common numerical methods, such as finite element methods (FEMs) combined with time-stepping schemes, exhibit limitations that might be unacceptable [3,4,5]: spurious oscillations commonly known as Gibb’s phenomenon, dispersion and dissipation errors or chattering when constitutive impact laws are implemented. Also, most energy-preserving numerical schemes dedicated to contact dynamics feature numerical dispersion issues [6].

In the framework of undamped linear continuous systems, natural modes of vibration are characterized by their natural frequencies (eigenvalues) and normalized shapes (eigenfunctions) [7]. In the phase space, linear modes can be seen as continuous families of periodic orbits describing two-dimensional planes. For nonlinear dynamical systems, the natural modes of vibration are known to form two-dimensional manifolds in the phase space tangent to the previously mentioned planes at equilibrium points [8]. These manifolds are invariant, i.e., for any initial condition on the manifold, the solution will remain on it as time advances [9]. Additionally, the nonlinear natural frequency of an orbit depends on the total energy of the latter.

Most investigations and developments on nonlinear modal analysis, conventionally within a finite-dimensional framework or equivalent, have dealt with smooth nonlinearities [8], i.e., nonlinear terms differentiable with respect to the unknown of the problem, mostly polynomial functions of the displacement and velocity. The continuous mechanical system investigated in this contribution involves a unilateral contact condition stricto sensu. As a consequence, displacements, velocities and accelerations are not differentiable with respect to time and space in the usual sense. Such systems are named nonsmooth systems [10]. Classical tools of nonlinear modal analysis rely on smoothness and thus no longer apply. Accordingly, “nonlinear normal modes” (NNMs) of vibration for nonsmooth systems will be referred to as nonsmooth modes (NSMs), defined as one-parameter continuous families of periodic nonsmooth orbits.

The common method to approximate solutions of continuous systems described by partial differential equations is to first obtain, through a semi-discretization in space, a finite-dimensional nonlinear ordinary differential equation solely depending on time. Unilateral constraints can then be incorporated via regularization to enable the use of classical nonlinear modal analysis [11,12,13,14,15,16,17]; the main issue lies in the high computational effort induced by the contact stiffness. Another strategy consists in preserving the nonsmooth nature of the system. It can be handled via appropriate time-stepping nonsmooth numerical schemes [18] or semi-analytic derivations [19, 20] involving energy-preserving impact laws. A few closed-form solutions in the form of periodic shock waves of an elastic string vibrating against a point obstacle are reported using the method of characteristic lines [21, 22]. This string system shares similarities with the bar considered in the present work for which a single continuous family of periodic solutions was exhibited through analytical considerations [23]. In the remainder, this family will be shown to form the first NSM of the system. The current work proposes an approach to numerically approximate any NSM.

By definition of NSMs, their computation relies on periodicity: the state of the system at time $t_0$ must be recovered at some $t_0+T$ where T is the period, requiring numerical methods that preserve total energy and are not prone to numerical dispersion. A considerable amount of research has been devoted to this topic with limited success [6, 24, 25]. In the present work, the wave finite element method (WFEM) [26] is implemented in order to numerically approximate the modes of vibration of a one-dimensional finite elastic bar subject to frictionless unilateral contact constraints. The WFEM is a shock-capturing method—similar to the Godunov method [27] commonly used in computation fluid dynamics—which consists in finding and tracking waves propagating in a mechanical system. Such shock waves are expected because of the unilateral contact condition. The proposed method does not introduce artificial dissipation of energy nor numerical dispersion [26, 28]. Multidimensional problems incorporating contact conditions are not targeted in this work due to the expected intricate interaction of compressional and shear waves.

The paper is organized as follows. The one-dimensional system of interest is outlined in Sect. 2, where three different configurations are detailed: unstressed, prestressed and statically grazing. The capability of the WFEM to handle unilateral contact dynamics is illustrated in Sect. 3 through a benchmark problem offering an exact solution. The overall strategy capable of performing nonsmooth modal analysis is described in Sects. 4 and  5. The approximate nonsmooth modes are then characterized in Sect. 6. Comparison with periodically forced responses is undertaken in Sect. 7. The implementation of WFEM is thoroughly detailed in “Appendix A” for a one-dimensional problem. The enforcement of contact constraints within WFEM is explained in “Appendix B”.

Fig. 1

One-dimensional finite elastic bar subject to unilateral contact constraints

2 System of interest

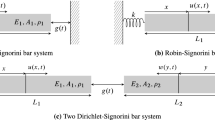
The system of interest is a homogeneous elastic bar of length L and constant cross-sectional area S rigidly fixed to the ground at its left end whose right end is subject to a conservative unilateral constraint as shown in Fig. 1. Within the framework of infinitely small transformations, the unknown displacement, velocity, strain and stress fields are denoted by u(x, t), v(x, t), $\varepsilon (x,t)$ and $\sigma (x,t)$, respectively, where $x\in \mathopen {[}0\,;L\mathclose {]}$ is the coordinate of a point of the bar along its longitudinal axis in the initial configuration and t denotes time. The quantity r(t) is the unilateral contact force emerging at $x=L$. The mass per unit volume is denoted by $\rho >0$, and $E>0$ stands for Young’s modulus which are both by assumption, space and time independent. Any elastic wave traveling within the bar thus propagates at constant velocity $c=\sqrt{E/\rho }$. The signed distance between the right end of the bar and the obstacle, or gap function, is defined as $g(u(L,t))=g_0-u(L,t)$, where $g_0$ is the signed distance between the unconstrained resting position and the obstacle. In linear elasticity, the stresses read $\sigma =E \varepsilon$ where the axial strains $\varepsilon =u_{,x}$ should be physically admissible, that is $u_{,x}>-1$. Stresses are related to the contact force by $\sigma (L,t)=E u_{,x}(L,t)=r(t)/S$. Unless stated otherwise, there is no other external force acting on the system, either per unit length or pointwise at the boundary. The full formulation reads:

• Local equation:

  $$\begin{aligned} \rho u_{,tt} - E u _{,xx} = 0, \quad \forall x\in \mathopen {]}0\,;L\mathclose {[},\quad \forall t > 0 \end{aligned}$$

  (1)

  where $(\bullet )_{,tt}$ stands for the second derivative in time and $(\bullet )_{,xx}$ for the second derivative in space.

• Homogeneous fixed (Dirichlet) boundary condition (BC) at $x=0$ and $\forall t > 0$:

  $$\begin{aligned} u(0,t)=0 \end{aligned}$$

  (2)

• Signorini complementarity condition at $x=L$ and $\forall t > 0$:

  $$\begin{aligned} g(u(L,t))\ge 0, \quad r(t)\le 0,\quad r(t)g(u(L,t))=0 \end{aligned}$$

  (3)

• Initial conditions $\forall x \in \mathopen {]}0\,;L\mathclose {[}$:

  $$\begin{aligned} u(x,0)=u_0(x), \quad v(x,0)=v_0(x) \end{aligned}$$

  (4)

  where $u_0$ and $v_0$ are prescribed functions.

This problem has a unique solution which conserves the total energy [29]. The local equation is the wave equation defined on a finite domain. D’Alembert’s exact solution is the sum of backward and forward traveling waves propagating with velocity c and reads $\forall x\in \mathopen {[}0\,;L\mathclose {]}$ and $\forall t>0$ [2]:

$$\begin{aligned} 2u(x,t)=u_0^{\star }(x\!+\!ct)+u_0^{\star }(x\!-\!ct)+\frac{1}{c}\!\int ^{x+ct}_{x-ct}\!\! v_0^{\star }(s) \mathop {}\!\mathrm {d}s \end{aligned}$$

(5)

where $u_0^{\star }$ and $v_0^{\star }$ are periodic extensions on the real axis of $u_0$ and $v_0$ defined on $\mathopen {[}0\,;L\mathclose {]}$ only. The period of $u_0^\star$ and $v_0^\star$ depends on the boundary conditions considered.

Nontrivial periodic solutions of the contact problem described by Eqs. (1)–(4) are successions of free phases (open gap) and contact phases (closed gap). They can therefore be understood as the combination of solutions to an hyperbolic partial differential equation with a switching boundary condition at $x=L$ between vanishing stress when the gap is open to prescribed displacement when the gap is closed. The nonlinearity in the formulation comes from the fact that the time of switch depends on the solution. There is also a subtlety in the BC switch at $x=L$: an open gap implies $u_{,x}(L,\cdot )=0$ while a closed gap implies a nonhomogeneous prescribed displacement of the form $u(L,\cdot )=g_0$. Accordingly, when the gap is open, BCs at $x=0$ and $x=L$ are homogeneous and will be referred to as fixed–free BCs in the remainder. For a closed gap, the BC at $x=0$ is homogeneous while the BC at $x=L$ is nonhomogeneous: they will be referred as fixed–fixed BCs.

The question is now to find the two functions $u_0$ and $v_0$ generating a time periodic state of the system which satisfies local Eq. (1) and properly switches between fixed–free and fixed–fixed BCs to comply with the unilateral contact conditions (3). This is achieved using the wave finite element method.

3 Illustration of the capabilities of WFEM

The WFEM is detailed, including a readily implementable algorithm, in “Appendices A” (the WFEM method itself) and “B” (unilateral contact conditions in WFEM). In the sequel, governing Eqs. (1)–(4) are equivalently recast in terms of stresses and velocities stacked in a state vector $\mathbf {q}$. The system is discretized simultaneously in space and time with mesh sizes $\varDelta x=L/N$ and $\varDelta t = \varDelta x/c$, respectively, where N is the number of cells used for space discretization. The overall dynamics is approximated by $\mathbf {Q}^{(n)} = \mathbf {A}\mathbf {Q}^{(n-1)}$ where $\mathbf {Q}^{(n)}=[\mathbf {Q}_1^{(n)} \ldots \mathbf {Q}_N^{(n)}]$ and $\mathbf {Q}_i^{(n)}$ stands for the averaged state $\mathbf {q}$ in cell $\mathcal {C}_i$ at time $t_n=n\varDelta t$. The matrix $\mathbf {A}$ encompasses stiffness and inertial terms as well as the appropriate boundary conditions. Two matrices are constructed: $\mathbf {A}=\mathbf {A}_\text {f}$ for free–free BCs (open gap) and $\mathbf {A}=\mathbf {A}_\text {c}$ for fixed–free BCs (closed gap).

In this section, the capabilities of the WFEM are succinctly illustrated on a unilaterally constrained linearly elastic finite bar benchmark, for which analytical solutions are known [3]. It can be compared to other time integration schemes based on a semi-discretization in space through the commonly used FEM [28]. The problem consists in an unclamped homogeneous elastic rod of length L and constant cross-sectional area S bouncing against an obstacle due to a distributed internal force, as shown in Fig. 2. Parameters reported in [3] are considered and listed in Table 1. The displacement (retrieved from stress via an integration in space), velocity, contact force and total energy are depicted for an isolated periodic solution in Fig. 3, for $N=100$ cells. Total energy and periodicity are accurately preserved, and the nonsmooth behavior is well recovered. Curves in Fig. 3 and the exact curves are undistinguishable [28]. In contrast, traditional numerical schemes dedicated to contact dynamics and commonly based on the standard FEM show spurious oscillations on the contact displacement and stress [5]. Moreover, these oscillations do not disappear when the time step decreases and might increase instead. Various solutions have been proposed to alleviate these difficulties, mainly by adapting the time-domain discretization. They all fail by either adding nonphysical damping, or not strictly respecting the contact constraint. This is partly explained by the inability of standard finite elements to properly propagate information. Also, the implementation of an impact law yields unavoidable drawbacks, such as chattering if energy conservation is targeted [4]. None of these issues are present with WFEM that produces accurate approximations with a reasonable number of cells. This can be partly explained by the fact that shock wave propagation is accurately captured by this scheme.

Fig. 2

Benchmark bouncing homogeneous elastic bar (used in Sect. 3)

Table 1 Simulation parameters for the considered benchmark, from [3]

Fig. 3

Periodic motion of the bouncing bar obtained by WFEM

4 Periodic solutions

NSMs are regarded as continuous families of periodic solutions satisfying the local equations and the boundary conditions including the unilateral contact conditions. Finding a periodic solution translates into finding initial conditions $u_0(x)$ and $v_0(x)$ and a period T which generate a solution satisfying Eqs. (1)–(4) in conjunction with the periodicity conditions

$$\begin{aligned} \left\{ \begin{aligned} \,&u(x,t+T)=u(x,t)\\&v(x,t+T)=v(x,t)\end{aligned}\right. ,\quad \forall x\in \mathopen {[}0\,;L\mathclose {]},\quad \forall t>0. \end{aligned}$$

(6)

Without loss of generality, it is assumed that a period starts with a free phase at $t=0$ and ends with a contact phase at $t=T$. In the general case, a pattern of free and contact phases will arise within one period. The k successive transition instants between free and contact phases are denoted by $T_i$ with $0<T_1<\cdots<T_{k-1}< T_k=T$ and are unknown. The sought solution is then an unknown combination of functions of the form (5) where $u_0^\star$ and $v_0^\star$ switch between fixed–free BCs over $\mathopen {[}0\,;T_1\mathclose {]}$, $\mathopen {[}T_2\,;T_3\mathclose {]}$, etc. and fixed–fixed BCs over $\mathopen {[}T_1\,;T_2\mathclose {]}$, $\mathopen {[}T_3\,;T_4\mathclose {]}$, etc., which must be periodic in time. Connecting these portions of D’Alembert solutions in order to form a periodic solution is quite a formidable task.

The WFEM approximately solves the above problem by building two matrices, $\mathbf {A}_{\text {f}}$ for the fixed–free BC and $\mathbf {A}_{\text {c}}$ for the fixed–fixed BC, so that mapping an initial state to the current state after a succession of free and contact phases is straightforward via Eq. (40). In contrast to more commonly used time integration schemes based on FEM, the WFEM perfectly preserves energy (in this one-dimensional configuration at least), which is crucial for the computation of periodic solutions. Additionally, for the problem at hand, this scheme is not prone to numerical dispersion and does not suffer from the well-known Gibb’s phenomenon commonly observed in unilateral contact dynamics [3].

The FEM framework without regularization of the complementarity conditions in continuous time is used for the calculation of nonsmooth modes in [19, 20, 30]. However, the formulation relies on a space discretization and hence requires the incorporation of an impact law—for instance, Newton’s impact law—to ensure the well-posedness of the problem. Since energy conservation is necessary to find nonsmooth modes, a perfectly elastic impact law should be considered, from which would emanate impulsive dynamics and chattering. This excludes periodic motions with “lasting” nonimpulsive contact phases similar to those of the periodically bouncing elastic bar exposed earlier. “Lasting” contact phases can only be obtained with a dissipative inelastic impact law. By simultaneously discretizing the governing equations in space and time in accordance with the characteristic lines, the WFEM accurately propagates shock waves. This probably explains why no impact law is needed in this framework; however, the authors are not aware of a formal proof of this assertion.

5 Nonsmooth modal analysis

Nonsmooth modal analysis characterizes vibratory mechanical systems with nonsmooth nonlinearities [18, 19, 30] by searching for one-parameter continuous families of periodic trajectories forming manifolds in the phase space. In this work, the targeted solutions are assumed to comprise free phases (open gap) as well as contact phases (closed gap), as described in Sect. 4. An example of an admissible periodic solution with two free phases and two contact phases is depicted in Fig. 4.

Fig. 4

Admissible periodic bar end displacement with closed and open gap switches

5.1 Problem formulation

As stated previously, the motion is uniquely determined by the initial conditions. The aim is to find such initial conditions which generate a periodic motion in the spirit of shooting methods [31]. If such periodic solutions exist, the formulation reduces to finding their period T and the appropriate initial conditions satisfying

$$\begin{aligned} \mathbf {q}(x,T) = \mathbf {q}(x,0),\quad \forall x \in \mathopen {[}0\,;L\mathclose {]}. \end{aligned}$$

(7)

In the discrete setting of the WFEM, this reduces to finding $n_T$ and the vector of initial conditions $\mathbf {Q}^{(0)}$ such that $\mathbf {Q}^{(n_T)} = \mathbf {Q}^{(0)}$ where $n_T$ is the number of steps required to cover the period T. In their simplest incarnation, the sought periodic solutions are only composed of one free phase and one contact phase per period¹ even though more complicated patterns are expected to exist. Accordingly, the solution is assumed to be in open contact (free phase) for m consecutive steps and in closed contact (contact phase) for p consecutive steps. Invoking Eq. (40), the state of the system after $n_T=m+p$ time steps emanating from initial state $\mathbf {Q}^{(0)}$ reads

$$\begin{aligned} \mathbf {Q}^{(n_T)}=\mathbf {A}_\text {c}^{p}\mathbf {A}_\text {f}^{m}\mathbf {Q}^{(0)}, \end{aligned}$$

(8)

with the origin of time taken at the beginning of the free phase. Both matrices $\mathbf {A}_\mathrm {c}$ and $\mathbf {A}_\mathrm {f}$ are known, see “Appendix A”. The duration of free and contact phases corresponding to periodic motions is not known a priori, so the integers m and p leading to acceptable solutions are unknowns of the problem. By enforcing the periodicity conditions, Eq. (8) simplifies to

$$\begin{aligned} (\mathbf {A}_\text {c}^{p}\mathbf {A}_\text {f}^{m}-\mathbf {I})\mathbf {Q}^{(0)}=\mathbf {0}. \end{aligned}$$

(9)

An initial condition $\mathbf {Q}^{(0)}$ satisfying Eq. (9) is called a potential solution for given p and m. Indeed, potential solutions may not be actual solutions of the initial problem: nothing prevents them from penetrating the rigid foundation during free phase and/or the corresponding contact force could be nonnegative: these conditions cannot be enforced in Eq. (9). Consequently, potential solutions are called admissible solutions if they satisfy the following additional conditions:

COND1 :

Free phase: $u_{N+1/2}^{(n)}\leqslant g_0$ and $r^{(n)}=0$ for $n=0, 1, \ldots , m$.

COND2 :

Contact phase: $u_{N+1/2}^{(n)} = g_0$ and $r^{(n)} \leqslant 0$ for $n=m+1, m+2, \ldots , m+p$.

COND3 :

Material impenetrability: $\varepsilon ^{(n)}_i > -1$ for $n=0, 1, \ldots , m+p$ and $i=1,\ldots ,N$.

where $u_{N+1/2}^{(n)}\approx u(L,T)$ and $\varepsilon ^{(n)}_i$ is the discretized strain field, both retrieved from discretized stresses. To summarize, periodic solutions satisfying contact conditions are obtained by solving the problem: Find $m \in \mathbb {N}^*$, $p \in \mathbb {N}^*$, and initial condition $\mathbf {Q}^{(0)}\in \mathbb {R}^{2N}$ such that Eq. (9) together with COND1, COND2 and COND3 is simultaneously satisfied.

5.2 Solution procedure

For specified m and p, a periodic motion necessarily corresponds to an initial condition which is in the kernel of the operator $\mathbf {S}_{T}=\mathbf {A}_\text {c}^{p}\mathbf {A}_\text {f}^{m} - \mathbf {I}$ as highlighted in Eq. (9), that is $\mathbf {Q}^{(0)} \in \ker \mathbf {S}_{T}$. The dimension h of $\ker \mathbf {S}_{T}$ depends on the doublet (m, p). A nontrivial solution may exist only if $h>0$. If $h>0$ and $\{\mathbf {e}_1,\mathbf {e}_2,\ldots ,\mathbf {e}_h \}$ is a basis of $\ker \mathbf {S}_{T}$, then $\mathbf {Q}^{(0)} = \alpha _1 \mathbf {e}_1 + \alpha _2 \mathbf {e}_2 + \ldots + \alpha _h \mathbf {e}_h$ for some $\alpha _1, \alpha _2,\ldots ,\alpha _h$. The state $\mathbf {Q}^{(n)}$ is completely determined by $\mathbf {Q}^{(0)}$ via Eq. (46). Accordingly, $\mathbf {Q}^{(n)}$ can be expressed in terms of the coefficients $\alpha _1, \alpha _2,\ldots ,\alpha _h$ only and it suffices to find appropriate values such that COND1, COND2 and COND3 are satisfied.

Finding m, p such that $h>0$ is achieved by systematically computing h for every combination of m and p within a given range. Once an admissible solution is known, other admissible solutions can be straightforwardly found in its vicinity. As soon as a family of periodic orbits—involving one contact phase and one free phase—emerges, it defines a nonsmooth mode of vibration.

6 Results and discussion

Nonsmooth modes of vibration of the system described in Sect. 2 are now constructed. The parameters E, $\rho$ and L are arbitrarily chosen to be unity and units are discarded. The results are obtained for 1000 cells and time step is calculated accordingly, i.e., $\varDelta t=\varDelta x/c = 1/{1000}$.

In the linear framework (that is without the contact conditions), linear natural frequencies of vibration denoted $\omega _k$ for fixed–free boundary conditions and $\varOmega _k$ for fixed–fixed boundary conditions are

$$\begin{aligned} \begin{aligned}&\omega _k=\frac{(2k-1)\pi c}{2L}=(2k-1)\omega _1,\quad k\in \mathbb {N}^* \\&\varOmega _k=\frac{k\pi c}{L}=k\varOmega _1,\quad k\in \mathbb {N}^*. \end{aligned} \end{aligned}$$

(10)

It is expected that the slightly damped linear system under consideration periodically forced in a neighborhood of these frequencies will resonate. Conversely, in the nonlinear framework (that is with contact conditions), such frequencies do not have the same physical interpretation anymore: the nonlinear system will resonate close to other unknown frequencies which are calculated by the nonsmooth modal analysis, for a given level of energy. The nonlinear system can also feature internal resonances where two or more NSMs interact [32]; for instance, driving the system in the neighborhood of a high-frequency NSM may activate a large amplitude low-frequency NSM [8]. Note that the system of interest satisfies a complete internal resonance condition in the sense that $\omega _k$ and $\varOmega _k$, $k=2,\ldots ,\infty$ are all multiples of $\omega _1$ and $\varOmega _1$, respectively. Moreover, a nonlinear system may exhibit subharmonic and superharmonic resonances in the vicinity of $(p\omega _k)/q$, for p, q positive integers such that $0<p/q<1$ and $1<p/q$, respectively [8].

Fig. 5

Frequency–energy plot in the range $[\omega _1,\varOmega _1]$ for $g_0>0$  , $g_0=0$  and $g_0<0$  with a few subharmonics of linear modes  . (Color figure online)

In this work, frequency–energy plots are preferably used, quoting [8]: “a nonlinear modal motion is represented by a point in such plots, which are drawn at a frequency corresponding to the minimal period of the periodic motion and at an energy equal to the conserved total energy during the periodic motion. A branch, represented by a solid line, is a family of nonlinear modal motions possessing the same qualitative features.” The terminologies “branch” and “backbone curve” are used interchangeably in the remainder. The reported frequencies are normalized with respect to $\omega _1$, and the energy is normalized with respect to the energy of the first linear mode grazing orbit satisfying

$$\begin{aligned} \max _{t\in \mathbb {R}} u(L,t)=g_0. \end{aligned}$$

(11)

When the calculated periodic solutions have one free phase and one contact phase, admissible solutions are only found when $h=1$ for various (m, p). For $h\geqslant 2$, potential solutions failed to satisfy COND1 and COND2 simultaneously and hence the distinction between potential and admissible. Admissible solutions were found only when h equals the number of contact phases. Additionally, recent developments, out of the scope of the present paper, have shown that if a periodic trajectory belongs to a continuum parameterized by T, then the displacement must be piecewise linear with respect to time and space. Thus, if a periodic solution does not satisfy this property, it is either isolated or part of a continuum of orbits sharing the same period.

A previous investigation on the first main NSM [23] showed that the duration of the contact phase $p\varDelta t$ is related linearly to the duration of free phase $m\varDelta t$ when a solution belongs to a family of periodic orbits. Numerical experiments suggest that other branches could present similar relations, which are employed to bound the range where m and p are iterated for each potential backbone curve. Once a solution is found, a point in a NSM branch is defined by the total energy of the admissible periodic motion and the respective frequency $\omega =2\pi /T$, see Fig. 5.

If the initial gap is positive $g_0>0$ (unstressed bar at rest), NSM branches arise in the vicinity of the linear natural frequencies $\omega _k$ and subharmonics $p\omega _k/q$ for $p,q\in \mathbb {N}^*$, and present a hardening behavior. For a “negative” gap $g_0<0$ (prestressed bar at rest), the NSM branches start in the vicinity of the linear natural frequencies $\varOmega _k$ and display a softening behavior. Finally, if the bar is statically grazing with the rigid foundation (grazing bar at rest, that is $g_0=0$), then the NSM branches are the vertical asymptotes common to the previous backbone curves, as shown in Figs. 5 and 6 for the first and second NSM, respectively. Internal resonance branches, explored in Sect. 6.3, are omitted in these figures. Identical results were already computed for the first main NSM only [23]. Also, a similar behavior has been observed in the frequency–energy plot of simplified discrete models for the unstressed case with penalized contact constraints [11, 12] and with a nonsmooth formulation [18].

Fig. 6

Frequency–energy plot in the range $[\omega _2,\varOmega _2]$ for $g_0>0$  , $g_0=0$  and $g_0<0$  with a few subharmonics of linear modes  . (Color figure online)

The frequency–energy dependence exhibited by NSM is a typical feature of nonlinear systems [8]. Interestingly, when $g_0=0$ the system mimics a linear behavior where the frequency and the shape of the orbits do not depend on their energy. However, the behavior remains globally nonlinear because of the BC switches.

Though the behavior and ranges of frequencies of the NSM branches depend on the sign of $g_0$, they “converge” to the branches of $g_0=0$ when $g_0\rightarrow 0$, as shown in Fig. 7 for the main NSM branch in $[\omega _1,\varOmega _1]$. In other words, there is no difference between NSMs with very small positive initial gap, zero initial gap or very small initial negative gap. Moreover, the normalized shape of the backbone curves depend only on the sign of $g_0$. Without loss of generality and for illustration purposes, $g_0=\pm \,10^{-3}$ or $g_0=0$ in the remainder.

In the following sections, a detailed study of the NSM branches is presented. It should be noted that all the results were obtained numerically. The proposed results have to be understood as conjectures.

Fig. 7

First NSM branch as a function of $g_0$. Energy is not normalized. The backbone curves for $g_0>0$  and $g_0<0$  slowly “approach” the backbone curve for $g_0=0$  when $g_0\rightarrow 0$. (Color figure online)

6.1 Main backbone curves

The main backbone curves are defined as the NSM branches, in the frequency–energy plot, starting in the vicinity of:

• $\omega _k$, the k-th linear natural frequency for fixed–free BC, for positive initial gap $g_0>0$,

• $\varOmega _k$, the k-th linear natural frequency for fixed–fixed BC, for negative initial gap $g_0<0$.

• For $g_0=0$, the main backbone curve is a vertical line asymptotic to its two above counterparts. Such asymptotes are located at $\omega _1(\omega _k/\omega _1+1)^2/(\omega _k/\omega _1+2)$.

Periodic motions corresponding to the main backbone curves in the range $[\omega _1,\varOmega _1]$ are depicted in Fig. 8. Such piecewise linear displacements were already observed as isolated periodic solutions, without describing a continuum [21, 22]. However, previous numerical investigations to locate families of periodic orbits were inaccurate because of numerical dispersion stemming from the space semi-discretization [12, 18].

Fig. 8

Periodic motions on the main NSM in the range $\mathopen {[}\omega _1\,;\varOmega _1\mathclose {]}$ for one contact phase per period, corresponding to points “a”  , “b”  and “c”  in Fig 5: unstressed (top), initially grazing (center) and prestressed (bottom). (Color figure online)

A generic space–time plot of the displacement of the bar is provided in Fig. 9. The solution is the combination of interacting forward and backward traveling waves which propagate along the characteristic lines ($t=\pm \, x/c$), as opposed to the linear counterpart modal motions which are sinusoidal standing waves as shown in Fig. 10 [2].

Fig. 9

Generic space–time displacement field of the main NSM in the range $\mathopen {[}\omega _1\,;\varOmega _1\mathclose {]}$ for $g_0>0$

Fig. 10

Generic space–time displacement field of the first linear mode (linear fixed–free bar without contact constraints) at $\omega _1$

Fig. 11

Invariant manifold corresponding the main backbone curve in the vicinity of $\omega _1$ plotted in the cross section $(u_{N+1/2},v_{N+1/2},u_{3/2})$. Gray surface: Poincaré cross section $u_{N+1/2}=g_0$. Periodic orbit  . Intersections between NSM and the Poincaré cross section  . (Color figure online)

Fig. 12

Grazing displacement of the contacting end at $\omega _1$. First linear mode  and first main NSM  . (Color figure online)

Every periodic solution corresponding to the main backbone curve comprises exactly one free phase and one contact phase. For a positive as well as negative initial gap, the contact phase duration increases while the free phase duration decreases as the frequency of vibration increases. When the initial gap is zero, periodic motions have constant period equal to $T=3L/c$ and the duration of contact closure is L / c while the free phase time is 2L / c. It should also be noted that the contact force associated with all the depicted motions is piecewise constant on a period. The invariant manifold in the unstressed case is plotted in the cross section $(u_{N+1/2}, v_{N+1/2}, u_{3/2})$—i.e., (displacement of the contacting end, velocity of the contacting end, displacement of the right-hand side interface of cell $\mathcal {C}_1$)—of the state space in Fig. 11. The linear portion of the first mode corresponds to an ellipse (like essentially all linear modes). The linear and nonlinear portions of the manifold are not continuously connected because of the internal resonance property. This is visualized in Fig. 12 which shows the grazing periodic displacements for the first linear mode and first main NSM, both having frequency $\omega _1$. It should be understood that any autonomous solution of frequency $\omega _1$ shall be expressed as an infinite Fourier sequence separated in space and time of the form

$$\begin{aligned} u(x,t)=\sum ^\infty _{k=1} \sin (\omega _k x/c)(a_k\cos (\omega _k t) + b_k\sin (\omega _k t)) \end{aligned}$$

(12)

where $\omega _k=(2k-1)\pi c/(2 L)=(2k-1)\omega _1$, $k\in \mathbb {N}^*$, are the linear natural frequencies; the coefficients $a_k$ and $b_k$ are computed from the initial conditions [2] and are not of interest here. In other words, the full internal resonance condition enjoyed by the system is such that the latter exhibits infinitely many solutions of frequency $\omega _1$, the piecewise linear grazing solution being one of them. Accordingly, a discontinuity in the manifold is made possible.

The above internal resonance condition can be annihilated by changing the BC at $x=0$ from Dirichlet type to Robin type saying that the bar is attached to a spring of stiffness $\delta$ at $x=0$: $ESu_{,x}(0,t)-\delta u(0,t)=0$. The solution can still be expressed as an infinite Fourier sequence

$$\begin{aligned} u(x,t)=\sum ^\infty _{k=1} \phi _k(x)(a_k\cos (\omega _k t) + b_k\sin (\omega _k t)) \end{aligned}$$

(13)

similar to Eq. (12) with $\phi _k(x)=p_k\cos (\omega _k x\!/\!c) + \sin (\omega _k x\!/\!c)$ where $p_k=\cot (\omega _k L/c)$. The $\omega _k$ are now solutions to the transcendental equation $ES \omega =c\delta \cot (\omega L/c)$ and are no longer commensurate [7]. Assuming that the grazing solution of the first NSM has frequency $\omega _1$ (this should be proven!), it will necessarily see the sole contribution of the first linear mode, which is the only motion of frequency $\omega _1$ in sequence (13), that is:

$$\begin{aligned} u(x,t)= \phi _1(x)(a_1\cos (\omega _1 t) + b_1\sin (\omega _1 t)). \end{aligned}$$

(14)

This necessarily induces a continuous connection between linear and nonlinear grazing trajectories. To summarize, the above argument stipulates that the internal resonance condition is necessary to see a discontinuity in the modal manifold between the linear and the nonlinear portions. However, this is not a sufficient condition.

Fig. 13

Generic space–time displacement field of the main NSM in the range $\mathopen {[}\omega _2\,;\varOmega _2\mathclose {]}$. Node of vibration  . (Color figure online)

Figure 13 depicts the generic space–time plot (irrespective of $g_0$) of the second main backbone curve in the range $[\omega _2,\varOmega _2]$ showing that the periodic solutions have one “node of vibration” along x—similar to the second linear mode of the fixed–free bar [2], depicted in Fig. 14. The displacement $u(L,\cdot )$ also features one contact phase per period, by assumption. Furthermore, for $g_0=0$, the period is 5L / (4c) comprising one contact phase of duration L / (4c) and one free phase of duration L / c, irrespective of the energy of the system.

For illustration purposes, only the first two main NSMs are shown in this section. However, the presented approach can be also used to find higher frequency NSM which requires a smaller time step $\varDelta t$ and therefore higher computational effort. Periodic solutions corresponding to the main backbone curves for higher frequencies display a similar structure: one free phase, one contact phase and nodes of vibration along x.

Fig. 14

Generic space–time displacement field of the second linear mode (linear fixed–free bar without contact constraints) at $\omega _2$. Node of vibration  . (Color figure online)

Fig. 15

Periodic motions in the vicinity of $\omega _2/2=3\omega _1/2$ (top), $\omega _3/3=5\omega _1/3$ (top center), $\omega _4/4=7\omega _1/4$ (bottom center) and $\omega _4/2=7\omega _1/2$ (bottom) corresponding, respectively, to points “d,” “e,” “f” and “g” in Figs. 5 and 6

6.2 Subharmonic backbone curves

For $g_0>0$, it was observed empirically that a subharmonic backbone curve emanates in the right vicinity of a fixed–free BCs linear subharmonic resonance frequency (vertical dashed lines in Figs. 5 and 6):

$$\begin{aligned} \omega =\frac{2k(n+1)-1}{n+1}\omega _1, \quad n,k\in \mathbb {N}^*. \end{aligned}$$

(15)

For $g_0<0$, a subharmonic backbone curve starts in the left vicinity of $\varOmega _k$ and shares an asymptote with the subharmonic backbone curve for positive initial gap. Furthermore, for $g_0=0$, a subharmonic backbone curve is asymptotic to its above counterparts. Several numerical experiments suggest that the asymptotes (vertical brown lines in Figs. 5, 6) are located at

$$\begin{aligned} \omega =\frac{\omega _1(n+1)(\omega _k/\omega _1+1)^2}{\omega _k/\omega _1(n+1) + n + 2}, \quad n,k\in \mathbb {N}^*. \end{aligned}$$

(16)

The number of computable subharmonics is determined by the discretization time step; for example, Figs. 5 and 6 display only six branches while the time step was $\varDelta t=10^{-3}$. Four periodic solutions corresponding to subharmonic backbone curves are depicted in Fig. 15 for $g_0>0$.

These plots suggests that the periodic motions present n grazing instants together with one contact phase, when the NSM branch starts in the vicinity of the n-th subharmonic of $\omega _k$, as inferred from Eq. (15). The displacement of the contacting end for points “d” and “g” (see Fig. 6) is similar; however, the latter has higher frequency. Such feature is also expected in periodic motions around subharmonics of higher NSM.

Moreover, periodic solutions belonging to distinct NSM branches coexist when the bar is prestressed ($g_0<0$), see point “h” in Fig. 6. The corresponding periodic displacements of the contacting end are plotted in Fig. 16 where the period of vibration is the same. Here, the solutions have longer free phases and increasing number of grazing instants with higher energy. These grazing instants coincide with the BC switching time of lower energy solutions.

Fig. 16

Periodic motions with same frequency for $g_0<0$ corresponding to points “h” in Fig. 6: low energy (top) to high energy (bottom)

Interestingly, extensive numerical experiments show that NSM branches do not appear in the range of frequencies $[\varOmega _k, \omega _{k+1}]$, $k\in \mathbb {N}^*$; the reason for this is unknown.

Fig. 17

Main NSM branch around $\omega _1$ with additional internal resonance branches

6.3 Internal resonance branches

The intrinsic discrete nature of the employed numerical algorithm is such that WFEM cannot capture an actual continuum of solutions (see Sect. 5). However, the periodic solutions previously presented all belong to numerically “apparent” continua parametrized by the energy where the solutions possess similar qualitative and quantitative features. The proposed approach also leads to sparse periodic solutions, see clouds of points in Fig. 17. Presumably, these points are also part of a complicated network of backbone curves stemming from main and subharmonic branches; however, they are much more challenging to capture numerically because of the high-frequency content in the corresponding mode shapes, see Fig. 18. These points seem to be organized on internal resonances backbone curves [8] emanating from the main one in the vicinity of the frequencies

$$\begin{aligned} \omega =2k\omega _1/(2k -1),\quad k=2,3,\dots \end{aligned}$$

(17)

Moreover, Fig. 17 shows that there are no internal resonance branches in the frequency ranges $[(2k-1)\omega _1/(2k-2);2k\omega _1/(2k-1)]$, $k=3,4,\dots$ This is not further explored in this work. Periodic motions featuring an internal resonance in the vicinity of $(\omega _3+\omega _1)/5 = 6\omega _1/5$ are displayed in Fig. 18. These solutions present two grazing instants and appear to correspond to a modal interaction between the first and third NSM. In contrast to solutions on the main and subharmonic backbone curves for $g_0>0$, the contact duration of internally resonant periodic motions decreases with increasing frequency: they exhibit a softening behavior.

Fig. 18

Internal resonances for $g_0>0$ in the vicinity of $(\omega _3+\omega _1)/5 = 6\omega _1/5$: points “a” (top) and “b” (bottom) in Fig. 17

It is difficult to compute the occurrence of internal resonances in systems involving unilateral contact. However, the data obtained by WFEM give suggestions about the existence of these NSM branches. The characterization of the periodic motions associated with internal resonances is helpful to predict the possible sudden resonance of real life applications, when vibrating around frequencies defined in Eq. (17).

6.4 Periodic solutions with two contact phases per period

The previous sections were devoted to solutions with one contact phase and one free phase per period, as expressed in Eq. (8). In this section, solutions with more than one contact phase per period are explored. The methodology is unchanged, but two additional unknowns (duration of second contact phase $\ell \varDelta t$ and duration of second free phase $m\varDelta t$, $\ell$ and $m\in \mathbb N^*$) arise in the new equation

$$\begin{aligned} (\mathbf {A}_\text {c}^{p}\mathbf {A}_\text {f}^{k}\mathbf {A}_\text {c}^{\ell }\mathbf {A}_\text {f}^{m} - \mathbf {I})\mathbf {Q}^{(0)} = \mathbf {0}, \end{aligned}$$

(18)

to be compared with Eq. (9). It appears that non trivial solutions $\mathbf {Q}^{(0)}$ can be found only if the contact phases have the same duration, that is $p=\ell$. This might be the consequence of the symmetry with respect to time and space of the wave equation. For the matrix $\mathbf {S}_{T}=\mathbf {A}_\text {c}^{p}\mathbf {A}_\text {f}^{k}\mathbf {A}_\text {c}^{p}\mathbf {A}_\text {f}^{m} - \mathbf {I}$, families of periodic solutions satisfying contact conditions were found only when $h=\dim (\ker \mathbf {S}_{T})=2$ suggesting that $\dim (\ker \mathbf {S}_{T})$ should equal the number of contact phases for periodic solutions to exist.

The solution procedure explained in Sect. 5.2 leads to a one-dimensional continuum of periodic orbits emerging in the vicinity of $\omega _2/5 =3\omega _1/5$, where $\omega _2=3\omega _1$, defining a subharmonic backbone curve with two contact phases, as illustrated in Fig. 19. This family of periodic orbits appears only for $g_0>0$ and presents hardening behavior. The corresponding space–time displacement field is shown in Fig. 20 for an arbitrary frequency. The asymptote of this NSM branch appears to be located at $2\omega _1/3$.

Fig. 19

NSM branch with two closed contacts per period in the vicinity of $\omega _2/5 =3\omega _1/5$  . First main NSM with one closed contact per period  ; $g_0>0$. (Color figure online)

The contacting end shown in Fig. 20 features one free phase with two grazing instants similar to the first subharmonic of the third NSM at $\omega _3/3$. Also, as in the case with one contact phase per period, the amplitude of the displacements and the duration of the contact phases get larger with the frequency of vibration. Interestingly, it resembles the two impact-per-period trajectories of a serial spring–mass system constrained by an obstacle with a purely elastic contact law [20]. In particular, the solutions have two axes of symmetry per period along the time axis, which are located in the middle of each free phase.

A finer discretization is required to obtain additional NSM branches with higher number of contact phases. These branches might be of interest for the prediction of vibratory responses where the elastic bar resonates for excitation frequencies much lower than the first linear natural frequency $\omega _1$.

Fig. 20

Generic space–time displacement field with two contact phases per period of the NSM branch around $\omega _2/5$

6.5 Stability analysis of periodic solutions

Due to the space–time coupled discretization and the conditional switching of boundary conditions, a rigorous stability analysis of the periodic orbits is a challenging task and remains an open problem left to future investigations. However, as a preliminary insight, the effects of a small sinusoidal perturbation on the initial conditions corresponding to the first main NSM were investigated by comparing the unperturbed and perturbed solutions time-integrated via WFEM over 1000 periods of the unperturbed solution. We found that the perturbed motion remains in the vicinity of the periodic motion, thus suggesting that a fraction of first main NSM motions are orbitally stable. This is illustrated in Fig. 21 which compares the unperturbed and perturbed motions, over the last period of integration $t\in [999T_a;1000T_a]$, corresponding to point “a” and $g_0>0$ in Fig. 5.

Fig. 21

Displacement of the contacting end after 1000$T_a$ for point “a” in Fig. 5: unperturbed  and perturbed  . (Color figure online)

7 Forced response of a mechanical system subject to contact constraints

One important purpose of performing nonsmooth modal analysis of a mechanical system is to predict its behavior when periodically forced [12, 30]. Accordingly, the frequency response of the previously investigated elastic bar with periodic external excitation is now compared to the NSM spectrum. The excitation consists in an external distributed harmonic force or a harmonically moving rigid wall that compresses the bar, see Fig. 22. The force acting on the bar is $f(x,t)= f_0(x)\sin (\omega t)$, and the displacement of the moving wall is $w(t)=w_{0}\sin (\omega t)$ where $\omega$ is the frequency of excitation and $w_0>g_0$. The gap function is now defined as $g(u(L,t),w(t))=g_0+w(t)-u(L,t)$. The system has been slightly damped by adding a velocity-dependent term with a small viscous damping coefficient in the left-hand side of Eq. (1). The forced response of this system is obtained for various amounts of damping and was computed using the WFEM version detailed in Algorithm 2 using a time-stepping approach not specifically targeting periodic motions.

Fig. 22

Elastic bar excited by a distributed harmonic force and/or a moving rigid wall

7.1 Periodically moving wall

The first tested configuration is $f_0=0$ and $w_0\ne 0$. The total energy of the steady-state solution averaged over one forcing period for increasing frequencies of excitation and various amounts of damping is shown in Figs. 23, 24 and 25 (top) for a positive, zero and negative initial gap, respectively.

In the frequency ranges where NSM branches do not exist, WFEM could not find externally forced periodic steady states. Instead, quasiperiodic or chaotic forced responses were detected. Calculating steady state for each frequency requires long computational times which complicates the construction of a detailed forced response.

7.2 Periodic distributed force

The second tested configuration is $f_0\ne 0$ and $w_0=0$, corresponding to the elastic bar excited by a distributed force. The results for a positive, zero and negative initial gap are depicted in Figs. 23, 24 and 25 (bottom), respectively.

Fig. 23

Periodically forced responses of the bar for various damping coefficients and $g_0>0$: harmonically moving wall (top) and harmonic distributed force (bottom)

Fig. 24

Periodically forced responses of the bar for various damping coefficients and $g_0=0$: harmonically moving wall (top) and harmonic distributed force (bottom)

Fig. 25

Periodically forced responses of the bar for various damping coefficients and $g_0<0$: harmonically moving wall (top) and harmonic distributed force (bottom)

For a positive gap and high frequencies, large damping confines the system to linear operating conditions. This is one of the reasons why the corresponding plots differ greatly. Moreover, similarly to the first configuration, quasiperiodic and chaotic solutions are observed in the frequency intervals where NSM branches do not exist. Presumably, there exist infinitely many backbones curves and corresponding “in-between” regions with no periodic solutions; only a few are plotted in Figs. 23, 24 and 25.

More importantly, the backbone curves obtained with the nonsmooth modal analysis provide an excellent approximation of the response resonances. In addition, the internal resonances of the system produce small protuberances in the forced response that coincide with the main resonance and subharmonic backbone curves.

The main advantage of the nonsmooth modal analysis is the characterization of the vibratory response without relying on very expensive numerical time integration procedures: via NSM as presented, the prediction of frequencies of excitation at which the system will vibrate with high energy is straightforward.

8 Conclusions

Families of periodic orbits (known as nonsmooth modes of vibration) of an autonomous finite elastic bar subject to frictionless unilateral contact are investigated in this work. Three cases were explored: unstressed ($g_0>0$), prestressed ($g_0<0$) and zero initial gap ($g_0=0$). The computation of periodic solutions was achieved using the wave finite element method (WFEM), chosen because it preserves energy and avoids numerical dispersion. This method consists in discretizing simultaneously in time and space the governing dynamic equations, resulting in a simple matrix form. Then, the problem of finding periodic solutions was formulated as finding a vector in the kernel of a matrix supplemented by complementarity conditions enforcing unilateral contact constraints. The presented methodology can be adapted to multiple contact phases per period or to systems coupled by unilateral contact conditions. However, it is presently limited to simplified one-dimensional problems with a single point of contact on the contact boundary.

It is shown that the elastic bar with unilateral contact has a rich dynamical behavior involving subharmonic resonances and internal resonances. Similar results are already reported in the literature [11, 12]. However, the proposed methodology does not necessitate regularized contact conditions. In this work, the unilateral contact conditions are treated as a switch between Dirichlet and Neumann-type boundary conditions when the gap opens or closes: from fixed–free BCs (no contact) to fixed–fixed BCs (contact) and vice-versa. The found nonlinear periodic solutions lying on a NSM are combinations of traveling waves with discontinuous wave fronts, as opposed to their linear counterpart (without contact conditions) which are standing harmonic waves. Also, the behavior of the NSMs depends on the gap at rest: hardening branches for $g_0>0$, softening branches for $g_0<0$ and discrete spectrum for $g_0=0$. Such behavior was already observed only for the first NSM [23]. Moreover, the frequency ranges at which NSM branches exist are conjectured.

Quasi-closed-form solutions can be extracted from the provided results. They could act as benchmark solutions for researchers designing advanced numerical schemes in unilateral contact dynamics. NSMs stability and the role of coexisting periodic solutions (same energy and frequency) need be further explored. The relevance of nonsmooth modal analysis was illustrated by the accurate prediction of periodically forced responses, irrespective of the way the external force is applied.

Extension of the proposed approach to multidimensional settings with several points of contact is a remarkable challenge as the nondispersive and energy-preserving properties of the WFEM in the one-dimensional context will then be lost. However, such extension seems feasible with Godunov-type discretization and shooting techniques by slightly relaxing the imposed periodicity conditions.

Appendices

Appendix A: Description of the wave finite element method

In this section, the WFEM, introduced by Shorr for the simulation of shock wave propagation in solids [26], is thoroughly described.

1.1 A.1 Hyperbolic system of conservation laws

Local Eq. (1) can be equivalently written as a system of two first-order partial differential equations in terms of velocities v(x, t) and stresses $\sigma (x,t)$

$$\begin{aligned} \left. \begin{aligned} \sigma _{,t} - E v_{,x}&= 0 \\ \rho v_{,t} - \sigma _{,x}&= 0 \end{aligned} \;\right\} , \quad \forall x\in \mathopen {]}0\,;L\mathclose {[},\quad \forall t > 0 \end{aligned}$$

(19)

where $(\bullet )_{,t}$ is the derivation in time and $(\bullet )_{,x}$ is the derivation in space of quantity $(\bullet )$ [33]. Recall that axial strains $\varepsilon =u_{,x}$ are bounded by nonphysical inter-penetration, which translates into $u_{,x}> -\,1$, see Sect. 2. Displacements can be straightforwardly recovered by space integration of the strains $u(x,\cdot \,)=\int _0^x u_{,s}(s,\cdot \,)\mathop {}\!\mathrm {d}s - u(0,\cdot \,)$, where $u(0,\cdot \,)=0$. By posing $\mathbf {q}=[\sigma v]^\top$, Eq. (19) can be recast as

$$\begin{aligned} \mathbf {q}_{,t} + \mathbf {B} \mathbf {q}_{,x}=\mathbf {0}\quad \text {where}\quad \mathbf {B}=\begin{bmatrix} 0&-E \\ - 1/\rho&0 \end{bmatrix}. \end{aligned}$$

(20)

The eigenvalues of matrix $\mathbf {B}$ are $\lambda _1 =-\sqrt{E/\rho }$ and $\lambda _2 = \sqrt{E/\rho }$, coinciding with the algebraic propagation velocity of the elastic wave: positive and negative for the two waves propagating in opposite directions. Since both eigenvalues are distinct and real, Eq. (20) is also referred to as a hyperbolic system of conservation laws [33].

Equation (20) involves time and space derivatives of $\mathbf {q}$. However, observing that $\mathbf {q}_{,t} + \mathbf {B} \mathbf {q}_{,x}=\mathbf {0}$ is a local form of the conservation law of $\mathbf {q}$ (implying $\mathbf {q}(\,\cdot \,,t)$ can only change due to fluxes at the boundaries) corresponding to the following integral form

$$\begin{aligned} \frac{\mathop {}\!\mathrm {d}}{\mathop {}\!\mathrm {d}t}\Bigl (\int ^{x_2}_{x_1}\mathbf {q}(x,t) \mathop {}\!\mathrm {d}x\Bigr )= \mathbf {B}\bigl (\mathbf {q}(x_1,t)-\mathbf {q}(x_2,t)\bigr ), \end{aligned}$$

(21)

it appears that the condition on the smoothness of $\mathbf {q}$ is no longer required. Therefore, $\mathbf {q}$ is allowed to exhibit discontinuities in time and space [34].

1.2 A.2 Discretization

The WFEM consists in dividing the spatial and temporal domain into grid cells of equal size and keeping track of an approximation to the integral of $\mathbf {q}$ within every single cell. As depicted in Fig. 26, the bar is discretized using a uniform grid of N cells. Each ith cell, denoted by $\mathcal {C}_i$, is delimited by the interval $(x_{i-1/2},x_{i+1/2})$. Similarly, time is discretized into intervals of equal length $\varDelta t=t_{n+1}- t_n$. The average of $\mathbf {q}(\,\cdot \,,t)$ over the ith cell at time $t_n$ is

$$\begin{aligned} \mathbf {Q}_i^{(n)} = \frac{1}{\varDelta x} \int _{x_{i-1/2}}^{x_{i+1/2}} \mathbf {q}(x,t_{n})\mathop {}\!\mathrm {d}x = \frac{1}{\varDelta x} \int _{\mathcal {C}_i} \mathbf {q}(x,t_n)\mathop {}\!\mathrm {d}x \end{aligned}$$

(22)

where $\varDelta x = x_{i+1/2} - x_{i-1/2}$ is the length of cell i. The integral form of conservation law (21) applied to cell $\mathcal {C}_i$ reads

$$\begin{aligned} \frac{\mathop {}\!\mathrm {d}}{\mathop {}\!\mathrm {d}t}\int _{\mathcal {C}_i}\mathbf {q}(x,t)\mathop {}\!\mathrm {d}x=\mathbf {B}\bigl (\mathbf {q}(x_{i-1/2},t) - \mathbf {q}(x_{i+1/2},t)\bigr ). \end{aligned}$$

(23)

This expression is now employed to develop an explicit time-stepping algorithm where $\mathbf {Q}_i^{(n+1)}$ is approximated by a function of $\mathbf {Q}_i^{(n)}$. Equation (23) is integrated between $t_n$ and $t_{n+1}$ yielding

$$\begin{aligned} \begin{aligned}&\int _{\mathcal {C}_i}\bigl (\mathbf {q}(x,t_{n+1})-\mathbf {q}(x,t_{n})\bigr )\mathop {}\!\mathrm {d}x \\&\quad =\int _{t_n}^{t_{n+1}} \bigl (\mathbf {B}\bigl (\mathbf {q}(x_{i-1/2},t) - \mathbf {q}(x_{i+1/2},t)\bigr )\bigr )\mathop {}\!\mathrm {d}t. \end{aligned} \end{aligned}$$

(24)

Fig. 26

Discretization of the spatial domain in grid cells at time $t_n$

Rearranging and dividing by $\varDelta x$ leads to

$$\begin{aligned} \frac{1}{\varDelta x}\int _{\mathcal {C}_i}\mathbf {q}(x,t_{n+1})\mathop {}\!\mathrm {d}x= & {} \frac{1}{\varDelta x}\Bigl ( \int _{\mathcal {C}_i}\mathbf {q}(x,t_{n})\mathop {}\!\mathrm {d}x \nonumber \\&-\int _{t_n}^{t_{n+1}} \mathbf {B}\mathbf {q}(x_{i+1/2},t)\mathop {}\!\mathrm {d}t \nonumber \\&+\int _{t_n}^{t_{n+1}} \mathbf {B}\mathbf {q}(x_{i-1/2},t)\mathop {}\!\mathrm {d}t\Bigr ).\nonumber \\ \end{aligned}$$

(25)

This equation describes how the cell average should be updated within a time step in order to satisfy the conservation of $\mathbf {q}$. In general, the two integrals involving $\mathbf {B}\mathbf {q}$ on the right-hand side of the equation cannot be evaluated exactly. Following [35], we pose

$$\begin{aligned} \mathbf {F}_{i\pm 1/2}^{(n)} \approx \frac{1}{\varDelta t}\int _{t_n}^{t_{n+1}}\mathbf {B}\mathbf {q}(x_{i\pm 1/2},t)\mathop {}\!\mathrm {d}t \end{aligned}$$

(26)

and Eq. (25) simply becomes

$$\begin{aligned} \mathbf {Q}^{(n+1)}_i=\mathbf {Q}^{(n)}_i-\frac{\varDelta t}{\varDelta x}\bigl (\mathbf {F}_{i+1/2}^{(n)}-\mathbf {F}_{i-1/2}^{(n)}\bigr ). \end{aligned}$$

(27)

The next subsection is dedicated to the computation of $\mathbf {F}_{i\pm 1/2}^{(n)}$, which are the time-averaged fluxes at $x=x_{i\pm 1/2}$.

Fig. 27

Reconstruction of $\mathbf {q}(x,t_n)$ from the average fluxes $\mathbf {Q}^{(n)}_i$

1.3 A.3 Approximation of the time–averaged fluxes

To approximate the fluxes at the interfaces defined by Eq. (26), the state $\mathbf {q}(x,t_n)$ at time $t_n$ is assumed to be a piecewise constant function defined for all x, constructed from the cell averages $\mathbf {Q}^{(n)}_i$ as depicted in Fig. 27. This piecewise reconstruction of the function $\mathbf {q}(x,t_n)$ is identical to the Godunov’s approach widely employed in computational fluid dynamics [36]. A suitable approximation of the flux $\mathbf {F}_{i+1/2}^{(n)}$ can be obtained by solving the problem, either numerically or exactly, of conservation law Eq. (20) together with the following discontinuous conditions at time $t_n$ [36]:

$$\begin{aligned} \begin{aligned} \sigma (x,t_n)= {\left\{ \begin{array}{ll} ~\sigma ^{(n)}_{i} &{} \text {if }x\leqslant x_{i+1/2}\\ ~\sigma ^{(n)}_{i+1} &{} \text {if }x>x_{i+1/2} \end{array}\right. }\\ v(x,t_n)= {\left\{ \begin{array}{ll} ~v^{(n)}_{i} &{} \text {if }x\leqslant x_{i+1/2}\\ ~v^{(n)}_{i+1} &{} \text {if }x>x_{i+1/2} \end{array}\right. } \end{aligned} \end{aligned}$$

(28)

which constitutes a Riemann problem centered at $x_{i+1/2}$ between cells $\mathcal {C}_i$ and $\mathcal {C}_{i+1}$ [36]. The solution to this Riemann problem consists of two shock waves propagating along the characteristic lines $x=\pm ct$, one moving to the left into cell $\mathcal {C}_i$ and one moving to the right into cell $\mathcal {C}_{i+1}$ as depicted in a space–time plot in Fig. 28. The shock wave traveling to the left, indicated by $\mathcal {W}_1$, propagates at velocity $s_1$ and connects the state $\mathbf {Q}^{(n)}_i$ and the interior state $\mathbf {Q}_i^*$ generated by such shock wave. Moreover, the solution $t\mapsto \mathbf {q}(x_{i+1/2},t)$ is constant over the time interval $[t_n,t_{n+1}]$.

Fig. 28

Structure of the solution to the Riemann problem depicted in a space–time plot

The Rankine–Hugoniot jump condition is proven to hold across any propagating discontinuity [37] which can be written for the left wave $\mathcal {W}_1$ propagating at velocity $s_1$ and the right wave $\mathcal {W}_2$ propagating at velocity $s_2$:

$$\begin{aligned} \begin{aligned} \mathcal {W}_1&\rightarrow {\left\{ \begin{array}{ll} ~ s_1 \bigl (\sigma ^*_{i} - \sigma ^{(n)}_{i}\bigr ) = - E\bigl (v^*_{i} - v^{(n)}_{i}\bigr ), \\ ~ \rho s_1 \bigl (v^*_{i} - v^{(n)}_{i}\bigr ) = -\bigl (\sigma ^*_{i} - \sigma ^{(n)}_{i}\bigr ) \end{array}\right. }\\ \mathcal {W}_2&\rightarrow {\left\{ \begin{array}{ll} ~ s_2\bigl (\sigma ^{(n)}_{i+1}-\sigma ^*_{i+1}\bigr )=-E\bigl (v^{(n)}_{i+1} - v^*_{i+1}\bigr ),\\ ~ \rho s_2 \bigl (v^{(n)}_{i+1} - v^*_{i+1}\bigr ) = -\bigl (\sigma ^{(n)}_{i+1} - \sigma ^*_{i+1}\bigr ). \end{array}\right. } \end{aligned} \end{aligned}$$

(29)

Because of material continuity, cells $\mathcal {C}_i$ and $\mathcal {C}_{i+1}$ cannot separate. This requires that the interior states must be equal across the material interface, $\mathbf {Q}^*_{i+1/2}=\mathbf {Q}_{i+1}^*=\mathbf {Q}_{i}^*$. By knowing that the shock speeds $s_1 = - s_2 = -\sqrt{E/\rho }=-c$ are known and constants, the intermediate state is approximated with $\mathbf {q}(x_{i+1/2},t)\approx \mathbf {Q}_{i+1/2}^*$ such that $t_{n}\leqslant t\leqslant t_{n+1}$ and can be calculated from Eq. (29):

$$\begin{aligned} \mathbf {Q}^*_{i+1/2}= & {} \begin{bmatrix} \sigma _{i+1/2}^* \\ v_{i+1/2}^* \end{bmatrix}\nonumber \\= & {} \frac{1}{2}\!\begin{bmatrix}\! \sigma ^{(n)} _{i+1}\!+\! \sigma ^{(n)} _{i} + \rho c \bigl (v^{(n)}_{i+1}-v^{(n)}_{i}\bigr )\\ v^{(n)} _{i+1} \!+\! v^{(n)} _{i}\!+\! \frac{1}{\rho c} \bigl (\sigma ^{(n)}_{i+1}-\sigma ^{(n)}_{i}\bigr ) \!\end{bmatrix}\!\!. \end{aligned}$$

(30)

Equation (30) is regarded as the exact solution of the Riemann problem involving linear elastodynamics [35, 38]. The flux approximation in Eq. (26) can be calculated with the solution of a Riemann problem at the cell interface as

$$\begin{aligned} \mathbf {F}_{i+1/2}^{(n)} \approx \frac{\mathbf {B}}{\varDelta t} \int _{t_n}^{t_{n+1}}\mathbf {Q}^*_{i+1/2}\mathop {}\!\mathrm {d}t \approx \mathbf {B} \mathbf {Q}^*_{i+1/2}. \end{aligned}$$

(31)

In a nonlinear framework for the local equation, a solution to the Riemann problem should be approximated numerically using Riemann solvers [39].

1.4 A. 4 Formulation for inner grid cells

Inserting Eq. (31) into Eq. (27) produces the iterative scheme

$$\begin{aligned} \mathbf {Q}^{(n+1)}_i = \mathbf {Q}^{(n)}_i - \frac{\varDelta t}{\varDelta x}\bigl (\mathbf {B} \mathbf {Q}^*_{i+1/2} - \mathbf {B} \mathbf {Q}^*_{i-1/2}\bigr ). \end{aligned}$$

(32)

Equation (32) describes the evolution in time of the states of the grid cells $\mathcal {C}_i$. This subsection provides the formulation for the inner cells, where $i=2,\ldots ,N-1$. The boundary cells $\mathcal {C}_1$ and $\mathcal {C}_N$ require a different treatment explained in the next subsection. Expressing the flux approximation, employing Eq. (31) on the right side of an inner cell yields

$$\begin{aligned} \mathbf {B} \mathbf {Q}^*_{i+1/2}{=}\frac{1}{2} \begin{bmatrix} -E\bigl (v^{(n)}_{i+1}+v^{(n)}_{i}+\frac{1}{\rho c}\bigl (\sigma ^{(n)}_{i+1}-\sigma ^{(n)}_{i}\bigr )\bigr )\\ -\frac{1}{\rho }\bigl (\sigma ^{(n)} _{i+1} + \sigma ^{(n)} _{i}+\rho c\bigl (v^{(n)}_{i+1}-v^{(n)}_{i}\bigr )\bigr )\end{bmatrix}. \end{aligned}$$

(33)

Performing the same operation on the left side of the cell reads

$$\begin{aligned} \mathbf {B} \mathbf {Q}^*_{i-1/2} {=} \frac{1}{2} \begin{bmatrix} -E\bigl ( v^{(n)} _{i} + v^{(n)}_{i-1} + \frac{1}{\rho c}\bigl (\sigma ^{(n)}_{i}-\sigma ^{(n)}_{i-1}\bigr ) \bigr ) \\ -\frac{1}{\rho }\bigl (\sigma ^{(n)} _{i} + \sigma ^{(n)} _{i-1} + \rho c \bigl (v^{(n)}_{i}-v^{(n)}_{i-1}\bigr )\bigr ) \end{bmatrix}. \end{aligned}$$

(34)

Accordingly, the total flux within an inner cell is the quantity $\mathbf {B} \mathbf {Q}^*_{i+1/2} - \mathbf {B} \mathbf {Q}^*_{i-1/2}$ which when substituted into Eq. (32) yields

$$\begin{aligned}&\begin{bmatrix} \sigma ^{(n+1)} _i\\v^{(n+1)}_i \end{bmatrix}\nonumber \\&\quad =\begin{bmatrix} \sigma ^{(n)} _i \\ v^{(n)}_i \end{bmatrix}+\frac{\varDelta t}{2 \varDelta x} \nonumber \\&\quad \times \begin{bmatrix} E\bigl (v^{(n)}_{i+1} - v^{(n)}_{i-1}\bigr ) + c\bigl (\sigma ^{(n)}_{i+1}-2\sigma ^{(n)}_{i} + \sigma ^{(n)}_{i-1}\bigr )\\ \frac{1}{\rho c} \bigl (\sigma ^{(n)}_{i+1} - \sigma ^{(n)}_{i-1}\bigr ) + c \bigl (v^{(n)}_{i+1}-2v^{(n)}_{i}+v^{(n)}_{i-1}\bigr ) \end{bmatrix}.\nonumber \\ \end{aligned}$$

(35)

Since the exact solution of a Riemann problem is being used, WFEM incorporates an appropriate time step $\varDelta t=\varDelta x/c$. Then, the stress and velocity of a grid cell $\mathcal {C}_i$ at time $t_{n+1}$ are calculated as

$$\begin{aligned} \begin{bmatrix} \sigma ^{(n+1)}_i \\ v^{(n+1)}_i \end{bmatrix} = \frac{1}{2} \begin{bmatrix} \sigma ^{(n)}_{i+1} + \sigma ^{(n)}_{i-1} + \rho c \bigl (v^{(n)}_{i+1} - v^{(n)}_{i-1}\bigr ) \\ v^{(n)}_{i+1}+v^{(n)}_{i-1} + \frac{1}{\rho c}\bigl (\sigma ^{(n)}_{i+1} - \sigma ^{(n)}_{i-1}\bigr ) \end{bmatrix}. \end{aligned}$$

(36)

The above strong assumption is suitable only for 1D elastodynamics problems, since the wave velocity and the direction of the propagation is known. Also, such assumption enforces energy conservation and eliminates numerical dissipation [26]. In the multidimensional framework, even though the waves velocities are known, the waves could propagate in various directions throughout the physical domain.

Equation (36) provides the main equation of the WFEM and characterizes how the average value $\mathbf {Q}_i^{(n)}$ of $\mathbf {q}$ in an inner cell $\mathcal {C}_i$ is updated at each time step. As required by the local conservation law (21) resulting from the absence of body forces, the evolution of the state of the inner cells depends only on the values of the adjacent cells. WFEM can be seen as the transference of the whole information embedded in cell $\mathcal {C}_i$ to its adjacent cells at each time step. Employing the latter approach to obtain the evolution of cell states, involving discontinuities such as shock and rarefaction waves, is well known by the Fluid Mechanics community employing finite volume methods [36].

1.5 A.5 Formulation for boundary grid cells

To compute the state of the boundary grid cells, the computational domain is extended by including additional cells on both boundaries, known as ghost cells [35], whose average values depend on the boundary conditions. This concept is taken from the finite volume methods. Figure 29 depicts ghost cells for a system discretized using N cells.

Fig. 29

Computational space domain with ghost cells

Equation (36) can then be used to update the average value on the boundary cells, which have now become inner cells. Only a single ghost cell is required at each boundary because the computation of the average value depends only on the states of the adjacent cells. For instance, the fixed–free elastic bar without the complementarity conditions of contact satisfies the two boundary conditions $u(0,t)=v(0,t)=0$ and $E u_{,x}(L,t)=\sigma (L,t)=0$. These conditions are used to define the average values within the ghost cells as follows:

$$\begin{aligned} \begin{aligned}&\text {At ghost cell}\,\, \mathcal {C}_0:\quad \left\{ \begin{aligned} \,&\sigma _0=\sigma _1 \\&v_0=-v_1, \end{aligned}\right. \quad \\&\text {At ghost cell }\mathcal {C}_{N+1}:\quad \left\{ \begin{aligned} \,&\sigma _{N+1}=-\sigma _N \\&v_{N+1}=v_N. \end{aligned}\right. \end{aligned} \end{aligned}$$

(37)

Such average values coincide with the theory of reflection of elastic waves from fixed and free boundaries [2], which states that stress waves reflect from a fixed boundary with the same sign and from a free boundary with the changed sign; similarly, velocity waves reflect from a fixed boundary with an opposite sign and from a free boundary with the same sign. The evolution of the average values of the boundary cells, $\mathcal {C}_1$ and $\mathcal {C}_N$, can be calculated by introducing the average values of Eq. (37) into Eq. (36), yielding for $\mathcal {C}_1$:

$$\begin{aligned} \mathbf {Q}_1^{(n+1)} = \frac{1}{2} \begin{bmatrix} \sigma ^{(n)}_{2} + \sigma ^{(n)}_{1} + \rho c \bigl (v^{(n)}_{2} + v^{(n)}_{1}\bigr ) \\ v^{(n)}_{2}-v^{(n)}_{1} + \frac{1}{\rho c}\bigl (\sigma ^{(n)}_{2} - \sigma ^{(n)}_{1}\bigr ) \end{bmatrix} \end{aligned}$$

(38)

and for $\mathcal {C}_{N}$:

$$\begin{aligned} \mathbf {Q}_N^{(n+1)} = \frac{1}{2} \begin{bmatrix} \sigma ^{(n)}_{N-1} -\sigma ^{(n)}_{N} + \rho c \bigl (v^{(n)}_{N} + v^{(n)}_{N-1}\bigr ) \\ v^{(n)}_{N}+v^{(n)}_{N-1} - \frac{1}{\rho c}\bigl (\sigma ^{(n)}_{N} + \sigma ^{(n)}_{N-1}\bigr ) \end{bmatrix}. \end{aligned}$$

(39)

1.6 A.6 WFEM generic algorithm

Altogether, the previous derivations lead to a set of equations that describe how $\mathbf {q}$ is updated in time for every cell. The different steps are summarized in Algorithm 1. Using $\varDelta t= \varDelta x/ c$ it computes, in the framework of linear elastodynamics, the propagation at finite speed c of a wave and accounts for the reflection conditions at the boundaries. By definition of $\varDelta t$, the CFL condition $\varDelta t\le \varDelta x/c$ is always satisfied, so the method is always stable [35, 40]. Additionally, because the global error is proportional to the discretization steps, the WFEM is first-order accurate in both space and time [26].

1.7 A.7 Matrix formulation

Similar to other numerical methods applied on linear systems, the WFEM can be rewritten in a convenient matrix form which facilitates the process of finding nonsmooth modes of vibration. More specifically, the state vector of the system $\mathbf {Q}^{(n)}=\bigl [\mathbf {Q}_1^{(n)} \ldots \mathbf {Q}_N^{(n)}\bigr ]^{\top }\in \mathbb {R}^{2N}$ at time $t_n$ satisfies the identity²

$$\begin{aligned} \mathbf {Q}^{(n)}=\mathbf {A}\mathbf {Q}^{(n-1)},\quad \forall n\ge 1 \end{aligned}$$

(40)

and $\mathbf {Q}^{(0)}$ is the initial state. The matrix $\mathbf {A}$ gathers stiffness and inertial terms as well as the type of boundary conditions. It is now derived for the fixed–free BC. In a matrix form, Eq. (36), which governs the evolution of inner cells, reads

$$\begin{aligned} \begin{bmatrix} \sigma ^{(n+1)}_i \\ v^{(n+1)}_i \end{bmatrix} = \frac{1}{2} \begin{bmatrix} 1&0&1&-\rho c&0&\rho c\\ -\frac{1}{\rho c}&0&\frac{1}{\rho c}&1&0&1 \end{bmatrix} \begin{bmatrix} \sigma ^{(n)}_{i-1} \\ \sigma ^{(n)}_{i} \\ \sigma ^{(n)}_{i+1} \\ v^{(n)}_{i-1} \\ v^{(n)}_{i} \\ v^{(n)}_{i+1} \end{bmatrix}. \end{aligned}$$

(41)

For the boundary cells in Eqs. (38) and (39), the matrix form follows as

$$\begin{aligned} \begin{bmatrix} \sigma ^{(n+1)}_1 \\ v^{(n+1)}_1 \end{bmatrix} = \frac{1}{2} \begin{bmatrix} 1&1&\rho c&\rho c\\ -\frac{1}{\rho c}&\frac{1}{\rho c}&-1&1 \end{bmatrix} \begin{bmatrix} \sigma ^{(n)}_{1} \\ \sigma ^{(n)}_{2} \\ v^{(n)}_{1} \\ v^{(n)}_{2} \end{bmatrix} \end{aligned}$$

(42)

and

$$\begin{aligned} \begin{bmatrix} \sigma ^{(n+1)}_N \\ v^{(n+1)}_N \end{bmatrix} = \frac{1}{2} \begin{bmatrix} 1&-1&\rho c&\rho c\\ -\frac{1}{\rho c}&-\frac{1}{\rho c}&1&1 \end{bmatrix} \begin{bmatrix} \sigma ^{(n)}_{N-1} \\ \sigma ^{(n)}_{N} \\ v^{(n)}_{N-1} \\ v^{(n)}_{N} \end{bmatrix}. \end{aligned}$$

(43)

Then, the block matrix $\mathbf {A}\in \mathbb {R}^{2N\times 2N}$ can be constructed using four $N\times N$ matrices $\mathbf {A}_1,\mathbf {A}_2,\mathbf {A}_3,\mathbf {A}_4$ whose expression can be derived from

$$\begin{aligned} \mathbf {A}_{\text {G}}(a,b,c,d) =\frac{1}{2} \begin{bmatrix} a&b&0&\dots&0&0&0\\ c&0&b&0&0&0\\ 0&c&0&0&0&0\\ \vdots&\ddots&\ddots&\ddots&\vdots \\ 0&0&0&0&b&0\\ 0&0&0&c&0&b\\ 0&0&0&\dots&0&c&d\\ \end{bmatrix} \end{aligned}$$

(44)

with $\mathbf A_1{=}\mathbf {A}_{\text {G}}(-1,1,1,1)$, $\mathbf A_2{=} \rho c\mathbf {A}_{\text {G}}(-1,1,-1,-1)$, $\mathbf A_3= \mathbf {A}_{\text {G}}(1,1,-1,1)/\rho c$, and $\mathbf A_4= \mathbf {A}_{\text {G}}(1,1,1,-1)$. Then, block matrix $\mathbf {A}$ is written as

$$\begin{aligned} \mathbf A = \begin{bmatrix} \mathbf A_1&\mathbf A_2 \\ \mathbf A_3&\mathbf A_4 \end{bmatrix}. \end{aligned}$$

(45)

Another matrix $\mathbf {A}$ can be constructed in the same way for the fixed–fixed BC. Finally, the unknown $\mathbf {Q}^{(n)}$ can be directly expressed in terms of the initial conditions $\mathbf {Q}^{(0)}$ from Eq. (40) by

$$\begin{aligned} \mathbf {Q}^{(n)}=\mathbf {A}^{n}\mathbf {Q}^{(0)} \end{aligned}$$

(46)

where $\mathbf {A}^{n}$ is known for each type of BC.

Fig. 30

Conditional switch for contact treatment in WFEM. a Inactive contact. b Active contact

Appendix B: Treatment of unilateral contact in WFEM

The unilateral contact constraints involved in the formulation are enforced using the concept of floating boundary conditions [26] which can be regarded as a conditional switch between fixed–free and fixed–fixed boundary conditions [41] when a penetration is detected during a time iteration, as illustrated in Fig. 30. In the continuous framework, these two boundary conditions are

• Fixed–free BC (inactive contact)

  $$\begin{aligned} u(0,t)=v(0,t)=0,\quad E u_{,x}(L,t)=\sigma (L,t)=0 \end{aligned}$$

  (47)

• Fixed–fixed BC (active contact)

  $$\begin{aligned} u(0,t)=v(0,t)=0,\quad u(L,t)=g_0 \rightarrow v(L,t)=0. \end{aligned}$$

  (48)

The gap function g(u(L, t)), which is a function of the displacement u(L, t), but not an explicit function of t, is discretized in time to calculate a possible penetration of the bar as

$$\begin{aligned} g^{(n)}=g_0 - u_{N+1/2}^{(n)} \end{aligned}$$

(49)

where $u_{N+1/2}^{(n)}$ is the displacement of the contacting interface which can be calculated by numerically integrating strains of the bar $u^{(n)}_{,x}$ at time $t_n$. This equality is used at each time step to check whether contact is active during the next iteration: if $g^{(n)}>0$, a free boundary condition is enforced while if $g^{(n)}\leqslant 0$, a fixed boundary condition is considered via the change of matrix $\mathbf {A}$.

Based on the theory of reflection of elastic waves from boundaries [2], the state of the ghost cell $\mathcal {C}_{N+1}$ is updated as follows

• Active contact [$g^{(n)}\leqslant 0$]

  $$\begin{aligned} \left\{ \begin{aligned} \,&\sigma _{N+1}=\sigma _N \\&v_{N+1}=-v_N \\ \end{aligned}\right. \end{aligned}$$

  (50)

• Inactive contact [$g^{(n)}>0$]

  $$\begin{aligned} \left\{ \begin{aligned} \,&\sigma _{N+1}=-\sigma _N \\&v_{N+1}=v_N \\ \end{aligned}\right. \end{aligned}$$

  (51)

Equation (36) is subsequently used to calculate the evolution of the average values inside the boundary cell $\mathcal {C}_N$, as detailed in Sect. 1. Additionally, the contact force $r^{(n)}$ is calculated by employing Eq. (30):

$$\begin{aligned} r^{(n)} = \mathcal {S}\bigl (\sigma ^{(n)}_N - \rho c v^{(n)}_N\bigr ). \end{aligned}$$

(52)

The sign of this quantity is tracked to locate the time of release, when the bar returns to free condition at $x=L$. Algorithm 1 is modified to include the floating boundary conditions as described in Algorithm 2.

From the matrix formulation of the WFEM in Eq. (40), two matrices $\mathbf {A}$ shall then be distinguished: $\mathbf {A}_{\text {f}}$ for the fixed–free condition (no contact) and $\mathbf {A}_{\text {c}}$ for the fixed–fixed condition (contact). Both matrices embed the same stiffness and inertial terms of the system of interest; the only unshared information are the boundary conditions. To summarize, the developed WFEM with floating boundary conditions is a numerically conservative and stable scheme able to properly propagate shock waves induced by a switch in the boundary conditions, the latter being governed by complementarity constraints.