Generation mechanism and evolution of five-state meshing behavior of a spur gear system considering gear-tooth time-varying contact characteristics

Abstract

Teeth disengagement or back-side teeth engagement induced by backlash reduces the transmission quality and dynamic performance of gear systems, and the accurate interpretation of multi-state meshing behavior can provide guidance for structural optimization and performance evaluation. Therefore, the multi-state meshing behavior of the gear system is elaborated. A new nonlinear dynamic model of a spur gear system with five-state meshing behavior is established based on the time-varying backlash and contact ratio. The time-varying meshing stiffness and time-varying backlash considering the elastic contact of gear teeth, gear temperature rise and lubrication are included in the model. The five-state meshing behavior is clearly characterized by constructing five Poincaré maps, and its generation mechanism is revealed using dynamic meshing force time history, teeth relative displacement time history and phase portrait. The bifurcation and evolution of five-state meshing behavior are analyzed under the effects of load factor, meshing frequency and error coefficient. The results show that the mutation in the direction of dynamic meshing force leads to teeth disengaging and back-side single- or double-tooth contact, forming multi-state meshing behavior. Bifurcation caused by parameter changes greatly affects the evolution of five-state meshing behavior, particularly grazing bifurcation can decrease the number of teeth disengagement. Chaotic behavior or trajectory expansion inspires multi-state meshing vibration of the system. Previous gear system models could not reveal these phenomena due to ignoring the multi-state meshing behavior.

1 Introduction

Gear transmission is a basic key component for transmitting motion and power in mechanical equipment and is commonly used in critical fields such as aviation, ships, vehicles, wind power generation, and manufacturing. The dynamic instability and vibration caused by teeth meshing of the gear system has always been a concern for scholars and engineers [1,2,3,4]. Accurate elaboration of gear-tooth contact characteristics is the basis of dynamic modeling and analysis of gear systems [5,6,7]. The multi-state meshing behavior of the gear system, such as single-tooth drive-side meshing, double-tooth drive-side meshing, single-tooth back-side meshing and double-tooth back-side meshing, is possible due to the interaction between single and double teeth alternately meshing as well as backlash. This exacerbates the contact impact vibration, dynamics instability, and gear failure of the gear system [8, 9]. Therefore, this paper is dedicated to studying the possible multi-state meshing behavior of gear systems, analyzing its generation mechanism and evolution process, and exploring the inherent law between multi-state meshing behavior and dynamic response.

The study on the characteristics of single- and double-tooth alternating meshing mainly focuses on the time-varying meshing stiffness [10]. The contact areas of single and double teeth along the tooth profile or line of action were accurately identified according to contact ratio [11]. Yang et al. [12] considered the influence of single- and double-tooth meshing characteristics and derived an analytically model of time-varying meshing stiffness of the spur gear system including Hertzian contact stiffness, bending stiffness and axial compressive stiffness based on the energy method. Subsequently, Tian [13] added shearing stiffness on the base of the Yang’s model. Wang [14] and Sainsot [15] evaluated the effect of the fillet-foundation deflection and added the fillet-foundation stiffness based on Tian’s model. The jump of time-varying meshing stiffness is observed in these studies when the single-tooth and double-tooth meshing are switched, which causes periodic meshing impact between the gear teeth. Thus, the studies on the tooth profile modification are carried out by many scholars in order to reduce shock and vibration during the gear mesh [16]. Recently, various models of the time-varying meshing stiffness under faulty gears are developed, such as cracked gears [17,18,19], tooth surface pitting [20], and tooth surface wear [21]. Although diverse time-varying meshing stiffness models have been obtained considering various influencing factors, the effects of tooth surface temperature rise and lubrication are rarely reported in the current literature. Gear temperature rise and lubrication are indispensable in gear transmission. Therefore, it is necessary to establish a comprehensive time-varying meshing stiffness model including elastic deformation, thermal deformation, and oil film thickness deformation in the single- and double-tooth areas for the analyses of time-varying meshing characteristics and dynamics of gear systems. In addition, it is worth noting that single-tooth and double-tooth meshes are rarely considered in the nonlinear dynamic modeling and analysis of gear systems in the previous studies.

At present, the meshing vibration of the gear system is equivalently simplified to the coupling vibration between two rotating bodies connected by a spring and a damper [22,23,24], which is convenient for modeling and analysis. In these studies, the gear contact characteristics are only described by time-varying meshing stiffness with single and double teeth [25,26,27]. However, the real time-varying contact characteristics are ignored, such as the time-varying geometric properties of the meshing point along the tooth profile and the contact behaviors of gear teeth induced by backlash and contact ratio (single-tooth drive-side meshing, double-tooth drive-side meshing, single-tooth back-side meshing and double-tooth back-side meshing).

The constant backlash can clearly describe the drive-side engagement, disengagement and back-side contact of the gear systems [12, 28], but it cannot effectively distinguish between single and double teeth during drive-side or back-side tooth meshing. Nevertheless, this can be accurately identified by the time-varying backlash [29]. Due to gear installation and machining errors, tooth surface wear and tooth deformation, the backlash is time-varying along the tooth profile [30,31,32,33,34,35]. Therefore, numerous calculation models of time-varying backlash involving various influencing factors were proposed for different purposes. Li et al. [30] used a first-order sine function to characterize the time-varying backlash caused by the deformation of the support bearing and the transmission shaft. Chen et al. [31] established a random fluctuation model of backlash including the influence of random factors. Chen et al. [32] proposed the dynamic backlash model by deriving the relationship between the gear center distance and backlash. Based on the finite element method, Wang et al. [33] established a time-varying backlash model considering the geometric error of the gear and the deviation of the gear center distance. Wu et al. [34] established a time-varying backlash model that accumulates with the amount of wear according to the static tooth surface wear prediction model. Chen et al. [35] developed a fractal model of the time-varying backlash of a gear system based on the fractal theory. Although these models describe the time-varying properties of backlash, they cannot distinguish between single and double teeth during drive-side and back-side meshing since the gear-tooth contact characteristics are not considered. As such, the time-varying contact behavior and multi-state meshing behavior of the gear system cannot be precisely elaborated. The authors proposed a new calculation model of the time-varying backlash of the spur gear system considering the influence of the elastic deformation, thermal deformation, oil film thickness deformation at the meshing point [29], which can accurately identify the multi-state meshing behavior.

Based on the time-varying backlash model, this paper proposes a new nonlinear dynamic model of the involute spur gear system including five-state meshing behavior, such as single-tooth drive-side meshing, double-tooth drive-side meshing, teeth disengaging, single-tooth back-side meshing and double-tooth back-side meshing. The time-varying backlash and the time-varying meshing stiffness considering elastic contact, gear temperature rise and lubrication are calculated in detail, and are introduced into the model of the gear system established in this work. Furthermore, the mechanism of multi-state meshing behavior is analyzed, and the bifurcation and evolution of five-state meshing behavior under the influence of meshing frequency, load factor and transmission error factor are investigated in detail via phase diagram, Poincaré map, bifurcation plot and time history chart of the dynamic meshing force. Some new and interesting results that were impossible to obtain in previous studies were observed. This research can provide a useful reference for dynamic performance optimization, parameter design and further study of gear transmission system, such as gear-tooth meshing-impact dynamics.

The remainder of this paper is structured as follows. In Sect. 2, a nonlinear dynamic modeling of a spur gear pair based on time-varying meshing characteristics is derived strictly. Classification of multi-state meshing behavior is presented in Sect. 2.1, and the dynamic modellings of different meshing states are established based on 2nd Newtonian law in Sect. 2.2, and the dimensionless normalized model of the spur gear pair with five-state meshing behavior is described in Sect. 2.3. Also, time-varying backlash, time-varying meshing stiffness and time-varying meshing damping are calculated in Sect. 3. Further, some results and discussions are described in Sect. 4. Finally, some conclusions are outlined in Sect. 5.

2 Modeling of a spur gear system with five-state meshing behavior

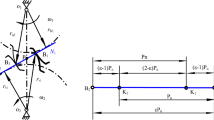
Under low-speed and heavy-load conditions, the gear system is in a state of drive-side tooth mesh. However, under high-speed and light-load conditions, backlash induces periodic teeth disengagement or back-side tooth contact behavior. Therefore, the multi-state meshing behavior of the gear system under complex and time-varying conditions is possible. In order to have a better understanding of the multi-state meshing characteristics, it is assumed that the gear pair is rigidly supported and only the torsional vibration of the gear pair is taken into account. A simplified physical model of an involute spur gear pair with drive-side and back-side tooth meshes is shown in Fig. 1. $T_{i}$, $I_{i}$, $\theta_{i}$ and $R_{{{\text{b}} i}}$ are the torques, mass moment of inertia, torsional vibration displacement and base circle radius of pinion and gear, where i = p represents pinion and i = g represents gear. Drive-side and back-side tooth meshes are considered in this work. The red line is drive-side line of action (Drive-side LoA), and the blue line is back-side line of action (back-side LoA). $k_{\text{d}} (\tau )$, $\mu_{\text{d}} (\tau )$, $e_{\text{d}} (\tau )$ and $c_{\text{d}} (\tau )$ are the time-varying meshing stiffness, time-varying friction coefficient, comprehensive transmission error and time-varying meshing damping alone Drive-side LoA, where τ is dimensional time. Also, $k_{\text{k}} (\tau )$, $\mu_{\text{k}} (\tau )$, $e_{\text{k}} (\tau )$ and $c_{\text{k}} (\tau )$ are the time-varying meshing stiffness, time-varying friction coefficient, comprehensive transmission error and time-varying meshing damping alone back-side LoA. $\overline{D}(\tau )$ is half of the time-varying backlash of the spur gear pair.

Fig. 1

A simplified physical model with considering drive-side and back-side tooth meshes

2.1 Classification of multi-state meshing behavior

Figure 2 is a schematic diagram of drive-side and back-side tooth meshes for a spur gear pair. $R_{i}$ and $R_{{{\text{a}} i}}$ are the pitch radius and addendum radius, respectively. $\varepsilon_{\text{m}}$ is the contact ratio of the gears, which is $1.0 < \varepsilon_{\text{m}} < 2.0$. Thus, the alternate meshing between single tooth and double teeth is obtained along Drive-side LoA or back-side LoA. Let $\overline{x} = R_{bp} \theta_{p} - R_{bg} \theta_{g} - e(\tau )$ be the relative displacement of meshing gear teeth. $e(\tau )$ is the comprehensive transmission error, which is $e(\tau ) = e_{\text{d}} (\tau )$ for drive-side meshing and $e(\tau ) = e_{k} (\tau )$ for back-side meshing. Based on the moving position of the meshing point and the geometric relationship between $\overline{x}$ and $\overline{D}(\tau )$, five meshing states of the spur gear system and their corresponding boundary conditions are summarized as follows.

• (i) Double-tooth drive-side meshing state (AB and CD areas in Fig. 2). The boundary condition is $\overline{x} \ge \overline{D}(\tau )$ and $nT_{\text{m}} \le \tau \le (\varepsilon_{\text{m}} - 1)nT_{\text{m}} \;(n = 0,1,2, \cdots )$;

• (ii) Single-tooth drive-side meshing state (BC area in Fig. 2). The boundary condition is $\overline{x} \ge \overline{D}(\tau )$ and $(\varepsilon_{\text{m}} - 1)nT_{\text{m}} < \tau \le (n + 1)T_{\text{m}}$;

• (iii) Double-tooth back-side meshing state ($A^{\prime}B^{\prime}$ and $C^{\prime}D^{\prime}$ areas in Fig. 2). The boundary condition is $\overline{x} \le - \overline{D}(\tau )$ and $nT_{\text{m}} \le \tau \le (\varepsilon_{\text{m}} - 1)nT_{\text{m}}$;

• (iv) Single-tooth back-side meshing state ($B^{\prime}C^{\prime}$ area in Fig. 2). The boundary condition is $\overline{x} \le - \overline{D}(\tau )$ and $(\varepsilon_{\text{m}} - 1)nT_{\text{m}} < \tau \le (n + 1)T_{\text{m}}$;

• (v) Teeth disengaged state. The boundary condition is $|\overline{x}| < \overline{D}(\tau )$ and $nT_{\text{m}} \le \tau \le (n + 1)T_{\text{m}}$.

Fig. 2

A meshing schematic diagram of a spur gear pair with drive-side and back-side tooth meshes

Herein, $T_{\text{m}} { = }{{2{\uppi }} \mathord{\left/ {\vphantom {{2{\uppi }} {(z_{\text{p}} \omega_{\text{p}} )}}} \right. \kern-\nulldelimiterspace} {(z_{\text{p}} \omega_{\text{p}} )}}$ is a complete meshing cycle including single-tooth and double-tooth meshes (pitch AC or $A^{\prime}C^{\prime}$). $z_{\text{p}}$ and $\omega_{\text{p}}$, respectively, represent the tooth number and rotational angular velocity of pinion. According to the above five meshing states, the corresponding dynamic models are, respectively, established below.

2.2 Dynamic models of the spur gear pair under different meshing states

2.2.1 Double-tooth drive-side meshing

Figure 3 is the force analysis diagram at the meshing points under double-tooth drive-side meshing state. There are two pairs of gear teeth participating in the meshing at the same time. The load is unevenly distributed on the two pairs of gear teeth. $F_{{{\text{Np}} 1}}$, $F_{{{\text{Np}} 2}}$, $F_{{{\text{N}} {\text{g}} 1}}$, and $F_{{{\text{N}} {\text{g}} 2}}$ are the forces acting on the pinion and gear, which are along drive-side LoA. $F_{fp1}$, $F_{{{\text{fp}} 2}}$, $F_{{{\text{fg}} 1}}$, and $F_{{{\text{fg}} 2}}$ are the friction forces acting on the pinion and gear, which are perpendicular to the direction of Drive-side LoA. According to the principle of gear transmission and 2nd Newtonian law, the absolute torsional vibration equation of the pinion and gear under double-tooth drive-side meshing state can be obtained by Eq. (1).

$$ \left\{ \begin{gathered} I_{\text{p}} \ddot{\theta }_{\text{p}} + R_{{\text{bp}}} F_{{{\text{Np}} 1}} + S_{dp1} (\tau )F_{{{\text{fp}} 1}} + R_{{\text{bp}}} F_{{{\text{Np}} 2}} + S_{dp2} (\tau )F_{{{\text{fp}} 2}} = T_{\text{p}} \hfill \\ I_{\text{g}} \ddot{\theta }_{\text{g}} - R_{{\text{bg}}} F_{{{\text{Ng}} 1}} - S_{dg1} (\tau )F_{{{\text{fg}} 1}} - R_{{\text{bg}}} F_{{{\text{Ng}} 2}} - S_{dg2} (\tau )F_{{{\text{fg}} 2}} = - T_{\text{g}} \hfill \\ \end{gathered} \right. $$

(1)

where $F_{{{\text{Np}} 1}}$, $F_{{{\text{Np}} 2}}$, $F_{{{\text{N}} {\text{g}} 1}}$ and $F_{{{\text{N}} {\text{g}} 2}}$ can be written as:

$$ F_{{{\text{Np1}}}} = F_{{{\text{Ng1}}}} = L_{{{\text{d1}}}} (\tau )F_{{\text{m}}} ,F_{{{\text{Np2}}}} = F_{{{\text{Ng2}}}} = L_{{{\text{d2}}}} (\tau )F_{{\text{m}}} $$

(2)

where $L_{{{\text{d1}}}} (\tau )$ and $L_{{{\text{d2}}}} (\tau )$ are the load sharing ratio (see Ref. [36]). $F_{{\text{m}}}$ is the dynamic meshing force, which can be calculated by Eq. (3).

$$ F_{{\text{m}}} = \overline{k}_{\text{d}} (\tau )\left[ {\overline{x} - \overline{D}(\tau )} \right] + c_{{\text{d}}} (\tau )\dot{\overline{x}} $$

(3)

Fig. 3

A schematic diagram of force analysis of the spur gear pair under double-tooth drive-side meshing state

In Eq. (1), $F_{fp1}$, $F_{{{\text{fp}} 2}}$, $F_{{{\text{fg}} 1}}$ and $F_{{{\text{fg}} 2}}$ can be expressed as:

$$ F_{{{\text{fp1}}}} = F_{{{\text{fg1}}}} = \mu_{{{\text{d1}}}} (\tau )L_{{{\text{d}} 1}} (\tau )F_{{\text{m}}} ,F_{{{\text{fp2}}}} = F_{{{\text{fg2}}}} = \mu_{{{\text{d2}}}} (\tau )L_{{{\text{d}} 2}} (\tau )F_{{\text{m}}} $$

(4)

where $\mu_{{{\text{d}}i}} (\tau )$ is the friction coefficient, and its direction related to the relative slip velocity of two gears [37, 38], see Sect. 3.4 for details.

$S_{dp1} (\tau )$, $S_{dp2} (\tau )$, $S_{{{\text{dg}} 1}} (\tau )$ and $S_{{{\text{dg}} 2}} (\tau )$ in Eq. (1) are the friction moments of the tooth pairs, respectively, which can be written as:

$$ \left\{ \begin{gathered} S_{dp1} (\tau ) = (R_{{\text{bp}}} + R_{{\text{bg}}} )tan\alpha - \sqrt {R_{{\text{ag}}}^{2} - R_{{\text{bg}}}^{2} } + R_{{\text{bp}}} \omega_{\text{p}} \tau \hfill \\ S_{dg1} (\tau ) = \sqrt {R_{{\text{ag}}}^{2} - R_{{\text{bg}}}^{2} } - R_{{\text{bp}}} \omega_{\text{p}} \tau \hfill \\ \end{gathered} \right.,\left\{ \begin{gathered} S_{dp2} (\tau ) = S_{dp1} (\tau + T_{0} ) \hfill \\ S_{dg2} (\tau ) = S_{dg1} (\tau + T_{0} ) \hfill \\ \end{gathered} \right. $$

(5)

Therefore, the relative torsion dynamic equation of the spur gear pair under the double-tooth drive-side meshing state can be got by subtracting the two formulas in Eq. (1), as expressed in Eq. (6).

$$ m_{\text{e}} \ddot{\overline{x}} + [1 + \mu_{{{\text{d}} 1}} (\tau )g_{d1} (\tau )L_{{{\text{d}} 1}} (\tau ) + \mu_{{{\text{d}} 2}} (\tau )g_{d2} (\tau )L_{{{\text{d}} 2}} (\tau )][\overline{k}_{\text{d}} (\tau )(\overline{x} - \overline{D}(\tau )) + c_{d} \dot{\overline{x}}] = \overline{F}_{\text{m}} + \overline{F}_{\text{h}} (\tau ) $$

(6)

where $m_{\text{e}} = {{I_{\text{p}} I_{\text{g}} } \mathord{\left/ {\vphantom {{I_{\text{p}} I_{\text{g}} } {(R_{{\text{bp}}}^{2} I_{\text{g}} + R_{{\text{bg}}}^{2} I_{\text{p}} )}}} \right. \kern-\nulldelimiterspace} {(R_{{\text{bp}}}^{2} I_{\text{g}} + R_{{\text{bg}}}^{2} I_{\text{p}} )}}$ is the equivalent mass of the gear pair. $\overline{F}_{\text{h}} (\tau ) = - m_{e} \ddot{e}_{d} (\tau )$ is the error excitation force of the gear pair. $g_{dj} (\tau ) = {{\left( {R_{{\text{bp}}} I_{\text{g}} S_{dpj} (\tau ) + R_{{\text{bg}}} I_{\text{p}} S_{dgj} (\tau )} \right)} \mathord{\left/ {\vphantom {{\left( {R_{{\text{bp}}} I_{\text{g}} S_{dpj} (\tau ) + R_{{\text{bg}}} I_{\text{p}} S_{dgj} (\tau )} \right)} {\left( {R_{{\text{bp}}}^{2} I_{\text{g}} + R_{{\text{bg}}}^{2} I_{\text{p}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {R_{{\text{bp}}}^{2} I_{\text{g}} + R_{{\text{bg}}}^{2} I_{\text{p}} } \right)}}\;\;(j = 1,2)$ is the equivalent friction arm of the tooth pair. $\overline{F}_{\text{m}} = {{\left( {R_{{\text{bp}}} I_{g} T_{p} + R_{bg} I_{\text{p}} T_{\text{g}} } \right)} \mathord{\left/ {\vphantom {{\left( {R_{{\text{bp}}} I_{g} T_{p} + R_{bg} I_{\text{p}} T_{\text{g}} } \right)} {\left( {R_{{\text{bp}}}^{2} I_{\text{g}} + R_{{\text{bg}}}^{2} I_{\text{p}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {R_{{\text{bp}}}^{2} I_{\text{g}} + R_{{\text{bg}}}^{2} I_{\text{p}} } \right)}}$ is the average torque of the gear pair.

2.2.2 Single-tooth drive-side meshing

Figure 4 is the force analysis diagram at the meshing point under single-tooth drive-side meshing state. There is one pair of gear tooth engaging. The total load acts on the one pair of gear tooth. According to the principle of gear transmission and 2nd Newtonian law, the absolute torsional vibration equation of the pinion and gear under single-tooth drive-side engaging state can be obtained by Eq. (7).

$$ \left\{ \begin{gathered} I_{\text{p}} \ddot{\theta }_{\text{p}} + R_{{\text{bp}}} F_{{{\text{Np}} 2}} + S_{dp2} (\tau )F_{{{\text{fp}} 2}} = T_{\text{p}} \hfill \\ I_{\text{g}} \ddot{\theta }_{\text{g}} - R_{{\text{bg}}} F_{{{\text{Ng}} 2}} - S_{dg2} (\tau )F_{{{\text{fg}} 2}} = - T_{\text{g}} \hfill \\ \end{gathered} \right. $$

(7)

where

$$ F_{{{\text{Np}} 2}} { = }F_{{{\text{Ng}} 2}} { = }F_{m} ,F_{fp2} { = }F_{fg2} { = }\mu_{{{\text{d}} 2}} (\tau )F_{m} $$

(8)

Fig. 4

A schematic diagram of force analysis of gear teeth under single-tooth drive-side meshing state

Therefore, the relative torsion dynamic equation of the spur gear pair under the single-tooth drive-side meshing state can be written as:

$$ m_{\text{e}} \ddot{\overline{x}} + [1 + \mu_{{{\text{d}} 2}} (\tau )g_{d2} (\tau )][\overline{k}_{\text{d}} (\tau )(\overline{x} - \overline{D}(\tau )) + c_{d} \dot{\overline{x}}] = \overline{F}_{\text{m}} + \overline{F}_{\text{h}} (\tau ) $$

(9)

2.2.3 Double-tooth back-side meshing

When the back-side tooth engages, the rotation direction of the gears remains unchanged, and the back-side tooth profile of gear pushes the drive-side tooth profile of pinion to transmit motion and power along back-side LoA. Figure 5 is a schematic diagram of the force analysis of the gear pair at the meshing points under double-tooth back-side meshing state. Based on 2nd Newtonian law, the absolute torsional vibration equation of the pinion and gear under double-tooth back-side meshing state can be obtained by Eq. (10).

$$ \left\{ \begin{gathered} I_{\text{p}} \ddot{\theta }_{\text{p}} - R_{{\text{bp}}} F_{{{\text{Np}} 1}} - S_{kp1} (\tau )F_{{{\text{fp}} 1}} - R_{{\text{bp}}} F_{{{\text{Np}} 2}} - S_{kp2} (\tau )F_{{{\text{fp}} 2}} = T_{\text{p}} \hfill \\ I_{\text{g}} \ddot{\theta }_{\text{g}} + R_{{\text{bg}}} F_{{{\text{Ng}} 1}} + S_{kg1} (\tau )F_{{{\text{fg}} 1}} + R_{{\text{bg}}} F_{{{\text{Ng}} 2}} + S_{kg2} (\tau )F_{{{\text{fg}} 2}} = - T_{\text{g}} \hfill \\ \end{gathered} \right. $$

(10)

where $F_{{{\text{Np}} 1}}$, $F_{{{\text{Np}} 2}}$, $F_{{{\text{N}} {\text{g}} 1}}$ and $F_{{{\text{N}} {\text{g}} 2}}$ can be expressed as:

$$ F_{{{\text{Np}} 1}} { = }F_{{{\text{Ng}} 1}} { = }L_{k1} (\tau )F_{m}, F_{{{\text{Np}} 2}} { = }F_{{{\text{Ng}} 2}} { = }L_{k2} (\tau )F_{m} $$

(11)

where $L_{{{\text{k1}}}} (\tau )$ and $L_{{{\text{k2}}}} (\tau )$ are the load distribution coefficients of the first and second meshing tooth pairs under double-tooth back-side meshing state [36]. $F_{{\text{m}}}$ is the total dynamic meshing force along back-side LoA, which can be calculated by Eq. (12).

$$ F_{{\text{m}}} = \overline{k}_{k} (\tau )\left[ { - \overline{x} - \overline{D}(\tau )} \right] - c_{{\text{k}}} (\tau )\dot{\overline{x}} $$

(12)

Fig. 5

A schematic diagram of force analysis of gear teeth under double-tooth back-side meshing state

Also, $F_{fp1}$, $F_{{{\text{fp}} 2}}$, $F_{{{\text{fg}} 1}}$ and $F_{{{\text{fg}} 2}}$ can be expressed as:

$$ F_{{{\text{fp1}}}} = F_{{{\text{fg1}}}} = \mu_{{{\text{k1}}}} (\tau )L_{{{\text{k1}}}} (\tau )F_{{\text{m}}} ,F_{{{\text{fp2}}}} = F_{{{\text{fg2}}}} = \mu_{{{\text{k}}2}} (\tau )L_{{{\text{k}}2}} (\tau )F_{{\text{m}}} $$

(13)

where $\mu_{{{\text{k1}}}} (\tau )$ and $\mu_{{{\text{k2}}}} (\tau )$ are the friction coefficients along back-side LoA.

In Eq. (10), $S_{{{\text{kp}} 1}} (\tau )$, $S_{{{\text{kp}} 2}} (\tau )$, $S_{{{\text{kg}} 1}} (\tau )$ and $S_{{{\text{kg}} 2}} (\tau )$ are the friction moments of the tooth pairs at the meshing points under back-side tooth meshing, respectively, which can be expressed as:

$$ \left\{ \begin{gathered} S_{kp1} (\tau ) = \sqrt {R_{{\text{ap}}}^{2} - R_{{\text{bp}}}^{2} } - R_{{\text{bg}}} \omega_{g} \tau \hfill \\ S_{kg1} (\tau ) = (R_{{\text{bp}}} + R_{{\text{bg}}} )tan\alpha - \sqrt {R_{{\text{ap}}}^{2} - R_{{\text{bp}}}^{2} } + R_{{\text{bg}}} \omega_{g} \tau \hfill \\ \end{gathered} \right.,\left\{ \begin{gathered} S_{kp2} (\tau ) = S_{kp1} (\tau + T_{m} ) \hfill \\ S_{kg2} (\tau ) = S_{kg1} (\tau + T_{m} ) \hfill \\ \end{gathered} \right., $$

(14)

Thus, the relative torsion dynamic equation of the spur gear pair under the double-tooth back-side meshing state can be achieved by Eq. (15).

$$ m_{\text{e}} \ddot{\overline{x}} - [1 + \mu_{k1} (\tau )g_{k1} (\tau )L_{k1} (\tau ) + \mu_{k2} (\tau )g_{k2} (\tau )L_{k2} (\tau )][\overline{k}_{k} (\tau )( - \overline{x} - \overline{D}(\tau )) - c_{k} \dot{\overline{x}}] = \overline{F}_{\text{m}} + \overline{F}_{\text{h}} (\tau ) $$

(15)

where $g_{kj} (t) = {{(R_{{\text{bp}}} I_{\text{g}} S_{kpj} (t) + R_{{\text{bg}}} I_{\text{p}} S_{kgj} (t))} \mathord{\left/ {\vphantom {{(R_{{\text{bp}}} I_{\text{g}} S_{kpj} (t) + R_{{\text{bg}}} I_{\text{p}} S_{kgj} (t))} {(R_{{\text{bp}}}^{2} I_{\text{g}} + R_{{\text{bg}}}^{2} I_{\text{p}} )}}} \right. \kern-\nulldelimiterspace} {(R_{{\text{bp}}}^{2} I_{\text{g}} + R_{{\text{bg}}}^{2} I_{\text{p}} )}}\;\;(j = 1,2)$ is the equivalent friction arm of the tooth pairs at the meshing point under back-side tooth meshing state.

2.2.4 Single-tooth back-side meshing

Figure 6 is a schematic diagram of the force analysis of the gear pair at the meshing point under single-tooth back-side meshing state. Based on 2nd Newtonian law, the absolute torsional vibration equation of the pinion and gear can be got by Eq. (16).

$$ \left\{ \begin{gathered} I_{\text{p}} \ddot{\theta }_{\text{p}} - R_{{\text{bp}}} F_{{{\text{Np}} 2}} - S_{kp2} (\tau )F_{{{\text{fp}} 2}} = T_{\text{p}} \hfill \\ I_{\text{g}} \ddot{\theta }_{\text{g}} + R_{{\text{bg}}} F_{{{\text{Ng}} 2}} + S_{kg2} (\tau )F_{{{\text{fg}} 2}} = - T_{\text{g}} \hfill \\ \end{gathered} \right. $$

(16)

Fig. 6

A schematic diagram of force analysis of gear teeth under single-tooth back-side meshing state

where $F_{{{\text{Np}} 2}} \,= \,F_{{{\text{Ng}} 2}} \,= \,F_{m}$ and $F_{fp2} \,= \,F_{fg2} \,= \,\mu_{k2} (\tau )F_{m}$.

Therefore, the relative torsion dynamic equation of the spur gear pair under the single-tooth back-side meshing state can be expressed by Eq. (17).

$$ m_{\text{e}} \ddot{\overline{x}} - [1 + \mu_{k2} (\tau )g_{k2} (\tau )][\overline{k}_{k} (\tau )( - \overline{x} - \overline{D}(\tau )) - c_{k} \dot{\overline{x}}] = \overline{F}_{\text{m}} + \overline{F}_{\text{h}} (\tau ) $$

(17)

2.2.5 Teeth disengaged state

The pinion and gear are separated from each other under teeth disengaged state, and there is no movement and power transmission between the gear pair. The two meshing gears can be used as two mutually independent rotating bodies. Figure 7 is a schematic diagram of the gear pair under teeth disengaged state. According to 2nd Newtonian law, the absolute torsional vibration equation of the pinion and gear under teeth disengaged state can be written as:

$$ \left\{ \begin{gathered} I_{\text{p}} \ddot{\theta }_{\text{p}} = T_{\text{p}} \hfill \\ I_{\text{g}} \ddot{\theta }_{\text{g}} = - T_{\text{g}} \hfill \\ \end{gathered} \right. $$

(18)

Fig. 7

A schematic diagram of the gear pair under teeth disengaged state

Therefore, the relative torsion dynamic equation of the spur gear pair under teeth disengaged state can be obtained by Eq. (19).

$$ m_{\text{e}} \ddot{\overline{x}} = \overline{F}_{\text{m}} + \overline{F}_{\text{h}} (\tau ) $$

(19)

2.3 Dimensionless normalized model of the spur gear system with five-state meshing behavior

Based on the dynamic models of the spur gear pair under five meshing states as well as their boundary conditions, a normalized nonlinear dynamic model with multiple states is obtained by introducing a meshing force function, $f(\overline{x},\overline{D}(\tau ))$, and a meshing state function, $h(\tau ,\overline{x})$, as expressed in Eq. (20). Double-tooth drive-side meshing, single-tooth drive-side meshing, double-tooth back-side meshing, single-tooth back-side meshing and teeth disengaged states are included in this model.

$$ m_{\text{e}} \ddot{\overline{x}} - h(\tau ,\overline{x})f(\overline{x},\overline{D}(\tau )) = \overline{F}_{\text{m}} + \overline{F}_{\text{h}} (\tau ) $$

(20)

where $f(\overline{x},\overline{D}(\tau ))$ and $h(\tau ,\overline{x})$ can be expressed as Eqs. (21) and (22), respectively.

$$ f(\bar{x},\bar{D}(\tau )) = \left\{ {\begin{array}{*{20}l} {\bar{k}_{\text{d} } (\tau )\left[ {\bar{x} - \bar{D}(\tau )} \right] - c_{d} (\tau )\dot{\bar{x}}} \hfill & {(\bar{x} \ge \bar{D}(\tau ))} \hfill \\ 0 \hfill & {(|\bar{x}| < \bar{D}(\tau ))} \hfill \\ {\bar{k}_{k} (\tau )\left[ {\bar{x} + \bar{D}(\tau )} \right] - c_{k} (\tau )\dot{\bar{x}}} \hfill & {(\bar{x} \le - \bar{D}(\tau ))} \hfill \\ \end{array} } \right. $$

(21)

$$ h(\tau ,\overline{x}) = \left\{ \begin{gathered} h_{{\text{dt}}} (\tau ,\overline{x})\;\;\;\;nT_{\text{m}} \le \tau < (\varepsilon_{m} - 1)T_{\text{m}} \;\;(n = 0,1,2 \cdots ) \hfill \\ h_{st} (\tau ,\overline{x})\;\;\;\;(\varepsilon_{m} - 1)T_{\text{m}} \le \tau < (n + 1)T_{\text{m}} \hfill \\ \end{gathered} \right. $$

(22)

where $h_{{\text{dt}}} (\tau ,\overline{x})\;$ and $h_{st} (\tau ,\overline{x})$, respectively, represent the meshing state function of the double-tooth and the single-tooth meshes, which can be written as:

$${h_{{\mathop{\rm dt}\nolimits} }}(\tau ,\bar x) = \left\{ \begin{array}{l} 1 + {\mu _{{\mathop{\rm d}\nolimits} 1}}(\tau ){g_{d1}}(\tau ){L_{{d1}}}(\tau ) + {\mu _{{\mathop{\rm d}\nolimits} 2}}(\tau ){g_{d2}}(\tau ){L_{{d2}}}(\tau )\;\;\;\;\;(\bar x \ge \bar D(\tau ))\\ 0\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (|\bar x| < \bar D(\tau ))\\ 1 + {{\mu }_{{k1}}}(\tau ){g_{k1}}(\tau ){L_{{k1}}}(\tau ) + {{\mu }_{{k2}}}(\tau ){g_{{k2}}}(\tau ){L_{{k2}}}(\tau )\;\;\;\;\;(\bar x \le - \bar D(\tau )) \end{array} \right.,$$

(23)

$${h_{st}}(\tau ,\bar x) = \left\{ \begin{array}{l} 1 + {\mu _{{\mathop{\rm d}\nolimits} 2}}(\tau ){g_{d2}}(\tau \quad (\bar x \ge \bar D(\tau ))\\ 0\quad \quad \quad \quad \quad \quad \quad (|\bar x| < \bar D(\tau ))\\ 1 + {{\mu }_{{k2}}}(\tau ){g_{{k2}}}(\tau )\quad (\bar x \le - \bar D(\tau )) \end{array} \right.$$

(24)

Some dimensionless parameters are defined as: $\omega_{\text{n}} = \sqrt {{{k_{{\text{av}}} } \mathord{\left/ {\vphantom {{k_{{\text{av}}} } {m_{\text{e}} }}} \right. \kern-\nulldelimiterspace} {m_{\text{e}} }}}$ is the natural frequency of the gear pair, where $k_{{\text{av}}}$ is the average meshing stiffness. $\omega = {{\omega_{h} } \mathord{\left/ {\vphantom {{\omega_{h} } {\omega_{\text{n}} }}} \right. \kern-\nulldelimiterspace} {\omega_{\text{n}} }}$ is the dimensionless meshing frequency, where $\omega_{h}$ is the dimensional meshing frequency. $t = {\tau \mathord{\left/ {\vphantom {\tau {\omega_{\text{n}} }}} \right. \kern-\nulldelimiterspace} {\omega_{\text{n}} }}$ is dimensionless time. $D(t) = {{\overline{D}(t)} \mathord{\left/ {\vphantom {{\overline{D}(t)} {D_{\text{c}} }}} \right. \kern-\nulldelimiterspace} {D_{\text{c}} }}$ is the dimensionless time-varying backlash, $D_{\text{c}}$ is the characteristic size. The remaindered dimensionless parameters are $x_{3} = {{\overline{x}} \mathord{\left/ {\vphantom {{\overline{x}} {D_{c} }}} \right. \kern-\nulldelimiterspace} {D_{c} }}$, $k_{d} (t) = {{\overline{k}_{d} (\tau )} \mathord{\left/ {\vphantom {{\overline{k}_{d} (\tau )} {(m_{\text{e}} \omega_{n}^{2} )}}} \right. \kern-\nulldelimiterspace} {(m_{\text{e}} \omega_{n}^{2} )}}$, $k_{k} (t) = {{\overline{k}_{k} (\tau )} \mathord{\left/ {\vphantom {{\overline{k}_{k} (\tau )} {(m_{\text{e}} \omega_{n}^{2} )}}} \right. \kern-\nulldelimiterspace} {(m_{\text{e}} \omega_{n}^{2} )}}$, $\xi_{{\text{d}}} (t) = {{c_{{\text{d}}} } \mathord{\left/ {\vphantom {{c_{{\text{d}}} } {(m_{\text{e}} \omega_{\text{n}} )}}} \right. \kern-\nulldelimiterspace} {(m_{\text{e}} \omega_{\text{n}} )}} = 2\varsigma \sqrt {k_{{\text{d}}} (t)}$, $\xi_{{\text{k}}} (t) = {{c_{{\text{k}}} } \mathord{\left/ {\vphantom {{c_{{\text{k}}} } {(m_{\text{e}} \omega_{\text{n}} )}}} \right. \kern-\nulldelimiterspace} {(m_{\text{e}} \omega_{\text{n}} )}} = 2\varsigma \sqrt {k_{{\text{k}}} (t)}$, $\varepsilon \omega^{2} \cos (\omega t) = {{\overline{F}_{\text{h}} (t)} \mathord{\left/ {\vphantom {{\overline{F}_{\text{h}} (t)} {D_{\text{c}} }}} \right. \kern-\nulldelimiterspace} {D_{\text{c}} }}$, $F = {{\overline{F}_{m} } \mathord{\left/ {\vphantom {{\overline{F}_{m} } {(m_{\text{e}} D_{c} \omega_{\text{n}}^{2} )}}} \right. \kern-\nulldelimiterspace} {(m_{\text{e}} D_{c} \omega_{\text{n}}^{2} )}}$.

Thus, the dimensionless form of Eq. (20) is expressed by Eq. (25).

$$ \ddot{x}_{3} + h(t,x_{3} )\left[ {k(t)f(x_{3} ,D(t)) + \xi \dot{x}_{3} } \right] = F + \varepsilon \omega^{2} \cos (\omega t) $$

(25)

where

$$ f(x_{3} ,D(t)) = \left\{ \begin{gathered} k_{\text{d}} (t)\left[ {x_{3} - D(t)} \right] + \xi_{\text{d}} \dot{x}_{3} \;\;\;\;\;\;(x_{3} \ge D(t)) \hfill \\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(|x_{3} | < D(t)) \hfill \\ k_{\text{k}} (t)\left[ {x_{3} + D(t)} \right] + \xi_{k} \dot{x}_{3} \;\;\;\;\;\;(x_{3} \le - D(t)) \hfill \\ \end{gathered} \right., $$

(26)

$$ h(t,x_{3} ) = \left\{ \begin{gathered} h_{{\text{dt}}} (t,x_{3} )\;\;\;\;\;\;nT_{\text{m}} \le t < (\varepsilon_{m} - 1)T_{\text{m}} \;\;(n = 0,1,2 \cdots ) \hfill \\ h_{st} (t,x_{3} )\;\;\;\;\;\;(\varepsilon_{m} - 1)T_{\text{m}} \le t < (n + 1)T_{\text{m}} \hfill \\ \end{gathered} \right., $$

(27)

$${h_{dt}}(t,{x_3}) = \left\{ \begin{array}{l} 1 + {\mu _{d1}}(t){g_{d1}}(t){L_{d1}}(t) + {\mu _{d2}}(t){g_{d2}}(t){L_{d2}}(t)\quad ({x_3} \ge D(t))\\ 0\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (|{x_3}| < D(t))\\ 1 + {\mu _{k1}}(t){g_{k1}}(t){L_{k1}}(t) + {\mu _{k2}}(t){g_{k2}}(t){L_{k2}}(t)\quad ({x_3} \le - D(t)) \end{array} \right.,$$

(28)

$${h_{st}}(t,{x_3}) = \left\{ \begin{array}{l} 1 + {\mu _{d2}}(t){g_{d2}}(t)\quad \quad ({x_3} \ge D(t))\\ 0\quad \quad \quad \quad \quad \quad \quad \quad (|{x_3}| < D(t))\\ 1 + {\mu _{k2}}(t){g_{k2}}(t)\quad \quad ({x_3} \le - D(t)) \end{array} \right.$$

(29)

The dimensionless dynamic meshing force F_m is calculated by Eq. (30).

$$ F_{m} = h(t,x_{3} )\left[ {k(t)f(x_{3} ,D(t)) + \xi \dot{x}_{3} } \right] $$

(30)

Therefore, the dimensionless normalized expression of nonlinear dynamic model of the spur gear pair including five states (such as double-tooth drive-side meshing, single-tooth drive-side meshing, double-tooth back-side meshing, single-tooth back-side meshing, and teeth disengaging) and time-varying meshing parameters (such as time-varying meshing stiffness, time-varying meshing damping, and time-varying backlash) is obtained, as written in Eq. (25). This model provides a basis for the study of nonlinear dynamics and multi-state meshing behavior of a spur gear system. Due to the significant importance of the time-varying meshing parameters to the nonlinear dynamics and meshing characteristics of the gear system, the time-varying backlash, the time-varying meshing stiffness, and the time-varying meshing damping considering the elastic deformation and thermal deformation at the meshing point for gear teeth as well as the deformation of the oil film thickness are calculated, as seen from Sect. 3.1

3 Calculating of time-varying parameters

3.1 Time-varying backlash

Time-varying backlash can identify multi-state meshing behavior of spur gear system. The elastic deformation of gear tooth and the deformation of the oil film thickness increase backlash, and the thermal deformation of tooth reduces backlash. It is assumed that the gear pair is installed as standard, thus the time-varying backlash, D(t), is expressed as [29]:

$$ D(t){\text{ = d}}_{{0}} + d(t) $$

(31)

where $d_{0}$ is the amount of static backlash, which refers to the tooth side clearance reserved in the design and is considered a constant. $d(t)$ is a time variable caused by the elastic deformation and thermal deformation of gear teeth as well as the oil film thickness deformation at the meshing point. $d(t)$ can be obtained by Eq. (31) [29].

$$ d(t) = \left[ {\delta_{{\text{e}}} (t) - \delta_{{\text{t}}} (t) - h_{oil} (t)} \right]cos(2\alpha ) $$

(32)

where α is the pressure angle. $\delta_{{\text{e}}} (t)$, $\delta_{{\text{t}}} (t)$ and $h_{oil} (t)$ are the elastic deformation amount, thermal deformation amount and oil film thickness deformation at the meshing point, respectively. The detailed calculation of these deformations can be found in Ref. [29].

The parameter properties of the studied gear pair are shown in Table 1. The static backlash amount is $d_{0} = 200{\mu m}$ in this work. The distribution characteristics of the time-varying backlash along the action line are shown in Fig. 8. AB and CD represent the double-tooth meshing areas, and BC is the single-tooth meshing area. The time-varying backlash in the single-tooth area is greater than the one in the double-tooth areas. The backlash jumps when switching between single and double teeth, such as B and C points. Additionally, the time-varying backlash can be regarded as a constant in the single-tooth and double-tooth areas due to its very small change, as shown in Fig. 8. Therefore, half of the dimensionless time-varying backlash is Ds = 0.89 in the single-tooth area and Dd = 0.79 in the double-tooth areas. This helps to identify and analyze the single-tooth and double-tooth meshing behavior of the gear pair.

Table 1 Parameter properties of the studied spur gear system

Fig. 8

The time-varying backlash along the tooth profile or LoA

3.2 Time-varying meshing stiffness

The accuracy of the time-varying meshing stiffness model reflects the precision and validity of the dynamic model of the gear system. The mesh stiffness is mainly characterized by the elastic stiffness in the dynamic modeling and analysis of the gear systems [10,11,12,13,14,15]. Recently, many improved time-varying meshing stiffness models have been proposed to consider different influencing factors. Ma et al. [39] established an improved time-varying mesh stiffness considering the effects of ETC, nonlinear contact stiffness, revised fillet-foundation stiffness, and tooth profile modification. Also, various time-varying stiffness calculation models including the effects of crack propagation path [40], the realistic spalling morphology [41], and roughness [42] are obtained. However, the influence of gear temperature is not considered in these time-varying mesh stiffness models. The thermal deformation caused by the tooth temperature is of great significance for the meshing stiffness of spur gear systems during gear meshing. This thermal deformation is different from the elastic deformation caused by the contact load, such as Hertzian contact deformation, shear deformation, bending deformation and axial compression deformation, etc. In this paper, the stiffness caused by thermal deformation is defined as temperature stiffness. As the reviewer said, the temperature stiffness should be an elastic stiffness considering the effect of temperature. However, there is a certain difference between elastic stiffness and temperature stiffness. That is, the elastic stiffness does not depend on the change of the load, but the temperature stiffness is positively correlated with the load when the thermal deformation is constant. Therefore, in order to highlight this difference, the temperature stiffness is defined additionally. The temperature stiffness and the oil film stiffness caused by the oil film thickness deformation have an important influence on the time-varying meshing stiffness of the gear system. Thus, a comprehensive time-varying meshing stiffness model, $k_{m} (t)$, including elastic stiffness, temperature stiffness and oil film stiffness is developed in this paper, as expressed as Eq. (33).

$$ \frac{1}{{k_{m} (t)}}{ = }\frac{1}{{k_{{\text{e}}} (t)}} + \frac{1}{{k_{{\text{t}}} (t)}} + \frac{1}{{k_{{{\text{oil}}}} (t)}} $$

(33)

where $k_{e} (t)$, $k_{{\text{t}}} (t)$ and $k_{{{\text{oil}}}} (t)$ are elastic stiffness, temperature stiffness and oil film stiffness, respectively. The elastic stiffness, $k_{e} (t)$, includes bending stiffness $k_{{{\text{eb}}}} (t)$, axial compression stiffness $k_{{{\text{ea}}}} (t)$, shear stiffness $k_{{{\text{es}}}} (t)$, fillet-foundation stiffness $k_{{{\text{ef}}}} (t)$ and Hertzian contact stiffness $k_{{{\text{eh}}}}$, which can be written as in Eq. (34) [12,13,14,15].

$$ \frac{1}{{k_{e} (t)}}{ = }\frac{1}{{k_{{{\text{eh}}}} }} + \frac{1}{{k_{{{\text{eb}}}} (t)}} + \frac{1}{{k_{{{\text{ea}}}} (t)}} + \frac{1}{{k_{{{\text{es}}}} (t)}} + \frac{1}{{k_{{{\text{ef}}}} (t)}} $$

(34)

The temperature stiffness, $k_{{\text{t}}} (t)$, can be calculated by Eq. (35).

$$ k_{{\text{t}}} (t){ = }\frac{{F_{{\text{m}}} }}{{\delta_{{\text{t}}} (t)}} $$

(35)

where $F_{{\text{m}}}$ and $\delta_{{\text{t}}} (t)$ are the dynamic meshing force and thermal deformation amount at the meshing point, respectively.

The oil film stiffness, $k_{{{\text{oil}}}} (t)$, can be got by Eq. (36) [43].

$$ k_{{{{\rm oil}}}} (t) = \frac{{\Delta F_{m} }}{{\Delta H_{{{{\rm oil}}}} (t)}} $$

(36)

where $\Delta F_{m}$ is the change in load, and $\Delta H_{{{\text{oil}}}} (t)$ is the change in oil film thickness caused by $\Delta F_{m}$.

The studied gear parameters are seen from Table 1. The oil film stiffness $k_{{{\text{oil}}}} (t)$, temperature stiffness $k_{{\text{t}}} (t)$, elastic stiffness $k_{e} (t)$ as well as comprehensive time-varying meshing stiffness $k_{m} (t)$ along the action line (LoA) for one tooth pair are shown in Fig. 9a and b. It is thus clear that the introduction of oil film stiffness and temperature stiffness reduces the comprehensive time-varying meshing stiffness. In contrast, the temperature stiffness has a greater effect on the comprehensive time-varying meshing stiffness, while the effect of the oil film stiffness is small due to its larger value.

Fig. 9

The changes of the time-varying meshing stiffness along the action line (LoA): a The oil film stiffness $k_{{{\text{oil}}}} (t)$; b Elastic stiffness $k_{e} (t)$, temperature stiffness $k_{{\text{t}}} (t)$ and comprehensive time-varying meshing stiffness $k_{m} (t)$

According to the boundary conditions of single-tooth engagement and double-tooth engagement in the time domain: single-tooth engagement $(\varepsilon_{m} - 1)T_{\text{m}} \le t < (n + 1)T_{\text{m}}$ and double-tooth engagement $nT_{\text{m}} \le t < (\varepsilon_{m} - 1)T_{\text{m}} \;\;(n = 0,1,2 \cdots )$, the expression of the comprehensive time-varying meshing stiffness calculation model under single- and double-tooth engaging conditions is expressed as Eq. (37).

$$ \frac{1}{{k_{m} (t)}}{ = }\left\{ \begin{gathered} \frac{1}{{k_{{{\text{eh}}i}} }} + \frac{1}{{k_{{{\text{eb}}i}} (t)}} + \frac{1}{{k_{{{\text{ea}}i}} (t)}} + \frac{1}{{k_{{{\text{es}}i}} (t)}} + \frac{1}{{k_{{{\text{ef}}i}} (t)}} + \frac{1}{{k_{{{\text{t}}i}} (t)}} + \frac{1}{{k_{{{\text{oil}}i}} (t)}}\;,\;\;\;\;\;\;\;\;\;(\varepsilon_{m} - 1)T_{\text{m}} \le t < (n + 1)T_{\text{m}} \hfill \\ \sum\limits_{i = }^{2} {\left( {\frac{1}{{k_{{{\text{eh}}i}} }} + \frac{1}{{k_{{{\text{eb}}i}} (t)}} + \frac{1}{{k_{{{\text{ea}}i}} (t)}} + \frac{1}{{k_{{{\text{es}}i}} (t)}} + \frac{1}{{k_{{{\text{ef}}i}} (t)}} + \frac{1}{{k_{{{\text{t}}i}} (t)}} + \frac{1}{{k_{{{\text{oil}}i}} (t)}}} \right),\;\;\;\;\;nT_{\text{m}} \le t < (\varepsilon_{m} - 1)T_{\text{m}} \;\;} \hfill \\ \end{gathered} \right. $$

(37)

A comparison of the time-varying meshing stiffness in this paper with the one in the published literatures is carried out in order to verify the proposed model including the temperature stiffness and oil film stiffness, as illustrated in Fig. 10. The dark blue curve is the time-varying meshing stiffness calculated by the proposed model including the temperature stiffness and oil film stiffness. The red curve represents the time-varying meshing stiffness calculated from the published literature models [10,11,12,13,14,15], which is only the elastic stiffness. The stiffness proposed in this paper is less than the stiffness in the literature because the temperature stiffness and oil film stiffness are considered. However, the stiffness changes of the two models are consistent and within the same order of magnitude. Notably, the thermal deformation caused by temperature changes and oil film thickness deformation can reduce the meshing stiffness of the gear system. Therefore, the influence of temperature and lubrication cannot be ignored in the analysis of gear meshing vibration.

Fig. 10

A comparison between the stiffness proposed in this article and the stiffness of published literature

3.3 Time-varying meshing damping

The meshing damping of the spur gear pair is related to the meshing stiffness. Thus, the time-varying meshing damping $c_{m} (t)$ of the spur gear pair can be calculated by Eq. (38).

$$ c_{m} (t)\,{ = }\,2\varsigma \sqrt {m_{e} k_{m} (t)} $$

(38)

where $\varsigma$ is the meshing damping rate and is $\varsigma = 0.07$ in this work.

3.4 Time-varying friction coefficient under EHL

The oil film stiffness under the elastohydrodynamic lubrication (EHL) condition is calculated in this work, so the time-varying friction coefficient under EHL condition is referred to in the dynamic modeling and analysis of the gear system. Based on the studies of He et al. [44], the time-varying friction formula for the ith meshing tooth pair are expressed as Eq. (39).

$$ \mu_{i} (t) = \lambda_{i} (t)e^{{f(SR_{i} (t),P_{hi} (t),\eta_{{{\text{M}} ,}} R_{{\text{aavg}}} )}} P_{{{\text{h}} i}}^{{b_{2} }} \left| {SR_{i} (t)} \right|^{{b_{3} }} \cdot {{(v_{ei} (t)} \mathord{\left/ {\vphantom {{(v_{ei} (t)} 2}} \right. \kern-\nulldelimiterspace} 2})^{{b_{6} }} \eta_{\text{M}}^{{b_{7} }} \rho_{{{\text{r}} i}}^{{b_{8} }} (t) $$

(39a)

$$ f(SR_{i} (t),P_{hi} (t),\eta_{{{\text{M}} ,}} R_{{\text{aavg}}} ) = b_{1} + b_{4} |SR_{i} (t)|P_{{{\text{h}} i}} (t)\lg \eta_{\text{M}} + b_{5} {\text{e}}^{{ - |SR_{i} (t)P_{hi} (t)\lg \eta_{\text{M}} |}} + b_{9} {\text{e}}^{{R_{{\text{aavg}}} }} $$

(39b)

where $R_{{\text{aavg}}} = (R_{{{\text{a}} 1}} + R_{a2} )/2$ is the averaged surface roughness and $\eta_{\text{M}} = 0.058$ is the dynamic viscosity of the oil entering. The maximum Hertzian pressure $P_{hi} (t)$ of the ith meshing tooth pair is written as Eq. (40).

$$ P_{hi} (t) = \sqrt {{{f_{e} } \mathord{\left/ {\vphantom {{f_{e} } {\left[ {{\uppi }\rho_{r} (t)(\frac{{1 - v^{2} }}{E})} \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {{\uppi }\rho_{r} (t)(\frac{{1 - v^{2} }}{E})} \right]}}} $$

(40)

Herein, $f_{e}$ is the unit normal load, and $\rho {}_{ri}(t)$ is the composite relative radius of curvature of the ith meshing tooth pair.

In Eq. (39), $SR_{i} (t) = 2v_{si} (t)/v_{ei} (t)$ is the dimensionless slide-to-roll ratio of the ith meshing tooth pair. $v_{si} (t)$ is the sliding velocity of the ith meshing tooth pair. $v_{ei} (t)$ is the entraining velocity of the ith meshing tooth pair. $\lambda_{i} (t)$ is the direction coefficient of the friction force and can be obtained by the Eq. (41).

$$ \lambda_{i} (t) = sgn\left[ {v_{{{\text{s}} i}} (t)} \right] $$

(41)

Herein, sgn [•] is the sign function, used to determine the direction of friction force.

4 Results and discussion

4.1 Characterization of five-state meshing behavior

Based on the analysis in Sect. 2.1, five-state meshing behavior of the spur gear system, such as double-tooth drive-side meshing, single-tooth drive-side meshing, double-tooth back-side meshing, single-tooth back-side meshing as well as teeth disengaging, is obtained. Therefore, the existence areas of the five-state meshing behavior in the phase plane can be observed according to the numerical relationship between the teeth relative displacement and time-varying backlash, as shown in Fig. 11. Ds is half of the dimensionless backlash in the single-tooth area and Dd is half of the dimensionless backlash in the double-tooth areas, where Ds > Dd.

Fig. 11

The existence area of five meshing states in the phase plane

As shown in Fig. 11, single-tooth drive-side meshing only occurs in area I (x₃ ≥ Ds). Single-tooth disengagement occurs in $I{\text{I}} \cup {\text{III}} \cup {\text{IV}}$ area (|x₃|< Ds). Single-tooth back-side meshing only occurs in $V$ area (x₃ ≤ -Ds). Also, double-tooth drive-side meshing occurs in ${\text{I}} \cup {\text{II}}$ area (x₃ ≥ Dd). Double-tooth disengagement only occurs in ${\text{III}}$ area (|x₃|< Dd). Double-tooth back-side meshing occurs in $IV \cup V$ area (x₃ ≤ -Dd). Additionally, area $I$ only appears single-tooth and double-tooth drive-side meshes, where the phase orbit is characterized by the symbol Γ1. area $II$ appears single-tooth disengagement and double-tooth drive-side meshing, where the phase orbit is characterized by Γ2. area $III$ appears single-tooth disengagement, where the phase orbit is characterized by Γ3. area $IV$ appears single-tooth disengagement and double-tooth back-side meshing, where the phase orbit is characterized by Γ4. area $V$ appears single-tooth and double-tooth back-side meshes, where the phase orbit is characterized by Γ5.

In order to clearly solve and identify the five-state meshing behavior of the gear system, five different Poincaré mapping sections can be constructed based on Fig. 11, such as time-period mapping section, single-tooth disengagement mapping section, single-tooth back-side contact mapping section, double-tooth disengagement mapping section, and double-tooth back-side contact mapping section below.

• (1) Time-period mapping section: ${\Sigma _n} = \left\{ {({x_3},{{\dot x}_3},t) \in {R^2} \times {R^ + },\bmod (t,2\pi /\omega ) = 0} \right\}$;

• (2) Single-tooth disengagement mapping section: ${\Sigma _p} = \left\{ {({x_3},{{\dot x}_3},t) \in {R^2} \times {R^ + },{x_3} = Dd} \right\}$;

• (3) Single-tooth back-side contact mapping section: ${\Sigma _q} = \left\{ {({x_3},{{\dot x}_3},t) \in {R^2} \times {R^ + },{x_3} = - Dd} \right\}$;

• (4) Double-tooth disengagement mapping section: ${\Sigma _r} = \left\{ {({x_3},{{\dot x}_3},t) \in {R^2} \times {R^ + },{x_3} = Ds} \right\}$;

• (5) Double-tooth back-side contact mapping section: ${\Sigma _s} = \left\{ {({x_3},{{\dot x}_3},t) \in {R^2} \times {R^ + },{x_3} = - Ds} \right\}$.

According to the five different Poincaré mapping sections above, the multi-state meshing behavior of the gear system can be characterized by the symbol n-p-q-r-s. n represents the number of system periodic motion; p represents the number of single-tooth disengagement; q represents the number of single-tooth back-side meshing; r represents the number of double-tooth disengagement; s represents the number of double-tooth back-side meshing. If p, q, r or s is zero, it indicates that the there is no single-tooth disengagement, single-tooth back-side engagement, double-tooth disengagement, or double-tooth back-side engagement occurring. Thus, the multi-state meshing behavior and nonlinear dynamics of the gear system are obtained by analyzing the characteristics of n-p-q-r-s.

4.2 Mechanism of multi-state meshing behavior

The nonlinear dynamic equation, Eq. (25), of the spur gear system including five-state meshing behavior and time-varying meshing parameters is solved numerically by using fourth-order Runge–Kutta method. The mechanism of five-state meshing behavior is analyzed in this section by means of phase diagrams, Poincaré maps and dynamic meshing force time history diagrams.

4.2.1 Drive-side tooth meshing state

The system dimensionless parameters ω = 0.3, F = 0.1 and ε = 0.15 are fixed. Figure 12a and b shows the phase diagram and the time history diagram of the corresponding dynamic meshing force, respectively. The relative displacement of the system is always greater than half of the single-tooth and double-tooth backlash, x₃ > Ds = 0.89 and x₃ > Dd = 0.79. Also, the dynamic meshing force of the system is always greater than zero, F_m > 0.0. It means that the drive-side tooth meshing persists under this parameter condition, and there are no teeth disengagement and back-side tooth meshing. The teeth relative displacement and relative speed of the gear system jump between single tooth and double teeth more obviously because of their small vibration amplitude, as shown in Fig. 12a.

Fig. 12

Drive-side tooth meshing state: a phase diagram; b time history diagram of the dynamic meshing force

4.2.2 Drive-side tooth meshing and teeth disengaged states

ω = 0.3 and F = 0.1 are fixed and other parameters are kept unchanged. Figure 13a is the phase diagram and Poincaré map where both drive-side tooth mesh and teeth disengagement are observed. The symbol “•” represents Poincaré mapping point. The system performs a stable period-1 behavior as shown in Fig. 13a, and the phase orbit is distributed in I, II and III regions, as in red marked by Γ1, blue marked by Γ2 and purple marked by Γ3. Figure 13b is the time history diagram of the corresponding dynamic meshing force F_m. F_m changes periodically between greater than zero (F_m > 0) and equal to zero (F_m = 0). This means that the drive-side tooth mesh and teeth disengagement occur periodically. The disengagement state occurs in the single-tooth area and the double-tooth area. As shown in Fig. 13b, when the drive-side tooth mesh (F_m > 0) transitions to the teeth disengagement (F_m = 0), the dynamic meshing force has two sudden changes, namely: F_m > 0 → F_m = 0 → F_m < 0 → F_m = 0 → F_m > 0 → F_m = 0 → F_m < 0 → F_m = 0 (partially enlarged in the picture).

Fig. 13

Drive-side tooth meshing and teeth disengaged state: a phase diagram and Poincaré map; b time history diagram of the dynamic meshing force

In order to reveal the mechanism of teeth disengagement, it is necessary to analyze the mutation process of dynamic meshing force in detail. Figure 14 shows the changes of the dynamic meshing force and teeth relative displacement in the time domain when the drive-side tooth mesh is transferred to the teeth disengagement. The dynamic meshing force of the system jumps periodically, and the force of the double-tooth area (double-tooth F_m) is greater than that of the single-tooth area (single-tooth F_m).

Fig. 14

Mechanism of the transition from drive-side tooth meshing to teeth disengagement

The dynamic meshing forces are greater than zero before point F1, and the system performs drive-side tooth meshing state. At point F1, the single-tooth F_m decreases to zero, and then increases in the opposite direction (see area F1F2). In the F1F2 area, the system is still in contact with the single-tooth drive-side because the teeth relative displacement is greater than half of the single-tooth backlash (x₃ > Ds). However, the meshing gear teeth tend to separate from each other due to the change in the direction of the meshing force. At point F2, the relative displacement is equal to half of the single-tooth backlash (x₃ = Ds) and the single-tooth F_m suddenly becomes zero. It indicates that the meshing gear teeth are about to separate. Subsequently, teeth relative displacement is smaller than half of the single-tooth backlash, and the single-tooth meshing force is equal to zero, and thus the single-tooth disengagement occurs in the area F2F3. Double-tooth drive-side meshing persists in F2F3 since double-tooth F_m is greater than zero and the teeth relative displacement is higher than half of the double-tooth backlash (x₃ > Dd). The double-tooth meshing force decreases to zero at point F3 and then increases in the opposite direction (see area F3F4). In the F3F4 area, the system is in double-tooth drive-side contact state because the relative displacement is still greater than half of the double-tooth backlash (x₃ > Dd). But the meshing teeth tend to separate from each other due to the change of the direction of the meshing force. At F4, x₃ = Dd and double-tooth F_m = 0 mean that the meshing gear teeth are about to separate. And then, the relative displacement is less than half of the double-tooth backlash (x₃ < Dd) and the dynamic meshing force is equal to zero (F_m = 0). The system is completely disengaged after F4.

Therefore, the transition process from drive-side tooth mesh to teeth disengagement occurs in the F1F4 area. The mechanism of gear teeth disengagement is described as follows. The single-tooth dynamic meshing force first decreases to zero and then increases in the opposite direction until the relative teeth displacement is equal to the half value of the single-tooth backlash (point F2). Then the teeth disengagement occurs in the single-tooth area (such as F2F3 area). Subsequently, the double-tooth dynamic meshing force decreases to zero, and then increases in the opposite direction. Until the relative teeth displacement is equal to the half value of the double-tooth backlash (point F4), the double-tooth dynamic meshing force suddenly decreases to zero, and then the system is completely in a state of teeth disengagement. Thus, the dynamic meshing force experienced two sudden changes in the direction, respectively, in the single-tooth and double-tooth areas, resulting in the occurrence of gear teeth disengagement.

4.2.3 Back-side tooth meshing and teeth disengaged states

Take ω = 1.4, other parameters are consistent with those in Fig. 13. Figure 15a is the phase diagram and Poincaré map of the gear system where double-tooth drive-side mesh (Γ1 and Γ2), single-tooth drive-side mesh (Γ1), double-tooth back-side mesh (Γ4 and Γ5), single-tooth back-side mesh (Γ5) and teeth disengagement (Γ3) are observed. The system performs a stable period-3 behavior and its phase orbit are distributed in I, II, III, IV and V regions. The meshing state of the system becomes extremely complicated. Figure 15b shows the time history of the corresponding dynamic meshing force F_m, which changes periodically between greater than zero (F_m > 0), equal to zero (F_m = 0) and less than zero (F_m < 0). It indicates that the single-tooth drive-side meshing, double-tooth drive-side meshing, single-tooth back-side meshing, double-tooth back-side meshing and teeth disengagement appear periodically as shown in Fig. 15a. Additionally, when the drive-side tooth meshing (F_m > 0) transitions to teeth disengaging (F_m = 0) or the back-side tooth meshing (F_m < 0) transitions to teeth disengaging (F_m = 0), the dynamic meshing force has undergone two sudden changes, such as local magnifications in the picture. The mutation process from drive-side tooth engagement to teeth disengagement is the same as that in Fig. 14. However, the mutation process from back-side tooth meshing to teeth disengagement is analyzed in detail below.

Fig. 15

Drive-side tooth meshing and teeth disengaged state: a phase diagram and Poincaré map; b time history diagram of the dynamic meshing force

Figure 16 shows the changes of dynamic meshing force F_m and teeth relative displacement x₃ in the time domain when the back-side tooth meshing transitions to teeth disengagement. The dynamic meshing forces are less than zero, and the system performs the back-side tooth meshing state before point F1. At F1, the absolute value of single-tooth F_m is reduced to zero and then increases in the opposite direction (see area F1F2). Between F1 and F2, the single-tooth drive-side contact persists because the teeth relative displacement is less than half of the negative value of single-tooth backlash (x₃ < −Ds). However, the contact teeth tend to separate from each other in the single-tooth area because of the change in the direction of the dynamic meshing force (single-tooth F_m). At F2, the relative displacement is equal to half of the negative value of single-tooth backlash (x₃ = −Ds) and the single-tooth F_m suddenly becomes zero. It means that the back-side meshing teeth are about to separate. Subsequently, the relative displacement is greater than half of the negative value of single-tooth backlash (x₃ > −Ds), and the single-tooth meshing force is equal to zero, so the single-tooth disengagement appears between F2 and F3. However, double-tooth back-side meshing persists in the F2F3 area because double-tooth F_m is less than zero and the teeth relative displacement is lower than half of the negative value of double-tooth backlash (x₃ < -Dd). The double-tooth meshing force decreases to zero at point F3 and then increases in the opposite direction (see area F3F4). The double-tooth drive-side contact state persists because the relative displacement is less than half of the negative value of double-tooth backlash (x₃ < −Dd) between F3 and F4. But the double-tooth meshing teeth tend to separate from each other due to the change of the meshing force in direction. At F4, x₃ = −Dd and single-tooth F_m = 0 indicate that double-tooth meshing teeth are about to separate. Subsequently, the relative displacement is larger than half of the negative value of double-tooth backlash (x₃ > −Dd) and the dynamic meshing force is equal to zero (F_m = 0). The completely teeth disengagement is obtained after F4.

Fig. 16

Mechanism of the transition from back-side tooth meshing to teeth disengagement

Therefore, the transition process from back-side tooth meshing to teeth disengagement appears in the F1F4 area. The single-tooth dynamic meshing force first changes in direction between F1 and F2. And then single-tooth back-side teeth disengagement occurs between F2 and F3. Subsequently, the double-tooth dynamic meshing force changes in direction between F3 and F4. Finally, the system enters a completely teeth disengaged state after point F4. Similarly, the mutation in the direction of the dynamic meshing force leads to the occurrence of teeth disengagement.

4.3 Bifurcation and evolution of five-state meshing behavior

Due to time-varying meshing stiffness, time-varying backlash, dynamic transmission error, and switching between different meshing states, the gear system becomes a non-smooth nonlinear strong time-varying system. The five-state meshing behavior and nonlinear dynamics caused by the system parameters have a significant impact on the transmission efficiency and motion quality of the system. The effects of meshing frequency, load factor, and transmission error coefficient on the nonlinear dynamics of five-state meshing behavior of the gear system are discussed in detail as follows.

4.3.1 Effect of meshing frequency

Take F = 0.13 and ε = 0.25 and the meshing frequency ω is used as the control parameter. Based on five different Poincaré mapping sections established in Sect. 3.1, the bifurcation diagram of the five-state meshing behavior of the system and the corresponding top Lyapunov exponent (TLE) are shown in Fig. 17a–d increasing in ω. Figure 17a is the bifurcation diagram in time-period mapping section Σ_n in blue. In Fig. 17b, the bifurcation diagrams in single-tooth disengagement mapping section Σ_p and single-tooth back-side contact mapping section Σ_q are in magenta and green, respectively. In Fig. 17c, the bifurcation diagrams in double-tooth disengagement mapping section Σ_r and double-tooth back-side contact mapping section Σ_s are in red and grass green, respectively. Figure 17d shows the corresponding top Lyapunov exponent (TLE), which is used to analyze the dynamic stability of the system. TLE value less than zero indicates a stable periodic behavior, and TLE value greater than zero means an unstable chaotic behavior. TLE value is approximately equal to zero or jumps indicate the bifurcation or sudden change of the dynamic behavior of the system, such as the black dot “•” (A, B, C, D, E and F).

Fig. 17

Bifurcation diagrams in different Poincaré mapping sections and corresponding top Lyapunov exponent (TLE) with the increase in ω. a time-period mapping section in blue; b single-tooth disengagement mapping section in magenta and single-tooth back-side contact mapping section in green; c double-tooth disengagement mapping section in red and double-tooth back-side contact mapping section in grass green; d top Lyapunov exponent (TLE)

When the meshing frequency ω is small (left side of point A), the system shows a stable 1-0-0-0-0 behavior, where no teeth disengagement and back-side tooth meshing occur. The corresponding TLE values are lower than zero. Figure 18a shows the phase portrait and Poincaré map calculated for ω = 0.2 where the symbol “•” is Poincaré mapping point. The vibration amplitude between single-tooth and double-tooth is obviously jumping due to the slight vibration. The time history of the corresponding dynamic meshing force is shown in Fig. 18b, which is always greater than zero. With the increase in ω, single-tooth disengagement appears at point A. The system performs a stable 1-1-0-0-0 behavior between A and B points. The phase portrait and Poincaré map are displayed in Fig. 18c as ω = 0.5. The phase portrait crosses the half of the value of single-tooth backlash (Ds = 0.89), where Γ1 is the portrait of single-tooth and double-tooth drive-side meshing portrait and Γ2 is the portrait of single-tooth disengagement and double-tooth drive-side mesh. Figure 18d shows the corresponding meshing force in time domain. It is observed that the dynamic meshing force is equal to zero in the single-tooth area (see partial enlargement), and the dynamic meshing force in the double-tooth area is always greater than zero. This means that the single-tooth disengagement occurs periodically.

Fig. 18

Phase portraits, Poincaré maps, and time histories of dynamic meshing force. a Phase portrait and Poincaré mapping as ω = 0.2; b Dynamic meshing force as ω = 0.2; c Phase portrait and Poincaré mapping as ω = 0.5; d Dynamic meshing force as ω = 0.5; e Phase portrait and Poincaré mapping as ω = 0.68; f Dynamic meshing force as ω = 0.68; g Phase portrait and Poincaré mapping as ω = 0.74; h Dynamic meshing force as ω = 0.74; i Phase portrait and Poincaré mapping as ω = 0.87; j Dynamic meshing force as ω = 0.87; k Poincaré mapping as ω = 1.05; l Dynamic meshing force as ω = 1.05; m Phase portrait and Poincaré mapping as ω = 1.75; n Dynamic meshing force as ω = 1.75; m Phase portrait and Poincaré mapping as ω = 2.0

At B, 1-1-0-0-0 behavior jumps and transitions to a 1-1-1-1-1 behavior and then the system performs a stable 1-1-1-1-1 behavior between B and C points. The multi-state dynamics of the system become more complicated. The phase trajectory of the system passes through half of the value and half of the negative value of the single-tooth and double-tooth backlash, as marked by Γ1, Γ2, Γ3, Γ4 and Γ5, as shown in Fig. 18e. The phase trajectory of the system becomes smoother than that of Fig. 18a and c due to the expansion of its topology, and thus the jump of vibration amplitude between single and double teeth is not obvious. The corresponding dynamic meshing force changes periodically between greater than zero (drive-side meshing), equal to zero (disengagement) and less than zero (back-side meshing), as illustrated in Fig. 18f. Also, the mutation of the meshing force is observed when the drive-side meshing transitions to disengagement or back-side meshing transitions to disengagement.

At C, 1-1-1-1-1 behavior shifts to a stable 1-1-0-1-0 behavior. Single-tooth and double-tooth back-side meshes disappear for 1-1-0-1-0, but single-tooth and double-tooth disengagements persist. Phase trajectories of different meshing states are marked by the symbols Γ1, Γ2 and Γ3 as shown in Fig. 18g. The dynamic meshing force of the system appears periodically between greater than zero and equal to zero, as seen from Fig. 18h. 1-1-0-1-0 behavior enters a short chaotic behavior via period-doubling bifurcation sequence and then degenerates to a stable 2-2-0-2-0 behavior by inverse period-doubling bifurcation sequence. The phase orbit and dynamic meshing force in time domain of 2-2-0-2-0 behavior are shown in Fig. 18i and j. 2-2-0-2-0 behavior degenerates to 2-1-0-1-0 behavior via grazing bifurcation at point D. Then 2-1-0-1-0 behavior turns into chaos at point E. The chaotic attractor in time-period Poincaré mapping section is depicted in Fig. 18k and the corresponding dynamic meshing force is shown in Fig. 18l. The meshing force changes periodically between F_m > 0, F_m = 0 and F_m < 0. Thus, the single-tooth and double-tooth disengagements as well as single-tooth and double-tooth back-side meshes are observed in chaos. As ω increases further, the chaos degenerates into a 2-1-1-1-1 behavior, and then 2-1-1-1-1 behavior enters chaos. Subsequently, the chaos degenerates into a 3-1-1-1-1 behavior. The phase trajectory of the system crosses Ds, -Ds, Dd and -Dd, as shown in Fig. 18m. The five-state meshing behaviors are observed as marked by Γ1, Γ2, Γ3, Γ4 and Γ5. The time history of the corresponding dynamic meshing force is shown in Fig. 18n, which appears periodically between F_m > 0, F_m = 0 and F_m < 0. 3-1-1–1-1 behavior transfers to a 1-1-0-1-0 behavior at point F. The system performs drive-side tooth mesh, single-tooth and double-tooth disengagements after F. Figure 18o is the phase portrait and Poincaré map of 1-1-0-1-0.

Therefore, the system performs a stable drive-side meshing state when the meshing frequency ω is small. With the increase in ω, the system gradually appeared multi-state meshing behavior such as single-tooth and double-tooth disengagement, double-tooth back-side meshing and single-tooth back-side meshing. The multi-state meshing behavior of the system become complicated decreasing ω. In addition, the bifurcation, periodic jump, and chaos are found between B and F points (0.5 < ω < 2.0). Teeth disengagements and back-side meshes caused by bifurcation or chaos are also obtained in this area. Bifurcations such as B, C, D, E and F points not only modify the type of motion, but also change the multi-state meshing behavior of the system. Also, chaotic behavior stimulates tooth disengagement and back-side tooth contact, forming a multi-state meshing behavior. When ω is large (to the right of point F), although the system exhibits a stable period-1 behavior, the single-tooth and double-tooth disengagement still occurs, as seen from 1-1-0-1-0 behavior.

4.3.2 Effect of load factor

ω = 1.3 and ε = 0.12 are fixed, and other parameters remain unchanged. Figure 19 shows the bifurcation diagrams of the gear system in different Poincaré sections and TLE diagram with the decrease in load factor F. When F is large (on the right of point A), the system exhibits a 1-1-0-1-0 behavior, which is a period-1 motion and the corresponding TLE values are less than zero. Only the single- and double-tooth disengagements are observed and no back-side teeth mesh occurring for 1-1-0-1-0 behavior. The phase portrait and Poincaré map are depicted in Fig. 20a, and the phase trajectories in different meshing states are marked by Γ1, Γ2 and Γ3, respectively. The corresponding dynamic meshing force is shown in Fig. 20b, which changes periodically between F_m > 0 and F_m = 0.

Fig. 19

Bifurcation diagrams in different Poincaré mapping sections and top Lyapunov exponent (TLE) with the decrease in F. a time-period mapping section in blue; b single-tooth disengagement mapping section in magenta and single-tooth back-side contact mapping section in green; c double-tooth disengagement mapping section in red and double-tooth back-side contact mapping section in grass green; d top Lyapunov exponent (TLE)

Fig. 20

Phase portraits, Poincaré maps and time histories of dynamic meshing force. a Phase portrait and Poincaré mapping as F = 0.16; b Dynamic meshing force as F = 0.16; c Phase portrait and Poincaré mapping as F = 0.117; d Dynamic meshing force as F = 0.117; e Phase portrait and Poincaré mapping as F = 0.103; f Dynamic meshing force as F = 0.103; g Phase portrait and Poincaré mapping as F = 0.11; h Dynamic meshing force as F = 0.11; i Poincaré mapping as F = 0.09; j Dynamic meshing force as F = 0.09; k Poincaré mapping as F = 0.07; l Dynamic meshing force as F = 0.07; m Phase portrait and Poincaré mapping as F = 0.02; n Dynamic meshing force as F = 0.02

With the decrease in F, 1-1-0-1-0 behavior creates a 2-2-0-2-0 behavior via period-double bifurcation at B point where TLE value is equivalent to zero. And then the system performs a stable period-2 motion and there are two single-tooth disengagements and two double-tooth disengagements for 2–2-0–2-0. The phase portrait and dynamic meshing force are illustrated in Fig. 20c and d, respectively. 2–2-0–2-0 transitions to 2–2-0-1-0 at B point by grazing bifurcation and the phase portrait is described in Fig. 20e where the curve Γ2 is tangent to the straight line Dd, and then double-tooth disengaging is reduced once. The phase trajectory crosses x₃ = Ds twice and crosses x₃ = Dd once, as indicated in Fig. 20f. The corresponding dynamic meshing force is illustrated in Fig. 20g.

At C point, 2-2-0-1-0 jumps and transitions to a 4-2-0-2-0 behavior. Figure 20h and i shows the phase trajectory and dynamic meshing force in time domain for 4-2-0-2-0. Subsequently, 4-2-0-2-0 enters into a chaotic behavior by short period-double bifurcations and TLE values of the chaotic behavior are higher than zero. Figure 20j is Poincaré mapping diagram of chaos calculating for F = 0.09, and Fig. 20k is the corresponding dynamic meshing force. The dynamic meshing force changes periodically between F_m > 0 and F_m = 0, and no F_m < 0 appearing. Thus, there is not any back-side teeth mesh occurring for the chaos. However, the chaotic attractor enlarges at E point and then single-tooth and double-tooth back-side meshes appear. The enlarged chaotic attractor is depicted in Fig. 20l and the corresponding dynamic meshing force is shown in Fig. 20m where F_m < 0 is observed.

As F is further decreased to point F, the chaotic behavior degenerates to a 3-1-1-1-1 behavior. The system performs a stable period-3 behavior, but the teeth disengagements and back-side tooth mesh persist as shown in Fig. 20n. The corresponding dynamic meshing force changes periodically between F_m > 0, F_m = 0 and F_m < 0 as shown in Fig. 20o.

Therefore, when the load factor is large, the system behaves as a stable period-1 behavior. The multi-state meshing behavior is simple, and only single-tooth and double-tooth disengagements occur. As decreasing in load factor F, the system undergoes period-doubling and grazing bifurcations, and five-state meshing behavior is gradually observed. In addition, grazing bifurcation (B point) reduces the number of double-tooth disengagement. Bifurcation changes the multi-state meshing behavior of the system. Additionally, the single-tooth and double-tooth back-side meshes are gradually observed. Both the multi-state meshing behavior and nonlinear dynamics become complicated decreasing in F.

4.3.3 Effect of transmission error coefficient

Take F = 0.05 and ω = 1.3, Fig. 21 shows the bifurcation diagrams of the five-state meshing behavior of the system with the increase in transmission error coefficient ε. When ε is small (left of point A), the system behaves as a stable 1-0-0-0-0 behavior, and the corresponding TLE value is less than zero. There is a complete drive-side meshing state is observed, and no disengagement and back-side meshing appearing. The system exhibits a flutter motion in the range of extremely small vibration amplitude, as shown in Fig. 22a calculating for ε = 0.012.

Fig. 21

Bifurcation diagrams in different Poincaré mapping sections and corresponding top Lyapunov exponent (TLE) with the increase in ε. a time-period mapping section in blue; b single-tooth disengagement mapping section in magenta and single-tooth back-side contact mapping section in green; c double-tooth disengagement mapping section in red and double-tooth back-side contact mapping sectionin grass green; d top Lyapunov exponent (TLE)

Fig. 22

Phase portraits, Poincaré maps and time histories of dynamic meshing force. a Phase portrait and Poincaré mapping as ε = 0.012; b Phase portrait and Poincaré mapping as ε = 0.028; c Dynamic meshing force as ε = 0.028; d Phase portrait and Poincaré mapping as ε = 0.04; e Dynamic meshing force as ε = 0.04; f Poincaré mapping as ε = 0.07; g Dynamic meshing force as ε = 0.07; h Phase portrait and Poincaré mapping as ε = 0.0985; i Dynamic meshing force as ε = 0.0985; j Poincaré mapping as ε = 0.25; k Dynamic meshing force as ε = 0.25

With the decreasing in ε, single-tooth disengagement is observed at A point and then 1-1-0-0-0 behavior is obtained between A and B points. The phase portrait and Poincaré map are depicted in Fig. 22b, and the corresponding dynamic meshing force is shown in Fig. 22c. The phase portrait crosses x₃ = Ds, as marked by Γ1 and Γ2. At B, 1-1-0-0-0 behavior jumps to 2-1-0-1-0 behavior. The system performs a period-2 motion and appears double-tooth disengagement between B and C points. Figure 22d is the phase portrait and Poincaré map of 2-1-0-1-0 behavior. The phase portrait crosses x₃ = Ds and x₃ = Dd, as marked with Γ1, Γ2 and Γ3. The corresponding dynamic meshing force changes periodically between F_m > 0 and F_m = 0. Drive-side mesh, single-tooth disengagement and double-tooth disengagement occur periodically during gears operating.

2-1-0-1-0 behavior jumps at C and D points, and then enters chaos. The corresponding TLE value is higher than zero. Poincaré map and dynamic meshing force of the chaos are shown in Fig. 22f and g as ε = 0.07. The meshing force changes between F_m > 0 and F_m = 0. Single-tooth and double-tooth disengagements persist, but no back-side meshing occurs for the chaotic behavior. However, the chaotic behavior degenerates into 6-2-2-2-2 behavior at point E. Single-tooth and double-tooth back-side meshes are observed. The phase portrait passes through x₃ = Ds, -Ds, Dd and -Dd, as shown in Fig. 22h. The phase trajectories under different meshing states are marked with Γ1, Γ2, Γ3, Γ4 and Γ5. The dynamic meshing force changes periodically between F_m > 0, F_m = 0 and F_m < 0, as shown in Fig. 22i.

Subsequently, 6-2-2–2-2 behavior enters to chaos via a short period-doubling bifurcation sequence. Teeth disengagements and back-side tooth meshes persist for the chaotic behavior. Furthermore, the chaotic behavior degenerates into a 6-1-2-1-2 behavior at point F. 6-1-2-1-2 behavior exists in a larger range of ε and then enters chaos after a series of bifurcation and evolution. Figure 22j and k shows the Poincaré map and dynamic meshing force of the chaotic behavior. The dynamic meshing force alternates between F_m > 0, F_m = 0 and F_m < 0. Teeth disengagements and back-side meshes always occur.

Therefore, when ε is small, the system exhibits a complete drive-side meshing state without disengagement and back-side meshing. With the increase in ε, however, single-tooth disengagement occurs at point A, and then double-tooth disengagement appears at point B. Single-tooth and double-tooth back-side meshes are observed at point E. Subsequently, teeth disengagements and back-side tooth meshing persist after point F. In addition, the system behaves as a stable periodic behavior when the transmission error coefficient ε is small. Periodic jumps and bifurcation points are obtained increasing in ε, such as B, C, D, E and F points. The system performs chaotic and periodic behaviors where teeth disengagements and back-side tooth engagements are observed as ε is large. Bifurcation leads to gear tooth disengagement and back-side tooth contact, resulting in multi-state meshing behavior. The type of multi-state meshing behavior is also changed through bifurcation or periodic jump, such as B and E point. The transmission error coefficient ε greatly affects the nonlinear dynamics as well as multi-state meshing behavior of the gear system. When the motion trajectory is enlarged or chaotic, the system behaves as a multi-state meshing behavior.

In order to demonstrate the advantages of the proposed model, the nonlinear vibration obtained from the traditional method is compared with the proposed method. A bifurcation diagram with the increase in the transmission error coefficient ε is calculated by the traditional model, as shown in Fig. 23, which corresponds to Fig. 21a.

Fig. 23

The bifurcation diagram with the increase in ε in time-period Poincaré mapping section

Comparing Fig. 21a and Fig. 23, when ε is small (at the left of F), the two bifurcation graphs have a certain similarity, and the evolutionary trend of dynamic behavior is basically the same. However, the difference is that the period-2 behavior near point B cannot be revealed in Fig. 23, and the position of the bifurcation point E (chaotic behavior degenerates to period-6 behavior) is advanced, and the parameter range of the period-6 behavior is shortened in Fig. 21a compared to Fig. 23. When ε is large (at the right of point F), the bifurcation diagrams obtained by the two methods are quite different. The dynamic behavior obtained by the traditional method mainly shows periodic behavior when ε is large, while the dynamic behavior obtained by the proposed model mainly shows period-6 behavior and chaotic behavior, and the nonlinear vibration of the gear system is unstable and complex. Therefore, compared with the traditional model, the proposed model in this work can better reflect the dynamical characteristics of the influence of the transmission error coefficient ε on the gear system. The proposed model in this work has certain advantages.

Notably, based on the actual engaging process of the gear pair, a dimensionless normalized model of the gear pair system including five-state mesh is established. Then five different Poincaré mapping sections are obtained according to the switching conditions between different meshing states. Based on this, the multi-state meshing behavior is clearly characterized, and the evolutionary mechanisms of single-tooth or double-tooth disengagement and back-side tooth contact are well revealed. However, these behaviors and phenomena cannot be obtained in the traditional model because the multi-state meshing characteristics are not considered.

5 Conclusions

The time-varying contact characteristics of an involute spur gear system considering backlash and contact ratio are elaborated. A new nonlinear dynamic model of the gear system with five-state meshing behavior, such as single-tooth drive-side mesh, double-tooth drive-side mesh, teeth disengagement, single-tooth back-side mesh, and double-tooth back-side mesh, is established in this work. The time-varying meshing stiffness and time-varying backlash considering the elastic contact of gear teeth, gear temperature rise and lubrication are calculated and introduced into this model. The generation mechanism of multi-state meshing behavior is revealed by using dynamic meshing force time history and phase portrait. The bifurcation and evolution of five-state meshing behavior are analyzed separately under the effects of meshing frequency, load factor and transmission error coefficient. The nonlinear vibration obtained from the traditional method has been compared with the proposed method to demonstrate the advantages of the model. Some beneficial conclusions are obtained as follows:

• (1) Five different meshing states of a spur gear system and their boundary conditions are clearly described. A dimensionless normalized nonlinear dynamic model of the gear system including five-state meshing behavior together with the effects of time-varying backlash and time-varying meshing stiffness are elaborated. The time-varying backlash and time-varying meshing stiffness are calculated in detail with the considerations of the elastic contact of the gear teeth, and the gear temperature rise and lubrication.

• (2) The mutation in the direction of the dynamic meshing force results in the disengagement of gear teeth, and then five-state meshing behavior is observed. This mutation occurs successively in the single- and double-tooth meshing regions. The five-state meshing behavior is well characterized by constructing five different Poincaré mapping sections, such as time-period mapping section Σ_n, single-tooth disengagement mapping section Σ_p, single-tooth back-side contact mapping section Σ_q, double-tooth disengagement mapping section Σ_r, and double-tooth back-side contact mapping section Σ_s.

• (3) The meshing frequency, load factor, and transmission error coefficient greatly affect the nonlinear dynamics and multi-state meshing behavior of the gear system. When meshing frequency or load factor is small, the system behaves as a complete drive-side tooth meshing state and a stable period-1 behavior. The multi-state meshing behavior, bifurcation, and chaotic behavior gradually occur as meshing frequency or load factor increase. The multi-state meshing behavior stimulates the complexity of the nonlinear dynamics of the gear system. In addition, grazing bifurcation reduces the number of double-tooth disengagement. These phenomena, however, cannot be obtained in the traditional method due to the neglect of the multi-state meshing behavior.

This paper provides a scientific basis for the parameter optimization design, dynamic performance improvement and reliable application of the gear transmission system, and also lays a foundation for further research of the gear system in meshing-contact impact characteristics.