Dynamic characteristics of spur gear pair considering meshing impact and multi-state meshing

Abstract

Meshing impact is caused by boundary impact, mesh-in impact, mesh-out impact and switching impact of meshing teeth pair for gear pair. To study the characteristics of these impacts and their influence on the system dynamic performance, meshing impact is classified according to multi-state meshing. Calculation models of switching impact including impact force and impact time are established based on Hertz contact theory. Calculation model of boundary impact including drive-side boundary impact and back-side boundary impact is constructed on the principle of conservation of energy. An improved nonlinear dynamics model of spur gear pair considering meshing impact is established as multi-state meshing and time-varying parameters are included. It is solved in C program language by Runge–Kutta method numerically. Five representative typical cases are selected to discuss the characteristics and possible motion patterns of the system after considering the meshing impact. The influences of meshing frequency and load coefficient on the system dynamic characteristics and nonlinear dynamics are investigated according to bifurcation diagrams with and without considering the meshing impact and other well-known crucial tools in nonlinear dynamics analysis. Motion transition mechanism of the system considering meshing impact is discussed. The relationship between input and output torque is attempted to deduce according to dimensionless parameters and the engineering significance of the influence for dimensionless load coefficient on the system dynamic characteristics is discussed. It provides a theoretical basis for revealing meshing impact mechanism of the system and further reducing the impact.

1 Introduction

Vibration and dynamic characteristics of the gear transmission system have always been key issues for scholars in engineering and science since a nonlinear dynamics model of a spur gear pair proposed by Kahraman and Singh in 1990 [1]. The model is constantly improved and perfect for instant its number for degrees of freedom considered is increasing. 3-DOF model [2,3,4], 6-DOF model [5,6,7,8], 8-DOF model [9, 10], 12-DOF model [11] and so on have emerged in addition to the single DOF model [12,13,14,15,16]. The transmission stages have also developed from one-stage gear transmission [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16] to two-stage [17] and even multi-stage transmission [18, 19]. The effects of bearings [20, 21], rotors [22, 23] and supports [2] are gradually introduced to the models. Various time-varying parameters are gradually improved in the model such as time-varying meshing stiffness [11, 12], time-varying friction coefficient [13, 23], time-varying backlash [24], elastodynamic lubrication [25,26,27] and tooth pitch deviation [28, 29]. The research object is also extended from spur gear to helical gear [30, 31], face gear [32] and so on.

Meshing impact of the gear transmission system affects its dynamic vibration directly. The impact in meshing has been extensively studied by theoretical or experimental methods. Parey and Tandon [33] proposed a model of the impact velocity for the gear pair that links the vibration signal obtained by measurable method. Chen et al. [34] researched the impact characteristics of convex gear transmission system by using backlash and static transmission error experiments. The primary problem of impact for gear transmission system is the calculation of impact force [35,36,37,38,39] and the determination of impact position [38]. Hu et al. [35] extracted the meshing impact signal in the experiment to calculate the meshing impact force. Li et al. [40] established an adaptive cascade stochastic resonance method for shock feature extraction in gear fault diagnosis. Tong et al. [41] proposed a model to identify the local resonance caused by gear meshing impact. Xiang et al. [42] established an improved model of gear contact force to distinguish its collision and meshing states. Mu et al. [43] proposed a vibration control optimization design method of spiral bevel gears according to meshing impact model. Rigaud and Perret-Liaudet [44] conducted an experimental study on the tooth slap caused by vibration and impact between teeth of spur cylindrical gear. Ma et al. [45] proposed an analytical model of the circular arc tooth line cylindrical gear by the finite element method at different impact positions. The researches on the impact of gears mainly focus on the off-line meshing, contact impact, mesh-in impact and mesh-out impact. There is little study on the teeth impact caused by meshing in or out for the current tooth pair.

The nonlinear dynamics model and the meshing impact of the gear transmission system have been studied widely and deeply, respectively. But nonlinear dynamics model coupling meshing impact is still rare and the multi-state meshing is not found yet. Meshing impact affects importantly the dynamic characteristics of gear teeth and it is closely related to their meshing state. Shi et al. [46] first proposed the multi-state meshing theory of the gear transmission and used it to establish the nonlinear dynamic model with considering multi-state meshing of spur gear pair based on this. After that, they built a calculation model of the time-varying backlash and meshing stiffness for spur gear pair based on its multi-state meshing characteristics [24]. The accuracy of the multi-state meshing characteristics for the gear transmission was proved by experiments when they measured the tooth surface contact temperature of a spur gear pair based on Seebeck effect [47]. Tang et al. [48] spoke highly of the multi-state meshing modeling method proposed in Ref. [24] and improved it. Gear meshing state is divided into drive-side teeth meshing, back-side teeth contacting and tooth disengagement with different number of teeth pairs according to the backlash and contact ratio of gear transmission based on multi-state meshing theory [24, 46, 47]. The impact of gear teeth can be accurately identified according to multi-state meshing characteristics.

All these studies provide the basis and possibility for more precise identification of the meshing state and more accurate study of the role between gears according to the engineering practice of gear transmission. Therefore, spur gear pair proposed by Kahraman and Singh [1] is taken as the research object of this paper. An improved dynamics model of spur gear pair will be established when meshing impact, time-varying parameters and multi-state meshing are considered. Influence of meshing impact and parameters on the dynamic characteristics will be analyzed. It is organized as follows. The absolute rotation equation of spur gear pair considering multi-state meshing is discussed in Sect. 2. Classification and calculation methods of meshing impact with multi-state meshing will be proposed in Sect. 3. The rotation equation of spur gear pair is dimensionless considering the impact and multi-state meshing in Sect. 4. Dynamic characteristics of meshing impact will be discussed according to numerical calculated results in Sect. 5. The influence of meshing impact on the system dynamic characteristics and its engineering value are discussed according to the relationship between output and input torque in Sect. 6. Some conclusions will be drawn in Sect. 7.

2 Absolute rotation equation of spur gear pair with multi-state meshing

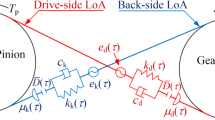
Single stage involute spur gear pair is the simplest form of gear transmission and the basis of all gear transmission forms. The support of the gear pair is assumed by rigid mounts as the influences of bearings and the flexure of the shafts are not considered in this work. A single stage spur gear pair meshing considering its torsional vibration is represented in Fig. 1 [1]. $T_{i}$, $\theta_{i}$, $R_{bi}$ and $I_{i}$ (i = p, g) is the input torque and output torque, the dynamic angular displacements, the base circle radius and the mass moments of inertia of the pinion (i = p) and gear (i = g), respectively. $e(t)$ is the comprehensive transmission error along the action line and $t$ is time. $k(t)$ and $c_{{\text{m}}}$ is the time-varying meshing stiffness and meshing damping coefficient, respectively. $\overline{D}$ and $\mu$ is half of backlash and the friction coefficient of the tooth surface, respectively. Parameters of the system corresponding to the test rig [47] that do not affect the universality of this work are listed in Table 1.

Fig. 1

Schematic of single stage spur gear pair meshing [1]

Table 1 Parameters of the studied gears corresponding to the test rig [47]

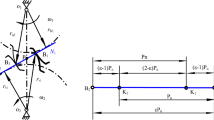
There are three meshing regions along the action line, N₁N₂ determined by its contact ratio $\varepsilon_{{\text{m}}}$ = 1.595 which is more than 1.0 and less than 2.0 for spur gear pair according to the gear transmission principle. They are meshing regions of double-pair teeth (AB and CMo) and meshing region of single-pair teeth (BC) as depicted in Fig. 2 [49], where $\omega_{i}$ (i = p, g) is the angular speed of the pinion (i = p) and gear (i = g), respectively. A is the point of mesh-in. Mo is the point of mesh-out. P is the pitch point. Switching points of double-to- single and single-to-double are B and C, respectively. The division of meshing region and the calculation of switching time has been proved to be correct by Ref. [47] in the experiment of measuring the tooth surface contact temperature for the spur gear pair listed in Table 1.

Fig. 2

Region diagram of multi-state meshing for spur gear pair

Backlash is reserved in designing to prevent jamming which occurs in the gear transmission process. It leads to drive-side teeth meshing, back-side teeth contacting and tooth disengagement. There are five meshing states such as drive-side meshing of single-pair teeth (MSds), drive-side meshing of double-pair teeth (MSdd), tooth disengagement, back-side contacting of single-pair teeth (MSks) and back-side contacting of double-pair teeth (MSkd) in the spur gears transmission process [46]. Schematic of the forces acting on the gear teeth under meshing and contacting states are shown in Fig. 3 and that of tooth disengagement is not shown because there is no force acting on the teeth in this case. N₁N₂ is the action line under drive-side meshing and M₁M₂ is the action line under back-side contacting. $F_{{{\text{f}}ijc}}$ and $F_{{{\text{N}}ijc}}$ represents the friction forces and positive pressures acting on the teeth where i = p, g represents the pinion and gear, j = 1, 2 represents the number of the meshing teeth pair and its value relates to meshing region along the action line, c = d, k represents the drive- side teeth meshing and back-side teeth contacting in order, respectively. Absolute rotation equations of spur gear pair under different meshing states is established in Eq. (1) according to Fig. 3 based on 2^nd Newton law.

$$ \left\{ \begin{gathered} I_{\text{p}} \ddot{\theta }_{\text{p}} \pm R_{{\text{bp}}} F_{{{\text{Np}} 1c}} \pm S_{p1c} (t)F_{{{\text{fp}} 1c}} \pm R_{{\text{bp}}} F_{{{\text{Np}} 2c}} \pm S_{p2c} (t)F_{{{\text{fp}} 2c}} = T_{\text{p}} \hfill \\ I_{\text{g}} \ddot{\theta }_{\text{g}} \mp R_{{\text{bg}}} F_{{{\text{Ng}} 1c}} \mp S_{g1c} (t)F_{{{\text{fg}} 1c}} \mp R_{{\text{bg}}} F_{{{\text{Ng}} 2c}} \mp S_{g2c} (t)F_{{{\text{fg}} 2c}} = - T_{\text{g}} \hfill \\ \end{gathered} \right.,\quad \left( {c = {\text{d}},{\text{k}}} \right) $$

(1)

where $S_{ijc} (t)$(i = p, g; j = 1,2; c = d, k) is the friction arm of the tooth on the pinion (i = p) and gear (i = g) for the jth teeth pair under drive-side teeth meshing (c = d) and back-side teeth contacting (c = k) state. The upper operator in $\pm$ and $\mp$ corresponds to c = d and the lower one corresponds to c = k. They can be obtained as Eq. (2) [46].

$$ \left\{ \begin{gathered} S_{{p1{\text{d}}}} (t) = (R_{{\text{bp}}} + R_{{\text{bg}}} )tan\alpha - \sqrt {R_{{\text{ag}}}^{2} - R_{{\text{bg}}}^{2} } + R_{{\text{bp}}} \omega_{\text{p}} t \hfill \\ S_{g1d} (t) = \sqrt {R_{{\text{ag}}}^{2} - R_{{\text{bg}}}^{2} } - R_{{\text{bp}}} \omega_{\text{p}} t \hfill \\ S_{p1k} (t) = \sqrt {R_{{\text{ap}}}^{2} - R_{{\text{bp}}}^{2} } - R_{{\text{bg}}} \omega_{g} t \hfill \\ S_{g1k} (t) = (R_{{\text{bp}}} + R_{{\text{bg}}} )tan\alpha - \sqrt {R_{{\text{ap}}}^{2} - R_{{\text{bp}}}^{2} } + R_{{\text{bg}}} \omega_{g} t \hfill \\ \end{gathered} \right. $$

(2a)

$$ S_{i2c} (t) = S_{i1c} (t + T_{0} ),\quad \left( {i = {\text{p}},{\text{g}};\,c = {\text{d}},{\text{k}}} \right) $$

(2b)

Fig. 3

Schematic of the forces acting on the teeth under different states: a MSds, b MSdd, c MSks, d MSkd

Positive pressures, $F_{{{\text{N}}ijc}}$ in Eq. (1) can be obtained as Eq. (3) according to their definitions and Fig. 3.

$$ F_{{{\text{N}}i{1}c}} = L_{1c} (t)F_{{{\text{m}}c}} ,\quad F_{{{\text{N}}i{2}c}} = L_{2c} (t)F_{{{\text{m}}c}} ,\quad \left( {i = {\text{p}},{\text{g}}; c = {\text{d}},{\text{k}}} \right) $$

(3)

where $L_{jc} (t)$ is the load distribution ratio of the jth teeth pair under drive-side teeth meshing state (c = d) and back-side teeth contacting state (c = k). They can be obtained as Eq. (4) according to Ref. [46].

$$ L_{jc} (t) = \left\{ {\begin{array}{*{20}l} {\frac{1}{3}\left( {1 + \frac{{\eta_{{{\text{C}} c}} (t) - \eta_{{\text{A}c}} }}{{\eta_{{\text{D}c}} - \eta_{{\text{A}c}} - 1}}} \right),} \hfill & {\eta_{{\text{A}c}} \le \eta_{{{\text{C}} c}} (t) \le \eta_{{\text{D}c}} - 1} \hfill \\ {1,} \hfill & {\eta_{{\text{D}c}} - 1 \le \eta_{{{\text{C}} c}} (t) \le \eta_{{\text{A}c}} + 1} \hfill \\ {\frac{1}{3}\left( {1 + \frac{{\eta_{{{\text{C}} c}} (t) - \eta_{{\text{D}c}} }}{{\eta_{{\text{A}c}} - \eta_{{\text{D}c}} + 1}}} \right),} \hfill & {\eta_{{\text{A}c}} + 1 \le \eta_{{{\text{C}} c}} (t) \le \eta_{{\text{D}c}} } \hfill \\ \end{array} } \right.,\quad \left( {c = {\text{d}},{\text{k}}} \right) $$

(4)

where $\eta_{{\text{Ad}}} = \frac{{z_{\text{p}} }}{2\pi }\sqrt {R_{{\text{ag}}}^{2} /R_{{\text{bp}}}^{2} - 1}$ and $\eta_{{\text{Ak}}} = \frac{{z_{\text{g}} }}{2\pi }\sqrt {R_{{\text{ap}}}^{2} /R_{{\text{bg}}}^{2} - 1}$ denote the profile parameters at meshing point A corresponding to the drive-side teeth meshing state and the back-side teeth contacting state, respectively. $\eta_{{\text{Dd}}} =$ $\frac{{z_{\text{p}} }}{2\pi }\sqrt {R_{{\text{ap}}}^{2} /R_{{\text{bp}}}^{2} - 1}$ and $\eta_{{\text{Dk}}} = \frac{{z_{\text{g}} }}{2\pi }\sqrt {R_{{\text{ag}}}^{2} /R_{{\text{bg}}}^{2} - 1}$ denote the profile parameters at meshing point Mo corresponding to the drive-side teeth meshing state and the back-side teeth contacting state, respectively. $\eta_{{\text{Cd}}} =$$\frac{{z_{\text{p}} }}{2\pi }\sqrt {R_{{\text{dp}}}^{2} (t)/R_{{\text{bp}}}^{2} - 1}$ and $\eta_{{\text{Ck}}} = \frac{{z_{\text{g}} }}{2\pi }\sqrt {R_{{\text{kg}}}^{2} (t)/R_{{\text{bg}}}^{2} - 1}$ is the time-varying profile parameter changing along line AMo corresponding to the drive-side teeth meshing state and the back-side teeth contacting state, respectively. Here, $R_{{{\text{a}} i}}$ is addendum circle radius of the pinion (i = p) and gear (i = g), respectively. The meshing radius, $R_{ijc} (t)$ (i = p, g; c = d, k) can be written as Eq. (5) as the back-side teeth contacting state is considered.

$$ \left\{ \begin{gathered} R_{p1c} (t) = \sqrt {R_{{\text{bp}}}^{2} + [(R_{{\text{bp}}} + R_{{\text{bg}}} )tan\alpha - \sqrt {R_{{\text{ag}}}^{2} - R_{{\text{bg}}}^{2} } + R_{{\text{bp}}} \omega_{\text{p}} \;t]^{2} } \hfill \\ R_{g1c} (t) = \sqrt {R_{{\text{bg}}}^{2} + [\sqrt {R_{{\text{ag}}}^{2} - R_{{\text{bg}}}^{2} } - R_{{\text{bp}}} \omega_{\text{p}} \;t]^{2} } \hfill \\ R_{i2c} (t) = R_{i1c} (t + T_{0} ) \hfill \\ \end{gathered} \right. $$

(5)

The load acting on the teeth is distributed to every meshing teeth pair in the double-pair teeth meshing region according to the number of the meshing teeth pair and the meshing position of spur gear pair. Its time-varying load distribution ratio has been obtained by solving Eq. (4) as shown in Fig. 4 taking c = d. It can be seen from Fig. 4 that there are sudden changes in the load distribution ratio at the four key meshing points, A, B, C and Mo. It means that the load jumps at these points and they result in the impact at these points. They will be discussed in SubSect. 3.1 in details.

Fig. 4

Load distribution ratio of meshing position along the action line, N₁N₂

Dynamic meshing force, $F_{{{\text{m}}c}}$ in Eq. (3) can be obtained by Eq. (6) when it is considered composed of elastic force and damping force according to Eq. (1).

$$ F_{{{\text{m}}c}} = k(t)(R_{bp} \theta_{pc} \mp R_{bg} \theta_{{{\text{g}} c}} \mp e(t) - \overline{D}) + c_{{\text{m}}} (R_{bp} \dot{\theta }_{pc} \mp R_{bg} \dot{\theta }_{{{\text{g}} c}} \mp \dot{e}(t)),\quad \left( {c = {\text{d}},{\text{k}}} \right) $$

(6)

Friction forces, $F_{{{\text{f}}ijc}}$ in Eq. (1) can be obtained as Eq. (7) according to their relationships to positive forces after introducing Eqs. (6) to (3).

$$ F_{{{\text{f}}i{1}c}} = \lambda_{{{1}c}} (t)\mu_{{{1}c}} (t)L_{1c} (t)F_{{{\text{m}}c}} ,\quad F_{{{\text{f}}i{2}c}} = \lambda_{{{2}c}} (t)\mu_{{{2}c}} (t)L_{{{2}c}} (t)F_{{{\text{m}}c}} ,\quad \left( {i = {\text{p}},{\text{g}};\,c = {\text{d}},{\text{k}}} \right) $$

(7)

where $\mu_{jc} (t)$ (j = 1,2; c = d,k) is time-varying friction coefficient of the jth teeth pair corresponding to the drive-side teeth meshing state and the back-side teeth contacting state and they can be obtained according to Ref. [46]. $\lambda_{jc} (t)$(j = 1,2; c = d,k) is the direction coefficient of the friction force for the jth teeth pair corresponding to the drive-side teeth meshing state and the back-side teeth contacting state. They can be defined as Eq. (8).

$$ \lambda_{jc} (t) = sgn[v_{jc} (t)] $$

(8)

Herein, sgn(•) is the sign function and $v_{jc} (t)\;$ is the slip velocity of the tooth surface of the jth teeth pair corresponding to the drive-side teeth meshing state and the back-side teeth contacting state which can be written as Eq. (9).

$$ v_{jc} (t) = R_{pjc} (t)sin(\alpha_{pjc} (t))\omega_{\text{p}} - R_{gjc} (t)sin(\alpha_{gjc} (t))\omega_{\text{g}} ,\quad \left( {j = {1},{2};\,c = {\text{d}},{\text{k}}} \right) $$

(9)

where $\alpha_{ijc} (t) = {\text{arc}}\cos [R_{{{\text{bp}}}} /R_{ijc} (t)]$ (i = p,g; j = 1,2; c = d,k) is the pressure angle at meshing or contacting points.

Absolute rotation equation of spur gear pair under tooth disengagement state is shown in Eq. (10).

$$ \left\{ \begin{gathered} I_{\text{p}} \ddot{\theta }_{\text{p}} = T_{\text{p}} \hfill \\ I_{\text{g}} \ddot{\theta }_{\text{g}} = - T_{\text{g}} \hfill \\ \end{gathered} \right.,\quad \left( {c = {\text{d}},{\text{k}}} \right) $$

(10)

3 Meshing impact of spur gear pair

3.1 Classification of meshing impact for spur gear pair according to multi-state meshing determined by contact ratio and backlash

Meshing characteristics of gear transmission system is very complex determined by the backlash and contact ratio. The relative position and the action state of the force for the interacting teeth pair are different at different times. Accordingly, the meshing impact is different. A clear classification of the meshing impact is the basis for its calculation. Classification of meshing impact for spur gear pair considering multi-state meshing is shown in Fig. 5 and the distribution of phase trajectories is shown in the phase plane, respectively. Boundary in drive-side boundary impact and back-side boundary impact is omitted for simplicity in Fig. 5. Double- to-single switching impact and single-to-double switching impact are collectively referred to as switching of meshing teeth in Fig. 5. Time, t is main control parameter and $\Delta t$ is the time step. Arrows in Fig. 5 indicate the moving direction of the phase trajectory, and different colors are used to distinguish the type of motion and impact. It is discussed in detail to prepare for the calculation of meshing impact.

Fig. 5

Calculation process of meshing impact for spur gear pair considering multi-state meshing. Arrows indicate the moving direction of the phase trajectory, and different colors are used to distinguish the type of motion and impact

For the convenience of discussion, several quantities will be used first and their specific meanings will be discussed in detail in Sect. 3.4. $\dot{x}$ is the dimensionless relative velocity and $x$ is the dimensionless relative displacement. D is the dimensionless half backlash. t is the dimensionless time. $F_{{\text{i}}}$ is the dynamic meshing force. $[F_{{\text{N}}} ]_{{\text{m}}}$ is the critical mesh-in force and $[F_{{\text{N}}} ]_{{\text{c}}}$ is the critical contact-in force.

From a macro perspective, the meshing states can be roughly divided into three types according to the relative relationship between x and D:

Drive-side teeth meshing when $x \ge D$ which is marked by ① in Fig. 5;

Tooth disengagement when $D > x > - D$ which is marked by ③ in Fig. 5;

Back-side teeth contacting when $x \le - D$ which is marked by ④ in Fig. 5.

There are two different consequences when the relative position of meshing teeth pair is at special boundaries such as $x = D$ and $x = - D$, respectively. It depends on the state of the dynamic meshing force:

Mesh-in deduced by drive-side boundary impact when $x = D$ which is marked by ② in Fig. 5 and the dynamic meshing force $F_{{\text{i}}} \le$$[F_{{\text{N}}} ]_{{\text{m}}}$;

Separation of teeth pair caused by drive-side boundary impact when $x = D$ which is marked by ⑥ in Fig. 5 and the dynamic meshing force $F_{{\text{i}}}$ > $[F_{{\text{N}}} ]_{{\text{m}}}$;

Separation of teeth pair caused by back-side boundary impact when $x = - D$ which is marked by ⑦ in Fig. 5 and the dynamic meshing force $F_{{\text{i}}}$ > $[F_{{\text{N}}} ]_{{\text{c}}}$;

Back-side teeth contacting caused by back-side boundary impact when $x = - D$ as marked ⑧ in Fig. 5 and the dynamic meshing force $F_{{\text{i}}} \le$$[F_{{\text{N}}} ]_{{\text{c}}}$.

Switching impact of meshing teeth pair will occur as the gear pair is under drive-side teeth meshing or back-side teeth contacting. The switching impact under drive-side teeth meshing as marked ⑤ in Fig. 5 is discussed when it is considered as the same as the one under back-side teeth contacting. A complete meshing process of any tooth can be depicted as coming into meshing at mesh-in point A → double-pair teeth meshing in the region AB → switching to single-pair teeth meshing at point B → single-pair teeth meshing in the region BC → switching to double-pair teeth meshing at point C → double-pair teeth meshing in the region CMo → exiting meshing at mesh-out point Mo according to Fig. 2. The gear operation is the repetition of this process on each tooth and the load acting on each tooth jumps at points A, B, C and Mo as shown in Fig. 4. The jumping of the load results in four different types of impact. It can be divided into four types when the ith teeth pair is taken as the studied one.

• (1) Mesh-in impact. It is caused by the coming into meshing of the ith teeth pair at mesh-in point, A.

• (2) Mesh-out impact. It is caused by the exiting meshing of the ith teeth pair at mesh-out point, Mo.

• (3) Double-to-single switching impact. It is caused by the exiting meshing of the (i-1)th teeth pair at the switching point B. The exiting meshing of the (i-1)th teeth pair will cause the mesh-out impact of (i-1)th teeth pair. But it causes the change of the load acting on the ith teeth pair at point B as shown in Fig. 4. This impact is called as double-to-single impact because its generation mechanism is different to the mesh-out impact for the ith teeth pair.

• (4) Single-to-double switching impact. It is caused by the coming into meshing of the (i + 1)th teeth pair at the switching point C. The coming into meshing of the (i + 1)th teeth pair will cause the mesh-in impact of (i + 1)th teeth pair. But it causes the change of the load acting on the ith teeth pair at point C as shown in Fig. 4. This impact is called as single-to-double impact because its generation mechanism is different to the mesh-in impact for the ith teeth pair.

The independent mesh-in impact exists only at the starting of the gear operation. Mesh-in impact mainly involves in single-to-double switching impact on other cases. Similarly, the independent mesh-out impact exists only at the stop time of the gear operation. Mesh-out impact mainly involves in double-to-single switching impact on other cases. There are two types switching impact during the normal operation. They are single-to-double switching impact and double-to-single switching impact. That is the impact at point A is similar to the one at point C and the impact at point B is same to the one at point Mo in the stable operation.

In a word, the impact in the running gear transmission system mainly includes boundary impact and switching impact. Switching impact includes double-to-single switching impact (relating to mesh-out impact) and single-to-double switching impact (relating to mesh-in impact). Impact time and impact force are two important factors of their impact characteristics. Their calculation methods will be discussed in Sects. 3.2 and 3.3 in details, respectively. Boundary impact includes drive-side boundary impact and back-side boundary impact. Their calculation methods will be discussed in SubSect. 3.4.

3.2 Calculation method of impact time for switching impact based on Hertz contact theory

The distances from the centers of the pinion and gear to meshing points of the jth teeth pair, $R_{{pj{\text{d}}}} (t)$ and $R_{{gj{\text{d}} }} (t)$ (j = 1,2) are called as radii of the meshing points and can be obtained by the Eq. (11) according to Ref. [46], respectively.

$$ \left\{ \begin{gathered} R_{p1d} (t) = \sqrt {R_{{\text{bp}}}^{2} + [(R_{{\text{bp}}} + R_{{\text{bg}}} )tan\alpha - \sqrt {R_{{\text{ag}}}^{2} - R_{{\text{bg}}}^{2} } + R_{{\text{bp}}} \omega_{\text{p}} \;t]^{2} } \hfill \\ R_{g1d} (t) = \sqrt {R_{{\text{bg}}}^{2} + [\sqrt {R_{{\text{ag}}}^{2} - R_{{\text{bg}}}^{2} } - R_{{\text{bp}}} \omega_{\text{p}} \;t]^{2} } \hfill \\ R_{i2d} (t) = R_{i1d} (t + T_{0} ),\quad (i = {\text{p,g}}) \hfill \\ \end{gathered} \right. $$

(11)

where $T_{0} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {z_{\text{p}} \omega }}} \right. \kern-0pt} {z_{\text{p}} \omega }}$ is a meshing cycle between double-pair teeth and single-pair teeth as $z_{\text{p}}$ is teeth number of the pinion. $\omega = \omega_{{\;{\text{h}} }} /\omega_{\text{n}}$ is the dimensionless meshing frequency as $\omega_{\;h}$ is the meshing frequency and $\omega_{\text{n}} = \sqrt {k_{{\text{av}}} /m_{\text{e}} }$ is the system natural frequency, where $k_{{\text{av}}}$ is the system average meshing stiffness. $\alpha$ is the pressure angle of the gears.

In this study, gears are assumed isolated from other inertias in the system as in Refs. [34, 36, 38, 39]. The tooth surfaces in the contact zone for spur gear pair are closer to cylinders with radii $R_{{pj{\text{d}}}} (t)$ and $R_{{gj{\text{d}} }} (t)$ and length of tooth width. The elastic impact is only considered in the switching impact of meshing teeth pair. The impact can be equivalent to the midpoint of the tooth width when the gears are simply regarded as two elastomers and the impact force is consistent along the length of the cylinder in the elastic impact. Therefore, the teeth impacting can be simplified to two spheres with radii $R_{{pj{\text{d}}}} (t)$ and $R_{{gj{\text{d}} }} (t)$. Their equivalent masses are expressed as $m_{1}$ and $m_{2}$, respectively. Impact force, $F_{{\text{i}}} (t)$ produced when the two teeth (equivalent elastic spheres) impact with the relative velocity, $v_{0}$. The amount of proximity between the centers of two equivalent spheres is expressed as $\delta (t)$ when center displacements of the two equivalent elastic spheres are $u_{1} (t)$ and $u_{2} (t)$, respectively. The relationship between $F_{{\;{\text{i}}}} (t)$ and $\delta (t)$ can be obtained from Eq. (12) assuming that they on the contact surface satisfy the Hertz contact theory.

$$ \frac{{{\text{d}}^{2} \delta (t)}}{{{\text{d}}t^{2} }} = - \frac{1}{{m_{{\text{e}}} }}F_{{\text{i}}} (t) $$

(12)

where $m_{{\text{e}}} = m_{1} m_{2} /(m_{1} + m_{2} )$ and it can also be calculated as $m_{{\text{e}}} = I_{{\text{p}}} I_{{\text{g}}} /(I_{{\text{p}}} R_{{{\text{bp}}}}^{2} + I_{{\text{g}}} R_{{{\text{bg}}}}^{2} )$ according to the parameters of the gears approximately. $\delta (t) = u_{1} (t) + u_{2} (t)$.

The contact condition can be obtained by Eq. (13) according to Hertzian impact theory [50] especially the exponent from the impact of two cylinders [51].

$$ F_{{\;{\text{i}}}} (t) = k(t)\;\delta^{3/2} (t) $$

(13)

where $k(t) = 1/(1/k_{\text{h}} + 1/k_{{\text{b}ji}} + 1/k_{{\text{a}ji}} + 1/k_{{\text{s}ji}} + 1/k_{\text{f}} )$ is the time-varying meshing stiffness of the gear system where $k_{\text{h}}$, $k_{{\text{b}ji}}$ (j = p,g and i = 1,2), $k_{{\text{a}ji}}$ j = p,g; i = 1,2), $k_{{\text{s}ji}}$ (j = p,g; i = 1,2) and $k_{f}$ is the Hertzian contact stiffness, bending stiffness of the ith gear pair for the pinion (j = p) and gear(j = g), axial compressive stiffness, shearing stiffness and the fillet-foundation stiffness of spur gear pair when the double-pair teeth meshing regions and single-pair teeth meshing region are considered, respectively. Its calculation results can be obtained in Fig. 6 according to Ref. [46].

Fig. 6

Time-varying meshing stiffness along the line of action, N₁N₂

Equation (12) can be written as Eq. (14) by substituting Eq. (13) into Eq. (12) and eliminating $F_{{\;{\text{i}}}} (t)$.

$$ \frac{{{\text{d}}^{2} \delta (t)}}{{{\text{d}}t^{2} }} = - \frac{k(t)}{{m_{{\text{e}}} }}\;\delta^{3/2} (t) $$

(14)

Equation (15) can be obtained by integrating Eq. (14) with initial condition $\frac{{{\text{d}}\delta (t)}}{{{\text{d}}t}}\left| {_{t = 0} } \right. = v_{0}$.

$$ \left( {\frac{{{\text{d}}\delta (t)}}{{{\text{d}}t}}} \right)^{2} - v_{0}^{2} = - \frac{4k(t)}{{5m_{{\text{e}}} }}\delta (t)^{5/2} $$

(15)

The impact process can be divided into compression and recovery stages. ${\text{d}}\delta (t_{0} )/{\text{d}}t = v_{0}$ at the beginning of compression stage and ${\text{d}}\delta (t_{{\text{s}}} )/{\text{d}}t = 0$ at the ending of compression stage as $t_{{\text{s}}}$ is the compression time. $\delta_{\max } (t)$ can be obtained as Eq. (16) at the ending of compression stage.

$$ \delta_{\max } = \left( {\frac{{5m_{{\text{e}}} v_{0}^{2} }}{{4k(t_{{\text{s}}} )}}} \right)^{2/5} $$

(16)

The max impact force can be obtained as Eq. (17) when Eq. (16) is substituted into Eq. (13).

$$ F_{{{\text{i}}\max }} = k(t_{{\text{s}}} )\left( {\frac{{5m_{{\text{e}}} v_{0}^{2} }}{{4k(t_{{\text{s}}} )}}} \right)^{3/5} $$

(17)

The expression of the compression time, $t_{{\text{s}}}$ can be expressed in the form of first Euler integral by separating the variables from Eq. (15) and integrating the time and shown in Eq. (18) as let $\overline{\delta } = [\delta (t)/\delta_{\max } ]^{5/2}$. The lower integral limit is taken at the beginning of compression and there are t = 0, δ(t) = 0 and $\overline{\delta }$ = 0. The upper limit of integration is taken at the end of compression and there are t = $t_{{\text{s}}}$, δ(t) = $\delta_{\max }$ and $\overline{\delta }$ = 1.

$$ t_{{\text{s}}} = \frac{{2\delta_{\max } }}{{5v_{0} }}\int_{0}^{1} {\frac{{ \, \overline{\delta }^{ - 3/5} }}{{\sqrt {1 - \overline{\delta }} }}} {\text{d}}\overline{\delta } = \frac{{2\delta_{\max } }}{{5v_{0} }}\int_{0}^{1} { \, \overline{\delta }^{(2/5 - 1)} (1 - \overline{\delta })^{(1/2 - 1)} } {\text{d}}\overline{\delta } $$

(18)

The compression time, $t_{{\text{s}}}$ can be obtained as Eq. (19) by solved Eq. (18) according to β Function calculation method.

$$ t_{{\text{s}}} = 1.88\left( {\frac{{m_{{\text{e}}} }}{k(t)}} \right)^{2/5} \left( {\frac{1}{{v_{0} }}} \right)^{1/5} $$

(19)

The recovery time, $t_{{\text{r}}}$ can be obtained as Eq. (20) assuming that tooth deformation is not completely elastic deformation.

$$ t_{{\text{r}}} = 1.88\left( {\frac{{m_{{\text{e}}} }}{k(t)}} \right)^{2/5} \left( {\frac{1}{{e_{{\text{r}}} v_{0} }}} \right)^{1/5} $$

(20)

where $e_{{\text{r}}}$ is the recovery coefficient and it can be obtained according to the material reference manual.

It can be seen that the compression time, $t_{{\text{s}}}$ and the recovery time, $t_{{\text{r}}}$ are determined by the meshing stiffness and the initial relative velocity, $v_{0}$ at the impact points. The value of the meshing stiffness can be obtained according to Fig. 5. There are two methods to calculate the initial relative velocity. One is calculated according to the radii of the meshing points (shown in Eq. (11)) and the angular velocity ($\omega_{{\text{p}}}$, $\omega_{{\text{g}}}$). The other is calculated according to the relative velocity in the nonlinear dynamics model established in Sect. 2. It is found that the latter is more accurate than the former because the comprehensive transmission error is considered in it. The latter will be used to calculate the initial relative velocity in the paper. Each impact point is refined into an interval due to consider the impact time. The action region of gear teeth along the action line N₁N₂ can be illustrated as Fig. 7 because the impact time (including compression time and recovery time) are considered. Each action interval and its corresponding time boundary can be obtained according to Fig. 7.

Fig. 7

Teeth action region along the line of action, N₁N₂

• (1) mesh-in impact interval AA₁, $0 \le t \le \Delta t_{1}$,

• (2) double-pair teeth meshing interval A₁B, $\Delta t_{1} \le t \le (\varepsilon_{{\text{m}}} - 1)T_{0} - \Delta t_{2}$,

• (3) switching impact interval of double-to-single BB₁, $(\varepsilon_{{\text{m}}} - 1)T_{0} - \Delta t_{2} \le t \le (\varepsilon_{{\text{m}}} - 1)T_{0}$,

• (4) single-pair teeth meshing interval B₁C, $(\varepsilon_{{\text{m}}} - 1)T_{0} \le t \le T_{0}$,

• (5) switching impact interval of single-to-double CC₁, $T_{0} \le t \le T_{0} + \Delta t_{3}$,

• (6) double-pair teeth meshing interval C₁Mo, $T_{0} + \Delta t_{3} \le t \le \varepsilon_{{\text{m}}} T_{0} - \Delta t_{4}$,

• (7) mesh-out impact interval MoMo₁, $\varepsilon_{{\text{m}}} T_{0} - \Delta t_{4} \le t \le \varepsilon_{{\text{m}}} T_{0}$.

$\Delta t_{i} = t_{{{\text{s}}i}} + t_{{{\text{r}}i}}$(i = 1,2,3,4) above in each impact interval can be calculated according to the impact type easily.

3.3 Calculation method of impact force for switching impact

The max impact force, $F_{{{\text{i}}\max }}$ has been obtained according to Eq. (17). This is its maximum in the impact interval. It increases from meshing force at the beginning point of the impact interval in the compression stage and decreases to meshing force at the end point of the impact interval in the recovery stage. Peng et al. [49] found the impact force increased according to the sinusoidal law in the compression stage and decreased according to the cosine law in the recovery stage when they studied the elastic impact of a sphere on a large plate. Calculation equation of the impact force can be established as Eq. (21) inspired by this.

$$ F_{{\text{i}}} (t) = \left\{ \begin{gathered} F_{{{\text{i}}\max }} \sin (\omega_{{\text{s}}} t + \varphi_{{\text{s}}} )\quad \quad t \in [0,t_{{\text{s}}} ] \hfill \\ F_{{{\text{i}}\max }} \cos (\omega_{{\text{r}}} t + \varphi_{{\text{r}}} )\quad \;\,\,t \in [0,t_{{\text{r}}} ] \hfill \\ \end{gathered} \right. $$

(21)

where $\omega_{{\text{s}}}$ and $\omega_{{\text{r}}}$ is the compression and recovery frequency, respectively. $\varphi_{{\text{s}}}$ and $\varphi_{{\text{r}}}$ is the compression and recovery phase angle, respectively. They can be calculated as follows according to the initial and boundary conditions.

Dynamic meshing forces at impact start time and end time are recorded as $F_{{{\text{ms}}}}$ and $F_{{{\text{me}}}}$, respectively. The initial and boundary conditions of compression stage can be expressed as Eq. (22).

$$ \left\{ \begin{gathered} F_{{{\text{ms}}}} = F_{{{\text{i}}\max }} \sin (\omega_{{\text{s}}} t + \varphi_{{\text{s}}} ),\quad t = 0 \hfill \\ F_{{{\text{i}}\max }} = F_{{{\text{i}}\max }} \sin (\omega_{{\text{s}}} t + \varphi_{{\text{s}}} ),\quad t = t_{{\text{s}}} \hfill \\ F_{{{\text{i}}\max }} = F_{{{\text{i}}\max }} \cos (\omega_{{\text{r}}} t + \varphi_{{\text{r}}} ),\quad t = 0 \hfill \\ F_{{{\text{me}}}} = F_{{{\text{i}}\max }} \cos (\omega_{{\text{r}}} t + \varphi_{{\text{r}}} ),\quad t = t_{{\text{r}}} \hfill \\ \end{gathered} \right. $$

(22)

It can be obtained by solving Eq. (22) as shown in Eq. (23).

$$ \left\{ \begin{gathered} \varphi_{{\text{s}}} = {\text{arc}}\sin (F_{{{\text{ms}}}} /F_{{{\text{i}}\max }} ) \hfill \\ \omega_{{\text{s}}} = [\pi - 2{\text{arc}}\sin (F_{{{\text{ms}}}} /F_{{{\text{i}}\max }} )]/t_{{\text{s}}} \hfill \\ \varphi_{{\text{r}}} = 0 \hfill \\ \omega_{{\text{r}}} = {\text{arc}}\cos (F_{{{\text{me}}}} /F_{{{\text{i}}\max }} )/t_{{\text{r}}} \hfill \\ \end{gathered} \right. $$

(23)

Impact forces of every impact type can be obtained by introducing Eq. (23) to Eq. (21) when the dynamic meshing forces, $F_{{{\text{ms}}}}$ and $F_{{{\text{me}}}}$ are calculated by solving the system dynamics equation. A nonlinear dynamics equation including switching impact of the spur gear pair will be established in Sect. 4 when the multi-state meshing determined by the backlash and contact ratio are considered.

3.4 Calculation method of drive-side and back-side boundary impact

Let $\overline{x} = \pm R_{bp} \theta_{p} \mp R_{bg} \theta_{\text{g}} \mp e(t)$ represent the relative displacement of the spur gear system along the line of action N₁N₂ (the operator is the upper one in $\pm$ and $\mp$) and M₁M₂ (the operator is the lower one in $\pm$ and $\mp$) according to Eq. (1). Drive-side boundary impact will occur when the gear pair reaches the drive-side boundary, $\overline{x} = \overline{D}$ from tooth disengagement and back-side boundary impact will occur when it reaches the back-side boundary, $\overline{x} = - \overline{D}$ from tooth disengagement. Drive-side boundary impact will result in separation of teeth pair or drive-side teeth meshing. Back-side boundary impact will result in separation of teeth pair or back-side teeth contacting. The results are determined by the relationship between the dynamic meshing force and the critical mesh-in force, $[F_{{\text{N}}} ]_{{\text{m}}}$ or contact-in force, $[F_{{\text{N}}} ]_{{\text{c}}}$.

A pair of meshing gears meets Eq. (24) according to the gear meshing principle.

$$ R_{\text{g}} \dot{\theta }_{\text{g}} = R_{\text{p}} \dot{\theta }_{\text{p}} $$

(24)

where $R_{i}$(i = p, g) is pitch radius of the pinion (i = p) and gear (i = g), respectively.

Equation (25) can be obtained when Eq. (24) is substituted into Eq. (1).

$$ I_{\text{g}} R_{\text{p}} \left( {T_{\text{p}} \mp R_{{\text{bp}}} F_{{{\text{Np}} 1}} \mp S_{p1c} (t)F_{{{\text{fp1}}}} \mp R_{{\text{bp}}} F_{{{\text{Np}} 2}} \mp S_{p2c} (t)F_{{{\text{fp2}}}} } \right) = I_{\text{p}} R_{{\text{g}}} \left( { - T_{\text{g}} \pm R_{{\text{bg}}} F_{{{\text{Ng}} 1}} \pm S_{g1c} (t)F_{{{\text{fg1}}}} \pm R_{{\text{bg}}} F_{{{\text{Ng}} 2}} \pm S_{g2c} (t)F_{{{\text{fg2}}}} } \right) $$

(25)

The critical mesh-in force, $[F_{{\text{N}}} ]_{{\text{m}}}$ and contact-in force, $[F_{{\text{N}}} ]_{{\text{c}}}$ can be approximated by the quasi-static positive pressure $F_{{{\text{N}}ij{\text{d}}}}$ along N₁N₂ and $F_{{{\text{N}}ij{\text{k}}}}$ along M₁M₂ shown in Fig. 3, respectively. They can be obtained according to Eq. (26).

$$ \left\{ \begin{gathered} [F_{{\text{N}}} ]_{{\text{m}}} = \frac{{R_{\text{p}} T_{\text{p}} I_{\text{g}} + R_{{\text{g}}} I_{\text{p}} T_{\text{g}} }}{{R_{\text{p}} I_{\text{g}} R_{{\text{bp}}} + R_{{\text{g}}} I_{\text{p}} R_{{\text{bg}}} + A_{c} + B_{c} }} \hfill \\ [F_{{\text{N}}} ]_{{\text{c}}} = - \frac{{R_{\text{p}} T_{\text{p}} I_{\text{g}} + R_{{\text{g}}} I_{\text{p}} T_{\text{g}} }}{{R_{\text{p}} I_{\text{g}} R_{{\text{bp}}} + R_{{\text{g}}} I_{\text{p}} R_{{\text{bg}}} + A_{c} + B_{c} }} \hfill \\ \end{gathered} \right. $$

(26)

where $A_{c} = \mu_{c} \lambda_{1c} (t)\gamma_{1c} (t)\left[ {R_{\text{p}} I_{\text{g}} S_{p1c} (t) + R_{{\text{g}}} I_{\text{p}} S_{g1c} (t)} \right]$, $B_{c} = \mu_{c} \lambda_{2c} (t)\gamma_{2c} (t)\left[ {R_{\text{p}} I_{\text{g}} S_{p2c} (t) + R_{{\text{g}}} I_{\text{p}} S_{g2c} (t)} \right]$. $\gamma_{1c} (t)$ and $\gamma_{2c} (t)$ can be obtained by Eq. (27).

$$ \gamma_{ic} (t) = \left\{ \begin{gathered} L_{ic} (t),{ 0} \le {\text{t}} \le {(}\varepsilon_{{\text{m}}} { - 1)}T_{0} \hfill \\ 0,{ (}\varepsilon_{{\text{m}}} { - 1)}T_{0} \le t \le T_{0} \, \hfill \\ \end{gathered} \right.,\quad \left( {i = {1},{ 2}; \, c = {\text{d}},{\text{ k}}} \right) $$

(27)

The kinetic energy of drive-side boundary impact or back-side boundary impact will all convert into elastic potential energy if the heat and damping dissipation caused by tooth friction are not considered according to energy conversation law. It is as Eq. (28).

$$ \frac{1}{2}m_{{\text{e}}} (1 - e_{{\text{r}}}^{2} )v_{0 - }^{2} = \int_{0}^{\delta } {k(t)\delta^{3/2} {\text{d}}\delta = \frac{2}{5}k(t)\delta^{5/2} } $$

(28)

where $v_{0 - }$ represents the velocity before drive-side boundary impact or back-side boundary impact and it can be calculated according to Eq. (1). The impact force after drive-side boundary impact or back-side boundary impact can be obtained as Eq. (29) according to Eq. (28).

$$ F_{{\text{i}}} (t) = \left[ {\frac{5}{4}k^{2/3} (t)m_{{\text{e}}} (1 - e_{{\text{r}}}^{2} )v_{0 - }^{2} } \right]^{3/5} $$

(29)

The gear teeth are in a compressed state under the action of quasi-static positive pressure when the spur gear pair is engaged. The impact force in the recovery stage for drive-side boundary impact or back-side boundary impact causes the meshing teeth to separate in the case of drive-side boundary impact or back-side boundary impact. The boundary determination condition can be obtained according to Eqs. (30) and (33). They are as follows.

Separation of teeth pair caused by drive-side boundary impact when $F_{{\text{i}}} > [F_{{\text{N}}} ]_{{\text{m}}}$ and its relative displacement and velocity can be obtained as Eq. (30).

$$ \overline{x} = \overline{D},\quad \dot{\overline{x}}_{ + } = - e_{{\text{r}}} \dot{\overline{x}}_{ - } $$

(30)

where $\dot{\overline{x}}_{ + }$ and $\dot{\overline{x}}_{ - }$ represents the velocity after and before impact.

Mesh-in caused by drive-side boundary impact when $F_{{\text{i}}} \le [F_{{\text{N}}} ]_{{\text{m}}}$ and its relative displacement and velocity can be obtained as Eq. (31).

$$ \overline{x} = \overline{D},\quad \dot{\overline{x}}_{ + } = e_{{\text{r}}} \dot{\overline{x}}_{ - } $$

(31)

Separation of teeth pair caused by back-side boundary impact when $F_{{\text{i}}} < [F_{{\text{N}}} ]_{{\text{c}}}$ and its relative displacement and velocity can be obtained as Eq. (32).

$$ \overline{x} = - \overline{D},\quad \dot{\overline{x}}_{ + } = - e_{{\text{r}}} \dot{\overline{x}}_{ - } $$

(32)

Back-side contacting caused by back-side boundary impact when $F_{{\text{i}}} \ge [F_{{\text{N}}} ]_{{\text{c}}}$ and its relative displacement and velocity can be obtained as Eq. (33).

$$ \overline{x} = - \overline{D},\quad \dot{\overline{x}}_{ + } = e_{{\text{r}}} \dot{\overline{x}}_{ - } $$

(33)

4 Non-dimensional nonlinear dynamics model of spur gear pair considering meshing impact

The nonlinear dynamics model of spur gear pair considering meshing impact and multi-state meshing is non-smooth and nonlinear. It is difficult to obtain its analytical solution. Numerical methods are usually used to study its dynamic characteristics. The variables in the equation belong to different scales, such as the order of magnitude for time-varying meshing stiffness and backlash is $10^{8}$ and $10^{ - 3}$, respectively. In order to avoid the overflow of large numbers and the submergence of decimals in the numerical solution, it is necessary to make the equations dimensionless. In addition, dimensionless can effectively expand the observation range of parameters in the study. To this end, this section will discuss the dimensionless processing of equations.

The backlash function of the gear transmission system shown in Eq. (34) can be used to reveal its meshing state as $\overline{x} = \pm R_{bp} \theta_{p} \mp R_{bg} \theta_{\text{g}} \mp e(t)$.

$$ f(\overline{x}) = \left\{ \begin{gathered} \overline{x} - \overline{D}, \, \overline{x} \ge \overline{D} \hfill \\ 0, \, \left| {\overline{x}} \right| < \overline{D} \hfill \\ \overline{x} + \overline{D}, \, \overline{x} \le - \overline{D} \hfill \\ \end{gathered} \right. $$

(34)

Relative rotation equation of spur gear pair can be normalized as Eq. (35) by introducing backlash function when the first equation subtracts the second equation in Eqs. (1) and (34), respectively. Dynamic meshing force, $F_{{{\text{m}}c}}$ can be normalized as $k(t)f(\overline{x}) \pm c_{{\text{m}}} \dot{\overline{x}}$, too.

$$ m_{\text{e}} \ddot{\overline{x}} \pm \left[ {1 + \lambda_{1c} (t)\mu_{1c} (t)g_{1c} (t)L_{1c} (t) + \lambda_{2c} (t)\mu_{2c} (t)g_{2c} (t)L_{2c} (t)} \right][k(t)f(\overline{x}) \pm c_{{\text{m}}} \dot{\overline{x}}] = \overline{F}_{\text{m}} + \overline{F}_{\text{h}} (t) $$

(35)

where $\overline{F}_{{\text{m}}} = {{\left( {R_{{\text{bp}}} I_{g} T_{p} + R_{bg} I_{\text{p}} T_{\text{g}} } \right)} \mathord{\left/ {\vphantom {{\left( {R_{{\text{bp}}} I_{g} T_{p} + R_{bg} I_{\text{p}} T_{\text{g}} } \right)} {\left( {I_{\text{g}} R_{{\text{bp}}}^{2} + I_{\text{p}} R_{{\text{bg}}}^{2} } \right)}}} \right. \kern-0pt} {\left( {I_{\text{g}} R_{{\text{bp}}}^{2} + I_{\text{p}} R_{{\text{bg}}}^{2} } \right)}}$ is the average actuating force component. $\overline{F}_{\text{h}} (t) =$ $- m_{e} \ddot{e}(t)$ is the internal actuating force of the gear pair. $g_{jc} (t) = [R_{{\text{bp}}} I_{\text{g}} S_{pjc} (\tau ) + R_{{\text{bg}}} I_{\text{p}} S_{gjc} (\tau )]/$$(I_{\text{g}} R_{{\text{bp}}}^{2} + I_{\text{p}} R_{{\text{bg}}}^{2} )$ is the equivalent friction moment of the jth teeth pair under drive-side teeth meshing (c = d) and back-side teeth contacting (c = k) state.

The dimensionless backlash, $D = \overline{D}/D_{\text{c}}$ is obtained when a feature size, $D_{c}$, is defined which is generally taken as equal to a backlash value. The remaining dimensionless variables are $x = \overline{x}/D_{c}$, $\overline{F} =$ $\overline{F}_{m} /(m_{\text{e}} D_{c} \omega_{\text{n}}^{2} )$, $\zeta = c_{{\text{m}}} /(m_{\text{e}} \omega_{\text{n}} )$, $k_{\text{m}} (t) =$ $k(t)/$$(m_{\text{e}} \omega_{n}^{2} )$ and $F_{\text{h}} (t)$ = $\overline{F}_{\text{h}} (t)/(m_{\text{e}} D_{c} \omega_{\text{n}}^{2} ) =$$\varepsilon \omega^{2} \cos (\omega {\kern 1pt} t)$. The dimensionless time is $\tau = t\omega_{\text{n}}$. The normalized non-dimensional nonlinear dynamics model including impact of spur gear pair considering the multi-state meshing can be obtained as Eq. (36) based on Eqs. (30)–(33) and (35) replacing $t$ with $\tau$.

$$ \left\{ \begin{gathered} \ddot{x} + h(x,\tau )F(x,\tau ) = \overline{F} + \varepsilon \omega^{2} \sin (\omega \tau ),\quad x \ne \pm D \hfill \\ \dot{x}_{ + } = e_{r} \dot{x}_{ - } ,\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad x = D \wedge F_{{\text{i}}} (\tau ) \le [F_{{\text{N}}} ]_{{\text{m}}} \hfill \\ \dot{x}_{ + } = - e_{r} \dot{x}_{ - } ,\quad \quad \quad \quad \quad \quad \quad \;\quad \quad \quad x = D \wedge F_{{\text{i}}} (\tau ) > [F_{{\text{N}}} ]_{{\text{m}}} \hfill \\ \dot{x}_{ + } = - e_{r} \dot{x}_{ - } ,\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad x = - D \wedge F_{{\text{i}}} (\tau ) < [F_{{\text{N}}} ]_{{\text{c}}} \hfill \\ \dot{x}_{ + } = e_{r} \dot{x}_{ - } ,\quad \quad \quad \quad \quad \quad \quad \;\quad \quad \quad x = - D \wedge F_{{\text{i}}} (\tau ) \ge [F_{{\text{N}}} ]_{{\text{c}}} \hfill \\ \end{gathered} \right. $$

(36)

where $h(x,\tau )$ is the state function of spur gear pair which including the single-pair and double-pair teeth meshing and contacting, tooth disengagement when four impact states corresponding to drive-side teeth meshing state are considered. It can be described as Eq. (37) which reflects the meshing position shown in Fig. 7.

$$ h(x,\tau ) = \left\{ \begin{gathered} 1 + \lambda_{{1{\text{d}}}} (\tau )\mu_{{1{\text{d}}}} (\tau )g_{{1{\text{d}}}} (\tau )L_{{1{\text{d}}}} (\tau ) + \lambda_{{2{\text{d}}}} (\tau )\mu_{{2{\text{d}}}} (\tau )g_{{2{\text{d}}}} (\tau )L_{{2{\text{d}}}} (\tau ), \, \tau_{{\text{A}}} < \tau \le \, \tau_{{{\text{A}}_{1} }} \hfill \\ h_{{{\text{dt}}}} (x,\tau ), \, \quad \quad \,\quad \quad \quad \quad \, \tau_{{{\text{A}}_{1} }} < \tau \le \tau_{{\text{B}}} \, \hfill \\ 1 + \lambda_{{2{\text{d}}}} (\tau )\mu_{{2{\text{d}}}} (\tau )g_{{2{\text{d}}}} (\tau ), \, \quad \; \, \tau_{{\text{B}}} < \tau \le \tau_{{{\text{B}}_{1} }} \hfill \\ h_{{{\text{st}}}} (x,\tau ), \, \quad \quad \,\quad \quad \quad \quad \, \tau_{{{\text{B}}_{1} }} < \tau \le \tau_{{\text{C}}} \hfill \\ 1 + \lambda_{{1{\text{d}}}} (\tau )\mu_{{1{\text{d}}}} (\tau )g_{{1{\text{d}}}} (\tau )L_{{1{\text{d}}}} (\tau ) + \lambda_{{2{\text{d}}}} (\tau )\mu_{{2{\text{d}}}} (\tau )g_{{2{\text{d}}}} (\tau )L_{{2{\text{d}}}} (\tau ), \, \,\, \, \tau_{{\text{C}}} < \tau \le \tau_{{{\text{C}}_{1} }} \hfill \\ h_{{{\text{dt}}}} (x,\tau ), \, \quad \quad \quad \quad \quad \quad \, \tau_{{{\text{C}}_{1} }} < \tau \le \, \tau_{{\text{D}}} \hfill \\ 1 + \lambda_{{1{\text{d}}}} (\tau )\mu_{{1{\text{d}}}} (\tau )g_{{1{\text{d}}}} (\tau ), \, \quad \; \, \tau_{{\text{D}}} < \tau \le \, \tau_{{{\text{D}}_{1} }} \hfill \\ \end{gathered} \right. $$

(37)

where $h_{{{\text{dt}}}} (x,\tau )$ and $h_{{{\text{st}}}} (x,\tau )$ is the state function of MSdd or MSkd and MSds or MSks, respectively. They can be described as Eqs. (38) and (39), respectively.

$$ h_{{{\text{dt}}}} (x,\tau ) = \left\{ \begin{gathered} 1 + \lambda_{{1{\text{d}}}} (\tau )\mu_{{1{\text{d}}}} (\tau )g_{{1{\text{d}}}} (\tau )L_{{1{\text{d}}}} (\tau ) + \lambda_{{2{\text{d}}}} (\tau )\mu_{{2{\text{d}}}} (\tau )g_{{2{\text{d}}}} (\tau )L_{{2{\text{d}}}} (\tau ), \, x \ge D \hfill \\ 0,\quad \, \quad \;\quad \;\; \, \quad \, \left| x \right| < D \hfill \\ 1 + \lambda_{{1{\text{k}}}} (\tau )\mu_{{1{\text{k}}}} (\tau )g_{{1{\text{k}}}} (\tau )L_{{1{\text{k}}}} (\tau ) + \lambda_{{{\text{2k}}}} (\tau )\mu_{{{\text{2k}}}} (\tau )g_{{{\text{2k}}}} (\tau )L_{{{\text{2k}}}} (\tau ) \, x \le - D \hfill \\ \end{gathered} \right. $$

(38)

$$ h_{{{\text{st}}}} (x,\tau ) = \left\{ \begin{gathered} 1 + \lambda_{{1{\text{d}}}} (\tau )\mu_{{1{\text{d}}}} (\tau )g_{{1{\text{d}}}} (\tau ) \, x \ge D \hfill \\ 0\quad \;\; \, \left| {\overline{x}} \right| < D \hfill \\ 1 + \lambda_{{1{\text{k}}}} (\tau )\mu_{{1{\text{k}}}} (\tau )g_{{1{\text{k}}}} (\tau ) \, \overline{x} \le - D \hfill \\ \end{gathered} \right. $$

(39)

$F(x,\tau )$ in Eq. (36) is called dynamic force which acts on the teeth pair corresponding to different meshing states. It is just the dynamic meshing force when the system is under teeth meshing or contacting state, but it is the coupling result of the dynamic meshing force and meshing impact force when the system is under meshing impact state. It can be expressed as Eq. (40).

$$ F(x,\tau ) = \left\{ \begin{gathered} F_{i} (\tau ), \, \tau_{{\text{A}}} < \tau \le \tau_{{{\text{A}}_{1} }} \hfill \\ k(\tau )f(x) + \zeta \dot{x}, \, \tau_{{{\text{A}}_{1} }} < \tau \le \tau_{{\text{B}}} \hfill \\ F_{i} (\tau ), \, \tau_{{\text{B}}} < \tau \le \tau_{{{\text{B}}_{1} }} \, \hfill \\ k(\tau )f(x) + \zeta \dot{x}, \, \tau_{{{\text{B}}_{1} }} < \tau \le \tau_{{\text{C}}} \hfill \\ F_{i} (\tau ), \, \tau_{{\text{C}}} < \tau \le \tau_{{{\text{C}}_{1} }} \hfill \\ k(\tau )f(x) + \zeta \dot{x}, \, \tau_{{{\text{C}}_{1} }} < \tau \le \tau_{{{\text{Mo}}}} \hfill \\ F_{i} (\tau ), \, \tau_{{{\text{Mo}}}} < \tau \le \tau_{{{\text{D}}_{1} }} \hfill \\ \end{gathered} \right. $$

(40)

where $F_{i} (\tau )$ should be calculated according to its impact type and the impact time introduced in SubSects. 3.2 and 3.3. Non-dimensional backlash function, $f(x)$ can be expressed as Eq. (41) by substituting the dimensionless quantities into Eq. (34).

$$ f(x) = \left\{ \begin{gathered} x - D,\;\;\;\;\;\;\;\;x \ge D \hfill \\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\; - D < x < D \hfill \\ x + D,\;\;\;\;\;\;\;\;x \le - D \hfill \\ \end{gathered} \right. $$

(41)

5 Numerical results

A nonlinear dynamics system considering meshing impact with multi-state meshing is described in Eq. (36) and it is strongly non-smooth because of backlash is included and time-varying because there are so many time-varying variables are considered including time-varying meshing stiffness, time-varying friction, load distribution ratio and the comprehensive transmission error. It is very difficult to obtain its analytical solution because of its nonlinearity, non-smoothness and time-varying variability. The numerical analyses method is widely used to investigate the system nonlinear dynamics. Our C programming based on 4-order Runge–Kutta method is used to solve the nonlinear dynamics equation in the paper. The nonlinear dynamics, meshing states and meshing impact of the system are studied. Some well-known crucial tools in nonlinear dynamics analysis are used such as phase portraits which can clearly reveal the interval of phase trajectory, Poincaré mappings which are used to judge the period of system motion, time history diagrams of dynamic force which are mainly used to reveal the change of meshing force and impact force, bifurcation diagrams which are used to reflect the transition process of system motion, the corresponding top Lyapunov exponent (TLE) diagrams which are used to distinguish whether the motion of the system is periodic or chaotic and the type of bifurcation and so on. Five typical phase portraits are used to discuss the system dynamics characteristics when meshing impact is considered in SubSect. 5.1. Effects of two control variables such as meshing frequency and load coefficient on the system impact and vibration characteristics are analyzed that is from a global perspective in SubSect. 5.2.

5.1 Five typical cases

There are eight cases of the system motions when the meshing impact including mesh-in impact, single- to-double switching impact, double-to-single switching impact, drive-side boundary impact and back-side boundary impact are considered as shown in Fig. 5. They either appear in a single form or in a combined form in the system corresponding to different working conditions. Five representative typical forms of motion by their phase portraits are listed in Fig. 8 as Eq. (36) are solved numerically. Their trend of the phase trajectory is clockwise. The black dashed line represents x = D or x = -D. The sky blue in the phase trajectory represents MSdd and MSkd and the magenta represents MSds and MSks when solid lines represent phase trajectory with meshing impact and dashed lines in Fig. 8c–e represent phase trajectory without considering meshing impact.

Fig. 8

Phase portraits of five representative typical cases: a $\overline{F}$ = 0.0202, ω = 1.2, ξ = 0.2, ε = 0.15, D = 1.0; b $\overline{F}$ = 0.0311, ω = 1.2, ξ = 0.2, ε = 0.15, D = 1.0; c $\overline{F}$ = 0.09, ω = 1.2, ξ = 0.15, ε = 0.2, D = 1.0; d $\overline{F}$ = 0.14, ω = 1.2, ξ = 0.2, ε = 0.14, D = 1.0; e $\overline{F}$ = 0.1, ω = 1.2, ξ = 0.08, ε = 0.03, D = 1.0. The sky blue “blue square” (0, 204, 255) represents MSdd and MSkd and the magenta “magenta square” (255, 0, 255) represents MSds and MSks. Solid lines represent the phase trajectory with meshing impact and dotted lines in (c), (d) and (e) represent the phase trajectory without meshing impact

Figure 8a is obtained as the variables are taken as $\omega$ = 1.2, $\overline{F}$ = 0.0202, $\xi$ = 0.2, $\varepsilon$ = 0.15, D = 1.0. There are six cases in it. All cases except ④ and ⑧ shown in Fig. 5 appear in the phase portrait. The phase trajectory under tooth disengagement (③) comes to the drive-side boundary, x = D and the mesh-in caused by drive-side boundary impact (②) after many times separation of teeth pair caused by drive-side boundary impact (⑥) leads the teeth pair to drive-side teeth meshing (①). Double-to-single switching impact and single-to-double switching impact (⑤) exist in the drive-side teeth meshing process. Tooth disengagement occurs in the single-pair teeth meshing. There are two trends of phase trajectory under tooth disengagement states. One is to return directly to the drive-side boundary, x = D without reaching the back-side boundary, x = -D. The other is to return to the drive-side boundary, x = D after separation of teeth pair caused by back-side boundary impact (⑦). This is an interesting phenomenon because the teeth pair is during busy drive-side boundary impact, tooth disengagement, back-side boundary impact. This should be the most extreme rattling.

Figure 8b is obtained as the parameters are taken as $\overline{F}$ increases to 0.0311 and other four parameters are same as Fig. 8a. The impact in the motion of the system and the motion pattern caused by it have changed significantly. There are still six cases in it. All cases except ⑥ and ⑦ shown in Fig. 5 appear in the phase portrait. Separations of teeth pair caused by drive-side boundary impact and back-side boundary impact do not appear again. The motion of the system has become much softer. The phase trajectory under tooth disengagement (③) comes to the drive-side boundary, x = D and the mesh-in caused by drive-side boundary impact (②) leads the teeth pair to drive-side teeth meshing (①). Double-to-single switching impact and single- to-double switching impact (⑤) exist in the drive-side teeth meshing process. Tooth disengagement occurs in the single-pair teeth meshing. Back-side contacting (⑧) occurs after back-side boundary impact. Double-to-single switching impact and single-to-double switching impact exist in the back-side teeth contacting process. Teeth pair disengages in the single-pair teeth meshing region (in magenta) under drive-side teeth meshing state and they disengage in the double-pair teeth meshing region (in sky blue) under back-side teeth contacting state.

Figure 8c is obtained as the parameters are taken as $\omega$ = 1.2, $\overline{F}$ = 0.09, $\xi$ = 0.15, $\varepsilon$ = 0.2, D = 1.0. Solid lines represent the motion of the system with meshing impact considered while the dashed lines represent the one without considering meshing impact. The impact in the motion of the system and the motion pattern caused by it have changed significantly. The phase trajectory does not reach the back-side boundary, x = -D and the phenomena relating to back-side do not appear in this case. There are four cases in it. They are ①, ②, ⑤ and ⑥ shown in Fig. 5. Mesh-in caused by the drive-side boundary impact (②) leads the system to drive-side teeth meshing (①) after times of separation of teeth pair caused by the drive-side boundary impact (⑥). This process is shown in the enlarged area AB in the figure. Double-to-single switching and single-to-double switching exist in the case. Tooth disengagement occurs in the region of single-pair teeth meshing. The dashed lines exhibit the phase trajectory of the system without considering impact. It is the calculation result of the most popular model at present. It can be seen from the calculation results of the two models that the meshing impact changes the motion characteristics under the condition of this parameter. From the local situation of this case, the system motion is a period-2 one when considering the meshing impact and it is period-1 motion without considering the meshing impact. In addition, the amplitude of the system state variables also changed.

Figure 8d is obtained as the parameters are taken as $\omega$ = 1.2, $\overline{F}$ = 0.14, $\xi$ = 0.2, $\varepsilon$ = 0.14, D = 1.0. The meaning of lines and colors in it is the same as that in Fig. 8c. The motion of the system under this parameter is relatively simple compared to Fig. 8c. It is period-1 motion whether meshing impact is considered or not. The system enters drive-side teeth meshing (①) after mesh-in caused by the drive-side boundary impact (②) when the phase trajectory of tooth disengagement region reaches the drive-side boundary as considering the meshing impact. There is not separation of teeth pair caused by drive-side boundary impact. Double-to-single switching impact occurs in the drive-side teeth meshing region. It disengages at point C as shown in the figure and the point falls in the single pair teeth meshing region, too. The amplitude of the system state variables is reduced by meshing impact.

Figure 8e is obtained as the parameters are taken as $\omega$ = 1.2, $\overline{F}$ = 0.1, $\xi$ = 0.08, $\varepsilon$ = 0.03, D = 1.0. The meaning of lines and colors in it is the same as that in Fig. 8c. The system motion under this parameter is period-1 one whether meshing impact is considered or not. There is only drive-side teeth meshing (①) in the system. Double-to-single switching impact (in the region of AB shown in the figure) and single-to-double switching impact (in the region of AB shown in the figure) leads to the obvious jump of the phase trajectory of the system and also significantly changes the amplitude of the system state quantity (including two system state variables). The phase trajectory of the system becomes unsmooth compared to that without considering meshing impact (dashed line).

It can be seen that the meshing impacts affect the dynamic characteristics of spur gear pair in a different way. Firstly, they change the system state variables comparing the phase trajectory considering meshing impact to the one without considering meshing impact. But they have no obvious effect of the meshing states. Secondly, the number of motion period for the system may be changed by meshing impact. Thirdly, the influence of meshing impact on the system dynamic characteristics is related to the value of its parameters. It will be investigated in the next subsection.

5.2 Analysis of vibro-impact characteristics for spur gear pair

The effect of different variables on the system nonlinear dynamic characteristics will be analyzed in this subsection as the Poincaré section, $\Gamma_{\text{n}} = \left\{ {(x,\dot{x},t) \in {\mathbf{R}}^{2} \times {\mathbf{R}}^{ + } ,\;\bmod (t,2\pi /\omega ) = 0} \right\}$ is defined. The influences of meshing frequency and load coefficient on the dynamics of the spur gear pair considering meshing impact within gear operation cycle will be analyzed systematically according to phase portraits, Poincaré mappings, bifurcation diagrams, top Lyapunov exponent (TLE) diagrams and diagram of the dynamic force versus time, respectively.

5.2.1 The effect of meshing frequency

Meshing frequency is the most important parameter of the gear transmission system. It directly changes the transmission speed of the gear pair and has a very important effect on the system dynamics. Bifurcation diagrams of the spur gear pair with meshing impact (in red) and without considering meshing impact (in blue) are obtained in Fig. 9a as $\omega$$\in$ [0.5,1.5], $\zeta$ = 0.2, $\varepsilon$ = 0.14, $D = 1.0$, $\overline{F}$ = 0.08 as time-varying meshing stiffness, k(t) is calculated as shown in Fig. 6 dynamically. The corresponding TLE diagram with meshing impact is shown in Fig. 9b. The meshing impact affects the nonlinear dynamics obviously compared to two bifurcation diagrams in Fig. 9a. Its motion transition process will be analyzed in detail and Ai(i = 1, 2, …, 9) are used to represent the bifurcation points for the convenience of analysis and explanation.

Fig. 9

Bifurcation and TLE diagrams of spur gear pair with increase in meshing frequency, $\omega$: a Bifurcation diagrams considering meshing impact (in red) and without considering meshing impact (in blue); b TLE diagram considering meshing impact. Ai(i = 1, 2, …, 9) represent the bifurcation points for the convenience of analysis and explanation. (Color figure online)

It can be seen from Fig. 9a that the system motion is a stable period-1 one as the meshing frequency falls in the left of point A₁ ($\omega$ < 0.61). Its TLE is less than 0 and it means that the motion is periodic one as shown in Fig. 9b. The meshing impact does not change the type of the system motion and increases the amplitude of the relative displacement and velocity of the system slightly comparing the bifurcation diagrams in red and blue in Fig. 9a. The corresponding Poincaré mapping and phase portrait is shown in Fig. 10a as its diagram of the dynamic force, F versus time is shown in Fig. 10b as $\omega$ = 0.6, respectively. There is tooth disengagement existing in the system because there are x < D and F = 0 as shown in Fig. 10a and b and the system enters drive- side teeth meshing (①) after mesh-in caused by the drive-side boundary impact (②). The effect of double-to- single switching impact and single-to-double switching impact is obvious because the phase trajectory has two times obvious mutations as shown in Fig. 10a. The change amplitude of state variables for single-to-double is smaller than that of double-to-single because the single-to-double switching impact is smaller than that of double-to-single as shown in Fig. 10b.

Fig. 10

Poincaré mappings and phase portraits, diagrams of dynamic forces versus time with different values of ω: a Poincaré mapping and phase portrait, ω = 0.6; b Diagram of dynamic force versus time, ω = 0.6; c Poincaré mapping and phase portrait, ω = 0.63; d Diagram of dynamic force versus time, ω = 0.63; e Poincaré mapping and phase portrait, ω = 0.7; f Diagram of dynamic force versus time, ω = 0.7; g Poincaré mapping, ω = 0.95; h Diagram of dynamic force versus time, ω = 0.95; (i) Poincaré mapping, ω = 0.96; j Diagram of dynamic force versus time, ω = 0.96; k Poincaré mapping and phase portrait, ω = 1.05; l Diagram of dynamic force versus time, ω = 1.05; m Poincaré mapping and phase portrait, ω = 1.2; n Diagram of dynamic force versus time, ω = 1.2; o Poincaré mapping and phase portrait, ω = 1.45; p Diagram of dynamic force versus time, ω = 1.45. The sky blue “blue square” (0, 204, 255) represents double-pair teeth meshing and the magenta “magenta square” (255, 0, 255) represents single-pair teeth meshing. (Color figure online)

The period-1 motion transits to period-2 one by saddle-node bifurcation with the increasing of the system meshing frequency to point A₁ ($\omega$ = 0.61). The TLE < 0 means that the bifurcation is not a doubling one and there is also no grazing. The corresponding Poincaré mapping and phase portrait is shown in Fig. 10c and its diagram of the dynamic force, F versus time is shown in Fig. 10d as $\omega$ = 0.63, respectively. Tooth disengagement exists still in the system. The meshing impact changed the motion type and the amplitude of the system state variables as shown in Fig. 9a but did not eliminate the tooth disengagement state existing in the system as shown in Fig. 10d. There is twice drive-side boundary impact. Its dynamic force shows an obvious change trend of period-2 as shown in Fig. 10d. This period-2 motion degenerates to period-1 one at point A₂ ($\omega$ = 0.656) by inverse-doubling bifurcation and its TLE = 0 at this point as shown in Fig. 9b. This period-1 motion continues until the system meshing frequency increases to point A₄ ($\omega$ = 0.938) except the transient chaos at $\omega$ = 0.755 (A₃). The corresponding Poincaré mapping and phase portrait is shown in Fig. 10e and the diagram of the dynamic force, F versus time is shown in Fig. 10f as $\omega$ = 0.7, respectively. The transient chaos at $\omega$ = 0.755(A₃) can be proved by that its TLE is greater than zero at this point as shown in Fig. 9b.

The period-2 motion degenerates to a period-1 one through saddle-node bifurcation with the increasing of the system meshing frequency to point A₄ ($\omega$ = 0.938) according to its TLE less than zero at the bifurcation point A₄. Grazing bifurcation deduced by which the phase trajectory of the system is tangent to the boundary, x = D changes the amplitude of the system state variables for this period-2 motion with the increasing of the system meshing frequency to point A₅ ($\omega$ = 0.96) but this motion remains as period-2 still. The corresponding Poincaré mapping and phase portrait is shown in Fig. 10g and the diagram of the dynamic force, F versus time is shown in Fig. 10h of the period-2 motion as $\omega$ = 0.95 before the grazing bifurcation, respectively. Jumping of the amplitude for relative velocity at drive-side boundary and turning on the phase trajectory at switching of meshing pair can be seen clearly in Fig. 10g. Time of tooth disengagement shortens comparing Fig. 10h with Fig. 10b, d and f. The corresponding Poincaré mapping and phase portrait is shown in Fig. 10i and the diagram of the dynamic force, F versus time is shown in Fig. 10j of the grazing motion as $\omega$ = 0.96, respectively. Time of tooth disengagement is further shortened by the grazing comparing Fig. 10j with Fig. 10h. It can be seen from Fig. 10i that the phase trajectory is tangent to the drive-side boundary, x = D. Twice drive-side boundary impact decreases to one times by the grazing bifurcation and the phase trajectory moves towards drive-side teeth meshing comparing Fig. 10i with Fig. 10g.

Crisis changes the period-2 motion to chaos with the increasing of the system meshing frequency to point A₆ ($\omega$ = 1.023) according to its TLE greater than zero at the bifurcation point A₆. This chaos degenerates to a period-8 motion with the increasing of the system meshing frequency to point A₇ ($\omega$ = 1.04) by the inverse doubling bifurcation sequence. The corresponding Poincaré mapping and phase portrait is shown in Fig. 10k and the diagram of the dynamic force, F versus time is shown in Fig. 10(l) as $\omega$ = 1.05, respectively. There are four times drive-side boundary impact as shown in Fig. 10k. The period-8 window soon disappears and the system enters chaos again with the increasing of the system meshing frequency to point A₈ ($\omega$ = 1.06). The Poincaré mapping is shown in Fig. 10m and the diagram of the dynamic force, F versus time is shown in Fig. 10n as $\omega$ = 1.2, respectively.

The chaos degenerates to a period-1 motion by inverse doubling bifurcation sequences quickly with the increasing of the system meshing frequency to point A₉ ($\omega$ = 1.375) as shown in the enlarge window locally of Fig. 9a. The phase portrait and the corresponding Poincaré mapping of the period-1 motion is shown in Fig. 10o and the diagram of the dynamic force, F versus time is shown in Fig. 10p as $\omega$ = 1.45, respectively. After that, the system is in period-1 motion and its phase trajectory gradually moves to the right with the increase of meshing frequency but tooth disengagement always exists under the condition of this parameter.

It can be seen from the red and blue bifurcation diagrams in Fig. 9a that the system motion with meshing impact (in red) and is the same to the one without considering meshing impact (in blue) when the meshing frequency is smaller than A₁, regions of A₂A₃, A₃A₄ and A₅A₆. That is the influence of meshing impact on the dynamic characteristics of the system is not very obvious which can be basically ignored when the meshing frequency is less than 1.0. Its influence can not be ignored when the meshing frequency is greater than 1.0 and less than 1.5. This should also be the reason why the dynamic model without considering meshing impact is applicable for a long time.

There are some interesting phenomena. Most of tooth disengagement occurs in the single-pair teeth meshing region as shown in Fig. 10a, c, e, g, i and k. It will soon disappear if tooth disengagement occurs in the double-pair teeth meshing region as shown in Fig. 10g and i. In addition, the dynamic force amplitude of double-to-single switching is basically greater than that of single-to-double switching.

5.2.2 The effect of load coefficient

Load is another important parameter of the gear transmission system because it directly reflects the power transmission ability and level of the gear pair. Bifurcation diagrams of the system considering meshing impact (in red) and without considering meshing impact (in blue) are obtained in Fig. 11a as $\overline{F}$$\in$[0.02,0.2], $\zeta = 0.2$, $\varepsilon = 0.15$, D = 1.0, $\omega$ = 1.2 and time-varying meshing stiffness is calculated as Fig. 6 dynamically. The corresponding TLE diagram considering meshing impact is shown in Fig. 11b. The meshing impact affects obviously the nonlinear dynamics when the load coefficient is less than $\overline{F} < 0.08$ as shown in Fig. 11a. It leads the system motion to be simple. There is no effect when the system is in the period-1 motion as the load coefficient is large. Its motion transition process will be analyzed in detail and Bi(i = 1, 2, …, 6) represent the bifurcation points for the convenience of analysis and explanation.

Fig. 11

Bifurcation and TLE diagrams of the spur gar pair with the increasing of load coefficient, $\overline{F}$: a Bifurcation diagrams considering meshing impact (in red) and without considering meshing impact (in blue); b TLE diagram considering meshing impact. Bi(i = 1, 2, …, 6) represent the bifurcation points for the convenience of analysis and explanation

The system motion is chaotic one when the load coefficient $\overline{F}$ < 0.0385(B₁) from Fig. 11a. Its TLE is more than 0 and it means that the motion is chaos as shown in Fig. 11b. Poincaré mapping is shown in Fig. 12a and the diagram of the dynamic force, F versus time is shown in Fig. 12b as $\overline{F}$ = 0.03, respectively. Its dynamic force changes irregularly and the dynamic force amplitude of single-to-double switching is greater than that of double-to-single switching. A small window of period-1 motion appears in a narrow region as the load coefficient greater than $\overline{F}$ = 0.0385 (B₁) and less than $\overline{F}$ = 0.0401 (B₂). The corresponding Poincaré mapping and phase portrait is shown in Fig. 12c and the diagram of the dynamic force, F versus time is shown in Fig. 12d of the period-1 motion as $\overline{F}$ = 0.04, respectively. It can be seen from Fig. 12d that the dynamic force amplitude of double-to-single switching is greater than that of single-to- double switching. Tooth disengagement appears in the system because there are x < D and F ≤ 0 as shown in Fig. 12c and d. The system enters drive-side teeth meshing (①) after mesh-in caused by the drive-side boundary impact (②) and enters tooth disengagement in single pair teeth meshing region.

Fig. 12

Poincaré mappings and phase portraits, diagrams of dynamic forces versus time with different values of $\overline{F}$: a Poincaré mapping, $\overline{F}$ = 0.03; b Diagram of dynamic force versus time, $\overline{F}$ = 0.03; c Poincaré mapping and phase portrait, $\overline{F}$ = 0.04; d Diagram of dynamic force versus time, $\overline{F}$ = 0.04; e Poincaré mapping and phase portrait, $\overline{F}$ = 0.06; f Diagram of dynamic force versus time, $\overline{F}$ = 0.06; g Poincaré mapping and phase portrait, $\overline{F}$ = 0.08; h Diagram of dynamic force versus time, $\overline{F}$ = 0.08; i Poincaré mapping and phase portrait, $\overline{F}$ = 0.125; j Diagram of dynamic force versus time, $\overline{F}$ = 0.125; k Poincaré mapping and phase portrait, $\overline{F}$ = 0.145; l Diagram of dynamic force versus time, $\overline{F}$ = 0.145; m Poincaré mapping and phase portrait, $\overline{F}$ = 0.16; n Diagram of dynamic force versus time, $\overline{F}$ = 0.16. The sky blue “blue square” (0, 204, 255) represents double-pair teeth meshing and the magenta “magenta square” (255, 0, 255) represents single-pair teeth meshing. (Color figure online)

Chaotic motion comes back from period-1 motion by the crisis with the increasing of the load coefficient to point B₂ ($\overline{F}$ = 0.0401). Poincaré mapping is shown in Fig. 12e and the diagram of the dynamic force, F versus time is shown in Fig. 12f as $\overline{F}$ = 0.06, respectively. The dynamic force amplitude of double-to-single switching is greater than that of single-to-double switching. The chaos degenerates to a period-2 motion by saddle-node bifurcation with the increasing of the load coefficient to $\overline{F}$ = 0.079(B₃) as shown in Fig. 11a. The corresponding Poincaré mapping and phase portrait is shown in Fig. 12g and the diagram of the dynamic force, F versus time is shown in Fig. 12h of the period-2 motion as $\overline{F}$ = 0.08, respectively. The dynamic force changes in period-2 law with time obviously as shown in Fig. 12h and the dynamic force amplitude of double-to-single switching is greater than that of single-to-double switching.

The period-2 motion degenerates to period-1 one by an inverse doubling bifurcation with the increasing of the load coefficient to point B₄ ($\overline{F}$ = 0.1191). The corresponding Poincaré mapping and phase portrait is shown in Fig. 12i and the diagram of the dynamic force, F versus time is shown in Fig. 12j of the period-1 motion as $\overline{F}$ = 0.125, respectively. The amplitude of double-to-single switching impact is less than that of single-to-double switching impact as shown in Fig. 12j. Grazing occurs with the increasing of the load coefficient to point B₆ ($\overline{F}$ = 0.145). The corresponding Poincaré mapping and phase portrait is shown in Fig. 12k and the diagram of the dynamic force, F versus time is shown in Fig. 12l of this grazing as $\overline{F}$ = 0.145, respectively. This grazing eliminates the tooth disengagement of the system. It is in stable period-1 motion when the load coefficient greater than $\overline{F}$ = 0.145(B₆). The corresponding Poincaré mapping and phase portrait is shown in Fig. 12m and the diagram of the dynamic force, F versus time is shown in Fig. 12n of the period-1 motion as $\overline{F}$ = 0.16, respectively. It can be seen from Fig. 12m and n that there is only drive-side teeth meshing in the system and x > D, F > 0.

The transition of the system motion near B₅ cannot be ignored. It is known from the above that the system enters period-1 motion with the increasing of the load coefficient to point B₄ ($\overline{F}$ = 0.1191) and its phase portrait is shown in Fig. 12i. It can be seen that from Fig. 12c, g and i that tooth disengagement occurs in the region of the single-pair teeth meshing. The phase trajectory gradually moves to the right with the increasing of the load coefficient. Tooth disengagement occurs in the region of the double-pair teeth meshing and the phase trajectory begins to entangle as shown in Fig. 13a. Doubling bifurcation sequences lead the system motion to chaos after period-2 motion (Fig. 13b), period-4 motion (Fig. 13c) and so on. The corresponding Poincaré mapping and the phase portrait of the chaos is shown in Fig. 13d. The chaos degenerates to periodic motion immediately by inverse doubling bifurcation sequences. Phase portraits and the corresponding Poincaré mappings of period-4 motion, period-2 motion and period-1 motion are shown in Fig. 13e-g, respectively.

Fig. 13

Poincaré mappings and phase portraits with different values of $\overline{F}$: a period-1 motion, $\overline{F}$ = 0.1293; b period-2 motion, $\overline{F}$ = 0.12936; c period-4 motion, $\overline{F}$ = 0.12938; d chaos, $\overline{F}$ = 0.1294; e period-4 motion, $\overline{F}$ = 0.12942; f period-2 motion, $\overline{F}$ = 0.12944; g period-1 motion, $\overline{F}$ = 0.1295. The sky blue “blue square” (0, 204, 255) represents double pair teeth meshing and the magenta “magenta square” (255, 0, 255) represents single pair teeth meshing. (Color figure online)

There is a great difference between the system motions considering meshing impact (in red) and without considering meshing impact (in blue) as can be seen from Fig. 11a. The system motion without considering meshing impact is chaos when the load coefficient is small and it degenerates to period-2 motion and stable period-1 motion immediately with the increase in the load coefficient as shown in Fig. 11a. The influence of the load is so small that it is unreasonable in the actual system. Meshing impact can not be ignored in the dynamic equation of the gear transmission system.

There is also an abscissa, $\eta_{{\text{T}}} \in$[0, 3.68] in the upper of Fig. 11a. It is a new idea presented in this work. It will be discussed in detail in Sect. 6. The reasons for some phenomena in Fig. 8 will be further discussed, too.

6 Discussions

Dimensionless treatment is a common method of numerical solution of equations which is conducive to get convergent numerical solutions quickly and accurately. However, the meaning of some parameters will change due to dimensionless processing. This will bring some difficulties in understanding and engineering application. For example, load coefficient here, $\overline{F}$ is directly called as load in some literature on the dynamics of the gear transmission system. In fact, it is a dimensionless parameter as $\overline{F} = \overline{F}_{m} /(m_{\text{e}} D_{c} \omega_{\text{n}}^{2} )$ where $\overline{F}_{{\text{m}}} = (R_{{\text{bp}}} I_{g} T_{p} +$$R_{bg} I_{\text{p}} T_{\text{g}} )/$$(I_{\text{g}} R_{{\text{bp}}}^{2} + I_{\text{p}} R_{{\text{bg}}}^{2} )$ as introduced above. It is difficult to directly reflect the input torque, output torque or their relative relationship because it is a compound quantity of input torque and output torque. A quantity is defined to interpret the calculation result in order to make the calculation results better guide the engineering practice. $\eta_{{\text{T}}}$ is used to represent the ratio of input torque to output torque as shown in Eq. (42).

$$ \eta_{{\text{T}}} = T_{{\text{p}}} /T_{{\text{g}}} $$

(42)

It can be further transformed into the corresponding relationship with the load coefficient, $\overline{F}$ as shown in Eq. (43).

$$ \eta_{{\text{T}}} = \frac{{R_{{{\text{bp}}}}^{2} I_{{\text{g}}} + R_{{{\text{bg}}}}^{2} I_{{\text{p}}} }}{{R_{{{\text{bp}}}} I_{{\text{g}}} T_{{\text{g}}} }}m_{\text{e}} D_{c} \omega_{\text{n}}^{2} \overline{F} - \frac{{R_{{{\text{bg}}}} I_{{\text{p}}} }}{{R_{{{\text{bp}}}} I_{{\text{g}}} }} $$

(43)

In the design of gear transmission, the input torque is generally determined according to the output torque and they should meet the relationship in Eq. (44).

$$ T_{{\text{g}}} \le i\eta T_{{\text{p}}} $$

(44)

where $i = z_{{\text{g}}} /z_{{\text{p}}}$ is transmission ratio. $\eta$ is gearing efficiency and it is taken as 1.0 here.

The critical conditions which the pinion can drive the gear when the output torque is given should meet the Eq. (45).

$$ \eta_{{\text{T}}} \ge [\eta_{{\text{T}}} ] = \eta z_{{\text{p}}} /z_{{\text{g}}} $$

(45)

Values of $\eta_{{\text{T}}}$ and $[\eta_{{\text{T}}} ]$ can be obtained and they have been marked in the upper of Fig. 11a as another abscissa according to the principles and methods in the design of gear transmission when the output torque is given as $T_{{\text{g}}}$ = 20 ${\text{N}} \cdot {\text{m}}$. There are several interesting phenomena that deserve an in-depth discussion.

Firstly, the value of $\overline{F}$ cannot be too small because $\eta_{{\text{T}}}$ will be negative if it is small according to its definition. The pinion cannot drive the gear according to the definition of $\eta_{{\text{T}}}$ when $\eta_{{\text{T}}}$ < $[\eta_{{\text{T}}} ]$. Corresponding to the value of $[\eta_{{\text{T}}} ]$ = 0.8077 in this work, the value of $\overline{F}$ is $\overline{F}_{{\text{B}}}$ = 0.0597.

This can explain the phenomena in Figs. 8a and b. Back-side boundary impact occurs in Fig. 8a and b. $\overline{F}$ = 0.0202 in Fig. 8a and $\overline{F}$ = 0.0311 in Fig. 8b. They are both less than the critical value of $\overline{F}_{{\text{B}}}$ = 0.0597. That is, $\overline{F}$ is too small, so the pinion cannot drive the gear.

In the actual gear transmission process, there will be no case that $\eta_{{\text{T}}}$ is less than $[\eta_{{\text{T}}} ]$, corresponding to $\overline{F}$ less than $\overline{F}_{{\text{B}}}$. However, it will occur during the starting and stopping of the drive motor. Therefore, the starting and stopping characteristics of the drive motor will affect whether there will be back-side boundary impact in gear transmission system. It will even affect the service life of the gear transmission system.

Coincidentally, the value range of $\overline{F}$ corresponding to back-side boundary impact in the dynamic model considering meshing impact (in red as shown in Fig. 11a) exactly corresponds to the range of chaotic motion in the dynamic model without considering meshing impact (in blue as shown in Fig. 11a). This further explains that the value of $\overline{F}$ cannot be too small.

Secondly, the value of $\overline{F}$ cannot be too large. Although it can be seen from Fig. 11a that tooth disengagement of the system will disappear as $\overline{F}$ $\ge$ 0.145(B₆). In fact, the best matching between input and output is not achieved at this time.

Thirdly, back-side boundary impact can be avoided if $\overline{F}$ is not too small (as long as the pinion can drive the gear). Tooth disengagement can be avoided by a reasonable combination of parameters as shown in Fig. 8d in addition to taking a larger value of $\overline{F}$ $\ge$ 0.145(B₆) shown in Fig. 11a.

7 Conclusions

Calculation methods of different meshing impact are proposed. An improved nonlinear dynamics model of spur gear pair including the multi-state meshing due to backlash and contact ratio and time-varying parameters is established when the action mechanism of meshing impact is considered. The research methods and results of spur gear transmission are also the easiest to be extended to other forms of gear transmission as it is the simplest and most basic transmission form. Some conclusions are as follows.

Firstly, there are two categories of meshing impact in spur gear pair. One is boundary impact including drive- and back-side boundary impact. The other is switching impact including mesh-in impact, mesh-out impact, single-to-double switching impact and double-to-single switching impact for a pair of teeth which can be merged into single-to-double and double-to-single switching impact for a spur gear pair.

Secondly, the nonlinear dynamic model of the gear transmission system which the meshing impact and multi-state meshing characteristics are considered can be used to reveal better the system dynamic characteristics. The change of load at meshing state switching point is transformed from the original jump to gradual change after the meshing impact is introduced to the nonlinear dynamics model. The meshing impact changes the motion characteristics including the number of motion cycles and the amplitude of the relative displacement and relative velocity. It can better reflect the engineering practice of gear meshing. Meshing impact is a factor that must be paid enough attention to.

Finally, different parameters affect the nonlinear dynamics of the system while their influence law and change mode are different. The meshing frequency which is regarded as the motion parameter mainly makes the motion complex and the transmission unstable. From the perspective of engineering practice, the value of dimensionless load coefficient is meaningful only within a certain range. Too small value has nothing to do with the transmission but may be related to the start and stop characteristics of the drive motor. Excessive value belongs to power mismatch in engineering practice which has no practical significance. Back-side contacting or impact only occurs when the load coefficient is very small. In order to eliminate tooth disengagement, either a large load coefficient corresponding to large input torque and small output torque should be selected or a reasonable combination of parameters should be selected.