Long-Time Asymptotics for the Spin-1 Gross–Pitaevskii Equation

Abstract

On the basis of the spectral analysis of the $4\times 4$ Lax pair associated with the spin-1 Gross–Pitaevskii equation and the scattering matrix, the solution to the Cauchy problem of the spin-1 Gross–Pitaevskii equation is transformed into the solution to the corresponding Riemann–Hilbert problem. The Deift–Zhou nonlinear steepest descent method is extended to the Riemann–Hilbert problem, from which a model Riemann–Hilbert problem is established with the help of distinct factorizations of the jump matrix for the Riemann–Hilbert problem and a decomposition of the matrix-valued spectral function. Finally, the long-time asymptotics of the solution to the Cauchy problem of the spin-1 Gross–Pitaevskii equation is obtained.

1 Introduction

The phenomenon of Bose–Einstein condensation attracts the attention of many researchers, which are related to the superfluidity of liquid helium and the superconductivity of metals [24, 29]. The dynamics of a Bose–Einstein condensate (BEC) can be described by means of an effective mean-field theory and the relevant model is a classical nonlinear evolution equation, the so-called Gross–Pitaevskii (GP) equation [25, 35]. The spin-1 GP equation can also be used to describe the soliton dynamics in spinor Bose–Einstein condensates [27]. The integrability of the spin-1 GP equation was studied by applying the Painlevé singularity structure analysis [28]. The spin-1 GP equation admits the application of the inverse scattering transform and Hirota bilinear method under appropriate conditions, which makes it possible to generate various exact analytical solutions relevant to physical applications [43]. The initial-boundary value problems for the spin-1 GP equations on the half-line and on a finite interval were studied by Fokas method [41, 42].

The inverse scattering transformation is a major achievement of twentieth-century mathematics [2, 20], by which exact solutions to the initial value problems for many integrable nonlinear evolution equations have been obtained in the reflectionless case. However, one can not solve this problem in a closed form unless in the case of reflectionless potentials. A natural idea is to study the asymptotic behavior of solutions to such problems. There were a number of progresses in this subject, particularly significant among them is the nonlinear steepest descent method [18] (also called Deift–Zhou method) for oscillatory Riemann–Hilbert (RH) problems. Subsequently, this method is applied to study the long-time asymptotic behavior for integrable nonlinear evolution equations associated with $2\times 2$ matrix spectral problems, such as the KdV equation, modified nonlinear Schrödinger equation, sine-Gordon equation, derivative nonlinear Schrödinger equation, Camassa-Holm equation and so on [3, 7, 8, 14, 17, 19, 23, 26, 30, 31, 34, 37, 38, 40]. Recently, Lenells has derived the long-time asymptotics for initial-boundary value problems of the mKdV equation and the derivative nonlinear Schrödinger equation using the Deift–Zhou nonlinear steepest descent method [4, 32].

However, when it comes to the nonlinear evolution equations related to the higher-order matrix spectral problems, the analysis process becomes very difficult. To the best of our knowledge, among the integrable nonlinear evolution equations associated with the $3\times 3$ matrix spectral problem, only the coupled nonlinear Schrödinger equation, Sasa–Satuma equation, cmKdV equation and Degasperis–Procesi equation have been studied for long-time asymptotic properties [9, 21, 22, 33]. There are important differences in dealing with these equations. In the case of the coupled nonlinear Schrödinger equation, Sasa–Satuma equation and cmKdV equation, there are two different eigenvalues in the main parts of their spectral problems. Thus in the process of direct and inverse problems, the block $2\times 2$ formalisms can be adopted and the Jost solutions are determined by the respective Volterra integral equations, which are the keys to building the RH formalisms. When dealing with the Degasperis–Procesi equation, it becomes complicated because the main part of its spectral problem has three different eigenvalues, which require the development of essential $3\times 3$ formalism. As in [9, 10], the authors introduced crucial transformations that make the leading terms of the $3\times 3$ matrix Lax pair into the product of (x, t)-independent and (x, t)-dependent factors and then diagonalize the (x, t)-independent part. The Jost solutions in this case are constructed by resorting to the Fredholm integral equations, which are important to establish the RH formalism. Apart from the Degasperis–Procesi equation [15], such equations that have $3\times 3$ matrix Lax pairs and three different eigenvalues are the Ostrovsky–Vakhnenko equation and the Novikov equation [11,12,13]. Therefore, it is of great significance to study the long-time asymptotics of integrable nonlinear evolution equations associated with higher-order matrix spectral problems.

In this paper, we shall extend the Deift–Zhou nonlinear steepest descent method to study the long-time asymptotics for the Cauchy problem of the spin-1 GP equation

$$\begin{aligned} {\left\{ \begin{array}{ll} iq_{1t}+q_{1xx}+2(|q_1|^2+2|q_0|^2)q_1+2q_0^2q_{-1}^*=0,\\ iq_{0t}+q_{0xx}+2(|q_1|^2+2|q_0|^2+|q_{-1}|^2)q_0+2q_1q_{-1}q_0^*=0,\\ iq_{-1t}+q_{-1xx}+2(2|q_0|^2+|q_{-1}|^2)q_{-1}+2q_0^2q_1^*=0,\\ q_0(x,0)=q_0^0(x),\quad q_1(x,0)=q_1^0(x),\quad q_{-1}(x,0)=q_{-1}^0(x), \end{array}\right. } \end{aligned}$$

(1.1)

associated with a $4\times 4$ matrix spectral problem, where $q_{1}(x,t)$, $q_{0}(x,t)$ and $q_{-1}(x,t)$ are three potentials, the initial values $q_0^0(x)$, $q_1^0(x)$ and $q_{-1}^0(x)$ lie in the Schwartz space ${\mathscr {S}}({\mathbb {R}})=\{f(x)\in C^\infty ({\mathbb {R}}):\sup _{x\in {\mathbb {R}}}|x^\alpha \partial ^\beta f(x)|<\infty ,\forall \alpha ,\beta \in {\mathbb {N}}\}$ and they are assumed to be generic so that $\det X_1$, $\det X_2$ and $\det X_4$ defined in the following context are nonzero in $\mathbb {C_+}\cup {\mathbb {R}}$, ${\mathbb {R}}$ and ${\mathbb {C}}_-\cup {\mathbb {R}}$ (Fig. 1), respectively. However, using the Deift–Zhou nonlinear steepest descent method, it is extremely difficult to study the long-time asymptotics for the Cauchy problem of the spin-1 GP equation because of the structure of the $4\times 4$ matrix spectral problem. The innovation of this paper mainly includes the following aspects. (i) All the $4\times 4$ matrices in this paper are expressed in the form of $2\times 2$ blocks, and each element of the block matrix is a $2\times 2$ matrix, which is different from the multi-component Manakov case. Therefore, the estimates in analysis is much more difficult because it is a matrix rather than a scalar. (ii) The triangular decomposition of the initial jump matrix is a key step in the Deift–Zhou nonlinear steepest descent method, which can be realized by introducing a RH problem in the multi-component Manakov case. However, in the case of the spin-1 GP equation associated with $4\times 4$ matrix spectral problem, we have to introduce two different matrix RH problems and give the decomposition of the jump matrix of the initial RH problem. In general, the solution of a matrix RH problem cannot be given in an explicit form, so it is a challenge to solve two matrix RH problems. Fortunately, we find that the determinants of the two solution matrices to the two matrix RH problems satisfy two scalar RH problems, and their solutions can replace the solutions of the matrix RH problems with the controlled error terms. (iii) The final model problem has a new form, which consists of four matrix-valued functions rather than the scalar functions. In the multi-component Manakov case, the corresponding functions satisfy Weber’s equation by a change of variable. In the case of the spin-1 GP equation associated with $4\times 4$ matrix spectral problem, the relevant equations make up of matrix-valued functions, they can not be transformed to Weber’s equation directly. But we find that the relevant matrix-valued functions can be reduced to diagonal forms by utilizing the properties of them. Then they satisfy the Weber’s equation and their components can be expressed by the parabolic cylinder functions. Finally, the model problem can be solved with the aid of the asymptotic expansion of the parabolic cylinder function, from which the long-time asymptotics for the Cauchy problem of the spin-1 GP equation are obtained.

The main result of this paper is expressed as follows:

Theorem 1.1

Let $(q_{1}(x,t),q_{0}(x,t),q_{-1}(x,t))$ be the solution for the Cauchy problem of the spin-1 GP equation (1.1) and the initial values $q_0^0(x)$, $q_1^0(x)$ , $q_{-1}^0(x)\in {\mathscr {S}}({\mathbb {R}})$. Assume that the determinants of the matrix-valued spectral functions $X_1(k)$, $X_2(k)$ and $X_4(k)$ defined in (2.13) are nonzero in $\mathbb {C_+}\cup {\mathbb {R}}$, ${\mathbb {R}}$ and $\mathbb {C_-}\cup {\mathbb {R}}$, respectively, which excludes soliton-type phenomena. Then, for $|x/t|<C$, the long-time asymptotics of the solution to the Cauchy problem of the spin-1 GP equation has the form

$$\begin{aligned} (q_{1}(x,t),q_{0}(x,t),q_{-1}(x,t))=\frac{\sqrt{\pi }(\delta ^0)^2e^{-\frac{\pi \nu }{2}}e^{\frac{-3\pi i}{4}}}{\sqrt{t}\Gamma (-i\nu )\det \gamma ^\dag (k_0)}(\gamma _{22}^*(k_0),-\gamma _{21}^*(k_0),\gamma _{11}^*(k_0))+O(\frac{\log t}{t}), \end{aligned}$$

(1.2)

where C is a fixed constant, $\Gamma (\cdot )$ is the Gamma function and the $\gamma _{ij}(k)$ is the (i, j) entry of the matrix-valued function $\gamma (k)$ defined in (2.22), and

$$\begin{aligned} \delta ^0= & {} e^{2itk_0^2}(8t)^{-\frac{i\nu }{2}}e^{\chi (k_0)},\quad k_0=-\frac{x}{4t},\\ \nu= & {} -\frac{1}{2\pi }\log (1+|\gamma (k_0)|^2+|\det \gamma (k_0)|^2),\\ \chi (k_0)= & {} \frac{1}{2\pi i}\Big [\int _{k_0-1}^{k_0}\log \left( \frac{1+|\gamma (\xi )|^2+|\det \gamma (\xi )|^2}{1+|\gamma (k_0)|^2+|\det \gamma (k_0)|^2}\right) \, \frac{\mathrm {d}\xi }{\xi -k_0}\\&+\int _{-\infty }^{k_0-1}\log \left( 1+|\gamma (\xi )|^2+|\det \gamma (\xi )|^2\right) \, \frac{\mathrm {d}\xi }{\xi -k_0}\Big ]. \end{aligned}$$

The structure of the paper is as follows. In Sect. 2, we begin with the $4\times 4$ matrix Lax pair of the spin-1 GP equation. A basic RH problem can be constructed through the Jost solutions and the scattering matrix. In Sect. 3, the RH problem is studied with the aid of the Deift–Zhou nonlinear steepest descent method, from which a model RH problem is derived. Finally, the long-time asymptotics of the solution to the Cauchy problem of the spin-1 GP equation is obtain through solving the model problem.

2 The Basic Riemann–Hilbert Problem

In this section, we shall derive the basic RH problem from the initial problem for the spin-1 GP equation (1.1). Let us consider a $4\times 4$ matrix Lax pair of the spin-1 GP equation:

$$\begin{aligned} \psi _x= & {} (-ik\sigma _4+U)\psi , \end{aligned}$$

(2.1a)

$$\begin{aligned} \psi _t= & {} (-2ik^2\sigma _4+V)\psi , \end{aligned}$$

(2.1b)

where $\psi$ is a matrix-valued function and k is the spectral parameter, $\sigma _4={\mathrm {diag}}(1,1,-1,-1)$,

$$\begin{aligned} U=\left( \begin{array}{cccc} 0&{}0&{}q_1&{}q_0\\ 0&{}0&{}q_0&{}q_{-1}\\ -q_1^*&{}-q_0^*&{}0&{}0\\ -q_0^*&{}-q_{-1}^*&{}0&{}0\\ \end{array}\right) ,\\ V=2kU+i\sigma _4(U_x-U^2). \end{aligned}$$

(2.2)

For convenience, the matrix U is written as the block form

$$\begin{aligned} U= \left( \begin{array}{cc} \mathbf{0 }_{2\times 2} &{}\quad q\\ -q^\dag &{}\quad \mathbf{0 }_{2\times 2}\\ \end{array}\right) , \end{aligned}$$

(2.3)

where

$$\begin{aligned} q=\left( \begin{array}{cl} q_1&{}q_0\\ q_0&{}q_{-1}\\ \end{array}\right) . \end{aligned}$$

(2.4)

Let $\mu =\psi e^{ik\sigma _4x+2ik^2\sigma _4t}$, where the matrix exponential $e^{\sigma _4}={\mathrm {diag}}(e,e,e^{-1},e^{-1})$. Then we have by using (2.1) that

$$\begin{aligned} \mu _x= & {} -ik[\sigma _4,\mu ]+U\mu , \end{aligned}$$

(2.5)

$$\begin{aligned} \mu _t= & {} -2ik^2[\sigma _4,\mu ]+V\mu , \end{aligned}$$

(2.6)

where $[\sigma _4,\mu ]=\sigma _4\mu -\mu \sigma _4$. We introduce the matrix Jost solutions $\mu _\pm$ of equation (2.6) by the Volterra integral equations:

$$\begin{aligned} \mu _\pm (k;x,t)=I_{4\times 4}+\int _{\pm \infty }^xe^{ik\sigma _4(\xi -x)}U(k;\xi ,t)\mu _\pm (k;\xi ,t)e^{-ik\sigma _4(\xi -x)}\, \mathrm {d}\xi , \end{aligned}$$

(2.7)

with the assumptions $\mu _\pm \rightarrow I_{4\times 4}$ as $x\rightarrow \pm \infty$, where $I_{4\times 4}$ is the $4\times 4$ identity matrix. Let $\mu _\pm$= ($\mu _{\pm L},\mu _{\pm R})$, where $\mu _{\pm L}$ denote the first and the second columns of the $4\times 4$ matrices $\mu _{\pm }$, and $\mu _{\pm R}$ denote the third and the fourth columns of the $4\times 4$ matrices $\mu _{\pm }$.

Lemma 2.1

The matrix Jost solutions $\mu _\pm (k;x,t)$ have the properties:

(i) $\mu _{-L}$ and $\mu _{+R}$ is analytic in the upper complex k-plane ${\mathbb {C}}_+$;

(ii) $\mu _{+L}$ and $\mu _{-R}$ is analytic in the lower complex k-plane ${\mathbb {C}}_-$;

(iii) $\det \mu _\pm =1$, and $\mu _\pm$ satisfy the symmetry conditions $\mu _\pm ^\dag (k^*)=\mu _\pm ^{-1}(k)$, where Ҡ" denotes the Hermite conjugate.

Proof

The $4\times 4$ matrix-valued functions $\mu _{\pm }$ are written as the $2\times 2$ block forms $(\mu _{\pm ij})_{2\times 2}$. A simple computation shows that

$$\begin{aligned} e^{ik\sigma _4(\xi -x)}U\mu _\pm e^{-ik\sigma _4(\xi -x)}= \left( \begin{array}{cc} q\mu _{\pm 21} &{}\quad e^{2ik(\xi -x)}q\mu _{\pm 22}\\ -e^{-2ik(\xi -x)}q^\dag \mu _{\pm 11} &{}\quad -q^\dag \mu _{\pm 12}\\ \end{array}\right) . \end{aligned}$$

Then the analytic properties of the Jost solutions $\mu _\pm$ can be obtained from the exponential term in the Volterra integral equation (2.8). Note that U has the symmetry relation $U^\dag (k^*)=-U(k)$ and $\mu _\pm ^{-1}$ satisfies

$$\begin{aligned} (\mu _\pm ^{-1})_x=-ik[\sigma _4,\mu _\pm ^{-1}]-\mu _\pm ^{-1}U, \end{aligned}$$

(2.8)

which implies the symmetry relation of $\mu _\pm$. Finally, $\det \mu _\pm =1$ are due to the traceless of U and the asymptotic properties of $\mu _\pm$ as follows

$$\begin{aligned} \begin{aligned} (\det \mu _\pm )_x&={\mathrm {tr}}[({\mathrm {adj}}\mu _\pm )(\mu _\pm )_x]\\&={\mathrm {tr}}\{({\mathrm {adj}}\mu _\pm )[-ik(\sigma _4\mu _\pm -\mu _\pm \sigma _4)+U\mu _\pm ]\}\\&=-ik{\mathrm {tr}}({\mathrm {adj}}\mu _\pm ){\mathrm {tr}}(\sigma _4\mu _\pm -\mu _\pm \sigma _4)+{\mathrm {tr}}({\mathrm {adj}}\mu _\pm ){\mathrm {tr}}(U){\mathrm {tr}}(\mu _\pm )\\&=0, \end{aligned} \end{aligned}$$

(2.9)

where ${\mathrm {adj}}X$ is the adjoint of matrix X and ${\mathrm {tr}}X$ is the trace of matrix X. $\quad \square$

Because $\mu _\pm e^{-ik\sigma _4 x-2ik^2\sigma _4 t}$ satisfy the same differential equations (2.1a) and (2.1b), they are linear related. There exists a $4\times 4$ scattering matrix s(k) such that

$$\begin{aligned} \mu _-=\mu _+ e^{-ik\sigma _4 x-2ik^2\sigma _4 t}s(k)e^{ik\sigma _4 x+2ik^2\sigma _4 t},\quad \det s(k)=1. \end{aligned}$$

(2.10)

From the symmetry property of $\mu _\pm$, the scattering matrix s(k) has symmetry condition

$$\begin{aligned} s^\dag (k^*)=s^{-1}(k). \end{aligned}$$

(2.11)

We express s(k) in block form, as shown in (2.4)

$$\begin{aligned} s(k)=\left( \begin{array}{cc} X_1(k) &{}\quad X_2(k)\\ X_3(k) &{}\quad X_4(k)\\ \end{array}\right) . \end{aligned}$$

(2.12)

Using (2.12), we have

$$\begin{aligned} X_1^\dag (k^*)= & {} \left( X_1(k)-X_2(k)X_4^{-1}(k)X_3(k)\right) ^{-1}, \end{aligned}$$

(2.13)

$$\begin{aligned} X_3^\dag (k^*)= & {} \left( X_3(k)-X_4(k)X_2^{-1}(k)X_1(k)\right) ^{-1}. \end{aligned}$$

(2.14)

A direct calculation shows from the evaluation of (2.11) at $t=0$ that

$$\begin{aligned} s(k)=\lim _{x\rightarrow +\infty }e^{ik\sigma _4 x}\mu _-(k;x,0)e^{-ik\sigma _4 x}, \end{aligned}$$

(2.15)

which implies

$$\begin{aligned} X_2= & {} \int _{-\infty }^{+\infty }q(\xi ,0)\mu _{-22}(k;\xi ,0)e^{2ik\xi }\, \mathrm {d}\xi , \end{aligned}$$

(2.16)

$$\begin{aligned} X_4= & {} I_{2\times 2}-\int _{-\infty }^{+\infty }q^\dag (\xi ,0)\mu _{-12}(k;\xi ,0)\, \mathrm {d}\xi . \end{aligned}$$

(2.17)

Let

$$\begin{aligned} M(k;x,t)= {\left\{ \begin{array}{ll} \left( \mu _{-L}(k)X_1^{-1}(k),\mu _{+R}(k)\right) , &{} k\in {\mathbb {C}}_+,\\ \left( \mu _{+L}(k),\mu _{-R}(k)X_4^{-1}(k)\right) , &{} k\in {\mathbb {C}}_-.\\ \end{array}\right. } \end{aligned}$$

(2.18)

From the analytic properties of $\mu _\pm$ in Lemma 2.1 and (2.11), it is easy to see that $X_1$ and $X_4$ are analytic in ${\mathbb {C}}_+$ and ${\mathbb {C}}_-$, respectively. Then M(k; x, t) is analytic for $k\in {\mathbb {C}}\backslash {\mathbb {R}}$. For convenience, we introduce the notations. For any matrix function $A(\cdot )$, we define $|A|=\sqrt{{\mathrm {tr}}(A^\dag A)}$ and $\Vert A(\cdot )\Vert _p=\Vert |A(\cdot )|\Vert _p$ .

Fig. 1

The contour on ${\mathbb {R}}$

Theorem 2.1

The piecewise-analytic function M(k; x, t) determined by (2.19) satisfies the RH problem

$$\begin{aligned} {\left\{ \begin{array}{ll} M_+(k;x,t)=M_-(k;x,t)J(k;x,t),\quad k\in {\mathbb {R}},\\ M(k;x,t)\rightarrow I_{4\times 4},\quad k\rightarrow \infty , \end{array}\right. } \end{aligned}$$

(2.19)

where $M_+(k;x,t)$ and $M_-(k;x,t)$ denote the limiting values as k approaches the contour ${\mathbb {R}}$ from the left and the right along the contour, respectively, the oriented contour is on ${\mathbb {R}}$ in Fig. 1,

$$\begin{aligned} J= \left( \begin{array}{cc} I_{2\times 2}+\gamma (k)\gamma ^\dag (k^*) &{}\quad -\gamma (k)e^{-2it\theta }\\ -\gamma ^\dag (k^*) e^{2it\theta } &{}\quad I_{2\times 2}\\ \end{array}\right) ,\\ \theta (k)=\frac{x}{t}k+2k^2,\quad \gamma (k)=X_2(k)X_4^{-1}(k), \end{aligned}$$

(2.20)

and function $\gamma (k)$ lies in the Schwartz space and satisfies

$$\begin{aligned} \sup _{k\in {\mathbb {R}}}|\gamma (k)|<\infty . \end{aligned}$$

(2.21)

In addition, the solution of RH problem (2.20) exists and is unique, and

$$\begin{aligned} q(x,t)=2i\lim _{k\rightarrow \infty }(kM(k;x,t))_{12} \end{aligned}$$

(2.22)

solves the Cauchy problem of the spin-1 GP equation (1.1).

Proof

Combining with the expression of M(k; x, t) and the scattering relation (2.11), we can obtain the jump condition and the corresponding RH problem (2.20) by straightforward calculations. According to the Vanishing Lemma [1], the solution of the RH problem (2.20) is existent and unique because of the positive definiteness of the jump matrix J(k; x, t). Notice that M(k; x, t) has the asymptotic expansion

$$\begin{aligned} M(k;x,t)=I_{4\times 4}+\frac{M_1(x,t)}{k}+\frac{M_2(x,t)}{k^2}+O(k^{-3}). \end{aligned}$$

(2.23)

We can obtain (2.24) as long as we substitute the asymptotic expansion into (2.6). $\quad \square$

3 Long-Time Asymptotic Behavior

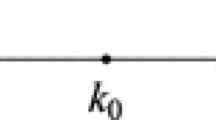
In this section, we begin with the basic RH problem (2.20) and analyze the long-time asymptotic behavior of the solution to the Cauchy problem of the spin-1 GP equation (1.1) by the nonlinear steepest descent method. It is worth noting that the stationary point $k_0=-x/(4t)$, which makes $\mathrm {d}\theta /\mathrm {d}k=0$. In order to use the nonlinear steepest descent method, we deform the contour of the RH problem and our main goal is to construct a model RH problem. After reorientation, extending, cut and rescaling, we obtain the long-time asymptotics of the solution to the Cauchy problem of the spin-1 GP equation (1.1).

3.1 The first transformation: reorientation

Finding the factorization forms of the jump matrix is the key step of the nonlinear steepest descent method. In the case of the RH problem (2.20), there are two different triangular factorizations for jump matrix J(k; x, t). In order to have a unified form for the two decompositions, We introduce two other RH problems and construct a new RH problem based on the RH problem (2.20).

The two triangular factorizations of J(k; x, t) are

$$\begin{aligned} J= {\left\{ \begin{array}{ll} \left( \begin{array}{cc} I_{2\times 2} &{}\quad -e^{-2it\theta }\gamma (k)\\ 0 &{}\quad I_{2\times 2}\\ \end{array}\right) \left( \begin{array}{cc} I_{2\times 2} &{}\quad 0\\ -e^{2it\theta }\gamma ^{\dag }(k^{*}) &{}\quad I_{2\times 2}\\ \end{array}\right) ,\\ \left( \begin{array}{cc} I_{2\times 2} &{}\quad 0\\ -e^{2it\theta }\gamma ^{\dag }(k^{*})D_1^{-1} &{}\quad I_{2\times 2}\\ \end{array}\right) \left( \begin{array}{cc} D_1 &{}\quad 0\\ 0 &{}\quad D_2\\ \end{array}\right) \left( \begin{array}{cc} I_{2\times 2} &{}\quad -e^{-2it\theta }D_1^{-1}\gamma (k)\\ 0 &{}\quad I_{2\times 2}\\ \end{array}\right) , \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} D_1=I_{2\times 2}+\gamma (k)\gamma ^{\dag }(k^{*}),\quad D_2=\left( I_{2\times 2}+\gamma ^{\dag }(k^{*})\gamma (k)\right) ^{-1}. \end{aligned}$$

(2.24)

We introduce two $2\times 2$ matrix-valued function $\delta _1(k)$ and $\delta _2(k)$ that satisfy the RH problems

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\delta _{1+}(k)=\delta _{1-}(k)(I_{2\times 2}+\gamma (k)\gamma ^{\dag }(k^{*})),\quad k\in (-\infty ,k_0),\\ &{}\delta _1(k)\rightarrow I_{2\times 2},\quad k\rightarrow \infty , \end{array}\right. } \end{aligned}$$

(2.25)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\delta _{2+}(k)=(I_{2\times 2}+\gamma ^{\dag }(k^{*})\gamma (k))\delta _{2-}(k),\quad k\in (-\infty ,k_0),\\ &{}\delta _2(k)\rightarrow I_{2\times 2},\quad k\rightarrow \infty , \end{array}\right. } \end{aligned}$$

(3.1)

respectively. The solutions of the above two RH problems exist and are unique because of Vanishing Lemma [1]. From the uniqueness, we have the symmetry relations $\delta _j^{-1}(k)=\delta _j^\dag (k^*), (j=1,2)$. Then a simple calculation shows that for $j=1,2$,

$$\begin{aligned} |\delta _{j+}|^2= & {} {\left\{ \begin{array}{ll} 2+|\gamma (k)|^2, &{} k\in (-\infty ,k_0),\\ 2, &{} k\in (k_0,+\infty ), \end{array}\right. }\end{aligned}$$

(3.2)

$$\begin{aligned} |\delta _{j-}|^2= & {} {\left\{ \begin{array}{ll} 2-\frac{2|\det \gamma (k)|^2+|\gamma (k)|^2}{1+|\det \gamma (k)|^2+|\gamma (k)|^2}, &{} k\in (-\infty ,k_0),\\ 2, &{} k\in (k_0,+\infty ). \end{array}\right. } \end{aligned}$$

(3.3)

Hence, by the maximum principle, we have for $j=1,2$,

$$\begin{aligned} \vert \delta _j(k)\vert \leqslant {\mathrm {const}}<\infty ,\quad k\in {\mathbb {C}}. \end{aligned}$$

(3.4)

We define the matrix-valued spectral function

$$\begin{aligned} \rho (k)= {\left\{ \begin{array}{ll} \gamma (k), &{} k\in (k_0,+\infty ),\\ -\left( I_{2\times 2}+\gamma (k)\gamma ^{\dag }(k^{*})\right) ^{-1}\gamma (k), &{} k\in (-\infty ,k_0),\\ \end{array}\right. } \end{aligned}$$

(3.5)

and

$$\begin{aligned} M^\Delta (k;x,t)=M(k;x,t)\Delta ^{-1}(k), \end{aligned}$$

where

$$\begin{aligned} \Delta (k)=\left( \begin{array}{cc} \delta _1(k) &{}\quad 0\\ 0 &{}\quad \delta _2^{-1}(k)\\ \end{array}\right) . \end{aligned}$$

Fig. 2

The oriented contour on ${\mathbb {R}}$

We reverse the orientation for $k\in (k_0,+\infty )$ as shown in Fig. 2 and $M^\Delta (k;x,t)$ satisfies the RH problem on the reoriented contour

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}M^\Delta _+(k;x,t)=M^\Delta _-(k;x,t)J^\Delta (k;x,t),\quad k\in {\mathbb {R}},\\ &{}M^\Delta (k;x,t)\rightarrow I_{4\times 4},\quad k\rightarrow \infty ,\\ \end{array}\right. } \end{aligned}$$

(3.6)

where the jump matrix $J^\Delta (k;x,t)$ has a decomposition

$$\begin{aligned} \begin{aligned} J^\Delta (k;x,t)&= \left( \begin{array}{cc} I_{2\times 2} &{}\quad 0\\ e^{2it\theta }\delta _{2-}^{-1}(k)\rho ^\dag (k^*)\delta _{1-}^{-1}(k) &{}\quad I_{2\times 2}\\ \end{array}\right) \left( \begin{array}{cc} I_{2\times 2} &{}\quad e^{-2it\theta }\delta _{1+}(k)\rho (k)\delta _{2+}(k)\\ 0 &{}\quad I_{2\times 2}\\ \end{array}\right) \\&\triangleq (b_-)^{-1}b_+. \end{aligned} \end{aligned}$$

(3.7)

3.2 Extend to the augmented contour

In this subsection, we first split the spectral function $\rho (k)$ into an analytic part and a small nonanalytic remainder. It provides an effective approach to decompose the triangular matrices $b_\pm$ in (3.9). Then we can construct a new RH problem on a augmented contour based on the decomposition of the triangular matrices.

For convenience, we define $L=\{k=k_0+ue^{\frac{3\pi i}{4}}:u\in (-\infty ,+\infty )\}$, and $A\lesssim B$ for two quantities A and B if there exists a constant $C>0$ such that $|A|\leqslant CB$.

Theorem 3.1

The matrix-valued spectral function $\rho (k)$ have the decompositions

$$\begin{aligned} \rho (k)=h_1(k)+h_2(k)+R(k),\quad k\in {\mathbb {R}}, \end{aligned}$$

(3.8)

where R(k) is a piecewise-rational function, $h_2(k)$ has a analytic continuation to L and they admit the following estimates

$$\begin{aligned}&\vert e^{-2it\theta (k)}h_1(k)\vert \lesssim \frac{1}{(1+\vert k\vert ^{2})t^{l}}, \quad k\in {\mathbb {R}}, \end{aligned}$$

(3.9)

$$\begin{aligned}&\vert e^{-2it\theta (k)}h_2(k)\vert \lesssim \frac{1}{(1+\vert k\vert ^{2})t^{l}}, \quad k\in L, \end{aligned}$$

(3.10)

for an arbitrary positive integer l. The Schwartz conjugate of $\rho (k)$ shows that

$$\begin{aligned} \rho ^\dag (k^*)=h_1^\dag (k^*)+h_2^\dag (k^*)+R^\dag (k^*), \end{aligned}$$

(3.11)

and $e^{2it\theta (k)}h_1^\dag (k^*)$ and $e^{2it\theta (k)}h_2^\dag (k^*)$ have the same estimates on ${\mathbb {R}}\cup L^*$.

Proof

At first, we consider the function $\rho (k)$ for $k\in (k_0,+\infty )$ and it has a similar process for $k\in (-\infty ,k_0)$. In order to replace the function $\rho (k)$ by a rational function with well-controlled errors, we expand $(k-i)^{m+5}\rho (k)$ in a Taylor series around $k_0$,

$$\begin{aligned} (k-i)^{m+5}\rho (k)=\mu _0+\mu _1(k-k_0)+\cdots +\mu _m(k-k_0)^m+\frac{1}{m!}\int _{k_0}^k((\xi -i)^{m+5}\rho (\xi ))^{(m+1)}(k-\xi )^m\, \mathrm {d}\xi . \end{aligned}$$

(3.12)

Then we define

$$\begin{aligned} R(k)= & {} \dfrac{\sum _{j=0}^m\mu _j(k-k_0)^j}{(k-i)^{m+5}}, \end{aligned}$$

(3.13)

$$\begin{aligned} h(k)= & {} \rho (k)-R(k). \end{aligned}$$

(3.14)

So the following result is straightforward

$$\begin{aligned} \left. \frac{\mathrm {d}^j\rho (k)}{\mathrm {d}k^j}\right| _{k=k_0}=\left. \frac{\mathrm {d}^jR(k)}{\mathrm {d}k^j}\right| _{k=k_0},\quad 0\leqslant j\leqslant m. \end{aligned}$$

(3.15)

For the convenience, we assume that $m=4p+1, p\in {\mathbb {Z}}_+$. Set

$$\begin{aligned} \alpha (k)=\frac{(k-k_0)^p}{(k-i)^{p+2}}. \end{aligned}$$

(3.16)

By the Fourier inversion, we arrive at

$$\begin{aligned} (h/\alpha )(k)=\int _{-\infty }^{+\infty }e^{is\theta }\widehat{(h/\alpha )}(s)\, \bar{\mathrm {d}}s, \end{aligned}$$

(3.17)

where

$$\begin{aligned} \widehat{(h/\alpha )}(s)= & {} \int _{k_0}^{+\infty }e^{-is\theta }(h/\alpha )(k)\, \bar{\mathrm {d}}\theta (k), \end{aligned}$$

(3.18)

$$\begin{aligned} \bar{\mathrm {d}}s= & {} \frac{\mathrm {d}s}{\sqrt{2\pi }},\quad \bar{\mathrm {d}}\theta =\frac{\mathrm {d}\theta }{\sqrt{2\pi }}. \end{aligned}$$

(3.19)

From (3.14), (3.16) and (3.18), it is easy to see that

$$\begin{aligned} (h/\alpha )(k)=\frac{(k-k_0)^{m+1-p}}{(k-i)^{m+3-p}}g(k,k_0)=\frac{(k-k_0)^{3p+2}}{(k-i)^{3p+4}}g(k,k_0), \end{aligned}$$

(3.20)

where

$$\begin{aligned} g(k,k_0)=\frac{1}{m!}\int _0^1((k_0+u(k-k_0)-i)^{m+5}\rho (k_0+u(k-k_0)))^{(m+1)}(1-u)^m\, \mathrm {d}u. \end{aligned}$$

(3.21)

Noting that

$$\begin{aligned} \left| \frac{\mathrm {d}^j}{\mathrm {d}k^j}g(k,k_0)\right| \lesssim 1, \end{aligned}$$

(3.22)

we have

$$\begin{aligned}&\int _{k_0}^{+\infty }\left| \left( \frac{\mathrm {d}}{\mathrm {d}\theta }\right) ^j(h/\alpha )(k(\theta ))\right| ^2\, |\bar{\mathrm {d}}\theta |\\&\quad =\int _{k_0}^{+\infty }\left| \left( \frac{1}{4k-4k_0}\frac{\mathrm {d}}{\mathrm {d}k}\right) ^j(h/\alpha )(k)\right| ^2(4k-4k_0)\, \bar{\mathrm {d}}k\\&\quad \lesssim \int _{k_0}^{+\infty }\left| \frac{(k-k_0)^{3p+2-2j}}{(k-i)^{3p+4}}\right| ^2(k-k_0)\, \bar{\mathrm {d}}k\lesssim 1,\quad {\mathrm {for}}\quad 0\leqslant j\leqslant \frac{3p+2}{2}. \end{aligned}$$

Using the Plancherel formula [36],

$$\begin{aligned} \int _{-\infty }^{+\infty }(1+s^2)^j\left| \widehat{(h/\alpha )}(s)\right| ^2\, \mathrm {d}s \lesssim 1, \end{aligned}$$

(3.23)

we split h(k) into two parts

$$\begin{aligned} \begin{aligned} h(k)&=\alpha (k)\int _{t}^{+\infty }e^{is\theta }\widehat{(h/\alpha )}(s)\, \bar{\mathrm {d}}s+\alpha (k)\int _{-\infty }^{t}e^{is\theta }\widehat{(h/\alpha )}(s)\, \bar{\mathrm {d}}s\\ \triangleq&h_1(k)+h_2(k). \end{aligned} \end{aligned}$$

(3.24)

For $k\geqslant k_0$, we have

$$\begin{aligned}&|e^{-2it\theta }h_1(k)|\leqslant |\alpha (k)|\int _t^{+\infty }\left| \widehat{(h/\alpha )}(s)\right| \, \bar{\mathrm {d}}s\\&\quad \lesssim \left| \frac{(k-k_0)^p}{(k-i)^{p+2}}\right| \left( \int _{t}^{+\infty }(1+s^2)^{-r}\, \mathrm {d}s\right) ^{1/2}\left( \int _{t}^{+\infty }(1+s^2)^{r}\left| \widehat{(h/\alpha )}(s)\right| ^2\, \mathrm {d}s\right) ^{1/2}\\&\quad \lesssim t^{-r+\frac{1}{2}}, \quad {\mathrm {for}}\quad r\leqslant \frac{3p+2}{2}. \end{aligned}$$

Noting (2.22), it is not difficult to prove that

i) ${{\mathrm {Re}}}(i\theta )>0$ when ${\mathrm {Re}}k>k_0, {\mathrm {Im}}k<0$ or ${\mathrm {Re}}k<k_0, {\mathrm {Im}}k>0$;

ii) ${\mathrm {Re}}(i\theta )<0$ when ${{\mathrm {Re}}}k>k_0, {\mathrm {Im}}k>0$ or ${{\mathrm {Re}}}k<k_0, {\mathrm {Im}}k<0$.

Then $h_2(k)$ has an analytic continuation to the line $\{k=k_0+ue^{-\frac{\pi i}{4}}:u\in [0,+\infty )\}$. On this line,

$$\begin{aligned} |e^{-2it\theta }h_2(k)|&\leqslant e^{-2t{\mathrm {Re}}(i\theta )}\left| \frac{(k-k_0)^p}{(k-i)^{p+2}}\right| \int _{-\infty }^t\left| e^{is\theta }\widehat{(h/\alpha )}(s)\right| \, \bar{\mathrm {d}}s\\&\lesssim \frac{u^pe^{-t{\mathrm {Re}}(i\theta )}}{|k-i|^{p+2}}\int _{-\infty }^te^{(s-t){\mathrm {Re}}(i\theta )}\left| \widehat{(h/\alpha )}(s)\right| \, \mathrm {d}s\\&\lesssim \frac{u^pe^{-t{\mathrm {Re}}(i\theta )}}{|k-i|^{p+2}}\left( \int _{-\infty }^t(1+s^2)^{-1}\, \mathrm {d}s\right) ^{1/2}\left( \int _{-\infty }^t(1+s^2)\left| \widehat{(h_1/\alpha )}(s)\right| ^2\, \mathrm {d}s\right) ^{1/2}\\&\lesssim \frac{u^pe^{-t{\mathrm {Re}}(i\theta )}}{|k-i|^{p+2}}, \end{aligned}$$

where

$$\begin{aligned} \theta (k)=2(k-k_0)^2-2k_0^2. \end{aligned}$$

(3.25)

Then we arrive at ${\mathrm {Re}}(i\theta )=2u^2$ and

$$\begin{aligned} |e^{-2it\theta }h_2(k)|&\lesssim \frac{(\sqrt{t}u)^pe^{-2u^2t}u^p}{|k-i|^{p+2}(\sqrt{t}u)^p}\lesssim \frac{1}{|k-i|^{2}t^{p/2}}. \end{aligned}$$

(3.26)

This accomplishes the estimates of $h_1(k)$ and $h_2(k)$ for $k\geqslant k_0$. In the case of $k<k_0$, it is similar. To sum up, we let l be an arbitrary positive integer and p is sufficiently large such that $(3p+1)/2$ and p/2 are greater than l. Then we can obtain (3.11) and (3.12). $\quad \square$

Based on the result of Theorem 3.1, $b_\pm$ have decompositions

$$\begin{aligned} b_{+}=b^{o}_{+}b^{a}_{+}=(I_{4\times 4}+\omega ^{o}_{+})(I_{4\times 4}+\omega ^{a}_{+}),\quad b_{-}=b^{o}_{-}b^{a}_{-}=(I_{4\times 4}-\omega ^{o}_{-})(I_{4\times 4}-\omega ^{a}_{-}), \end{aligned}$$

(3.27)

where

$$\begin{aligned}&\omega ^{o}_{+}= \left( \begin{array}{cc} 0 &{}\quad e^{-2it\theta }\delta _{1+}(k)h_1(k)\delta _{2+}(k)\\ 0 &{}\quad 0\\ \end{array}\right) ,&\omega ^{a}_{+}= \left( \begin{array}{cc} 0 &{}\quad e^{-2it\theta }\delta _{1+}(k)(h_2(k)+R(k))\delta _{2+}(k)\\ 0 &{}\quad 0\\ \end{array}\right) ;\\&\omega ^{o}_{-}= \left( \begin{array}{cc} 0 &{}\quad 0\\ e^{2it\theta }\delta _{2-}^{-1}(k)h_1^\dag (k^*)\delta _{1-}^{-1}(k) &{}\quad 0\\ \end{array}\right) ,&\omega ^{a}_{-}= \left( \begin{array}{cc} 0 &{}\quad 0\\ e^{2it\theta }\delta _{2-}^{-1}(k)(h_2^\dag (k^*)+R^\dag (k^*))\delta _{1-}^{-1}(k) &{}\quad 0\\ \end{array}\right) . \end{aligned}$$

Fig. 3

The oriented contour $\Sigma$

Define the oriented contour $\Sigma$ by $\Sigma ={\mathbb {R}}\cup L\cup L^*$ as in Fig. 3. Set

$$\begin{aligned} M^\sharp (k;x,t)= {\left\{ \begin{array}{ll} M^\Delta (k;x,t), &{} k\in \Omega _{1}\cup \Omega _{2},\\ M^\Delta (k;x,t)(b_+^a)^{-1}, &{} k\in \Omega _{3}\cup \Omega _{4},\\ M^\Delta (k;x,t)(b_-^a)^{-1}, &{} k\in \Omega _{5}\cup \Omega _{6}.\\ \end{array}\right. } \end{aligned}$$

(3.28)

From the analytic properties of $b_\pm ^a$ in Theorem 3.1, $M^\sharp (k;x,t)$ is analytic in ${\mathbb {C}}\backslash \Sigma$.

Lemma 3.1

$M^\sharp (k;x,t)$ is the solution of the RH problem

$$\begin{aligned} {\left\{ \begin{array}{ll} M^\sharp _+(k;x,t)=M^\sharp _-(k;x,t)J^\sharp (k;x,t), &{} k\in \Sigma ,\\ M^\sharp (k;x,t)\rightarrow I_{4\times 4}, &{} k\rightarrow \infty , \end{array}\right. } \end{aligned}$$

(3.29)

where the jump matrix $J^\sharp (k;x,t)$ satisfies

$$\begin{aligned} J^\sharp (k;x,t)= & {} (b_-^\sharp )^{-1}b_+^\sharp , \end{aligned}$$

(3.30)

$$\begin{aligned} b_-^\sharp= & {} {\left\{ \begin{array}{ll} I, &{} k\in L,\\ b_-^a, &{} k\in L^*,\\ b_-^o, &{} k\in {\mathbb {R}},\\ \end{array}\right. }\quad b_+^\sharp = {\left\{ \begin{array}{ll} b_+^a, &{} k\in L,\\ I, &{} k\in L^*,\\ b_+^o, &{} k\in {\mathbb {R}}.\\ \end{array}\right. } \end{aligned}$$

(3.31)

Proof

According to the RH problem (3.8) and the decomposition of $b_\pm$, the jump condition (3.32) is obtained by a simple calculation. The normalized condition of $M^\sharp (k;x,t)$ can be derived from the convergence of $b_\pm$ as $k\rightarrow \infty$. We first consider the case of $k\in \Omega _{3}$. Based on the boundedness of $\delta _1(k)$ and $\delta _2(k)$ in (3.6), and the definition of R(k) and $h_2(k)$ in (3.15) and (3.26), we have

$$\begin{aligned}&\vert e^{-2it\theta }\delta _{1+}(k)(h_2(k)+R(k))\delta _{2+}(k)\vert \\&\quad \lesssim \vert e^{-2it\theta }h_2(k)\vert +\vert e^{-2it\theta }R(k)\vert \\&\quad \lesssim |\alpha (k)|e^{-t{\mathrm {Re}}(i\theta )}\left| \int _{-\infty }^te^{i(s-t)\theta }\widehat{(h/\alpha )}(k)\, \mathrm {d}s\right| +\dfrac{\vert \sum _{j=0}^m\mu _j(k-k_0)^j\vert }{\vert (k-i)^{m+5}\vert }\\&\quad \lesssim \dfrac{1}{\vert k-i\vert ^{2}}+\dfrac{1}{\vert k-i\vert ^{5}}. \end{aligned}$$

Then we obtain that $M^\sharp (k;x,t)\rightarrow I_{4\times 4}$ when $k\in \Omega _{3}$ and $k\rightarrow \infty$. In other domains, the result can be similarly proved. $\quad \square$

In the following, we construct the solution of the above RH problem (3.31) by using the approach in [5]. Assume that

$$\begin{aligned} \omega ^\sharp _\pm =\pm (b^\sharp _\pm -I_{4\times 4}), \quad \omega ^\sharp =\omega ^\sharp _++\omega ^\sharp _-, \end{aligned}$$

(3.32)

and define the Cauchy operators $C_\pm$ on $\Sigma$ by

$$\begin{aligned} (C_\pm f)(k)=\int _\Sigma \frac{f(\xi )}{\xi -k_\pm }\frac{\mathrm {d}\xi }{2\pi i},\quad k\in \Sigma ,\ f\in {\mathscr {L}}^2(\Sigma ), \end{aligned}$$

(3.33)

where $C_+f(C_-f)$ denotes the left (right) boundary value for the oriented contour $\Sigma$ in Fig. 3. We introduce the operator $C_{\omega ^\sharp }:{\mathscr {L}}^2(\Sigma )+{\mathscr {L}}^\infty (\Sigma )\rightarrow {\mathscr {L}}^2(\Sigma )$ by

$$\begin{aligned} C_{\omega ^{\sharp }}f=C_+\left( f\omega ^\sharp _-\right) +C_-\left( f\omega ^\sharp _+\right) \end{aligned}$$

(3.34)

for a $4\times 4$ matrix-valued function f. Suppose that $\mu ^\sharp (k;x,t)\in {\mathscr {L}}^2(\Sigma )+{\mathscr {L}}^\infty (\Sigma )$ is the solution of the singular integral equation

$$\begin{aligned} \mu ^\sharp =I_{4\times 4}+C_{\omega ^\sharp }\mu ^\sharp . \end{aligned}$$

Then

$$\begin{aligned} M^\sharp (k;x,t)=I_{4\times 4}+\int _\Sigma \dfrac{\mu ^\sharp (\xi ;x,t)\omega ^\sharp (\xi ;x,t)}{\xi -k} \, \frac{\mathrm {d}\xi }{2\pi i} \end{aligned}$$

(3.35)

solves RH problem (3.31). Indeed,

$$\begin{aligned} \begin{aligned} M_\pm ^\sharp (k)&=I_{4\times 4}+C_\pm (\mu ^\sharp (k)\omega ^\sharp (k))\\&=I_{4\times 4}+C_\pm (\mu ^\sharp (k)\omega _+^\sharp (k))+C_\pm (\mu ^\sharp (k)\omega _-^\sharp (k))\\&=I_{4\times 4}\pm \mu ^\sharp (k)\omega _\pm ^\sharp (k)+C_{\omega ^\sharp }\mu ^\sharp (k)\\&=\mu ^\sharp (k) b_\pm ^\sharp (k). \end{aligned} \end{aligned}$$

(3.36)

It is obvious that

$$\begin{aligned} M_+^\sharp =\mu ^\sharp b_+^\sharp =M_-^\sharp (b_-^\sharp )^{-1}b_+^\sharp =M_-^\sharp J^\sharp . \end{aligned}$$

(3.37)

Theorem 3.2

The solution q(x, t) for the Cauchy problem of the spin-1 GP equation (1.1) is expressed by

$$\begin{aligned} q(x,t)=-\frac{1}{\pi }\left( \int _\Sigma \left( (1-C_{\omega ^\sharp })^{-1}I_{4\times 4}\right) (\xi )\omega ^\sharp (\xi )\, \mathrm {d}\xi \right) _{12}. \end{aligned}$$

(3.38)

Proof

From (2.24), (3.30) and (3.37), we arrive at

$$\begin{aligned} \begin{aligned} q(x,t)&=2i\lim _{k\rightarrow \infty }\left( kM^\Delta (k;x.t)\right) _{12}\\&=2i\lim _{k\rightarrow \infty }\left( kM^\sharp (k;x.t)\right) _{12}\\&=-\frac{1}{\pi }\left( \int _\Sigma \mu ^\sharp (\xi )\omega ^\sharp (\xi )\,\mathrm {d}\xi \right) _{12}\\&=-\frac{1}{\pi }\left( \int _\Sigma ((1-C_{\omega ^\sharp })^{-1}I_{4\times 4})(\xi )\omega ^\sharp (\xi )\,\mathrm {d}\xi \right) _{12}. \end{aligned} \end{aligned}$$

(3.39)

$\square$

3.3 The third transformation

In this subsection, the RH problem on the contour $\Sigma$ is converted to a RH problem on the contour $\Sigma ^\prime =\Sigma \backslash {\mathbb {R}}=L\cup L^*$ and we figure out the estimates of the errors between the two RH problems.

From (3.29), (3.33) and (3.34), we find that $\omega ^\sharp$ is made up of the terms including $h_1(k)$, $h_1^\dag (k^*)$, $h_2(k)$, $h_2^\dag (k^*)$, R(k) and $R^\dag (k^*)$. Because $\omega ^\sharp$ is the sum of different terms, we can split $\omega ^\sharp$ into three parts: $\omega ^\sharp =\omega ^a+\omega ^b+\omega ^\prime$, where $\omega ^a=\omega ^\sharp |_{{\mathbb {R}}}$ and is made up of the terms including $h_1(k)$ and $h_1^\dag (k^*)$; $\omega ^b=0$ on $\Sigma \backslash (L\cup L^*)$ and is made up of the terms including $h_2(k)$ and $h_2^\dag (k^*)$; $\omega ^\prime$=0 on $\Sigma \backslash \Sigma ^\prime$ and is made up of the terms including R(k) and $R^\dag (k^*)$.

Let $\omega ^e=\omega ^a+\omega ^b$. So $\omega ^\sharp =\omega ^e+\omega ^\prime$. Then we immediately get the following estimates.

Lemma 3.2

For arbitrary positive integer l, as $t\rightarrow \infty$, we have the estimates

$$\begin{aligned}&\Vert \omega ^a\Vert _{{\mathscr {L}}^1({\mathbb {R}})\cap {\mathscr {L}}^2({\mathbb {R}})\cap {\mathscr {L}}^\infty ({\mathbb {R}})}\lesssim t^{-l}, \end{aligned}$$

(3.40)

$$\begin{aligned}&\Vert \omega ^b\Vert _{{\mathscr {L}}^1(L\cup L^*)\cap {\mathscr {L}}^2(L\cup L^*)\cap {\mathscr {L}}^\infty (L\cup L^*)}\lesssim t^{-l}, \end{aligned}$$

(3.41)

$$\begin{aligned}&\Vert \omega ^\prime \Vert _{{\mathscr {L}}^2(\Sigma )}\lesssim t^{-\frac{1}{4}},\quad \Vert \omega ^\prime \Vert _{{\mathscr {L}}^1(\Sigma )}\lesssim t^{-\frac{1}{2}}. \end{aligned}$$

(3.42)

Proof

We first consider the case of $\omega ^a$. It is necessary to compute $|\omega ^a|$ if we want to give the estimates for $\Vert |\omega ^a|\Vert _{{\mathscr {L}}^p({\mathbb {R}})}$. Notice the boundedness of $\delta _1(k)$ and $\delta _2(k)$ in (3.6) and the estimates in Theorem 3.1, we have

$$\begin{aligned} |\omega ^a|&=\left( \left| e^{-2it\theta }\delta _1(k)h_1(k)\delta _2(k)\right| ^2+\left| e^{2it\theta }\delta _2^{-1}(k)h_1^\dag (k^*)\delta _1^{-1}(k)\right| ^2\right) ^{\frac{1}{2}}\\&\leqslant \left| e^{-2it\theta }\delta _1(k)h_1(k)\delta _2(k)\right| +\left| e^{2it\theta }\delta _2^{-1}(k)h_1^\dag (k^*)\delta _1^{-1}(k)\right| \\&\lesssim \left| e^{-2it\theta }h_1(k)\right| +\left| e^{2it\theta }(k)h_1^\dag (k^*)\right| \\&\lesssim \frac{1}{(1+\vert k\vert ^{2})t^{l}}, \end{aligned}$$

which leads the estimates (3.42). Similarly, we can prove by a simple calculation that (3.43) also holds. Next, we prove estimate (3.44). Noting the definition of R(k) in (3.15), we have

$$\begin{aligned} |R(k)|=\dfrac{\vert \sum _{j=0}^m\mu _j(k-k_0)^j\vert }{\vert (k-i)^{m+5}\vert }\lesssim \dfrac{1}{1+\vert k\vert ^{5}}. \end{aligned}$$

(3.43)

Resorting to ${\mathrm {Re}}(i\theta )=2u^2$ on $L=\{k=k_0+ue^{\frac{3\pi i}{4}}:u\in (-\infty ,+\infty )\}$, we arrive at

$$\begin{aligned} \left| e^{-2it\theta }\delta _1(k)R(k)\delta _2(k)\right| \lesssim e^{-4tu^2}(1+|k|^5)^{-1}. \end{aligned}$$

It is similar for $R^\dag (k^*)$ on $L^*$ that

$$\begin{aligned} \left| e^{2it\theta }\delta _2^{-1}(k)R^\dag (k^*)\delta _1^{-1}(k)\right| \lesssim e^{-4tu^2}(1+|k|^5)^{-1}. \end{aligned}$$

Then (3.44) holds through direct computations. $\quad \square$

From Proposition 2.23 and Corollary 2.25 in [18], we know that operator $(1-C_{\omega ^\prime })^{-1}:{\mathscr {L}}^2(\Sigma )\rightarrow {\mathscr {L}}^2(\Sigma )$ exists and is uniformly bounded and

$$\begin{aligned} \Vert (1-C_{\omega ^\prime })^{-1}\Vert _{{\mathscr {L}}^2(\Sigma )}\lesssim 1,\quad \Vert (1-C_{\omega ^\sharp })^{-1}\Vert _{{\mathscr {L}}^2(\Sigma )}\lesssim 1. \end{aligned}$$

(3.44)

Lemma 3.3

As $t\rightarrow \infty$, then

$$\begin{aligned} \int _\Sigma ((1-C_{\omega ^\sharp })^{-1}I_{4\times 4})(\xi )\omega ^\sharp (\xi ) \, \mathrm {d}\xi = \int _{\Sigma ^\prime }((1-C_{\omega ^\prime })^{-1}I_{4\times 4})(\xi )\omega ^\prime (\xi ) \, \mathrm {d}\xi +O(t^{-l}). \end{aligned}$$

(3.45)

Proof

It is easy to see that

$$\begin{aligned} \begin{aligned}&\left( (1-C_{\omega ^\sharp }\right) ^{-1}I_{4\times 4})\omega ^\sharp = \left( (1-C_{\omega ^\prime })^{-1}I_{4\times 4}\right) \omega ^\prime +\left( (1-C_{\omega ^\prime })^{-1}(C_{\omega ^\sharp }-C_{\omega ^\prime })(1-C_{\omega ^\sharp })^{-1}I_{4\times 4}\right) \omega ^\sharp \\&\quad \quad +\,((1-C_{\omega ^\prime })^{-1}I_{4\times 4})(\omega ^\sharp -\omega ^\prime )\\&\quad =\left( (1-C_{\omega ^\prime })^{-1}I_{4\times 4}\right) \omega ^\prime +\omega ^e+\left( (1-C_{\omega ^\prime })^{-1}(C_{\omega ^e}I_{4\times 4})\right) \omega ^\sharp \\&\quad \quad +\,((1-C_{\omega ^\prime })^{-1}(C_{\omega ^\prime }I_{4\times 4}))\omega ^e +\left( (1-C_{\omega ^\prime })^{-1}C_{\omega ^e}(1-C_{\omega ^\sharp })^{-1}\right) (C_{\omega ^\sharp }I_{4\times 4})\omega ^\sharp . \end{aligned} \end{aligned}$$

(3.46)

From Lemma 3.2 and (3.46), we get

$$\begin{aligned} \begin{aligned}&\Vert \omega ^e\Vert _{{\mathscr {L}}^1(\Sigma )} \leqslant \Vert \omega ^a\Vert _{{\mathscr {L}}^1({\mathbb {R}})}+\Vert \omega ^b\Vert _{{\mathscr {L}}^1(L\cup L^*)}\lesssim t^{-l},\\&\begin{aligned} \left\| \left( (1-C_{\omega ^\prime })^{-1}(C_{\omega ^e}I_{4\times 4})\right) \omega ^\sharp \right\| _{{\mathscr {L}}^1(\Sigma )}&\leqslant \Vert (1-C_{\omega ^\prime })^{-1} C_{\omega ^e}I_{4\times 4}\Vert _{{\mathscr {L}}^2(\Sigma )}\Vert \omega ^\sharp \Vert _{{\mathscr {L}}^2(\Sigma )}\\&\leqslant \Vert (1-C_{\omega ^\prime })^{-1}\Vert _{{\mathscr {L}}^2(\Sigma )}\Vert C_{\omega ^e}I_{4\times 4}\Vert _{{\mathscr {L}}^2(\Sigma )}\\&\quad \times (\Vert \omega ^a\Vert _{{\mathscr {L}}^2({\mathbb {R}})}+\Vert \omega ^b\Vert _{{\mathscr {L}}^2(L\cup L^*)}+\Vert \omega ^\prime \Vert _{{\mathscr {L}}^2(\Sigma )})\\&\lesssim \Vert \omega ^e\Vert _{{\mathscr {L}}^2(\Sigma )}(t^{-l}+t^{-l}+t^{-\frac{1}{4}}) \lesssim t^{-l-\frac{1}{4}}, \end{aligned}\\&\begin{aligned} \left\| \left( (1-C_{\omega ^\prime })^{-1}(C_{\omega ^\prime }I_{4\times 4})\right) \omega ^e\right\| _{{\mathscr {L}}^1(\Sigma )}&\leqslant \Vert (1-C_{\omega ^\prime }^{-1}) C_{\omega ^\prime }I_{4\times 4}\Vert _{{\mathscr {L}}^2(\Sigma )}\Vert \omega ^e\Vert _{{\mathscr {L}}^2(\Sigma )}\\&\leqslant \Vert (1-C_{\omega ^\prime }^{-1})\Vert _{{\mathscr {L}}^2(\Sigma )}\Vert C_{\omega ^\prime }I_{4\times 4}\Vert _{{\mathscr {L}}^2(\Sigma )}\Vert \omega ^e\Vert _{{\mathscr {L}}^2(\Sigma )}\\&\lesssim \Vert \omega ^\prime \Vert _{{\mathscr {L}}^2(\Sigma )}(\Vert \omega ^a\Vert _{{\mathscr {L}}^2({\mathbb {R}})}+\Vert \omega ^b\Vert _{{\mathscr {L}}^2(L\cup L^*)}) \lesssim t^{-l-\frac{1}{4}}, \end{aligned}\\&\left\| \left( (1-C_{\omega ^\prime })^{-1}C_{\omega ^e}(1-C_{\omega ^\sharp })^{-1}\right) (C_{\omega ^\sharp }I_{4\times 4})\omega ^\sharp \right\| _{{\mathscr {L}}^1(\Sigma )}\\&\leqslant \Vert (1-C_{\omega ^\prime })^{-1}C_{\omega ^e}(1-C_{\omega ^\sharp })^{-1}(C_{\omega ^\sharp }I_{4\times 4})\Vert _{{\mathscr {L}}^2(\Sigma )}\Vert \omega ^\sharp \Vert _{{\mathscr {L}}^2(\Sigma )}\\&\leqslant \Vert (1-C_{\omega ^\prime })^{-1}\Vert _{{\mathscr {L}}^2(\Sigma )}\Vert (1-C_{\omega ^\sharp })^{-1}\Vert _{{\mathscr {L}}^2(\Sigma )}\Vert C_{\omega ^e}\Vert _{{\mathscr {L}}^2(\Sigma )}\Vert C_{\omega ^\sharp }I_{4\times 4}\Vert _{{\mathscr {L}}^2(\Sigma )}\Vert \omega ^\sharp \Vert _{{\mathscr {L}}^2(\Sigma )}\\&\lesssim \Vert \omega ^e\Vert _{{\mathscr {L}}^\infty (\Sigma )}\Vert \omega ^\sharp \Vert ^2_{{\mathscr {L}}^2(\Sigma )} \lesssim t^{-l-\frac{1}{2}}. \end{aligned} \end{aligned}$$

Substituting the above estimates into (3.48), the proof is completed. $\quad \square$

Lemma 3.4

As $t\rightarrow \infty$, the solution q(x, t) for the Cauchy problem of the spin-1 GP equation (1.1) has the asymptotic estimate

$$\begin{aligned} q(x,t)=-\frac{1}{\pi }\left( \int _{\Sigma ^\prime }((1-C_{\omega ^\prime })^{-1}I_{4\times 4})(\xi )\omega ^\prime (\xi )\, \mathrm {d}\xi \right) _{12}+O(t^{-l}). \end{aligned}$$

(3.47)

Proof

A direct consequence of (3.40) and (3.47). $\quad \square$

Set

$$\begin{aligned} M^\prime (k;x,t)=I_{4\times 4}+\int _{\Sigma ^\prime }\frac{\mu ^\prime (\xi ;x,t)\omega ^\prime (\xi ;x,t)}{\xi -k} \, \frac{\mathrm {d}\xi }{2\pi i}, \end{aligned}$$

where $\mu ^\prime =(1-C_{\omega ^\prime })^{-1}I_{4\times 4}$. Then (3.49) is equivalent to

$$\begin{aligned} q(x,t)=2i\lim _{k\rightarrow \infty }(kM^\prime )_{12}+O(t^{-l}). \end{aligned}$$

(3.48)

Noting that $M^\sharp (k;x,t)$ in (3.37) is the solution of RH problem (3.31), we can construct a RH problem that $M^\prime (k;x,t)$ satisfies

$$\begin{aligned} {\left\{ \begin{array}{ll} M_+^\prime (k;x,t)=M_-^\prime (k;x,t)J^\prime (k;x,t), &{} k\in \Sigma ^\prime , \\ M^\prime (k;x,t)\rightarrow I_{4\times 4}, &{} k\rightarrow \infty ,\\ \end{array}\right. } \end{aligned}$$

(3.49)

where

$$\begin{aligned} J^\prime= & {} (b_-^\prime )^{-1}b_+^\prime =(I_{4\times 4}-\omega _-^\prime )^{-1}(I_{4\times 4}+\omega _+^\prime ),\\ \omega ^\prime= & {} \omega _+^\prime +\omega _-^\prime ,\\ b_+^\prime= & {} {\left\{ \begin{array}{ll} \left( \begin{array}{cc} I_{2\times 2} &{} e^{-2it\theta }\delta _1(k)R(k)\delta _2(k)\\ 0 &{} I_{2\times 2}\\ \end{array}\right) , &{} k\in L,\\ I_{4\times 4}, &{} k\in L^*,\\ \end{array}\right. }\\ b_-^\prime= & {} {\left\{ \begin{array}{ll} I_{4\times 4}, &{} k\in L,\\ \left( \begin{array}{cc} I_{2\times 2} &{}\quad 0\\ -e^{2it\theta }\delta _2^{-1}(k)R^\dag (k^*)\delta _1^{-1}(k) &{}\quad I_{2\times 2}\\ \end{array}\right) , &{} k\in L^*.\\ \end{array}\right. } \end{aligned}$$

3.4 Rescaling and further reduction of the RH problems

Though the leading-order asymptotics for the solution of the Cauchy problem of the spin-1 GP equation (1.1) is transformed to an integral on $\Sigma ^\prime$ through the stationary point $k_0$ as in (3.49), the solution of the corresponding RH problem (3.51) still can not be written in explicit form. So we convert the contour to a cross through the origin and introduce the oriented contour $\Sigma _0=\{k=ue^{\frac{\pi i}{4}}:u\in {\mathbb {R}}\}\cup \{k=ue^{-\frac{\pi i}{4}}:u\in {\mathbb {R}}\}$ in Fig. 4.

Fig. 4

The oriented contour $\Sigma _0$

Define the scaling operator

$$\begin{aligned} \begin{aligned} N:&{\mathscr {L}}^2(\Sigma ^\prime )\rightarrow {\mathscr {L}}^2(\Sigma _0),\\&f(k)\mapsto (Nf)(k)=f\left( k_0+\frac{k}{\sqrt{8t}}\right) . \end{aligned} \end{aligned}$$

(3.50)

Let ${{\hat{\omega }}}=N\omega ^\prime$. Then for a $4\times 4$ matrix-valued function f,

$$\begin{aligned} NC_{\omega ^\prime }f=N\left( C_+(f\omega _-^\prime )+C_-(f\omega _+^\prime )\right) =C_{{{\hat{\omega }}}}Nf, \end{aligned}$$

(3.51)

which means $C_{\omega ^\prime }=N^{-1}C_{{{\hat{\omega }}}}N$. Notice that $\omega ^\prime$ is made up of these terms $\delta _1(k)$, $\delta _1^{-1}(k)$, $\delta _2(k)$ and $\delta _2^{-1}(k)$. However, $\delta _1(k)$ and $\delta _2(k)$ can not be found in explicit form because they satisfy the matrix RH problems (3.2) and (3.3). If we consider the determinants of the two RH problems, they become the same scalar RH problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \det \delta _{+}(k)=(1+|\gamma (k)|^2+|\det \gamma (k)|^2)\det \delta _{-}(k),\quad k\in (-\infty ,k_0),\\ \det \delta (k)\rightarrow 1,\quad k\rightarrow \infty , \end{array}\right. } \end{aligned}$$

(3.52)

which can be solved by the Plemelj formula [1]

$$\begin{aligned} \det \delta (k)=(k-k_0)^{i\nu }e^{\chi (k)}, \end{aligned}$$

(3.53)

where

$$\begin{aligned} \nu&=-\frac{1}{2\pi }\log (1+|\gamma (k_0)|^2+|\det \gamma (k_0)|^2),\\ \chi (k)&=\frac{1}{2\pi i}\Big (\int _{k_0-1}^{k_0}\log \left( \frac{1+|\gamma (\xi )|^2+|\det \gamma (\xi )|^2}{1+|\gamma (k_0)|^2+|\det \gamma (k_0)|^2}\right) \, \frac{\mathrm {d}\xi }{\xi -k}\\&\quad +\int _{-\infty }^{k_0-1}\log \left( 1+|\gamma (\xi )|^2+|\det \gamma (\xi )|^2\right) \, \frac{\mathrm {d}\xi }{\xi -k}\\&\quad -\log (1+|\gamma (k_0)|^2+|\det \gamma (k_0)|^2)\log (k-k_0+1)\Big ). \end{aligned}$$

Resorting to the symmetry relations of $\delta _1(k)$ and $\delta _2(k)$, we arrive at $|\det \delta (k)|\lesssim 1$ for $k\in {\mathbb {C}}$. A direct computation shows by the scaling operator act on the exponential term and $\det \delta (k)$ that

$$\begin{aligned} N(e^{-it\theta }\det \delta )=\delta ^0\delta ^1(k), \end{aligned}$$

where $\delta ^0$ is independent of k and

$$\begin{aligned} \delta ^0=e^{2itk_0^2}(8t)^{-\frac{i\nu }{2}}e^{\chi (k_0)}. \end{aligned}$$

(3.54)

Set ${\hat{L}}=\{\sqrt{8t}ue^{-\frac{\pi i}{4}}:u\in {\mathbb {R}}\}$. In a way similar to the proof of Lemma 3.35 in [18], we obtain by a straightforward computation that

$$\begin{aligned}&\left| (NR)(k)(\delta ^1(k))^2-R(k_0\pm )k^{2i\nu }e^{-\frac{1}{2}ik^2}\right| \lesssim \frac{\log t}{\sqrt{t}},\quad k\in {\hat{L}}, \end{aligned}$$

(3.55)

$$\begin{aligned}&\left| (NR^\dag )(k^*)(\delta ^1(k))^{-2}-R^\dag (k_0\pm )k^{-2i\nu }e^{\frac{1}{2}ik^2}\right| \lesssim \frac{\log t}{\sqrt{t}},\quad k\in {\hat{L}}^*, \end{aligned}$$

(3.56)

where

$$\begin{aligned} R(k_0+)=\gamma (k_0),\quad R(k_0-)=-\left( I_{2\times 2}+\gamma (k_0)\gamma ^\dag (k_0)\right) ^{-1}\gamma (k_0). \end{aligned}$$

Then we obtain the expression of ${{\hat{\omega }}}$:

$$\begin{aligned}&{{\hat{\omega }}}={\hat{\omega }}_+= \left( \begin{array}{cc} 0 &{}\quad (Ns_1)(k)\\ 0 &{}\quad 0\\ \end{array}\right) , \quad k\in {\hat{L}}, \end{aligned}$$

(3.57)

$$\begin{aligned}&{{\hat{\omega }}}={\hat{\omega }}_-= \left( \begin{array}{cc} 0 &{}\quad 0\\ (Ns_2)(k) &{}\quad 0\\ \end{array} \right) ,\quad k\in {\hat{L}}^*, \end{aligned}$$

(3.58)

where

$$\begin{aligned} s_1(k)=e^{-2it\theta }\delta _1(k)R(k)\delta _2(k),\quad s_2(k)=e^{2it\theta }\delta _2^{-1}(k)R^\dag (k^*)\delta _1^{-1}(k). \end{aligned}$$

(3.59)

Lemma 3.5

As $t\rightarrow \infty$ and $k\in {\hat{L}}$,

$$\begin{aligned} \vert (N{{\tilde{\delta }}}_1)(k)\vert \lesssim t^{-1},\quad \vert (N{{\tilde{\delta }}}_2)(k)\vert \lesssim t^{-1}, \end{aligned}$$

(3.60)

where

$$\begin{aligned} {{\tilde{\delta }}}_1(k)= & {} e^{-2it\theta }[\delta _1(k)R(k)-\det \delta (k)R(k)],\\ {{\tilde{\delta }}}_2(k)= & {} e^{-2it\theta }[R(k)\delta _2(k)-\det \delta (k)R(k)]. \end{aligned}$$

Proof

We first consider the case of ${{\tilde{\delta }}}_1(k)$. Another case is similar. Noting that $\delta _1(k)$ and $\det \delta (k)$ satisfy the RH problems (3.2) and (3.54), respectively, then ${{\tilde{\delta }}}_1(k)$ satisfies

$$\begin{aligned} {\left\{ \begin{array}{ll} {{\tilde{\delta }}}_{1+}(k)={{\tilde{\delta }}}_{1-}(k)(1+|\gamma (k)|^2+|\det \gamma (k)|^2)+e^{-2it\theta }f(k),\quad k\in (-\infty ,k_0),\\ {{\tilde{\delta }}}_1(k)\rightarrow 0,\quad k\rightarrow \infty , \end{array}\right. } \end{aligned}$$

(3.61)

where $f(k)=\delta _{1-}(k)\left( \gamma (k)\gamma ^\dag (k^*)-(|\gamma (k)|^2+|\det \gamma (k)|^2)I_{2\times 2}\right) R(k)$. This RH problem can be solved as follows

$$\begin{aligned} {{\tilde{\delta }}}_1(k)= & {} X(k)\int _{-\infty }^{k_0}\frac{e^{-2it\theta (\xi )}f(\xi )}{X_{+}(\xi )(\xi -k)}\, \frac{\mathrm {d}\xi }{2\pi i},\\ X(k)= & {} {\mathrm {exp}}\left\{ \frac{1}{2\pi i}\int _{-\infty }^{k_0}\frac{\log (1+|\gamma (\xi )|^2+|\det \gamma (\xi )|^2)}{\xi -k}\, \mathrm {d}\xi \right\} . \end{aligned}$$

Resorting to the definition of $\rho (k)$ in (3.7), one deduces that

$$\begin{aligned} \begin{aligned}&\left( \gamma (k)\gamma ^\dag (k^*)-(|\gamma (k)|^2+|\det \gamma (k)|^2)I_{2\times 2}\right) R(k)\\&\quad =\left[ (|\gamma (k)|^2+|\det \gamma (k)|^2)I_{2\times 2}-\gamma (k)\gamma ^\dag (k^*)\right] (\rho (k)-R(k))-\det \gamma (k){\mathrm {adj}}\gamma ^\dag (k^*), \end{aligned} \end{aligned}$$

(3.62)

where ${\mathrm {adj}}X$ is the adjoint of matrix X. From Theorem 3.1, $\rho -R=h_1+h_2$. Similarly, ${\mathrm {adj}}\gamma ^\dag (k^*)$ also has a decomposition ${\mathrm {adj}}\gamma ^\dag ={\tilde{h}}_1+{\tilde{h}}_2+{\tilde{R}}$. We split f(k) into three parts $f=f_1+f_2+f_3$, where $f_1$ consists of the terms including $h_1$ and ${\tilde{h}}_1$, $f_2$ consists of the terms including $h_2$ and ${\tilde{h}}_2$, $f_3$ consists of the terms including ${\tilde{R}}$. Notice that $|(|\gamma |^2+|\det \gamma |^2)I_{2\times 2}-\gamma \gamma ^\dag |$ is consist of the modulus of the components of $\gamma$ and $\det \gamma$. Then $f_2$ and $f_3$ have an analytic continuation to $L_t=\{k=k_0-\frac{1}{t}+ue^{\frac{3\pi i}{4}}:u\in (0,+\infty )\}$ (Fig. 5).

Fig. 5

The contour $L_t$

Moreover, $f_1(k)+f_2(k)=O((k-k_0)^l)$ and they satisfy

$$\begin{aligned}&\vert e^{-2it\theta }f_{1}(k)\vert \lesssim \frac{1}{(1+\vert k\vert ^{2})t^{l}}, \quad k\in {\mathbb {R}}, \end{aligned}$$

(3.63)

$$\begin{aligned}&\vert e^{-2it\theta }f_{2}(k)\vert \lesssim \frac{1}{(1+\vert k\vert ^{2})t^{l}}, \quad k\in L_{t}. \end{aligned}$$

(3.64)

As $k\in {\hat{L}}$, we arrive at

$$\begin{aligned} (N\tilde{\delta _1})(k)&=X(\frac{k}{\sqrt{8t}}+k_{0})\int _{k_0-\frac{1}{t}}^{k_0}\frac{e^{-2it\theta (\xi )}f(\xi )}{X_+(\xi )(\xi -k_0-\frac{k}{\sqrt{8t}})}\, \frac{\mathrm {d}\xi }{2\pi i}\\&\quad +X(\frac{k}{\sqrt{8t}}+k_{0})\int _{-\infty }^{k_0-\frac{1}{t}}\frac{e^{-2it\theta (\xi )}f_1(\xi )}{X_+(\xi )(\xi -k_0-\frac{k}{\sqrt{8t}})}\, \frac{\mathrm {d}\xi }{2\pi i}\\&\quad +X(\frac{k}{\sqrt{8t}}+k_{0})\int _{-\infty }^{k_0-\frac{1}{t}}\frac{e^{-2it\theta (\xi )}f_2(\xi )}{X_+(\xi )(\xi -k_0-\frac{k}{\sqrt{8t}})}\, \frac{\mathrm {d}\xi }{2\pi i}\\&\quad +X(\frac{k}{\sqrt{8t}}+k_{0})\int _{-\infty }^{k_0-\frac{1}{t}}\frac{e^{-2it\theta (\xi )}f_3(\xi )}{X_+(\xi )(\xi -k_0-\frac{k}{\sqrt{8t}})}\, \frac{\mathrm {d}\xi }{2\pi i}\\&\triangleq A_{1}+A_{2}+A_{3}+A_4, \end{aligned}$$

and a direct calculation shows that

$$\begin{aligned}&\vert A_1\vert \lesssim \left| \int _{k_0-\frac{1}{t}}^{k_0}\frac{e^{-2it\theta (\xi )}f(\xi )}{X_+(\xi )(\xi -k_0-\frac{k}{\sqrt{8t}})}\, \mathrm {d}\xi \right| \lesssim t^{-1},\\&\vert A_2\vert \lesssim \int _{-\infty }^{k_0-\frac{1}{t}}\frac{|e^{-2it\theta (\xi )}f_1(\xi )|}{|\xi -k_0-\frac{k}{\sqrt{8t}}|}\, \mathrm {d}\xi \lesssim t^{-l}\sqrt{2}t\int _{-\infty }^{0}\frac{1}{1+\xi ^2}\, \mathrm {d}\xi \lesssim t^{-l+1}. \end{aligned}$$

Similarly, we can evaluate $A_{3}$ along the contour $L_{t}$ instead of the interval $(-\infty ,k_0-\frac{1}{t})$ because of Cauchy’s Theorem, and $|A_{3}|\lesssim t^{-l+1}$. For $\xi \in L_t$,

$$\begin{aligned} \vert A_4\vert \lesssim \sqrt{2}t^{-1}\int _{-\infty }^{k_0-\frac{1}{t}}\frac{1}{1+|\xi |^5}\, \mathrm {d}\xi \lesssim t^{-1}. \end{aligned}$$

Then the estimates for $|(N{{\tilde{\delta }}}_1)(k)|$ and $|(N{{\tilde{\delta }}}_2)(k)|$ is similarly computed. $\quad \square$

Corollary 3.1

When $k\in {\hat{L}}^*$ and as $t\rightarrow \infty$,

$$\begin{aligned} \vert (N{\hat{\delta }}_1)(k)\vert \lesssim t^{-1},\quad \vert (N{\hat{\delta }}_2)(k)\vert \lesssim t^{-1}, \end{aligned}$$

(3.65)

where

$$\begin{aligned} {\hat{\delta }}_1(k)= & {} e^{2it\theta }[R^\dag (k^*)\delta _1^{-1}(k)-(\det \delta (k))^{-1}R^\dag (k^*)],\\ {\hat{\delta }}_2(k)= & {} e^{2it\theta }[\delta _2^{-1}(k)R^\dag (k^*)-(\det \delta (k))^{-1}R^\dag (k^*)]. \end{aligned}$$

Next, we construct $\omega ^0$ on the contour $\Sigma _0$. Let

$$\begin{aligned}&\omega ^0=\omega ^0_+= {\left\{ \begin{array}{ll} \left( \begin{array}{cc} 0 &{}\quad (\delta ^0)^2k^{2i\nu }e^{-\frac{1}{2}ik^2}\gamma (k_0)\\ 0 &{}\quad 0\\ \end{array}\right) , &{} k\in \Sigma _0^1,\\ \left( \begin{array}{cc} 0 &{}\quad -(\delta ^0)^2k^{2i\nu }e^{-\frac{1}{2}ik^2}(I_{2\times 2}+\gamma (k_0)\gamma ^\dag (k_0))^{-1}\gamma (k_0)\\ 0 &{}\quad 0\\ \end{array}\right) , &{} k\in \Sigma _0^3,\\ \end{array}\right. }\\&\omega ^0=\omega ^0_-= {\left\{ \begin{array}{ll} \left( \begin{array}{cc} 0 &{}\quad 0\\ (\delta ^0)^{-2}k^{-2i\nu }e^{\frac{1}{2}ik^2}\gamma ^\dag (k_0) &{}\quad 0\\ \end{array}\right) , &{} k\in \Sigma _0^2,\\ \left( \begin{array}{cc} 0 &{}\quad 0\\ -(\delta ^0)^{-2}k^{-2i\nu }e^{\frac{1}{2}ik^2}\gamma ^\dag (k_0)(I_{2\times 2}+\gamma (k_0)\gamma ^\dag (k_0))^{-1} &{}\quad 0\\ \end{array}\right) , &{} k\in \Sigma _0^4.\\ \end{array}\right. } \end{aligned}$$

(3.66)

It follows from (3.57) and (3.58) that, as $t\rightarrow \infty$,

$$\begin{aligned} \Vert {{\hat{\omega }}}-\omega ^0\Vert _{{\mathscr {L}}^1(\Sigma _0)\cap {\mathscr {L}}^2(\Sigma _0)\cap {\mathscr {L}}^\infty (\Sigma _0)} \lesssim \frac{\log {t}}{\sqrt{t}}. \end{aligned}$$

(3.67)

Theorem 3.3

As $t\rightarrow \infty$, the solution q(x, t) for the Cauchy problem of the spin-1 GP equation (1.1) is

$$\begin{aligned} \begin{aligned} q(x,t)=-\frac{1}{\pi \sqrt{8t}}\left( \int _{\Sigma _0}((1-C_{\omega ^0})^{-1}I_{4\times 4})(\xi )\omega ^0(\xi )\, \mathrm {d}\xi \right) _{12}+O\left( \frac{\log t}{t}\right) . \end{aligned} \end{aligned}$$

(3.68)

Proof

A simple computation shows that

$$\begin{aligned}&\left( (1-C_{{{\hat{\omega }}}})^{-1}I_{4\times 4}\right) {{\hat{\omega }}}-\left( (1-C_{\omega ^0})^{-1}I_{4\times 4}\right) {\omega ^0}\\&\quad =\left( (1-C_{{{\hat{\omega }}}})^{-1}I_{4\times 4}\right) ({{\hat{\omega }}}-{\omega ^0})+(1-C_{{{\hat{\omega }}}})^{-1}(C_{{{\hat{\omega }}}}-C_{\omega ^0})(1-C_{\omega ^0})^{-1}I_{4\times 4}{\omega ^0}\\&\quad =({{\hat{\omega }}}-{\omega ^0})+\left( (1-C_{{{\hat{\omega }}}})^{-1}C_{{{\hat{\omega }}}}I_{4\times 4}\right) ({{\hat{\omega }}}-{\omega ^0})+(1-C_{{{\hat{\omega }}}})^{-1}(C_{{{\hat{\omega }}}}-C_{\omega ^0})I_{4\times 4}{\omega ^0}\\&\qquad +(1-C_{{{\hat{\omega }}}})^{-1}(C_{{{\hat{\omega }}}}-C_{\omega ^0})(1-C_{\omega ^0})^{-1}C_{\omega ^0}I_{4\times 4}{\omega ^0}. \end{aligned}$$

Utilizing the triangle inequality and the inequalities (3.70), we have

$$\begin{aligned} \int _{\Sigma _0}\left( (1-C_{{{\hat{\omega }}}})^{-1}I_{4\times 4}\right) (\xi ){{\hat{\omega }}}(\xi )\,\mathrm {d}\xi =\int _{\Sigma _0}\left( (1-C_{\omega ^0})^{-1}I_{4\times 4}\right) (\xi ){\omega ^0}(\xi )\,\mathrm {d}\xi +O\left( \frac{\log {t}}{\sqrt{t}}\right) . \end{aligned}$$

According to (3.53), we obtain by using a simple change of variable that

$$\begin{aligned} \begin{aligned}&\int _{\Sigma ^\prime }\left( (1-C_{\omega ^\prime })^{-1}I_{4\times 4}\right) (\xi )\omega ^\prime (\xi )\,\mathrm {d}\xi \\&\quad =\int _{\Sigma ^\prime }\left( N^{-1}(1-C_{{{\hat{\omega }}}})^{-1}NI_{4\times 4}\right) (\xi )\omega ^\prime (\xi )\,\mathrm {d}\xi \\&\quad =\int _{\Sigma ^\prime }\left( (1-C_{{{\hat{\omega }}}})^{-1}I_{4\times 4}\right) ((\xi -k_0)\sqrt{8t})N\omega ^\prime ((\xi -k_0)\sqrt{8t})\,\mathrm {d}\xi \\&\quad =\frac{1}{\sqrt{8t}}\int _{\Sigma _0}\left( (1-C_{{{\hat{\omega }}}})^{-1}I_{4\times 4}\right) (\xi ){{\hat{\omega }}}(\xi )\,\mathrm {d}\xi \\&\quad =\frac{1}{\sqrt{8t}}\int _{\Sigma _0}\left( (1-C_{\omega ^0})^{-1}I_{4\times 4}\right) (\xi )\omega ^0(\xi )\,\mathrm {d}\xi +O\left( \frac{\log t}{t}\right) .\\ \end{aligned} \end{aligned}$$

Then (3.71) can be deduced from (3.49). $\quad \square$

For $k\in {\mathbb {C}}\backslash \Sigma _0$, set

$$\begin{aligned} M^0(k;x,t)=I_{4\times 4}+\int _{\Sigma _0}\frac{\left( (1-C_{\omega ^0})^{-1}I_{4\times 4}\right) (\xi )\omega ^0(\xi )}{\xi -k} \, \frac{\mathrm {d}\xi }{2\pi i}. \end{aligned}$$

(3.69)

Then $M^0(k;x,t)$ is the solution of the RH problem

$$\begin{aligned} {\left\{ \begin{array}{ll} M^0_+(k;x,t)=M^0_-(k;x,t)J^0(k;x,t), &{} k\in \Sigma _0, \\ M^0(k;x,t)\rightarrow I_{4\times 4}, &{} k\rightarrow \infty , \end{array}\right. } \end{aligned}$$

(3.70)

where $J^0=(b^0_-)^{-1}b^0_+=(I_{4\times 4}-\omega _-^0)^{-1}(I_{4\times 4}+\omega _+^0)$. In particular, we have

$$\begin{aligned} M^0(k)=I_{4\times 4}+\frac{M^0_1}{k}+O(k^{-2}), \quad k\rightarrow \infty . \end{aligned}$$

(3.71)

From (3.72) and (3.74), the coefficients of the term $k^{-1}$ is as follows

$$\begin{aligned} M^0_1=-\int _{\Sigma _0}\left( (1-C_{\omega ^0})^{-1}I_{4\times 4}\right) (\xi )\omega ^0(\xi )\, \frac{\mathrm {d}\xi }{2\pi i}. \end{aligned}$$

(3.72)

Corollary 3.2

As $t\rightarrow \infty$, the solution q(x, t) for the Cauchy problem of the spin-1 GP equation (1.1) is

$$\begin{aligned} q(x,t)=\frac{i}{\sqrt{2t}}\left( M_1^0\right) _{12}+O\left( \frac{\log t}{t}\right) . \end{aligned}$$

(3.73)

Proof

Substituting (3.75) into (3.71), we immediately obtain (3.76). $\quad \square$

3.5 Solving the model problem

In this subsection, we focus on $M_1^0$ and the RH problem that $M^0(k;x,t)$ satisfies. This RH problem can be transformed into a model problem, from which the explicit expression of $M_1^0$ can be obtained through the standard parabolic cylinder function. For this purpose, we introduce

$$\begin{aligned} \Psi (k)=H(k)k^{i\nu \sigma _4}e^{-\frac{1}{4}ik^2\sigma _4},\quad H(k)=(\delta ^0)^{-\sigma _4}M^0(k)(\delta ^0)^{\sigma _4}. \end{aligned}$$

(3.74)

It is easy to see from (3.73) that

$$\begin{aligned} \Psi _+(k)=\Psi _-(k)v(k_0),\quad v=e^{\frac{1}{4}ik^2\sigma _4}k^{-i\nu \sigma _4}(\delta ^0)^{-\sigma _4}J^0(k)(\delta ^0)^{\sigma _4} k^{i\nu \sigma _4}e^{-\frac{1}{4}ik^2{\sigma _4}}. \end{aligned}$$

(3.75)

The jump matrix is independent of k along each of the four rays $\Sigma _0^1, \Sigma _0^2, \Sigma _0^3, \Sigma _0^4$, so

$$\begin{aligned} \frac{\mathrm {d}\Psi _+(k)}{\mathrm {d}k}=\frac{\mathrm {d}\Psi _-(k)}{\mathrm {d}k}v(k_0). \end{aligned}$$

(3.76)

Combining (3.78) and (3.79), we obtain

$$\begin{aligned} \frac{\mathrm {d}\Psi _+(k)}{\mathrm {d}k}+\frac{1}{2}ik\sigma _4\Psi _+(k)=\left( \frac{\mathrm {d}\Psi _-(k)}{\mathrm {d}k}+\frac{1}{2}ik\sigma _4\Psi _-(k)\right) v(k_0). \end{aligned}$$

(3.77)

Then $(\mathrm {d}\Psi /\mathrm {d}k+\frac{1}{2}ik\sigma _4\Psi )\Psi ^{-1}$ has no jump discontinuity along each of the four rays. In addition, from the relation between $\Psi (k)$ and H(k), we have

$$\begin{aligned} \left( \frac{\mathrm {d}\Psi (k)}{\mathrm {d}k}+\frac{1}{2}ik\sigma _4\Psi (k)\right) \Psi ^{-1}(k)&=\frac{\mathrm {d}H(k)}{\mathrm {d}k}H^{-1}(k)-\frac{ik}{2}H(k)\sigma _4 H^{-1}(k)\\&\quad +\frac{i\nu }{k}H(k)\sigma _4 H^{-1}(k)+\frac{1}{2}ik\sigma _4\\&=O(k^{-1})+\frac{i}{2}(\delta ^0)^{-\sigma _4}[\sigma _4, M^0_1](\delta ^0)^{\sigma _4}. \end{aligned}$$

It follows by the Liouville’s Theorem that

$$\begin{aligned} \frac{\mathrm {d}\Psi (k)}{\mathrm {d}k}+\frac{1}{2}ik\sigma _4\Psi (k)=\beta \Psi (k), \end{aligned}$$

(3.78)

where

$$\begin{aligned} \beta =\frac{i}{2}(\delta ^0)^{-\sigma _4}[\sigma _4, M^0_1](\delta ^0)^{\sigma _4} =\left( \begin{array}{cc} 0 &{}\quad \beta _{12}\\ \beta _{21} &{}\quad 0 \end{array}\right) . \end{aligned}$$

Moreover,

$$\begin{aligned} (M_1^0)_{12}=-i(\delta ^0)^2\beta _{12}. \end{aligned}$$

(3.79)

The RH problem (3.73) shows that

$$\begin{aligned} \sigma _4(M^0(k^*))^\dag \sigma _4=(M^0(k))^{-1}, \end{aligned}$$

(3.80)

which implies that $\beta _{12}=\beta _{21}^\dag$. Set

$$\begin{aligned} \Psi (k) =\left( \begin{array}{cc} \Psi _{11}(k) &{}\quad \Psi _{12}(k)\\ \Psi _{21}(k) &{}\quad \Psi _{22}(k)\\ \end{array}\right) , \end{aligned}$$

and $\Psi _{ij}(k)(i,j=1,2)$ are all $2\times 2$ matrices. From (3.81) and its differential we obtain

$$\begin{aligned}&\frac{\mathrm {d}^{2}\Psi _{11}(k)}{\mathrm {d}k^{2}}+\left[ (\frac{1}{2}i+\frac{1}{4}k^2)I_{2\times 2}-\beta _{12}\beta _{21}\right] \Psi _{11}(k)=0, \end{aligned}$$

(3.81)

$$\begin{aligned}&\beta _{12}\Psi _{21}(k)=\frac{\mathrm {d}\Psi _{11}(k)}{\mathrm {d}k}+\frac{1}{2}ik\Psi _{11}(k), \end{aligned}$$

(3.82)

$$\begin{aligned}&\frac{\mathrm {d}^{2}\beta _{12}\Psi _{22}(k)}{\mathrm {d}k^{2}}+\left[ (-\frac{1}{2}i+\frac{1}{4}k^2)I_{2\times 2}-\beta _{12}\beta _{21}\right] \beta _{12}\Psi _{22}(k)=0, \end{aligned}$$

(3.83)

$$\begin{aligned}&\Psi _{12}(k)=(\beta _{12}\beta _{21})^{-1}\left( \frac{\mathrm {d}\beta _{12}\Psi _{22}(k)}{\mathrm {d}k}-\frac{1}{2}ik\beta _{12}\Psi _{22}(k)\right) . \end{aligned}$$

(3.84)

For the convenience, we assume that the $2\times 2$ matrices $\beta _{12}$ and $\beta _{12}\beta _{21}$ have the forms

$$\begin{aligned} \beta _{12}=\left( \begin{array}{cc} A &{}\quad B \\ C &{}\quad D \\ \end{array}\right) ,\quad \beta _{12}\beta _{21}= \left( \begin{array}{cc} {\tilde{A}} &{}\quad {\tilde{B}} \\ {\tilde{C}} &{}\quad {\tilde{D}} \\ \end{array}\right) . \end{aligned}$$

(3.85)

Set $\Psi _{11}=(\Psi _{11}^{(ij)})_{2\times 2}$. We consider the (1,1) entry and (2,1) entry of equation (3.84) that are

$$\begin{aligned}&\frac{\mathrm {d}^{2}\Psi _{11}^{(11)}(k)}{\mathrm {d}k^{2}}+(\frac{1}{2}i+\frac{1}{4}k^2)\Psi _{11}^{(11)}(k)-{\tilde{A}}\Psi _{11}^{(11)}(k)-{\tilde{B}}\Psi _{11}^{(21)}(k)=0, \end{aligned}$$

(3.86)

$$\begin{aligned}&\frac{\mathrm {d}^{2}\Psi _{11}^{(21)}(k)}{\mathrm {d}k^{2}}+(\frac{1}{2}i+\frac{1}{4}k^2)\Psi _{11}^{(21)}(k)-{\tilde{C}}\Psi _{11}^{(11)}(k)-{\tilde{D}}\Psi _{11}^{(21)}(k)=0. \end{aligned}$$

(3.87)

If we set s satisfies ${\tilde{B}} {\tilde{C}}=(s-{\tilde{D}})(s-{\tilde{A}})$, then (3.89) becomes

$$\begin{aligned} \frac{\mathrm {d}^{2}}{\mathrm {d}k^{2}}[{\tilde{C}}\Psi _{11}^{(11)}(k)+(s-{\tilde{A}})\Psi _{11}^{(21)}(k)]+(\frac{1}{2}i+\frac{1}{4}k^2-s)[{\tilde{C}}\Psi _{11}^{(11)}(k)+(s-{\tilde{A}})\Psi _{11}^{(21)}(k)]=0. \end{aligned}$$

(3.88)

It is obvious that we can transform the above equations to Weber’s equations by simple change of variables. As is well known, the standard parabolic-cylinder function $D_{a}(\zeta )$ and $D_{a}(-\zeta )$ constitute the basic solution set of Weber’s equation

$$\begin{aligned} \frac{\mathrm {d}^{2}g(\zeta )}{\mathrm {d}\zeta ^{2}}+\left( a+\frac{1}{2}-\frac{\zeta ^{2}}{4}\right) g(\zeta )=0, \end{aligned}$$

whose general solution is denoted by

$$\begin{aligned} g(\zeta )=C_{1}D_{a}(\zeta )+C_{2}D_{a}(-\zeta ), \end{aligned}$$

where $C_1$ and $C_2$ are two arbitrary constants. Set $a=is$,

$$\begin{aligned} {\tilde{C}}\Psi _{11}^{(11)}(k)+(s-{\tilde{A}})\Psi _{11}^{(21)}(k)=c_1D_a(e^{\frac{\pi i}{4}}k)+c_2D_a(e^{-\frac{3\pi i}{4}}k), \end{aligned}$$

(3.89)

where $c_1$ and $c_2$ are constants. First, the solution $c_1D_a(e^{\frac{\pi i}{4}}k)+c_2D_a(e^{-\frac{3\pi i}{4}}k)$ is nontrivial, otherwise the large k expansion of $\Psi (k)$ is false. Besides, notice that as $k\rightarrow \infty$,

$$\begin{aligned} \Psi _{11}(k)\rightarrow k^{i\nu }e^{-\frac{1}{4}ik^2}I_{2\times 2}. \end{aligned}$$

(3.90)

From [39], the parabolic-cylinder function has a asymptotic expansion

$$\begin{aligned} D_{a}(\zeta )= {\left\{ \begin{array}{ll} \zeta ^{a}e^{-\frac{\zeta ^{2}}{4}}(1+O(\zeta ^{-2})), &{} \left| \arg {\zeta }\right|<\frac{3\pi }{4},\\ \zeta ^{a}e^{-\frac{\zeta ^{2}}{4}}(1+O(\zeta ^{-2}))-\frac{\sqrt{2\pi }}{\Gamma (-a)}e^{a\pi i+\frac{\zeta ^{2}}{4}}\zeta ^{-a-1}(1+O(\zeta ^{-2})), &{} \frac{\pi }{4}<\arg {\zeta }<\frac{5\pi }{4},\\ \zeta ^{a}e^{-\frac{\zeta ^{2}}{4}}(1+O(\zeta ^{-2}))-\frac{\sqrt{2\pi }}{\Gamma (-a)}e^{-a\pi i+\frac{\zeta ^{2}}{4}}\zeta ^{-a-1}(1+O(\zeta ^{-2})), &{} -\frac{5\pi }{4}<\arg {\zeta }<-\frac{\pi }{4}, \end{array}\right. } \end{aligned}$$

(3.91)

as $\zeta \rightarrow \infty$, where $\Gamma (\cdot )$ is the Gamma function. Along the line $k=\sigma e^{-\frac{\pi i}{4}}(\sigma >0)$, using the asymptotic expansion (3.93) and (3.94) to evaluate the left-hand side and the right-hand side of (3.92), we get that $c_1={\tilde{C}}k^{i\nu -a}e^{\frac{-a\pi i}{4}}$ and $c_2=0$. In the meantime, $\Psi _{11}^{(11)}(k)$ and $\Psi _{11}^{(21)}(k)$ are not linear dependent because they satisfy the asymptotic expansion (3.93). The equality (3.92) shows that the coefficient of $\Psi _{11}^{(21)}(k)$ is unique, which means that s is unique. Combining with the definition of s, we have ${\tilde{B}}={\tilde{C}}=0$. Hence, we assume that $\beta _{12}\beta _{21}={\mathrm {diag}}(d_1,d_2)$ and (3.84) becomes

$$\begin{aligned} \frac{\mathrm {d}^{2}}{\mathrm {d}k^{2}}\left( \begin{array}{cc} \Psi _{11}^{(11)} &{}\quad \Psi _{11}^{(12)} \\ \Psi _{11}^{(21)} &{}\quad \Psi _{11}^{(22)} \\ \end{array}\right) +(\frac{1}{2}i+\frac{1}{4}k^2)\left( \begin{array}{cc} \Psi _{11}^{(11)} &{}\quad \Psi _{11}^{(12)} \\ \Psi _{11}^{(21)} &{}\quad \Psi _{11}^{(22)} \\ \end{array}\right) -\left( \begin{array}{cc} d_1\Psi _{11}^{(11)} &{}\quad d_1\Psi _{11}^{(12)} \\ d_2\Psi _{11}^{(21)} &{}\quad d_2\Psi _{11}^{(22)} \\ \end{array}\right) =0. \end{aligned}$$

(3.92)

It can be seen that $\Psi _{11}^{(11)}$, $\Psi _{11}^{(12)}$ and $\Psi _{11}^{(21)}$, $\Psi _{11}^{(22)}$ satisfy the same equation, respectively. Set ${\tilde{a}}=id_1$, similar to (3.92), $\Psi _{11}^{(12)}$ can be expressed by the linear combination of $D_{{\tilde{a}}}(e^{\frac{\pi i}{4}}k)$ and $D_{{\tilde{a}}}(e^{-\frac{3\pi i}{4}}k)$. Notice that $\Psi _{11}^{(12)}\rightarrow 0$ as $k\rightarrow \infty$ and the asymptotic expansion (3.94), $\Psi _{11}^{(12)}=0$. A similar computation shows that $\Psi _{11}^{(21)}=0$. Then $\Psi _{11}(k)$ is a diagonal matrix and set $a_1=id_1$, $a_2=id_2$, we have

$$\begin{aligned} \Psi _{11}^{(11)}= & {} c_1^{(1)}D_{a_1}(e^{\frac{\pi i}{4}}k)+c_2^{(1)}D_{a_1}(e^{-\frac{3\pi i}{4}}k), \end{aligned}$$

(3.93)

$$\begin{aligned} \Psi _{11}^{(22)}= & {} c_1^{(2)}D_{a_2}(e^{\frac{\pi i}{4}}k)+c_2^{(2)}D_{a_2}(e^{-\frac{3\pi i}{4}}k), \end{aligned}$$

(3.94)

where $c_1^{(j)}$, $c_2^{(j)}(j=1,2)$ are constants. A similar analysis can be applied for $\Psi _{22}(k)$ and we have

$$\begin{aligned} A\Psi _{22}^{(11)}= & {} c_1^{(3)}D_{-a_1}(e^{-\frac{\pi i}{4}}k)+c_2^{(3)}D_{-a_1}(e^{\frac{3\pi i}{4}}k), \end{aligned}$$

(3.95)

$$\begin{aligned} D\Psi _{22}^{(22)}= & {} c_1^{(4)}D_{-a_2}(e^{-\frac{\pi i}{4}}k)+c_2^{(4)}D_{-a_2}(e^{\frac{3\pi i}{4}}k), \end{aligned}$$

(3.96)

where $c_1^{(j)}$, $c_2^{(j)}(j=3,4)$ are constants. Next, we first consider the case when $\arg {k}\in (-\frac{\pi }{4},\frac{\pi }{4})$. Notice that as $k\rightarrow \infty$,

$$\begin{aligned} \Psi _{11}(k)k^{-i\nu }e^{\frac{ik^{2}}{4}}\rightarrow I_{2\times 2}, \quad \Psi _{22}(k)k^{i\nu }e^{-\frac{ik^{2}}{4}}\rightarrow I_{2\times 2}. \end{aligned}$$

Then we arrive at

$$\begin{aligned}&\Psi _{11}^{(11)}(k)=\Psi _{11}^{(22)}(k)=e^{\frac{\pi \nu }{4}}D_{a_1}(e^{\frac{\pi i}{4}}k), \quad a_1=a_2=i\nu ,\\&\Psi _{22}^{(11)}(k)=\Psi _{22}^{(22)}(k)=e^{\frac{\pi \nu }{4}}D_{-a_1}(e^{-\frac{\pi i}{4}}k). \end{aligned}$$

Besides, the parabolic cylinder function follows that [6]

$$\begin{aligned} \frac{\mathrm {d}D_{a}(\zeta )}{\mathrm {d}\zeta }+\frac{\zeta }{2}D_{a}(\zeta )-aD_{a-1}(\zeta )=0. \end{aligned}$$

(3.97)

Then we have

$$\begin{aligned} \Psi _{21}(k)=\beta _{12}^{-1}a_1e^{\frac{\pi \nu }{4}}e^{\frac{\pi i}{4}}D_{a_1-1}(e^{\frac{\pi i}{4}}k). \end{aligned}$$

For $\arg {k}\in (\frac{\pi }{4},\frac{3\pi }{4})$ and $k\rightarrow \infty$,

$$\begin{aligned} \Psi _{11}(k)k^{-i\nu }e^{\frac{ik^{2}}{4}}\rightarrow I_{2\times 2}, \quad \Psi _{22}(k)k^{i\nu }e^{-\frac{ik^{2}}{4}}\rightarrow I_{2\times 2}. \end{aligned}$$

We obtain

$$\begin{aligned}&\Psi _{11}^{(11)}(k)=\Psi _{11}^{(22)}(k)=e^{-\frac{3\pi \nu }{4}}D_{a_1}(e^{-\frac{3\pi i}{4}}k), \quad a_1=a_2=i\nu ,\\&\Psi _{22}^{(11)}(k)=\Psi _{22}^{(22)}(k)=e^{\frac{\pi \nu }{4}}D_{-a_1}(e^{-\frac{\pi i}{4}}k), \end{aligned}$$

which imply

$$\begin{aligned} \Psi _{21}(k)=\beta _{12}^{-1}a_1e^{-\frac{3\pi \nu }{4}}e^{-\frac{3\pi i}{4}}D_{a_1-1}(e^{-\frac{3\pi i}{4}}k). \end{aligned}$$

Along the ray $\arg k=\frac{\pi }{4}$, one infers

$$\begin{aligned} \Psi _{+}(k)=\Psi _{-}(k) \left( \begin{array}{cc} I_{2\times 2} &{}\quad 0\\ \gamma ^\dag (k_0) &{}\quad I_{2\times 2}\\ \end{array}\right) . \end{aligned}$$

(3.98)

Notice the (2, 1) entry of the RH problem,

$$\begin{aligned} \beta _{12}^{-1}a_1e^{\frac{\pi (i+\nu )}{4}}D_{a_1-1}(e^{\frac{\pi i}{4}}k)=e^{\frac{\pi \nu }{4}}D_{-a_1}(e^{\frac{3\pi i}{4}}k)\gamma ^\dag (k_0)+\beta _{12}^{-1}a_1e^{-\frac{\pi (3\nu +3i)}{4}}D_{a_1-1}(e^{-\frac{3\pi i}{4}}k). \end{aligned}$$

The parabolic-cylinder function satisfies [6]

$$\begin{aligned} D_{a}(\zeta )=\frac{\Gamma (a+1)}{\sqrt{2\pi }}\left( e^{\frac{1}{2}a\pi i}D_{-a-1}(i\zeta )+e^{-\frac{1}{2}a\pi i}D_{-a-1}(-i\zeta )\right) . \end{aligned}$$

(3.99)

We can split the term of $D_{-a_1}(e^{\frac{3\pi i}{4}}k)$ into the terms of $D_{a_1-1}(e^{\frac{\pi i}{4}}k)$ and $D_{a_1-1}(e^{-\frac{3\pi i}{4}}k)$. By separating the coefficients of the two independent functions, we obtain

$$\begin{aligned} \beta _{12}=\frac{\nu \sqrt{2\pi }e^{-\frac{\pi \nu }{2}}e^{\frac{3\pi i}{4}}}{\Gamma (-i\nu +1)\det \gamma ^\dag (k_0)} \left( \begin{array}{cc} \gamma _{22}^*(k_0) &{}\quad -\gamma _{21}^*(k_0)\\ -\gamma _{12}^*(k_0) &{}\quad \gamma _{11}^*(k_0) \end{array}\right) . \end{aligned}$$

(3.100)

Finally, we can obtain (1.2) from (3.76), (3.82) and (3.103).