1 Introduction

Signal amplification of driven resonators is essential in engineering applications involving nano- and micro-electro-mechanical-systems (N/MEMS). The importance of signal amplification stems from the need to operate above the noise-floor of the device with a large signal-to-noise ratio in order to use these tiny resonators for sensitive detection of displacement [1], mass [2], force [3], torque [4], and charge [5]. Due to its practical significance, signal amplification has received a considerable amount of attention [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. Diverse methods have been devised for signal amplification including electrical means, such as lock-in amplifiers [21] and phase-locked loops [22], where the backaction from the inherently noisy electrical amplifier needs to be treated, and mechanical means, where the motion of the resonator is mechanically preamplified by a large factor before being transduced into an electrical signal.

The realm of mechanical amplification is vast and includes numerous distinguishable techniques, such as bifurcation-topology amplification [9], strong mechanical coupling amplification [12], and parametric amplification [7]. The latter, i.e., parametric amplification—the process of amplifying a driven resonator with a parametric pump at twice its oscillation frequency and with a phase-delay—is a well-established concept and the most widely used technique with applications ranging from radio engineering [23] to cavity optomechanics [24].

In this study we present a relatively simple amplification scheme in which a pair of driven mechanical resonators are mutually coupled. One resonator (the secondary) decays much faster than the primary resonator and can serve as an amplifier for the primary resonator. The amplification of the primary resonator depends on the coupling between the resonators and the driving frequency of the secondary resonator. Specifically, when the coupling is linear and the driving frequency of the secondary resonator is close to the eigenfrequency of the primary resonator, a significant enhancement in the drive level of the primary resonator is obtained, and when the coupling is nonlinear (quadratic) and the driving frequency of the secondary resonator is close to twice the eigenfrequency of the primary resonator, a parametric amplification is obtained.

In general, coupled N/MEMS resonators can exhibit diverse and complex dynamics [25,26,27,28,29], which may be used in various engineering applications, such as filters, mixers, and sensors [14, 30,31,32]. However, when one of the resonator decays significantly faster than the other resonator, it can be adiabatically eliminated [33]. Therefore, the complex dynamics reduces considerably, and the resulting dynamical system (after the adiabatic elimination) consists of a single resonator (the slow decaying resonator) that is being modified by the coupling to the fast decaying resonator.

Using the method of adiabatic elimination, our amplification technique comes from a straightforward generalization of a previous study that was conducted on the undriven counterpart of the dynamical system under consideration [34]. The previous study, Ref. [34], showed that in the undriven system, the linear and nonlinear characteristics of the primary resonator can be altered in a significant manner. Therefore, as we show in the present analysis, in the driven system it is possible to both modify the characteristics of the primary resonator and amplify its response.

This paper is organized as follows: In Sect. 2, we formulate the problem and show that the motion of the relatively fast decaying secondary resonator can be eliminated from the governing equation of the primary resonator under the adiabatic approximation for times that are considerably larger than the relaxation time of the secondary resonator. In Sect. 3, we conduct an asymptotic analysis and obtain the main results of the paper, consisting of closed-form expressions for the amplified response of the primary resonator. In addition, we present numerical validation of our theoretical predictions. Finally, in Sect. 4 we summarize our main findings, discuss their implications and suggest potential future work.

2 Problem formulation

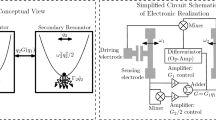
We consider a system consisting of a pair of driven resonators that are mutually coupled (Fig. 1).

Fig. 1
figure 1

Conceptual view and simplified circuit schematic of an electronic realization. Left panel: Two resonators are mutually coupled via the interaction potential \(-q_2G(q_1)\). The primary resonator \(q_1\) has a nonlinear conservative restoring force, \(-U'(q_1)\), a weak linear dissipation \(-\varGamma _1\dot{q}_1\), and a resonant drive \(F_1\cos (\omega _{F_1}t+\theta )\), where \(\omega _{F_1}\approx \sqrt{U''(0)}\). The secondary resonator has a linear conservative restoring force \(-\omega _2^2q_2\), a relatively strong linear dissipation \(-\varGamma _2\dot{q}_2\), and a non-resonant drive \(F_2\cos (\omega _{F_2}t)\). The dissipation is indicated by the wiggly lines, which indicates that the secondary resonator is more heavily damped than the primary resonator. Right panel: For N/MEMS, the motion of each resonator is detected using a parallel-plate capacitive sensing technique. The signal from the primary resonator is fed into a mixer, amplifiers (for control of the different coefficients of G), and an adder to form the function \(G(q_1)\). The signal \(G(q_1)\) is then fed into the driving electrode of the secondary resonator along with the external drive \(F_2\cos (\omega _{F_2}t)\), and to a differentiator and a mixer, which multiplies the signal \(G'(q_1)\) with \(q_2\), and finally, the mixed signal \(q_2G'(q_1)\) is fed into the driving electrode of the primary resonator along with the external drive \(F_1\cos (\omega _{F_1}t+\theta )\)

Full size image

The primary resonator \(q_1\) is driven resonantly by an excitation \(F_1\cos (\omega _{F_1}t+\theta )\) and oscillates around its stable equilibrium \(q_1=0\) with a large amplitude and nonlinear restoring forces that stem from a potential \(U(q_1)\). The secondary resonator \(q_2\) is driven by a non-resonant excitation \(F_2\cos (\omega _{F_2}t)\), i.e., the drive frequency \(\omega _{F_2}\) is not close to its eigenfrequency \(\omega _2\), and oscillates linearly with small amplitude around its stable equilibrium \(q_2=0\). The two resonators are coupled via an interaction potential \(U_{\mathrm{inter}}(q_1,q_2)\). Since \(|q_1|\gg |q_2|\), we assume that the interaction potential depends nonlinearly on \(q_1\) and linearly on \(q_2\), i.e., \(U_{\mathrm{inter}}=-q_2G(q_1)\). Therefore, the Hamiltonian of the system is given by

$$\begin{aligned}&{\mathcal {H}}=p_1^2/2+p_2^2/2+U(q_1)+\omega _2^2q_2^{2}/2-q_2G(q_1)\nonumber \\&\quad -q_1F_1\cos (\omega _{F_1}t+\theta )-q_2F_2\cos (\omega _{F_2}t) , \end{aligned}$$
(1)

where \(p_1\) and \(p_2\) are the conjugate momenta (normalized by mass) of \(q_1\) and \(q_2\), respectively, i.e., \(p_{1,2}=\dot{q}_{1,2}\). The governing equations of \(q_1\) and \(q_2\) are formally given by \(\ddot{q}_k=\dot{p}_k=-2\varGamma _k\dot{q}_k-\partial {\mathcal {H}}/\partial q_k\), and can be explicitly written as

$$\begin{aligned} \ddot{q}_1&=-2\varGamma _1\dot{q}_1-U'(q_1)+F_1\cos (\omega _{F_1}t+\theta )+q_2G'(q_1),\nonumber \\ \end{aligned}$$
(2)
$$\begin{aligned} \ddot{q}_2&=-2\varGamma _2\dot{q}_2-\omega _2^{2}q_2+F_2\cos (\omega _{F_2}t)+G(q_1), \end{aligned}$$
(3)

where the dot symbol denotes a time derivative, the prime symbol denotes a differentiation of a function with respect to its single variable, and \(-2\varGamma _k\dot{q}_k\) models the linear friction force experienced by resonator k (\(k=1,2\)). Moreover, both resonators are lightly damped (\(\varGamma _k/\omega _k\ll 1\)), and the secondary resonator decays much faster than the primary resonator (\(\varGamma _2/\varGamma _1\gg 1\)).

Equation (3) is linear in \(q_2\); therefore, in a similar spirit to the analysis of [34] we can formally solve for \(q_2\) in terms of its Green’s function

$$\begin{aligned}&q_2(t)=e^{-\varGamma _2t}\left[ q_2(0)\cos (\omega _{2d}t)+\frac{p_2(0)}{\omega _{2d}}\sin (\omega _{2d}t)\right] \nonumber \\&\qquad \qquad +\frac{1}{\omega _{2d}}\int \limits _0^t[F_2\cos (\omega _{F_2}\tau )\nonumber \\&\qquad \qquad +G(q_1(\tau ))]e^{-\varGamma _2(t-\tau )}\sin (\omega _{2d}(t-\tau ))d\tau .\nonumber \\ \end{aligned}$$
(4)

Because we consider a lightly damped system (\(\varGamma _k/\omega _k\ll 1\)), the damped eigenfrequency of the secondary resonator in Eq. (4) can be replaced by the undamped eigenfrequency, i.e., \(\omega _{2d}=\omega _2\sqrt{1-(\varGamma _2/\omega _2)^2}\approx \omega _2\). By substitution of Eq. (4) into Eq. (2), we find that

$$\begin{aligned}&\ddot{q}_1=-2\varGamma _1\dot{q}_1-U'(q_1)+F_1\cos (\omega _{F_1}t+\theta )\nonumber \\&\quad +G'(q_1)(L[q_1,t]+M(t)), \end{aligned}$$
(5)

where

$$\begin{aligned}&L[q_1,t]=\frac{1}{\omega _{2}}\int \limits _0^t[F_2\cos (\omega _{F_2}\tau )\nonumber \\&\qquad \qquad \quad +G(q_1(\tau ))]e^{-\varGamma _2(t-\tau )}\sin (\omega _{2}(t-\tau ))d\tau ,\nonumber \\ \end{aligned}$$
(6)
$$\begin{aligned}&\quad M(t)=e^{-\varGamma _2t}\left[ q_2(0)\cos (\omega _{2}t)+\frac{p_2(0)}{\omega _{2}}\sin (\omega _{2}t)\right] . \end{aligned}$$
(7)

The functional \(L[q_1,t]\) is the driven response (by the external excitation and the primary resonator) of the secondary resonator and M(t) is the response of the secondary resonator to its initial state.

3 Asymptotic analysis

To analyze Eq. (5), we make a number of standard assumptions that are relevant to weakly nonlinear resonators, i.e., that all effects other than the inertia (\(\ddot{q}_1\)) and linear stiffness [\(U''(0)\cdot q_1\)] of resonator are small. Specifically, we assume a weak nonlinear interaction between the resonators \([G'(q_1)(L[q_1,t]+M(t))/|U''(0)\cdot q_1|\ll 1]\), a weak damping \((|2\varGamma _1\dot{q}_1|/|U''(0)\cdot q_1|\ll 1)\), and a weak drive of the primary resonator \((F_1/|U''(0)\cdot q_1|\ll 1)\). Under these assumptions, we can use the method of averaging to derive evolution equations for the slow variations of the amplitude and phase of the primary resonator [35, 36].

To this end, we make the following coordinate transformation \(q_1(t)={\mathcal {A}}(t)e^{i\omega _{F_1}t}+{\mathcal {A}}^{*}(t)e^{-i\omega _{F_1}t}\) and \(\dot{q}_1(t)=i\omega _{F_1}[{\mathcal {A}}(t)e^{i\omega _{F_1}t}-{\mathcal {A}}^{*}(t)e^{-i\omega _{F_1}t}]\), where \({\mathcal {A}}^{*}\) is the complex conjugate of \({\mathcal {A}}\) and the complex amplitude \({\mathcal {A}}(t)\) remains almost constant over the period \(T=2\pi /\omega _{F_1}\). Consequently, \(G(q_1(t))\) can be replaced by its Fourier series \(G(q_1(t))=\sum _nc_n({\mathcal {A}}(t),{\mathcal {A}}^{*}(t))e^{in\omega _{F_1}t}\), where \(c_{-n}=c_{n}^*\), and the functional, \(L[q_1,t]\), can be rewritten as

$$\begin{aligned}&L[q_1,t]=\frac{F_2}{\omega _{2}}\int \limits _0^te^{-\varGamma _2(t-\tau )}\nonumber \\&\quad \sin (\omega _{2}(t-\tau ))\cos (\omega _{F_2}\tau )d\tau \nonumber \\&\quad +\int \limits _0^t\sum _{n}\frac{c_n(\tau )}{2i\omega _{2}}[e^{-\varGamma _2(t-\tau )+i[n\omega _{F_1}\tau +\omega _{2}(t-\tau )]}\nonumber \\&\quad -e^{-\varGamma _2(t-\tau )+i[n\omega _{F_1}\tau -\omega _{2}(t-\tau )]}]d\tau . \end{aligned}$$
(8)

Because \(c_n(t)\) are functions of \({\mathcal {A}}(t)\) and \({\mathcal {A}}^*(t)\), they also vary slowly in time. Hence, to the leading order, we can approximate Eq. (8) in the following way

$$\begin{aligned}&L[q_1,t]\approx \frac{F_2}{\omega _{2}}\int \limits _0^te^{-\varGamma _2(t-\tau )}\sin (\omega _{2}(t-\tau ))\cos (\omega _{F_2}\tau )d\tau \nonumber \\&\quad +\sum _{n}\frac{c_n(t)}{2i\omega _{2}}\int \limits _0^t[e^{-\varGamma _2(t-\tau )+i[n\omega _{F_1}\tau +\omega _{2}(t-\tau )]}\nonumber \\&\quad -e^{-\varGamma _2(t-\tau )+i[n\omega _{F_1}\tau -\omega _{2}(t-\tau )]}]d\tau \nonumber \\&\quad =F_2[k_{1}\cos (\omega _{F_2}t-\varphi )\nonumber \\&\quad -k_{2}e^{-\varGamma _2t}\cos (\omega _{F_2}t-\psi )]\nonumber \\&\quad +\sum _{n}\frac{c_n(t)}{2\omega _{2}}e^{in\omega _{F_1}t}\nonumber \\&\quad \left[ \frac{1-e^{-[\varGamma _2+i(n\omega _{F_1}-\omega _{2})]t}}{-(n\omega _{F_1}-\omega _{2})+i\varGamma _2}+\frac{1-e^{-[\varGamma _2+i(n\omega _{F_1}+\omega _{2})]t}}{(n\omega _{F_1}+\omega _{2})-i\varGamma _2}\right] , \end{aligned}$$
(9)

where

$$\begin{aligned} k_1&=\frac{\sqrt{(\omega _{2}^2-\omega _{F_2}^2+\varGamma _2^2)^2+(2\omega _{F_2}\varGamma _2)^2}}{[(\omega _2-\omega _{F_2})^2+\varGamma _2^2][(\omega _2+\omega _{F_2})^2+\varGamma _2^2]},\tan \varphi \nonumber \\&\quad =\frac{2\omega _{F_2}\varGamma _2}{\omega _{2}^2-\omega _{F_2}^2+\varGamma _2^2}\nonumber \\ k_2&=\frac{\sqrt{(\omega _{2}^2-\omega _{F_2}^2+\varGamma _2^2)^{2}+(\varGamma _2/\omega _{2})^2(\omega _{2}^2+\omega _{F_2}^2+\varGamma _2^2)^2}}{[(\omega _2-\omega _{F_2})^2+\varGamma _2^2][(\omega _2+\omega _{F_2})^2+\varGamma _2^2]},\nonumber \\&~\tan \psi =\frac{\varGamma _2}{\omega _{2}}\quad \frac{\omega _{2}^2+\omega _{F_2}^2+\varGamma _2^2}{\omega _{2}^2-\omega _{F_2}^2+\varGamma _2^2}. \end{aligned}$$
(10)

We note that for \(t\gg \varGamma _2^{-1}\), the functional \(L[q_1,t]\) is simplified considerably and reduces to

$$\begin{aligned}&L[q_1,t]\approx k_{1}F_2\cos (\omega _{F_2}t-\varphi )\nonumber \\&\quad +\sum _n\frac{\omega _2^2-n^2\omega _{F_1}^2-2in\omega _{F_1}\varGamma _2}{(\omega _2^2-n^2\omega _{F_1}^2)^2 +(2n\omega _{F_1}\varGamma _2)^2}c_n(t)e^{in\omega _{F_1}t}. \end{aligned}$$
(11)

Hence, we effectively eliminated the secondary resonator and obtained from Eq. (5) the following evolution equation of the primary resonator

$$\begin{aligned}&\ddot{q}_1+U'(q_1)=F_1\cos (\omega _{F_1}t+\theta )\nonumber \\&\quad +k_{1}G'(q_1)F_2\cos (\omega _{F_2}t-\varphi )\nonumber \\&\quad -2\varGamma _1\dot{q}_1+G'(q_1)\sum _n\nonumber \\&\quad \frac{\omega _2^2-n^2\omega _{F_1}^2-2in\omega _{F_1}\varGamma _2}{(\omega _2^2-n^2\omega _{F_1}^2)^2+(2n\omega _{F_1}\varGamma _2)^2}c_n(t)e^{in\omega _{F_1}t}. \end{aligned}$$
(12)

Moreover, this approximation applies even for internal-resonance situations, where \(\omega _2\) is close to a multiple of \(\omega _1\). That is, no further assumptions are needed (other than \(\varGamma _2\gg \varGamma _1\) and a weakly nonlinear system) for the validity of Eq. (12) even in cases where \(\omega _2\approx \omega _1,~\omega _2\approx 2\omega _1\) or \(\omega _2\approx 3\omega _1\).

In the remainder of this paper, we focus only on times that are considerably larger than the relaxation time of the secondary resonator \(t\gg \varGamma _2^{-1}\), where the secondary resonator is adiabatically tracking the primary resonator [37]. We have also assumed here that the functions \(c_n(t)\) vary slowly over the time \(\varGamma _2^{-1}\), which is a restriction on the nonlinearity and the decay rate of the primary resonator. For the weak coupling that we consider here, the only terms to keep in the sum over n of Eq. (12) are the resonant terms, which oscillate with slowly varying amplitude and phase at the same frequency as \(q_1(t)\). For linear coupling, where \(G(q_1)\propto q_1\) and \(G'(q_1)\) is constant, the resonant terms are associated with the fundamental harmonic (\(n=\pm 1\)), whereas for quadratic coupling in which \(G(q_1)\propto q_1^2\) and \(G'(q_1)\) is a linear function of \(q_1\), we have to keep the second (\(n=\pm 2\)) and zeroth (\(n=0\)) harmonics. The same arguments hold for the external excitation of the secondary resonator \(F_2\cos (\omega _{F_2}t)\), i.e., for constant \(G'\), only a drive frequency \(\omega _{F_2}\approx \omega _1\) will lead to a resonant term (under the assumption of weak excitation, where \(|U''(0)\cdot q_1|\gg k_1 G' F_2\)), and if we take into account the term \(\propto q_1\) in \(G'(q_1)\), only a drive frequency \(\omega _{F_2}\approx 2\omega _1\) will lead to a resonant term. These distinctions are used in the analysis of the next subsections.

3.1 Essential leading-order nonlinear terms

In what follows, we restrict our attention to the essential leading-order nonlinear terms. We assume that both \(U(q_1)\) and \(G(q_1)\) are analytic functions and hence can be expanded to a Taylor series. Thus, the potential of the primary resonator can be explicitly written as a Taylor expansion truncated at quartic order \(U(q_1)=\omega _1^2q_1^2/2+\gamma q_1^4/4\), where the non-secular term \(\beta q_1^3/3\) renormalizes \(\gamma \) to the second order in \(\beta \), which we assume to have been taken into account. Similarly, \(G(q_1)\) can represented as \(G(q_1)=G_{1}q_1+G_2q_1^2/2+O(q_1^3)\), where \(G_1\equiv G'(0)\) and \(G_2\equiv G''(0)\). Therefore, we obtain the following complex amplitude equation of the primary resonator

$$\begin{aligned} \mathcal {\dot{A}}=&- \varGamma _1\mathcal {A}\left( 1+\alpha _1\frac{\varGamma _2}{\varGamma _1}+\alpha _2\frac{\varGamma _2}{\varGamma _1}|\mathcal {A}|^2\right) \nonumber \\&-i\mathcal {A}\left\{ \delta \omega _1+\alpha _1\left( \frac{\omega _2^2-\omega _{1}^2}{2\omega _{1}}\right) +\left[ \alpha _2\left( \frac{3\omega _2^2-20\omega _{1}^2}{4\omega _{1}}+\frac{8\omega _{1}}{\omega _2^2}(\varGamma _2^2+\omega _{1}^2) \right) -\frac{3\gamma }{2\omega _{1}}\right] |\mathcal {A}|^2 \right\} \nonumber \\&-\frac{i}{4\omega _{1}}(F_1\exp ( i\theta )+k_1G_1F_2\exp \{i[(\omega _{F_2}-\omega _{F_1})t-\varphi ]\}\nonumber \\&+k_1G_2\mathcal {A}^*F_2\exp \{i[(\omega _{F_2}-2\omega _{F_1})t-\varphi ]\}), \end{aligned}$$
(13)

where we replaced \(\omega _{F_1}\) with \(\omega _1\) in the various coefficients of Eq. (13) other than the detuning parameter \(\delta \omega _1=\omega _{F_1}-\omega _1\), since it leads to higher corrections that can be ignored at the current level of approximation. Accordingly, the coupling to the secondary resonator is captured by the terms with the coefficients

$$\begin{aligned}&\alpha _1=\frac{G_{1}^2}{(\omega _2^2-\omega _{1}^2)^2+(2\varGamma _2\omega _{1})^2},\nonumber \\&\quad \alpha _2=\frac{G_2^2}{(\omega _2^2-4\omega _{1}^2)^2+(4\varGamma _2\omega _{1})^2}. \end{aligned}$$
(14)

Hence, as shown in Ref. [34], the interaction of the primary resonator with the secondary resonator modifies the linear and nonlinear restoring forces of the primary resonator and leads to:

  1. 1.

    An increase in the linear decay rate \(\varGamma _{1\mathrm eff}=\varGamma _1+\alpha _{1}\varGamma _2\)

  2. 2.

    Addition of new nonlinear cubic (van der Pol type) damping term \(-\alpha _2\varGamma _2|{\mathcal {A}}|^2{\mathcal {A}}\)

  3. 3.

    A shift in the eigenfrequency \(\varDelta \omega _1=\alpha _{1}(\omega _2^2-\omega _1^2)/(2\omega _1)\)

  4. 4.

    A modification to the Duffing nonlinearity \(-i\alpha _{2}\left[ (3\omega _2^2-20\omega _1^2)/(4\omega _1)+8\omega _{1}(\varGamma _2^2+\omega _1^2)/\omega _2^2 \right] |{\mathcal {A}}|^2{\mathcal {A}}\)

Moreover, in the current setup of driven resonators, the interaction of the primary resonator with the secondary resonator also modifies the external drive. In particular, there are two cases that lead to additional resonant driving force:

  • Case I: where \(\omega _{F_2}=\omega _{F_1}\), and the uncoupled direct external drive term \(F_1e^{i\theta }\) in Eq. (13) is replaced by \(F_1e^{i\theta }+k_1G_1F_2e^{-i\varphi }\), which modifies both the amplitude and phase of the direct external drive. The parametric drive in Eq. (13), \(k_1G_2{\mathcal {A}}^*F_2e^{-i(\omega _{F_1}t+\varphi )}\), is averaged to zero. Hence, in this case, Eq. (13) is consistent with the complex amplitude equation that is obtained from the averaging method for the following phenomenological model

    $$\begin{aligned}&\ddot{q}_1+2(\varGamma _{1\mathrm eff}\dot{q}_1+\alpha _2\varGamma _2q_1^2)\dot{q}_1+{\tilde{\omega }}_1^2q_1\nonumber \\&\quad +{\tilde{\gamma }} q_1^3={\tilde{F}} \cos (\omega _{F_1}t+\chi ), \end{aligned}$$
    (15)

    where the square of the shifted eigenfrequency is given by \({\tilde{\omega }}_1^2=\omega _1^2-\alpha _{1}(\omega _2^2-\omega _1^2)\), the modified Duffing parameter is given by \({\tilde{\gamma }}=\gamma -(2\alpha _{2}/3)[( 3\omega _2^2-20\omega ^{2}_1)/4+8\omega _{1}^2(\varGamma _2^2+\omega _1^2)/\omega _2^2 ]\), the modified amplitude and phase of the direct drive in Eq. (15) are given by \({\tilde{F}}=[F_1^2+2k_1G_1F_1F_2\cos (\theta +\varphi )+k_1^2G_1^2F_2^2]^{1/2}\) and \(\tan \chi =(F_1\sin \theta -k_1G_1F_2\sin \varphi )/(F_1\cos \theta +k_1G_1F_2\cos \varphi )\).

  • Case II: where \(\omega _{F_2}=2\omega _{F_1}\), and the direct external drive \(F_1e^{i\theta }\) remains unmodified because the term \(k_1G_1F_2e^{i(\omega _{F_1}t-\varphi )}\) is averaged to zero; however, there is an additional parametric drive term \(k_1G_2{\mathcal {A}}^*F_2e^{-i\varphi }\) that can lead to non-trivial dynamical outcomes. In this case, Eq. (13) is consistent with the complex amplitude equation that is obtained from the averaging method for the following phenomenological model

    $$\begin{aligned}&\ddot{q}_1+2(\varGamma _{1\mathrm eff}\dot{q}_1+\alpha _2\varGamma _2q_1^2)\dot{q}_1\nonumber \\&\quad +[{\tilde{\omega }}_1^2-k_{1}G_2F_2\cos (\omega _{F_2}t-\varphi )]q_1\nonumber \\&\quad +{\tilde{\gamma }} q_1^3=F_1\cos (\omega _{F_1}t+\theta ). \end{aligned}$$
    (16)

These two cases are considered in detail in the following subsections.

3.2 The case of \(\omega _{F_2}=\omega _{F_1}\)

While the modified linear (\({\tilde{\omega }}_1, \varGamma _{1\mathrm eff}\)) and nonlinear (\(\alpha _2\varGamma _2,{\tilde{\gamma }}\)) characteristics of the primary resonator have been discussed in Ref. [34], the variation of the drive amplitude \({\tilde{F}}\) and phase \(\chi \) are new phenomena that deserve further attention. We focus here on the dynamical systems, where in addition to the large difference in the relaxation times \(\varGamma _2/\varGamma _1\gg 1\), there is a large difference in resonators eigenfrequencies \(\omega _2/\omega _1\gg 1\). These conditions occur frequently in the nonlinear interactions between MEMS (primary) resonators and NEMS (secondary) resonators [38,39,40].

Fig. 2
figure 2

Variation of the direct drive normalized amplitude (\({\tilde{F}}/F_1\)) and phase (\(\chi \)) of the primary resonator as a function of the linear coupling to the secondary resonator \((G_1)\) for \(\varGamma _2/\varGamma _1=F_{2}/F_{1}=10^3, \theta =0\), and different frequency ratios: \(\omega _{2}/\omega _1=10\) (magenta), \(\omega _{2}/\omega _1=20\) (blue), \(\omega _{2}/\omega _1=30\) (green), \(\omega _{2}/\omega _1=40\) (red), and \(\omega _{2}/\omega _1\rightarrow \infty \) (dashed black), which is equivalent to the case of no linear coupling (\(G_1=0\)). Left panel: The normalized drive amplitude increases significantly as the frequency ratio decreases. Right panel: The phase of the direct drive undergoes an insignificant variation as long as the eigenfrequency of the secondary resonator is an order of magnitude higher than the eigenfrequency of the primary resonator

Full size image

From Fig. 2, we see that for a finite frequency ratio \(\omega _2/\omega _1\), there is a major enhancement of the drive amplitude due to the coupling with the secondary resonator (e.g., \({\tilde{F}}\approx 50F\) for \(\omega _{2}/\omega _1=10\) and \(G_1=4.9\)), and a minor variation of the phase (e.g., \(\chi \approx -0.02\) for \(\omega _{2}/\omega _1=10\) and \(G_1=4.9\)). These results suggest that we can use the linear coupling of the resonators \(G_1\) to amplify the response of the primary resonator.

To further understand how the interaction with the secondary resonator changes the forced response of the primary resonator, we write the complex amplitude in polar representation \({\mathcal {A}}=ae^{i\phi }/2\) and consider the evolution of the amplitude a and phase \(\phi \)

$$\begin{aligned} \dot{a}&=-\left( \varGamma _{1\mathrm eff}+ \frac{\alpha _2\varGamma _2a^{2}}{4}\right) a\nonumber \\&+\frac{{\tilde{F}}}{2\omega _1}\sin (\chi -\phi ), \end{aligned}$$
(17)
$$\begin{aligned} {\dot{\phi }}&=-\delta {\tilde{\omega }}_1+\frac{3{\tilde{\gamma }} a^2}{8\omega _1}\nonumber \\&-\frac{{\tilde{F}}}{2\omega _1a}\cos (\chi -\phi ), \end{aligned}$$
(18)

where \(\delta {\tilde{\omega }}_1=\omega _{F_1}-{\tilde{\omega }}_1\). For the steady-state response we set \(\dot{a}={\dot{\phi }}=0\), and obtain from Eqs. (17) and (18) the following well-known response curve of a forced Duffing resonator with nonlinear damping [41]

$$\begin{aligned}&a^2\left[ \left( \delta {\tilde{\omega }}_1-\frac{3{\tilde{\gamma }} a^2}{8\omega _1}\right) ^2+\left( \varGamma _{1\mathrm eff}\right. \right. \nonumber \\&\quad \left. \left. +\frac{\alpha _2\varGamma _2a^{2}}{4}\right) ^{2} \right] =\left( \frac{{\tilde{F}}}{2\omega _1} \right) ^2. \end{aligned}$$
(19)

A standard stability analysis of this nonlinear response indicates the expected results for a forced Duffing resonator, with upper and lower stable branches of the response that are connected by the middle unstable branch of the response [35].

To illustrate the amplification of the primary resonator response due to the linear coupling of the resonators \(G_1\), we use the following set of system parameters: \(\omega _1=1,\omega _2=10, \varGamma _1=10^{-3},\varGamma _2=1,F_1=10^{-3},F_2=1,G_1=4, G_2=0,\gamma =0.01\), which yields almost a threefold increase in the linear decay rate \(\varGamma _{1\mathrm eff}/\varGamma _1=2.63\), an 8% downward shift of the eigenfrequency \(\varDelta \omega _1/\omega _1=0.08\), and a forty times stronger driving force \({\tilde{F}}/F=41\). The numerically validated modified response curve is shown in Fig. 3 along with the response of the non-interacting primary resonator \((G=0)\). It is clear that the response is greatly enhanced due to the interaction with the secondary resonator. Specifically, the maximal amplitude of the response curve, \(a_{\mathrm{max}}\), which satisfy the backbone curve equation \(\omega _{\mathrm{max}}={\tilde{\omega }}_1+3\gamma a_{\mathrm{max}}^2/(8\omega _1)\), is given by \(a_{\mathrm{max}}={\tilde{F}}/(2\omega _1\varGamma _{1\mathrm eff})\). Therefore, the maximal amplitude is increased by more than an order of magnitude, and the ratio between the maximal amplitude with and without coupling is given by \(a_{\mathrm{max}}/(a_{\mathrm{max}}|_{G=0})=\varGamma _1{\tilde{F}}/(\varGamma _{1\mathrm eff}F )=15.59\). Moreover, due to the variations in the eigenfrequency \({\tilde{\omega }}_1\) and in the maximal amplitude \(a_{\mathrm{max}}\), the frequency of the maximal amplitude also increases by \(14.34\%\), and is explicitly given by \(\omega _{\mathrm{max}}={\tilde{\omega }}_1+3\gamma {\tilde{F}}^2/(32\omega _1^3\varGamma _{1\mathrm eff}^2)\).

Fig. 3
figure 3

Amplitude response curve of the primary resonator for the case of \(\omega _{F_2}=\omega _{F_1}\). The red/blue curves are the responses that are obtained by analytically solving Eq. (19) with/without coupling to the secondary resonator, respectively. The solid/dashed curves indicate stable/unstable branches of the responses. The black squares and gray dots indicate the sweep-up (increasing \(\omega _{F_1}\)) and sweep-down (decreasing \(\omega _{F_1}\)) values, respectively, of the numerically calculated amplitude of the primary resonator, which are obtained by performing numerical time integration of the original dynamical system, Eqs. (2) and (3)

Full size image

3.3 The case of \(\omega _{F_2}=2\omega _{F_1}\)

In this case, we have a combined parametric and directly driven Duffing resonator with nonlinear damping, and the polar evolution equations are given by

$$\begin{aligned} \dot{a}&=-\left( \varGamma _{1\mathrm eff}+ \frac{\alpha _2\varGamma _2a^{2}}{4}\right) a-\frac{ F_1}{2\omega _1}\sin (\phi -\theta )\nonumber \\&-\frac{k_1G_2F_2}{4\omega _1}a\sin (2\phi +\varphi ), \end{aligned}$$
(20)
$$\begin{aligned} {\dot{\phi }}&=-\delta {\tilde{\omega }}_1+\frac{3{\tilde{\gamma }} a^2}{8\omega _1}-\frac{F_1}{2\omega _1a}\cos (\phi -\theta )\nonumber \\&-\frac{k_1G_2F_2}{4\omega _1}\cos (2\phi +\varphi ). \end{aligned}$$
(21)
Fig. 4
figure 4

Amplitude response curve of the primary resonator for the case of \(\omega _{F_2}=2\omega _{F_1}\). The red/blue curves are the response curves obtained by analytically solving Eqs. (22) and (23) with/without coupling to the secondary resonator, respectively. The solid/dashed curves indicate stable/unstable branches of the responses. The black squares and gray dots indicate the sweep-up (increasing \(\omega _{F_1}\)) and sweep-down (decreasing \(\omega _{F_1}\)) values, respectively, of the numerically calculated amplitude of the primary resonator, which are obtained by performing numerical time integration of the original dynamical system, Eqs. (2)-(3)

Full size image

For the steady-state response, we set \(\dot{a}={\dot{\phi }}=0\), and obtain from Eqs. (20)-(21) the following equation of response curve

$$\begin{aligned}&a^2\left[ \left( \delta {\tilde{\omega }}_1-\frac{3{\tilde{\gamma }} a^2}{8\omega _1}\right) ^2+\left( \varGamma _{1\mathrm eff}+ \frac{\alpha _2\varGamma _2a^{2}}{4}\right) ^{2} \right] \nonumber \\&\quad =\frac{4F_1^2+4ak_1G_2F_1F_2\cos (\theta +\varphi +\phi )+a^2k_1^2G_2^2F_2^2}{16\omega _1^{2}},\nonumber \\ \end{aligned}$$
(22)

and the following auxiliary equation for the phase \(\phi \)

$$\begin{aligned}&\frac{ak_1G_2F_2\cos (2\phi +\varphi )+2F_1\cos (\phi -\theta )}{ak_1G_2F_2\sin (2\phi +\varphi )+2F_1\sin (\phi -\theta )}\nonumber \\&\quad =\frac{8\omega _1\delta {\tilde{\omega }}_{1}-3{\tilde{\gamma }} a^2}{8\omega _1\varGamma _{1\mathrm eff}+2\omega _1\alpha _2\varGamma _2a^{2}}. \end{aligned}$$
(23)

As recently shown in Ref. [20], Eqs. (22) and (23) can generate intricate amplitude response curves that differ drastically from the standard directly driven Duffing resonator and include isolas, dual peaks, loops, and flat resonant peaks. However, we are interested here in a relatively simple response curve, which is amplified by the induced parametric excitation from the secondary resonator. To this end, we set \(\theta =-\pi /4\) [20] and use the following set of system parameters: \(\omega _1=1,\omega _2=10, \varGamma _1=10^{-3},\varGamma _2=1,F_1=10^{-3},F_2=1,G_1=0, G_2=5,\gamma =0.13\), which yields a drastic reduction in the Duffing nonlinearity \({\tilde{\gamma }}/\gamma =2.57\times 10^{-2}\) (97.43%), a cubic nonlinear damping with a coefficient of \(\alpha _2\varGamma _{2}=2.7\times 10^{-3}\), and a parametric drive level of \(k_1G_2F_2=0.05\). The numerically validated modified response curve is shown in Fig. 4 along with the response of the non-interacting primary resonator \((G=0)\). Note that for \(G\ne 0\) the response curve is significantly more intricate, where there are both an isola (due to symmetry-breaking) and Duffing bistability. Therefore, the response curve exhibits four saddle-node bifurcations and frequency regions with three stable branches [20]. Moreover, it is clear that the response of the primary resonator is amplified significantly due to the interaction with the secondary resonator. In particular, the maximal amplitude of the response curve, \(a_{\mathrm{max}}\), is increased by almost an order of magnitude, where \(a_{\mathrm{max}}/(a_{\mathrm{max}}|_{G=0})=8.41\), and its frequency \(\omega _{\mathrm{max}}\) is barely changed by the interaction with secondary resonator (less than 1% variation).

4 Closing remarks

We analyzed the nonlinear interaction of mutually coupled driven resonators with significantly different decay rates. We considered a resonantly driven slowly decaying nonlinear (primary) resonator, which is nonlinearly coupled to a non-resonantly driven relatively fast decaying linear (secondary) resonator. We showed that when the drive frequency of the secondary resonator is close to either the eigenfrequency or twice the eigenfrequency of the primary resonator, the interaction between the resonators can be exploited to mechanically amplify the response of the primary resonator. In particular, the linear coupling between the resonators can be used to enhance the direct drive of the primary resonator when the drive frequency of the secondary resonator is close to the eigenfrequency of the primary resonator, and the quadratic coupling between the resonators can be used to parametrically pump the response of the primary resonator when the drive frequency of the secondary resonator is close to twice the eigenfrequency of the primary resonator.

We proposed a relatively simple amplification technique that can be analyzed theoretically in closed-form due to the large difference in the relaxation times of the resonators. Such systems of coupled resonators with large difference in their relaxation times are frequently encountered in coupling between MEMS (primary) and NEMS (secondary) resonators [38,39,40]. This amplification technique came from a straightforward generalization of a previous study on a similar undriven system [34], where it was shown that the linear and nonlinear characteristics of the primary resonator can be altered in a significant manner. Taken together the finding of the earlier analysis [34] and the current study, we conclude that such a driven dynamical system can be used to tailor a desired response curve of the primary resonator with prescribed linear and nonlinear characteristics, and a specified amplification.

In future studies, we plan to develop methods for designing and tuning the coupling between the resonators in a mechanical manner. Mechanical realization of the coupling between the resonators can help to reduce the noise in the system by avoiding the use of inherently noisy electrical circuitry. To this end, we will use tools of structural optimization such as those described in Ref. [42], which will guide us in adjusting the coupling terms in our reduced-order models of the resonators.