Tuning linear and nonlinear characteristics of a resonator via nonlinear interaction with a secondary resonator

Abstract

We conside the dynamics of a nonlinear resonator that is nonlinearly coupled to a linear resonator that has a relatively short decay time. In this case, the secondary (linear) resonator adiabatically tracks the primary (nonlinear) resonator. This model, which is motivated by ongoing experimental work in nano-resonators, is analyzed analytically and numerically to show that the linear and nonlinear characteristics of the primary resonator can be altered in a significant manner by the coupling to the secondary resonator. Such an arrangement may provide a practical means of tuning resonator characteristics in applications.

1 Introduction

Nano- and micro-electromechanical systems (N/MEMS) resonators are widely used in a variety of applications that include inertial sensing, signal processing, switching, and timing [1,2,3,4]. These devices possess inherent compatibility with semiconductor technology, the ability to fulfill miniaturization requirements, and offer some improved performance metrics when compared to their purely electrical analogs [5,6,7,8].

As the size of N/MEMS resonators is reduced, their vibrations become nonlinear already for small amplitudes [9]. Nonlinear stiffness effects in N/MEMS resonators commonly arise from multiple sources, such as finite deformations that lead to nonlinear strain–displacement relationships [10,11,12] and the nonlinear nature of the electrostatic forces in capacitive N/MEMS [13,14,15]. Nonlinear damping in N/MEMS resonators can be derived from a microscopic model, which account for nonlinear coupling between the resonator and a thermal bath [16, 17], or from a macroscopic model, which accounts for material viscoelasticity and geometric nonlinearities [18].

While the linear stiffness and linear damping, which are associated with the natural frequency and the nominal quality factor (or decay time), respectively, are of obvious interest for any resonant N/MEMS application, the nonlinear stiffness and nonlinear damping can also influence significantly the device figures of merits. Examples include the degradation of frequency precision due to amplitude modulation (AM) to phase modulation (PM) conversion that arises from Duffing nonlinearity [19, 20], and the degradation of nanotube and graphene nano-resonators quality factors due to nonlinear van der Pol-type damping [21].

Numerous studies considered different methods of tuning the linear and nonlinear characteristics of N/MEMS resonators. DeMartini et al. [22] experimentally demonstrated a means to tune linear and nonlinear characteristics of parametrically excited MEMS resonators by adjusting the drive DC and AC excitation voltages, and the configurations of their non-interdigitated capacitive comb fingers. Saghafi et al. [23] conducted a theoretical and numerical study of a bilayer microbeam and considered ways to tune the magnitude of intrinsic nonlinear effects and the beam dynamic range by varying the beam geometry. Li et al. [24] experimentally demonstrated a systematic control of the Duffing nonlinearity in MEMS resonators using shape optimization techniques.

Several experimental observations [25,26,27] have shown that when N/MEMS resonators are operated in 1:3 internal resonance conditions, the low-frequency vibrational mode can experience: (i) a significant frequency stabilization [25] (which implies that the effects of the Duffing nonlinearity are considerably reduced), (ii) an increase in the decay rate due to mode hybridization [26], and (iii) amplitude dwell in which the fast-frequency vibrational mode compensates for the low-frequency vibrational mode losses and practically eliminates its decay for a finite time [27]. In a recent study [28], the authors theoretically analyzed the 1:3 internal resonance of nanomechanical modes and showed that it can lead to a variety of anomalous decay behaviors, where both increase (as observed by [26]) and decrease (as observed by [27]) in the decay rate of the low-frequency mode can be obtained. Moreover, it was shown that the coupling between the two modes can result in an increase in the effective linear damping of the low-frequency mode for sufficiently large amplitude, even when the system is far from internal resonance [28]. In this work, we further theoretically explore such interactions and show that they can be used to tune the linear and nonlinear characteristics of a primary resonator when it is coupled to a relatively fast-decaying secondary resonator. The results developed here are related to the seminal work on a classical oscillators coupled to a bath of linear oscillators [29, 30]. Furthermore, the results of the current analysis can be viewed as a special case, with important potential applications (e.g., manipulation of MEMS resonator characteristics), of the more general analyses of [16, 31].

The paper is organized as follows: In Sect. 2, we formulate the problem and show that the motion of the relatively fast-decaying secondary resonator can be eliminated from the governing equation under the adiabatic approximation. In Sect. 3, we conduct an asymptotic analysis and obtain the main results of the paper, consisting of closed-form expressions for the modified linear and nonlinear characteristics of the primary resonator. In Sect. 4, we numerically validate our analytical predictions. In Sect. 5, we summarize our main findings and discuss their implications. We also include an appendix which briefly describes the microscopic theory of a resonator that interacts with a medium [16, 19, 32], since it provided the theoretical inspiration for the current work.

2 Problem formulation

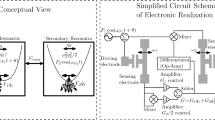
We consider a system with two resonators that are mutually coupled. Figure 1 depicts a conceptual view of such a system with a simplified circuit schematic for the electronic realization of the coupling between the resonators. This realization, via electronic coupling, is chosen for the sake of clarity due to its simplicity; however, one can consider other types of coupling between the resonators, such as mechanical [33] and optical [34].

Fig. 1

Conceptual view and simplified circuit schematic of an electronic realization. Left panel: conceptually, the two resonators mutually and nonlinearly coupled via an interaction potential, $-q_2G(q_1)$. The primary resonator $(q_1)$ has a nonlinear conservative restoring force, $-U'(q_1)$, and weak linear dissipation, $-\varGamma _1\dot{q}_1$. The bath resonator has a linear conservative restoring force, $-\omega _2^2q_2$, and a relatively strong linear dissipation, $-\varGamma _2\dot{q}_2$. Right panel: For micro-mechanical systems, the motion of each resonator is detected using a parallel-plate capacitive sensing technique. The signal from the primary resonator is fed into a mixer, amplifiers (for control of different coefficients of G), and an adder to form the function $G(q_1)$. The signal $G(q_1)$ is then fed into the driving electrode of the bath resonator, and to a differentiator and a mixer, which multiplies the signal $G'(q_1)$ with $q_2$, and finally, the mixed signal $q_2G'(q_1)$ is being fed into the driving electrode of the primary resonator

We assume that the primary resonator (with coordinate $q_1$) can experience a large amplitude oscillation around its stable equilibrium, $q_1=0$, and its potential $U(q_1)$, provides a nonlinear restoring force. The secondary resonator (with coordinate $q_2$) is linear and oscillates with small amplitude around its stable equilibrium, $q_2=0$. To be consistent with the above assumptions, we model the interaction potential of the two resonators as $U_\mathrm{inter}=-q_2G(q_1)$. Thus, the Hamiltonian of the system is given by

$$\begin{aligned} \mathcal {H}=p_1^2/2+U(q_1)+p_2^2/2+\omega _2^2q_2^{2}/{2} -q_2G(q_1). \end{aligned}$$

(1)

The equations of motion of the resonators with the inclusion of linear damping are formally given by $\ddot{q}_k=\dot{p}_k=-2\varGamma _k\dot{q}_k-\partial \mathcal {H}/\partial q_k$ and can be explicitly written as

$$\begin{aligned} \ddot{q}_1&=-2\varGamma _1\dot{q}_1-U'(q_1)+q_2G'(q_1), \end{aligned}$$

(2)

$$\begin{aligned} \ddot{q}_2&=-2\varGamma _2\dot{q}_2-\omega _2^{2}q_2+G(q_1), \end{aligned}$$

(3)

where the overdot denotes a time derivative, the prime symbol differentiation of a function with respect to its single variable, and $-2\varGamma _k\dot{q}_k$ models the linear friction force experienced by resonator k with $k=1,2$. Furthermore, we assume that both resonators are lightly damped ($\varGamma _k/\omega _k\ll 1$) and that the decay times satisfy $\varGamma _2/\varGamma _1\gg 1$ so that the secondary resonator will adiabatically track the primary resonator [28].

We formally solve Eq. (3) in terms of its Green’s function, i.e.,

$$\begin{aligned} q_2(t)&=\mathrm{e}^{-\varGamma _2t}\left[ q_2(0)\cos (\omega _{2d}t)+\frac{p_2(0)}{\omega _{2d}}\sin (\omega _{2d}t)\right] \nonumber \\&\quad +\frac{1}{\omega _{2d}}\int _0^tG(q_1(\tau ))\mathrm{e}^{-\varGamma _2(t-\tau )}\sin (\omega _{2d}(t-\tau ))\mathrm{d}\tau , \end{aligned}$$

(4)

where, due to the low level of damping in the system ($\varGamma _k/\omega _k\ll 1$), we approximate the secondary resonator damped eigenfrequency $\omega _{2d}$ by its undamped eigenfrequency $\omega _2$, i.e., $\omega _{2d}=\omega _2\sqrt{1-(\varGamma _2/\omega _2)^2}\approx \omega _2$. Upon inserting Eq. (4) into Eq. (2), we find that

$$\begin{aligned} \ddot{q}_1=-2\varGamma _1\dot{q}_1-U'(q_1)+G'(q_1)(L[q_1]+F), \end{aligned}$$

(5)

where

$$\begin{aligned} L[q_1]=&\frac{1}{\omega _{2}}\int _0^tG(q_1(\tau ))\mathrm{e}^{-\varGamma _2(t-\tau )}\sin (\omega _{2}(t-\tau ))\mathrm{d}\tau , \end{aligned}$$

(6)

$$\begin{aligned} F(t)=&\mathrm{e}^{-\varGamma _2t}\left[ q_2(0)\cos (\omega _{2}t)+\frac{p_2(0)}{\omega _{2}}\sin (\omega _{2}t)\right] . \end{aligned}$$

(7)

The functional $L[q_1]$ describes the retarded reaction of the secondary resonator on the primary resonator, and F(t) describes the response of the primary resonator to the initial state of the secondary resonator.

3 Asymptotic analysis

For weakly nonlinear interaction between the resonators, we can use the method of averaging [35, 36], i.e., we assume that $q_1(t)=\mathcal {A}(t)\mathrm{e}^{i\omega _1t}+\mathcal {A}^{*}(t)\mathrm{e}^{-i\omega _1t}$ and $\dot{q}_1(t)=i\omega _1[\mathcal {A}(t)\mathrm{e}^{i\omega _1t}-\mathcal {A}^{*}(t)\mathrm{e}^{-i\omega _1t}]$, where $\mathcal {A}^{*}$ is the complex conjugate of $\mathcal {A}$, and the complex amplitude $\mathcal {A}(t)$ remains almost constant over the period $T=2\pi /\omega _1$ of the linearized resonator, $\omega _1^2=U''(0)$. Thus, $G(q_1(t))$ can be replaced by its Fourier series $G(q_1(t))=\sum _nc_n(\mathcal {A}(t),\mathcal {A}^{*}(t))\mathrm{e}^{in\omega _1t}$, where $c_{-n}=c_{n}^*$. Consequently, the functional $L[q_1]$ can be rewritten as

$$\begin{aligned} L[q_1]=\int _0^t\sum _{n}\frac{c_n(\tau )}{2i\omega _{2}}[\mathrm{e}^{-\varGamma _2(t-\tau )+i[n\omega _1\tau +\omega _{2}(t-\tau )]} -\mathrm{e}^{-\varGamma _2(t-\tau )+i[n\omega _1\tau -\omega _{2}(t-\tau )]}]\mathrm{d}\tau . \end{aligned}$$

(8)

Since $c_n(t)$ are functions of $\mathcal {A}(t)$ and $\mathcal {A}^*(t)$, they also vary slowly in time. Thus, to the leading order we can approximate Eq. (8) as follows:

$$\begin{aligned} L[q_1]\approx&\sum _{n}\frac{c_n(t)}{2i\omega _{2}}\int _0^t[\mathrm{e}^{-\varGamma _2(t-\tau )+i[n\omega _1\tau +\omega _{2}(t-\tau )]} -\mathrm{e}^{-\varGamma _2(t-\tau )+i[n\omega _1\tau -\omega _{2}(t-\tau )]}]\mathrm{d}\tau \nonumber \\ =&\sum _{n}\frac{c_n(t)}{2\omega _{2}}\mathrm{e}^{in\omega _1t} \left[ \frac{1-\mathrm{e}^{-[\varGamma _2+i(n\omega _1-\omega _{2})]t}}{-(n\omega _1-\omega _{2})+i\varGamma _2}+\frac{1-\mathrm{e}^{-[\varGamma _2+i(n\omega _1+\omega _{2})]t}}{(n\omega _1+\omega _{2})-i\varGamma _2}\right] . \end{aligned}$$

(9)

For times that are larger than the relaxation time of the secondary resonator, $t\gg \varGamma _2^{-1}$, the functional $L[q_1]$ is further simplified and yields

$$\begin{aligned} L[q_1]\approx \sum _n\frac{\omega _2^2-n^2\omega _1^2-2in\omega _1\varGamma _2}{(\omega _2^2-n^2\omega _1^2)^2+(2n\omega _1\varGamma _2)^2}c_n(t)\mathrm{e}^{in\omega _1t}. \end{aligned}$$

(10)

Hence, for $t\gg \varGamma _2^{-1}$, the equation of motion of the primary resonator, Eq. (5), reduces to

$$\begin{aligned} \ddot{q}_1+U'(q_1)&=-2\varGamma _1\dot{q}_1+G'(q_1)\nonumber \\&\quad \sum _n\frac{\omega _2^2-n^2\omega _1^2-2in\omega _1\varGamma _2}{(\omega _2^2-n^2\omega _1^2)^2+(2n\omega _1\varGamma _2)^2}c_n(t)\mathrm{e}^{in\omega _1t}. \end{aligned}$$

(11)

This approximation applies even for resonant situations, where $\omega _2$ is close to a multiple of $\omega _1$.

In what follows, we focus only on times that are larger than the relaxation time of the secondary resonator, $t\gg \varGamma _2^{-1}$, where the secondary resonator is adiabatically tracking the primary resonator and acts as a thermal reservoir. In fact, we have also assumed here that the functions $c_n(t)$ vary slowly over the time $\varGamma _2^{-1}$. This is a restriction on the nonlinearity and the decay rate of the primary resonator.

For the weak coupling that we consider, the only terms to keep in the sum over n in Eq. (11) are the resonant terms, which oscillate, with the slowly varying amplitude and phase, at the same frequency as $q_1(t)$. For $G' =$ constant, these are terms with $n=\pm 1$, whereas if we take into account the term $\propto q_1$ in $G'(q_1)$, we have to keep the resonant terms with $n=\pm 2$ and $n=0$. This is used in the calculation in the next section.

Fig. 2

Variation in the normalized linear damping ($\varGamma _\mathrm{eff}/\varGamma _1$) and frequency ($\tilde{\omega }_1/\omega _1$) parameters of the primary resonator as a function of the normalized eigenfrequency of the secondary resonator $(\omega _2/\omega _1)$ for $\varGamma _2/\varGamma _1=10^3$ and different levels of the linear coupling strength: $G_1=0.2$ (black), $G_1=0.4$ (purple), $G_1=0.6$ (blue), $G_1=0.8$ (green), and $G_1=1$ (red). Left panel: The effective linear damping reaches its maximum value when the two resonators interact resonantly at $\omega _2/\omega _1=1$ (indicated by the vertical dashed line). Right panel: The primary resonator shifted eigenfrequency increases for $\omega _2<\omega _1$ and decreases for $\omega _2>\omega _1$. We emphasize that the theory applies for weak coupling of the resonators, which means that we only study the regime where $|\tilde{\omega }_1 - \omega _1|\ll \omega _1$. (Color figure online)

3.1 Essential leading-order nonlinear terms

Restricting our attention to the essential leading-order nonlinear terms, we take $U(q_1)=\omega _1^2q_1^2/2+\gamma q_1^4/4$; the non-secular term $\beta q_1^3/3$ renormalizes $\gamma$, to the second order in $\beta$, which we assume to have been taken into account. Furthermore, we assume that $G(q_1)$ can be similarly represented, $G(q_1)=G_{1}q_1+G_2q_1^2/2+O(q_1^3)$, where $G_1\equiv G'(0)$ and $G_2\equiv G''(0)$. Consequently, we obtain the following approximated equation for the complex amplitude of the primary resonator

$$\begin{aligned} \mathcal {\dot{A}}=&- \varGamma _1\mathcal {A}\left( 1+\alpha _1\frac{\varGamma _2}{\varGamma _1}+\alpha _2\frac{\varGamma _2}{\varGamma _1}|\mathcal {A}|^2\right) \nonumber \\&-i\mathcal {A}\left\{ \alpha _1\left( \frac{\omega _2^2-\omega _1^2}{2\omega _1}\right) +\left[ \alpha _2\left( \frac{3\omega _2^2-20\omega _1^2}{4\omega _1}\right. \right. \right. \nonumber \\&\left. \left. \left. +\frac{8\omega _{1}}{\omega _2^2}(\varGamma _2^2+\omega _1^2) \right) -\frac{3\gamma }{2\omega _1}\right] |\mathcal {A}|^2 \right\} , \end{aligned}$$

(12)

where the coupling to the secondary resonator is captured by the terms with coefficients

$$\begin{aligned}&\alpha _1=\frac{G_{1}^2}{(\omega _2^2-\omega _1^2)^2+(2\varGamma _2\omega _1)^2},\nonumber \\&\alpha _2=\frac{G_2^2}{(\omega _2^2-4\omega _1^2)^2+(4\varGamma _2\omega _1)^2}. \end{aligned}$$

(13)

From Eq. (12), we deduce that the interaction of the primary resonator with the secondary resonator modifies the linear and nonlinear terms in the equation of motion for the coordinate $q_1$ of the primary resonator. To be specific, we see that at the leading order, the interaction between the two resonators leads to the following changes in this equation: (i) an increase in the linear decay rate $\varGamma _{1\mathrm eff}=\varGamma _1+\alpha _{1}\varGamma _2$; (ii) the addition of new nonlinear cubic (van der Pol type) damping term $-\alpha _2\varGamma _2|\mathcal {A}|^2\mathcal {A}$; (iii) a shift in the eigenfrequency $\varDelta \omega _1=\alpha _{1}(\omega _2^2-\omega _1^2)/(2\omega _1)$; and (iv) a modification to the Duffing nonlinearity $-i\alpha _{2}\left[ (3\omega _2^2-20\omega _1^2)/(4\omega _1)+8\omega _{1}(\varGamma _2^2+\omega _1^2)/\omega _2^2 \right] |\mathcal {A}|^2\mathcal {A}$. Hence, Eq. (12) is consistent with the complex amplitude equation that one gets from the averaging method for the following phenomenological model

$$\begin{aligned} \ddot{q}_1+2(\varGamma _{1\mathrm eff}\dot{q}_1+\alpha _2\varGamma _2q_1^2)\dot{q}_1+\tilde{\omega }_1^2q_1+\tilde{\gamma } q_1^3=0,\qquad \end{aligned}$$

(14)

where the square of the shifted eigenfrequency is given by $\tilde{\omega }_1^2=\omega _1^2-\alpha _{1}(\omega _2^2-\omega _1^2)$, and the modified Duffing parameter is given by $\tilde{\gamma }=\gamma -\frac{2}{3}\alpha _{2}[( 3\omega _2^2-20\omega ^{2}_1)/4+8\omega _{1}^2(\varGamma _2^2+\omega _1^2)/\omega _2^2 ]$.

Fig. 3

Variation in the normalized nonlinear damping ($\omega _1\alpha _2\varGamma _{2}/\gamma$) and stiffness (i.e., Duffing, $\tilde{\gamma }/\gamma$) parameters of the primary resonator as a function of the normalized eigenfrequency of the secondary resonator $(\omega _2/\omega _1)$ for $\varGamma _2/\varGamma _1=10^3,~\gamma =1$ and different levels of the nonlinear coupling strength: $G_2=1$ (black), $G_2=2$ (purple), $G_2=3$ (blue), $G_2=4$ (green), and $G_2=5$ (red). Left panels: The van der Pol damping reaches its maximum value when the two resonators interact resonantly at $\omega _2/\omega _1=2$ (indicated by the vertical dashed line). Right panel: The modified Duffing parameter $\tilde{\gamma }$ can deviate dramatically from its nominal value $\gamma$ at relatively low frequencies of the secondary resonator and can even change sign. (Color figure online)

We note that the linear characteristics (i.e., the linear damping and eigenfrequency) are functions of the linear coupling strength $G_1$ and therefore can be tuned by variation of $G_1$ (Fig. 2). Due to the presence of a Lorentzian function $\alpha _1(\omega _2)$ in the effective linear damping $\varGamma _{1\mathrm eff}=\varGamma _1+\alpha _{1}\varGamma _2$, it reaches a maximum value when the eigenfrequencies of the isolated secondary and primary resonators are equal, $\omega _2=\omega _1$. This result is not surprising as it corresponds to a resonant interaction between the resonators, which only occurs when $\omega _2\approx \omega _1$ for linear coupling. Alternatively, this coupling-induced decay rate can be understood in terms of the standard Fermi golden rule [37]. It is quadratic in the linear coupling strength $G_1$ and is proportional to the “density of states” $1/[(\omega _2^2-\omega _1^2)^2+(2\varGamma _2\omega _1)^2]$ of the effective reservoir provided by the secondary resonator. The primary resonator shifted eigenfrequency $\tilde{\omega }_1$ increases for $\omega _2<\omega _1$ and decreases for $\omega _2>\omega _1$. This change in the shifted eigenfrequency $\tilde{\omega }_1$ can be related to a linear anti-crossing (eigenvalue veering) with a frequency splitting of the two eigenfrequencies of the linearly coupled ($G_1\ne 0,~G_2=0$) dynamical system [38].

Similarly, the nonlinear characteristics (i.e., the van der Pol damping and modified Duffing parameter) are functions of the nonlinear quadratic coupling strength $G_2$ and therefore can be tuned by variation of $G_2$ (Fig. 3). Due to the presence of a Lorentzian function $\alpha _2(\omega _2)$ in the van der Pol damping term $2\alpha _2\varGamma _2q_1^2\dot{q}$, it reaches a maximum value when the eigenfrequency of the secondary resonator is close to twice the eigenfrequency of the primary resonator, $\omega _2\approx 2\omega _1$. The result can be understood as a nonlinear resonant interaction between the resonators, which can only occur when $\omega _2\approx 2\omega _1$ for this type of quadratic coupling, provided $\varGamma _1\ll \omega _1$ and $\varGamma _2\ll \omega _2$. Alternatively, this can also be understood in terms of the Fermi golden rule, where $G_2$ is the “matrix element” of the interaction and $1/[(\omega _2^2-4\omega _1^2)^2+(4\varGamma _2\omega _1)^2]$ is the “density of states” of the effective reservoir provided by the secondary resonator at twice the eigenfrequency of the primary resonator. The modified Duffing parameter $\tilde{\gamma }$ can deviate dramatically from its nominal value $\gamma$ for a range of frequency ratios of the resonators $(\omega _2/\omega _1<5)$ and in the vicinity of the nonlinear resonance condition ($\omega _2=2\omega _1$). More importantly, it can also change sign, i.e., changing from hardening nonlinearity $(\tilde{\gamma }>0)$ to softening nonlinearity $(\tilde{\gamma }<0)$. This variation of $\tilde{\gamma }$ leads to a peculiar change in the effective vibration frequency $\omega _1^\mathrm{eff}\approx \tilde{\omega }_1+3\tilde{\gamma }|\mathcal {A}|^2/2\tilde{\omega }_1$, which is attributed to a nonlinear counterpart of frequency anti-crossing due to nonlinear resonance [28]. However, as we show in the following subsection, even for significantly higher frequencies (say, $\omega _2/\omega _1=10$), which are far from nonlinear resonance conditions, $\tilde{\gamma }$ can be twofold smaller than its nominal value $\gamma$.

3.2 Analytical solution of the complex amplitude equation

Equation (12) yields the following pair of evolution equations for the complex amplitude modulus and argument ($\mathcal {A}=|\mathcal {A}|\mathrm{e}^{i\phi }$)

$$\begin{aligned} \mathcal {|\dot{A}|}&=-|\mathcal {A}|(\varGamma _{1\mathrm eff}+\alpha _2\varGamma _2|\mathcal {A}|^2), \end{aligned}$$

(15)

$$\begin{aligned} \dot{\phi }&=-\varDelta \omega _1+\frac{3\tilde{\gamma }}{2\omega _1}|\mathcal {A}|^2. \end{aligned}$$

(16)

Equations (15)–(16) can be solved in closed form

$$\begin{aligned} |\mathcal {A}(t)|&=|\mathcal {A}(0)|\mathrm{e}^{-\varGamma _{1\mathrm eff}t}\nonumber \\&\quad \left[ 1+\frac{\alpha _2\varGamma _2}{\varGamma _{1\mathrm eff}}|\mathcal {A}(0)|^2(1-\mathrm{e}^{-2\varGamma _{1\mathrm eff}t})\right] ^{-1/2}, \end{aligned}$$

(17)

$$\begin{aligned} \phi (t)&=\phi (0)-\varDelta \omega _1t+\frac{3\tilde{\gamma }}{4\omega _1\alpha _2\varGamma _2}\ln \nonumber \\&\quad \left[ 1+\frac{\alpha _2\varGamma _2}{\varGamma _{1\mathrm eff}}|\mathcal {A}(0)|^2(1-\mathrm{e}^{-2\varGamma _{1\mathrm eff}t})\right] . \end{aligned}$$

(18)

From the closed-form solution of the amplitude (modulus), Eq. (17), we can deduce the following: due to the presence of the van der Pol damping ($-\alpha _2\varGamma _2|\mathcal {A}|^2\mathcal {A}$), which arises from the nonlinear interaction $(G_2,\alpha _2)$ between $q_1$ and $q_2$, we see that if $\alpha _2\varGamma _2|\mathcal A(0)|^2/\varGamma _{1\mathrm eff}\sim O(1)$ or bigger, then the amplitude of the primary resonator $(2|\mathcal A(t)|)$ will decay in a non-exponential manner (faster than exponential), and the decay will become exponential only for large time, where $t\gg \varGamma _{1\mathrm eff}^{-1}$. These asymptotic non-exponential and exponential decays of the amplitude are given by

$$\begin{aligned} |\mathcal {A}(t)|=&|\mathcal {A}(0)|\left[ 1+2\alpha _2\varGamma _2|\mathcal {A}(0)|^2t\right] ^{-1/2}~~~\mathrm{for}~~\varGamma _{1 \mathrm{eff}}t \ll 1, \end{aligned}$$

(19)

$$\begin{aligned} |\mathcal {A}(t)|=&\sqrt{\frac{\varGamma _{1\mathrm eff}|\mathcal {A}(0)|^2}{\varGamma _{1\mathrm eff}+\alpha _2\varGamma _2|\mathcal {A}(0)|^2}}\mathrm{e}^{-\varGamma _{1\mathrm eff}t}~~~~~\mathrm{for}~~\varGamma _{1 \mathrm{eff}}t \gg 1. \end{aligned}$$

(20)

Similarly, from the closed-form solution of the phase (argument), Eq. (18), we deduce the following: For $\tilde{\gamma }/\gamma \ne 1$ and $3(\tilde{\gamma }-\gamma )/(4\omega _1\alpha _2\varGamma _2)\sim O(1)$ or bigger, the phase dynamics is highly affected by the nonlinear interaction $(G_2,\alpha _2)$ between $q_1$ and $q_2$, and for large time, where $t\gg \varGamma _{1\mathrm eff}^{-1}$, there is only a linear shift of the eigenfrequency due to the linear interaction of the resonators $(G_1,\alpha _1)$. These asymptotic behaviors of the phase are given by

$$\begin{aligned} \phi (t)&=\phi (0)+\frac{3\tilde{\gamma }}{4\omega _1\alpha _2\varGamma _2}\ln \nonumber \\&\quad \left[ 1+\frac{\alpha _2\varGamma _2}{\varGamma _{1\mathrm eff}}|\mathcal {A}(0)|^2(1-\mathrm{e}^{-2\varGamma _{1\mathrm eff}t})\right] ~\mathrm{for}~\varGamma _{1 \mathrm{eff}}t \ll 1, \end{aligned}$$

(21)

$$\begin{aligned} \phi (t)&=\phi (0)+\frac{3\tilde{\gamma }}{4\omega _1\alpha _2\varGamma _2}\ln \nonumber \\&\quad \left[ 1+\frac{\alpha _2\varGamma _2}{\varGamma _{1\mathrm eff}}|\mathcal {A}(0)|^2\right] -\varDelta \omega _1t~~~~~~~~~\mathrm{for}~\varGamma _{1 \mathrm{eff}}t \gg 1 \end{aligned}$$

(22)

In the remainder of this paper, we use a fixed set of system parameters: $\omega _1=1,~\omega _2=10,~\varGamma _1=10^{-3},~\varGamma _2=1,~G_1=4,G_2=5,~\gamma =1$, to illustrate the linear and nonlinear characteristics of the primary resonator. Figure 4 depicts the amplitude and phase dynamics of the primary resonator for the initial conditions $\mathcal A(0)=10i$. Due to the linear interaction of the resonators $(G_1,\alpha _1)$, there is almost a threefold increase in the linear decay rate $\varGamma _{1\mathrm eff}/\varGamma _1=2.63$, and the eigenfrequency is shifted downward by 8%, $\varDelta \omega _1/\omega _1=0.08$. The nonlinear interaction of the resonators $(G_2,\alpha _2)$ is responsible for the van der Pol nonlinear damping term with a coefficient of $\alpha _2\varGamma _2=2.7\times 10^{-3}$, which significantly changes the amplitude dynamics and leads to a non-exponential decay, and for a twofold decrease in the Duffing parameter $\tilde{\gamma }/\gamma =0.49$. The asymptotic behaviors of Eqs. (19)–(22) clearly govern the amplitude and phase dynamics at small and large times.

Fig. 4

Analytical estimations of the amplitude and phase dynamics of the primary resonator. Left panel: amplitude dynamics according to the closed-form solution (black curve) Eq. (17) and its asymptotic behaviors for $t\rightarrow 0$ (blue curve), i.e., $|\mathcal {A}(0)|\left[ 1+2\alpha _2\varGamma _2|\mathcal {A}(0)|^2t\right] ^{-1/2}$, and $t\rightarrow \infty$ (red curve), i.e., $\sqrt{\frac{\varGamma _{1\mathrm eff}|\mathcal {A}(0)|^2}{\varGamma _{1\mathrm eff}+\alpha _2\varGamma _2|\mathcal {A}(0)|^2}}\mathrm{e}^{-\varGamma _{1\mathrm eff}t}$. Right panel:  Phase dynamics according to the closed-form solution (black curve) Eq. (18) and its asymptotic behaviors for $t\rightarrow 0$ (blue curve), i.e., $\phi (0)+\frac{3\tilde{\gamma }}{4\omega _1\alpha _2\varGamma _2}\ln \left[ 1+\frac{\alpha _2\varGamma _2}{\varGamma _{1\mathrm eff}}|\mathcal {A}(0)|^2(1-\mathrm{e}^{-2\varGamma _{1\mathrm eff}t})\right]$, and $t\rightarrow \infty$ (red curve), i.e., $\phi (0)+\frac{3\tilde{\gamma }}{4\omega _1\alpha _2\varGamma _2}\ln \left[ 1+\frac{\alpha _2\varGamma _2}{\varGamma _{1\mathrm eff}}|\mathcal {A}(0)|^2\right] -\varDelta \omega _1t$. (Color figure online)

Fig. 5

Numerical and theoretical predictions of the amplitude and phase dynamics of the primary resonator. The amplitude (left panel) and phase (right panel) dynamics are shown for three different initial conditions: (i) $A_1(0)=10i,~A_2(0)=0.01$—gray curves, (ii) $A_1(0)=i,~A_2(0)=0.01$—blue curves, and (iii) $A_1(0)=0.1i,~A_2(0)=0.01$—red curves. The light solid curves indicate the result of the direct numerical integration of Eqs. (23)–(24), and the dark dashed curves indicate the theoretical predictions from Eqs. (17)–(18). The inset in the left panel shows the time evolution of the amplitude on the time interval $0<\varGamma _1t<0.02$

4 Numerical validation

To validate our single-mode theoretical approximation, we rewrite the full equations, Eqs. (2)–(3), in terms of the complex amplitudes, i.e., $q_k(t)=A_k(t)\mathrm{e}^{i\omega _kt}+A_k^{*}(t)\mathrm{e}^{-i\omega _kt}$ and $\dot{q}_k(t)=i\omega _k[A_k(t)\mathrm{e}^{i\omega _kt}-A_k^{*}(t)\mathrm{e}^{-i\omega _kt}]$, where $k=1,2$, and set $U(q_1)=\omega _1^2q_1^2/2+\gamma q_1^4/4$, $G(q_1)=G_1q_1+G_2q_1^2/2$. Thus, we obtain the following equations for the evolution of the complex amplitudes

$$\begin{aligned} \dot{A}_1&=\frac{\mathrm{e}^{-i\omega _1t}}{2i\omega _1}[q_{2}(G_1+G_2q_1)-\gamma q_1^3-2\varGamma _1\dot{q}_1], \end{aligned}$$

(23)

$$\begin{aligned} \dot{A}_2&=\frac{\mathrm{e}^{-i\omega _2t}}{2i\omega _2}\left[ \left( G_1+\frac{G_2}{2}q_{1}\right) q_{1}-2\varGamma _2\dot{q}_2\right] . \end{aligned}$$

(24)

Note that no approximations were made in the derivation of Eqs. (23)–(24), and they yield exact solutions for the complex amplitudes, $A_1(t)$ and $A_2(t)$, of the full equations, Eqs. (2)–(3). Hence, by solving Eqs. (23)–(24) numerically we can confirm the approximate asymptotic behavior of the complex amplitude, $\mathcal {A}(t)=|\mathcal {A}(t)|\mathrm{e}^{i\phi (t)}$, given by Eqs. (17)–(18). Figure 5 shows a comparison between the numerically calculated exact equations and the theoretical approximation for the same system parameters as in Fig. 4 ($\omega _1=1,~\omega _2=10,~\varGamma _1=10^{-3},~\varGamma _2=1,~G_1=4,G_2=5,~\gamma =1$) and three different initial conditions: (i) High initial energy of the primary resonator—$A_1(0)=10i$ and $A_2(0)=0.01$. (ii) Moderate initial energy of the primary resonator—$A_1(0)=i$ and $A_2(0)=0.01$, and (iii) low initial energy of the primary resonator—$A_1(0)=0.1i,~A_2(0)=0.01$. Note that these three cases can actually be captured by a single case starting from high initial energy of the primary resonator; however, for the sake of exposition, we treat them separately.

Direct numerical integration of the full equations and the theoretical estimates are in excellent agreement (Fig. 5). In fact, the only clear difference between the numerics and the theory is the presence of fast oscillations that appear in the numerical solutions of the amplitude and phase (see the inset of the left panel in Fig. 5) due to the presence of non-secular terms that are not filtered out in the full equations, Eqs. (23)–(24). The numerical results also confirm that the nonlinear effects are most pronounced for high initial energy of the primary resonator $(|A_1(0)|^2)$, that is, at the beginning of the ring down $(t\rightarrow 0)$, and as the system decays toward its zero energy state $(t\rightarrow \infty )$, only linear effects persist. Note that the current numerical integration only validates the theory for a specific set of parameters and hence can be considered only as a validation to the proof of concept. A detailed numerical analysis that includes parameter sensitivity analysis and numerical investigation of the theory limitations are out of the scope of the current paper and will be considered in future studies.

5 Closing remarks

In this paper, we analyzed the nonlinear interaction of mutually coupled resonators with significantly different decay rates, namely slowly decaying nonlinear (primary) resonator, which is nonlinearly coupled to a relatively fast-decaying linear resonator. We showed that such an interaction can change both the linear and nonlinear characteristics of the primary resonator. That is, by coupling a nonlinear resonator to relatively fast-decaying linear resonator, we can change its eigenfrequency, linear damping, and Duffing parameter and add new nonlinear van der Pol damping term to the resonator dynamics.

Theoretically, we view this interaction between resonators with significantly different decay rates as a discrete and finite version of the microscopic theory of a resonator that interacts with a medium, where the “medium” is the secondary resonator. Due to the nature of this interaction (only two resonators), the modified linear and nonlinear characteristics of the primary resonator depend on the eigenfrequency of the secondary resonator rather than on a continuous spectrum as in the standard case, in which the medium is modeled by infinite number of harmonic oscillators (see “Appendix” for brief description of the standard model of the bath with a large number of degrees of freedom and with a quasi-continuous frequency spectrum).

Practically, the results of this paper show a potential method for tuning parameters in nano- and micro-mechanical systems, allowing one to adjust the response of a resonator according to desired specifications by controlling its interaction with a fast-decaying linear resonator. This ability to tailor a desired nonlinear response of a resonator can be extremely useful in NEMS and MEMS applications. A prime example is in the case of closed loop oscillators used in timekeeping, and the ability to reduce the Duffing nonlinearity is an important step in reducing noise [39,40,41,42].

Appendix A: Brief discerption of the microscopic theory of a resonator that interacts with a medium

We consider the total Hamiltonian of a nonlinear resonator with a potential U(x) that is coupled to a medium of harmonic oscillators. The analysis is well-known [16, 19, 31, 32, 43,44,45,46]; here, we briefly outline it for completeness. The total Hamiltonian includes the resonator Hamiltonian $\mathcal {H}_r$, the medium Hamiltonian $\mathcal {H}_m$, and the interaction Hamiltonian $\mathcal {H}_\mathrm{inter}$ and reads

$$\begin{aligned} \mathcal {H}=\frac{v^2}{2}+U(x)+\frac{1}{2}\sum _k(p_k^2+\omega _k^2q_k^2)-G(x)\sum _k\epsilon _kq_k. \end{aligned}$$

(25)

The equations of motion resulting from Eq. (25) are

$$\begin{aligned} \ddot{x}&=-U'(x)+G'(x)\sum _k\epsilon _kq_k, \end{aligned}$$

(26)

$$\begin{aligned} \ddot{q}_k&=-\omega _k^2q_k+\epsilon _kG(x). \end{aligned}$$

(27)

We formally solve Eq. (27) in terms of its Green’s function, i.e.,

$$\begin{aligned} q_k(t)&=q_k(0)\cos (\omega _{k}t)+\frac{p_k(0)}{\omega _{k}}\sin (\omega _{k}t) \nonumber \\&+\frac{\epsilon _k}{\omega _{k}}\int _0^tG(x(\tau ))\sin (\omega _{k}(t-\tau ))\mathrm{d}\tau . \end{aligned}$$

(28)

Upon inserting Eq. (28) into Eq. (26), we find that

$$\begin{aligned} \ddot{x}=-U'(x)+G'(x)(L[x]+F), \end{aligned}$$

(29)

where

$$\begin{aligned} L[x]=&\sum _k\frac{\epsilon _k^{2}}{\omega _{k}}\int _0^tG(x(\tau ))\sin (\omega _{k}(t-\tau ))\mathrm{d}\tau , \end{aligned}$$

(30)

$$\begin{aligned} F(t)=&\sum _k\epsilon _k\left[ q_k(0)\cos (\omega _{k}t)+\frac{p_k(0)}{\omega _{k}}\sin (\omega _{k}t)\right] . \end{aligned}$$

(31)

Using integration by parts, we can rewrite Eq. (30) as

$$\begin{aligned} L[x]=&-G(x(t))\sum _k\frac{\epsilon _k^{2}}{\omega _{k}^2}+G(x(0))\sum _k\frac{\epsilon _k^{2}}{\omega _{k}^2}\cos (\omega _{k}t)\nonumber \\&-\sum _k\frac{\epsilon _k^{2}}{\omega _{k}^2}\int _0^t\dot{x}(\tau )G'(x(\tau ))\cos (\omega _{k}(t-\tau ))\mathrm{d}\tau . \end{aligned}$$

(32)

We assume that the medium contains an infinite number of harmonic oscillators with a continuous spectrum. Consequently, we approximate the sum over k as an integral. Toward this end, we define the spectral density of the bath as $g(\omega )\mathrm{d}\omega =\sum _{\omega<\omega _k<\omega +\mathrm{d}\omega }\epsilon _k^{2}/\omega _{k}^2$.

Using Eq. (32) along with the assumption of a continuous spectrum of the medium, we rewrite Eq. (29) as

$$\begin{aligned}&\ddot{x}+G'(x)\int _0^t\varGamma (t-\tau )\dot{x}(\tau )G'(x(\tau ))\mathrm{d}\tau \nonumber \\&\quad +V_\mathrm{ren}'(x)=G'(x)\tilde{F}, \end{aligned}$$

(33)

where $\varGamma (t-\tau )=\int _{-\infty }^{\infty }g(\omega )\cos (\omega (t-\tau ))\mathrm{d}\omega$ is the memory of the friction, $V_\mathrm{ren}(x)=U(x)+\frac{1}{2}G^2(x)\int _{-\infty }^{\infty }g(\omega )\mathrm{d}\omega$ is the renormalized potential of the resonator, and $\tilde{F}=F+G(x(0))\int _{-\infty }^{\infty }g(\omega )\cos (\omega t)\mathrm{d}\omega$ is a noise term.

The statistical properties of the noise term F are determined as follows: We assume that at $t=0$, the interaction between the bath and the resonator is turned on and considers an ensemble of initial states in which x(0) is held fixed but the initial bath variables $q_k(0),p_k(0)$ are drawn at random from a canonical distribution characterized by a temperature T, i.e.,

$$\begin{aligned} \mathcal {P}(\{q_k,p_k\}|x(0)=x)\propto \mathrm{e}^{-\mathcal {H}_m/k_BT}. \end{aligned}$$

(34)

With this conditional probability for the bath variables, the noise term F obeys the fluctuation–dissipation relations

$$\begin{aligned} \langle F\rangle _{\mathcal {P}}=0,~\langle F(t) F(\tau )\rangle _{\mathcal {P}}=k_BT\varGamma (t-\tau ), \end{aligned}$$

(35)

and hence, it is a colored Gaussian noise. Note that for a flat spectrum of the bath weighted with the coupling (the so-called Ohmic dissipation), we can use the Markovian approximation, where $\varGamma (t-\tau )=2\langle g\rangle \delta (t-\tau )$ and $\langle g\rangle /\pi$ is the averaged value of the spectrum. Hence, Eq. (33) reduces to

$$\begin{aligned} \ddot{x}+2\langle g\rangle G'^2(x)\dot{x}+V_\mathrm{ren}'(x)=G'(x) F, \end{aligned}$$

(36)

and F becomes a white Gaussian noise.

Comparison between Eqs. (14) and (36) reveals that, for both cases of discrete and continuous spectrum baths, the linear coupling is the source of the induced linear damping and the shift in the eigenfrequency of the resonator, and the nonlinear coupling leads to nonlinear damping and modifications in the nonlinear conservative terms of the resonator. However, for the case of a continuous spectrum bath there are also fluctuating back-action terms that come along with the damping terms and balance them, i.e., the linear damping is associated with an additive noise term $2\langle g\rangle G'^2(0)\dot{x}\longleftrightarrow G'(0)\tilde{F}$ and the nonlinear damping with a multiplicative noise $2\langle g\rangle [G'^2(x)-G'^2(0)]\dot{x}\longleftrightarrow [G'(x)-G'(0)]\tilde{F}$.