1 Introduction

Extracting internal structural features in complex systems has been of constant concern to researchers. As an important information carrier of complex systems, time series is widely studied. The complexity of time series is closely related to a variety of dynamic characteristics of time series, such as long-range correlation [1], multifractal characteristics [2], chaotic characteristics [3] and so on. The existence of these characteristics makes time series show varying degrees of complexity. Researchers hope to reveal the dynamic evolution of complex systems by analyzing the dynamic patterns of time series. In order to study the dynamic characteristics of time series, many methods have been put forward so far, such as Lyapunov index [4], fractal dimension [5], complex network [6], and information entropy [7]. The research on the complexity of time series has been the focus of researchers for a long time. And it is of significant importance to study the complexity of time series. Many researchers have applied time series analysis in various fields, such as climate systems [8, 9], eco-epidemiological system [10] and economic system [11].

Among many methods, symbolic time series analysis and information entropy have attracted the attention of scholars. Symbolic time series analysis includes symbolization of time series [12,13,14] and analysis of symbolic sequence, and it is a fast, simple and effective signal processing method [15]. By reducing the interference of some data information and capturing large-scale features of data sequence, high-resolution data can be converted into low-resolution data to extract dynamic characteristics and reduce noise sensitivity of signal analysis. Permutation analysis [7], one of common symbolic methods, has been applied to time series to quantify appearance already. It is computed with an ordinal symbolization rule by comparing neighboring values in time series. Then, complexity measures have been proposed to characterize the resulting symbolic sequence, a very popular one being the permutation entropy (PE). However, the main disadvantage of permutation entropy (PE) is that no information is retained other than ranking when ordinal pattern of each time series is extracted. Therefore, weighted permutation entropy is proposed [16]. The weighting method makes it possible to detect sudden changes in data and assign more weights to conventional spike patterns. In addition, the traditional entropy algorithm, which is based on a single scale, does not consider the inherent multiple time scales of complex systems [17]. Hence, Costa proposes a new method called multiscale entropy (MSE) to calculate entropy at multiscale [18]. For a given discrete time series \(\left\{ x_{i}\right\} _{i=1}^{N}\), multiple coarse-grained time series are constructed by averaging the data points within nonoverlapping windows of increasing length s. Entropy can represent dynamic systems from different perspectives, and plays an important role in measuring the complexity of time series [19,20,21].

In the field of nonlinear time series research, it is highly praised to use the complex network method [6, 22] to describe the dynamic characteristics of time series. The idea of transforming time series into complex network also opens up a new river of nonlinear time series research. This idea connects the research of time series with the method of graph theory, which makes it possible to apply graph theory to the study of dynamic pattern of time series. A key problem to be solved in the research of sequential network is how to transform the dynamic evolution of time series into complex networks. Different complex network construction methods determine that the dynamic information of time series at different levels is mapped to the network topology. Masoller uses symbolic ordinal analysis and network representation to characterize the evolution of dynamic systems in 2015 [13]. Moreover, it has been proved that correlation charts [23, 24], recurrence charts [25,26,27] and visibility charts [28,29,30,31] can provide relevant information, such as qualitative changes and sudden changes in early warning indicators.

In this study, we use the transition graph method to construct temporal network. Sequential network itself is a directed graph, but each link in the network has no weight added, so amplitude information is often ignored when capturing dynamic information of time series. We get the dynamic information of the sequence by adding weight in the link. In addition, the traditional entropy method is only a measure of uncertainty. Higher entropy only means higher uncertainty (or randomness), but does not mean higher complexity of system dynamics. Therefore, the multiscale method is used to research the coarse grain sequence instead of the original time series for measuring the complexity.

In this paper, a new method combining symbolic time series analysis and complex network is proposed, which is called weighted link entropy (WLE). The main contribution of this paper is to construct weighted digraph in sequential network to obtain the dynamic information about amplitude of time series. We extend the permutation analysis to complex networks to compute node entropy and link entropy, which are defined from the perspective of network construction. In addition, weighted link entropy is extended to multiscale weighted link entropy (MWLE), thus studying multiple inherent scales of complex systems through coarse grain time series. We analyze multiscale weighted link entropy of Shangzheng, Shenzheng, HSI, S&P500, DJI, NQCI, FTSE, FCHI and GDAXI stock closing prices. In order to accurately test the validity of the proposed method, we consider time series generated by logistic map, tent map, Gaussian-modulated sinusoidal pulses model and Binomial multifractal model.

The rest of this paper is organized as follows. Section 2 presents methods adopted in this study. In Sects. 3 and 4, results of simulation data and empirical data are presented respectively. Section 5 gives the conclusions.

2 Methodologies

2.1 Permutation entropy and weighted permutation entropy

We consider the embedded representation of time series \(\left\{ x_{t}\right\} _{t=1}^{T}\) and the embedded expression of its time delay \(X_{j}^{m, \tau }=\left\{ x_{j}, x_{j+\tau }, \ldots , x_{j+(m-1) \tau }\right\} \), \(j=1,2, \ldots T-(m-1) \tau \), where m represents the embedding dimension and \(\tau \) represents the time delay. Each vector in \(N=T-(\mathrm {m}-1) \tau \) sub-vector will generate m! ordinal symbols, so the m! order permutation entropy is defined as

$$\begin{aligned} H(m, \tau )=-\sum _{i: \pi _{i}^{m, \tau } \in \Pi } p\left( \pi _{i}^{m, \tau }\right) \ln p\left( \pi _{i}^{m, \tau }\right) \end{aligned}$$
(1)

where \(p\left( \pi _{i}^{m, \tau }\right) \) is defined as

$$\begin{aligned} p\left( \pi _{i}^{m, \tau }\right) =\frac{\Vert \left\{ j: j \le N,\right. {type} \left. \left( X_{j}^{m, \tau }\right) =\pi _{i}^{m, \tau }\right\} \Vert }{N} \end{aligned}$$
(2)

where type() represents the mapping from the schema space to the symbol space, \(\Vert \cdot \Vert \) stands for set. An alternative way of writing \(p\left( \pi _{i}^{m, \tau }\right) \) is

$$\begin{aligned} p\left( \pi _{i}^{m, \tau }\right) =\frac{\sum _{j \le N} \mathbf {1}_{u:\mathrm {type}(u)=\pi _{i}}\left( X_{j}^{m, \tau }\right) }{\sum _{j \le N} \mathbf {1}_{u: \mathrm {type}(u) \in \Pi }\left( X_{j}^{m, \tau }\right) } \end{aligned}$$
(3)

where \(\mathbf {1}_{A}(u)\) denotes the indicator function of set A defined as \(\mathbf {1}_{A}(u)=1\) if \(u \in A\) and \(\mathbf {1}_{A}(u)=0\) if \(u \notin A\). Obviously, \(0 \le H(m, \tau ) \le \log (m !)\).

In general, the ordinal representation s(t) of x(t) has M different symbols. According to the dynamics of the system, not all possible symbols will appear in the sign sequence s(t), because dynamics does not allow the appearance of some ’forbidden mode’ [32, 33], or the length of time series x(t) is limited, so there will be no ’missing mode’ [34]. Therefore, the symbol type M that actually appears in the symbol sequence is less than or equal to m!.

However, the main disadvantage of permutation entropy (PE) is that it does not retain any information except the order structure when the order pattern of each time series is extracted, so the amplitude information of most time series could be lost [16]. In order to overcome this defect, weighted permutation entropy (WPE) is proposed by Fadlalah in 2013. The procedure of calculating the WPE is briefly described as follows: Each vector \(X^{m}_{j}\) is weighted with the weight value \(w_{j}\), instead of being weighted uniformly. The weighted relative frequencies are calculated as

$$\begin{aligned} p_{w}\left( \pi _{i}^{m, \tau }\right) =\frac{\sum _{j \le N} \mathbf {1}_{u: \mathrm {type}(u)=\pi _{i}}\left( X_{j}^{m, \tau }\right) w_{j}}{\sum _{j \le N} \mathbf {1}_{u: \mathrm {type}(u) \in \Pi }\left( X_{j}^{m, \tau }\right) w_{j}} \end{aligned}$$
(4)

Note that \(\sum _{i} p_{w}\left( \pi _{i}^{m}\right) =1\). The weight value \(w_{j}\) is the variance of each vector \(X^{m}_{j}\) as

$$\begin{aligned} w_{j}=\frac{1}{m} \sum _{k=1}^{m}\left[ x_{j+k-1}-\bar{X}_{j}^{m}\right] ^{2} \end{aligned}$$
(5)

where \(\bar{X}_{j}^{m}\) is the arithmetic mean:

$$\begin{aligned} \bar{X}_{j}^{m}=\frac{1}{m} \sum _{k=1}^{m} x_{j+k-1} \end{aligned}$$
(6)

WPE is then computed as

$$\begin{aligned} H_{w}(m, \tau )=-\sum _{i: \pi _{i}^{m, \tau } \in \Pi } p_{w}\left( \pi _{i}^{m, \tau }\right) \ln p_{w}\left( \pi _{i}^{m, \tau }\right) \end{aligned}$$
(7)

2.2 Network construction

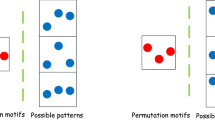
We transform a time series x(t) into a sequence of symbols s(t) by using the ordinal pattern representation with symbols of length m. In this case, symbols are defined by considering groups of m consecutive values in the time series. For example, for \(m= 2\) there are two ordinal patterns: \(x(t)<x(t+1)\) gives symbol \('01'\) and \(x(t)>x(t+1)\) gives symbol \('10'\).

Weight of a node i is the relative number of times symbolioccurs in sequence s(t):

$$\begin{aligned} p_{i}=\frac{1}{L} \sum _{t=1}^{L} n[s(t)=i] \end{aligned}$$
(8)

where n is the count of occurrence times of node i, L is length of sequence s(t), \(p_{i}\) is standardized, \(\sum _{i=1}^{M} p_{i}=1\). \(s_{p}\) is entropy of the distribution of node weights:

$$\begin{aligned} s_{p}=-\sum _{i=1}^{M} p_{i} \log p_{i} \end{aligned}$$
(9)

In sequence s(t), the relative degree of symbol i followes by symbol j is the weight of a link \(w_{i,j}\):

$$\begin{aligned} w_{i j}=\frac{\sum _{t=1}^{L-1} n[s(t)=i, s(t+1)=j]}{\sum _{t=1}^{L-1} n[s(t)=i]} \end{aligned}$$
(10)

Since \(\sum _{j=1}^{M} w_{i j}=1, \forall i\), we can calculate entropy of the weight distribution of each link:

$$\begin{aligned} s_{i}=-\sum _{j=1}^{M} w_{i j} \log w_{i j} \end{aligned}$$
(11)

Then the heterogeneity of network is represented by the distribution of \(s_{i}\) value. We propose to use the first moment of \(s_{i}\) value distribution, namely, the average node entropy of network:

$$\begin{aligned} s_{n}=\frac{1}{M} \sum _{i=1}^{M} s_{i} \end{aligned}$$
(12)

If all nodes have only one outgoing link, then \(s_{i}=0\), \(s_{n}=0\), sign j that comes after sign i is completely predictable. The largest \(s_{i}=\log M\) occurs in \(s_{n}=\log M\), where the sign sequence is completely random, any sign in sequence follows sign i with the same probability \(\frac{1}{M}\). Therefore, \(0 \le s_{n} \le \log M\).

2.3 Weighted link entropy and multiscale weighted link entropy

2.3.1 Weighted link entropy

However, when link entropy extracts information in time series, only ordinal pattern is considered, so amplitude information could be lost. For example, Fig. 1 shows how the same ordinal link pattern can originate from different \(m+\tau \) dimensional vectors. Therefore, we define weighted link entropy (WLE) in the following steps.

Fig. 1
figure 1

Two examples of possible patterns corresponding to the same link, \(m=3\), \(\tau =1\)

Full size image

First, we define weighted node entropy (WNE). Each vector \(X^{m}_{j}\) is weighted with the weight value \(w_{j}\), instead of being weighted uniformly.

Step 1 Equation 8 can be expressed as follows:

$$\begin{aligned} p_{i}=\frac{\sum _{t=1}^{L} n[s(t)=i]}{\sum _{t=1}^{L} \sum _{i=1}^{M} n[s(t)=i]} \end{aligned}$$
(13)

Step 2 We add weights to the nodes,

$$\begin{aligned} wp_{i}=\frac{\sum _{t=1}^{L} n[s(t)=i] w_{t}}{\sum _{t=1}^{L} \sum _{i=1}^{M} n[s(t)=i] w_{t}} \end{aligned}$$
(14)

Step 3 \(w_{t}\) is defined in Eqs. 5, 6, and then the weighted node entropy (WNE) can be calculated as

$$\begin{aligned} wsp=-\sum _{i=1}^{M} wp_{i} \log wp_{i} \end{aligned}$$
(15)

Then based on the concept of weighted node entropy, we propose weighted link entropy (WLE):

Step 1 Equation 10 can be written as

$$\begin{aligned} w_{i j}=\frac{\sum _{t=1}^{L-1} n[s(t)=i, s(t+1)=j]}{\sum _{t=1}^{L-1} \sum _{j=1}^{M} n[s(t)=i, s(t+1)=j]} \end{aligned}$$
(16)

Step 2 We add weights to links:

$$\begin{aligned} w p_{i j}=\frac{\sum _{t=1}^{L-1} n[s(t)=i, s(t+1)=j]\left( \frac{w_{t}+w_{t+1}}{2}\right) }{\sum _{t=1}^{L-1} \sum _{j=1}^{M} n[s(t)=i, s(t+1)=j]\left( \frac{w_{t}+w_{t+1}}{2}\right) } \end{aligned}$$
(17)

Step 3 The entropy of weighted link distribution is calculated as

$$\begin{aligned} hwp_{i}=-\sum _{i=1}^{M} wp_{i j} \log wp_{i j} \end{aligned}$$
(18)

Step 4 Using the first moment of \(hwp_{i}\) distribution, the weighted link entropy wsn is calculated as

$$\begin{aligned} wsn=\frac{1}{M} \sum _{i=1}^{M} hwp_{i} \end{aligned}$$
(19)
Fig. 2
figure 2

The produce of weighted node and weighted link, \(m=3\), \(\tau =1\)

Full size image

The produce of weighted node and weighted link can be seen in Fig. 2. The embedding dimension is set to 3 and time delay \(\tau =1\), each sub-vector \(\{x(t),x(t+1),x(t+2)\}\) will generate 6 ordinal symbols. Therefore the network is allowed to build 6 nodes and 36 links. We assign weights \({w_{i}}\) to each node, and \(\{(w_{i}+w_{i+1})/2\}\) to each link.

2.3.2 Multiscale weighted link entropy

The coarse-grained time series is constructed by using the following equation.

$$\begin{aligned} y_{j}^{(s)}=\frac{1}{s} \sum _{i=(j-1) s+1}^{j s} x_{i} \end{aligned}$$
(20)

where s represents the scale factor and \(1 \le j \le N / s\). The length of each coarse-grained time series is equal to the length of original time series divided by the scale factor s. We calculate entropy of each coarse-grained time series as a function of scale factor s and then plot as a function of the scale factor. In the sense of multiscale, the weighted link entropy (WLE) we calculate is extended to multiscale weighted link entropy (MWLE).

3 Simulated data results

3.1 Logistic model and tent model

We start by presenting the results of the analysis of simulated time series for the logistic map and the tent map [35]. The equations and parameters are:

  • logistic map:\(x_{i+1}=r x_{i}\left( 1-x_{i}\right) \)

  • Tent map:\(x_{i+1}=r x_{i}\) if \(x_{i}<0.5\), \(x_{i+1}=r\left( 1-x_{i}\right) \) if \(x_{i} \ge 0.5\)

The analysis is performed with a time series of length \(L= 6000\) and patterns of length \(m= 3\). When analyzing empirical data, we focus on the different performance of weighted node entropy and weighted link entropy.

Fig. 3
figure 3

Analysis of the logistic map, parameter range \(3.5 \le r \le 4\), subgraphes from top to bottom are bifurcation diagram of logistic model, the diagram of Lyapunov index, weighted node entropy and weighted link entropy, respectively

Full size image
Fig. 4
figure 4

Analysis of the tent map, parameter range \(1 \le r \le 2\), subgraphes from top to bottom are bifurcation diagram of logistic model, the diagram of Lyapunov index, weighted node entropy and weighted link entropy, respectively

Full size image

Both logistic map and tent map have similar bifurcation sequences (except for the periodic windows in the logistic map). Thus, assuming similar bifurcation sequence gives rise to similar dynamical behaviors, similar symbolic networks which depend on control parameters will be obtained. In several previous studies, Lyapunov index (LE) can well measure the chaotic state of logistic map and tent map. The system is in chaotic motion when the Lyapunov index (LE) is positive. The trends of \(ws_{p}\) and \(ws_{n}\), which change with parameters are essentially similar to Lyapunov index’s. In the visibility diagram, the direct relationship between network entropy and LE is established by identifying Pesin [4]. Therefore, these results show that the above network entropy can indeed capture non-trivial properties of dynamics.

Indeed, it is observed in Figs. 3 and 4 that \(ws_{n}\) displays more informatioin on the complexity inside systems. For example, \(ws_{n}\) has a wider range of variations when the system is in a chaotic state and can detect minute changes of the complexity of systems. The trend of \(ws_{n}\) is more similar to that of LE, which can be understood in the following terms. On the one hand, \(ws_ {p}\) only represents the distribution of weighted nodes, but on this basis \(ws_ {n}\) contains weighted link which increases the connection between two nodes, so that a more robust network structure is built. So the values of \(ws_{n}\) will change more greatly when the system is chaotic, and subtle fluctuation in the systems will be also detected. On the other hand, with the increase of map parameters, new patterns will appear in the symbol sequence, which produce new nodes and links in symbol network. Althrough the frequency of occurrence of the new ordinal patterns is small in the initial state and their appearance does not produce mutation variations in \(ws_ {p}\), the new links will not necessarily have small entropies. Therefore, they can induce mutation variations in the average link entropy.

3.2 Gaussian-modulated sinusoidal pulses model

In order to study the different performances of WLE and WNE in signals with noise, we try a series of sinusoidal pulses with Gaussian modulation amplitude attenuation and sinusoidal pulses has Gaussian white noise which has mean \(\mu = 0 \) and variance \(\sigma ^{2}= 0.2\). Gaussian-modulated sinusoidal train with a frequency of 10 kHz, a pulse repetition frequency of 1 kHz and an amplitude attenuation rate of 0.9. It’s sampling rate is 50 kHz. The value of \(\tau \) is set to 1 and m is set to 4. We use the window length of 50 and the window moving length of 10.

Fig. 5
figure 5

Node entropy, weighted node entropy, link entropy and weighted link entropy in Gaussian sine pulse (left) and Gaussian sine pulse with Gaussian white noise (right)

Full size image

In the left figure of Fig. 5, when Gaussian white noise is not added to the Gaussian sinusoidal pulse signal, node entropy and link entropy do not well represent amplitude attenuation characteristics of signal, which means that information about amplitude is lost when ordinal structure is extracted separately. However, WNE and WLE always discard the part of the signal displaying the pulse, which can clearly distinguish the burst and stagnation regions of the pulse train. In the right figure of Fig. 5, after adding gaussian white noise with variance \(\sigma ^{2}= 0.2\), WNE is greatly affected and changes dramatically, showing an obvious upward trend, since the system tends to be more chaotic. In this case, the amplitude information is not the main factor to determine the value of WNE. On the contrary, WLE is relatively robust and stable. Therefore, whether to add noise or not does not affect the value of MLE. Entropy value remains at a relatively stable level, which can well measure the change of amplitude.

Table 1 The mean and variance of NE, WNE, LE and WLE in Gaussian sine pulse and Gaussian sine pulse with Gaussian white noise
Full size table

Table 1 records the mean and variance of node entropy, weighted node entropy, link entropy and weighted link entropy in Gaussian sinusoidal pulse and Gaussian sinusoidal pulse with Gaussian white noise. After adding Gaussian white noise, the system tends to be more chaotic. Its randomness and uncertainty increase, which is in line with the reality that the mean of all entropy value increases significantly in a more chaotic system. The variance of weighted entropy are larger than that of general permutation entropy on account of the fact that adding weight can capture more amplitude information of ordinal pattern. What’s more, the weighted link entropy \(WS_{n}\) fluctuates in a smaller range, compared with the weighted node entropy \(WS_{p}\) in both two sets of signals.

Fig. 6
figure 6

PE, WPE and WLE values for different variance of Gaussian white noise added in Gaussian sinusoidal pulse. The signal used is the same as that described in Fig. 5

Full size image

To observe the change of entropy under different SNR, we change the variance of Gaussian white noise added in Fig. 6. As expected, all of three entropy measures increase with the increase of the SNR since the effect of noise contributes to more complexity. WLE increases at a higher pace than WPE, which reflects a better robustness when noise is added.

3.3 Binomial multifractal series

The binomial multifractal time series, which is very popular due to it’s spike structures, is suitable for study in complex models [36]. The binomial multifractal time series contains some spiky portions as shown in Fig. 7. The given series of \(N=2^{n_{\max }}\) numbers i with \( i = 1,2,...,N\) is defined by

$$\begin{aligned} x_{i}=a^{n(i-1)}(1-a)^{n_{\max }-n(i-1)} \end{aligned}$$
(21)

where \(0.5<a<1\) is a parameter and n(i) is the number of digits equal to 1 in the binary representation of the index i. In the following study, we generate binomial multifractal series with \(a=0.75\), and the length of \(\left\{ x_{i}\right\} \) is set to be \(2^{10}\) and \(2^{16}\).

Fig. 7
figure 7

The sample of binomial multifractal series with \(a = 0.75\) of length \(2^{16}\)

Full size image

Then, multiple inherent dynamics of time series based on multiscale analysis is explored. We estimate the multiscale WNE and multiscale WLE of \(x_{i}\) for different embedding dimension \(m = 3,4\) and different length N, which are presented in Fig. 8. Some important observations can be found from the subplots: (i) the value of \(ws_ {p}\) is always larger than that of \(ws_ {n}\), but their changing trend is similar. And the changing range of \(ws_ {p}\) is larger than that of \(ws_ {n}\) on multiple time scales. The calculation of WLE is based on network and its links, which helps to weaken the influence of small fluctuations (which may be caused by noise). Also, it gives weight to regular patterns, which leads to higher predictability. (ii) the MWNE of time series when \(m = 4\) is always larger than that of \(m = 3\), but the change of MWLE is not obvious at different m. On the contrary, neither of them changes significantly in different length N of time series.

Fig. 8
figure 8

MWPE and MWLE analysis of different embedding dimension m and different length N of two time series

Full size image

4 Empirical data results

4.1 Research on the complexity of time series during financial crisis

The financial market is a complex system with various interactions [37] and has a strong self-organization ability. It is still a huge challenge to study its nonlinearity and uncertainty. Financial markets often exhibit unexpected phenomena, such as systemic breakdowns. In the past 20 years, the global currency crisis in 1998, the dotcom crash in 2001, the global financial crisis in 2008, the European debt crisis in 2012, the Chinese crisis in 2015–2016 and the US stock market crisis in early 2019 are all tipical financial crisis events. Therefore, it is of great significance to quantify the changes of complexity before, during and after the crisis in financial systems, providing early warning indicators of qualitative changes. The key idea is how to quantify some patterns of complex systems, which subsequently indicate the changes of internal complexity of system. A significant advantage of this approach is that it can be compared with the corresponding time series to monitor and detect key changes. Furtherfore these quantitative measures of complexity can be used in the diagnosis process and in the prediction of future changes.

We use the daily closing price data of Shanghai Composite Index from January 1, 2006 to December 29, 2016. We collect the original sample data from finance of yahoo (http://finance.yahoo.com/). The length of sliding window is set to 100, and the window moving length is 30. In practice, the normalized log-returns are considered. When the stock indes is denoted as x(t), the log-returns is defined as \(g(t)=\log (x(t))-\log (x(t-1))\), and then the normalized log-returns are \(R(t)=(g(t)-\langle g(t)\rangle ) / \sigma \), where \(\sigma \) is the standard deviation of the series g(t). And \(<*>\) is the time average of the series g(t). We obtain the data covering 3647 days as shown in Fig. 9.

In this time series, there are two distinct mutation periods, corresponding to the global financial crisis of 2008 and the China crisis of 2015–2016, resprctively. Under the framework of sliding window algorithm, the specific time of the two mutation periods can be observed through the mean value and variance. Correspondingly, the entropy changes of weighted node entropy and weighted link entropy can also be seen when these two mutation events occur. We determine the point in time of mutation by comparing the average change of entropy in time period. It can be seen in Table 2 that period 2 and period 5 are smaller than the average of their two adjacent time periods obviously. Significantly, the change of WLE and WNE is noted much earlier than the actual crisis event time, which provides an early warning. It can be explained that the internal structure of systems changes before certain sudden changes, and entropy is an effective tool to quantify these structural patterns. In addition, the range of entropy change is different due to the different impact degree of these two crisis events. Measures of complexity can be used as indicators or precursors of the phenomenon of crisis if they show a clear pattern across all crises, such as a decrease or increase in the early stages of the crisis (Fig. 10).

Fig. 9
figure 9

Daily closing prices and normalized log-returns of Shanghai Composite Index

Full size image
Fig. 10
figure 10

The closing price, mean value, variance, weighted node entropy, weighted link entropy of Shangzheng stock index from January 1, 2006 to December 31, 2016

Full size image
Table 2 The mean of four indicators in pre crisis, mid crisis, post crisis respectively
Full size table

4.2 Multiscale research on different stock markets

The financial time series we use is daily closing prices of nine stock indexes: three American stock indexes S&P500, DJI and NQCI, three Chinese stock indexes Shangzheng, Shenzheng and HSI together with three European stocks indexes FTSE100, FCHI and GDAXI. The data are recorded from January 1, 2006 to December 31, 2020. After removing asynchronous data, we obtain data covering 3647 days as shown in Fig. 11. We collect the original sample data from finance of yahoo (http://finance.yahoo.com/).

By observing the closing prices of nine indexes in Fig. 11 and the normalized log-returns of nine indexes in Fig. 12, we can find that there are three obvious oscillations in given time interval, which are the global financial crisis in 2008, the European debt crisis in 2012 and the China crisis in 2015–2016. The three stocks of American stock market fluctuat greatly in the 2008 financial crisis, followed by the European debt crisis, and the 15–16 China crisis has the least impact on them. In comparison, the three stocks of China’s stock market show a great degree of volatility in 2008 financial crisis and the 15–16 China crisis. However, they do not show any obvious change in European crisis except HSI index. In addition, the three stocks of European stock market show volatility at all three corresponding time points, but the degree is not obvious compared with the other two stock markets in 2008 and 2015, which can be regarded as being affected by the stock markets of two other regions.

Fig. 11
figure 11

Closing prices of nine stock indexes

Full size image
Fig. 12
figure 12

Normalized log-returns of nine stock indexes

Full size image

When the embedding dimension \(m=3\), WLE of these three stock markets at multiple scales and of pairwise comparison is analyzed. Stock data has strong noise interference. Even so, there are some interesting conclusions that can be found on multiple time scales. (i) The Shangzheng and Shenzheng indexes have similar trends on multiple scales, while the HSI index is similar to several indexes in the US and European stock markets. HSI index is greatly influenced by the international stock market from 2006 to 2020. (ii) In Chinese stock market and American stock market, the general trends of these three stocks we use are generally similar, while the three indexes of European stock market are obviously different. These three stocks in European stock market come from different countries. The conclusion about the difference of similarity is basically consistent with the fact above (Figs. 13, 14, 15).

Fig. 13
figure 13

WLE of six stocks in Chinese and American stock markets at different time scales, embedding dimension \(m=3\)

Full size image
Fig. 14
figure 14

WLE of six stocks in Chinese and European stock markets at different time scales, embedding dimension \(m=3\)

Full size image
Fig. 15
figure 15

WLE of six stocks in American and European stock markets at different time scales, embedding dimension \(m=3\)

Full size image

Then, we study the influence of different embedding dimensions on the results, setting \(m=4\) and then \(m=5\). When \(m = 4\), there are 24 nodes and 576 links in the network. When \(m = 5\), the network allows 120 nodes and 14,400 links to be built. Rich links tend to make the network more robust and not be vulnerable to extreme values and noise. In Fig. 16, a very obvious phenomenon is that the entropy of FTSE 100 and FCHI indexes is obviously different from other stocks, which is more pronounced in Fig. 17. In multiple time scales, it is easy to distinguish the sequences with different features in the same cluster. In large time scales, multiscale entropy can better extract the intrinsic characteristics of information, which further demostrates the necessity of applying multiple scales to MLE.

The similarity of stock markets in different regions can be measured better in a larger embedding dimension. In the analysis of embedding dimension \(m=5\), European stock market and American stock market are completely separated, while Chinese stock market is between them. When the embedding dimension is 4, although the stock markets in different regions can be roughly distinguished, the effect is not obvious in some time scales. However, when the embedding dimension is large, it requires longer length of time series and takes longer time to run. Therefore, how to select an appropriate embedding dimension needs to be further solved.

Fig. 16
figure 16

WLE of nine stocks in Chinese, American and European stock markets at different time scales, embedding dimension \(m=4\)

Full size image
Fig. 17
figure 17

WLE of nine stocks in Chinese, American and European stock markets at different time scales, embedding dimension \(m=5\)

Full size image

5 Conclusion and discussion

Fig. 18
figure 18

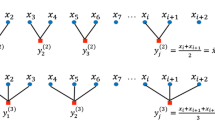
a A simple example to explain how the sequential network predicts the next most probable symbol in the symbol sequence through transitions, thus inferring the variations of values in ordinal time series, and \(W_{ij}\) stands for different links. b A simple example of the two periodic time series which can eventually be mapped to the same class of regular networks

Full size image

In this paper, we propose a hybrid method which combines symbolic time series analysis and complex networks to measure the complexity of nonlinear system. On the basis of traditional permutation entropy, this paper puts forward the concept of node and link, and then proposes weighted link entropy. Compared with traditional permutation entropy, the WLE can measure amplitude information since adding weights in temporal networks. What’s more, the research extends WLE to multiple scales. Therefore, WLE retains most of characteristics of weighted permutation entropy, and also takes into account the multiple time scales inherent in complex systems.

Through numerical simulation experiments, we prove the superiority of the WLE method. In previous studies, Lyapunov exponent is a good indice to show the chaotic characteristics of nonlinear dynamic system. Our research shows that weighted link entropy is not only very similar to it, but also can identify the mutation of dynamic systems. Moreover, the robustness of WLE when noise is added is further demonstrated. Hence, these results show that network entropy can capture the nontrivial characteristics of dynamics.

In the empirical analysis, we find that WLE can predict the occurrence of financial crisis and effectively measure the inherent complexity of major events in the financial market in the framework of moving window algorithm. In multiple scales, the focus of our research is the similarity of different regions of stock markets. And the results demostrate that multiscale entropy can measure the similarity of different stock markets.

In summary, the complexity of time series is studied by weighted time series network in this paper. The proposed method can indeed quantify the dynamic pattern information of time series in simulation and real data applications. Compared with the traditional weighted permutation entropy, our method can obtain more dynamic information of time series and has better anti-noise ability. In addition, in studying the mutation behavior of financial stock markets and measuring the similarity of stock markets, we arrive at a conclusion that our proposed method is effective. However, how to choose the appropriate embedding dimension needs to be further solved in practical application.

Our approach can identify changes in the symbolic dynamics of these systems, for example, the appearance of new symbols or the appearance of new transitions, which result in variations of the network measures. What’s more, it provides additional predictive power for time series analysis, as identifying nodes with one outgoing link will allow us to identify the symbol sequence, those for which we know which is the next most probable symbol in the symbol sequence. And then in time series analysis, entropy is used to measure the uncertainty of these symbols and transitions, thereby indicating the change of system chaos. However, some time series can eventually be mapped to the same class of regular networks, such as periodic and irregular time series. It means that it is of significant importance to choose symbolization methods. These above conclusions are explained in Fig. 18. Therefore, further studies should be performed to determine the correspondence between different network characteristics and different types of dynamics as well.