Modified generalized multiscale sample entropy and surrogate data analysis for financial time series

Abstract

Complexity in time series is an intriguing feature of living dynamical systems such as financial systems, with potential use for identification of system state. Multiscale sample entropy (MSE) is a popular method of assessing the complexity in various fields. Inspired by Tsallis generalized entropy, we rewrite MSE as the function of q parameter called generalized multiscale sample entropy and surrogate data analysis ($q\hbox {MSE}$). qMSDiff curves are calculated with two parameters q and scale factor $\tau$, which consist of differences between original and surrogate series $q\hbox {MSE}$. However, the distance measure shows some limitation in detecting the complexity of stock markets. Further, we propose and discuss a modified method of generalized multiscale sample entropy and surrogate data analysis ($q\hbox {MSE}_\mathrm{SS}$) to measure the complexity in financial time series. The new method based on similarity and symbolic representation ($q\hbox {MSDiff}_\mathrm{SS}$) presents a different way of time series patterns match showing distinct behaviors of complexity and $q\hbox {MSDiff}_\mathrm{SS}$ curves are also presented in two ways since there are two influence factors. Simulations are conducted over both synthetic and real-world data for providing a comparative study. The evaluations show that the modified method not only reduces the probability of inducing undefined entropies, but also performs more sensitive to series with different features and is confirmed to be robust to strong noise. Besides, it has smaller discrete degree for independent noise samples, indicating that the estimation accuracy may be better than the original method. Considering the validity and accuracy, the modified method is more reliable than the original one for time series mingled with much noise like financial time series. Also, we evaluate $q\hbox {MSDiff}_\mathrm{SS}$ for different areas of financial markets. The curves versus q of Asia are greater than those of America and Europe. Moreover, American stock markets have the lowest $q\hbox {MSDiff}_\mathrm{SS}$, indicating that they are of low complexity. While the curves versus $\tau$ help to research their complexity from a different aspect, the modified method makes us have access to analyzing complexity of financial time series and distinguishing them.

1 Introduction

Recently, the study on the complexity of real data which is regulated by its environment or mechanism in both spatial and temporal domains, such as financial time series, has drawn considerable attention [1,2,3,4]. Financial time series are usually nonlinear processes where complex and chaotic behaviors frequently emerge, and it is believed that adequate methods are needed for analysis of data from such systems. Rich information is contained in financial time series, so it is an important aspect to research. A key measure of information is known as entropy, which is the rate of information production as it has a strong relation with nonlinear time series and dynamical systems. Entropy is widely applied into various fields [6,7,8,9,10] since it is a measure of degree of uncertainty to detect the system complexity and we also pay much attention to it. It is usually expressed by the average number of bits needed to store or communicate one symbol in a message [5, 11].

Many entropy-based methods have been proposed such as Boltzmann–Gibbs entropy [12, 13], transfer entropy [14, 15] and approximate entropy [16, 17] and then successfully used to investigate the features of complexity, correlation and multifractality. Pincus [16] introduced a family of measures termed approximate entropy (ApEn) for the analysis of short and noisy time series which is a regularity statistic and widely used in medicine and physiology. Sample entropy (SampEn) is a modification of approximate entropy proposed by Richman et al. [18]. It has the advantage of being less dependent on length of data and showing relative consistency over a broader range of possible values of parameters. Although these two methods both measure the degree of randomness of a time series and have been also used with short datasets [19], contradictory findings occur in real-world datasets obtained in health and disease states [20] because there is no straightforward relationship between regularity and complexity. To avoid these limitations, Costa et al. [21] introduced the multiscale entropy (MSE) to take into account the information contained in multiple scales which can present the complexity more comprehensively.

Based above, the multivariate financial time series are widely concerned in current process of quantifying the dynamical properties of the complex phenomena in financial systems. Thus, many modified methods based on SampEn and MSE have been proposed to explore the nonlinear natures of financial markets nowadays. Ahmed and Mandic introduced multivariate sample entropy (MSampEn) in order to generalize the univariate MSE to the multivariate case and evaluate its evolution over multiple time scales to perform the multivariate multiscale entropy (MMSE) analysis [22]. Moreover, MMSE has been effectively applied in analyzing the multivariate time series in financial market for the first time by Lu and Wang [23]. They quantify the complexity of four generated trivariate time series for each stock trading hour in China stock markets, including the SSE and the SZSE, for a new trial and illustrate many new findings. Mao et al. [24] also test the transfer entropy between multivariate time series and characterize the information flow among financial time series.

Theiler et al. [3] thought of surrogate data generation for nonlinearity hypothesis testing for time series analysis. This method is quoted in a new method for complex system analysis called generalized sample entropy and surrogate data analysis by Silva and Murta Jr. [25]. Generalized statistical formalism and the technique of surrogate data are combined in this method. The surrogate data are generated by simply shuffling the original time series, yielding in a time series with exactly the same time distribution but with no time correlation, and then they calculate the generalized sample entropy of original time series and surrogate ones. The generalized form of SampEn (qSampEn), a function of q parameter, gives a richer perspective to analyze the data.

Inspired by MSE, we extend the method proposed by Silva and Murta Jr to multiple scales, denoted as generalized multiscale sample entropy and surrogate data analysis ($q\hbox {MSE}$). However, we find that the distance measure, known as the infinite norm between two compared vectors, may lead to the loss of information of time series and an average idea can be more reliable. When it comes to financial time series such as stock markets, we pay attention to many aspects of information, among which complexity and the changing trend are of significance. So symbolic representation for financial time series is also in need. Since the distance between two template vectors can be inversely regarded as similarity to some extent, we develop another way to quantify the degree of similarity. Based on symbolic representation, we modify the distance measure in $q\hbox {MSE}$. At last, we further put forward a modification of $q\hbox {MSE}$ and we name it as modified generalized multiscale sample entropy and surrogate data analysis based on similarity and symbolic representation ($q\hbox {MSE}_\mathrm{SS}$). $q\hbox {MSE}_\mathrm{SS}$ is confirmed to be useful for time series mingled with much noise like financial time series by comparison of experiments with synthetic data with $q\hbox {MSE}$ and $q\hbox {MSE}_\mathrm{SS}$. Then, we apply $q\hbox {MSE}_\mathrm{SS}$ to stock markets and research their complexity.

The remainder of the paper is organized as follows. Section 2 gives a brief review to the SampEn, MSE, generalized sample entropy and surrogate data analysis and our new method of $q\hbox {MSE}$ and $q\hbox {MSE}_\mathrm{SS}$. Section 3 provides a comparative study to evaluate the effectiveness of $q\hbox {MSE}$ and $q\hbox {MSE}_\mathrm{SS}$ by using artificial time series from two aspects. Section 4 is devoted to apply $q\hbox {MSE}_\mathrm{SS}$ to real-world data and illustrate our analysis. Finally, conclusions are made in Sect. 5.

2 Methodology

2.1 Sample entropy and multiscale sample entropy

The multiscale sample entropy (MSE) is proposed on the basis of sample entropy (SampEn) by Costa et al. [21]. Firstly, we briefly review the SampEn [18]. Let N be the length of the time series, m be the length of sequences to be compared, and r be the tolerance for accepting matches. Given a time series $\varvec{x}=\{x_{1},x_{2},\ldots , x_{N}\}$ of N points, the SampEn method is summarized as follows:

Step 1 Construct template vectors $x_{m}(i)$ through the sets of points $\varvec{x}$ from i to $i+m-1$ with dimension m

$$\begin{aligned} x_{m}(i)=\{ x_{i+k}:0\le k\le m-1 \},\quad 1\le i\le N-m. \end{aligned}$$

(1)

Step 2 For each $x_{m}(i)$, the distance between vectors $x_{m}(i)$ and $x_{m}(j)$ is defined by the infinite norm:

$$\begin{aligned} d(x_{m}(i), x_{m}(j))= & {} \max \{|x_{i+k}-x_{j+k}|:0\le k\le m-1 \},\nonumber \\&\quad 1\le i,j\le N-m,j\ne i. \end{aligned}$$

(2)

Step 3 An instance where a vector $x_{m}(j)$ is within r of $x_{m}(i)$ is called a m-dimensional template match. To exclude self-matches, we must have $j\ne i$. Next, we give a specific definition. For $x_{m}(1)$, count the number of template matches $n_{1}^{(m)}$, then from $x_{m}(2)$ to $x_{m}(N-m)$, obtain the number of template matches for themselves in turn. $n^{(m)}$ is defined as the sum of $n_{i}^{(m)}$ ($1\le i \le N-m$). Finally, let $n^{(m)}$ be the total number of m-dimensional template matches. Repeat the above process for $m=m+1$, and $n^{(m+1)}$ is obtained to represent the total number of $m+1$-dimensional template matches.

Step 4 Sample entropy is defined with the equation:

$$\begin{aligned} SampEn(\varvec{x},m,r,N)=\ln n^{(m)}(r)- \ln n^{(m+1)}(r) \end{aligned}$$

(3)

In the MSE method, we first use coarse-graining procedure to construct consecutive coarse-grained time series $\varvec{y^\tau }$ from the original time series $\varvec{x}$ on different scale factor $\tau$.

$$\begin{aligned} \begin{aligned} \varvec{y^\tau }&=\{y_{1}^{\tau }, y_{2}^{\tau }, \ldots , y_{p}^{\tau }\},\\ \mathrm{where} \; y_{j}^{\tau }&= \frac{1}{\tau }\sum _{i=(j-1)\tau +1}^{j\tau }x_{i}, \quad 1\le j\le N/\tau . \end{aligned} \end{aligned}$$

(4)

For scale factor $\tau =1$, the time series $\varvec{y^1}$ is the original series $\varvec{x}$. Then, for each given $\tau$, the original series is divided into $N/\tau$ coarse-grained series [27]. For each coarse-grained series $\varvec{y^\tau }$, the MSE is defined by the SampEn algorithm.

$$\begin{aligned} \hbox {MSE}(\varvec{x},m,r,N,\tau )=\ln n^{(m)}(r,\tau )- \ln n^{(m+1)}(r,\tau ). \end{aligned}$$

(5)

2.2 Generalized sample entropy and surrogate data analysis

Silva and Murta Jr. proposed a new method for complex system analysis which is called generalized sample entropy and surrogate data analysis in [25]. It offers a window into the complex system from a new perspective [28] and allows us to gain a new insight of the complexity analysis.

Inspired by Tsallis generalized entropy, a kind of nonadditive statistics [12], they rewrite SampEn as a function of q parameter. Tsallis entropy ($S_{q}$), a generalization of Boltzmann–Gibbs–Shannon (BGS) entropy [13], has proven to be suitable for complex and multifractal systems since it exceeds the domain of applicability for classical BGS entropy [29]. The discrete form of $S_{q}$ is given by

$$\begin{aligned} S_{q}=\frac{1-\sum _{i=1}^{W}p_{i}^{q}}{q-1}, \end{aligned}$$

(6)

or

$$\begin{aligned} S_{q}=\sum _{i}^{W}p_{i}log_{q}(1/p_{i}), \end{aligned}$$

(7)

where $p_{i}$ is the probability that the system has in state i, W is the amount of possible states of the system, and q is the entropic index. Equation (2) further derives the general form for logarithm function [26], namely, q-logarithm, defined as

$$\begin{aligned} \begin{aligned} \hbox {log}_{q}(x)&=\frac{x^{1-q}-1}{1-q},\\ (x\in \mathbb {R}_{+}^{*}; q\in \mathbb {R}; \mathrm{log}_{1}(x)&=log(x)). \end{aligned} \end{aligned}$$

(8)

Then, consider the time series $\varvec{x}$, qSampEn is defined as

$$\begin{aligned} qSampEn(\varvec{x},m,r,N,q)= & {} \hbox {log}[n^{(m)}\oslash _{q}n^{(m+1)}]\nonumber \\= & {} \hbox {log}_{q}n^{(m)}(r)\nonumber \\&-\hbox {log}_{q}n^{(m+1)}(r). \end{aligned}$$

(9)

Generalized sample entropy and surrogate data analysis is divided into four steps as follows:

Step 1:

Generate 100 surrogate series for each given time series by shuffling the original signal.

Step 2:

Calculate qSampEn for each surrogate series and their mean values, denoted as $qSampEn_{\overline{\mathrm{surr}}}$.

Step 3:

Calculate qSampEn for original time series, denoted as $qSampEn_\mathrm{orig}$.

Step 4:

Calculate the difference:

$$\begin{aligned} qSDiff=qSampEn_\mathrm{orig}-qSampEn_{\overline{\mathrm{surr}}}. \end{aligned}$$

They use qSDiff to evaluate the influence of the entropic index of qSampEn. And it is obtained vs. entropic index q so that we can assess the contribution of this index.

2.3 Generalized multiscale sample entropy and surrogate data analysis ($q\hbox {MSE}$)

We extend the algorithm to multiscale analysis,

$$\begin{aligned} q\hbox {MSE}(\varvec{x},m,r,N,q,\tau )&=log[n^{(m)}\oslash _{q}n^{(m+1)}]\nonumber \\&=log_{q}n^{(m)}(r,\tau )\nonumber \\&\quad -log_{q}n^{(m+1)}(r,\tau ), \end{aligned}$$

(10)

then generalized multiscale sample entropy and surrogate data analysis is divided into four steps as follows:

Step 1:

Generate 100 surrogate series for each given time series by shuffling the original signal.

Step 2:

Calculate $q\hbox {MSE}$ for each surrogate series and their mean values, denoted as $q\hbox {MSE}_{\overline{\mathrm{surr}}}$.

Step 3:

Calculate $q\hbox {MSE}$ for original time series, denoted as $q\hbox {MSE}_\mathrm{orig}$.

Step 4:

Calculate the difference:

$$\begin{aligned} q\hbox {MSDiff}=q\hbox {MSE}_\mathrm{orig}-q\hbox {MSE}_{\overline{\mathrm{surr}}}. \end{aligned}$$

When $q=1$, $q\hbox {MSE}$ becomes the original method that Silva and Murta Jr. have proposed.

2.4 Modified generalized multiscale sample entropy and surrogate data analysis based on similarity and symbolic representation ($q\hbox {MSE}_\mathrm{SS}$)

Furthermore, if we want to investigate the trend for financial time series, we think of similarity and symbolic representation. In this way, we propose a modified method based on $q\hbox {MSE}$ to quantify the degree of similarity and complexity correspondingly. The new method, modified multiscale sample entropy based on similarity and symbolic representation, consists of the following procedures:

Firstly, construct consecutive coarse-grained time series $\varvec{x^\tau }$ with the scale factor $\tau$ by Eq. (4) and symbolize $\varvec{x^\tau }$. We get 1 if the component of $\varvec{x^\tau }$ is positive, otherwise we get 0. In this way, a binary representation $\varvec{y^\tau }$ is obtained. For practical study, 1 represents the increase of the stock market so it has a practical purpose.

Secondly, get template vectors $y^\tau _{m}(i)$ with an overlapped sliding window of length m from the signed series $\varvec{y^\tau }$ by Eq. (1):

Thirdly, define two functions f and s to calculate the similarity between two template vectors. f is a symbolic function between two template vectors $y^\tau _{m}(i)$ and $y^\tau _{m}(j)$ such that we will obtain a binary vector $count^\tau _{m}(i,j)$ of length m where there is a 1 in the position which the corresponding scalar components of two template vectors are equal.

$$\begin{aligned} f=\left\{ \begin{array}{ll} 0&{}\quad \text {if }y^\tau _{m}(i+k)\ne y^\tau _{m}(j+k),\\ 1&{}\quad \text {if }y^\tau _{m}(i+k)= y^\tau _{m}(j+k). \end{array}\right. \end{aligned}$$

The similarity s of the two compared vectors under the function f is as follows:

$$\begin{aligned}&s(y^\tau _{m}(i),y^\tau _{m}(j))=\frac{\#\,\mathrm{of} \ 1 \mathrm{in count}^\tau _{m}(i,j)}{m},\nonumber \\&\quad \quad 1\le i,j\le N-m,\quad j\ne i. \end{aligned}$$

(11)

Then, we count template matches. An instance where a vector $y^\tau _{m}(j)$ is beyond r of $y^\tau _{m}(i)$ is called a m-dimensional template match. Here, the condition ji guarantees that self-matches are excluded. For $y^\tau _{m}(1)$, we count the number of template matches named as $n_{1}^{(m)}$ by comparing $s(y^\tau _{m}(1),y^\tau _{m}(j))$ and r, then from $y^\tau _{m}(2)$ to $y^\tau _{m}(N-m)$, we get the number of template matches for themselves in turn. The sum of $n_{i}^{(m)}$ ($1\le i \le N-m$) is assigned to $n^{(m)}$. Finally, let $n^{(m)}$ represent the total number of m-dimensional template match. Repeat the above process for $m=m+1$, and the total number of $m+1$-dimensional template matches is set to $n^{(m+1)}$.

Finally, the modified generalized multiscale sample entropy is

$$\begin{aligned} q\hbox {MSE}_\mathrm{SS}(\varvec{x},m,r,N,q,\tau )= & {} \hbox {log}[n^{(m)}\oslash _{q}n^{(m+1)}]\nonumber \\= & {} \hbox {log}_{q}n^{(m)}(r,\tau )\nonumber \\&-\hbox {log}_{q}n^{(m+1)}(r,\tau ). \end{aligned}$$

(12)

Modified generalized multiscale sample entropy and surrogate data analysis based on similarity and symbolic representation is also divided into four steps as follows:

Step 1:

Generate 100 surrogate series for each given time series by shuffling the original signal.

Step 2:

Calculate $q\hbox {MSE}_\mathrm{SS}$ for each surrogate series and their mean values, denoted as $q\hbox {MSE}_{\mathrm{SS}\, \overline{\mathrm{surr}}}$.

Step 3:

Calculate $q\hbox {MSE}_\mathrm{SS}$ for original time series, denoted as $q\hbox {MSE}_{{\mathrm{SS}\, orig}}$.

Step 4:

Calculate the difference:

$$\begin{aligned} q\hbox {MSDiff}_\mathrm{SS}=q\hbox {MSE}_{\mathrm{SS\,orig}}-q\hbox {MSE}_{\mathrm{SS}\, \overline{\mathrm{surr}}}. \end{aligned}$$

In the new method, $q\hbox {MSDiff}_\mathrm{SS}$ is assigned to evaluate the influence of the entropic index and the scale factor of $q\hbox {MSE}_\mathrm{SS}$. And it is obtained versus entropic index q and scale factor $\tau$ giving us access to researching the contribution of these two parameters, respectively. The choice of threshold r is very important for our study due to the change of similarity measure. On the premise that n is the maximum number of 0, we can tolerate in $\hbox {count}^\tau _{m}(i,j)$, we set $m=2$, $n=1$, and r as follows for the modified method:

$$\begin{aligned} r=\frac{1}{2}\left( \frac{m-n}{m+1}+\frac{m-n}{m}\right) . \end{aligned}$$

(13)

3 Comparative study

3.1 Accuracy test

Here, we apply 1/f noise to evaluate the effectiveness of the two methods $q\hbox {MSE}$ and $q\hbox {MSE}_\mathrm{SS}$ since a previous study [30] has demonstrated the reliability of this kind of noise. All the values are obtained for 30 independent 1/f noise samples; the length of each sample is 2000 or 4000.

Table 1 Means, SDs and CVs of qMSDiff at different q for 1/f noises

Table 2 Means, SDs and CVs of $q\hbox {MSDiff}_\mathrm{SS}$ at different q for 1/f noises

Tables 1 and 2 show the means, standard deviations (SDs) and coefficients of variation (CVs) of qMSDiff and $q\hbox {MSDiff}_\mathrm{SS}$ obtained vs. entropic index q. q varies from − 2 to 2 with step of 0.5. It is obvious that the absolute values of means and SDs both increase as q increases. The means for $q\hbox {MSE}$ when $q=1.5$ and 2 are extremely high; they change a lot compared with other q values, and this is totally unscientific when applied into real data. So $q\hbox {MSE}$ may lose validity at certain q values. However, this limitation doesn’t occur for $q\hbox {MSE}_\mathrm{SS}$. The CVs for both method remain a state of decrease with q increasing. For CVs under these two different length, note that they are relatively small at the longer length 4000, meaning that results for each simulation are much more concentrated. What’s more, the CVs for $q\hbox {MSDiff}_\mathrm{SS}$ under length 2000 and 4000 are both lower than those for qMSDiff, indicating that the modified method $q\hbox {MSE}_\mathrm{SS}$ has smaller discrete degree, and thus the estimation accuracy may be better than $q\hbox {MSE}$.

Tables 3 and 4 represent these three statistics of qMSDiff and $q\hbox {MSDiff}_\mathrm{SS}$ obtained vs. scale factor $\tau$. $\tau$ varies from 1 to 10 with step of 1. Different results are found with comparison to Tables 1 and 2. The CVs for both method remain a state of increase with the increase in $\tau$. However, there exists a similar evaluation that they are relatively small at the longer length 4000, meaning that results for each simulation are much more concentrated. We also notice the CVs for $q\hbox {MSDiff}_\mathrm{SS}$ under length 2000 and 4000 are both lower than those for qMSDiff. The absolute values of means for $q\hbox {MSE}$ roughly decrease when $\tau$ increases except for the scale factor 5 under length of 2000 which may mean 1/f noise lose complexity at large scales. As far as we are concerned [20], the complexity of 1/f noise almost remains unchanged or becomes large since it has nonstationarity and no regularity. So $q\hbox {MSE}$ describes its feature not well. However, the results for $q\hbox {MSDiff}_\mathrm{SS}$ are much more reliable and they fit in with the irregularity that the samples have.

Table 3 Means, SDs and CVs of qMSDiff at different $\tau$ for 1/f noises

Table 4 Means, SDs and CVs of $q\hbox {MSDiff}_\mathrm{SS}$ at different $\tau$ for 1/f noises

3.2 Sensitivity test

In this subsection, experiments with synthetic data, logistic map, are performed by comparison test to show the sensitivity of different kinds of data and resistance to the noise for $q\hbox {MSE}$ and $q\hbox {MSE}_\mathrm{SS}$. The logistic map, a polynomial mapping (equivalently, recurrence relation) of degree 2, often cited as an archetypal example of how complex, chaotic behavior can arise from very simple nonlinear dynamical equations is a well-known archetypal example. Mathematically, the logistic map is written as

$$\begin{aligned} x_{i+1}=ax_{i}(1-x_{i}). \end{aligned}$$

(14)

We are keenly aware of the rich dynamics logistic map has in different ranges. For each value of a, we analyze a time series of length 2000 where the control parameter $a\in [3.5,4]$ with a step size $\Delta a = 0.1$. Evaluations are conducted on two aspects including entropic index q and scale factor $\tau$. White noise of standard deviation 0.01 and mean 0 is then added to the original time series to research the resistance for two methods.

Figure 1 presents the surfaces of qMSDiff (Fig. 1a) and $q\hbox {MSDiff}_\mathrm{SS}$ (Fig. 1b) versus entropic index q for logistic map with the control parameter $a\in [3.5,4]$. For all values of a, the curves of qMSDiff share a same changing trend with q. At negative q values, they are almost zero and then reach a maximum for $0<q<1$. We can’t see the maximum clearly because the value is also very small. The curves of qMSDiff begin to decrease after they reach the maximum. Although the trend is the same, the extent of the decline of different qMSDiff curves varies. That is the only way of distinguishing time series with different a. However, the rich dynamics of the logistic map should have been exhibited from various aspects, so the qMSDiff is not sensitive to the changes of dynamics for logistic map. Compared with the curves of qMSDiff, those of $q\hbox {MSDiff}_\mathrm{SS}$ are much more abundant. Different trends for time series with various a and q spread out. For time series with a from 3.5 to 3.65, $q\hbox {MSDiff}_\mathrm{SS}$ are negative with all q values and they show a decreasing trend with the increasing q. When a is beyond of 3.65, richer features for logistic map appear. There is also a trend analogous to that of qMSDiff, first almost remains unchanged and begins decreasing after reaching a maximum. When a becomes 3.8, the $q\hbox {MSDiff}_\mathrm{SS}$ curves show a monotonically increasing trend and they are all positive. The extent of increase begins to reduce when a is larger and with a about 4, the $q\hbox {MSDiff}_\mathrm{SS}$ curves almost remains close to 0. That means complexity is not lost even in the shuffled version of time series. Different trends of curves and the extents of these trends can be used to characterize and distinguish series. The modified method contains rich information of time series.

Next, we will take a look at the test of two methods in the face of noise. Results are shown in Fig. 2 (surfaces of qMSDiff (Fig. 2a) and $q\hbox {MSDiff}_\mathrm{SS}$ (Fig. 2b) against white noise versus entropic index q). It is obvious that the modified method is robust to noise since the curves almost remain unchanged. There is also no change about the trends with the original method, but the specific values of qMSDiff against white noise change a lot compared to those calculated with original time series. Besides, there are many points disappeared when a is larger than 3.65 which is a fact of significance attention. Undefined entropy occurs when noise is fit in the time series. When we explore the complexity of time series, this kind of limitation will affect the result. So qMSDiff performs worse than $q\hbox {MSDiff}_\mathrm{SS}$ not only in the description of time series with various features, but also in the presence of noise.

To get a comparison of MSE and our method, we set $q=1$ and only test on the original series (logistic series x4 with $a=3.8$ is selected) instead of shuffling the data, our method is then denoted as MSE$_\mathrm{SS}$. For logistic series x4 with $a=3.8$, we add different degrees of noise to it and test the MSE and MSE$_\mathrm{SS}$ at certain scale. Each case of experiments is carried out 500 times independently, and through the means and error bars of sample entropies, we give a comparison from Fig. 3.

Symbolic representation allows us to view the time series from an aspect not so concrete, leading to a relatively small entropy value compared to MSE. Correspondingly, we reduce the complexity to some extent. With the degree of noise increasing, entropies calculated by MSE algorithm go with a sustainable growth, illustrating that MSE algorithm is sensible to noise. While entropies calculated by MSE$_\mathrm{SS}$ algorithm almost remain unchanged, MSE$_\mathrm{SS}$ has a stronger resistance for noise than MSE. Besides, the error bars for MSE$_\mathrm{SS}$ is lower than those of MSE, also indicating that the results by MSE$_\mathrm{SS}$ are more consistent than those by MSE. Next, we will test the performance of qMSDiff and $q\hbox {MSDiff}_\mathrm{SS}$.

Fig. 1

qMSDiff surface (a) and $q\hbox {MSDiff}_\mathrm{SS}$ surface (b) calculated for logistic map with the control parameter $a\in [3.5,4]$ and the entropic index $q\in [-\,2,2]$

Fig. 2

qMSDiff surface (a) and $q\hbox {MSDiff}_\mathrm{SS}$ surface (b) calculated for logistic map in the face of noise with the control parameter $a\in [3.5,4]$ and the entropic index $q\in [-\,2,2]$

Fig. 3

Mean of the MSE analysis (up) and MSE$_\mathrm{SS}$ analysis (down) for logistic series x4 with $a=3.8$ in face of noise

In order to better show the surfaces of qMSDiff (Fig. 4a) and $q\hbox {MSDiff}_\mathrm{SS}$ (Fig. 4b) versus scale factor $\tau$ for logistic map, we choose some specific values of parameter a. As we all know, with a between 3.449 and 3.544, from almost all initial conditions the population will approach permanent oscillations among four values resonating with the periodicity. When a is beyond 3.569, logistic map is the onset of chaos, at the end of the period-doubling cascade. At last, four groups of logistic map time series ($a=3.5$ for {x1},$a=3.6$ for {x2},$a=3.7$ for {x3}, $a=3.8$ for {x4}) are considered. Distinct features of four groups series are well shown in two methods. We can distinguish these four groups series due to the different information they possess. The two methods both present the periodicity of {x1}. The difference between {x1} and {x2} is not obvious in Fig. 4a, while we can easily distinguish them in Fig. 4b since there exists scale invariance for {x1} at certain scales. Both {x3} and {x4} are kinds of chaos except for the extent, so it is difficult to separate them if we directly observe the original time series. Such limitation also occurs in Fig. 4a, in which the curves are very similar. However, by using $q\hbox {MSE}_\mathrm{SS}$ in Fig. 4b, this problem is solved since {x4} is much more irregular and $q\hbox {MSDiff}_\mathrm{SS}$ values gradually stabilize with the scale factor increasing.

Figure 5 shows us the test of $q\hbox {MSE}$ (Fig. 5a) and $q\hbox {MSE}_\mathrm{SS}$ (Fig. 5b) when noise is added to the original four group time series. Values obtained by $q\hbox {MSE}_\mathrm{SS}$ change a little compared with those without noise except for {x1} under the scale factor of 4 and 8. Since {x1} have periodicity, noise may have a relatively big affect at certain scales. Curves of $q\hbox {MSE}$ are not as well as those of $q\hbox {MSE}_\mathrm{SS}$. It seems that noise has a big influence for this method. Although there is no big change for {x1} and {x2}, the trend of {x3} changes a lot. Besides, there is a undefined entropy for {x3} at scale 1. For {x4}, more undefined entropy occurs making us have no access to the research of complexity. So $q\hbox {MSE}$ is not reliable for time series with less regularity and it may lose accuracy for time series mingled with much noise like financial time series.

Fig. 4

qMSDiff surface (a) and $q\hbox {MSDiff}_\mathrm{SS}$ surface (b) calculated for logistic map with the control parameter $a\in [3.5,4]$ and the scale factor $\tau \in [1,10]$

Fig. 5

qMSDiff surface (a) and $q\hbox {MSDiff}_\mathrm{SS}$ surface (b) calculated for logistic map in the face of noise with the control parameter $a\in [3.5,4]$ and the scale factor $\tau \in [1,10]$

From the comparison, we can see that $q\hbox {MSE}_\mathrm{SS}$ performs better in characterizing time series containing rich information and has a much more accurate result.

4 Results and discussions

4.1 Real-world data

Financial time series usually are considered with high complexity. Nowadays, stock markets have been more and more attracted to investigators. In this section, we apply the modified method $q\hbox {MSE}_\mathrm{SS}$ to real-world data to research the complexity and similarity between stock markets. The daily records of six stock exchange indices during the period 2006–2016 are obtained from Yahoo Finance. Here, we use log-returns as proxies for volatility of stock exchange indices. Let $\varvec{S}=\{S_{1},S_{2},\ldots , S_{n}\}$ be the vector of daily indexes, and use the log-return of $\varvec{S}$ to obtain $\varvec{x}=\{x_{1},x_{2},\ldots , x_{N}\}$ of length N which describes the financial time series.

$$\begin{aligned} x_i=\ln S{_{i+1}}-\ln S{_i},\quad 1\le i\le N(=n-1). \end{aligned}$$

(15)

The datasets consist of HSI (Hang Seng Index, Asia), SSE (SSE Composite Index, Asia), DJI (Dow Jones Industrial Average, America), S&P500 (S&P 500 Index, America), CAC40 (Cotation Assiste en Continu 40, Europe) and SMI (Swiss Market Index, Europe). The index values are nonstationary and may provide bad results in stock analysis. So we take the log-returns of indices as the objectives to smooth the sequence. Besides, log-returns have its practical purpose in financial analysis. On the basis of mathematical analysis, it can be seen as the relative return of stocks. The log-returns of six stock markets are presented in Fig. 6.

Fig. 6

Log-returns of HSI (a), SSE (b), DJI (c), S&P500 (d), CAC40 (e) and SMI (f) during the period 2006–2016

4.2 Complexity analysis with $q\hbox {MSE}_\mathrm{SS}$ and $q\hbox {MSDiff}_\mathrm{SS}$

Figure 7 displays the relation between $q\hbox {MSDiff}_\mathrm{SS}$ obtained by $q\hbox {MSE}_\mathrm{SS}$ algorithm and the entropic index q. Results indicate that stock markets in Asia, like HSI and SSE, have relatively large qSDiff$_\mathrm{SS}$ values compared with the other four stock markets. qSDiff$_\mathrm{SS}$ values for HSI and SSE are close to zero or positive, while others’ are negative. As is known to us, in the shuffled version of time series with regularity, the regularity of time series is lost so that the $q\hbox {MSDiff}_\mathrm{SS}$ should be negative. The performance of DJI, S&P500, CAC40 and SMI all makes sense. The zero or positive values of HSI and SSE indicate us when the stock markets are shuffled, the regularity or irregularity is remained, meaning that they may have higher complexity. When q is increasing, the six stock markets show different changing tendency. $q\hbox {MSDiff}_\mathrm{SS}$ values of American markets and European markets decrease with the increasing q, while Asian markets have no tendency of decreasing. The extent of decline of American markets and European markets is different; we can see that $q\hbox {MSDiff}_\mathrm{SS}$ of DJI and S&P500 falls faster than CAC40 and SMI. It seems that American markets have the lowest complexity. Besides, stock markets from different areas are completely separated and $q\hbox {MSDiff}_\mathrm{SS}$ values of the markets in the same area are much closer. That means stock markets in the same area are more likely to share a similar complexity and there exists similarity among them. This is also consistent with facts because the business behavior of the stock markets in the same area are influenced by similar rules and the mutual influence between markets [24].

Fig. 7

qSDiff$_\mathrm{SS}$ data plotted versus q parameter for SSE, HSI, DJI, S&P500, CAC40 and SMI

Figure 8 shows us the relation between $q\hbox {MSDiff}_\mathrm{SS}$ obtained by $q\hbox {MSE}_\mathrm{SS}$ algorithm and the scale factor $\tau$. Stock markets from the same area tend to have a similar change when observed with a scale factor. Obviously, the six group data are divided into three types due to their diverse features. At scale factor $\tau =1$, also the six points at $q=1$ in Fig. 7, the order from big to small of $q\hbox {MSDiff}_\mathrm{SS}$ is SSE, HSI, CAC40, SMI, DJI and S&P500. $q\hbox {MSDiff}_\mathrm{SS}$ values of SSE and HSI are close to 0 with $\tau$ varying from 1 to 8, and it indicates that the two stock markets may have the scale invariance considering the surrogate data analysis. Earlier researches find that generally sample entropy decreases with the increasing $\tau$. On the one hand, some positive and negative data in calculation are offset in multiscale analysis of log-return series for sample entropy and this makes the entropy decrease [24]. On the other hand, when stock markets are seen under large scales, original series is highly coarse-grained and the information contained reduces causing a smaller entropy which just goes to show stock markets are less complex. The scale invariance aware us of the fact that complexity is not lost under large scales. Shuffled data are also complex, and for this reason the entropy for SSE and HSI of original series is almost the same as that of shuffled series. So the $q\hbox {MSDiff}_\mathrm{SS}$ is close to 0. For SSE at $\tau =10$ and HSI at $\tau =9$, the shuffled series may show more regularity than original series, so the difference is positive. If $q\hbox {MSDiff}_\mathrm{SS}$ curves remain almost unchanged with scale factor, then the series is believed to have high complexity.

Curves of DJI and S&P500 both have a peak value, and they appear at $\tau =3$&4. The peak value may mean that series have a higher complexity. After the appearance of peak values, $q\hbox {MSDiff}_\mathrm{SS}$ of DJI begins to decrease while $q\hbox {MSDiff}_\mathrm{SS}$ of S&P500 first decreases like DJI at the next scale and then increases. Monotonic changes after peak values both can give a reflection on the change of complexity due to the scale factor. The negative values show a lower complexity. So the complexity of S&P500 is considered to increase at large scales. Peak values also occur for curves of CAC40 and SMI. Besides, there are two peak values for each stock market. $q\hbox {MSDiff}_\mathrm{SS}$ values of CAC40 are all negative except for those with scale factor $\tau =4$&9. The two positive points indicate higher complexity than others. $q\hbox {MSDiff}_\mathrm{SS}$ values of SMI are all negative except for those with scale factor $\tau =5$&8. This interesting phenomenon of peak values makes us think about periodicity. Peak values correspond to the scale factor where the complexity begins to change. When we deal with series with scale factor $\tau =4$&5, we take 4 or 5 days’ information as a whole and the information contained in the next trading day may be the same as that in the first day. Then, the scale factor $\tau =8$&9 can also be a signal of periodicity. Different stock markets’ periodicity may be different due to unknown factors such as level of development and system mechanism. As a result, $q\hbox {MSDiff}_\mathrm{SS}$ values against the scale factor can also be applied to research the complexity and distinguish stock markets of different areas.

Fig. 8

qSDiff$_\mathrm{SS}$ data plotted versus scale factor $\tau$ for SSE, HSI, DJI, S&P500, CAC40 and SMI

We extend the MSE$_\mathrm{SS}$ to multivariate situations to get a comparison with Lu [23] and apply it into real-world data and select the high-frequency (5-min interval) returns of Shanghai Stock Exchange (SSE) and Shenzhen Stock Exchange (SZSE) from November 1, 2013 to February 18, 2016 with 26784 data points (5-min returns) to research the complexity in stock markets. The 5-min interval records are obtained from Wind database. We also use log-returns as proxies for volatility of stock exchange indices.

Fig. 9

$q\hbox {MSE}_\mathrm{SS}$ analysis of $Y_{1}$ (up) and $Y_{2}$ (down) for SSE and SZSE

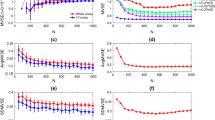
SSE and SZSE trade 4 h a day, so there are 48 high-frequency (5-min interval) data every trading day. For multivariate analysis, we divide the 48 5-min returns into 12 groups and there are four 5-min returns contained in each group. By connecting each group of data with the corresponding set of data on the same time of the next day, we can generate 12 groups of 5-min return series, denoted as $X_{1},X_{2},X_{3},\ldots ,X_{12}$. In each group, there are 2232 data points. At last, let $Y_{1}=[X_{1},X_{2},X_{3}]$ for the 1st hour, $Y_{2}=[X_{4},X_{5},X_{6}]$ for the 2nd hour, $Y_{3}=[X_{7},X_{8},X_{9}]$ for the 3rd hour, $Y_{4}=[X_{10},X_{11},X_{12}]$ for the 4th hour and we generate 4 trivariate time series in this way. Then, we show an analysis for the 4 trivariate time series from SSE and SZSE and make a comparison. Results are shown in Figs. 9 and 10. Figure 11 represents the mean of entropy values for $Y_{1},Y_{2},Y_{3},Y_{4}$ of SSE and SZSE.

We can see that all of the $q\hbox {MSE}_\mathrm{SS}$ curves decrease with the increasing scale factor except for some certain scales, which means that the multivariate return series contain more useful information at the smaller scales. It follows the rule that the higher the degree of coarse-grained, the smaller the resolution. In this study, the degree of coarse-grained exactly show the scale factor. So they contain less information at large scales. Besides, the $q\hbox {MSE}_\mathrm{SS}$ values of four trivariate time series from the SZSE are correspondingly larger than those from the SSE. Generally, a lower entropy means less complexity, indicating that the stock returns in each hour from the SZSE are more dynamically complex than those from the SSE. We also have some findings that different from some traditional conclusions. There is not a trend of monotonic decreases when the scale factor increases. At some certain scale, for instance, $\tau =6$, 11, the $q\hbox {MSE}_\mathrm{SS}$ values begin to increase. At scale $\tau =6$, the entropy value begins to increase, and the state lasts for 4 scales. At scale $\tau =11$, the entropy value begins to increase again, and the state lasts until we increase $\tau$ to 20. We can get different information through different scales, and the scale factor where the entropy value began to increase is an important point for periodicity. When $\tau =5$, we take 1 week’s information together, the contained information may have similarity with that of the previous week.

The $q\hbox {MSE}_\mathrm{SS}$ values for $Y_{1},Y_{2},Y_{3},Y_{4}$ at scale $\tau =1$ from the SSE are 0.22259, 0.20828, 0.20564, 0.19458, and the $q\hbox {MSE}_\mathrm{SS}$ values for $Y_{1},Y_{2},Y_{3},Y_{4}$ at scale $\tau =1$ from the SZSE are 0.23733, 0.23452, 0.23193, 0.20216. Moreover, at each scale, the values for $Y_{1},Y_{2},Y_{3},Y_{4}$ have a tendency of decreasing, so the system complexity of SSE and SZSE in the forenoon is significantly higher than that in the afternoon. The difference between $q\hbox {MSE}_\mathrm{SS}$ values of $Y_{1}$ for the two markets is lower than those of $Y_{2}$. Similar findings are found for $Y_{3}$ and $Y_{4}$, showing that the markets are more complex when the trading begins than when the trading has begun for some time. From Fig. 11, we can say the SSE is of less complexity than the SZSE to some extent.

Fig. 10

$q\hbox {MSE}_\mathrm{SS}$ analysis of $Y_{3}$ (up) and $Y_{4}$ (down) for SSE and SZSE

Fig. 11

Mean of $q\hbox {MSE}_\mathrm{SS}$ of $Y_{1},Y_{2},Y_{3},Y_{4}$ for SSE and SZSE

5 Conclusion

In this paper, inspired by MSE [21] and generalized sample entropy and surrogate data analysis [22], we introduce a new method, called generalized multiscale sample entropy and surrogate data analysis ($q\hbox {MSE}$), which is just the combination. To better research the complexity and the changing trend of series mingled with much noise, we develop $q\hbox {MSE}$ through symbolizing time series and modifying the distance measure to a modified method and we name it as modified generalized multiscale sample entropy and surrogate data analysis based on similarity and symbolic representation ($q\hbox {MSE}_\mathrm{SS}$).

The effectiveness tests of the two new methods are provided with two kinds of synthetic data. Results of 1/f noise obtained by surrogate data analysis qMSDiff and $q\hbox {MSDiff}_\mathrm{SS}$ indicate the modified method $q\hbox {MSE}_\mathrm{SS}$ has smaller discrete degree and can describe its feature better; thus, the estimation accuracy may be better than $q\hbox {MSE}$. qMSDiff and $q\hbox {MSDiff}_\mathrm{SS}$ values are calculated individually against entropic index q and scale factor $\tau$. Experiments with logistic map are also performed by comparison test to show the sensitivity of different kinds of data and resistance to the noise for $q\hbox {MSE}$ and $q\hbox {MSE}_\mathrm{SS}$. It is observed that $q\hbox {MSE}$ is not sensitive to the changes of dynamics for logistic map, while the modified method contains rich information of time series and better characterize original time series. When we add a noise of the same extent to logistic map, qMSDiff values by $q\hbox {MSE}$ change a lot and even cause the appearance of undefined entropy. $q\hbox {MSE}_\mathrm{SS}$ can perfectly avoid the problem due to the application of symbolization in it. Moreover, it shows a good robustness to noise so it can be used to the analysis of series with much noise like financial time series.

The disadvantage of symbolic representation of time series is that it may lose some information since we are not dealing with original data directly, but the new approach pays more attention to the trend of series so symbolic representation is reliable. When we consider a symbolic representation of a time series, we should decide the number of symbols according to the actual needs. Considering a financial series, the most important information we want to get is whether it will increase or not. So two symbols are enough to meet our demand.

Real-world data of six stock markets including SSE, HSI, DJI, S&P500, CAC40 and SMI are also tested to measure the complexity. $q\hbox {MSDiff}_\mathrm{SS}$ values are calculated versus entropic index q and scale factor $\tau$ correspondingly. Considering $q\hbox {MSDiff}_\mathrm{SS}$ values versus entropic index q, HSI and SSE have relatively large $q\hbox {MSDiff}_\mathrm{SS}$ values compared with the other 4 stock markets. Curves of HSI and SSE almost have no change with the increasing q, while those of DJI, S&P500, CAC40 and SMI all decrease. Further, the extent of decline of the four stock markets is different. American markets fall faster than European markets. Correspondingly, American stock markets have a less complex feature. Besides, stock markets from different areas are completely separated and $q\hbox {MSDiff}_\mathrm{SS}$ values of the markets in the same area are much closer. We consider that stock markets in the same area exist similarity. $q\hbox {MSDiff}_\mathrm{SS}$ values versus scale factor $\tau$ give more information of stock markets from another aspect. Six stock markets are divided into three types due to their diverse features which just correspond to their location. $q\hbox {MSDiff}_\mathrm{SS}$ values of SSE and HSI tend to have a scale invariance except for some very large scales. Complexity is still remained with the scale changing. So Asian markets are the most complex. Curves of DJI and S&P500 both have a peak value where the series have a higher complexity. Then, $q\hbox {MSDiff}_\mathrm{SS}$ of DJI begins to decrease, while $q\hbox {MSDiff}_\mathrm{SS}$ of S&P500 first decreases like DJI at the next scale and then increases. So the complexity of S&P500 is considered to increase at large scales and DJI has a low complexity with a relatively large scale. There are two peak values for each stock market of CAC40 and SMI, and $q\hbox {MSDiff}_\mathrm{SS}$ values of them are all negative except the two peak values. Scale factors with peak values show a periodicity of stock markets, and they are points where the complexity begins to change.

$q\hbox {MSDiff}_\mathrm{SS}$ values against entropic index q and scale factor $\tau$ can both be used to explore the complexity and distinguish stock markets of different areas. There are still many other areas that need further study. Symbolization method can be developed according to the data from different fields. It will also be a good attempt to combine the proposed method in this paper with some other entropy-based methods.