Nonlinear dynamics and flutter of plate and cavity in response to supersonic wind tunnel start

Abstract

The transient response of a plate and a cavity is investigated in a supersonic wind tunnel start experiment where the freestream flow inside the test section reaches turbulent flow at Mach 2. Experimentally measured plate displacement time history shows flutter onset, transition to limit cycle oscillation, and stabilization at a static deformed state during the 30 s run. To analyze and interpret the measured plate response, a fully coupled aero-thermal-acousto-elastic analysis is carried out. A theoretical–computational model is formulated with a nonlinear structural plate model, acoustic pressure equation for the stationary fluid in a cavity, and the first-order Piston Theory aerodynamics. A linear stability analysis is performed that includes the nonlinear added stiffness due to an initial deformation to investigate the combined effects of freestream coupling and temperature differential on system stability. Also, direct time integration of the nonlinear fluid structural equations of motion is performed using experimentally measured flow parameters as inputs. All stability transitions are captured using the theoretical model with good agreement with experiment for transitions from no flutter to flutter/limit cycle oscillations (LCO) although the theoretical LCO amplitude is approximately $50\%$ larger than measured. The system’s sensitivity to cavity coupling, temperature differential, thickness calibration, static pressure differential, and turbulent pressure fluctuations are investigated. Lastly, snap-through buckling analyses in response to periodic and quasi-static excitations are conducted.

1 Introduction

Nonlinear plate dynamics in supersonic flows has been an active field of research in the past several decades [3, 4, 26, 27]. In practical applications, plates constitute a basic building block in various types of aerial vehicles, while in basic research, they are used to investigate the fundamental physics typical to the high-speed vehicle environment. Structural nonlinearity in flat plates becomes important for deflections of the order of its thickness [10] which usually has to be small to comply with weight requirements. This constraint is a core challenge for most aerospace structures and is the leading reason why numerous experimental, computational, and theoretical studies were and are to this day, conducted to develop and improve fluid–structure models for this family of problems.

Prior literature on fluid–structure interaction (FSI) of plates in supersonic flow shows that different parameters affect flutter onset condition and the nonlinear dynamics after flutter onset. Yuen and Lau [35] considered the effect of in-plane load and computationally showed that for a sufficiently large load several modes of limit cycle oscillations are possible. In a computational study by Nydick et al. [29], the effects of aerodynamic heating, plate curvature, and a shock upstream of the plate were shown to have strong effect on the system’s dynamics. Several experimental [21, 32] and computational [18, 19] studies have shown that static pressure differential, which causes an initial static deformation of the plate, substantially stiffens the plate, postpones flutter, and affects the dynamics in post-flutter conditions. Amabili and Pellicano investigated the nonlinear flutter of circular cylindrical plates (or in this case, shells) including the effects of geometric imperfections and different in-plane boundary constraints [1, 2]. Overall, correlation between theory and experiment shows that the existing models predict flutter onset accurately for this wide range of effects [11] but there is a clear lack of experimental data on plate dynamics beyond flutter onset. Currao et al. [8] are among those who plan to change this as demonstrated by their recent computational design study of a panel flutter experiment in a short duration supersonic wind tunnel facility.

Other works considered the dynamics of stable plates (i.e., in sub-flutter conditions) in response to shockwave, boundary layer, external excitation, and their combined interaction. Clemens and Narayanaswamy [7] provide an excellent review on the low-frequency unsteadiness in shockwave/turbulent boundary layer interaction which may lead to frequency lock-in with the structure’s natural frequencies. Casper et al. [5] conducted an experimental study of the interaction of a conical curved plate responding to the turbulent flow oscillations in the boundary layer of a supersonic flow. Whalen et al. [33, 34] carried out an experimental study of a flat plate mounted on a compression corner in Mach 6 with transitional and turbulent boundary layers. The compression ramp angle was varied and changes in the natural frequencies of the plate were measured. Using a theoretical–computational model [19], it was shown that aerodynamic heating and static pressure differential were the dominant factors in the variation of natural frequencies. It is important to note that in order to analyze the effect of static pressure differential on natural frequencies, the analysis must include the contribution of added nonlinear stiffness due to static deformation.

Another aspect of nonlinear plate dynamic that has been investigated, although predominately without fluid coupling, is snap-through buckling (or mode jumping). Ehrhardt and Virgin recently did experimental work on buckled plates with uniform and localized heating [14]. They showed that for a given plate temperature several stable buckled states exist, and by applying a sufficiently large external force, the plate transitioned from one state to another. Other experimental [15, 22] and theoretical [6, 25] studies investigated the postbuckling dynamics of laminate composite and isotropic plates.

It is clear from the above mentioned studies that most computational and experimental literature considered phenomena associated with nonlinear plate dynamics separately. Moreover, the experimental wind tunnel instability studies were predominantly interested in flutter onset and not transition to limit cycle oscillation (LCO) or its characteristics, e.g. amplitude and frequency content. In this work, results obtained in recent experimental campaign [31] are utilized in a theoretical computational investigation of the coupled aero-thermal-acousto-elastic problem. In the current configuration an initially flat plate is the elastic wall of a closed volume cavity on one side. On the other side the plate is exposed to the freestream flow that starts stationary and accelerates to a turbulent Mach 2 flow in a transient supersonic wind tunnel start. Thus the plate is dynamically coupled to the freestream flow and the stationary fluid inside the cavity. Also, its temperature is increasing due to heat flux from the boundary layer, and it is excited by turbulent pressure fluctuations. The goal of the current study is to asses the accuracy of the proposed theoretical model in predicting the response of a path dependent nonlinear system to the transient process of supersonic wind tunnel start. Transition times to and from instability are considered as well as the behavior during LCO and the model’s sensitivity to several parameters is investigated.

This work is organized as follows. In Sect. 2, the fluid–structure system is modeled and solution methods are described. In Sect. 3, the experimental configuration, parameters, and measurements are described. In Sect. 4, the results are presented and discussed. The Results and Discussion section consists of (in this order): experimentally measured plate displacement, theoretical model calibration and assumptions (on temperature differential and the natural frequencies), fluid–structure system sensitivity to the presence of cavity, sensitivity to choice of plate thickness (nominal vs calibrated), sensitivity to static pressure differential (between freestream and cavity), sensitivity to turbulent pressure fluctuations. The results section ends with snap-through calculations in response to periodic and quasi-static external loads.

2 Theoretical model

2.1 Theoretical–computational model derivation

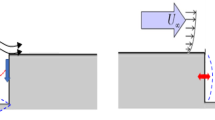
A theoretical–computational fluid–structure model is derived to analyze the coupled plate, freestream, and cavity dynamics as shown schematically in top and side views in Figs. 1 and 2, respectively. The model includes mechanical and thermal loadings that are characteristic to plates in supersonic FSI problems which are expected to affect the system’s stability and nonlinear response [11]. Static pressure differential $\Delta p_s$ and temperature differential $\Delta T$ are shown in Fig. 1 and may generally vary in space and time. $\Delta p_s$ may be calculated with theory or measured experimentally and is independent of the plate dynamics. $\Delta T$ may be determined by solving the heat equation with an empirical heat flux model or obtained from experiments. Distributed in-plane boundary stiffness along the edges of the plate is modeled as shown in Fig. 2 and denoted by K(y). Considering the in-plane edge constraint is important when a nonlinear structural response is expected, e.g., due to limit cycle oscillation (LCO) or large static deformation, because it may strongly affect the instability onset condition and the LCO amplitude [16, 17, 32].

Fig. 1

Plate top view with freestream flow, static pressure differential, and support and plate temperatures

Fig. 2

Side view of plate, freestream flow, cavity, and in-plane edge stiffness K(y), cross section at $-b/2< y < + b/2$

The nonlinear structural model derivation begins with formulating the elastic and kinetic energies of a flat von Kármán plate with general in-plane stiffness distribution at the edges in terms of three displacement components. This approach is in contrast to previous literature where the Airy’s stress function and a single transverse displacement are employed. Then, the Rayleigh–Ritz method is applied by modally expanding the three displacement components and calculating the spatial energy integral. This removes the dependence on spatial coordinates and reduces the problem to time domain. Lagrange’s Equations are utilized with the elastic and kinetic energies in modal form to obtain the system of equations of motion. External, aerodynamic, and acoustic pressure forces are added as nonconservative forces. Finally, the in-plane inertia is neglected and the system of equations is reduced using algebra to a single transverse displacement component as shown in Eq. (1). The modal expansion of w(x, y, t) is shown in Eq. (2). Note that if large plate imperfections are present, the in-plane inertia could be retained to improve the accuracy of the model. In that case, dynamical equations for the in-plane displacement would be included and the plate would become a shell.

$$\begin{aligned}&M_{nk} \ddot{w}_k + C_{nk} \dot{w}_k + G^{(1)}_{nk} w_k - \Delta T K^{Th}_{nk} w_k \nonumber \\&\quad +D^{(2)}_{nkrs} w_k w_r w_s + Q_n= 0 \end{aligned}$$

(1)

$$\begin{aligned}&w(x,y,t) = \sum _i^{N_w} w_i(t) \psi _i^w(x,y) \end{aligned}$$

(2)

For detailed derivation and explicit forms of the structural matrices, the reader is referred to [16, 17]. The linear thermal load matrix $K^{Th}_{nk}$ is the sum of thermal matrices of all displacement components as defined in [16, 17] with an additional assumption that $\Delta T(t)$ is uniform in space. The in-plane boundary stiffness is manifested through $K^{Th}_{nk}$ and the nonlinear stiffness tensor $D^{(2)}_{nkrs}$. External loads are added through the generalized force term $Q_n$ as defined in Eq. (3).

$$\begin{aligned} Q_n = \int \limits _{A}^{} \Delta p(x,y,t) \psi _n^w \,\mathrm{d}A \end{aligned}$$

(3)

Aerodynamics are modeled using first order Piston Theory (PT) which dictates the following relation between pressure perturbation and local motion of a structure, one side of which is under a freestream flow with properties $\rho _{\infty }(t)$, $U_{\infty }(t)$, $M_{\infty }(t)$

$$\begin{aligned} \Delta p_{PT} = \frac{\rho _{\infty } U_{\infty }}{M_{\infty }} \Big ( \frac{\partial w}{\partial t} + U_{\infty }\frac{\partial w}{\partial x} \Big ) \end{aligned}$$

(4)

The application of this form of PT in freestream flow is appropriate under certain conditions, i.e., sufficiently high Mach number or very high (reduced) frequency as discussed in [12, 19], and the motions must be sufficiently small that the product of Mach number times deflection/chord ratio is small compared to one. The smallest reduced frequency considered in this work is of order one while deformations are in the order of two plate thicknesses. Thus, first-order PT is expected to provide a reasonable approximation. The expression in Eq. (4) is transformed to modal coordinates either through the nonconservative force term in Lagrange’s equations or by expansion in and projection on the modal coordinates $\psi ^w_n$. The resulting aerodynamic damping and stiffness matrices are defined implicitly as follows

$$\begin{aligned} Q_n^{PT}= & {} \frac{\rho _{\infty } U_{\infty }}{M_{\infty }} \bigg ( \bar{A}_{{\dot{w}}_{nk}} \dot{w}_k + U_{\infty } \bar{A}_{{w}_{nk}} w_k \bigg ) \nonumber \\= & {} \frac{\rho _{\infty } U_{\infty }}{M_{\infty }} \bigg ( \dot{w}_k \int \limits _{A}^{} \psi _{k}^w \psi _n^w \,\mathrm{d}A + U_{\infty } w_k \int \limits _{A}^{} \psi _{x_k}^w \psi _n^w \,\mathrm{d}A \bigg )\nonumber \\ \end{aligned}$$

(5)

Properties of the freestream flow were separated from the aerodynamic matrices in contrast to authors’ previous works [16, 17, 19] mentioned above. This is to emphasize the temporal variation of these parameters in the formulation of the coupled model and the computational scheme.

A uniform static pressure differential is added which, in contrast to PT aerodynamics, is independent of the plate’s motion. Continuing the same reasoning as above with regard to definitions, the following generalized force is included in the model with $\Delta p_s(t)$ as a parameter

$$\begin{aligned} Q_n^s = \Delta p_s \bar{Q}_n^s= \Delta p_s \int \limits _{A}^{} \psi _n^w \,\mathrm{d}A \end{aligned}$$

(6)

Lastly, the stationary air inside a closed cavity is modeled as inviscid, potential fluid governed by the acoustic equation

$$\begin{aligned} \nabla ^2 p_c - \frac{1}{a_c^2} \frac{\partial ^2 p_c}{\partial ^2 t} = 0 \end{aligned}$$

(7)

With boundary conditions in a rectangular volume

$$\begin{aligned}&\frac{\partial p_c}{\partial n} = 0 \end{aligned}$$

(8a)

on rigid walls at $x = 0,a \quad y = \pm b/2 \quad z = -d_c$

$$\begin{aligned} \frac{\partial p_c}{\partial n} = -\rho _c \frac{\partial ^2 w}{\partial ^2 t} \end{aligned}$$

(8b)

on the elastic wall (plate) at $z = 0$.

The wave equation with boundary conditions are transformed to modal coordinates using Green’s second identity and modal expansion of the cavity pressure according to Eq. (9) where $\psi _i^c(x,y,z)$ are the eigenfunctions of the spatial operator in Eq. (7).

$$\begin{aligned} p_c(x,y,z,t) = \sum _i^{N_c} P_i(t) \psi _i^c(x,y,z) \end{aligned}$$

(9)

Substituting the boundary conditions in Eq. () into Green’s identity and calculating the modal integrals, the following matrices are defined

$$\begin{aligned} M^c_{nk}= & {} \int \limits _{V}^{} \psi ^c_n \, \psi ^c_k \,\mathrm{d}V \end{aligned}$$

(10a)

$$\begin{aligned} K^c_{nk}= & {} - \int \limits _{V}^{} \psi ^c_n \, \nabla ^2 \psi ^c_k \,\mathrm{d}V \end{aligned}$$

(10b)

$$\begin{aligned} L^c_{nk}= & {} \int \limits _{A}^{} \psi ^c_n|_{z=0} \, \psi ^w_k \,\mathrm{d}A \end{aligned}$$

(10c)

And the modal governing equation is obtained

$$\begin{aligned} \frac{1}{a_c^2} M^c_{nk} \ddot{P}_k + K^c_{nk} P_k = - \rho _c L^c_{nk} \ddot{w}_k \end{aligned}$$

(11)

The plate motion has been introduced as a forcing term on the RHS of Eq. (11) which establishes a one way coupling. To complete the two-way coupling, cavity pressure perturbation is added to the structural system of equation using the term in Eq. (12).

$$\begin{aligned} Q_n^c = - L^c_{kn} P_k \end{aligned}$$

(12)

The ambient static pressure and temperature inside the cavity may vary with respect to time. The fluid density $\rho _c$ is calculated with the state equation using the freestream static pressure and pressure differential across the plate as follows

$$\begin{aligned} \rho _c = \frac{p_{\infty } - \Delta p_s}{R T_c} \end{aligned}$$

(13)

The speed of sound inside the cavity $a_c$ depends only on temperature which in this work is assumed constant.

In certain cases [11, 13], a simplified version for the cavity model may replace the acoustic equation in Eq. (7). When a steady-state equilibrium solution for the plate deformation under the combined loads of freestream flow, pressure, and temperature differentials, and cavity resistance is of interest the following stiffness term may be included in the LHS of Eq. (1)

$$\begin{aligned} Q^{c,ss}_n = \frac{\rho _c a_c^2}{a b d_{c}} A^c_{nk} w_k =\frac{\rho _c a_c^2}{a b d_{c}} w_k \int \limits _{A}^{} \psi ^w_n \mathrm{d}A \cdot \int \limits _{A}^{} \psi ^w_k \mathrm{d}A \end{aligned}$$

(14)

The added stiffness term in Eq. (14) accounts for the fluid’s resistance to change in volume while neglecting the added mass effect (which is a reasonable assumption for a steady-state equilibrium). It can be shown by using a single first mode for the cavity pressure expansion in Eq. (9) (which is simply $\psi ^c_1 = 1$) together with Eq. (), that under this assumption there is a static relation between cavity pressure and plate displacement, i.e., Eq. (14).

Further details on the different forms of the cavity model can be found in [9].

2.2 Modal equations of motion

The coupled governing system of equations in modal coordinates is shown in Eq. () with the fluid–structure terms identified and underlined.

$$\begin{aligned}&\underbrace{ M_{nk} \ddot{w}_k + C_{nk} \dot{w}_k + G^{(1)}_{nk} w_k -\Delta T K^{Th}_{nk} w_k }_{\mathrm{linear}\ \mathrm{plate}\ \mathrm{model}} +\underbrace{ D^{(2)}_{nkrs} w_k w_r w_s }_{\mathrm{NL}\ \mathrm{structural}\ \mathrm{stiffness}} \nonumber \\&\quad + \underbrace{ \frac{\rho _{\infty } U_{\infty }}{M_{\infty }} \bigg ( \bar{A}_{{\dot{w}}_{nk}} \dot{w}_k + U_{\infty } \bar{A}_{{w}_{nk}} w_k \bigg ) }_{\mathrm{PT}\ \mathrm{aerodynamics}} -\underbrace{ L^c_{kn} P_k }_{\mathrm{cavity}\ \mathrm{coupling}} \nonumber \\&\quad + \underbrace{\Delta p_s \bar{Q}^s_n}_{\mathrm{static}\ \mathrm{pressure}\ \mathrm{differential}} = 0 \end{aligned}$$

(15a)

$$\begin{aligned}&\underbrace{ \rho _c L^c_{nk} \ddot{w}_k }_{\mathrm{plate}\ \mathrm{coupling}} +\underbrace{\frac{1}{a_c^2} M^c_{nk} \ddot{P}_k +K^c_{nk} P_k }_{\mathrm{acoustic}\ \mathrm{wave}\ \mathrm{eqn.}} = 0 \end{aligned}$$

(15b)

The above is a system of second order ordinary differential equations in time of size $N^w + N^c$. The unknowns are the modal coordinates $w_n$ and $P_n$ with their respective initial conditions for displacement and velocity provided. The properties $\Delta T, \rho _{\infty }, U_{\infty }, M_{\infty }, \Delta p_s$, and $T_c$ may generally vary in time. Future work will consider the heat equation to calculate the nonuniform $\Delta T$ which in general depends on the plate’s motion. This extension will make the thermal matrix ${K}^{Th}$ a third order tensor and include summation over the modal coordinates of the temperature distribution across the plate.

2.3 Solution methods

The dynamic response of the fluid–structure system during wind tunnel start is analyzed by employing two solution approaches. First, the equations of motion are integrated with respect to time for a given set of initial conditions and time varying parameters. With this approach, the transient response of the plate to wind tunnel start is computed and correlated with experiment and the system’s sensitivity to random fluid boundary-layer pressure fluctuations is investigated. Second, a linear stability analysis is carried out to provide more insight into the time response and the intermittent instability transitions measured in the wind tunnel. For all computations in this work, the modal coordinates describing the spatial motion of the plate consisted of combinations of 8 chordwise and four spanwise modes totaling in 32 coordinates. For the cavity, modes describing the acoustic pressure distribution consisted of combinations of 6 chordwise, 3 spanwise, and 3 transverse direction modes totaling in 54 coordinates. Products of the one-dimensional clamped–clamped beam-mode shapes [24] were used for the plate deformation basis functions $\psi ^w_n(x,y)$ as detailed in authors’ previous works [16, 17, 19]. For the cavity mode shapes $\psi ^c_n (x,y,z)$, products of cosine functions were used [11].

The system in Eq. () is reduced to first order and integrated with MATLAB’s ode45 function (a routine based on the Runge–Kutta method with a variable time-step). Initial conditions are set to zero in all coordinates to describe a static plate at the beginning of the wind tunnel start. Turbulent pressure fluctuations inside the fluid boundary layer are modeled by introducing a noise signal to the pressure differential $\Delta p_s (t)$. This simple model was shown by Miller et al. [28] to demonstrate how acoustic noise may affect instability onset and time to reaching LCO for a one-dimensional plate in supersonic flow. The noise signal is characterized by the sound pressure level (SPL) in decibel which relates to the root-mean-square (rms) of the signal as follows

$$\begin{aligned} p_{\mathrm{rms}} = p_{\mathrm{ref}} \times 10^{SPL/20} \end{aligned}$$

(16)

A Gaussian white noise is generated with rms of $p_{\mathrm{rms}}$ and cutoff frequency of 3000 Hz and summed with $\Delta p_s$. Frequency cutoff range was chosen to include structural and cavity natural modes as well as all fluid–structure instability branches in the range of considered parameters (more on this in Sect. 4.3). This approach assumes turbulent fluctuations that are uniform in space and do not impact the local freestream parameters used to calculate the aerodynamic pressure in Eq. (4). And thus this analysis is mostly qualitative and serves as first-order approximation. Future work will use experimental measurements or results from Computational Fluid Dynamics (CFD) for a more accurate analysis.

An eigenvalue problem is formulated to calculate the fluid–structure system’s natural frequencies, mode shapes and determine its stability. In this work the plate experiences combined loads due to interaction with cavity and freestream flow, in-plane temperature differential, and static pressure differential. The first three are easily included in a linear analysis using the linear part of the model in Eq. (15a) with the simplified version of the cavity from Eq. (14). But the latter is an external forcing and thus the equilibrium state about a deformed plate steady-state must be considered to include the contribution of the nonlinear stiffness term underlined in Eq. (). Thus a steady-state solution is obtained by time marching the full fluid–structure system with $\Delta p_s$ and an additional added damping term (to facilitate reaching the steady state efficiently). Then the full system in Eq. () is dynamically linearized about the nonlinear static equilibrium state due to all loads and a harmonic form of solution in both displacement and cavity pressure is assumed according to Eq. (17).

$$\begin{aligned} \begin{Bmatrix} \bar{w} \\ \bar{P} \end{Bmatrix} =\begin{Bmatrix} \hat{w} \\ \hat{P} \end{Bmatrix} e^{i \lambda t},\quad \lambda = \omega + \zeta \omega i \end{aligned}$$

(17)

Substituting Eq. (17) in the dynamically linearized form of Eq. () produces a quadratic eigenvalue problem. Its solution produces $2\times (N_w + N_c)$ pairs of complex eigenvalues $\lambda _n$ and mode shapes $\hat{w}_n, \hat{P}_n$. By eliminating eigenvalues with repeating real parts (natural frequencies) there are $N_w + N_c$ pairs. Natural frequencies and modal damping ratio are calculated from the remaining eigenvalues according to Eq. (17). Further details on this analysis with full derivation can be found in [16, 17, 19].

3 Experiment configuration and parameters

3.1 The elastic plate

A plate was manufactured [31] by machining a $305 \times 152 \times 12.7 \, \hbox {mm}$ block of AISI 4140 alloy steel leaving a thin rectangular all-clamped edges flat plate with geometrical and material parameters as listen in Table 1. The thicker external frame of the steel block was used to install the plate flush with the wind tunnel wall. Figure 3 shows a photograph of the plate and frame structure. The plate surface is covered with white paint and a random pattern is applied using a fine-tipped permanent marker. A 3D Digital Image Correlation (DIC) system is utilized to measure the displacement of 153 points across the plate surface at a rate of 5 kHz.

Table 1 Material and geometrical properties of the plate and cavity

Fig. 3

Plate with 3D DIC random pattern and locations of displacement and temperature measurements [31]. Freestream flow direction is down

Table 2 Natural modal frequencies and damping—theory (th) and experiment (exp)

Fig. 4

RC-19 test section schematic showing the plate, cavity, and an optional shock generator [31]

Modal testing of the structure was conducted using an impact hammer. The plate, with its much thicker frame, was placed on bungee cords during the test to effectively isolate the structure. The first six measured natural frequencies and estimated damping ratios are shown in Table 2 along with theoretical frequencies for two plate thicknesses, nominal $h_\mathrm{nom}$ and calibrated $h_\mathrm{cal}$. The nominal thickness is the measured thickness of the manufactured model, while the calibrated thickness was calculated to match the first natural frequency $f_1 = 375\,\hbox {Hz}$ and thus is $7\%$ greater than $h_\mathrm{nom}$. This form of calibration is common among structural engineers as it effectively accounts for uncertainties in the geometrical as well as the material properties listed in Table 1. Note that for $h_\mathrm{nom}$, modes 2 through 6 are remarkably close to the measured values but for $h_\mathrm{cal}$ the difference between theory and experiment increases substantially with mode number. Fluid–structure system’s sensitivity to thickness choice is further investigated in Sect. 4.4, but for the rest of this work $h_\mathrm{nom}$ is utilized. Estimated modal damping ratios obtained in the same test are also presented. A simple theoretical model for aerodynamic damping at current structural parameters is not available considering the relatively small reduced natural frequency, i.e., $f_1 b / a_{\infty } \approx 0.7$ [11]. Aerodynamic modal damping of the first mode based on Piston Theory is 20 times greater than measured and thus damping in Table 2 is attributed mostly to the structure.

3.2 The supersonic wind tunnel

Experiments were conducted at the AFRL Research Cell 19 (RC-19) Mach 1.5–3 continuous supersonic wind tunnel to refine new measurement techniques and investigate FSI phenomena in supersonic flow. Of all the wind tunnel tests conducted, discussed and analyzed in [31], this work focuses on the transient wind tunnel start in which a complex fluid–structure response was measured that included transitions between different stability and instability states. A schematic of the wind tunnel test section, plate, and cavity is shown in Fig. 4.

Figure 5 shows the measured and calculated transient flow parameters used in all computations shown in this work unless otherwise stated. The shaded region shows the approximate time interval during which the flow is subsonic inside the wind tunnel test section. Wind tunnel stagnation pressure $p_0$ was measured with a static pressure transducer in the settling chamber. The cavity pressure was measured with a low-frequency (static) pressure transducer connected to a pressure tap. Freestream static pressure at the plate’s surface $p_{\infty }$ in the supersonic time interval was calculated using isentropic flow relations with the freestream flow Mach number in Table 3 and the measured value of $p_0$. In the subsonic interval $p_{\infty }$ was approximated using the measured displacement response in Fig. 6. Because the subsonic portion of the test is not the key focus of this work, assumptions considered here are reasonable and primarily serve as closure. Note that the wind tunnel is pressurized to approximately 21 kPa at the beginning of the test and thus all pressures agree at the first second of the measured data. The calculated static pressure differential $\Delta p_s$ is also plotted with a separate ordinate on the right hand side. For a large part of the response the static pressure differential is approximately constant at 3 kPa. Temperature differential $\Delta T$ was measured with a pair of thermocouples: one near the plate’s edge as shown in Fig. 3 and another on its thicker frame.

Fig. 5

Stagnation, cavity, freestream, and differential pressures and measured $\Delta T$ time histories

Table 3 Supersonic freestream and cavity properties

Fig. 6

Experiment—measured displacement versus time at $x/a = 1/4$ [31]

Fig. 7

Theory—displacement versus time with cavity, $1.0 \times \Delta T$

Fig. 8

Theory—displacement versus time with cavity, $1.25 \times \Delta T$

Fig. 9

Theory—displacement versus time with cavity, $1.5 \times \Delta T$

Table 3 shows the supersonic freestream properties, the boundary layer thickness at the leading edge (LE), and stationary fluid temperature inside the cavity. While this configuration of the wind tunnel is designed to produce a freestream flow of Mach 2 inside the test section, measurements in [31] as well as the static displacement of the plate at the end of the transient response support the lower value in Table 3. The unit Reynolds number was calculated based on freestream properties at the end of the wind tunnel start transient and the flow at the plate’s surface is turbulent according to [31]. The boundary layer to plate length ratio is $\delta / a \approx 0.03$, which is sufficiently small to justify an inviscid flutter stability analysis [11]. Transient measurements of temperature inside the cavity is not available, and thus it is assumed constant. This assumption is reasonable considering the stagnation temperature of the wind tunnel of $T_0 = 389\,\hbox {K}$ is relatively small.

Further details on the wind tunnel facility, configuration, and measuring equipment are available in [31].

4 Results and discussion

4.1 Measured plate displacement

Figure 6 shows the time history of transverse displacement measured with the DIC system at $25\%$ chord length during the wind tunnel start transient [31]. At $t \approx 5\,\hbox {s}$, the plate is forced by the wind tunnel start expansion shock which marks the point of supersonic regime start in all of the following computational results. The magnitude of the peak displacement due to the moving shock has been used to approximate the peak value of $\Delta p_s (t \approx 5\,\hbox {s})$ in Fig. 5. From $t \approx 8\,\hbox {s}$ the oscillation amplitude varies over time with a maximum of $w / h \approx 1.5$ at $t = 24\,\hbox {s}$.

As the wind tunnel stagnation pressure rises, the aerodynamic forces increase, while the plate also heats up due to the increasingly turbulent boundary layer. In simple cases, the increase in freestream pressure and plate temperature are both likely to increase the amplitude and frequency of LCO and may even lead to structural failure. But because the cavity and the freestream flow static pressures are not exactly equal, i.e., a static pressure differential $\Delta p_s$ is present, the plate deformation becomes large enough for the nonlinear stiffness contribution to become significant and stabilize the plate at $t \approx 25\,\hbox {s}$. In the last 5 s of the response the plate vibrates with small amplitude about a deformed equilibrium in response to the turbulent freestream flow.

In all following computations, the time history of the plate displacement is considered at $x/a = 1/4$ and the experimental results from Fig. 6 are overlaid on top with a partially transparent red curve.

4.2 Theoretical model calibration and assumptions

Results were computed with the theoretical-computational model described in Sect. 2. The structural linear stiffness $G^{(1)}_{nk}$ and damping $C_{nk}$ matrices in Eq. (15a) were calibrated by substituting the theoretical with measured values from Table 2. In-plate boundary stiffness was set to $\frac{K_{bc} a}{E h} = 1000$ which very closely approximates zero displacement in-plane boundary conditions [16, 17]. The first-order Piston Theory aerodynamic term is activated when the flow inside the test section becomes supersonic as classified by the unshaded area on Fig. 5, while the static pressure differential is active throughout the whole computation.

Fig. 10

Theory—displacement versus time, no cavity, $1.25 \times \Delta T$

Temperature differential between the plate and its massive support is assumed uniform which in reality is not likely the case. Note that the plate temperature is measured near its edge as shown in Fig. 3. To account for uncertainties in spatial distribution of the plate temperature, the measured $\Delta T$ time history in Fig. 5 was scaled by several constants and the computed responses were correlated with experimental data. Figures 7, 8 and 9 show results for scalings of $1.0 \times \Delta T$, $1.25 \times \Delta T$, and $1.5 \times \Delta T$, respectively. The discussion on $\Delta T$ scaling calibration will focus on the second half of the response, i.e., $t = 15\,\hbox {s}$ and on. Figure 7 shows that computational results based on the nominal (measured) $\Delta T$ do not agree with experiment in the last 7 s of the response, where the plate is expected to oscillate and then stabilize. Figure 9 shows results for the largest scaling considered of $1.5 \times \Delta T$. It is clear that now the scaling is too large because the plate reaches equilibrium early at $t = 19\,\hbox {s}$. Also, the theoretical static displacement at the end of the response is greater than measured which suggests that the value of $\Delta T$ at the end of the transient should be reduced.

Figure 8 shows the computed time response of displacement with the calibrated scaling of $1.25 \times \Delta T$. In this final case, the plate transitions from large amplitude oscillation to small vibrations within 1 s of the experimentally measured transition time of $t \approx 24\,\hbox {s}$. Additionally, good agreement in the final static displacement is now obtained. Perhaps the most important conclusion is that while the temperature can be scaled to give even better correlation between theory and experiment, the theoretical results are not especially sensitive to a reasonable range of possible scaling values. For all following computations, a scaling value of 1.25 will be used and the effect of $\Delta T$ scaling will be further discussed in the next subsection using linear stability analysis.

4.3 Fluid–structure stability with and without cavity

Figures 8 and 10 show the theoretical (calibrated) displacement time history computed with and without cavity, respectively. Both cases show a reasonable qualitative agreement with the experiment although both overestimate the magnitude of the large amplitude oscillation region by at least $50\%$ of the experiment (shaded region). There is very little experimental data on LCO amplitudes of plates in post-flutter conditions [11]. Nevertheless, theoretical and computational studies have shown [11, 16, 17, 32] that the amplitude of LCO of an all-clamped plate in post flutter conditions is sensitive to the assumptions made about the in-plane boundary conditions, structural and aerodynamic damping, and boundary layer thickness (which ultimately affects the aerodynamic forces). In this work, fully clamped in-plane edges are assumed which is the most conservative assumption possible, i.e., the LCO amplitude is expected to be at minimum for that parameter. Thus the more likely causes for theory’s overestimation of the amplitude are the aerodynamic forces and internal structural damping. The use of Piston Theory for flutter analysis is justified by prior literature [11] as was mentioned in Sect. 2, but for the more complicated behavior at post-flutter condition LCO a more accurate model is likely needed which considers the boundary layer. Also, structural damping may increase during complicated modes of motion and varying frequencies [23]. And the assumption made about $\Delta T$ distribution may also have impact on LCO amplitude. For more accurate correlation future studies will utilize more temperature and displacement measuring points, and an aerodynamic model that includes the effect of boundary layer.

Both theoretical models fail to predict the moderate amplitude oscillation that start at $t \approx 9\,\hbox {s}$. A possible explanation for the dynamics in this region may be the wind tunnel stagnation pressure reaching $80\%$ of its maximum value which at some point causes the BL at the plate’s surface transition from laminar to transitional, and finally to turbulent, which may lead to large pressure oscillations. In the last 5 s of the response, for both with and without cavity, the theoretical models stabilize and vibrate about the same equilibrium state which suggests that the cavity provides very little resistance to a static deformation at current fluid properties.

Additional insight into the fluid–structure dynamics can be obtained by investigating stability maps in the $p_{\infty }$ versus $\Delta T$ plane generated using the eigenvalue problem approach described in Sect. 2.3. In many cases, the flutter and buckling problems are considered independently such that $p_{\infty }$ is increased until flutter onset condition is found and similarly with $\Delta T$ for buckling. For structures in supersonic flow, the two problems are coupled and must be treated simultaneously for accurate results. Figures 11 and 12 show fluid–structure stability maps computed without and with coupled cavity dynamics. Important to note that the computation of these maps assumes small perturbations about a steady-state equilibrium of a deformed plate due to combined static loads of freestream, cavity resistance (when present), static pressure differential $\Delta p_s$, and temperature differential $\Delta T$.

Fig. 11

Stability map for $\Delta p_s = -3\,\hbox {kPa}$, no cavity

Fig. 12

Stability map for $\Delta p_s = -3\,\hbox {kPa}$, with cavity

Figure 11 shows regions of stability and flutter of a plate coupled with the freestream flow and ignoring the cavity effect. The experimentally measured (and scaled) trajectory is plotted with crosses marking 5 s ticks. For example, it is possible to conclude that first onset of flutter is expected at $t \approx 11\,\hbox {s}$ which is consistent with the time series in Fig. 10. In the final 5 s of the response the trajectory curve leaves the flutter region. This is consistent with the final stabilization of the plate. A colormap is overlaid over the regions of instability to show the magnitude of the dominant unstable mode’s imaginary part of the eigenvalue. The value of $Re(\lambda ) = \zeta \omega$ is associated with the rate of growth towards instability according to Eq. (17).

Figure 12 shows stability map for the coupled structure–cavity–freestream system. The main flutter region (in the shape of two connected spikes) remained similar to shown in Fig. 11 but with a slight offset to the left. The clear difference is the appearance of additional instability regions labeled A and B. These regions appear when the natural frequencies of the structure (altered by the freestream interaction) and the cavity frequencies coalesce. A and B regions are characterized by a comparatively light instability suggested by the lower $\zeta \omega$ values. Note that regions of combined flutter and cavity resonance are also observed.

Figure 12 also shows the three scaled $\Delta T$ trajectories discussed in Sect. 4.2. The dynamics of each case at the last 10 s of the response in Figs. 7, 8, and 9 are consistent with their corresponding trajectory on the map. The $1.0 \times \Delta T$ trajectory ends inside the flutter region, as previously noted. The $1.5 \times \Delta T$ curve crosses all instability regions swiftly and spends more time in the stable region than other cases. The $1.25 \times \Delta T$ case agrees best with experiment.

Fig. 13

Fluid–structure natural frequencies’ versus $\Delta T$ for $\Delta p_s = -3\,\hbox {kPa}$, $p_{\infty } = 41\,\hbox {kPa}$, with cavity

Fig. 14

Theory—displacement versus time with cavity $1.25 \times \Delta T$, and calibrated thickness $h = h_{\mathrm{cal}}$

Lastly, the eigenprobem approach is also used to analyze the variation of natural frequencies of the fluid–structure system for a constant value of $p_{\infty }$. Figure 13 shows natural frequencies versus $\Delta T$ for $p_{\infty } = 41\,\hbox {kPa}$, a value which from the stability map on Fig. 12 shows to cross all instability regions. The figure shows that the two separate flutter regions represent a two-mode flutter instability for the same modes pair characterized by frequencies in the range of $f_{\mathrm{flutter}} =310:375\,\hbox {Hz}$. On the other hand, region A instability occurs when the first cavity mode (first chordwise mode), which is almost independent of $\Delta T$, coalesces with a higher order structural mode at $f_{A} = 700\,\hbox {Hz}$ and becomes unstable. A similar instability occurs in Region B at a higher frequency of $f_{A} = 1875\,\hbox {Hz}$ which is not included in the range of frequencies plotted. The zeroth mode of the cavity, also called the Helmholtz mode, is shown with an approximately constant frequency of zero.

4.4 Results sensitivity to thickness calibration

In Sect. 3.1, the theoretical natural frequencies of the plate were presented for two plate thicknesses, the nominal measured $h_\mathrm{nom}$ and calibrated $h_\mathrm{cal}$. The thickness value h affects all structural matrices, that is mass, damping, linear stiffness, and nonlinear stiffness. And while calibrating the linear stiffness and damping matrices leads to exact agreement in some modal parameters between theory and experiment, the nonlinear stiffness tensor in Eq. (15a) depends on h and remains uncalibrated. Thus the choice of h is expected to impact the nonlinear dynamics of the structure more than the linear.

Figure 14 shows the time response computed with $h_\mathrm{cal}$ and scaled temperature differential of $1.25 \times \Delta T$. In terms of stability, flutter onset takes place at the same time as in previously discussed results in Fig. 8 for $h_\mathrm{nom}$, but in this case the plate stabilizes approximately 2 s earlier. A major difference in the qualitative behavior is observed in post-flutter dynamics in Fig. 14 where oscillations are highly non-periodic and possibly chaotic. Also a short stabilization is observed at $t = 16\,\hbox {s}$ which is attributed to the crossing of a stable region on the stability map. Figure 15 shows the stability map for $h_\mathrm{cal}$ where substantial shifts in instability regions of type B are observed. Recall that regions B correspond to instability due to coalescence of structural and cavity modes at approximately 1875 Hz. It appears that for $h_\mathrm{cal}$ the cavity and plate frequencies cross at substantially different $\Delta T$ values. Overall, the nonlinear dynamics observed in the time responses of both cases suggest that $h_\mathrm{nom}$ produces results closer to those measured in the experiment and thus justify the choice made in Sect. 3.1.

Fig. 15

Stability map for $\Delta p_s = -3\,\hbox {kPa}$, with cavity and calibrated thickness $h = h_{\mathrm{cal}}$

4.5 Stability sensitivity to static pressure differential

In the above discussion, the system’s linear dynamic stability was investigated with a static pressure differential of $\Delta p_s =-3\,\hbox {kPa}$, which is the approximate value measured inside the wind tunnel throughout a substantial period of the transient start process. To investigate the effect of $\Delta p_s$ on fluid–structure linear stability, Fig. 16 is plotted showing the stability map with zero static pressure differential. In contrast to previous maps, a buckling instability region has appeared with zero frequency at the unstable mode although the experiment trajectory stays far from it. The important conclusion from this figure is that in the absence of $\Delta p_s$ there are no additional stability zones on the experiment trajectory path and because the plate’s temperature may rise to even greater values, the system is expected to enter deeper into the flutter region. This result is consistent with the fact that a flat plate is more likely to become unstable than a deformed plate because the latter benefits from the increased stiffness due to the structural nonlinear terms underlined in Eq. (15a).

Fig. 16

Stability map for $\Delta p_s = 0\,\hbox {kPa}$, with cavity

Fig. 17

Theory—displacement versus time, with cavity and no static pressure differential $\Delta p_s = 0\,\hbox {kPa}$, $1.25 \times \Delta T$

Figure 17 shows the time response of a plate computed with the same temperature, freestream and cavity properties but with static pressure differential set to zero at all times. In contrast to previous cases the plate remains ideally flat until flutter onset at $t\approx 11\,\hbox {s}$ when the temperature differential reaches a critical value of $\Delta T = 4\,\hbox {K}$ (determined from Fig. 16). Past flutter onset, a non-periodic oscillation starts with amplitude that varies with $\Delta T$.

Fig. 18

Theory—displacement versus time, with cavity and 135 dB noise, $1.25 \times \Delta T$

Fig. 19

Theory—displacement versus time, with cavity and 140 dB noise, $1.25 \times \Delta T$

4.6 Sensitivity to turbulent pressure fluctuations

Figures 18 and 19 show the plate’s response during the wind tunnel start transient with added acoustic noise in the $\Delta p_s$ input with rms of 135dB and 140dB (as described in Sect. 2.3), respectively. Acoustic noise may, in some cases, lead to snap-through buckling and shorten time to reaching LCO as demonstrated by Miller et al. [28]. The current computation’s aim is to investigate the plate’s sensitivity during its unstable phase (in the time interval of $t=10{:}26\,\hbox {s}$) to acoustic noise.

In both considered rms cases, the response amplitude up to $t = 5.5\,\hbox {s}$ is relatively large due to the absence of aerodynamic damping which was activated only when the freestream flow became supersonic. Compared with experiment it is clear that such levels of noise were not present in the experiment in this time interval. At $t \approx 11\,\hbox {s}$ both cases begin to flutter at approximately the same time and large amplitude oscillation begins. Surprisingly, both cases stabilize 2 s earlier than the case without noise shown in Fig. 12 which suggests that noise may facilitate transition between the different stability regions in some cases. Once stabilized at $t \approx 23\,\hbox {s}$, both cases vibrate with small amplitude about the deformed state. The considered noise levels are too small to induce snap-through buckle in this configuration.

4.7 Snap-through buckling and flutter

In the final 5 s of the measured plate displacement time history on Fig. 6, the plate reaches a static equilibrium. Vibrations about the deformed state may be caused by acoustic noise that originates in the turbulent boundary layer, periodic loads due to other systems on a high-speed vehicle, or even simple slow (quasi-static) changes in the static pressure differential due to climb, descent, or internal pressurization. The effects of periodic and quasi-static excitation modes on a deformed (although stable) plate are investigated to further demonstrate the nonlinear nature of plates in supersonic flow.

Fig. 20

Small vibration response to periodic excitation at $f_{\mathrm{ext}} = 350\,\hbox {Hz}$ and amplitude $A_{\mathrm{ext}} = 1150\,\hbox {Pa}$—(top) displacement time series, (bottom) phase-plane

Fig. 21

Snap-through response to periodic excitation at $f_{\mathrm{ext}} = 350\,\hbox {Hz}$ and amplitude $A_{\mathrm{ext}} = 1200\,\hbox {Pa}$—(top) displacement time series, (bottom) phase-plane (trajectory ends at time marked by the red dashed line). (Color figure online)

The steady state equilibrium at the end of the wind tunnel start is the focus of two snap-through instability computations. In both cases the static deformed shape is first computed for $\Delta p_{s_0} = \pm 3\,\hbox {kPa}$, $p_{\infty } = 41\,\hbox {kPa}$ and $\Delta T = 14.2\,\hbox {K}$. Then, a periodic or slowly increasing (or decreasing) term is added to the uniform static pressure differential term as described in Eqs. (18a) and (18b), respectively.

$$\begin{aligned} \Delta p_s(t)= & {} \Delta p_{s_0} + A_\mathrm{ext} sin(2 \pi f_\mathrm{ext} t) \end{aligned}$$

(18a)

$$\begin{aligned} \Delta p_s(t)= & {} \Delta p_{s_0} +\Delta \dot{p}_s t \end{aligned}$$

(18b)

Periodic excitation was applied with a frequency of $f_\mathrm{ext} =350\,\hbox {Hz}$ which is slightly below the first natural frequency of the plate at the considered conditions (see Fig. 13). Excitation amplitudes $A_\mathrm{ext}$ were increased until snap-through onset. Figures 20 and 21 show results for excitation amplitudes of $A_\mathrm{ext} = 1150\,\hbox {Pa}$ and $A_\mathrm{ext} = 1200\,\hbox {Pa}$ which fall slightly below and after snap-through onset, respectively. Both figures show the displacement time response (top) and a phase-space trajectory (bottom) in the first modal coordinate’s velocity versus displacement plane.

Excitation amplitude below snap-through onset results in a relatively small and periodic oscillation about the deformed state as shown in Fig. 20. The phase-plane plot shows that the energy input is not sufficient for the trajectory to leave the attractor’s proximity. On the other hand, a larger excitation amplitude considered in Fig. 21 leads to large amplitude and non-periodic oscillation. The phase-space trajectory of the snap-through buckled plate escapes the original equilibrium area and goes back and forth-between two attractors. Snap-through onset amplitude of excitation $A_\mathrm{ext}$ is expected to vary with frequency $f_\mathrm{ext}$ and thus chaos boundaries can be plotted on a $A_\mathrm{ext}$ versus $f_\mathrm{ext}$ plane [30]. Qualitatively, this behavior is similar to the dynamics of the Duffing’s equation which was investigated experimentally and computationally by Gottwald et al. [20].

For the excitation of the second mode to induce snap-through, the static pressure differential was increased at a rate of $\Delta \dot{p}_s = 1000 \, \hbox {Pa/s}$ as shown on the bottom plot of Fig. 22 with the corresponding displacement time history above it. Note that the $\Delta p_s$ increase was halted when a value of 3000 Pa was reached and shortly the oscillation stopped. When $\Delta p_s$ reaches a values of zero, the displacement is not equal to zero which means the plate is in buckled and stable equilibrium. This is also an indicator that there is hysteresis in the transition between two or more states. A similar computation is conducted for a different sign of initial static pressure differential $\Delta p_{s_0} = +3000\,\hbox {Pa}$ with a decrease rate of $\Delta \dot{p}_s = -1000 \, \hbox {Pa/s}$. Figure 23 shows a $\Delta p_s$ versus displacement plot for increasing and decreasing static pressure differentials. Both cases start at a static equilibrium with displacement of one plate thickness and flutter onset occurs at approximately $\Delta p_{s_F} \approx \pm 600\,\hbox {Pa}$. The demonstrated hysteresis loop presents an additional challenge for designers who plan to utilize plates in their nonlinear regime in supersonic flight.

Fig. 22

Displacement and $\Delta p_s$ versus time for increasing static pressure differential applied at a rate of $\Delta \dot{p}_s = 1000 \, \hbox {Pa/s}$ until $t = 6\,\hbox {s}$

Fig. 23

$\Delta p_s$ versus displacement for increasing (black) and decreasing (red) static pressure differential applied at a rate of $\Delta \dot{p}_s = \pm 1000 \, \hbox {Pa/s}$. (Color figure online)

5 Conclusion

A theoretical computational model of a plate in supersonic flow with cavity was presented and correlated with measurements taken in a transient wind tunnel start experiment. The model’s sensitivity to key parameters was investigated in terms of transition to and from stability by direct time integration of the equations of motion and a linear stability analysis that included the contribution of nonlinear stiffness due to initial static deformation. Responses to random, periodic, and quasi-static excitations were computed and snap-through onset conditions obtained. The following key conclusions are drawn from the results:

• 1. Considering the simplifying assumptions made about the aerodynamic forces and pressure and temperature differentials distribution, a good correlation between theory and experiment was demonstrated. LCO amplitudes predicted with theory were greater than measured. Future studies will consider a more accurate aerodynamic model with the effect of boundary layer in an attempt to improve agreement in LCO amplitude.

• 2. Temperature differential calibration is necessary when a local measurement from experiment is used together with a uniform distribution assumption. It is likely that better agreement in LCO amplitude between theory and experiment could be obtained for a more accurate modeling of $\Delta T$ distribution. Future studies will include spatial measurements of temperature.

• 3. Dynamic coupling between the plate and cavity had a relatively small effect on the plate’s response. While some small shifts in the fluter boundaries were observed on stability maps, the overall dynamic time response was very similar for with and without cavity. Important to note that instability due to plate cavity resonance was the main difference between the two cases, but in the considered time scales this form of instability did not manifest in the plate’s response.

• 4. Thickness calibration was shown to have an effect on the post-flutter dynamics. In many engineering applications the thickness (or a different geometrical or material parameter) are adjusted to match the first experimental and theoretical natural frequency. This approach may have impact on the nonlinear terms which are likely governed by the real/nominal geometrical thickness.

• 5. Static pressure differential was shown to be a key parameter in the experimentally measured plate dynamics. Without static pressure differential it is not likely the plate will reach a stable state after flutter onset. Thus measuring $\Delta p_s(t) = p_{\infty } - p_{\mathrm{cav}}$ is crucial for accurate time response prediction.

• 6. Acoustic pressure fluctuations were shown to have minor effect on transition to and from LCO. For sufficiently large oscillation rms values, a stable deformed plate is expected to transition between states (snap-through). This is similar to computations done in the snap-through buckling section.

• 7. Periodic and quasi-static modes of excitation were applied to compute snap-through buckling of an initially static deformed plate. Both cases demonstrate the challenging nonlinearities engineers may encounter when designing future supersonic vehicles. These include hysteresis, rapid transition between stable states and large amplitude non-periodic oscillations.