Fuzzy dynamics of multibody systems with polymorphic uncertainty in the material microstructure

Abstract

This paper deals with the fuzzy dynamics of multibody systems with polymorphic uncertainty in the material microstructure. Macroscopic material properties are obtained using fuzzy-stochastic FEM based computational homogenization. In particular, the spectral stochastic local FEM is utilized to simulate a representative volume element of the microstructure. Forward dynamics of the macroscopic system is modeled using the Graph Follower algorithm. Thereby we propagate the uncertainty from the lowest level of material microstructure to the highest level of multibody dynamics. Differences in the propagation of epistemic and aleatoric uncertainties to the macroscale and their influence on the multibody dynamics are discussed. A particular example of a multibody system used in this paper is a multistory frame, whereby the considered heterogeneous material is a cement-based concrete.

1 Introduction

In general, the analysis of technical systems in engineering applications requires precisely defined physical quantities. These quantities can be parameters such as material properties or geometrical values. Examining dynamical systems, for example, often requires certain deterministic quantities that lead to an output in form of a deterministic mapping. The approximative solution of the underlying differential equations of motion is usually found by using numerical time integration schemes.

However, in reality these parameters are afflicted with uncertainty. Real heterogeneous materials possess always either uncertain material properties, some kind of geometrical uncertainty in the microstructure, or both types. In many cases, the influence of these uncertainties cannot be neglected without loss of accuracy. Thus, a non-deterministic modeling technique is required.

Uncertainties can be divided in two types [1, 2]. Aleatoric uncertainty originates from the natural variability of the microstructure and cannot be reduced [2]. This type of uncertainties can be modeled using stochastic approaches. Epistemic uncertainty derives from insufficient knowledge regarding the microstructure and parameter distribution, imperfection of the analytical models, and experimental limitations. It can be described using fuzzy set theory [3]. If both types of uncertainties are present, the system is subject to polymorphic uncertainty [2].

The two most widely used approaches for uncertainty propagation are stochastic analysis [4,5,6,7,8,9] and fuzzy analysis [10,11,12]. These mathematical tools may be potentially applied to the same classes of problems. However, they require different input quantities, provide different outputs, and follow different strategies while propagating uncertainties.

The most widely accepted approach is to use stochastic analysis for aleatoric problems with sufficient and precise statistical data. In the case that additional information can be received, the model can be improved using Bayesian updates. Fuzzy analysis is often preferred for models with lack of experimental data, and contradictory or imprecise information. It is suited to describe measurement errors and errors resulting from model simplifications. The different treatment of aleatoric and epistemic uncertainties is motivated by a number of studies [13,14,15,16]. Fuzzy set theory was developed by Zadeh in the sixties [3] and is explained in detail in [10, 11]. In “Appendix 1” a brief reiteration of fuzzy numbers and fuzzy set theory is given. Based on the extension principle, the approach allows the transition from deterministic mappings to fuzzy mappings [10, 11, 17].

This paper deals with fuzzy dynamics of multibody systems with polymorphic uncertainties in the material microstructure modeled using fuzzy-stochastic FEM and the Graph Follower algorithm. We apply the homogenization scheme presented in [18]. Aleatoric uncertainties are modeled using the stochastic local FEM [19]. Epistemic uncertainties are modeled using the extended transformation method for fuzzy numbers [20]. Here, the microscopic material model is considered to be fuzzy-stochastic, while the macroscopic material properties are described only by fuzzy parameters.

The specific example used in this paper is concrete, a typical heterogeneous material consisting of a cement paste matrix filled with coarse aggregates. Mechanical properties of heterogeneous materials may strongly differ depending on the aggregate volume fraction, aggregate size and stiffness, and cement quality. The effective macroscopic properties of heterogeneous materials are estimated from the response of the underlying microstructure by homogenization. The classical homogenization approach considers a deterministic representative volume element of the microstructure. The response is then transferred to the macroscale. For an overview of existing deterministic homogenization techniques we refer to [21].

In contrast to that, in this paper the material model of concrete contains polymorphic uncertainty and requires a mixed fuzzy-stochastic description. There are four specific sources of uncertainties in the considered concrete model—two aleatoric uncertainties and two epistemic uncertainties: random aggregate sizes, random aggregate distribution within the matrix, measurement error, and error resulting from model simplification. Aleatoric uncertainties influence microscopic quantities and are important when considering local phenomena like crack growth, plasticity and damage. On the macroscale, an averaging procedure is applied. Thus, no parameter spread resulting from aleatoric uncertainties in the microstructure needs to be considered. Epistemic uncertainties cannot be averaged due to their nature. The data spread resulting from epistemic uncertainties is therefore transferred from the microscale to the macroscale.

The paper focuses on epistemic uncertainty in the forward dynamics simulation for the specific example of a multistory frame. For this, the uncertain parameter determined by the fuzzy-stochastic finite element analysis of the microstructure of concrete is integrated. Following [22] and [23], the fuzzy mapping of the dynamical system is determined from the deterministic mapping. In [22], an efficient numerical method called Graph Follower algorithm is developed, which is used for the simulation of forward dynamics with epistemic parameter-uncertainty. Based on this algorithm, the discrete envelopes in fuzzy forward dynamics for a multistory frame are determined.

2 Notation

In this work, we distinguish between deterministic and non-deterministic variables, vectors and tensors, matrices and operators. The following notation is used:

• Second order tensors and vectors are denoted by bold (e.g. $\varvec{\mathrm {F}}$) and bold italic (e.g. $\varvec{x}$) scripts, respectively.

• Random variables, second order tensors and vectors are represented [24, 25] as functions of the elementary event $\omega$, e.g. $g(\omega )$, $\varvec{\mathrm {F}}(\omega )$, $\varvec{\theta }(\omega )$.

• A random field is any function of the spatial coordinates $\varvec{x}$ and the elementary event $\omega$ (e.g. $G(\varvec{x},\omega )$).

• Fuzzy numbers, vectors, and matrices are denoted by a tilde like, e.g. $\tilde{p}$.

• Capital calligraphic letters are used for the domains of functions and sets (e.g. $\mathcal {D}$, $\mathcal {S}$, $\mathcal {F}$).

• Bold calligraphic letters denote function spaces like, e.g. the Hilbert space $\varvec{\mathcal {H}}$.

• Differential operators are denoted by capital upright letters, e.g. $\mathrm {D}(\varvec{x},\omega )$.

• In particular ${{\,\mathrm{div}\,}}$ and ${{\,\mathrm{grad}\,}}$ denote divergence and gradient operators.

3 Non-deterministic finite element method

3.1 Stochastic finite element method

In contrast to the usual deterministic FEM the stochastic version works with random parameters thus requiring some preliminary definitions. Let the Euclidean space $\mathbb {E}$ represent the physical space with coordinates $x_i$ assembled in the vector $\varvec{x}$. The stochastic FEM (SFEM) requires in addition the definition of the stochastic space $\mathbb {S}$ [4]. This is the space of random variables (RVs) with the basis set of RVs arranged in the vector $\varvec{\theta }$. For convenience the basis random variables in form of truncated Gaussian RVs with zero mean and unit variance parameter are chosen. The implementation of the truncated Gaussian RVs instead of normal Gaussian RV is motivated by the natural limitations of physical processes (e.g. particle radii cannot tend to infinity) and also for reasons of numerical integration stability [26].

All other random variables can be described as a possible nonlinear mapping of the basic set of RVs [24, 25]. Thus, the stochastic space $\mathbb {S}$ can be visualized similar to the physical space $\mathbb {E}$ with coordinates $\theta _i$ assembled in the vector $\varvec{\theta }$ [19, 27,28,29]. Thus, all other random variables are functions in $\mathbb {S}$. Note that the basis RVs are independent and their joint probability density function $f_{\Theta }$ (pdf) represents the product of all individual pdfs from the basic set of RVs.

By this definition the SFEM may be regarded as normal deterministic FEM, only in the n-dimensional physical-stochastic product space [19, 27,28,29].

Galerkin-type FEM as considered in the present work is based on the concept of a Hilbert space of functions. For this the physical domain $\mathcal {D}\subset \mathbb {E}$, the stochastic domain $\mathcal {S}\subset \mathbb {S}$, and the tensor product domain $\mathcal {V}=\mathcal {D}\times \mathcal {S}$ are defined. Following [4] the physical Hilbert space $\varvec{\mathcal {H}}$ of functions defined over the domain $\mathcal {D}$, the stochastic Hilbert space $\varvec{\mathcal {Q}}$ of functions defined over the domain $\mathcal {S}$, and the tensor product Hilbert space $\varvec{\mathcal {W}}=\varvec{\mathcal {H}} \times \varvec{\mathcal {Q}}$ of functions defined over the domain $\mathcal {V}$ are introduced. Physical, stochastic, and product spaces with corresponding domains are depicted in Fig. 1.

Fig. 1

Physical, stochastic, and product spaces $\mathbb {E}$, $\mathbb {S}$, and $\mathbb {E}\times \mathbb {S}$ with corresponding physical, stochastic, and product domains $\mathcal {D}$, $\mathcal {S}$, and $\mathcal {V}=\mathcal {D}\times \mathcal {S}$

SFEM shape functions belong to the space $\varvec{\mathcal {W}}$, thus integration is performed over the domain $\mathcal {V}$.

In this work the stochastic local FEM (SL-FEM) approach is used, which requires unified treatment of physical and stochastic dimensions. Thereby, local quadratic n-dimensional serendipity-type shape functions [19] are used for the discretization of the domain $\mathcal {V}$.

Let $\langle ~\rangle$ denote the inner product in the physical-stochastic product space.

$$\begin{aligned} \langle g_1(\varvec{x},\omega ) g_2(\varvec{x},\omega ) \rangle := \int \limits _\mathcal {D}\int \limits _\mathcal {S} g_1(\varvec{x},\varvec{\theta })g_2(\varvec{x},\varvec{\theta }) \mathrm {d}\varvec{x} f_{\Theta } \mathrm {d}\varvec{\theta }, \end{aligned}$$

(1)

where $f_{\Theta }$ is the joint probability density function of the basis random variables.

Next, a random differential operator $\mathrm {D}(\varvec{x},\omega )$ is considered such that

$$\begin{aligned} \mathrm {D}(\varvec{x},\omega )\varvec{q}(\varvec{x},\omega )=f(\varvec{x},\omega ), \end{aligned}$$

(2)

where $f(\varvec{x},\omega )$ is the random loading and $\varvec{q}(\varvec{x},\omega )$ is the unknown function.

Thus, Galerkin projections of the differential operator $\mathrm {D}(\varvec{x},\omega )$ and the unknown function $\varvec{q}(\varvec{x},\omega )$ onto the basis $\varvec{\varphi }(\varvec{x},\omega )$ yield

$$\begin{aligned}&\varvec{q}(\varvec{x},\omega )=\sum \limits _{i=1}^{N_q}\varvec{q}_i\varphi _i(\varvec{x},\omega ), \end{aligned}$$

(3)

$$\begin{aligned}&\left\langle \left[ \mathrm {D}(\varvec{x},\omega )\varvec{q}(\varvec{x},\omega )-f(\varvec{x},\omega ) \right] \varphi _i(\varvec{x},\omega ) \right\rangle =0,\nonumber \\&\quad \forall i=1,\ldots ,~N_q, \end{aligned}$$

(4)

where $N_q$ is the number of basis functions.

For a 2D linear mechanical problem the differential operator in (2) reads

$$\begin{aligned} \begin{aligned}&\mathrm {D}(\varvec{x},\omega )\varvec{q}(\varvec{x},\omega ):=-{{\,\mathrm{div}\,}}{{\varvec{\sigma }}}\big ({{\varvec{\varepsilon }}}(\varvec{x},\omega ) \big ),\\&f(\varvec{x},\omega ):=\varvec{f}(\varvec{x},\omega ),\\ \end{aligned} \end{aligned}$$

(5)

where $\varvec{q}(\varvec{x},\omega )$ corresponds to the random deformation map describing the position of material points, $\varvec{f}(\varvec{x},\omega )$ denotes the random body forces and ${{\varvec{\sigma }}}$ and ${{\varvec{\varepsilon }}}$ represent the stress tensor and the linear strain tensor, respectively. Please note that the ${{\,\mathrm{div}\,}}$ and $\mathrm {D}$ involve differentiation only with respect to the physical coordinates $\varvec{x}$.

For simplicity of representation, the random deformation map is rewritten using matrix notation:

$$\begin{aligned} \begin{aligned}&\varvec{q}(\varvec{x},\omega )=\varvec{x}+\varvec{u}(\varvec{x},\omega ), \\&\varvec{u}(\varvec{x},\omega ) = {{\varvec{\varphi }}}(\varvec{x},\omega ) \varvec{U} = \begin{bmatrix} \varphi _1(\varvec{x},\omega ) \varvec{\mathrm {I}}&\varphi _2(\varvec{x},\omega ) \varvec{\mathrm {I}}&\dots \end{bmatrix} \varvec{U} , \\&\varvec{\varepsilon }=\varvec{\mathrm {D}} \varvec{u}(\varvec{x},\omega ) = \begin{bmatrix} \frac{\partial }{\partial x_1}&0 \\ 0&\frac{\partial }{\partial x_2} \\ \frac{\partial }{\partial x_2}&\frac{\partial }{\partial x_1} \end{bmatrix} \varvec{u}(\varvec{x},\omega ) = \varvec{\mathrm {B}}(\varvec{x},\omega ) \varvec{U}, \\&\varvec{\sigma }(\varvec{x},\omega )=\varvec{\mathrm {E}}\varvec{\varepsilon }(\varvec{x},\omega ), \end{aligned} \end{aligned}$$

where $\varvec{\mathrm {I}}$ is the identity matrix and the matrix $\varvec{\mathrm {E}}$ represents Hooke’s law, e.g. for plane strain problems reading

$$\begin{aligned} \varvec{\mathrm {E}}=\frac{E}{[1+\nu ][1-2\nu ]}\begin{bmatrix} 1-\nu&\nu&0\\ \nu&1-\nu&0\\ 0&0&\frac{1}{2}[1-2\nu ] \end{bmatrix}, \end{aligned}$$

(6)

where E and $\nu$ are Young’s modulus and Poisson’s ratio, respectively.

Here, $\varvec{U}$ is a vector of coefficients in the finite approximation of (3)

$$\begin{aligned} \varvec{U}=\begin{bmatrix} \varvec{u}_1\\ \varvec{u}_2\\ \vdots \\ \varvec{u}_n \end{bmatrix}, ~~~ \varvec{u}_i=\begin{bmatrix} u_{i1}\\ u_{i2}\\ \vdots \end{bmatrix}, \end{aligned}$$

where $u_{ij}$ represents the jth component of the displacement field projected onto the ith basis function.

Thus, Galerkin projections yield the necessary condition of the total mechanical energy minimum:

$$\begin{aligned} \begin{aligned}&\varvec{\mathrm {K}}\cdot \varvec{U} = \varvec{F}^{ext}, \\&\varvec{\mathrm {K}}:=\left\langle \varvec{\mathrm {B}}^t \varvec{\mathrm {E}} \varvec{\mathrm {B}} \right\rangle ,\\ \end{aligned} \end{aligned}$$

(7)

where $\varvec{\mathrm {K}}$ is the linear elastic stiffness matrix, $\varvec{\mathrm {B}}^t$ is the transposed matrix $\varvec{\mathrm {B}}$, and vector $\varvec{F}^{ext}$ represents external loading. Finally a deformed state is obtained as:

$$\begin{aligned} \varvec{q}(\varvec{x},\omega )=\varvec{x}+ {{\varvec{\varphi }}}(\varvec{x},\omega ) \varvec{U}. \end{aligned}$$

3.2 Fuzzy finite element analysis

In many cases the system parameters cannot be obtained exactly due to many reasons: lack of knowledge regarding the microstructure, limited accuracy of the fitting procedure, imperfection of the model (which can be fitted to the experimental data but never coincides with them), noisy experimental data, insufficient number of experimental samples, etc. Based on the source of uncertainties, available input data, and required output, either the probabilistic or the non-probabilistic description of the problem parameters may be used. The most well-developed non-probabilistic techniques are interval arithmetic, evidence theory, and fuzzy arithmetic [10, 11].

The fuzzy problem description may be preferred if the available data is coarse or inconsistent, but more specific than only upper and lower bounds, or in case the sensitivity with respect to the parameter spread size is studied. The discussion on a fuzzy description for the considered problem is presented in detail in [18].

In case of different types of uncertainties present in the system, one refers to polymorphic uncertainties. In this case the interval-stochastic, fuzzy-stochastic or evidence theory is applied. All of these approaches use p-boxes instead of precise cumulative probability distribution functions of input parameters. That is the reason why an alternative terminology for this techniques is often used: the imprecise probability. The combination of random variables and fuzzy numbers used to describe imprecision in the considered problem [18] results naturally in a fuzzy-stochastic problem treatment.

The structure of the proposed fuzzy-stochastic homogenization framework is as follows [18]. Based on the experimental data we design a stochastic representative volume element. Parametrized distributions like, e.g. truncated Gaussian or truncated log-normal, are used to fit statistical data. The distribution parameters and material properties cannot be estimated exactly and, thus, become fuzzy numbers. Every sample generated by fuzzy arithmetic is an independent stochastic problem and is solved separately (Fig. 2). The SFEM output is then analyzed in order to construct the response surface for every quantity of interest, e.g. for the homogenized stress mean value. Response surfaces are used to extract $\mathrm {min}$ and $\mathrm {max}$ values of the quantities of interest for every $\alpha$-cut. Finally fuzzy response curves are plotted representing upper and lower bounds for every $\alpha$-cut.

Fig. 2

Structure of the fuzzy-stochastic FEM based homogenization framework

4 Computational homogenization of heterogeneous materials with polymorphic uncertainties in the microstructure

4.1 Description of random particle positions

In this section we briefly explain the approach which is used to describe heterogeneous materials with randomly distributed circular particles of different sizes. Let us consider firstly a material with circular particles of equal size and then generalize this approach to the case of random particle sizes.

An attempt to describe the particle positions in terms of random variables results in a large and complex system of random variables with strongly nonlinear dependencies between them. Due to the fact that particles are non-overlapping, inequalities should be used to restrict the particle positions. However, the extremely high complexity of such a description necessitates some alternative approach.

The traditional description of random particle distributions is based on the concept of a n-point probability density. The one-point probability density represents the relative density of particles. Thereby, higher one-point probability results in higher particle density in the given area. Interparticle distance is characterized by the two-point probability density function. For the considered case of uniform one-point probability function and homogeneous particle distribution, the two-point probability density may be considered as the probability to find the next particle in a certain distance from the given particle. Thereby the direction of search is not important.

In many cases the interparticle distance plays the key role in the determination of mechanical stresses. Thus, material models based on a two-point probability density function are proven to be very accurate. Examples of that kind of models may be found in e.g. [30]. The model presented in [30] considers only one particle (center) surrounded by an infinite set of particles with random distances to the center. The disadvantage of this approach is that the interparticle distances between the surrounding particles are not considered. Figure 3 demonstrates the particle distribution generated using the two-point probabilities only. Note that the non-overlapping restriction and distribution homogeneity, which were mentioned earlier, are not fulfilled. Moreover, the introduction of any restrictions on the distances between the surrounding particles requires the use of three-, four-, five-, and n-point distribution density functions, thus, resulting in an extremely complex system of random variables.

Another disadvantage of two-point probability models is that there are particles next to the center along some direction, which are extremely far and have only a very weak influence on the deformed state around the center (Fig. 4). Due to the fact that mechanical laws are strongly local, only the interparticle distance to the direct neighbors should be considered. Thus, an advanced material model must distinguish between direct neighbors and the rest of the particles and must account for the interparticle distances between surrounding particles.

Fig. 3

Particle distribution around the center particle generated using the two-point probabilities only. The non-overlapping restriction and distribution homogeneity are not fulfilled

Fig. 4

Two-point probability considers all presented particles as neighbors, however only the direct neighbors influence the deformed state near the center

Thus, an alternative approach consists in an application of the Delaunay triangulation with further statistical analysis. Let us generate randomly distributed particles of equal sizes and perform triangulation considering the particle centers as nodal points (Fig. 5). Delaunay triangulation determines the nearest particles (neighbors) to the given particle and evaluate the distances to direct neighbors only.

Fig. 5

Delaunay triangulation of the randomly distributed circular inclusions of equal sizes. For every given particle the number of neighbor particles and distances to the direct neighbors are known

Two important statistical estimations may be obtained from the produced triangulation: the distribution of interparticle distances between direct neighbors (Fig. 6) and the statistics on the number of direct neighbors (Fig. 7). The interparticle distance is always bigger or equal to the particle diameter. Thus, the non-overlapping condition is fulfilled automatically. The number of direct neighbors is bigger or equal three and the most probable number is six. Using these two statistical measures one may generate consistent random samples with the considered properties (homogeneity, non-overlapping restriction, etc.). The presented statistical data looks like first order statistics, but contains also the information from the two-point distribution function and more.

Fig. 6

Distribution of the distances between direct neighbors in a Delaunay triangulation. The smallest distance is equal to the particle diameter, thus, particles are non-overlapping

Fig. 7

Number of direct neighbors in a Delaunay triangulation. The smallest number is three, the most frequently observed number of neighbors is six

The interparticle distance is an important quantity for the estimation of the micromechanical stresses. However, observations demonstrate that the homogenized stress values exhibit strong dependency only on some averaged (integral) quantity, namely the volume fraction. This is also the underlying reason that the well-known Mori-Tanaka homogenization technique requires only three input quantities: particle size, particle shape and volume fraction. The simulations performed in [31] demonstrate that a single unit cell with volume fraction corresponding to the volume fraction of the material with randomly distributed particles provides already a good approximation for homogenized stresses. Thus, the volume fraction is the dominating factor for the estimation of homogenized stresses.

In order to take into account the volume fraction we switch from the Delaunay triangulation to its dual—the Voronoi tessellation (Fig. 8). The Voronoi tessellation divides the total area into the cells associated with particles such that every cell contains all material points which are closer to the associated particle than to any other particle. This division is unique for the given Delaunay triangulation. The Voronoi tessellation contains the same statistical information as the triangulation. The number of edges of a Voronoi cell is equal to the number of direct neighbors. The distance to the edge is half of the distance to the corresponding neighbor.

Fig. 8

The Voronoi tessellation divides the total area into the cells associated with particles such that the every cell contains all material points which are closer to the associated particle than to any other particle. The Voronoi tessellation is the dual to the Delaunay triangulation

The average stress values in neighboring cells are only weakly correlated. Let us divide the Voronoi cells into triangular elements as depicted in Fig. 9. The triangular elements $\varOmega _1$ and $\varOmega _2$ associated with particles $P_1$ and $P_2$, respectively, are equal and symmetric. For all material points in $\varOmega _1$ the closest particle is by definition $P_1$, the second closest is $P_2$. Let us consider that the deformed state in the region $\varOmega _1\cup \varOmega _2$ is defined principally by the distances to these two particles and the influence of other particles is neglected. In this case the deformed states in the $P_1$-cell and the $P_2$-cell are correlated and the correlation is determined by the relative area of $\varOmega _1$. In average every cell contains 6 triangular components, thus the correlation is weak.

Fig. 9

Symmetric triangular components of two neighbor cells possessing close deformed states

The local volume fraction of every Voronoi cell is given by $\nu _i=\pi r^2 / A_i$, where $A_i$ is the cell area. Considering the normalized radius $r_n=r/a$, where $a=\sqrt{A}/2$, we obtain $\nu _i=\pi /4 ~[r_n]_i^2$. The variable $r_n$ is evaluated accounting for the two-point probability density function, the number of direct neighbors, the inequality restriction, the correlation between these quantities, and is directly related to the local volume fraction.

The total volume fraction $\nu _f$ is related to the local volume fraction as

$$\begin{aligned} \nu _f=\sum \limits _{i=1}^{N}\frac{A_i}{A_{total}} \nu _i=\sum \limits _{i=1}^{N}\frac{A_i}{A_{total}}\frac{\pi }{4}[r_n]_i^2, \end{aligned}$$

(8)

where N is the total number of particles and $A_{total}$ is the total area. For convenience we divide the total range of values into bins $A_k$. By introducing the new weight function $w_k$ such that

$$\begin{aligned} w_k=\sum \limits _{\forall i: A_i\in A_k} \frac{A_i}{A_{total}}, \end{aligned}$$

(9)

the total volume fraction reads as

$$\begin{aligned} \nu _f=\sum \limits _{k=1}^{K} w_k \frac{\pi }{4}[r_n]_k^2. \end{aligned}$$

(10)

Similarly, the average $r_n$ is simply $\sum \nolimits _{k=1}^{K}w_k [r_n]_k$. Similar expressions hold also for other quantities. Thus, in general the weight $w_k$ determines the partition of the whole sample possessing a $r/a=[r_n]_k$ ratio, i.e. in the limit case $w(r_n)$ is the probability density of $r_n(\omega )$.

Fig. 10

Part of the virtual sample with non-overlapping inclusions divided into Voronoi cells (a) and Apollonius cells (b). Note the Voronoi edges intersecting the inclusions’ boundaries

In the case of random particle radii the Voronoi tessellation fails. If the traditional Voronoi tessellation is used the Voronoi cell edges may intersect the inclusions boundaries (Fig. 10a). Thus in our previous work we proposed an improved model based on the so-called Apollonius diagram (additively weighted Voronoi diagram), its dual is the Apollonius graph also sometimes called the Delaunay graph of disks (Fig. 10b). The computation of the Apollonius graph is a non-trivial problem due to the highly complex predicates and curvilinear edges of the Apollonius diagram. In the general case these edges are hyperbolic curves. We used a specialized package of the Computational Geometry Algorithms Library [32] in order to compute the Apollonius diagrams.

In the case, when the Apollonius diagram is used instead of Voronoi tessellation, the weight $w_k$ of every single realization of $r_n$ is also the sum of the relative areas of all cells possessing corresponding r / a-ratio.

4.2 Stochastic representative volume element

Homogenization considers typically two separate scales: the macro scale and the micro scale. Thereby macroscopic material properties are obtained from the simulation of the microscopic model. In the case of random material microstructures the microscopic model should be large enough to exhibit all macroscopic properties, thus resulting in extremely high computational costs. Thus the ergodicity assumption is often used, which states that averaging over one large sample is equivalent to averaging over an ensemble of small samples. Thereby time and computer power demanding simulations can be replaced by the analysis of one small stochastic representative volume element (RVE), however, including statistical information about the microstructural variability.

In our work we utilize the homogenization framework proposed in [18]. Thus the following simplifications are required:

• Following [33, 34], aggregates are presented by round particles.

• Aggregates are distributed within the matrix fully randomly and uniformly without preferred directions.

• The shape of the stochastic ergodic RVE is rectangular.

The corresponding uncertainties are considered:

• Random particle radii (modeled as random variables),

• Random particle distribution within the matrix (statistical data obtained from the additively weighted Voronoi diagram),

• Error in statistical data (two fuzzy variables),

• Imprecise information about the particle stiffness (fuzzy Young’s modulus of particles).

Based on the maximum entropy principle the particle radii distribution is considered to be log-normal and described in terms of scale and position parameters $\sigma _r$ and $\mu _r$:

$$\begin{aligned} r(\omega )=\exp (\mu _r+\sigma _r \theta (\omega )), \end{aligned}$$

(11)

where $\theta (\omega )$ is the truncated Gaussian variable.

The cumulative probability density function (cdf) of the log-normal radii distribution is presented in Fig. 11. The random radius $r(\omega )$ is expressed here in normalized units. Based on data presented in [33, 35] the radius varies by a factor of ten.

Fig. 11

The cumulative probability density function (cdf) of the log-normal radii distribution. The random radius $r(\omega )$ is expressed in normalized units

The random particle distribution is evaluated in a few steps as described in Sect. 4.1:

• Real materials possess randomly distributed non-overlapping inclusions. One may divide microscopic material samples into cells wherein every cell represents the set of material points that are closer in some sense to the associated inclusion than to any other.

• The cell area distribution can be estimated statistically based on the analysis of microscopic samples.

• The statistical information is implemented into the considered RVE model.

Based on the data presented in the literature [33, 35] the total volume fraction may be considered in the range [0  0.5], but in most cases it is equal 0.2.

Figure 12 demonstrates the statistical area distribution plotted versus the reduced radius $r_n$ for materials with volume fraction of particles $\nu _f=0.2$. The dashed area in the right part of the figure depicts physically impossible values of $r_n$. If $r_n\ge \sqrt{\frac{\pi }{4}}$ the area of the inclusion is bigger than the area of the Apollonius cell, thus impossible for non-overlapping inclusions. Two vertical blue lines $r_n=0.13$ and $r_n=0.87$ are limits covering 99.27% of the entire sample area. Cells lying outside these limits are depicted by blue color. Only the cells inside these limits are used for the evaluation of $w(r_n)$. We truncate the distribution at this point for numerical reasons in order to avoid long tails with nearly zero probability in the resulting pdf.

Fig. 12

Area of the Apollonius cells $A^{cell}$ plotted versus $r_n=r/a$. The dashed area in the right part of the picture represents physically impossible values of $r_n$

The obtained cdf of $r_n(\omega )$ is presented in Fig. 13. The purple curve represents a histogram obtained from Fig. 12. This distribution is non-Gaussian. For further applications the reduced radius $r_n(\omega )$ should be represented as a nonlinear mapping of the truncated Gaussian basis random variable [18]. The mapping curve $r_n(\theta (\omega )):~\theta (\omega )\rightarrow \mathbb {R}$ is computed from the expression $f_r(r) \mathrm {d}r=f_\theta (\theta ) \mathrm {d}\theta$, where $f_r(r)$ and $f_\theta (\theta )$ are the probability density functions. The obtained function is approximated by a cubic polynomial. To this end, we introduce a new random variable which is a cubic polynomial of the truncated Gaussian variable $\theta (\omega )$:

$$\begin{aligned} \begin{aligned}&p_n(\omega )=\sum \limits _{i=1}^4 a_ih_i(\theta (\omega )),\\&h_1(\theta (\omega ))=[1+2\theta (\omega )][1-\theta (\omega )]^2,\\&h_2(\theta (\omega ))=\theta (\omega )[1-\theta (\omega )]^2,\\&h_3(\theta (\omega ))=\theta (\omega )^2[3-2\theta (\omega )],\\&h_4(\theta (\omega ))=\theta (\omega )^2[\theta (\omega )-1],\\ \end{aligned} \end{aligned}$$

(12)

where the $h_i$ are cubic Hermite splines.

This model includes 4 parameters $a_i$. The convenience of the Hermite representation is that two parameters, namely $a_1$ and $a_3$ are immediately evaluated from the function values at the ends of the interval. Thus only the parameters $a_2$ and $a_4$ need to be found from curve fitting. The fitting curve does not perfectly coincide with the experimental curve, thus we introduce some variation to the parameters $a_2$ and $a_4$ [18].

Based on the results of curve fitting we design two triangular fuzzy numbers: $\tilde{a}_2$ with support [0.001,  0.3145] and modal value $\bar{a}_2=0.1$ which is obtained from curve fitting; and $\tilde{a}_4$ with support [0.001,  0.9975] and modal value $\bar{a}_4=0.1692$. The two crisp model parameters are $a_1=0.1337$ and $a_3=0.8663$. The obtained function $p_n$ is an approximation of the empirical curve $r_n$ and includes two fuzzy parameters, therefore it cannot be visualized as one single curve, but as lower and upper limits, i.e. the p-box (black lines in Fig. 13).

Fig. 13

Experimental cumulative distribution function of $r_n(\omega )$ and the p-box containing the underlying experimental curve

Thereby the normalized radius is described by a fuzzy-stochastic variable with three non-deterministic parameters.

We consider here a rectangular RVE with size parameter a and total area $A=4a^2$. The area of the RVE is considered to exhibit the same distribution density function as the areas of the cells. The influence of the cell’s shape is not considered, thus, we lose some part of the statistical information in order to reduce the number of model parameters. This is a necessary model simplification.

Thereby we propose to use a statistically similar representative volume element [36]. The idea is to provide some substitute or surrogate model, which possesses some statistical properties of the original model, specifically the relation between the particle radius and the area around the particle. The statistically similar stochastic model is simple and contains only one particle. By varying the particle radii distribution in a one-particle model we may control not only the average stress, but also the maximum and minimum stress and the stress standard deviation in the stochastic system.

All simulation are performed with periodic boundary conditions applied to the boundaries of the RVE. The macroscopic loading transfered from the macroscale is presented by the macroscopic strain tensor ${\bar{{\varvec{\varepsilon }}}}$.

The use of periodic boundary conditions for the statistically similar (substitute) model is motivated by a number of studies demonstrating that periodic boundary conditions are the most reliable and converge faster than Dirichlet or traction boundary conditions [21, 31, 37]. They are often used even if the model is not periodic [21, 31], because Dirichlet and traction boundary conditions result in over- and underestimation for the stress [21, 31, 37, 38] in computational homogenization. Periodic boundary conditions do not necessarily represent topological periodicity of the microstructure. They are in this case just some particular mathematical abstraction satisfying the Hill-Mandel condition and resulting in faster convergence compared to Dirichlet and traction boundary conditions.

Moreover the simple comparison of the homogenized stresses in periodic composites modeled with only one particle in the unit cell and composites with random microstructure, performed in [31], demonstrated close homogenized stress values in both models. Thus, one of the conclusions made in [31] is that one unit cell with only one centered particle and periodic boundary conditions is already a good approximation for the model with randomly distributed particles at least in engineering applications.

Thus the resulting stochastic RVE is a rectangular RVE with the size 2a, where $a=1$, with one circular particle possessing random radius $r_n(\omega )$. Due to the periodic boundary conditions the particle position inside the RVE does not influence the homogenized stress values, thus for the sake of simplicity we consider only a model with the particle in the center of the RVE.

In case of two physical and one stochastic coordinates the stochastic RVE can be considered as a stack of thin sheets with deterministic 2D RVEs in each of them, i.e. every horizontal slice of the stochastic RVE corresponds to some deterministic model. Thus the vertical dimension represents the evolution of the microstructure by varying the random parameter (Fig. 14).

Fig. 14

The stochastic representative volume element for a 2D problem considering a random particle radius

Material properties of the cement matrix are presented by the Young’s modulus $E_m=20$ GPa and the Poisson’s ratio $\nu _m=0.3$ [33, 35]. The Poisson’s ratio of the particles is $\nu _i=\nu _m=0.3$. The Young’s modulus of the aggregates is roughly four times higher than the Young’s modulus of the cement matrix, also the experimental estimations of the aggregate stiffness contain often large measurement error. Therefore we consider the Young’s modulus of the particles to be a triangular fuzzy number with modal value $\bar{E}_i=80$ GPa [35] and the support [75,   85] GPa.

We model a particle as a jump in the elastic properties ($C^{-1}$-continuity), whereby the displacements are $C^0$-continuous. We assume for simplicity a constant Poisson’s ratio $\nu =0.3$. In the general case the Poisson’s ratio is also a random field. An interesting analysis for the case of fluctuating Poisson’s ratio is presented, e.g. in [39].

Thus, here only the elastic modulus is a random field and is given as

$$\begin{aligned} \tilde{E}(\varvec{x},\omega )=E_m+\frac{1}{2}[\tilde{E}_i-E_m]\big [ 1-\mathrm {sign} z\big (\varvec{x},\omega \big )\big ], \end{aligned}$$

(13)

where $E_m$ and $E_i$ are the Young’s moduli of the matrix and the particle, respectively; $z\big (\varvec{x},\omega \big )$ is a cone-like level-set function [26], which indicates whether the material point with coordinates $\varvec{x}$ belongs to the matrix or to the particle ($z<0$: particle, $z>0$: matrix).

$$\begin{aligned} z\big (\varvec{x},\omega \big )=r(\omega )\left[ \sqrt{\frac{x_1^2}{r(\omega )^2}+\frac{x_2^2}{r(\omega )^2}}-1\right] . \end{aligned}$$

(14)

4.3 Simulation results for computational homogenization

The simulations presented in this section were performed using 12 element layers in the stochastic dimensions due to the large radius variation. The mesh generated for one arbitrary fuzzy sample is depicted in Fig. 15. Lilac is used to depict inclusion, orange corresponds to the elastomer matrix.

Fig. 15

Finite element discretization of the physical-stochastic domain $\mathcal {V}$. Lilac depicts inclusion, orange corresponds to the elastomer matrix

Three fuzzy parameters $\tilde{a}_2$, $\tilde{a}_4$ and $\tilde{E}$ are sampled using the extended transformation method [20] with 5 $\alpha$-cuts thus resulting in 225 fuzzy samples.

The simulations were performed for two different load cases:

$$\begin{aligned} \begin{aligned}&{{\varvec{\varepsilon }}}^{(1)}\widehat{=}\begin{bmatrix} 0.01&0 \\ 0&0.01 \end{bmatrix},&{{\varvec{\varepsilon }}}^{(2)}\widehat{=}\begin{bmatrix} 0&0.01 \\ 0.01&0 \end{bmatrix}. \end{aligned} \end{aligned}$$

(15)

The homogenized stresses are obtained as functions of the basis random variable $\theta (\omega )$ for every fuzzy sample (Fig. 16). The effective macroscopic stress is obtained by averaging all curves along $\theta (\omega )$, thus, presenting the mean stress value. Figure 17 demonstrates the mean stress values rearranged into $\alpha$-cuts. The reconstructed mean homogenized stress membership function is slightly asymmetric

Fig. 16

Stochastic homogenized stress curves plotted versus the basis random variable $\theta (\omega )\in [-3,~3]$. Different curve colors correspond to different $\alpha$-cuts

Fig. 17

Mean homogenized stress values $\bar{\sigma }_{11}({{\varvec{\varepsilon }}}^{(1)})$ rearranged into $\alpha$-cuts. Different curve colors correspond to different $\alpha$-cuts

The effective macroscopic Young’s modulus is computed by substituting the mean homogenized stresses ${\bar{{\varvec{\sigma }}}}({\bar{{\varvec{\varepsilon }}}}_1)$ and ${\bar{{\varvec{\sigma }}}}({\bar{{\varvec{\varepsilon }}}}_2)$ into the solution for linear isotropic homogeneous materials.

$$\begin{aligned} \begin{aligned}&\sigma _{11}({{\varvec{\varepsilon }}}^{(1)})=\frac{E}{[1+\nu ][(1-2\nu ]} \varepsilon ^{(1)}_{11} , \\&\varepsilon ^{(2)}_{12}=\frac{1+\nu }{E}\sigma _{12}({{\varvec{\varepsilon }}}^{(2)}) . \end{aligned} \end{aligned}$$

(16)

Solving the linear Eq. (16) for every fuzzy sample yields the fuzzy Young’s modulus depicted in Fig. 18. Note that the Young’s modulus is well approximated by a triangular fuzzy number with modal value $\bar{E}=24.7561$ GPa and support [22.7626,  25.8312] GPa. Modal value and spread of the effective Young’s modulus perfectly coincide with the experimental data presented in [35].

Fig. 18

Fuzzy effective Young’s modulus evaluated from the homogenized stress mean values

5 Fuzzy uncertainty in forward dynamics

This section describes the concept of fuzzy uncertainty in forward dynamics. The Graph Follower algorithm developed in [22] to efficiently compute the envelopes in fuzzy forward dynamics simulation is explained briefly. The uncertain parameters are modeled as triangular numbers. One fuzzy parameter is the fuzzy effective Young’s modulus evaluated from the homogenized stress mean values depicted in Fig. 18. The time integrator used in this paper is the variational integrator which has shown several advantages in fuzzy forward dynamics [22].

5.1 Continuous fuzzy forward dynamics

Following [22], the concept of fuzzy uncertainty in forward dynamics in the continuous setting is briefly introduced in the following.

We consider convex fuzzy quantities $\tilde{\pmb {p}} \in \mathbb {F}(K)$ with membership function $\mu _{\tilde{\pmb {p}}}: K \rightarrow [0,1]$ on a compact set K, see Fig. 19 and e.g. [11]. Only at the modal value $\bar{\pmb {p}}$, the membership function takes the value 1. For the $\alpha$-cut $\alpha _k \in [0,1]$, the $\alpha$cut set $\pmb {P}_{\alpha _k}$ of $\tilde{\pmb {p}}$ is defined as the support of membership function values greater or equal to $\alpha _k$, i.e. $\pmb {P}_{\alpha _k} = \lbrace \pmb {p} \in K: \mu _{\tilde{\pmb {p}}}(\pmb {p}) \ge \alpha _k \rbrace$.

Fig. 19

Membership function $\mu _{\tilde{p}}$ of convex fuzzy parameter $\tilde{p}$

In the time interval $[t_0, t_N] \subset \mathbb {R}$, consider a dynamical system

$$\begin{aligned} \dot{\pmb {y}}(t;\pmb {p}) = \pmb {F}(\pmb {y}(t;\pmb {p}); \pmb {p}) \end{aligned}$$

(17)

with temporally constant and independent parameters $\pmb {p}$ and the state $\pmb {y}(t;\pmb {p}) \in \mathbb {R}^{N_y}$. Along the solution, a scalar valued deterministic mapping $f: [t_0, t_N] \rightarrow \mathbb {R}$ can be written as

$$\begin{aligned} f\left( t; \pmb {p}\right) = \bar{f}(\pmb {y}(t;\pmb {p});\pmb {p}). \end{aligned}$$

(18)

It’s smoothness is controlled by the smoothness of $\bar{f}$ and $\pmb {y}$ (if $\bar{f}$ and $\pmb {y}$ are k times continuously differentiable, so is f). When considering fuzzy parameters $\tilde{\pmb {p}}$, corresponding to the deterministic mapping (18), the fuzzy mapping $\tilde{f}: [t_0, t_N] \times K \rightarrow \mathbb {F}(\mathbb {R})$ maps time and fuzzy parameters onto a fuzzy quantity $\tilde{f}$, whose membership function $\mu _{\tilde{f}}: \mathbb {R} \rightarrow [0,1]$ consequently depends on t and $\tilde{\pmb {p}}$ as well.

By determining the $\alpha$-cut sets $F_{\alpha _k}\left( t;\tilde{\pmb {p}}\right) = \lbrace z \in \mathbb {R}: \mu _{\tilde{f}}(z,t;\tilde{\pmb {p}}) \ge \alpha _k \rbrace$, the fuzzy output $\tilde{f}(t;\tilde{\pmb {p}})$ at the time t can be found. With the help of $\alpha$-cut optimization [11], the upper and lower bound of $F_{\alpha _k}\left( t;\tilde{\pmb {p}}\right)$ can be computed for all $t\in [t_0, t_N]$. They form the upper and lower envelope of the fuzzy output quantity $\tilde{f}$ at a certain $\alpha$-cut, see Fig. 20.

Fig. 20

The deterministic mapping f in combination with fuzzy parameters $\tilde{\pmb {p}}$ yields the fuzzy mapping $\tilde{f}$ with envelopes shown for $\alpha$-cut $\alpha _k$

5.2 Discrete fuzzy forward dynamics

This concept in now transferred to the temporally discrete setting as in [22]. In computational dynamics, a time stepping scheme performs the forward integration and the deterministic mapping (18) is approximated by the discrete deterministic mapping

$$\begin{aligned} \begin{aligned}&f_d: \lbrace t_0, t_1,\ldots ,t_N \rbrace \rightarrow \mathbb {R}, \\&f_d(t_j;\pmb {p}) \approx f(t_j;\pmb {p}), \quad j=0,1,\ldots ,N. \end{aligned} \end{aligned}$$

(19)

with shorthand notation $f_j(\pmb {p})$, and the discrete fuzzy mapping $\tilde{f}_j \in \mathbb {F}(\mathbb {R})$ at every time node $\tilde{f}_j(\tilde{\pmb {p}})$.

As in the continuous setting, $\alpha$-cuts discretize both the fuzzy parameters and the fuzzy output into $\alpha$-cut sets $\pmb {P}_{\alpha _k}$ and $F_{j,\alpha _k}\left( \tilde{\pmb {p}}\right)$. According to Nguyens’s principle [40], the latter can be computed as

$$\begin{aligned} \begin{aligned} F_{j,\alpha _k}(\tilde{\pmb {p}})&= \lbrace z \in \mathbb {R}: z = f_j \left( \pmb {p}\right) ,\, \pmb {p} \in \pmb {P}_{\alpha _k} \rbrace \\&= [f_{j,\alpha _k}^{(-1)}(\varvec{p}^{(-1,\alpha _k)^*}), f_{j,\alpha _k}^{(+1)}(\varvec{p}^{(+1,\alpha _k)^*})] \end{aligned} \end{aligned}$$

(20)

where the interval bounds can be determined by solving the global optimization problems

$$\begin{aligned} f_{j,\alpha _k}^{(s)}(\varvec{p}^{(s,\alpha _k)^*}) = -s \min _{\pmb {p} \in \pmb {P}_{\alpha _k}}(-s f_j(\pmb {p})), \quad s = \mp 1 \end{aligned}$$

(21)

for the optimal parameters $\varvec{p}^{(s,\alpha _k)^*}$. Computing the upper and lower bound in (20) for all time nodes yields the discrete upper and lower envelopes of the discrete fuzzy output at a certain $\alpha$-cut.

The objective function in (21) involves the evaluation of the discrete deterministic mapping $f_j(\pmb {p})$, thus, forward dynamics steps are necessary which may cause high computational effort. In [22], three different formulations of the general $\alpha$-optimization problems (21) are formulated and compared. Based on the third proposed optimization problems, the so-called approximative optimization problems, the best results regarding the numerical behavior and the accuracy were obtained [22]. Hence, the approximative optimization problems are shortly explained in the following.

Optimization Problem (OP)

The approximative optimization problems for $\alpha$-cut optimization around $\pmb {p}^{(0)} \in \pmb {P}_{\alpha _k}$ with the optimization variables $\pmb {p} \in \pmb {P}_{\alpha _k}$ and $k\in \mathbb {N}^{+}$ read

$$\begin{aligned}&f_j^{(\kappa )}(\varvec{p}^{(s,\alpha _k)^*};\pmb {p}^{(0)}) = -s \min _{\pmb {p} \in \pmb {P}_{\alpha _k}} \left( -s f_j^{(\kappa )}(\pmb {p};\pmb {p}^{(0)}) \right) , \nonumber \\&\qquad s=\mp 1. \end{aligned}$$

(22)

The idea is to approximate the discrete deterministic mapping $f_j(\pmb {p})$ locally around a guessed parameter $\pmb {p}^{(0)}$ by a Taylor polynomial $f_j^{(\kappa )}(\pmb {p};\pmb {p}^{(0)})$ of order $\kappa$ and to represent and compute the necessary derivatives very efficiently with the concept of multiple internal numerical differentiation (MIND) introduced in [22]. Hence, only $f_j(\pmb {p}^{(0)})$ and its derivatives have to be determined by forward dynamics integration and MIND, respectively. Forward dynamics integration is not required for any other parameter $\pmb {p} \in \pmb {P}_{\alpha _k}$ to evaluate the objective function in the optimization of the approximate problems in (22). See [22] for an elaborate presentation and technical details.

5.3 Graph follower algorithm

The determination of the discrete fuzzy mapping as the fuzzy output of the dynamical system requires the computation of the $\alpha$-cut sets on each $\alpha$-cut $\alpha _k, k = 1,2,..,N_{\alpha }$ for all time nodes $t_j, j = 0,1,..,N$. The Graph Follower (GF) algorithm can be used to find the upper and lower envelopes on each $\alpha$-cut. Note that despite the local approximation of the discrete deterministic mapping around $\pmb {p}^{(0)}$, the approximative optimization problems (22) require global optimization in $\pmb {P}_{\alpha _k}$. The GF algorithm developed in [22] offers a sophisticated combination of local optimization and forward dynamics steps together with an appropriate post-processing to avoid the need of global optimization. It is demonstrated to beat benchmark methods with regard to accuracy and efficiency.

The concept of the algorithm is based on the fact that discrete envelopes consist piecewise of graph-segments of the discrete deterministic mapping. Furthermore, a storage contains all previously computed graphs. Consider an $\alpha$-cut $\alpha _k$. At $j=0$, arbitrary parameters $\pmb {p}^{(0)}$ are chosen and (22) is solved for the upper and lower bound parameters $\varvec{p}^{(s,\alpha _k)^*}$. Then the complete graphs $f^{(s)}_d(t_j;\varvec{p}^{(s,\alpha _k)^*})$ are computed for $j=0,1,\ldots ,N$ and stored in the storage. They are followed to the next time node ($j=1$), where the optimized parameters are used as initial guess for the next optimization problems, yielding optimal parameters and adding two new graphs of the discrete deterministic mapping to the storage. From now on, the parameters corresponding to the best graph in storage serve as initial guess for the optimization problem at the next time node. So far, only locally optimal upper and lower bounds have been computed. However, a post-processing step compares these with all graphs available in the storage and—based on this set—the best envelopes are determined. This procedure is illustrated in Figs. 21, 22, 23, 24 and 25. The plots are snapshots from a video visualizing the GF algorithm for the fuzzy dynamics of a damped pendulum with fuzzy uncertainty in $N_p=6$ parameters and the force in the pendulum bar being the output. It has been created by the first author of [22] and can be accessed at http://ltd.tf.uni-erlangen.de/Research/Research.htm.

Fig. 21

Discrete fuzzy mapping—initial guess for optimization

Fig. 22

Discrete fuzzy mapping—determination of an optimal graph with new parameters

Fig. 23

Discrete fuzzy mapping—initial guess for the next time step

Fig. 24

Postprocessing step for the optimal result

Fig. 25

Resulting discrete fuzzy mapping

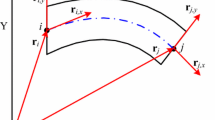
6 Fuzzy dynamics of a multistory frame

In this section, an example is introduced illustrating results of the combination of the GF algorithm with the data of the microstructure achieved in Sect. 4.3. Figure 26 shows the considered multistory frame which is a commonly used model in civil engineering applications and Fig. 27 illustrates a simplified version of the system, which is equivalent in case of rigid floors and purely bending columns. It is modeled as a damped spring mass system similar to [41, 42]. The columns are assumed to be made of the concrete, i.e. the heterogeneous material with polymorphic uncertainty in the microstructure (Sect. 4). The implementation of the GF algorithm for a similar example (same structure but different uncertainty) in [22] is used as a basis to determine the output of the system in form of a fuzzy mapping.

6.1 Model configuration

The masses $m_1$, $m_2$ and $m_3$ build the floors of the building. For simplicity, the parameters for the masses, which are modeled as fuzzy triangular numbers, are based on arbitrary example values. Based on [41], the supporting vertical columns are modeled as linear springs with the spring stiffness $k_z = \frac{24 EI}{l_z^3}$, $z = 1,2,3$, with lengths $l_1 = 2.50\,{\mathrm{m}}$ and $l_2 = l_3 = 2.70\,{\mathrm{m}}$ and bending stiffness EI.

Fig. 26

Model of the multistory frame; based on [11]

Fig. 27

Simplified model of the multistory frame; based on [11]

The system is described by the configuration vector $\varvec{q}(t;\pmb {p}) = [q_1(t;\pmb {p}) ~~ q_2(t;\pmb {p}) ~~ q_3(t;\pmb {p})]^T \in \mathbb {R}^3$. Further, $\varvec{q}(t_0) = \varvec{q}_0$ and $\dot{\varvec{q}}(t_0) = \dot{\varvec{q}}_0$ are the initial conditions of the system caused by a previous earthquake. They are defined as $\varvec{q}_0 = \begin{bmatrix}10,&30,&80 \end{bmatrix}$ mm and $\dot{\varvec{q}}_0 = \begin{bmatrix}0.0,&-0.5,&-0.5 \end{bmatrix} \frac{\mathrm {m}}{\mathrm {s}}$ for the first, second and third floor, respectively. The mass matrix $\varvec{M}(\pmb {p})$ includes the three masses of the horizontal bars of the frame while the vertical bars are not afflicted with any mass. $\varvec{K}(\pmb {p})$ defines the stiffness matrix of the system.

The system is further influenced by viscous dampers with the damping coefficients $d_1=d_2=d_3=50 \frac{\mathrm {Ns}}{\mathrm {m}}$. Altogether, the dynamical system contains 16 parameters (including the initial conditions $\varvec{q}^0$, $\dot{\varvec{q}}^0$).

The equations of motions can be written as

$$\begin{aligned} \begin{aligned}&\dot{\varvec{y}}(t;\pmb {p}) = \varvec{F}(\varvec{y}(t;\pmb {p});\pmb {p}) \\&\quad =\begin{bmatrix} \varvec{v}(t;\pmb {p}) \\ -\varvec{M}^{-1}(\pmb {p}) \cdot [\varvec{K}(\pmb {p}) \cdot \varvec{q}(t;\pmb {p}) + \varvec{D}(\pmb {p}) \cdot \dot{\varvec{q}}(t;\pmb {p})] \end{bmatrix} \end{aligned} \end{aligned}$$

(23)

with the damping matrix $\varvec{D}(\pmb {p})$ and the damping force $-\varvec{D}(\pmb {p}) \cdot \dot{\varvec{q}}(t;\pmb {p})$.

Only $N_p=4$ specific parameters are considered to be uncertain values modeled as fuzzy triangular numbers. The bending stiffness EI consist of the Youngs Modulus E and the area moment of inertia I. The latter one is a deterministic value which is set to $1.0\,{\mathrm{m}}^{4}$. The parameter E is considered to be a fuzzy parameter and modeled as a fuzzy triangular number determined in Sect. 4.3. In reality, the weight of the floors in large buildings is dependent on several factors such as the furniture or human load. Hence, masses of the horizontal bars of the multistory frame can vary and it is hardly possible to determine the masses at every time of every day. Thus, these parameters are also afflicted with epistemic uncertainty. The modal masses of the floors are set based on the values in [11]. The spread of the upper and lower support amounts to 5% with regard to the modal value. Therefore, the triangular fuzzy number of the masses are set as shown in Table 1.

Table 1 Multistory frame—values for fuzzy triangular numbers; based on [11]

6.2 Numerical investigation

The deterministic mapping is defined as the displacement $\varvec{q}_1$, $\varvec{q}_2$ and $\varvec{q}_3$ of the first, second and third mass, respectively, leading to $\bar{f}^{q_i}(\varvec{y}(t;\pmb {p});\pmb {p}) = q_i(t;\pmb {p}), i = 1,2,3$.

At first, only the Young’s modulus E is considered as a fuzzy parameter while the masses hold deterministic values, thus $N_p = 1$. Five $\alpha$-cuts $\alpha = [ 0, ~~ 0.25, ~~ 0.5, ~~ 0.75, ~~1]$ are considered. Figures 28, 29 and 30 show the corresponding discrete envelopes which are determined with the algorithm explained above. The span between upper and lower envelopes is relatively small due to the considerably low deviation between deterministic value and associated support values.

The graph in Fig. 28 shows a comprehensible progress regarding the deviation and the curve has a minimum of $-0.293\,\mathrm{m}$. While the second graph spreads already to almost $-0.382\,\mathrm{m}$, the displacement of the third floor shows a typical irregular motion influenced by all three displacements of the different floors and therefore also the biggest spread.

As mentioned above, masses of the floors of a multistory building vary. Moreover, the behavior of the graph over a longer time is an interesting factor. Figures 31, 32, 33 show a longer period of the simulation for the displacements including the fuzzy parameters $m_1, m_2$ and $m_3$.

Fig. 28

Forward dynamics for the first floor of the multistory frame with fuzzy Young’s modulus

Fig. 29

Forward dynamics for the second floor of the multistory frame with fuzzy Young’s modulus

Fig. 30

Forward dynamics for the third floor of the multistory frame with fuzzy Young’s modulus

Fig. 31

Forward dynamics for the first floor of the frame for a duration of $30\,\mathrm{s}$ with fuzzy Young’s modulus and fuzzy masses

Fig. 32

Forward dynamics for the second floor of the multistory frame for a duration of $30\,\mathrm{s}$ with fuzzy Young’s modulus and fuzzy masses

Fig. 33

Forward dynamics for the third floor of the multistory frame for a duration of $30\,\mathrm{s}$ with fuzzy Young’s modulus and fuzzy masses

The difference of the support values is $200\,{\mathrm{kg}}$ in the first, $100\,{\mathrm{kg}}$ in the second and $50\,{\mathrm{kg}}$ in the third floor. This can be considered a realistic value considering human weights assuming the amount of people in the building only varies between one and three people in the different stories. The graphs indicate an increase of the spread with time while the displacement values vary between $-\,0.32$ and $0.32\,\mathrm{m}$, $-\,0.45$ and $0.45\,\mathrm{m}$ and $-\,0.6$ and $0.6\,\mathrm{m}$ for the first, second and third floor, respectively, roughly reiterating after one cycle of approximately $14\,\mathrm{s}$. Moreover, the spread increases due to the additional fuzzy parameters of the masses.

To evaluate the influences of the fuzzy Young’s modulus versus the fuzzy masses on the fuzzy mapping, firstly the Young’s modulus and secondly the masses are defined as deterministic values for the displacement of the third floor, see Figures 34 and 35, respectively.

Fig. 34

Forward dynamics for the third floor with fuzzy masses $m_1, m_2, m_3$—the Young’s modulus E is defined as a deterministic value

Fig. 35

Forward dynamics for the third floor with fuzzy Young’s modulus E—masses $m_1, m_2, m_3$ are defined as deterministic values

Based on the results, the mass seems to have an irregular influence on the fuzzy mapping of the simulation, which increases clearly over time. However, considering that three masses are included, the influence of the weight still seems to be smaller than when only considering the Young’s modulus as a fuzzy parameter, see Fig. 35, which shows a growing of the spread over time.

7 Discussion on numerical efficiency

The key aspect in the application of the Graph Follower algorithm is the reduction of computational costs in fuzzy dynamic simulations. This approach allows a drastic reduction of computational costs since only a relatively small amount of trajectories needs to be evaluated. However, if the studied system includes thousands of degrees of freedom, the simulation becomes infeasible. In this case an alternative treatment of a discrete system can be useful. First of all, a discrete system can be replaced by a reduced model with a relative small number of degrees of freedom. The system dependency on fuzzy parameters can be further simplified by introducing a set of intervening variables [43]. The idea is to represent the most essential system dependencies in terms of new variables, which have some useful properties. E.g. the studied system must exhibit a nearly linear dependency on the intervening variables. This property of the intervening variables can strongly increase the efficiency of the Graph Follower algorithm.

Another alternative is to replace a dynamic system by a suitable metamodel. We would like to highlight here the approach [44], which includes fuzzy parameters into the metamodel. This approach is based on machine learning. The metamodel is trained to provide the correct upper and lower bounds for the quantity of interest for the given fuzzy input. I.e. it is optimized for needs of fuzzy dynamic. High efficiency of this approach is demonstrated on examples of the failure probability estimation in fuzzy dynamic systems.

In case of the Monte-Carlo method used instead of the $\alpha$-cut optimization, method efficiency can be improved by using the quasi Monte-Carlo method [45]. In particular, the interval quasi Monte-Carlo method, which is suitable for imprecise probabilities and fuzzy problems, is proposed recently [46].

Further reduction of computational costs can be achieved by application of the reduced order modeling to the fuzzy-stochastic homogenization problem [47, 48]. Alternative stochastic reduction methods are presented also in [45].

Thus, the proposed methodology demonstrate a large potential for further modifications. It can be improved by incorporation of order reduction techniques, metamodels, and efficient dynamic models.

8 Summary and conclusions

In this paper, we demonstrate an example of uncertainty propagation from the lowest level, i.e the material’s microstructure, to the very top level of dynamic simulations. We estimate the influence of the considered microscopic uncertainties on the behavior of the entire engineering construction. The sequential application of two novel uncertainty propagation techniques is demonstrated, namely the fuzzy-stochastic FEM based homogenization [18] and the Graph Follower algorithm [22].

On the micro level we consider four sources of uncertainties, namely the variable size of the concrete aggregates, the random aggregate positions (aleatoric uncertainties), and the imprecisely known mechanical properties of aggregates (epistemic uncertainty). The first two uncertainties are modeled using a probabilistic approach. In contrast, the third uncertainty (resulting from the insufficient knowledge) is modeled using fuzzy arithmetic. Moreover, while transferring the uncertainty associated with random aggregate distribution into the representative volume element of the microstructure, some simplifications and numerical evaluations are required, thus, resulting in additional epistemic uncertainties. Therefore the final model of the material’s microstructure contains already five different sources of uncertainties.

Homogenized material properties are obtained by averaging over the volume of the RVE and over the parameters defining the natural variability of the microstructure. In contrast, the epistemic uncertainties cannot be averaged due to their nature. The data spread resulting from the epistemic uncertainties is therefore transferred to the macroscale and results in the fuzzy Young’s modulus of the concrete.

The validation of the presented fuzzy-stochastic FEM based homogenization scheme is performed by comparing the data with experimental investigations. The modal value and the spread of the macroscopic Young’s modulus completely agree with the empirical data presented in the literature.

The fuzzy Young’s modulus is then used for the fuzzy forward dynamics simulation of a multistory frame. The displacement of the upper floor is considered to be a valuable parameter for construction planning having the largest spread of displacement, since the first and second floor influence the displacement of the third floor. The results show an increasing spread between upper and lower envelope with ongoing time. The spread of the upper and lower envelope is larger when considering the Young’s modulus as the only fuzzy parameter compared to the results when considering the three masses as the only fuzzy parameters. This leads to the conclusion that uncertainties in masses have a lower influence on the fuzzy mapping of the simulation than uncertainties in the Young’s modulus.

Based on these results, the correct estimation of the Young’s modulus in the presence of polymorphic uncertainty by the methods described in this paper is even more important for the outcome.

Appendix A: Short introduction to fuzzy set theory

The history of fuzzy numbers began in 1965 with the introduction of fuzzy sets [3] which are an extension of the classical set theory based on the notion of different grades of membership.

Let us briefly repeat some basic definitions from fuzzy set theory [3]. In the case of a fuzzy set $\tilde{\mathcal {P}}$ the grade of membership of p is defined by the membership function $\mu _{\tilde{\mathcal {P}}}(p) \in [0,~1]$. Here $\mu _{\tilde{\mathcal {P}}}(p)=1$ means that the element p entirely belongs to the set $\tilde{\mathcal {P}}$, $\mu _{\tilde{\mathcal {P}}}(p)=0$ means that p is not a member of the set $\tilde{\mathcal {P}}$. In the case of a conventional set $\mathcal {P}$ the membership function of an element p may have only two values $\mu _{\mathcal {P}}(p)\in \{0,~1\}$, i.e. the element can only belong to or not belong to the set $\mathcal {P}$.

For practical applications, a few very important types of fuzzy sets are fuzzy numbers, fuzzy intervals, crisp numbers, and crisp intervals. A fuzzy number $\tilde{a}$ is the convex fuzzy set over the universal set $\mathbb {R}$ with the membership function $\mu _{\tilde{a}}(p) \in [0,~1]$, where $\mu _{\tilde{a}}(p)=1$ only for one single value of $p=\bar{a}$ called the modal value. The fuzzy interval $\tilde{A}$ is the convex fuzzy set defined similarly to the fuzzy number, however with the difference that $\mu _{\tilde{A}}(p)=1$ holds for some interval called modal interval $\bar{A}$. A crisp interval A can be considered as the fuzzy set of points such that $\mu _{A}(p)=1$, if $p\in A$, and $\mu _{A}(p)=0$ otherwise. The crisp number a is then the fuzzy set with the membership function given by the Kronecker delta function $\mu _a(p)=\delta (p,a)$. Figure 36 represents from left to right: crisp number $p=1$, crisp interval [2,  3], symmetric triangular fuzzy number with $\bar{p}=4.5$, fuzzy interval with the modal interval $p\in [6.5,~7.5]$, and the arbitrary non-convex subnormal fuzzy set with nonzero membership function on the interval $p\in [9,~11]$.

Fig. 36

Membership function plotted for (from left to right): crisp number, crisp interval, symmetric triangular fuzzy number, fuzzy interval, and the arbitrary non-convex subnormal fuzzy set

Zadeh’s extension principle is used to perform unary and binary arithmetical operations of fuzzy numbers. Due to the high complexity of calculations performed using the extension principle, an alternative approach was proposed in the literature. The fuzzy numbers are reduced to sets of nested intervals for different degrees of membership, i.e. $\alpha$-cuts (Fig. 37). These intervals are also called intervals of confidence [10]. Lower and upper bounds for every quantity of interest are then evaluated for every $\alpha$-cut. Collection of intervals of confidence for output quantity results naturally in the reconstruction of the output’s membership function.

Fig. 37

Triangular fuzzy number with modal value m decomposed into 6 $\alpha$-cuts

In most cases, two optimization problems must be solved for every $\alpha$-cut. However, if the evaluation of the system is costly, the optimization approach becomes too expensive. As an alternative one may use the extended transformation method [10].