1 Introduction

As a solution to the Schrödinger equation, the Airy wave packet exhibits remarkable and interesting properties [1], including self-accelerating, self-healing and nondiffracting behavior. In free space, compared with the linear propagation of traditional beam, Airy beam’s propagation trajectory is bent and is not affected by external forces or other potential fields, researchers call it self-accelerating beam. Some Airy-related beams also have self-accelerating property, such as Airy Gaussian beam [1]. Novel self-accelerating wave packets have been explored extensively, from one-dimensional pulses [2] and two-dimensional beams [3] to three-dimensional spatiotemporal wave packets [4]. It has been demonstrated that these distinctive wave packets, which have propagation properties that are independent from the ambient environment, are important across the range from fundamental research to practical applications such as particle manipulation [5], imaging [6] and plasmons [7].

The vortex, as a typical optical effect, has attracted considerable attention because of its isolated dark spot structure that carries orbital angular momentum [8]. A topological charge indicates that the phase rotating around the center will change by \(2\pi \). Vortex beams with topological charges are mutually spatially orthogonal, this feature provides vortex beams with an additional spatial dimension to carry information, and their potential applications can thus be expanded considerably [9]. Reference [10] has demonstrated optical communication experimentally using orbital angular momentum multiplexing in fibers. Optical vortices have also been used as tweezers to assemble DNA biomolecules [11]. Research into the propagation of optical vortices that have been superimposed on Airy wave packets has attracted considerable attention [12,13,14].

For a long time, the generation of novel spatiotemporal optical wave packets that are impervious to both dispersion and diffraction has posed an interesting challenge [15]. Recently, tremendous efforts have been made by researchers to generate spatiotemporal wave packets in both linear and nonlinear backgrounds [16,17,18,19]. Nonlocal means that the response of the medium in a point depends on the intensity in the vicinity of this point. Nonlocality has attracted considerable interest for its potential applications to nematic liquid crystals and lead glasses [20, 21]. More recently, as the generic model of Schördinger equation with nonlocal nonlinearity presented, the evolution dynamics of spatiotemporal wave packets in nonlocal nonlinear media have received much attention [22,23,24].

Among the various wave packets available, the complex-variable-function distribution [25] represents a rather intriguing phenomenology in the form of its rotating modes. However, to the best of our knowledge, the propagation of novel spatiotemporal wave packets with helical phases, particularly the propagation of self-accelerating Hermite complex-variable-function Gaussian (SHCG) wave packets carrying multi-order vortices in nonlocal nonlinear media, remains an open subject for research. In this paper, we investigate the various modes of localized SHCG wave packets carrying topological charges, and their dynamic evolution properties in highly nonlocal nonlinear media are discussed. Increasing the distribution factor will cause the intensity layout to cluster more closely around the center, while the vortices will be farther away. The SHCG wave packets can reverse the positions of their temporal side lobes. The simulated results agree well with the theoretical results under the high nonlocality condition. The interesting features of SHCG wave packets will provide new ideas for the regulation of the multi-dimensional optical field.

2 Mode of SHCG wave packets in highly nonlocal nonlinear media

The nonlinear Schrödinger equation is not only important in studies of physical system properties, but also plays a crucial role in describing the optical dynamics of real problems [26, 27]. In a general class of media, when the propagation of a spatiotemporal wave packet \(U(x,y,\tau ,z)\) with a nonlinear nonlocal response is considered, the evolution obeys the nonlocal nonlinear Schrödinger equation [26, 28]

$$\begin{aligned} 2i\frac{\partial U}{\partial z}+\frac{1}{k}\bigg (\frac{\partial ^{2} U}{\partial x^{2}}+\frac{\partial ^{2} U}{\partial y^{2}}\bigg )-k_{g}\frac{\partial ^2 U}{\partial \tau ^2}+2k\frac{\varDelta n}{n_{0}} U=0, \end{aligned}$$
(1)

where x and y are the transverse coordinates, \(\tau \) represents the time coordinate, k is the wave number in the media without nonlinearity, and \(k_{g}=\partial ^2 k/\partial \omega ^2 \vert _{ \omega _{0}}\) is the group velocity dispersion evaluated at the carrier frequency \(\omega _{0}\). \(\varDelta n=n_{1}\int \int _{-\infty }^{\infty } R(r-r')|U(r',z)|^{2}d^{2}r'\) is the nonlinear perturbation of the refraction index, \(n_{1}\) is the nonlinear index coefficient, \(n_{0}\) is the linear refractive index of the media, r and \(r'\) are two-dimensional transverse coordinates, and R represents the physically reasonable nonlocal response function. Here, the Gaussian function \(\alpha ^2/(2\pi )\exp [-\alpha ^2 r^2/(2w_{0}^2)]\) is selected as the normalized symmetrical real spatial response function of the media [25], where \(\alpha =w_{0}/w_{1}\) is the nonlocality degree of the wave packet in the nonlocal nonlinear media, \(w_{0}\) is the spatial scaling parameter, and \(w_{1}\) is the characteristic length of the response.

Underlying the dimensionless coordinates \((X, Y, T, Z)=(x/w_{0}\), \(y/w_{0}\), \(\tau /\tau _{0}\), z/L), \(\tau _{0}\) is the temporal scaling parameter, \(L=kw_{0}^{2}\) is the diffraction length, and \(D=\tau _{0}^{2}/\left| k_{g} \right| \) is the dispersion length. It is assumed that both the dispersion and the diffraction have the same effect along the propagation direction (i.e., L=D), and we consider the anomalous dispersion (i.e., \(k_{g}<0\)). In the case of high nonlocality, Eq. (1) can be applied to the (3+1) dimensional Snyder–Mitchell model [28,29,30,31], which can be simplified into the following normalized dimensionless form

$$\begin{aligned} 2i\frac{\partial U}{\partial Z}+\bigg (\frac{\partial ^2}{\partial X^2}+\frac{\partial ^2}{\partial Y^2}+\frac{\partial ^2}{\partial T^2}\bigg ) U -\beta ^2(X^2+Y^2) U=0, \end{aligned}$$
(2)

where \(\beta =\sqrt{P_{0}/P_{c}}\) is related to the power ratio, \(P_{0}\) is the input power, \(P_{c}=n_{0}/(\gamma n_{1}L^{2})\) is the critical power for soliton propagation, and \(\gamma \) is the material parameter related to R. We note that Eq. (1) is nonlinear, while Eq. (2) is linear. The idea behind this important simplification is from Snyder and Mitchell [28]. By using the method of separation of variables [29], the solution to Eq. (2) can be written as the multiplication of two functions denoted by F(X, Y, Z) and A(T, Z):

$$\begin{aligned} U=F(X,Y,Z)A(T,Z). \end{aligned}$$
(3)

We consider the finite-energy Airy distribution with a chirp factor in the temporal dimension \(A(T,0)=Ai(T)e^{a T+ic T^{2}}\). Here, \(a(0<a\leqslant 1)\) is the decay factor required to enable the physical realization, and c is the chirp factor [32]. Considering the effect of initial frequency chirp on Airy pulse propagation, the chirped Airy distribution propagating in an optical fiber is discussed in Ref. [32]. The following can then be obtained as

$$\begin{aligned} \begin{aligned} A(T,Z)&=\sqrt{\eta }Ai\bigg [\eta \big (T-\frac{\eta }{4}Z^{2}+iaZ\big )\bigg ]\\&\quad \exp \bigg [a \eta (T-\frac{\eta }{2} Z^{2})\bigg ]\\&\quad \times \exp \bigg [i\eta \big (c T^{2}+\frac{\eta }{2}TZ+\frac{a^{2}}{2} Z-\frac{\eta ^{2}}{12}Z^{3}\big )\bigg ], \end{aligned} \end{aligned}$$
(4)

where \(\eta =1/(1+2cZ)\). Other exact solutions to the one-dimensional Schrödinger equation can be used as the temporal distributions to explore spatiotemporal wave packets; the chirped Airy function is just one of these solutions [1]. After substituting Eq. (3) into Eq. (2), we obtain

$$\begin{aligned} 2i\frac{\partial F}{\partial Z}+\frac{\partial ^2 F}{\partial X^2}+\frac{\partial ^2 F}{\partial Y^2} -\beta ^{2}(X^{2}+Y^{2})F=0. \end{aligned}$$
(5)

The initial Hermite complex-variable-function Gaussian part can be expressed as

$$\begin{aligned} F(X,Y,0)=H_{m}(\xi _{0})\exp \bigg (-\frac{X^{2}+Y^{2}}{2}\bigg ), \end{aligned}$$
(6)

where \(H_{m}(\cdot )\) is the mth-order Hermite polynomial, \(\xi _{0}=(X+iY)/b\), and b is the distribution factor. The solution to Eq. (5) can be expressed as

$$\begin{aligned} F(X,Y,Z)= & {} \frac{H_{m}(\xi )}{w(Z)}\nonumber \\&\exp \bigg [-\frac{X^{2}+Y^{2}}{2w^{2}(Z)}\nonumber \\&+i\frac{X^{2}+Y^{2}}{2M(Z)}-i\theta (Z)\bigg ], \end{aligned}$$
(7)

where \(\xi =(X+iY)/[bw(Z)]\exp [i\theta (Z)]\), \(w(Z)=[\cos ^{2}(\beta Z)+\sin ^{2}(\beta Z)/\beta ^2]^{1/2}\), \(M(Z)=\beta [\tan (\beta Z)+\beta ^2\cot (\beta Z)]/(1-\beta ^2)\), and \(\theta (Z)=\arctan [\tan (\beta Z)/\beta ]\). Equation (7) shows that the radius of the wave packet is related to \(\beta \) when the complex-variable-function and the distribution factor b are given. The complex-variable-function Gaussian distribution is a more general solution that contains rotating elliptical Gaussian distribution.

The highly nonlocal nonlinear solution to Eq. (2) can now be constructed as

$$\begin{aligned} \begin{aligned} U=&\frac{H_{m}(\xi )}{w(Z)}\\&\exp \bigg [-\frac{X^{2}+Y^{2}}{2w^{2}(Z)}+i\frac{X^{2}+Y^{2}}{2M(Z)}-i\theta (Z)\bigg ]\\&\quad \times \sqrt{\eta }Ai\bigg [\eta \big (T-\frac{\eta }{4}Z^{2}+iaZ\big )\bigg ]\\&\exp \bigg [a \eta (T-\frac{\eta }{2} Z^{2})\bigg ]\\&\quad \times \exp \bigg [i\eta \big (c T^{2}+\frac{\eta }{2}TZ\\&+\frac{a^{2}}{2} Z-\frac{\eta ^{2}}{12}Z^{3}\big )\bigg ]. \end{aligned} \end{aligned}$$
(8)

The solution is called the SHCG wave packet, which is because the structure is determined by the product of the temporal self-accelerating distribution and the spatial multi-order Hermite complex-variable-function Gaussian distribution.

3 Analysis and discussion

Fig. 1
figure 1

a1–f1 Snapshots describing the initial second-order SHCG wave packets with different b. a2–f2 The normalized transverse intensity, the corresponding cross lines and insets display the related phase distributions

Full size image

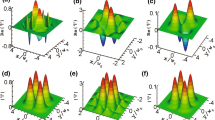
We begin by discussing the wave packet properties in the highly nonlocal nonlinear limit to gain a physical insight into the SHCG wave packets, which are demonstrated in the two spatial transverse coordinates as well as in temporal coordinate. Figure 1 shows various examples of 3D second-order SHCG wave packets with their main lobes in front and the transverse layout varying from a ring in Fig. 1a1 to an elliptical ring in Fig. 1b1, side-by-side vortices in Fig. 1c1, a butterfly shape in Fig. 1d1, a number eight shape in Fig. 1e1 and a solid round shape in Fig. 1f1. Figure 1a2 shows the transverse intensity distribution as a ring with an isolated dark spot with two topological charges. In Fig.  1b2–e2, as the distribution factor increases, the transverse intensity distribution becomes clustered more closely around the center, while the two vortices move farther away from the center. When b is large enough, Eq. (6) is nearly equal to the Gaussian function and the vortices disappeared while the Gaussian plot can be seen clearly in Fig. 1f2. b characterizes the distribution of the SHCG wave packet from the wave packet center and provides a way to capture the scale or degree of being spread out.

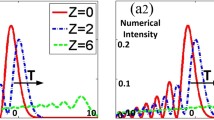
Figure 2 shows that the entire SHCG wave packet rotates smoothly while basically maintaining its profile; the rotation period is \(\pi \). The physical essence of the rotation phenomenon is that the energy flow in the wave packet cross section is not uniformly distributed, which results in the redistribution of the energy flow. Figure 2a–c shows that the wave packets are self-accelerating in the positive T direction while keeping their main lobes at the front. It is important to note that because of the negative chirp factor \((c <0)\), \(\eta \) in Eq. (8) becomes negative, and the wave packets in Fig.  2d–f reverse their positions to have their temporal side lobes at the front while still self-accelerating. In addition, by observing some particular profiles, we can expect that they are distinguished in real physics; e.g., when \(\beta =1\), the input power equaling the critical power, the diffraction is balanced exactly by the nonlinearity, the wave packets propagate stably.

Fig. 2
figure 2

Propagation dynamic of the second-order SHCG wave packets with a and d \(Z=\pi /3\), b and e \(Z=2\pi /3\), c and f \(Z=\pi \). a–c \(b=1\) and \(c=0\), d–f \(b=2\) and \(c=-1\). The insets in a and d display temporal profile plots, the red solid lines with \(Z=\pi /3\), the blue dotted lines with \(Z=2\pi /3\) and the green point lines with \(Z=\pi \). \(\beta =1\)

Full size image

Although the visible rotation comes from a nonzero angular momentum, not all wave packets with nonzero angular momentum will rotate. It can be found that the vortex Ince–Gaussian soliton [33], which is also a solution of the Snyder–Mitchell model, does not rotate during propagation. To discuss the rotation characteristics of SHCG wave packets in the highly nonlocal limit, we consider the magnitude of the transverse angular velocity (i.e., the angle rotated per unit propagation distance) \(V=d \theta (Z)/d Z=1/w^{2}(Z)\). V is inversely proportional to \(w^{2}(Z)\) and thus behaves periodically. It is like the movement of the rigid body in mechanics, if the wave packet is narrowed (or broadened) while keeping the total “mass” contents, its angular velocity increases (or decreases). The rotation period of the wave packets is \(\pi /\beta \), which decreases with increasing \(\beta \). The transverse angular velocity is not related to the form of the wave packet and is only dependent on the power ratio. The SHCG wave packets periodically oscillating when the balance between diffraction and nonlinearity is broken. When the input power is lower than the critical power (i.e., \(\beta <1\)), the angular velocity initially decreases before increasing back to 1, as shown in Fig. 3a. Nevertheless, the reverse occurs when the input power is greater than the critical power (i.e., \(\beta >1\)), with the angular velocity initially increasing and then decreasing back to 1, as shown in Fig. 3b.

Fig. 3
figure 3

Comparison of the magnitude of the angular velocity with different \(\beta \)

Full size image
Fig. 4
figure 4

The third-order SHCG wave packets with \(b=1\). a The normalized transverse intensity and the corresponding cross lines. The analytical wave packets with b \(Z=0\) and c \(Z=2\). The related numerical simulation at \(Z=2\) by using the split step Fourier transform d \(\alpha =0.001\), e \(\alpha =0.2\) and f \(\alpha =0.25\). The insets display the related phase distributions

Full size image

In addition, we perform the numerical calculations of Eq. (1) to verify the results of the theoretical analysis. The propagation dynamics of the third-order SHCG wave packets are shown in Fig. 4. The normalized transverse intensity and the corresponding cross lines of the third-order SHCG wave packets are shown in Fig. 4a, while the insets in Fig.  4b–f show the changes in the phase distribution. The most obvious features are the phase singularity and the intensity singularity, while the shape of this singularity is influenced by the three topological charges. Comparison shows that the numerical simulation results in Fig. 4d agree well with the results of the theoretical analysis in Fig. 4c under the high nonlocality (\(\alpha =0.001\)) condition. It is natural to consider what may occur when the degree of nonlocality changes. The approximations of the analytical results are slightly worse in Fig. 4e and f because the degree of nonlocality has become weaker. The less \(\alpha \) is, the higher the nonlocality is. The degree of nonlocality is the relative width of the response function with respect to the wave packet, and it thus changes dynamically when the wave packet spreads or contracts. It is difficult to prove anything rigorously for an arbitrary degree of nonlocality, but what we have discussed here provides strong support for the existence of observable nonlinear modes in the laboratory experiments.

Fig. 5
figure 5

The fourth-order SHCG wave packets with \(b=0.8\). a The normalized transverse intensity and the corresponding cross lines. The analytical wave packets with b \(Z=0\) and c \(Z=2\). The related numerical simulation to different perturbations at \(Z=2\) with d \(\epsilon =0\), e \(\epsilon =0.1\) and f \(\epsilon =0.3\). The insets display the phase distributions. \(\alpha =0.001\)

Full size image

Furthermore, the stabilities are affected by the various perturbation conditions are analyzed. The normalized transverse intensity and the corresponding cross lines of the fourth-order SHCG wave packets are shown in Fig. 5a, while the insets in Fig.  5b–f display the phase distribution evolution of the fourth order vortices. The initial condition is supposed to be \(U+\epsilon \phi \), where \(\epsilon \) is the perturbation parameter and \(\phi \) is a random complex function with a maximum amplitude that is lower than that of the SHCG wave packets. Comparison of Fig. 5d with the analytical results in Fig. 5c shows that the numerically simulation results agree well with the theoretical analysis results under the zero perturbation (\(\epsilon =0\)) condition. However, the difference between the numerical simulation results and the theoretical analysis results becomes huge when \(\epsilon =0.3\) (Fig. 5f), although the difference is too small to distinguish when \(\epsilon =0.1\) (Fig. 5e). In a numerical simulation, a stable SHCG wave packet propagates, while the initial wave packet is perturbed by noise. This may not constitute a rigorous proof of the stability of the wave packet; however, it paves the way to the experimental observation in the highly nonlocal nonlinear media and is further expected to introduce significant novelties in nonlinear optics.

4 Summary

In conclusion, we have studied the propagation properties of localized SHCG wave packets carrying multi-order vortices in highly nonlocal nonlinear media. Analytical results are obtained by solving the (3+1) dimensional Snyder–Mitchell model, and the stable rotation of the entire wave packets is shown. When the distribution factor is larger, the transverse intensity distribution becomes clustered more closely around the center, while the vortices move farther away from the center. It is important to note that the wave packets reverse the positions of their temporal side lobes to face the front because of negative chirp factors. The SHCG wave packets propagate stably when the input power is equal to the critical power, which means that the diffraction effects are balanced exactly by the material nonlinearity. In addition, the evolution of the SHCG wave packets shows that the angular velocity is generally a function of the power ratio, independent of the distribution factor. The physics behind the rotation phenomenon is the inhomogeneity of the energy flow within the SHCG wave packet cross section. In the numerically simulations, the simulated results agree well with the theoretical results under the high nonlocality condition. Furthermore, the related numerical simulation snapshots of the SHCG wave packets under different perturbation conditions are discussed. Although the numerical simulation may not constitute a rigorous proof of the stability of the wave packet, it does provide strong support for the existence of observable nonlinear modes in the laboratory experiments.

These SHCG wave packets have shown good intensity stability during propagation, which has not only expanded the recently introduced spatiotemporal wave packets significantly, but also has provided new ideas for the propagation and regulation of the multi-dimensional optical field.