1 Introduction

In the wake of the discovery of soliton, abundant localized structures, describing real problems in physical and engineering fields including nonlinear optics, plasma physics and condensed matter physics, have aroused great interest [1–6]. In local nonlinear case, authors investigated many localized structures, such as spatial similaritons [7, 8], spatiotemporal solitons [5], Peregrine solitons [9, 10] and breathers [11]. In nonlocal nonlinear case, authors have also studied various localized structures, including vector Hermite–Gaussian spatial solitons [12], necklace solitons [13] and Hermite–Bessel solitons [14].

In recent years, the study of higher-dimensional localized structures [15–20] in parity-time (\(\mathcal {PT}\))-symmetric nonlinear media has become an interesting topic since Musslimani et al. [21] introduced the concept of \(\mathcal {PT}\)-symmetry from the quantum mechanics to the nonlinear optics. However, spatiotemporal Hermite–Bessel solitons in \(\mathcal {PT}\)-symmetric nonlocal nonlinear media are hardly studied. As we all know, the nonlocality can promote the stability of vector solitons [22] and prevent beam collapse and stabilize multidimensional solitons [23].

The coupled dual waveguides with balanced gain and loss were firstly used to realize the \(\mathcal {PT}\) symmetry in optics [24]. In these nonlocal nonlinear media, the nonlinearity of a material at a particular point depends on the wave intensity at all other material points. Considering the nonlocal case, we can use coupled nonlocal nonlinear Schrödinger equation (NNSE) with the equal gain and loss to describe the propagation of optical solitons. In (3+1)-dimensional inhomogeneous nonlocal nonlinear media with the equal gain and loss, the coupled NNSE with variable coefficients has the form

$$\begin{aligned}&\text {i}\frac{\partial u_1}{\partial t}+\frac{1}{2}\beta (t) \left( \frac{\partial ^2 u_1}{\partial x^2}+\frac{\partial ^2u_1}{\partial y^2}+\frac{\partial ^2u_1}{\partial z^2}\right) \nonumber \\&\quad +\,\triangle n_1(\mathbf r ,t)u_1=\nu (t)(-u_2+\text {i}\gamma u_1),\nonumber \\&\text {i}\frac{\partial u_2}{\partial t}+\frac{1}{2}\beta (t) \left( \frac{\partial ^2 u_2}{\partial x^2}+\frac{\partial ^2u_2}{\partial y^2}+\frac{\partial ^2u_2}{\partial z^2}\right) \nonumber \\&+\,\triangle n_2(\mathbf r ,t)u_2=\nu (t)(-u_1-\text {i}\gamma u_2), \end{aligned}$$
(1)

where \(\mathbf r =(x,y,z)\) with two dimensionless transverse coordinates x, y and the evolution coordinate t related to the propagation distance in optics and the time in Bose–Einstein condensates, and \(u_j(\mathbf r ,t),j=1,2\) represent two normalized complex mode components. Parameter \(\beta (t)\) is the diffraction coefficient, and the nonlocal nonlinear coefficients are expressed as \(\triangle n_1(\mathbf r ,t)=\int _{-\infty }^{+\infty }R(\mathbf r -\mathbf r ')(\chi _1(t)|u_1|^2+\chi (t)|u_2|^2)d\mathbf r \) and \(\triangle n_2(\mathbf r ,t)=\int _{-\infty }^{+\infty }R(\mathbf r -\mathbf r ')(\chi (t)|u_1|^2+\chi _1(t)|u_2|^2)d\mathbf r \) with the response function \(R(\mathbf r -\mathbf r ')=\exp [-\frac{|\mathbf r -\mathbf r '|^2}{\sigma ^2}]/(\pi \sigma ^2)\). If \(\sigma \rightarrow 0\) and \(\sigma \rightarrow \infty \), Eq. (1) possesses local cubic and strongly nonlocal nonlinearities, respectively. The coupling between the modes is embodied in the first term of right side, and the \(\mathcal {PT}\)-balanced gain and loss are expressed as the opposite signs of the \(\gamma \) term in the second term of the first and second equations, respectively.

In this paper, we focus on the (3+1)-dimensional coupled NNSE with variable coefficients (1) in the strongly nonlocal case and derive analytical spatiotemporal Hermite–Bessel soliton solution. The control of expansion of spatiotemporal Hermite–Bessel soliton in different axis directions is studied in the diffraction decreasing system (DDS). Moreover, the periodic compression and expansion of spatiotemporal Hermite–Bessel solitons in different axis directions are also discussed in the periodic distributed amplification system (PDAS).

2 Spatiotemporal Hermite–Bessel soliton solution

When the gain/loss term is small enough (\(\gamma \le 1\)), the energy through linear coupling is transferred from the core with gain to the lossy one, and modes can be excited in the system by input pulses but do not arise spontaneously. Without loss of generality, it is convenient to make a change of variable with \(\gamma =\sin (\theta )\). Considering the following transformation

$$\begin{aligned}&u_1(t,x,y,z)=v(t,x,y,z), u_2(t,x,y,z)\nonumber \\&\quad =\pm v(t,x,y,z)\exp {(\pm \text {i} \theta )},\end{aligned}$$
(2)

Equation (1) is transformed into a single equation

$$\begin{aligned}&\text {i}v_t+\frac{\beta (t)}{2} \nabla ^2 v\nonumber \\&\quad -\,(\chi _1+\chi )\triangle n(\mathbf r ,t)v\pm \nu (t)\cos (\theta )v=0, \end{aligned}$$
(3)

with \(\triangle n(\mathbf r ,t)=\int _{-\infty }^{+\infty }R(\mathbf r -\mathbf r ')|v|^2d\mathbf r \).

If the nonlinearity is strongly nonlocal in the non-\(\mathcal {PT}\)-symmetric case, the governing equation of propagation of pulse can be simplified into the linear Snyder–Mitchell model [25]. In this paper, we consider the strongly nonlocal medium in the \(\mathcal {PT}\)-symmetric case, which means that the degree of nonlocality \(\sigma \) in the nonlinear response function is rather more than wave characteristic width. Using Taylor’s series to expand the response function, the nonlinear refraction index \(\triangle n(\mathbf r ,t)\) in Eq. (3) is expressed as \(\triangle n(\mathbf r ,t)\approx x^2+y^2+z^2\).

If diffraction and nonlocal nonlinearity satisfy the relation

$$\begin{aligned} \chi (t)+\chi _1(t)=\frac{\delta \beta (t)}{W^4(t)}, \end{aligned}$$
(4)

and using the transformation

$$\begin{aligned}&v=\frac{\rho _0}{W^{3/2}(t)}V\left[ T\equiv \frac{\Lambda (t)}{W_0W(t)},X\equiv \frac{x}{W(t)},\right. \nonumber \\&Y\left. \equiv \frac{y}{W(t)},Z\equiv \frac{z}{W(t)}\right] \exp \nonumber \\&\qquad \left\{ \text {i}\left[ \cos (\theta )\Gamma (t)-\frac{s_0W_0}{2W(t)}r^2\right] \right\} , \end{aligned}$$
(5)

with the width \(W(t)=W_0[1-s_0\Lambda (t)]\), the accumulated diffraction \(\Lambda (t)=\int ^t_0\beta (\tau )\text {d}\tau \), \(\Gamma (t)=\int _0^t\nu (\tau )d\tau \) and constants \(\rho _0,W_0,s_0\), Equation (3) turns into

$$\begin{aligned}&\text {i} V_T+\frac{1}{2}(V_{XX}+V_{YY}+V_{ZZ})\nonumber \\&\quad -\delta (X^2+Y^2+Z^2)V=0. \end{aligned}$$
(6)

From transformations (2) and (5) with soliton solution of Eq. (6) obtained similarly to the procedure in [14], Eq. (1) with the strongly nonlocal case possesses solution

$$\begin{aligned}&u_1{=}\frac{\rho _0k}{w_1(t) w_2^{1/2}(t)W^{3/2}(t)}[\cos (m\phi ){+}\text {i}q\sin (m\phi )]J_m\nonumber \\&\quad \times \left[ \frac{\mu _n^m}{A_0W^2(t)} \text {sech}(\frac{\sqrt{2}\delta \Lambda (t)}{W_0W(t)})(x^2+y^2)\right] \nonumber \\&\quad \times H_l\left( \frac{z}{w_2(t)W(t)}\right) \nonumber \\&\quad \times \exp \left\{ -\frac{z^2}{w_2^2(t)W^2(t)}+\text {i}[\cos (\theta )\Gamma (t)\right. \nonumber \\&\quad \left. -\frac{s_0W_0}{2W(t)}r^2{+}a(t)+c_1(t)(X^2{+}Y^2){+}c_2(t)Z^2]\right\} ,\nonumber \\ \end{aligned}$$
(7)
$$\begin{aligned}&u_2(t,x,y,z)=\pm u_1(t,x,y,z)\exp {(\pm \text {i} \theta )}, \end{aligned}$$
(8)

where \(J_m(\cdot )\) and \(H_l(\cdot )\) are Bessel function with the nth zero point value \(\mu _n^m\) [14] and Hermite polynomials of the lth order, respectively. Five functions are expressed as \(a(t)=-\frac{\sqrt{2}\lambda _1}{12\delta }[\tanh (\sqrt{2}\delta T)+2\text {sech}(\sqrt{2}\delta T)] -\frac{2l+1}{4}\arctan [\frac{\sqrt{\lambda _2}\sin (2\delta T)}{\cos ^2(\delta T)-\lambda _2\sin ^2(\delta T)}], c_1(t)=\frac{\sqrt{2}}{2}\delta \tanh (\sqrt{2}\delta T),c_2(t)=\frac{\delta (\lambda _2-1)\sin (2\delta T)}{2[\cos ^2(\delta T)+\lambda _2\sin ^2(\delta T)]}, w_1(t)=w_{10}\text {sech}^2(\sqrt{2}\delta T),\) and \( w_2(t)=\sqrt{w_{20}^2\cos ^2(\delta T)+\sin ^2(\delta T)/(\delta ^2w_{20}^2)}\). The modulation depth of the pulse intensity \(q\in [0,1]\), the constant \(k=\frac{1}{A_0J_{m+1}(\mu _n^m)} \sqrt{\frac{P}{\sqrt{\pi }(1+q^22^{l-1}l!)}} \), X, Y, Z and T are expressed in the transformation (5), the azimuthal angle \(\phi \) in the transverse plane (X, Y) and constants \(A_0,\rho _0,w_{10},w_{20}\lambda _1,\lambda _2,\delta \) and P.

3 Evolutional behaviors of spatiotemporal Hermite–Bessel solitons

At first, we focus on different localized structures of spatiotemporal Hermite–Bessel soliton solution (7) by modulating different values of m and l. In order to discuss this problem, we choose the diffraction function \(\beta (t)\) as [26, 27]

$$\begin{aligned} \beta (t)=\beta _{0}\exp (-\sigma t), \end{aligned}$$
(9)

where \(\beta _{0}\) and \(\sigma \) are two positive parameter related to diffraction. When \(\sigma >0\), this system corresponds to the typical DDS.

Fig. 1
figure 1

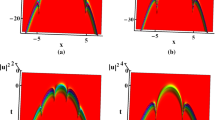
(Color online) Intensity distributions of spatiotemporal Hermite–Bessel soliton for \(q=0,n=1\) at \(t=40\) in the DDS: a–c \(m=0,1,2\) with \(l=0\) and d–f \(m=0,1,2\) with \(l=1\). Parameters are chosen as \(\delta =0.5,s_0=-0.15,\beta _0=0.3,\sigma =0.03,\rho _0=1,A_0=0.5,W_0=0.8,w_{10}=0.2,w_{20}=0.25,P=15\)

Full size image
Fig. 2
figure 2

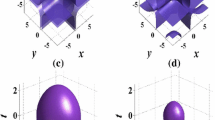
(Color online) Intensity distributions of spatiotemporal Hermite–Bessel soliton for \(q=1,n=1\) at \(t=40\) in the DDS: a, b \(m=1,2\) with \(l=0\) and c, d \(m=1,2\) with \(l=1\). Parameters are chosen as the same as those in Fig. 1

Full size image

When we fix parameters as \(\delta =0.5,s_0=-0.15,\beta _0=0.3,\sigma =0.03,\rho _0=1,A_0=0.5,W_0=0.8,w_{10}=0.2,w_{20}=0.25,P=15\) and \(q=0,n=1\), Fig. 1 exhibits Hermite–Bessel solitons in the DDS with different l and m. If \(m=0\), Hermite–Bessel soliton clusters can be constructed in Fig. 1a, d. Strikingly, the layer of Hermite–Bessel soliton clusters along the vertical (z-axis) direction is determined by \(l+1\), and there is one cylinder-like structure in each layers. If \(m\ne 0\), Hermite–Bessel soliton clusters can be constructed in Fig. 1b, c, e, f. In this case of \(q=0\), multipole Hermite–Bessel soliton clusters can be constructed. These multipole patterns display symmetric structures, namely some big shell structures exist in the center, and some small shell structures encircle these big shell structures. Moreover, the more the distance of the shells to the center, the smaller the shape of the shells. From Fig. 1b, c, e, f, we see that the layer of multipole soliton clusters along the vertical (z-axis) direction is also fixed by \(l+1\). Moreover, in each longitudinal layers, the number of big shell structures in the center is decided by 2m, and the layer number of small shells around big shell structures along the radial direction is determined by \(m+1\).

When \(q=1\), Hermite–Bessel soliton clusters possess closed structures. Similarly to the case of \(q=0\) in Fig. 1, the layer of clusters along the vertical (z-axis) direction is also decided by \(l+1\) in Fig. 2. In each layers, a cylinder is located in the center, and some rings around this central cylinder. The width of ring along the vertical (z-axis) direction would be smaller with the distance to the center. Different from the case of \(q=0\) in Fig. 1, the layer number of rings around the central cylinder along the radial direction is determined by 2m.

Fig. 3
figure 3

(Color online) The evolution of Hermite–Bessel soliton corresponding to Fig. 1d at \(t=10,50,150\) in the DDS. Parameters are chosen as the same as those in Fig. 1

Full size image

In the following, we study evolutional behaviors of spatiotemporal Hermite–Bessel soliton in the DDS by choosing different time for solution (7). Figure 3 exhibits the evolution of Hermite–Bessel soliton corresponding to Fig. 1d at \(t=10,50,150\) in the DDS. The amplitude of soliton is decided by \(\frac{\rho _0k}{w_1(t) w_2^{1/2}(t)W^{3/2}(t)}\), and the widths along vertical (z-axis) and radial (x, y-axes) directions are determined by \(w_2(t)W(t)\) and W(t), respectively. From Fig. 3, the width along vertical (z-axis) direction decreases as time goes on; however, the width along radial (x, y-axes) direction increases with time process. It is clear that the expansion and compression of widths along different directions appear in these structures at the same time. This phenomenon is not reported for spatiotemporal locations in Refs. [15, 17, 28, 29].

At last, we discuss the expansion and compression of Hermite–Bessel soliton in the following PDAS [30]

$$\begin{aligned} \beta (t)=\beta _{0}\cos (t)\exp (-\sigma t), \end{aligned}$$
(10)

where \(\beta _{0}\) is a parameter related to the initial peak power in system. In this system, the alternating regions of positive and negative values of \(\beta \) help the eventual stability of solutions [31, 32]. Specially, Eq. (10) with \(\sigma =0\) is the inhomogeneous system with a periodic modulation in [33].

Fig. 4
figure 4

(Color online) a The variation of amplitude and widths in z-axis direction (100 times) and x, y-axes directions (80 times) in the PDAS, b–d the expansion and compression of Hermite–Bessel soliton corresponding to Fig. 2a at \(t=0,5,180\). Parameters are chosen as the same as those in Fig. 1 except for \(\sigma =0.05\)

Full size image

Compared with the expansion and compression behavior of Hermite–Bessel soliton in different directions in Fig. 3, we can also discuss the periodic expansion and compression behavior of Hermite–Bessel soliton in the PDAS. Figure 4 exhibits a periodical variation of the width of the Hermite–Bessel soliton in Fig. 2a. The changes of amplitude and widths in z-axis direction and x, y-axes directions in the PDAS are exhibited in Fig. 4a. In order to show the change of widths clearly, we enlarge their demonstrations 100 times for the width in z-axis direction and 80 times for the widths in x, y-axes directions in Fig. 4a. From Fig. 4b–d, widths in z-axis direction and x, y-axes directions of Hermite–Bessel soliton periodically change; however, they have opposite trends of alteration in the PDAS. The width in z-axis direction increases from \(t=0\) in Fig. 4b to \(t=5\) in Fig. 4c and then decreases from \(t=5\) in Fig. 4c to \(t=180\) in Fig. 4d. On the contrary, the widths in x, y-axes direction reduce from \(t=0\) in Fig. 4b to \(t=5\) in Fig. 4c and then attenuate from \(t=5\) in Fig. 4c to \(t=180\) in Fig. 4d. Clearly, these expansion and compression behaviors of Hermite–Bessel soliton in different directions appear periodically with the evolution of time.

4 Conclusions

In conclusion, we review the main points offered in this paper:

\(\bullet \) Analytical spatiotemporal Hermite–Bessel soliton solutions are derived.

We study a (3+1)-dimensional coupled NNSE in the inhomogeneous strongly nonlocal nonlinear \(\mathcal {PT}\)-symmetric media and obtain analytical spatiotemporal Hermite–Bessel soliton solutions. Different localized structures of spatiotemporal Hermite–Bessel soliton solution (7) can be constructed by modulating different values of m and l.

\(\bullet \) Different localized structures are studied.

If \(m=0\), the layer of Hermite–Bessel soliton clusters along the vertical (z-axis) direction is determined by \(l+1\), and there is one cylinder-like structure in each layers. If \(m\ne 0\) and \(q=0\), multipole Hermite–Bessel soliton clusters display symmetric structures. The layer of multipole soliton clusters along the vertical (z-axis) direction is also fixed by \(l+1\). Moreover, in each longitudinal layers, the number of big shell structures in the center is decided by 2m, and the layer number of small shells around big shell structures along the radial direction is determined by \(m+1\). When \(q=1\), Hermite–Bessel soliton clusters possess closed structures. The layer of clusters along the vertical (z-axis) direction is also decided by \(l+1\). In each layers, a cylinder is located in the center, some rings around this central cylinder, and the layer number of rings around the central cylinder along the radial direction is determined by 2m.

\(\bullet \) The control of Hermite–Bessel soliton is discussed.

The control of expansion and compression of spatiotemporal Hermite–Bessel soliton in different axis directions is studied in the diffraction decreasing system. Moreover, the periodic compression and expansion of spatiotemporal Hermite–Bessel solitons in different axis directions are also discussed in the periodic distributed amplification system.