Intraspecific competition of predator for prey with variable rates in protected areas

Abstract

In this present study, we systematically explore the periodicity (almost periodic nature) of a dynamical system in time-varying environment, which portrays a special case of prey–predator model governed by non-autonomous differential equations. In particular, we investigate the dynamical characteristics of the underlying prey–predator model by considering modified Leslie–Gower-type model with Crowley–Martin functional response with time-dependent periodic variation of model parameters in a prey reserve area. We show the existence of globally stable periodic solutions. This perpetual prey oscillation results in persistent interference among predator, causing reduced feeding rate at high prey density. A comparative study between the two methods used to prove the existence of periodic (almost periodic) solution of the considered non-autonomous system is also discussed. After showing permanence, existence, uniqueness and global attractivity of the periodic (almost periodic) solution analytically, we demonstrate the typical prey and predator dynamics in time-varying environment using several numerical examples. Partial rank correlation coefficient technique is performed to address how the model output is affected by changes in a specific parameter disregarding the uncertainty over the rest of the parameters.

1 Introduction

Process-based ecological models often include time-dependent nonlinear processes [27, 50], this suggests that the contribution of each parameter to the variation in model outputs may also change with time. For example, in forest growth models, the coupled nonlinear reduction in stomatal conductance and hydraulic conductivity as trees age will inevitably influence physiological processes such as photosynthesis, biomass allocation, etc. [27, 43]. Thereby, some parameters influential at young stand ages may decline in influence in older stands and vice versa [47]. Time-dependent variation analysis of system parameters is a significant part of the successful development in process-based ecological models [57] because these models are often complex and can be richly parameterized [58]. One significant example is the culture of Hilsa fish harvesting at Ganges–Brahmaputa–Meghna (GBM) basin of northern Bay of Bengal. Age or body size is considered to be one of the most significant traits of a species because it correlates many aspects of its biology, from life history to ecology [7, 37, 49]. Different case studies on Hilsa fish at GBM basin reflect a real scenario of ecological and economic status of India and Bangladesh. De and Datta [12] carried out an experiment on Tenualosa ilisha (Hamilton) commonly known as Hilsa, of the freshwater zone of Hooghly estuary to estimate the length-weight relationship of Hilsa fish. It is well known that the rate of growth of fish population varies due to the periodic changes of the ecosystem including changes in food availability, salinity, temperature, density-dependent growth factors, etc. [25, 38, 40]. Fish population biology is impacted by several factors like physiological factors of birth, death etc., seasonal effects of environment, climate change, physio-chemical factors of ocean, fishing effort, harvesting, etc. which are all time-dependent system parameters. The literature shows that the temporal fluctuations in the physical environment are major drivers of population fluctuation yet there has been a little theoretical attention to predict the characteristics of the resultant population fluctuation [1, 8, 10, 16, 29, 51, 56]. When the temporal inhomogeneity of the environment is incorporated, a model must be non-autonomous and the concerned research includes the consideration of periodic and almost periodic coefficients as the relevant environmental factors fluctuate periodically (almost periodically) in time [2, 6, 41, 52].

Protected area is where the prey seeks refuge in order to stay away from the predation risk and this surely has an effect on the prey–predator coexistence [26]. Since the predator cannot access the prey in the reserved area and considering the predator to be a generalist here, i.e., the predator has other food resources and it also feeds on the available prey [11]. This situation leads to intraspecific competition among predator population [44, 45, 55]. Such a scenario is modeled and temporal inhomogeneity is incorporated in this research.

Our objectives of this present study are to formulate model with periodic and almost periodic system parameters and study the dynamical characteristics of this non-autonomous prey–predator system which describes a particular ecological scenario. This work carries a complete dynamical analysis of the proposed model and establishes the existence of a unique, globally attractive periodic (almost periodic) solution of the model system using comparison lemma, coincidence degree theorem and constructing a suitable Lyapunov functional. The system describes the following ecological scenario:

• According to the diet variation, here predator is generalist type [4, 23, 24]. For so, we consider here modified Leslie–Gower-type model [4, 23, 24, 29].

• The interference among predator is regardless of whether a particular individual is currently handling prey or searching for prey [10, 24, 36]. Here we consider Crowley and Martin [10]-type functional response of predator which represents the interference among themselves [24, 53].

• Predator’s foraging efficiency is affected by the prey refuge intensity [14, 22, 23, 26, 31, 33, 35, 51, 54, 56] and we incorporate degree or strength of prey refuge [22, 23, 26] in the Crowley–Martin functional response term [10, 24]. This describes the negative feedback on the predator feeding over the range of prey density by decreasing encounter of prey density.

So, the non-autonomous modified Leslie–Gower prey–predator system with Crowley–Martin functional response and prey reserve is given by:

$$\begin{aligned}&\frac{\mathrm{d}x(t)}{\mathrm{d}t} = x(t)\Big ( a(t)-b(t)x(t) \nonumber \\&\quad -\frac{c(t)(1-m)y(t)}{a_1(t)+a_2(t) (1-m)x(t)+a_3(t)y(t)+a_4(t)(1-m)x(t)y(t)}\Big ), \nonumber \\&\frac{\mathrm{d}y(t)}{\mathrm{d}t} = y(t)\Big (d(t) - \frac{e(t)y(t)}{k(t)+(1-m)x(t)}\Big ). \end{aligned}$$

(1)

Here x(t) is the size of prey population and y(t) is the size of predator population. It is also assumed that the refuge protecting mx of prey, where $m \in [0, 1)$, is constant and hence $(1-m)x$ is only prey available to predator. All the coefficients $a_i(t),a(t),b(t),c(t),d(t),e(t),k(t)$ ($i=1,2,3,4$) are continuous and bounded above and below by positive constants with ecological meaning as follows:

a(t):

Prey population growth rate in the absence of predator,

b(t):

Strength of competition among individual of prey species,

c(t):

Maximum value which per capita reduction rate of prey can attain,

d(t):

Growth rate of predator,

e(t):

Maximum value which per capita reduction rate of predator can attain,

$a_1(t)$:

Measures the half saturation of prey species,

$a_2(t)$:

Measures the handling time on the feeding rate,

$a_3(t)$:

Coefficient of interference among predator,

$a_4(t)$:

Coefficient of interference among predators at high prey density.

The rest of the paper is structured as follows. Some preliminary results used in this study are given in Sect. 2. In Sect. 3, we establish boundedness, permanence and global asymptotic stability of the model system (1). We derive sufficient conditions for the existence and global asymptotic stability of a periodic solution in Sect. 4. In Sect. 5, we also discuss the existence of a unique almost periodic solution. In Sect. 6, numerical examples are provided to validate analytical findings. Ecological interpretation of the obtained analytical findings are given in the last section.

2 Lemmas and definitions

Here we introduce some notations, definitions and lemmas in order to present sufficient conditions for the existence of a positive periodic and almost periodic solutions.

Definition 2.1

The solution set of the model system (1) is ultimately bounded if $\exists \, S>0$ such that for every solution (x(t), y(t)) of (1), $\exists \, T >0$ such that $\Vert (x(t),y(t))\Vert < S$, $\forall \, t \ge t_0+T$, where S is independent of particular solution while T may depend on the solution.

Definition 2.2

(Equicontinuous family of functions) Let E be any compact metric space. Let C(E) denote set of continuous functions defined on E and $f \in A \subseteq C(E)$. A is said to be equicontinuous family of functions if $\forall \, \epsilon>0\, \exists \, \delta >0$ such that

$$\begin{aligned} d(x,y)< \epsilon \Longleftrightarrow \vert f(x)- f(y) \vert < \epsilon \quad \forall \quad f \in A. \end{aligned}$$

Definition 2.3

(Globally attractive solution) A bounded positive solution $X(t) = ({\hat{x}}(t),{\hat{y}}(t))$ of the model system (1) with $X(0) > 0$ is said to be globally attractive (globally asymptotically stable), if any other solution $Y(t) = (x(t),y(t))$ of the system (1) with $Y(0)>0$ satisfies $\displaystyle {\lim _{t \rightarrow +\infty } \vert X(t)-Y(t) \vert = 0}$.

Definition 2.4

The upper right Dini (upper right) derivative for a function $V: {\mathbb {R}} \rightarrow {\mathbb {R}}$ is defined as

$$\begin{aligned} D^+V(t) = \displaystyle {\limsup _{h \rightarrow 0^+}\frac{V(t+h)-V(t)}{h}}. \end{aligned}$$

Lemma 2.5

[5] Let $\zeta$ be a real number and h be a nonnegative function defined on $[\zeta ,+\infty )$ such that h is integrable on $[\zeta ,+\infty )$ and is uniformly continuous on $[\zeta ,+\infty )$. Then ${\displaystyle {\lim _{t\rightarrow +\infty }}}h(t) = 0$.

Lemma 2.6

(Brouwer fixed-point theorem) [3] Let ${\bar{\varUpsilon }}$ be a closed bounded convex subset of ${\mathbb {R}}^n$. Let $\rho$ be a continuous operator that maps ${\bar{\varUpsilon }}$ into itself. Then the operator $\rho$ has at least one fixed point in ${\bar{\varUpsilon }}$, i.e., $\exists$ a point ${\hat{x}} \in {\bar{\varUpsilon }}$ such that $\rho ({\hat{x}}) = {\hat{x}}$.

Definition 2.7

(Almost periodic solution) [18] A function f(t, x), where f is an m-vector, t is a real scalar and x is an n-vector, is said to be almost periodic in t uniformly with respect to $x \in X \subset {\mathbb {R}}^n$, if f(t, x) is continuous in $t \in {\mathbb {R}}$ and $x \in X$, and if for any $\epsilon >0$, it is possible to find a constant $l(\epsilon ) >0$ such that in any interval of length $l(\epsilon )$ there exists a $\tau$ such that the inequality

$$\begin{aligned}&\vert \vert f(t+\tau ,x)-f(t,x) \vert \vert \\&\quad = {\sum } _{i =1}^{m} \vert f_{i}(t+\tau ,x)-f_{i}(t,x) \vert <\epsilon \end{aligned}$$

is satisfied for all $t \in {\mathbb {R}}$, $x \in X$. The number $\tau$ is called an $\epsilon$-translation number of f(t, x).

Definition 2.8

A function $f: {\mathbb {R}} \rightarrow {\mathbb {R}}$ is said to be asymptotically almost periodic function if there exist an almost-periodic function q(t) and a continuous function r(t) such that

$$\begin{aligned} f(t) = q(t)+r(t), \, r \in R \, \hbox {and} \, r(t) \rightarrow 0 \, \hbox {as} \, t \rightarrow \infty . \end{aligned}$$

Definition 2.9

[19, 20] Let Y and Z be two Banach spaces. Let L :  Dom $L \subset Y \rightarrow Z$ be a linear map, and $N: Y \rightarrow Z$ be a continuous mapping. The operator L is called Fredholm operator of index 0 if dim Ker L = codim Im $L < +\infty$ and Im L is closed in Z. If L is a Fredholm mapping of index zero and there exist continuous projections $P : Y \rightarrow Y$ and $Q: Z \rightarrow Z$ such that Im $P=$ Ker L, Ker Q = Im $L =$ Im $(I-Q)$, it follows that $L \vert$ Dom $L \cup \text {Ker} P:\, (I-P)X \rightarrow$ Im L is invertible. We denote the inverse of the map by $K_P$. If $\varUpsilon$ is an open-bounded subset, the mapping L is called L-compact on ${\bar{\varUpsilon }}$ if $QN({\bar{\varUpsilon }})$ is bounded and $K_p(I-Q)N: {\bar{\varUpsilon }} \rightarrow Y$ is compact. Since Im Q is isomorphic to Ker L, then there exists an isomorphism J: Im Q $\rightarrow$ Ker L.

Definition 2.10

[13, 19] Let $\varUpsilon \subset {\mathbb {R}}^n$ be an open and bounded, $f \in C^1(\varUpsilon ,{\mathbb {R}}^n) \cap C({\overline{\varUpsilon }},{\mathbb {R}}^n)$ and $y \in {\mathbb {R}}^n /f(\partial \varUpsilon \cup N_f)$, i.e., y is a regular value of f. Here, $N_f = \{ x \in \varUpsilon : J_f(x) = 0 \}$, the critical set of f and $J_f$ is the Jacobian of f at x. Then the degree deg $\{f, \varUpsilon , y\}$ is defined by

$$\begin{aligned} \hbox {deg}\{f,\varUpsilon , y\} = {\displaystyle {\sum _{x \in f^{-1}y}}} \hbox {sgn} \, J_f(x). \end{aligned}$$

(2)

For more details about Degree Theory, one can refer Deimling [13].

Definition 2.11

(Homotopy invariance) Let $\varOmega \subset {\mathbb {R}}^n$ be an open and bounded set and $V(\varOmega ) = \{ f \in C({\bar{\varOmega }},{\mathbb {R}}^n): 0 \in f(\partial \varOmega ) \}$. Then the mapping $\hbox {deg}(.,\varOmega ):V(\varOmega )\rightarrow {\mathbb {Z}}$ is well defined. Moreover, if $h:[0,1]\times {\bar{\varOmega }} \rightarrow {\mathbb {R}}^n$ is continuous and such that $0 \notin h(t, \partial \varOmega )$ for all $t \in [0,1]$ then $\hbox {deg}(h(t,.),\varOmega )$ does not depend on t. If we “deform with continuity,” a function $f \in V(\varOmega )$ into another function $g \in \varOmega$ then $\hbox {deg}(f,\varOmega ) = \hbox {deg}(g,\varOmega )$, with the essential assumption that no zeros appear in $\partial \varOmega$ throughout the homotopy.

Lemma 2.12

(Continuation theorem) [19] Let L be a Fredholm mapping of index zero and N be a L-compact on ${\bar{\varUpsilon }}$. Furthermore, assume

• (i) for each $\lambda \in (0,1)$, $x \in \partial \varUpsilon \cup Dom L, Lx \ne \lambda Nx$,

• (ii) for each $x \in \partial \varUpsilon \cup Ker L, QNx \ne 0$ and $\hbox {deg} \{ JQN,\varUpsilon \cup Ker L, 0 \} \ne 0$.

Then the operator equation $Lx = Nx$ has at least one solution in ${\bar{\varUpsilon }}\cup Dom L$.

Now we introduce the following function space with its norm, which will be valid throughout the paper. Denote

$$\begin{aligned} X= & {} Z \\= & {} \Big \{ w(t) = (u,v)^T \in C({\mathbb {R}},{\mathbb {R}}^2)\ \vert w(t+\omega ) = w(t) \Big \}, \end{aligned}$$

equipped with norm

$$\begin{aligned} \Vert w \Vert = \max _{t \in [0,\omega ]} \Vert w(t)\Vert = \max _{t \in [0,\omega ]} \Vert u(t)\Vert + \max _{t \in [0,\omega ]} \Vert v(t)\Vert , \end{aligned}$$

for $(u,v) \in X$. Obviously, X and Z both are Banach spaces when they are endowed with the above norm $\Vert .\Vert$.

3 General non-autonomous case: positivity, permanence and global attractivity

Assume that $a(t),b(t),c(t),d(t),e(t),k(t),a_i(t)$ are continuous and bounded for $i = 1,2,3,4$. Let ${\mathbb {R}}^2_+ = \{(x,y) \in {\mathbb {R}}^2 \vert x \ge 0, y \ge 0\}$. Let g(t) be a continuous and bounded function defined on ${\mathbb {R}}$. Let $g_L$ and $g_M$ denote $\displaystyle {\inf _{t \in {\mathbb {R}}}} g(t)$ and $\displaystyle {\sup _{t \in {\mathbb {R}}}} g(t)$, respectively. It is obvious that the coefficients of the model system (1) must satisfy

$$\begin{aligned}&\displaystyle {\min _{i = 1,2,3,4}} \{ a_L, b_L, c_L, d_L, e_L, k_L, a_{i_{L}} \} > 0, \\&\displaystyle {\max _{i = 1,2,3,4}} \{ a_M, b_M, c_M, d_M, e_M, k_M, a_{i_{M}} \} < \infty . \end{aligned}$$

Lemma 3.1

The positive cone is positively invariant with respect to the model system (1).

Proof

The proof is similar to the proof given in [14]. $\square$

Now we state a theorem that will help us to show the boundedness and permanence of the model system (1).

Theorem 3.2

If

$$\begin{aligned} a_La_{1_{L}} > (1 -m)c_M M_{2}^{\epsilon }, \end{aligned}$$

(3)

then the set defined by

$$\begin{aligned} \kappa _\epsilon := \big \{ (x,y) \in {\mathbb {R}}^2 \vert m_1^\epsilon \le x \le M_1^\epsilon , m_2^\epsilon \le y \le M_2^\epsilon \big \},\nonumber \\ \end{aligned}$$

(4)

is positively invariant with respect to the system (1), where

$$\begin{aligned} M_1^\epsilon:= & {} \displaystyle {\frac{a_M}{b_L}}+\epsilon , \\ m_1^\epsilon:= & {} \displaystyle {\frac{a_La_{1_{L}}-c_M(1-m)M_2^\epsilon }{a_{1_{L}}b_M}}-\epsilon , \\ M_2^\epsilon:= & {} \displaystyle {\frac{d_M(M_1^\epsilon +k_M)}{e_L}} + \epsilon , \\ m_2^\epsilon:= & {} \displaystyle {\frac{d_L(m_1^\epsilon +k_L)}{e_M}} - \epsilon , \end{aligned}$$

and $\epsilon \ge 0$ is sufficiently small so that $m_1^\epsilon > 0$.

Proof

For the proof of this theorem, one can refer [1].

$\square$

The following theorem follows immediately from Theorem 3.2.

Theorem 3.3

Suppose that the time-dependent coefficients satisfy

$$\begin{aligned} m > 1 - \frac{a_L a_{1_{L}}}{c_MM_2}, \end{aligned}$$

(5)

Then the model system (1) is permanent.

Remark 3.4

Here $a_La_{1_{L}}>(1-m)c_M$ implies that $a_Ma_{1_{M}}>(1-m)c_L$ as $a_M > a_L$, $a_{1_{M}} > a_{1_{L}}$ and $c_M > c_L$. In addition, we would like to remark here that all the solutions of the model system (1) are ultimately bounded above under the restriction (5). One can also prove that the set $\kappa _\epsilon \ne \phi$, i.e., the model system (1) has at least one bounded positive solution (Definition 2.1).

Remark 3.5

For the same value of coefficient functions as in the Example 6.1 (Sect. 6) and sufficiently small value of $\epsilon$, one can show that the sufficient conditions of Theorem 3.2 are well satisfied. Moreover, one can also compute the set $\kappa _{\epsilon }$. Here for $\epsilon = 0$, (3) is same as (5). Hence if $\kappa _{\epsilon }$ is positively invariant in model system (1), then the system (1) is permanent. Here it is important to mention that permanence ensures the existence of a positively invariant region, while it does not provide any information about $\omega$ and $\varOmega$ and which is ensured by Theorem 3.2.

Theorem 3.6

Let $(\sum )$ denote the set of solutions $\chi (t) = (x(t),y(t))^T$ of system (1) on ${\mathbb {R}}$ satisfying $m_1 \le x(t) \le M_1$ and $m_2 \le y(t) \le M_2$ for $t \in {\mathbb {R}}$. Then $(\sum ) \ne \phi$.

Proof

For the proof of Theorem 3.6, one can refer [30]. The proof follows similarly. $\square$

Theorem 3.7

Let $Y(t) = (x_1(t),y_1(t))$ be a bounded positive solution of the model system (1). If the condition of Theorem 3.3 along with

$$\begin{aligned}&\inf _{t \in R} \Big \{ b(t)-\frac{c(t)(1-m)\Big [a_2(t)(1-m)M_{2}^{\epsilon }+a_4(t)(1-m){M_{2}^{\epsilon }}^{2} \Big ]}{(a_1(t)+a_2(t)(1-m)m_{1}^{\epsilon }+a_3(t)m_{2}^{\epsilon }+a_4(t)(1-m)m_{1}^{\epsilon }m_{2}^{\epsilon })^2} \nonumber \\&\quad -\frac{e(t)(1-m)M_{2}^{\epsilon }}{(k(t)+(1-m)m_{1}^{\epsilon })^2}\Big \}>0,\nonumber \\&\inf _{t \in R} \Big \{-\frac{c(t)(1-m)\left[ a_1(t)+a_2(t)(1-m)M_{1}^{\epsilon } \right] }{(a_1(t)+a_2(t)(1-m)m_{1}^{\epsilon } +a_3(t)m_{2}^{\epsilon }+a_4(t)(1-m)m_{1}^{\epsilon }m_{2}^{\epsilon })^2} \nonumber \\&\quad +\frac{e(t)\Big [k(t)+(1-m)m_{1}^{\epsilon } \Big ]}{(k(t)+(1-m)M_{1}^{\epsilon })^2} \Big \} >0 \end{aligned}$$

(6)

hold, then any two positive solutions $X(t) = (x(t),y(t))$ and $Y(t) = (x_1(t),y_1(t))$ of the model system (1) satisfy $\displaystyle {\lim _{t \rightarrow \infty } \vert X(t)-Y(t) \vert = 0}$, i.e., $(x_1(t),y_1(t))$ is globally attractive.

Proof

Let $X(t) = (x(t),y(t))$ be any bounded positive solution of model system (1). Hence, there exists $T>0$ such that $(x(t),y(t)) \in \kappa _\epsilon$ and $(x_1(t),y_1(t)) \in \kappa _\epsilon$ for all $t \ge t_0+T$,

i.e., Theorem 3.2 gives that for an enough small $\epsilon > 0$, $\exists$ a $T >0$ such that

$$\begin{aligned}&m_1^\epsilon< x(t)< M_1^\epsilon , \quad m_2^\epsilon< y(t)< M_2^\epsilon , \nonumber \\&m_1^\epsilon< x_1(t)< M_1^\epsilon , \quad m_2^\epsilon< y_1(t)< M_2^\epsilon , \end{aligned}$$

(7)

for all $t \ge T$. Define $\zeta (t,x(t),y(t)) = a_1(t)+(1-m)a_2(t)x(t)+a_3(t)y(t)+(1-m)a_4(t)x(t)y(t)$.

Let $G_1(t) = \vert \ln x(t) - \ln x_1(t) \vert$.

The Dini derivative of $G_1(t)$ along the solution of (3) gives

$$\begin{aligned}&D^+G_1(t) \\&\quad = \text {sgn}(x(t)-x_1(t))\Big ( \frac{{\dot{x}}(t)}{x(t)}-\frac{\dot{x_1}(t)}{x_1(t)} \Big )\\&\quad = \text {sgn}(x(t)-x_1(t)) \\&\qquad \Big [-b(t)(x(t)-x_1(t))-c(t)(1-m) \Big (\frac{y(t)}{\zeta (t,x(t),y(t))}\\&\quad \qquad -\frac{y_1(t)}{\zeta (t,x_1(t),y_1(t))}\Big )\Big ]\\&\quad = -b(t) \vert x(t)-x_1(t) \vert \\&\qquad -\text {sgn}(x(t)-x_1(t))c(t)(1-m) \\&\qquad \Big (\frac{y(t) \zeta (t,x_1(t),y_1(t))-y_1(t)\zeta (t,x(t),y(t))}{(\zeta (t,x(t), y(t)))(\zeta (t,x_1(t),y_1(t)))}\Big )\\&\quad \le -b(t) \vert x(t)-x_1(t) \vert \\&\qquad +c(t)(1-m) \\&\Big (\frac{(1-m)y_1(t)(a_2(t)+a_4(t)y(t))}{\zeta (t,x_1(t),y_1(t)).\zeta (t,x(t),y(t))}\vert x(t)-x_1(t) \vert \\&\quad \qquad +\frac{(a_1(t)+(1-m)a_2(t)x_1(t))}{\zeta (t,x_1(t),y_1(t)) .\zeta (t,x(t),y(t))}\vert y(t)-y_1(t) \vert \Big ). \end{aligned}$$

Furthermore, consider $S_2(t) = \vert \ln y(t)-\ln y_1(t) \vert$.

The upper right derivative of $S_2(t)$ is given by

$$\begin{aligned} D^+G_2(t)= & {} \text {sgn}(y(t)-y_1(t))\Big ( \displaystyle {\frac{{\dot{y}}(t)}{y(t)}-\frac{\dot{y_1}(t)}{y_1(t)}} \Big )\\= & {} \text {sgn}(y(t)-y_1(t))e(t) \\&\Big (\displaystyle {\frac{y_1(t)}{(1-m)x_1(t)+k(t)}-\frac{y(t)}{(1-m)x(t)+k(t)}}\Big )\\= & {} \text {sgn}(y(t)-y_1(t))e(t) \\&\Big (\frac{(1-m)y_1(t)(x(t)-x_1(t))}{((1-m)x_1(t)+k(t))((1-m)x(t)+k(t))}\\&+\frac{(k(t)+(1-m)x_1(t))(y_1(t)-y(t))}{((1-m)x_1(t)+k(t))((1-m)x(t)+k(t))}\Big )\\\le & {} \frac{e(t)(1-m)y_1(t)}{((1-m)x_1(t)+k(t))((1-m)x(t)+k(t))} \\&\vert x(t) -x_1(t) \vert \\&-\frac{e(t)(k(t)+(1-m)x_1(t))}{((1-m)x_1(t)+k(t))((1-m)x(t)+k(t))} \\&\vert y(t)-y_1(t) \vert . \end{aligned}$$

Combining the two functions $G_i(t), i = 1,2$, we obtain $G(t) = G_1(t)+G_2(t)$. For $t \ge t_0 +T$, we have

$$\begin{aligned} D^+G(t)\le & {} -\left[ b(t)-\frac{c(t)(1-m)\Big [a_2(t)(1-m)M_{2}^{\epsilon }+a_4(t)(1-m){M_{2}^{\epsilon }}^{2} \Big ]}{(a_1(t)+a_2(t)(1-m)m_{1}^{\epsilon }+a_3(t)m_{2}^{\epsilon }+a_4(t)(1-m)m_{1}^{\epsilon }m_{2}^{\epsilon })^2} -\frac{e(t)(1-m)M_{2}^{\epsilon }}{(k(t)+(1-m)m_{1}^{\epsilon })^2}\right] \\&\quad \vert x(t)-x_1(t) \vert \\&-\left[ -\frac{c(t)(1-m)\left[ a_1(t)+a_2(t)(1-m)M_{1}^{\epsilon } \right] }{(a_1(t)+a_2(t)(1-m)m_{1}^{\epsilon } +a_3(t)m_{2}^{\epsilon }+a_4(t)(1-m)m_{1}^{\epsilon }m_{2}^{\epsilon })^2} +\frac{e(t)\Big [k(t)+(1-m)m_{1}^{\epsilon } \Big ]}{(k(t)+(1-m)M_{1}^{\epsilon })^2}\right] \\&\quad \vert y(t)-y_1(t) \vert . \end{aligned}$$

The above inequality takes the following form:

$$\begin{aligned}&D^+G(t) \le - \rho \big [\vert x(t)-x_1(t)\vert +\vert y(t)-y_1(t)\vert \big ], \nonumber \\&\quad t\ge t_0 +T, \end{aligned}$$

(8)

where

$$\begin{aligned} \rho&= \min \left\{ \inf _{t \in R} \left\{ b(t)- \frac{c(t)(1-m)\Big [a_2(t)(1-m)M_{2}^{\epsilon } +a_4(t)(1-m){M_{2}^{\epsilon }}^{2} \Big ]}{(a_1(t)+a_2(t)(1-m)m_{1}^{\epsilon }+a_3(t) m_{2}^{\epsilon }+a_4(t)(1-m)m_{1}^{\epsilon }m_{2}^{\epsilon })^2} -\frac{e(t)(1-m)M_{2}^{\epsilon }}{(k(t)+(1-m)m_{1}^{\epsilon })^2}\right\} \right. \end{aligned}$$

and

$$\begin{aligned}&\inf _{t \in R} \left\{ -\frac{c(t)(1-m)\left[ a_1(t)+a_2(t)(1-m)M_{1}^{\epsilon } \right] }{(a_1(t)+a_2(t)(1-m)m_{1}^{\epsilon } +a_3(t)m_{2}^{\epsilon }+a_4(t)(1-m)m_{1}^{\epsilon }m_{2}^{\epsilon })^2} +\frac{e(t)\Big [k(t)+(1-m)m_{1}^{\epsilon } \Big ]}{(k(t)+(1-m)M_{1}^{\epsilon })^2} \Big \} \right\} >0. \end{aligned}$$

Integrating the above relation (8) from $t_0 +T$ to t, we obtain

$$\begin{aligned}&G(t)+\rho \int ^t_{t_0 +T} \Big [\vert x(s)-x_1(s)\vert +\vert y(s)-y_1(s)\vert \Big ]\mathrm{d}s \\&\quad< G(t_0 +T) < + \infty \quad t\ge t_0 +T, \end{aligned}$$

which gives

$$\begin{aligned}&\displaystyle {\limsup _{t \rightarrow \infty }} \int ^t_T \Big [\vert x(s)-x_1(s)\vert +\vert y(s)-y_1(s)\vert \Big ]\mathrm{d}s \\&\quad< \displaystyle {\frac{G(t_0 +T)}{\rho }} < + \infty . \end{aligned}$$

One can easily observe that $\vert x(t)-x_1(t) \vert$ and $\vert y(t)-y_1(t) \vert$ are uniformly continuous on $[t_0 +T,+\infty )$. Thus, we have

$$\begin{aligned} \displaystyle {\lim _{t\rightarrow \infty }}\vert x(t)-x_1(t)\vert = 0, \displaystyle {\lim _{t\rightarrow \infty }}\vert y(t)-y_1(t) \vert = 0, \end{aligned}$$

which completes the proof. $\square$

Remark 3.8

One can also show that above property also holds for any two positive solutions with positive initial values, i.e., we can establish the global asymptotic stability of the model system (1). For $a_4(t) = 0$, the model system (1) reduces to non-autonomous modified Leslie–Gower-type predator-prey system with Beddington–DeAngelis functional response while for $a_4(t) = 0$ and $a_3(t) = 0$, the system (1) reduces to non-autonomous modified Leslie–Gower-type predator-prey system with Holling type II functional response. The above analysis remains valid.

4 Periodicity

Apart from general non-autonomous models, in this section, the parameters involved with the concerned model system (1) are considered to be periodic as relevant environmental factors fluctuate periodically in time [41]. We derive some sufficient conditions for existence of a positive periodic solution of the resulting periodic non-autonomous system followed by the global attractivity of a boundary positive solution using Lemmas 2.6 and 2.12.

Here, we assume that $a(t+\omega ) = a(t), b(t+\omega ) = b(t), c(t+\omega ) = c(t), d(t+\omega ) = d(t), e(t+\omega ) = e(t), k(t+\omega ) = k(t), a_1(t+\omega ) =a_1(t), a_2(t+\omega ) =a_2(t), a_3(t+\omega ) =a_3(t), a_4(t+\omega ) =a_4(t)$ i.e., all the parameters in the system (1) are $\omega$-periodic in t. Denote the mean value of a continuous and periodic function $\psi (t)$ with period $\omega$ by ${\hat{\psi }} = \frac{1}{\omega }\int _0^\omega \psi (t)\mathrm{d}t$.

Let $(x(t, t_0, (x_0,y_0)), y(t, t_0, (x_0,y_0)))$ denote the solution of the model system (1) through the point $(t_0,(x_0,y_0))$. Define a map $\varphi : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2$ by

$$\begin{aligned}&\varphi (x_0,y_0) \\&\quad = (x(t_0+\omega , t_0, (x_0,y_0)), y(t_0+\omega , t_0, (x_0,y_0))), \\&\qquad (x_0,y_0) \in {\mathbb {R}}^2. \end{aligned}$$

Hence, Theorem 3.2 assures the invariance of the set $\kappa _\epsilon$ under the operator $\varphi$ defined above, i.e., $\varphi (\kappa _\epsilon ) \subset \kappa _\epsilon$. The shift operator $\varphi$ is continuous as the solution of the system (1) is continuous with respect to initial value. It is not difficult to observe that the set $\kappa _\epsilon$ is a bounded, closed and convex set in ${\mathbb {R}}^2$. Thus by Brouwer fixed point theorem (one can refer Lemma 2.6), $\varphi$ has at least one fixed point in $\kappa _\epsilon$, i.e., $\exists$ $(x_1,y_1) \in \kappa _\epsilon$ such that $(x_1,y_1) = (x(t_0+ \omega , t_0, (x_1,y_1)), y(t_0+ \omega , t_0, (x_1,y_1)))= \varphi (x_1,y_1)$. Hence, the model system (1) posses at least one positive periodic solution say $(x_1,y_1)$ and $(x_1,y_1) \in \kappa _\epsilon$ is assured by the invariance of $\kappa _\epsilon$. This can be summarized in the following theorem:

Theorem 4.1

If the condition (4) of Theorem 3.3 holds, then the model system (1) has at least one positive periodic solution of period $\omega$, say $(x_1,y_1)$, which lies in $\kappa _\epsilon$.

In Theorem 4.1, the existence of a positive periodic solution is proved using the supremum and infimum (bounds) of the parameters. Now in the next theorem, we use an alternative approach, i.e., the continuation theorem is in coincidence degree theory for the existence of a positive periodic solution.

Theorem 4.2

Assume that the following conditions hold:

$$\begin{aligned} {\hat{a}} > \widehat{\Big ( \frac{c}{a_3} \Big )}, \end{aligned}$$

(9)

Then the model system (1) has at least one positive $\omega$ periodic solution.

Proof

Making the change of variables $x(t) = \exp \{ u(t) \}, y(t) = \exp \{ v(t) \}$, the system (1) can be rewritten as follows:

$$\begin{aligned} \frac{\mathrm{d}u(t)}{\mathrm{d}t}= & {} a(t)-b(t) \exp \{u(t)\} \nonumber \\&-\frac{c(t)(1-m) \exp \{v(t)\}}{a_1(t)+a_2(t)(1-m) \exp \{u(t)\}+a_3(t) \exp \{v(t)\}+a_4(t)(1-m) \exp \{u(t)\} \exp \{v(t)\}},\nonumber \\ \frac{\mathrm{d}v(t)}{\mathrm{d}t}= & {} d(t) - \frac{e(t) \exp \{v(t)\}}{k(t)+(1-m)\exp \{u(t)\}}. \end{aligned}$$

(10)

Now we define the operators L, N and projectors P, Q as follows:

$$\begin{aligned}&L: \text {Dom} L \subset X \rightarrow X, L w = L \left[ \begin{array}{cc} u \\ v \end{array} \right] = \left[ \begin{array}{cc} \frac{\mathrm{d}u}{\mathrm{d}t} \\ \frac{\mathrm{d}v}{\mathrm{d}t} \end{array} \right] , P, Q: X \rightarrow X, P w = Q w = \left[ \begin{array}{cc} {\hat{u}} \\ {\hat{v}} \end{array} \right] = \left[ \begin{array}{cc} \frac{1}{\omega } \int _0^\omega u(t)\mathrm{d}t \\ \frac{1}{\omega } \int _0^\omega v(t)\mathrm{d}t \end{array} \right] ,N:X \rightarrow X,\\&Nw = \left[ \begin{array}{cc} N_1(t) \\ N_2(t) \end{array} \right] = \left[ \begin{array}{cc} a(t)-b(t) \exp \{u(t)\}-\frac{c(t)(1-m) \exp \{v(t)\}}{a_1(t)+a_2(t)(1-m) \exp \{u(t)\} +a_3(t) \exp \{v(t)\}+a_4(t)(1-m) \exp \{u(t)\} \exp \{v(t)\}} \\ d(t) - \frac{e(t) \exp \{v(t)\}}{k(t)+(1-m)\exp \{u(t)\}} \end{array} \right] . \end{aligned}$$

Thus, it is not difficult to observe that the domain of L in X is the whole space and

$$\begin{aligned} \text {Ker} L= & {} \{ (u,v) \in X \vert (u(t),v(t) = (p_1,p_2) \in {\mathbb {R}}^2) = {\mathbb {R}}^2 \},\\ \text {Im} L= & {} \Bigg \{ (u,v) \in X \vert \int _0^\omega u(t)\mathrm{d}t = 0, \int _0^\omega v(t)\mathrm{d}t = 0 \Bigg \}, \end{aligned}$$

and dim Ker L = codim Im $L = 2$. Since ImL is closed in X, L is a Fredholm mapping of index zero. One can easily observe that P is continuous projection such that Im $P =$ Ker L, Ker $P =$ Im $L =$ Im $(I-Q)$. Furthermore, the generalized inverse (to L) $K_P:$ Im $L \rightarrow$ Dom $L \cap$ Ker P exists and is given by

$$\begin{aligned} K_P(w)= & {} \int _0^tw(s)\mathrm{d}s-\frac{1}{\omega }\int _0^\omega \int _0^tw(s)\mathrm{d}s\mathrm{d}t = K_P\left[ \begin{array}{cc} u \\ v \end{array} \right] \\= & {} \left[ \begin{array}{cc} \int _0^tu(s)\mathrm{d}s-\frac{1}{\omega }\int _0^\omega \int _0^tu(s)\mathrm{d}s\mathrm{d}t \\ \int _0^tv(s)\mathrm{d}s-\frac{1}{\omega }\int _0^\omega \int _0^tv(s)\mathrm{d}s\mathrm{d}t \end{array} \right] . \end{aligned}$$

$\square$

Clearly, QN and $K_P(I-P)N$ are continuous. By the Arzela-Ascoli theorem, it is not difficult to prove that $(K_P(I-P)N({\bar{\varOmega }})$ for any bounded open set $\varOmega \in X$. Moreover, $PN({\bar{\varOmega }})$ is bounded. So N is L-compact on ${\bar{\varOmega }}$.

Corresponding to the operator equation $Lx = \lambda Nx$ for each $\lambda \in (0,1)$, we have

$$\begin{aligned}&\frac{\mathrm{d}u(t)}{\mathrm{d}t} =\lambda \Bigg (a(t)-b(t) \exp \{u(t)\} \nonumber \\&\quad -\frac{c(t)(1-m) \exp \{v(t)\}}{a_1(t)+a_2(t)(1-m) \exp \{u(t)\}+a_3(t) \exp \{v(t)\}+a_4(t)(1-m) \exp \{u(t)\} \exp \{v(t)\}}\Bigg ),\nonumber \\&\frac{\mathrm{d}v(t)}{\mathrm{d}t} = \lambda \Bigg ( d(t) - \frac{e(t) \exp \{v(t)\}}{k(t)+(1-m)\exp \{u(t)\}}\Bigg ). \end{aligned}$$

(11)

If $(u(t),v(t)) \in X$ is an arbitrary solution of the system (11) for certain $\lambda \in (0,1)$, we obtain

$$\begin{aligned}&{\hat{a}}\omega = \int _0^\omega \Bigg (b(t) \exp \{u(t)\} \nonumber \\&+\frac{(1-m)c(t) \exp \{v(t)\}}{a_1(t)+a_2(t)(1-m) \exp \{u(t)\}+a_3(t) \exp \{v(t)\}+a_4(t)(1-m) \exp \{u(t)\} \exp \{v(t)\}}\Bigg )\mathrm{d}t, \nonumber \\&{\hat{d}}\omega = \int _0^\omega \frac{e(t) \exp \{v(t)\}}{k(t)+(1-m)\exp \{u(t)\}}\mathrm{d}t. \end{aligned}$$

(12)

From (11) and (12), we have

$$\begin{aligned}&\int _0^\omega \Big \vert \frac{\mathrm{d}u}{\mathrm{d}t} \Big \vert \mathrm{d}t \le \lambda \int _0^\omega a(t)\mathrm{d}t+ \lambda \int _0^\omega \Bigg ( b(t) \exp \{u(t)\} \nonumber \\&+\frac{(1-m)c(t) \exp \{v(t)\}}{a_1(t)+a_2(t)(1-m) \exp \{u(t)\}+a_3(t) \exp \{v(t)\} +a_4(t)(1-m) \exp \{u(t)\} \exp \{v(t)\}}\Bigg )\mathrm{d}t< 2{\hat{a}}\omega , \nonumber \\&\int _0^\omega \Big \vert \frac{\mathrm{d}v}{\mathrm{d}t} \Big \vert \mathrm{d}t \le \lambda \int _0^\omega d(t)\mathrm{d}t + \lambda \int _0^\omega \frac{e(t) \exp \{v(t)\}}{k(t)+(1-m)\exp \{u(t)\}}\mathrm{d}t < 2{\hat{d}}\omega . \end{aligned}$$

(13)

As $(u(t),v(t)) \in X$, $\exists \, \mu _i, \nu _i \in [0,\omega ], i = 1,2$, such that

$$\begin{aligned} u(\mu _1)= & {} \min _{t \in [0,\omega ]}u(t), u(\nu _1) = \max _{t \in [0,\omega ]}u(t), v(\mu _2) \nonumber \\= & {} \min _{t \in [0,\omega ]}v(t), v(\nu _2) = \max _{t \in [0,\omega ]}v(t). \end{aligned}$$

(14)

It follows from (12) and (14) that

$$\begin{aligned} {\hat{a}} \omega \ge \int _0^\omega b(t)\exp \{ u(\mu _1)\}\mathrm{d}t = {\hat{b}} \omega \exp \{u(\mu _1 )\} \end{aligned}$$

which in turn gives $u(\mu _1) \le \ln (\frac{{\hat{a}}}{{\hat{b}}})$, and hence we obtain

$$\begin{aligned} u(t) \le u(\mu _1)+\int _0^\omega \Big \vert \frac{\mathrm{d}u}{\mathrm{d}t}\Big \vert \mathrm{d}t \le \ln (\frac{{\hat{a}}}{{\hat{b}}})+2{\hat{a}}\omega := \varTheta _1.\nonumber \\ \end{aligned}$$

(15)

Moreover, from the first equation of (12) and equation (14), one can easily obtain that

$$\begin{aligned} {\hat{a}}\omega\le & {} \int _0^\omega \Bigg ( b(t) \exp \{u(\nu _1)\} \frac{c(t)}{a_3(t)}\Bigg )\mathrm{d}t \\= & {} \widehat{\Big ( \frac{c}{a_3} \Big )}\omega +{\hat{b}}\omega \exp \{u(\nu _1)\}. \end{aligned}$$

Thus we find $u(\nu _1) \ge \ln \Bigg (\Big ( {\hat{a}}- \widehat{\frac{c}{a_3}}\Big )\Bigg )\Big /{\hat{b}}$, and hence

$$\begin{aligned} u(t)\ge & {} u(\nu _1)-\int _0^\omega \Big \vert \frac{\mathrm{d}u}{\mathrm{d}t} \Big \vert \mathrm{d}t \nonumber \\\ge & {} \ln \Bigg \{ \ln \Bigg ( {\hat{a}}- \widehat{\Big ( \frac{c}{a_3}}\Big )\Bigg )\Big /{\hat{b}} \Bigg \} -2{\hat{a}}\omega := \varTheta _2.\nonumber \\ \end{aligned}$$

(16)

Thus (16) together with (15) implies that $\displaystyle {\max _{t \in [0,\omega ]}} \vert u(t) \vert \le \max \{ \vert \varTheta _1 \vert , \vert \varTheta _2 \vert \} :=D_1$. Furthermore, from (14), we have

$$\begin{aligned} \frac{\mathrm{d}v}{\mathrm{d}t}\Big \vert _{t = \mu _2} = \frac{\mathrm{d}v}{\mathrm{d}t}\Big \vert _{t = \nu _2} = 0. \end{aligned}$$

Hence second equation of (11) implies that

$$\begin{aligned}&\frac{\mathrm{d}v}{\mathrm{d}t}\Big \vert _{t = \mu _2} = 0 = \lambda \Bigg ( d(\mu _2) - \frac{e(\mu _2) \exp \{v(\mu _2)\}}{k(\mu _2)+(1-m)\exp \{u(\mu _2)\}}\Bigg ), \\&\quad \Longrightarrow \mathrm{d}(\mu _2) = \frac{e(\mu _2) \exp \{v(\mu _2)\}}{k(\mu _2)+(1-m)\exp \{u(\mu _2)\}}. \end{aligned}$$

Hence, we obtain

$$\begin{aligned}&\exp {v(\mu _2)} \le \Big ( k_M+(1-m)\exp \{\theta _1\} \Big ) \Big [ \frac{d}{e} \Big ]_M\nonumber \\&\quad \Longrightarrow v(\mu _2) \le \ln \Bigg \{ \Big ( k_M+(1-m)\exp \{\theta _1\} \Big ) \Big [ \frac{d}{e} \Big ]_M \Bigg \} := \varTheta _3.\nonumber \\ \end{aligned}$$

(17)

On the other hand, it follows from second equation of (11) that

$$\begin{aligned}&\frac{\mathrm{d}v}{\mathrm{d}t}\Big \vert _{t = \nu _2} = 0 = \lambda \Bigg ( d(\nu _2) - \frac{e(\nu _2) \exp \{v(\mu _2)\}}{k(\nu _2)+(1-m)\exp \{u(\nu _2)\}}\Bigg ) \nonumber \\&\Longrightarrow&\exp \{v(\nu _2)\} = \frac{d(\nu _2)[(1-m)\exp \{u(\nu _2)\}+k(\nu _2)}{e(\nu _2)} \nonumber \\&\Longrightarrow&v(\nu _2) \ge \ln \Bigg \{ \Big ( k_L+(1-m)\exp \{\theta _3\} \Big ) \Big [ \frac{d}{e} \Big ]_L \Bigg \} := \varTheta _4.\nonumber \\ \end{aligned}$$

(18)

Here, Eqs. (15), (16), (17) and (18) imply that $\varTheta _2 \le u(t) \le \varTheta _1$ and $\varTheta _4 \le \varTheta _3$ for $t \in [0,\omega ]$. Equations (17) and (18) together give that ${\max _{t \in [0,\omega ]}v(t)} \le \max \{ \vert \varTheta _3, \varTheta _4 \vert \} := D_2$. Obviously, $D_1$ and $D_2$ are independent of $\lambda$. Define $D = D_1+D_2+D_3$, where $D_3>0$ is taken sufficiently large such that $D_3>\vert l_1 \vert + \vert L_1 \vert +\vert l_2 \vert +\vert L_2 \vert$.

For $\mu \in [0,1]$ and $(u,v) \in {\mathbb {R}}^2$, consider the following algebraic equations

$$\begin{aligned}&{\hat{a}}-{\hat{b}} \exp \{u\}-\frac{1}{\omega }\int _0^\omega \nonumber \\&\quad \frac{\mu c(t) \exp \{v\}}{a_1(t)+a_2(t) \exp \{u\}+a_3(t) \exp \{v\}+a_4(t)\exp \{u\} \exp \{v\}}\mathrm{d}t = 0,\nonumber \\&{\hat{d}} - \frac{1}{\omega }\int _0^\omega \frac{e(t) \exp \{v\}}{k(t)+(1-m) \exp \{u\}}\mathrm{d}t = 0. \end{aligned}$$

(19)

One can easily show that any solution $(u_1,v_1)$ of the above equations satisfies

$$\begin{aligned} l_1 \le u_1 \le L_1, l_2 \le v_1 \le L_2. \end{aligned}$$

(20)

Particularly, we take $\varOmega = \{ (u,v)^T \in X: \Vert z \Vert < D \}$. Thus we conclude that for each $\lambda \in (0,1)$, every solution x of $Lx = \lambda Nx$ is such that $x \notin \partial \varOmega$, i.e., $\varOmega$ satisfies the condition (i) of Lemma 2.12. Furthermore, when $(u,v) \in \partial \varOmega \cup Ker L = \partial \varOmega \cup {\mathbb {R}}^2$, (u, v) is a constant vector in ${\mathbb {R}}^2$ with norm $\Vert (u,v) \Vert = \vert u \vert +\vert v \vert = D$. Then from the definition of D and (20), we have $PNw = PN(u,v)^T \ne 0$, because if $PNw = PN(u,v)^T = 0$, then $(u,v)^T$ is a constant solution of (19) with $\mu = 1$. Hence, we have $\Vert (u,v)\Vert \le D_1+D_2$ which is contradictory to $\Vert (u,v)^T \Vert = D$. Thus, we have

$$\begin{aligned} PNw= & {} PN \left[ \begin{array}{cc} u \\ v \end{array} \right] = \left[ \begin{array}{cc} {\hat{a}}-{\hat{b}} \exp \{u\}-\frac{1}{\omega }\int _0^\omega \frac{\mu c(t) \exp \{v\}}{a_1(t)+a_2(t) \exp \{u\}+a_3(t) \exp \{v\}+a_4(t)\exp \{u\} \exp \{v\}}\mathrm{d}t \\ {\hat{d}} - \frac{1}{\omega }\int _0^\omega \frac{e(t) \exp \{v\}}{k(t)+(1-m) \exp \{u\}}\mathrm{d}t \end{array} \right] \ne \left[ \begin{array}{cc} 0 \\ 0 \end{array} \right] . \end{aligned}$$

Thus, it is clear that the requirement of the condition (ii) of Lemma 2.12 is accomplished.

Now we need to compute the Brouwer degree of the map PN. For this, we define a homotopy and use its invariance property. Consider the homotopy

$$\begin{aligned} H_\mu w = H_\mu \left[ \begin{array}{cc} u \\ v \end{array} \right] = \mu QN \left[ \begin{array}{cc} u \\ v \end{array} \right] +(1-\mu )G\left[ \begin{array}{cc} u \\ v \end{array} \right] , \end{aligned}$$

where $\mu \in [0,1]$ and

$$\begin{aligned} G \left[ \begin{array}{cc} u \\ v \end{array} \right] = \left[ \begin{array}{cc} {\hat{a}}-{\hat{b}}\exp \{u\} \\ {\hat{d}} - \frac{1}{\omega }\int _0^\omega \frac{e(t) \exp \{v\}}{k(t)+(1-m) \exp \{u\}}\mathrm{d}t \end{array} \right] . \end{aligned}$$

(21)

From (20), we know that $H_{\mu } w = \Big (u,v\Big )^T \ne (0,0)^T$ on $\partial \varOmega \cap$ Ker L. Define $J(= I):$ Im $P \rightarrow$ Ker L, as Im $P =$ Ker L. Hence, due to invariance property of homotopy of topological degree (refer the Definition 2.11), we obtain

$$\begin{aligned}&\deg \Big ( JPN(u,v)^T,\varOmega \cap \text {Ker} L, (0,0)^T \Big ) \\&\quad = \deg \Big (PN, \varOmega \cap \text {Ker} L, (0,0)^T \Big ) \\&\quad = \deg \Big (G, \varOmega \cap \text {Ker} L, (0,0)^T \Big ). \end{aligned}$$

It can be easily observed that the algebraic equations $G\big ((u,v)^T\big ) = 0$, i.e.,

$$\begin{aligned}&{\hat{a}}-{\hat{b}}\exp \{ u \} = 0, \\&{\hat{d}} - \frac{1}{\omega }\int _0^\omega \frac{e(t) \exp \{v\}}{k(t)+(1-m) \exp \{u\}}\mathrm{d}t = 0 \end{aligned}$$

have unique solution ${\tilde{w}} = ({\tilde{u}},{\tilde{v}})^T \in \varOmega \cap$ Ker L. Let det M stand for determinant of matrix M while $J_f(w)$ denote the Jacobian matrix of the function f at the point w. Then one can obtain that

$$\begin{aligned}&\deg \Big ( JPN(u,v)^T,\varOmega \cap \text {Ker} L, (0,0)^T \Big )\\&\quad = \text {sgn} \Big ( \text {det} J_G ({\tilde{w}})\Big ) \ne 0. \end{aligned}$$

Thus, we have verified all the requirements of Lemma 2.12 and hence the equation $Lx = Nx$, i.e., Eq. (10) has at least one $\omega$-periodic solution in Dom $L \cap {\overline{\varOmega }}$ say $(u_1(t),v_1(t))$. As $x_1(t) = \exp \{u_1(t)\}$, $y_1(t) = \exp \{ v_1(t) \}$, hence $\big (x_1(t),y_1(t)\big )$ is an $\omega$-periodic solution of system (1). This completes the proof.

Remark 4.3

One can observe that Theorem 4.2 ensures the existence of a periodic solution under certain restriction on the prey reserve m. It determines a threshold value of prey reserve m while this is not the case in Theorem 4.1. Numerical simulation also shows that the prey reserve m, where $m \in (0,1]$, does not affect the existence of a periodic solution. This ensures the betterment of Theorems 4.2 over 4.1. As far as the sufficient condition for the existence of at least one periodic solution is concerned, both Theorems 4.1 and 4.2 give only one sufficient condition. Theorem 4.2 gives only one sufficient condition for the existence of a periodic solution because of $k_M+\exp (\varTheta _1) >0$. We should notice that in case of density-dependent predator death rate we must have addition parametric restriction along with (9).

Remark 4.4

One can observe that the prey co-ordinate, $x_1(t)$ of the $\omega$-periodic solution $(x_1(t),0)$ of the system (1) is the $\omega$-periodic solution of the time-dependent periodic Logistic equation discussed in [17]. The global attractivity of the positive $\omega$-periodic solution of the model system (1) can be discussed in the similar fashion as we have done for the general non-autonomous model system in Sect. 3 while the global attractivity of the boundary $\omega$-periodic solution can be discussed as in [17]. The $\omega$-periodic solution $(x_1(t),0)$ of the non-autonomous model system (1) reduces to boundary equilibrium $(\frac{a}{b},0)$ of the corresponding autonomous model system.

5 Almost periodicity

Almost periodic solutions of ecological models have received significant attention from researchers during last few decades [8]. The concept was introduced by H. Bohr in his magnificent papers published in Acta Mathematica [6]. A function $g: R \rightarrow R$ is called almost periodic if $g(x+\tau ) = g(x)$ is satisfied with an arbitrary degree of accuracy by infinitely many values of $\tau$, those values being spread over the whole range from $-\infty$ to $+\infty$ in such a way as not to leave empty intervals of arbitrary great length. For detailed study of almost periodic functions and its properties, we refer to [59]. The coefficients of a model system are taken to be almost periodic when the various components of environment are periodic with not necessarily commensurate periods (e.g., seasonal effects of weather, food supplies, mating habits and harvesting) [30], i.e., when the periods of the components of environment are rationally independent. Thus, assumption that the parameters in model system are almost periodic makes the model more realistic.

In this section, we ensure the existence of almost periodic solution of the model system (1), which is more general concept than periodicity, under the assumption that $a(t),b(t),c(t),d(t),e(t),a_1(t)$, $a_2(t)$, $a_3(t)$ and $a_4(t)$ are almost periodic in t.

Let

$$\begin{aligned} x(t) = \exp ({\bar{x}}(t)), \quad y(t) = \exp ({\bar{y}}(t)). \end{aligned}$$

Then the model system (1) becomes in the following form

$$\begin{aligned} \frac{\mathrm{d}{\bar{x}}(t)}{\mathrm{d}t}= & {} a(t)-b(t)\exp ({\bar{x}}(t)) \nonumber \\&\quad -\frac{c(t)(1-m)\exp ({\bar{y}}(t))}{a_1(t)+a_2(t)(1-m)\exp ({\bar{x}}(t))+a_3(t)\exp ({\bar{y}}(t))+a_4(t)(1-m)\exp ({\bar{x}}(t))\exp ({\bar{y}}(t))},\nonumber \\ \frac{\mathrm{d}{\bar{y}}(t)}{\mathrm{d}t}= & {} d(t) - \frac{e(t)\exp ({\bar{y}}(t))}{k(t)+(1-m)\exp ({\bar{x}}(t))}. \end{aligned}$$

(22)

From Theorem 3.2, one can easily prove the following result

Theorem 5.1

If $a_La_{1_{L}} > (1 -m)c_M M_{2}^{\epsilon }$, then the set defined by

$$\begin{aligned} \kappa _\epsilon ^*&:= \big \{ (x,y) \in {\mathbb {R}}^2 \vert \ln (m_1^\epsilon ) \le x \le \ln (M_1^\epsilon ), \ln (m_2^\epsilon )\\&\le y \le \ln (M_2^\epsilon )\big \}, \end{aligned}$$

is positively invariant with respect to the model system (22), where $m_1^\epsilon , M_1^\epsilon , m_2^\epsilon , M_2^\epsilon$ are defined in Theorem 3.2.

In order to prove that the main result of this section, we shall first introduce the following lemma. Consider the ordinary differential equation

$$\begin{aligned} x'=f(t,x), \quad f(t,x) \in C(R\times D, R^n), \end{aligned}$$

(23)

where D is an open set in $R^n$ and f(t, x) is almost periodic in t uniformly with respect to $x \in D$.

In order to show the existence of an almost-periodic solution of (23), we consider the product system of (23)

$$\begin{aligned} x'=f(t,x), \quad y'=f(t,y). \end{aligned}$$

(24)

Lemma 5.2

(cf. Theorem 19.1 of [59]) Suppose that there exists a Lyapunov function V(t, x, y) defined on $[0, +\infty )\times D \times D$ that satisfies the following conditions:

• 1. $\alpha (||x-y||)\le V(t,x,y) \le \beta (||x-y||)$, where $\alpha (\gamma )$ and $\beta (\gamma )$ are continuous, increasing and positive definite.

• 2. $|V(t,x_1,y_1)-V(t,x_2,y_2)| \le K(||x_1-x_2||+||y_1-y_2||)$, where $K>0$ is a constant.

• 3. $V'(t,x,y)\le -\mu V(|x-y|)$, where $\mu >0$ is a constant.

Furthermore, suppose that the system (23) has a solution that remains in a compact set $S \subset D$ for all $t \ge t_0 \ge 0$. Then system (23) has a unique almost-periodic solution in S, which is uniformly asymptotically stable in D.

Theorem 5.3

If $a_La_{1_{L}} > (1 -m)c_M M_{2}^{\epsilon }$ and

$$\begin{aligned}&\inf _{t \in R} \left[ b(t)-\frac{c(t)(1-m)\left[ a_2(t)(1-m)M_{2}^{\epsilon }+a_4(t)(1-m){M_{2}^{\epsilon }}^{2} \right] }{(a_1(t)+a_2(t)(1-m)m_{1}^{\epsilon }+a_3(t)m_{2}^{\epsilon }+a_4(t)(1-m)m_{1}^{\epsilon }m_{2}^{\epsilon })^2}\right. \\&\quad \left. -\frac{e(t)(1-m)M_{2}^{\epsilon }}{(k(t)+(1-m)m_{1}^{\epsilon })^2} \right]>0,\\&\inf _{t \in R} \left[ - \frac{c(t)(1-m)\left[ a_1(t)+a_2(t)(1-m)M_{1}^{\epsilon } \right] }{(a_1(t)+a_2(t) (1-m)m_{1}^{\epsilon }+a_3(t)m_{2}^{\epsilon }+a_4(t)(1-m)m_{1}^{\epsilon }m_{2}^{\epsilon })^2}\right. \\&\quad \left. +\frac{e(t)\left[ k(t)+(1-m)m_{1}^{\epsilon } \right] }{(k(t)+(1-m)M_{1}^{\epsilon })^2}\right] >0, \end{aligned}$$

where $m_1^\epsilon , M_1^\epsilon , m_2^\epsilon , M_2^\epsilon$ are defined in Theorem 3.2, then the model system (1) has a unique positive almost-periodic solution, which is globally asymptotically stable and uniformly globally stable in $\kappa _\epsilon$.

Proof

For $(x, y) \in {\mathbb {R}}^{2}_{+}$, we define $||(x, y)^{T} ||=x+y$. In order to prove that the model system (1) has a unique positive almost-periodic solution, which is uniformly asymptotically stable in $\kappa _\epsilon$, it is equivalent to show that model system (22) has a unique almost-periodic solution to be uniformly asymptotically stable in $\kappa _\epsilon ^*$.

Consider the product system of (22)

$$\begin{aligned} \nonumber \frac{\mathrm{d}{\bar{x}}_{1}(t)}{\mathrm{d}t}= & {} a(t)-b(t)\exp ({\bar{x}}_{1}(t)) \\&-\frac{c(t)(1-m)\exp ({\bar{y}}_{1}(t))}{a_1(t)+a_2(t)(1-m)\exp ({\bar{x}}_{1}(t))+a_3(t) \exp ({\bar{y}}_{1}(t))+a_4(t)(1-m)\exp ({\bar{x}}_{1}(t))\exp ({\bar{y}}_{1}(t))}, \nonumber \\ \frac{\mathrm{d}{\bar{y}}_{1}(t)}{\mathrm{d}t}= & {} d(t) - \frac{e(t)\exp ({\bar{y}}_{1}(t))}{k(t)+(1-m)\exp ({\bar{x}}_{1}(t))}, \nonumber \\ \frac{\mathrm{d}{\bar{x}}_{2}(t)}{\mathrm{d}t}= & {} a(t)-b(t)\exp ({\bar{x}}_{2}(t)) \nonumber \\&-\frac{c(t)(1-m)\exp ({\bar{y}}_{2}(t))}{a_1(t)+a_2(t)(1-m)\exp ({\bar{x}}_{2}(t))+a_3(t) \exp ({\bar{y}}_{2}(t))+a_4(t)(1-m)\exp ({\bar{x}}_{2}(t))\exp ({\bar{y}}_{2}(t))}, \nonumber \\ \frac{\mathrm{d}{\bar{y}}_{2}(t)}{\mathrm{d}t}= & {} d(t) - \frac{e(t)\exp ({\bar{y}}_{2}(t))}{k(t)+(1-m)\exp ({\bar{x}}_{2}(t))}. \end{aligned}$$

(25)

Now we define a Lyapunov function on $\left[ 0, +\infty \right) \times \kappa _\epsilon ^* \times \kappa _\epsilon ^*$ as follows-

$$\begin{aligned} V(t, {\bar{x}}_{1}, {\bar{y}}_{1}, {\bar{x}}_{2}, {\bar{y}}_{2})= & {} |{\bar{x}}_{1}(t)-{\bar{x}}_{2}(t)| \\&+|{\bar{y}}_{1}(t)-{\bar{y}}_{2}(t)|. \end{aligned}$$

Then condition 1 of Lemma 5.2 is satisfied for $\alpha (\gamma ) = \beta (\gamma )=\gamma$ for $\gamma \ge 0$. Additionally

$$\begin{aligned}&|V(t, {\bar{x}}_{1}, {\bar{y}}_{1}, {\bar{x}}_{2}, {\bar{y}}_{2}) - V(t, {\bar{x}}_{1}, {\bar{y}}_{1}, {\bar{x}}_{2}, {\bar{y}}_{2})|\nonumber \\&\quad = (|{\bar{x}}_{1}(t)-{\bar{x}}_{2}(t)|+|{\bar{y}}_{1}(t)-{\bar{y}}_{2}(t)|)\nonumber \\&\qquad -(|{\bar{x}}_{3}(t)-{\bar{x}}_{4}(t)|+|{\bar{y}}_{3}(t)-{\bar{y}}_{4}(t)|)\nonumber \\&\quad \le |{\bar{x}}_{1}(t)-{\bar{x}}_{3}(t)|+|{\bar{y}}_{1}(t)-{\bar{y}}_{3}(t)|\nonumber \\&\qquad +|{\bar{x}}_{2}(t)-{\bar{x}}_{4}(t)|+|{\bar{y}}_{2}(t)-{\bar{y}}_{4}(t)| \nonumber \\&\quad \le ||({\bar{x}}_{1}(t), {\bar{y}}_{1}(t))-({\bar{x}}_{3}(t), {\bar{y}}_{3}(t))|| \nonumber \\&\qquad +||({\bar{x}}_{2}(t), {\bar{y}}_{2}(t))-({\bar{x}}_{4}(t), {\bar{y}}_{4}(t))||, \end{aligned}$$

(26)

which shows that condition 2 of Lemma 5.2 is also satisfied.

Let $({\bar{x}}_{i}(t), {\bar{y}}_{i}(t))^{T}, i=1,2$, be any two solutions of (22) defined on $\left[ 0, +\infty \right) \times \kappa _\epsilon ^* \times \kappa _\epsilon ^*$. Calculating the right derivative of V(t) along the solutions of (22), we obtain

$$\begin{aligned} \begin{aligned} D^{+}V(t) =&A \times \text {sgn}({\bar{x}}_{1}(t)-{\bar{x}}_{2}(t)) \\&+B \times \text {sgn}({\bar{y}}_{1}(t)-{\bar{y}}_{2}(t)), \end{aligned} \end{aligned}$$

(27)

where

$$\begin{aligned}&A=-b(t)(\exp ({\bar{x}}_{1}(t))-\exp ({\bar{x}}_{2}(t))) \\&\qquad -\left( \frac{c(t)(1-m)\exp ({\bar{y}}_{1}(t))}{a_1(t)+a_2(t)(1-m)\exp ({\bar{x}}_{1}(t))+a_3(t)\exp ({\bar{y}}_{1}(t))+a_4(t)(1-m)\exp ({\bar{x}}_{1}(t))\exp ({\bar{y}}_{1}(t))} \right. \\&\qquad \left. - \frac{c(t)(1-m)\exp ({\bar{y}}_{2}(t))}{a_1(t)+a_2(t)(1-m)\exp ({\bar{x}}_{2}(t))+a_3(t)\exp ({\bar{y}}_{2}(t))+a_4(t)(1-m)\exp ({\bar{x}}_{2}(t))\exp ({\bar{y}}_{2}(t))} \right) ,\\&B=-\left( \frac{e(t)\exp ({\bar{y}}_{1}(t))}{k(t)+(1-m)\exp ({\bar{x}}_{1}(t))}-\frac{e(t)\exp ({\bar{y}}_{2}(t))}{k(t)+(1-m)\exp ({\bar{x}}_{2}(t))} \right) . \end{aligned}$$

After some algebraic calculation, we obtain

$$\begin{aligned}&A\times \text {sgn}({\bar{x}}_{1}(t)-{\bar{x}}_{2}(t)) \\&\quad \le \left[ -b(t)+\frac{c(t)(1-m)\left[ a_2(t)(1-m) M_{2}^{\epsilon }+a_4(t)(1-m){M_{2}^{\epsilon }}^{2} \right] }{(a_1(t)+a_2(t)(1-m)m_{1}^{\epsilon }+a_3(t) m_{2}^{\epsilon }+a_4(t)(1-m)m_{1}^{\epsilon } m_{2}^{\epsilon })^2} \right] |\exp ({\bar{x}}_{1}(t)) -\exp ({\bar{x}}_{2}(t))|\\&\qquad +\frac{c(t)(1-m)\left[ a_1(t)+a_2(t)(1-m)M_{1}^{\epsilon } \right] }{(a_1(t)+a_2(t)(1-m) m_{1}^{\epsilon }+a_3(t) m_{2}^{\epsilon }+a_4(t)(1-m)m_{1}^{\epsilon }m_{2}^{\epsilon })^2}\\&\qquad |\exp ({\bar{y}}_{1}(t))-\exp ({\bar{y}}_{2}(t))| \end{aligned}$$

and

$$\begin{aligned}&B\times \text {sgn}({\bar{y}}_{1}(t)-{\bar{y}}_{2}(t)) \\&\quad \le -\frac{e(t)\left[ k(t)+(1-m)m_{1}^{\epsilon } \right] }{(k(t)+(1-m)M_{1}^{\epsilon })^2} |\exp ({\bar{y}}_{1}(t))-\exp ({\bar{y}}_{2}(t))|\\&\qquad + \frac{e(t)(1-m)M_{2}^{\epsilon }}{(k(t)+(1-m)m_{1}^{\epsilon })^2} |\exp ({\bar{x}}_{1}(t))-\exp ({\bar{x}}_{2}(t))|. \end{aligned}$$

Note that

$$\begin{aligned} \begin{aligned} \exp ({\bar{x}}_{1}(t))-\exp ({\bar{x}}_{2}(t))&=\exp (\rho _1(t))({\bar{x}}_1(t)-{\bar{x}}_2(t)),\\ \exp ({\bar{y}}_{1}(t))-\exp ({\bar{y}}_{2}(t))&=\exp (\rho _1(t))({\bar{y}}_1(t)-{\bar{y}}_2(t)), \end{aligned}\nonumber \\ \end{aligned}$$

(28)

where $\rho _1(t)$ lies between ${\bar{x}}_{1}(t)$ and ${\bar{x}}_{2}(t)$ and $\rho _2(t)$ lies between ${\bar{y}}_{1}(t)$ and ${\bar{y}}_{2}(t)$. Hence, we obtain

$$\begin{aligned}&D^{+}V(t) \le -\left[ b(t)-\frac{c(t)(1-m)\left[ a_2(t)(1-m) M_{2}^{\epsilon }+a_4(t)(1-m){M_{2}^{\epsilon }}^{2} \right] }{(a_1(t)+a_2(t)(1-m)m_{1}^{\epsilon }+a_3(t) m_{2}^{\epsilon }+a_4(t)(1-m)m_{1}^{\epsilon }m_{2}^{\epsilon })^2}\right. \\&\left. -\frac{e(t)(1-m)M_{2}^{\epsilon }}{(k(t)+(1-m)m_{1}^{\epsilon })^2} \right] m_{1}^{\epsilon } |{\bar{x}}_1(t)-{\bar{x}}_2(t)|\\&-\left[ -\frac{c(t)(1-m)\left[ a_1(t)+a_2(t)(1-m)M_{1}^{\epsilon } \right] }{(a_1(t)+a_2(t)(1-m)m_{1}^{\epsilon } +a_3(t)m_{2}^{\epsilon }+a_4(t)(1-m)m_{1}^{\epsilon }m_{2}^{\epsilon })^2}\right. \\&\left. +\frac{e(t)\left[ k(t)+(1-m)m_{1}^{\epsilon } \right] }{(k(t)+(1-m)M_{1}^{\epsilon })^2}\right] m_{2}^{\epsilon } |{\bar{y}}_1(t)-{\bar{y}}_2(t)|\\&\le -\mu (|{\bar{x}}_1(t)-{\bar{x}}_2(t)| +|{\bar{y}}_1(t)-{\bar{y}}_2(t)|)\\&= -\mu ||({\bar{x}}_{1}(t), {\bar{y}}_{1}(t))-({\bar{x}}_{2}(t), {\bar{y}}_{2}(t))||, \end{aligned}$$

where

$$\begin{aligned}&\mu = \min \left\{ \inf _{t \in {\mathbb {R}}}\left\{ \left[ b(t)-\frac{c(t)(1-m)\left[ a_2(t)(1-m)M_{2}^{\epsilon } +a_4(t)(1-m){M_{2}^{\epsilon }}^{2} \right] }{(a_1(t)+a_2(t)(1-m)m_{1}^{\epsilon }+a_3(t)m_{2}^{\epsilon } +a_4(t)(1-m)m_{1}^{\epsilon }m_{2}^{\epsilon })^2}\right. \right. \right. \\&\left. \left. \left. -\frac{e(t)(1-m)M_{2}^{\epsilon }}{(k(t)+(1-m)m_{1}^{\epsilon })^2} \right] m_{1}^{\epsilon }\right\} \right. \end{aligned}$$

and

$$\begin{aligned}&\left. \inf _{t \in {\mathbb {R}}}\left\{ \left[ -\frac{c(t)(1-m)\left[ a_1(t)+a_2(t)(1-m)M_{1}^{\epsilon } \right] }{(a_1(t)+a_2(t)(1-m)m_{1}^{\epsilon }+a_3(t) m_{2}^{\epsilon }+a_4(t)(1-m)m_{1}^{\epsilon } m_{2}^{\epsilon })^2}\right. \right. \right. \\&\quad \left. \left. \left. +\frac{e(t)\left[ k(t)+(1-m)m_{1}^{\epsilon } \right] }{(k(t)+(1-m)M_{1}^{\epsilon })^2} \right] m_{2}^{\epsilon }\right\} \right\} >0. \end{aligned}$$

Hence condition 3 of Lemma 5.2 is also satisfied. Therefore, by Theorem 5.1 and Lemma 5.2, it can be concluded that the model system (22) has a unique almost-periodic solution $({\bar{x}}^*(t), {\bar{y}}^*(t))$ (say) in $\kappa _\epsilon ^*$, which is uniformly asymptotically stable in $\kappa _\epsilon ^*$. Hence the model system (1) has a unique positive almost-periodic solution $({\bar{x}}^*(t), {\bar{y}}^*(t))$ in $\kappa _\epsilon ^*$, which is uniformly asymptotically stable in $\kappa _\epsilon ^*$. From Theorem 3.7, we have that $({\bar{x}}^*(t), {\bar{y}}^*(t))$ is globally asymptotically stable, which completes the proof. $\square$

6 Examples and numerical simulation

In order to show analytical results obtained in the previous sections graphically, we numerically simulate the solutions of our model system (1). For this, we consider the following examples:

Example 6.1

Consider $a(t) = 3$, $b(t) = 2+\cos t$, $c(t) = 1.4$, $d(t) = 1+0.03 \cos t$, $e(t) = 3$, $m = 0.7$, $a_1(t) = k(t) = 0.2+0.1 \sin t$, $a_2(t) = 3+0.2 \sin t$, $a_3(t) = 2+ \cos t$, $a_4(t) = 0.01+0.01 \sin t$ and $\omega = 2\pi$ then the model system (1) takes the following form

$$\begin{aligned}&\frac{\mathrm{d}x(t)}{\mathrm{d}t} = x(t)\Bigg ( 3-(2+ \cos t) x(t) \nonumber \\&-\frac{1.4(1-0.7)y(t)}{0.2+0.1 \sin t +0.3(3+0.2 \sin t)x(t)+(2+ \cos t)y(t) +0.3(0.01+0.01 \sin t)x(t)y(t)}\Bigg ), \nonumber \\&\frac{\mathrm{d}y(t)}{\mathrm{d}t} = y(t)\Bigg (1+0.03 \cos t - \frac{3y(t)}{0.2+0.1 \sin t +0.3 x(t)}\Bigg ). \end{aligned}$$

(29)

By easy calculations, one can obtain that ${\hat{a}} = 3, {\hat{b}} = 2, {\hat{c}} = 1.4, {\hat{d}} = 1, {\hat{e}} = 2, {\hat{a}}_3 = 2$ and furthermore

$$\begin{aligned} {\hat{a}} = 3 > \widehat{\Big ( \frac{c}{a_3} \Big )} = \Big (\frac{{\hat{c}}}{{\hat{a}}_3} \Big ) = \frac{ 1.4}{2} = 0.7. \end{aligned}$$

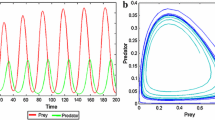
Thus, the parametric values in Example 6.1 satisfy condition (9). Hence, the model system (29) has at least one globally attractive positive $2\pi$-periodic solution. Its phase-plane diagram is shown in Fig. 1i. We plot here three trajectories (denoted by blue, red and green curves) which start from three different initial points (denoted by black bullets) and they gradually converge to the $2\pi$-periodic limit cycle (denoted by thick black closed loop). Figure 1ii, iii is the time series representation of prey (x) and predator (y), respectively, of the system (29).

Fig. 1

Phase-plane diagram (i) and time series solutions (ii, iii) of system (29). Parameters are written in the text

Example 6.2

Consider $m = 0.7$, $a(t) = 3.2$, $b(t) = 2+ \cos t$, $c(t) = 1.5$, $d(t) = 2+\frac{1}{30} \cos t$, $e(t) = 0.5$, $k(t) = \frac{1}{5}+ \frac{1}{10} \sin t$, $a_1(t) = \frac{1}{5} + \frac{1}{10} \sin t$, $a_2(t) = 3+\frac{1}{5} \sin t$, $a_3(t) = 2 + \cos t$, $a_4(t) = \frac{1}{20}+\frac{1}{30} \sin t$, then the model system (1) takes the following form:

$$\begin{aligned}&\frac{\mathrm{d}x(t)}{\mathrm{d}t} = x(t)\Bigg ( 3.2-(2+\cos t) x(t) \nonumber \\&\quad -\frac{1.5y(t)}{\frac{1}{5}+\frac{1}{10}\sin t+(3+\frac{1}{5}\sin t) x(t) +(2+\cos t)y(t)+(\frac{1}{20}+\frac{1}{30})x(t)y(t)}\Bigg ), \nonumber \\&\frac{\mathrm{d}y(t)}{\mathrm{d}t} = y(t)\Bigg (2+\frac{1}{30} \cos t - \frac{0.5y(t)}{\frac{1}{5}+\frac{1}{10}\sin t+(1-m)x(t)}\Bigg ). \end{aligned}$$

(30)

One can compute bounds of all the time-dependent coefficients. Here, $a_L = a_M = 3.2, b_L = 1, b_M = 3, c_L = c_M = 1.5, d_L = \frac{1}{60}, d_M = \frac{1}{12}, e_L = e_M = 3, a_{1_{L}} = \frac{1}{10}, a_{1_{M}} = \frac{3}{10}, a_{2_{L}} = \frac{14}{5}, a_{2_{M}} = \frac{16}{5}, a_{3_{L}} = a_{3_{M}} = 3, a_{4_{L}} = \frac{1}{60}, a_{4_{M}} = \frac{1}{12}, M_1 = 3.2, M_2 =0.14$. Furthermore we have

$$\begin{aligned} a_La_{1_{L}} = 0.32 > 0.189 = (1-m)c_MM_2. \end{aligned}$$

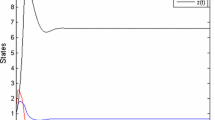
Thus the parametric values mentioned in the Example 6.2 satisfy the condition (5). Hence, Theorem 3.3 ensures that the model system (30) is permanent which can also be ensured from Fig. 2ii, iii. More precisely, phase plane diagram is shown in Fig. 2i (representation is carrying the similar meaning of Fig. 1i) while the integral curves are shown in Fig. 1ii (for prey (x)) and Fig. 1iii (for predator (y)), respectively.

Fig. 2

Phase-plane diagram (i) and time series solutions (ii, iii) of the system (30). Parameters are written in the text

Example 6.3

Let $a(t) = 9.9+ \sin 5t$, $b(t) = 10.9$, $c(t) = 0.3 + 0.19 \sin 5t$, $m = 0.7$, $a_1(t) = 8+ \cos 11t$, $a_2(t) = 10+ \sin 3t$, $a_3(t) = 5$, $a_4(t) = 0.1$, $d(t) = 0.5 + 0.29 \sin 3t$, $e(t) = 12 + 0.2 \sin 13t$, $k(t) = 2$, then the model system (1) becomes:

$$\begin{aligned}&\frac{\mathrm{d}x(t)}{\mathrm{d}t} = x(t)\Bigg ( 9.9+ \sin 5t -10.9 x(t) \nonumber \\&\quad -\frac{0.3(0.3 + 0.19 \sin 5t) y(t)}{8+ \cos 11t + 0.3(10+ \sin 3t)x(t)+5 y(t) +(0.1)(0.3) x(t)y(t)}\Bigg ), \nonumber \\&\frac{\mathrm{d}y(t)}{\mathrm{d}t} = y(t)\Bigg (0.5 + 0.29 \sin 3t - \frac{(12 + 0.2 \sin 13t)y(t)}{2+0.3x(t)}\Bigg ). \end{aligned}$$

(31)

By simple numerical computations, one can obtain that $a_L = 8.9, a_M = 10.9, b_L = b_M = 10.90, c_L = 0.11, c_M = 0.49, d_L = 0.21, d_M = 0.79, e_L = 11.8, e_M = 12.2, k_L = k_M = 2, a_{1_{L}} = 7, a_{1_{M}} = 9, a_{2_{L}} = 9, a_{2_{M}} = 11, a_{3_{L}} = a_{3_{M}} = 5, = 0.09, a_{4_{L}} = a_{4_{M}} = 0.1, = 0.5, M_1 = 1, M_2 = 0.20, m_1 = 0.82, m_2 = 0.04$ and furthermore

$a_La_{1_{L}} = 62.3 > (1-m)c_MM_2 = 0.147 \times 0.04 = 0.0059$ and

$$\begin{aligned}&\inf _{t \in R} \Big \{ b(t)- \frac{c(t)(1-m)\Big [a_2(t)(1-m)M_{2}^{\epsilon }+a_4(t)(1-m){M_{2}^{\epsilon }}^{2} \Big ]}{(a_1(t)+a_2(t)(1-m)m_{1}^{\epsilon }+a_3(t)m_{2}^{\epsilon }+a_4(t)(1-m)m_{1}^{\epsilon }m_{2}^{\epsilon })^2} \\&\quad -\frac{e(t)(1-m)M_{2}^{\epsilon }}{(k(t)+(1-m)m_{1}^{\epsilon })^2}\Big \}=10.754>0, \end{aligned}$$

and

$$\begin{aligned}&\inf _{t \in R}\Big \{- \frac{c(t)(1-m)[a_1(t)+a_2(t)(1-m)M_{1}^{\epsilon }]}{(a_1(t)+a_2(t)(1-m)m_{1}^{\epsilon } +a_3(t)m_{2}^{\epsilon }+a_4(t)(1-m)m_{1}^{\epsilon }m_{2}^{\epsilon })^2}\\&\quad +\frac{e(t)\left[ k(t)+(1-m)m_{1}^{\epsilon } \right] }{(k(t)+(1-m)M_{1}^{\epsilon })^2}\Big \}=5.009 >0. \end{aligned}$$

Thus the parametric values in the Example 6.3 satisfy conditions (5) and (6) stated in Theorems 3.3 and 3.7. Hence Theorem 3.7 ensures the global attractivity (global asymptotic stability) of the bounded positive solution (x(t), y(t)) of the system (31). Here, in Fig. 3i, we draw the globally attractive periodic solution whereas in Fig. 3ii, iii we show its time series solutions for prey (x) and predator (y), respectively.

Fig. 3

Phase-plane diagram (i) and time series solutions (ii, iii) of the system (31). Parameters are written in the text

Example 6.4

Let $a(t) = 5$, $b(t) = 3+\sin t$, $c(t) = 2.5$, $d(t) = 0.22 + 0.05 \cos t$, $e(t) = 1$, $m = 0.9$, $a_1(t) = 0.5$, $k(t) = 0.2$, $a_2(t) = 0.9 + 0.01 \cos t$, $a_3(t) = 1+ 0.0001 \sin t$, $a_4(t) = 3 + 0.1 \sin t$, and let $\epsilon = 0.0001$ and $\omega = 2 \pi$ then the model system (1) takes the following form:

$$\begin{aligned} \frac{\mathrm{d}x(t)}{\mathrm{d}t}= & {} x(t)\Bigg ( 5-(3+\sin t) x(t) \nonumber \\&-\frac{((1-0.9)2.5 y(t)}{0.5 + (0.1)(0.9 + 0.01 \cos t)x(t)+(1+ 0.001 \sin t)y(t) +(0.1)(3 +0.1 \sin t)x(t)y(t)}\Bigg ), \nonumber \\ \frac{\mathrm{d}y(t)}{\mathrm{d}t}= & {} y(t)\Bigg (0.22+0.05 \cos t - \frac{y(t)}{0.2 + (1-0.9)x(t)}\Bigg ). \end{aligned}$$

(32)

By simple calculations, one can obtain that $b_M = 4$, $b_L = 2$, $d_M = 0.27$, $d_L = 0.17$, $a_{2_{M}} = 0.91$, $a_{2_{L}} = 0.89$, $a_{3_{M}} = 1.001$, $a_{3_{L}} = 0.999$, $a_{4_{M}} = 3.1$, $a_{4_{L}} = 2.9$, $M_1 = 1.25, M_2 = 0.392, m_1 = 1.2, m_2 = 0.238$ and furthermore

$$\begin{aligned}&a_La_{1_{L}} = 2.5> (1-m)c_MM_2 = 0.09790675, \\&\inf _{t \in R} \Big \{ b(t)-\frac{c(t)(1-m)\Big [a_2(t)(1-m)M_{2}^{\epsilon }+a_4(t)(1-m){M_{2}^{\epsilon }}^{2} \Big ]}{(a_1(t)+a_2(t)(1-m)m_{1}^{\epsilon }+a_3(t)m_{2}^{\epsilon }+a_4(t)(1-m)m_{1}^{\epsilon }m_{2}^{\epsilon })^2} \\&\quad -\frac{e(t)(1-m)M_{2}^{\epsilon }}{(k(t)+(1-m)m_{1}^{\epsilon })^2}\Big \}=1.594>0 \end{aligned}$$

and

$$\begin{aligned}&\inf _{t \in R}\Big \{- \frac{c(t)(1-m)[a_1(t)+a_2(t)(1-m)M_{1}^{\epsilon }]}{(a_1(t)+a_2(t)(1-m)m_{1}^{\epsilon } +a_3(t)m_{2}^{\epsilon }+a_4(t)(1-m)m_{1}^{\epsilon }m_{2}^{\epsilon })^2}\\&\quad +\frac{e(t)\left[ k(t)+(1-m)m_{1}^{\epsilon } \right] }{(k(t)+(1-m)M_{1}^{\epsilon })^2}\Big \}=3.006 >0. \end{aligned}$$

Thus the parametric values in the Example 6.4 satisfy conditions (5) and (6) stated in Theorems 3.3 and 3.7. Hence, Theorem 3.7 ensures the global attractivity of the bounded positive solution (x(t), y(t)) of the system (32). Also,

$$\begin{aligned} {\hat{a}} = 5 > \widehat{\Big ( \frac{c}{a_3} \Big )} = \Big (\frac{{\hat{c}}}{{\hat{a}}_3} \Big ) = 2.5. \end{aligned}$$

Thus the parametric values in the Example 6.4 satisfy condition (9). Hence the model system (32) has at least one globally attractive positive $2\pi$-periodic solution. In Fig. 6i, we draw the globally attractive periodic solution and in Fig. 6ii, iii we show its time series solutions for prey (x) and predator (y), respectively.

Fig. 4

Phase-plane diagram (i) and time series solutions (ii, iii) of the system (33). Parameters are written in the text

Example 6.5

(Existence of Almost Periodic Solution) Let $a(t) = 14+ \cos (t), b(t) = 12+\cos (\sqrt{3}t)$, $c(t) = 1.5+\sin (t)$, $d(t) = 2 + 0.2 \sin (\sqrt{5}t)$, $e(t) = 12+ 0.2 \sin (\sqrt{13} t)$, $m = 0.7$, $a_1(t) = k(t) = 0.2 + 0.1 \sin t$, $a_2(t) = 3 + 0.2 \sin (\sqrt{7}t)$, $a_3(t) = 2+\cos (t)$, $a_4(t) = 0.01+0.001 \sin (t)$, then the model system (1) takes the following form:

$$\begin{aligned} \frac{\mathrm{d}x(t)}{\mathrm{d}t}= & {} x(t)\Bigg ( 14+ \cos (t)-(12+\cos (\sqrt{3}t)) x(t) \nonumber \\&-\frac{(1-0.7)(1.5+\sin (t)) y(t)}{(0.2 + 0.1 \sin t)+(3 + 0.2 \sin (\sqrt{7}t))(1-0.7)x(t) +(2+\cos (t))y(t)+(1-0.7)(0.01+0.001 \sin t)x(t)y(t)}\Bigg ), \nonumber \\ \frac{\mathrm{d}y(t)}{\mathrm{d}t}= & {} y(t)\Bigg (2 + 0.2 \sin (\sqrt{5}t) - \frac{(12+ 0.2 \sin (\sqrt{13} t))y(t)}{(0.2 + 0.1 \sin (t))+(1-0.7)x(t)}\Bigg ). \end{aligned}$$

(33)

By simple calculations, one can obtain that $a_L=13$, $a_M=15$, $b_M = 13$, $b_L = 11$, $c_L=0.5$, $c_M=2.5$, $e_L=11.8$, $e_M=12.2$ $a_{1_{L}} = 0.1$, $a_{1_{M}} = 0.3$ $d_M = 2.2$, $d_L = 1.8$, $a_{2_{M}} = 3.2$, $a_{2_{L}} = 2.8$, $a_{3_{M}} = 3$, $a_{3_{L}} = 1$, $a_{4_{M}} = 0.011$, $a_{4_{L}} = 0.009$, $M_1 = 1.363, M_2 = 0.310, m_1 = 0.821, m_2 = 0.136$ and furthermore

$$\begin{aligned}&a_La_{1_{L}} = 1.3> (1-m)c_MM_2 = 0.2326, \\&\inf _{t \in R} \Big \{ b(t)- \frac{c(t)(1-m)\Big [a_2(t)(1-m)M_{2}^{\epsilon }+a_4(t)(1-m){M_{2}^{\epsilon }}^{2} \Big ]}{(a_1(t)+a_2(t)(1-m)m_{1}^{\epsilon }+a_3(t)m_{2}^{\epsilon }+a_4(t)(1-m)m_{1}^{\epsilon }m_{2}^{\epsilon })^2} \\&\quad -\frac{e(t)(1-m)M_{2}^{\epsilon }}{(k(t)+(1-m)m_{1}^{\epsilon })^2}\Big \}=1.65011>0 \end{aligned}$$

and

$$\begin{aligned}&\inf _{t \in R}\Big \{- \frac{c(t)(1-m)[a_1(t)+a_2(t)(1-m)M_{1}^{\epsilon }]}{(a_1(t)+a_2(t)(1-m)m_{1}^{\epsilon } +a_3(t)m_{2}^{\epsilon }+a_4(t)(1-m)m_{1}^{\epsilon }m_{2}^{\epsilon })^2}\\&\quad +\frac{e(t)\left[ k(t)+(1-m)m_{1}^{\epsilon } \right] }{(k(t)+(1-m)M_{1}^{\epsilon })^2}\Big \}=12.734 >0. \end{aligned}$$

Thus the parametric values in the Example 6.5 satisfy conditions of Theorem 5.3. One can observe that the model system (33) posses a unique positive almost periodic solution which is globally attractive and it has been portrayed by phase-plane diagram in Fig. 4i and corresponding time series in Fig. 4ii for prey x and Fig. 4iii for predator y, respectively.

Fig. 5

Phase-plane diagrams of the system (30) with different strengths of prey refuge parameter m. Parameters are written in the text

Another significant point stressed by the modeling of [28] is the importance of a “temporal refuge” in the management of resistance. Hence the temporal refuge allows for better control of resistant of target population [46, 48]. Marine habitat, in particular, becomes complex in presence of oyster and coral reefs, mangroves, sea grass beds and salt marshes [21]. In lakes, habitat heterogeneity is most commonly present in the form of littoral zone vegetation or a depth-gradient diversity [15]. Terrestrial and aquatic vegetation diversity are not constant for any system in nature, these are temporal effects on the system and sometime give resistance to system functioning by creating habitat complexity or refuge [39]. To observe the dynamical behavior of the system (1) with variation of prey refuge intensity, we fix the values of all parameters as in Example 6.2 except m. Here also we observe the impact of temporal variation of prey refuge intensity m(t) on the same system.

Then it is observed that the sufficient condition (5) for permanence is well satisfied for all $m \in [0,1)$. Here for $m = 0$, we have $a_La_{1_{L}} = 0.32 > 0.210 = (1-m)c_MM_2$ while for $m = 0.99$ we have $a_La_{1_{L}} = 0.32 > 0.0021 = (1-m)c_MM_2$. One can also observe that both the species co-exist periodically for all $m \in [0,1)$. Moreover, the predator species co-exist for all values of m which also justify the additional food for predator species. The phase plane diagrams of the model system (1) are shown in Fig. 5i–iv for different values of prey reserve $m=0.1,0.35,0.25+0.1\sin t, 0.7+0.1\cos \sqrt{5}t$, respectively.

Fig. 6

Phase-plane diagram (i) and time series solutions (ii, iii) of the system (32). Parameters are given in the text

6.1 Sensitivity analysis

The outputs of deterministic models are governed by the model input parameters, which may exhibit some uncertainty in their determination or selection. We employed a global sensitivity analysis to assess the impact of uncertainty and the sensitivity of the outcomes of the numerical simulations to variations in each parameter of the system (1) using Latin Hypercube Sampling (LHS) and partial rank correlation coefficients (PRCC). LHS is a stratified sampling without replacement technique which allows for an efficient analysis of parameter variations across simultaneous uncertainty ranges in each parameter [32]. PRCC measures the strength of the relationship between the model outcome and the parameters, stating the degree of the effect that each parameter has on the outcome. Thus, sensitivity analysis determines the parameters with the most significant impact on the outcome of the numerical simulations of the model. To generate the LHS matrices, we assume that all the model parameters are uniformly distributed. Then a total of 200 simulations of the model per LHS run were carried out, using the baseline values are: Example 6.1 $\implies$ Fig. 7a, b, Example 6.2 $\implies$ Fig. 7c, d, Example 6.3 $\implies$ Fig. 7e, f, Example 6.4 $\implies$ Fig. 7g, h and Example 6.5 $\implies$ Fig. 7i, j and the ranges as 25% from the baseline values (in either direction). Note that the PRCC values lie between − 1 and 1. Positive (negative) values indicate a positive (negative) correlation of the parameter with the model output. A positive (negative) correlation implies that a positive (negative) change in the parameter will increase (decrease) the model output. Note that the PRCC values lie between -1 and 1. Positive (negative) values indicate a positive (negative) correlation of the parameter with the model output. A positive (negative) correlation implies that a positive (negative) change in the parameter will increase (decrease) the model output. The larger the absolute value of the PRCC, the greater the correlation of the parameter with the output. The PRCC values are depicted as bar graphs in Fig. 7a, c, e, g, i and its time evolution is illustrated in Fig. 7b, d, f, h, j.

Fig. 7

a Bar graphs of partial rank correlation coefficients (PRCC) of the parameters of the system (29) and b time course plots of the PRCCs of the parameters of the system (29) at 10 different time points (days 20, 40, 60, 80, 100, 120, 140, 160, 180, 200). Model parameters were sampled 1000 times. Baseline parameters are in the text

7 Concluding remarks

Variability in environmental factors plays critical role in the feasibility, uniqueness and shaping intrinsic population dynamics. For example, nature of environmental variability captured in the form of noise has evidently been shown to determine population extinction risk [34, 42]. We have discussed about an example on life history of hilsa fish at GBM basin in our introduction. Also by real and empirical data several authors describe the impact of temporal fluctuations of system parameters on their cultured system [15, 21, 28, 39, 46, 48]. In particular, prey–predator relationship is one of the basic links among populations which determine population dynamics and trophic structure of our environment. Classic prey–predator model has commonly been studied in idiosyncratic fashion, without considering variability in the surrounding environment in which population grow and survive. In this paper, environmental variability is captured in the model parameters with time-dependent periodic functions, which makes the model non-autonomous in nature. We have then studied population dynamics of non-autonomous modified Leslie–Gower prey–predator model with Crowley–Martin functional response which incorporates the effect of degree or strength of prey refuge.

Table 1 Comparative results obtained by using Brouwer fixed point theorem and continuation theorem in coincidence degree theory

Firstly, we have carried out the global qualitative behavior (permanence and global asymptotic stability) of the general non-autonomous proposed model by constructing a suitable Lyapunov function and using comparison theorem of differential equation. We have also investigated the periodicity and almost periodicity of this model system. One can notice that for $\epsilon = 0$, the conditions (3) and (5) are same. Hence the existence of a positively invariant set is sufficient for the permanence of the system. Moreover, the equations (5) and (8) provide the sufficient conditions for permanence and global asymptotic stability of the model system (1), respectively. The condition (5) also provides threshold level of the prey reserve m for permanence. We have shown that permanence condition (5) is sufficient for the existence of positive periodic solution using Brouwer fixed-point theorem. The condition (9) has ensured the existence of a positive periodic solution using continuation theorem (coincidence degree theorem).

Theorem 4.1 determines a threshold value of prey reserve m while the sufficient condition (9) obtained from Theorem 4.2 is independent of prey reserve m which is also supported by numerical simulation. This implies the betterment of Theorem 4.2 over Theorem 4.1. This also concludes that the prey reserve leaves no effect on the periodic coexistence scenario. The obtained results for the non-autonomous model system (1) are contrast with those of autonomous model system studied in [31] and consistent with Chen et al. [9] who showed that the prey refuge has no influence on permanence of the concerned autonomous model system. Some of the comparative results obtained by using Brouwer fixed point theorem and continuation theorem in coincidence degree theory are presented in the following Table 1. We have also discussed more general case than the existence of periodic solution, i.e., the existence of a unique globally asymptotically stable positive almost periodic solution has been established under certain sufficient parametric conditions (refer Theorem 5.3).

At last, we have also validated our analytical findings with respect to different sets of time-varying system parameters (hypothetical) except prey refuge intensity (m) through numerical simulations in Sect. 6 and also these are considered to agree and illustrate the effectiveness of analytical findings. But sometimes depending upon the environmental conditions and ecological health, prey refuge intensity is not fix and it varies with time and in this situation output of the dynamical system is different than the system with constant refuge in density [15, 21, 28, 39, 46, 48]. We have shown that the temporal impact on prey refuge intensity and its corresponding dynamical output by considering this parameter as periodic function through Fig. 5iii, iv. By these two figures, it is clear that periodic fluctuation of the considered system varies with different periodic prey refuge intensity. So, temporal variability of prey refuge can also motive that type of system along with other periodic and almost periodic system parameters.

PRCC sensitivity analysis gives us a conclusion that sensitivity of any parameter strongly depends upon the parameter estimation. High, intermediate and low PRCC values for same parameter for the same system are shown by the choices of different parameter sets. In the present study, in the model system (1), the involved variables x and y are only functions of the time. However in more general model systems, one can also consider the diffusion of the involved variables. Therefore, the variables x and y become space and time dependent and the associated ecological model system is given by parabolic nonlinear partial differential equations. The interested readers may refer to [60] and [61], which may help in understanding the analysis of the model system. In [60], authors have discussed a biological model system involving one species while in [61] authors have discussed a model system involving one species and a chemical signal.