Fractional-order adaptive fault-tolerant control for a class of general nonlinear systems

Abstract

This paper proposes a series of fractional-order control methods (FOCMs) based on fractional calculus (FC) for a class of general nonlinear systems. In order to deal with the nonlinearities and uncertainties caused by both external and internal factors, the designed control schemes are adaptive, robust, fault-tolerant and do not involve detailed information of the system model. Besides, FC is combined to improve the control performance, especially in higher control accuracy, better anti-interference ability and stronger robustness. For a comprehensive consideration of the practical systems, three different actuator conditions are separately discussed, and the FOCMs are established aiming at these three different situations, respectively, and proved by theoretical analysis. The inverted pendulum system is adopted as simulation object, and the fractional-order schemes are verified and compared with integer-order controller and traditional PID controller. Simulation results make it clear that the proposed FOCMs are superior to other two schemes in control precision, robustness and anti-interference ability.

1 Introduction

Refer to most research on the nonlinear systems, a great number of efforts have been devoted to study the control methods. For example, PID control [1, 2], adaptive fuzzy control [3], sliding mode control [4], etc. [5, 6], are widely used for the nonlinear systems. Since nearly all the practical systems are prone to nonlinearity, it brings the problem into researchers’ view: how can the designed controllers excellently deal with the nonlinearities and uncertainties when the practical influencing factors are taken into consideration?

In recent years, a lot of works have been done for the nonlinear systems to handle the problems caused by both external environments and internal situations. For example, in [7, 8], the systems were considered with unpredictable disturbances and input limitations. Besides, as a significant factor having an effect on system safety performance, actuator failures also cannot be ignored when it comes to the controller design, that is, the controller is required to have a capacity of fault tolerance  [9, 10]. Furthermore, due to the linear or nonlinear way the control inputs act on the system, Ali et al. [11] and Song et al. [12], respectively, proposed control methods for the affine and non-affine nonlinear systems. Also, some special actuator characteristics like asymmetric saturation and asymmetric dead zone  [13] should be noted and well addressed [14]. From the above analysis, it can be concluded that although some studies have been put forward to cope with the nonlinearities and uncertainties, very few of them have noticed the parameter perturbations and considered the different actuator conditions simultaneously. In addition, most existing works have a requirement for the specific values of the system parameters [4], which are difficult to acquire in the practical systems. And for the research on fault-tolerant control methods (e.g.,  [15]), most of them tend to be fairly complicated and have difficulty in applications. Thus, it is necessary for this paper to establish a control scheme, which does not rely on the unknown system parameters and can well adapt to the parameter changes as well as different actuator conditions. Simultaneously, the controller should also have a capacity of fault tolerance in order to guarantee the safety performance of the system in the presence of unpredictable actuator failures. Motivated by the above analysis, an integer-order adaptive fault-tolerant control method can be proposed, which has an analogous structure in [16]. However, considering the work is described in integer-order form, it is almost certain that it has deficiency in control effects, and it is still a problem that how to improve the control performance when the practical systems have a higher requirement for control accuracy, anti-interference capacity and robustness [17]?

With regard to the issue above, fractional calculus (FC) is considered [18]. Different from traditional integer-order conception, fractional derivatives and integrals can better reflect the system characteristics and can describe the practical systems more accurately [19,20,21]. Furthermore, with the development of technology, the complicated calculation of FC can be well solved  [22], and more and more attention has been attracted to FC-based control method design to improve the control performance. This is because FC has genetic attenuation property, which is reflected in that FC has an attenuated memory and it is a storage based on the current time. Specifically, according to the definition of FC, it can be seen as an integral transformation of the function which only focuses on the information close to the current time while integer-order stores all the information from the beginning to the present [23]. With this special characteristic of FC, the control energy can be released gently to make appropriate correction under the current time. It means that the control system can implement suitable control actions although system inertia and time delay exist, thus less oscillation process and smaller overshoot can be realized. As a result, comparing with the integer-order controllers, FC-based controllers ensure better system performance, especially in higher control accuracy and better anti-interference capacity aspects [24]. Today, more and more researchers have noted this special property of FC, and the research on FC-based control methods has been increasingly raised. For example, Espinosa et al. [25] adopted fractional-order control to realize accurate tracking control of the system, and a FC-based sliding mode control method was derived to deal with the system uncertainty  [26]. According to  [27], it has been proved that the FOCM can better achieve the stable-state performance than integer-order method and classical PID method. In  [28], Adeleh et al. addressed the tracking problem of a class of nonlinear dynamic systems and achieved better tracking results with the utilization of FC-based methods. Besides, by comparing the fractional-order PID controller with integer-order PID and traditional PID control methods, the superiority of fractional-order control was certified [29]. From the mentioned studies, it is not difficult to summarize that the FC-based control method can achieve better control performance than integer-order control method, which provides evidence for its application in this paper.

Inspired by the analysis above, the paper puts forward a series of fractional-order adaptive fault-tolerant control methods based on FC, with the purpose to cope with the parametric uncertainty and nonlinearity, external disturbances as well as unpredictable actuator failures of a class of nonlinear systems, and simultaneously improve the control performance. In sum, the innovations are concluded as below:

• 1. A series of control methods are established for a class of general nonlinear systems, which are adaptive, fault-tolerant and do not rely on the detailed information of the system model. The controller can deal with the system nonlinearities and uncertainties, as well as different actuator conditions.

• 2. The FC is combined so as to improve the control performance. Theoretical analysis and simulation studies jointly prove that the FOCM can realize higher control accuracy, better anti-interference ability and stronger robustness than integer-order method and PID method.

• 3. The proposed FOCMs can be easily established with simple structure, which are more favorable to practical applications compared with currently available methods.

The rest of the paper is organized as follows: In Sect. 2, three different actuator conditions are separately discussed, for which three system dynamic models are established, respectively, and some assumptions are put forward as the basis of the following analysis. A series of FOCMs based on FC are proposed aiming at three different actuator situations in Sect. 3, and the systems under the control schemes are proved to be stable by Lyapunov stability theory and Matignon’s stability theorem. In Sect. 4, the inverted pendulum system is employed as simulation object, and the FOCMs under three conditions are tested and compared with integer-order controller and traditional PID controller, which certifies the superiority of the fractional-order schemes. Finally, some conclusions are drawn in Sect. 5.

2 Model establishment and problem statement

Consider a class of general nonlinear systems which have their form as follows:

$$\begin{aligned} \begin{aligned}&\dot{x}_k=x_{k+1},\;\;\;k=1,2,\ldots ,n-1\\&\dot{x}_n=g(X)u_a+f(X) \end{aligned} \end{aligned}$$

(1)

where $x_k\in R$ is the system state with $k=1,2,\ldots ,n$, and X is the state vector that $X=[x_1,x_2,\ldots ,x_n]^T$. In addition, it should be mentioned that $x_1=x$ is defined for convenience. $u_a$ is the actual control input of the system. g(X) represents the time-varying and uncertain control gain of the system. f(X) is the lumped uncertainties considering external disturbances and system nonlinearities.

In order to describe the practical systems more comprehensively, three different actuator situations are analyzed.

Case 1

Actuator under healthy condition

In this situation, the designed control input can totally work on the system, which means

$$\begin{aligned} \begin{aligned}&\dot{x}_k=x_{k+1},\;\;\;k=1,2,\ldots ,n-1\\&\dot{x}_n=g(X)u+f(X) \end{aligned} \end{aligned}$$

(2)

where u is the object to be addressed in the paper.

Although the above dynamic model can generally describe most systems, there still exist inevitable actuator failures which could cause serious safety problem to the system. Thus, it is necessary to consider the actuator faults during the modeling process.

Case 2

Actuator failures with linear characteristics

Note that u to be designed under this condition is not the same as $u_a$ any more, as the relationship between these two factors can be described as $u_a=\rho u+\delta$, in which $\rho$ is named “actuator health indicator” and is identically defined in [30]. It should be mentioned that $\rho$ reflects the degree of actuator failure and satisfies $0<\rho <1$, for the actuator is assumed to be partly faulty instead of totally invalid in this paper, thus u can always have an effect on $u_a$. It is readily shown that the involvement of $\rho$ has previously considered the possible actuator faults in the controller design, which makes the system does not rely on precise fault detection and diagnosis [15]. $\delta$ is the part brought about by actuator failures, which is uncertain and bounded. Then, the system dynamic model in this case can be rewritten as

$$\begin{aligned} \begin{aligned}&\dot{x}_k=x_{k+1},\;\;\;k=1,2,\ldots ,n-1\\&\dot{x}_n=g(X)\rho u+g(X)\delta +f(X) \end{aligned} \end{aligned}$$

(3)

where $u_a=\rho u+\delta$ is applied, and other symbols are defined the same as before.

Case 3

Actuator failures with nonlinear characteristics

In this case, the actuator is described with some nonlinear characteristics like asymmetric saturation and asymmetric dead zone, which can be intuitively seen in Fig. 1. $\psi (u)$ is a nonlinear function of u, where $u_r>0$ and $u_l>0$ represent the uncertain saturation values of $\psi (u)$. Thus, u affects the system in a nonlinear way that $u_a=\rho \psi (u)+\zeta$, where $\zeta$ is defined the same as $\delta$. Then, the system dynamic model can be presented as

$$\begin{aligned} \begin{aligned}&\dot{x}_k=x_{k+1},\;\;\;k=1,2,\ldots ,n-1\\&\dot{x}_n=g(X)\rho \psi (u)+g(X)\zeta +f(X) \end{aligned} \end{aligned}$$

(4)

with other notations having the same meanings as described before.

Fig. 1

Actuator with asymmetric saturation and asymmetric dead zone characteristics

It can be summarized from the above description that in case 1, the system is affine nonlinear system with healthy actuator. In case 2, the system is affine system considering actuator failures. While the system in case 3 is in the non-affine form with actuator failures. To our best knowledge, very few research has simultaneously considered the different actuator conditions, and the paper will fill this gap.

In this work, the control objective is to design a suitable controller with the purpose to realize asymptotically stable tracking of the ideal system trajectories. Three actuator conditions are separately discussed, that is, considering the actuator under completely healthy condition ($u_a=u$), actuator failures with linear characteristics ($u_a=\rho u+\delta$) and actuator failures with nonlinear characteristics ($u_a=\rho \psi (u)+\zeta$). Specifically, for the system described by formula (2), (3) and (4), the designed control input u can make sure that the tracking error $E=[e_1,e_2,\ldots ,e_n]^T (e_1=e)$ converges toward 0 as $t\rightarrow \infty$, where $E=X-X^*$, with $X^*=[x_1^*,x^*_2,\ldots ,x^*_n]^T (x_1^*=x^*)$ representing the ideal system trajectory.

Before introducing the control laws, the following assumptions should be given first.

Assumption 1

The control gain is unknown but satisfies the constrain that there exists unknown constants $\underline{\lambda }$ and $\bar{\lambda }$ making $0<\underline{\lambda }\le |g(X)|\le \bar{\lambda }<\infty$, which ensures the boundedness of $g(\cdot )$. Besides, it is assumed that $g(\cdot )>0$ without loss of generality in this work.

Assumption 2

There is $|f(X)|\le \omega _0+\omega _1|x|+\omega _2|x^{(1)}|+\cdots +\omega _n|x^{(n-1)}|\le \omega \phi (X)$, in which $\phi (X)>0$ is a scale function of X and satisfies $\phi =1+|x|+|x^{(1)}|+\cdots +|x^{(n-1)}|$. $\omega \ge 0$ is an unknown constant which has $\omega =max\{\omega _0,\omega _1,\ldots ,\omega _n\}$ with $i=0,1,\ldots ,n$. It is assumed that the boundedness of X indicates the boundedness of $\phi$ and further ensures f to be bounded.

Assumption 3

There are unknown constants $\bar{\delta }>0$ and $\bar{\zeta }>0$, respectively, making $\delta$ and $\zeta$ satisfy $0<|\delta |\le \bar{\delta }<\infty$ and $0<|\zeta |\le \bar{\zeta }<\infty$.

Assumption 4

The ideal system state $x^*$, together with its derivatives (from 1st order to the nth order) are thought to be known, smooth and bounded.

Remark 1

It should be stressed that these assumptions are commonly used in the existing works and suitable for most nonlinear systems. Assumptions 1 and 4 are always utilized to address the tracking control problem for the systems (2)(3)(4) [31]. Assumption 2 makes it feasible to extract core information from the system uncertainties, and it can be done for any practical systems with only crude model information [32]. For Assumption 3, in line with most existing research on fault-tolerant control [33], it can be assumed that the faults vary slowly enough with time so as to realize fault detection and diagnosis, while Assumption 3 does not have such variation rate restriction, which is more practical.

3 Control method design and stability analysis

Before the controller design, some explanations about FC should be introduced firstly.

For the fractional integration, it often means Riemann–Liouville (R–L) integral, but for fractional differential, there are several definitions can be referred to [34]. Caputo definition is applied in this paper, since the initial condition for the Caputo differential equations has the same form as integer-order differential equations, and it has widespread applications in practical modeling process [35]. When we mention fractional integral and Caputo derivative, it usually refers to the left R–L integral and the left Caputo derivative, respectively. The mathematical explanations are presented as follows.

Definition 1

[36] The left-sided R–L fractional integral on $[t_0,T]$

$$\begin{aligned} _{t_0}I_t^{r}f(t)=\frac{1}{\varGamma (r)}\int _{t_0}^t (t-\tau )^{r-1}f(\tau )\mathrm{{d}}\tau \end{aligned}$$

(5)

where $r>0$ is the fractional order. $t>t_0$. $\varGamma (z)=\int _o^\infty e^{-t}t^{z-1}dt$ is Euler Gamma function with $Re(z)>0$.

Definition 2

[36] The left-sided Caputo fractional derivative on $[t_0,T]$

$$\begin{aligned} _{t_0}D_t^rf(t)=\frac{1}{\varGamma (n-r)}\int _{t_0}^t (t-\tau )^{n-r-1}f^{(n)}(\tau )\mathrm{{d}}\tau \end{aligned}$$

(6)

where $r>0$ and n is a positive integer satisfying $n-1<r<n$. $t>t_0$. Besides, it is worth noting that f(t) is function belonging to the space of absolutely continuous function that $f(t)\in AC^n([t_0,T])$.

In addition, the following property holds:

Property 1

[36] Suppose that $0<r<1$, then

$$\begin{aligned} {_{t_0}D_t^{r}}{_{t_0}I_t^{r}}f(t)=f(t) \end{aligned}$$

(7)

where $f(t)\in C[t_0,T]$.

Based on these preparations, the control laws can be proposed with separately taking the three different actuator conditions into consideration.

3.1 Controller design under healthy actuator condition $(u_a=u)$

In order to carry out the control law design, the following filtered variable should be proposed firstly

$$\begin{aligned} s_0=\alpha _1e_1+\alpha _2e_2+\cdots \alpha _{n-1}e_{n-1}+e_n \end{aligned}$$

(8)

which can be written as

$$\begin{aligned} s_0=\alpha _1e+\alpha _2e^{(1)}+\cdots +\alpha _{n-1}e^{(n-2)}+e^{(n-1)} \end{aligned}$$

(9)

where $\dot{e}_k=e_{k+1}(k=1,2,\ldots ,n-1)$ is employed. $\alpha _k$ with $k=1,2,\ldots ,n-1$ are constants chosen by the designer with the constrain that the polynomial in the form of $p^{(n-1)}+\alpha _{n-1}p^{(n-2)}\cdots +\alpha _1p$ satisfies Hurwitz condition. According to [37], it can be proved that if $s_0$ is proved to be asymptotically stable, e and its derivatives (up to $(n-1)$th order) will converge toward 0 as $t\rightarrow \infty$. Furthermore, the boundedness of $s_0$ indicates the boundedness of e and its derivatives.

To put forward the FOCM, the generalized fractional-order filtered variable should be adopted:

$$\begin{aligned} s=s_0+\beta _0I_t^{r}s_0 \end{aligned}$$

(10)

where $\beta >0$ is selected by the designer, and r is the fractional order which satisfies $0<r<1$. 0 and t are, respectively, lower and upper bound of the fractional integral. In order to carry out the controller design, the following Lemma is needed.

Lemma 1

Consider the following autonomous system

$$\begin{aligned} _0D_t^rx(t)=ax(t),\;\;\;x(0)=x_0 \end{aligned}$$

(11)

where $0<r<1$. Using the result of Matignon [38], it can be proved that the system is stable and its state x will decay toward 0 if and only if

$$\begin{aligned} |arg(a)|>r\pi /2 \end{aligned}$$

(12)

Refer to the formula (10), when s turns to be 0, the linear fractional-order system appears as

$$\begin{aligned} s_0+\beta _0I_t^{r}s_0=0 \end{aligned}$$

(13)

Take the rth order Caputo derivative of the above equation by using the Property 1, there is

$$\begin{aligned} _0D_t^rs_0=-\beta s_0 \end{aligned}$$

(14)

Considering $0<r<1$ in this work, one has $0<r\pi /2<\pi /2$. Besides, since $\beta >0$, it is readily shown that $|arg(-\beta )|=\pi >r\pi /2$ holds. According to Lemma 1, it is not different to gain that the system (14) is stable and its state $s_0$ will converge toward 0 when $t\rightarrow \infty$.

So far, it can be seen that if s converges toward 0 as $t\rightarrow \infty$, then, one has $\lim \limits _{t\rightarrow \infty }s_0=0$, which further ensures e and its derivatives converge to 0 as $t\rightarrow \infty$. Thus, the problem to be dealt with in this paper turns to designing a suitable controller to make sure that $s\rightarrow 0$ as $t\rightarrow \infty$.

Remark 2

It is noted that if we design (10) as $s=s_0+\varrho \int _0^ts_0d\tau$ with $\varrho >0$, an integer-order control method can be established refer to [16]. Since the integer-order method has the similar design and proof process with the FOCM in this paper, it will not be elaborated any more.

To continue the analysis, integrate (2) and (10), then, the following formula can be gained

$$\begin{aligned} \begin{aligned} \dot{s}=&g(X)u+f(X)-x^{*(n)}+\alpha _{n-1}e^{(n-1)}+\cdots \\&+\alpha _1e^{(1)}+\beta \frac{\mathrm{{d}}}{\mathrm{{d}}t}{_0I_t^{r}s_0} \end{aligned} \end{aligned}$$

(15)

where $\frac{\mathrm{{d}}}{\mathrm{{d}}t}{_0I_t^{r}s_0}$ can be calculated. Let $f(X)-x^{*(n)}+\alpha _{n-1}e^{(n-1)}+\cdots +\alpha _1e^{(1)}+\beta \frac{d}{dt}{_0I_t^{r}s_0}$ be $h(X,X^*)$ for simplification, one has

$$\begin{aligned} \dot{s}=gu+h(X,X^*) \end{aligned}$$

(16)

By uniting like terms in $h(\cdot )$, it can be seen that there exists bounded uncertain constant term in h, which has $|\omega _0|+|-x^{*(n)}|+|\alpha _{n-1}x^{*(n-1)}|+\cdots +|\alpha _1x^{*(1)}|\le b_0$. Similarly, x and its derivatives can be extracted with $b_1=|\alpha _1|+|\omega _2|,b_2=|\alpha _2|+|\omega _3|,\cdots ,b_{n-1}=|\alpha _{n-1}|+|\omega _n|$. Then one has

$$\begin{aligned} \begin{aligned} |h|\le&b_0+b_1|x^{(1)}|+\cdots +b_{n-1}|x^{(n-1)}|\\&+\beta |\frac{\mathrm{{d}}}{\mathrm{{d}}t}{_0I_t^{r}s_0}|+\omega _1|x|\le b\varphi \end{aligned} \end{aligned}$$

(17)

in which $b_i\ge 0, i=0,1,\cdots n-1$. b is an unknown constant satisfying $b=max\{b_0,b_1,\ldots , b_{n-1},\beta ,\omega _1\}$, and $\varphi =1+|x^{(1)}|+\cdots +|x^{(n-1)}|+|\frac{\mathrm{{d}}}{\mathrm{{d}}t}{_0I_t^{r}s_0}|+|x|$. Then, the following theorem can be put forward.

Theorem 1

Consider the general system described by formula (2) with healthy actuator. If the controller is designed as

$$\begin{aligned} u= & {} -c_0s-\hat{b}\varphi sign(s) \end{aligned}$$

(18)

$$\begin{aligned} \dot{\hat{b}}= & {} \mu _0\varphi |s| \end{aligned}$$

(19)

in which $c_0>0$ and $\mu _0>0$ are chosen by the designer, and $\hat{b}$ is the estimation of b, the asymptotically stable tracking of the system can be ensured.

Proof

Choose Lyapunov function candidate as

$$\begin{aligned} V=\frac{1}{2}s^2+\frac{1}{2\underline{\lambda }\mu _0} (b-\underline{\lambda }\hat{b})^2 \end{aligned}$$

(20)

then the derivative of the above equation can be gained that

$$\begin{aligned} \dot{V}=s\dot{s}-\frac{\dot{\hat{b}}}{\mu _0}(b-\underline{\lambda }\hat{b}) \end{aligned}$$

(21)

By utilizing formula (16), there is

$$\begin{aligned} \dot{V}=gus+hs-\frac{\dot{\hat{b}}}{\mu _0}(b-\underline{\lambda }\hat{b}) \end{aligned}$$

(22)

Then, one can developed by (18) with Assumption 1 that

$$\begin{aligned} \dot{V}\le -c_0\underline{\lambda }s^2-\underline{\lambda } \hat{b}\varphi |s|+b\varphi |s|-\frac{\dot{\hat{b}}}{\mu _0} (b-\underline{\lambda }\hat{b}) \end{aligned}$$

(23)

where $s\cdot sign(s)=|s|$ and $|h|\le b\varphi$ are applied. Then, the following formula can be obtained with (19) that

$$\begin{aligned} \dot{V}\le -c_0\underline{\lambda }s^2\le 0 \end{aligned}$$

(24)

Thus, it can be gained that $V\in \ell _\infty$, which further ensures that $s\in \ell _\infty$ and $\hat{b}\in \ell _\infty$. Hence, e and its derivatives (up to $(n-1)$th order) are bounded according to the analysis above. Then, one has $\varphi \in \ell _\infty$ and $u\in \ell _\infty$, and it can be readily shown that $\dot{s}\in \ell _\infty$, which means s is uniformly continuous. Simultaneously, it has $\int _{0}^{t}c_0\underline{\lambda } s^2d\epsilon \le V(0)<\infty$. Then, it can be concluded that $s\rightarrow 0$ as $t\rightarrow \infty$ with Barbalat theorem. Finally, e and its derivatives converge to 0 when $t\rightarrow \infty$ can be gained by Lemma 1 and the aforementioned analysis, which means the asymptotically stable tracking of the system can be guaranteed by the proposed control method. $\square$

Remark 3

It is worth noting that although it is difficult to acquire the exact value of b, we can easily calculate $\varphi$, which contains some core information of h.

3.2 Controller design considering actuator failures with linear characteristics $(u_a=\rho u+\delta )$

In this subsection, the controller is designed to achieve control objective and simultaneously cope with the actuator failures. Specifically, combine (3) and (10), the following equation can be drawn that

$$\begin{aligned} \begin{aligned} \dot{s}=&g(X)\rho u+g(X)\delta +f(X)-x^{*(n)}\\&+\alpha _{n-1}e^{(n-1)}+\cdots +\alpha _1e^{(1)} +\beta \frac{d}{dt}{_0I_t^{r}s_0} \end{aligned} \end{aligned}$$

(25)

To simplify the above formula, let $g(X)\delta +f(X)-x^{*(n)}+\alpha _{n-1}e^{(n-1)}+\cdots +\alpha _1e^{(1)}+\beta \frac{d}{dt}{_0I_t^{r}s_0}$ be $y(X,X^*)$ like before, there is

$$\begin{aligned} \dot{s}=g\rho u+y(X,X^*) \end{aligned}$$

(26)

From the aforementioned analysis and assumptions, we can similarly have

$$\begin{aligned} \begin{aligned} |y|\le&m_0+m_1|x^{(1)}|+\cdots +m_{n-1}|x^{(n-1)}|\\&+\beta |\frac{d}{dt}{_0I_t^{r}s_0}|+\omega |x|\le m\varphi \end{aligned} \end{aligned}$$

(27)

where $m=max\{m_0,m_1,\ldots ,m_{n-1},\beta ,\omega _1\}$ is an uncertain constant, and $\varphi =1+|x^{(1)}|+\cdots +|x^{(n-1)}|+|\frac{d}{dt}{_0I_t^{r}s_0}|+|x|$ has the same definition as before. Besides, make $g\rho$ be $\sigma$, then $\sigma >0$ can be concluded from Assumption 1 and the above analysis, and one has $0<\underline{\sigma }\le |\sigma |\le \bar{\sigma }<\infty$, in which $\underline{\sigma }$ and $\bar{\sigma }$ are unknown positive constants. Then here comes

$$\begin{aligned} \dot{s}=\sigma u+y(\cdot ) \end{aligned}$$

(28)

thus the theorem can be drawn below.

Theorem 2

If the general system is considered as described in formula (3), it can be proved that the following controller can guarantee asymptotically stable tracking of the system

$$\begin{aligned} u= & {} -d_0s-\hat{m}\varphi sign(s) \end{aligned}$$

(29)

$$\begin{aligned} \dot{\hat{m}}= & {} \eta _0\varphi |s| \end{aligned}$$

(30)

where $d_0>0$ and $\eta _0>0$ are control parameters selected by the designer, and $\hat{m}$ is the estimation of m.

Proof

The Lyapunov function candidate is selected as

$$\begin{aligned} V=\frac{1}{2}s^2+\frac{1}{2\underline{\sigma }\eta _0} (m-\underline{\sigma }\hat{m})^2 \end{aligned}$$

(31)

Then, treat the above equation like before and simultaneously utilize formula (29) and (30), we can finally gain

$$\begin{aligned} \dot{V}\le -d_0\underline{\sigma }s^2\le 0 \end{aligned}$$

(32)

together with the fact that $\int _{0}^{t}d_0\underline{\sigma } s^2d\epsilon \le V(0)<\infty$, similar result can be gained following the same argument as the proof of Theorem 1. $\square$

3.3 Controller design considering actuator failures with nonlinear characteristics $(u_a=\rho \psi (u)+\zeta )$

With taking actuator characteristics like asymmetric saturation and asymmetric dead zone into consideration, this subsection focuses on controller design when the system is a non-affine nonlinear system. Recall the dynamic system described by (4), a smooth function $\chi (u)$ is proposed to approximate the nonlinear function $\psi (u)$ [39], which has

$$\begin{aligned} \chi (u)=\frac{u_{\varpi }e^{\gamma u}-u_{\varpi }e^{-\gamma u}}{e^{\gamma u}+e^{-\gamma u}} \end{aligned}$$

(33)

Note that $\gamma >0$ is chosen by the designer and probably leads to different approximation results with different values. Besides, $u_\varpi >0$ is the uncertain saturation value of the function. In line with Eq.  (33), one has

$$\begin{aligned} \psi (u)=\chi (u)+\theta (u) \end{aligned}$$

(34)

where $\theta (u)$ refers to the approximation error and satisfies $0<|\theta (u)|\le \theta _0<\infty$, in which $\theta _0$ is an unknown constant. Then, the Lagrange Mean Value Theorem can be applied since $\chi (u)$ is a smooth and continues function, that is

$$\begin{aligned} \chi (u)-\chi (0)=\chi '(\xi )u \end{aligned}$$

(35)

with $\chi '(\xi )=\frac{\partial \chi }{\partial u}|_{u=\varepsilon }$. It should be noted that if $u>0$, $\xi \in (0,u)$, otherwise, if $u<0$, there is $\xi \in (u,0)$. Then, the system dynamic model can be further gained

$$\begin{aligned} \begin{aligned}&\dot{x}_k=x_{k+1},\;\;\;k=1,2,\ldots ,n-1\\&\dot{x}_n=g\rho \chi '(\xi )u+g\rho \theta (u)+g\zeta +f(X) \end{aligned} \end{aligned}$$

(36)

in which $\chi (0)=0$ is applied. With the filtered variable proposed as (10), there is

$$\begin{aligned} \begin{aligned} \dot{s}=&g\rho \chi '(\xi )u+g\rho \theta (u)+g\zeta +f(X)-x^{*(n)}\\&+\alpha _{n-1}e^{(n-1)}+\cdots +\alpha _1e^{(1)}+\beta \frac{d}{dt}{_0I_t^{r}s_0} \end{aligned} \end{aligned}$$

(37)

Considering the assumptions and analysis, the equation above is similarly dealt with as before, then

$$\begin{aligned} \dot{s}=g\rho \chi '(\xi )u+q(X,X^*) \end{aligned}$$

(38)

can be obtained, which has

$$\begin{aligned} \begin{aligned} |q|\le&v_0+v_1|x^{(1)}|+\cdots +v_{n-1}|x^{(n-1)}|\\&+\beta |\frac{d}{dt}{_0I_t^{r}s_0}|+\omega |x|\le v\varphi \end{aligned} \end{aligned}$$

(39)

with $v=max\{v_0,v_1,\ldots ,v_{n-1},\beta ,\omega \}$, and $\varphi$ has the same definition as before. For simplification, make $g\rho \chi '(\xi )$ be $\tau$, then one has

$$\begin{aligned} \dot{s}=\tau u+q(\cdot ) \end{aligned}$$

(40)

Since $\tau$ can be either positive or negative, it is assumed that $\tau >0$ here without loss of generality, and there exist positive constants $\underline{\tau }$ and $\bar{\tau }$ satisfying $0<\underline{\tau }\le |\tau |\le \bar{\tau }<\infty$. Thus, the theorem can be put forward.

Theorem 3

Consider the system described by formula (4). The controller is designed as

$$\begin{aligned} u= & {} -k_0s-\hat{v}\varphi sign(s) \end{aligned}$$

(41)

$$\begin{aligned} \dot{v}= & {} \iota _0\varphi |s| \end{aligned}$$

(42)

where $k_0>0$ and $\iota _0>0$ are selected by the designer, $\hat{v}$ is the estimation of v, then the asymptotically stable tracking of the system can be ensured.

Proof

Choose Lyapunov function candidate as

$$\begin{aligned} V=\frac{1}{2}s^2+\frac{1}{2\underline{\tau }\iota _0} (v-\underline{\tau }\hat{v})^2 \end{aligned}$$

(43)

Then, treat the formula in the similar way, it can be finally concluded that

$$\begin{aligned} \dot{V}\le -k_0\underline{\tau }s^2\le 0 \end{aligned}$$

(44)

With $\int _{0}^{t}k_0\underline{\tau } s^2d\epsilon \le V(0)<\infty$, the conclusion can be drawn by utilizing the same argument in the proof of Theorem 1. $\square$

Remark 4

From all above analysis, it can be concluded that the proposed control methods are in the similar forms under different actuator conditions, which means they can cope with different actuator situations only by adjusting control parameters. Besides, the controllers do not involve detailed information of the system except the measurable and known amount and are provided with simple structure which are easy to be established. All these advantages make the FOCMs proposed in this paper have a potential in applications.

Fig. 2

The schematic diagram of the inverted pendulum system

4 Simulation studies

4.1 Simulation results

Comparison of the methods in the simulation part is the comparison of the integer-order control method and the fractional-order control method established in this paper, and the comparison between the two kinds of methods and the traditional PID method. As Fig. 2 shows, the inverted pendulum system is adopted for the validation of the theorems, since it is a typical multivariate and nonlinear system, which has the dynamic model taken from [40]:

$$\begin{aligned} \begin{aligned}&\dot{x}_1=x_2\\&\dot{x}_2=h(X)u_a+f(X) \end{aligned} \end{aligned}$$

(45)

where $x_1$ and $x_2$ represent the swing angle and swing speed, respectively, and $X=[x_1,x_2]^T$ is the state vector. To simplify the following analysis, it is defined that $x_1=x$. $u_a$ is the actual control input of the system. h(X) is the uncertain control gain which has

$$\begin{aligned} h(X)=\frac{cos(x)/(m_c+m)}{l(4/3-mcos^2x/(m_c+m))} \end{aligned}$$

(46)

and f(X) represents lumped uncertainties that

$$\begin{aligned} f(X)=\frac{gsinx-ml\dot{x}^2cosxsinx/(m_c+m)}{l(4/3-mcos^2x/(m_c+m))} \end{aligned}$$

(47)

For the above analysis, g is gravitational acceleration. $m_c$ is the mass of the car while m is the mass of the pendulum. l represents half length of the pendulum. It should be mentioned that, in fact, h(X) and f(X) can be selected in other forms as long as they satisfy the assumptions, and the designed methods are still applicable. The system parameters are chosen as $g=9.8m/s^2$, $m_c=1kg$, $m=0.1kg$, $l=0.5m$, which are only used for simulation and not involved in the controller design.

Table 1 Values of control parameters

Deal with the inverted pendulum system as described before. Similarly, three actuator conditions are separately considered, and fractional-order controller, integer-order controller and traditional PID controller are compared under each condition. It should be mentioned that during the simulation process, all the control parameters are selected in principle to gain the best possible simulation results so as to make the conclusions more persuasive. Specifically, all the selected parameters are presented in Table 1.

Condition 1

The inverted pendulum system with healthy actuator $(u_a=u)$

(a) Fractional-order controller Firstly, the fractional-order filtered variables $s_0$ and s are chosen as

$$\begin{aligned} s_0= & {} \alpha e+\dot{e} \end{aligned}$$

(48)

$$\begin{aligned} s= & {} s_0+\beta _0I_t^{r}s_0 \end{aligned}$$

(49)

and the control laws can be finally concluded below:

$$\begin{aligned} u= & {} -c_1s-\hat{p}\kappa _1sign(s) \end{aligned}$$

(50)

$$\begin{aligned} \dot{\hat{p}}= & {} \mu _1\kappa _1|s| \end{aligned}$$

(51)

here $\kappa _1>0$ is the scale function which has the form as $\kappa _1=1+|x|+|\dot{x}|+|sinx|+|cosx|+|\frac{\mathrm{{d}}}{\mathrm{{d}}t}{_0I_t^{r}s_0}|$. $\hat{p}$ is the estimation of the uncertain parameter p.

Fig. 3

Tracking results and errors under healthy actuator

(b) Integer-order controllerFor comparison, an integer-order control method is also proposed. Specifically, choose the integer-order filtered variable as

$$\begin{aligned} \bar{s}=s_0+\varrho \int _{0}^{t}s_0\,\mathrm{{d}}\tau \end{aligned}$$

(52)

in which $s_0$ has the same structure as (48). Treat the inverted pendulum system in the same way, then the integer-order controller is designed to achieve asymptotically stable tracking of the system that

$$\begin{aligned} u= & {} -c_2\bar{s}-\hat{p}\kappa _2sign(\bar{s}) \end{aligned}$$

(53)

$$\begin{aligned} \dot{\hat{p}}= & {} \mu _2\kappa _2|\bar{s}| \end{aligned}$$

(54)

with $\kappa _2=1+|x|+|\dot{x}|+|sinx|+|cosx|$.

(c) PID controller In addition, traditional PID control method is also tested on the inverted pendulum system during the simulation for contrast, and the parameters can be determined by continuous tuning.

As is shown in Fig. 3, it can be clearly seen that when the actuator is completely healthy, the three control methods can achieve the tracking control objective while the fractional-order control scheme ensures better control performance. Specifically, in Fig. 3a, c the enlarged parts make it obvious that fractional-order scheme realizes more precise tracking results than other two methods. More intuitive results can be seen from Fig. 3b, d, where higher control accuracy of the developed FOCM is enlarged. It is shown that the tracking errors with FOCM are smaller than the errors gained by integer-order and PID method. Especially, compared with PID controller, the FC-based method shows great advantages in smaller overshoot and greater stability, proving its feasibility in practical nonlinear systems.

Fig. 4

Actuator faults simulated

Fig. 5

Tracking results and errors considering actuator failures with linear characteristics

Condition 2

Considering actuator failures with linear characteristics $(u_a=\rho u+\delta )$

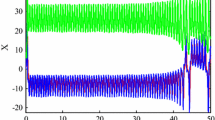
In this condition, the actuator is assumed to be partly invalid so as to verify the capacity of fault tolerance of the designed controller. The selection of $\rho$ and $\delta$ is shown in Fig. 4, from which it can be seen that the health indicator is time-varying and brings uncertain interference to the system. It should be mentioned that they can also be chosen in other forms with the assumptions. As is shown in Fig. 5a, b, similar with Condition 1, the fractional-order controller realizes more precise tracking of the ideal system trajectories than other two control methods. Additionally, in (d), larger chattering phenomenon appears with the PID control method when the actuator failures exist. However, the FOCM can still guarantee stable tracking with highest precision and smallest vibration. Furthermore, as the FOCM achieves better control performance than other two control schemes under uncertain actuator failures and disturbances, the stronger robustness and better anti-interference characteristics of fractional-order method can also be proved.

Fig. 6

Tracking results and errors considering actuator failures with nonlinear characteristics

Fig. 7

The control action of the controllers under three cases

Condition 3

Considering actuator failures with nonlinear characteristics $(u_a=\rho \psi (u)+\zeta )$

In this case, $\rho$ is the same as that in Condition 2 and $\zeta$ is selected identical to $\delta$. $\psi (u)$ adopted for simulation is that

$$\begin{aligned} \psi (u)= {\left\{ \begin{array}{ll} -9&{} u<-9\\ 1.5(u+3)&{} -9\le u<-3\\ 0&{} -3\le u<0\\ 0&{} 0\le u<5\\ 2u-10&{} 5\le u<10\\ 10&{} u\ge 10\\ \end{array}\right. } \end{aligned}$$

(55)

It can be observed from Fig. 6 that the superiority of FOCM is even more evident when the actuator is considered with nonlinear characteristics like asymmetric saturation and asymmetric dead zone. Larger tracking errors and more chattering phenomenon appear with integer-order and PID schemes; however, the fractional-order method still ensures highest control precision. Especially, in Fig. 6c, d, there exists obvious chattering in the integer-order and PID cases when the system switches the speed direction, and it takes more than 1s for the system to overcome the perturbation. Yet fractional-order method has only slight vibration and can quickly restore stable state, which means that the FOCM has a better capacity to deal with the external disturbances in spite of the input constrains. This further certifies stronger robustness and better anti-interference ability of the developed methods.

Table 2 RMS of the controllers under three cases

Furthermore, the control action of the three controllers under three different conditions is presented in Fig. 7, and in order to quantitatively describe the performance of the controllers in terms of energy consumption, the values of RMS are calculated, respectively, which can be seen in Table 2. It is shown that the FOCM achieves the smallest RMS in each condition, indicating the least energy consumption during the control process, which further proves its potential in applications.

Remark 5

In fact, the control parameters involved in the developed FOCMs can be set by the designer quite arbitrarily and do not need continues tuning as long as they satisfy the preset requirement (e.g., $\alpha >0, 0<r<1$). However, we try to achieve a best possible result for comparison. The problem of how the control performance specifically depends on these control parameters is not discussed in this paper, which is expected to be solved in the future work.

4.2 Analysis of advantages

From the above simulation results, it can be concluded that compared with traditional PID method, fractional-order control scheme can realize the tracking control objective with higher control accuracy, less vibration, smaller overshoot and stronger robustness. This is because the calculation of fractional calculus can be seen as integral transformation of the function which has ${_{0}I_t^{r}}f(t)=\int _0^t\phi (t-\tau )\cdot f(\tau )\mathrm{{d}}\tau$, where the weight function has the properties that $\lim \limits _{t\rightarrow 0^+}\phi (\cdot )=\infty$ and $\lim \limits _{t\rightarrow \infty }\phi (\cdot )=0$. Thus, the FOCM makes appropriate corrections with the help of FC while PID control implements excessive control actions. Besides, the FOCM has a capacity of fault tolerance and is more effective for the complicated nonlinear systems. As for the integer-order control method, it can also be proved that all the fractional-order cases perform better than the integer-order ones.

Recall the chosen of s in formula (49). When s is proved to be asymptotically stable, we gain the fractional-order linear equation as

$$\begin{aligned} _0D_t^rs_0+\beta s_0=0 \end{aligned}$$

(56)

which has the solution as

$$\begin{aligned} s_0(t)=T_{r,1}(t)s_0(0) \end{aligned}$$

(57)

where

$$\begin{aligned} T_{r,1}(t)=\sum \limits _{k=0}^\infty \frac{(-\beta )^kt^{rk}}{\varGamma (rk+1)}\approx \frac{1}{\varGamma (1-r)}(-\beta )^{-1}t^{-r} \end{aligned}$$

is Mittag-Leffler function [38]. Especially, when r turns to be 1, which means the system is described by integer-order, one has

$$\begin{aligned} T_{1,1}(t)=\sum \limits _{k=0}^\infty \frac{(-\beta )^kt^{k}}{\varGamma (k+1)} =\sum \limits _{k=0}^{\infty }\frac{(-\beta )^kt^k}{k!}=exp(-\beta t), \end{aligned}$$

thus it has readily shown that the fractional-order system decays toward 0 in the form of $t^{-r}$, while the decay type of integer-order system is $exp(-\beta t)$. It illustrates that the energy transfer is slowly with the help of FC. Thus, when the overshoot or disturbances appears, the FOCMs implement the control action gently to make suitable corrections and can make up the shortcomings caused by the high-frequency actuator switching. Then, smaller error and less oscillation can be achieved, which makes the fractional-order controller has higher precision, better anti-interference ability and stronger robustness than integer-order methods.

5 Conclusion

Considering the nonlinearities and uncertainties of a class of general nonlinear systems, a series of fractional-order control methods (FOCMs) are put forward, which are adaptive, robust, fault-tolerant and do not refer to detailed information of the system model. Based on the fractional calculus (FC), the fractional-order controller has advantages in higher control precision, better anti-interference ability and stronger robustness. Three different actuator conditions are considered, for which, the FOCMs are established, respectively, and Lyapunov stability proof and Matignons stability theorem are combined to illustrate the effectiveness of them. The inverted pendulum system is chosen as simulation object, and the fractional-order schemes are compared with both integer-order and PID control methods. Simulation results have proved the superiority of the FC-based FOCMs, which is consistent with the theoretical analysis.