Reliability of a class of nonlinear systems under switching random excitations

Abstract

Systems subjected to switching random excitations are practically significant because they include many safety-critical systems such as power plants and communication networks. In this paper, the reliability of multi-degree, nonlinear, non-integrable Hamiltonian systems subjected to switching random excitations is investigated. Such a system is formulated as a continuous–discrete hybrid based upon the Markov jump theory. Stochastic averaging is applied to suppress the rapidly varying parameters of the Markov jump process in order to generate a probability-weighted diffusion equation. The associated backward Kolmogorov equation is then set up, from which the approximate reliability function and probability density of first passage time are obtained. The utility and accuracy of this approximate procedure are demonstrated by two examples.

1 Introduction

In system modeling, the excitations that systems undergo may change abruptly due to environmental disturbances or component failures. Abruptly changing loads occur in many fields, for example in power plants, communication networks, large-scale structures and so on. The presence of such loads complicates the dynamic response and often diminishes system reliability. Development of methodology for nonlinear structures subjected to switching random excitations (SREs) is much deserving.

Markov jump system (MJS) is basically a continuous–discrete hybrid formulated as a continuous system that can take on different forms, the number of which is finite. Such a model can adequately describe the system response under abruptly changing loads. It has received increasing attention from researchers since first introduced by Krasovskii and Lidskii [1] in 1961. In recent years, research in Markov jump systems has concerned with issues such as stationary response [2], stochastic stability [3,4,5], optimal vibration control [6, 7] and robustness [8]. Most of the published results are formulated for linear MJSs and are rarely applicable to nonlinear MJSs. However, the actual engineering structures are usually nonlinear, and it is important that they can operate reliably.

Reliability is mainly concerned with the question of safety, such as the safety of a building under seismic excitation and the performance of a vehicle under irregular road excitation. In structural systems, reliability is frequently addressed by the first passage problem—a classic and challenging problem in stochastic theory. Only when the response is a diffusion process is there a rigorous theory. At present, the reliability function of random systems is normally determined by the backward Kolmogorov (BK) equation. In multi-degree-of-freedom systems, the associated BK equation is a high-dimensional partial differential equation, which is not amenable to exact solution. Although Monte Carlo simulation can be used to solve the first passage problem, the method requires a large amount of computing time and core memory. The stochastic averaging method, which can effectively reduce the size of high-dimensional stochastic systems, greatly facilitates the solution of resulting BK equations. In recent years, the reliability of systems under white noise excitation [9,10,11], Poisson white noise excitation [12], wideband random excitation [13], combined harmonic force and white noise excitation [14, 15], and combined harmonic force and wideband noise excitation [16, 17] has received a great deal of attention. However, there is little research in the reliability of nonlinear systems under abruptly changing noise.

The purpose of this paper is to present an approximate method for the reliability of nonlinear, Markov jump, quasi-non-integrable Hamiltonian systems. This paper is organized as follows. In Sect. 2, the equation for such systems is set up, and the stochastic averaging method is applied to derive an averaged Itô stochastic differential equation for the Hamiltonian. The BK equation for the reliability function of the averaged system is established in Sect. 3. Utility and accuracy of the proposed method are demonstrated in Sect. 4 by two examples, wherein comparison is made of numerical results obtained by direct Monte Carlo simulation and analytical results obtained by solving the averaged BK equation. A summary of findings is given in Sect. 5.

2 Problem formulation

2.1 Model of switching random excitations

The excitation that structures undergo may switch randomly from one intensity grade to another. Assume that the switching of intensity grades follows the Markov jump rules. The SRE can be expressed as

$$\begin{aligned} {\upxi }^{{a}}\left( {t} \right) ={\upxi }^{\left[ {s}\left( {t} \right) \right] }{(t)}, \end{aligned}$$

(1)

where ${\upxi }^{{a}}\left( {t} \right)$ denotes the actual random excitation that structures undergo and s(t) is a Markov process representing the intensity grade of the excitation. In applications, the intensity grades are usually finite, so that s(t) takes values from a finite set ${S} =\{1,2,\ldots ,l$. In addition, ${\upxi }^{\left( u \right) }( {t} )(u\in {S})$ denotes the $u\hbox {th}$ grade random excitation, which is Gaussian white noise with zero mean and density $2{D}^{(u)}$.

The Markov jump process s(t) is characterized by its transition probability matrix given by

$$\begin{aligned}&\Pr \left\{ {{s}\left( {t}+\vartriangle \right) =j} \vert {{s}\left( {t} \right) =i}\right\} \nonumber \\&\quad =\left\{ {\begin{array}{l} {\lambda }_{ij}\Delta +{o}\left( {\Delta } \right) {,}\quad i \ne j\\ {{1+\lambda }}_{ij}{\Delta +{o}}\left( {\Delta } \right) {,}\quad i=j,\\ \end{array} } \right. \end{aligned}$$

(2)

where $\vartriangle \,>0$ is a sufficiently small positive number and ${\lambda }_{ij}>0$ denotes the transition rate from grade i to grade $j\,(i\ne j)$ such that

$$\begin{aligned} {\lambda }_{ii}=-\sum \nolimits _{\begin{array}{c} j=1 \\ j\ne i \end{array}}^l {\lambda }_{ij}. \end{aligned}$$

(3)

2.2 Nonlinear stochastic system with SREs

Consider an n-degree-of-freedom (DOF) nonlinear system with SREs. The motion of the system is governed by n second-order stochastic differential equations in the generalized displacements. These second-order equations can always be recast as 2n first-order equations in the Hamiltonian formulation:

$$\begin{aligned} {\dot{{q}}}_{i}= & {} \frac{{\partial } {\tilde{{H}}}^{'}}{{\partial }{p}_{i}} \end{aligned}$$

(4)

$$\begin{aligned} {\dot{{p}}}_{i}= & {} -\frac{{\partial }{\tilde{{H}}}^{{'}}}{{\partial }{q}_{i}} -\upvarepsilon {\tilde{{c}}}_{ij}^{{'}}\left( {\mathbf{q,p}} \right) \frac{{\partial }{\tilde{{H}}}^{{'}}}{{\partial }{p}_{j}}+ {\varepsilon }^{{1}/{2}}{f}_{ij}\left( {\mathbf{q,p}} \right) {\upxi }_{k}^{a},\nonumber \\ \end{aligned}$$

(5)

where $i,j=1,2,\ldots ,n; k=1,2,\ldots ,m$; ${q}_{i}$ and ${p}_{i}$ are the generalized displacements and momenta, respectively; and $\mathbf{q}={{(}{{ q}}_{{1}},{q}_{{2}},\ldots ,{q}_{n}{)}}^{{{T}}}$ and $\mathbf{p}={{(}{p}_{{1}},{p}_{{2}},\ldots ,{p}_{n}{)}}^{{T}}$. The Hamiltonian ${\tilde{{H}}}^{{'}}={\tilde{{H}}}^{{'}}({\mathbf{q,p}})$ can be written in terms of the kinetic and potential energy terms in the form ${\tilde{{H}}}^{{'}}={T}(\mathbf{p})+{U}(\mathbf{q})$. The parameter $\varepsilon$ is usually small, so that the damping term $-\varepsilon {\tilde{{c}}}_{ij}^{{'}}\left( {\mathbf{q,p}} \right) \frac{{\partial }\tilde{{H}}^{{'}}}{{\partial }{p}_{j}}$ is weak. As described in Eq. (1), the switching random excitations ${\upxi }_{k}^{{(}u{)}}\left( {t} \right) {(}u\in {S})$ are independent Gaussian white noises with zero means and correlation function

$$\begin{aligned} {E}\left( {\upxi }_{k}^{{(}u{)}}\left( {t} \right) {\upxi }_{l}^{{(}u{)}}\left( {t}+\uptau \right) \right) =2{D}_{kl}^{{(}u{)}}{\updelta (\uptau )}. \end{aligned}$$

(6)

Equations (4) and (5) can be converted to the following Itô stochastic differential equations by adding the Wong–Zakai correction terms:

$$\begin{aligned} {\text {d}{q}}_{i}= & {} \frac{{\partial }{\tilde{{H}}}^{{'}}}{{\partial }{p}_{i}}\text {d}{t}, \end{aligned}$$

(7)

$$\begin{aligned} {\text {d}{p}}_{i}= & {} \left( -\frac{{\partial }{\tilde{{H}}}^{{'}}}{{\partial }{q}_{i}}-\varepsilon {\tilde{{c}}}_{ij}^{{'}}\left( {\mathbf{q,p}} \right) \frac{{\partial }\tilde{{H}}^{{'}}}{{\partial }{p}_{j}}-\varepsilon {{{D}}}_{kl}^{\left[ {s}\left( {t} \right) \right] }{\sigma }_{jl}^{\left[ {s}\left( {t} \right) \right] }\frac{{\partial }{\sigma }_{ik}^{\left[ {s}\left( {t} \right) \right] }}{{\partial }{p}_{j}} \right) \text {d}{t}\nonumber \\&+\,{{\varepsilon }}^{{1}/{2}} {\upsigma }_{ik}^{\left[ {s}\left( {t} \right) \right] }\left( {\mathbf{q,p}} \right) \text {d}{B}_{k}{(t),} \end{aligned}$$

(8)

where ${B}_{k}{(t)}$ are standard Wiener processes, and

$$\begin{aligned} {\upsigma }_{ik}^{\left[ {s}\left( {t} \right) \right] }\left( {{\mathbf {q}},{\mathbf {p}}} \right) \text {d}{B}_{k}{(t)}={f}_{ij}\left( {{\mathbf {q}}},{\mathbf {p}} \right) {\upxi }_{k}^{\left[ {s}\left( {t} \right) \right] }\text {d}{t}. \end{aligned}$$

(9)

The Wong–Zakai correction terms can be split into two parts such that

$$\begin{aligned} {\varepsilon }{D}_{kl}^{\left[ {s}\left( {t} \right) \right] }{\upsigma }_{jl}^{\left[ {s}\left( {t} \right) \right] }\frac{{\partial }{\upsigma }_{ik}^{\left[ {s}\left( {t} \right) \right] }}{{\partial }{p}_{j}}=\varepsilon {\tilde{{g}}}^{\left[ {s}\left( {t} \right) \right] }\left( {\mathbf{q}} \right) +\varepsilon {{\tilde{{d}}}}^{\left[ {s}\left( {t} \right) \right] }\left( {\mathbf{q,p}} \right) \frac{{\partial }{\tilde{{H}}}^{{'}}}{{\partial }{p}_{j}}.\nonumber \\ \end{aligned}$$

(10)

The conservative part ${\varepsilon }{\tilde{{g}}}^{\left[ {s}\left( {t} \right) \right] }\left( {\mathbf{q}} \right)$ alters the conservative forces, and the dissipative part ${\varepsilon }\tilde{{d}}^{\left[ {s}\left( {t} \right) \right] }\left( {\mathbf{q,p}} \right) \frac{{\partial }\tilde{{H}}^{{'}}}{{\partial }{p}_{j}}$ modifies the damping forces. Combining these two parts with $\frac{{\partial }{\tilde{{H}}}^{{'}}}{{\partial }{q}_{i}}$ and ${\varepsilon }{\tilde{{c}}}_{ij}^{{'}}\frac{{\partial }{\tilde{{H}}}^{{'}}}{{\partial }{p}_{j}}$, Eqs. (7) and (8), respectively, become

$$\begin{aligned} {\text {d}{q}}_{{i}}= & {} \frac{{\partial }{\tilde{{ H}}}^{{[s(t)]}}}{{\partial }{p}_{i}}\text {d}{t,} \end{aligned}$$

(11)

$$\begin{aligned} {\text {d}{p}}_{{i}}= & {} \left( -\frac{{\partial }{\tilde{{H}}}^{{[s(t)]}}}{{\partial }{q}_{i}}-\varepsilon {\tilde{{c}}}_{ij}^{{[s(t)]}}\left( {\mathbf{q,p}} \right) \frac{{\partial }{\tilde{{H}}}^{{[s(t)]}}}{{\partial }{p}_{j}} \right) \text {d}{t}\nonumber \\&+\,{\varepsilon }^{{1}/{2}}{\upsigma }_{ik}^{\left[ {s}\left( {t} \right) \right] }\left( {\mathbf{q,p}} \right) \text {d}{B}_{k}{(t),} \end{aligned}$$

(12)

where ${\tilde{{H}}}^{{[s(t)]}}$ and ${\tilde{{ c}}}_{ij}^{{[s(t)]}}$ are the switched Hamiltonian and the coefficients of damping as modified by the Wong–Zakai correction. These terms are given by

$$\begin{aligned} {\tilde{{H}}}^{{[s(t)]}}= & {} {T}(\mathbf{p})+{U}(\mathbf{q})+\varepsilon {\tilde{\mathbf{U}}}^{\left[ {s}\left( {t} \right) \right] }{(\mathbf{q}),} \end{aligned}$$

(13)

$$\begin{aligned} {\tilde{{c}}}_{ij}^{{[s(t)]}}= & {} {{\tilde{{c}}}}_{ij}^{{'}}\left( {\mathbf{q,p}} \right) +{\tilde{{d}}}^{\left[ {s}\left( {t} \right) \right] }\left( {\mathbf{q,p}} \right) . \end{aligned}$$

(14)

The system described by Eqs. (11) and (12) is a nonlinear stochastic hybrid system possessing Markov jumps. Reliability of the original system can now be studied in the framework of Markov jump hybrid systems.

Under the assumption of ergodicity of s(t), limiting averaging principle can be applied [18, 19]. The Markov jump system (1) is then reduced to a probability-weighted one without Markov jump parameter and, as ${\varepsilon \rightarrow 0}$,

$$\begin{aligned} {\text {d}{q}}_{i}= & {} \frac{{\partial {H}(\mathbf{q,p};{\varvec{\mu }} )}}{{\partial }{p}_{i}}\text {d}{t,} \end{aligned}$$

(15)

$$\begin{aligned} {\text {d}{p}}_{i}= & {} \left( -\frac{\partial {H}({\mathbf{q,p}};{\varvec{\mu }} )}{{\partial }{q}_{i}}-\varepsilon {{\bar{{c}}}}_{ij}\left( {\mathbf{q,p}};{\varvec{\mu }} \right) \frac{\partial {H}({\mathbf{q,p}};{\varvec{\mu }} )}{{\partial }{p}_{j}} \right) \text {d}{t}\nonumber \\&+\,{{\varepsilon }}^{{1}/{2}} {\bar{\sigma }}_{ik}\left( {\mathbf{q,p}};{\varvec{\mu }}\right) \text {d}{B}_{k}{(t),} \end{aligned}$$

(16)

where ${\varvec{\mu }}=\left[ {\mu }^{{(1)}},{\mu }^{{(2)}},\ldots , {\mu }^{{(}l{)}} \right] ^{{T}},{\mu }^{{(}u{)}}$ is the stationary probability distribution of s(t) for ${s(t)}=u$ satisfying [2]

$$\begin{aligned} \sum \nolimits _{u=1}^l {\mu }^{{(}u{)}} {\lambda }_{ui}=0,\qquad \qquad \qquad i\in {S}, \end{aligned}$$

(17)

and the transition rates ${\lambda }_{ui}$ are given in Eq. (3). Using the normalization condition $\sum \nolimits _{u=1}^l {\mu }^{{(}u)} =1$, the stationary probability distribution ${\mu }^{{(}u{)}}$can be calculated. In the above equations, ${H}({\mathbf{q,p}};{\varvec{\mu }})$, ${{\bar{{c}}}}_{ij}\left( {\mathbf{q,p}};{\varvec{\mu }} \right)$ and ${\bar{\upsigma }}_{ik}\left( {\mathbf{q,p}};{\varvec{\mu }}\right)$ are given by

$$\begin{aligned} {H}({\mathbf{q,p}};{\varvec{\mu }})= & {} \sum \nolimits _{u\in {S}} {\left[ {\tilde{{H}}}^{\left( u \right) }({\mathbf{q,p}})\cdot {\mu }^{{(}u{)}} \right] ,} \nonumber \\ {\bar{{c}}}_{ij}\left( {\mathbf{q,p}};{\varvec{\mu }} \right)= & {} \sum \nolimits _{u\in {S}} {\left[ {\tilde{{c}}}_{ij}^{{(}u{)}}({\mathbf{q,p}})\cdot {\mu }^{{(}u{)}} \right] ,} \nonumber \\ {{\bar{\sigma }}}_{ik}\left( {\mathbf{q,p}};{\varvec{\mu }} \right)= & {} \sum \nolimits _{u\in {S}} {\left[ {\upsigma }_{ij}^{{(}u{)}}({\mathbf{q,p}})\cdot {\mu }^{{(}u{)}} \right] .} \end{aligned}$$

(18)

The stochastic differential ${H}={H}({\mathbf{q,p}};{\varvec{\mu }} )$ can be derived from Eqs. (15) and (16) using the Itô differential rule [20]

$$\begin{aligned} \text {d}{H}= & {} \varepsilon \left( -{\bar{{c}}}_{ij}\frac{{\partial {H}}}{{\partial }{p}_{i}}\frac{{\partial {H}}}{{\partial }{p}_{j}}{+}\frac{{1}}{{2}}{\bar{\upsigma }}_{ik}{{\bar{\upsigma }}}_{jk} \frac{{\partial }^{{2}}{H}}{{\partial }{p}_{i}{\partial }{p}_{j}} \right) \text {d}{t}\nonumber \\&+\,{\varepsilon }^{{1}/{2}}{\bar{\sigma }}_{ik} \frac{\partial {H}}{{\partial }{p}_{i}}\text {d}{B}_{k} \left( {t} \right) . \end{aligned}$$

(19)

Since ${\varepsilon }$ is a small parameter, the above relation indicates that H is a slowing varying process, while the generalized displacements ${q}_{{1}},{q}_{{2}},\ldots {{,q}}_{n}$ and generalized momenta ${p}_{{1}},{p}_{{2}},\ldots ,{p}_{n}$ are usually rapidly varying processes with respect to time. By a theorem of Khasminskii [21], H converges to a one-dimensional diffusion process E as $\varepsilon \rightarrow 0$. The Itô equation for this diffusion process is obtained by time averaging of Eq. (19). The effect of stochastic averaging is to average out the rapidly varying processes so as to yield an equation for the slowly varying process H, which is essential for describing the long-term behavior of the system.

Time averaging of Eq. (19) can be conducted by traditional methods [22] because the original Markov jump system (1) has been reduced to a probability-weighted one without the Markov jump parameters by applying the limiting averaging principle. Making use of Eq. (15), time averaging can be replaced by space averaging with respect to ${p}_{{1}}$ (${p}_{i}$ may be used instead). Upon stochastic averaging, the limiting process E satisfies of the equation

$$\begin{aligned} \text {d}{E}=\bar{{m}}\left( {E};{\varvec{\mu }} \right) \text {d}{t}+{\bar{\sigma }}\left( {E};{\varvec{\mu }} \right) \text {d}{B}\left( {t} \right) , \end{aligned}$$

(20)

where ${B}\left( {t} \right)$ is unit Wiener process. The drift coefficient $\bar{{m}}\left( {E};{\varvec{\mu }} \right)$ and diffusion coefficient ${\bar{\upsigma }}\left( {E};{\varvec{\mu }} \right)$ are given by

$$\begin{aligned}&{\bar{{m}}}\left( {E};{\varvec{\mu }} \right) \nonumber \\&\quad = \frac{{1}}{{T}\left( {E};{\varvec{\mu }} \right) }\nonumber \\&\quad \quad \int \nolimits _{\omega } \left( -\varepsilon {{\bar{{c}}}}_{ij}\frac{\partial {H}}{{\partial }{p}_{i}}\frac{\partial {H}}{{\partial }\mathrm {p}_{j}}+\frac{{1}}{{2}}{\varepsilon }{\bar{\sigma }}_{ik} {\bar{\sigma }}_{jk}\frac{{\partial }^{{2}}{H}}{{\partial }{p}_{i}{\partial }{p}_{j}} \right) \left( \frac{\partial {H}}{{\partial }{p}_{{1}}} \right) ^{{-1}}d{\mathbf{z}},\nonumber \\ \end{aligned}$$

(21)

$$\begin{aligned}&\left\{ {\bar{\sigma }}\left( {E};{\varvec{\mu }} \right) \right\} ^{{2}}=\frac{{1}}{{T}\left( {E};{\varvec{\mu }} \right) }\int \nolimits _{\omega } {{\varepsilon }{\bar{\sigma }}_{ik}} {\bar{\sigma }}_{jk}\frac{\partial {H}}{{\partial } {p}_{i}}\frac{\partial {H}}{{\partial } {p}_{j}}\left( \frac{\partial {H}}{{\partial } {p}_{{1}}} \right) ^{{-1}}d{\mathbf{z}},\nonumber \\ \end{aligned}$$

(22)

where ${\mathbf{z}}=\left( {q}_{{1}},{q}_{{2}},\ldots ,{q}_{n}, {p}_{{2}},\ldots ,{p}_{n} \right)$ is a vector of order 2n–1, the region of integration is $\omega =\left\{ \mathbf{z}:{H}\left( {q}_{{1}},{q}_{{2}},\ldots ,{q}_{n},0,{p}_{{2}},\ldots ,{p}_{n} \right) <{E} \right\}$ and the parameter

$$\begin{aligned} {T}\left( {E};{\varvec{\mu }} \right) =\int \nolimits _{\omega } {\left( \frac{\partial {H}}{{\partial }{p}_{{1}}} \right) ^{{-1}}d{\mathbf{z}}}. \end{aligned}$$

(23)

It is intuitive to replace E by H in Eq. (20) even though E is only an approximation and is not equal to H. Equation (20) can be extended so that

$$\begin{aligned} \text {d}{H}={\bar{{m}}}\left( {H};{\varvec{\mu }} \right) \text {d}{t}+{\bar{\sigma }}\left( {H};{\varvec{\mu }}\right) \text {d}{B}\left( {t} \right) , \end{aligned}$$

(24)

where the drift coefficient ${\bar{{m}}}\left( {H};{\varvec{\mu }} \right)$ and diffusion coefficient ${\bar{\sigma }}\left( {H};{\varvec{\mu }} \right)$ are given by replacing E with H in Eqs. (21) and (22). The MJS as governed by Eqs. (4) and (5) possesses an energy envelope given approximately by the solution H of Eq. (24).

3 Reliability analysis

For most engineering structures, H represents the total energy. There often exists a critical value ${H}_{{c}}$ that the structure or some components of the structure will fail if the total energy of the structure exceeds that critical value. Let ${R}={R}\left( {t}\left| {H}_{{0}} \right. \right)$ be the reliability function, which is defined as the probability of the concerned system being in the safe region $\omega _{{H}}=\left[ 0, \right. \left. {H}_{{c}} \right)$ given the initial Hamiltonian ${H}_{{0}}\in \omega _{{H}}$. The conditional reliability function ${R}\left( {t}\left| {H}_{{0}} \right. \right)$ can be obtained by solving the following BK equation

$$\begin{aligned} \frac{\partial {R}}{\partial {t}}={\bar{{m}}} \left( {H}_{{0}};{\varvec{\mu }} \right) \frac{\partial {R}}{{\partial }{H}_{{0}}}{+}\frac{{1}}{{2}}{\bar{\upsigma }}^{{2}}\left( {H}_{{0}};{\varvec{\mu }}\right) \frac{{\partial }^{{2}}{R}}{{\partial }{H}_{{0}}^{{2}}}, \end{aligned}$$

(25)

together with the initial condition

$$\begin{aligned} {R}\left( {0}\vert {H}_{{0}}\right) =1,\qquad \qquad \qquad {H}_{{0}}\in \omega _{{H}}, \end{aligned}$$

(26)

and boundary conditions

$$\begin{aligned} \begin{array}{ll} {R}\left( {t}\vert {H}_{{c}}\right) =0,&{} {t}\ge 0,\\ {R}\left( {t}\vert {0}\right) ={finite}, &{} {t}\ge 0.\\ \end{array} \end{aligned}$$

(27)

In Eq. (25), ${\bar{{m}}}\left( {H}_{{0}};{\varvec{\mu }}\right)$ and ${\bar{\sigma }}\left( {H}_{{0}};{\varvec{\mu }}\right)$ are the same as in Eqs. (21) and (22) with H(t) replaced by the initial state ${H}\left( {0} \right) ={H}_{{0}}$. Let the time of first passage be T. Then the probability distribution function ${F}\left( {t}\vert {H}_{{0}}\right)$ and the conditional probability density function ${p}\left( {t}\vert {H}_{{0}}\right)$ of the first passage time can be obtained as follows

$$\begin{aligned} {F}\left( {t}\vert {H}_{{0}}\right)= & {} {P}\left\{ {{T}<{t}}\vert {{H}\left( {0} \right) ={H}_{{0}}\in \omega }\right\} =1-{R}\left( {t}\vert {H}_{{0}}\right) ,\nonumber \\ \end{aligned}$$

(28)

$$\begin{aligned} {p}\left( {t}\vert {H}_{{0}}\right)= & {} \frac{\partial {F}\left( {t}\vert {H}_{{0}}\right) }{\partial {t}}=-\frac{\partial {R}\left( {t}\vert {H}_{{0}}\right) }{\partial {t}}. \end{aligned}$$

(29)

It can be seen that boundary conditions (27) are only “qualitative,” which is of little use for obtaining quantitative solution. However, when ${\bar{{m}}}\left( {H}_{{0}};{\varvec{\mu }}\right)$ and ${\bar{\sigma }}\left( {H}_{{0}};{\varvec{\mu }}\right)$ satisfy certain conditions, the qualitative boundary conditions (27) can be replaced by a quantitative one [9, 23]. If $\mathop {\hbox {lim}}\limits _{{H}_0 \rightarrow 0} {{\bar{\upsigma }}\left( {H}_{{0}};{\varvec{\mu }}\right) =0}$ and $\mathop {\hbox {lim}}\limits _{{H}_0 \rightarrow 0}{{\bar{\mathrm{m}}}\left( {H}_{{0}};{\varvec{\mu }}\right) \ne 0}$, boundary conditions (27) can be replaced by

$$\begin{aligned} \frac{\partial {R}}{\partial {t}}={\bar{{m}}}\left( {H}_{{0}};{\varvec{\mu }} \right) \frac{\partial {R}}{{\partial }{H}_{{0}}},\qquad \qquad {H}_{{0}}=0. \end{aligned}$$

(30)

If $\mathop {\hbox {lim}}\limits _{{H}_0 \rightarrow 0}{{\bar{\upsigma }}}\left( {H}_{{0}};{\varvec{\mu }} \right) =0$ and $\mathop {\hbox {lim}}\limits _{{H}_0 \rightarrow 0}{\bar{{m}}}\left( {H}_{{0}};{\varvec{\mu }}\right) =0$, boundary conditions (27) can be replaced by

$$\begin{aligned} \frac{\partial {R}}{\partial {t}}=0,\qquad \qquad {H}_{{0}}=0. \end{aligned}$$

(31)

4 Examples

To demonstrate the validity and perhaps accuracy of the method presented in this paper, two examples will be presented. The switching random excitations are described by Eq. (1), where s(t) is assumed to be a two-form Markov jump process. That means s(t) takes values from ${S}=\left\{ {1,2} \right\}$. The transition rate matrix L of s(t) can be prescribed by

$$\begin{aligned} {L}=\left[ {\begin{array}{ll} {\lambda }_{{11}} &{} {\lambda }_{{12}}\\ {\lambda }_{{21}} &{} {\lambda }_{{22}}\\ \end{array} } \right] =\left[ {\begin{array}{ll} -\,v_{{1}} &{} v_{{1}}\\ v_{{2}} &{} -\,v_{{2}}\\ \end{array} } \right] . \end{aligned}$$

(32)

The stationary probabilities ${\mu }^{{(1)}}$ and ${\mu }^{{(2)}}$ are calculated by applying Eq. (17) and the normalization condition $\sum \nolimits _{u=1}^l {\mu }^{{(}u{)}} =1$ to yield

$$\begin{aligned} {\mu }^{{(1)}}=\frac{v_{{2}}}{v_{{1}}+v_{{2}}},\qquad \qquad {\mu }^{{(2)}}=1-{\mu }^{\left( {1} \right) }. \end{aligned}$$

(33)

Three special cases are considered with

$$\begin{aligned} {L}_{{1}}=\left[ {\begin{array}{cc} -2 &{} {2}\\ {2} &{} -2\\ \end{array} } \right] , \quad {L}_{{2}}=\left[ {\begin{array}{cc} {-1} &{} {1}\\ {2} &{} {-2}\\ \end{array} } \right] , \quad {L}_{{3}}=\left[ {\begin{array}{cc} {-2} &{} {2}\\ {1} &{} {-1}\\ \end{array} } \right] . \end{aligned}$$

(34)

The system jumps between the two forms with equal probabilities if ${L}={L}_{{1}}$. Observe that the system is more likely to take the form $s(t) = 1$ if ${L}={L}_{{2}}$. Finally, the system is more likely to take the form $\hbox {s(t)} = 2$ if ${L}={L}_{{3}}$.

Figure 1 shows the sample time history of noise and the jumps with ${L}={L}_{{1}}$ to make them understood easily.

Fig. 1

a Sample time history of random excitation with ${L}={L}_{{1}}$; b sample time history of the jumps with ${L}={L}_{{1}}$

Fig. 2

Reliability function of system (35). a Analytical results; b Monte Carlo simulation

Examples 1

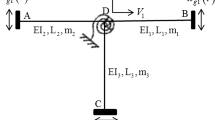
Consider the following nonlinear quasi-non-integrable Hamilton system with switching random excitations:

$$\begin{aligned}&{{\ddot{{x}}}}_{{1}}+\left( {\beta }_{{1}}{-}{\upalpha }_{{1}}{x}_{{1}}^{{2}} \right) {\dot{{x}}}_{{1}}+{\omega }_{{1}}^{{2}}{x}_{{1}}+a{\omega }_{{1}}^{{2}}\left( {\omega }_{{1}}^{{2}}{x}_{{1}}^{{2}}+{\omega }_{{2}}^{{2}}{x}_{{2}}^{{2}} \right) {x}_{{1}}\nonumber \\&\quad ={c}_{{1}}{\upxi }_{{1}}^{a}\left( {t} \right) +{c}_{{3}}{x}_{{1}}{\upxi }_{{3}}^{a}\left( {t} \right) +{c}_{{5}}{\dot{{x}}}_{{1}}{\upxi }_{{5}}^{a}\left( {t} \right) ,\nonumber \\&{{\ddot{{x}}}}_{{2}}+\left( {\beta }_{{2}}{-}{\upalpha }_{{2}}{x}_{{2}}^{{2}} \right) {\dot{{x}}}_{{2}}+{\omega }_{{2}}^{{2}}{x}_{{2}}+a{\omega }_{{2}}^{{2}}\left( {\omega }_{{1}}^{{2}}{x}_{{1}}^{{2}}+{\omega }_{{2}}^{{2}}{x}_{{2}}^{{2}} \right) {x}_{{2}}\nonumber \\&\quad ={{c}}_{{2}}{\upxi }_{{2}}^{a}\left( {t} \right) +{c}_{{4}}{x}_{{2}}{\upxi }_{{4}}^{a}\left( {t} \right) +{c}_{{6}}{\dot{{x}}}_{{2}}{\upxi }_{{6}}^{a}\left( {t} \right) , \end{aligned}$$

(35)

where ${\beta }_{i},{\upalpha }_{i}{}\left( i=1,2 \right) ,{c}_{k}{}\left( k=1,2,\ldots ,6 \right)$ and a are constants; ${\omega }_{i} \left( i=1,2 \right)$ are the natural frequencies of the above systems; ${\upxi }_{k}^{a}\left( {t} \right) \left( k=1,2,\ldots ,6 \right)$ are switching random excitations described by Eq. (1); ${\upxi }_{k}^{\left( u \right) }\left( {t} \right) \left( u\in {S},k=1,2,\ldots ,6 \right)$ denote the uth grade random excitations, which are independent Gaussian white noise with zero mean and intensity ${{2D}}_{k}^{\left( u \right) }\left( k=1,2,\ldots ,6 \right)$.

Let ${q}_{{1}}={x}_{{1}},{p}_{{1}}={\dot{\mathrm{x}}}_{{1}}, {q}_{{2}}={x}_{{2}},{p}_{{2}}={\dot{\mathrm{x}}}_{{2}},$ Eq. (35) can be rewritten in the form of Eqs. (4) and (5). The Hamiltonian associated with system (35) is

$$\begin{aligned} {\tilde{{H}}}^{{'}}=\frac{{1}}{{2}}{p}_{{1}}^{{2}}+\frac{{1}}{{2}}{p}_{{2}}^{{2}}+{U}\left( {{\mathbf {q}}} \right) , \end{aligned}$$

(36)

where

$$\begin{aligned} {U}\left( {{\mathbf {q}}} \right) =\frac{{1}}{{2}}{\omega }_{{1}}^{{2}}{q}_{{1}}^{{2}} +\frac{{1}}{{2}}{\omega }_{{2}}^{{2}}{q}_{{2}}^{{2}} +\frac{{1}}{{4}}a{{(}{\omega }_{{1}}^{{2}}{q}_{{1}}^{{2}} +{\omega }_{{2}}^{{2}}{q}_{{2}}^{{2}}{)}}^{{2}}.\nonumber \\ \end{aligned}$$

(37)

The excitation terms for Eq. (35) are only associated with displacements and velocities, respectively. As a consequence, the Wong–Zakai correction terms are only related to the velocities, namely ${H}={\tilde{{H}}}^{{'}}$. Using the stochastic averaging method for quasi-non-integrable Hamiltonian system under switching random excitations described previously, one obtains the averaged Itô stochastic differential equation for the Hamiltonian

$$\begin{aligned} \text {d}{H}={\bar{{m}}}\left( {H};{\varvec{\mu }} \right) \text {d}{t}+{\bar{\upsigma }}({H};{\varvec{\mu }})\text {d}{B(t)}. \end{aligned}$$

(38)

The drift and diffusion coefficients are

$$\begin{aligned} {\bar{{m}}}\left( {H};{\varvec{\mu }}\right)= & {} \frac{{1}}{{T}\left( {H};{\varvec{\mu }} \right) }\int \nolimits _{\omega } \left( \left( -{\beta }_{{1}}+{{\upalpha }}_{{1}}{q}_{{1}}^{{2}} \right) \right. {p}_{{1}}^{{2}}\nonumber \\&+\,\left( -{\beta }_{{2}}+{\upalpha }_{{2}}{q}_{{2}}^{{2}} \right) {p}_{{2}}^{{2}}+{c}_{{1}}^{{2}}{D}_{{1}}+{c}_{{2}}^{{2}}{D}_{{2}}\nonumber \\&+\,{c}_{{3}}^{{2}}{D}_{{3}}{q}_{{1}}^{{2}}+{c}_{{4}}^{{2}}{D}_{{4}}{q}_{{2}}^{{2}}+{2}{c}_{{5}}^{{2}}{{D}_{{5}}{p}}_{{1}}^{{2}}\nonumber \\&{+2}{c}_{{6}}^{{2}}{D}_{{6}}\left. {p}_{{2}}^{{2}} \right) \left( \frac{\partial {H}}{{\partial }{p}_{{1}}} \right) ^{{-1}}d{\mathbf{z}}, \end{aligned}$$

(39)

$$\begin{aligned} {{\bar{\sigma }}}^{{2}}\left( {H};{\varvec{\mu }} \right)= & {} \frac{{1}}{{T}\left( {H};{\varvec{\mu }}\right) }\int \nolimits _\omega {\left( {2c} \right. _{{1}}^{{2}}{D}_{{1}}{p}_{{1}}^{{2}}+{2}{c}_{{2}}^{{2}}{D}_{{2}}} {p}_{{2}}^{{2}}\nonumber \\&+\,{{2c}}_{{3}}^{{2}}{D}_{{3}}{q}_{{1}}^{{2}}{p}_{{1}}^{{2}}+{{2c}}_{{4}}^{{2}}{D}_{{4}}{q}_{{2}}^{{2}}{p}_{{2}}^{{2}}\nonumber \\&+\,{2}{c}_{{5}}^{{2}}{{D}_{{5}}{p}}_{{1}}^{{4}}+{2}{c}_{{6}}^{{2}}{D}_{{6}}\left. {p}_{{2}}^{{4}} \right) \left( \frac{\partial {H}}{{\partial } {p}_{{1}}} \right) ^{{-1}}\text {d}{} \mathbf{z},\nonumber \\ \end{aligned}$$

(40)

where ${\mathbf{z}}{=}\left( {q}_{{1}},{q}_{{2}},{p}_{{2}} \right)$, $\omega {=}\left\{ {\mathbf{z}}:{{H}}\left( {q}_{{1}},{q}_{{2}},{{0,p}}_{{2}} \right) {\le } {H} \right\}$,

$$\begin{aligned} {T}\left( {H};{\varvec{\mu }}\right)= & {} \int \nolimits _{\omega } {\left( \frac{\partial {H}}{{\partial }{p}_{{1}}} \right) ^{{-1}}d{\mathbf{z}},} \end{aligned}$$

(41)

$$\begin{aligned} {D}_{i}= & {} \sum \nolimits _{u\in {S}} {D}_{i}^{{(}u{)}} {\mu }^{{(}u{)}}, \qquad \qquad i=1,2,\ldots ,6.\nonumber \\ \end{aligned}$$

(42)

Using the transformations ${p}_{{1}}=\sqrt{{2}\left( \text {H-U} \right) } {\text {cos}}\upphi$, ${p}_{{2}}=\sqrt{{2}\left( \text {H-U} \right) } \text {sin}\,\upphi$ and ${q}_{{1}}=\frac{r}{{\omega }_{{1}}}\text {cos }\theta ,{q}_{{2}}=\frac{r}{{\omega }_{{2}}}\text {sin }\theta$, the integrals in Eqs. (39–41) can be completed as follows:

$$\begin{aligned}&{\bar{{m}}}\left( {H};{\varvec{\mu }}\right) \nonumber \\&\quad ={c}_{{1}}^{{2}}{D}_{{1}}+{c}_{{2}}^{{2}}{D}_{{2}}+\left( -{\beta }_{{1}}-{\beta }_{{2}}+{2}{c}_{{5}}^{{2}}{D}_{{5}}{+2}{c}_{{6}}^{{2}}{D}_{{6}} \right) \nonumber \\&\quad \quad \times \,\left( {H}-\frac{{1}}{{4}}{R}^{{2}}{-}\frac{a}{{12}}{R}^{{4}} \right) \nonumber \\&\quad \quad +\,\left( \frac{{\upalpha }_{{1}}}{{4}{\omega }_{{1}}^{{2}}}+\frac{{\upalpha }_{{2}}}{{4}{\omega }_{{2}}^{{2}}} \right) \left( {H}{R}^{{2}}{-}\frac{{1}}{{3}}{R}^{{4}}{-}\frac{{1}}{{8}}{R}^{{6}} \right) \nonumber \\&\qquad +\,\frac{{1}}{{4}}\left( \frac{{c}_{{3}}^{{2}}{D}_{{3}}}{{\omega }_{{1}}^{{2}}}+\frac{{c}_{{4}}^{{2}}{D}_{{4}}}{{\omega }_{{2}}^{{2}}} \right) {R}^{{2}}, \end{aligned}$$

(43)

$$\begin{aligned}&{\bar{\sigma }}^{{2}}\left( {H};{\varvec{\mu }} \right) \nonumber \\&\quad =2\left( {c}_{{1}}^{{2}}{D}_{{1}}+{c}_{{2}}^{{2}}{D}_{{2}} \right) \left( {H}-\frac{{1}}{{4}}{R}^{{2}}-\frac{a}{{12}}{R}^{{4}} \right) \nonumber \\&\qquad +\,\frac{{1}}{{2}}\left( \frac{{c}_{{3}}^{{2}}{D}_{{3}}}{{\omega }_{{1}}^{{2}}}+\frac{{c}_{{4}}^{{2}}{D}_{{4}}}{{\omega }_{{2}}^{{2}}} \right) \left( {H}{R}^{{2}}-\frac{{1}}{{3}}{R}^{{4}}-\frac{{1}}{{8}}{R}^{{6}} \right) \nonumber \\&\qquad {+3}\left( {c}_{{5}}^{{2}}{D}_{{5}}+{c}_{{6}}^{{2}}{D}_{{6}} \right) \left( {H}^{{2}}{-H}\left( \frac{{1}}{{2}}{R}^{{2}}+\frac{a}{{6}}{R}^{{4}} \right) \nonumber \right. \\&\qquad \left. +\ ,\frac{{1}}{{12}}{R}^{{4}}+\frac{{1}}{{16}}{R}^{{6}}+\frac{a^{{2}}}{{80}}{R}^{{8}} \right) , \end{aligned}$$

(44)

$$\begin{aligned}&{T}\left( {H};{\varvec{\mu }}\right) =\frac{{2}{\uppi }^{{2}}}{{\omega }_{{1}}{\omega }_{{2}}}{R}^{{2}}, \end{aligned}$$

(45)

where R is the positive root of the equation

$$\begin{aligned} \frac{a}{{4}}{R}^{{4}}+\frac{{1}}{{2}}{R}^{{2}}={H}. \end{aligned}$$

(46)

The BK equation for system (35) has the same form as Eq. (25). The associated quantitative boundary condition is described by Eq. (27). Set the critical energy of system (35) by ${H}_{{{c}}}=1$. When total energy ${H}\left( {t} \right)$ is equal to or larger than ${H}_{{{c}}}$, system (35) is damaged. Then, the BK equation will be solved by using finite difference method [9], where the step length ${\Delta }{H}_{{0}}=1.0\times {{10}}^{-2}$ and $\Delta {t}=5\times {{10}}^{-3}$. To validate the accuracy of the analytical results, direct simulation from Eq. (35) are also obtained by Runge–Kutta method, where step length of time is set as $\Delta {t}=5\times {{10}}^{{-3}}$, and ${5\times }{{10}}^{{6}}$ samples are used for statistics.

Some numerical results are shown in Figs. 2, 3, 4, 5, 6 for the chosen parameters: ${\omega }_{{1}}=1$, ${\omega }_{{2}}=2$, ${\beta }_{{1}}=0.01$, ${\beta }_{{2}}=0.01$, ${\alpha }_{{1}}=0.01$, ${\alpha }_{{2}}=0.01$, $a=1$, ${c}_{{1}}=0.1$, ${c}_{{2}}=0.1$, ${c}_{{3}}=0.1$, ${c}_{{4}}=0.1$, ${c}_{{5}}=0.1$, ${c}_{{6}}=0.1$, ${D}_{{1}}^{\left( {1} \right) }=2$, ${D}_{{2}}^{\left( {1} \right) }=2$, ${D}_{{3}}^{\left( {1} \right) }=2$, ${D}_{{4}}^{\left( {1} \right) }=2$, ${D}_{{5}}^{\left( {1} \right) }=2$, ${D}_{{6}}^{\left( {1} \right) }=2$, ${D}_{{1}}^{\left( {2} \right) }=1$, ${D}_{{2}}^{\left( {2} \right) }=1$, ${D}_{{3}}^{\left( {2} \right) }=1$, ${D}_{{4}}^{\left( {2} \right) }=1$, ${D}_{{5}}^{\left( {2} \right) }=1$, ${D}_{{6}}^{\left( {2} \right) }=1$ and ${L}={L}_{{1}}$. Figure 2 shows the reliability function ${R}({t}| {H}_{{0}})$ of system (35) as a function of the initial energy ${H}_{{0}}$ and time t. Figure 3 displays ${R}({t}|{H}_{{0}})$ of system (35) as a function of t for the different initial energy ${H}_{{0}}$. It can be seen that the reliability function is a monotonic decreasing function of the initial energy and time. In addition, the reliability function diminishes more sharply with larger initial energy value. This is because that, for large ${H}_{{0}}$, the initial energy value is closer to the critical energy ${H}_{{{c}}}$ and the system’s energy is easier to cross the critical value. That is to say, the system will have a relatively small reliability. Monte Carlo simulation of Eq. (35) is also conducted, and the results are provided for comparison. The results from direct simulation of Eq. (35) are shown in Fig. 2b and as colored dots in Figs. (3) and (4). Note that the two results are in excellent agreement, demonstrating the validity and accuracy of the proposed procedure.

The probability density function (PDF) of first passage time of system (35) is plotted in Fig. 4. As ${H}_{{0}}$ decreases, the peak of the PDF curve drifts to the right, which indicates that a small decrease in the initial energy can dramatically increase the mean value of first passage time. Figure 4 shows that as ${H}_{{0}}$ increases the PDF curve gets thinner. This is not surprise; for larger ${H}_{{0}}$, the system is easier to damage, which indicates that the PDF of first passage time only has significant value in a relatively small time interval.

Fig. 3

Reliability function of system (35) as a function of t. “Dashed” curves from analytical results; “dots” from Monte Carlo simulation

Fig. 4

Probability density function of first passage time of system (35). “Dashed” curves from analytical results; “dots” from Monte Carlo simulation

In Fig. 5, the reliability functions of system (35) are shown when the transition rates are defined by the three transition matrices in Eq. (34) and when the excitation is assumed to be fixed at ${s}\left( {t} \right) =1$ and ${s(t)} = 2$. When the system operates in the form ${s}\left( {t} \right) =2$, it has a smaller intensity of random excitation than when it operates in the form ${s(t)} = 1$. Figure 5 shows that the switching of the random excitation has significant influence on the reliability of system (35). Figure 5 shows that the reliability function has the largest value when ${s}\left( {t} \right) =2$, and that it decreases as the system cycles through ${L}={L}_{{3}}$, ${L}={L}_{{1}}$, ${L}={L}_{{2}}$ and ${s(t)} = 1$. This is because that when the system cycles from ${s}\left( {t} \right) =2$ through ${L}={L}_{{3}}$, ${L}={L}_{{1}}$, ${L}={L}_{{2}}$ to ${s(t)}= 1$, the probability of the switch random excitation staying in the larger intensity form ${s(t)}=1$ is increasing.

Fig. 5

Reliability function of system (35) with ${L}={L}_{{3}}$, ${L}={L}_{{1}}$, ${L}={L}_{{2}}$ in Eq. (34) and when the system is fixed at ${s(t)}=1$ and ${s(t)}=2$. “Dashed” curves from analytical results; “dots” from Monte Carlo simulation

Fig. 6

When ${H}_{{0}}=0.1,$ time histories of the total energy of system (35) for different initial conditions. a${x}_{{10}}=0,{x}_{{20}}=0,{\dot{\mathrm{x}}}_{{10}}=0,{\dot{{x}}}_{{20}}=\sqrt{{2}{H}_{{0}}} {;}$b${x}_{{10}}=0,{x}_{{20}}=0,{\dot{\mathrm{x}}}_{{10}}=-\sqrt{{2}{H}_{{0}}},{\dot{{x}}}_{{20}}=0;$c${x}_{{10}}=0,{x}_{{20}}=0,{\dot{\mathrm{x}}}_{{10}}=0,{\dot{{x}}}_{{20}}=-\sqrt{{2}{H}_{{0}}} {;}$d${x}_{{10}}=0,{x}_{{20}}=0,{\dot{\mathrm{x}}}_{{10}}=\sqrt{{2}{H}_{{0}}},{\dot{{x}}}_{{20}}=0$

Figure 6 displays sample time histories of the total energy of system (35) for different initial conditions. The blue line represents the curve of the total energy, the green line represents the critical energy, and the red line shows the time when the total energy of system (35) crosses the critical energy for the first time. The first passage of the total energy of system (35) out of the safety region can therefore be visualized.

Examples 2

As a second example, a simplified nonlinear vehicle suspension system subjected to switching random road roughness is considered. The nonlinear stochastic motion equations of this vehicle suspension system can be written in the following dimensionless form:

$$\begin{aligned}&{\ddot{{x}}}_{{1}}+{c}\left( {\dot{{x}}}_{{1}}-{\dot{{x}}}_{{2}} \right) {+}{{\omega }}_{{1}}^{{2}}\left( {x}_{{1}}-{x}_{{2}} \right) +\alpha \left( {x}_{{1}}-{x}_{{2}} \right) ^{{3}}=0,\nonumber \\&{\ddot{{x}}}_{{2}}+{c}\left( {\dot{{x}}}_{{2}}-{\dot{{x}}}_{{1}} \right) {+}{\omega }_{{1}}^{{2}}\left( {x}_{{2}}-{x}_{{1}} \right) +\alpha \left( {x}_{{2}}-{x}_{{1}} \right) ^{{3}}\nonumber \\&\quad \quad {+}{\omega }_{{2}}^{{2}}{x}_{{2}}={{\upxi }}^{a}\left( {t} \right) , \end{aligned}$$

(47)

where ${x}_{1}$ and ${x}_{2}$ denote the non-dimensional displacements of vehicle body and wheel, respectively; c is the coefficient of the damping between the body and the wheel; ${\alpha }$ is the coefficient of the nonlinear stiffness; ${\omega }_{i}\left( i=1,2 \right) ,{c}$ and ${\alpha }$ are constants; and ${\upxi }^{a}\left( {t} \right)$ is the switching random excitation representing the road roughness. For simplicity, only two irregularity grades are considered here: ${\upxi }^{{(1)}}\left( {t} \right)$ for high-intensity irregularity and ${\upxi }^{{(2)}}\left( {t} \right)$ for low-intensity irregularity. Let ${q}_{{1}}={x}_{{1}},{p}_{{1}}={\dot{\mathrm{x}}}_{{1}},{q}_{{2}}={{x}}_{{2}},{p}_{{2}}={\dot{\mathrm{x}}}_{{2}},$ Eq. (47) can be rewritten in the form of Eqs. (4) and (5). The Hamiltonian associated with system (47) is

$$\begin{aligned} {\tilde{\mathrm{H}}}^{{'}}=\frac{{1}}{{2}}{p}_{{1}}^{{2}}{+}\frac{{1}}{{2}}{p}_{{2}}^{{2}}+{U}\left( {{\mathbf {q}}} \right) , \end{aligned}$$

(48)

where

$$\begin{aligned} {U}\left( {{\mathbf {q}}} \right) =\frac{{1}}{{2}}{\omega }_{{1}}^{{2}}\left( {q}_{{1}}-{q}_{{2}} \right) ^{{2}}{+}\frac{{1}}{{2}}{\omega }_{{2}}^{{2}}{q}_{{2}}^{{2}}{+}\frac{{1}}{{4}}{\alpha }{{(}{q}_{{1}}-{q}_{{2}}{)}}^{{4}}.\nonumber \\ \end{aligned}$$

(49)

Fig. 7

Reliability function of system (47). a Analytical results; b Monte Carlo simulation

Fig. 8

a Conditional reliability function of system (47); b conditional PDF of first passage time of system (45). “Dashed” curves from analytical results; “dots” from Monte Carlo simulation

Since the excitation specified in Eq. (47) is independent of velocities, the Wong–Zakai correction terms are zero. As a result, ${H}={\tilde{{H}}}^{{'}}$. Applying the method explained previously, one obtains the averaged Itô stochastic differential equation for the Hamiltonian as

$$\begin{aligned} \text {d}{H}={\bar{{m}}}\left( {H};{\varvec{\mu }} \right) \text {d}{t}+{\bar{\upsigma }}({H};{\varvec{\mu }} )\text {d}{B(t)}. \end{aligned}$$

(50)

The drift and diffusion coefficients are

$$\begin{aligned}&{\bar{{m}}}\left( {H};{\varvec{\mu }} \right) \nonumber \\&\quad =\frac{{1}}{{T}\left( {H};{\varvec{\mu }}\right) }\nonumber \\&\quad \quad \times \,\int \nolimits _{\omega }\left( -{{cp}}_{{1}}^{{2}}-{c}{p}_{{2}}^{{2}} +{2c}{p}_{{1}}{p}_{{2}} {+D} \right) \left( \frac{\partial {H}}{{\partial }{p}_{{1}}} \right) ^{{-1}}d{\mathbf{z},} \nonumber \\ \end{aligned}$$

(51)

$$\begin{aligned}&{\bar{\sigma }}^{{2}}\left( {H};{\varvec{\mu }} \right) \nonumber \\&\quad =\frac{{2D}}{{T}\left( {H};{\varvec{\mu }}\right) }\int \nolimits _{\omega } {p}_{{2}}^{{2}} \left( \frac{\partial {H}}{{\partial }{p}_{{1}}} \right) ^{{-1}}\text {d}{} \mathbf{z}, \end{aligned}$$

(52)

where $\mathbf{z}$, $\omega$, ${T}\left( {H};{\varvec{\mu }}\right)$ are identical to those in Example 1, and

$$\begin{aligned} {D}=\sum \nolimits _{{u}\in {S}} {D}^{\left( {u} \right) } {\mu }^{{(u)}}. \end{aligned}$$

(53)

Introduce the same transformations as in Example 1, it is found that

$$\begin{aligned}&{\bar{{m}}}\left( {H};{\varvec{\mu }} \right) \nonumber \\&\quad ={D+c} \int \nolimits _{0}^{{2\uppi }} \left[ -{2H}{R}^{{2}}{+}\frac{{1}}{{2}}\left( \frac{\text {cos}\theta }{{\omega }_{{1}}}-\frac{\text {sin}\theta }{{\omega }_{{2}}} \right) ^{{2}}{R}^{{2}}\nonumber \right. \\&\quad \quad {+}\,\frac{{1}}{{6}} \left( \frac{\text {cos}\theta }{{\omega }_{{1}}}-\,\frac{\text {sin}\theta }{{\omega }_{{2}}} \right) ^{{4}}{R}^{{4}} \nonumber \\&\qquad \left. {+}\,\frac{{1}}{{2}}{\text {sin}}^{{2}}{\theta }{R}^{{4}} \right] {d}\theta \big / \int \nolimits _{0}^{{2\uppi }} {R}^{{2}} \text {d}{\theta ,} \end{aligned}$$

(54)

$$\begin{aligned}&{\bar{\sigma }}^{{2}}\left( {H};{\varvec{\mu }} \right) \nonumber \\&\quad ={D}\int _{0}^{{2\uppi }} \left[ {2H}{R}^{{2}}{-}\frac{{1}}{{2}}\left( \frac{\text {cos}\theta }{{\omega }_{{1}}}-\frac{\text {sin}\theta }{{\omega }_{{2}}} \right) ^{{2}}{R}^{{2}}\nonumber \right. \\&\qquad \left. -\,\frac{{1}}{{6}} \right. \left( \frac{\text {cos}\theta }{{\omega }_{{1}}}{-}\frac{\text {sin}\theta }{{\omega }_{{2}}} \right) ^{{4}}{R}^{{4}} \nonumber \\&\quad \quad \left. -\,\frac{{1}}{{2}}{\text {sin}}^{{2}}{\theta }{R}^{{4}} \right] {d}\theta \big / \int \nolimits _{0}^{{2\uppi }} {R}^{{2}} \text {d}\theta , \end{aligned}$$

(55)

$$\begin{aligned}&{T}\left( {H};{\varvec{\mu }} \right) =\frac{{\uppi }}{{\omega }_{{1}}{\omega }_{{2}}}\int _{0}^{{2\uppi }} {{R}^{{2}}\text {d}{\theta }}, \end{aligned}$$

(56)

where R is the positive root of the equation

$$\begin{aligned}&{\frac{{\alpha }}{{4}}\left( \frac{\text {cos}\theta }{{\omega }_{{1}}}-\frac{\text {sin}\theta }{{\omega }_{{2}}} \right) }^{{4}}{R}^{{4}}{+}\frac{{1}}{{2}}{{\omega }_{{1}}^{{2}}\left( \frac{\text {cos}\theta }{{\omega }_{{1}}}{-}\frac{\text {sin}\theta }{{\omega }_{{2}}} \right) }^{{2}}{R}^{{2}}\nonumber \\&\quad +\,\frac{{1}}{{2}}{\omega }_{{2}}^{{2}}{\text {sin}}^{{2}}{\theta }{R}^{{2}}={H}. \end{aligned}$$

(57)

For vehicle suspension system, the total energy represents the vibration level which is related to driving safety and ride comfort. A critical value is defined so that if the value of energy is larger than the critical value, the car is unsafe or that the vibration of the vehicle is beyond human tolerance. Then, the BK equation governing the reliability function ${R}\left( {t}\left| {H}_{{0}} \right. \right)$ of system (47) can be set up in the form of Eq. (25). Solving the BK equation, the reliability function and the PDF of the first passage time of system (47) for different initial conditions can be obtained.

Fig. 9

Conditional reliability function of system (47) with ${L}={L}_{{1}}$, ${L}={L}_{{2}}$, ${L}={L}_{{3}}$ in Eq. (34) and when the system is fixed at ${s}\left( {t} \right) =1$ and ${s}\left( {t} \right) =2$. “Dashed” curves from analytical results; “dots” from Monte Carlo simulation

Fig. 10

When ${H}_{{0}}=0.01$, time histories of the total energy of system (47) for different initial conditions. a${x}_{{10}}=0,{x}_{{20}}=0,{\dot{\mathrm{x}}}_{{10}}=0,{\dot{{x}}}_{{20}}=\sqrt{{2}{H}_{{0}}} {;}$b${x}_{{10}}=0,{x}_{{20}}=0,{\dot{\mathrm{x}}}_{{10}}=-\sqrt{{2}{H}_{{0}}},{\dot{{x}}}_{{20}}=0;$c${x}_{{10}}=0,{x}_{{20}}=0,{\dot{\mathrm{x}}}_{{10}}=0,{\dot{{x}}}_{{20}}=-\sqrt{{2}{H}_{{0}}} {;}$d${x}_{{10}}=0,{x}_{{20}}=0,{\dot{\mathrm{x}}}_{{10}}=\sqrt{{2}{H}_{{0}}},{\dot{{x}}}_{{20}}=0$

Analytical results are shown as continuous curves in Figs. 7 and 8 for the chosen parameters ${\omega }_{{1}}=1$, ${\omega }_{{2}}=1$, ${c}=0.01$, $\alpha =1$, ${D}^{\left( {1} \right) }=0.02$, ${D}^{\left( {2} \right) }=0.01$ and ${L}={L}_{{1}}$. Figure 7 shows the reliability function ${R}({t}|{H}_{{0}})$ of system (47) as a function of the initial energy ${H}_{{0}}$ and time t. Figure 8 displays ${R(t}|{H}_{{0}})$ of system (47) as a function of t for the different initial energy ${H}_{{0}}$. Similar to Example 1, the reliability function is found to be a monotonic decreasing function of the initial energy and time. In addition, the reliability function diminishes more sharply with larger initial energy value. Again, results from Monte Carlo simulation are also shown in Fig. 7b and color dots in Fig. 8 for comparison. It is seen that the agreement is excellent.

In Fig. 9, the conditional reliability function of system (47) is shown when the transition rates are defined by the three transition matrices in Eq. (34) and when the system is fixed at ${s}\left( {t} \right) =1$ and ${s}\left( {t} \right) =2$. It can also be seen that neglecting the switching character of random excitations could introduce large errors in the evaluation of reliability function.

Figure 10 shows sample time histories of the total energy of system (47) for different initial conditions. Again, the blue line represents the curve of the total energy, the green line represents the critical energy, and the red line shows the time when the total energy of system (47) crosses the critical energy for the first time. The first passage of the total energy of system (47) out of the safety region can therefore be visualized.

5 Conclusions

Systems subjected to switching random excitations are practically significant because they include many safety-critical systems such as power plants and communication networks. In this paper, an approximate procedure for the reliability analysis of multi-degree-of-freedom, nonlinear, non-integrable Hamiltonian systems subjected to switching random excitation has been proposed. Such a system is first formulated in terms of a continuous–discrete hybrid based upon the Markov jump theory. Upon stochastic averaging of the Markov jump process, the hybrid system is reduced to a probability-weighted Itô equation. The associated backward Kolmogorov equation is then set up, from which the reliability function and probability density of first passage time are obtained. To demonstrate the utility and accuracy of the proposed approximate method, two examples have been provided, wherein the approximate analytical results are compared with those from Monte Carlo simulation. It has been found that the analytical results are generally in good agreement with Monte Carlo simulation. In both examples, the reliability function decreases as time progresses, or as the initial energy or the intensity of the switching random excitations increases. It has also been observed that neglecting the switching character of random excitations can introduce serious errors in the evaluation of reliability.