1 Introduction

Estimation of time variant reliability of dynamical systems, in which randomness exists in both the system parameter specifications and the external excitations, remains one of the most challenging problems in stochastic mechanics. This problem usually consists of determining the probability that the state of the dynamical system remains within a specified safe domain at all times over a given time duration. Evaluating this probability is of paramount importance in the safety assessment of structural or mechanical systems subjected to loads such as earthquake, wind, wave, guideway unevenness or moving traffic. A review of works on stochastic modelling of uncertainties and reliability estimation of dynamical systems can be found in [1,2,3]. In practical applications, the reliability is determined by estimating its complement, the probability of failure. Several complicating features make exact solution of the failure probability generally infeasible. These complexities include the presence of strong nonlinearity in the system behaviour, nonlinear and (or) implicitly defined performance functions, large number of mechanical degrees of freedom (dof), and non-stationary and (or) non-Gaussian nature of applied loading, among others.

In the approximate analytical/semi-analytical approaches, the time variant reliability is commonly evaluated based on out-crossing theory through Rice’s formula [4,5,6], or diffusion theory through numerical solution of the Kolmogorov equation [7,8,9,10]. These methods were originally developed in the context of deterministic dynamical systems, but have been subsequently extended to estimate the reliability of systems involving parameter uncertainties. Some approaches are the fast integration technique [11], methods based on asymptotic reliability analysis [12, 13], and methods based on Taylor series expansion of the failure probability [14]. Although the above methods provide important insights into the problem, they are often based on assumptions which are only asymptotically valid, and their ability to tackle many of the afore-mentioned complexities is rather limited. Recent research efforts focus on the development of the probability density evolution method [15, 16] that can handle more general cases, but its applicability for reliability analysis of white noise-driven dynamical systems is not well studied. Such representations for loads are often employed in engineering problems [17].

The Monte Carlo simulation (MCS) methods, on the other hand, are eminently suited to tackle a wide range of complexities and form powerful alternatives to the analytical procedures. These methods, however, typically need to be reinforced with strategies to control the sampling variance, in the absence of which the methods become computationally infeasible, especially in the estimation of small failure probabilities. Several variance reduction techniques have been developed for estimating the reliability of dynamical systems. For the particular case where the system parameters are characterized as deterministic and the applied excitations are modelled as random processes, one could model the random excitation by an equivalent set of random variables by using time discretization or series representations (such as, Fourier or Karhunen–Loeve expansion). The performance function defining the failure event can further be expressed in terms of extremes of the relevant response processes. This transforms the time variant reliability estimation problem into a high-dimensional time invariant reliability problem, which can be subsequently tackled using variance reduction schemes such as the importance sampling methods [18, 19], subset simulation methods [20,21,22], line sampling technique [23], or the Markov chain particle splitting methods [24]. When the structural response process is Markovian in nature, as in the case of white noise or filtered white noise-driven dynamical systems, an alternative approach for variance reduction is to employ the Girsanov probability measure transformation technique [17]. Importance sampling methods based on this principle introduce carefully chosen artificial control forces to the dynamical system which nudge the response trajectories towards the failure region. Subsequently, an unbiased estimator for the failure probability is derived by correcting for the artificial modification to the system dynamics. The main challenge in applying this method lies with the selection of the control force which, if selected judiciously, leads to significant reduction in the sampling variance. These controls could be open loop (chosen a priori, and, hence, independent of the response process), or closed loop (chosen adaptively, and, hence, dependent on the response process as it evolves). Several studies focus on open loop Girsanov controls which are obtained by solving a distance minimization problem [25,26,27]. However, improved variance reduction is achieved by using closed loop controls which can be derived based on results from optimal stochastic control theory [28, 29], or by numerical solution of the Bellman equation [30].

When randomness in both external excitation and system parameters are considered, the estimation of time variant reliability becomes considerably more involved. One way to proceed is to introduce an extended vector of random variables, comprising of the random system parameters and the equivalent set of random variables representing the random excitation. Failure probability estimation is then performed in the high dimensional space of the extended random vector using time invariant reliability methods. The benchmark study reported in [31] gives a comprehensive account of the performance of the subset simulation methods, the line sampling technique and other variance reduction schemes for this setting. An alternative approach in the literature consists of a two-step procedure: the first step estimates the failure probability conditional on the random system parameters, and the second step estimates the unconditional probability of failure through integration over the space of random parameters. In the existing studies based on this approach [32,33,34,35], the conditional probability of failure is estimated through importance sampling of the uncertain loading using the methods presented in [18, 25]. Subsequently, importance sampling [32,33,34], or line sampling [35] in the space of random system parameters is employed to evaluate the unconditional probability of failure. The performance of these approaches depends on the appropriate selection of certain algorithmic parameters, which, in turn, requires prior knowledge of the failure domain. The importance sampling method suggested in [32] requires identification of a so-called design point in the random parameter space to construct the sampling density. In the method based on line sampling [35], the unconditional failure probability is estimated by generating random lines parallel to an important direction defined by the afore-mentioned design point. The above methods are effective only when the important region contributing to the failure probability lies in the vicinity of a unique design point. In the method presented in [34], the importance sampling density in the random parameter space is determined by constructing a surrogate model for the conditional instantaneous failure probabilities, i.e. the probability of failure at specific time instants, of the dynamical system. The approach is more robust as it does not rely on the determination of design points. However, the efficiency of the method depends on a proper choice of the surrogate model which may not be straight-forward, especially in the presence of a large number of random system parameters.

The present study aims at developing an efficient strategy for estimating the time variant reliability of randomly excited uncertain dynamical systems. In the proposed approach, a two-step estimation procedure is adopted. The first step involves estimation of the failure probability conditional on the random system parameters. In implementing this step, two existing approaches are employed, which are: (a) analytical approximation based on threshold crossing statistics [4, 36], and (b) closed loop control based Girsanov’s transformation method [29]. In the second step, the unconditional probability of failure is determined by estimating the expectation of the conditional failure probability with respect to the random parameters. The main contribution of this paper lies in developing an efficient simulation-based method to estimate the expectation in the second step of the proposed method. To accomplish this, a framework is introduced that transforms the problem of estimating the expectation into a hypothetical reliability estimation problem through the inclusion of an auxiliary random variable. This enables evaluation of the unconditional failure probability using simulation-based reliability estimation methods which do not require prior knowledge of the failure domain. This is in contrast with the afore-mentioned existing studies based on importance sampling and line sampling. In particular, the study investigates the application of alternative versions of the Markov chain splitting methods, such as the subset simulation method [20] and the particle splitting methods [24], in this context. The novel aspect of the present study, thus, essentially lies in meeting the challenges posed by the need to combine details of alternative tools such as closed loop Girsanov’s control-based importance sampling and the Markov chain splitting algorithms for the problem on hand. The efficacy of the proposed methods is demonstrated through numerical studies on single degree of freedom (sdof) linear/nonlinear oscillators driven by Gaussian white noise, and a multi-degree of freedom (mdof) linear system subjected to filtered non-stationary Gaussian excitation. It is noted that the latter problem is one of the benchmark reliability examples studied earlier in [31].

2 Problem formulation

2.1 Uncertain dynamical system

Consider a randomly parametered dynamical system with governing equation of the form

$$\begin{aligned}&{\mathbf {M}}\left( {\varvec{{\varTheta }}} \right) \ddot{{{\textit{\textbf{V}}}}}\left( t \right) +{\textit{\textbf{D}}}\left[ {{{\varvec{\varTheta }}},{\textit{\textbf{V}}}\left( t \right) ,\dot{{{\textit{\textbf{V}}}}}\left( t \right) ,t} \right] ={\textit{\textbf{F}}}\left( t \right) ; \, \nonumber \\&{\textit{\textbf{V}}}\left( 0 \right) ={\textit{\textbf{V}}}_{0}, \, \dot{{{\textit{\textbf{V}}}}}\left( 0 \right) =\dot{{{\textit{\textbf{V}}}}}_{0}; \, t\ge 0 \end{aligned}$$
(1)

where a dot represents derivative with respect to time t. This semi-discretized equation of motion can be obtained, for instance, from spatial discretization of a continuum system using the finite element method. Here, \({\textit{\textbf{V}}}\left( t \right) \) is the \(n\times 1\) nodal displacement vector, \({\mathbf {M}}\) is the \(n\times n\) mass matrix, \({\textit{\textbf{F}}}\left( t \right) \) is the external excitation modelled as a \(n\times 1\) vector-valued random process, \({\textit{\textbf{D}}}\) is a \(n\times 1\) vector of nonlinear function of system states, and \({\varvec{{\varTheta }}} \) is the \(n_{s} \times 1\) vector of uncertain system parameters which are modelled as random variables with joint probability density function (pdf) \(p_{{\varvec{{\varTheta }}} } \left( {\varvec{\theta }} \right) \). The initial conditions \({\textit{\textbf{V}}}_{0} \) and \(\dot{{{\textit{\textbf{V}}}}}_{0} \) are taken to be deterministic. The components of \({\textit{\textbf{F}}}\left( t \right) \), in general, could be non-stationary, non-white, and (or) non-Gaussian. When non-white excitations are considered, \({\textit{\textbf{F}}}\left( t \right) \) is taken to be the output of a set of additional linear/nonlinear filters driven by Gaussian white noise excitations. Similarly, the components of \({\varvec{{\varTheta }}}\) could be dependent and non-Gaussian, and it is assumed that \({\textit{\textbf{F}}}\left( t \right) \) and \({\varvec{{\varTheta }}} \) are independent.

We define a p-dimensional extended state vector \({\textit{\textbf{X}}}\left( t \right) \) which comprises of the dynamical system states \({\textit{\textbf{V}}}\left( t \right) , \, \dot{{{\textit{\textbf{V}}}}}\left( t \right) \), and the additional state variables associated with the augmented filter equations (leading to the definition of \({\textit{\textbf{F}}}\left( t \right) )\). In this setting, the governing equation (1) can be cast as a stochastic differential equation (SDE) of the form

$$\begin{aligned} \hbox {d}{\textit{\textbf{X}}}\left( t \right) ={\textit{\textbf{A}}}\left[ {{\varvec{{\varTheta }}}, {\textit{\textbf{X}}}\left( t \right) ,t} \right] \hbox {d}t+\varvec{\upsigma }\left[ {{\varvec{{\varTheta }}}, {\textit{\textbf{X}}}\left( t \right) ,t} \right] \hbox {d}{\textit{\textbf{B}}}\left( t \right) ; {\textit{\textbf{X}}}\left( 0 \right) ={\textit{\textbf{X}}}_{0}; \, t\ge 0 \end{aligned}$$
(2)

Here, \({\textit{\textbf{A}}}\left[ {{\varvec{{\varTheta }}}, {\textit{\textbf{X}}}\left( t \right) ,t} \right] \) and \(\varvec{\upsigma }\left[ {{\varvec{{\varTheta }}}, X\left( t \right) ,t} \right] \) are, respectively, the \(p\times 1\) drift vector and \(p\times q\) diffusion matrix, \(B\left( t \right) \) is a q-dimensional zero mean Brownian motion process with covariance function \({E}_{\mathrm{P}} \left[ {\left( {{\textit{\textbf{B}}}\left( {t_{1} +{\Delta } t} \right) -{\textit{\textbf{B}}}\left( {t_{1} } \right) } \right) \left( {{\textit{\textbf{B}}}\left( {t_{2} +{\Delta } t} \right) -{\textit{\textbf{B}}}\left( {t_{2} } \right) } \right) ^{\mathrm{T}}} \right] ={\mathbf {C}}{\Delta } t\delta \left( {t_{1} -t_{2} } \right) ; \, t_{1},t_{2} \ge 0\), \(\left( {{\Omega },{\mathcal {F}},\hbox {P}} \right) \) is the probability space associated with the above SDE, \({E}_{\mathrm{P}} \left[ \cdot \right] \) is the expectation operator with respect to the probability measure P, and \(\delta \left( \cdot \right) \) is the Dirac delta function.

2.2 Time variant reliability problem

In problems of time variant reliability analysis, one compares a dynamic response of interest \(h\left[ {{\varvec{{\varTheta }}}, \, {\textit{\textbf{X}}}\left( t \right) } \right] \) against an acceptable threshold level \(h^{*}\), and the system is taken to be safe if the response remains below \(h^{*}\) at all times over the duration of the random excitation. The reliability of the system is thus defined by the probability \({\textit{\textbf{P}}}_{\mathrm{R}} =\hbox {P}\left[ {\left\{ {h\left[ {{\varvec{{\varTheta }}}, {\textit{\textbf{X}}}\left( t \right) } \right] <h^{*}\forall t\in \left[ {0,T} \right] } \right\} } \right] \), where \(\left[ {0,T} \right] \) is the time duration over which the excitation acts. The probability of failure \(P_{\mathrm{F}} =1-P_{\mathrm{R}} \) is subsequently obtained as

$$\begin{aligned} P_{\mathrm{F}} =1-\hbox {P}\left[ {\left\{ {h\left[ {{\varvec{{\varTheta }}}, {\textit{\textbf{X}}}\left( t \right) } \right]<h^{*}\forall t\in \left[ {0,T} \right] } \right\} } \right] =\hbox {P}\left[ {\left\{ {h^{*}-\mathop {\max }\limits _{0<t\le T} h\left[ {{\varvec{{\varTheta }}}, {\textit{\textbf{X}}}\left( t \right) } \right] \le 0} \right\} } \right] \end{aligned}$$
(3)

One can, in principle, estimate the failure probability by the direct Monte Carlo method. In this approach, the estimator for the probability of failure is given by the expression \(\hat{{P}}_{\mathrm{F}} =\frac{1}{N}\sum \nolimits _{i=1}^N {I}\left\{ h^{*}-\mathop {\max }\nolimits _{0<t\le T} h\left[ {{\varvec{\theta }} ^{i}, {\textit{\textbf{X}}}^{i}\left( t \right) } \right] \le 0 \right\} \). Here, \({I}\left\{ \cdot \right\} \) denotes the indicator function for the failure event, \({\varvec{\theta }}^{i};i=1,\ldots ,N\) are independent realizations of \({\varvec{{\varTheta }}}\) distributed according to \(p_{{\varvec{{\varTheta }}} } \left( {\varvec{\theta }} \right) \), and \({\textit{\textbf{X}}}^{i}\left( t \right) \) is a sample realization of the state vector \({\textit{\textbf{X}}}\left( t \right) \) obtained by solving Eq. (2) for \({\varvec{\theta }} ={\varvec{\theta }}^{i}\). It can be shown that the number of samples needed by the direct Monte Carlo estimator to meet a target coefficient of variation is inversely proportional to the magnitude of \(P_{\mathrm{F}}\). Therefore, when \(P_{\mathrm{F}} \) is small, which is typically the case in engineering problems, the computational cost associated with this approach becomes considerable because a large number of samples would be needed to generate accurate estimates. The variance of the direct Monte Carlo estimator can be reduced by using advanced Monte Carlo methods known as variance reduction techniques. The present study proposes a framework that combines the potential of two variance reduction schemes, namely, the Markov chain splitting methods and Girsanov’s transformation-based importance sampling, to estimate the failure probability.

To this end, it is noted that the probability of failure in Eq. (3) can be alternatively expressed as

$$\begin{aligned} P_{\mathrm{F}} ={E}_{\mathrm{P}} \left[ {{I}\left\{ {h^{*}-\mathop {\max }\limits _{0<t\le T} h\left[ {{\varvec{{\varTheta }}}, {\textit{\textbf{X}}}\left( t \right) } \right] \le 0} \right\} } \right] ={E}_{\left\{ {{\varvec{{\varTheta }}} \, {\textit{\textbf{B}}}} \right\} } \left[ {{I}\left\{ {h^{*}-\mathop {\max }\limits _{0<t\le T} h\left[ {{\varvec{{\varTheta }}}, {\textit{\textbf{X}}}\left( t \right) } \right] \le 0} \right\} } \right] \end{aligned}$$
(4)

Here, \({I}\left\{ \cdot \right\} \) is the indicator function and \({E}_{\left\{ {{\varvec{{\varTheta }}} \, {\textit{\textbf{B}}}} \right\} } \left[ \cdot \right] \) denotes expectation with respect to the uncertain system parameters and loads. The above equation considers the simultaneous presence of randomness in both excitation and system parameters in calculating the failure probability. The envisaged method first considers the probability of failure conditional on a given value of the parameter vector \({\varvec{{\varTheta }}} ={\varvec{\theta }} \). This conditional probability is defined as

$$\begin{aligned} P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{\theta }} \right) ={E}_{{\textit{\textbf{B}}}} \left[ {\left. {{I}\left\{ {h^{*}-\mathop {\max }\limits _{0<t\le T} h\left[ {{\varvec{{\varTheta }}}, {\textit{\textbf{X}}}\left( t \right) } \right] \le 0} \right\} } \right| {\varvec{{\varTheta }}} ={\varvec{\theta }} } \right] =\hbox {P}\left[ {\left. {\left\{ {h^{*}-\mathop {\max }\limits _{0<t\le T} h\left[ {{\varvec{{\varTheta }}}, {\textit{\textbf{X}}}\left( t \right) } \right] \le 0} \right\} } \right| {\varvec{{\varTheta }}} ={\varvec{\theta }} } \right] \nonumber \\ \end{aligned}$$
(5)

The probability of failure in Eq. (4) is then given by

$$\begin{aligned} P_{\mathrm{F}} ={E}_{{\varvec{{\varTheta }}} } \left[ {{E}_{B} \left[ {\left. {{I}\left\{ {h^{*}-\mathop {\max }\limits _{0<t\le T} h\left[ {{\varvec{{\varTheta }}}, {\textit{\textbf{X}}}\left( t \right) } \right] \le 0} \right\} } \right| {\varvec{{\varTheta }}} } \right] } \right] ={E}_{{\varvec{{\varTheta }}} } \left[ {P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{{\varTheta }}} \right) } \right] =\int {P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{\theta }} \right) p_{{\varvec{{\varTheta }}} } \left( {\varvec{\theta }} \right) \hbox {d}{\varvec{\theta }} } \end{aligned}$$
(6)

where \({E}_{{\textit{\textbf{B}}}} \left[ \cdot \right] \) and \({E}_{{\varvec{{\varTheta }}} } \left[ \cdot \right] \) denote expectation with respect to the random excitation and the random system parameters, respectively. Section 3 reviews two available approaches to estimate \(P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{\theta }} \right) \). These approaches are extended in Sect. 4 to develop an efficient strategy for estimating the probability of failure including uncertainty in both system parameters and excitation.

3 Estimation of probability of failure conditional on random system parameters

In this section, estimation of the conditional failure probability \(P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{\theta }} \right) \) for a given value of the parameter vector \({\varvec{{\varTheta }}} ={\varvec{\theta }} \) is discussed. Two existing approaches are employed: in the first approach, an analytical approximation of \(P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{\theta }} \right) \) is obtained based on out-crossing theory, and, in the second approach, \(P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{\theta }} \right) \) is evaluated by a Monte Carlo simulation strategy that uses Girsanov’s probability measure transformation technique to achieve sampling variance reduction. The details of these methods are briefly outlined in the subsequent sections.

3.1 Analytical approximation based on out-crossing theory

In this approach, an estimate of the conditional failure probability \(P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{\theta }} \right) \) is obtained by counting the number of times the response \(h\left[ {{\varvec{\theta }},{\textit{\textbf{X}}}\left( t \right) } \right] \) up-crosses the threshold \(h^{*}\) in the time duration \(\left[ {0,T} \right] \). Let \(\eta ^{+}\left( {h^{*};{\varvec{\theta }},0,T} \right) \) be the number of out-crossings from the safe domain. Under the assumption that the out-crossing events are independent \(\eta ^{+}\left( {h^{*};{\varvec{\theta }},0,T} \right) \) is approximated by a Poisson random variable, and an analytical estimate of \(P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( \theta \right) \) is obtained as [37]

$$\begin{aligned} \hat{{P}}_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} }^{A} \left( {{\varvec{\theta }}} \right) =\hbox {P}\left[ {\left\{ {\eta ^{+}\left( {h^{*};{\varvec{\theta }},0,T} \right) >0} \right\} } \right] =1-\exp \left( {-\int \limits _0^T {\nu ^{+}\left( {h^{*},{\varvec{\theta }},t} \right) \hbox {d}t} } \right) \end{aligned}$$
(7)

The quantity \(\nu ^{+}\left( {h^{*},{\varvec{\theta }},t} \right) \) is the mean rate of up-crossing the threshold \(h^{*}\) at time t and can be obtained according to the Rice formula \(\nu ^{+}\left( {h^{*},{\varvec{\theta }},t} \right) =\int \nolimits _0^\infty {\dot{{s}}f\left( {h^{*},\dot{{s}};{\varvec{\theta }},t} \right) \hbox {d}\dot{{s}}} \), where \(f\left( {s,\dot{{s}};{\varvec{\theta }},t} \right) \) denotes the joint pdf of the response \(h\left[ {{\varvec{\theta }},X\left( t \right) } \right] \) and its velocity at time t [4].

When the response \(h\left[ {{\varvec{\theta }},{\textit{\textbf{X}}}\left( t \right) } \right] \) is a stationary/non-stationary Gaussian random process, such as in linear systems subjected to Gaussian excitations, the joint pdf of the response and its time derivative can be explicitly derived analytically, based on which the mean up-crossing rate can be computed. The exact analytical expression of the mean up-crossing rate of Gaussian response processes across a specified threshold has been reported in the existing literature [36, 38]. For certain types of nonlinear systems driven by stationary Gaussian white noise, this joint pdf can also be determined exactly based on the procedure outlined in [36]. However, for general nonlinear systems, an approximation to this joint pdf is needed, deducing which is seldom straight-forward. In such cases, Monte Carlo simulation-based approaches provide a powerful alternative to analytical approximations for estimating the conditional probability of failure.

3.2 Girsanov’s transformation-based importance sampling

The underlying principle in the Girsanov transformation method is to modify the dynamical system by introducing an artificial control force that drives the response trajectories towards the failure region. An unbiased estimator for \(P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( \theta \right) \) is subsequently obtained by introducing a correction term, known as the Radon–Nikodym derivative, that corrects for the addition of the artificial controls. For this purpose, associated with Eq. (2), one considers the controlled dynamical system governed by the Ito’s SDE,

$$\begin{aligned}&\hbox {d}\tilde{{{\textit{\textbf{X}}}}}\left( t \right) ={\textit{\textbf{A}}}\left[ {{\varvec{\theta }}, \tilde{{{\textit{\textbf{X}}}}}\left( t \right) ,t} \right] \hbox {d}t+\varvec{\upsigma }\left[ {{\varvec{\theta }},\tilde{{{\textit{\textbf{X}}}}}\left( t \right) ,t} \right] {\textit{\textbf{u}}}\left[ {{\varvec{\theta }},\tilde{{{\textit{\textbf{X}}}}}\left( t \right) ,t} \right] \hbox {d}t+\varvec{\upsigma }\left[ {{\varvec{\theta }},\tilde{{{\textit{\textbf{X}}}}}\left( t \right) ,t} \right] \hbox {d}\tilde{{{\textit{\textbf{B}}}}}\left( t \right) ; \nonumber \\&\hbox {d}R\left( t \right) =-R\left( t \right) \left( {{\textit{\textbf{u}}}\left[ {{\varvec{\theta }} ,\tilde{{{\textit{\textbf{X}}}}}\left( t \right) ,t} \right] } \right) ^{\mathrm{T}}{\mathbf {C}}^{-1}\hbox {d}\tilde{{{\textit{\textbf{B}}}}}\left( t \right) \nonumber \\&\tilde{{{\textit{\textbf{X}}}}}\left( 0 \right) ={\textit{\textbf{X}}}_{0}; \, R\left( 0 \right) =R_{0}; \, 0\le t\le T \end{aligned}$$
(8)

where \({\textit{\textbf{u}}}\left[ {{\varvec{\theta }} ,\tilde{{{\textit{\textbf{X}}}}}\left( t \right) ,t} \right] \) is the q-dimensional vector-valued control force, \(R\left( t \right) \) is the scalar correction process, \(\tilde{{{\textit{\textbf{X}}}}}\left( t \right) \) is the biased state corresponding to the modified input, and \(\tilde{{{\textit{\textbf{B}}}}}\left( t \right) \) is an Ito’s process given by \(\hbox {d}\tilde{{{\textit{\textbf{B}}}}}\left( t \right) =-{\textit{\textbf{u}}}\left[ {{\varvec{\theta }} ,\tilde{{{\textit{\textbf{X}}}}}\left( t \right) ,t} \right] \hbox {d}t+\hbox {d}{\textit{\textbf{B}}}\left( t \right) ;\,\tilde{{{\textit{\textbf{B}}}}}\left( 0 \right) =0;t\ge 0\). In the above equation, the initial condition \(R_{0} \) is typically set to 1. According to the Girsanov theorem [17], the addition of control forces transforms the probability measure associated with the uncontrolled SDE such that \(\tilde{{{\textit{\textbf{B}}}}}\left( t \right) \) is a zero mean correlated Brownian motion process with respect to the transformed measure. Assuming \(R_{0} =1\), an estimator for \(P_{\left. {\mathrm{F}} \right| {\varvec{{\varvec{{\varTheta }}}}} } \left( {\varvec{\theta }} \right) \) based on the above modified SDE is obtained as

$$\begin{aligned} \hat{{P}}_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} }^{\mathrm{GT}} \left( {\varvec{\theta }} \right) =\frac{1}{N_{\mathrm{I}} }\sum \limits _{j=1}^{N_{\mathrm{I}} } {R^{j}\left( T \right) {I}\left\{ {h^{*}-\mathop {\max }\limits _{0<t\le T} h\left[ {{\varvec{\theta }}, \tilde{{{\textit{\textbf{X}}}}}^{j}\left( t \right) } \right] \le 0} \right\} } \end{aligned}$$
(9)

where \(\tilde{{{\textit{\textbf{X}}}}}^{j}\left( t \right) , \, R^{j}\left( t \right) ;j=1,\ldots ,N_{\mathrm{I}} \) are random draws from Eq. (8). The salient feature of this importance sampling scheme is the choice of the control \({\textit{\textbf{u}}}\left[ {{\varvec{\theta }},\tilde{{{\textit{\textbf{X}}}}}\left( t \right) ,t} \right] \) which, if selected judiciously, can significantly reduce the sampling variance of \(\hat{{P}}_{\left. {\mathrm{F}} \right| {\varvec{{\varvec{{\varTheta }}}}} }^{\mathrm{GT}} \left( {\varvec{\theta }} \right) \). As has been previously mentioned, several alternative strategies for devising variance reducing Girsanov controls have been studied in the existing literature. In the present study, \(P_{\left. {\mathrm{F}} \right| {\varvec{{\varvec{{\varTheta }}}}} } \left( {\varvec{\theta }} \right) \) is estimated by employing the closed loop Girsanov control developed in a recent study by the present authors [29]. The novelty of this control force lies in the fact that it is applicable to mdof systems driven by non-stationary Gaussian excitation, unlike other existing closed loop controls which have been studied primarily in the context of stationary white noise-driven sdof oscillators, and it leads to significant sampling variance reduction as compared to open loop controls. The procedure for deducing this Girsanov control, as outlined in [29], is described in Annexure A of the accompanying electronic supplementary material (ESM).

4 Estimation of the unconditional probability of failure

4.1 Framework for estimating the probability of failure

In order to estimate the unconditional probability of failure \(P_{\mathrm{F}} ={E}_{{\varvec{{\varTheta }}} } \left[ {P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{{\varTheta }}} \right) } \right] \), it is expedient to express the expectation in Eq. (6) as an equivalent expectation of the form \({E}_{{\textit{\textbf{Z}}}} \left[ {{I}\left\{ {g\left( {\textit{\textbf{Z}}} \right) \le 0} \right\} } \right] \), for a suitably defined random vector Z and a performance function \(g\left( {\textit{\textbf{Z}}} \right) \). To this end, an auxiliary random variable \(\xi \) distributed uniformly in \(\left[ {0,1} \right] \) and independent of \({\varvec{{\varTheta }}}\) is introduced [11]. Since \(0\le P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{{\varTheta }}} \right) \le 1\) for a specified value of \({\varvec{{\varTheta }}} \), the following identity holds:

$$\begin{aligned} P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{{\varTheta }}} \right) ={E}_{\xi } \left[ {{I}\left\{ {\xi \le P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{{\varTheta }}} \right) } \right\} } \right] \end{aligned}$$
(10)

Therefore, by combining Eqs. (6) and (10), one gets

$$\begin{aligned} P_{\mathrm{F}}= & {} {E}_{{\varvec{{\varTheta }}} } \left[ {{E}_{\xi } \left[ {{I}\left\{ {\xi \le {E}_{{\textit{\textbf{B}}}} \left[ {\left. {{I}\left\{ {h^{*}-\mathop {\max }\limits _{0<t\le T} h\left[ {{\varvec{{\varTheta }}}, {\textit{\textbf{X}}}\left( t \right) } \right] \le 0} \right\} } \right| {\varvec{{\varTheta }}} } \right] } \right\} } \right] } \right] \nonumber \\= & {} {E}_{\left\{ {{\varvec{{\varTheta }}} \, \xi } \right\} } \left[ {{I}\left\{ {\xi -{E}_{{\textit{\textbf{B}}}} \left[ {\left. {{I}\left\{ {h^{*}-\mathop {\max }\limits _{0<t\le T} h\left[ {{\varvec{{\varTheta }}}, {\textit{\textbf{X}}}\left( t \right) } \right] \le 0} \right\} } \right| {\varvec{{\varTheta }}} } \right] \le 0} \right\} } \right] \nonumber \\= & {} {E}_{\left\{ {{\varvec{{\varTheta }}} \, \xi } \right\} } \left[ {{I}\left\{ {\xi -P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{{\varTheta }}} \right) \le 0} \right\} } \right] ={E}_{{\textit{\textbf{Z}}}} \left[ {{I}\left\{ {g\left( {\textit{\textbf{Z}}} \right) \le 0} \right\} } \right] =\hbox {P}\left[ {\left\{ {g\left( {\textit{\textbf{Z}}} \right) \le 0} \right\} } \right] \end{aligned}$$
(11)

where \({\textit{\textbf{Z}}}=\left\{ {\xi \, {\varvec{{\varTheta }}} } \right\} \) is a \(\left( {n_{s} +1} \right) \)-dimensional random vector with pdf \(p_{{\textit{\textbf{Z}}}} \left( z \right) =p_{{\varvec{{\varTheta }}} } \left( {\varvec{\theta }} \right) \) for \(\xi \in \left[ {0,1} \right] \) and \(p_{{\textit{\textbf{Z}}}} \left( z \right) =0\) otherwise. The above equation represents a hypothetical time invariant reliability problem with performance function given by \(g\left( {\textit{\textbf{Z}}} \right) =\xi -P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{{\varTheta }}} \right) \).

The problem of estimating the failure probability in Eq. (11) can now be tackled by using Monte Carlo simulations augmented with a suitable variance reduction scheme. The present study employs a specific class of variance reduction techniques, known as the Markov chain particle splitting methods. The basic idea in this class of methods is to express the event \(E=\left\{ {g\left( {\textit{\textbf{Z}}} \right) \le 0} \right\} \) as an intersection of M intermediate nested events \(E_{1},\ldots ,E_{M} \) such that \(E_{1} \supset E_{2} \supset \ldots \supset E_{M} =E\). Consequently, the probability of the event E can be computed as a product of conditional probabilities:

$$\begin{aligned} P_{\mathrm{F}} =\hbox {P}\left[ E \right] =\hbox {P}\left[ {\bigcap \limits _{k=1}^M {E_{k} } } \right] =\prod \limits _{k=1}^M {\hbox {P}\left[ {\left. {E_{k} } \right| E_{k-1} } \right] } =\prod \limits _{k=1}^M {p_{k} } \end{aligned}$$
(12)

Here, \(E_{0} \) is the certain event. The intermediate events are selected such that the conditional probabilities \(p_{k} =\hbox {P}\left[ {\left. {E_{k} } \right| E_{k-1} } \right] ;k=1,\ldots ,M\) are much larger than \(\hbox {P}\left[ E \right] \). In this way, the original problem of estimating the small probability of the rare event E reduces to a problem of computing a sequence of larger conditional probabilities that can be efficiently estimated with fewer samples. The intermediate events are defined as \(E_{k} =\left\{ {g\left( {\textit{\textbf{Z}}} \right) \le b_{k} } \right\} ;k=1,\ldots ,M\) where the threshold levels satisfy the condition \(b_{1}>b_{2}>\cdots >b_{M} =0\).

Depending on the manner in which the intermediate events, i.e. the threshold levels \(b_{1},\ldots ,b_{M-1} \), are selected, and the strategy employed to generate conditional samples for estimating \(\hbox {P}\left[ {\left. {E_{k} } \right| E_{k-1} } \right] ;k=1,\ldots ,M\), alternative particle splitting algorithms can be developed. In this study, three existing algorithms are considered, namely, the subset simulation (SS) method [20], the generalized splitting (GS) method [39], and the multiple-chain Holmes–Diaconis–Ross (mHDR) method [24]. The salient features of these methods are provided in Annexure B of the ESM, and further details can be found in [24]. The resulting estimators for the unconditional failure probability \(P_{\mathrm{F}} \) are discussed in the following section.

4.2 Proposed estimators for the probability of failure

By embedding the estimator for \(P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{{\varTheta }}} \right) \) into the framework of the Markov chain particle splitting methods, alternative estimators for the unconditional failure probability are obtained. These estimators are listed in Box 1. It is noted that the proposed estimators require repeated evaluations of the function \(g\left( {\textit{\textbf{Z}}} \right) \), and hence \(P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{{\varTheta }}} \right) \). For instance, the estimator of \(P_{\mathrm{F}} \) based on the SS and mHDR methods requires \(MN_{\mathrm{O}} \) estimations of \(P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{{\varTheta }}} \right) \), once for each of the \(N_{\mathrm{O}} \) samples \(\left\{ {z^{k-1,1},\ldots ,z^{k-1,N_{\mathrm{O}} }} \right\} \) simulated in the domain \(E_{k-1};k=1,\ldots ,M\). This implies that if \(P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{{\varTheta }}} \right) \) is estimated by Girsanov’s transformation, i.e. when \(\hat{{P}}_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{\theta }} \right) =\hat{{P}}_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} }^{\mathrm{GT}} \left( {\varvec{\theta }} \right) \) in Box 1, one has to determine a total of \(MN_{\mathrm{O}} \) Girsanov controls \({\textit{\textbf{u}}}\left[ {{\varvec{\theta }} ^{k-1,i},\tilde{{{\textit{\textbf{X}}}}}\left( t \right) ,t} \right] ;k=1,\ldots M;i=1,\ldots ,N_{\mathrm{O}} \). As has been discussed in Annexure A of the ESM, the control force \({\textit{\textbf{u}}}\left[ {{\varvec{\theta }}^{k-1,i},\tilde{{{\textit{\textbf{X}}}}}\left( t \right) ,t} \right] \) is randomly chosen from a set of m closed loop controls \({\textit{\textbf{u}}}^{r}\left[ {{\varvec{\theta }}^{k-1,i},\tilde{{{\textit{\textbf{X}}}}}\left( t \right) ,t} \right] ;r=1,\ldots ,m\), where each control promotes an instantaneous failure event. Thus, determination of each Girsanov control requires further evaluation of m instantaneous level control forces.

Box 1. Failure probability estimator based on Markov chain particle splitting methods

Method

Estimator

mHDR

\(\hat{{P}}_{\mathrm{F}} =\prod \nolimits _{k=1}^M {\hat{{p}}_{k} } =\prod \nolimits _{k=1}^M {\left( {\frac{1}{N_{\mathrm{O}} }\sum \nolimits _{i=1}^{N_{\mathrm{O}} } {{I}\left\{ {g\left( {z^{k-1,i}} \right) \le b_{k} } \right\} } } \right) } =\prod \nolimits _{k=1}^M {\left( {\frac{1}{N_{\mathrm{O}} }\sum \nolimits _{i=1}^{N_{\mathrm{O}} } {{I}\left\{ {\xi ^{k-1,i}-\hat{{P}}_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {{\varvec{\theta }}^{k-1,i}} \right) \le b_{k} } \right\} } } \right) } \)

GS

\(\hat{{P}}_{\mathrm{F}} =\frac{N_{M} }{N_{\mathrm{O}} }\prod \nolimits _{k=2}^M {{p}'_{k} } \)

SS

\(\hat{{P}}_{\mathrm{F}} =\rho ^{M-1}\hat{{p}}_{M} =\rho ^{M-1}\frac{1}{N_{\mathrm{O}} }\sum \nolimits _{i=1}^{N_{\mathrm{O}} } {{I}\left\{ {g\left( {z^{M-1,i}} \right) \le 0} \right\} } =\rho ^{M-1}\frac{1}{N_{\mathrm{O}} }\sum \nolimits _{i=1}^{N_{\mathrm{O}} } {{I}\left\{ {\xi ^{M-1,i}-\hat{{P}}_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {{\varvec{\theta }}^{M-1,i}} \right) \le 0} \right\} } \)

Remarks:

1.

\(z^{k-1,i}=\left\{ {{\begin{array}{*{20}c} {\xi ^{k-1,i}} &{} {{\varvec{\theta }}^{k-1,i}} \\ \end{array} }} \right\} ;i=1,2,\ldots ,\) are the samples of Z generated in the \(\left( {k-1} \right) -\hbox {th}\) conditional level. These samples are drawn from the pdf \(p_{Z} \left( {\left. z \right| z\in E_{k-1} } \right) \) using direct MCS for \(k=1\), and using Markov chain Monte Carlo (MCMC) method for \(k>1\).

2.

\(\hat{{p}}_{1},\ldots ,\hat{{p}}_{M} \) are Monte Carlo estimators of the probabilities \(\hbox {P}\left[ {\left. {E_{k} } \right| E_{k-1} } \right] ;k=1,\ldots ,M\).

3.

\({p}'_{2},\ldots ,{p}'_{M} \) are parameters of the GS method. These correspond to approximate a priori values of the probabilities \(\hbox {P}\left[ {\left. {E_{k} } \right| E_{k-1} } \right] ;k=2,\ldots ,M\). The procedure for obtaining these parameters is outlined in box B1 of Annexure B in the ESM.

4.

\(\rho \) is a parameter of the SS method. It represents a pre-fixed value for the sample estimates of the probabilities \(\hbox {P}\left[ {\left. {E_{k} } \right| E_{k-1} } \right] ;k=1,\ldots ,M-1\). In this study, \(\rho \) is taken equal to 0.1.

5.

\(\hat{{P}}_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {{\varvec{\theta }}^{k-1,i}} \right) \) is an estimate of \(P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{{\varTheta }}} \right) \) for \({\varvec{{\varTheta }}} ={\varvec{\theta }}^{k-1,i}\) computed using equations (7) or (9).

6.

\(N_{\mathrm{O}} \) is the sample size for the conditional probability estimators \(\hat{{p}}_{1},\ldots ,\hat{{p}}_{M} \).

7.

\(N_{M} \) is the number of samples generated in the \(\left( {M-1} \right) \hbox {-th}\) conditional level that fall in the region \(E_{M} \), i.e. number of samples from the set \(\left\{ {{ \begin{array}{*{20}c} {z^{M-1,1}} &{} {z^{M-1,2}} &{} \cdots \\ \end{array} }} \right\} \) for which \(g\left( z \right) \le 0\).

For linear systems, where the instantaneous level controls can be analytically obtained in closed form, this does not pose any significant difficulty. However, for nonlinear systems, the approach would become computationally intractable since, in this case, the controls \({\textit{\textbf{u}}}^{r}\left[ {{\varvec{\theta }}^{k-1,i},\tilde{{{\textit{\textbf{X}}}}}\left( t \right) ,t} \right] ;r=1,\ldots ,m\) are obtained through numerical solution of the optimization problem in Eq. (A3) of Annexure A. To alleviate this difficulty, a simplification is proposed, wherein for every \(k\in \left\{ {1,\ldots ,{\textit{\textbf{M}}}} \right\} \), the controls \({\textit{\textbf{u}}}\left[ {{\varvec{\theta }} ^{k-1,i},\tilde{{{\textit{\textbf{X}}}}}\left( t \right) ,t} \right] ;i=1,\ldots ,N_{\mathrm{O}} \) are replaced by a representative control \({\textit{\textbf{u}}}\left[ {{\varvec{\theta }} ^{k-1,\mathrm{rep}},\tilde{{{\textit{\textbf{X}}}}}\left( t \right) ,t} \right] \). The points \({\varvec{\theta }} ^{k-1,\mathrm{rep}};k=1,\ldots ,{\textit{\textbf{M}}}\) are obtained as follows. For \(k=1\), in all the three methods (SS, GS and mHDR), \({\varvec{\theta }}^{0,\mathrm{rep}}\) is taken as the mean value of the random vector \({\varvec{{\varTheta }}} \), i.e. \({\varvec{\theta }} ^{0,\mathrm{rep}}={E}_{\mathrm{P}} \left[ {\varvec{{\varTheta }}} \right] \). In order to determine \({\varvec{\theta }}^{k-1,\mathrm{rep}}\) for the successive levels, a sequence of points \({\textit{\textbf{Y}}}_{1},\ldots ,{\textit{\textbf{Y}}}_{m-1} \) are obtained such that \({\textit{\textbf{Y}}}_{k};k\in \left\{ {1,\ldots ,{\textit{\textbf{M}}}-1} \right\} \) lies in the region \(E_{k} \). The algorithm for obtaining \({\textit{\textbf{Y}}}_{1},\ldots ,{\textit{\textbf{Y}}}_{m-1} \) is stated in box B1 of Annexure B in the ESM. Subsequently, in the GS and mHDR methods, the representative points for \(k\ge 2\) are obtained as \({\varvec{\theta }} ^{k-1,\mathrm{rep}}={\textit{\textbf{Y}}}_{k-1} \). To determine \({\varvec{\theta }}^{k-1,\mathrm{rep}}\) in the SS method, a parameter \(\rho =0.1\) is considered and the function values \(g\left( {z^{k-2,i}} \right) ;i=1,\ldots ,N_{\mathrm{O}} \) are sorted in ascending order. Let \(b_{\rho }^{k-1} \) denote the \(\rho N_{\mathrm{O}} \hbox {-th}\) largest value in the sorted sequence. The representative point is taken as \({\varvec{\theta }} ^{k-1,\mathrm{rep}}={\textit{\textbf{Y}}}_{d} \) where d is the smallest integer such that \(b_{d} \le b_{\rho }^{k-1} \).

From the above discussion, it follows that when \(P_{\left. {\mathrm{F}} \right| {{{{\Theta }}} }} \left( {\varvec{{\varTheta }}} \right) \) is estimated by Girsanov’s transformation, the conditional probability estimators \(\hat{{p}}_{k};k\in \left\{ {1,\ldots ,{\textit{\textbf{M}}}} \right\} \) in Box 1 are of the following form:

$$\begin{aligned}&\hat{{p}}_{k} =\frac{1}{N_{\mathrm{O}} }\sum \limits _{i=1}^{N_{\mathrm{O}} } {{I}\left\{ {g\left( {z^{k-1,i}} \right) \le b_{k} } \right\} } =\frac{1}{N_{\mathrm{O}} }\sum \limits _{i=1}^{N_{\mathrm{O}} } {{I}\left\{ {\xi ^{k-1,i}-\hat{{P}}_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} }^{\mathrm{GT}} \left( {{\varvec{\theta }}^{k-1,i}} \right) \le b_{k} } \right\} } \nonumber \\&\quad =\frac{1}{N_{\mathrm{O}} }\sum \limits _{i=1}^{N_{\mathrm{O}} } {{I}\left\{ {\xi ^{k-1,i}-\left\{ {\frac{1}{N_{\mathrm{I}} }\sum \limits _{j=1}^{N_{\mathrm{I}} } {\left( {\sum \limits _{r=1}^m {w_{r} \left( {{\varvec{\theta }}^{k-1,\mathrm{rep}}} \right) \frac{1}{R_{r}^{j} \left( T \right) }} } \right) ^{-1}{I}\left\{ {h^{*}-\mathop {\max }\limits _{0<t\le T} h\left[ {{\varvec{\theta }}^{k-1,i}, \tilde{{{\textit{\textbf{X}}}}}^{j}\left( t \right) } \right] \le 0} \right\} } } \right\} \le b_{k} } \right\} }\nonumber \\ \end{aligned}$$
(13)

The expression for \(\hat{{P}}_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} }^{\mathrm{GT}} \left( {{\varvec{\theta }}^{k-1,i}} \right) \) in the above equation follows from the discussion in Annexure A of the ESM. To estimate \(\hat{{p}}_{k} \) based on the above equation, for a given \(\left( {i,j} \right) ; \, i\in \left\{ {1,\ldots ,N_{\mathrm{O}} } \right\} ,j\in \left\{ {1,\ldots ,N_{\mathrm{I}} } \right\} \), an index \(\lambda _{ij} \in \left\{ {1,\ldots ,m} \right\} \) is sampled according to the probability mass function \(\hbox {P}\left[ {\lambda _{ij} =a} \right] =w_{a} \left( {{\varvec{\theta }}^{k-1,\mathrm{rep}}} \right) ;a=1,\ldots ,m\). The weights \(w_{a} \left( {{\varvec{\theta }}^{k-1,\mathrm{rep}}} \right) ;a=1,\ldots ,m\) are computed based on the procedure outlined in Annexure A. The sample realizations \(\tilde{{\textit{\textbf{X}}}}^{j}\left( t \right) \) and \(R_{r}^{j} \left( t \right) \) are obtained by solving the system of SDEs

$$\begin{aligned} \begin{array}{l} \left\{ {{ \begin{array}{*{20}c} {\hbox {d}\tilde{{\textit{\textbf{X}}}}\left( t \right) } \\ {\begin{array}{l} \hbox {d}R_{1} \left( t \right) \\ \, \vdots \\ \hbox {d}R_{m} \left( t \right) \\ \end{array}} \\ \end{array} }} \right\} =\left\{ {{ \begin{array}{*{20}c} {A\left[ {{\varvec{\theta }}^{k-1,i},\tilde{{\textit{\textbf{X}}}}\left( t \right) ,t} \right] +\varvec{\upsigma }\left[ {{\varvec{\theta }}^{k-1,i},\tilde{{\textit{\textbf{X}}}}\left( t \right) ,t} \right] {\textit{\textbf{u}}}^{\lambda _{ij} }\left[ {{\varvec{\theta }} ^{k-1,\mathrm{rep}},\tilde{{\textit{\textbf{X}}}}\left( t \right) ,t} \right] } \\ {\begin{array}{l} -R_{1} \left( t \right) {\textit{\textbf{u}}}^{1}\left[ {{\varvec{\theta }}^{k-1,\mathrm{rep}},\tilde{{\textit{\textbf{X}}}}\left( t \right) ,t} \right] ^{\mathrm{T}}{\mathbf {C}}^{-1}\left( {{\textit{\textbf{u}}}^{\lambda _{ij} }\left[ {{\varvec{\theta }}^{k-1,\mathrm{rep}},\tilde{{\textit{\textbf{X}}}}\left( t \right) ,t} \right] -{\textit{\textbf{u}}}^{1}\left[ {{\varvec{\theta }}^{k-1,\mathrm{rep}},\tilde{{\textit{\textbf{X}}}}\left( t \right) ,t} \right] } \right) \\ \quad \vdots \\ -R_{m} \left( t \right) {\textit{\textbf{u}}}^{m}\left[ {{\varvec{\theta }}^{k-1,\mathrm{rep}},\tilde{{\textit{\textbf{X}}}}\left( t \right) ,t} \right] ^{\mathrm{T}}{\mathbf {C}}^{-1}\left( {{\textit{\textbf{u}}}^{\lambda _{ij} }\left[ {{\varvec{\theta }}^{k-1,\mathrm{rep}},\tilde{{\textit{\textbf{X}}}}\left( t \right) ,t} \right] -{\textit{\textbf{u}}}^{m}\left[ {{\varvec{\theta }}^{k-1,\mathrm{rep}},\tilde{{\textit{\textbf{X}}}}\left( t \right) ,t} \right] } \right) \\ \end{array}} \\ \end{array} }} \right\} \hbox {d}t \\ \quad +\left\{ {{ \begin{array}{*{20}c} {\varvec{\upsigma }\left[ {{\varvec{\theta }}^{k-1,i},\tilde{{\textit{\textbf{X}}}}\left( t \right) ,t} \right] } \\ {\begin{array}{l} -R_{1} \left( t \right) {\textit{\textbf{u}}}^{1}\left[ {{\varvec{\theta }}^{k-1,\mathrm{rep}},\tilde{{\textit{\textbf{X}}}}\left( t \right) ,t} \right] ^{\mathrm{T}}{\mathbf {C}}^{-1} \\ \quad \vdots \\ -R_{m} \left( t \right) {\textit{\textbf{u}}}^{m}\left[ {{\varvec{\theta }}^{k-1,\mathrm{rep}},\tilde{{\textit{\textbf{X}}}}\left( t \right) ,t} \right] ^{\mathrm{T}}{\mathbf {C}}^{-1} \\ \end{array}} \\ \end{array} }} \right\} \hbox {d}\tilde{\textit{\textbf{B}}}^{\lambda _{ij} }\left( t \right) \\ \end{array} \end{aligned}$$
(14)

with initial conditions \(\tilde{{\textit{\textbf{X}}}}\left( 0 \right) ={\textit{\textbf{X}}}_{0} , \, R_{r} \left( 0 \right) =1;r=1,\ldots ,m\). The governing SDE for \(R_{r} \left( t \right) ;r=1,\ldots ,m\) stated above can be obtained from Eq. (A10).

Finally, it is noted that the computational time needed to implement the proposed methods scales approximately linearly, individually with respect to \(N_{\mathrm{O}} \) and \(N_{\mathrm{I}} \). A reduction in the computational time is possible by adopting parallelization. Estimation of the unconditional probability of failure can be parallelized when the mHDR method is used for deconditioning the conditional failure probability. Specifically, the probabilities \(\hbox {P}\left[ {\left. {E_{k} } \right| E_{k-1} } \right] ;k=2,\ldots ,M\) at the different levels can be estimated in parallel. Within each level, the computation of \(\hat{{p}}_{k} \), i.e. the estimator of \(\hbox {P}\left[ {\left. {E_{k} } \right| E_{k-1} } \right] \), requires evaluation of the function \(g\left( Z \right) =\xi -P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{{\varTheta }}} \right) \) for the \(N_{\mathrm{O}} \) samples \(\left\{ {z^{k-1,1},\ldots ,z^{k-1,N_{\mathrm{O}} }} \right\} \) distributed according to \(p_{Z} \left( {\left. z \right| z\in E_{k-1} } \right) \). These \(N_{\mathrm{O}} \) evaluations of \(g\left( Z \right) \) can be done in parallel. For every sample, \(z^{k-1,i}=\left\{ {{ \begin{array}{*{20}c} {\xi ^{k-1,i}} &{} {{\varvec{\theta }}^{k-1,i}} \\ \end{array} }} \right\} \), \(P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {{\varvec{\theta }}^{k-1,i}} \right) \) is evaluated either by analytical approximation, or by Girsanov’s transformation. In the latter case, evaluation of the estimator \(\hat{{P}}_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} }^{\mathrm{GT}} \left( {{\varvec{\theta }} ^{k-1,i}} \right) \) in Eq. (13) requires an additional \(N_{\mathrm{I}}\) evaluation of the dynamical system for each sample \({\varvec{\theta }}^{k-1,i}\). These additional \(N_{\mathrm{I}} \) evaluations can also be parallelized. However, when the SS and GS methods are employed, one cannot completely parallelize the estimation of the unconditional probability of failure. For these methods, only evaluation of the estimator \(\hat{{P}}_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} }^{\mathrm{GT}} \left( {{\varvec{\theta }}^{k-1,i}} \right) \) can be parallelized. In the present study, however, we have not explored issues related to parallelizing the computational steps.

5 Numerical illustrations

The procedures discussed in the previous section are now illustrated by considering two numerical examples. The first example considers a nonlinear single dof system subjected to stationary white noise excitation. The second pertains to a ten storey linear frame excited by filtered non-stationary Gaussian excitation. The latter example is a benchmark example reported in [31]. These problems are analysed using three alternative methods designated as follows: (a) method 1—the proposed procedure with \(\hat{{P}}_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{\theta }} \right) \) in Box 1 taken equal to the analytical approximation \(\hat{{P}}_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} }^{A} \left( {\varvec{\theta }} \right) \) (b) method 2—the proposed procedure with \(\hat{{P}}_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{\theta }} \right) \) in Box 1 taken equal to the Girsanov transformation-based estimator \(\hat{{P}}_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} }^{\mathrm{GT}} \left( {\varvec{\theta }} \right) \), and (c) method 3—large-scale direct Monte Carlo simulation which provides a benchmark for the estimates obtained from the other methods. In methods 1 and 2, the unconditional failure probability \(P_{\mathrm{F}} \) is estimated using the three alternative estimators described in Box 1, i.e. the estimators based on the SS, GS and mHDR methods. In the SS and GS methods, the Markov chains in the conditional levels are generated based on the procedure outlined in [20, 39]. In methods 2 and 3, integration of the governing SDE is performed using order 1.5 explicit stochastic Runge–Kutta method [40] with a time step of \({\Delta } t=0.01\,\hbox {s}\) in example 1 and \({\Delta } t=0.005\,\hbox {s}\) in example 2.

5.1 Example 1: nonlinear single degree of freedom oscillator

In this example, a sdof nonlinear oscillator subjected to stationary random excitation is considered. The governing equation of the system is written as

$$\begin{aligned}&\ddot{{V}}\left( t \right) +\dot{{V}}\left( t \right) \left[ {2\eta \omega +0.5\varepsilon \left( {\omega ^{2}V^{2}\left( t \right) +\dot{{V}}^{2}\left( t \right) +0.5\alpha V^{4}\left( t \right) } \right) } \right] +\omega ^{2}V\left( t \right) +\alpha V^{3}\left( t \right) =W\left( t \right) \nonumber \\&V\left( 0 \right) =0, \, \dot{{V}}\left( 0 \right) =0;t\ge 0 \end{aligned}$$
(15)

Here, \(W\left( t \right) \) is a zero mean Gaussian white noise process with auto-covariance \({E}_{\mathrm{P}} \left[ {W\left( t \right) W\left( {t+\tau } \right) } \right] =\sigma ^{2}\delta \left( \tau \right) \). The state space of the associated Ito’s SDE is given by\({{{\textit{\textbf{X}}}}}\left( t \right) =\left\{ {{ \begin{array}{*{20}c} {V\left( t \right) } &{} {\dot{{V}}\left( t \right) } \\ \end{array} }} \right\} \). The parameters \(\eta \), \(\omega \), \(\sigma \), \(\varepsilon \), and \(\alpha \) are modelled as correlated non-Gaussian random variables with distribution properties as given in Table 1. These random variables are collectively represented by a random vector \({\varvec{{\varTheta }}} \). A Nataf model [37] for the joint pdf \(p_{{\varvec{{\varTheta }}} } \left( {\varvec{\theta }} \right) \) is adopted. The failure event is defined in terms of the maximum steady state displacement. The problem on hand thus consists of determining the probability of failure \(P_{\mathrm{F}} =\hbox {P}\left[ {\left\{ {h^{*}-\mathop {\max }\nolimits _{t_{0}<t\le t_{0} +T} h\left[ {{\varvec{{\varTheta }}}, {\textit{\textbf{X}}}\left( t \right) } \right] \le 0} \right\} } \right] =\hbox {P}\left[ {\left\{ {h^{*}-\mathop {\max }\nolimits _{t_{0} <t\le t_{0} +T} V\left( t \right) \le 0} \right\} } \right] \). Here, \(h^{*}\) denotes the safe limit on displacement, \(t_{0} \) denotes the time needed for the response to reach steady state, and T denotes the duration over which the reliability is analysed. In the numerical work, we take \(t_{0} =10\,\hbox {s}\) and \(T=35\,\hbox {s}\).

Table 1 Example 1; quantities modelled as random variables and their properties
Full size table

The problem is solved for two cases: (i) case 1—here, the system is assumed to be linear (i.e. \(\alpha =0\) and \(\varepsilon =0)\), and (ii) case 2—here, nonlinearity is considered with \(\alpha \) and \(\varepsilon \) as stated in Table 1. In each case, different threshold values are selected and the failure probability is computed based on methods 1–3. It may be recalled that, in method 1, the conditional failure probability \(P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{\theta }} \right) \) for a given threshold \(h^{*}\), and for a given realization \({\varvec{\theta }} \) of the parameter vector, is estimated using the analytical approximation based on out-crossing theory. Here, one needs to determine the mean up-crossing rate of the threshold \(h^{*}\) by the response process \(h\left[ {{\varvec{\theta }}, X\left( t \right) } \right] \). This, in turn, requires knowledge of the joint pdf of the response process and its time derivative at different time instants. For the system defined by Eq. (15), an exact analytical expression for the joint pdf can be determined by solving the underlying Fokker–Planck equation [36]. Accordingly, the steady state joint pdf of the response is obtained as

$$\begin{aligned} f\left( {s,\dot{{s}};{\varvec{\theta }} } \right) =C_{0} \exp \left[ {-\frac{2\eta \omega }{\sigma ^{2}}\left\{ {\dot{{s}}^{2}+\omega ^{2}s^{2}+0.5\alpha s^{4}+\frac{0.25\varepsilon }{\eta \omega }\left( {\dot{{s}}^{2}+\omega ^{2}s^{2}+0.5\alpha s^{4}} \right) ^{2}} \right\} } \right] \end{aligned}$$
(16)

where \(C_{0} \) is the normalization constant. In the above equation, the variable s denotes the response, and \(\dot{{s}}\) denotes its time derivative. The steady state mean up-crossing rate \(\nu ^{+}\left( {h^{*},{\varvec{\theta }} } \right) \) can subsequently be determined by integrating the joint pdf according to the Rice formula stated in Sect. 3.1, i.e. according to the expression \(\nu ^{+}\left( {h^{*},{\varvec{\theta }} } \right) =\int \nolimits _0^\infty {\dot{{s}}} f\left( {s,h^{*};{\varvec{\theta }} } \right) \hbox {d}\dot{{s}}\). In the numerical work, \(\nu ^{+}\left( {h^{*},{\varvec{\theta }} } \right) \) is evaluated by numerical integration. To implement methods 1 and 2, the sample size \(N_{\mathrm{O}} \) for the failure probability estimators listed in Box 1 is taken equal to 200. In method 2, the sample size for the Girsanov transformation based estimator for \(P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{\theta }} \right) \) is taken as \(N_{\mathrm{I}} =5\). In the mHDR method, the number of Markov chains in each level is taken as 10, and an additional 125 samples are employed in each level to allow for dissipation of initial transients in MCMC sampling. During the burn-in phase, \(P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{\theta }} \right) \) is evaluated using the out-crossing statistic-based analytical approximation method. To implement method 3, a sample size of \(3\times 10^{6}\) is used. A total of 175 equi-spaced up-crossing time instants (i.e. \(m = 175\)) in the time window 10–45 s are selected to determine the Girsanov controls in method 2 (see, [29] for further details).

Tables 2 and 3 summarize the estimates of \(P_{\mathrm{F}} \) obtained from the proposed methods, i.e. methods 1 and 2, for cases 1 and 2, respectively. Here, \(\hat{{P}}_{\mathrm{F}} \) and \(\delta _{\hat{{P}}_{\mathrm{F}} } \) are the mean and coefficient of variation of the sample estimates of \(P_{\mathrm{F}} \) from 25 independent runs. The acceptability of the failure probability estimates obtained from the proposed methods is assessed by comparing the results with corresponding large-scale direct Monte Carlo simulation-based estimates (method 3). From Tables 2 and 3, it may be observed that, for different threshold levels, the mean of the failure probability estimates obtained using methods 1 and 2 shows satisfactory agreement with the estimates from method 3. Tables 2 and 3 also compare the coefficient of variation of the estimates of \(P_{\mathrm{F}} \) (numbers in parenthesis) obtained using the alternative particle splitting algorithms. It may be observed that the coefficient of variation of the estimator based on the GS method is relatively less, while the estimators based on the mHDR and SS methods show broadly similar levels of sampling variance.

Table 2 Example 1; estimates of \(P_{\mathrm{F}}\) from methods 1, 2, and 3 for case 1 (linear system)
Full size table
Table 3 Example 1; estimates of \(P_{\mathrm{F}}\) from methods 1, 2, and 3 for case 2 (nonlinear system)
Full size table

An idea of the computational effort needed to implement method 2 can be obtained by examining Table 4, where the total sample size and the CPU time needed to implement the method on a Intel(R) Core(TM) i7-3770 CPU@3.40 GHz processor with 8 GB ram have been reported. Here, \(T_{\mathrm{A}} \) denotes the time needed to determine the algorithmic parameters of the particle splitting methods. The quantities \(T_{\mathrm{R}} \) and \(N_{\mathrm{Tot}}\), respectively, denote the total time and the total number of SDE evaluations required to obtain a single estimate of \(P_{\mathrm{F}} \) during reliability analysis. The results noted in this table are averaged over 25 independent runs, and \(N_{\mathrm{Tot}} \) is rounded to the nearest integer. From these tables, it may be observed that the quantity \(T_{\mathrm{A}} \) is significantly higher for case 2 as compared to case 1. This is because in case 2, the constrained optimization problem for determining the representative Girsanov controls is solved numerically due to nonlinear nature of the system. In order to obtain the same coefficient of variation as in method 2, the sample size required in direct MCS (method 3) is approximately \(N_{\mathrm{Tot}} = \, 2.8\times 10^{4}\) for \(h^{*}=0.46\,\hbox {m}\) in case 1, and approximately \(N_{\mathrm{Tot}} =2.5\times 10^{4}\) for \(h^{*}=0.36\,\hbox {m}\) in case 2. Finally, it is noted that in method 1 the failure probability conditional on the random systems parameters is estimated via analytical approximation procedures based on out-crossing rate statistics. Hence, the quantity \(N_{\mathrm{Tot}}\), which denotes the number of SDE evaluations needed for reliability estimation, is not applicable for this method. However, for the sake of completeness, we provide the computational time needed to estimate the failure probability based on method 1 (using the mHDR method), which is approximately \(T_{\mathrm{R}} =30.3\,\hbox {s}\) for \(h^{*}=0.46\,\hbox {m}\) in case 1, and approximately \(T_{\mathrm{R}} =36.0\,\hbox {s}\) for \(h^{*}=0.36\,\hbox {m}\) in case 2. The time required for determining the algorithmic parameters in method 1 is the same as in method 2.

Table 4 Example 1; computational effort needed to implement method 2 for cases 1 and 2
Full size table

5.2 Example 2: ten storey linear frame

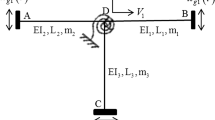
This example considers a randomly excited ten storey linear frame which constitutes one of the benchmark reliability examples studied in [31]. The frame is idealized as a mass-spring-dashpot system with mass \(m_{i} \), stiffness parameter \(k_{i} \) and damping ratio \(\eta _{i} \), \(i=1,\ldots ,10\). The governing equation of motion is written as

$$\begin{aligned}&{\mathbf {M}}_{{\mathbf {s}}} \ddot{{{\textit{\textbf{V}}}}}\left( t \right) +{\mathbf {C}}_{{\mathbf {s}}} \dot{{{\textit{\textbf{V}}}}}\left( t \right) +{\mathbf {K}}_{{\mathbf {s}}} {\textit{\textbf{V}}}\left( t \right) =-{\textit{\textbf{P}}}\left( t \right) \nonumber \\&{\textit{\textbf{V}}}\left( 0 \right) =0, \, \dot{{{\textit{\textbf{V}}}}}\left( 0 \right) =0;t\ge 0 \end{aligned}$$
(17)

where \(V\left( t \right) =\left\{ {{ \begin{array}{*{20}c} {V_{1} } &{} \cdots &{} {V_{10} } \\ \end{array} }} \right\} ^{\mathrm{T}}\) is the displacement vector, and \(\mathbf{M }_{\mathbf{s}}\), \(\mathbf{C }_{\mathbf{s}} \), and \(\mathbf{K }_{\mathbf{s}} \) are the mass, damping, and stiffness matrices given by

$$\begin{aligned} {\mathbf {M}}_{{\mathbf {s}}}= & {} \left[ {{ \begin{array}{*{20}c} {m_{1} } &{} 0 &{} 0 &{} \cdots &{} 0 \\ 0 &{} {m_{2} } &{} 0 &{} \cdots &{} 0 \\ \cdot &{} \cdot &{} \cdot &{} \cdots &{} \cdot \\ 0 &{} \cdots &{} 0 &{} 0 &{} {m_{10} } \\ \end{array} }} \right] , {\mathbf {C}}_{{\mathbf {s}}} =\left[ {{\begin{array}{*{20}c} {c_{1} +c_{2} } &{} {-c_{2} } &{} 0 &{} \cdots &{} 0 \\ {-c_{2} } &{} {c_{2} +c_{3} } &{} {-c_{3} } &{} \cdots &{} 0 \\ \cdot &{} \cdot &{} \cdot &{} \cdots &{} \cdot \\ 0 &{} \cdots &{} 0 &{} {-c_{10} } &{} {c_{10} } \\ \end{array} }} \right] \\ {\mathbf {K}}_{{\mathbf {s}}}= & {} \left[ {{ \begin{array}{*{20}c} {k_{1} +k_{2} } &{} {-k_{2} } &{} 0 &{} \cdots &{} 0 \\ {-k_{2} } &{} {k_{2} +k_{3} } &{} {-k_{3} } &{} \cdots &{} 0 \\ \cdot &{} \cdot &{} \cdot &{} \cdots &{} \cdot \\ 0 &{} \cdots &{} 0 &{} {-k_{10} } &{} {k_{10} } \\ \end{array} }} \right] \end{aligned}$$

The damping coefficients are given by \(c_{i} =2\eta _{i} \sqrt{m_{i} k_{i}}\). The random excitation \({\textit{\textbf{P}}}\left( t \right) \) is taken as \({\textit{\textbf{P}}}\left( t \right) =f\left( t \right) \left\{ {{\begin{array}{*{20}c} {m_{1} } &{} \cdots &{} {m_{10} } \\ \end{array} }} \right\} ^{\mathrm{T}}\). The input \(f\left( t \right) \) is modelled as a filtered non-stationary Gaussian white noise excitation according to the equation

$$\begin{aligned} f\left( t \right) =\omega _{d}^{2} x_{d} \left( t \right) +2\eta _{d} \omega _{d} \dot{{x}}_{d} \left( t \right) -\omega _{g}^{2} x_{g} \left( t \right) -2\eta _{g} \omega _{g} \dot{{x}}_{g} \left( t \right) \end{aligned}$$
(18)

where \(\left\{ {{ \begin{array}{*{20}c} {x_{d} } &{} {\dot{{x}}_{d} } &{} {x_{g} } &{} {\dot{{x}}_{g} } \\ \end{array} }} \right\} ^{\mathrm{T}}\) is defined by the linear system

$$\begin{aligned}&\ddot{{x}}_{d} \left( t \right) +2\eta _{d} \omega _{d} \dot{{x}}_{d} \left( t \right) +\omega _{d}^{2} x_{d} \left( t \right) =e\left( t \right) W\left( t \right) \nonumber \\&\ddot{{x}}_{g} \left( t \right) +2\eta _{g} \omega _{g} \dot{{x}}_{g} \left( t \right) +\omega _{g}^{2} x_{g} \left( t \right) =2\eta _{d} \omega _{d} \dot{{x}}_{d} \left( t \right) +\omega _{d}^{2} x_{d} \left( t \right) \nonumber \\&x_{d} \left( 0 \right) =0; \, \dot{{x}}_{d} \left( 0 \right) =0; \, x_{g} \left( 0 \right) =0; \, \dot{{x}}_{g} \left( 0 \right) =0 \end{aligned}$$
(19)

Here, \(e\left( t \right) \) is a modulating function that imparts non-stationarity to the input, and \(W\left( t \right) \) is a zero mean Gaussian white noise process with \({E}_{\mathrm{P}} \left[ {W\left( t \right) W\left( {t+\tau } \right) } \right] ={\mathcal {I}}\, \left( {e\left( t \right) } \right) ^{2}\delta \left( \tau \right) \). The modulating function is given by

$$\begin{aligned} e\left( t \right) =\left\{ {{ \begin{array}{ll} 0 &{} t\le 0\,\hbox {s} \\ t/2 &{} 0\,\hbox {s}\le t\le 2\,\hbox {s} \\ 1 &{} 2\,\hbox {s}\le t\le 10\,\hbox {s} \\ \exp \left( {-0.1\left( {t-10} \right) } \right) &{} \hbox {10\,s}\le t\le 20\,\hbox {s} \\ \end{array} }} \right. \end{aligned}$$
(20)

The numerical values of the parameters in Eq. (18) are taken as \(\omega _{d} =15\,{\hbox {rad/s}}\), \(\omega _{g} =0.3\,{\hbox {rad/s}}\), \(\eta _{d} =0.8\), \(\eta _{g} =0.995\) and \({\mathcal {I}}=0.08\,{\hbox {m}^{2}/s^{\hbox {3}}}\). The structural parameters \(m_{i},k_{i} \), and \(\eta _{i} \) are modelled as independent Gaussian random variables with statistical properties as listed in Table 5. These choices follow the models adopted in the definition of the benchmark exercise [31]. The state space of the Ito’s SDE associated with Eqs. (17) and (19) is given by \({\mathbf {X}}\left( t \right) =\left\{ {{ \begin{array}{*{20}c} {{{\textit{\textbf{V}}}}\left( t \right) } &{} {\varvec{\dot{{V}}}\left( t \right) } &{} {x_{g} \left( t \right) } &{} {\dot{{x}}_{g} \left( t \right) } &{} {x_{d} \left( t \right) } &{} {\dot{{x}}_{d} \left( t \right) } \\ \end{array} }} \right\} ^{\mathrm{T}}\).

Table 5 Example 2; statistical properties of the random structural parameters
Full size table
Table 6 Example 2; comparison of failure probability estimates and coefficient of variation of the estimators
Full size table

To define the failure condition, two response measures are considered: (i) the first floor displacement given by \(h_{1} \left[ {{\varvec{{\varTheta }}},{\textit{\textbf{X}}}\left( t \right) } \right] ={\textit{\textbf{V}}}_{1} \left( t \right) \), and (ii) the relative displacement between the ninth and the tenth floors given by \(h_{2} \left[ {{\varvec{{\varTheta }}},{\textit{\textbf{X}}}\left( t \right) } \right] ={\textit{\textbf{V}}}_{10} \left( t \right) -{\textit{\textbf{V}}}_{9} \left( t \right) \). The probability of failure is evaluated for the following cases: (i) case 1—here, the failure event is defined by the exceedance of the maximum value of the response \(h_{1} \left[ {{\varvec{{\varTheta }}},{\textit{\textbf{X}}}\left( t \right) } \right] \) over the threshold \(h_{1}^{*} =0.057\,\hbox {m}\), (ii) case 2—this case is similar to the previous case except that \(h_{1}^{*} \) is taken equal to 0.073 m, and (iii) case 3—here, the failure event is defined by the exceedance of the maximum value of the response \(h_{2} \left[ {{\varvec{{\varTheta }}},{\textit{\textbf{X}}}\left( t \right) } \right] \) over the threshold \(h_{2}^{*} =0.013\,\hbox {m}\). In each case, the reliability is analysed over the transient domain encompassing the duration 0–20 s.

The probability of failure is estimated based on the proposed methods, i.e. methods 1 and 2, using the alternative estimators listed in Box 1. While implementing method 1, as has been already noted, the mean up-crossing rate of the response \(h_{i} \left[ {{\varvec{{\varTheta }}},{\textit{\textbf{X}}}\left( t \right) } \right] \) over the corresponding threshold \(h_{i}^{*} \) needs to be evaluated. For this purpose, in the present study, the analytical expression reported in [38] is employed. For the estimators in Box 1, the sample size \(N_{\mathrm{O}} \) is taken equal to 250 for method 1 and equal to 200 for method 2. In method 2, the sample size in the Girsanov transformation-based estimator for \(P_{\left. {\mathrm{F}} \right| {\varvec{{\varTheta }}} } \left( {\varvec{\theta }} \right) \) is taken as \(N_{\mathrm{I}} =3\). Here, the Girsanov control is determined using 480 equi-spaced up-crossing time instants from the time window 6–18 s. In each case, 15 independent realizations of \(P_{\mathrm{F}} \) are obtained using methods 1 and 2, and the mean and coefficient of variation of the estimates are computed. The results are summarized in Table 6. This table also compares the estimates obtained using the proposed approach with the results obtained from two existing methods reported in [31], namely, the subset simulation method (SubSim) and the spherical subset simulation method (S\(^{\mathrm {3}})\). The results from few other variance reduction methods are also available in [31], but they are not reproduced here. The estimates from large-scale direct Monte Carlo simulation (i.e. method 3 with \(2.98\times 10^{7}\) samples) are also reported in these tables.

From Table 6, it is observed that the failure probability estimates obtained from method 2 agree well with those from large-scale direct Monte Carlo results, while the estimates from method 1 are marginally higher. The sampling variance associated with the proposed methods can be assessed based on the coefficient of variation, \(\delta _{\hat{{P}}_{\mathrm{F}} } \), reported in the table. The quantity \(N_{\mathrm{Tot}} \) in Table 6 denotes the average number of dynamical system evaluations needed to obtain a single estimate of \(P_{\mathrm{F}} \), and \({\Delta } =\delta _{\hat{{P}}_{\mathrm{F}} } \sqrt{N_{\mathrm{Tot}} } \) is the unit coefficient of variation. Based on the values of \(\delta _{\hat{{P}}_{\mathrm{F}} } \) and \({\Delta } \) reported in Table 6, it is concluded that the performance of method 2 is comparable with most of the other existing method.

6 Conclusions

The study considers the problem of time variant reliability analysis of randomly parametered and randomly excited dynamical systems. Two alternative approaches to tackle the problem are explored. The first approach shows that, when an approximate analytical solution of the failure probability conditional on the system parameters is known, it can form the basis for obtaining estimates of the unconditional reliability of the dynamical system by applying the Markov chain splitting techniques. The second approach demonstrates the feasibility of combining Girsanov’s transformation, based on closed loop controls, with the Markov chain splitting methods, to estimate the probability of failure. In order to avoid construction of control forces for every realization of the uncertain system parameters, a strategy to construct representative closed loop Girsanov’s controls, which can be used for an ensemble of realization of system parameters, is suggested. Numerical studies on linear/nonlinear systems demonstrate that the failure probability estimates obtained from the proposed methods compare well with those obtained from large-scale direct Monte Carlo simulations. Finally, it is noted that the determination of algorithmic parameters in the proposed methods requires prior knowledge of an approximate analytical estimate of the failure probability conditional on the random system parameters. For general nonlinear dynamical systems, this approximate solution based on out-crossing rate statistics is often difficult to obtain. A possible strategy to reinforce the proposed framework, in order to estimate the time variant reliability of general nonlinear dynamical systems, could be to combine the developed methods with equivalent linearization techniques. This aspect of the problem requires further exploration and remains as a topic for future work. In addition, extensions of the proposed methods to estimate time variant system reliability of randomly parametered dynamical systems, with multiple failure modes arranged in series, parallel, or combined series and parallel configurations, is currently being pursued by the present authors.