1 Introduction

A rotor is becoming more used widely in mechanical system [1], such as aero-engines, large blowers, machine tools, etc. With the precision development of mechanical manufacturing, precision requirements are improved gradually when machine tools manufacture workpieces. A rotor structure is the most important part of most of machine tools. Therefore, dynamic changes of the rotor structure should be monitored to avoid occurrence of faults. These show that online monitoring of a rotor system is still an urgent problem to be solved.

Misalignments [2] in a rotor system are a common fault. Great misalignment will cause some damage to the system. At present, many scholars have focused on many rotor misalignment studies. Gibbons [3] established the parallel misaligned rotor model and provided the expression of the forces and moments generated by parallel misalignment. Sekhar and Prabhu [4] applied the high-order finite element method and added the force and torque generated by flexible coupling misalignment to analyze the misalignment of the rotor–bearing system. Xu and Marangoni [5] analyzed the rotor misalignment and unbalance coupling faults. The results showed that the fundamental frequency amplitude (\(\hbox {A}_{1}\)) and the double frequency amplitude (\(\hbox {A}_{2}\)) dominate the vibration spectrum of the system response. Sudhakar and Sekhar [6] summarized the effect of different modeling methods on system response, condition monitoring technique, and fault identification. Qi et al. [7] used the RBF network to classify the collected vibration signals. The results verified the effectiveness of this method. Yao et al. [8] proposed a virtual phase torque diagram method for self-sensing motor drive system to detect misalignment angles and identified misalignment in different directions. Sawalhi et al. [9] used the finite element method to establish the dynamic model and proposed a function to express the relationship between coupled bending stiffness and eccentric force, when the angle of rotation and the amount of parallel eccentricity change. It was found that the lower harmonics and higher harmonics of the rotor system increase with the increase of the rotational speed. Tuckmantel and Cavalca [10] studied the system misalignment under two different modeling methods and found that the higher harmonics appeared in system response. The EMD method was introduced by Lei et al. [11], and Lei summarized the latest application of EMD in the diagnosis of rotary machine. Rai and Mohanty [12] used the intrinsic mode function in the HHT transform to study the system response in the frequency domain and used it for fault identification. These diagnostic methods are all methods of linear theoretical analysis.

In references mentioned above, these methods of fault extraction have certain effectiveness, but they all neglect the nonlinear phenomena of the systems. However, nonlinear problems [13,14,15] are inevitable in the systems. Linear theory has certain limitations when studying dynamic behaviors of such systems. With introduction of nonlinear method of Volterra series, these problems will be expected to be solved. Some scholars [16,17,18] used the method of Volterra series to diagnose mechanical faults, but Volterra series is quite complex and cannot be applied to all nonlinear problems. Generalized frequency response functions (GFRFs) are a concept based on Volterra series. Researchers [19, 20] used GFRFs to study the nonlinear output of the system. Since GFRFs are a multidimensional function, it is difficult to use for accurate calculations in practical problems. To solve this problem, Lang and Billings [21] and Lang et al. [22]proposed NOFRFs. It is a one-dimensional function that allows the output of a nonlinear system [23,24,25] to be solved in a manner of solving a linear system. Peng et al. [26] used NOFRFs to detect the cracked beams and found the sub-resonances in the nuclear values of NOFRFs.

When a nonlinear system is excited by harmonic inputs [27], the higher harmonic response representing nonlinear components [28] will be found in the response of the nonlinear system. However, traditional linear theoretical analysis methods have certain weakness when analyzing these nonlinear components. With the development of NOFRFs, scholars [29,30,31] began to pay close attention to indexes based on NOFRFs for diagnosing mechanical faults. However, these indexes weaken ratio of the high-order nonlinear components in the nonlinear system response, which result in the decrease of their sensitivity for detecting faults of a nonlinear system.

Based on these indexes proposed in [29,30,31], the new method, named the variable weighted contribution rate of NOFRFs used to enhance the high-order nonlinear [32] components, is proposed in this paper. Through the study of the weighted contribution rate, it is found that the contribution rate Rn(2) is a single-valued function, which increase first and then decrease against the independent variable \(\rho \), so it will have a unique maximum. Newton–Raphson iterative method will be used to extract this maximum in this paper. Based on the maximum extracted, we propose the new detection index MR, which represents the maximum value of the single-valued function Rn(2). In this study, the rotor system with slight misalignment is simulated by using the lumped mass model, and the output response of the rotor system with slight misalignment is analyzed. We find that the index MR in diagnosis of the rotor system with slight misalignment is more sensitive than the traditional methods, and the index MR can be used to detect faults in nonlinear system. Based on the experimental platform of the rotor system, rotor experiments with slight misalignment are performed. The experimental results also verify the effectiveness of the index MR for detecting the rotor system with slight misalignment.

Section 2 introduces the relevant theory of NOFRFs. Section 3 establishes a mathematical model of the misaligned rotor system. The simulations which compare the application of new method proposed in this paper and the traditional methods on slight misalignment fault of the rotor system are performed in Sect. 4. The results are confirmed by experiment to be presented in Sect. 5. Finally, conclusions are given in Sect. 6.

2 Related theory of NOFRFs

2.1 NOFRFs under harmonic inputs

Linear methods were used to investigate system fault diagnosis in most of literatures. In a linear system, the relationship between input and output is expressed by a transfer function \(H(j\omega )\). Therefore, transfer function of the system can be obtained according to the input and output of the system.

$$\begin{aligned} Y(j\omega )=H(j\omega )X(j\omega ) \end{aligned}$$
(1)

where \(Y(j\omega )\) and \(X(j\omega )\) are the frequency domain expressions of the linear system time domain output y(t) and input x(t) after Fourier transform, respectively, and their relationship is shown in Fig. 1.

Fig. 1
figure 1

Frequency domain response of linear systems

Full size image

However, when harmonic inputs are loaded into a nonlinear system, its response will contain the nonlinear components. Linear theory will fail to analyze these nonlinear components.

By virtue of a concept of transfer function of a linear system, GFRFs are regarded as a transfer function as extension of a linear system into a nonlinear system. Therefore, the relationship of input and output of a nonlinear system can be expressed as

$$\begin{aligned} Y(j\omega )=\sum _{n=1}^N {Y_n (j\omega )} \end{aligned}$$
(2)

where

$$\begin{aligned}&Y_n (j\omega )=\frac{1/n^{1/2}}{(2\pi )^{n-1}}\nonumber \\&\quad \times \int _{\omega _1 +\cdots +\omega _n =\omega } {H_n (j\omega _1 ,\ldots ,j\omega _n )} \prod _{i=1}^n {X(j\omega )} \mathrm{d}\sigma _{n\omega }\nonumber \\ \end{aligned}$$
(3)

where N is the maximum order of the system nonlinearity, \(Y_{n}(j\omega )\) is the frequency domain expression of the nth order output response of the system, and \(H_{n}(j\omega )\) is the nth order GFRFs. It can be seen from the expression of \(H_{n}(j\omega )\) that GFRFs are multidimensional functions, and its dimension increases with increasing of the order of GFRFs. As the order increases, the corresponding amount of calculation of GFRFs becomes larger. Therefore, the “dimensional disaster” limits the development of GFRFs in field of faults diagnosis.

To solve this problem caused by dimension, Lang and Billings [21] proposed the concept of NOFRFs. Its specific expression is defined as

$$\begin{aligned} G_n (j\omega )=\frac{\int _{\omega _1 +\cdots +\omega _n =\omega } {H_n (j\omega _1 ,\ldots ,j\omega _n )} \prod \nolimits _{i=1}^n {X(j\omega _i )} \mathrm{d}\sigma _{n\omega } }{\int _{\omega _1 +\cdots +\omega _n =\omega } {\prod \nolimits _{i=1}^n {X(j\omega _i )} } \mathrm{d}\sigma _{n\omega } } \end{aligned}$$
(4)

on the condition that

$$\begin{aligned} \int _{\omega _1 +\cdots +\omega _n =\omega } {\prod _{i=1}^n {X(j\omega _i )} } \mathrm{d}\sigma _{n\omega } \ne 0 \end{aligned}$$
(5)

By means of Eqs. (2)–(4), it can be concluded that the relationship of input and output of a nonlinear system can be expressed as

$$\begin{aligned} Y(j\omega )= & {} \sum _{n=1}^N {Y_n (j\omega )} =\sum _{n=1}^N {G_n (j\omega )} X_n (j\omega ) \end{aligned}$$
(6)
$$\begin{aligned} X_n (j\omega )= & {} \frac{1/n^{1/2}}{(2\pi )^{n-1}}\int {_{\omega _1 +\cdots +\omega _n =\omega } \prod _{i=1}^n {X(j\omega )} \mathrm{d}\sigma _{n\omega }}\nonumber \\ \end{aligned}$$
(7)

where \(G_{n}(j\omega )\) can be estimated according to the method provided in [21]. Furthermore, \(G_{n}(j\omega )\) can be regarded as the transfer function of the nonlinear system. Therefore, the relationship between input and output in a nonlinear system can be displayed in Fig. 2. As shown in Fig. 2, the relationship between input and output of the nonlinear system can be expressed as the relationship between input and output of a plurality of linear systems, that is, \(H(j\omega )\) is equal to \(G_{1}(j\omega )\).

Based on the theory of NOFRFs, a response of a nonlinear system is presented in the form Eq. (6). When N approaches to infinity, a nonlinear system response is approximately equivalent to the sum of the response of N order linear subsystems. The transfer function of each order linear subsystem contains the nonlinearity of the system. To a certain extent, this reduces the calculation amount of a nonlinear system and avoids the problem caused by dimensionality. Therefore, there are immense research significances of NOFRFs in engineering fault diagnosis.

Fig. 2
figure 2

Frequency domain response of nonlinear systems

Full size image

When a harmonic \(u(t)=a\hbox {sin}(\omega t)\) is loaded into a system, the system frequency domain output can be expressed as [29]

$$\begin{aligned}&Y(jk\omega )\nonumber \\&\quad =\sum _{n=2}^{[(N-k+1)/2]} G_{k+2(n-1)} (jk\omega )U_{k+2(n-1)} (jk\omega ),\nonumber \\&\quad k=0,1,2,\ldots ,N \end{aligned}$$
(8)

This system frequency domain input is defined as

$$\begin{aligned} U_n (j(-n+2k)\omega )=\frac{1}{2^{n}}\frac{n!}{k!(n-k)!}\left| a \right| ^{n} \end{aligned}$$
(9)

The \(G_{n}(j\omega )\) based NOFRFs can be simplified to

$$\begin{aligned}&G_n (j(-n+2k)\omega )\nonumber \\&\quad =H_n \left( {\overbrace{j\omega ,\ldots ,j\omega }^k,\overbrace{-j\omega ,\ldots ,-j\omega }^{n-k}} \right) \end{aligned}$$
(10)

According to Eqs. (8)–(10), assuming \(N = 4\), nonlinear features of the system can be fully expressed, and other high-order [33] effects are ignored. In consequence, the frequency domain output and input of the system can be written as

$$\begin{aligned} \begin{aligned} Y(j\omega )&=G_1 (j\omega )U_1 (j\omega )+G_3 (j\omega )U_3 (j\omega ) \\ Y(j2\omega )&=G_2 (j2\omega )U_2 (j2\omega )+G_4 (j2\omega )U_4 (j2\omega ) \\ Y(j3\omega )&=G_3 (j3\omega )U_3 (j3\omega ) \\ Y(j4\omega )&=G_4 (j4\omega )U_4 (j4\omega ) \end{aligned} \end{aligned}$$
(11)

According to reference [21], when two different magnitudes a are selected to excite the nonlinear system, the first four NOFRFs of the nonlinear system can be obtained, namely \(G_{1}(j\omega )\), \(G_{2}(j\omega )\), \(G_{3}(j\omega )\), \(G_{3}(j3\omega )\), \(G_{4}(j2\omega )\), and \(G_{4}(j4\omega )\).

Fig. 3
figure 3

Jeffcott’s finite element model of the misaligned rotor system

Full size image

2.2 Proposal of variable weighted contribution rate

Nonlinear characteristics and related indexes can be used directly to detect the system faults. In the process of actual solution, the increase of nonlinear order of a system leads to decreasing amplitude of high-order NOFRFs, which makes it difficult to extract the amplitude. High-order NOFRFs play an important role in the detection of nonlinear system faults. Therefore, extraction of high-order nonlinear features is very necessary. Based on this, the new method is proposed in this paper to weight high-order NOFRFs so that the contribution rate of high-order NOFRFs to the response of the system increases. The specific weighting process is written as

$$\begin{aligned} T_n (j\omega )=\frac{G_n (j\omega )}{n^{\rho }} \end{aligned}$$
(12)

where \(T_{n}(j\omega )\) represents the weighted\( G_{n}(j\omega )\), \(n^{\rho }\) represents a weighted coefficient, and \(\rho \) is an independent variable. It can be found that the weighted method adopted in this paper is variable weighted, that is, the weighting will change with change of the independent variable \(\rho \). When \(\rho < 0\), as the nonlinear order of the system increases, the weighting of the high-order NOFRFs is greater, namely

$$\begin{aligned} 1=\frac{T_1 (j\omega )}{G_1 (j\omega )}<\frac{T_2 (j\omega )}{G_2 (j\omega )}<\cdots <\frac{T_n (j\omega )}{G_n (j\omega )} \end{aligned}$$
(13)

The weighted process can enhance the contribution rate of high-order NOFRFs of a system response, thus achieving the purpose of enhancing the high-order nonlinear features.

The basic theory of the variable weighted contribution rate of NOFRFs is conveyed above, which is expressed as:

$$\begin{aligned} Rn(n)= & {} \frac{\int \nolimits _{-\infty }^{+\infty } {\left| {T_n (j\omega )} \right| \mathrm{d}\omega } }{\sum \nolimits _{i=1}^N {\int \nolimits _{-\infty }^{+\infty } {\left| {T_i (j\omega )} \right| \mathrm{d}\omega } } }\nonumber \\= & {} \frac{\int \nolimits _{-\infty }^{+\infty } {\left| {\frac{G_n (j\omega )}{n^{\rho }}} \right| \mathrm{d}\omega } }{\sum \nolimits _{i=1}^N {\int \nolimits _{-\infty }^{+\infty } {\left| {\frac{G_i (j\omega )}{i^{\rho }}} \right| \mathrm{d}\omega } } }, \nonumber \\&1\le n\le N,\,\,\rho \in (-\infty ,0) \end{aligned}$$
(14)

The contribution rate of high-order nonlinear features \(G_{n}(j\omega )\) (\(n > 1\)) in the system is amplified by weighted process. The weighted contribution rate Rn(n) contains the order n of nonlinearity, which causes the weight increase as the order of nonlinearity increases. Only when the independent variable \(\rho \) is less than zero, the weighted coefficient \(n^{\rho }\) will be less than one, so that high-order nonlinear features of the system can be amplified. Therefore, the weighted contribution rate Rn solves the problem of difficult extraction of high order NOFRFs values.

Fig. 4
figure 4

Simplified model of the mechanical system of the misaligned rotor system

Full size image

3 Mathematical model of misaligned rotor system

Jeffcott rotor system [34] with angle misalignment will be used as an example in this paper. A schematic diagram of Jeffcott angle misaligned rotor system is shown in Fig. 3. In this paper, the method of lumped mass is used to model the angular misalignment rotor system. The rotor system is divided into 4 shaft segments. Each shaft segment has two nodes, so the rotor system has a total of five nodes.

The shaft and motor of the system are connected by a flexible coupling. Assuming there is a certain deflection angle \(\alpha \) between the shaft and motor, this will result in a misalignment torque T at the coupling. In order to calculate the misalignment torque, motor axis is projected onto the xoy plane, and \(\beta \) represents angle between the projection axis and the x-axis, as shown in Fig. 4. The misalignment torque T is decomposed to obtain

$$\begin{aligned} T_z =T\cos \alpha ,\,\,T_s =T\sin \alpha \end{aligned}$$
(15)

where \(T_{Z}\) and \(T_{S}\) are the torque of T decomposing to the rotor direction and perpendicular to the rotor direction, respectively. Decompose \(T_{S}\) again to obtain

$$\begin{aligned} T_x =T\sin \alpha \cos \beta ,\,\,T_y =T\sin \alpha \sin \beta \end{aligned}$$
(16)

According to Euler equation of motion, \(T_{x}\), \(T_{y}\), and \(T_{z}\) can be written as

$$\begin{aligned} \begin{aligned} T_x&=I_x \dot{\omega }_x +\omega _y \omega _z (I_z -I_y ) \\ T_y&=I_y \dot{\omega }_y +\omega _y \omega _z (I_x -I_z ) \\ T_z&=I_z \dot{\omega }_z +\omega _y \omega _x (I_y -I_x ) \end{aligned} \end{aligned}$$
(17)

where \(I_{x}\), \(I_{y}\), and \(I_{z}\) represent moment of the inertia about thex,y, and z axes, respectively, and \(\omega _{x}\), \(\omega _{y}\), and \(\omega _{z}\) represent the angular velocity of the rotor.

Due to the rotor system only rotates around the z-axis, Eq. (17) can be turned into

$$\begin{aligned} T\cos \alpha =I_R \vartheta _R \end{aligned}$$
(18)

where \(\vartheta _{R}\) represents the angular acceleration of the rotor and \(I_{R}\) represents the polar moment of inertia of the rotor.

In the misaligned rotor system, angular velocity should satisfy the following relationship [35]

$$\begin{aligned} \frac{\omega _R }{\omega _M }=\frac{C}{1+D\cos (2\theta _M )} \end{aligned}$$
(19)

where \(\omega _{R}\) is the angular velocity of the rotor, \(\omega _{M}\) is the angular velocity of the motor, and \(\theta _{M}\) is the angle of rotation of the motor, \(C=\frac{4\cos \alpha }{3+\cos 2\alpha }\), \(D=\frac{1-\cos 2\alpha }{3+\cos 2\alpha }\).

The differential calculation at Eq. (19) can be obtained

$$\begin{aligned} \frac{\vartheta _R }{\omega _M }= & {} \frac{2\omega _M CD\sin 2\theta _M }{(1+D\cos 2\theta _M )^{2}} \end{aligned}$$
(20)
$$\begin{aligned} \vartheta _R= & {} \frac{2CD\sin (2\omega _M t)}{[1+D\cos (2\omega _M t)]^{2}}\omega _{_M }^2 \end{aligned}$$
(21)

Substitute Eq. (21) into Eq. (18) to obtain the misalignment torque T

$$\begin{aligned} T=\frac{2I_R \omega _{_M }^2 CD\sin (2\omega _M t)}{\cos \alpha [1+D\cos (2\omega _M t)]^{2}} \end{aligned}$$
(22)

Therefore, the governing equation for the angular misalignment rotor system is defined as

$$\begin{aligned} \left\{ {\begin{array}{l} \mathbf{M}\ddot{{\varvec{x}}}+(\mathbf{C}+\mathbf{G})\dot{{\varvec{x}}}+\mathbf{K}x=\mathbf{F}_e +T_x \\ \mathbf{M}\ddot{{\varvec{y}}}+(\mathbf{C}+\mathbf{G})\dot{{\varvec{y}}}+\mathbf{K}y=\mathbf{F}_e +T_y \\ \end{array}} \right. \end{aligned}$$
(23)

where M, C, G, K, \(\mathbf{F}_{e}\), \(\mathbf{T}_{x}\) and \(\mathbf{T}_{y}\) are the mass matrix, damping matrix, gyro matrix, stiffness matrix, unbalanced vector force, and misalignment vector torques of the rotor system in the x and y directions, respectively.

Table 1 Simulation parameters of the misaligned rotor system
Full size table
Fig. 5
figure 5

Time domain response at different misalignment angles

Full size image

The rest of simulation parameters are listed in Table 1. In addition, Newmark-\(\beta \) [36] method is used to solve Eq. (23), and vibration response of each node of the angular misaligned rotor system can be obtained at excitation speed of 1200 r/min. According to the method provided in [21], two different system excitations are required to calculate the NOFRFs value of the system. In this paper, the system excitations are changed by changing unbalanced mass of the rotor. The NOFRFs value of the system can be obtained from the two system inputs and outputs obtained.

Fig. 6
figure 6

Poincare section diagram at different misalignment angles

Full size image
Fig. 7
figure 7

Frequency domain response at different misalignment angles

Full size image

4 Fault feature extraction of misaligned rotor system

4.1 Extraction of response features based on the traditional methods

Based on the above analysis, the response feature curves can be obtained by simulating the angle misaligned rotor system, as shown in Figs. 5, 6, 7 and 8.

It can be concluded from Fig. 5 that the amplitude of time domain response changes slightly in the process of \(\alpha \) changing from \(0^{\circ }\) to \(0.35^{\circ }\), but the corresponding peak of time domain is relatively obvious in subsequent changes of the same interval. In other words, the maximum value of the time domain response is increased in the process of increasing the deflection angle \(\alpha \), but the amount of change is small. In actual engineering application, when the deflection angle \(\alpha \) changes slightly, it is not enough to identify change of \(\alpha \) only by the time domain response of the systems. This will affect manufacturing accuracy of machine tools.

Fig. 8
figure 8

Axis trajectory diagram at different misalignment angles

Full size image

The four points of Poincare section are almost coincident as shown in Fig. 6 when the deflection angle \(\alpha \) takes \(0^{\circ }\), \(0.35^{\circ }\), \(0.7^{\circ }\) and \(1.05^{\circ }\), respectively. And these four points successively move toward left upper side, as the increasing of deflection angle \(\alpha \). This indicate that they can be regarded approximately as a same periodic motion when \(\alpha \) adopts these four numerical values. In addition, the four axial trajectories displayed in Fig. 8 also show the same coincident tendency. However, from Figs. 5, 6 and 8, it can be concluded that the corresponding curve changes become apparent gradually as the misalignment is aggravated, but the amount of change is small.

The frequency domain response of the rotor system with misalignment will show a manifest double frequency, but it is found from Fig. 7 that the fundamental frequency is unchanged basically and the double frequency amplitude is almost zero in the case of slight misalignment, losing the obvious feature of misalignment of rotor systems. Therefore, only small changes in the deflection angle will not be recognized from these changes from Figs. 5, 6, 7 and 8. We attempt to find a suitable index to identify the slight changes in the deflection angle.

4.2 Fault feature extraction based on weighted contribution rate Rn

Through the analysis in Sect. 2.2, we propose the variable weighted contribution rate Rn based on NOFRFs. By virtue of the assumption in Sect. 2.1 that \(N=4\) is sufficient to express the nonlinear characteristics of a system, variation curves of Rn(1)–Rn(4) are obtained by using the method of concentrated mass model and the variable weighted contribution rate, as shown in Fig. 9.

Fig. 9
figure 9

Rn curves at different misalignment angles (a–d)

Full size image

As the independent variable \(\rho \) changes, as shown in Fig. 9, among the four curves of Rn(1)-Rn(4), only Rn(2) and Rn(3) show a tendency of increasing first and then decreasing. In addition, it can be seen from the zooms in Fig. 9b, c that as the misalignment angle increases gradually the value of Rn(2) increases and the value of Rn(3) decreases when the independent variable \(\rho \) is constant. But as the misalignment angle increases, the nonlinearity of the system increases. In theory, the magnitude of Rn(3) can be used to detect the severity of the faults, but it is logically opposite to the increase of nonlinearity. Therefore, this paper does further research on the Rn(2) function.

The specific expression of Rn(2) can be derived from Eq. (14) as follows

$$\begin{aligned} Rn(2)= & {} \frac{\int \nolimits _{-\infty }^{+\infty } {\left| {T_2 (j\omega )} \right| \mathrm{d}\omega } }{\sum \nolimits _{i=1}^N {\int \nolimits _{-\infty }^{+\infty } {\left| {T_i (j\omega )} \right| \mathrm{d}\omega } } }\nonumber \\= & {} \frac{\int \nolimits _{-\infty }^{+\infty } {\left| {\frac{G_2 (j\omega )}{2^{\rho }}} \right| \mathrm{d}\omega } }{\sum \nolimits _{i=1}^N {\int \nolimits _{-\infty }^{+\infty } {\left| {\frac{G_i (j\omega )}{i^{\rho }}} \right| \mathrm{d}\omega } } }, \,\,\rho \in (-\infty ,0)\nonumber \\ \end{aligned}$$
(24)

Denote \(\int \nolimits _{-\infty }^{+\infty } {\left| {G_i (j\omega )} \right| \mathrm{d}\omega } =\varphi _i\) in Eqs. (24), and (24) be written as

$$\begin{aligned} Rn(2)=\frac{\frac{\varphi _2 }{2^{\rho }}}{\sum \nolimits _{i=1}^N {\frac{\varphi _i }{i^{\rho }}} }, \,\,\rho \in (-\infty ,0) \end{aligned}$$
(25)

It can be seen from Eq. (25) that Rn(2) is a function of the independent variable \(\rho \), and define \(H(\rho )={ Rn}(2)\)

$$\begin{aligned} H(\rho )=\frac{\frac{\varphi _2 }{2^{\rho }}}{\sum \nolimits _{i=1}^N {\frac{\varphi _i }{i^{\rho }}} }, \,\,\rho \in (-\infty ,0) \end{aligned}$$
(26)
Fig. 10
figure 10

MR curves at different speeds

Full size image

According to the analysis in Sect. 2.1, only the first four-order NOFRFs of the nonlinear system are considered here, so Eq. (26) can be expressed as

$$\begin{aligned}&H(\rho )=\frac{1}{2^{\rho }\frac{\varphi _1 }{\varphi _2 }+(\frac{2}{3})^{\rho }\frac{\varphi _3 }{\varphi _2 }+(\frac{1}{2})^{\rho }\frac{\varphi _4 }{\varphi _2 }+1}, \nonumber \\&\quad \rho \in (-\infty ,0) \end{aligned}$$
(27)

Let us also define \(g(\rho )\) as

$$\begin{aligned} g(\rho )=\frac{\mathrm{d}H(\rho )}{\mathrm{d}\rho } \end{aligned}$$
(28)

Under certain working conditions, \(\frac{\varphi _i}{\varphi _2}\), \(i=1,\,3,\,4\) in the function \(H(\rho )\) is constant. Therefore, it can be summarized from Eq. (27) that the function \(H(\rho )\) is a single-valued function. Therefore, \(H(\rho )\) has a maximum value as shown in Fig. 9b. Based on the above analysis, denote \(g(\rho )\) be derivative function of \(H(\rho )\). Solving the function \(g(\rho ) = 0\), then there must be only one solution \(\rho _{0}\) to this equation. In order to extract \(\rho _{0}\), Newton–Raphson iterative method is used to solve \(\rho _{0}\) in this paper. Newton–Raphson iterative method is one of the important methods for solving nonlinear equations [37, 38]. Its biggest characteristic is that it has the square convergence rate when an equation has a single root and can be used to solve multiple and complex roots of an equation. Therefore, this method is used widely. However, Newton–Raphson iterative method requires a suitable initial value to ensure the convergence and the accuracy of results. Therefore, this paper uses dichotomy to choose the suitable initial value of Newton–Raphson iterative algorithm. It can be seen from Fig. 9b that the solution interval of dichotomy is approximately \((-4, 0)\). Dichotomy is performed in this interval to solve \(\rho _{0}\). The \(\rho _{0}\) is brought into the function \(H(\rho )\), and define \({ MR}= H(\rho _{0})\).

4.3 Index MR based on NOFRFs

From the analysis in Sect. 4.2, the maximum value of the weighted contribution rate Rn(2) is extracted as the new index MR. In the process of extracting new index, it is ignored whether the independent variable \(\rho \) takes same value. It can be seen from Fig. 9b that the value of the independent variable \(\rho \) is approximately equal when the weighted contribution rate Rn(2) reaches the maximum value at different declination angles, so it can be ignored here whether the independent variable \(\rho \) takes the same value. The implication of the variable weighted proposed in this paper refers to variation of the independent variable \(\rho \) in process of change of the contribution rate index Rn (as shown in Fig. 9).

For the misalignment rotor system, the three speeds are simulated and the index MR is extracted. The results are shown in Fig. 10. As it can be found in Fig. 10, the indexes MR increase monotonously with increase of the declination angle \(\alpha \), and amplitude of the indexes MR increase gradually during the increase of rotation speed.

To illustrate that the index MR is more suitable for identifying working conditions of the slight misaligned rotor system, index MR is compared with the traditional fault extraction methods. The results are shown in Fig. 11. In Fig. 11, index MR is more suitable for diagnosing slight misalignment faults than \(\hbox {A}_{1}\)(fundamental frequency amplitude) and \(\hbox {A}_{2}\)(double frequency amplitude) [39] when the deflection angle \(\alpha \) changes.

Fig. 11
figure 11

Variation curves of \(\hbox {A}_{1}\), \(\hbox {A}_{2}\) and MR

Full size image
Table 2 Relative change rates of \(\hbox {A}_{1}\), \(\hbox {A}_{2}\) and MR at different misalignment angles
Full size table

Define the relative rate of change \(\eta \)

$$\begin{aligned} \eta _i =\frac{M_i -M_{i-\delta } }{M_{i-\delta } },\,\,i=0.15^{\circ },0.3^{\circ },0.45^{\circ },\ldots ,1.05^{\circ } \end{aligned}$$
(29)

where \(M_{i}\) represents the magnitude of MR, \(\hbox {A}_{1}\), and \(\hbox {A}_{2}\), i represents the misalignment angle, \(\delta /^{o}\) indicates the misalignment angle step, and the step length in the experiment is \(0.15^{\circ }\), \(\eta _{i}\) indicates the relative rate of current misalignment angle relative to previous one.

Fig. 12
figure 12

MR curves under two different mass excitations with the same rate of change

Full size image

Table 2 lists the relative change rate of index MR, \(\hbox {A}_{1}\), and \(\hbox {A}_{2}\) when deflection angle \(\alpha \) changes. It can also be concluded from Table 2 that the index MR is more suitable for diagnosing slight misalignment faults than \(\hbox {A}_{1}\) and \(\hbox {A}_{2}\).

4.4 Robustness analysis

To illustrate that the index MR proposed in this paper is suitable for fault detection of the slightly misaligned rotor system, this section elaborates its robustness.

Fig. 13
figure 13

MR curves under two different mass excitations with different rates of change

Full size image

Figure 12 is a graph of the index MR drawn when the relative changes in the two mass excitations are kept constant. In the two mass excitations, the magnitude of the second mass excitation is increased by 1% based on the first mass excitation. In addition, the first mass excitation of the second curve is the second mass excitation of the first curve in the adjacent two MR curves, and ten curves in Fig. 12 are obtained under such a regulation. Fig. 13 is a graph of the index MR plotted in the case where the first mass excitation is fixed but the second mass excitation is changed. And the second mass excitation is increased by 0.3% from the first mass excitation, and finally ten curves are obtained under two mass excitations relative change (i.e., case1 indicates that the relative change of the two mass excitations is 0.3%, and case2 indicates that the relative change of the two mass excitations is 0.6%, etc.). Figure 14 is an index MR graph drawn under speed fluctuation. The adjacent two rotation speeds are sequentially increased by 0.2%, and finally ten curves under the change of rotation speed are obtained.

Fig. 14
figure 14

MR curves under speed fluctuation

Full size image

In Fig. 13 that the monotonous increase trend of the curve of case10 is not obvious, that is, when the first four orders of NOFRFs of the rotor system are calculated, the two mass excitations cannot be too much difference. In addition, it can be seen from Figs. 12, 13 and 14 that the change trend (a monotonous increase trend) of the index MR curves in each figure is the same, and it can be found that the changed parameter has a weak influence on the index MR. These indicate that the index MR has certain stability for detecting the slight misalignment of the rotor system, and it can also be used to qualitatively detect the variation of the misalignment angle. It also proves that the index MR has certain superiority for detecting the slight misalignment of the rotor system.

Figures 12, 13 and 14 show more clearly that the index MR proposed in this paper is robust. Due to the proposed method takes into account the combination of robustness and dynamic performance in the design process, these results are achieved.

5 Experimental verification

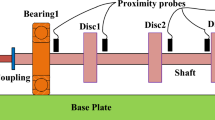
The experimental equipment is shown in Fig. 15. In order to obtain the first four orders of NOFRFs of system, it requires two loads of different amplitudes a. In the process of experiments in this paper, these two excitations were obtained by changing unbalanced mass, as shown in Fig. 15. Twice data of the system response under unbalanced mass should be collected simultaneously at the same speed. The rotation speed in the experiment was the same as the simulation, i.e., 1200 rpm. Misalignment angle in the experiment was changed by changing number of shims, each of shim having a thickness of 3 mm, as shown in Fig. 15. A total of four experiments were carried out in this paper, i.e., the normal condition of case 1, the addition of one shim (misalignment angle is \(0.35^{\circ }\)) in case 2, the addition of two shims (misalignment angle is \(0.7^{\circ }\)) in case 3, and the addition of three shims (misalignment angle is \(1.05^{\circ }\)) in case 4.

$$\begin{aligned} {\eta }'_i =\frac{{M}'_i -{M}'_{i-{\delta }'} }{{M}'_{i-{\delta }'} },\,\,i=0.35^{\circ },0.7^{\circ },1.05^{\circ } \end{aligned}$$
(30)

where \(M'_{i}\) represents magnitude of MR, \(\hbox {A}_{1 }\) and \(\hbox {A}_{2},i\) represents misalignment angle, \(\delta '/^{o}\) indicates misalignment angle step, and the step length in experiment is \(0.35^{\circ }\), \(\eta '_{i}\) indicates relative rate of current misalignment angle relative to the previous one.

Fig. 15
figure 15

Experimental equipment

Full size image

It can be seen from Fig. 16 that the magnitude of index MR increases when the deflection angle changes, which are consistent with the simulation results. By comparing with \(\hbox {A}_{1}\) and \(\hbox {A}_{2}\), it can be concluded that the index MR is more practical than the traditional fault feature extraction methods when identifying of the slight misaligned faults. In Table 3, the relative change rate \(\eta ^{\prime }\) of index MR is more stable compared with \(\hbox {A}_{1}\) and \(\hbox {A}_{2}\) when the deflection angle increases. Based on the analysis in Sect. 4.3, the results in simulation and experiment are roughly the same. These imply that both the simulation and the experiment confirm practicability of the index MR. The index MR has certain research significance in the weak faults diagnosis.

Fig. 16
figure 16

Variation curves of \(\hbox {A}_{1}\), \(\hbox {A}_{2}\) and MR

Full size image

6 Conclusion

The experiment and the simulation of the rotor system with slight misalignment are performed in this paper. During the research, it is found that response of the fault system under harmonic inputs contains nonlinear components. These weak nonlinear components will be ignored in the traditional fault extraction methods. In this study, the novel method for extracting nonlinear features in the frequency domain is introduced. The lumped mass mathematical model is established to simulate the slight misalignment rotor system and it is found that this method has a certain effectiveness to analyze the simulation results.

Table 3 Relative change rates of \(\hbox {A}_{1}\), \(\hbox {A}_{2}\) and MR at different misalignment angles
Full size table

However, the high-order nonlinear features are not obvious in the existing fault extraction methods based on NOFRFs due to very weak nonlinear features. In order to further enhance the high-order nonlinear features of response, we propose the theoretical method, namely the variable weighted contribution rate of NOFRFs. This method contains the nonlinear order n of the system, and it can amplify the high-order nonlinear features when the independent variable \(\rho \) changes, which makes the higher-order nonlinear features easier to extract. The analysis of the weighted contribution rate implies that Rn(2) is a single-valued function that is incremented first and then decremented and has a unique maximum. Based on these theories, Newton–Raphson iterative method is used to solve the maximum value, and a new index MR based on the maximum is proposed for detecting slight misalignment of the rotor system. In addition, the new method is compared with the traditional fault extraction methods through experiments and simulations.

The results demonstrate that index MR has better adaptability than the traditional fault extraction methods for the misalignment rotor system when deflection angle changes. Experiments and simulations have confirmed that the index MR has immense research implications in the rotor system fault diagnosis. The property of the index MR in other mechanical faults and structural damages detection will be discussed in future study.