Oil-film instability simulation in an overhung rotor system with flexible coupling misalignment

Abstract

Aiming at the oil-film instability of the sliding bearings at high speeds, this paper systematically investigates oil-film instability laws of an overhung rotor system with parallel and angular misalignments in the run-up and run-down processes. A finite element (FE) model of the overhung rotor system considering the gyroscopic effect is established, and the sliding bearings are simulated by a nonlinear oil-film force model based on the assumption of short-length bearings. Moreover, the effectiveness of the FE model is also verified by comparing our simulation results with the experimental results in the published literature. In the run-up and run-down processes with constant angular acceleration, the effects of parallel misalignment (PM) and angular misalignment (AM) on oil-film instability laws are simulated. The results show that under the perfectly aligned condition, the onsets of the first and second vibration mode instability in the run-down process are less than those in the run-up process due to the hysteresis effect. Under the misalignment conditions, the misalignment of the coupling can delay the onset of the first vibration mode instability and decrease its vibration amplitude. In comparison with the PM, the amplitudes of multiple frequency components are more obvious under the given AM conditions. Moreover, in the run-up and run-down processes with different misalignment conditions, the variation of the dominant vibration energy was observed according to the rotating frequency $f_{\mathrm{r}}$, the first-mode whirl/whip frequency $f_{\mathrm{n}1}$, the second-mode whirl/whip frequency $f_{\mathrm{n}2}$, or the their combinations, such as $f_{\mathrm{r}}$–$2f_{\mathrm{n}2}$.

1 Introduction

Studies on the dynamic characteristics of a rotor–bearing system are frequently required in the design of modern high-speed rotating machines, such as turbines, turbo-compressors and generators. Nowadays, some rotating machines are designed for high speed, more flexibility to pursue larger operating range, which will increase the risk of the fluid-induced instability. When the instability occurs, excessive vibrations at the first- or second-mode oil whip frequency can be observed, which is at typically subsynchronous speed. The instability may cause the unstable operation, high-level vibration of the system, rubbing between the rotor and stator, which will lead to potential damage of the rotating machinery.

The most common unstable phenomena such as oil whirl and oil whip have already been studied widely. In order to better simulate the nonlinearity of the sliding bearings, Muszynska [1] developed a nonlinear oil-film force model based on a series of experimental results. Adopting the Muszynska’s model, Ding et al. [2] investigated the Hopf bifurcation of a rotor/seal system and discussed the level of unbalance on the bifurcation of non-synchronized whirl. On the basis of the short-length bearing assumption, Capone [3, 4] proposed a nonlinear oil-film force model, with which he shows high agreement between the simulation results and the experimental results. Furthermore, his model shows excellent accuracy and convergence. Based on Capone’s model, Adiletta et al. [5] analyzed the possible chaotic motions stemming from the nonlinear response of the bearings, while Jing et al. [6, 7] studied the nonlinear dynamic behavior of the bearings considering the oil whip phenomenon. Moreover, de Castro et al. [8] investigated the instability threshold of a rotor system influenced by the amount of unbalance, rotor arrangement form and bearing parameters. Ding et al. [9] analyzed the non-stationary dynamic responses of the system during speed-up with a constant angular acceleration in a multi-bearing rotor, while Cheng et al. [10] investigated the nonlinear dynamic behavior of a rotor–bearing–seal coupled system. Ma et al. [11] proposed a rotor system with two disks and investigated the effects of different eccentric phase angles between two disks on oil-film instability. Adopting Capone’s model and a variational approximate finite bearing model, Liu et al. [12] analyzed stability characteristics of the inclined rotor–bearing system by numerical simulation and experimental results.

Zhang and Xu [13] developed a model of nonlinear oil-film force acting on a journal with unsteady motion and discussed nonlinear oil-film whip instability of a rigid Jeffcott rotor supported by short-length journal bearings. Xie et al. [14] studied the complicated behavior of a flexible rotor–bearing system with two unbalanced disks based on Zhang’s model [13]. Ding and Leung [15] analyzed non-stationary processes of a rotor–bearing system by taking the rotating angular speed as the control parameter. Ding and Zhang [16] investigated the dynamics of a continuous rotor–bearing–seal system based on the standard Galerkin method and the nonlinear Galerkin method.

The literature mentioned above mostly deal with the first flexural mode instability. However, for some rotating machines, the operational speed may be greater than several orders of the critical speeds. Under this condition, the high-order mode instability may appear, such as the second flexural mode instability mentioned in [1, 11, 17]. Muszynska [18] indicated that the second-mode whirl would occur under some special rotating speeds and this phenomenon has been observed experimentally and reported from machinery field data (see Fig. 1). Moreover, in the turbocharger rotor–bearing system, the instability caused by full-floating ring bearings also have similar laws, such as instabilities of inner oil-film (Sub1: conical mode, Sub2: translatory mode) and instability of outer oil-film (Sub3: instability of outer oil-film, conical mode) in [19–22].

Fig. 1

Spectrum cascade of vibration response of a steam turbine-driven compressor [18]

In rotating machines, misalignment is one of the most common problems, which can induce many other malfunctions. Considering the coupling effects of the flexible coupling misalignment and oil-film whirl/whip, the oil-film instability laws will be more complicated. However, limited attention [23, 24] has been paid to the problem compared to unbalance, bearing damage [25], crack [26], rub-impact [27], and fluid-induced vibrations [28, 29]. El-Shafei et al. [23] presented an experimental research on the oil whirl and oil whip in plain journal bearings and analyzed the effects of the supply pressure, unbalance of middle disk, unbalance of overhung disk, offset misalignment, and angular misalignment on the oil-film instability. Their results show that angular misalignment can significantly delay the onset of instability. Wan et al. [24] performed theoretical and experimental studies on the dynamic response of a multi-disk rotor system with flexible coupling misalignment. Their results indicate that the coupling misalignment can delay the occurrence of the first vibration mode instability and suppress the system vibration.

In order to understand the complicated oil-film instability mechanism considering the coupling effects of flexible coupling misalignment and oil-film whirl/whip, in this study, a rotor system provided in [23] is adopted as the research object, and the sliding bearings are simulated by a nonlinear oil-film force model (Zhang’s model [13]). The typical first-mode/second-mode whip phenomenon is produced in the run-up and run-down processes under parallel/annular misalignment conditions. The simulation results are compared with the experimental results to verify the validity of the model.

This paper is organized as follows: in Sect. 2, a FE model of an overhung rotor–bearing system with coupling misalignment is developed (see Sect. 2.1), and the model is verified by comparing the simulation results with the experimental results (see Sect. 2.2). In Sect. 3, three simulation conditions will be presented: the aligned overhung rotor system, the parallel misalignment, and the angular misalignment in Sects. 3.1, 3.2 and 3.3, respectively. Finally, the conclusions of this work are shown in Sect. 4.

2 Modeling of an overhung rotor system with coupling misalignment and model validation

2.1 Modeling of an overhung rotor with coupling misalignment

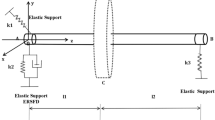
An overhung rotor–bearing system attached with four identical disks and one coupling and supported by two oil-lubricated bearings, as shown in Fig. 2. In order to study the rotor–bearing system efficiently, the FE model of the rotor–bearing system is simplified according to the following assumptions:

• (a) The shaft is divided into 13 Timoshenko beam elements and 14 nodes; each node has four degrees of freedom as is shown in Fig. 3. Note that $x_{A}, y_{A}$ and $\theta _{xA}, \theta _{yA}$ denote lateral displacements and angular displacements, and subscripts $A$ and $B$ denote two adjacent nodes $A$ and $B$ in the shaft, respectively.

• (b) The rigid disks and the coupling are simulated by lumped mass elements which are superimposed upon the corresponding shaft nodes. These elements are simulated by the mass $m_{d}, m_{c}$, the diametric and polar moments of inertia ($I_{dd}, I_{dc}$ and $I_{pd}, I_{pc})$; meanwhile, the gyroscopic effects of the disks are also considered. In Fig. 3, subscript $C$ denotes node $C$ on the rigid disk.

• (c) The left and right bearings are identical and simulated by nonlinear oil-film forces [13].

Fig. 2

Schematic view of the overhung rotor–bearing system, nodes, and elements

Fig. 3

FE model schematic view of a shaft element and rigid disk

The general displacement vector of a beam element for the shaft $\varvec{u}^{e }$ can be expressed as

$$\begin{aligned} \varvec{u}^{e}=[x_A \;y_A \;\theta _{xA} \;\theta _{yA} \;x_B \;y_B \;\theta _{xB} \;\theta _{yB} ]^{\mathrm{T}}, \end{aligned}$$

(1)

where the superscript $e$ stands for element number. The general displacement vector of a rigid disk $\varvec{u}_d^e$ is given as

$$\begin{aligned} \varvec{u}_d^e ={\begin{array}{llll} {[x_C }&{} {y_C }&{} {\theta _{xC} }&{} {\theta _{yC} ]^{\mathrm{T}}} \\ \end{array} }. \end{aligned}$$

(2)

The mass, stiffness and gyroscopic matrixes of shaft and disk/coupling elements are denoted as ${\varvec{M}}^{e}, {\varvec{ K}}^{e}, {\varvec{G}}^{e},{\varvec{M}}_d^e , {\varvec{G}}_d^e$ [30].

Considering the nonlinear oil-film forces, unbalance exciting force, the forces and bending moments caused by coupling misalignment and the rotor gravity, the dynamic equations of the rotor–bearing system can be written as:

$$\begin{aligned} \varvec{M}{\ddot{\varvec{q}}}+\left( {\omega \varvec{G}+\varvec{C}} \right) {\dot{\varvec{q}}}+\varvec{Kq}=\varvec{F}_u +\varvec{F}_b -\varvec{F}_g +\varvec{Q}, \end{aligned}$$

(3)

where M, K,C and $\omega$ G are the mass, stiffness, damping, and gyroscopic matrixes of the system. q denotes the displacement vector. F $_{u}$ represents the excitation force due to the disk unbalanced mass and its eccentricity during the run-up and run-down processes, which only exists at disk 1 (node 6). F $_{b}$ denotes the nonlinear oil-film force vectors of the sliding bearings at node 2 and node 10 (see Fig. 2). ${\varvec{F}}_{g}$ denotes the vector related to gravity in $y$ direction. Q are the excitation forces/moments caused by misalignment of the coupling; they are treated as excitations on the coupling (node 1), and only the $f_{\mathrm{r}}, 2f_{\mathrm{r}}, 3f_{\mathrm{r}}$ and $4f_{\mathrm{r}}$ harmonic components are considered [24, 31, 32].

The nodal force vector ${\varvec{F}}_{u}$ at node 6 is given as follows:

$$\begin{aligned} \varvec{F}_u =\left[ {\begin{array}{l} f_{ux} \\ f_{uy} \\ M_{ux} \\ M_{uy} \\ \end{array}} \right] =\left[ {\begin{array}{l} me\dot{\theta }^{2}\cos \theta +me\ddot{\theta }\sin \theta \\ me\dot{\theta }^{2}\sin \theta -me\ddot{\theta }\cos \theta \\ 0 \\ 0 \\ \end{array}} \right] , \end{aligned}$$

(4)

where $\theta$ is the angular displacement in torsional direction.

The excitation forces/moments Q caused by coupling misalignment at node 1 are given as follows:

$$\begin{aligned} \varvec{Q}=\left[ {{\begin{array}{l} {F_{x2} \left( {\sin \left( {\omega t} \right) +\sin \left( {2\omega t} \right) +\sin \left( {3\omega t} \right) +\sin \left( {4\omega t} \right) } \right) } \\ {F_{y2} \left( {\cos \left( {\omega t} \right) +\cos \left( {2\omega t} \right) +\cos \left( {3\omega t} \right) +\cos \left( {4\omega t} \right) } \right) } \\ {M_{x2} \left( {\sin \left( {\omega t} \right) +\sin \left( {2\omega t} \right) +\sin \left( {3\omega t} \right) +\sin \left( {4\omega t} \right) } \right) } \\ {M_{y2} \left( {\cos \left( {\omega t} \right) +\cos \left( {2\omega t} \right) +\cos \left( {3\omega t} \right) +\cos \left( {4\omega t} \right) } \right) } \\ \end{array} }} \right] . \end{aligned}$$

(5)

The forces and bending moments which the coupling imposes on the machine shaft are expressed by $F_{x2}, F_{y2}, M_{x2}, M_{y2}$ in $x$ and $y$ directions, as are shown in Fig. 4. The parallel or angular misalignment parameters ($\Delta X_{1}, \Delta X_{2}, \Delta Y_{1}, \Delta Y_{2},\theta _{3})$, bending spring rate per degree per diskpack ($K_{b})$, and the centre of articulation ($Z_{3})$ are also displayed in the figure. Care must be used to follow the sign convention shown in Fig. 4 [32]. Assuming that $z_{1}$ is the driving side, that (+) $T_{q}$ is applied as shown in Fig. 4 and that the rotation is in the same direction as the applied torque, the reaction forces, and moments that the coupling acts on the shaft can be expressed as follows [32].

Fig. 4

Coordinate system of the coupling positions: a parallel misalignment, b angular misalignment

For parallel misalignment:

$$\begin{aligned} \left\{ {\begin{array}{l} F_{x2} =(T_q \sin \varphi _1 -k_b \theta _1 +T_q \sin \varphi _2 +k_b \theta _2 )/Z_3 \\ F_{y2} =-(T_q \sin \theta _1 +k_b \varphi _1 +T_q \sin \theta _2 -k_b \varphi _2 )/Z_3 \\ M_{x2} =T_q \sin \theta _2 -k_b \varphi _2 \\ M_{y2} =T_q \sin \varphi _2 +k_b \theta _2 \\ \end{array}} \right. , \end{aligned}$$

(6)

where the misalignment angles $\theta _{1}, \theta _{2}, \varphi _{1}$ and $\varphi _{2}$ can be obtained by the Eq. (7).

$$\begin{aligned} \left\{ {\begin{array}{l} \theta _1 =\hbox {sin}^{-1}(\Delta X_1 /Z_3 ) \\ \varphi _1 =\hbox {sin}^{-1}(\Delta Y_1 /Z_3 ) \\ \end{array}}\right. , \quad \left\{ {\begin{array}{l} \theta _2 =\hbox {sin}^{-1}(\Delta X_2 /Z_3 ) \\ \varphi _2 =\hbox {sin}^{-1}(\Delta Y_2 /Z_3 ) \\ \end{array}} \right. . \end{aligned}$$

(7)

For angular misalignment:

$$\begin{aligned} \left\{ {\begin{array}{l} F_{x2} =T_q \sin \theta _3 /Z_3 \\ F_{y2} =k_b \theta _3 /Z_3 \\ M_{x2} =-k_b \theta _3 \\ M_{y2} =T_q \sin \theta _3 \\ \end{array}} \right. . \end{aligned}$$

(8)

According to the short-length bearing theory, the nonlinear oil-film force vectors ${\varvec{F}}_{b}$ at nodes 2 and 10 can be written as:

$$\begin{aligned} \varvec{F}_{bi} =\left[ {{\begin{array}{l} {F_{bxi} } \\ {F_{byi} } \\ {M_{bxi} } \\ {M_{byi} } \\ \end{array} }} \right] =\sigma \left[ {{\begin{array}{l} {f_{bxi} } \\ {f_{byi} } \\ 0 \\ 0 \\ \end{array} }} \right] (i=2,10), \end{aligned}$$

(9)

where $i$ denotes the node number, $f_{bxi}$ and $f_{byi}$ are dimensionless oil-film forces [13] where the dimensionless ${\tilde{\varvec{q}}}=\frac{{\mathbf {q}}}{c}$ and ${\dot{\tilde{\varvec{q}}}}=\frac{\dot{\varvec{q}}}{c\omega }$ are applied and $\sigma$ is as follow:

$$\begin{aligned} \sigma =\eta \omega \frac{D}{2}L\left( {\frac{D}{2c}} \right) ^{2}\left( {\frac{L}{D}} \right) ^{2}, \end{aligned}$$

(10)

here, $\eta , L, D$ and $c$ are oil viscosity, bearing length, journal diameter and mean radial clearance, respectively.

In practical engineering, most structures are multiple-degree-of-freedom systems, whose damping is mostly assumed by using Rayleigh damping theory, namely the damping matrix is obtained by superposition of mass matrix and stiffness matrix. This simulation method of energy dissipation has a lot of numerical advantages, and it can meet the needs of the general structure dynamics analysis. In this paper, the Rayleigh damping form is applied and obtained by the following formula [33]:

$$\begin{aligned} \varvec{C}= & {} \alpha _1 \varvec{M}+\beta _1 \varvec{K},\end{aligned}$$

(11)

$$\begin{aligned} \alpha _1= & {} \frac{60\left( {\omega _{\mathrm{n}2} \xi _1 -\omega _{\mathrm{n}1} \xi _2 } \right) \omega _{\mathrm{n}1} \omega _{\mathrm{n}2}}{\pi \left( \omega _{\mathrm{n}2}^2 -\omega _{\mathrm{n}1}^2 \right) }, \beta _1 =\frac{\pi \left( {\omega _{\mathrm{n}2} \xi _2 -\omega _{\mathrm{n}1} \xi _1 } \right) }{15\left( \omega _{\mathrm{n}2}^2 -\omega _{\mathrm{n}1}^2 \right) }, \end{aligned}$$

(12)

where $\omega _{\mathrm{n}1}$ and $\omega _{\mathrm{n}2}$ are the first and second natural frequencies (rev/min); $\xi _{1}$ and $\xi _{2}$ are the first and second modal damping ratios, respectively. In this paper, $\xi _{1}=0.02$ and $\xi _{2}=0.04$.

In this paper, Eq. (3) is solved by using Newmark’s integration method, which is a reliable algorithm to solve nonlinear equations in the time domain. In order to keep the accuracy and efficiency of the simulation, the calculation time increment is $1\times 10^{-5}\,\hbox {s}$. The spectrum cascade and top views of them are used to show the change of the frequency components under different misalignment levels.

2.2 Model validation

In this section, the simulation results are compared with the experimental results in [23] in order to examine the FE model validity. The detailed geometric dimensioning of the rotor is shown in Fig. 2, and the other parameters are listed in Table 1. Aiming at a well balanced and aligned overhung rotor [23], the measured amplitude spectrum (see Fig. 5a) at 5800 rev/min shows the oil whip component (OW) and its harmonics such as $2\times \hbox {OW}\; \hbox {and}\; 3\times \hbox {OW}$. Moreover, the first and second critical speed components also appear. For the simulation without unbalance, the amplitude spectrum of the rotor shows only the first-mode whip frequency $f_{\mathrm{n}1}$ and its harmonics (see Fig. 5b). The difference between the experimental result and simulation result is because the test rig is not balanced perfectly under practical condition. For the simulation with unbalance, the amplitude spectrum shows $f_{\mathrm{n}1}, f_{\mathrm{r}1}$, combination frequency components of $f_{\mathrm{n}1 }$ and $f_{\mathrm{r}1}$ (see Fig. 5c), which are similar to those [23]. The comparison indicates that the FE model of the rotor system considering nonlinear oil-film forces can accurately simulate the fluid-induced instability.

Table 1 Model parameters of the overhung rotor system

Fig. 5

Amplitude spectra at 5800 rev/min under case 1: a experimental results [23], b simulation results without unbalance, c simulation results with unbalance

In order to validate the accuracy of the coupling misalignment model, the comparison between the simulation results and the experimental results [23] is displayed in Fig. 6. The measured results show that the coupling misalignment mainly causes the $2f_{\mathrm{r}}$ component and the angular misalignment can delay the onset of instability more significantly than the parallel misalignment (see Fig. 6a, b). The similar instability phenomenon can also be observed in the simulation results (see Fig. 6c, d). For the parallel misalignment, the simulation results indicate that $f_{\mathrm{r}}$ and its harmonics are dominant; however, the measured results show the oil whip becoming dominant under the instability condition. Some reasons may lead to the different behavior, such as the difference between the simulation parameters and the physically real operating state and damping effects. On the whole, the FE model of the system can reproduce the fluid-instability law accurately under the coupling misalignment conditions.

Fig. 6

Spectrum cascades comparison between the experimental and simulation results under coupling misalignment conditions: a measured result under parallel misalignment [23], b measured result under angular misalignment [23], c simulation result under parallel misalignment, d simulation result under angular misalignment

3 Simulations and discussions

In this section, three effects on the instability law are simulated based on the FE model: (i) the angular acceleration $\alpha$, (ii) parallel misalignment, and (iii) angular misalignment. The simulation conditions are shown in Fig. 7, and the parameters related to specific coupling misalignments are listed in Table 2.

Fig. 7

Simulation parameters diagram

Table 2 Parameters of the coupling misalignment

3.1 Simulation 1 for the aligned overhung rotor system

Assuming that there exists an unbalance (unbalance moment of $1.89\times 10^{-4}$ $\hbox {kg/m}^{-1}$) at disk 1 and other disks are perfectly balanced for the aligned rotor system with constant angular acceleration, different run-up and run-down processes are performed by changing the angular acceleration $\alpha$ from 0 to $125\,\hbox {rad/s}^{2}$ with an increment of $25\,\hbox {rad/s}^{2}$. It is worth noting that the value of the angular acceleration $\alpha$ is negative in the run-down process and $\alpha =0\,\hbox {rad/s}^{2}$ corresponds to steady-state condition. The angular displacement $\theta$($t$) can be expressed as follows:

$$\begin{aligned} \theta (t)=\omega _0 t+1/2\alpha t^{2}, \end{aligned}$$

(13)

where $\omega _{0}$ is the initial angular velocity and $t$ the acceleration time.

Spectrum cascades of the right bearing in $y$ direction with angular acceleration at 0, 25 and $125\,\hbox {rad/s}^{2}$ are displayed in Figs. 8 and 9. The first and second unstable thresholds under $\alpha =0\sim 125\,\hbox {rad/s}^{2}$ conditions are depicted in Fig. 10. In these figures, points $\hbox {P}_{1}$ and $\hbox {P}_{2}$ denote the first and second unstable thresholds, respectively. The main characteristics of the obtained results are summarized as follows:

• (1) The frequency components at $\alpha =0$, 25 and $125\, \hbox {rad/s}^{2}$ all show the first- and second-mode whirl/whip frequencies $f_{\mathrm{n}1}$ and $f_{\mathrm{n}2}$, rotating frequency $f_{\mathrm{r}}$, and complicated combination frequency components about $f_{\mathrm{n}1}, f_{\mathrm{n}2}$ and $f_{\mathrm{r}}$, such as $2f_{\mathrm{n}2}, f_{r}-f_{\mathrm{n}1}, \hbox {and} f_{\mathrm{r}}+f_{\mathrm{n}1}$. (see Figs. 8 and 9).

• (2) In comparison with the steady-state condition ($\alpha =0\, \hbox {rad/s}^{2})$, it is clear that under transient situations ($\alpha =25$ and $125\,\hbox {rad/s}^{2})$, the onsets of the first- and second-mode instability are greater than those at $\alpha =0\,\hbox {rad/s}^{2}$ in the run-up process; however, they are all less than those at $\alpha =0\,\hbox {rad/s}^{2}$ in the run-down process (see Figs. 8 and 9). Larger $\alpha$ has a greater hysteresis effect on the onset of oil-film instability in comparison with $\alpha =0\,\hbox {rad/s}^{2}$ because of the tangential inertia force caused by run-up and run-down processes.

• (3) For the run-up and run-down processes, under small acceleration conditions ($\alpha \in [0, 50]\,\hbox {rad/s}^{2})$, the first- and second-mode instability thresholds all monotonically increase and decrease, respectively. However, the first- and second-mode instability thresholds are tending toward stability under large acceleration conditions ($\alpha \in [75, 125]\,\hbox {rad/s}^{2})$, as is shown in Fig. 10.

Fig. 8

Spectrum cascade of the right bearing in $y$ direction at $a=0$  rad/s$^{2}$

Fig. 9

Spectrum cascades of the right bearing in $y$ direction: a1 run-up process at $\alpha =25\,\hbox {rad/s}^{2}$, a2 run-down process at $\alpha =25\,\hbox {rad/s}^{2}$, b1 run-up process at $\alpha =125\,\hbox {rad/s}^{2}$, b2 run-down process at $\alpha =125\,\hbox {rad/s}^{2}$.

Fig. 10

Unstable thresholds under different angular accelerations

3.2 Simulation 2 for the parallel misalignment

In this section, the effects of PM on the oil-film instability of the rotor system are discussed under four different coupling PM conditions involving different misalignment levels. In the run-up and run-down processes, time-domain waveforms of the left and right bearings under PM condition-1 are shown in Fig. 11a, b, respectively. The rotating speed increases from 6 to 19,506 rev/min and decreases from 19,506 to 6 rev/min. Spectrum cascades corresponding to the time-domain waveforms in Fig. 11 are shown in Fig. 12, where the run-up and run-down processes are exhibited in one figure to give a better understanding of the differences between them. In order to display the abscissa of spectrum cascades conveniently, the left-hand ordinate is denoted by time not rotating speed. The top views of spectrum cascades of the left bearing under four different PM conditions at $\alpha =25\, \hbox {rad/s}^{2}$ are shown in Fig. 13. The main characteristics of the obtained results are summarized as follows:

• (1) The displacement of the left bearing is larger than that of the right bearing at low rotating speeds, and the non-synchronous frequency components for the left bearing are more complicated than those for the right bearing, which are due to the shorter distance between the left bearing and the misaligned coupling (see Figs. 11 and  12). These phenomena also indicate that the PM has greater influence on the left bearing than on the right bearing.

  Apparently, the transform of system energy can be observed, in which the dominant vibration energy of the system transfers from $f_{\mathrm{r}}$ via $f_{\mathrm{n}1}$ and $f_{\mathrm{n}2}$ to $f_{\mathrm{r}}$-$2\!f_{\mathrm{n}2}$ in the run-up process and from $f_{\mathrm{r}}$-$2\!f_{\mathrm{n}2}$ via $f_{\mathrm{n}2}$ and $f_{\mathrm{n}1}$ to $f_{\mathrm{r}}$ in the run-down process (see Figs. 12a, 13a–c). Under PM condition-4, the dominant vibration energy $f_{\mathrm{n}1}$ is replaced by $f_{\mathrm{r}}$, which indicates that the larger PM level can suppress the first-mode instability by decreasing its amplitude. Meanwhile, the amplitude of multiple frequency components, such as $2\!f_{\mathrm{r}}, 3\!f_{\mathrm{r}}$ and $4\!f_{\mathrm{r}}$, increases with the ascending PM levels, as is shown in Fig. 13.

• (2) The durations of the first- and second-mode instability are different in the run-up and the run-down processes under four PM conditions. Because of the hysteresis effect, the duration of the first-mode instability in the run-up process is longer than that in the run-down process, while the duration of the second-mode instability is shorter than that in the run-down process (see Figs. 12 and 13).

• (3) The onsets of the first and second vibration mode instabilities with PM faults in the run-up processes are equal to or larger than those in the run-up processes without PM faults, except for the second-mode instability under PM condition-4, which may be because the high PM level has an influence on the transform of system energy. Furthermore, in the run-down process, the change in the law of the onset of the first-mode instability is not regular and the onset of the second-mode instability has an increasing trend with the ascending PM level under $\alpha =25\,\hbox {rad/s}^{2}$.

Fig. 11

Time-domain waveforms of the left and right bearings in $y$ direction under the PM condition-1 ($\alpha =25$  rad/s$^{2}$): a left bearing, b right bearing

Fig. 12

Spectrum cascades under the PM condition-1 ($\alpha =25\, \hbox {rad/s}^{2})$: a left bearing, b right bearing

Fig. 13

Top views of the spectrum cascades of the left bearing under four different PM conditions ($\alpha =25$ rad/s$^{2}$): a condition-1, b condition-2, c condition-3, d condition-4

Fig. 14

Top views of the spectrum cascades of the left bearing under four different AM conditions ($\alpha =25\,\,\hbox {rad/s}^{2})$: a condition-1, b condition-2, c condition-3, d condition-4

3.3 Simulation 3 for the angular misalignment

Under four angular misalignment conditions where the misalignment level also increases successively, the results corresponding to run-up and run-down processes at $\alpha =25\,\hbox {rad/s}^{2}$ are shown in Fig. 14. The obtained results are summarized as follows:

• (1) Under four different AM conditions, the durations of the first- and second-mode instabilities and the transform law of system energy resemble those under the PM conditions. There are some differences under AM condtion-4, where the frequency component $f_{\mathrm{r}}/2$ with larger amplitude appears and the vibration amplitude is amplified at the intersection points of $f_{\mathrm{r}}/2$ and $2\!f_{\mathrm{n}2}$.

• (2) In contrast to the transient results without AM fault, the transient results with AM faults show some interesting phenomena. In the run-up process, the onset of the first-mode instability is delayed, while the onset of the second-mode instability is less than or equal to that in the run-up process without AM fault. In the run-down process, the onset of the first-mode instability changes little and that of the second-mode instability increases slightly.

• (3) In comparison with the PM conditions, the amplitudes of multiple frequency components are more obvious under the given AM conditions (see Fig. 14). Under large AM conditions, such as condtion-4, $f_{\mathrm{r}}$ and $2\!f_{\mathrm{r}}$ are dominant.

4 Conclusions

Based on finite element method, this work systematically illustrates the effects of angular acceleration, parallel misalignment (PM), and angular misalignment (AM) on the oil-film instability laws of a flexible rotor–bearing system in the run-up and run-down processes. The variation of dominant vibration energy of the system under different frequency components, such as $f_{\mathrm{r}}, f_{\mathrm{n}1}, f_{\mathrm{n}2}$, and $f_{\mathrm{r}}$–$2\!f_{\mathrm{n}2}$, were examined. The dominant vibration energy $f_{\mathrm{n}1}$ is replaced by $f_{\mathrm{r}}$ under the large misalignment level, which indicates that the larger misalignment levels can suppress the amplitude of $f_{\mathrm{n}1}$. In the run-up process, smaller misalignment levels also delay the onset of the second vibration mode instability; however, the instability may occur in advance under the larger misalignment levels. Furthermore, the amplitudes of multiple frequency components under PM conditions are more obvious than that under the AM conditions. Moreover, $f_{\mathrm{r}}$ and $2\!f_{\mathrm{r}}$ are dominant under the large AM level, and the frequency component $f_{\mathrm{r}}/2$ with larger amplitude was also observed and its amplitude is amplified at the crossings of $f_{\mathrm{r}}/2$ and $2\!f_{\mathrm{n}2}$.