Application of Multiple-Model Estimation Method to Rotor Fault Diagnosis

Abstract

The diagnosis and prediction of rotor fault is a key problem of rotor dynamics. In this investigation, a Multiple Model Estimator (MME) based method for typical rotor fault diagnosis is proposed. On a test rotor, crack and misalignment faults are produced respectively. Aiming at the test rotor, the normal, crack and misalignment rotor models are built accordingly. Based on these rotor models, a MME built with Kalman filters is setup with considering different crack and misalignment parameters. Via the estimation of the measured responses of the test rotor by MME, the rotor faults are identified successfully. It is proved that this proposed method is effective in the fault diagnosis, especially in the early stage of rotor faults.

1 Introduction

At present, the diagnosis methods on rotor faults mainly focus on feature identification of vibration signals, such as orbit of rotor center, frequency spectrum and so on [1]. All these methods usually need the help of engineer’s pre-knowledge or experiences. Although several artificial intelligence diagnosis methods have been used in the mechanical diagnosis such as neural network, rough sets etc., the accuracy of all these methods depend strongly on the quantity of fault cases and data. Therefore, the application of these methods is confined in many practical diagnoses.

Multiple-model Estimation method [2], which is strong in analyzing the problem with uncertainty or changing structure, parameter as well as transforming a complex problem into a simple one, has been used in many fields such as maneuver object tracing, failure detection and segregation. It has covered many fields, such as medical signals process, process control [3, 4], etc.

In this study, the MME built with Kalman filters will be employed to identify the crack and misalignment fault produced on a test rotor. It is expected to identify the faults effectively.

2 Rotor Models

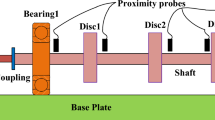
In this investigation, a Bently RK4 test rotor is used to produce the crack and misalignment fault respectively. From view of rotordynamics, it can be modeled as a Jeffcott rotor, shown in Fig. 1. The mass, stiffness and damping of the rotor are denoted by m, k, c. The eccentricity distance and revolving speed of the disk are denoted by $e,\omega$. By using the knowledge of rotor dynamics, the dynamical models for the normal and fault rotors can be built [5, 6].

Fig. 1

Jeffcott rotor

2.1 Normal Rotor Model

$$\left[ {\begin{array}{*{20}c} m & 0 \\ 0 & m \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\mathop x\limits^{..} } \\ {\mathop y\limits^{..} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} c & 0 \\ 0 & c \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\dot{x}} \\ {\dot{y}} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} k & 0 \\ 0 & k \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {me\omega^{2} \cos \omega t} \\ {me\omega^{2} \sin \omega t} \\ \end{array} } \right\}$$

(1)

Since rotors always has mass eccentricity, the dynamical equation for the rotor with unbalance can then be obtained as Eq. (1). Where the key parameters of the rotor are $m = 0.943\,{\text{kg}},\,K = 41{,}757\,{\text{N}}/{\text{m}},c = 10.91\,{\text{N}}\,{\text{s}}/{\text{m}}$, $\omega = 20\,{\text{Hz}}$, $e = 23.6\,\upmu{\text{m}}$.

2.2 Crack Rotor Model

There are many models for crack rotor’s dynamic behavior analysis. We adopt the square wave model which has considered the crack opening and closing effect.

$$\begin{aligned} & \left[ {\begin{array}{*{20}c} m & 0 \\ 0 & m \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\mathop x\limits^{..} } \\ {\mathop y\limits^{..} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} c & 0 \\ 0 & c \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\dot{x}} \\ {\dot{y}} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} k & 0 \\ 0 & k \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right\} - \frac{1}{2}f(\omega t) \cdot \Delta k \\ & \quad \times \,\left[ {\begin{array}{*{20}c} {1 + \cos 2\omega t} & {\sin 2\omega t} \\ {\sin 2\omega t} & {1 - \cos 2\omega t} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {me\omega^{2} \cos \omega t} \\ {me\omega^{2} \sin \omega t} \\ \end{array} } \right\} \\ \end{aligned}$$

(2)

$$f(\omega t) = \frac{ 1}{ 2} - \frac{ 2}{\pi }{\cos}\, \omega {\text{t}} + \frac{ 2}{ 3\pi }{{\cos}} \,3\omega {\text{t}} - \frac{ 2}{ 5\pi }{{\cos}} \,5\omega {\text{t}}$$

where, Δk is the decrease of shaft stiffness caused by crack. $f(\omega t)$ is the function to approach the opening and closing effect of the crack [1].

2.3 Misalignment Rotor Model

The misalignment of coupling includes parallel misalignment and angle misalignment, the unified dynamics equation of the two cases is:

$$\begin{aligned} & \left[ {\begin{array}{*{20}c} m & 0 \\ 0 & m \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\mathop x\limits^{..} } \\ {\mathop y\limits^{..} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} c & 0 \\ 0 & c \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\dot{x}} \\ {\dot{y}} \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} k & 0 \\ 0 & k \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right\} \\ & \quad = \,\left\{ {\begin{array}{*{20}c} {me\omega^{2} \cos \omega t + 2M\Delta e\omega^{2} \cos (2\omega t)} \\ {me\omega^{2} \sin \omega t + 2M\Delta e\omega^{2} \sin (2\omega t)} \\ \end{array} } \right\} \\ \end{aligned}$$

(3)

$\Delta e$ is the equivalent unbalance caused by misalignment, M is the mass of coupling.

3 Multiple-Model Estimation

3.1 Structure of Multiple-Model Adaptive Kalman Filters

Multiple-Model estimator consists of a parallel Kalman filter library and hypothesis tracking method. Every filter in the library has a specific system model. According to its own model and input vector u, every Kalman filter feedbacks the estimation $\hat{X}_{i}$ of the current system. Then, it uses the estimated value to form the predicted value of measurement vector Z. And the residual error $r_{i}$, which is calculated by Z subtracting the actual measurement vector, is the similarity of filter model and actual system model. In hypothesis tracking method, residual error is used to calculate conditional probability p _i of each Kalman filter model with the condition of measured values. p _i is used to evaluate the accuracy of the estimated value of each Kalman filter. Then use the probability weighted average of each state estimated value to calculate the hybrid state estimated value $\hat{X}_{MME}$ of actual system. The diagram of a multiple model estimator can be plotted as Fig. 2.

Fig. 2

Multiple model estimator

3.2 Multiple-Model Kalman Filters Equation

$$\left\{ {\begin{array}{*{20}l} {X_{i} (t_{k} ) =\Phi _{i} X_{i} (t_{k - 1} ) + B_{i} u(t_{k - 1} ) +\Gamma _{i} w_{i} (t_{k - 1} )} \hfill \\ {Z_{i} (t_{k} ) = H_{i} X_{i} (t_{k} ) + v_{i} (t_{k} )} \hfill \\ \end{array} } \right.$$

(4)

In which, X _i , Φ _i , B _i and Γ _i are state vector, state-transition matrix, control input matrix, noise input matrix of the ith Kalman filter model, respectively. u is the control input vector of the system; w _i is discrete dynamic white noise with zero-mean, and its auto-covariance is

$$E\left\{ {w_{i} (t_{k} )w_{i}^{T} (t_{j} )} \right\} = \left\{ {\begin{array}{*{20}l} {Q_{i} ,\quad t_{k} = t_{j} } \hfill \\ {0,\quad \;\; t_{k} \ne t_{j} } \hfill \\ \end{array} } \right.$$

(5)

In which, the measured vector, output matrix, measured discrete dynamic white noise of the ith Kalman filter model are respectively denoted by Z _i , H _i and v _i , v _i and w _i are mutually related. Both v _i and w _i have zero-mean, and the auto-covariance is

$$E\left\{ {v_{i} (t_{k} )v_{i}^{T} (t_{j} )} \right\} = \left\{ {\begin{array}{*{20}l} {R_{i} , \quad t_{k} = t_{j} } \hfill \\ {0,\quad \;\;t_{k} \ne t_{j} } \hfill \\ \end{array} } \right.$$

(6)

Both Kalman filter models and actual system models are linear models, but the dimension of them may be different. In many cases, Kalman filter models are the simplifications of actual system models (the state of Kalman filter models are always the subset of the actual system models).

The Kalman filters algorithm adopted the models above to calculate the time that Kalman filters state estimation need to update the best prediction and measurement, to update the best estimated equation and error covariance matrices of the state estimation. The time updating equations of state estimation of the Kalman filters, which are based on the Kalman filter models, are as follows:

$$\left\{ {\begin{array}{*{20}l} {\hat{X}_{i} (t_{k}^{ - } ) =\Phi _{i} \hat{X}_{i} (t_{k - 1}^{ + } ) + B_{i} u(t_{k - 1} )} \hfill \\ {\hat{Z}_{i} (t_{k}^{ - } ) = H_{i} \hat{X}_{i} (t_{k}^{ - } )} \hfill \\ \end{array} } \right.$$

(7)

$\hat{X}_{i}$ is state estimation vector of the ith Kalman filter; $\hat{Z}_{i} (t_{k}^{ - } )$ is the prediction of the measured vector of the ith Kalman filter before t _k ; $t_{k}^{ - }$ is the time point before the updating of the kth measured quantity. $t_{k - 1}^{ + }$ is the time point after the updating of the $k - 1$th measured quantity.

The time updating equation of covariance matrix of the state estimation error is:

$$P_{i} (t_{k}^{ - } ) =\Phi _{i} P_{i} (t_{k - 1}^{ + } )\Phi _{i}^{T} +\Gamma _{i} Q\Gamma _{i}^{T}$$

(8)

The actual measurement updating of state estimation of Kalman filter is given by:

$$\hat{X}_{i} (t_{k}^{ + } ) =\Phi _{i} \hat{X}_{i} (t_{k}^{ - } ) + K_{i} (t_{k} )r_{i} (t_{k} )$$

(9)

In which, the gain of Kalman filter is given by:

$$K_{i} (t_{k} ) = P_{i} (t_{k}^{ - } )H_{i}^{T} A_{i} (t_{k} )^{ - 1}$$

(10)

The residual error variance matrix which is calculated by Kalman filter is given by:

$$A_{i} (t_{k} ) = H_{i} P_{i} (t_{k}^{ - } )H_{i}^{T} + R_{i}$$

(11)

The residual error vector is a subtraction of the measured value Z and the Kalman filter estimated value $H_{i} \hat{X}_{i} (t_{k}^{ - } )$ which is based on the previous measured value, that is:

$$r_{i} (t_{k} ) = Z(t_{k} ) - H_{i} \hat{X}_{i} (t_{k}^{ - } )$$

(12)

The updating equation of variance matrix of the state estimation is:

$$P_{i} (t_{k}^{ + } ) = P_{i} (t_{k}^{ - } ) - K_{i} (t_{k} )H_{i} P_{i} (t_{k}^{ - } )$$

(13)

The error covariance matrix of the state estimation can be calculated by (8), (10), (11) and (13) in advance. The time updating of state vectors is determined by (4). According to the measured value, measurement updating is calculated by (12) and (9) in real-time.

3.3 Hypothesis Test Algorithm

Hypothesis test algorithm (HTA) test the residual error of filters in Kalman filters set at the same time. If the models of Kalman filter match well with the actual models, the error will be a sequence of Gaussian white noise with zero-mean, and the variance is:

$$A_{i} = H_{i} P_{i}^{ - } H_{i}^{T} + R_{i}$$

(14)

Thus, with the condition of prior measured value $Z^{{t_{k - 1} }} = [Z^{T} (t_{1} ), \ldots ,Z^{T} (t_{k - 1} )]^{T}$ and parameter vector $a \in \left\{ {a_{1} ,a_{2} , \ldots ,a_{k} } \right\}$, the conditional probability density function of measured value $Z(t_{k} )$ of the ith Kalman filter model at the time point t _k is:

$$f_{{z(t_{k} )|a,z^{{t_{k - 1} }} }} (Z(t_{k} )|a_{i} ,Z^{{t_{k - 1} }} ) = \beta_{i} \exp \{ \bullet \}$$

(15)

In which, $\left\{ \bullet \right\} = \left\{ { - \frac{1}{2}r_{i}^{T} (t_{k} )A_{i}^{ - 1} r_{i} (t_{k} )} \right\},\beta_{i} = \frac{1}{{(2\pi )^{m/2} |A_{i} |^{1/2} }}$, m is the dimension of measured vector.

Suppose that the conditional probability of a hypothetic model is:

$$p_{i} (t_{k} ) = \Pr \left\{ {a = a_{i} |Z^{{t_{k} }} } \right\}$$

(16)

Then, the conditional probability of this hypothetic model can be given like this:

$$p_{i} (t_{k} ) = \frac{{f_{{z(t_{k} )|a,z^{{t_{k - 1} }} }} (Z(t_{k} )|a_{i} ,Z^{{t_{k - 1} }} )p_{i} (t_{k - 1} )}}{{\sum\nolimits_{j = 1}^{K} {f_{{z(t_{k} )|a,z^{{t_{k - 1} }} }} (Z(t_{k} )|a_{j} ,Z^{{t_{k - 1} }} )p_{j} (t_{k - 1} )} }}$$

(17)

The conditional probability of previous time point is used in this equation, and a weighting on the conditional probability density of current time point in this model is given. Then we take the weighting as numerator and normalize each hypothesized model, finally get the current time point’s conditional probability of this hypothesis.

We obtain the hybrid state estimation of the actual system through weighting and fusing the state estimated vectors of different models by conditional probabilities of hypothesis models.

$$\hat{X}_{MME} (t_{k} ) = \sum\limits_{i = 1}^{N} {p_{i} } (t_{k} )\hat{X}_{i} (t_{k} )$$

(18)

If the correct model was included in these models, and there is no jumping between these models, the probability of this model will converges to 1.

Those filers will neglect the new observation as the probability of the best model tends to 1, while others are 0. Through giving lean limits to model probabilities and standardizing the probabilities of other models, the shortcoming above can be avoided.

4 Construction of MME

4.1 Construction of Kalman Filters

Rewrite the normal, crack and misalignment rotor models in the formation of state-space equation:

$$\dot{X} = f(X,t)$$

(19)

The state variable is denoted by$X = [x,y,\dot{x},\dot{y}]^{T}$. Since the vibration quantity is always in two directions of the rotor, it can be deemed as observation quantity. The measuring equation is:

$$Z = \left[ {\begin{array}{*{20}c} {z_{1} } \\ {z_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} x \\ y \\ {\dot{x}} \\ {\dot{y}} \\ \end{array} } \right]$$

(20)

For the misalignment rotor, the Eq. 3 can be written as:

$$\left[ {\begin{array}{*{20}c} {\mathop x\limits^{.} } \\ {\mathop y\limits^{.} } \\ {\mathop x\limits^{..} } \\ {\mathop y\limits^{..} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ { - \frac{k}{m}} & 0 & { - \frac{c}{m}} & 0 \\ 0 & { - \frac{k}{m}} & 0 & { - \frac{c}{m}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} x \\ y \\ {\mathop x\limits^{.} } \\ {\mathop y\limits^{.} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\frac{{4M\Delta e\omega^{2} }}{m}\cos 2(\omega t - \phi )} \\ {\frac{{4M\Delta e\omega^{2} }}{m}\sin 2(\omega t - \phi )} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {e\omega^{2} \cos \omega t} \\ {e\omega^{2} \sin \omega t} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {w_{1} (t)} \\ {w_{2} (t)} \\ {w_{3} (t)} \\ {w_{4} (t)} \\ \end{array} } \right]$$

(21)

$$Z = \left[ {\begin{array}{*{20}c} {z_{1} } \\ {z_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} x \\ y \\ {\dot{x}} \\ {\dot{y}} \\ \end{array} } \right] + \left[ \begin{aligned} v_{1} (t) \hfill \\ v_{2} (t) \hfill \\ \end{aligned} \right]$$

(22)

The Kalman filters for misalignment rotor can then be built by Eqs. 21 and 22. In the same way, the Kalman filters for normal and crack rotor can also be obtained.

4.2 Construction of Multiple Model Estimators

The influence of a crack on a rotor is mainly manifested in the decrease on the shaft stiffness, which corresponds to the Δk in dynamics equation of rotor Eq. 2. As for a certain crack on a real rotor, the Δk cannot be known. Hence, in the multiple model estimators, several crack rotor models with different Δk are used to estimate the severity. In the same way, several misalignment rotor models with different equivalent misalignment quantity are also used in the estimator. The feature parameters of each model used in the built MME are listed in Table 1.

Table 1 Parameters of Kalman filter models

5 Fault Diagnosis of Test Rotor

In order to validate the effectiveness of the proposed method on rotor fault diagnosis, a lateral crack is machined on the shaft of the test rotor. Where, the width of the crack is 0.1 mm, and its depth is the 3/10 of the shaft diameter. The crack locates near the disk which is fixed at the mid-span of the shaft. A misalignment fault is also produced by a misalignment coupling, which connects the motor and the shaft. The frequency spectrums of measured dynamical responses at the disk of the normal, crack, misalignment rotor are plotted in Figs. 3, 4 and 5 respectively.

Fig. 3

Spectrum of normal rotor in vertical direction

Fig. 4

Spectrum of crack rotor in vertical direction

Fig. 5

Spectrum of misalignment rotor in vertical direction

Using the measured rotor responses of normal, crack and misalignment rotor as the input of the MME respectively, the estimated probabilities of each model are then can be obtained and given in Figs. 6, 7 and 8. The Fig. 6 shows that the probability of normal rotor converses to 1, that means the current state of rotor match the normal model of the test rotor well. This indicates that the rotor runs in normal state. Whereas, in Fig. 7, the probability of crack rotor with Δk = 0.12 converses to 1, that indicates that the rotor runs in state of crack fault and the shaft stiffness decrease its 12 %. Figure 8 shows that the probability of the estimator with Δe = 0.2 mm converses to 1, it indicates that misalignment exists on the rotor and the equivalent eccentricity is 0.2 mm. These three cases show that the MME identifies the rotor state successfully.

Fig. 6

Normal rotor diagnosis

Fig. 7

Crack rotor diagnosis

Fig. 8

Misalignment rotor diagnosis

As Fig. 4 shows, it is difficult to reason the rotor including a crack fault in terms of spectrum features. In Fig. 5, the 2X component can be observed obviously. In terms of pre-knowledge, it can be reasoned that a crack or misalignment may occur on the rotor, but it is difficult to make sure what exact fault it is. However, the MME can identify these two faults directly and definitely. It can also estimate the key feature parameters change. The above investigation proves that the proposed MME method has advantages in rotor fault diagnosis.

6 Conclusions

In this study, the normal, crack and misalignment rotor models are built to approach the corresponding test rotor states. Based these rotor models, a MME with Kalman filters is setup. Via experiments, the rotor faults are identified successfully and the key feature parameters of the faults can also be estimated. It is proved that this proposed method is effective in the fault diagnosis of rotor system.