1 Introduction

There are always the cross-phase modulation term and the relative velocity among different component fields in the multi-component coupled systems [1,2,3,4]. Compared to the scalar systems [5,6,7,8], there exist very abundant pattern dynamics for the localized waves in the multi-component coupled systems [1, 9, 10]. In recent years, the interactional solutions of the multi-component systems have been widely researched, which included bright-dark mixed solitons [11, 12], dark and anti-dark solitons [13, 14], the interactional solutions among rogue waves (RWs), solitons (bright and dark solitons) and breathers [15, 16], etc. Compared with the standard RWs in the scalar equations [5, 7], a mass of novel patterns for vector RWs have been constructed in the coupled systems [1, 17,18,19].

Utilizing the Kadomtsev–Petviashvili (KP) hierarchy reduction method, the bright-dark mixed solitons were constructed in the multi-component nonlinear Schrödinger (NLS) equation [11], Yajima–Oikawa (YO) system [12] and Mel’nikov system [20]. The interactions between multi-dark solitons and multi-anti-dark solitons were constructed in the scalar nonlocal NLS equation by Darboux transformation [13]. The general soliton solutions, such as dark–dark, dark and anti-dark, anti-dark and anti-dark solitons, for the nonlocal NLS equation with PT-symmetry for both zero and nonzero boundary conditions were given by KP hierarchy reduction method [14]. The line rogue waves with dark and anti-dark rational traveling waves were derived in the nonlocal Davey–Stewartson (DS) equation by Darboux transformation [21]. The semirational solutions including RWs interacting with multi-breather, RWs interacting with multi-bright or dark soliton were constructed in different systems [9, 15, 16, 22,23,24]. In recent years, RWs have been researched in a lot of documents [1, 3, 5, 17,18,19, 25,26,27,28]. In many documents [3, 5, 25,26,27,28], the first-order RW has one hump, and the second-order and third-order RWs can split into three and six first-order RWs, respectively. Here, we call these RW patterns the traditional structures. However, there have been some documents focusing on the RW pairs in different systems, such as the NLS equations [1], the Sasa–Satsuma equation [17], the cubic–quintic NLS equations [18] and the Fokas–Lenells equations [19]. In the RW pairs [1, 17,18,19], the first-order RW pairs can split into two traditional first-order RWs, and the second-order RW pairs can split into four or six traditional lower-order RWs. Here, we are interested in two kinds of the solutions for the coupled nonlinear system. The first one is the interactional solution among higher-order RWs, multi-bright (or dark) solitons and breathers; the other is the high-order RW pairs.

In this paper, we focus on the interactional solutions and some RW pairs for the following coupled Lakshmanan–Porsezian–Daniel (LPD) equations [29,30,31]

$$\begin{aligned} iq_{jt}+ & {} q_{jxx}+ 2\sum _{k=1}^{2}|q_k|^2q_j + \gamma \Bigg [q_{jxxxx}+ 2\sum _{k=1}^{2}|q_{kx}|^2q_{j}\nonumber \\&+ 2\sum _{k=1}^{2}q_kq_{kx}^{*}q_{jx} + 6\sum _{k=1}^{2}q_k^{*}q_{kx}q_{jx}+4\sum _{k=1}^{2}|q_{k}|^2q_{jxx}\nonumber \\&+ 4\sum _{k=1}^{2}q_k^{*}q_{kxx}q_j + 2\sum _{k=1}^{2}q_kq_{kxx}^{*}q_j\nonumber \\&+ 6\left( \sum _{k=1}^{2}|q_k|^2\right) ^2q_j\Bigg ]=0,\quad (j=1,2), \end{aligned}$$
(1)

where \(q_1\) and \(q_2\) are all the functions of x and t, they denote the complex envelopes of the electric field, and the nonnumeric subscripted variables stand for the corresponding partial differentiation. The symbol “\(^{*}\)” indicates the complex conjugate, and “||” is the modulus of a complex function. The parameter \(\gamma \) is a real constant and denotes the strength of higher-order dispersive and nonlinear effects. The coupled LPD system (1) is also called the fourth-order nonlinear Schrödinger system and can be used to describe the ultrashort pulses in the birefringent optical fiber [29,30,31].

The single component LPD equation was first derived in [32], and its integrability was researched by the Painlevé analysis method in [33]. The infinitely many conservation laws and bound-state solitons of the system (1) were given in [29]. In [30], the authors investigated the modulation instability and the first-order semirational solutions for the coupled LPD equations (1). The first- and second-order breather-to-soliton solutions and the effect of the parameter \(\gamma \) for the system (1) were all discussed in [31]. The soliton excitations and interactions for the three-component LPD equations were constructed by the bilinear method [34]. Besides, the higher-order semirational solutions of the three-component LPD system were derived through the generalized Darboux transformation (DT) method [35].

As far as we know, it has not been reported that there are the interactional solutions among higher-order RWs, multi-bright (dark) solitons and multi-breather for the coupled LPD equations (1). Furthermore, the higher-order RW pairs for the system (1) have also not been investigated. It is very meaningful to construct the higher-order interactional solutions and RW pairs for the coupled LPD equations (1). Combining the DT method and the limiting technique, we will separately construct the above two kinds of solutions for the system (1) in the double- and triple-root situation of the spectral characteristic equation.

The present paper is organized as follows. In Sect. 2, the Lax pair and the N-fold DT for the coupled LPD equations (1) are given. In Sect. 3, we consider the spectral characteristic equation own a double-root case, and the interactional solutions are derived, which include higher-order RWs interacting with multi-bright (dark) solitons and multi-breather. In Sect. 4, considering the triple-root situation of the spectral characteristic equation, we construct the higher-order RW pairs. The last section includes several conclusions and discussions.

2 Darboux transformations for the coupled LPD equations

The Lax pair of the coupled LPD equations (1) can be given as [30, 31]

$$\begin{aligned} \Psi _x=U\Psi =\begin{pmatrix} -i\xi &{}\quad q_1^{*}&{}\quad q_2^{*}\\ -q_1&{}\quad i\xi &{}\quad 0\\ -q_2&{}\quad 0&{}\quad i\xi \end{pmatrix}\Psi ,\nonumber \\ \Psi _t=V\Psi =\begin{pmatrix}V_{11}&{}\quad V_{12}&{}\quad V_{13}\\ V_{21}&{}\quad V_{22}&{}\quad V_{23}\\ V_{31}&{}\quad V_{32}&{}\quad V_{33} \end{pmatrix}\Psi , \end{aligned}$$
(2)

where \(\Psi (x,t)=(\psi _1,\psi _2,\psi _3)^{\mathrm{T}}\) (“T” denotes the transpose of a vector) is the function of the independent variables x and t. Besides, \(\Psi \) denotes the eigenfunction and \(\xi \) is the spectral parameter. It is easily found that the coupled LPD system (1) can be generated from the compatibility condition \(U_t - V_x + UV - VU=0\). Additionally, the concrete elements \(V_{sj}~(1\le s,j\le 3)\)  in the matrix V can be given as follows

$$\begin{aligned} V_{11}= & {} - 8i\gamma \xi ^4 + 4i \left( 1 + \sum _{k=1}^{2}|q_k|^2\right) \xi ^2\\&+ 2\gamma \sum _{k=1}^{2}(q_k^{*}q_{kx} - q_kq_{kx}^{*})\xi - i\sum _{k=1}^{2}|q_k|^2\\&- i\gamma \left[ \sum _{k=1}^{2}(|q_k|^2_{xx} - 3|q_{kx}|^2) \right. \\&\left. + 6|q_1|^2|q_2|^2 + 3\sum _{k=1}^{2}|q_k|^4\right] ,\\ V_{1j}= & {} 8\gamma q_{j-1}^{*}\xi ^3 + 4i\gamma q_{j-1x}^{*}\xi ^2\\&- 2\left( \gamma q_{j-1xx}^{*} + 2\gamma \sum _{k=1}^{2}|q_k|^2q_{j-1}^{*} + q_{j-1}^{*}\right) \xi \\&- iq_{j-1x}^{*} - i\gamma (q_{j-1xxx}^{*}+\\&3\sum _{k=1}^{2}|q_k|^2q_{j-1x}^{*}+3\sum _{k=1}^{2}q_kq_{kx}^{*}q_{j-1}^{*}),\quad (j=2,3),\\ V_{ss}= & {} 8i\gamma \xi ^4 - 4i\gamma |q_{s-1}|^2\xi ^2\\&+ 2\gamma (q_{s-1}q_{s-1x}^{*}-q_{s-1x}q_{s-1}^{*})\xi +i|q_{s-1}|^2 \\&+ i\gamma (|q_{s-1}|^2_{xx}3|q_{s-1x}|^2\\&+ 3\sum _{k=1}^{2}|q_k|^2|q_{s-1}|^2),\quad (s=2,3),\\ V_{s1}= & {} - 8\gamma q_{s-1}\xi ^3+4i\gamma q_{s-1x}\xi ^2\\&+ 2(\gamma q_{s-1xx}+2\gamma \sum _{k=1}^{2}|q_k|^2q_{s-1}+ q_{s-1})\xi \\&- i\gamma (q_{s-1xxx}+3\sum _{k=1}^{2}|q_k|^2q_{s-1x}\\&+ 3\sum _{k=1}^{2}q_{k}^{*}q_{kx}q_{s-1}),\quad (s=2,3),\\ V_{sj}= & {} -4i\gamma q_{s - 1}q_{j-1}^{*}\xi ^2+2 \gamma (q_{s-1}q_{j-1x}^{*}-q_{s-1x}q_{j-1}^{*})\xi \\&+ iq_{s-1}q_{j-1}^{*}+i\gamma [(q_{s-1}q_{j-1}^{*})_{xx}-3q_{s-1x}q_{j-1x}^{*}\\&+ 3\sum _{k=1}^{2}|q_k|^2q_{s-1}q_{j-1}^{*}],\quad (s,j=2,3,s{\ne }j). \end{aligned}$$

Based on the DT of Ablowitz–Kaup–Newell–Segur (AKNS) system [36], we can directly construct the corresponding generalized DT for the system (1). Suppose that \(\Psi _1(\xi _1+\delta )=(\psi _1,\psi _2,\psi _3)^\mathrm{T}\) is a special solution of the Lax pair (2) with \(q_1=q_1[0],~q_2=q_2[0]\) and \(\xi =\xi _1+\delta \) (\(\delta \) is an infinitesimal parameter), the eigenfunction \(\Psi _1(\xi _1+\delta )\) can be expanded as the Taylor series at \(\delta =0\)

$$\begin{aligned} \Psi _1=\Psi _1^{[0]}+\Psi _1^{[1]}\delta +\Psi _1^{[2]}\delta ^2+\cdots +\Psi _1^{[N]}\delta ^N+\cdots ,\nonumber \\ \end{aligned}$$
(3)

where

$$\begin{aligned} \Psi _1^{[j]}= & {} \left( \psi _1^{[j]},\psi _2^{[j]},\psi _3^{[j]}\right) ^\mathrm{T}\\ {}= & {} \dfrac{1}{j!}\dfrac{\partial ^j \Psi _1}{\partial \delta ^j}|_{\delta =0},\quad (j=0,1,2,3\ldots ). \end{aligned}$$

Based on the above facts, the N-fold generalized DT for the system (1) can be directly given in the following theorem. In order to avoid tedious calculation of determinant with high-order matrix, the iteration form of the DT is chosen in the following contents.

Theorem 1

Utilizing the iterative formulae, the N-fold generalized DT for the coupled LPD equations can be directly constructed as follows

$$\begin{aligned}&\Psi [N]=T[N]T[N-1]\ldots T[1]\Psi , \end{aligned}$$
(4)
$$\begin{aligned}&T[j]=(\xi -\xi _1^{*})\left( I-\frac{\Psi _1^{[j-1]}\Psi _1^{[j-1]\dag }}{\Psi _1^{[j-1]\dag }\Psi _1^{[j-1]}}\right) \nonumber \\&\quad \qquad \quad (j=1,2,3\ldots N),\end{aligned}$$
(5)
$$\begin{aligned}&\Psi _1[N-1]=\Psi _1^{[0]}+\sum _{s=1}^{N-1}T_1[s] \Psi _1^{[1]} \nonumber \\&\qquad \qquad \qquad \quad + \sum _{N-1}^{k}\sum _{s}^{k-1}T_1[k]T_1[s]\Psi _1^{[2]} +\cdots \nonumber \\&\qquad \qquad \qquad \quad +T_1[N-1]T_1[N-2] \ldots T_1[1]\Psi _1^{[N-1]}, \end{aligned}$$
(6)
$$\begin{aligned}&q_k[N]=q_k[N-1]\nonumber \\&\quad \qquad \quad +\frac{2i(\xi _1^{*}-\xi _1)\psi _{k+1}[N-1]\psi _1[N-1]^{*}}{|\psi _1[N-1]|^2+|\psi _2[N-1]|^2+|\psi _3[N-1]|^2},\nonumber \\&\quad \quad \quad \quad (k=1,2) \end{aligned}$$
(7)

where \(\Psi _1[N-1]=(\psi _1[N-1],\psi _2[N-1],\psi _3[N-1])^\mathrm{T}\) and \(T_1[j]=T[j]|_{\xi =\xi _1}\), the symbol “\(^{\dag }\)” represents Hermite conjugation, and I is the \(3\times 3\) identity matrix.

In order to generate the new solutions through the above-mentioned N-fold generalized DT formulae, we choose the following general plane wave solutions as the seed solutions for the coupled LPD equations (1) as

$$\begin{aligned} q_1[0]=l_1e^{i\theta _1},\quad q_2[0]=l_2e^{i\theta _2}, \end{aligned}$$
(8)

with

$$\begin{aligned}&\theta _1=m_1x+n_1t,\quad \quad \theta _2=m_2x+n_2t,\\&n_1=\gamma m_1^4-(12\gamma l_1^2+4\gamma l_2^2+1)m_1^2+6\gamma (l_1^2+l_2^2)^2\\&\qquad -4\gamma l_2^2 m_2(m_1+m_2)+2(l_1^2+l_2^2),\\&n_2=\gamma m_2^4-(12\gamma l_2^2+4\gamma l_1^2+1)m_2^2+6\gamma (l_1^2+l_2^2)^2\\&\qquad -4\gamma l_1^2 m_1(m_1+m_2)+2(l_1^2+l_2^2), \end{aligned}$$

where \(l_1,l_2,m_1\) and \(m_2\) are all real constants (\(l_1\ne l_2,~m_1\ne m_2\)).

When the functions \(q_i~(i=1,2)\) in the Lax pair (2) are chosen as the seed solutions (8), we find that the corresponding matrices U and V in the Lax pair (2) include some exponential function elements. Choosing the following gauge transformation \(\Psi =M\Phi \), the Lax pair including exponential function elements can be transformed into the new Lax pair with constant elements

$$\begin{aligned}&\Phi _x=(M^{-1}UM-M^{-1}M_x)\Phi \equiv U_0\Phi , \end{aligned}$$
(9)
$$\begin{aligned}&\Phi _t=(M^{-1}UM-M^{-1}M_t)\Phi \equiv V_0\Phi , \end{aligned}$$
(10)

where

$$\begin{aligned} M=\mathrm{diag}\left( e^{-\frac{i}{3}(\theta _1+\theta _2)},e^{\frac{i}{3}(2\theta _1-\theta _2)},e^{\frac{i}{3}(2\theta _2-\theta _1)}\right) , \end{aligned}$$

all the symbol “diag” in this paper denotes the diagonal matrix.

Utilizing the principle of diagonalization of matrices, the special vector solutions for the new Lax pair (9–10) can be directly derived. In order to solve the new Lax pair (9–10), the spectral characteristic equation of the matrix \(U_0\) in Eq. (9) should be considered, and it reads as

$$\begin{aligned}&{\zeta }^{3}-i\xi \,{\zeta }^{2}\nonumber \\&\quad + \left( \frac{1}{3}\,{m_{{1}}}^{2}+\frac{1}{3}\, \left( -2\,\xi -m_{{2}} \right) m_{{1}}+{\xi }^{2}\right. \nonumber \\&\quad \left. -\frac{2}{3}\,m_{{2}}\xi +{l_{ {1}}}^{2}+{l_{{2}}}^{2}+\frac{1}{3}\,{m_{{2}}}^{2} \right) \zeta \nonumber \\&\quad -{\frac{2\,i }{27}}{m_{{1}}}^{3} -\frac{i}{27}\left( -3\,\xi -3\,m_{{2}} \right) {m_{{1}}}^{ 2}\nonumber \\&\quad -\frac{i}{27}\left( -18\,{\xi }^{2}+21\,m_{{2}}\xi +9\,{l_{{1}}}^{2}-18\,{l_{ {2}}}^{2}-3\,{m_{{2}}}^{2} \right) \nonumber \\&m_{{1}}-{\frac{2\,i}{27}}{m_{{2}}} ^{3}\nonumber \\&\quad +\frac{i}{9}{m_{{2}}}^{2}\xi -\frac{i}{27}\left( -18\,{\xi }^{2}-18\,{l_{{1}}}^{2}+ 9\,{l_{{2}}}^{2} \right) m_{{2}}\nonumber \\&\quad -i \left( {\xi }^{2}+{l_{{1}}}^{2}+{l_{ {2}}}^{2} \right) \xi =0, \end{aligned}$$
(11)

where \(\xi \) is the spectral parameter of the Lax pair (2), and \(\zeta \) is the eigenvalue of the matrix \(U_0\).

From the spectral characteristic equation (11) of the matrix \(U_0\), we can find that \(U_0\) have three eigenvalues \(\zeta _j~(j=1,2,3)\) and Eq. (11) can be seen as one-variable cubic equation of \(\zeta \). Through considering the double-root and triple-root situations of the spectral characteristic equation (11), we will discuss two kinds of novel solutions for the coupled LPD equations (1). If Eq. (11) has a double-root, we give the higher-order interactional solutions among higher-order RWs, multi-bright (dark) solitons and multi-breather for the coupled LPD system (1). If Eq. (11) possesses a triple-root, we construct the higher-order RW pairs for the coupled LPD system (1).

3 Higher-order interactional solutions for the double-root case

In the content of this paper, the interactional solutions denote that higher-order RWs interact with multi-bright solitons, dark solitons and breathers. Besides, the interactional solutions can be also understood that the higher-order RWs are generated on a multi-solitons background or a multi-breather background. In order to construct this kind of interactional solutions, we consider that the spectral characteristic equation (11) owns a double-root and that the special solutions of the Lax pair (2) are the linear combination of all the fundamental solutions.

For convenience, we can choose \(m_1=m_2=0\) in the seed solutions (8), and the new seed solutions can be written as

$$\begin{aligned} q_1[0]=l_1e^{i\theta t},\quad q_2[0]=l_2e^{i\theta t}, \end{aligned}$$
(12)

with \(\theta =2(l_1^2+l_2^2)[3\gamma (l_1^2+l_2^2)+1]\). Beginning with the spectral parameter \(\xi \) and the seed solutions (12), the special vector solutions of the Lax pair (2) can be elaborately derived as

$$\begin{aligned} \Psi _1=\begin{pmatrix}(P_1e^{2i\xi ^2t+H_1}-P_2e^{2i\xi ^2t+H_1})e^{-\frac{i}{2}\theta t},\\ \rho _1(-P_2e^{2i\xi ^2t+H_1}+P_1e^{2i\xi ^2t+H_1})e^{\frac{i}{2}\theta t}-cl_2e^{H_2}\\ \rho _2(-P_2e^{2i\xi ^2t+H_1}+P_1e^{2i\xi ^2t+H_1})e^{\frac{i}{2}\theta t}+cl_1e^{H_2}\end{pmatrix},\nonumber \\ \end{aligned}$$
(13)

with

$$\begin{aligned}&P_1=\frac{(\xi -\sqrt{\xi ^2+l_1^2+l_2^2})^{\frac{1}{2}}}{\sqrt{\xi ^2+l_1^2+l_2^2}},\\&P_2=\frac{(\xi +\sqrt{\xi ^2+l_1^2+l_2^2})^{\frac{1}{2}}}{\sqrt{\xi ^2+l_1^2+l_2^2}}, ~\rho _1=\frac{l_1}{\sqrt{l_1^2+l_2^2}},~\\&\rho _2=\frac{l_2}{\sqrt{l_1^2+l_2^2}},\\&H_1=i\sqrt{\xi ^2+l_1^2+l_2^2}\left[ x-2\xi (1+2\gamma (l_1^2+l_2^2-2 \xi ^2))t\right. \\&\quad \left. +\sum _{k=1}^{N}S_kf^{2k}\right] , \quad H_2=i\xi (x+8\gamma \xi ^3t), \end{aligned}$$

where \(S_k=m_k+in_k\), c, \(m_k\) and \(n_k\) are all arbitrary real constants, and f is a real infinitesimal parameter. Choosing \(\tau =l_1^2+l_2^2\) and \(\xi =\xi _1=i(\sqrt{\tau }+f^2)\), the spectral characteristic equation (11) can own a double-root. At this point, we can expand the vector function \(\Psi _1\) at \(f=0\) as

$$\begin{aligned} \Psi _1=\Psi _1^{[0]}+\Psi _1^{[1]}f^2+\Psi _1^{[2]}f^4+\cdots +\Psi _1^{[N]}f^{2N}+\cdots , \end{aligned}$$

with \(\Psi _1^{[j]}=(\psi _1^{[j]},\psi _2^{[j]},\psi _3^{[j]})^\mathrm{T}=\dfrac{1}{(2j)!}\dfrac{\partial ^{2j} \Psi _1}{\partial f^{2j}}|_{f=0}~(j=0,1,2,3\ldots )\).

Here, we only give the concrete expressions of \(\Psi _1^{[0]}\) and \(\Psi _1^{[1]}\) as follows

$$\begin{aligned} \psi _1^{[0]}= & {} \tau ^{-1/4} \left( 1/2+i/2 \right) {\mathrm{e}^{-3\,i\tau \,t \left( \tau \, \gamma +1 \right) }}\\&\sqrt{2} \left( 24\,{\tau }^{2}t\gamma +4\,\tau \,t+2 \,i\sqrt{\tau }x+i \right) ,\\ \psi _2^{[0]}= & {} \tau ^{-5/4} \left( -1/2-i/2 \right) \\&\sqrt{2}l_{{1}} \left( 24\,{\tau }^{5 /2}\gamma \,t+4\,{\tau }^{3/2}t+2\,i\tau \,x-i \sqrt{\tau } \right) \\&\times { \mathrm{e}^{3\,i{\tau }^{2}t\gamma -i\tau \,t}} -cl_{{2}}{\mathrm{e}^{8\,i{\tau }^{2}\gamma \,t-\sqrt{\tau }x}},\\ \psi _3^{[0]}= & {} \tau ^{-5/4}\left( -1/2-i/2 \right) \\&\ \sqrt{2}l_{{2}} \left( 24\,{\tau }^{5 /2}\gamma \,t+4\,{\tau }^{3/2}t+2\,i\tau \,x-i\sqrt{\tau } \right) \\&\times {\mathrm{e}^{3\,i{\tau }^{2}t\gamma -i\tau \,t}} +cl_{{1}}{ \mathrm{e}^{8\,i{\tau }^{2}\gamma \,t -\sqrt{\tau }x}},\\ \psi _1^{[1]}= & {} {\tau }^{-3/4}( -1/24-1/24\,i) {\mathrm{e}^{-3\,i\tau \,( \gamma \, \tau +1) t}}\\&\sqrt{2}( -8\,i{\tau }^{3/2}{x}^{3}-48\,{\tau } ^{2}{x}^{2}t-288\,\gamma \,{\tau }^{3}{x}^{2}t\\&+1152\, i\gamma \,{\tau }^{7/2}x{t}^{2}\\&+ 3456\,i{\gamma }^{2}{\tau }^{9/2}x{t}^{2}+96\,i{\tau }^{5/2}x{ t}^{2}\\&+ 6912\,{\gamma }^{2}{\tau }^{5}{t}^{3}+1152\,\gamma \,{\tau }^{4}{t} ^{3}+64\,{\tau }^{3}{t}^{3}\\&+ 13824\,{\gamma }^{3}{\tau }^{6}{t}^{3}-12\,i \tau \,{x}^{2}\\&- 144\,{\tau }^{3/2}xt-288\,\gamma \,{\tau }^{5/2}xt+1728\,i \gamma \,{\tau }^{3}{t}^{2}\\&+1728\,i{\gamma }^{2}{\tau }^{4}{t}^{2}\\&+ 240\,i{ \tau }^{2}{t}^{2}-6\,i\sqrt{\tau }x-108\,\tau \,t-744\,{\tau }^{2}\gamma \,t\\&- 24\,i\tau \,m_{{1}}+24\,\tau \,n_{{1}}+3\,i),\\ \psi _2^{[1]}= & {} ( cl_{{2}}x-32\,i{\tau }^{3/2}\gamma \,ctl_{{2}}) {\mathrm{e}^ {-\sqrt{\tau }x+8\,i\gamma \,{\tau }^{2}t}}\\&+ \tau ^{-5/4}(1/24+1/24\,i) \sqrt{2}l_1\Omega {\mathrm{e}^{3\,i\gamma \,{\tau }^{2}t-i\tau \,t}},\\ \psi _3^{[1]}= & {} ( -cl_{{1}}x+32\,i{\tau }^{3/2}\gamma \,cl_{{1}}t) {\mathrm{e} ^{-\sqrt{\tau }x+8\,i\gamma \,{\tau }^{2}t}}\\&+ \tau ^{-5/4}( 1/24+1/24\,i) \sqrt{2}l_{{2}}\Omega {\mathrm{e}^{3\,i\gamma \,{\tau }^{2}t-i\tau \,t}},\\ \Omega= & {} -8\,i{\tau }^{3/2}{x}^{3} -48\,{\tau }^{2}{x}^{2}t-288\,\gamma \,{\tau }^{3}{x}^{2}t\\&+1152\,i\gamma \,{\tau }^{7/2}x{t}^{2}\\&+ 3456\,i{\gamma }^{2}{\tau }^{9/2}x{t}^{2}+96\,i{ \tau }^{5/2}x{t}^{2}\\&+ 6912\,{\gamma }^{2}{\tau }^{5}{t}^{3}\\&+ 64\,{\tau }^{3}{t}^{3}+1152\,\gamma \,{\tau }^{4}{t}^{3} +13824\,{\gamma }^{3}{\tau }^{6}{t}^{3}\\&+12\,i\tau \,{x}^{2}\\&- 48\,{\tau }^{3/2}xt+288\,\gamma \,{\tau }^{5/2} xt+576\,i\gamma \,{\tau }^{3}{t}^{2}\\&+144\,i{\tau }^{2}{t}^{2}\\&- 1728\,i{\gamma }^{2}{\tau }^{4}{t}^{2}-6\,i\sqrt{\tau }x-744\,\gamma \,{\tau }^{2} t\\&- 12\,\tau \,t-24\,i\tau \,m_{{1}}+24\,\tau \,n_{{1}}-3\,i. \end{aligned}$$

Choosing \(N=1\) in Theorem 1, we can directly derive the following concrete expressions of the first-order interactional solutions for the coupled LPD equations (1) as

$$\begin{aligned}&q_1[1]=l_1e^{i\theta t}+\dfrac{4l_1F_1e^{i\theta t}+cl_2F_2{\mathrm{e}^{11\,i{\tau }^{2}t\gamma +3\,i\tau \,t-\sqrt{\tau }x}}}{ {c}^{2}({l_{{1}}}^{2}+{l_{{2}}}^{2}) {\mathrm{e}^{-2\,\sqrt{{ \tau }}x}}+G}, \nonumber \\\end{aligned}$$
(14)
$$\begin{aligned}&q_2[1]=l_2e^{i\theta t}+\dfrac{4l_2F_1e^{i\theta t}-cl_1F_2{\mathrm{e}^{11\,i{\tau }^{2}t\gamma +3\,i\tau \,t-\sqrt{\tau }x}}}{{c}^{2}({l_{{1}}}^{2}+{l_{{2}}}^{2}) {\mathrm{e}^{-2\,\sqrt{{ \tau }}x}}+G}, \nonumber \\ \end{aligned}$$
(15)

with

Fig. 1
figure 1

The first-order interactional solutions \(\gamma =\frac{1}{100}\): case 1 (a, b) with \(l_1=0,l_2=-1,c=\frac{1}{50}\); case 2 (c, d) with \(l_1=1,l_2=-\frac{1}{2},c=\frac{1}{500}\)

Full size image
$$\begin{aligned} F_1= & {} \tau ^{-\frac{1}{2}}(-576\,{\tau }^{4}{\gamma }^{2}{t}^{2}-192\,{\tau }^{3}\gamma \,{t}^{2}\\&+ 48 \,i{\tau }^{2}t\gamma -16\,{\tau }^{2}{t}^{2}+8\,i\tau \,t-4\,\tau \,{x}^{2}+1),\\ F_2= & {} \root 4 \of {\tau }\sqrt{2}\left( 2-2\,i \right) \left( -24\,{\tau }^{2}\gamma \,t-4\,\tau \,t\right. \\&\left. + 2 \,i\sqrt{\tau }x+i \right) ,\quad \tau =l_1^2+l_2^2,\\ G= & {} \tau ^{-\frac{3}{2}}(576\,{\tau }^{4}{\gamma }^{2}{t}^{2}{l_{{1}}}^{2}\\&+ 576\,{\tau }^{4}{\gamma }^{2}{t}^{2}{l_{{2}}}^{2}\\&+ 576\,{\tau }^{5}{\gamma }^{2}{t}^{2}+192\,{ \tau }^{3}\gamma \,{t}^{2}{l_{{1}}}^{2}\\&+ 192\,{\tau }^{3}\gamma \,{t}^{2}{l _{{2}}}^{2}+192\,{\tau }^{4}\gamma \,{t}^{2}\\&+ 16\,{\tau }^{2}{t}^{2}{l_{{1}}}^{2}+16\,{\tau }^{2}{t}^{2}{l_{{2}}}^{2}\\&+ 16\,{\tau }^{3}{t}^{2}+4\, \tau \,{x}^{2}{l_{{1}}}^{2}+4\,\tau \,{x}^{2}{l_{{2}}}^{2}+4\,{\tau }^{2} {x}^{2}\\&- 4\,\sqrt{\tau }x{l_{{1}}}^{2}-4\,\sqrt{\tau }x{l_{{2}}}^{2}\\&+ 4\,{\tau }^{3/2}x+{l_{{1}}}^{2}+{l_{{2}}}^{2}+\tau ). \end{aligned}$$

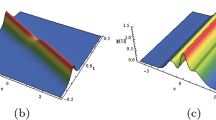
Case 1 When \(c\ne 0\), one of the two parameters \(l_1\) and \(l_2\) is zero, and we can get the first kind of the first-order interactional solutions. From Fig. 1a, b, we can find that \(q_1\) component is the first-order RW interacting with one bright soliton and \(q_2\) component is the first-order RW interacting with one dark soliton. In \(q_1\) component, the amplitude of the background that the RW emerges is almost zero, so the RW in Fig. 1a is not easily observed.

Case 2 When \(c\ne 0\), \(l_1l_2\ne 0\), the second kind of the first-order interactional solutions can be constructed. It is shown that the two components are all the first-order RW and one breather in Fig. 1c, d. Comparing with Fig. 1c , d, we can find that the breathers in \(q_1\) and \(q_2\) components are greatly different. In Fig. 1d, the amplitudes of the breather beyond the background are bigger than the ones under the background plane. However, the situation is opposite in Fig. 1c.

Choosing \(N=2\) in Theorem 1, the second-order interactional solutions can be similarly derived. The concrete expressions for the second-order interactional solutions are very tedious and complicated, and we omit them and only give the corresponding figures. In the following contents, the dynamics of the second-order interactional solutions will be discussed in detail.

Case 1 If \(c\ne 0\), one of the two parameters \(l_1\) and \(l_2\) is zero, and the first type of the second-order interactional solutions can be constructed. From Fig. 2, we can find that \(q_1\) component is the second-order RW coexisting with two bright solitons, and \(q_2\) component is the second-order RW coexisting with two dark solitons. When \(m_1=n_1=0\), the second-order RWs in the interactional solutions are the fundamental one, see Fig. 2a, b; when \(m_1n_1\ne 0\), the fundamental second-order RWs in Fig. 2a, b split into three first-order RWs, which forms the triangular pattern, see Fig. 2c, d. In Fig. 2a, the fundamental second-order RW in \(q_1\) component emerges on the top of two bright solitons and it can be seen easily. In Fig. 2c, the fundamental second-order RW splits into three first-order RWs, and we find that one first-order RW is generated on the top of one soliton and can be easily seen. However, the other two first-order RWs are generated on a plane with almost zero amplitude and cannot be find easily.

Case 2 If \(c\ne 0\), \(l_1l_2\ne 0\), the second type of the second-order interactional solutions can be derived. At this point, the two components are all the second-order RWs interacting with two-breather, see Fig. 3. The RWs in Fig. 3a, b are the fundamental second-order RWs with the condition \(m_1=n_1=0\). Choosing \(m_1n_1\ne 0\), the fundamental RWs in Fig. 3a, b can split into three first-order RWs, see Fig. 3c, d.

Utilizing the above Theorem 1, the more higher-order interactional solutions for the coupled LPD equations (1) can be constructed. It can be found that these solutions can be mainly classified as two types: (1) One component is the higher-order RWs and multi-bright solitons, and the other one is the higher-order RWs and multi-dark solitons; (2) two components are all the higher-order RWs and multi-breather.

Fig. 2
figure 2

Case 1: the second-order interactional solutions \(\gamma =\frac{1}{50},l_1=0,l_2=-1,c=\frac{1}{10^6}\): a, b the second-order fundamental RW interacts with two bright and dark solitons with \(m_1=n_1=0\); c, d the second-order RW of triangular pattern interacts with two bright and dark solitons with \(m_1=-n_1=400\)

Full size image
Fig. 3
figure 3

Case 2: the second-order interactional solutions \(\gamma =\frac{1}{50},l_1=1,l_2=-\frac{1}{2},c=\frac{1}{10^6}\): a, b the second-order fundamental RW interacts with two breathers with \(m_1=n_1=0\); c, d the second-order RW of triangular pattern interacts with two breathers with \(m_1=-n_1=400\)

Full size image

4 Higher-order rogue wave pairs for the triple-root case

Considering that the spectral characteristic equation (11) owns a triple-root, we can construct the novel RWs for the coupled LPD equations (1), which are called RW pairs. Here, the first-order RW pairs can split into two traditional first-order RWs, and the second-order RWs split into four or six traditional RWs.

Here, we will attempt to derive the higher-order RW pairs of the system (1) with the assumption that the characteristic equation (11) of \(U_0\) owns a triple-root. In order to get the triple-root, the following constraint conditions in the seed solutions (8) should be needed

$$\begin{aligned} \xi =\frac{3\sqrt{3}}{4}l_1i,\quad m_2=-m_1,\quad l_2=-l_1,\quad m_1=-\frac{1}{2}l_1. \end{aligned}$$

Without loss of generality, the parameter \(l_1\) can be chosen as \(l_1=1\), and then, the seed solutions (8) can be rewritten as

$$\begin{aligned} q_1[0]=e^{i\eta _1},\quad q_2[0]= - e^{i\eta _2}, \end{aligned}$$

with

$$\begin{aligned}&\eta _1=\left( \frac{321}{16}\gamma +\frac{15}{4}\right) t - \frac{1}{2}x,\\&\eta _2=\left( \frac{321}{16}\gamma +\frac{15}{4}\right) t+\frac{1}{2}x. \end{aligned}$$

In order to utilize the limiting technique, we set the spectral parameter as \(\xi =\xi _1=\frac{3\sqrt{3}}{4}i(1+\delta ^3)\), where \(\delta \) is a small parameter. Thus, the vector fundamental solution of the Lax pair (2) can be given as

$$\begin{aligned}&\Theta (\xi _1)=\mathrm{RM}\begin{pmatrix}e^{A_j},\\ (\zeta _j-i\xi _1+\frac{i}{2})e^{A_j},\\ (-\zeta _j+i\xi _1+\frac{i}{2})e^{A_j})\end{pmatrix}\nonumber \\&\quad (j=1,2,3), \end{aligned}$$
(16)

where

$$\begin{aligned} \mathrm{RM}= & {} \mathrm{diag}(e^{-\frac{i}{3}(\eta _1+\eta _2)},e^{\frac{i}{3}(2\eta _1-\eta _2)},e^{\frac{i}{3}(2\eta _2-\eta _1)}),\\ A_j= & {} \zeta _{{j}}x+\left[ \left( 4\,i\gamma \,{\xi _1}^{2}-{\frac{23}{4}}\,i \gamma -i\right) {\zeta _{{j}}}^{2}\right. \\&+ \left( 8\,\gamma \,{\xi _1}^{3}-\frac{15}{2} \,\gamma \,\xi _1-2\,\xi _1\right) \zeta _{{j}}\\&\left. + 4\,i\gamma \,{\xi _1}^{4}+\frac{11}{4}\, i\gamma \,{\xi _1}^{2}+i{\xi _1}^{2}-\frac{3}{2}\,i-{\frac{69}{8}}\,i\gamma \right] t, \end{aligned}$$

where \(\zeta _j\) admits the following one-variable cubic equation

$$\begin{aligned}&\zeta ^3+\frac{3\sqrt{3}}{4}(\delta +1)(\delta ^2-\delta +1)\zeta ^2\nonumber \\&\quad + \frac{9}{16}(-6\delta ^3+1+3\delta ^6)\zeta -\frac{3\sqrt{3}}{64}(9\delta ^4-9\delta ^3\nonumber \\&\quad +12\delta ^2+3\delta +1)(\delta +1)(3\delta ^2+3\delta -1)\nonumber \\&\quad (\delta ^2-\delta +1)=0. \end{aligned}$$
(17)

When \(\delta \rightarrow 0\), Eq. (17) can own the following triple-root \(\zeta _1=\zeta _2=\zeta _3=-\frac{\sqrt{3}}{4}\).

Choosing the spectral parameter \(\xi =\xi _1=\frac{3\sqrt{3}}{4}i(l_1+\delta ^3)\), the special vector solution of the Lax pair (2) can be written as

$$\begin{aligned} \Psi _2(\delta )=f\Xi _1+g\Xi _2+h\Xi _3, \end{aligned}$$
(18)

where

$$\begin{aligned} f= & {} \sum _{j=1}^{N}f_j\delta ^{3(N-1)},\\ g= & {} \sum _{j=1}^{N}g_j\delta ^{3(N-1)},\\ h= & {} \sum _{j=1}^{N}h_j\delta ^{3(N-1)}\\ \Xi _1= & {} \frac{1}{3}(\Theta _1+\Theta _2+\Theta _3),\\ \Xi _2= & {} \frac{3\sqrt{2}}{3\delta }(\Theta _1+\omega ^{*}\Theta _2+\omega \Theta _3),\\ \Xi _3= & {} \frac{3\sqrt{4}}{3\delta ^2}(\Theta _1+\omega \Theta _2+\omega ^{*}\Theta _3). \end{aligned}$$

Here, \(\omega =e^{\frac{2i\pi }{3}}\) and \(f_j,~g_j~h_j~(j=1,2,\ldots ,N)\) are all real constants. The vector eigenfunction \(\Psi _2(\delta )\) can be expanded as the following Taylor series at \(\delta =0\)

$$\begin{aligned} \Psi _2(\delta )=\Psi _2^{[0]}+\Psi _2^{[1]}\delta ^3+\cdots +\Psi _2^{[N]}\delta ^{3(N-1)}+\cdots , \end{aligned}$$

where \(\Psi _2^{[j]}=(\psi _2^{[j]},\phi _2^{[j]},\chi _2^{[j]})^\mathrm{T}=\dfrac{\partial ^{3j} \Psi _1}{(3j)!\partial \delta ^{3j}}|_{\delta =0}~(j=0,1,2,3\ldots )\).

Setting \(N=1\) in Eq. (7), the concrete expressions for the first-order RW pairs can be derived as

$$\begin{aligned}&q_1[1]=e^{i\eta _1}+\frac{3\sqrt{3}\phi _2[0]\psi _2[0]^{*}}{|\psi _2[0]|^2+|\phi _2[0]|^2+|\chi _2[0]|^2}, \nonumber \\\end{aligned}$$
(19)
$$\begin{aligned}&q_2[1]=-e^{i\eta _1}+\frac{3\sqrt{3}\chi _2[0]\psi _2[0]^{*}}{|\psi _2[0]|^2+|\phi _2[0]|^2+|\chi _2[0]|^2},\nonumber \\ \end{aligned}$$
(20)
Fig. 4
figure 4

The first-order rogue wave pairs with \(\gamma =\frac{1}{50},g_1=0,h_1=\frac{1}{2}\): a, b the fundamental RW pairs with \(f_1=0\); c, d the RW pairs consisted of two traditional first-order RWs with \(f_1=100\)

Full size image

with

$$\begin{aligned} {\psi _2[0]}= & {} \psi _2^{[0]}=1/8\,{\mathrm{e}^{-{\frac{185}{32}}\,it\gamma -{\frac{19}{4}}\,it-1/4\, \sqrt{3}x}}\\&\left( 228\,ih_{{1}}\sqrt{3}xt\gamma +24\,ih_{{1}}xt \sqrt{3}+3249\,h_{{1}}{t}^{2}{\gamma }^{2}\right. \\&+ 228\,ig_{{1}}t\gamma +1212\,ih_{{1}}t\gamma +684\,h_{{1}}{t}^{2}\gamma \\&+ 24\,ig_{{1}}t+120\,ih_{{1}} t-8\,g_{{1}}\sqrt{3}x - 32\,h_{{1}}\sqrt{3}x\\&\left. + 36\,h_{{1}}{t}^{2} -12\,h_{ {1}}{x}^{2}-8\,f_{{1}}-24\,g_{{1}}-48\,h_{{1}}\right) ,\\ \phi _2[0]= & {} \phi _2^{[0]}=-1/16\,{\mathrm{e}^{{\frac{457}{32}}\, it\gamma -it-1/2\,ix-1/4\,\sqrt{3} x}}\\&(- 228\,g_{{1}}t\gamma -528\,h_{{1}}t\gamma -24\,g_{{1}}t\\&- 48\,h_{{1}}t-24\,xg_{{1}}-72\,xh_{{1}}+36\,ih_{{1}}{t}^{2}\\&- 12\,ih_{{1}}{x}^{2} -8\,if_{{1}}-16\,h_{{1}}\sqrt{3}-16\,g_{{1}}\\&\sqrt{3}+228\,ig_{{1}}\sqrt{3}t\gamma +984\,ih_{{1}} \gamma \,\sqrt{3}t+684\,i\gamma \,txh_{{1}}\\&+ 3249\,ih_{{1}}{t}^{2} {\gamma }^{2}+684\,ih_{{1}}{t}^{2}\gamma +24\,ig_{{1}}\sqrt{3}t\\&+ 96\,ih_{{1}}\sqrt{3}t-8\,ig_{{1}}\sqrt{3}x-8\,ih_{{1}} \sqrt{3}x +72\,itxh_{{1}} \\&- 12\,h_{{1}}\sqrt{3}{x}^{2}-228\,h_{{1}}\sqrt{3}xt\gamma -24\,h_{{1}}xt\sqrt{3}\\&+ 684\,h_{{1}}{t}^{2}\sqrt{3}\gamma +3249\,h_{{1}}{t}^{2}\\&\sqrt{3}{\gamma }^{2}-8\,f_{{1}}\sqrt{3}+ 36\,h_{{1}}{t}^{2}\sqrt{3}),\\ \chi _2[0]= & {} \chi _2^{[0]}=-1/16\,{\mathrm{e}^{{\frac{457}{32}} \,it\gamma -it+1/2\,ix-1/4\,\sqrt{3} x}}\\&(- 228\,g_{{1}}t\gamma -528\,h_{{1}}t\gamma -24\,g_{{1}}t -48\,h_{{1}}t\\&+ 24\,xg_{{1}}+72\,xh_{{1}} +36\,ih_{{1}}{t}^{2} -12\,ih_{{1}}{x}^{2}\\&- 8\,if_{{1}} +16\,h_{{1}}\sqrt{3}+16\,g_{{1}}\sqrt{3}\\&+ 3249\,ih_{{1}}{t}^{2} {\gamma }^{2}+684\,ih_{{1}}{t}^{2}\gamma -8\,ig_{{1}}\sqrt{3}x\\&- 8\,ih_{{1}}\sqrt{3}x +12\,h_{{1}}\sqrt{3}{x}^{2}\\&- 228\,h_{{1}} \sqrt{3}xt\gamma -24\,h_{{1}}xt\sqrt{3}\\&- 984\,ih_{{1}}\gamma \,\sqrt{3}t-684\,i\gamma \,txh_{{1}}-228\,ig_{{1}} \sqrt{3}t\gamma \\&- 24\,ig_{{1}}\sqrt{3}t-96\,ih_{{1}}\sqrt{3}t-72\,itxh_{{1}}\\&- 684\,h_{{1}} {t}^{2}\sqrt{3} \gamma -3249\,h_{{1}}{t}^{2}\sqrt{3}{\gamma }^{2}\\&+ 8\,f_{{1}}\sqrt{3}- 36\,h_{{1}}{t}^{2}\sqrt{3}). \end{aligned}$$

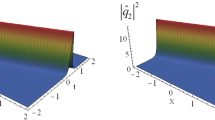
From Fig. 4 a, b, it is shown that the first-order fundamental RW pairs exist in the two components, and this kind of fundamental RW includes more than one peak above the background plane. Choosing \(f_1\ne 0\), the first-order fundamental RW pairs can split into two traditional first-order RWs, see Fig. 4c, d. Here, we give the density plot of the first-order RW pairs in \(q_1\) component with different \(\gamma \) to discuss the higher-order dispersive and nonlinear effects, see Fig. 5. When \(\gamma >0\), the two RWs are stretched and close together with increasing the absolute value of \(\gamma \), see Fig. 5a, c. Choosing \(\gamma =0\), the RWs without the effects of the higher-order terms are given in Fig. 5d. When \(\gamma <0\), the two RWs separate with each other with increasing the absolute value of \(\gamma \), see Fig. 5e, g.

Fig. 5
figure 5

The density plot of the RW pairs in Fig. (4): a\(\gamma =\frac{1}{50}\); b\(\gamma =\frac{1}{30}\); c\(\gamma =\frac{1}{5}\); d\(\gamma =0\); e\(\gamma =-\frac{1}{50}\); f\(\gamma =-\frac{1}{30}\); and g\(\gamma =-\frac{1}{5}\)

Full size image

Choosing \(N=2\) in Eq. (7), the expressions of the second-order RW pairs can be similarly constructed. Here, we omit the concrete expressions and only give the related figures. There exist six free parameters \(f_j,~g_j,~h_j~(j=1,2)\) in the expressions for the second-order RW pairs. Based on the above facts, the second-order RW pairs are expected to have more distribution patterns.

Fig. 6
figure 6

The second-order RW pairs with \(f_1=0, g_1=1, g_2=0, h_1=0, \gamma =\frac{1}{50}\): a, b the triangular pattern with \(f_2=0, h_2=100\); c, d the quadrilateral pattern with \(f_2=10000, h_2=0\)

Full size image
Fig. 7
figure 7

The second-order RW pairs with \(f_1=0, g_1=0, h_1=\frac{1}{100}, h_2=0, \gamma =\frac{1}{50}\): a, b the ring pattern 1 with \(f_2=0, g_2=1000\); c, d the ring pattern 2 with \(f_2=10000, g_2=0\)

Full size image

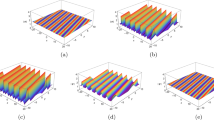
If \(g_1\ne 0\), the second-order RW pairs including four traditional first-order RWs are given, see Fig. 6. In Fig. 6a, b, we can find that one fundamental first-order RW pairs are located on the middle site and two traditional first-order RWs stand on two sides; these three RWs form an obtuse triangle pattern. In Fig. 6c, d, the first-order RW pairs in Fig. 6a, b all split into two traditional first-order RWs, which form a quadrilateral pattern. If \(g_1=0\), the second-order RW pairs consisted of six traditional first-order RWs are demonstrated in Fig. 7. It is shown that four traditional first-order RWs distribute around one fundamental first-order RW pairs in Fig. 7a, b, and these five RWs form the ring pattern 1. Changing these parameters, the fundamental first-order RW pairs in the ring pattern 1 can split into two traditional first-order RWs, which form the ring pattern 2, see Fig. 7c, d. Utilizing Theorem 1, other higher-order RW pairs can be constructed and we omit them here.

5 Conclusion

Utilizing the Darboux transformation and the limiting technique, we construct the higher-order interactional solutions and the higher-order RW pairs for the coupled LPD equations (1). We mainly consider the two situations of the roots for the spectral characteristic equation (11): the double-root and the triple-root. If the spectral characteristic equation owns a double-root, the higher-order interactional (semirational) solutions can be derived, which are mainly classified as two kinds: (1) One component is higher-order RWs interacting with multi-bright solitons, and the other one is higher-order RWs interacting with multi-dark solitons; (2) two components are all higher-order RWs coexisting with multi-breather. Considering the triple-root situation of the spectral characteristic equation, we can construct the higher-order RW pairs for the system (1), which are absolutely different from the traditional higher-order RWs. For the first-order RW pairs, it can split into two traditional first-order RWs, see Fig. 4c, d. Besides, the higher-order nonlinear and dispersive terms can affect the dynamics of the RW pairs, see Fig. 5. Choosing \(g_1=0\) or \(g_1\ne 0\), the second-order RW pairs can split into four or six traditional first-order RWs. It is shown that the four traditional first-order RWs can form the triangular pattern and the quadrilateral pattern in Fig. 6. Similarly, the six traditional first-order RWs form the ring pattern 1 and 2 in Fig. 7.

These results further reveal the dynamic structures of RWs in the multi-component coupled system, and we hope these kinds of solutions could be verified in physical experiments in the future.