Elastic and viscoelastic foundations: a review on linear and nonlinear vibration modeling and applications

Abstract

This paper presents a comprehensive review on different theoretical elastic and viscoelastic foundation models in oscillatory systems. The review covers the simplest foundation models to the most complicated one and fully tracks the recent theories on the topic of mechanical foundations. It is fully discussed why each theory has been developed, what limitations each one contains, and which approaches have been applied to remove these limitations. Moreover, corresponding theories about structures supported by such foundations are briefly reviewed. Subsequently, an introduction to popular solution methods is presented. Finally, several important practical applications related to the linear and nonlinear foundations are reviewed. This paper provides a detailed theoretical background and also physical understanding from different types of foundations with applications in structural mechanics, nanosystems, bio-devices, composite structures, and aerospace-based mechanical systems. The presented information of this review article can be used by researchers to select an appropriate kind of foundation/structure for their dynamical systems. The paper ends with a new idea of intelligent foundations based on nanogenerators, which can be exploited in future smart cities for both energy harvesting and self-powered sensing applications.

1 Introduction

Foundations are important parts of physical systems due to their wide range of applications in different science and engineering areas including mechanical, civil, electrical, nanotechnology, and even biotechnology. They are highly attractive for researchers because of their crucial applications in different systems. One of the principle focuses of researchers is to investigate dynamical behavior of foundations. Foundations play a pivotal role to preserve structural system under oscillations. In fact, it is inevitable to utilize foundations in a structural system to avoid mechanical failure. Therefore, three main criteria should be considered by engineers and researchers when they design a system under any type of oscillations. First, it is highly necessary to develop a continuum model for the structure; second, it is inescapable to develop a mathematical model for the foundations of the system; and the last one is a full model of the whole structural system, which considers the interaction between the foundation and the system rested on it.

Depending on the applications of the considered structural system, researchers have proposed several types of modelings for foundations. The first and simplest presentation for a foundation was proposed by Winkler. This model is known as the linear elastic Winkler model [1]. The main shortcoming of the linear elastic model is its failure in the presentation of viscoelastic behavior of materials. Therefore, a viscoelastic element has been added to the foundation models proposed by Winkler. Different arrangements can be assumed for the elastic and viscoelastic elements of a foundation, and accordingly, the original model of Winkler was improved by researchers with proposing several novel foundation models such as Kelvin–Voigt, Maxwell, Zener, Poynting-Thomson, and Burger [2,3,4]. In the aforesaid models, elements of foundations show independent reactions to any external load. In addition, they react uniformly to an applied load whether the load is uniform or not; and the deflection of top layer of foundation is discontinuous (Fig.7).

Two-parameter models are known as the models that a layer connects top ends of foundation’s element to each other. Accordingly, the force–displacement functions for this type of foundations are continuous (because the top ends of elements are joined by a shear layer—see Fig.7). The main examples of these types of foundations include Filonenko–Borodich [5], Hetenyi [6], Pasternak [7], Vlasov [8], and Reissner [9] models. Filonenko–Borodich, Hetenyi, and Pasternak models have been developed based on Winkler model, while Vlasov and Reissner models have been proposed in accordance with the theory of the elastic continuum model [10]. According to the type of study or type of foundation–structure, all of these models can be assumed to be continuous or discrete. The multilayered foundations have been proposed to model foundations with different layers. The multilayered models are mostly used in studying railway track vibration, soil interaction vibration, and ground-borne vibration. In addition, partial and discontinuous foundation models can be implemented in modeling structures, which are partially supported by a foundation. Furthermore, a few approaches have been utilized in order to strengthen foundations against settlements. Therefore, reinforced foundation has been proposed by adding reinforcements to a foundation. Floating foundations are designed to isolate ground-borne vibrations.

The above-mentioned foundations have the same reactions in both compression and tensile conditions. In fact, this is not the actual behavior in most of the practical cases. As a result, tensionless and bilinear models have been suggested [11, 12]. In these models, possible separations can occur between supporting and supporter, which cause nonlinearity in the response of foundation even in the case of having a foundation with linear nature. The reaction of material in large deflections and under heavy loading has prompted the researchers to use nonlinear models [13]. Most of the materials have a nonlinear response with respect to the tension/compression loading; in the small displacements, however, the linear models can provide an acceptable accuracy. In general, the nonlinear model is more practical and more realistic [14]. Also, friction nonlinearity has been observed in the behavior of foundations due to foundation fillers. Another important case in the hierarchy of foundations evolution is randomness feature. Uncertainty in the foundation parameters is introduced as one of the reasons, which results in random vibrations. Randomness has been considered along the continuous foundation and in the stiffness, damping, and loss factor of them [15,16,17]. Nonlinear fractional foundation can be introduced as the last model, which can be used for modeling different types of substrates. This model, in addition to load-dependent properties, which are presented by nonlinear elements, describes frequency-dependent properties of foundations by fractional elements [18].

The category of structures includes a beam/string and a membrane/plate/shell on a foundation. The problem of a beam on a foundation is mostly used for modeling railway tracks, bridges, pavements, and runways, among which the railway track problem is the most wide-spreading topic [19, 20]. A plate resting on a foundation can describe the behavior of panel element, floor systems, and slab foundations. Also, the behavior of rotor disks, parts of a clutch, and housings of different electrical as well as mechanical equipment can be presented by the plate theory. Liquid storage tanks and pipelines, to name but a few, are the problems which can be modeled by a shell on a foundation. Strings and membranes are widely used in biomechanics and in modeling of music instruments. Another possible type is the oscillations of nanosystems on linear or nonlinear foundations.

There are a few review studies pertinent to the present topic, i.e., the history of beam/plate on elastic foundation as well as interaction between soil and structure were reported in [21,22,23]. Fryba [24] covered the content of beams and plates on foundation subjected to moving loads, till 1999. However, a review paper on the study of foundation theories and their applications has not been addressed so far.

The principal objective of this paper is to provide a comprehensive survey on the different theories of foundations, from the simplest to the evolution of the most complicated one, nonlinear fractional foundations. Accordingly, the present review is started from the simplest presentation of a foundation to the most complicated model. Types of structures, the practical usage of the models, and impediments for the applications of each one are comprehensively provided. In addition, a few solution methods are presented [25]. Finally, a few attractive, state-of-the-art field studies of flexible structures resting on elastic/viscoelastic foundations are introduced.

2 Theoretical foundation models

2.1 Linear elastic and viscoelastic models

2.1.1 Winkler model

Winkler first modeled an Euler–Bernoulli beam on an elastic foundation as a railroad track [1]. This model of foundation is based on the hypothesis that the every point’s reaction is proportional to the point’s displacement, and the springs are linear and independent as described in Eq. (1). The reaction force of foundation is [1]:

$$\begin{aligned} p\left( {x,t} \right) =kw\left( {x,t} \right) , \end{aligned}$$

(1)

where w(x, t) is the vertical displacement and k is the stiffness of linear springs. As a result, this theory leads to the same answer in both compressions and tensions. This kind of mechanical behavior is called bilateral (bilateral foundation) (Fig. 1).

Fig. 1

Winkler model

Fig. 2

Kelvin–Voigt model

Fig. 3

Maxwell model

In the mathematical modeling, the method of describing the mechanics of a foundation is based on idealizing its behavior. The linear one-parameter model of Winkler is the simplest one; however, due to the various properties of different materials and soils (granular soils, clay soils, wet soils, pressured soils, etc.), more parameters should be involved to represent the behavior of materials used as a foundation. The following models, presented in the next parts, are developed based on the Winkler model. In fact, researchers have started with the Winkler theory and have inserted more parameters and elements into the Winkler model in order to present a more accurate reaction behavior for a structural foundation.

Fig. 4

Zener model

Fig. 5

Poynting-Thomson models a: type 1, b: type 2

2.1.2 Kelvin–Voigt model

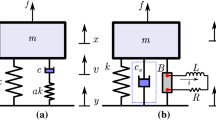
One weakness of Winkler model is the lack of viscoelastic elements. Kelvin–Voigt model includes the viscoelastic behavior and presents the behavior of a media with a series of discrete springs parallel with dampers (as shown in Fig. 2). In another word, Kelvin–Voigt enters the effects of viscoelasticity into the elastic Winkler model. The relation between the restoring force and displacement is found using the following relation [4]:

$$\begin{aligned} p\left( {x,t} \right) =kw\left( {x,t} \right) +c\dot{w}\left( {x,t} \right) , \end{aligned}$$

(2)

where c is the damping of viscous elements. The Kelvin–Voigt model has been used in several works including nonlinear frequency analysis of beam on Kelvin–Voigt foundation, finite element formulation of infinite beam on Kelvin–Voigt foundation, and wave propagation study of an infinite beam on the foundation [26,27,28].

2.1.3 Maxwell model

In this model, a series of springs along with dampers are placed as shown in Fig. 3. The reaction force of the foundation can be calculated from the following equation [4]:

$$\begin{aligned}&\left. {{\begin{array}{l} {p(x,t)=k\Delta _1 (x,t)=c\dot{\Delta }_2 (x,t)} \\ {w(x,t)=\Delta _\mathrm{tot} \left( {x,t} \right) =\Delta _1 (x,t)+\Delta _2 (x,t)} \\ \end{array} }} \right\} \nonumber \\&\quad \Rightarrow \frac{\partial w(x,t)}{\partial t}=\frac{1}{k}\frac{\partial p(x,t)}{\partial t}+\frac{1}{c}p(x,t), \end{aligned}$$

(3)

where p(x, t) is the foundation reaction, $\Delta _1 (x,t)$ and $\Delta _2 (x,t)$ are the displacement changes of spring elements and damper elements, respectively (presented in Fig. 3). Hatada et al. modeled the assembly of braces and viscous dampers, which are used in tall buildings by the model of Maxwell. In their analysis, the Maxwell model was selected because of the arrangement of the braces and dampers [29]. Soukup and Volek used the Maxwell model to describe viscoelastic behavior of plates, and then, they conducted stress analysis for a thin plate [30].

2.1.4 Zener model

Zener model—also known as standard linear solid (SLS) model—consists of the Winkler and Maxwell models in parallel (Fig. 4) with the following force–displacement relation [4]:

$$\begin{aligned}&\left. {{\begin{array}{l} {p(x,t)=k_2 \Delta _2 (x,t)+k_1 \Delta _{s1} (x,t)=k_2 \Delta _2 (x,t)+c_1 \dot{\Delta }_{d1} (x,t)} \\ {w(x,t)=\Delta _\mathrm{tot} \left( {x,t} \right) =\Delta _{s1} (x,t)+\Delta _{d1} (x,t)=\Delta _2 (x,t)} \\ \end{array} }} \right\} \nonumber \\&\quad \Rightarrow \frac{\partial w(x,t)}{\partial t}=\frac{\frac{\partial p(x,t)}{\partial t}+\frac{k_1 }{c_1 }p(x,t)-k_1 k_2 w(x,t)}{k_1 +k_2 }. \end{aligned}$$

(4)

Muscolino and Palmeri [31] used SLS model in combination with state space formulation to describe the vibrations of a beam rested on a foundation; Hörmann et al. presented the response of a beam on a foundation with considering the generalized Zener model [32].

Fig. 6

Burger model

Fig. 7

a Winkler foundation, b two-parameter foundation

2.1.5 Poynting-Thomson model

This kind of foundation is built by an arrangement of three damper and spring elements. The arrangement can have various combinations, two of which are presented in Fig. 5.

The force–displacement relation for the first type of Poynting-Thomson model (Fig. 5a) can be expressed as:

$$\begin{aligned}&\left. {{\begin{array}{l} {p(x,t)=k_1 \Delta _1 (x,t)=k_2 \Delta _2 (x,t)+c_2 \dot{\Delta }_2 (x,t)} \\ {w(x,t)=\Delta _\mathrm{tot} \left( {x,t} \right) =\Delta _1 (x,t)+\Delta _2 (x,t)} \\ \end{array} }} \right\} \nonumber \\&\quad \Rightarrow k_1 \frac{\partial w(x,t)}{\partial t}+\frac{k_1 k_2 }{c_2 }w(x,t)=\frac{\partial p(x,t)}{\partial t}\nonumber \\&\qquad +\frac{k_1 +k_2 }{c_2 }p(x,t), \end{aligned}$$

(5)

and for the second type (presented in Fig. 5b) we have:

$$\begin{aligned}&\left. {{\begin{array}{l} {p(x,t)=c_1 \dot{\Delta }_1 (x,t)=k_2 \Delta _2 (x,t)+c_2 \dot{\Delta }_2 (x,t)} \\ {w(x,t)=\Delta _\mathrm{tot} \left( {x,t} \right) =\Delta _1 (x,t)+\Delta _2 (x,t)} \\ \end{array} }} \right\} \nonumber \\&\quad \Rightarrow k_2 \frac{\partial w(x,t)}{\partial t}+c_2 \frac{\partial ^{2}w(x,t)}{\partial t^{2}}=\frac{c_2 }{c_1 }\frac{\partial p(x,t)}{\partial t}\nonumber \\&\qquad +\frac{c_1 +k_2 }{c_1 }p(x,t). \end{aligned}$$

(6)

In the above equations, p(x, t) shows the foundation reaction force. Poynting-Thomson model is widely used in modeling dynamic characteristics of viscoelastic materials [33, 34]. In fact, if the Maxwell model became attached to a spring/damper element in series, the Poynting-Thomson model is achieved. In Ref. [33], the effect of model parameters on the eigenvalues was scrutinized; particularly, the eigenvalues were calculated for different values of $k_1$, till $k_1 \rightarrow \infty$ in which the Poynting-Thomson model becomes equivalent to the Maxwell model.

2.1.6 Burger model

Burger model considers four spring and damper elements, which can be placed in different combinations. One well-known combination is the placement of the Kelvin–Voigt model series with the Maxwell model (presented in Fig. 6). The restoring force of the foundation can be calculated as [4]:

$$\begin{aligned}&\left. {{\begin{array}{l} {p(x,t)=k_1 \Delta _2 (x,t)=c_1 \dot{\Delta }_2 (x,t)=k_2 \Delta _3 (x,t)+c_2 \dot{\Delta }_3 (x,t)} \\ {w(x,t)=\Delta _\mathrm{tot} \left( {x,t} \right) =\Delta _1 (x,t)+\Delta _2 (x,t)+\dot{\Delta }_3 (x,t)} \\ \end{array} }} \right\} \nonumber \\&\quad \Rightarrow \left[ {\frac{\partial ^{2}}{\partial t^{2}}+\left( {\frac{k_1 }{c_1 }+\frac{k_1 }{c_2 }+\frac{k_2 }{c_2 }} \right) \frac{\partial }{\partial t}+\frac{k_1 k_2 }{c_1 c_2 }} \right] p(x,t)\nonumber \\&\qquad =\left[ {\frac{k_1 k_2 }{c_2 }\frac{\partial }{\partial t}+k_1 \frac{\partial ^{2}}{\partial t^{2}}} \right] w(x,t). \end{aligned}$$

(7)

Displacement, damping, and stiffness of the elements are shown in Fig. 6. Dey et al. showed the excellent potential of Burger model in presenting time-dependent behavior of continuum media subjected to cyclic loads [3]. They observed a satisfactory agreement by performing a curve fitting between the observed results and results from mathematical model. After that, they developed the inverse analysis formulation in order to estimate burger’s parameters [35].

Fig. 8

Filonenko–Borodich model

Fig. 9

Hetenyi model

Because of the fact that Winkler model uses only one parameter—as outlined previously—in the modeling foundation reactions, this model is known as one-parameter model. One-parameter model does not consider the interactions between springs, and it reacts uniformly whether it is subjected to a uniform load or not, i.e., every point of this model reacts proportionally to the load, which is applied to the point. It should be noted that, in one-parameter model, the point’s displacement is independent of the load applied to other points (Fig. 7). Consequently, inaccurate results emerge in practical cases. Kelvin–Voigt, Maxwell, Zener, Poynting-Thomson, and Burger models have the same shortcoming. Therefore, two-parameter foundations are presented to address the above issue [2]. The two-parameter model refers to the foundations in which a top layer has connected the ends of springs or dampers to each other. As a result, continuity is created in the displacement and restoring force of adjacent points (Fig. 7b). Different assumptions and constrains have been considered for the top layer of the two-parameter model, and based on them, several two-parameter models have been developed such as Filonenko–Borodich, Hetenyi, Pasternak, Vlasov, and Reissner.

Filonenko–Borodich, Hetenyi, and Pasternak models are developed based on Winkler model. These models have been initially developed based on Winkler theory; and by adding some elements and constants, the continuous functions for displacement and restoring force are provided. Vlasov and Reissner models are originated from the continuous model, and by the use of some constrains, they provide the force–displacement relation for the foundation.

2.1.7 Filonenko–Borodich model

In this model, the reaction of springs is not independent and the ends of springs are connected to each other by a tensioned, massless membrane. The equilibrium equation in the direction of z, which represents the reaction of the foundation, is [5]:

$$\begin{aligned} p\left( {x,t} \right) =kw\left( {x,t} \right) -T\frac{\partial ^{2}w\left( {x,t} \right) }{\partial x^{2}}, \end{aligned}$$

(8)

where T is the tensile force of the membrane. A schematic sketch of the Filonenko–Borodich model is depicted in Fig. 8.

2.1.8 Hetenyi model

The reaction of springs is not independent in this model either. An Euler–Bernoulli beam (in one-dimensional problems) or a thin plate (in two-dimensional problems) provides the connection between the springs of Winkler model. The beam or the plate is shown in Fig. 9, which is considered without mass and has only bending reaction.

The relation between force and displacement through this foundation is [6]

$$\begin{aligned} p\left( {x,t} \right) =kw\left( {x,t} \right) +k_1 \frac{\partial ^{2}w\left( {x,t} \right) }{\partial x^{2}}, \end{aligned}$$

(9)

where $k_{1}=EI$, the flexural rigidity of the beam, or $k_1=D$ is flexural rigidity of the plate [6].

2.1.9 Pasternak model

In this section, the most well-known two-parameter foundation model (the Pasternak model) is described. In the Pasternak model, the foundation elements are assumed to be connected by a layer, which acts as a horizontal linkage of vertical elements. The elastic, viscoelastic, and generalized Pasternak models are introduced in this section.

2.1.9.1 Elastic Pasternak model In the Pasternak model, an elastic shearing layer connects the end top of springs (Fig. 10). The layer only undergoes lateral shear deformations.

In order to derive the restoring force of the Pasternak foundation, an element of shearing layer is considered as shown in Fig. 11.

Fig. 10

Elastic Pasternak model

Fig. 11

An element of shearing layer

Fig. 12

Viscoelastic Pasternak model

It is assumed that the foundation material is homogenous and isotropic, accordingly, we will have:

$$\begin{aligned} \left\{ {\begin{array}{l} \tau _{xz} =G\frac{\partial w\left( {x,y} \right) }{\partial x} \\ \tau _{yz} =G\frac{\partial w\left( {x,y} \right) }{\partial y} \\ \end{array}} \right. , \end{aligned}$$

(10)

in which G is the coefficient of viscosity due to shear deformations. According to the Newton’s law for elastic materials, the shear force per unit length of the shearing layer is as below:

$$\begin{aligned} \left\{ {\begin{array}{l} N_x =\int \limits _0^1 {\tau _{xz} \mathrm{d}z=} G\frac{\partial w\left( {x,y,t} \right) }{\partial x} \\ N_y =\int \limits _0^1 {\tau _{xz} \mathrm{d}z=} G\frac{\partial w\left( {x,y,t} \right) }{\partial y} \\ \end{array}} \right. . \end{aligned}$$

(11)

The force–displacement relation is achieved by writing the equilibrium equation of forces in the direction of z as below[7]:

$$\begin{aligned} p\left( {x,y,t} \right) =kw\left( {x,y,t} \right) -G\nabla ^{2}w\left( {x,y,t} \right) . \end{aligned}$$

(12)

Fig. 13

Generalized viscoelastic Pasternak foundation under a Timoshenko beam [36]

Fig. 14

Kerr-type foundation[44]

2.1.9.2 The viscoelastic Pasternak In this section, the concept of the Pasternak foundation is extended to the case of viscoelastic one. Therefore, elastic elements are stood in parallel with viscous elements, and instead of the elastic shearing layer, a viscoelastic layer is taken into account (depicted in Fig. 12).

Again, an element of viscoelastic layer is considered as Fig. 11. For this case, the shear forces through the unit length of sharing layer are obtained from the Newton’s law for viscoelastic materials as below:

$$\begin{aligned} \left\{ {\begin{array}{l} N_x =\mu \frac{\partial ^{2}w\left( {x,y,t} \right) }{\partial x\partial t} \\ N_y =\mu \frac{\partial ^{2}w\left( {x,y,t} \right) }{\partial y\partial t} \\ \end{array}} \right. , \end{aligned}$$

(13)

in which $\mu$ is the coefficient of elastic resistance due to shear deformations. The force–displacement relation in the direction of z is as follows:

$$\begin{aligned} p\left( {x,y,t} \right)&=kw\left( {x,y,t} \right) +c\frac{\partial w\left( {x,y,t} \right) }{\partial t}\nonumber \\&\quad -\mu \frac{\partial }{\partial t}\nabla ^{2}w\left( {x,y,t} \right) . \end{aligned}$$

(14)

2.1.9.3 The generalized Pasternak Younesian and Kargarnovin added momentum reaction to the viscoelastic Pasternak model and called the model as the generalized Pasternak viscoelastic foundation. The momentum transmitted from foundation to the structure is expressed as [36]:

$$\begin{aligned} M\left( {x,t} \right) =k_\phi \phi \left( {x,t} \right) +c_\phi \frac{\partial \phi \left( {x,t} \right) }{\partial t}, \end{aligned}$$

(15)

where $k_\phi$ and $c_\phi$ are the rotational stiffness and damping, respectively. The relation of force–displacement can be written in the form of Eq. (14) (Fig. 13).

Zhaohua and Cook [37] introduced the use of two-parameter foundations under beam elements. They related the second parameter to shear deformations or bending properties and presented the following general equation for the restoring force of two-parameter foundations:

$$\begin{aligned} p\left( {x,t} \right) =kw\left( {x,t} \right) -k_1 \frac{\partial ^{2}w\left( {x,t} \right) }{\partial x^{2}}, \end{aligned}$$

(16)

where k is Winkler’s modulus and $k_1$ is the second parameter related to the interactions between springs. Equation (16) is the presentation of the Pasternak model. It was concluded that when $k_1$ is not large, the Winkler foundation can provide a reliable result. On the contrary, when $k_1$ is large and especially is close to k, the use of Winkler model leads to considerable error [37]. Since the introduction of two-parameter foundation models, the Pasternak model has attracted the most attentions among different types of two-parameter foundations, and it is considered as the most generalized two-parameter foundation [38,39,40,41]. Wang and Stephens investigated the effect of shear layer by comparing the natural frequencies of a beam resting on the Winkler and Pasternak foundation and demonstrated that the shear layer increases the frequencies [42]. Shen [43] studied the buckling and post-buckling phenomena for orthotropic rectangular plates resting on a Pasternak foundation. They showed that the post-buckling phenomenon is strongly influenced by the foundation parameters.

2.1.10 Kerr (three-parameter) model

Three-parameter model was suggested by Kerr [44] and also known as the Kerr-type foundation. The foundation was introduced as the development of Pasternak model in which the foundation is consisted of a beam embedded into an elastic media as presented in Fig. 14. Accordingly, three independent parameters represent the restoring force of the foundation that is $c\,(\mathrm{kN}{/}\mathrm{m}^{3}), k\,(\mathrm{kN}{/}\mathrm{m}^{3})$, and $G\,(\mathrm{kN}{/}\mathrm{m})$. By using these three parameters, a wide range of viscoelastic materials can be mathematically modeled. The deflection response of the foundation can be achieved by solving the following equation [44]:

$$\begin{aligned} \left( {1+\frac{k}{c}} \right) p\left( {x,t} \right)&-\frac{G}{c}\nabla ^{2}p\left( {x,t} \right) =kw\left( {x,t} \right) \nonumber \\&\quad -G\nabla ^{2}w\left( {x,t} \right) , \end{aligned}$$

(17)

where c and k are the constants of elastic springs, G is the flexural rigidity, and w(x, t) is the displacement of foundation surface. The foundation was mainly used to model the behavior of flexible soil and can present the boundary condition between a structure and soil.

Avramidis and Morfidis accomplished a comparison between the response of one-, two-, and three-parameter foundation models and showed that the Kerr-type foundation provides more realistic results for the considered case [45]. Hetenyi [46] presented the general procedure for analyzing beams on Kerr-type foundation using an analytical scheme. The procedure presented by Hetenyi can provide dynamic response of a beam on Kerr foundation subjected to any kind of load and boundary conditions. Based on exact solution of the governing differential equation, Morfidis formulated the problem of a Timoshenko beam on the three-parameter foundation in matrices form and investigated the natural frequency of the vibrations of the structure [47, 48]. Limkatanyu et al. [49] derived the stiffness matrix for the foundation based on the virtual force principle. Wang and Zhang used the three-parameter foundation to model the adhesive layer between curved beam structures and fiber-reinforced polymer (FRP) plates [50]. They also used the three-parameter model to satisfy the boundary condition of zero shear stress at the edge of adhesive joints [51]. Wang et al. studied parametric instability of an inextensional beam taking into account Winkler, Pasternak, and Kerr foundations [52].

2.1.11 Half-space model

The half-space foundation has been proposed for the modeling of infinite/semi-infinite problems. Based on the Hertz contact theory, when the contact surface is small compared with the problem dimensions, the foundation medium can be presented by a half-space medium. A half-space medium is considered as Fig. 15 $(z>0,\infty<x<\infty ,\infty<y<\infty )$. These kinds of media are chosen based on the load type [e.g., Fig. 15 is appropriate for a normal loading F(x, y, t)].

Fig. 15

System of a half-space medium [24]

The equation which governs the motion of an isotropic elastic half-space in the direction of x and subjected to the load of F(x, y, z, t) is [24] (the same relation can be written in y and z directions)

$$\begin{aligned} \left( {\lambda +G} \right) \frac{\partial \theta }{\partial x}+G\nabla ^{2}u_x +F_x =\rho \frac{\partial ^{2}u_x }{\partial t^{2}}, \end{aligned}$$

(18)

where

• $u_x ( {x,y,z,t})$: displacement in x direction

• $\rho$: density of the media

• $\nabla ^2$: Laplace operator

• $F_x ( {x,y,z,t})$: force per unit volume in the direction of x

• $\theta$: volume relative change

• $\lambda =\frac{\nu E}{(1+\nu )(1-2\nu )}$: Lame’s constant

• $G=\frac{E}{2(1+\nu )}$: shear modulus

In order to simplify this type of foundation, a few idealized models have been presented by researchers with consideration of elastic continuum model. These models are isotropic elastic continuum, anisotropic elastic continuum, and inhomogeneous elastic continuum. Study of different structures such as beams and plates on half-space foundation has attracted attentions of vibration engineers. But these simplified models are still complicated to be used. The following two-parameter models are also developed based on continuum theory, which can provide the continuity between the spring’s elements, and are usually more preferable than the half-space model.

Fig. 16

Vlasov model

2.1.12 Vlasov model

The Vlasov model is also considered as a two-parameter foundation. This method simplifies the model of an elastic continuous medium by imposing a few constraints on the top layer. Using the constraints and variational method, Vlasov presented a relation similar to Eq. (16) as the force–displacement relation of a continuous medium. Here, a summary for the case of Vlasov model is presented [53]. Considering Fig. 16 as the case of a plane strain of the elastic layer in $x\hbox {-}z$ plane, the displacement components are as below:

$$\begin{aligned} u( {x,z} )=0,\quad \hbox {w}( {x,z} )=w( x )h( z ), \end{aligned}$$

(19)

where the function h(z) provides the vertical variations of displacement. For a linear variation case, the function can be considered as:

$$\begin{aligned} h( z )=1-\frac{z}{H}, \end{aligned}$$

(20)

in which H is the vertical thickness of elastic medium. By the use of stress–strain relation and the Lagrange’s principle of virtual work, the force–displacement relation of the Vlasov foundation can be expressed as:

$$\begin{aligned} p( x )=kw( x )-k_1 \frac{\mathrm{d}^{2}w(x)}{\mathrm{d}x^{2}}, \end{aligned}$$

(21)

in which

$$\begin{aligned} \begin{array}{l} k=\frac{E_0}{\left( {1-v_0^2} \right) }\int \limits _0^H \left( \frac{\mathrm{d}h\left( z \right) }{\mathrm{d}z} \right) ^{2}\mathrm{d}z,\quad k_1 =\frac{E_0}{2\left( {1+v_0} \right) }\int \limits _0^H {\left( {h\left( z \right) } \right) ^{2}\mathrm{d}z} \\ E_0 =\frac{E_s }{\left( {1-v_s^2 } \right) },\quad v_0 =v_s \left( {1-v_s } \right) \\ \end{array}, \end{aligned}$$

(22)

where $E_s$ is the elastic modulus and $v_s$ is the Poisson’s ratio of elastic media. The procedure to achieve the first and second parameters of Vlasov model also can provide a general understanding about the nature of shear and elastic modulus used in the Pasternak and other two-parameter models. Mullapudi and Ayoub showed the importance of considering the second parameter in the mathematical modeling of soil reaction forces. They also presented an iterative algorithm in order to calculate parameters of a soil medium, which are presented by Vlasov and Pasternak model [54]. Ozgan and Daloglu used finite element analysis to study vibrations of a plate on Vlasov foundation [55]. In their considered vibrating system, the Vlasov model was used to present the interactions between soil and the plate.

Fig. 17

Discrete Winkler model

Fig. 18

Discrete Kelvin–Voigt model

2.1.13 Reissner model

Reissner model is also developed to make the half-space model less complicated. It is based on the assumption that all the stresses in z-plane of a soil layer (as presented in Fig. 16) with thickness of H are zero:

$$\begin{aligned} \sigma _x =\sigma _y =\tau _{xy} =0. \end{aligned}$$

(23)

Also, the following constraints on the displacements of the contact and bottom surfaces of the foundation are considered as:

$$\begin{aligned} \left. u \right| _{z=0} =0;\hbox { }\left. u \right| _{z=H} =\left. w \right| _{z=H} =0. \end{aligned}$$

(24)

Based on the assumption of elastic as well as isotropic material, the following relation is derived from the governing equations of a continuum medium [53]:

$$\begin{aligned}&c_1 w\left( {x,y,t} \right) -c_2 \nabla ^{2}w\left( {x,y,t} \right) =p\left( {x,y,t} \right) \nonumber \\&\quad -\,\frac{c_2 }{4c_1 }\nabla ^{2}p\left( {x,y,t} \right) , \end{aligned}$$

(25)

in which $c_1=\frac{E}{H},c_{2}=\frac{HG}{3}$ and E, G, and H are Young’s modulus, shear modulus, and thickness of foundation, respectively. Zhang demonstrated the superiority of using Reissner model over using Winkler model by studying contacts between a beam and a foundation [56]. Nobili used the Reissner foundation model as the mathematical model of soil media [57].

2.2 Discrete models

All of the above-mentioned models describe continuous foundations; however, the foundation can be presented in a discrete form. Railway track, for example, is a structure, which is actually supported by a discrete foundation, and in the case that the length of considered system is finite, the discrete model is more appropriate. On the contrary, for the infinite problem, the foundation is usually assumed to be continuous. Therefore, all of the presented theories for different models can be expanded to the discrete models. The reaction force of discrete Winkler foundation, which contains linear springs, can be described by the following equation:

$$\begin{aligned} p\left( x \right) =k\sum _{i=1}^n {w\left( {x_i } \right) \delta \left( {x-x_i } \right) } , \end{aligned}$$

(26)

in which $x_i$ is the location of ith spring and $\delta$ is the Dirac function (Fig. 17).

And for the Kelvin–Voigt model, the relation can be expressed as:

$$\begin{aligned} p\left( x \right) =k\sum _{i=1}^n {w\left( {x_i } \right) \delta \left( {x-x_i } \right) } +c\sum _{i=1}^n {\dot{w}\left( {x_i } \right) \delta \left( {x-x_i } \right) } . \end{aligned}$$

(27)

The reaction force can be developed for the other foundation models (such as Maxwell and Poynting-Thomson) (Fig. 18).

Over time, due to settlements and decompositions, the foundations (especially soils) act like a multilayer model in which the properties of each layer are different. In this case, multilayered models have provided more realistic responses than single-layered or continuous half-space models. In the next section, we discuss multilayered models.

Fig. 19

a Continuous two-layered model; b discrete two-layered model

Fig. 20

Three-layered model of railway track including ballast mass[59]

2.3 Multilayered models

Based on the type of analysis, structure/foundation, and range of frequency, the number of considered layers varies in the mathematical/numerical modeling of a foundation. Single-layer model is utilized when the subgrade is rigid or its stiffness is much larger than the stiffness of the considered foundations. For analysis of railway vibrations, the single-layer model is implemented when the frequency of vibration is low. Multilayered models are usually used in the modeling of structures on soil foundation and for high-frequency modeling of railway track. Furthermore, when the ground-borne vibration is transmitted to nearby structures, it is necessary to consider the lower layers in the modeling of soil/foundation interactions [58].

2.3.1 Two-layered model

Analyzing dynamical behavior of ballasted railway tracks is mostly done by the implementation of two-layered models. Generally, these models are simple, which considers the effects of main components (rail, rail pads, sleepers, and ballast) into mathematical modeling. Researchers have used both continuous and discrete two-layered models to study dynamics of ballasted railway tracks [58] (Fig. 19).

The mass and stiffness of beneath layers can be inserted into the model by the aid of three-layered and poly-layered (more than three) models.

2.3.2 Three-layered model

For the modeling of railway track, three-layered foundation models are used with taking into account the effects of track–soil interactions, ballast mass, stiffness as well as the damping of soil (presented in Fig. 20) [59].

2.3.3 Poly-layered model

As the properties of soil are layered, it is best to use the poly-layered models to describe the soil-based foundations (Fig. 21). Ai and Cai have conducted research on the poly-layered soil foundation. The layers are assumed to be in contact, and thus, the boundary condition between the layers can be presented as Eq. (28). They first derived the stiffness matrix for a single layer, and based on the boundary conditions between the layers, the matrix was then extended to n layers. The finite element method, boundary element method, and analytical layer element method were used to solve the considered problem [60, 61].

$$\begin{aligned} \left. {\left[ {{\begin{array}{l} {-\,\tau _{xz} \left( {x_i ,z_i^- } \right) } \\ {-\,\sigma _{xz} \left( {x_i ,z_i^- } \right) } \\ {u\left( {x_i ,z_i^- } \right) } \\ {w\left( {x_i ,z_i^- } \right) } \\ \end{array} }} \right] } \right| _i =\left. {\left[ {{\begin{array}{l} {\tau _{xz} \left( {x_i ,z_i^+ } \right) } \\ {\sigma _{xz} \left( {x_i ,z_i^+ } \right) } \\ {u\left( {x_i ,z_i^+ } \right) } \\ {w\left( {x_i ,z_i^+ } \right) } \\ \end{array} }} \right] } \right| _{i+1} . \end{aligned}$$

(28)

Fig. 21

Poly-layered soil foundation [61]

Fig. 22

a Structure on partially distributed supporter; b foundation with discontinuity

Fig. 23

Schematic of reinforced soil bed and the simulated model [68]

2.4 Partially distributed and discontinuous models

In the practical problems, partially distributed supporters and discontinuous foundations are frequently used. The partial configuration of a foundation directly influences buckling load of beams/columns. Stability and control of beams, pipes, and strings on partial foundations have been examined considering the effects of partial configuration of the foundation [62]. In the case of stability analysis, the stability, critical velocity, and flutter velocity of fluid conveying pipes depend on the attachment ratio (the ratio of the length of partial foundation over the entire length of the system) and also the foundation parameters [63]. The governing equations are usually in the form of integro-differential equations [64]. Stojanovic [65] presented the natural frequencies, mode shapes, and maximum deflection of beams on Winkler/Pasternak foundations taking into account the size and location of discontinuity (Fig. 22).

Fig. 24

Floating slab tracks [72, 73]

Fig. 25

Different kinds of lift-up phenomena due to types of loading

2.5 Reinforced model

Settlement is a potential phenomenon in soft foundations (for example in soft soils), where shearing resistance is weak. A soft substrate can experience partial or total subsidence due to sudden and complex loadings. For insuring a structure against settlement, the reinforced foundations have been introduced and utilized (especially in order to reinforce the shearing strength). Placement of a granular layer on top of a soft soil is highly effective on the settlement characteristics of the system. The study of settlement and foundation reinforcement is usually conducted considering the example of a beam on a foundation.

Dey conducted a study to provide a comparison between stress distribution in the foundation of a reinforced and unreinforced elastic foundation bed. He showed that the stress distribution in the reinforced foundation is higher and more uniform than in the unreinforced one. As a result, the reinforced foundation enhances settlement characteristics and decreases the non-uniformness of contact stress [66]. Maheshwari et al. studied reinforced foundation coated by a beam subjected to a moving load. The model of a membrane placed between two Pasternak layers was assumed as the reinforcement, and the underlying soil was considered as Winkler model [67]. They showed that flexural vibrations are significantly influenced by geotextile stiffness, granular fill compressibility, and the load condition. Dey et al. reinforced a soft clay soil using granular fills and geosynthetic layer. They presented the model of a footing on soil as the model of a beam on an elastic foundation. A footing, also known as a shallow foundation, is used under walls and buildings to distribute loads on a wider area and preserve structures from large concentrated loads. Different models such as Winkler, Maxwell, Pasternak, and a tensioned membrane were used in modeling of the foundation [68, 69] (Fig. 23).

2.6 Floating model

Floating foundations (known as floating slabs in the field of railway engineering) are used in tunnels and urban areas where the vibration control/isolation is critical. This foundation can drastically reduce the transmitted vibrations to nearby structures and buildings. In the structure of a floating slab track, the rail is placed on a concrete slab foundation by the use of rail pads, and the slab is rested on a compressible mat layer (the mat is known as the slab mat and usually is rubber bearings or steel springs); and a resonance frequency is assigned to the slab, which is calculated from the ratio of mass slab and mat stiffness. The floating slab tracks effectively work at the frequencies higher than the resonance frequency at which the slab detached from the underlying layer, and as a result, high reduction in vibration transmission is provided. A few researchers have studied the optimum resonance frequency using both experimental and theoretical techniques. Their research shows that the optimal resonance frequency is in the range of 8–16 Hz [70,71,72]. The mathematical and simulation of the problem is was performed by the use of continuous/discrete multilayered models (Fig. 24).

2.7 Nonlinear models

In this section, nonlinear models are presented. These models are classified according to the type of nonlinearity. The types of nonlinearity (or the sources of nonlinearity) in the system of a flexible structure on a foundation are divided into three branches: nonlinearity from the lift-up phenomena, nonlinearity due to amplitude dependency behavior of foundation, and nonlinearity due to friction from the fillers, which are used in the formation of foundation elements.

2.7.1 Lift-off nonlinearity

Bilateral model (a model of foundation which has the same behavior in both compression and tension cases) is not an actual representative for the most of practical cases. A foundation model may present different behavior under tension and pressure loads; it is also possible that it only reacts in one direction and has a neutral behavior in the other direction. Initially, it was assumed that a foundation can only react in compression case; therefore, the idea of tensionless foundations or unilateral foundation was brought up. Separation between structure and foundation is a very common assumption in the modeling of tensionless foundations (as presented in Fig. 25). This phenomenon results in emergence of nonlinearity in the force–displacement behavior.

Weitsman studied a beam subjected to a moving load rested on a tensionless Winkler foundation. He related the speed of load to the lift-up phenomenon and named the speed at which the separation takes place as the critical speed [74]. Choros and Adams [75] showed that several lift-ups are possible in overcritical region and presented closed-form solutions for such problems, which are valid for contact and noncontact regions. Celep et al. [11] investigated the effect of tensionless parameters on the response of a beam. They showed once such models undergo lift-ups, nonlinearity appears in the static and dynamic analysis. In this case, the nonlinear equation described the behavior of engineering foundations better than those of linear ones.

Farshad and Shahinpoor [12] used a bilinear elastic foundation, which considers different responses for foundation in compression and tension cases. They extracted two equations for foundation in compression and tension and combined them into one valid equation for the whole region under the consideration. The problem was solved by a perturbation method. An iteration procedure was presented by Bhattiprolu et al. [76] to solve lift-off problem of a beam on a viscoelastic foundation. Based on partitioning a beam, Johnson and Kouskoulas linearized the nonlinear equation, which describes the problem of the beam on bilinear foundations [77]. Celep used eigenvalues of a beam as an approximation of displacement function of rectangular plates. He employed an auxiliary function to present the tensionless behavior of plates on Winkler foundation [78]; for the circular plates, he presented a method to solve the lift-up problem by minimizing the total potential energy of the system [79].

Dynamic response of a beam on a tensionless two-parameter foundation was studied by Celep et al. considering different types of boundary conditions [80]. Ahmadian et al. [81] studied vibrations of a beam rested on a Pasternak foundation and subjected to a periodical moving load. The focus of their research was on the reduction in separation between load and beam by adjusting the parameters of considered foundation.

Fig. 26

a Force displacement behavior of nonlinear friction model, b updating reference point during motion [104]

2.7.2 Cubic nonlinearity

Nonlinear foundation was first proposed to develop more accurate model for the behavior of soil. Beaufait and Hoadley approximated the nonlinear behavior of a foundation using a bilinear curve. This foundation was only active in compression condition. Then, they used the midpoint difference method, which is an effective approach for dealing with higher-order equations in the presence of discontinuities [82]. Birman [83] explored the effect of hardening nonlinearity on the natural frequencies of a beam. He used a cubic relation between the displacement and the foundation reaction as below:

$$\begin{aligned} p\left( x \right) =kw\left( x \right) \pm k_3 w^{3}\left( x \right) , \end{aligned}$$

(29)

where the positive sign stands for hardening nonlinearity and the negative sign stands for softening nonlinearity. Kou and Lee [84] considered a non-uniform beam problem on nonlinear foundation and solved it using the perturbation method. They showed that the response of a vibrating system can be obtained from solving linear ordinary differential equations, which are extracted based on perturbation technique. Harden and Hutchinson conducted a practical and numerical study on the nonlinear behavior of foundations in order to model seismic energy dissipation in rocking dominant structures. The problem was modeled by a beam on the nonlinear Winkler foundation [85]. Bhattiprolu et al. [86] used a nonlinear viscoelastic foundation to model restoring force of flexible polyurethane foams, which are used in furniture and automotive industry. They applied different types of excitation loading to a structure on the foundation for two cases, namely the bilateral foundation (the structure was stuck to the foundation so the foundation acts same in pressure and tension) and the unilateral foundation (the structure was not stuck to the foundation so the foundation acts only in one direction) [87].

Wu and Thompson [88] considered the effect of preload on the nonlinear behavior of the pad and ballast stiffness in railway track and observed that the preload improves damping effect at low frequencies. They observed that the supports around the load point are stiffened; and at more than 2 m away from the load point, the effect of preload is negligible [89]. They investigated the effect of linearity and nonlinearity on the wheel–rail impact for soft, medium, and hard types of rail pad. It was shown that the linear model is not appropriate for wheel–rail impact problem [90] because the points which are subjected to large deformation react stiffer than other ones.

Nguyen et al. [91] proposed a new general model which includes the shear characteristic of Pasternak foundation, the linear as well as nonlinear features of nonlinear Winkler foundation. In addition, they considered the effect of foundation mass on the maximum deflections and observed maximum deflections are influenced by foundation mass in high velocity range. Şimşek [92] studied a microbeam on three-layered foundation (shear, linear, and nonlinear layers). Effects of nonlinear foundation on the large amplitude of a beam were examined by Kanani et al. [93]. The foundation includes nonlinear Winkler and shear layer of Pasternak foundations. They concluded that increasing the nonlinear parameter of foundation can magnify nonlinearity of the system. On the other hand, linear and shear parameters can weaken the nonlinearity. Since the nonlinearity is influenced by the above-mentioned parameters, the nonlinearity of vibrations can be controlled or even omitted by the aid of linear and shear parameters. Civalek stated that the effect of shear and nonlinear parameters on the amplitude of oscillations is highly significant in comparison with the linear model [94]. Senalp [95] examined the influences of damping and speed of load on nonlinear response of beams considering a nonlinear foundation.

Younesian et al. provided the response of an infinite beam on nonlinear Kelvin–Voigt foundation under harmonic moving load, investigated chaotic behavior of beam on foundation with cubic nonlinearity, presented frequency response of an imperfect beam on nonlinear foundation, and employed variational iteration method as an analytical method to solve nonlinear problems of beams on a foundation [96,97,98,99]. Coskun considered nonlinearity in the governing equation due to both cubic and lift-off nonlinearity and studied lift-off phenomenon for a beam resting on a tensionless Pasternak and Winkler foundation. By investigating the effects of foundation parameters on beam/foundation contact as well as noncontact length, Coskun showed the effects of foundation nonlinearity on contact length [100,101,102].

2.7.3 Friction nonlinearity

The nonlinearity due to friction is mainly used for rubber springs. Because of several advantages, rubber springs are conventionally used in railway vehicles and bushings. Berg conducted several experimental tests on the rubber springs subjected to harmonic excitation at low frequencies and reported a force–displacement curve for the spring as shown in Fig. 26a. He showed that the sharp corners are due to frictional nature of rubber fillers. Therefore, a friction force was inserted into the model of rubber springs, and the springs were modeled by three elements: elastic, viscous, and friction [103].

A reference point is defined as $(x_s,p_{fs})$ on the graph of force–displacement, which is updated during any motion; and the nonlinear force depends on the displacement and the reference state (as shown in Fig. 26b). This force is expressed by the following relation [103, 104]:

$$\begin{aligned} p_f =p_{fs}&+\frac{x-x_s }{x_2 \left( {1-sign\left( {\dot{x}} \right) \frac{p_{fs} }{p_{f\max } }} \right) +\mathrm{sign}\left( {\dot{x}} \right) \left( {x-x_s } \right) }\nonumber \\&\quad \left( {p_{f\max } -\mathrm{sign}\left( {\dot{x}} \right) p_{fs} } \right) , \end{aligned}$$

(30)

where $p_{f\max }$ is the maximum of friction force; $x_2$ is the displacement which is started from $x=0,p_f=0$. It increases monotonically as it is needed for the force to reach to $p_{f}=p_{f\max }/2$. Use of this relation provides the effect of changes of stiffness in small amplitudes [105].

The model presented by Berg has been widely used and adopted for presenting behavior of rubber springs in different frequency ranges and load amplitudes [106].

2.8 Random model

Random vibrations occur due to random excitations from a stochastic load or randomness of structure parameters. Elements of a structure might experience deteriorations due to erosion, frictions, and heavy loadings over a period of time [16]. In railway engineering, the randomness usually has been observed in irregularities of rail and stiffness, damping as well as loss factor of the track foundation. The random parameter can be expressed by a mean value plus a variance. Accordingly, we have the following form for a random stiffness:

$$\begin{aligned} k\left( x \right) =k_0 +k_\varepsilon \left( x \right) , \end{aligned}$$

(31)

in which $k_{0}$ is the mean value of spring stiffness and $k_\varepsilon (x)$ is the longitudinal variations of stiffness.

Fryba et al. [107] considered a beam resting on a foundation with random stiffness and uncertain damping coefficient subjected to a moving load. They performed a stochastic finite element analysis for evaluating the deflection and the bending moment variances [17]. It was found that the influence of stiffness randomness is far more important than the effect of uncertainty in damping. Also, it was observed that increasing the velocity enhances the subcritical region and decreases the supercritical region due to the stochastic effects. Naprstek and Fryba [108] considered the practical use of the last case as the railway track structure and included track irregularity randomness in the equations. Younesian et al. studied a foundation with random stiffness [109] and random loss factor [16] as the supporter of a Timoshenko beam subjected to a moving load. They presented the dynamic responses in the form of variance–mean by the use of first-order two-dimensional perturbation method.

Andersen and Nielsen investigated a beam on the Kelvin foundation with stochastic vertical stiffness. A shear layer was used to modify the foundation’s model. They explored how variations of stiffness affect beam response and indicated correlation length of the stiffness variation increases dynamic response of the beam [110]. Koziol et al. [111] proposed the stiffness of foundation as a function of the space variable. They presented a comparison between Adomian’s decomposition method and Bourret’s approximation as the solution methods of the problem of a beam on the random foundation [112]. Schevenels et al. [113] studied the wave propagation in an Euler–Bernoulli beam on a random foundation. They also studied the effects of correlation length on the wave propagation. It was observed that spatial variations can have an influence on the dynamic response only when the amplitude of correlation length is near the amplitude of wavelength. Jagtap et al. [114] considered the randomness problem of a structure on a foundation taking into account the thermal variation. Singh et al. [115] investigated stochastic responses of composite plates on nonlinear shear-deformable foundation. The randomness was considered in material properties and foundation parameters [116]. Kumar et al. [117] studied nonlinear vibration of a random nonlinear foundation covered by a composite laminated plate. The randomness was considered in different parameters and sensitivity analysis was performed to find their effect on the transverse deflection of a plate. Among the different parameters which were considered in the sensitivity analysis, the elastic constants have shown the most important influence.

2.9 Fractional model

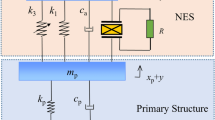
Till here, the nonlinear model is introduced as the model which can enter the effect of heavy loadings or large displacement into calculations. Thus, the displacement-dependent feature of foundations is already satisfied by the use of nonlinear models. However, a few parameters of foundations are frequency dependent. Loss factor, for example, is a parameter which is moderately influenced by the frequency of vibrations. Therefore, the fractional model has been introduced to present frequency-dependent features of a foundation. In Fig. 27, an example of using fractional element for rail pads suggested by Zhu et al. [117] is illustrated.

Fig. 27

Rail pad model suggested by Zhu et al.[117]

The reaction force of the fractional element can be presented by the following equation:

$$\begin{aligned} p=C_a { }_0^G D_t^\alpha x, \end{aligned}$$

(32)

in which p and x are the reaction force and the deflection of fractional element. $D_{t}^{\alpha }$ denotes the fractional derivative of $\alpha$th order for x. For the systems including fractional as well as nonlinear elements (i.e., cubic hardening nonlinearity), the time-domain governing equation is a nonlinear fractional differential equation (NFDE) type, for example

$$\begin{aligned}&\ddot{x}\left( t \right) +c\dot{x}\left( t \right) +kx\left( t \right) \nonumber \\&\quad +\, k_N x^{3}\left( t \right) +k_\alpha D^{\alpha }x\left( t \right) =F_\mathrm{ext} \left( t \right) +lD^{\alpha }p\left( t \right) ,\nonumber \\ \end{aligned}$$

(33)

where $F_\mathrm{ext} \left( t \right)$ is the external applied load, $p\left( t \right)$ is the fractional force through fractional elements, l and $k_\alpha$ are fractional parameters of foundation model which are specified from experimental tests.

Berg [103] used a five-parameter model in describing the behavior of rubber springs in primary suspension of railway vehicles in accordance with elastic, viscous, and friction forces. He presented a procedure in which all the five parameters can be calculated only with two force–displacement measurement tests. However, he stated that more accurate model is desirable at high frequencies. Fenander [118] provided experimental analysis on rubbers and showed that the parameters of such foundations are frequency dependent. Hence, he proposed a fractional derivative model to describe the frequency-dependent behavior of the foundation in a practical application (as the model of rail pads in a railway track) [119]. Zhu et al. [105] presented an amplitude- and frequency-dependent rail pad model including a fractional element corresponding to the frequency-dependent behavior plus a nonlinear element representing amplitude-dependent behavior. They compared their proposed model with the traditional viscous model and demonstrated that the traditional model overestimates stiffness and damping at high frequencies [18]. Zhang and Zhu [120] used a fractional derivative, nonlinear friction model to surmount the frequency-dependent behavior of the model. Hosseinkhani and Younesian studied the vibro-acoustic analysis of a railway track including fractional and nonlinear elements. Based on a parametric analysis, they showed that deflections, stresses, and radiated acoustic pressure from the railway track can be controlled by fractional parameters [121]. They also provided the closed-form solution for dynamic response of a plate on the most generalized form of foundation model, i.e., generalized stiffness and generalized damping (linear, nonlinear, and fractional damping) [122].

Paola et al. investigated exponential distance-decaying and fractional power distance-decaying functions to present the restoring force of a foundation. The former model yielded to an integro-differential governing equation, while the latter results in fractional differential one with better results [123]. Cammarata and Zingales [124] showed that the fractional model can present the relation between the force and displacement as well as distance-decaying.

Fig. 28

Beam subjected to a general load

3 Structures on foundations

In this part, different models of structures on a foundation are presented. According to the dimensions, the structures are classified into one-dimensional structure (beam and string) on a foundation and two-dimensional structures (plate, shell, and membrane) on a foundation. Applications, theories, and mathematical formulations of each one are briefly illustrated.

3.1 Beam on a foundation

Many practical experiments and problems in various fields, such as aerospace, physics, biomechanics, and railway engineering, as one special case, have been efficiently handled by the model of beams on a foundation. The railway track is consisted of a rail and foundation. The foundation, also known as the track support, includes sleepers, rail pads, and the ballast. Each component undergoes complicated different loads, and consequently they react differently according to the amplitude, frequency, and type of the applied load [19, 22]. The fundamental of foundation theories and their behavior in the presence of different load conditions is already covered in Sect. 2.

Four theories exist for presenting the behavior of a beam to name, the Euler–Bernoulli, Rayleigh, shear, and Timoshenko. Euler–Bernoulli model neglects the effects of rotary inertia and deformation, but the Timoshenko model considers both of them. The theory of Rayleigh beam is positioned between the Euler–Bernoulli and Timoshenko theories, which considers effects of rotation of cross section. The shear model is also a model between the Euler–Bernoulli and Timoshenko and only includes the effect of shear deformation.

3.1.1 Euler–Bernoulli beam

Euler–Bernoulli model is also known as shear-indeformable beam, classical beam, and thin beam theory. It is the simplest model among the above-mentioned beam theories, since it neglects the effects of rotary inertia and transverse shear deformations. The Euler–Bernoulli theory can be derived based on the three-dimensional elasticity theory, by the use of Newton’s second law, or by the generalized Hamiltonian’s principle [125]. This theory is valid when the thickness of a beam is less than $\frac{1}{20}$ wavelength of the deformations. For an Euler–Bernoulli beam resting on a foundation subjected to a general load as presented in Fig. 28, a differential element can be considered (Fig. 29), in which $V\left( {x,t} \right)$ and a $M\left( {x,t} \right)$ are the shear force and bending moment, respectively. Therefore, the governing equation is expressed as

$$\begin{aligned} EI\frac{\partial ^{4}w\left( {x,t} \right) }{\partial x^{4}}+\rho A\frac{\partial ^{2}w\left( {x,t} \right) }{\partial t^{2}}+p\left( {x,t} \right) =f\left( {x,t} \right) , \end{aligned}$$

(34)

in which $p\left( {x,t} \right)$ is the foundation reaction. In the following part of this review article, a few fundamental works related to the study of Euler–Bernoulli beam on a foundation are presented.

Tanahashi formulated the problem of Euler–Bernoulli beam on a two-parameter foundation in order to obtain displacement and stress functions [126]. Ansari et al. [127] employed the Galerkin method and the multiple time scales method (MTSM) to investigate nonlinear frequency of a beam on a foundation subjected to a moving load. They studied the effects of load, nonlinear stiffness, and damping parameters on the frequency response of a railway track using MTSM. Results of their research show the internal and external resonances for their objective structure [26, 128].

Fig. 29

Differential element of Euler–Bernoulli beam [125]

Younesian et al. [96] presented analytical solution for vibrations of a beam rested on a nonlinear foundation using variational iteration method (VIM). In another paper, they performed frequency analysis of a cracked Euler–Bernoulli beam. In order to analyze the considered problem, they divided the beam into two parts, and the crack was modeled by a rotational spring [97]. Nayfeh and Lacarbonara [129] compared two approaches, namely discretization method and direct method, for solving quadratic, cubic nonlinear differential equations to obtain primary resonance and sub-harmonic resonance of the considered structure. It was concluded that the discretization method leads to erroneous responses; therefore, in some special cases (when quadratic nonlinearity exists), the discretization method is not an applicable procedure.

Dimitrovová and Varandas [130] studied the effects of sudden change in the stiffness of a foundation under a beam, modeled by Euler–Bernoulli theory, with the specific attention to the application in high-speed trains. Influences of load velocity and amplitude as well as foundation stiffness on the dynamic response of Euler–Bernoulli beam were investigated by Jorge et al. [131]. Yuan et al. [132] used a double Euler–Bernoulli beam model to present the behavior of floating slab track.

Nagaya and Kato [133] suggested the use of non-symmetric piecewise linear support for presenting the non-symmetric, nonlinear behavior of magnetic levitation supports. Levitation supports are widely used in linear vehicle guideways. They used a combination of Laplace transformation, Fourier series expansion, and the residue theorem for analyzing the model subjected to a stationary decaying force. Lee [134] analyzed the same model on the condition that the load is moving with a constant speed. He employed Hamiltonian’s principle and the mode method to investigate the difference between the transient response of piecewise linear support and linear support.

Using the model of a beam on a nonlinear foundation, Li et al. [135] investigated the possibility of chaos for the model of a vehicle moving on a road by Melnikov method. Norouzi and Younesian investigated the chaotic vibration in the Euler–Bernoulli beam on a nonlinear foundation. They analyzed the effect of foundation parameters on the chaotic behavior of the considered structure [98].

Naidu and Rao [136] presented the results corresponding to the effects of various boundary conditions on free vibration and stability behavior of uniform beams and columns resting on a nonlinear foundation. Hui [137] examined buckling and post-buckling behavior of an infinite beam on a nonlinear foundation using Koiter’s general and Koiter’s improved theory. It was found that if only the linear foundation is used, post-buckling behavior is unstable, while the nonlinear foundation can provide stability. Sheinman and Adan developed [138] a nonlinear higher-order shear deformation theory to study the effect of imperfection on the vibration of a beam rested on a nonlinear elastic foundation. It was shown that imperfection is highly effective on foundation behavior in the case of softening nonlinearity. Santee and Gonçalves obtained the post-buckling load for a beam on a nonlinear foundation as a function of beam parameters, foundation parameters, as well as load parameters. They also investigated the conditions in which the beam remains stable [139]. Fallah and Aghdam [140] presented analytical solution for the post-buckling analysis of a beam on a nonlinear foundation with shearing layer and tensile force. They used Euler–Bernoulli and von Karman’s assumption to develop the governing equation [141].

3.1.2 Rayleigh beam

Rayleigh improved the Euler–Bernoulli beam theory by including the effects of rotary inertia or the inertia due to axial displacement. The theory of Rayleigh beam on a foundation is obtained by considering the effect of rotatory inertia in Eq. (34) [125]:

$$\begin{aligned} EI\frac{\partial ^{4}w\left( {x,t} \right) }{\partial x^{4}}&-\rho I\frac{\partial ^{4}w\left( {x,t} \right) }{\partial x^{2}\partial t^{2}}+\rho A\frac{\partial ^{2}w\left( {x,t} \right) }{\partial t^{2}}\nonumber \\&\quad +p\left( x \right) =f\left( {x,t} \right) . \end{aligned}$$

(35)

The term $\rho I\frac{\partial ^{4}w}{\partial x^2 \partial t^2}$ stands for the effect of rotatory inertia. Nevertheless, there are not many studies about Rayleigh theory, and in the most cases, Euler–Bernoulli or Timoshenko models are used to model vibrations of beams.

Dynamics of Rayleigh beam on nonlinear foundation subjected to moving load were studied by Hryniewicz [142]. The aim was to analyze the response of an infinite Rayleigh beam. Oni and Omolofe considered prestresses in Rayleigh beam and presented the resonance condition [143]. The effect of rotatory inertia on the resonance condition showed that increasing the rotatory inertia decreases the risk of resonance. Kim studied the effects of rotatory inertia on the stability and frequencies of Rayleigh beam–columns under variable harmonic load [144]. When the effect of rotatory inertia was considered, the first frequency increased while no change was observed for the second frequency.

3.1.3 Shear beam

The shear model improves the Euler–Bernoulli model by including effect of shear distortion [145]. The governing equations of the motion of the shear beam model are [145]:

$$\begin{aligned} \begin{array}{l} \rho A\frac{\partial ^{2}w\left( {x,t} \right) }{\partial t^{2}}+k^{*}AG\left( {\frac{\partial \phi \left( {x,t} \right) }{\partial x}-\frac{\partial ^{2}w\left( {x,t} \right) }{\partial x^{2}}} \right) +p\left( x \right) =f\left( {x,t} \right) \\ EI\frac{\partial ^{2}\phi \left( {x,t} \right) }{\partial x^{2}}-k^{*}AG\left( {\phi \left( {x,t} \right) -\frac{\partial w\left( {x,t} \right) }{\partial x}} \right) =0 \\ \end{array}, \end{aligned}$$

(36)

where A is the area of cross section, $k^{*}$ is the shear coefficient of section, and $\phi$ is the rotation angle of cross section. This model is mostly used to examine dynamic behavior of tall buildings [146].

Fig. 30

A Timoshenko beam subjected to a general load

3.1.4 Timoshenko beam

Timoshenko or thick beam theory was first introduced by Stephen Timoshenko in 1921 [147]. The theory considers the effects of both rotary inertia and shear deformations [148]. Assuming we have the following set of equations for a beam rested on a foundation and subjected to an external load based on the Timoshenko beam theory (as it is shown in Fig. 30):

$$\begin{aligned} \begin{array}{l} \rho A\frac{\partial ^{2}w\left( {x,t} \right) }{\partial t^{2}}+k^{*}AG\left( {\frac{\partial \phi \left( {x,t} \right) }{\partial x}-\frac{\partial ^{2}w\left( {x,t} \right) }{\partial x^{2}}} \right) +p\left( x \right) =f\left( {x,t} \right) \\ EI\frac{\partial ^{2}\phi \left( {x,t} \right) }{\partial x^{2}}-k^{*}AG\left( {\phi \left( {x,t} \right) -\frac{\partial w\left( {x,t} \right) }{\partial x}} \right) =\rho I\frac{\partial ^{2}\phi \left( {x,t} \right) }{\partial t^{2}} \\ \end{array}. \end{aligned}$$

(37)

Accordingly, several researchers presented different methods to evaluate shear coefficient of Timoshenko beam theory [149,150,151]. Natural frequencies of Timoshenko beam were analyzed in [42, 152, 153]. Attarnejad et al. [154] used differential transform method to extract natural frequencies of Timoshenko beam on a two-parameter foundation. Chen et al. [155]investigated the effects of Poisson’s ratio and foundation parameters on the natural frequencies of the thick beam, using a mixed method, which combines the methods of state space and the differential quadrature (DQ). They observed that increasing the Poisson’s ratio decreases the natural frequencies. Since the Poisson’s ratio is different for different materials and the Poisson’s ratio affects natural frequencies, the type of material can be considered as an important criterion in designing the properties of a structure. Mo et al. [156] investigated the effect of shear deformation and nonlinearity of foundation on the nonlinear frequency of Timoshenko beam and showed the frequency is highly influenced by these two parameters.

Zhu and Leung studied nonlinearity due to the geometry of Timoshenko beam using FEM scheme [157]. These nonlinear vibrations caused intensive axial stresses to the beam, while the level of vibrations is highly influenced by the foundation parameters. Arboleda-Monsalve et al. [158] considered generalized boundary conditions for Timoshenko beam on a foundation and presented the corresponding dynamic stiffness matrix and load vector. Sapountzakis and Kampitsis used boundary element method to deal with arbitrary boundary condition of Timoshenko beam-columns on a nonlinear foundation. They utilized the average acceleration approach in combination with the modified Newton–Raphson method to solve the obtained coupled nonlinear equations [62]. Kargarnovin et al. investigated the comfort of passengers of high-speed trains passing on a bridge. They probed the effects of foundation parameters (stiffness of rail pad and ballast), suspension parameters, and track irregularities. Rail and bridge were modeled by Timoshenko beam [159, 160].

3.2 String on a foundation

Belts, cables, and ropes are the elements that are modeled by string. It is highly needed to model the transverse vibrations of the aforesaid structures [161, 162] owing to their critical applications.

Strings are preloaded by a tensile load (shown as T in Fig. 31b) and can withstand tensile forces. For a string rested on a foundation subjected to a general load, depicted in Fig. 31a, the governing equation is derived as:

$$\begin{aligned} \rho \frac{\partial ^{2}w\left( {x,t} \right) }{\partial t^{2}}+p\left( {x,t} \right) =\frac{\partial }{\partial x}\left( {T\frac{\partial w\left( {x,t} \right) }{\partial x}} \right) +f\left( {x,t} \right) , \end{aligned}$$

(38)

where p(x, t) is the restoring force of foundation.

Fig. 31

a Full body diagram of a vibrating string, b free body diagram of the string element

Fig. 32

a A schematic of membrane on a general foundation in x–z plane, b schematic of tensioned membrane in x–y plane, c free diagram of a membrane element [125]

Metrikine [163] investigated responses of an infinite string on a nonlinear foundation subjected to a moving load whether or not the speed of load is slower than the speed of wave. It was observed when the speed of load exceeds the speed of wave in the string, the symmetry of the string response was violated and a wave response was observed behind the load position. This model aims to represent the behavior of catenary system in high-speed trains. Gottlieb and Cohen studied oscillations of a string on an elastic foundation, with concentration on its application in modeling mechanisms of the mammalian cochlea [164]. Demeio and Lenci conducted nonlinear analysis of cables on nonlinear foundation using MTSM [165].

3.3 Membrane on a foundation

Membranes have a wide range of applications in modeling acoustical and musical instruments, and in biomechanics. Behavior of skull, skin, and air vehicle wings can be presented by the membrane theory.

A membrane is defined as a flexible structure whose one dimension is thin compared to other dimensions. The membrane is subjected to an initial tension and due to that bears tensile forces (the force of T in Fig. 32). It withstands no shear or bending loads. The membrane theory can be considered as the string theory whose displacement is a function of two spatial variables; however, the string displacement has only one spatial direction. The equation of transverse vibration, by writing Newton’s second law in the direction of z, is expressed as [125, 166]:

$$\begin{aligned}&T_x \frac{\partial ^{2}w\left( {x,y,t} \right) }{\partial x^{2}}+2T_{xy} \frac{\partial ^{2}w\left( {x,y,t} \right) }{\partial x\partial y}\nonumber \\&\qquad +\,T_y \frac{\partial ^{2}w\left( {x,y,t} \right) }{\partial y^{2}}+f\left( {x,y,t} \right) \nonumber \\&\quad =\rho h\frac{\partial ^{2}w\left( {x,y,t} \right) }{\partial t^{2}}+p(x,y,t). \end{aligned}$$

(39)

Mack and McQueary [167] developed the general perturbation method for solving the oscillations of a circular membrane on the elastic foundation with cubic nonlinearity taking into account the first nonlinear periodic mode. Soares and Gonçalves studied nonlinear vibrations of a pre-stretched membrane on a foundation with hardening and softening nonlinearities [168]. Effects of foundation parameters and initial stretching ratios on the frequency–amplitude were investigated. It was shown that increasing the stretching ratio leads to higher natural frequencies.

3.4 Plate on a foundation

Geometrically, a plate is a membrane which can bear bending forces. Plates are thicker than membranes; nevertheless, one of its dimensions is still thin compared with the two other dimensions. The following equation governs the vibrations of the plate illustrated in Fig. 33:

$$\begin{aligned} D\nabla ^{4}w\left( {x,y,t} \right)&+\rho h\frac{\partial ^{2}w\left( {x,y,t} \right) }{\partial t^{2}}+p(x,y,t)\nonumber \\&\quad =f\left( {x,y,t} \right) , \end{aligned}$$

(40)

where $D=\frac{Eh^{3}}{12(1-\nu ^2)}$ is the flexural rigidity; and in Fig. 33b, Q is the shearing force and M is the bending moment.

Fig. 33

a Schematic of a plate on a general foundation and subjected to general loading b free diagram of a plate element [125]

Yamaki [169] and Dumir [170] are among the first researchers in the nonlinear analysis of plates on foundation and in presenting solution method for the problem, of a plate with different shapes under different loads taking into account various boundary conditions. Sincar [171] analyzed a simply supported plate resting on a weak nonlinear foundation subjected to a certain initial condition to calculate the fundamental frequency of plate. He applied the Galerkin method to the governing equation for extracting the related partial differential equation, and afterward, Lindstedt’s perturbation method was employed to obtain the fundamental frequency. Collet and Pouget [172] used the two-dimensional nonlinear Schrodinger equation to study the behavior of a thin plate on a nonlinear foundation in small-amplitude limits. The equation paved the way for analyzing the appearance of localized modes and waves excited by modulational instability. They investigated the effects of material nonlinearity and geometric dispersion on the system’s vibrations modes [173].

Vibration analysis can be used as the method of studying frequency resonances for components of a structure and as the method of designing them to be resonance free (if it is desired). In connection with this subject, Chien and Chen studied nonlinear vibrations of plates resting on a nonlinear foundation [174,175,176].They found that besides the vibration amplitude, modulus ratio, and foundation stiffness, initial stresses affect frequency responses of laminate plates. The nonlinear governing equation was derived using the Galerkin method and was solved numerically by the use of Runge–Kutta method. Younesian et al. [177] presented a closed-form solution for the dynamic response of a plate on a nonlinear foundation and investigated sensitivity of frequency resonances with respect to the initial amplitude of plate. Ping et al. [178] studied the bifurcation and chaos behavior of circular plates on a foundation with Duffing equation.

Reissner considered a simplified version of a spherical shell problem as a uniform infinite elastic plate. He modeled the foundation as a nonlinear one, and he investigated post-buckling behavior for both quadratic and cubic foundations [179]. Chai [180] formulated nonlinear vibration and post-buckling behavior of unsymmetrically laminated imperfect shallow cylindrical panels using the dynamic Marguerre-type equations. He used mixed condition as the boundary condition and investigated the effect of such parameters as parabolically varying rotational constraint, in-plane edge tension, vibration mode, curvature and geometric imperfection, and rotational edge stiffness. Effects of complex mechanical load on post-buckling behavior of flat and curved panels were investigated by Librescu and Lin [181]. Lin and Librescu [182] considered the case of geometrical imperfection of flat/curved plates on a nonlinear foundation subjected to thermo-mechanical loading. They showed that achieving to higher buckling load and lower snapping phenomenon is possible by increasing the foundation moduli.

In the post-buckling region, an unstable phenomenon called mode jumping may occur. This phenomenon can unbalance the equilibrium configurations and devastate the system. Imperfections, boundary conditions, and foundation configurations affect the onset of mode jumping [183]. This can be prevented by appropriate selection of foundation parameters [64]. The mode jumping is investigated in post-buckling of beams and plates resting on a foundation in [64, 184, 185].

3.5 Shell on a foundation

The last two-dimensional flexible structure on a foundation, in the present category, is shell. Shells are employed to model dynamical behavior of curved-shape component of many practical structures, which are used in aerospace vehicles, automotive, and buildings. A shell is a curved plate and bear bending moment. The governing equation is:

$$\begin{aligned}&D\nabla ^{4}w\left( {x,y,t} \right) +\rho h\frac{\partial ^{2}w\left( {x,y,t} \right) }{\partial t^{2}}+p(x,y,)\nonumber \\&\qquad =f\left( {x,y,t} \right) -\left( \frac{1}{R_x }\frac{\partial ^{2}\phi (x,y,t)}{\partial y^{2}}\right. \nonumber \\&\quad \left. +\,\frac{1}{R_y }\frac{\partial ^{2}\phi (x,y,t)}{\partial x^{2}}-\frac{2}{R_{xy} }\frac{\partial ^{2}\phi (x,y,t)}{\partial x\partial y}\right) . \end{aligned}$$

(41)

Most of the engineering materials show nonlinear behavior in the presence of large deformations. According to that, Jain and Nath [13] investigated the softening, hardening nonlinear behavior of a foundation under clamped orthotropic shallow spherical shells. It was shown that by increasing the hardening nonlinearity of the foundation, the maximum deformation decreases.

Based on Ritz’s variational and the R-function methods, a new method was presented by Kurpa et al. [186] in order to deal with the problem of orthotropic shallow shells on the Pasternak foundation. Ramachandran and Murthy [187] studied snap-through phenomenon as well as the influence of large amplitude on the flexural vibrations of a shallow cylindrical shell resting on the Winkler foundation. The same topic was considered by Massalas and Kafousias [188] in which the foundation was a nonlinear one. They obtained an analytical expression for the first natural frequency of the considered structure. Sofiyev [189] investigated the large-amplitude vibration and frequency–amplitude characteristics of FGM cylindrical shells interacting with the nonlinear Winkler elastic foundation. They studied the effects of shell characteristics on the nonlinear frequency parameters.

4 Methods of solution

Since the beginning of the vibration analysis of beams, plates, and shells on foundations, different kinds of solution methods have been presented and developed for extracting, discretizing, and solving their governing equations.

The first step in the mathematically modeling of the vibration problem is deriving the governing equation. A few methods such as Newton’s law, Hamilton’s principle, D’Alembert’s principle, and energy method are applied to derive the governing equation of the motion [190]. Then, a discretizing method (the Galerkin method and the Ritz method) must be utilized to decouple the equation into time and space domain. The obtained time-domain differential equation is the most important equation that needs to be analyzed. According to the structure, assumptions, requirement, and simplifications, which are considered in the formulation, the time-domain governing equation can appear in the form of ordinary differential equation (ODE), nonlinear differential equation (NDE), and nonlinear/linear fractional differential equation (FDE). According to the type of equation, several numerical, approximate, and analytical methods have been developed. A few of these methods and their applications are presented in this section. Accordingly, a general overview on the most well-known solution methods pertinent to the problem of flexible structures on a foundation is discussed.

4.1 Analytical/approximate methods

Analytical methods are in the priority of the methods because they provide exact and closed-form solutions for the developed mathematical model. Nevertheless, analytical methods are usually hard to be applied or they need several simplification assumptions. In this regard, analytical/approximate methods have been developed. The analytical/approximate methods have succeeded to provide advantages of analytical methods, to some extent. They usually present the response of the problem in the form of a series which converge to the exact solution. In this part, three of analytical/approximate methods named variational iteration method (VIM), homotopy analysis method (HAM), and Adomian decomposition method (ADM) are first described. Then, perturbation techniques and differential transform method are introduced.

VIM is one of the methods which can be used in extracting solution of differential equations and in conducting frequency analysis of nonlinear systems. It is known as an analytical/approximate method [191]. VIM has an approximately high speed of convergence. The method has been exploited by a few researches to present semi-analytical solution for the problem of a structure rested on a foundation. For example, researchers have developed analytical solution for the free oscillations of a beam on nonlinear foundations [96]. In addition, free vibration analysis of a beam on elastic foundation was conducted using VIM in [192]. The use of VIM for buckling problems was presented by Atay and Coşkun [193] and by Baghani et al. [194].

HAM is considered as a reliable and straightforward approximate/analytical technique for nonlinear oscillation problems [195]. Pirbodaghi et al. [196] presented analytical expression for the dynamic response of laminated composite plates resting on a nonlinear foundation using the homotopy analysis method. Jafari-Talookolae et al.[197] investigated laminated composite beams on a nonlinear foundation. The time-domain equation was extracted by Ritz method, and the exact solution was obtained by HAM where the HAM was truncated at third approximation. Younesian et al. [177] considered the problem of plate on a foundation. They showed that both HAM and VIM can solve NDEs. HAM was also used by Shahlaei-Far et al., taking into account both quadratic and cubic nonlinearity for the foundation [198].

Adomian decomposition method (ADM) is based on the expansion of the solution to an infinite series. In this method, the Adomian’s polynomial is employed to enable the convergence of nonlinear terms. The analytical solutions of Euler–Bernoulli, Rayleigh, and Timoshenko beams on a foundation have been obtained using ADM [142, 199, 200]. The method was utilized for dealing with nonlinear terms of the formulation [201], non-uniform beams [202, 203], and random foundations [112]. Hryniewicz and Kozioł [204, 205] combined wavelet approximation with ADM in order to present analytical method for vibrations of a Timoshenko beam rested on a nonlinear foundation. Arefi employed the Adomian decomposition method to evaluate the response of Euler–Bernoulli beam on a nonlinear foundation considering the effects of nonhomogeneous index [206].

Perturbation techniques and their applications in solving different problems are explained in [207] among which multiple time scales method (MTSM) is a well-established and widely used approach in the vibration analysis of structures [127, 208]. These techniques are applicable for two kinds of problems: strongly nonlinear and small deflection; weakly nonlinear and large deflection. They are mostly used for obtaining frequency and harmonic responses as well as investigating stability conditions [16, 99]. Lancioni and Lenci [209] utilized perturbation technique as a semi-analytical method and the finite element algorithm as a numerical method for solving the problem of Euler–Bernoulli beam on a nonlinear foundation. Zarubinskaya and Van Horssen studied the initial boundary value problem, which represents the behavior of a simply supported plate on a weakly nonlinear elastic foundation. Two time scales perturbation method was used to achieve the approximate solution of plates on foundations [210]. Mareishi et al. [211] used MTSM to derive frequency response of free and forced vibrations of FG nanobeams on a nonlinear supporter.

Differential transform method (DTM) is a semi-analytical approach in solving differential equations, and it is based on Taylor series expansion. Attarnejad et al. [154] assessed the application and accuracy of DTM for extracting natural frequencies of the Timoshenko beam on a two-parameter foundation. They observed as the number of terms in DTM grows, the accuracy of transverse displacement and bending angle of rotation increases, and by considering about 20 terms in the DTM, the relative error in the calculation of the natural frequencies becomes zero. Balkaya et al. [212] solved the differential equation of the vibrations of Euler–Bernoulli and Timoshenko beams on a Pasternak foundation (as the model of soil). Exact solution and natural frequencies of a beam on the soil foundation were obtained by the method of differential transform in Ref [213].

4.2 Numerical methods

Numerical methods are used for solving the complicated problems when finding a closed-form solution to be difficult or impossible. Analytical approaches present exact responses and provide direct solutions of the equation. However, these methods are sometimes difficult to be exploited and they lose their functionality. In this regard, the numerical methods are employed [214,215,216,217]. The numerical methods use assumptions and constraints, which make finding the solution of the most complicated problems possible. Finite element and boundary element methods (FEM and BEM) are utilized to deal with the effects of complicated geometry and boundary conditions. FEM has been used for analyzing vibrations of different kinds of structure on Winkler, two-parameter, and nonlinear foundations [194, 217,218,219,220,221]. In this context, extraction of stiffness, mass matrices as well as force vector have been developed by several works [47, 222, 223]; in implementation of FEM, the kind of theory considered for structures (i.e., the Euler–Bernoulli, Rayleigh, Shear, and Timoshenko theories for one-dimensional structures; membrane, plate, and shell theories for two-dimensional structures) is an important case either [220, 224, 225]. Lua and Teng studied buckling of shells on a nonlinear elastic foundation. They used finite element formulation and presented a number of discrete data points in order to model the foundation reaction–displacement relationship in a general form [226]. Hong et al. [227] applied the discrete data points to model the nonlinear behavior of elastic foundation and studied the large deflection analysis of shells and plates on tensionless foundation using a finite element scheme. Finite element method was developed by Jorge et al. [228] for a railway track system, while analytical solution was not available for the problem. They modeled the system as a beam on bilinear foundation with different stiffness in tension and compression. The effect of different stiffness was investigated on rail deflection and critical velocity of load (the velocity above which rail deflection increases significantly). It was observed as the stiffness in tension increases, this critical velocity also increases. Stojanovic used p-version of the finite element method for the problem of a Timoshenko beam rested on a nonlinear foundation. He implemented the method to the general case of beams/plates on a foundation taking into account the effects of variable discontinuity and geometric nonlinearity [65].

Boundary element method (BEM) is a well-known method for analyzing dynamics of structures. It is especially used to solve free and forced vibration of a foundation under a structure. The method also is applied for deriving stiffness as well as mass matrices, and therefore, analyzing the eigenvalue problems [214, 229, 230]. Dynamic response of a beam on a foundation subjected to cyclic load [231], Reissner plates on an elastic foundation [232], soil structures [233] have been analyzed using BEM.

Ding et al. [234] solved the governing equation of the Euler–Bernoulli beam on a nonlinear foundation using the Galerkin and Runge–Kutta method. The Galerkin method proposes the response of a problem as an infinite series of multiple trial functions. This infinite series must be truncated at a point. Therefore, Ding et al. investigated the convergence of the Galerkin method. They pointed out that the convergence rate of the method increases as the nonlinear parameter of the foundation increases and it decreases as the linear parameter of foundation increases. The combination of Runge–Kutta and Galerkin methods was used by Yang et al. [235] in order to deal with the problem of Timoshenko beam on a foundation. They also investigated the convergence for the case of Timoshenko beam and showed that shear modulus of the beam plays an important role on the rate of convergence. Chen et al. [174] also used the Galerkin and Runge–Kutta methods to solve the governing differential equation of plates.

Fig. 34

Reproduced with permission [58], Copyright 2015, Elsevier

Application of half-space model in ground-borne vibration analysis.

Fig. 35

A model of vehicle–pavement interactions [244]

Fig. 36

Reproduced with permission [248], Copyright 2008, Elsevier

Catenary system.

5 Practical applications

5.1 Mechanical/structural applications

The most well-known and tangible applications of the model of a structure resting on a foundation can be found in mechanical, civil, and railway engineering systems. The model of railway track, bridges, pavements, and soil–tank interactions are a few applications among which railway track has gained the attraction of several researchers. Investigating the behavior of railway track was one of the primary stimuli to the implementation of a beam on a foundation. The railway track includes a rail (modeled with one of the beam theories) fastened to sleepers. Rail pads are embedded between rail and sleeper. Sleepers are placed on the ballast. Each of these components undergoes complicated loading force with different frequency range and reacts based on the applied loading. Therefore, different models have been developed to formulate vibrations of the track. Puzavac et al. [236] assumed that the stress–deformation relation of railway track is based on Winkler model. They considered geometry deteriorations in the track and investigated the effect of stiffness on the vertical quality of track geometry. Fenander used a fractional foundation model to present the frequency-dependent properties of the railway track [119]. Wu and Thompson [237] used double-Timoshenko beam to study high-frequency behavior of a railway track [238,239,240].

In order to study the induced vibration from railway track loads or from highway loads to adjacent buildings and structures, the two-dimensional models such as structures on a half-space foundation (Fig. 34) and plates on a foundation were used [135, 241,242,243].

However, in the case of one-dimensional pavements (Fig. 35), the model of a Timoshenko/Euler–Bernoulli beam on a foundation can be used [244,245,246]. In addition to track, the overhead catenary system is modeled by a string on a foundation with varying stiffness [165, 247, 248].

The interaction forces between vehicle and pavement, vehicle and road, and rail and track are important. In this regard, the dynamics of vehicle and road/pavement need to be investigated. In the present review article, the dynamics of vehicle is outside of its scope, and its effects can be considered in the problem as a concentrated moving load. The model of foundation can be considered as a layered plate on a foundation [249]. In Ref [250], nonlinear dynamics of vehicle–road interactions is studied. The road was modeled as a simply supported double plate on a foundation. The nonlinear viscoelastic behavior of the foundation was presented by a nonlinear Kelvin–Voigt model. Yang et al. studied the effects of coupling action on the car–road interactions. They also studied the effects of roughness amplitude on coupling action. They showed that as the roughness amplitude of road decreases, the effects of coupling action become more considerable; therefore, the effects of coupling action cannot be neglected when a vehicle is running on a smooth surface [251].

Modeling bridges in railway and highways is a similar subject. Brun et al. [252] considered the model of a bridge using the Euler–Bernoulli beam theory rested on a foundation. Parametrically excited vibrations of a bridge on a nonlinear foundation were studied by Zhou et al. [253]. Human-induced vibrations can be assumed as a structure on a foundation. Pavements and pedestrian bridge are the primary examples for the human-induced vibrations on a foundation [254, 255]. Also, bridges are supported by piles (columns). These piles are located on a foundation. Accordingly, many papers have been published to investigate vibrations of piles on foundations. Methods for increasing their strength and effects of their vibration on adjacent structures were also fully discussed in [256, 257] (Fig. 36).

Polyurethane foams used in furniture and automotive industry usually present complex nonlinear behaviors. They usually are modeled as a foundation under a beam or a plate. In this regard, Bhattiprolu conducted vibration analysis of beams/plates on nonlinear Polyurethane foams [76, 86, 258]. Tanks, slabs, buildings, and pipes are other structures, which are placed on viscoelastic foundations with the aim of vibration reduction [189, 219] (Fig. 37).

Fig. 37

Sketch of a shell on a foundation as the model of storage tanks or pipes interacting with soil

Fig. 38

Reproduced with permission [261], Copyright 2006, Springer

Model of pipelines in the deep sea.

5.2 Marine pipelines

The model of infinite/semi-infinite cables/beams on a foundation is considered as the system of marine pipelines or moorings as shown in Fig. 38a [259, 260]. Vibration-induced forces play a key role in stability and safety of these structures. The foundation, which is substrate of sea, acts only in compression (unilateral foundation) and includes linear as well as nonlinear coefficients (Fig. 38b). The applied load is composed of constant distributed load due to the weight and boundary harmonic excitations. Demeio and Lenci [261] transformed the moving-boundary problem of cables on unilateral foundation to a fixed-boundary problem by changing variables. They investigated forced nonlinear dynamics of such systems. In their other works, resonance harmonics of these continuous systems were investigated using perturbation techniques [262]. They also studied both stability and nonlinear vibrations of the structures [165, 263]. In order to install pipelines in deepwaters, an analytical model is proposed by Wang et al. [264]. Zan et al. [265] presented a method to determine nonlinear matrix for the system of J-lay pipelines. Gong et al. [266] studied dynamics of S-lay pipelines on nonlinear hysteretic soil using finite element method.

5.3 Aerospace applications

The effects of foundation parameters on the vibration suppression and their effects on preventing unwanted phenomenon are important and substantial in aerospace structures where structures undergo a combination of elastic forces, thermal forces, and aerodynamic forces. Because of their lightweight and astonishing bending rigidity, sandwich and composite plates/beams are used in this field. The model of structures on a foundation (Fig. 39) is widely used in modeling aerospace plates and shells [267,268,269]. Fluttering motion and thermal buckling are undesirable phenomena, which endanger safety and stability of the flight vehicle [270]. External surface of an aerospace vehicle, which is subjected to aerodynamic forces, suffers from self-excited oscillations (fluttering motion). Chai et al. [271] investigated the effects of elastic foundation to avoid supersonic flutter of aerospace panels subjected to aero-thermo-elastic forces. Rao and Rao[270] employed the finite element method to examine the effects of elastic foundation on the supersonic flutter of short panels. Goldman and Dowell studied nonlinear dynamic of fluttering plates on an elastic foundation. A nonlinear form was considered for the interaction force between the plate and the foundation [272].

Fig. 39

Reproduced with permission [271], Copyright 2017, Elsevier

Model of a sandwich plate in supersonic airflow.

5.4 Biomechanics applications

Vibration analysis of human body is important from HSE aspects, and also, highly needed for designing artificial organs. In this regard, some parts of human body can be represented by the aforementioned models; i.e., human skull can be modeled by a membrane, tissues, and vessels are modeled by a string, and skin is modeled by a thin layer on a soft substrate. Since the concentration of the present paper is on the foundations, in this section, we investigate the cochlea which is one of the important parts of the mammalian auditory system [273]. Cochlea is divided into two channels by a membrane called basilar membrane (BM). Actual shape of cochlea is spiral; however, for presenting traveling waves features, the unwrapped model is an appropriate simplified assumption (Fig. 40a). The dynamic problem of basilar membrane is considered as a fluid–structure interaction (FSI) example, as the membrane is between two fluid-filled channels. The structural part is considered as a beam on a foundation (in 2-D models) and a plate on a foundation (in 3-D ones) (Fig. 40b). The dynamic equation of structural part is as below:

$$\begin{aligned} m\ddot{Z}\left( {x,t} \right) +c\dot{Z}\left( {x,t} \right) +k(x)Z\left( {x,t} \right) =F_f \left( {x,t} \right) , \end{aligned}$$

(42)

in which m is the mass of MB per unit length, c is the damping coefficient, $F_f(x,t)$ is the force due to fluid traction, and Z(x, t) is the displacement of MB in the direction of z. The longitudinal variable stiffness of the BM is developed as an exponential function in the following form [274]:

$$\begin{aligned} k\left( x \right) =k_0 e^{-ax}, \end{aligned}$$

(43)

where $k_0$ and a are constant values. According to the frequency of input sound, the amplitude of traveling waves reaches a maximum at a different section of BM. These astounding characteristics provide the sensitivity of human ear to different frequencies.

Fig. 40

Schematic diagram of basilar membrane with longitudinal varying stiffness suggested by Ren et al. [275]; a 2-D model of cochlea, b schematic of BM and varying stiffness attached to it

Vibration patterns and fluid properties of the cochlear stimulated by input sound with different frequencies have been studied in Ref. [275]. Effective mechanical properties of BM such as stiffness and damping on the response of cochlear were studied by Ren et al. [276]. Meaud and Grosh considered longitudinal coupling of the basilar membrane BM and the tectorial membrane in the mathematical modeling of cochlear mechanics, and investigated these effects on the tuning of cochlea [277].

Tissues, vessels, aneurysms, and skin are the other parts of body which have been modeled and studied using the aforesaid mechanisms. In order to study surface morphological post-buckling, Xu and Potier-Ferry presented a macroscopic framework of a thin layer on a soft foundation as the model of wrinkle surfaces (for example human skin or other living tissues [278]). The layer was presented using the plate theory, and the foundation was presented by the theory of linear isotropic elasticity. They investigated the onset of instability due to post-buckling phenomenon [279]. Buckling phenomenon in wrinkle surfaces results in slight variation in wrinkle amplitude and wavelength. Owing to complexity of geometry and boundary conditions, the numerical methods are employed to study these problems [280]. Analyzing mechanical properties of skin is crucial to create artificial skin and also detect skin lesions as well as under skin disease [281, 282]. Sasai et al.[283] designed a tactile sensor to measure mechanical properties of skin by touching it. The probe can report stiffness of skin surface and stiffness of deeper tissues.

Pamplona and Mota [284] used the model of a membrane filled by a fluid on a rigid/elastic foundation to study skin expansion phenomena during skin surgeries. The foundation was considered to be both elastic and rigid, because surface of human body has different stiffness; fatty tissues, for example, were considered as elastic foundations. Patil et al. [285] studied the effects of substrate layer on the mechanical behavior of membranes during inflation and deflation. The model was based on the contact between cells or a cell and a deformable substrate (Fig. 41).

Wakeling and Nigg conducted an experimental study to determine the frequency and damping coefficients of soft tissues in leg. Free vibrations of the tissue were measured by an acceleration sensor attached to the skin. The frequency and damping of vibrations were determined from the response of harmonic vibrations [286]. David and Humphrey presented the model of intracranial saccular aneurysms by a membrane submerged in a viscous fluid. Bifurcation and instabilities due to natural frequencies of saccular aneurysms were found as the reasons of saccular aneurysm raptures. They studied fluid and viscoelasticity of the material from the stability viewpoint [287].

5.5 Nanoresonators and foundations

Vibrations of nanoresonators including nanobeams, nanotubes, nanowires, graphene sheets, and nanoplates have been fascinating for researchers in the area of applied mechanics, structural analysis and vibrations [288, 289]. Plenty of articles have been published so far to investigate the vibrations of the nanoresonators. Herein, we briefly review the vibrations of nanoresonators considering different types of foundations. We first start with vibration analysis of nanobeams, which can include nanotubes and nanowires as well. Recently, Eyebe et al. studied nonlinear vibrations of a nanobeam rested on fractional-order viscoelastic Pasternak foundations [290]. Lei et al. studied vibrations of viscoelastic damped nanobeams using nonlocal Timoshenko beam theory rested on Kelvin–Voigt elastic foundation [291]. Malekzadeh and Shojaee investigated surface and nonlocal effects on the nonlinear free vibration of non-uniform nanobeams rested on a damped Winkler foundations using both Timoshenko and Euler–Bernoulli beam theory [292]. Askari and Esmailzadeh studied nonlinear vibrations of fluid conveying nanotubes rested on the nonlinear Winkler foundation using the nonlocal Euler–Bernoulli beam theory considering both thermal and surface effects [293]. They also studied forced vibrations of curved carbon nanotubes and higher modes of carbon nanotubes rested on nonlinear Winkler–Pasternak foundations using nonlocal Euler–Bernoulli beam theory [294,295,296,297,298,299]. In another work, Askari et al. studied nonlinear vibrations of nanobeam considering Winkler–Pasternak foundation with quadratic rational Bezier arc curvature [300]. Another model was also developed by them using the nonlocal Rayleigh beam theory to investigate the vibrations of nanobeams considering Winkler and Pasternak foundations [301].

Fig. 41

reproduced with permission [284], Copyright 2012, Elsevier

Model of inflated membrane on a foundation used in numerical study.

Kiani has published several papers in which he studied vibrations of nanowires, nanobeams, and nanotubes rested on a foundation based on different beam theories [302,303,304,305]. Su et al. studied both free and forced vibrations of nanowires rested on an elastic substrate. They considered Winkler, Pasternak, and also generalized substrate models for the considered foundation of the nanowire [306]. Rahmanian et al. investigated free vibrations of carbon nanotubes rested on a nonlinear Winkler foundation using nonlocal models. They showed that by increasing the foundation stiffness, the natural frequencies incline to specific values which are related to the clamped conditions[307]. Sadri et al. analyzed vibrations of double-walled carbon nanotube resonators embedded in an elastic medium utilizing the variational iteration method [308]. They showed that enhancing the stiffness of the surrounding elastic medium increases the nonlinear frequencies [308]. Saadatnia and Esmailzadeh studied chaotic flexural vibrations of carbon nanotubes under axial loads rested on Winkler and Pasternak foundations [309]. Zhang investigated transverse vibrations of embedded nanowires under axial compression considering the higher-order surface effects and Winkler foundation model [310]. Nonlinear vibration of nanobeams was modeled using nonlocal Euler Bernoulli beam theory by Togun and Bagdatlı. The considered foundation in their modeling is in the form of linear Winkler–Pasternak [311].

Graphene sheets and nanoplates have also attracted researchers to investigate their vibrations when they are rested on a foundation. A few of recent examples can be started with a research in which a nanoplate rested on a nonlinear Winkler Pasternak foundation was used for ultra-high small mass sensing. The high nonlinearity of the stiffness allows the system to have higher sensitivity in order to detect a very tiny mass in the scale of femtogram [312, 313]. Zhang et al. analyzed thermo-electro-mechanical vibration of piezoelectric nanoplates resting on viscoelastic foundations using nonlocal Kirchhoff plate theory. They showed that decreasing the foundation stiffness increases the effect of nonlocal parameter on the natural frequencies of nanoplates [314]. Two-parameter elastic foundations were utilized by Sobhy as the model of foundation for determining the natural frequency of the orthotropic nanoplates [315]. Very recently, Fan et al. determined exact solutions for forced vibrations of completely free orthotropic rectangular nanoplates with a viscoelastic foundation. They used the Kelvin–Voigt foundation for the modeling of the foundation of nanoplates [316]. Anjomshoa and Tahani obtained natural frequency of orthotropic circular and elliptical nanoplates embedded in an elastic medium. In order to model the elastic medium, they used the damped Winkler and Pasternak foundations [317].

6 Conclusions and future work

In the present work, we reviewed theoretical models of foundations considering a wide range of linear and nonlinear elastic and viscoelastic models. We first focused on Winkler model and discussed the evolution and theoretical background of this principal model. Afterwards, we presented theories of Kelvin–Voigt, Maxwell, Zener, Poynting-Thomson, Burger, Filonenko-Borodich, Hetenyi, and Pasternak models. A comprehensive review was also provided on discrete, multilayered, partially distributed supporter and discontinuous, reinforced, floating, and nonlinear models. Different types of nonlinear models including lift-off, cubic, and friction nonlinearities were fully discussed. We then focused on the random and fractional models. After fully reviewing different types of foundations, their applications in different structural systems such as beams, plates, strings, membranes, and shell were presented. A few approximate and numerical approaches were investigated to show their potential for analyzing structural systems rested on foundations. Very last part of this review article shows the applications of reviewed foundations in different systems including mechanical/structural application, marine pipelines, aerospace devices, biomechanics, and nanoresonators. This review article can be used by researchers from different disciplines as a comprehensive and technical source for better understanding of mechanical foundations, and their potential applications in different systems. The research in this area can be categorized into three different branches:

• The first branch is related to foundation models and development of novel theories in order to have a more accurate and reliable models for substrates and mediums in different systems.

• The second branch contains the solution methods for analyzing the developed mathematical models in accordance with these foundation models.

• Applications of the foundation models in different systems can be considered as the last main category of research in this area. Vibration behavior of many structures can be investigated taking into account different foundation models presented in this research.

Accordingly, researchers can extend vibration modeling of different types of structures in macro- to nanoscale using the presented foundation models in this review article. Furthermore, new foundation models can be developed considering fractional nonlinearity and fractional damping. The practical applications of these foundation models can be studied for different structural systems such as bridges and railways for the sake of vibration suppression.

The mechanical behavior of foundation should be also investigated under the effect of different parameters such as thermal variation and cyclic loads. For designing the structural systems, this review article can provide useful information to select an appropriate foundation model taking into account the stability, control, and vibrations of the targeted system.

Thus far, several interesting models and practical applications have been suggested for the mechanical foundations, but there is a lack of research on the implementation of intelligent materials into mechanical foundations. However, the field of foundation modeling is still in progress and many exciting works will be published in future; herein, we plan to propose a new area of research based on the foundation models and recently proposed technology of nanogenerators (NGs) to develop the intelligent foundation [318]. NGs, especially triboelectric nanogenerators (TENGs), have been recently proposed to convert wasted kinetic energy to electrical power. TENGs can be easily embedded in mechanical foundations to harvest the kinetic energy applied to the vibrating system, and use it for energy harvesting or self-powered sensing. In fact, the dissipated mechanical energy through the foundation can be scavenged with adding TENG part. With using this new technology in foundation, we can develop intelligent foundation for different parts of our cities and transportation systems including railways, parks, roads, and even sidewalks [319] (Fig. 42).

Fig. 42

Conceptual design of intelligent foundation using nanogenerators [319]

The technology of nanogenerators should be investigated by vibration engineers and material scientists to develop intelligent foundations for both energy harvesting and transportation monitoring applications. It opens a new door to researchers from different areas such as networks systems, vibrations, materials, IoT, and smart cities to propose new mathematical modeling of intelligent foundations, optimize and select the required materials, and fabricate the intelligent foundation of future.