1 Introduction

The influence of moving loads on foundations has been the subject of numerous investigations in structural mechanics. When the concentrated load moves with constant velocity along infinite foundations, a relatively simple “steady-state” solution can be obtained [1]. The extensive researches on the dynamic response analysis of beams on foundations under moving loads have been summarized in review articles by Fryba [2], Wang et al. [3], and Beskou and Theodorakopoulos [4].

In most of the published researches on the topic of response of an infinite beam resting on a foundation under moving loads, the foundation is assumed as linear elastic one. Sheehan and Debnath [5] presented an analytical solution of the dynamic response of an infinite beam on an elastic foundation with axial load. Zheng et al. [6] studied the instability analysis of a beam resting on a viscoelastic foundation and subjected to a moving mass–spring–damper system. Metrikine and his colleagues investigated the dynamic instability of a mass moving along an axially compressed beam on a viscoelastic foundation [7]; an oscillator moving along a beam on an elastic half-space [8]; a mass moving along a beam on a periodically inhomogeneous foundation [9]; a moving two-mass oscillator on a beam on a viscoelastic foundation [10, 11]; a bogie moving on a flexibly supported beam [12]; a moving particle on a periodically supported infinitely long string [13]. Sun et al. proposed a closed-form solution of the deflection of a beam on linear subgrade subjected to a moving line load [14], a harmonic line load [15], moving loads [16], a platoon of moving dynamic loads [17] and a beam on multilayered viscoelastic media under a moving dynamic distributed load [18]. Dimitrovová [19] studied the vibration induced by a load moving along a beam resting on a piece-wise homogeneous viscoelastic foundation. Mackertich [20] investigated the vibration of a beam on elastic foundation excited by a moving and vibration mass. Chen et al. [21] established the dynamic stiffness matrix of a beam on viscoelastic foundation to a harmonic moving load. Kargarnovin and Younesian [22] checked the response of a beam supported by a Pasternak viscoelastic foundation. Ruge and Birk [23] compared the dynamic stiffness of Timoshenko and Euler–Bernoulli beams on Winkler foundation. ÇalIm [24] analyzed the dynamic behavior of beams on Pasternak-type viscoelastic foundation subjected to time-dependent loads. Mazilu et al. [25] analyzed the vibration of a three-mass oscillator moving along a viscoelastic supported Timoshenko beam.

With the development of the studies on dynamic response of a beam resting on a linear foundation, researchers began to pay attention to beams on a nonlinear foundation. In practice the foundation is highly nonlinear. Dahlberg [26] experimentally found that the influence of foundation’s nonlinearity on a railway track were quite significant and cannot be omitted. Wu and Thompson [27] found that linear track models are not appropriate for wheel/track impact. Kargarnovin et al. [28] compared the responses of a nonlinear and equivalent linear viscoelastic model, and they found that the results are completely different at low frequencies. Furthermore, Hryniewicz [29] found that the nonlinearity of the foundation increases the amplitude of vibration under certain conditions. Ansari, Esmailzadeh and Younesian [30] found that for the nonlinear foundation in the high-speed range, increasing the gradient of the deflection with respect to the load speed is much larger than that of the linear foundation. Ding et al. [31] studied the convergence of the Galerkin method for the dynamic response of finite beam resting on a nonlinear foundation with viscous damping subjected to a moving concentrated load, they also found that nonlinear parameter of the foundation has significant influence on the dynamic response and the convergence.

It should be remarked that the literature on infinite beams on nonlinear foundations is rather limited. To the author’s best knowledge, in previous work, only Kargarnovin et al. [28] and Hryniewicz [29] studied the response of an infinite beam on a nonlinear foundation. Based on the nonlinear cubic Winkler foundation, Kargarnovin et al. [28] studied the response of an infinite Timoshenko beam subjected to a harmonic moving load, the authors considered the shear modulus of the beams, without taking into account the shear parameter of the foundation. Hryniewicz [29] discussed the dynamic response of an infinite Rayleigh beam subjected to moving load without considering the shear modulus of the beam or the foundation. However, there was no literature on the dynamic response of an infinite beam on a nonlinear foundation considering the shear deformable beams and shear modulus of the foundation at the same time.

According to the modeling of the mechanical behavior of the road or railway and the subgrade, the earliest mathematical model adopted is the Winkler elastic foundation [32]. The Winkler foundation is assumed as a series of mutually independent vertical spring. Pasternak-type foundation is introduced to account for the interaction among the linear elastic springs [33]. With linear-plus-cubic stiffness, Tsiatas compared finite beams on nonlinear Winkler’s foundation and nonlinear Pasternak’s foundation [34]. He found that even for small nonlinearity in the foundation the linear analysis is inadequate to predict the real response of the beam and the deflection of the beam is more sensitive in case of the nonlinear Pasternak foundation. Sapountzakis and Kampitsis investigated the nonlinear response of shear deformable finite Timoshenko–Rayleigh beams resting on nonlinear three-parameter viscoelastic foundation [35]. They found the effect of shear deformation is significant, the discrepancy between the results of the linear and the nonlinear analyses is remarkable and the damping coefficient is of paramount importance for beams on viscoelastic foundation. The investigation draws the conclusion that the nonlinear three-parameter foundation including material damping is a very practical model for dynamic loading cases. However, there have been no investigations about the infinite Timoshenko beam on nonlinear Pasternak foundation.

Euler–Bernoulli [1, 5–10, 13–19, 31, 34], Rayleigh [29] and Timoshenko [11, 12, 20–24, 28, 35] beam theories were used for modeling the beam. Timoshenko [36] proposed a beam theory which adds the effect of shear as well as the effect of rotation to the Euler–Bernoulli beam. Ruge and Birk compared the Timoshenko and the Euler–Bernoulli beam on the Winkler foundation in the frequency-domain [23]. They found the physically more realistic Timoshenko beam model offers additional numerical advantages in unbounded domains. Although the infinite Timoshenko beam on foundation is extensively studied, the works on infinite Timoshenko beams on nonlinear foundation are rather limited.

Although several methods (for example, the normal-mode analysis [19], the dynamic-stiffness method [21], the boundary element method [35]) were used to dealing with an infinite beam on a foundation, the integral transformation is the most common used one and also is a powerful tool for dealing with dynamical problems for such case. There are two approaches for dealing with nonlinear term in the governing equations, namely, a perturbation method [28] and the Adomian decomposition method without linearization or perturbation [29]. In this paper, these two methods were, respectively, used to deal with the nonlinear term from the foundation reaction, and then the integral transformations were employed for the dynamic response of the infinite Timoshenko beam incurred by a moving load. The derivation process proves that the two methods give the consistent result for current issues.

The present paper is organized as follows. Section 2 establishes the governing equations for the transverse vibration of an infinite Timoshenko beam on a nonlinear viscoelastic foundation subjected to a moving concentrated force. Section 3 employs the Adomian decomposition method to determine the dynamic responses of the beams. Section 4 applies the perturbation method to analyze the governing equations under the infinite boundary conditions. Section 5 presents some numerical examples to demonstrate the effects of the related parameters on the dynamic response. Section 6 ends the paper with the concluding remarks.

2 Equation of motion

The system under investigation is an infinite elastic Timoshenko beam resting on nonlinear viscoelastic foundation and subjected to a moving load, as shown in Fig. 1. The speed of the moving load is assumed to be constant. Consider a homogeneous beam with a constant cross-section A, a second moment of area I, a shear modulus G, a effective shear area k ∗ A, a density ρ and a modulus of elasticity E. The foundation is taken as a nonlinear Pasternak foundation with liner-plus-cubic stiffness and viscous damping with four parameters as follows [35]:

(1)

where P represents the force induced by the foundation per unit length of the beam, k 1 and k 3 are the linear and nonlinear foundation parameters, respectively, G p and c are the shear parameter and the damping coefficient of the foundation, respectively, t is the time, x is the spatial coordinate along the axis of the beam, u(x,t) is the vertical displacement function. Using the Hamilton principle and considering the Timoshenko beam theory, one can develop the governing differential equations of motion for the beam as [28]

$$ \everymath{\displaystyle} \begin{array} {l} \rho A\frac{\partial^{2}u( x,t )}{\partial t^{2}} + k^{*}AG\biggl[ \frac{\partial \psi ( x,t )}{\partial x} - \frac{\partial^{2}u( x,t )}{\partial x^{2}} \biggr] \\ \noalign{\vspace*{6pt}} \quad {}+ P( x,t ) = F_{0}\delta( x - vt ), \\ \noalign{\vspace*{6pt}} \rho I\frac{\partial^{2}\psi ( x,t )}{\partial t^{2}} - EI\frac{\partial^{2}\psi ( x,t )}{\partial x^{2}} + k'AG\\ \noalign{\vspace*{6pt}} \quad {}\times \biggl[ \psi( x,t ) - \frac{\partial u( x,t )}{\partial x} \biggr] + k_{f}\psi( x,t )\\ \quad {} + c_{f}\frac{\partial \psi ( x,t )}{\partial t} = 0 \\ \end{array} $$
(2)

where F 0 and v are the magnitude of the load and the load speed, k f and c f are foundation rocking stiffness and damping coefficients, ψ(x,t) is the slope function due to bending of the beam, δ(x−vt) is the Dirac delta function used to deal with the moving concentrated load, which be defined by

$$ \int_{ - \infty }^{ + \infty } \delta( x - x_{0} ) f( x ) = f( x_{0} ) $$
(3)
Fig. 1
figure 1

The model of the Timoshenko beam on a nonlinear viscoelastic Pasternak foundation

Full size image

3 Adomian decomposition method

Since the beam is infinitely long, it is convenient to define the moving coordinate system as follows:

$$ \eta = x - vt $$
(4)

The displacement of the infinite beam becomes time invariant, in the steady-state. And the following results are obtained:

$$ \everymath{\displaystyle} \begin{array} {l} u_{,t} = - v \bar{u}',\qquad u_{,tt} = v^{2} \bar{u}'', \\ \noalign{\vspace*{6pt}} u_{,x} = \bar{u}',\qquad u_{,xx} = \bar{u}'', \\ \noalign{\vspace*{6pt}} \psi_{,t} = - v\bar{\psi}',\qquad \psi_{,tt} = v^{2}\bar{\psi}'', \\ \noalign{\vspace*{6pt}} \psi_{,x} = \bar{\psi}',\qquad \psi_{,xx} = \bar{\psi}'' \\ \end{array} $$
(5)

where \(\bar{u}\) and \(\bar{\psi}\) are the displacement and slope of steady-state, a comma preceding x or t denotes partial differentiation with respect to x or t, and the prime indicates differentiation with respect to η. Substitution (5) into (2) yield

$$ \everymath{\displaystyle} \begin{array} {l} \rho Av^{2} \bar{u}'' + k^{*}AG \bigl( \bar{ \psi}' - \bar{u}'' \bigr) + k_{1} \bar{u} + k_{3}\bar{u}^{3} - cv\bar{u}' \\ \noalign{\vspace*{6pt}} \quad {}- G_{p}\bar{u}'' = F_{0}\delta( \eta), \\ \noalign{\vspace*{6pt}} \rho Iv^{2}\bar{\psi}'' - EI\bar{\psi}'' + k^{*}AG \bigl( \bar{\psi} - \bar{u}' \bigr) + k_{f}\bar{\psi} \\ \noalign{\vspace*{6pt}} \quad {} - c_{f}v\bar{ \psi}' = 0 \\ \end{array} $$
(6)

Since the beam length is considered to be infinite, the boundary conditions are

(7)

Equation (6) can be rewritten as

$$ \everymath{\displaystyle} \begin{array} {l} L_{1}\bar{u}( \eta) + L_{2}\bar{\psi} ( \eta) = F_{0}\delta( \eta) - k_{3}\bar{u}^{3}( \eta), \\ \noalign{\vspace*{6pt}} - L_{2}\bar{u}( \eta) + L_{3}\bar{ \psi} ( \eta) = 0 \\ \end{array} $$
(8)

where

(9)

3.1 Decomposition

The method of Adomian decomposition has been applied to a rather wide class of nonlinear partial differential equations [29, 37]. The nonlinear term is represented as a series of Adomian polynomials. In order to solve (8) via the Adomian decomposition method, \(\bar{u}\) and \(\bar{\psi}\) can be decomposed into the form of the infinite sum of series

$$ \bar{u}( \eta) = \sum_{j = 0}^{ + \infty } \bar{u}_{j}( \eta) ,\qquad \bar{\psi} ( \eta) = \sum _{j = 0}^{ + \infty } \bar{\psi}_{j}( \eta) $$
(10)

The nonlinear term can be decomposed as [29]

$$ \bar{u}^{3}( \eta) = \sum_{j = 0}^{ + \infty } A_{j}( \eta) $$
(11)

where the series A j (j=0,1,2,…) are polynomials, called Adomian polynomials which can be expressed as [29]

$$ A_{j} = \sum_{n = 1}^{j} c( n,j ) \bigl[ \bar{u}_{0}^{3}( \eta) \bigr]^{(n)} , \quad n \ge 1 $$
(12)

It is to be noted that in this scheme, the sum of the subscripts in each term of the A j are equal to j. The c(n,j) are products of n components of \(\bar{u}\) whose subscripts sum to j, divided by the factorial of the number of repeated subscripts. Thus

(13)

So here A j are given as

$$ \everymath{\displaystyle} \begin{array} {l} A_{0}( \eta) = \bar{u}_{0}^{3},\qquad A_{1}( \eta) = 3 \bar{u}_{0}^{2}\bar{u}_{1}, \\ \noalign{\vspace*{4pt}} A_{2}( \eta) = 3\bar{u}_{0}^{2} \bar{u}_{2} + 3 \bar{u}_{1}^{2}\bar{u}_{0}, \\ \noalign{\vspace*{4pt}} A_{3}( \eta) = \bar{u}_{1}^{3} + 3\bar{u}_{0}^{2}\bar{u}_{3} + 6 \bar{u}_{0}\bar{u}_{1}\bar{u}_{2}, \ldots \\ \end{array} $$
(14)

Substitution of (10) and (11) into (8) yield

(15)

In the following computations, the infinite series only keep the first two terms in (14). So that (15) can be rewritten in recursive form [29]:

$$ \everymath{\displaystyle} \begin{array}{l} \left\{ \begin{array}{l} L_{1}\bar{u}_{0}( \eta) + L_{2}\bar{ \psi}_{0}( \eta) = F_{0}\delta( \eta) \\ \noalign{\vspace*{3pt}} - L_{2}\bar{u}_{0}( \eta) + L_{3}\bar{\psi}_{0}(\eta) = 0 \\ \end{array}\right. \\ \noalign{\vspace*{6pt}} \left\{ \begin{array}{l} L_{1} \bar{u}_{j}( \eta) + L_{2}\bar{\psi}_{j}( \eta) = - k_{3}A_{j - 1}( \eta) \\ \noalign{\vspace*{3pt}} - L_{2}\bar{u}_{j}( \eta) + L_{3}\bar{\psi}_{j}( \eta) = 0 \\ \end{array}\right. \end{array} $$
(16)

where j=1,2.

3.2 Integral transformation

Substitution of (9) into the first part of (16) yield

$$ \everymath{\displaystyle} \begin{array} {l} \bigl( \rho Av^{2} - k^{*}AG - G_{p} \bigr)\bar{u}_{0}^{\prime \prime } - cv\bar{u}_{0}^{\prime } + k_{1}\bar{u}_{0} \\ \noalign{\vspace*{3pt}} \quad {} + k^{*}AG\bar{\psi}_{0}^{\prime } = F_{0}\delta( \eta) \\ \noalign{\vspace*{3pt}} \bigl( \rho Iv^{2} - EI \bigr)\bar{ \psi}_{0}^{\prime \prime } - c_{f}v\bar{\psi}_{0}^{\prime } + \bigl( k^{*}AG + k_{f} \bigr)\bar{\psi}_{0} \\ \noalign{\vspace*{3pt}} \quad {} - k^{*}AG\bar{u}_{0}^{\prime } = 0 \\ \end{array} $$
(17)

and then application of complex Fourier transform

(18)

leads to [22]

(19)

U 0(ξ) and Ψ 0(ξ) which Green’s functions can be solved from (19):

(20)

where

(21)

Now, if an inverse Fourier transform is taken of both sides of (17), then we will get

(22)

To calculate integrals of (22), it is necessary to employ the residue theorem. According to residue theorem, the integrals of (22) are returned to the sum of residues at poles. The poles are the roots of B 10 ξ 4+B 20 ξ 3+B 30 ξ 2+B 40 ξ+B 50=0. Considering the boundary conditions of an infinite beam [29], the closed form solutions are obtained as

$$ \everymath{\displaystyle} \begin{array} {rcl} \bar{u}_{0}( \eta)& = & \frac{1}{2\pi} \operatorname{Re} s\biggl\{ \frac{B_{60}\xi^{2} + B_{70}\xi + B_{80}}{B_{10}\xi^{4} + B_{20}\xi^{3} + B_{30}\xi^{2} + B_{40}\xi + B_{50}} \mathrm{e}^{\mathrm{i}\xi \eta } \biggr\} \biggl|_{{\xi = \xi _{l}}} \\ \noalign{\vspace*{8pt}} &=& \frac{1}{2\pi} \biggl[ 2\pi \mathrm{i} \sum _{\operatorname{Im} \xi _{j} > 0} \lim_{\xi \to \xi _{j}}( \xi - \xi_{j} )U_{0}( \xi) \mathrm{e}^{\mathrm{i} \xi \eta } + \pi \mathrm{i} \sum _{\operatorname{Im} \xi _{j} = 0} \lim_{\xi \to \xi _{j}} (\xi - \xi_{j})U_{0}( \xi) \mathrm{e}^{\mathrm{i} \xi \eta } \biggr] \\ \noalign{\vspace*{8pt}} \bar{\psi}_{0}( \eta) &=& \frac{1}{2\pi} \operatorname{Re} s\biggl\{ \frac{\mathrm{i} k^{*}AGF_{0}\xi}{B_{10}\xi^{4} + B_{20}\xi^{3} + B_{30}\xi^{2} + B_{40}\xi + B_{50}} \mathrm{e}^{\mathrm{i} \xi \eta } \biggr\} \biggl|_{{\xi = \xi _{l}}} \\ \noalign{\vspace*{8pt}} &=& \frac{1}{2\pi} \biggl[ 2\pi \mathrm{i} \sum _{\operatorname{Im} \xi _{j} > 0} \lim_{\xi \to \xi _{j}} ( \xi - \xi_{j} )\varPsi_{0}( \xi) \mathrm{e}^{\mathrm{i} \xi \eta } + \pi \mathrm{i} \sum _{\operatorname{Im} \xi _{j} = 0} \lim_{\xi \to \xi _{j}} (\xi - \xi_{j}) \varPsi_{0}( \xi) \mathrm{e}^{\mathrm{i} \xi \eta } \biggr] \\ \end{array} $$
(23)

for η≥0, where ξ j in the first part of (23) is the pole of U 0(ξ) in upper half part of the complex plane and ξ j in the second part of (23) is the pole of Ψ 0(ξ) in upper half part of the complex plane and

$$ \everymath{\displaystyle} \begin{array} {rcl} \bar{u}_{0}( \eta) &=& \frac{1}{2\pi} \operatorname{Re} s\biggl\{ \frac{B_{60}\xi^{2} + B_{70}\xi + B_{80}}{B_{10}\xi^{4} + B_{20}\xi^{3} + B_{30}\xi^{2} + B_{40}\xi + B_{50}} \mathrm{e}^{\mathrm{i} \xi \eta } \biggr\} \biggl|_{{\xi = \xi _{l}}} \\ \noalign{\vspace*{8pt}} &=& \frac{1}{2\pi} \biggl[ - 2\pi \mathrm{i} \sum _{\operatorname{Im} \xi _{j} < 0} \lim_{\xi \to \xi _{j}} ( \xi - \xi_{j} )U_{0}( \xi) \mathrm{e}^{\mathrm{i} \xi \eta } - \pi \mathrm{i} \sum _{\operatorname{Im} \xi _{j} = 0} \lim_{\xi \to \xi _{j}} (\xi - \xi_{j})U_{0}( \xi) \mathrm{e}^{\mathrm{i} \xi \eta } \biggr] \\ \noalign{\vspace*{8pt}} \bar{\psi}_{0}( \eta) &=& \frac{1}{2\pi} \operatorname{Re} s\biggl\{ \frac{\mathrm{i}k^{*}AGF_{0}\xi}{B_{10}\xi^{4} + B_{20}\xi^{3} + B_{30}\xi^{2} + B_{40}\xi + B_{50}} \mathrm{e}^{\mathrm{i} \xi \eta } \biggr\} \biggl|_{{\xi = \xi _{l}}} \\ \noalign{\vspace*{8pt}} &=& \frac{1}{2\pi} \biggl[ - 2\pi \mathrm{i} \sum _{\operatorname{Im} \xi _{j} < 0} \lim_{\xi \to \xi _{j}} ( \xi - \xi_{j} )\varPsi_{0}( \xi) \mathrm{e}^{\mathrm{i} \xi \eta } - \pi \mathrm{i} \sum _{\operatorname{Im} \xi _{j} = 0} \lim_{\xi \to \xi _{j}} (\xi - \xi_{j}) \varPsi_{0}( \xi) \mathrm{e}^{\mathrm{i} \xi \eta } \biggr] \\ \end{array} $$
(24)

for η≤0, where ξ j in the first part of (24) is the pole of U 0(ξ) in lower half part of the complex plane and ξ j in the second part of (24) is the pole of Ψ 0(ξ) in lower half part of the complex plane.

When the integrals of (22) have high order poles, the closed form solutions are obtained as

$$ \everymath{\displaystyle} \begin{array} {rcl} \bar{u}_{0}( \eta) &=& \frac{1}{2\pi} \operatorname{Re} s \biggl\{ \frac{B_{60}\xi^{2} + B_{70}\xi + B_{80}}{B_{10}\xi^{4} + B_{20}\xi^{3} + B_{30}\xi^{2} + B_{40}\xi + B_{50}} \mathrm{e}^{\mathrm{i} \xi \eta } \biggr\} \biggl|_{\xi = \xi _{l}} \\ \noalign{\vspace*{8pt}} &=& \frac{1}{2\pi} \lim_{\xi \to \xi _{l}} \frac{\mathrm{d}}{\mathrm{d}\xi} \biggl\{ \frac{B_{60}\xi^{2} + B_{70}\xi + B_{80}}{(\xi - \xi_{1})(\xi - \xi_{2})} \mathrm{e}^{\mathrm{i}\xi \eta } \biggr\} \\ \noalign{\vspace*{8pt}} \bar{\psi}_{0}( \eta) &=& \frac{1}{2\pi} \operatorname{Re}s \biggl\{ \frac{\mathrm{i}k^{*}AGF_{0}\xi}{B_{10}\xi^{4} + B_{20}\xi^{3} + B_{30}\xi^{2} + B_{40}\xi + B_{50}} \mathrm{e}^{\mathrm{i} \xi \eta } \biggr\} \biggl|_{\xi = \xi _{l}} = \frac{1}{2\pi} \lim_{\xi \to \xi _{l}} \frac{\mathrm{d}}{\mathrm{d}\xi} \biggl\{ \frac{\mathrm{i} k^{*}AGF_{0}\xi}{(\xi - \xi_{1})(\xi - \xi_{2})} \mathrm{e}^{\mathrm{i}\xi \eta } \biggr\} \\ \end{array} $$
(25)

where ξ l in the first part of (25) is the second order pole of U 0(ξ),ξ 1 and ξ 2 are the first order poles. ξ l in the second part of (25) is the second order pole of Ψ 0(ξ),ξ 1 and ξ 2 are the first order poles.

Now the second part of (16) is considered. For j=1 and 2, the second part of (16) can be rewritten as

$$ \everymath{\displaystyle} \begin{array} {l} \bigl( \rho Av^{2} - k^{*}AG - G_{p} \bigr)\bar{u}_{1}^{\prime \prime } - cv\bar{u}_{1}^{\prime }\\ \noalign{\vspace*{6pt}} \quad {} + k_{1}\bar{u}_{1} + k^{*}AG\bar{\psi}_{1}^{\prime } = - k_{3} \bar{u}_{0}^{3} \\ \noalign{\vspace*{6pt}} \bigl( \rho Iv^{2} - EI \bigr)\bar{ \psi}_{1}^{\prime \prime } - c_{f}v\bar{\psi}_{1}^{\prime } + \bigl( k^{*}AG + k_{f} \bigr)\bar{\psi}_{1}\\ \noalign{\vspace*{6pt}} \quad {} - k^{*}AG\bar{u}_{1}^{\prime } = 0 \\ \end{array} $$
(26)

and

$$ \everymath{\displaystyle} \begin{array} {l} \bigl( \rho Av^{2} - k^{*}AG - G_{p} \bigr)\bar{u}_{2}^{\prime \prime } - cv\bar{u}_{2}^{\prime } + k_{1}\bar{u}_{2}\\ \noalign{\vspace*{6pt}} \quad {} + k^{*}AG\bar{\psi}_{2}^{\prime } = - 3k_{3} \bar{u}_{0}^{2}\bar{u}_{1} \\ \noalign{\vspace*{6pt}} \bigl( \rho Iv^{2} - EI \bigr)\bar{ \psi}_{2}^{\prime \prime } - c_{f}v\bar{\psi}_{2}^{\prime } + \bigl( k^{*}AG + k_{f} \bigr)\bar{\psi}_{2}\\ \noalign{\vspace*{6pt}} \quad {} - k^{*}AG\bar{u}_{2}^{\prime } = 0 \\ \end{array} $$
(27)

Using a similar procedure for (17) and using appropriate Green’s functions and the convolution integral theorem, the closed form solutions are obtained as

(28)
(29)

where \(\tilde{u}_{1}( \eta)\) and \(\tilde{\psi} _{1}( \eta)\) can be determined by

$$ \everymath{\displaystyle} \begin{array} {l} L_{1}\tilde{u}_{1}( \eta) + L_{2}\tilde{\psi}_{1}( \eta) = \delta( \eta) \\ \noalign{\vspace*{6pt}} - L_{2}\tilde{u}_{1}( \eta) + L_{3}\tilde{\psi}_{1}( \eta) = 0 \\ \end{array} $$
(30)

The same procedure is applicable in the case of Euler–Bernoulli beams. In this case, the equations of motion can be derived as [31]

(31)

Using the same procedure, a closed form solution can be calculated as

(32)

Using the same method of residue theorem, (32) will be solved.

4 Perturbation method

Introducing a dimensionless variable as follows:

$$ u(x,t) \leftrightarrow\frac{k_{3}}{k_{1}}\sqrt{\frac{I}{A}} u(x,t) $$
(33)

Substituting (33) into (2) leads to

$$ \everymath{\displaystyle} \begin{array} {l} \rho Au_{,tt} + Y \psi_{,x} - qu_{,xx} + k_{1}u + \varepsilon u^{3} + cu_{,t} \\ \noalign{\vspace*{6pt}} \quad {} - G_{p}u_{,xx} = \frac{F_{0}Y}{q}\delta( x - vt ) \\ \noalign{\vspace*{6pt}} \rho IY\psi_{,tt} - EIY\psi_{,xx} + qY \psi - q^{2}u_{,x} + k_{f}Y\psi \\ \noalign{\vspace*{6pt}} \quad {} + c_{f}Y\psi_{,t} = 0 \\ \end{array} $$
(34)

where q=k ∗ AG, \(Y = q\frac{k_{3}}{k_{1}}\sqrt{\frac{I}{A}}\), \(\varepsilon = k_{3}(\frac{q}{Y})^{2}\). Introducing coordinate transformation η=x−vt, and substituting (5) into (34) yields

(35)

One assumes an expansion of dimensionless displacement [28]

$$ \everymath{\displaystyle} \begin{array} {l} \bar{u}( \eta) = \bar{u}_{0}( \eta) + \bar{u}_{1}( \eta)\varepsilon + \bar{u}_{2}( \eta)\varepsilon^{2} + \cdots, \\ \noalign{\vspace*{6pt}} \bar{\psi} ( \eta) = \bar{\psi}_{0}( \eta) + \bar{\psi}_{1}( \eta)\varepsilon + \bar{\psi}_{2}( \eta) \varepsilon^{2} + \cdots \\ \end{array} $$
(36)

Substituting (36) into (35), and then equating coefficients ε 0, ε 1 and ε 2 in the resulting equation, one obtains

(37)
(38)
(39)

where

(40)

where k=0,1,2.

Equations (37)–(39) and (17), (26), and (27) are exactly the same. Therefore, these equations can be solved via integral transformation, and the procedure exactly same as the procedure for solving (16). That is to say, for approximate analysis the steady-state of infinite beams on nonlinear cubic foundation, the Adomian decomposition method based on 2-term truncation are accordant with the second order term perturbation method. But the perturbation method depend on ε, which must be very small one.

5 Numerical results

In this part, numerical examples are given for parametric research. The physical and geometrical properties of the Timoshenko beam, foundation and the moving load are listed in Table 1.

Table 1 Properties of the beam, foundation and load [28, 31]
Full size table

In part three, the decomposition series for the Adomian decomposition were gotten. But the convergence of the decomposition series has not been determined. According to [37, 38], let

(41)
(42)

The decomposition series equation (10) will converges rapidly to exact solution for 0≤α j <1, j=0,1,2,… . According to Table 1 and (40) and (41)

(43)
(44)
(45)
(46)
(47)

In the following computations, the infinite decomposition series equation (10) only keep the first three terms.

Using the prescribed method, a computer program has been provided to solve the problem. To realize the steady-state response, it is sufficient to study the vibration of any point of the beam. Hence, the point x=0 is used in the following numerical examples. As the first example, the dynamic response of the infinite Timoshenko beam is considered during passage of a moving load. Figure 2 shows the time history of the Timoshenko beam subjected to the moving concentrated force. For t<0, the transverse deflection increases with time, and the biggest deflection does not appear in the t=0, there is a little delay. After reaching to the biggest deflection, the transverse deflection decreases and tends to zero. And the growth speed of the transverse deflection is far greater than the reduced speed.

Fig. 2
figure 2

The approximately analytic solution of deflection of the beam

Full size image

The effects of the shear modulus of the Timoshenko beam and the shear modulus of the foundation on the deflection of the beam on the viscoelastic nonlinear foundation are illustrated in Figs. 3 and 4, respectively. From the observation of Figs. 3 and 4, it is found that the biggest deflection of the Timoshenko beam decrease with the increasing shear modulus of the beam and the increasing shear modulus of the foundation. Furthermore, Figs. 3 and 4 show that the contributions of the shear modulus of the beam and the shear modulus of the foundation on the deflection are significant, especially when the shear modulus of the beams and the shear modulus of foundations are not great ones. That is to say, the shear modulus of the beams and the shear modulus of foundations cannot be neglected for the dynamic response of infinite beams on nonlinear viscoelastic foundations. In Refs. [28] and [34], Kargarnovin et al. and Tsiatas have, respectively, shown that the shear modulus of the beams and the shear modulus of foundations have the significant influence on the dynamic response of infinite beams on the nonlinear foundation. In the present paper, the effects of the shear modulus of the beams and the shear modulus of foundations are investigated at the same time, and similar results are got as above mentioned two references. On the other side, the numerical results also indicate that the shear modulus of Timoshenko beams is not sensitive to the time-delays of the biggest deflection while the time-delays decreases with the increasing shear modulus of foundations.

Fig. 3
figure 3

Effect of the shear modulus of the Timoshenko beam on the deflection of the beam

Full size image
Fig. 4
figure 4

Effect of the shear modulus of the foundation on the deflection of the beam

Full size image

Figure 5 shows the effect of the modulus of the elasticity of the beam on the deflection of the Timoshenko beam on the viscoelastic nonlinear foundation. As is seen in this figure, the modulus of the elasticity of the Timoshenko beam has little effects on the transverse deflection of the Timoshenko beam. Specifically, there are only discernible differences between results for rather large different modulus of the elasticity of the Timoshenko beam.

Fig. 5
figure 5

Effect of the modulus of the elasticity of the Timoshenko beam on the deflection of the beam

Full size image

Figure 6 illustrates the effect of the damping coefficient of the foundation on the deflection of the Timoshenko beam on the viscoelastic nonlinear foundation. It should be noted that the viscoelastic foundation turn into an elastic Pasternak foundation when c=0. The numerical result shows that the damping coefficient of the foundation has significant influence on the dynamic response of the deflection of the Timoshenko beam and the deflection decrease with the increasing damping coefficient. Furthermore, the numerical result shows that the biggest deflection of the Timoshenko beam on the elastic Pasternak foundation appear when t=0. Moreover, the time the biggest deflection appeared is delayed with the increasing damping coefficient of foundations. Hence a larger value of the damping coefficient of foundations leads to a smaller deflection of the beam and the damping is one of the reasons of time-delay.

Fig. 6
figure 6

Effect of the damping coefficient of the foundation on the deflection of the beam

Full size image

The effects of the linear elasticity parameter of foundations on the deflection of the Timoshenko beam on the viscoelastic nonlinear foundation is displayed in Fig. 7. Figure 7 shows that the whole form of the deflection of the beam has little change with different linear elasticity parameter of foundations. Furthermore, the numerical results of Fig. 7 show that the biggest deflection of the beams decreased with increasing the linear elasticity parameter of foundation.

Fig. 7
figure 7

Effect of the linear elasticity parameter of the foundation on the deflection of the beam

Full size image

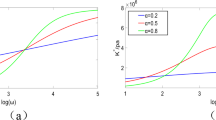
The effects of the nonlinear elasticity parameter of foundations on the deflection of the Timoshenko beam on the viscoelastic nonlinear foundation are displayed in Figs. 8–10. Figure 8 displays the effects of the nonlinear elasticity parameter of foundations on the vertical displacements of the beam at x=0 while t=0 versus the magnitude of the moving load. Figures 9 and 10, respectively, illustrate the dynamic response of the infinite Timoshenko beams with the different moving load. It is observed from Figs. 8–10 that the nonlinear elasticity parameter of foundations is an important parameter for influencing the dynamic response of the beam on the viscoelastic nonlinear foundation. Specifically, Fig. 8 shows that the deflection of the Timoshenko beams and the influence of the nonlinear elasticity parameter both increase with the increasing magnitude of the moving load F 0. Furthermore, the deflection of the beam increases with the increasing nonlinear parameter of foundation with a large moving load. It should be noted that this conclusion coincides with the research in Ref. [27]. On the contrary, a small moving load leads to the deflection of the Timoshenko beams decrease with the nonlinear elasticity parameter of the foundation. In addition, from the observation in Figs. 9 and 10, similar conclusions can be found for the effects of the nonlinear parameter on the dynamic response of the infinite beams. The comparison in Figs. 9 and 10 indicates that the influences of the nonlinear parameter increase with the increasing magnitude of the moving load. On the other side, both of Figs. 9 and 10 show that the whole form of the deflection of the beam has little change with different nonlinear elasticity parameter of foundations.

Fig. 8
figure 8

Effect of the nonlinear elasticity parameter of the foundation on the deflection of the beam versus the magnitude of the moving load

Full size image
Fig. 9
figure 9

Effect of the nonlinear elasticity parameter of the foundation on the deflection of the beam: F 0=50 kN

Full size image
Fig. 10
figure 10

Effect of the nonlinear elasticity parameter of the foundation on the deflection of the beam: F 0=65 kN

Full size image

Figures 11 and 12 show that the dynamic response change with the foundation rocking stiffness and damping coefficients on the deflection of the Timoshenko beams on the viscoelastic nonlinear foundation. As seen in this figure, the whole form has little change and the biggest deflection decrease with increasing foundation rocking stiffness and damping coefficients. It should be noted that the effects of the foundation rocking stiffness and damping coefficient have been investigated in Ref. [22]. In this paper, similar conclusions are drawn from the numerical results. In other words, the present paper proves that the influences of the rocking stiffness and damping coefficients of the foundation on the transverse deflection of the infinite beam on the foundation cannot be neglected.

Fig. 11
figure 11

Effect of the foundation rocking stiffness on the deflection of the beam

Full size image
Fig. 12
figure 12

Effect of the foundation damping coefficient on the deflection of the beam

Full size image

The effect of the velocity of the moving concentrated force on the deflection of the Timoshenko beam on the viscoelastic nonlinear foundation is displayed in Fig. 13. Figure 13 indicates that the biggest deflection of the Timoshenko beam decreases with the increasing moving velocity. Furthermore, the deflection of the beam is sensitive to the changing moving velocity. On the other hand, the numerical results in Fig. 13 proves that the whole form of the deflection of the Timoshenko beam on the viscoelastic nonlinear foundation has little change under different velocity of the moving concentrated force.

Fig. 13
figure 13

Influence of moving velocity of the load on the deflection of the beam

Full size image

As pointed out in Refs. [28, 29], the model of the beam is also an important aspect of influencing deflection of the beam resting on the viscoelastic foundation. The deflection of two different beam models on the viscoelastic nonlinear foundation is compared in Fig. 14. As is seen from the figure, the deflection of the Timoshenko beam close to the region of t=0 is lower than the Euler–Bernoulli beam’s. Furthermore, the deflection of the Timoshenko beam on the foundation is higher than the Euler–Bernoulli beam’s in other regions. It should be noted that the Timoshenko beam is usually considered more accurate than the Euler–Bernoulli beam [39]. Nevertheless, the Euler–Bernoulli beam is more acceptable for the dynamic response of the beam on the foundation in this investigation. It is because the Euler–Bernoulli beam overestimated the results of the dynamic response. In other words, the numerical results in Fig. 14 illustrates that the dynamic response from the Euler–Bernoulli beam theory provides more conservative estimate in track design.

Fig. 14
figure 14

Comparison of two different beam models from the deflection of the beam

Full size image

6 Conclusions

This paper is devoted to the dynamic response of infinite Timoshenko beams resting on nonlinear foundations with viscous damping acted upon subjected to a moving concentrated load. In conjunction with complex Fourier transformation, the Adomian decomposition method and a perturbation method are, respectively, used to deal with the nonlinear term from the foundation reaction. Moreover, the dynamic response distribution is obtained by using the presented Green function and the theorem of residues.

The present paper proves that the Adomian decomposition method and the perturbation method give a consistent result for current issues. Furthermore, it was found that the dynamic responses of infinite Timoshenko beams resting on nonlinear viscoelastic foundations decrease with growing of the shear modulus of the beam and the shear modulus of the foundation. Numerical results also illustrate that the dynamic responses decrease with the linear foundation parameter and damping coefficient. Specially, the influence of the nonlinear elasticity parameter of the foundation increase with the increasing magnitude of the moving load. Furthermore, a small moving load leads to the deflection of the Timoshenko beams decrease with the nonlinear elasticity parameter. Nevertheless, the deflection of the beam increase with the increasing nonlinear parameter under a large moving load. Moreover, numerical comparison shows that the biggest deflection of the Timoshenko beam is lower than the Euler–Bernoulli beam’s.