1 Introduction

The North American Free Trade Agreement (NAFTA) was signed between the USA, Mexico and Canada in November 1993 and ratified in January 1994. It is one of the world’s most important trading blocs. On the one hand, NAFTA seeks to liberalise trade between the USA, Mexico and Canada and promote trade in goods and services in the region by allowing the free flow of capital. On the other hand, it also seeks to strengthen links and promote cross-border investment between the stock markets of those countries [1, 17]. Numerous recent studies and a considerable body of research have shown strong integration and interdependence between NAFTA stock markets since the signing of the NAFTA agreement [1, 17, 25, 40]. These markets have become more closely linked under the NAFTA regime, especially as regards links between the USA and Mexico and between Canada and Mexico [1, 16, 17, 25, 40]. For these reasons, and in the wake of the 2008 global financial crisis, the study of the NAFTA as a complex system has become a multidisciplinary hot topic and has attracted great attention in recent years.

Financial stock markets have been an active area of research since the 1990s [46], and year after year mathematicians, statisticians and physicists have increasingly taken an interest in this type of research (known as “Econophysics”). Recent advances in the understanding of several economic phenomena (e.g. financial crises, financial market crashes and bubbles) and the analysis of the statistical properties of their corresponding variables use concepts and methods taken from physics (especially from statistical mechanics and the physics of complex systems) [19, 42, 44, 62].

A topic of particular interest is the study of the links between stock market indices (these are usually interconnected, particularly those that belong to trading blocs), which is mainly conducted by means of a large number of bivariate and multivariate correlation techniques in time (e.g. Pearson or Spearman correlation, correlation matrix or cross-correlation) or in frequency (e.g. cross-spectrum or spectral coherence) [64, 67, 80]. However, stock markets are not stationary and involve heterogeneous agents who make decisions on different time horizons (or “windows”) and operate on different timescales (or frequencies) [29, 32, 62, 67]. On the other hand, stock market indices may have a non-Gaussian distribution as well as containing outliers (i.e. inconsistent observations with the large part of population of observations). The presence of outliers can significantly reduce the efficiency of linear estimation algorithms derived on the assumptions that observations have Gaussian distributions [26, 75]. Therefore, it is extremely useful and necessary to use nonparametric correlation techniques (that do not rely on data belonging to any particular distribution) that are dynamic in time and/or frequency that allow to analyse the evolution in correlation in time or frequency, such as rolling window Spearman correlation [32, 52]. By contrast, financial markets are dynamic systems that can manifest nonlinearities (e.g. structural breaks, regime shifts, extreme volatility, etc.) [62, 69] and as such could elude common linear statistical tests, including linear causality tests [69].

Following this philosophy, the aim of this paper is to analyse dynamically the relationships between the three main NAFTA daily stock market indices over the 08/11/1991–16/03/2018 period, focusing on the pre-2008 crisis, 2008 crisis and post-2008 crisis periods. We propose the combined use of three advanced statistical methods. On the one hand, two nonparametric, nonlinear, non-stationary mathematical tools for analysing the evolution of correlation in time and in time–frequency to gain a deeper understanding of the dynamic system comprised by NAFTA country stock markets: (1) rolling window Spearman correlation and (2) wavelet coherence. On the other hand, we use a nonparametric, nonlinear causality test to analyse the cause–effect relationships in the time domain between NAFTA stock market indices. We split the full period studied into four sub-periods (1991–2001, 2002–2006, 2007–2011 and 2012–2018) chosen in such a way that they cover certain financial events of interest, e.g. the 2008 global financial crisis. We also analyse the full period (1991–2018). Such statistical methods have not been previously widely explored for the study of stock market indices. In particular, rolling window Spearman correlation via the Spearman estimator and wavelet coherence in combination with an areawise significance test have not been used previously to analyse financial time series and, to the best of our knowledge, these three statistical methods have never before been used individually or in combination to analyse NAFTA stock market indices.

The rest of the paper is organised as follows: Sect. 2 describes the data and methodologies used. Section 3 presents the results and discussion, and Sect. 4 concludes and provides some final remarks.

2 Material and methods

2.1 Data description

The data employed in this study comprise daily closing price indices from the USA (DJI), Mexico (IPC) and Canada (GSPTSE). All data sets cover the period from 8 November 1991 to 16 March 2018 (6876 data points). However, the causality analysis is performed in four sub-periods: (1) from 8 November 1991 to 31 December 2001 (the “unstable IPC period”, comprising 2647 data points); (2) from 2 January 2002 to 31 December 2006 (the “pre-2008 crisis period”, with 1305 data points); (3) from 2 January 2007 to 31 December 2011 (the “2008-crisis period”, with 1304 data points); and (4) from 2 January 2012 to 16 March 2018 (the “post-2008 crisis period”, with 1076 data points). The causality test also is applied to the full period from 8 November 1991 to 16 March 2018 (6875 data points). To cope with the different official holidays, we have adjusted the indices by using the last closing price corresponding to each official holiday. Data were obtained from Yahoo Finance.Footnote 1 All the analyses were conducted using daily log returns (called simply “returns” hereafter) (Fig. 1), that is, \(R_t = \log (S_t/S_{t-1}) =\varDelta \log S_t\), where \(S_t\) are the adjusted stock market indices at time t. The main advantage of the log returns is that the average correction of scale changes is incorporated without requiring additional correction factors (e.g. deflators or discounting factors). However, this transformation is nonlinear, and nonlinearity could strongly affect the statistical properties of a stochastic process [46]. Thus, nonlinear statistical analysis methods must be used to analyse these kinds of data.

Fig. 1
figure 1

Daily stock returns for the 08/11/1991–16/03/2018 period (the number of elements is 6875). The labels (x-axis above) indicate the most representative sociopolitical–economic events. 1. NAFTA treaty, 2. Tequila effect, 3. East Asian crisis, 4. Ruble crisis, 5. Long-Term Capital Management collapse, 6. Brazilian crisis, 7. Turkish crisis, 8. US subprime crisis, 9. Euro Area Sovereign Debt crisis, and 10. 11 September attacks

Full size image

2.2 Rolling window standard deviation

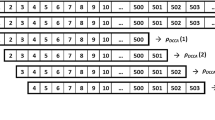
A rolling window analysis is often used to assess the model’s stability over time and is also very useful to analyse data whose statistical properties may change through time [11, 86]. We have estimated a 250-day rolling window standard deviation for each NAFTA stock market return (Fig. 2  describes graphically this process) to depict the trend in volatility visually. We have computed the rolling window standard deviation with windows of \(w = 250\) days or data points (one trading year), rolling forward one data point at a time and centred on time t (where the standard deviation value should be indexed, i.e. this value could be indexed left- or right-aligned or centred) as in [3, 22, 62]. We use the centred option to ensure that variations in the standard deviation are aligned with the variations in the returns rather than being shifted (towards the left or right). We obtained \(n-w+1\) (where \(n = 6875\) and \(w = 250\)) windows and therefore 6624 standard deviation values. We choose a window of 250 days because a shorter window would not have had enough data points to analyse longer timescales and a longer window would not isolate different events of interest at short and medium scales. However, other window lengths (125 and 500 days) were used to estimate the rolling window standard deviations to ensure this compromise. Our computational code to estimate the rolling window standard deviation for our analyses was programmed in R and uses the rollapply function from the R package Zoo.Footnote 2 Our R scripts are available upon request.

Fig. 2
figure 2

Graphical procedure to estimate the rolling window statistics (standard deviation and Spearman correlation), where w indicates the number of data points (250) and n is the size of the sample (6875) (modified from https://it.mathworks.com/help/econ/rolling-window-estimation-of-state-space-models.html)

Full size image

2.3 Rolling window Spearman correlation

Stock market prices are not necessarily stationary and normally distributed, so the conventional Pearson correlation is not the most suitable estimator for measuring links between stock market returns as it may lead to a biased estimation [83, 84]. We therefore use Spearman rank-order correlation that does not require variables with normal distribution (Gaussian), is based on the ranked values for each variable rather than the raw data and is known to be much more robust than the Pearson correlation, which means monotonic relationships, for instance nonlinear associations [65, 82, 84]. Spearman’s rank correlation coefficient can be estimated as follows [52]:

$$\begin{aligned} r_s = \frac{1}{n}\sum _{i=1}^{n}\left( \frac{R(i)-{\bar{R}}}{S_{n,R}}\right) \cdot \left( \frac{S(i)-{\bar{S}}}{S_{n,S}}\right) , \end{aligned}$$
(1)

where \({\bar{R}}\) and \({\bar{S}}\) are the sample means and \(S_{n,R}\) and \(S_{n,S}\) are the sample standard deviations calculated with the denominator n (sample size). The rank correlation (\(r_s\)) measures the degree of the monotonic relationship between two time series and takes values from −1 to 1 [52].

Spearman’s rank correlation is a useful initial approach for analysing correlation between two time series because it is an overall measure of association, but relationships between financial time series can vary over time [11, 65]. We apply the rolling window method to investigate the evolution of correlation over time from “short” (approximately less than 6 trading months) and “medium” (approximately between 6 and 12 trading months) to “long term” (more than 12 trading months) for the three pairs formed by the NAFTA stock market returns to deal with potential drawbacks occasioned by an overall measure of association and to find out whether correlations between the variables under analysis change over time. We compute the pairwise rolling window correlation for six windows—\(w = 30, 60, 125, 250, 500\) and 750 days or data points (from one and a half trading month to three trading years)—covering a wide range of variability, rolling forward one data point at a time, and centred (Fig. 2  describes graphically this process) on time t as in [3, 22, 62]. As in the last subsection, we use the centred option to ensure that variations in the correlation are aligned with the variations in the relationship of the returns rather than being shifted. Furthermore, these running correlation windows with different lengths help to carry out a comparison with the results of the other correlation method used here (see Sect. 3.3). Therefore, we obtain \(n - w + 1\) (where \(n = 6875\)) windows and, as a consequence, \(n - w + 1\) correlation coefficients.

A statistical significance (95% confidence level) test is applied to the rolling window Spearman’s rank correlation coefficients. This test takes into account the multiple testing/comparison problem (inflation of the Type I error) and thus includes p value adjustments (or corrections) following the false discovery rate method of Benjamini and Hochberg (BH) [8]. We have applied the BH method despite Bonferroni correction being frequently used to face the multiple testing/comparison problem for the following reasons. BH method is less conservative, performs much better (in terms of statistical power) than Bonferroni and is most adequate if a large number of comparisons are performed [8, 11]. Our computational code was also programmed in R to estimate the rolling window Spearman correlation and uses the running function from the R package gtoolsFootnote 3 [76] and the R native function p.adjust to perform the p value corrections. Our R scripts are available upon request.

Fig. 3
figure 3

Graphical procedure to perform rolling window spearman correlation analysis

Full size image

The computational procedure to estimate the rolling window Spearman correlation is presented in Fig. 3 and is described in detail in the following lines:

  1. 1.

    Input: two time series \(X_t\) and \(Y_t\) (stock market log returns in our case) for \(t=1,\ldots ,n\)

  2. 2.

    Compute the \(n - w + 1\) (number of windows; see Fig. 2) rolling window Spearman correlation coefficients (cor.XY) and p values (pval.XY) through the function running from the R package gtools\(^3\)

    1. (a)

      cor.XY\(<-\)running(\(X_t\), \(Y_t\), width=w, fun= corfun, align="center"), where corfun\(<-\)function(\(X_t\), \(Y_t\)){cor(\(X_t\), \(Y_t\), method="spearman")}

    2. (b)

      pval.XY\({<}-\)running(\(X_t\), \(Y_t\), width=w, fun= pvalfun, align="center"), where pvalfun\({<}{-}\)function(\(X_t\), \(Y_t\)){cor.test(\(X_t\), \(Y_t\), method="spearman")}

    where w is the size of the window (in our work we use windows with n=30, 60, 125, 250, 480 and 750 data points); align allows short subsets at both ends of the time series so that complete subsets are centred; cor and cor.test are native R functions to estimate correlations and their corresponding p values.

  3. 3.

    p value corrections following the method of Benjamini and Hochberg (BH) [8] as implemented in the native R function p.adjust:

    1. (a)

      Input: pval.XY obtained in Step 2 (b), i.e. \(n - w + 1\)p values \(p_1, p_2, \ldots , p_{n-w+1}\).

    2. (b)

      Sort the \(n - w + 1\)p values in ascending order \(p'_1 \le p'_2 \le \cdots \le p'_{n-w+1}\) to assign ranks, i.e. set the smallest p value has a rank of \(i=1\), then next smallest p value has \(i=2\), etc. (Note that for the case when there are p values with equal values the rank is obtained as the average of their corresponding ordinal ranks).

    3. (c)

      For a given false discovery rate \(\alpha \) (0.05 in our case), let k be the largest rank i such that \(p'_i \le \frac{i}{n-w+1}\alpha \) (the BH critical value). Declare all tests of rank \(1,2,\ldots ,i\) as significant with p values smaller or equal to \(p'(k)\).

  4. 4.

    Output: Spearman correlation coefficients with p values statistically significant obtained in 3 (c).

2.4 Wavelet coherence analysis

A vast number of studies investigating the correlation among stock markets are conducted using a large number of bivariate and multivariate correlation techniques in time (e.g. Pearson or Spearman correlation, correlation matrix or cross-correlation) or in frequency (e.g. cross-spectrum or spectral coherence), or by multivariate cointegration techniques and generalised VAR or (G)ARCH models [64, 67, 80]. However, cointegration theory can only tackle short-run versus long-run time horizons and the VAR or (G)ARCH approaches are sensitive to model specifications [41, 62]. In contrast, we may point out that stock markets are not necessarily stationary and involve heterogeneous agents who make decisions across different time horizons and operate on different timescales (frequencies) [29, 32, 62, 67].

A mathematical tool that can handle non-stationary time series and works in the combined time-and-scale domain is the wavelet correlation estimated through the wavelet transform (WT) [32, 59]. There are different methods or algorithms to compute the WT, e.g. the discrete wavelet transform (DWT), the maximal overlap discrete wavelet transform (MODWT), the multi-resolution analysis (MRA), or the wavelet packet decomposition (WPD). However, wavelet correlation via the (MO)DWT has been traditionally used to analyse relationships among stock markets time series [7, 15, 29, 32, 56, 62] in comparison with wavelet coherence obtained via the CWT, which has not been widely exploited to analyse relationships between this kind of time series (some exceptions are [2, 39, 45, 66, 77]). This paper makes use of the wavelet correlation obtained through the continuous wavelet transform (CWT) given its advantages over the other methods. For example, the wavelet correlation (obtained either by means of cross-correlation or by wavelet coherence) estimated through the CWT easily allows the evolution of correlation and the co-movements between two time series in time and scale (frequency) to be analysed at once [2, 48]. Furthermore, the CWT can be used with complex wavelet functions, such as Morlet; therefore, it is possible to estimate the phase difference (or phase coherence), which is very useful to obtain information on the delay or synchronisation (lead–lag relationships) between oscillations of the two time series under study [2, 61].

Fig. 4
figure 4

Graphical procedure to perform wavelet coherence analysis (modified from [38])

Full size image

We compute the wavelet coherence (WCO) obtained through the continuous wavelet transform (a graphical explanation is presented in Fig. 4) to analyse the relationships between the three stock market returns of the NAFTA countries in different time windows and frequency bands (scales). We follow the methodology for computing the WCO (and the wavelet spectrum for each variable analysed) proposed by Maraun and Kurths [48] and Maraun et al. [49], as implemented in the R package SOWAS [47]. The SOWAS package uses the CWT with the Morlet mother function. The CWT is defined for a time series \(X_t\) at time b and scale a (scales refer to 1/frequency) according to [10, 49] as

$$\begin{aligned} {W_X}(a,b) {=} \frac{1}{\sqrt{a}} \int _{-\infty }^{+\infty } X_tG^*\left( \frac{t-b}{a} \right) \hbox {d}t, \;\; a {>} 0,\qquad \end{aligned}$$
(2)

where \(G^*(t)\) denotes the complex conjugate of the Morlet function G(t) that is defined as

$$\begin{aligned} G_{a,b}(t) = \pi ^{-1/4} e^{i\omega _0 (\frac{t-b}{a})} e^{-(t-b)^2/2a^2} \end{aligned}$$
(3)

and \(\omega _0\) (the central frequency) determines the time/scale resolution and is equal to \(2\pi \) to satisfy the admissibility condition [24, 78]. It is important to point out that Fourier (wavelength) frequency f and wavelet scale a are not necessarily reciprocals, and it is necessary to rescale the result of the wavelet transform with a factor depending on the mother wavelet [48, 78]. For the case of Morlet, the conversion, that was deduced by [50], is given by

$$\begin{aligned} \frac{1}{f} = \frac{4\pi a}{\omega _o + \sqrt{2 + \omega _o^2}}, \end{aligned}$$
(4)

but, due to \(\omega _o=2\pi \) and from Eq. 4, it is obtained that \(a = \frac{1}{f}\) [50].

However, dealing with discrete time series \(X_t, t=0, 1,\ldots ,n-1\) with a uniform time step \(\delta t\), the integral in (2) has to be discretised, and the CWT of \(X_t\) becomes [2, 78]

$$\begin{aligned} {W}_t^X(a)= & {} \frac{\delta t}{\sqrt{a}} \sum _{i=0}^{n-1} X_t G^*\Big (\frac{i-t}{a}\delta t \Big ), \;\;\nonumber \\&\quad i=0,1,\ldots ,n-1 \end{aligned}$$
(5)

However, it is possible to calculate the wavelet transform from the discretised form (Eq. 5) for each value of a and t. In practice, we can also identify the computation for all the values of t simultaneously as a simple convolution of two sequences. This convolution can then be computed as a simple product in the Fourier space using the fast Fourier transform algorithm to go back and forth from time to spectral domain [2, 78]. As a consequence of working with finite-length time series, we inevitably suffer from boarder distortions as the values of the wavelet transform at the beginning and at the end of the series under scrutiny are always incorrectly computed. The values of the wavelet transform involve missing values of the series which are then artificially prescribed (the most common choices are zero padding or periodisation). The time–frequency region in which the wavelet transform suffers from these edge effects is called cone of influence (COI), and this region is unreliable and must be interpreted carefully [2, 45, 78].

The wavelet Morlet provides a good balance between scale (frequencies) and time localisations [34, 51] and is one of the best mother functions in terms of reproducing frequency [37, 61]. However, despite the WCO method (via Morlet) of Maraun and Kurths ([48]) having been successfully used to analyse different kinds of time series (e.g. ecological [58, 61], geophysical [48, 73], financial [14] among others), this method [48] (and other similar WCO methods, such as [34]) requires the time series analysed to be not far from a normal distribution [34, 48], but financial time series (and its returns) are not necessarily normally distributed [12, 46]. For this reason, it is highly recommendable to corroborate whether the time series under analysis fill this requirement. A typical way to establish where the time series are or are not normally distributed is to plot the histogram, the box-and-whisker or the Q–Q (quantile–quantile) of the series under study to verify visually their Gaussianity and/or to apply tests of normality to these series (e.g. Jarque–Bera test, Shapiro–Wilk for samples with \(\le \) 5000 data points or Kolmogorov–Smirnov or Anderson–Darling for samples >5000 data points). In the event that the time series under analyses are far from being normally distributed, a common way to tackle the lack of normality is to transform the target time series to be normally distributed (there are several methods to carry out this task, e.g. the Box–Cox, the Lambert W \(\times \) F, the Yeo-Johnson, the ordered quantile transformation and others)Footnote 4 and then use these transformed time series to carry out the WCO analysis. However, we should be cautious against rashly changing their PDF (probability density function) [34]. Fortunately, for the case when at least one of the time series analysed can be “modelled” by Gaussian white noise, the WCO method [48] used in our paper includes an approximation formula to easily calculate the critical value for the WCO significance on the 95% level (see end of this section).

Normalised wavelet coherence (WCO) is defined as the amplitude of the wavelet cross-spectrum (WCS) normalised by the smoothed wavelet spectrum of each signal or time series \(X_t\) and \(Y_t\), respectively, [2, 81], i.e.

$$\begin{aligned} \mathrm {R}_t^2(a) = \frac{| \langle a^{-1} \mathrm {W}_{t}^{XY}(a) \rangle |^2}{\langle a^{-1} | \mathrm {W}_t^X(a) |^2 \rangle \langle a^{-1} | \mathrm {W}_t^Y(a) |^2 \rangle }, \end{aligned}$$
(6)

where the WCS is given by \(W_t^{XY}(a)=W_t^X(a)W_t^{Y*}(a)\), \(W_t^X(a)\) and \(W_t^Y(a)\) are the wavelet power spectra of the time series, X(i) and Y(i), which are defined as \(<|W_t^X(a)|^2>\) and \(<|W_t^Y(a)|^2>\) [78, 81]. The \(\langle \rangle \) denotes a smoothing operator in time or scale (frequency), which must be applied at least to the numerator or denominator, otherwise WCO would be one [48, 61]. The smoothing is performed through the convolution with a constant-length window function in time or scale [48, 49]. The normalised wavelet coherence takes values between 0 and 1. A 0 value means that there is no link between the time series under study at the timescale considered; similarly, a value of 1 implies a perfect linear relationship [34, 48].

Fig. 5
figure 5

Wavelet phase coherence circle

Full size image

On the other hand, the wavelet phase coherence or phase difference (WPH) is defined as [2, 81]

$$\begin{aligned} {\phi }_{t}^{XY}(a)=\tan ^{-1} \Bigg (\frac{Im\big \{\langle a^{-1}{W}_{t}^{XY}(a)\rangle \}}{Re\big \{\langle a^{-1}{W}_{t}^{XY}(a)\rangle \big \}} \Bigg ), \end{aligned}$$
(7)

where Im and Re mean the real and imaginary parts of the \({W}_{t}^{XY}(a)\), respectively. The wavelet phase coherence provides information about the possible delay between two time series at time t on a scale a [10]. The phase coherence takes values from \(-\pi \) (\(-180^\circ \)) to \(\pi \) (180\(^\circ \)). The time series under study are either in (if \( -\pi /2 \le \mathrm {\phi }_{t}^{XY}(a) \le 0\) or \( 0 \le \mathrm {\phi }_{t}^{XY}(s) \le \pi /2\)) or out (if \( -\pi /2 \le \mathrm {\phi }_{t}^{XY}(s) \le -\pi \) or \( \pi /2 \le \mathrm {\phi }_{t}^{XY}(s) \le \pi \)) of phase (Fig. 5). A zero value indicates perfect synchrony between two time series. More details about wavelet phase coherence are given in [28, 34, 48].

A pointwise significance test of the results of the WCO is applied (90% confidence level) in our WCO analysis as a first approach. This test was proposed in [48] and is included in the R package SOWAS.Footnote 5 The pointwise statistical significance test for zero wavelet coherence is based on Monte Carlo simulations since such tests cannot easily (if not impossibly) be calculated analytically [48]. However, this test based on Monte Carlo simulation can only be used in the case of both time series under study being normally distributed or are not far from that being the case. Otherwise, and if at least one of these time series can be modelled by Gaussian white noise, the following approximation can be used [48]:

$$\begin{aligned} WCO_{95}= & {} 8.23\times 10^{-5}\omega _0^3 + 4.24\times 10^{-5}\omega _0^2\omega \nonumber \\&+ 1.13\times 10^{-5}\omega _0\omega ^2 + 1.54\times 10^{-5}\omega ^3 \nonumber \\&- 2.30\times 10^{-3}\omega _0^2 - 2.19\times 10^{-3}\omega _0\omega \nonumber \\&- 7.51\times 10^{-4}\omega ^2 + 2.05\times 10^{-2}\omega _0 \nonumber \\&+ 1.27\times 10^{-2}\omega + 0.95, \end{aligned}$$
(8)

where \(3 \le \omega _o \le 12\) (the central frequency) and \(0 \le \omega \le 25\) (smoothing length in scale direction a), i.e. this approximation is only valid for these intervals. The reason why only scale is used in Eq. 8 is due to the fact that smoothing in time direction is practically ineffective [48]. This approximation (8) is especially useful to save computational time when the statistical significance is estimated for the WCO of time series under scrutiny with a large number of elements.

On the other hand, the statistical significance estimated for the WCO is not free of the multiple testing or comparison problem (such as the rolling window Spearman correlation). A way to tackle this drawback is to apply a type of statistical significance correction to address the multiple comparison problem and to reduce false positive errors using, for example, Bonferroni corrections. However, Bonferroni often results in many true positives being rejected and is particularly permissive for correlated realisations. Overall, this kind of correction only states whether any coherency exists at all between the two time series without specifying at what scale and time. Therefore, Bonferroni corrections (and other similar methods) are not useful for this situation [48, 70]. Furthermore, a pointwise significance test could produce spurious results occurring in clusters or patches and should be used with caution (it is highly recommendable to estimate the WCO and its statistical significance for various smoothing windows—in time and scale, compare them, and select only the patches that appear in most) [48]. For this reason, Maraun et al. [49] propose an areawise significance test to overcome the intrinsic multiple testing problem of the pointwise significance test and to reduce spurious spectral patches as far as possible. This test uses information about the size and geometry of a detected spectro-temporal area or patch in the WCO to decide whether it is significant or not (details can be found in [49]) [49]. However, from a computational point of view the areawise test is only applicable for a significance level of 0.90 (that is, the areawise test is able of sorting out \(\sim \) 90% of the spuriously significant area from the pointwise test) [49]Footnote 6 We also use the areawise test of Maraun et al. [49] (also implemented in the R package SOWAS) in our analysis, and we would highlight that to the best of our knowledge, it is the first time that this test has been used to estimate the statistical significance of wavelet coherence to analyse financial time series.

A summary of the computational procedure to estimate the wavelet coherence analysis is presented below:

  1. 1.

    Input: two time series \(X_t\) and \(Y_t\) (stock market log returns in our case) for \(t=1,\ldots ,n\) and verify if both time series have a normal distribution, if not, use an adequate method to transform them to be normally distributed.

  2. 2.

    Estimate the discretised form of the continuous wavelet transform (Eq. 5) for both time series \(X_t\) and \(Y_t\).

  3. 3.

    Estimate the wavelet cross-spectrum for the time series \(X_t\) and \(Y_t\).

  4. 4.

    Estimate the wavelet coherence and phase difference by means of Eqs. 6 and 7 including the significance testing (pointwise and areawise).

  5. 5.

    (An additional step is included to operate the software.) The main inputs for SOWAS should be set up as follows: wco.s1\(<-\)wco(Xt, Yt, s0=0.05, noctave=8, nvoice=10,sw=0.5, tw=1.5, units= "Years", siglevel=0.90, arealsiglevel=0.90, phase=T) where s0 is the lowest calculated scale a, noctave is the number of octaves, nvoice number of voices per octave, sw and tw are the lengths of smoothing window in scale direction (given by 2*sw*nvoice + 1) and in time direction (given by 2*a*tw + 1), siglevel and arealsiglevel are the significance levels for the pointwise and areawise tests (for more details about the software SOWAS visit http://tocsy.pik-potsdam.de/wavelets/), and phase=T (TRUE) to estimate the phase coherence.

2.5 Nonlinear causality test

Financial markets are dynamic systems that could manifest nonlinearities (e.g. structural breaks, regime shifts or extreme volatility), especially when the time series under study contain a great many of data points [62, 63, 69]. [69] argues that these dynamic systems could elude common linear statistical tests, including linear causality tests. For this reason, many nonlinear causality tests have been developed to address nonlinear causality in bivariate analysis (see e.g. [4, 6, 35, 74]). However, here we use the test developed by Diks and Panchenko [18], as implemented in the C program GCTtest, which is freely available online.Footnote 7 [18] proposes a nonparametric, nonlinear Granger causality test to avoid over-rejection of the null hypothesis when the test is satisfied, as occurs in the causality test proposed by [35] (which is one of the main nonlinear causality tests used in economics and finance).

The nonlinear and nonparametric causality test of Diks and Panchenko [18] is described in the following lines. For a strictly stationary bivariate process \(\{ {X}_t, {Y}_t, t \ge 1 \}\), \(\{ {X}_t\}\) is a Granger cause of \(\{{Y}_t\}\) if past and current values of X contain additional information on future values of Y that is not contained in past and current Y values [18, 33]. The formal definition according to [18] is established in the following manner. For a strictly stationary bivariate time series process \(\{{X}_t, {Y}_t\}, t \in {Z}, \{{X}_t\}\) is a Granger cause of \(\{{Y}_t\}\) if, for some \(k \ge 1\)

$$\begin{aligned}&(Y_{t+1},\ldots , Y_{t+k})|({\mathscr {F}}_{X,t}, {\mathscr {F}}_{Y,t}) \nonumber \\&\quad \sim (Y_{t+1},\ldots , Y_{t+k})|{\mathscr {F}}_{Y,t}, \end{aligned}$$
(9)

where \({\mathscr {F}}_{X,t}\) and \({\mathscr {F}}_{Y,t}\) denote the information sets consisting of past observations of \({X}_t\) and \({Y}_t\) up to and including time t and \(\sim \) denotes equivalence in distribution [5, 18].

Note that although \(k \ge 1\), for simplification, Diks and Panchenko [18] limit the test for \(k=1\) (the case used most often). This is due to the fact that under the null hypothesis \(Y_{t+1}\) is conditionally independent of \(X_t, X_{t-1},\ldots ,\) given \(Y_t,Y_{t-1},\ldots ,\) and, in a nonparametric context, conditioning on the infinite past is not possible without a model restriction, such as an assumption that the order of the process is finite [5, 18]. Thus, in practice, conditional independence is tested using finite lags \(l_X\) and \(l_Y\) (\(l_X\) and \(l_Y\)\(\ge 1\)) [18]; then, the null hypothesis \(H_o\) “that past observations of \({\mathbf {X}}_t^{l_X}\) contain no additional information—beyond that in \({\mathbf {Y}}_t^{l_Y}\)—about \({Y}_{t+1}\)” is

$$\begin{aligned} H_o: {Y}_{t+1}|({\mathbf {X}}_t^{\text {{l}}_\text {X}};{\mathbf {Y}}_t^{\text {{l}}_\text {Y}}) \sim {Y}_{t+1}|{\mathbf {Y}}_t^{\text {{l}}_\text {Y}}, \end{aligned}$$
(10)

where \({\mathbf {X}}_t^{l_X} = (X_{t-l_X+1, \ldots , X_t})\) and \({\mathbf {Y}}_t^{l_Y} = (Y_{t-l_Y+1, \ldots , Y_t})\) are the so-called delay vectors.

For a strictly stationary bivariate time series, Eq. 10 comes down to a statement about the invariant distribution of the (\(l_X + l_Y + 1\))-dimensional vector \({\mathbf {W}}_t=({\mathbf {X}}_t^{l_X}, {\mathbf {Y}}_t^{l_Y}, {Z}_t)\), where \({Z}_t={Y}_{t+1}\) [5, 18]. To keep mathematical consistency, we also use the same notation as in Diks and Panchenko [18], and taking into account that the null hypothesis is a statement about the invariant distribution of \({\mathbf {W}}_t\), we drop the time index t and also consider \(l_X=l_Y=1\) as in [18]; thus, \({W}=({X}, {Y}, {Z})\) (which denotes a three-variate continuous random variable). Consequently, under the null, the conditional distribution of Z given \((X,Y) = (x,y)\) is the same as that of Z given \(Y = y\) [5, 18]. Therefore, the null hypothesis (Eq. 10) can be restated in terms of ratios of joint distributions. Particularly, the joint probability density function \(f_{X,Y,Z} (x,y,z)\) and its marginals must satisfy the relationship

$$\begin{aligned} \frac{f_{X,Y,Z}(x,y,z)}{f_{X,Y}(x, y)} = \frac{f_{Y,Z}(y,z)}{f_Y (y)} \end{aligned}$$
(11)

or equivalently

$$\begin{aligned} \frac{f_{X,Y,Z} (x,y,z)}{f_Y (y)} = \frac{f_{X,Y} (x,y)}{f_Y (y)} \frac{f_{Y,Z} (y,z)}{f_Y (y)} \end{aligned}$$
(12)

for each vector (x, y, z) in the support of (X, Y, Z) [18]. This explicitly states that X and Z are independent conditionally on \(Y = y\) for each fixed value of y [5, 18]. Diks and Panchenko [18] demonstrated that this reformulated null hypothesis \(H_o\) (Eq. 10) implies

$$\begin{aligned} q\equiv & {} {\mathbb {E}}[f_{X,Y,Z}(X,Y,Z)f_{Y}(Y) \nonumber \\&-f_{X,Y}(X,Y) f_{Y,Z}(Y,Z)] = 0, \end{aligned}$$
(13)

where \({\mathbb {E}}\) denotes the expectation operator. According to Diks and Panchenko [18], an estimator for q based on indicator functions is

$$\begin{aligned} T_n(\epsilon _n)= & {} \frac{(2\epsilon )^{-d_X-2d_Y-d_Z}}{n(n-1)(n-2)} \sum _i \left[ \sum _{k,k \ne i} \sum _{j,j \ne i} \left( \varvec{I}_{ik}^{XYZ}\varvec{I}_{ij}^{Y} \right. \right. \nonumber \\&\left. \left. -\varvec{I}_{ik}^{XY}\varvec{I}_{ij}^{YZ}\right) \right] , \end{aligned}$$
(14)

where \(\varvec{I}_{ij}^W = \varvec{I}(||W_i - W_j|| < \epsilon )\) (\(\varvec{I}\) is the indicator or characteristic function), \(W_i\) and \(W_j\) are elements of a \(d_W\)-variate random vector W, \(\epsilon \) is the bandwidth and n is the sample size [5, 18]. Taking into account that the local density estimators of a \(d_W\)-variate random vector W can be described as \({\hat{f}}_W(W_i)=\frac{(2\epsilon )^{-d_W}}{n-1}\sum _{j,j \ne i}\varvec{I}_{ij}^{W}\), the test statistic according to Diks and Panchenko [18] can be simplified as the sample scaled version of q (Eq. 13), i.e.

$$\begin{aligned} T_n(\epsilon _n) =&\frac{(n-1)}{n(n-2)} \sum _{i}\Bigg [{\hat{f}}_{X,Y,Z}(X_i,Y_i,Z_i){\hat{f}}_Y(Y_i)\nonumber \\&-{\hat{f}}_{X,Y}(X_i,Y_i){\hat{f}}_{Y,Z}(Y_i,Z_i)\Bigg ]. \end{aligned}$$
(15)

For the case \(\epsilon _n = Cn^{-\beta }\), with \(\beta \in \) (1/4, 1/3) and \(C > 0\), and for the lag 1, \(l_X = l_Y = 1\), the test statistics \(T_n\) (Eq. 15) are asymptotically normally distributed in the absence of dependence between vectors \({\mathbf {W}}_i\) and satisfies

$$\begin{aligned} \sqrt{n} \, \frac{(T_n(\epsilon _n) - q)}{S_n} \xrightarrow [\text {}]{\text {d}} N(0,1), \end{aligned}$$
(16)

where \(\xrightarrow [\text {}]{\text {d}}\) indicates convergence in distribution and \(S_n\) is an estimator of the asymptotic variance of \(T_n\) [5, 18].

Fig. 6
figure 6

Graphical procedure to perform nonlinear Granger causality

Full size image

The computational procedure (Fig. 6) to estimate the nonlinear causality test [18] is described as follows:

  1. 1.

    Input: two time series \(X_t\) and \(Y_t\) (stock market log returns in our case) for \(t=1,\ldots ,n\)

  2. 2.

    The bandwidth \(\epsilon _n\) is computed to each couple of time series (returns) as \(\epsilon _n = max(C^* n^{-2/7}, 1.5)\), where n is the number of data points and \(C^*\) the optimal “constant” is \(\approx 8\) for unfiltered financial returns time series [18].

  3. 3.

    The test is applied (using the software GCTtestFootnote 8) in both directions (\(X_t \rightarrow Y_t\) and \(Y_t \rightarrow X_t\)) using the parameters embeddim (embedding dimension; \(l_X=l_Y=1\)) and bandwidth (\(\epsilon _n\)) that are computed in step 3.

  4. 4.

    Output: T statistics and p values for \(X_t \rightarrow Y_t\) and \(Y_t \rightarrow X_t\).

Table 1 Descriptive statistic for the returns (\(R_t\)) of the stock market indices under study
Full size table

3 Results and discussion

3.1 Preliminary analysis

Basic descriptive statistics for returns are shown in Table1. The mean and median have practically the same values (zero) for all four sub-periods and for the full period studied. The minimum and maximum values for the four sub-periods are found in the crisis period (2007–2011), except for the IPC, where the maximum is found in the 1991–2001 “unstable” IPC period. Moreover, skewness (a measure of asymmetry) shows that \(R_t\) has an asymmetric probability distribution in all cases (except for the IPC in the crisis period) and a skewness value relatively close to zero. Additionally, practically none of the kurtosis values have a value close to 3Footnote 9 (except the GSPTSE for the pre-crisis period), indicating that none of the probability distributions of these time series appear to be normally distributed. To confirm this finding, we perform the Jarque–Bera test of the null hypothesis that the respective probability distribution of \(R_t\) are Gaussian (Chi-square with \(df = 2\)). The p values reported lead us to reject the null hypothesis in all cases. Note that this lack of normality for \(R_t\) is consistent with the well-known “stylised facts” of market returns, as pointed out in previous studies [12, 46]. Finally, the standard deviation, which is a measure of volatility, is practically at its highest for all three indices during the crisis period (2007–2011). This is expected because it is well known that volatility of financial markets increases during financial crises.

One of the most interesting features of the returns is a decrease in volatility on the IPC, which is most evident from 1991 to 2004 (Fig. 1). A decrease in volatility values on the IPC can clearly be seen in Fig. 7, which was obtained via a 250-day rolling window standard deviation for each stock market. Other window lengths (125 and 500 days) were used to estimate the rolling window standard deviations, but the result did not change substantially and they are therefore not reported. This result is consistent with the previous studies. For instance, [9] model changes in volatility in the Mexican Stock Exchange Index using a Bayesian approach for 1994–2016 and finds as an indirect result that periods of volatility coincide with different financial crises and that volatility decreases over time. Moreover, [13] statistically analyses the IPC index (through a simple moving average of its standard deviation) and finds, among other results, a clear decreasing trend in the standard deviation of the IPC from 1978 to 2006. The conclusion drawn is that the IPC shows compelling evidence of increased efficiency over time. By contrast, the volatility of the DJI and GSPTSE increases slightly over time for the full period studied (Fig. 7). This can be explained by the deep 2008 financial crisis (as observed in Fig. 7, the highest volatility values for DJI and GSPTSE are found during the 2008 crisis). This extreme volatility could affect the estimation of the linear trend in both indices. However, our results are consistent with other studies, such as [21], where the DJI index is found to show a considerable level of volatility for 1928–2009, and one that has been increasing in recent years. On the other hand, a noteworthy result presented in Fig. 7, over and above the expected strongly coupled DJI-GSPTSE system, is that the IPC has been trying to “follow” and “couple with” the DJI and GSPTSE since 1998 (though this is most noticeable from 2002 onwards). This result is a good indication of market integration in the NAFTA stock market system.

Fig. 7
figure 7

Rolling window standard deviation (continuous lines in black, green and blue) for returns and for the 08/11/1991–16/03/2018 period (the total number of elements is 6625 with a window length of 250 data points). Dashed lines indicate the linear trends for the rolling window standard deviations. Red lines indicate the lower and upper 95% confidence bounds. The labels (x-axis above) 1–10 are described in the legends. (Color figure online)

Full size image

3.2 Dynamic correlation in the time domain

The rolling window Spearman correlation for the NAFTA returns (Fig. 8) shows that there is a medium/high degree of correlation in all six windows, with a general increasing trend over time. The strongest relationship is in the DJI-GSPTSE pairing, which is expected because both indices belong to developed markets and the USA is Canada’s main trading partner. Moreover, the trade relationship between the USA and Canada is known to be the second largest in the world after that of China and the USA [23, 40]. By contrast, the relatively weakest correlations are found for the DJI–IPC and GSPTSE–IPC pairings, i.e. when the Mexican stock market is present. This result is also expected because the Mexican stock market belongs to an emerging market, and one which is not yet an efficient and competitive market as the corresponding markets in the USA or Canada. Despite this, there is a compelling evidence of increasing efficiency in the IPC over time [13].

The most conspicuous result is that the degree of correlation between NAFTA stock returns varies considerably over time and scale (from the short and medium to the long term), taking statistically significant values (5% level) running approximately from 0.10 to 0.85 (Fig. 8). This indicates that the relationships between NAFTA equity markets are highly time dependent. For example, although these correlations increase over the full period studied, there are sub-periods for which they decrease, e.g. approximately from 2011 to 2014. This decreasing correlation is present in all six windows but is more evident in the 250-, 500- and 750-day windows (Fig. 8d–f). This indicates that the main drivers influencing the decrease are related more to economic phenomena which are highly persistent or which took place over several years. A plausible explanation is that this may well be caused by indirect impacts of the recent global financial crisis, which lasted for many years (from the financial subprime crisis in 2007 and the Lehman Brothers bankruptcy in 2008 to the Euro Area Sovereign multi-year Debt Crisis that broke out in 2009). In other words, they can be explained by a slow recovery of the economy after a global financial crisis.

Fig. 8
figure 8

Rolling window Spearman correlations statistically significant (95% confidence level and taking into account multiple comparison corrections) for the NAFTA stock returns. The labels a–f correspond to the window length of 30, 60, 125, 250, 500 and 750 data points (days). The labels (x-axis above) 1–10 have been previously defined

Full size image

The increasing correlation is most pronounced for the DJI–IPC and GSPTSE–IPC pairings. It can be observed in all time windows, from short to long term, but is clearer on the longest scales (Fig. 8). This increasing correlation is most noticeable for the DJI–IPC pair in the 2008 crisis period, when their respective correlation values have the highest values for all the pairings analysed here. This means that the Mexican stock market is increasing its integration with the other two NAFTA stock markets, which is consistent with results reported by other authors [1, 16, 40, 60]. For instance, [60] investigate the evolving nature of NAFTA stock market interdependencies and their association with diversification gains from the perspective of US investors and find a time-varying long-term relationship. Furthermore, [40] have recently studied the impact of NAFTA on North American stock market linkages and found that NAFTA has increased links between the US and Mexican equity markets and between Canadian and Mexican markets. A strong relationship in the long term may be good indication of market integration between the US and Canadian stock markets and the Mexican market. However, from a financial investment viewpoint, this means high risk in diversification gains for North American stock market investors in the long-term perspective. That is, if the correlation between stock market returns is strong, a loss in one stock is likely to be accompanied by a loss in the other. This means that the benefits of diversification increase when the correlation between stock returns is low [1, 17]. On the other hand, countries with higher levels of correlation and integration in their stock markets have higher risk exposure to global financial turmoil (such as the 2008 financial crisis). This information is therefore useful for policymakers and managers.

3.3 Dynamic correlation in the time–frequency domain

Figures 9 and 10 present the estimated wavelet coherence (WCO) and phase coherence (WPH) for the NAFTA stock returns for the full period studied (08/11/1991–16/03/2018) after applying a (ordered quantile normalisation) transformation to these returns to be normally distributed.Footnote 10 Thin and thick contour lines denote statistically significant wavelet coherences (90% confidence level) obtained through the pointwise and areawise significance tests, respectively, and the black curve is the cone of influence (COI) in which edge effects cannot be ignored. In the wavelet coherence heat maps, the colour code for spectral power ranges from blue (low WCO values) to red (high WCO values). The phase coherence ranges from \(-\pi \) (\(-180^\circ \)) to \(\pi \) (180\(^\circ \)), where a zero value indicates that the two time series under analysis are synchronous. All heat maps show the wavelet coherence between two time series, where the name of the index presented first is the first time series and the other the second. We use the DJI as the first series in all cases because it is expected to lead the other indices, although this need not be the case. It should be highlighted that wavelet coherence techniques, e.g. the technique [48] used in our paper and other techniques such as those in [10, 34, 79], do not take into account the “causal” relationship between two time series, as was previously pointed out by [10, 57, 62, 63]. Thus, care must be taken when talking about leads and lags in wavelet coherence analysis.

The wavelet coherence results corroborate the previous results obtained using rolling window Spearman correlation (see Fig. 8, Sect. 3.2), i.e. there is a good degree of correlation between NAFTA stock returns, correlation is highly variable in time and in scale (frequency) and correlation increases not only over time but also over scale. This is most noteworthy for the DJI–IPC and GSPTSE–IPC pairings, particularly for the 2004–2011 period and for the DJI–GSPTSE pairing and for the period 1995–2004. However, it is clear that wavelet coherence provides more detail about correlation over time and overall over scales. For example, the WCO analysis (Fig. 9) enables to visualise the evolution of correlation between NAFTA returns at different scales (from short and medium to long term) and over time (from the beginning to the end of the time series under study). Furthermore, the WCO provides all this information in a single plot instead of several plots as the case of rolling window correlation (Fig. 8). In addition, WCO provides the phase difference between the two time series under scrutiny, which enables to analyse the lead–lag relationships.

Fig. 9
figure 9

Wavelet coherence (WCO) computed for the NAFTA stock returns after applying a normal distribution transformation. a WCO between DJI and IPC, b WCO between GSPTSE and IPC; and c WCO between DJI and GSPTSE. The area marked by the black lines indicates the cone of influence (COI) where edge effects become important. The solid thin and thick black contours enclose regions of 90% confidence obtained through the pointwise and the areawise tests, respectively. The letters A, B, C, D, E and F correspond to the scales of 30, 60, 125, 250, 500 and 750 data points (days)

Full size image
Fig. 10
figure 10

The wavelet phase coherence (WPH) computed for the NAFTA stock returns after applying a normal distribution transformation. a WPH between DJI and IPC, b WPH between GSPTSE and IPC; and c WPH between DJI and GSPTSE. The area marked by the black lines indicates the cone of influence (COI) where edge effects become important. The solid black contour encloses regions of 90% confidence obtained through the pointwise and the areawise tests, respectively. The letters A, B, C, D, E and F correspond to the scales of 30, 60, 125, 250, 500 and 750 data points (days)

Full size image

For the short-term scale band (Fig. 9, labels A and B on the right Y-axisFootnote 11), there is a moderate/strong level of wavelet coherence that appears “clustered” around 1996, 2002–2004, 2008–2011 and 2015–2016. This is clearer particularly for the DJI–IPC and GSPTSE–IPC pairings and in the 2008–2011 period. However, although these wavelet coherences are always in phase (Fig. 10) there is no preferential stock return that “leads” or “follows” the other. This also happens in the DJI–GSPTSE pairing, although there are other time intervals with moderate coherence and with no preferential direction in the phases, e.g. around 1996 or 2002–2004. These features indicate a common origin that could be related to financial contagion (at least during the 2008–2011 interval), i.e. significant increase in cross-market links after a shock to one country or group of countries [27]. Taking into account that wavelet coherence in the short term is more closely related to volatile events than to fundamental macroeconomic factors (trade monetary policy, common shocks, etc.), that there was a long global financial crisis during the 2008–2011 period and that several studies of other stock markets (e.g. [31, 36, 62, 68, 85], among others) have established that different financial markets tend to be more closely linked during financial crises, financial contagion seems to be the main mechanism for explaining this phenomenon.

Wavelet coherence in the medium-term band (Fig. 9 labels C and D on the right Y-axisFootnote 12) reveals interesting information. For example, coherence is stronger, as in the shorter timescales, but it is more noticeable that correlation increases not only over time but also in scale. These results confirm our findings obtained with the rolling window Spearman correlation (see Fig. 8, Sect. 3.2). However, the most noteworthy result is that in the medium-term statistical significant coherences (and in phase) are mainly present for the DJI–GSPTSE pairing and for the interval 1994–2005. This result corroborates the finding found through rolling window Spearman correlation (Fig. 8c, d). This result indicates that in the medium term and from 1994 to 2005, the economical and financial mechanisms behind this behaviour are mainly related to the economies of USA and Canada.

Finally, on the long-term scale band (Fig. 9, labels E and F on the right Y-axisFootnote 13), one of the most conspicuous results is that in 2005/2006–2011 with a frequency band of approximately between \(\sim \) 1 and 3 trading years, the wavelet coherence in the DJI–IPC and GSPTSE–IPC pairings shows strong correlation values which are in phase, and large statistical significant spectral regions (Figs. 9 and 10). This is clearly not due to chance. A likely explanation, in addition to macroeconomic factors that usually take place at lower scales, could be found in the effects of the 2008 global financial crisis (which originated in the USA), even though this phenomenon is often associated with short-term scales. The prolonged, persistent strong global financial crisis, considered to be one of the most serious ever reported [20, 30], could have influenced other economic factors, variables, agents, etc., not normally altered in non-crisis times. As a result, NAFTA stock markets entered a vicious circle (note that the direction of phases changes over time and scales), increasing correlation and interrelationships (“feedbacks”) between them. Lastly, on the longest scales (more than 3 trading years) the wavelet coherences (which are in phase) are strong and statistically significant (mainly obtained through the pointwise test) only for DJI–IPC pair. These strong co-movements and this close correlation in the long term for DJI and IPC stock returns could be explained by the interdependence and the increasing economic integration of these NAFTA markets, as pointed out by other authors [17, 43].

Fig. 11
figure 11

Nonlinear Granger causality test for the NAFTA stock returns. Details for the test estimation and statistics are provided in Table 2. The arrows in the solid lines indicate the causality direction between each stock return pairing (significance 5% level)

Full size image
Table 2 Pairwise nonlinear Granger causality test for the NAFTA stock returns
Full size table

3.4 Nonlinear causality

To gain more insight into the interrelations between pairs of all the daily stock returns under scrutiny in the time domain, we present and discuss the results obtained with the nonlinear bivariate causality test [18] applied to several sub-periods for NAFTA stock returns (Fig. 11 and Table 2). However, before discussing these results it is important to stress the following two points: (1) one-way causality indicates that changes in one stock return can cause changes in another; (2) two-way (or simultaneous) causality indicates that changes in one stock return can affect a second one, but changes in the second market can also affect the first. Two-way causality indicates a high degree of interaction between returns from two markets. From a financial perspective, causality in returns from two stock markets means that, to some extent, one market could be used to forecast the other. This information should be taken into account in portfolio diversification strategies [62, 63].

The most relevant result from our bivariate causality test is that there are nonlinear two-way causalities which are statistically significant in all the sub-periods analysed and for the full period. These results indicate that there is a strong level of interrelationship between NAFTA members and that there is feedback not only from the stock markets of the USA and Canada to Mexico, but also from that of Mexico to the USA and Canada. These results are consistent with the results presented previously and with those of other authors (e.g. [1, 17, 25, 43]), although our paper is the first to use a causality test to analyse the interrelationships between NAFTA stock markets. By contrast, there are three pairs of returns that do not show nonlinear causality but which pass the test of significance in the 2002–2001 and 2012–2018 sub-periods (Fig. 11 and Table 2): the pairs DJI–IPC and GSPTSE–DJI for the second sub-period and IPC-DJI for the fourth sub-period. Finally, an intriguing result is that all the pairs for the full period (1991–2018) show nonlinear causalities which are statistically significant, such as the first and especially the third sub-period (crisis period). In other words, more interrelationships are expected during crisis periods than non-crisis periods [62]. However, there is no clear explanation for this, so further research is needed.

4 Conclusions and final remarks

We here investigate for the first time the dynamic relationship between daily NAFTA stock market indices over the 8/11/1991–16/03/2018 period, focusing on the pre-2008 crisis, 2008 crisis and post-2008 crisis periods. To depict the trend in volatility in the NAFTA stock markets visually, we estimate a 250-day rolling window standard deviation for each NAFTA stock market return. This analysis reveals that volatility decreases for all three stock market indices (most markedly for the Mexican market (IPC)) throughout the period analysed, except for the 2008 financial crisis, where the highest volatility in the whole period of study is found.

We use the rolling window Spearman correlation and wavelet coherence to analyse the evolution of correlation in time and in time–frequency of NAFTA stock market indices. The Spearman correlation (nonparametric statistical technique) does not require variables with normal distribution (Gaussian), and stock market prices are not necessarily normally distributed. On the other hand, wavelet coherence is able to handle non-stationary time series (such as stock markets and other financial time series) and to lesser extent time series that are not far from a normal distribution (otherwise the target time series has to be transformed to be normally distributed) and works in the combined time and scale domain. The correlation (Spearman rolling window and wavelet coherence) between the pairs of indices analysed increases in the 2000–2011 period. However, this increasing correlation is interrupted around 2011/2012 and then falls noticeably before increasing again from 2015 onwards. The pairs that show the lowest correlation are those that involve the IPC.

On the other hand, to analyse the cause–effect relationships in the time domain between NAFTA stock markets, we apply a nonlinear, nonparametric causality test. Financial time series belong to dynamic systems that can manifest nonlinearities and as such could elude common linear statistical tests, including linear causality tests. For this reason, the test that we use is adequate to prevent this situation. That test reveals nonlinear two-way causality for all three indices for the intervals analysed, indicating that there are strong links between NAFTA members.

It must be highlighted that the statistical methods used in this paper, to the best of our knowledge, have never before been used individually or in combination to analyse NAFTA stock market indices. In particular, rolling window correlation via the Spearman estimator and wavelet coherence in combination with an areawise significance test have not been used previously to analyse financial time series.

A better understanding of NAFTA stock markets is vital for investors, economists and policymakers, especially in the wake of the recent global economic crisis, which was recognised as one of the most serious ever reported. Thus, our results are relevant to obtaining a better understanding of economic systems formed by countries with trade agreements, strong regional influence and interdependence.

Future directions of research include the combination between empirical analysis using advanced nonlinear, nonparametric and non-stationary statistical techniques (such as the techniques used in this paper), optimal control of parameters used as inputs for the statistical methods used to analyse the time series under study [53, 54], and sophisticated stochastic methods to model transition of stock fluctuations such as [71, 72] or [55].