1 Introduction

Nonlinear equations play an important role in various application areas, especially in robotics, image processing, system identification, optimization, and nonlinear control [1,2,3,4,5,6]. In addition, a lot of phenomena can be explained via solving nonlinear equations, which are usually difficult to be computed, especially analytically [7,8,9]. In the past decades, various numerical methods have been presented to find roots of nonlinear equations effectively [10,11,12,13,14]. Newton iteration is one of the most classic methods to solve nonlinear equations, and can converge to the root quadratically [10]. In addition, a great of researches have been devoted to the extensions of Newton iteration method by using different techniques for solving nonlinear equations, such as Adomian decomposition, Taylor series, and so on [10,11,12,13].

On the other hand, as a parallel-processing technique, neural dynamics (ND) attract a great of attention in the fields of neural computing and nonlinear dynamics [15,16,17]. In mathematics, neural dynamics can described as an ordinary differential equation, starting with one initial value and converging to the equilibrium state. It can also be regarded as a special kind of neural networks including the situation with one neuron and can be implemented in hardware [18,19,20]. As compared to the above-mentioned iterative algorithms, neural dynamics possesses excellent parallel-processing and potential hardware implementation abilities [17], In last decade, many ND models have been presented to solve nonlinear equations [21,22,23,24]. As a widely used model, the gradient neural dynamics (GND) was also developed to solve static nonlinear equations effectively [21, 22]. Due to the investigation to dynamic nonlinear equations, it was found that the GND model only solve static problems efficiently. When applied to dynamic nonlinear equations, it would generate a lagging error between the theoretical solution and the state output [23, 24].

To conquer this obstacle, in [23, 24], a special class of neural dynamics (called zeroing neural dynamics, ZND) has been developed for computing dynamic nonlinear equations via introducing a novel design method. It has been proved that the ZND model can achieve an exponential convergence. That is, the state output of the ZND model can converge to the theoretical solution exponentially. After that, various different nonlinear functions have been designed and applied to activate the ZND model, and the corresponding convergence speed can be further accelerated [15,16,17]. In particular, in [25], the sign-bi-power function is used to activate zeroing neural dynamics, and make such a model even achieve finite-time convergence (called finite-time ZND, FTZND). That is to say, the convergence speed of the FTZND model makes a great breakthrough (from infinite to finite time convergence). What is more, in [26,27,28,29,30,31], such a sign-b-power function and its variant have further been applied to nonlinear equations and linear matrix equations solving.

It should be noted that the design process of the above-mentioned ZND model for dynamic nonlinear equation is under ideal conditions and external additive noises are not considered. Simply put, the ZND model does not consider the negative effects of external disturbances on the solution accuracy of dynamic nonlinear equation in the previous work. Thus, the ZND model may have no inherently noise-tolerant property. Actually, external disturbances are unavoidable in practical applications. This happens all the time during the hardware implementation of neural dynamics. For better implementation of zeroing neural dynamics, the denoising property of the ZND model should be taken into account when applied to solving complex tasks. Based on these consideration, a robust nonlinear neural dynamics (RNND) is designed and proposed to solve dynamic nonlinear equation in front of external disturbances. In contrast to the ZND model, the presented RNND model simultaneously have the inherently noise tolerance and finite-time speedup features. Moreover, theses conclusions are supported by the rigorous theoretical analysis and numerical results. Besides, for demonstrating the superiority of RNND in the presence of external disturbances, the main features of the above-mentioned GND, ZND and FTZND models are comparatively summarized in Table 1 [21,22,23,24, 26, 27]. According to the comparison results shown in the table, it follows that RNND has the best performance under the same conditions. In particular, in [32,33,34], the ZND model was applied to motion planning and control of real systems, and it was proved to be effective in the presence of no noises. However, they do not discuss the influence of various noises to the ZND model. This work extends the ZND model to further address this problem by adopting a novel design mechanism.

Table 1 Features and distinctions of the proposed RNND model from GND [21, 22], ZND [23, 24] and FTZND models [26, 27] for nonlinear equation solving
Full size table

The rest of the current work is consist of four sections. As a basis for the research, in Sect. 2, the problem formulation is first given, and the corresponding ZND model is presented for comparative purposes. The design process and theoretical analysis of the RNND model for dynamic nonlinear equation are supplied in Sect. 3. Numerical verifications are presented in Sect. 4 to show the superiority of the RNND model in front of external disturbances. The conclusion part is presented in Sect. 5. Besides, at the end of this section, the key innovations of the current work can be generalized as below.

  1. 1.

    A robust nonlinear neural dynamics (RNND) is designed and proposed for modifying the existing zeroing neural dynamics (ZND) for dynamic nonlinear equation that does not own inherent noise tolerance and finite-time convergence performance at the same time. The proposed RNND model fills this gap to address this problem in a unified framework.

  2. 2.

    Theoretical analysis of the RNND model is provided in detail to guarantee the excellent performance. In addition, the upper bound of finite-time convergence for the RNND model is theoretically computed.

  3. 3.

    In front of different external noises, various computer simulations are conducted to show the advantages of the RNND model, as compared to the ZND model.

2 Problem formulation and preliminaries

In this part, let us consider the dynamic nonlinear equation as below [17, 26, 27]:

$$\begin{aligned} h(x(t),t)=0, \end{aligned}$$
(1)

where t denotes time, x(t) denotes dynamic state variable, and \(h(\cdot )\) denotes a smooth nonlinear function. Due to nonlinearity, dynamic nonlinear, Eq. (1) may have no solution. Therefore, we only consider the existence of at least one theoretical solution of (1) in the current work. The main aim of the current work is to design a robust nonlinear neural dynamics (RNND) to find a solution x(t) in the presence of external disturbances, which converges to one of theoretical solutions of (1) within finite time.

Before proposing the RNND model, let us review the design process of zeroing neural dynamics (ZND), which was widely established to solve nonlinear equation [21,22,23,24]. Note that the motivation of this work is inspired by the negative impact of additive noises on zeroing neural dynamics. As a comparative object, it is necessary to show the simple design process for the completeness of this work, which can be divided the following three steps.

  1. 1.

    According to the definition of dynamic nonlinear equation in (1), an error function is first constructed as \(e(t)=h(x(t),t)\). Obviously, if e(t) equals to 0, the corresponding variable x(t) is exactly the solution we want to find.

  2. 2.

    To force such an error function decrease to 0, the design mechanism for e(t) is defined as

    $$\begin{aligned} \frac{\text {d}e(t)}{\text {d}t}=\,-\delta \varphi (e(t)) \end{aligned}$$
    (2)

    where \(\delta \) represents the scaling factor and \(\varphi (\cdot )\) denotes a nonlinear function. It has been proved that the above design mechanism can make e(t) converge to zero exponentially provided that \(\varphi (\cdot )\) is a monotonously increased odd function.

  3. 3.

    Based on the above two steps, we can obtain the expanding first-order differential equation by substituting \(e(t)=h(x(t),t)\) into (2):

    $$\begin{aligned} \frac{\partial h}{\partial x} \frac{\text {d}x}{\text {d}t}+\frac{\partial h}{\partial t} =\,-\delta \varphi \left( h\big (x(t),t\big )\right) , \end{aligned}$$

    which gives rise to the following zeroing neural dynamics (ZND) for solving dynamic nonlinear Eq. (1):

    $$\begin{aligned} \frac{\partial h}{\partial x} \dot{x}(t)=\,-\delta \varphi \left( h\big (x(t),t\big )\right) -\frac{\partial h}{\partial t}, \end{aligned}$$
    (3)

    where x(t) represents the neural state of zeroing neural dynamics.

Note that ZND model (3) is proved to have an exponential convergence [23, 24]. Specifically, ZND model (3) can converge to one of theoretical solutions of dynamic nonlinear equations provided that \(\varphi (\cdot )\) is a monotonically increased odd function [23, 24].

As mentioned before, there is no existing neural dynamics that simultaneously achieve the noise-suppressing and finite-time convergence for solving dynamic nonlinear equation. However, such two excellent performances are always co-pursued in the neural-dynamic field, since they are highly demanded in practical applications. In the ensuing section, we will propose a robust nonlinear neural dynamics to fill this gap, and prove its finite-time convergence and noise-tolerant property.

3 Robust nonlinear neural dynamics

In order to solve dynamic nonlinear equation and satisfy the finite-time convergence and noise tolerance performance simultaneously, a robust nonlinear neural dynamics (RNND) is proposed in this section. The design process and theoretical analysis of the proposed RNND model are presented in details as below.

3.1 Design of RNND model

In this part, on the basis of design mechanism (2), we present the following novel nonlinear mechanism for e(t) [35, 36]:

$$\begin{aligned} \dot{e}(t)=\,-\delta _1\varphi _1(e(t))-\delta _2\varphi _2 \left( e(t)+\delta _1\int _0^t\varphi _1(e(\tau ))\text {d}\tau \right) , \end{aligned}$$
(4)

where \(\delta _1>0\) and \(\delta _2>0\) denote the scaling factors; and, \(\varphi _1(\cdot )\) and \(\varphi _2(\cdot )\) denote nonlinear activation functions. Due to the introduction of the integral sign and nonlinear activation functions, the novel design mechanism (4) can suppress additive noises and achieve finite-time convergence. In addition, for such a design mechanism, in the ensuing subsection, we will prove its inherently noise-tolerant and finite-time convergence property in theory. Before that, based on the above nonlinearly activated design mechanism, we first propose the robust nonlinear neural dynamics for solving dynamic nonlinear equation. Specifically, by defining \(e(t)=h(x(t),t)\), and extending design mechanism (4), the robust nonlinear neural dynamics (RNND) model is obtained as

$$\begin{aligned} \frac{\partial h}{\partial x}\dot{x}(t)= & {} - \delta _1\varphi _1\left( h\left( x(t),t\right) \right) - \,\delta _2\varphi _2\left( \phantom {\left. +\delta _1\int _0^t\varphi _1(h\left( x(\tau ),\tau \right) )\text {d}\tau \right) } h\left( x(t),t\right) \right. \nonumber \\&\left. +\delta _1\int _0^t\varphi _1(h\left( x(\tau ),\tau \right) )\text {d}\tau \right) -\frac{\partial h}{\partial t}, \end{aligned}$$
(5)

where \(\delta _1>0\), \(\delta _2>0\), \(\varphi _1(\cdot )\) and \(\varphi _2(\cdot )\) are defined as before. Since RNND model (5) is an equivalent extension of design formula (4) by defining \(e(t)=h(x(t),t)\), if design formula (4) is proven to be inherently noise tolerant and finite-time convergent, RNND model (5) will possess these superior property. In addition, for investigating the noise-suppressing property of the RNND model (5), the noise-polluted RNND model is directly presented by introducing external disturbance \(\eta \) as follows:

$$\begin{aligned} \frac{\partial h}{\partial x}\dot{x}(t)= & {} \,-\,\delta _1\varphi _1\left( h\left( x(t),t\right) \right) -\,\delta _2\varphi _2\left( \phantom {\left. +\delta _1\int _0^t\varphi _1(h\left( x(\tau ),\tau \right) )\text {d}\tau \right) } h\left( x(t),t\right) \right. \nonumber \\&\left. +\,\delta _1\int _0^t\varphi _1(h\left( x(\tau ),\tau \right) )\text {d}\tau \right) -\,\frac{\partial h}{\partial t}+\eta . \end{aligned}$$
(6)

Note that the RNND model (5) is an ideal model. The inherently noise-tolerant property will be investigated by using (6) to solve dynamic nonlinear equation.

3.2 Analysis of RNND model

In this section, three theorems are given to show the excellent speedup and noise-suppressing performance of the robust nonlinear neural dynamics.

Theorem 1

RNND model (5) converges to one of the theoretical solutions of dynamic nonlinear Eq. (1) as long as \(\varphi _1(\cdot )\) and \(\varphi _2(\cdot )\) are monotonically increasing odd functions.

Proof

As mentioned in the above subsection, RNND model (5) is a simple expansion of design formula (4) by defining \(e(t)=h(x(t),t)\). If design formula (4) is globally stable, RNND model (5) is also globally stable. Thus, we can equivalently analyze design formula (4). To prove the stability of (4), let us introduce the intermediate variable r(t), which is defined as

$$\begin{aligned} r(t)=e(t)+\delta _1\int _0^t \varphi _1(e(\tau ))\text {d}\tau , \end{aligned}$$
(7)

and the time derivative of r(t) is solved:

$$\begin{aligned} \dot{r}(t)=\dot{e}(t)+\delta _1\varphi _1(e(t)). \end{aligned}$$
(8)

Then, by merging (4), (7) and (8), the following result is obtained as

$$\begin{aligned} \dot{r}(t)=\,-\delta _2\varphi _2(r(t)). \end{aligned}$$
(9)

Thus, Lyapunov function candidate w(t) for (4) is devised as [with e(0) and r(0) given]:

$$\begin{aligned} w(t)=\frac{1}{2}\beta e^2(t)+\frac{1}{2}r^2(t), \end{aligned}$$
(10)

where \(\beta >0\) and \(v_0=v(0)=\beta e^2(0)/2+r^2(0)/2\). We easily have that w(t) is positive-definite. Now, let us compute its time derivative, which is presented as below:

$$\begin{aligned} \frac{\text {d}w(t)}{\text {d}t}= & {} \beta e(t)\dot{e}(t)+ r(t)\dot{r}(t)\nonumber \\= & {} \beta e(t)[\dot{r}(t)-\delta _1\varphi _1(e(t))]-\delta _2r(t)\varphi _2(r(t))\nonumber \\= & {} \,-\beta \delta _2e(t)\varphi _2(r(t))\nonumber \\&-\,\beta \delta _1e(t)\varphi _1(e(t)) -\delta _2r(t)\varphi _2(r(t)). \end{aligned}$$
(11)

If \(\dot{w}(t)\le 0\) is obtained, the global stability of design formula (4) is proven in the sense of Lyapunov stability theory.

For monotone increasing odd activation function \(\varphi _2(\cdot )\), we can use the mean-value theorem and obtain:

$$\begin{aligned} \varphi _2(r(t))-\varphi _2(0)=(r(t)-0)\frac{\partial \varphi _2(r(\xi ))}{\partial r}\mid _{r(\xi )\in R}. \end{aligned}$$
(12)

Besides, we have \(\varphi _2(0)=0\) and \(\partial \varphi _2(r(t))/{\partial r}>0\). As seen from (12), it is concluded:

$$\begin{aligned} |\varphi _2(r(t))|\le p_0|r(t)|, \end{aligned}$$

where \(p_0=\max \{{\partial \varphi _2(r(t))}/{\partial r}\}\mid _{r(t)\in R}>0\). Thus, we have

$$\begin{aligned} |e(t)\varphi _2(r(t))|\le & {} |e(t)|\cdot |\varphi _2(r(t))|\nonumber \\\le & {} p_0|e(t)|\cdot |r(t)|. \end{aligned}$$
(13)

Substituting (13) back into (11), we can obtain

$$\begin{aligned} \dot{w}(t)= & {} \,-\beta \delta _2e(t)\varphi _2(r(t)) -\beta \delta _1e(t)\varphi _1(e(t))-\delta _2r(t)\varphi _2(r(t))\nonumber \\\le & {} \beta \delta _2|e(t)\varphi _2(r(t))|-\beta \delta _1e(t)\varphi _1(e(t)) -\delta _2r(t)\varphi _2(r(t))\nonumber \\\le & {} \beta \delta _2p_0|e(t)|\cdot |r(t)| -\beta \delta _1p_1e^2(t)-\delta _2p_2r^2(t)\nonumber \\= & {} \,-\beta \left( \sqrt{\delta _1p_1}|e| -\frac{\delta _2p_0}{2\sqrt{\delta _1p_1}}|r(t)|\right) ^2\nonumber \\&-\,\beta \left( \frac{\delta _2p_2}{\beta } -\,\frac{\delta _2^2p_0^2}{4\delta _1p_1}\right) r^2(t), \end{aligned}$$
(14)

where \(p_1=\min \{{\partial \varphi _1(e(t))}/{\partial e}\}\mid _{e(t)\in R}>0\) and \(p_2=\min \{{\partial \varphi _2(r(t))}/{\partial r}\}\mid _{r(t)\in R}>0\) computed in the similar way. Thus, we have \(\dot{w}(t)\le 0\) if the following condition is met:

$$\begin{aligned} 0<\beta \le \frac{4\delta _1p_1p_2}{\delta _2p_0^2}. \end{aligned}$$
(15)

This fact guarantees the negative definiteness of \(\dot{w}(t)\). Therefore, on account of Lyapunov theory, we prove that nonlinear system (4) and the resultant RNND model (5) are both globally stable. That is to say, RNND model (5) converges to one of the theoretical solutions of dynamic nonlinear Eq. (1) as long as \(\varphi _1(\cdot )\) and \(\varphi _2(\cdot )\) are monotonically increasing odd functions. \(\square \)

Theorem 2

RNND model (5) is finite-time convergent, and the upper bound \(t_\text {f}\) is estimated as

$$\begin{aligned} t_\text {f}<\frac{\delta _1+\delta _2}{\delta _1\delta _2(1-\iota )}|e(0)|^{1-\iota }, \end{aligned}$$

as long as \(\varphi _1(x)=\varphi _2(x) =\psi ^\iota (x) +\psi ^{1/\iota } (x)\) with \(\iota \in (0,1)\) and \(\psi ^{\iota }(\cdot )\) defined as

$$\begin{aligned} \psi ^{\iota }(x)= \left\{ \begin{array}{ll} |x|^{\iota }, &{}\quad {\text {if}} \; x>0, \\ 0, &{}\quad {\text {if}} \, x=0, \\ -|x|^{\iota }, &{}\quad {\text {if}} \; x <0, \end{array}\right. \end{aligned}$$

where \(e(0)=h(x(0),0)\), and scaling factors \(\delta _1\) and \(\delta _2\) are defined as before.

Proof

We have obtained \(\dot{r}(t)=\,-\delta _2\varphi _2(r(t))\) by defining \(r(t)=e(t)+\delta _1\int _0^t\varphi _1(e(\tau ))\text {d}\tau \). In particular, if \(t=0\), we can obtain \(r(0)=e(0)\). For nonlinear system \(\dot{r}(t)=\,-\delta _2\varphi _2(r(t))\), we select the Lyapunov function candidate as \(q(t)=r^2(t)\), and its time derivative is computed as below:

$$\begin{aligned} \dot{q}(t)&=2r(t)\dot{r}(t)\\&=\,-2\delta _2r(t)\varphi _2(r(t))\\&=\,-2\delta _2\left( |r(t)|^{\iota +1}+|r(t)|^{\frac{1}{\iota }+1}\right) \\&\le -2\delta _2|r(t)|^{\iota +1}\\&=\,-2\delta _2 q^{\frac{\iota +1}{2}}(t). \end{aligned}$$

With \(q(0)=|r(0)|^2=|e(0)|^2\) given, by computing differential inequality \(\dot{q}(t)\leqslant -2\delta _2 q^{\frac{\iota +1}{2}}(t)\), we obtain:

$$\begin{aligned} q^{\frac{1-\iota }{2}}(t) \left\{ \begin{array}{ll} \le |r(0)|^{1-\iota }-{\delta _2t(1-\iota )}, &{}\quad \text {if}\, t\le \frac{|r(0)|^{1-\iota }}{\delta _2(1-\iota )}, \\ =0, &{} \quad \text {if}\, t>\frac{|r(0)|^{1-\iota }}{\delta _2(1-\iota )}. \end{array}\right. \end{aligned}$$

This fact reveals that \(q(t)=0\) when \(t>{|r(0)|^{1-\iota }}/ {\delta _2(1-\iota )}\). Owing to \(q(t)=r^2(t)\) and \(r(0)=e(0)\), one can also have that \(r(t)=0\) after \(t>{|e(0)|^{1-\iota }}/{\delta _2(1-\iota )}\). In other words, the upper bound \(t_\text {1}\) for r(t) is computed as

$$\begin{aligned} t_1<\frac{|e(0)|^{1-\iota }}{\delta _2(1-\iota )}. \end{aligned}$$

Thus, after the time period \(t_1\), it is easy to have \(r(t)=0\) and \(\dot{r}(t)=0\). Then, based on (8), we further have

$$\begin{aligned} \dot{e}(t)=\,-\delta _1\varphi _1(e(t)). \end{aligned}$$
(16)

Obviously, this nonlinear system (16) is similar with \(\dot{r}(t)=\,-\delta _2\varphi _2(r(t))\). Due to \(\varphi _1(\cdot )=\varphi _2(\cdot )\), from the above analysis, we directly compute the upper bound \(t_2\) of nonlinear system (16) as below:

$$\begin{aligned} t_2<\frac{|e(0)|^{1-\iota }}{\delta _1(1-\iota )}. \end{aligned}$$

In brief, based on the above discuss, it can be concluded that RNND model (5) is finite-time convergent, and the upper bound \(t_\text {f}=t_1+t_2\) is given as

$$\begin{aligned} t_\text {f}<\frac{\delta _1+\delta _2}{\delta _1\delta _2(1-\iota )}|e(0)|^{1-\iota }, \end{aligned}$$

as long as \(\varphi _1(x)=\varphi _2(x)=\psi ^\iota (x) +\psi ^{1/\iota }(x)\). The proof is thus completed. \(\square \)

Theorem 3

The noise-polluted RNND model (6) is capable of converging to one of theoretical solutions of (1) in front of unknown additive constant noise \(\eta \) as long as \(\varphi _1\) and \(\varphi _2\) are monotonically increasing odd functions.

Proof

It is easy to conclude that, by defining \(e(t)=h(x(t),t)\), the noise-polluted RNND model (6) is obtained from the following nonlinear system:

$$\begin{aligned} \dot{e}(t)= & {} \,-\delta _1\varphi _1(e(t))\nonumber \\&-\,\delta _2\varphi _2\left( e(t) +\delta _1\int _0^t \varphi _1(e(\tau ))\text {d}\tau \right) +\eta . \end{aligned}$$
(17)

Then, by defining \(r(t)=e(t)+\delta _1\int _0^t\varphi _1(e(\tau )) \text {d}\tau \), we can obtain

$$\begin{aligned} \dot{r}(t)=\,-\delta _2\varphi _2(r(t))+\eta . \end{aligned}$$
(18)

Therefore, Lyapunov function candidate for nonlinear system (17) is selected as

$$\begin{aligned} p(t)=\frac{1}{2}\left( \delta _2\varphi _2(r(t))-\eta \right) ^2, \end{aligned}$$

which is obviously positive definite. Next, \(\dot{p}(t)\) is computed as below:

$$\begin{aligned} \frac{\text {d}p(t)}{\text {d}t}= & {} \left( \delta _2\varphi _2(r(t))-\eta \right) \delta _2 \frac{\partial \varphi _2(r(t))}{\partial r} \dot{r}(t)\nonumber \\= & {} \,-\delta _2\frac{\partial \varphi _2(r(t))}{\partial r} \left( \delta _2\varphi _2(r(t))-\eta \right) ^2. \end{aligned}$$
(19)

Since \(\varphi _2\) is a monotonically increasing function, we know \({\partial \varphi _2(r(t))}/{\partial r>0}\). Hence, \(\dot{p}(t)\le 0\) (i.e., \(\dot{p}(t)\) is of negative definiteness). Based on Lyapunov theory, p(t) is capable of converging to 0. Here and now, \(\lim _{t\rightarrow \infty }\delta _2\varphi _2(r(t))-\eta =0\), i.e, \(\lim _{t\rightarrow \infty }r(t)=\varphi _2^{-1}(\eta /\delta _2)\). In other words, r(t) is finally convergent to \(\varphi _2^{-1} (\eta /\delta _2)\) and \(\lim _{t\rightarrow \infty }\dot{r}(t) =\,-\delta _2\varphi _2(r(t))+\eta =0\).

Furthermore, according to \(\dot{r}(t)=\dot{e}(t)+\delta _1\varphi _1(e(t))\) and \(\lim _{t\rightarrow \infty }\dot{r}(t)=0\), we can use Lasalle’s invariant set principle to analyze this problem [37, 38]. In this situation, \(\dot{e}(t)=\dot{r}(t)-\delta _1\varphi _1(e(t))\) reduces to

$$\begin{aligned} \dot{e}(t)=\,-\delta _1\varphi _1(e(t)), \end{aligned}$$
(20)

which is exactly the previously mentioned design formula (2). For this formula, we have proved that \(\lim _{t\rightarrow \infty }e(t)=0\). Furthermore, if the sign-bi-power function is used to activate (2), the error function will converge to zero in a finite period.

From the above analysis, we know that the error function e(t) produced by (6) is able to converge to 0 in front of unknown additive constant noise \(\eta \). In other words, the noise-polluted RNND model (6) is capable of converging to one of theoretical solutions of (1) in front of unknown additive constant noise \(\eta \). \(\square \)

4 Numerical verification

In this section, to validate the advantages of RNND model (5), zeroing neural dynamics (ZND) model (3) is comparatively applied to dynamic nonlinear equation solving. Note that the sign-bi-power function with \(\iota =0.5\) is adopted to activate ZND model (3) and RNND model (5). We consider the following dynamic nonlinear equation:

$$\begin{aligned} h(x(t),t)=x^2(t)-\cos ^2(2t)-4\cos (2t)-4=0, \end{aligned}$$
(21)

which can be converted into \(h(x(t),t)=[x(t)-\cos (2t)-2)][x(t) +\cos (2t)+2]=0\) via factorization of polynomial. Thus, the dynamic theoretical solutions for this problem are easily derived as \(x^*_1(t)=\cos (2t)+2\) and \(x^*_2(t)=\,-\cos (2t)-2\), which can be used to check the solution accuracy of such two neural dynamics. In this part, we mainly consider three cases for RNND model (5) and (ZND) model (3) to solve the above nonlinear equation. That is, such two models are simulated in the presence of zero noise (i.e., the ideal condition), additive constant noises, and additive time-varying noises.

Fig. 1
figure 1

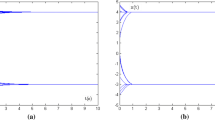
Computing results generated by the ZND model (3) beginning with 20 initial states \(x(0)\in [-4,4]\) with \(\delta =5\) in the presence of no noise. a Neural state output trajectories and theoretical solutions, where solid blue curves denote state output x(t), and dash red curves denote theoretical solution \(x^*(t)\). b The residual error trajectories

Full size image
Fig. 2
figure 2

Computing results generated by the RNND model (5) beginning with 20 initial states \(x(0)\in [-4,4]\) with \(\delta _1=\delta _2=5\) in the presence of no noise. a Neural state output trajectories and theoretical solutions, where solid blue curves denote state output x(t), and dash red curves denote theoretical solution \(x^*(t)\). b The residual error trajectories

Full size image
Fig. 3
figure 3

Computing results generated by the ZND model (3) starting from 20 randomly generated initial states \(x(0)\in [-4,4]\) with \(\delta =5\) in the presence of constant noise \(\eta =1\). a Neural state output trajectories and theoretical solutions, where solid blue curves denote state output x(t), and dash red curves denote theoretical solution \(x^*(t)\). b The residual error trajectories

Full size image

Case 1: Zero noise As mentioned before, ZND model (3) is proved to be effective to solve dynamic nonlinear equations in the ideal conditions (i.e., no noise). In this case, we continue to verify this conclusion by solving dynamic nonlinear Eq. (21) in the presence of zero noise. Beginning with 20 initial states \(x(0)\in [-4,4]\), the computing results of ZND model (3) for this issue are plotted in Fig. 1. As obtained in Fig. 1a, as long as x(0) is given, any of state variable trajectories x(t) is capable of converging to one of the theoretical solutions of dynamic nonlinear Eq. (21). Moreover, the convergence speed is very fast. After about finite time 0.4 s, state variable trajectories have overlapped with one of the theoretical solutions. Figure 1b plots the corresponding residual error trajectories, where the residual error is defined as |h(x(t), t)|. The results of Fig. 1b verify the conclusion of Fig. 1a. The corresponding residual errors immediately drop to 0 after about finite time 0.3 s. Below similar case, RNND model (5) is used to solve this dynamic nonlinear equation, and the computing results are plotted in Fig. 2. Compared with the results generated by ZND model (3) and RNND model (5), the solving performance is almost no difference between them. In other words, state variable trajectories x(t) of RNND model (5) are able to converge, and the finite convergence time is also about 0.4 s. For further verifying the theoretical analysis of RNND model (5), in this situation, the maximum upper bound is calculated according to the given maximum initial value as follows:

$$\begin{aligned} t_\text {f}<\frac{\delta _1+\delta _2}{\delta _1\delta _2(1-\iota )}|e(0)|^{1-\iota } =\frac{5+5}{5\times 5(1-0.5)}|4|^{1-0.5}=1.6. \end{aligned}$$

Obviously, as shown in the numerical results plotted in Fig. 1b, the convergence time of the RNND model (5) is within finite time 1 second, which is less than the above maximum upper bound. Theorem 2 is thus verified by the numerical results. In a word, both ZND model (3) and RNND model (5) are effective on solving dynamic nonlinear equations.

Fig. 4
figure 4

Computing results generated by the RNND model (5) beginning with 20 initial states \(x(0)\in [-4,4]\) with \(\delta _1=\delta _2=5\) in front of constant noise \(\eta =1\). a Neural state output trajectories and theoretical solutions, where solid blue curves denote state output x(t), and dash red curves denote theoretical solution \(x^*(t)\). b The residual error trajectories

Full size image
Fig. 5
figure 5

Residual error trajectories generated by different two models beginning with 20 initial states \(x(0)\in [-4,4]\) with \(\delta _1=\delta _2=\delta =5\) in front of time-varying noise \(\eta =0.8\sin (t)\). a By the ZND model (3). b By the RNND model (5)

Full size image

Case 2: Constant noise As we know, external disturbances are unavoidable in practical applications. This happens all the time during the hardware implementation of neural dynamics. In the previous work, the ZND model does not consider the negative effects of external disturbances on the solution accuracy of dynamic nonlinear equation. Thus, the ZND model may have no inherently noise-tolerant property. Now, let us first study the influence of constant noises in this part. In order to better show results, \(\eta =1\) is considered in ZND model (3) and RNND model (5) to solve dynamic nonlinear Eq. (21), and other conditions (e.g., design parameters \(\delta \) and \(\varepsilon \)) remain unchanged. The computing results of such two models are shown in Figs. 3 and 4. According to Fig. 3a generated by ZND model (3), we have the state variable trajectories x(t), starting from \(x(0)\in [-4,4]\), are no longer convergent to any of the theoretical solutions of dynamic nonlinear Eq. (21). There always exists some errors between them. Furthermore, as observed in Fig. 3b, the corresponding residual errors are always oscillating around the value of 0.5, instead of converging to zero. These results suggest that ZND model (3) cannot solve dynamic nonlinear Eq. (21) effectively in the presence of additive constant noises with relatively large lagging error existence. In contrast, under the same conditions, the computing results generated by RNND model (5) are shown in Fig. 4. As observed in Fig. 4a, even if in front of additive noise \(\eta =1\), the state variable trajectories x(t) of RNND model (5) are still convergent to one of the theoretical solutions of dynamic nonlinear Eq. (21). That is to say, RNND model (5) has a denoising property and is still effective in front of additive constant disturbances. Now, let us show the convergence results of the residual errors generated by RNND model (5), which are shown in Fig. 4b. In contrast to the convergence results of Fig. 2b, the finite convergence time is almost the same. In other words, the convergence speed of RNND model (5) is not affected by adding a constant noise, and finite-time convergence is also achieved. In addition, because the initial states are not changed, the maximum upper bound for RNND is the same as the first condition. By comparison, the conclusion of Theorem 2 is also validated. In a word, RNND model (5) has an inherently robust property in front of additive constant noises and simultaneously possesses the finite-time convergence property, while ZND model (3) becomes invalid. The results illustrate the superiority of RNND model (5) to ZND model (3).

Case 3: Time-varying noise In last case, let us consider additive time-varying noises. Similar to Case 2, only time-varying noise \(\eta =0.8\sin (t)\) is added in ZND model (3) and RNND model (5) to solve dynamic nonlinear Eq. (21), and other conditions remain unchanged. Due to the similarity of state variable trajectories, we only plot convergence trajectories of the residual errors produced by ZND model (3) and RNND model (5), which are shown in Fig. 5. As observed in this figure, it can be concluded that, in front of additive time-varying noise \(\eta =0.8\sin (t)\), the residual errors of ZND model (3) do not converge to zero, but keep oscillating along the trend of the function \(0.8\sin (t)\), while the residual errors of RNND model (5) are still convergent to zero with finite time. That is to say, even in front of additive time-varying noise \(\eta =0.8\sin (t)\), RNND model (5) is still effective on solving dynamic nonlinear equation, and simultaneously possesses the robustness and finite-time convergence property. The results in this case also verify the better performance of RNND model (5) than RNND model (5).

5 Conclusions

Inspired by the impact of additive noises on zeroing neural dynamics (ZND), in this work, a robust nonlinear neural dynamics (RNND) model has been designed to general dynamic nonlinear equation solving in the presence of external disturbances. Compared with ZND, the RNND model simultaneously achieves the superior robustness and finite-time convergence ability. Furthermore, the excellent performance of the RNND model has been analyzed in details. The convergence upper bound for RNND has also been calculated by solving a differential inequality. Various different simulations have demonstrated the effectiveness and advantages of the RNND model for nonlinear equation in front of different external disturbances. It should be mentioned that this is the first RNND model designed for dynamic nonlinear equation, which fills the gap existing in the field of zeroing neural dynamics either with the finite-time convergence performance or with the noise suppression property. The future work may lie in the theoretical analysis of the robustness of the RNND model in front of time-varying additive noises and the application of the RNND model to engineering application problems.