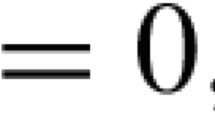On exponential convergence of nonlinear gradient dynamics system with application to square root finding

Abstract

Gradient dynamics systems and their exponential convergence theories are investigated in this paper. Differing from widely considered linear gradient dynamics system (LGDS), a class of nonlinear gradient dynamics system (NGDS) is investigated with the exponential convergence analyzed. As an application to scalar square root finding, by defining six different square-based nonnegative error-monitoring functions (i.e., energy functions), six different NGDSs are theoretically designed and proposed in the form of first-order differential equations. Moreover, inspired by the exponential convergence theory of the LGDS, for each of the six proposed NGDSs, the corresponding exponential convergence theory is proved rigorously based on Lyapunov theory. Numerical verification and comparison further illustrate the efficacy of the proposed six NGDSs, in which the main differences and respective usages, as well as the application background and condition, are discussed in detail.

1 Introduction

The gradient dynamics system (GDS) has now been regarded as a powerful alternative for online computation [1–5], such as matrix inversion [6], linear and nonlinear equations solving [7], in view of its high-speed processing nature and its convenience of hardware implementation in practical applications [8–13]. To effectively solve different linear and nonlinear problems, different classes of GDSs are thus obtained, i.e., the linear gradient dynamics systems (LGDSs) and the nonlinear gradient dynamics systems (NGDSs). Note that the LGDSs with application to online linear equations solving have been investigated by the previous work [7, 14]. However, to the best of the authors’ knowledge, there exists few research on their exponential convergence theories of NGDSs [7, 15]. Motivated by this reason, we thus design, propose and investigate different NGDSs as well as their application.

Being a case of nonlinear equations solving, the scalar square root finding in the form of $x^2-a=0$ is considered to be a basic mathematical operation arising in a wide variety of scientific and engineering applications, such as mathematical analysis [16–20], signal processing [21] and data regression [22]. Moreover, a majority of current microprocessors contain the square root implementation in the operation set. These systems must support and evaluate the operation (i.e., the computation of the square root) accurately and rapidly. Thus, many numerical algorithms are developed and investigated for scalar square root finding [23–25] and/or related to those used for division [26, 27]. As an application to the scalar square root finding, in this paper, the corresponding NGDS is theoretically designed and proposed by defining the square-based positive or at least lower-bounded function called the energy function (EF). More specifically, by defining six different EFs as the error-monitoring functions, six different NGDSs with each being depicted in the first-order differential equation are elegantly constructed to make the corresponding EFs exponentially converge to zero. Moreover, inspired by the previous work [7], the detailed theoretical analyses on exponential convergence of the proposed NGDSs are given based on Lyapunov theory [28–32] for the first time.

The rest of this paper is organized into the following sections. In Sect. 2, the design method of a GDS based on an EF is presented, and then, the exponential convergence for the resultant LGDS and NGDS is investigated. Section 3 proposes six different NGDSs based on six different EFs for scalar square root finding. Theoretical analyses about the exponential convergence of such proposed NGDSs are investigated in Sect. 4. Section 6 concludes this paper with final remarks. Before ending this section, it is worth pointing out the main contributions of this paper as follows.

• 1. The GDSs (including of LGDSs and NGDSs) with their exponential convergence are uniformly investigated in this paper. In addition, differing from the earlier-presented LGDSs, different NGDSs are designed, proposed and investigated by defining different EFs to find the scalar square root for the first time.

• 2. Based on Lyapunov theory, the exponential convergence of the proposed NGDSs is proven, which substantiates well the feasibility and validity of the proposed NGDSs for scalar square root finding.

• 3. A new approach on the definition of the EF for the GDS construction is introduced and also gives an inspiring direction on the research of dynamics system, especially the nonlinear dynamics system, which is guaranteed by the theoretical analysis.

• 4. Through the numerical verification and comparison, in which the main differences and respective usages, as well as the application background and condition are discussed in detail, the efficacy of the proposed six NGDSs is demonstrated well for scalar square root finding.

2 Nonlinear GDS and exponential convergence

In this section, the EF is designed as an error-monitoring function (i.e., a square-based energy function) for deriving a GDS. Specifically, by defining different EFs, different GDSs (i.e., LGDSs and NGDSs) can be obtained for linear and nonlinear problems solving. In addition, the exponential convergence of the LGDS and NGDS is investigated in this section. For better understanding and completeness, we present the following formal definition of EF.

Definition 1

The energy function (EF) denoted by $\varepsilon =\varepsilon (x)$, which is usually associated with GDS, is a norm-based or square-based scalar-valued nonnegative, or at least lower-bounded function (or termed, an error-monitoring function).

2.1 GDS design method

Based on the above definition, a GDS for problem solving (e.g., equation computing) can thus be established via an EF through the following steps.

Step 1. Following the gradient-descent design method [14], we define a square-based EF (i.e., $\varepsilon$) as the error-monitoring function to monitor the process of problem solving, e.g., equation computing.

Step 2. In order to force $\varepsilon$ to converge to zero, the negative of the gradient (i.e., $-\partial \varepsilon /\partial x$) is used as the descent direction, which leads to the so-called GDS design formula in the form of a first-order differential equation:

$$\begin{aligned} \dot{x}(t)=\frac{\hbox {d}{x(t)}}{\hbox {d}{t}}=-\gamma \frac{\partial \varepsilon }{\partial x}, \end{aligned}$$

(1)

where design parameter $\gamma >0 \in R$ is used to scale the convergence rate of GDS solution. Note that $\gamma$ corresponds to the reciprocal of a capacitance parameter, of which the value should be set as large as the hardware would permit, or appropriately large for modeling and experimental purposes [33].

Step 3. By adopting GDS design formula (1), the differential equation of a GDS (i.e., a dynamic equation) can thus be established for problem solving.

2.2 General application to equation solving

Our objective is to find the solution $\mathbf{x}\in R^{n}$ so as to make the following vector (or scalar when $n=1$) equation hold true:

$$\begin{aligned} f(\mathbf{x})=\mathbf{0}, \end{aligned}$$

(2)

where $f(\cdot ): R^{n} \rightarrow R^{n}$ denotes an function processing array. The GDS design method needs to define a square-based positive error function (or termed, EF) such as

$$\begin{aligned} \varepsilon (\mathbf{x})=\frac{1}{2}\Vert f(\mathbf{x})\Vert _{2}^{2}, \end{aligned}$$

where $\Vert \cdot \Vert _{2}$ denotes the two norm of a vector argument (or the absolute value of a scalar argument). Then, following GDS design formula (1), we can obtain the differential equation (termed as gradient dynamics) as below:

$$\begin{aligned} \dot{\mathbf{x}}(t)=-\gamma \frac{\partial \varepsilon }{\partial \mathbf{x}}=-\gamma \left( \frac{\partial f(\mathbf{x})}{\partial \mathbf{x}} \right) ^{\mathrm{T}}f(\mathbf{x}), \end{aligned}$$

where $^{\mathrm{T}}$ denotes the transpose operator, and $\gamma$ is defined as before.

Furthermore, based on Eq. (2), we can obtain two different forms of the GDS, i.e., the LGDS and the NGDS, as following two situations.

Situation 1. Consider nonsingular constant matrix $A$ in linear equation:

$$\begin{aligned} A\mathbf{x}-\mathbf{b}=\mathbf{0}, \end{aligned}$$

(3)

where coefficient matrix $A\in R^{n \times n}$ and coefficient vector $\mathbf{b} \in R^{n}$, while $\mathbf{x}\in R^{n}$ is the unknown vector to be obtained. For presentation convenience, let $\mathbf{x}^*\in R^{n}$ denote the theoretical solution of Eq. (3). Evidently, $f(\mathbf{x})=A\mathbf{x}(t)-\mathbf{b}$. Thus, we have $\varepsilon (\mathbf{x})=\Vert f(\mathbf{x})\Vert _{2}^{2} /2=\Vert A\mathbf{x}(t)-\mathbf{b}\Vert _{2}^{2} /2$. Following GDS design formula (1), we obtain the linear gradient dynamics system termed LGDS as below:

$$\begin{aligned} \dot{\mathbf{x}}(t)=-\gamma A^{\mathrm{T}}(A\mathbf{x}(t)-\mathbf{b}). \end{aligned}$$

(4)

Situation 2. Consider the following scalar square root problem:

$$\begin{aligned} x^2-a=0, \end{aligned}$$

(5)

where $a>0 \in R$ is a constant in this situation. Note that our objective in this work is to find $x\in R$ in real time such that the above nonlinear Eq. (5) holds true. For presentation convenience, let $x^*\in R$ denote a theoretical square root of $a$. Then, we have $\varepsilon (x)=f^{2}(x)/2=\left( x^2(t)-a\right) ^2 /2$. Following the above design procedure, we obtain the nonlinear gradient dynamics system termed NGDS as below:

$$\begin{aligned} \dot{x}(t)=-2\gamma x(t)\left( x^2(t)-a\right) . \end{aligned}$$

Thus, we constructed two classes of GDS, i.e., the LGDS and NGDS, based on different problems or equations to be solved.

2.3 Exponential convergence theory

In the previous research [7], the exponential convergence result of LGDS (4) has been proved and investigated (i.e., the following lemma).

Lemma 1

[7] Consider a nonsingular constant matrix $A\in R^{n \times n}$ in linear Eq. (3). The state vector $\mathbf{x}(t)\in R^{n}$ of LGDS (4) exponentially converges to the theoretical solution $\mathbf{x}^{*}=A^{-1}\mathbf{b}$ of linear Eq. (3). In addition, the exponential convergence rate is $\alpha \gamma$ with $\alpha$ denoting the minimum eigenvalue of $A^{ T }A$.

Inspired by Lemma 1, we have the exponential convergence theorem of the GDSs (i.e., LGDS and NGDS). Before presenting such a theorem, the following two definitions are given to lay a basis for further discussion [34].

Definition 2

An energy function $\varepsilon (t)$ of GDS starting with an initial state $\mathbf{x}(0)$ is said to be exponentially convergent if it satisfies

$$\begin{aligned} \varepsilon (t) \le \varepsilon (0) \hbox {exp}(-\beta t), \end{aligned}$$

(6)

where constant $\beta >0$ denotes the exponential convergence rate of $\varepsilon (t)$.

Definition 3

A trajectory $\mathbf{x}(t)$ of GDS starting from an initial state $\mathbf{x}(0)$ is said to be exponentially convergent if it satisfies

$$\begin{aligned} \Vert \mathbf{x}(t)-\mathbf{x}^{*}\Vert _2\le \mu \Vert \mathbf{x}(0)-\mathbf{x}^{*} \Vert _2 \hbox {exp} (-\lambda t), \forall t \ge 0,\nonumber \\ \end{aligned}$$

(7)

where constants $\mu >0$ and $\lambda >0$ exist.

Theorem 1

Starting with a randomly generated initial state $\mathbf{x}(0)$, gradient dynamics systems (GDSs), i.e., LGDS and NGDS, possess exponential convergence properties, if any of the following three conditions is satisfied.

• Condition 1. Equation (6) holds true.

• Condition 2. Equation (7) holds true.

• Condition 3. Equation $\Vert \partial \varepsilon /\partial \mathbf{x}\Vert _2^2\ge \alpha \varepsilon (t)$ holds true, $\exists \alpha >0$.

Proof

By Definition 2 or 3, the exponential convergence property of GDS is evident, if its energy function $\varepsilon (t)$ or state $\mathbf{x}(t)$ exponentially converges (i.e., Condition 1 or 2 holds true).

Furthermore, if Condition 3 holds true, then it follows from GDS design formula (1) that the time derivative of $\varepsilon (t)$ is

$$\begin{aligned} \dot{\varepsilon }(t)=\left( \frac{\partial \varepsilon }{\partial \mathbf{x}}\right) ^\mathrm{T}\frac{\hbox {d}\mathbf{x}}{\hbox {d}t}=\left( \frac{\partial \varepsilon }{\partial \mathbf{x}}\right) ^\mathrm{T}\dot{\mathbf{x}}(t)=-\gamma \left\| \frac{\partial \varepsilon }{\partial \mathbf{x}} \right\| _2^2. \end{aligned}$$

Applying Condition 3, we have

$$\begin{aligned} \dot{\varepsilon }(t)=-\gamma \left\| \frac{\partial \varepsilon }{\partial \mathbf{x}} \right\| _2^2 \le -\gamma \alpha \varepsilon (t). \end{aligned}$$

Therefore, with $\gamma \alpha >0$ being the exponential convergence rate, we obtain

$$\begin{aligned} \varepsilon (t) \le \varepsilon (0) \hbox {exp}( -\gamma \alpha t), \end{aligned}$$

which is exactly Eq. (6) and means that if Condition 3 is satisfied, then $\varepsilon (t)$ of GDS exponentially converges to zero. That is to say, by Definition 2, the GDS is exponentially convergent. The proof is thus completed.$\square$

In summary, we propose the exponential convergence theory of the GDSs in this section. Specifically, inspired by Lemma 1, we novelly extend the exponential convergence result to NGDS. Note that NGDSs are applied to square root finding with the detailed exponential convergence proofs given in Sect. 4.

3 Application to square root finding

In this section, based on different EFs, different NGDSs are developed and investigated for scalar square root finding via the presented GDS design method. For further discussion, the following lemma and definition are given as a basis for square root finding.

Lemma 2

[23] If scalar $a>0 \in R$ in (5) is constant, the theoretical square root $x^*\in R$ exists.

Definition 4

Specially, for online solution of scalar square root [i.e., (5)], we can define the following six different energy functions (EFs):

$$\begin{aligned} \varepsilon _{1}&= \frac{1}{2}\left( x^2(t)-a\right) ^2,\end{aligned}$$

(8)

$$\begin{aligned} \varepsilon _{2}&= \frac{1}{2}\left( \frac{1}{x^2(t)}-\frac{1}{a}\right) ^2,\end{aligned}$$

(9)

$$\begin{aligned} \varepsilon _{3}&= \frac{1}{2}\left( \frac{x^2(t)}{a}-1\right) ^2,\end{aligned}$$

(10)

$$\begin{aligned} \varepsilon _{4}&= \frac{1}{2}\left( \frac{a}{x^2(t)}-1\right) ^2, \end{aligned}$$

(11)

$$\begin{aligned} \varepsilon _{5}&= \frac{1}{2}\left( x(t)-\frac{a}{x(t)}\right) ^2,\end{aligned}$$

(12)

$$\begin{aligned} \varepsilon _{6}&= \frac{1}{2}\left( \frac{x(t)}{a}-\frac{1}{x(t)}\right) ^2. \end{aligned}$$

(13)

According to the GDS design method, these different EFs [i.e., (8)–(13)] can lead to different NGDSs. Firstly, let us consider GDS design formula (1) and EF (8). Then, we obtain the following nonlinear dynamic equation (i.e., a first-order nonlinear differential equation) of an NGDS for scalar square root finding.

$$\begin{aligned} \hbox {NGDS}_{1}:\dot{x}(t)=-2\gamma x(t)\left( x^2(t)-a\right) . \end{aligned}$$

(14)

Similarly, based on GDS design formula (1) and EFs (9)–(13), the following nonlinear dynamic equations of other NGDSs are obtained for scalar square root finding.

$$\begin{aligned}&\hbox {NGDS}_{2}:\dot{x}(t)=-2\gamma \frac{x^2(t)-a}{ax^5(t)},\end{aligned}$$

(15)

$$\begin{aligned}&\hbox {NGDS}_{3}:\dot{x}(t)=-2\gamma \frac{x(t)}{a}\left( \frac{x^2(t)}{a}-1\right) ,\end{aligned}$$

(16)

$$\begin{aligned}&\hbox {NGDS}_{4}:\dot{x}(t)=-2a\gamma \frac{x^2(t)-a}{x^5(t)},\end{aligned}$$

(17)

$$\begin{aligned}&\hbox {NGDS}_{5}:\dot{x}(t)=-\gamma \frac{\left( x^2(t)-a\right) \left( x^2(t)+a\right) }{x^3(t)},\end{aligned}$$

(18)

$$\begin{aligned}&\hbox {NGDS}_{6}:\dot{x}(t)=-\gamma \frac{(x^2(t)-a)(x^2(t)+a)}{a^2x^3(t)}. \end{aligned}$$

(19)

Thus, we obtain six different NGDSs [i.e., (14)–(19)] for scalar square root finding, which correspond to six different EFs [i.e., (8)–(13)].

Remark 1

By defining six different EFs (8)–(13), we develop six different NGDSs (14)–(19). Hence, it can provide many models for researchers or practitioners to choose. In practical applications, the practitioners could find and choose the most suitable EF and the corresponding NGDS in accordance with specific request. For example, we may find that NGDS (14) requires less components for hardware implementation.

4 Theoretical results and analyses

In the above section, we propose six different NGDSs (14)–(19) based on different EFs. In this section, we propose theorems as well as their corresponding proofs on the exponential convergence theories of NGDSs (14)–(19).

4.1 Exponential convergence analysis of $\hbox {NGDS}_{1}$

Let us consider $\hbox {NGDS}_{1}$ (14), we have the following results as the basis of its exponential convergence theory.

Lemma 3

Consider (5) and GDS design formula (1). Starting from an initial state $x(0)\ne 0$, the state $x(t)$ of $\hbox {NGDS}_{1}$ (14) is bounded. Specifically, the lower bound and upper bound are $\delta$ and $\zeta$, respectively, i.e.,

$$\begin{aligned} |x(t)|\ge \delta \in R, \end{aligned}$$

(20)

and

$$\begin{aligned} |x(t)|\le \zeta \in R. \end{aligned}$$

(21)

Proof

The boundness of the state $x(t)$ of $\hbox {NGDS}_{1}$ (14) can be discussed in the following four cases.

Case 1. If the initial state $x(0)>0$ satisfying $x(0)\ge x^*=\sqrt{a}$, then it follows Eq. (14) that $\dot{x}(t) \le 0, \forall t>0$. Therefore, the state $x(t)$ of $\hbox {NGDS}_{1}$ (14) is a monotonically nonincreasing function. Then, we have

$$\begin{aligned} x(0) \ge x(t) \ge x^*=\sqrt{a}>0. \end{aligned}$$

Case 2. If the initial state $x(0)>0$ satisfying $x(0)\le x^*=\sqrt{a}$, it follows Eq. (14) that $\dot{x}(t) \ge 0, \forall t>0$. Accordingly, the state $x(t)$ of $\hbox {NGDS}_{1}$ (14) is a monotonically nondecreasing function. Then, we obtain

$$\begin{aligned} 0<x(0) \le x(t) \le x^*=\sqrt{a}. \end{aligned}$$

Case 3. If the initial state $x(0)<0$ satisfying $x(0)\ge x^*=- \sqrt{a}$, it follows Eq. (14) that $\dot{x}(t) \le 0, \forall t>0$. Thus, the state $x(t)$ of $\hbox {NGDS}_{1}$ (14) is a monotonically nonincreasing function. Hence, we have

$$\begin{aligned} 0>x(0) \ge x(t) \ge x^*=- \sqrt{a}. \end{aligned}$$

Case 4. If the initial state $x(0)<0$ satisfying $x(0)\le x^*=- \sqrt{a}$, it follows Eq. (14) that $\dot{x}(t) \ge 0, \forall t>0$. Thus, the state $x(t)$ of $\hbox {NGDS}_{1}$ (14) is a monotonically nondecreasing function. As a result, we have

$$\begin{aligned} x(0) \le x(t) \le x^*=- \sqrt{a}<0. \end{aligned}$$

Therefore, based on the above discussion, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} x(0)\ge x(t) \ge x^{*}, &{}\hbox {if } \,x(0) \ge x^{*}= \sqrt{a}>0,\\ x(0)\le x(t)\le x^{*}, &{}\hbox {if } \, 0<x(0)\le x^{*}= \sqrt{a},\\ x(0)\ge x(t) \ge x^{*},&{}\hbox {if } \, 0>x(0) \ge x^{*}=- \sqrt{a}, \\ x(0)\le x(t) \le x^{*},&{}\hbox {if } \, x(0) \le x^{*}=- \sqrt{a}<0. \end{array}\right. } \end{aligned}$$

Since the initial state $x(0)$ and the theoretical solution $x^*$ are finite constants, we know that the state $x(t)$ of $\hbox {NGDS}_{1}$ (14) is bounded, i.e., (20) and (21) hold true. The proof is thus completed. $\square$

Corollary 1

Consider positive constant $a\in R$ involved in the nonlinear Eq. (5). Starting from an initial state $x(0)\ne 0$, the state $x(t)$ of $\hbox {NGDS}_{1}$ (14) will not be zero

$$\begin{aligned} x(t)\ne 0, \forall t>0. \end{aligned}$$

Besides, if the initial state $x(0)>0$, the state of (14) satisfies $x(t)>0$. On the contrary, if the initial state $x(0)<0$, the state of (14) satisfies $x(t)<0$.

Based on Lemma 3 and Corollary 1, we have the following theorem about the exponential convergence result of $\hbox {NGDS}_{1}$ (14).

Theorem 2

Consider constant $a>0 \in R$ involved in the nonlinear Eq. (5). Starting from an initial state $x(0)\ne 0$, $\hbox {NGDS}_{1}$ (14) possesses the exponential convergence property. That is, EF (8) exponentially converges to zero, and the state $x(t)$ of (14) exponentially converges to the theoretical scalar square root $x^*$ of the constant $a$.

Proof

To prove Theorem 2, i.e., the exponential convergence theorem of $\hbox {NGDS}_{1}$ (14), we can use Lyapunov theory [35]. Firstly, let us define a Lyapunov function candidate

$$\begin{aligned} {\L }_{1}(x(t))=\varepsilon _{1}=\frac{1}{2} (x^2(t)-a)^2\ge 0, \end{aligned}$$

(22)

which can be discussed in the following two cases.

Case 1. :

If $\varepsilon _{1}= (x^2(t)-a)^2/2=0$, then $x(t)=x^*=\pm \sqrt{a}$. The solution of the nonlinear Eq. (5) is found.

Case 2. :

If $\varepsilon _{1}= (x^2(t)-a)^2/2>0$, then $x(t)\ne x^*=\pm \sqrt{a}$.

As for Case 2, we derive the time derivative of Eq. (22) as

$$\begin{aligned} \dot{{\L }}_{1}(x(t))&= \dot{\varepsilon _{1}}=\frac{\hbox {d}\varepsilon _{1}}{\hbox {d} t} =\frac{\partial \varepsilon _{1}}{\partial x}\frac{\hbox {d} x}{\hbox {d} t} =\frac{\partial \varepsilon _{1}}{\partial x}\dot{x}\nonumber \\&= -\gamma \left( \frac{\partial \varepsilon _{1}}{\partial x} \!\right) ^2\!\!. \end{aligned}$$

(23)

Following from Eq. (22), we obtain the following first-order partial derivative of $\varepsilon _{1}$ with respect to $x$:

$$\begin{aligned} \frac{\partial \varepsilon _{1}}{\partial x}=2x(t)(x^2(t)-a), \end{aligned}$$

and we further have

$$\begin{aligned} \left( \frac{\partial \varepsilon _{1}}{\partial x} \right) ^2=4x^2(t)(x^{2}(t)-a)^2. \end{aligned}$$

By Lemma 3 and Corollary 1, $\exists \delta _{1}>0$, $\forall x(t)$, we have $x^2(t)\ge \delta _{1}$ [i.e., $-x^2(t)\le -\delta _{1}$], where $\delta _{1}$ is a positive constant. Thus, we have

$$\begin{aligned} \left( \frac{\partial \varepsilon _{1}}{\partial x} \right) ^2&= 4x^2(t)(x^{2}(t)-a)^2 \nonumber \\&\ge 4\delta _{1}(x^2(t)-a)^2=8\delta _{1}\varepsilon _{1}. \end{aligned}$$

(24)

Applying (23) and (24) yields

$$\begin{aligned} \dot{{\L }}_{1}(x(t))=\dot{\varepsilon _{1}}= - \gamma \left( \frac{\partial \varepsilon _{1}}{\partial x} \right) ^2 \le - 8 \gamma \delta _{1} \varepsilon _{1}. \end{aligned}$$

(25)

In this case, $\varepsilon _{1}\ne 0$, $\delta _{1} >0$, and $\gamma >0$. Let $\beta _{1}=8\gamma \delta _{1}>0$. Then, (25) can be simplified as

$$\begin{aligned} \dot{\varepsilon _{1}}(x(t))\le -\beta _{1}\varepsilon _{1}(x(t)). \end{aligned}$$

Thus, we have

$$\begin{aligned} {\L }_{1}(x(t))=\varepsilon _{1}(x(t)) \le \varepsilon _{1}(x(0))\hbox {exp}(-\beta _{1}t), \forall t\ge 0,\nonumber \\ \end{aligned}$$

(26)

which means that the energy function $\varepsilon _{1}$ exponentially converges to zero. That is, the EF (8) is exponentially convergent to zero.

Next, we prove the exponentially convergent property of the state $x(t)$ of $\hbox {NGDS}_{1}$ (14). By substituting (22) into (26), we obtain

$$\begin{aligned} \frac{1}{2} (x^2(t)-a)^2 \le \frac{1}{2} (x^2(0)-a)^2 \hbox {exp}(-\beta _{1}t), \end{aligned}$$

and further have

$$\begin{aligned} \Vert x^2(t)-a \Vert _2 \le \Vert x^2(0)-a\Vert _2\hbox {exp}\left( -\frac{1}{2} \beta _{1}t\right) . \end{aligned}$$

(27)

Note that (27) can also be rewritten as

$$\begin{aligned}&\Vert (x(t)-\sqrt{a})(x(t)+ \sqrt{a}) \Vert _2 \nonumber \\&\quad \le \Vert (x(0)\!- \!\sqrt{a})(x(0) \!+\! \sqrt{a})\Vert _2 \hbox {exp}\left( \!-\frac{1}{2} \beta _{1}t\right) \!.\qquad \end{aligned}$$

(28)

For (28), it can be discussed in the following two cases.

Case 1. If the given initial state $x(0)>0$, following from Lemma 3, we have $x(0)\ge x(t) \ge x^{*}= \sqrt{a}$ or $x(0)\le x(t)\le x^{*}= \sqrt{a}$. In this case, we can define a constant $\mu _{1}>0$ as

$$\begin{aligned} \mu _{1}=\!\left\| \frac{(x(0)+\! \sqrt{a})}{(x^*+\! \sqrt{a})} \right\| _2 \!\ge \! \left\| \frac{(x(0)+\! \sqrt{a})}{(x(t)+\! \sqrt{a})} \right\| _2\!>\! 0, \end{aligned}$$

or

$$\begin{aligned} \mu _{1}=\!\left\| \frac{(x(0)+\! \sqrt{a})}{(x(0)+\! \sqrt{a})} \right\| _2 \!\ge \! \left\| \frac{(x(0)+\! \sqrt{a})}{(x(t)+\! \sqrt{a})} \right\| _2\!>\!0. \end{aligned}$$

Thus, we have

$$\begin{aligned} \Vert x(t)-x^* \Vert _2 \le \mu _{1} \Vert x(0)- x^*\Vert _2 \hbox {exp}\left( -\frac{1}{2} \beta _{1}t\right) , \end{aligned}$$

which means that the state $x(t)$ of $\hbox {NGDS}_{1}$ (14) exponentially converges to the theoretical positive solution $x^{*}=\sqrt{a}$ of (5).

Case 2. If the given initial state $x(0)<0$, following from Lemma 3, then we have $x(0)\ge x(t) \ge x^{*}= -\sqrt{a}$ or $x(0)\le x(t)\le x^{*}= -\sqrt{a}$. In this case, the constant $\mu _{1}>0$ can be defined as another form

$$\begin{aligned} \mu _{1}= \left\| \frac{(x(0)- \sqrt{a})}{(x(0)- \sqrt{a})} \right\| _2\ge \left\| \frac{(x(0)- \sqrt{a})}{(x(t)- \sqrt{a})} \right\| _2> 0, \end{aligned}$$

or

$$\begin{aligned} \mu _{1}= \left\| \frac{(x(0)- \sqrt{a})}{(x^*- \sqrt{a})} \right\| _2\ge \left\| \frac{(x(0)- \sqrt{a})}{(x(t)- \sqrt{a})} \right\| _2> 0. \end{aligned}$$

Thus, we also have

$$\begin{aligned} \Vert x(t)-x^* \Vert _2 \le \mu _{1} \Vert x(0)- x^*\Vert _2 \hbox {exp}\left( -\frac{1}{2} \beta _{1}t\right) , \end{aligned}$$

which means that the state $x(t)$ of $\hbox {NGDS}_{1}$ (14) exponentially converges to the theoretical negative solution $x^{*}= -\sqrt{a}$ of (5).

Based on the above analysis, according to Theorem 1, we have the conclusion that $\hbox {NGDS}_{1}$ (14) processes the exponential convergence property. The proof is thus completed. $\square$

4.2 Exponential convergence analysis of $\hbox {NGDS}_{2}$

Based on the GDS design formula (1) and EF (9), we obtain the following $\hbox {NGDS}_{2}$ (15) for scalar square root finding. Besides, for $\hbox {NGDS}_{2}$ (15), we have the following exponentially convergent results.

Lemma 4

Consider (5) and GDS design formula (1). Starting from an initial state $x(0)\ne 0$, the state $x(t)$ of $\hbox {NGDS}_{2}$ (15) is bounded, specifically, lower-bounded and upper-bounded.

Proof

It can be generalized from the proof of Lemma 3. $\square$

Corollary 2

Consider positive constant $a\in R$ involved in the nonlinear Eq. (5). Starting from an initial state $x(0)\ne 0$, the state $x(t)$ of $\hbox {NGDS}_{2}$ (15) will not be zero

$$\begin{aligned} x(t)\ne 0, \forall t>0. \end{aligned}$$

Besides, if the initial state $x(0)>0$, the state of (15) satisfies $x(t)>0$. On the contrary, if the initial state $x(0)<0$, the state of (15) satisfies $x(t)<0$.

Based on Lemma 4 and Corollary 2, we have the following theorem about the exponential convergence result of $\hbox {NGDS}_{2}$ (15).

Theorem 3

Consider constant $a>0\in R$ involved in the nonlinear Eq. (5). Starting from an initial state $x(0)\ne 0$, $\hbox {NGDS}_{2}$ (15) possesses the exponential convergence property. That is, the EF (9) exponentially converges to zero, and the state $x(t)$ of (15) exponentially converges to the theoretical scalar square root $x^*$ of $a$.

Proof

To prove Theorem 3, we can use Lyapunov theory [35] as well. Let us define a Lyapunov function candidate as

$$\begin{aligned} {\L }_{2}(x(t))=\varepsilon _{2}= \frac{1}{2} \left( \frac{1}{x^2(t)}-\frac{1}{a} \right) ^2\ge 0, \end{aligned}$$

(29)

which can be discussed in the following two cases.

Case 1. :

If $\varepsilon _{2}= (1/x^2(t)-1/a)^2/2=0$, then $x(t)=x^*=\pm \sqrt{a}$. The solution of the nonlinear Eq. (5) is found.

Case 2. :

If $\varepsilon _{2}= (1/x^2(t)-1/a)^2/2>0$, then $x(t)\ne x^*=\pm \sqrt{a}$.

As for Case 2, we derive the time derivative of (29) as

$$\begin{aligned} \dot{{\L }}_{2}(x(t))&= \dot{\varepsilon _{2}}=\frac{\hbox {d}\varepsilon _{2}}{\hbox {d} t} =\frac{\partial \varepsilon _{2}}{\partial x}\frac{\hbox {d} x}{\hbox {d} t} =\frac{\partial \varepsilon _{2}}{\partial x}\dot{x}\nonumber \\&= -\gamma \left( \frac{\partial \varepsilon _{2}}{\partial x} \!\right) ^2\!\!. \end{aligned}$$

(30)

Following from Eq. (29), we obtain the first-order partial derivative of $\varepsilon _{2}$ with respect to $x$ as

$$\begin{aligned} \frac{\partial \varepsilon _{2}}{\partial x}=2\frac{x^2(t)-a}{ax^5(t)}, \end{aligned}$$

and we further have

$$\begin{aligned} \left( \frac{\partial \varepsilon _{2}}{\partial x} \right) ^2=4\frac{(x^{2}(t)-a)^2}{a^2x^{10}(t)}. \end{aligned}$$

In consideration of the corresponding Lemma 4 and Corollary 2, $\exists \zeta _{2}>0$, $\forall x(t)$, we have $x^2(t)\le \zeta _{2}$ [i.e., $-x^2(t)\ge -\zeta _{2}$] with $\zeta _{2}$ being a positive constant. Thus, we further have

$$\begin{aligned} \left( \frac{\partial \varepsilon _{2}}{\partial x} \right) ^2&= 4\frac{(x^{2}(t)-a)^2}{a^2x^{10}(t)} \nonumber \\&\ge 4\frac{(x^{2}(t)-a)^2}{a^{2}x^{4}(t)\zeta _{2}^{3}} = 8\frac{\varepsilon _{2}}{\zeta _{2}^{3}}. \end{aligned}$$

(31)

Applying (30) and (31) yields

$$\begin{aligned} \dot{{\L }}_{2}(x(t))&= \dot{\varepsilon _{2}}= - \gamma \left( \frac{\partial \varepsilon _{2}}{\partial x} \right) ^2\nonumber \\&\le - 8 \gamma \frac{\varepsilon _{2}}{\zeta _{2}^{3}}. \end{aligned}$$

(32)

In this case, $\varepsilon _{2}\ne 0$, $\zeta _{2} >0$, and $\gamma >0$. Let $\beta _{2}=8 \gamma /\zeta _{2}^{3}>0$. Then, (32) can be simplified as

$$\begin{aligned} \dot{\varepsilon _{2}}(x(t))\le -\beta _{2} \varepsilon _{2}(x(t)). \end{aligned}$$

Thus, we have

$$\begin{aligned} {\L }_{2}(x(t))=\varepsilon _{2}(x(t)) \le \varepsilon _{2}(x(0))\hbox {exp}(-\beta _{2}t), \forall t\ge 0,\nonumber \\ \end{aligned}$$

(33)

which means that the energy function $\varepsilon _{2}$ exponentially converges to zero. That is, EF (9) is exponentially convergent to zero.

Next, we prove the exponentially convergent property of the state $x(t)$ of $\hbox {NGDS}_{2}$ (15). By substituting (29) into (33), we obtain

$$\begin{aligned} \frac{1}{2} \left( \frac{1}{x^2(t)}-\frac{1}{a} \right) ^2 \le \frac{1}{2} \left( \frac{1}{x^2(0)}-\frac{1}{a} \right) ^2 \hbox {exp}(-\beta _{2}t), \end{aligned}$$

which can be simplified as

$$\begin{aligned} \left\| \frac{x^2(t)-a}{x^{2}(t)} \right\| _2 \le \left\| \frac{x^2(0)-a}{x^{2}(0)} \right\| _2 \hbox {exp}(-\frac{1}{2} \beta _{2}t). \end{aligned}$$

(34)

Note that (34) can be further rewritten as

$$\begin{aligned}&\left\| \frac{(x(t)-\sqrt{a})(x(t)+ \sqrt{a})}{x^{2}(t)} \right\| _2\nonumber \\&\quad \le \left\| \frac{(x(0)- \sqrt{a})(x(0)+ \sqrt{a})}{{x^{2}(0)}} \right\| _2 \hbox {exp}(-\frac{1}{2} \beta _{2}t). \nonumber \\ \end{aligned}$$

(35)

For (35), it can be discussed in the following two cases.

Case 1. If the given initial state $x(0)>0$, following from Lemma 4, then we have $x(0)\ge x(t) \ge x^{*}= \sqrt{a}$ or $x(0)\le x(t)\le x^{*}= \sqrt{a}$. In this case, we can define a constant $\mu _{2}>0$ as

$$\begin{aligned} \mu _{2}&= \left\| \frac{ x^{2}(0)(x(0)+ \sqrt{a})}{x^{2}(0)(x^*+ \sqrt{a})} \right\| _2\\&\ge \left\| \frac{ x^{2}(t)(x(0)+ \sqrt{a})}{x^{2}(0)(x(t)+ \sqrt{a})} \right\| _2 > 0, \end{aligned}$$

or

$$\begin{aligned} \mu _{2}&= \left\| \frac{ {x^*}^{2}(x(0)+ \sqrt{a})}{x^{2}(0)(x(0)+ \sqrt{a})} \right\| _2 \\&\ge \left\| \frac{ x^{2}(t)(x(0)+ \sqrt{a})}{x^{2}(0)(x(t)+ \sqrt{a})} \right\| _2 > 0. \end{aligned}$$

Thus, we have

$$\begin{aligned} \Vert x(t)-x^* \Vert _2 \le \mu _{2} \Vert x(0)- x^*\Vert _2 \hbox {exp}(-\frac{1}{2} \beta _{2}t), \end{aligned}$$

which means that the state $x(t)$ of $\hbox {NGDS}_{2}$ (15) exponentially converges to the theoretical positive solution $x^{*}=\sqrt{a}$ of (5).

Case 2. If the given initial state $x(0)<0$, following from Lemma 4, then we have $x(0)\ge x(t) \ge x^{*}= -\sqrt{a}$ or $x(0)\le x(t)\le x^{*}= -\sqrt{a}$. In this case, the constant $\mu _{2}>0$ can be defined as another form

$$\begin{aligned} \mu _{2}&= \left\| \frac{ { x^*}^{2}(x(0)- \sqrt{a})}{x^{2}(0)(x(0)- \sqrt{a})} \right\| _2\\&\ge \left\| \frac{ x^{2}(t)(x(0)- \sqrt{a})}{x^{2}(0)(x(t)- \sqrt{a})} \right\| _2 > 0, \end{aligned}$$

or

$$\begin{aligned} \mu _{2}&= \left\| \frac{ x^{2}(0)(x(0)- \sqrt{a})}{x^{2}(0)(x^*- \sqrt{a})} \right\| _2 \\&\ge \left\| \frac{ x^{2}(t)(x(0)- \sqrt{a})}{x^{2}(0)(x(t)- \sqrt{a})} \right\| _2 > 0. \end{aligned}$$

Thus, we also have

$$\begin{aligned} \Vert x(t)-x^* \Vert _2 \le \mu _{2} \Vert x(0)- x^*\Vert _2 \hbox {exp}(-\frac{1}{2} \beta _{2}t), \end{aligned}$$

which means that the state $x(t)$ of $\hbox {NGDS}_{2}$ (15) exponentially converges to the theoretical negative solution $x^{*}=-\sqrt{a}$ of (5).

Based on the above analysis, according to Theorem 1, we have the conclusion that $\hbox {NGDS}_{2}$ (15) processes the exponential convergence property. The proof is thus completed. $\square$

4.3 Exponential convergence analysis of $\hbox {NGDS}_{3}$

With the GDS design formula (1) and EF (10) exploited, $\hbox {NGDS}_{3}$ (16) is established for scalar square root finding.

Lemma 5

Consider (5) and GDS design formula (1). Starting from an initial state $x(0)\ne 0$, the state $x(t)$ of $\hbox {NGDS}_{3}$ (16) is bounded, specifically, lower-bounded and upper-bounded.

Corollary 3

Consider a positive constant $a\in R$ involved in the nonlinear Eq. (5). Starting from an initial state $x(0)\ne 0$, the state $x(t)$ of $\hbox {NGDS}_{3}$ (16) will not be zero

$$\begin{aligned} x(t)\ne 0, \forall t>0. \end{aligned}$$

Besides, if the initial state $x(0)>0$, the state of (16) satisfies $x(t)>0$. On the contrary, if the initial state $x(0)<0$, the state of (16) satisfies $x(t)<0$.

In addition, we have the following theorem about the exponentially convergent result of $\hbox {NGDS}_{3}$ (16).

Theorem 4

Consider constant $a>0\in R$ involved in the nonlinear Eq. (5). Starting from an initial state $x(0)$, $\hbox {NGDS}_{3}$ (16) possesses the exponential convergence property. That is, EF (10) exponentially converges to zero, and the state $x(t)$ of (16) exponentially converges to the theoretical scalar square root $x^*$ of $a$.

Proof

To prove Theorem 4, we can reuse Lyapunov theory [35]. Let us define a Lyapunov function candidate as

$$\begin{aligned} {\L }_{3}(x(t))=\varepsilon _{3}=\frac{1}{2} \left( \frac{x^2(t)}{a}-1 \right) ^2\ge 0, \end{aligned}$$

(36)

which can be discussed in the following two cases.

Case 1. :

If $\varepsilon _{3}= (x^2(t)/a-1)^2/2=0$, then $x(t)=x^*=\pm \sqrt{a}$. The solution of the nonlinear Eq. (5) is found.

Case 2. :

If $\varepsilon _{3}= (x^2(t)/a-1)^2/2>0$, then $x(t)\ne x^*=\pm \sqrt{a}$.

As for Case 2, we derive the time derivative of (36) as

$$\begin{aligned} \dot{{\L }}_{3}(x(t))&= \dot{\varepsilon _{3}}=\frac{\hbox {d}\varepsilon _{3}}{\hbox {d} t} =\frac{\partial \varepsilon _{3}}{\partial x}\frac{\hbox {d} x}{\hbox {d} t} = \frac{\partial \varepsilon _{3}}{\partial x}\dot{x}\nonumber \\&= -\gamma \left( \frac{\partial \varepsilon _{3}}{\partial x} \right) ^2. \end{aligned}$$

(37)

Based on (36), we obtain the following first-order partial derivative of $\varepsilon _{3}$ with respect to $x$:

$$\begin{aligned} \frac{\partial \varepsilon _{3}}{\partial x}=2\frac{x(t)}{a}\left( \frac{x^2(t)}{a}-1\right) , \end{aligned}$$

and we further have

$$\begin{aligned} \left( \frac{\partial \varepsilon _{3}}{\partial x} \right) ^2=4\frac{x^2(t)}{a^2}\left( \frac{x^2(t)}{a}-1\right) ^2. \end{aligned}$$

In view of the corresponding Lemma 5 and Corollary 3, $\exists \delta _{3}>0$, $\forall x(t)$, we have $x^2(t)\ge \delta _{3}$ [i.e., $-x^2(t)\le -\delta _{3}$], where $\delta _{3}$ is a constant. Therefore, we further have

$$\begin{aligned} \left( \frac{\partial \varepsilon _{3}}{\partial x} \right) ^2&= 4\frac{x^2(t)}{a^2}\left( \frac{x^2(t)}{a}-1\right) ^2 \\&\ge 4\delta _{3}\frac{(x^2(t)-a)^2}{a^4} = 8\frac{\delta _{3}}{a^{2}}\varepsilon _{3}. \end{aligned}$$

It follows from (37) that

$$\begin{aligned} \dot{{\L }}_{3}(x(t))&= \dot{\varepsilon _{3}}= - \gamma \left( \frac{\partial \varepsilon _{3}}{\partial x} \right) ^2\nonumber \\&\le - 8 \gamma \frac{\delta _{3}}{a^{2}}\varepsilon _{3}. \end{aligned}$$

(38)

In this case, $\varepsilon _{3}\ne 0$, $\delta _{3} >0$, and $\gamma >0$. Let $\beta _{3}=8 \gamma \delta _{3}/a^{2}>0$. Then, (38) can be simplified as

$$\begin{aligned} \dot{\varepsilon _{3}}(x(t))\le -\beta _{3}\varepsilon _{3}(x(t)). \end{aligned}$$

Consequently, we have

$$\begin{aligned} {\L }_{3}(x(t))=\varepsilon _{3}(x(t)) \le \varepsilon _{3}(x(0))\hbox {exp}(-\beta _{3}t), \forall t\ge 0,\nonumber \\ \end{aligned}$$

(39)

which means that the energy function $\varepsilon _{3}$ exponentially converges to zero. That is, EF (10) is exponentially convergent to zero.

Next, we prove the exponentially convergent property of the state $x(t)$ of $\hbox {NGDS}_{3}$ (16). By substituting (36) into (39), we obtain

$$\begin{aligned} \frac{1}{2} \left( \frac{x^2(t)}{a}-1 \right) ^2 \le \frac{1}{2} \left( \frac{x^2(0)}{a}-1 \right) ^2 \hbox {exp}(-\beta _{3}t), \end{aligned}$$

which can be simplified as

$$\begin{aligned} \Vert x^2(t)-a \Vert _2 \le \Vert x^2(0)-a\Vert _2 \hbox {exp}\left( -\frac{1}{2} \beta _{3}t\right) . \end{aligned}$$

(40)

Note that (40) can be also rewritten as

$$\begin{aligned}&\Vert (x(t)-\sqrt{a})(x(t)+ \sqrt{a}) \Vert _2 \le \Vert (x(0)- \sqrt{a})(x(0)\nonumber \\&\quad + \sqrt{a})\Vert _2 \hbox {exp}\left( -\frac{1}{2} \beta _{3}t\right) . \end{aligned}$$

(41)

For (41), it can be discussed in the following two cases.

Case 1. If the given initial state $x(0)>0$, following from Lemma 5, then we have $x(0)\ge x(t) \ge x^{*}= \sqrt{a}$ or $x(0)\le x(t)\le x^{*}= \sqrt{a}$. In this case, we can define a constant $\mu _{3}>0$ as

$$\begin{aligned} \mu _{3}= \left\| \frac{(x(0)+ \sqrt{a})}{(x^*+ \sqrt{a})}\right\| _2 \ge \left\| \frac{(x(0)+ \sqrt{a})}{(x(t)+ \sqrt{a})}\right\| _2 > 0, \end{aligned}$$

or

$$\begin{aligned} \mu _{3}= \left\| \frac{(x(0)+ \sqrt{a})}{(x(0)+ \sqrt{a})}\right\| _2 \ge \left\| \frac{(x(0)+ \sqrt{a})}{(x(t)+ \sqrt{a})}\right\| _2 > 0. \end{aligned}$$

Thus, we have

$$\begin{aligned} \Vert x(t)-x^* \Vert _2 \le \mu _{3} \Vert x(0)- x^*\Vert _2 \hbox {exp}\left( -\frac{1}{2} \beta _{3}t\right) , \end{aligned}$$

which means that the state $x(t)$ of $\hbox {NGDS}_{3}$ (16) exponentially converges to the theoretical positive solution $x^{*}=\sqrt{a}$ of (5).

Case 2. If the given initial state $x(0)<0$, following from Lemma 5, then we have $x(0)\ge x(t) \ge x^{*}= -\sqrt{a}$ or $x(0)\le x(t)\le x^{*}= -\sqrt{a}$. In this case, the constant $\mu _{3}>0$ can be defined as another form

$$\begin{aligned} \mu _{3}= \left\| \frac{(x(0)- \sqrt{a})}{(x(0)- \sqrt{a})}\right\| _2 \ge \left\| \frac{(x(0)- \sqrt{a})}{(x(t)- \sqrt{a})}\right\| _2 > 0, \end{aligned}$$

or

$$\begin{aligned} \mu _{3}= \left\| \frac{(x(0)- \sqrt{a})}{(x^*- \sqrt{a})}\right\| _2 \ge \left\| \frac{(x(0)- \sqrt{a})}{(x(t)- \sqrt{a})}\right\| _2 > 0. \end{aligned}$$

Thus, we have

$$\begin{aligned} \Vert x(t)-x^* \Vert _2 \le \mu _{3} \Vert x(0)- x^*\Vert _2 \hbox {exp}\left( -\frac{1}{2} \beta _{3}t\right) , \end{aligned}$$

which means that the state $x(t)$ of $\hbox {NGDS}_{3}$ (16) exponentially converges to the theoretical negative solution $x^{*}=-\sqrt{a}$ of (5).

Based on the above analysis, according to Theorem 1, we have the conclusion that $\hbox {NGDS}_{3}$ (16) processes the exponential convergence property. The proof is thus completed. $\square$

4.4 Exponential convergence analysis of $\hbox {NGDS}_{4}$

Following from GDS design formula (1) and EF (11), we have the $\hbox {NGDS}_{4}$ (17) for scalar square root finding.

Lemma 6

Consider (5) and GDS design formula (1). Starting from an initial state $x(0)\ne 0$, the state $x(t)$ of $\hbox {NGDS}_{4}$ (17) is bounded, specifically, lower-bounded and upper-bounded.

Corollary 4

Consider positive constant $a\in R$ involved in the nonlinear Eq. (5). Starting from an initial state $x(0)\ne 0$, the state $x(t)$ of $\hbox {NGDS}_{4}$ (17) will not be zero

$$\begin{aligned} x(t)\ne 0, \forall t>0. \end{aligned}$$

Besides, if the initial state $x(0)>0$, the state of (17) satisfies $x(t)>0$. On the contrary, if the initial state $x(0)<0$, the state of (17) satisfies $x(t)<0$.

In addition, we have the following theorem about the exponentially convergent result of $\hbox {NGDS}_{4}$ (17).

Theorem 5

Consider constant $a>0\in R$ involved in the nonlinear Eq. (5). Starting from an initial state $x(0)\ne 0$, $\hbox {NGDS}_{4}$ (17) possesses the exponential convergence property. That is, EF (11) exponentially converges to zero, and the state $x(t)$ of (17) exponentially converges to the theoretical scalar square root $x^*$ of $a$.

Proof

Similarly, we can define a Lyapunov function candidate as

$$\begin{aligned} {\L }_{4}(x(t))=\varepsilon _{4}=\frac{1}{2} \left( \frac{a}{x^2(t)}-1\right) ^2\ge 0, \end{aligned}$$

(42)

which can be discussed in the following two cases.

Case 1. If $\varepsilon _{4}= (a/x^2(t)-1)^2/2=0$, then $x(t)=x^*=\pm \sqrt{a}$. The solution of the nonlinear Eq. (5) is found.

Case 2. If $\varepsilon _{4}= (a/x^2(t)-1)^2/2>0$, then $x(t)\ne x^*=\pm \sqrt{a}$.

As for Case 2, we derive the time derivative of (42) as

$$\begin{aligned} \dot{{\L }}_{4}(x(t))&= \dot{\varepsilon _{4}}=\frac{\hbox {d} \varepsilon _{4}}{\hbox {d} t} =\frac{\partial \varepsilon _{4}}{\partial x}\frac{\hbox {d} x}{\hbox {d} t} = \frac{\partial \varepsilon _{4}}{\partial x}\dot{x}\nonumber \\&= -\gamma \left( \frac{\partial \varepsilon _{4}}{\partial x} \right) ^2. \end{aligned}$$

(43)

Following from (42), we obtain the first-order partial derivative of $\varepsilon _{4}$ with respect to as

$$\begin{aligned} \frac{\partial \varepsilon _{4}}{\partial x}=2a \frac{x^2(t)-a}{x^5(t)}, \end{aligned}$$

and we further have

$$\begin{aligned} \left( \frac{\partial \varepsilon _{4}}{\partial x} \right) ^2=4a^2\frac{(x^2(t)-a)^2}{x^{10}(t)}. \end{aligned}$$

Considering the corresponding Lemma 6 and Corollary 4, $\exists \zeta _{4}>0$, $\forall x(t)$, we have $x^2(t)\le \zeta _{4}$ [i.e., $-x^2(t)\ge -\zeta _{4}$], where $\zeta _{4}$ is a positive constant. Thus, we further have

$$\begin{aligned} \left( \frac{\partial \varepsilon _{4}}{\partial x} \right) ^2&= 4a^2\frac{(x^2(t)-a)^2}{x^{10}(t)} \nonumber \\&\ge 4a^2\frac{(x^2(t)-a)^2}{\zeta _{4}^{3}x^{4}(t)} = 8\frac{a^2\varepsilon _{4}}{\zeta _{4}^{3}}. \end{aligned}$$

(44)

Applying (42) and (44) yields

$$\begin{aligned} \dot{{\L }}_{4}(x(t))&= \dot{\varepsilon _{4}}= - \gamma \left( \frac{\partial \varepsilon _{4}}{\partial x} \right) ^2\nonumber \\&\le - 8 \gamma \frac{a^2\varepsilon _{4}}{\zeta _{4}^{3}}. \end{aligned}$$

(45)

In this case, $\varepsilon _{4}\ne 0$, $\zeta _{4} >0$, and $\gamma >0$. Let $\beta _{4}=8 \gamma a^2 / \zeta _{4}^{3}>0$. Then, (45) can be simplified as

$$\begin{aligned} \dot{\varepsilon _{4}}(x(t))\le -\beta _{4}\varepsilon _{4}(x(t)). \end{aligned}$$

Thus, we have

$$\begin{aligned} {\L }_{4}(x(t))=\varepsilon _{4}(x(t)) \le \varepsilon _{4}(x(0))\hbox {exp}(-\beta _{4}t), \forall t\ge 0,\nonumber \\ \end{aligned}$$

(46)

which means that the energy function $\varepsilon _{4}$ exponentially converges to zero. That is, EF (11) is exponentially convergent to zero.

Next, we prove the exponentially convergent property of the state $x(t)$ of $\hbox {NGDS}_{4}$ (17). By substituting (42) into (46), we obtain

$$\begin{aligned} \frac{1}{2} \left( \frac{a}{x^2(t)}-1\right) ^2 \le \frac{1}{2} \left( \frac{a}{x^2(0)}-1\right) ^2 \hbox {exp}(-\beta _{4}t), \end{aligned}$$

which can be simplified as

$$\begin{aligned} \left\| \frac{x^2(t)-a}{x^{2}(t)} \right\| _2 \le \left\| \frac{x^2(0)-a}{x^{2}(0)} \right\| _2 \hbox {exp}\left( -\frac{1}{2} \beta _{4}t\right) . \end{aligned}$$

(47)

Note that (47) can be further rewritten as

$$\begin{aligned}&\left\| \frac{(x(t)-\sqrt{a})(x(t)+ \sqrt{a})}{x^{2}(t)} \right\| _2\nonumber \\&\quad \le \left\| \frac{(x(0)- \sqrt{a})(x(0)+ \sqrt{a})}{{x^{2}(0)}} \right\| _2 \hbox {exp}\left( -\frac{1}{2} \beta _{4}t\right) .\nonumber \\ \end{aligned}$$

(48)

For (48), it can be discussed in the following two cases.

Case 1. If the given initial state $x(0)>0$, following from Lemma 6, then we have $x(0)\ge x(t) \ge x^{*}= \sqrt{a}$ or $x(0)\le x(t)\le x^{*}= \sqrt{a}$. In this case, we can define a constant $\mu _{4}>0$ as

$$\begin{aligned} \mu _{4}&= \left\| \frac{ x^{2}(0)(x(0)+ \sqrt{a})}{x^{2}(0)(x^*+ \sqrt{a})}\right\| _2\\&\ge \left\| \frac{ x^{2}(t)(x(0)+ \sqrt{a})}{x^{2}(0)(x(t)+ \sqrt{a})}\right\| _2 > 0, \end{aligned}$$

or

$$\begin{aligned} \mu _{4}&= \left\| \frac{ {x^*}^{2}(x(0)+ \sqrt{a})}{x^{2}(0)(x(0)+ \sqrt{a})}\right\| _2\\&\ge \left\| \frac{ x^{2}(t)(x(0)+ \sqrt{a})}{x^{2}(0)(x(t)+ \sqrt{a})}\right\| _2 > 0, \end{aligned}$$

Therefore, we have

$$\begin{aligned} \Vert x(t)-x^* \Vert _2 \le \mu _{4} \Vert x(0)- x^*\Vert _2 \hbox {exp}\left( -\frac{1}{2} \beta _{4}t\right) , \end{aligned}$$

which means that the state $x(t)$ of $\hbox {NGDS}_{4}$ (17) exponentially converges to the theoretical positive solution $x^{*}=\sqrt{a}$ of (5).

Case 2. If the given initial state $x(0)<0$, following from Lemma 6, then we have $x(0)\ge x(t) \ge x^{*}= -\sqrt{a}$ or $x(0)\le x(t)\le x^{*}= -\sqrt{a}$. In this case, $\exists \mu _{4}>0$, which can be defined as another form

$$\begin{aligned} \mu _{4}&= \left\| \frac{ {x^*}^{2}(x(0)- \sqrt{a})}{x^{2}(0)(x(0)- \sqrt{a})}\right\| _2\\&\ge \left\| \frac{ x^{2}(t)(x(0)- \sqrt{a})}{x^{2}(0)(x(t)- \sqrt{a})}\right\| _2 > 0, \end{aligned}$$

or

$$\begin{aligned} \mu _{4}&= \left\| \frac{ x^{2}(0)(x(0)- \sqrt{a})}{x^{2}(0)(x^*- \sqrt{a})}\right\| _2\\&\ge \left\| \frac{ x^{2}(t)(x(0)- \sqrt{a})}{x^{2}(0)(x(t)- \sqrt{a})}\right\| _2 > 0. \end{aligned}$$

As a result, we have

$$\begin{aligned} \Vert x(t)-x^* \Vert _2 \le \mu _{4} \Vert x(0)- x^*\Vert _2 \hbox {exp}\left( -\frac{1}{2} \beta _{4}t\right) , \end{aligned}$$

which means that the state $x(t)$ of $\hbox {NGDS}_{4}$ (17) exponentially converges to the theoretical negative solution $x^{*}=-\sqrt{a}$ of (5).

Based on the above analysis, according to Theorem 1, we have the conclusion that $\hbox {NGDS}_{4}$ (17) processes the exponential convergence property. The proof is thus completed. $\square$

4.5 Exponential convergence analysis of $\hbox {NGDS}_{5}$

With $\hbox {NGDS}_{5}$ design formula (1) and EF (12) exploited, the following $\hbox {NGDS}_{5}$ (18) is established for scalar square root finding.

Lemma 7

Consider (5) and GDS design formula (1). Starting from an initial state $x(0)\ne 0$, the state $x(t)$ of $\hbox {NGDS}_{5}$ (18) is bounded, specifically, lower-bounded and upper-bounded.

Corollary 5

Consider positive constant $a\in R$ involved in the nonlinear Eq. (5). Starting from an initial state $x(0)\ne 0$, the state $x(t)$ of $\hbox {NGDS}_{5}$ (15) will not be zero

$$\begin{aligned} x(t)\ne 0,\quad \forall t>0. \end{aligned}$$

Besides, if the initial state $x(0)>0$, the state of (18) satisfies $x(t)>0$. On the contrary, if the initial state $x(0)<0$, the state of (18) satisfies $x(t)<0$.

In addition, we have the following theorem about the exponentially convergent result of $\hbox {NGDS}_{5}$ (18).

Theorem 6

Consider constant $a>0\in R$ involved in the nonlinear Eq. (5). Starting from an initial state $x(0)$, $\hbox {NGDS}_{5}$ (18) possesses the exponential convergence property. That is, EF (12) exponentially converges to zero, and the state $x(t)$ of (18) exponentially converges to the theoretical scalar square root $x^*$ of $a$.

Proof

Let us define a Lyapunov function candidate as

$$\begin{aligned} {\L }_{5}(x(t))=\varepsilon _{5}=\frac{1}{2} \left( x(t)-\frac{a}{x(t)}\right) ^2\ge 0, \end{aligned}$$

(49)

which can be discussed in the following two cases.

Case 1. :

If $\varepsilon _{5}= (x(t)-a/x(t))^2/2=0$, then $x(t)=x^*=\pm \sqrt{a}$. The solution of the nonlinear Eq. (5) is found.

Case 2. :

If $\varepsilon _{5}= (x(t)-a/x(t))^2/2>0$, then $x(t)\ne x^*=\pm \sqrt{a}$.

As for Case 2, we derive the time derivative of (49) as

$$\begin{aligned} \dot{{\L }}_{5}(x(t))&= \dot{\varepsilon _{5}}=\frac{\hbox {d}\varepsilon _{5}}{\hbox {d} t} =\frac{\partial \varepsilon _{5}}{\partial x}\frac{\hbox {d} x}{\hbox {d} t} = \frac{\partial \varepsilon _{5}}{\partial x}\dot{x}\nonumber \\&= -\gamma \left( \frac{\partial \varepsilon _{5}}{\partial x} \right) ^2. \end{aligned}$$

(50)

Following from (49), we obtain the first-order partial derivative of $\varepsilon _{5}$ with respect to $x$ as

$$\begin{aligned} \frac{\partial \varepsilon _{5}}{\partial x}=\frac{(x^2(t)-a)(x^2(t)+a)}{x^3(t)}, \end{aligned}$$

and we further have

$$\begin{aligned} \left( \frac{\partial \varepsilon _{5}}{\partial x} \right) ^2=\frac{(x^2(t)-a)^{2}(x^2(t)+a)^{2}}{x^6(t)}. \end{aligned}$$

Considering Lemma 7 and Corollary 5, $\exists \eta _{5}>1$, $\forall x(t)$, we have

$$\begin{aligned} \eta _{5}\le \frac{(x^2(t)+a)^{2}}{x^4(t)}, \end{aligned}$$

where $\eta _{5}>1$ is a constant. Thus, we further have

$$\begin{aligned} \left( \frac{\partial \varepsilon _{5}}{\partial x} \right) ^2&= \frac{(x^2(t)-a)^{2}(x^2(t)+a)^{2}}{x^6(t)} \nonumber \\&\ge \frac{(x^2(t)-a)^{2}\eta _{5}}{x^2(t)} = 2\eta _{5}\varepsilon _{5}. \end{aligned}$$

(51)

Applying (50) and (51) yields

$$\begin{aligned} \dot{{\L }}_{5}(x(t))&= \dot{\varepsilon _{5}}= - \gamma \left( \frac{\partial \varepsilon _{5}}{\partial x} \right) ^2\nonumber \\&\le - 2 \gamma \eta _{5}\varepsilon _{5}. \end{aligned}$$

(52)

In this case, $\varepsilon _{5}\ne 0$, $\eta _{5} >0$ and $\gamma >0$. Let $\beta _{5}= 2 \gamma \eta _{5}>0$. Then, (52) can be simplified as

$$\begin{aligned} \dot{\varepsilon _{5}}(x(t))\le -\beta _{5}\varepsilon _{5}(x(t)). \end{aligned}$$

Thus, we have

$$\begin{aligned} {\L }_{5}(x(t))=\varepsilon _{5}(x(t)) \le \varepsilon _{5}(x(0))\hbox {exp}(-\beta _{5}t), \forall t\ge 0,\nonumber \\ \end{aligned}$$

(53)

which means that the energy function $\varepsilon _{5}$ exponentially converges to zero. That is, EF (12) is exponentially convergent to zero.

Next, let us prove the exponentially convergent property of the state $x(t)$ of $\hbox {NGDS}_{4}$ (17). By substituting (49) into (53), we obtain

$$\begin{aligned} \frac{1}{2} \left( x(t)-\frac{a}{x(t)}\right) ^2 \le \frac{1}{2} \left( x(0)-\frac{a}{x(0)}\right) ^2 \hbox {exp}(-\beta _{5}t), \end{aligned}$$

which can be simplified as

$$\begin{aligned} \left\| \frac{x^2(t)-a}{x(t)} \right\| _2 \le \left\| \frac{x^2(0)-a}{x(0)} \right\| _2 \hbox {exp}\left( -\frac{1}{2} \beta _{5}t\right) . \end{aligned}$$

(54)

Note that (54) can be also rewritten as

$$\begin{aligned}&\left\| \frac{(x(t)-\sqrt{a})(x(t)+ \sqrt{a})}{x(t)} \right\| _2 \nonumber \\&\quad \le \left\| \frac{(x(0)- \sqrt{a})(x(0)+ \sqrt{a})}{{x(0)}} \right\| _2 \hbox {exp}\left( -\frac{1}{2} \beta _{5}t\right) .\nonumber \\ \end{aligned}$$

(55)

For (55), it can be discussed in the following two cases.

Case 1. If the given initial state $x(0)>0$, following from Lemma 7, then we have $x(0)\ge x(t) \ge x^{*}= \sqrt{a}$ or $x(0)\le x(t)\le x^{*}= \sqrt{a}$. In this case, we can define a constat $\mu _{5}>0$ as

$$\begin{aligned} \begin{aligned} \mu _{5}&=\left\| \frac{ x(0)(x(0)+ \sqrt{a})}{x(0)(x^*+ \sqrt{a})}\right\| _2 \ge \left\| \frac{ x(t)(x(0)+ \sqrt{a})}{x(0)(x(t)+ \sqrt{a})}\right\| _2\\&> 0, \end{aligned} \end{aligned}$$

or

$$\begin{aligned} \begin{aligned} \mu _{5}&=\left\| \frac{ x^*(x(0)+ \sqrt{a})}{x(0)(x(0)+ \sqrt{a})}\right\| _2 \ge \left\| \frac{ x(t)(x(0)+ \sqrt{a})}{x(0)(x(t)+ \sqrt{a})}\right\| _2\\&> 0. \end{aligned} \end{aligned}$$

Thus, we have

$$\begin{aligned} \Vert x(t)-x^* \Vert _2 \le \mu _{5} \Vert x(0)- x^*\Vert _2 \hbox {exp}\left( -\frac{1}{2} \beta _{5}t\right) , \end{aligned}$$

which means that the state $x(t)$ of $\hbox {NGDS}_{5}$ (18) exponentially converges to the theoretical positive solution $x^{*}=\sqrt{a}$ of (5).

Case 2. If the given initial state $x(0)<0$, following from Lemma 7, then we have $x(0)\ge x(t) \ge x^{*}= -\sqrt{a}$ or $x(0)\le x(t)\le x^{*}= -\sqrt{a}$. In this case, the constant $\mu _{5}>0$ can be defined as another form

$$\begin{aligned} \begin{aligned} \mu _{5}&=\left\| \frac{ x^*(x(0)- \sqrt{a})}{x(0)(x(0)- \sqrt{a})}\right\| _2 \ge \left\| \frac{ x(t)(x(0)- \sqrt{a})}{x(0)(x(t)- \sqrt{a})}\right\| _2\\&> 0, \end{aligned} \end{aligned}$$

or

$$\begin{aligned} \begin{aligned} \mu _{5}&=\left\| \frac{ x(0)(x(0)- \sqrt{a})}{x(0)(x^*- \sqrt{a})}\right\| _2 \ge \left\| \frac{ x(t)(x(0)- \sqrt{a})}{x(0)(x(t)- \sqrt{a})}\right\| _2\\&> 0. \end{aligned} \end{aligned}$$

Thus, we have

$$\begin{aligned} \Vert x(t)-x^* \Vert _2 \le \mu _{5} \Vert x(0)- x^*\Vert _2 \hbox {exp}\left( -\frac{1}{2} \beta _{5}t\right) , \end{aligned}$$

which means that the state $x(t)$ of $\hbox {NGDS}_{5}$ (18) exponentially converges to the theoretical negative solution $x^{*}=-\sqrt{a}$ of (5).

Based on the above analysis, according to Theorem 1, we have the conclusion that $\hbox {NGDS}_{5}$ (18) processes the exponential convergence property. The proof is thus completed. $\square$

4.6 Exponential convergence analysis of $\hbox {NGDS}_{6}$

Similar to the analysis of $\hbox {NGDS}_{5}$ (18), based on EF (13), we obtain $\hbox {NGDS}_{6}$ (19) for scalar square root finding.

Lemma 8

Consider (5) and GDS design formula (1). Starting from an initial state $x(0)\ne 0$, the state $x(t)$ of $\hbox {NGDS}_{6}$ (19) is bounded, specifically, lower-bounded and upper-bounded.

Corollary 6

Consider positive constant $a\in R$ involved in the nonlinear Eq. (5). Starting from an initial state $x(0)\ne 0$, the state $x(t)$ of $\hbox {NGDS}_{6}$ (19) will not be zero

$$\begin{aligned} x(t)\ne 0, \forall t>0. \end{aligned}$$

Besides, if the initial state $x(0)>0$, the state of (19) satisfies $x(t)>0$. On the contrary, if the initial state $x(0)<0$, the state of (19) satisfies $x(t)<0$.

In addition, we have the following theorem about the exponentially convergent result of $\hbox {NGDS}_{6}$ (19).

Theorem 7

Consider constant $a>0\in R$ involved in the nonlinear Eq. (5). Starting from an initial state $x(0)$, $\hbox {NGDS}_{6}$ (19) possesses the exponential convergence property. That is, EF (13) exponentially converges to zero, and the state $x(t)$ of (19) exponentially converges to the theoretical scalar square root $x^*$ of $a$.

Proof

Let us define a Lyapunov function candidate as

$$\begin{aligned} {\L }_{6}(x(t))=\varepsilon _{6}=\frac{1}{2} \left( \frac{x(t)}{a}-\frac{1}{x(t)}\right) ^2\ge 0, \end{aligned}$$

(56)

which can be discussed in the following two cases.

Case 1. :

If $\varepsilon _{6}= (x(t)/a-1/x(t))^2/2=0$, then $x(t)=x^*=\pm \sqrt{a}$. The solution of the nonlinear Eq. (5) is found.

Case 2. :

If $\varepsilon _{6}= (x(t)/a-1/x(t))^2/2>0$, then $x(t)\ne x^*=\pm \sqrt{a}$.

As for Case 2, we derive the time derivative of (56) as

$$\begin{aligned} \dot{{\L }}_{6}(x(t))&= \dot{\varepsilon _{6}}=\frac{\hbox {d}\varepsilon _{6}}{\hbox {d} t} =\frac{\partial \varepsilon _{6}}{\partial x}\frac{\hbox {d} x}{\hbox {d} t} = \frac{\partial \varepsilon _{6}}{\partial x}\dot{x}\nonumber \\&= -\gamma \left( \frac{\partial \varepsilon _{6}}{\partial x} \right) ^2. \end{aligned}$$

(57)

Following from (56), we obtain the first-order partial derivative of $\varepsilon _{6}$ with respect to $x$ as

$$\begin{aligned} \frac{\partial \varepsilon _{6}}{\partial x}=\frac{(x^2(t)-a)(x^2(t)+a)}{a^{2}x^{3}(t)}, \end{aligned}$$

and we further have

$$\begin{aligned} \left( \frac{\partial \varepsilon _{6}}{\partial x} \right) ^2=\frac{(x^2(t)-a)^{2}(x^2(t)+a)^{2}}{a^{4}x^{6}(t)}. \end{aligned}$$

In consideration of Lemma 8 and Corollary 6, $\exists \eta _{6}>1$, $\forall x(t)$, we have

$$\begin{aligned} \eta _{6}\le \frac{(x^2(t)+a)^{2}}{x^4(t)}, \end{aligned}$$

where $\eta _{6}>1$ is a constant. Thus, we further have

$$\begin{aligned} \left( \frac{\partial \varepsilon _{6}}{\partial x} \right) ^2&= \frac{(x^2(t)-a)^{2}(x^2(t)+a)^{2}}{a^{4}x^{6}(t)} \nonumber \\&\ge \frac{\eta _{6}(x^2(t)-a)^{2}}{a^{4}x^2(t)} = 2\frac{\eta _{6}\varepsilon _{6}}{a^{2}}. \end{aligned}$$

(58)

Applying (57) and (58) yields

$$\begin{aligned} \dot{{\L }}_{6}(x(t))&= \dot{\varepsilon _{6}}= - \gamma \left( \frac{\partial \varepsilon _{6}}{\partial x} \right) ^2\nonumber \\&\le - 2 \gamma \frac{\eta _{6}\varepsilon _{6}}{a^{2}}. \end{aligned}$$

(59)

In this case, $\varepsilon _{6}\ne 0$, $\eta _{6} >0$ and $\gamma >0$. Let $\beta _{6}= 2 \gamma \eta _{6}/a^{2}>0$. Then, (59) can be simplified as

$$\begin{aligned} \dot{\varepsilon _{6}}(x(t))\le -\beta _{6}\varepsilon _{6}(x(t)). \end{aligned}$$

Thus, we have

$$\begin{aligned} {\L }_{6}(x(t))=\varepsilon _{6}(x(t)) \le \varepsilon _{6}(x(0))\hbox {exp}(-\beta _{6}t), \forall t\ge 0, \nonumber \\ \end{aligned}$$

(60)

which means that the energy function $\varepsilon _{6}$ exponentially converges to zero. That is, EF (13) is exponentially convergent to zero.

Next, let us prove the exponentially convergent property of the state $x(t)$ of $\hbox {NGDS}_{6}$ (19). By substituting (56) into (60), we obtain

$$\begin{aligned} \frac{1}{2} \left( \frac{x(t)}{a}-\frac{1}{x(t)}\right) ^2 \le \frac{1}{2} \left( \frac{x(0)}{a}-\frac{1}{x(0)}\right) ^2 \hbox {exp}(-\beta _{6}t), \end{aligned}$$

which can be simplified as

$$\begin{aligned} \left\| \frac{x^2(t)-a}{x(t)} \right\| _2 \le \left\| \frac{x^2(0)-a}{x(0)} \right\| _2 \hbox {exp}(-\frac{1}{2} \beta _{6}t). \end{aligned}$$

(61)

Note that (61) can be also rewritten as

$$\begin{aligned}&\left\| \frac{(x(t)-\sqrt{a})(x(t)+ \sqrt{a})}{x(t)} \right\| _2 \nonumber \\&\quad \le \left\| \frac{(x(0)- \sqrt{a})(x(0)+ \sqrt{a})}{{x(0)}} \right\| _2 \hbox {exp}(-\frac{1}{2} \beta _{6}t).\nonumber \\ \end{aligned}$$

(62)

For (62), it can be discussed in the following two cases.

Case 1. If the given initial state $x(0)>0$, following from Lemma 8, then we have $x(0)\ge x(t) \ge x^{*}= \sqrt{a}$ or $x(0)\le x(t)\le x^{*}= \sqrt{a}$. In this case, we can obtain a constant $\mu _{6}>0$ as

$$\begin{aligned} \begin{aligned} \mu _{6}&= \left\| \frac{ x(0)(x(0)+ \sqrt{a})}{x(0)(x^*+ \sqrt{a})}\right\| _2 \ge \left\| \frac{ x(t)(x(0)+ \sqrt{a})}{x(0)(x(t)+ \sqrt{a})}\right\| _2\\&> 0, \end{aligned} \end{aligned}$$

or

$$\begin{aligned} \begin{aligned} \mu _{6}&= \left\| \frac{ x^*(x(0)+ \sqrt{a})}{x(0)(x(0)+ \sqrt{a})}\right\| _2 \ge \left\| \frac{ x(t)(x(0)+ \sqrt{a})}{x(0)(x(t)+ \sqrt{a})}\right\| _2\\&> 0. \end{aligned} \end{aligned}$$

Thus, we have

$$\begin{aligned} \Vert x(t)-x^* \Vert _2 \le \mu _{6} \Vert x(0)- x^*\Vert _2 \hbox {exp}(-\frac{1}{2} \beta _{6}t), \end{aligned}$$

which means that the state $x(t)$ of $\hbox {NGDS}_{6}$ (19) exponentially converges to the theoretical positive solution $x^{*}=\sqrt{a}$ of (5).

Case 2. If the given initial state $x(0)<0$, following from Lemma 8, then we have $x(0)\ge x(t) \ge x^{*}= -\sqrt{a}$ or $x(0)\le x(t)\le x^{*}= -\sqrt{a}$. In this case, $\exists \mu _{6}>0$, which can be defined as another form

$$\begin{aligned} \begin{aligned} \mu _{6}&= \left\| \frac{ x^*(x(0)- \sqrt{a})}{x(0)(x(0)- \sqrt{a})}\right\| _2 \ge \left\| \frac{ x(t)(x(0)- \sqrt{a})}{x(0)(x(t)- \sqrt{a})}\right\| _2\\&> 0, \end{aligned} \end{aligned}$$

or

$$\begin{aligned} \begin{aligned} \mu _{6}&= \left\| \frac{ x(0)(x(0)- \sqrt{a})}{x(0)(x^*- \sqrt{a})}\right\| _2 \ge \left\| \frac{ x(t)(x(0)- \sqrt{a})}{x(0)(x(t)- \sqrt{a})}\right\| _2\\&> 0. \end{aligned} \end{aligned}$$

Thus, we have

$$\begin{aligned} \Vert x(t)-x^* \Vert _2 \le \mu _{6} \Vert x(0)- x^*\Vert _2 \hbox {exp}\left( -\frac{1}{2} \beta _{6}t\right) , \end{aligned}$$

which means that the state $x(t)$ of $\hbox {NGDS}_{6}$ (19) exponentially converges to the theoretical negative solution $x^{*}=-\sqrt{a}$ of (5).

Based on the above analysis, according to Theorem 1, we have the conclusion that $\hbox {NGDS}_{6}$ (19) processes the exponential convergence property. The proof is thus completed. $\square$

In summary, we construct six different NGDSs (14)–(19) for scalar square root finding, which correspond to six different EFs (8)–(13). More importantly, the exponential convergence theorems of such six different NGDSs are investigated completely.

Remark 2

Based on the above theoretical analyses, the proposed NGDSs are all effective for scalar square root finding, though they are based on different EFs. It may give us a new direction on the definition of the energy function for the dynamics system construction (specifically, the NGDS construction): i.e., the energy function is not only defined by following the definition equation of the problem to be solved [e.g., the nonlinear Eq. (5)], but also defined as other appropriate forms. More importantly, different dynamics systems with their exponential convergence theorems proven can thus be obtained by defining different EFs for the problem to be solved, which can be an inspiring direction on the research of dynamics system.

5 Numerical verification and comparison

In the previous sections, different NGDSs based on different EFs are proposed and investigated for scalar square root finding, and the corresponding theorems and proofs are given in detail. In this section, the corresponding MATLAB Simulink modeling of the proposed NGDSs (14)–(19) is firstly developed for possible circuit implementation and also for the final purpose of practical application. Then, two examples are presented to illustrate the exponential convergence performance and substantiate the efficacy of the proposed NGDSs. Based on the comparative results of the proposed six different NGDSs, the readers or practitioners can find respective usages of such NGDSs and choose a suitable NGDS for real problem solving.

The Simulink modeling can be viewed as a virtual implementation of a real system satisfying a set of requirements. Besides, the dynamic model developed in MATLAB Simulink environment can be extended to the hardware description language (HDL) code and then to the final FPGA and ASIC realization [36]. In view of this point, we develop the corresponding MATLAB Simulink modeling of the proposed NGDSs (14)–(19), which is shown in Figs. 1 and 2. As seen from Figs. 1 and 2, the structural complexities of NGDSs (14)–(19) are different from each other. Generally speaking, for the purpose of hardware implementation, it is desirable for practitioners to develop a simple system owning relatively low structural complexity. For a better illustration of the structural complexities of NGDSs (14)–(19), the number of components of NGDSs (14)–(19) in MATLAB Simulink modeling is listed in Table 1. Evidently, in terms of structural complexity, NGDS (14) requires less components and thus is a simpler model in terms of implementation compared with other NGDSs.

Fig. 1

Overall MATLAB Simulink modeling of NGDSs (14), (15) and (16). a Simulink modeling of NGDS (14). b Simulink modeling of NGDS (15). c Simulink modeling of NGDS (16)

Fig. 2

Overall MATLAB Simulink modeling of NGDSs (17), (18) and (19). a Simulink modeling of NGDS (17). b Simulink modeling of NGDS (18). c Simulink modeling of NGDS (19)

To illustrate the efficacy of the proposed NGDSs (14)–(19) for solving the scalar square root problem, the ensuing numerical example is presented.

Table 1 Number of components of NGDSs (14)–(19) in MATLAB Simulink modeling

Example 1

Let us consider the square root problem (5) with $a=\cos (\sin (10))+\log _{10}(414)$. Then, we have the following nonlinear equation:

$$\begin{aligned} x^2-\cos (\sin (10))-\log _{10}(414)=0. \end{aligned}$$

(63)

The proposed NGDSs (14)–(19) are firstly developed as MATLAB Simulink modeling and then exploited to solve problem (63). Corresponding results are illustrated in Figs. 3, 4, 5. Note that the numerical example is performed on a personal digital computer with a Pentium E5300 2.6 GHz CPU, 2 GB DDR3 memory and a Windows XP Professional operating system. Besides, positive and negative initial states $x(0)=1$ and $x(0)=-1$ are set, respectively, for each NGDS. As shown in Fig. 3, the $x(t)$ trajectories of each proposed NGDS denoted by solid curves all exponentially converge to the theoretical solutions denoted by dashed curves. In addition, we monitor the residual error $\Vert \epsilon \Vert _2=\Vert x^2(t)-\cos (\sin (10))-\log _{10}(414)\Vert _2$ during the scalar square root finding process. Figure 4 shows that the residual error $\Vert \epsilon \Vert _2$ of each NGDS exponentially converges to zero, which coincides with the theoretical analyses given in the previous sections. Moreover, from Figs. 3 and 4, one can readily find that NGDSs (14)–(19) possess different convergent performance for solving problem (63) in the perspective of computing time (or termed, convergent time) consumption . It needs about $0.05$ s for NGDS (14) to solve scalar square root problem (63), while it consumes more than $0.05$ s for other NGDSs [e.g., more than $4$ s for NGDS (15)] to solve the same problem. Therefore, in terms of computing time complexity, it would be more desirable for practitioners to choose NGDS (14) to solve this type of scalar square root problems.

Fig. 3

State $x(t)$ trajectories of NGDSs (14)–(19) for solving (63) with $\gamma =10$. a via NGDS (14). b via NGDS (15). c via NGDS (16). d via NGDS (17). e via NGDS (18). f via NGDS (19)

Fig. 4

Residual errors $\Vert \epsilon \Vert _2$ of NGDSs (14)–(19) for solving (63) with $\gamma =10$. a via NGDS (14). b via NGDS (15). c via NGDS (16). d via NGDS (17). e via NGDS (18). f via NGDS (19)

Fig. 5

Residual error $\Vert \epsilon \Vert _2$ of NGDS (15) for solving (63) with different values of $\gamma$ (a) with $\gamma =100$ (b) with $\gamma =$ 1,000 (c) with $\gamma =$ 10,000

Moreover, we can improve the exponential convergence performance of the proposed six NGDSs (14)–(19) by increasing the value of design parameter $\gamma$. As seen from Fig. 5, the convergence time of NGDS (15) can be expedited from around $0.4$ s to $0.04$ s and to $0.004$ s, as the value of $\gamma$ is set from $10^{2}$ to $10^{3}$ and to $10^{4}$, respectively. Note that the convergence performance of other NGDSs can also be improved by setting the design parameter $\gamma$ properly. That is to say, all the proposed NGDSs (14)–(19) are efficacy for solving the specific scalar square root problem if only the value of $\gamma$ is set appropriately in practical application.

In order to further investigate the benefits and disadvantages as well as respective usages of the proposed NGDSs (14)–(19), we present another numerical example, in which we find the application background and condition for each proposed NGDS.

Example 2

Let us consider the following nonlinear equations:

$$\begin{aligned}&x^2(t)-2.5\times 10^{-5}=0, \end{aligned}$$

(64)

$$\begin{aligned}&x^2(t)-2.5\times 10^{-3}=0, \end{aligned}$$

(65)

$$\begin{aligned}&x^2(t)-2.5\times 10^{-1}=0, \end{aligned}$$

(66)

$$\begin{aligned}&x^2(t)-2.5\times 10^{1}=0, \end{aligned}$$

(67)

$$\begin{aligned}&x^2(t)-2.5\times 10^{3}=0, \end{aligned}$$

(68)

$$\begin{aligned}&x^2(t)-2.5\times 10^{5}=0. \end{aligned}$$

(69)

As for the above nonlinear equations, the theoretical solutions $x^*$ of each scalar square root problem are $\pm 5\times 10^{-3}$, $\pm 5\times 10^{-2}$, $\pm 5\times 10^{-1}$, $\pm 5\times 10^{0}$, $\pm 5\times 10^{1}$ and $\pm 5\times 10^{2}$, respectively. In this numerical example, the scalar square root problems are investigated under the same conditions (with $\gamma =$ 1,000 and with the same initial states being set as $x^*\pm 1$) for comparative purpose.

Table 2 shows the computing time consumption for solving different scalar square root problems (64)–(69) via NGDSs (14)–(19) with $\gamma =$ 1,000. As seen from Table 2, the computing time of NGDS (14) decreases, as the absolute value of theoretical solutions to each scalar square root problem (denoted by SSRP) increases, for the reason that the NGDSs (14)–(19) have different parameters $\beta _{i}$ with $i=1, 2, \ldots 6$ (investigated in Sect. 4), which scale the exponential convergence rates. Such a numerical result shows that NGDS (14) is more suitable for the SSRP with a relatively large absolute value of solution in the practical applications. On the contrary, NGDS (15) is more suitable for the SSRP with a relatively small absolute value of solution in the practical applications, for the reason that the computing time of NGDS (15) decreases, as the absolute value of theoretical solutions of each SSRP decreases accordingly. In addition, NGDSs (16) and (19) have similar numerical results just like NGDS (15), which can also be seen from Table 2. Besides, NGDSs (17) and (18) both have a relatively stable computing performance; especially, NGDS (18) has the computing time of the order of $10^{-3}$ s for solving all of the six different SSRPs. Thus, NGDS (18) should have wider range of applications in real world.

Table 2 Computing time consumption (in seconds) for solving different SSRPs via NGDSs (14)–(19) with $\gamma =$ 1,000

In summary, the above numerical verification and comparison illustrated by two examples have fully shown the efficacy of the proposed six NGDSs (14)–(19) for scalar square root finding. Moreover, the main differences, benefits and disadvantages, as well as the application background and condition, have been discussed in detail for practitioners to choose a suitable NGDS for the specific scalar square root problem solving in practical applications.

6 Conclusions

In this paper, the GDSs, i.e., LGDS and NGDS, with their exponential convergence theories have been investigated. Based on different EFs [i.e., (8)–(13)], different NGDSs [i.e., (14)–(19)], which are different from the earlier-presented LGDSs, have been novelly designed, proposed and investigated in the form of the first-order nonlinear differential equations for square root finding. More importantly, theoretical analyses of the exponential convergence theorems of the proposed NGDSs have been proved based on Lyapunov theory, which has substantiated well the feasibility and validity of the proposed NGDSs for square root finding. Numerical verification and comparison including two illustrative examples have fully shown the efficacy of the proposed six NGDSs, in which the main differences and respective usages, as well as the application background and condition, have been discussed in detail.

As potential applications and a future research direction, we expect to investigate microprocessors which contain the square root implementation in the operation set based on the elegant NGDSs proposed in this paper.