Dynamic analysis of fractional-order predator–prey biological economic system with Holling type II functional response

Abstract

A fractional-order predator–prey biological economic system with Holling type II functional response is proposed. Local stability and Hopf bifurcation of predator–prey systems have been investigated in both commensurate and incommensurate fractional-order systems. We explore how the economic profit and fractional orders influence the local stability and Hopf bifurcation for the fractional-order predator–prey system. For an incommensurate system, we propose a new theory for the existence of Hopf bifurcation when the fractional orders are considered as bifurcation parameters. Several numerical examples are demonstrated to validate the theoretical results.

1 Introduction

Nowadays, fractional calculus has attained much attention as the novel mathematical model to describe various phenomena in nature [1,2,3,4]. Due to the non-local property of the fractional derivative, the fractional-order differential equations are more suitable than integer-order ones in biological, economic and social systems where memory effects are important. Several numerical methods have been proposed to obtain accurate approximations by handling the non-local property of fractional derivatives [5,6,7,8], and dynamical properties for the fractional-order systems have been studied [9,10,11,12,13,14].

The predator–prey model was studied to describe the relationship between two species in biological systems in which one predator feeds on the other prey. The first model was introduced by Lotka [15] and Volterra [16]. Holling type II functional response models have been investigated to describe more realistic predator–prey biological systems [17,18,19,20]. Recently, many predator prey models of fractional order have been proposed and their dynamical features studied in [21,22,23] In this paper, we consider the following fractional-order predator–prey biological economic model with Holling type II functional response [19],

$$\begin{aligned} \begin{aligned}&D^{\alpha _{1}}x(t)=x\left( d-kx-\frac{y}{a+x}-E\right) ,\\&D^{\alpha _{2}}y(t)=y\left( -r+\frac{bx}{a+x}\right) ,\\&0=E(px-c)-\upsilon , \end{aligned} \end{aligned}$$

(1)

where $\alpha _1,\alpha _2 \in (0,1)$; x and y represent the prey density and predator density at time t, respectively; d, r, a and b are positive constants that stand for prey intrinsic growth rate, predator mortality rate, half capturing saturation constant and maximal predator growth rate, respectively; $d/k>0$ is the carrying capacity of the prey; E(t) represents the harvest effort; p denotes harvesting reward per unit harvesting effort for unit weight; c represents harvesting cost per unit harvesting effort; $\upsilon$ is the economic profit; and the fractional derivative of order $\alpha$, $n-1 <\alpha \le n \in {\mathbb {Z}}^+$, is defined in the Caputo sense [24].

Definition 1

The Riemann–Liouville fractional integral of order $\beta \in R^{+}$ of the function $f(t),\,t>0$ is defined by

$$\begin{aligned} I^{\beta }f(t)=\int _{0}^{t}\frac{(t-s)^{\beta -1}}{\varGamma (\beta )}f(s) \hbox {d}s. \end{aligned}$$

Here, $\varGamma (\cdot )$ is the conventional Gamma function. Then the Caputo fractional differential operator of order $\alpha$ of $f(t),\,t>0~$ can be written by

$$\begin{aligned} D^{\alpha }f(t)=I^{n-\alpha }D^{n}f(t),~~D=\frac{\hbox {d}}{\hbox {d}t}. \end{aligned}$$

We refer to [1,2,3,4] for detailed analysis and discussions. In this paper, we mainly discuss the effects of economic profit $\upsilon$ and the fractional orders $\alpha _{1},\alpha _{2}$ on the dynamics of the system (1) in the region

$$\begin{aligned} R_{+}^{3}=\{(x,y,E)\mid x>0,y>0,E>0\}. \end{aligned}$$

It is well known that the economic profit $\upsilon$ is an important parameter to determine the dynamical properties [17,18,19,20]. As far as authors know, the stability analysis and the existence of Hopf bifurcation associated with both fractional orders $(\alpha _1,\alpha _2)$ and economic profit ${\upsilon }$ have not been addressed. In this paper, we provide the following results

• Stability regions with respect to $(\alpha _1,\alpha _2)$ when the economic profit $\upsilon$ varies. The stability regions are sensitive with the fractional orders. For the commensurate system, it is asymptotically stable for $\upsilon <s(\alpha )$, where $s(\alpha )$ is increasing with $s(0)=7/9$ and $s(1)=1/3$. For the incommensurate system, the area of stability region with respect to $(\alpha _1,\alpha _2)$ is decreasing when the economic profit $\upsilon$ is increasing (see Fig. 5).

• Existence of bifurcation versus an fractional order $\alpha$ or an economic profit $\upsilon$. For the incommensurate system, we provide a new theory of the existence of Hopf bifurcation by introducing a directional vector along the curve $h(\gamma (\alpha _1, \alpha _2))=0$, where the curve h is constructed by the stability condition (see Theorem 5).

Furthermore, we give several numerical simulations to support our analysis.

2 Preliminaries

In this section, we introduce stability analysis of the fractional-order system. Let us consider the nonlinear fractional orders autonomous system

$$\begin{aligned} \begin{aligned} D^{\alpha _{1}}x_{1}(t)&=f_{1}(x_{1},x_{2},\ldots ,x_{n}),\\ D^{\alpha _{2}}x_{2}(t)&=f_{2}(x_{1},x_{2},\ldots ,x_{n}),\\&\vdots \\ D^{\alpha _{n}}x_{n}(t)&=f_{n}(x_{1},x_{2},\ldots ,x_{n}), \end{aligned} \end{aligned}$$

(2)

with the initial values

$$\begin{aligned} x_{1}(0)=x_{01},x_{2}(0)=x_{02},\ldots , x_{n}(0)=x_{0n}, \end{aligned}$$

where $0<\alpha _{i}\le 1,~i=1,2,\ldots ,n.$ If $\alpha _{1}=\alpha _{2}=\cdots =\alpha _{n}=\alpha$, system (2) is called a commensurate order, otherwise it indicates an incommensurate order system.

Definition 2

The constant $(x_{1}^{eq},~x_{2}^{eq},\ldots ,x_{n}^{eq})$ is an equilibrium point of the fractional dynamic system (2), if and only if

$$\begin{aligned} f_{i}(x_{1}^{eq},x_{2}^{eq},\ldots ,x_{n}^{eq})=0,~~i=1,2,\ldots ,n. \end{aligned}$$

Theorem 1

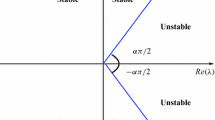
([4, 10]) Consider the commensurate nonlinear fractional-order system (2) with $0<\alpha _{1}=\cdots =\alpha _{n}=\alpha \le 1$. The equilibrium points of system (2), $\mathbf{x}^{eq}$, are locally asymptotically stable if all eigenvalues $\lambda _{i}$ of the Jacobian matrix J evaluated at the equilibrium points

$$\begin{aligned} J=\left[ \begin{array}{cccc} a_{11} &{}\quad a_{12} &{}\quad \ldots &{}\quad a_{1n} \\ a_{21} &{}\quad a_{22} &{}\quad \ldots &{}\quad a_{2n} \\ \vdots &{}\quad \vdots &{}\quad \ldots &{}\quad \vdots \\ a_{n1} &{}\quad a_{n2} &{}\quad \ldots &{}\quad a_{nn} \end{array} \right] , \end{aligned}$$

$$\begin{aligned} a_{ij}=\frac{\partial f_{i}}{\partial x_{j}}\mid _{\mathbf{x}^{eq}},~~i,j=1,2,\ldots ,n \end{aligned}$$

satisfy:

$$\begin{aligned} \left| \arg (\lambda _{i})\right| >\frac{\alpha \pi }{2}. \end{aligned}$$

Theorem 2

( [11]) Consider an incommensurate nonlinear fractional-order system (2) where $\alpha _{i}$’s are rational numbers between 0 and 1, for $i=1,2,\ldots ,n$. Let M be the least common multiple (LCM) of the denominators $u_{i}$ of $\alpha _{i}$’s, where $\alpha _{i}$$=\frac{v_{i}}{ u_{i}},$$(u_{i},v_{i})=1$ (the greatest common divisor of $u_{i}$ and $v_{i}$ is 1), $u_{i},v_{i}\in {\mathbb {Z}} ^{+},i=1,2,\ldots ,n$ and $\gamma =\frac{1}{M}$. Then, the equilibrium points of system (2) are locally asymptotically stable if and only if all the roots $\lambda$’s of the equation

$$\begin{aligned} \det \left( \begin{array}{cccc} \lambda ^{M \alpha _{1}}-a_{11} &{}\quad -a_{12} &{}\quad \ldots &{}\quad -a_{1n} \\ -a_{21} &{}\quad \lambda ^{M \alpha _{2}}-a_{22} &{}\quad \ldots &{}\quad -a_{2n} \\ \vdots &{}\quad \vdots &{}\quad \ldots &{}\quad \vdots \\ -a_{n1} &{}\quad -a_{n2} &{}\quad \ldots &{}\quad \lambda ^{M \alpha _{n}}-a_{nn} \end{array} \right) =0 \end{aligned}$$

(3)

satisfy:

$$\begin{aligned} \left| \arg (\lambda )\right| >\frac{\gamma \pi }{2}. \end{aligned}$$

3 Stability analysis

In this section, we investigate local stability analysis for the our model system (1) by using Theorems 1 and 2. To do this, we find an equilibrium point $(x_{0},y_{0},E_{0})$ by solving the following system:

$$\begin{aligned} \begin{aligned}&x\left( d-kx-\frac{y}{a+x}-E\right) =0,\\&y\left( -r+\frac{bx}{a+x}\right) =0,\\&E(px-c)-\upsilon =0, \end{aligned} \end{aligned}$$

(4)

which yields

$$\begin{aligned} \begin{aligned}&(x_{0},y_{0},E_{0})\\&\quad =\left( \frac{ar}{b-r},(a+x_{0})(d-kx_{0}-E_{0}),\frac{\upsilon }{px_{0}-c}\right) . \end{aligned} \end{aligned}$$

(5)

From the existence of the equilibrium point, we assume that

$$\begin{aligned} (b-r)>0,(d-kx_{0}-E_{0})>0,(px_{0}-c)>0. \end{aligned}$$

3.1 The commensurate nonlinear fractional-order system

Consider the commensurate nonlinear fractional-order system (1) with $\alpha _{1}=\alpha _{2}=\alpha ,~0<\alpha < 1$. The Jacobian matrix J of the system (1) evaluated at the equilibrium point $(x_{0},y_{0},E_{0})$ is

$$\begin{aligned} J=\left[ \begin{array}{cc} \frac{px_{0}E_{0}}{(px_{0}-c)}-kx_{0}+\frac{x_{0}y_{0}}{(a+x_{0})^{2}} &{}-\frac{x_{0}}{(a+x_{0})} \\ \frac{aby_{0}}{(a+x_{0})^{2}} &{} 0 \end{array} \right] , \end{aligned}$$

and the corresponding characteristic polynomial of the equilibrium point $(x_{0},y_{0},E_{0})$ is given by

$$\begin{aligned} \quad \quad \lambda ^{2}+a_{1}(\upsilon )\lambda +a_{2}(\upsilon )=0, \end{aligned}$$

(6)

where

$$\begin{aligned} \begin{aligned} a_{1}(\upsilon )&=kx_{0}-\frac{px_{0}E_{0}}{(px_{0}-c)}-\frac{x_{0}y_{0}}{(a+x_{0})^{2}}, \\ a_{2}(\upsilon )&=\frac{abx_{0}y_{0}}{(a+x_{0})^{3}}>0. \end{aligned} \end{aligned}$$

Then, it is easy to see by Theorem 1 that a sufficient condition for the local asymptotic stability at the equilibrium point $(x_{0},y_{0},E_{0})$ is

$$\begin{aligned} \left| \arg (\lambda _{i}(\upsilon ))\right| >\frac{\alpha \pi }{2}, i=1,2, \end{aligned}$$

(7)

where $\lambda _{i}(\upsilon )$ is the solution of the characteristic Eq. (6) and is given by

$$\begin{aligned} \lambda (\upsilon )=\frac{-a_1(\upsilon ) \pm \sqrt{ a^2_1(\upsilon )-4a_2(\upsilon )}}{2}. \end{aligned}$$

(8)

Since $a_2>0$, $\lambda _i(\upsilon )$ are negative real or complex conjugate with negative real part for $a_1>0$. In this case, the stability condition (7) is equivalent to the Routh–Hurwitz conditions [9].That is,

$$\begin{aligned} a_{1}^{2}\geqslant 4a_{2}, a_{1}>0, \text { or } a_{1}^{2}<4a_{2},a_{1}>0. \end{aligned}$$

(9)

For $a_1<0$, the solutions $\lambda _i(\upsilon )$ are positive real or complex conjugate with positive real part. Thus, we have the following equivalent condition for (7)

$$\begin{aligned} a_{1}<0,4a_{2}>a_{1}^{2},\left| \tan ^{-1}\left( \frac{\sqrt{4a_{2}-a_{1}^{2}}}{a_{1}}\right) \right| >\frac{\alpha \pi }{ 2}. \end{aligned}$$

(10)

3.2 An incommensurate nonlinear fractional-order system

Consider an incommensurate nonlinear fractional-order system (1), $\alpha _{1},\alpha _{2}\in (0,1)$ and $\alpha _{i}=v_{i} / u_{i}$ with $(u_{i},v_{i})=1, i=1,2$. Then, the equilibrium point $(x_{0},y_{0},E_{0})$ of the system in (5) is asymptotically stable if and only if all the roots $\lambda$’s of the equation

$$\begin{aligned} \det \left( \begin{array}{cc} \lambda ^{M\alpha _{1}}-a_{11} &{}\quad -a_{12} \\ -a_{21} &{}\quad \lambda ^{M\alpha _{2}}-a_{22} \end{array} \right) =0 \end{aligned}$$

(11)

satisfy the following condition

$$\begin{aligned} \left| \arg (\lambda )\right| >\frac{\gamma \pi }{2}, \end{aligned}$$

where M is the least common multiple of the denominators $u_{i}$, and $\gamma =1/M$.

3.3 Numerical illustrations

For all numerical simulations through this work, we choose the coefficients in the fractional-order system (1) [19]

$$\begin{aligned} a=0.5,b=2,d=2,r=1,p=4,c=1,k=2. \end{aligned}$$

Combined with the coefficients, the equilibrium point is evaluated as $(x_{0},y_{0},E_{0})=(0.5,1-\upsilon ,\upsilon )$ and the corresponding eigenvalues can be evaluated in (8)

$$\begin{aligned} \lambda =(3\upsilon -1 \pm \sqrt{9\upsilon ^2+2\upsilon -7})/4. \end{aligned}$$

(12)

For an integer system, the equilibrium point $(x_{0},y_{0},E_{0})$ is stable for $a_1(\upsilon )=0$. Since $a_1(\upsilon )=(1-3\upsilon )/4$, it is stable when $\upsilon =\upsilon _0=1/3$.

For a commensurate fractional-order system, the stability of the equilibrium point is followed by (9) and (10). Figure 1 shows the approximated solutions of x and y for $\alpha =0.9,0.95$ and 1 with $\upsilon =0.32$ and 0.333, respectively. For $\upsilon < \upsilon _0$, the eigenvalues are negative real values so that $\left| \arg (\lambda )\right| > \alpha \pi /2$. Thus, the equilibrium point is asymptotically stable for all $\alpha \in (0,1)$ in Fig. 1.

For $\upsilon >\upsilon _{0}$, the equilibrium point is unstable for $\alpha =1$ because of positive real eigenvalue. But, the stability for $\alpha \in (0,1)$ depends on the conditions (7). When $\upsilon =0.342$, the eigenvalues are given by $\lambda _{1,2}=0.0065\pm 0.5735 {i}$. Then if $\alpha < (2/\pi )\left| \arg (\lambda _{i})\right| =0.9927$, it is asymptotically stable. Figure 2a, b depicts the stability for $\alpha =0.9,0.95$, respectively. For $\upsilon =0.53$, the equilibrium point $(x_{0},y_{0},E_{0})=(0.5,0.47,0.53)$ has the eigenvalues $\lambda _{1,2}=0.1475\pm 0.4617{i}$. It is asymptotically stable for $\alpha <(2/\pi )\left| \arg (\lambda _{i})\right| = 0.8031$. Part (c) of Fig. 2 supports the stability of the equilibrium point for $\alpha =0.8$. However, for $\upsilon =0.55$, it is easy to see that the equilibrium point is asymptotic stable when $\alpha < 0.7774$. When $\alpha =0.8$, Fig. 2d shows that it is unstable. For the commensurate fractional-order system, it is shown that the system is asymptotically stable for $\upsilon < s(\alpha )$, where $s(\alpha )=\alpha \pi /2-\left| \arg (\lambda )\right|$. Here, $s(0)=7/9, s(1)=1/3$ and it is decreasing when $\alpha$ is increasing. The stability region with respect to $\alpha$ and $\upsilon$ is shown in Fig. 3.

Fig. 1

Plots of x and y with $\upsilon =0.32, 0.333$ and $x(0)=0.499, y(0)=0.666$

Fig. 2

Plots of x and y with $\upsilon =0.342, 0.53,0.55$ and $x(0)=0.4, y(0)=0.1$

Fig. 3

Stability region for the commensurate system

Fig. 4

Plots of x, y and E with $\upsilon =0.5$ and $x(0)=y(0)=0.48$ (left: $\alpha _1=0.7, \alpha _2=0.8$, right: $\alpha _1=0.8, \alpha _2=0.9$)

For the incommensurate fractional-order system, the eigenvalues can be evaluated by solving the characteristic equation (11) which may be a higher order of polynomial function depending on the fractional orders $\alpha _1,\alpha _2$. Let us set the economic profit to be $\upsilon =0.5$. Then the equilibrium point is $(x_{0},y_{0},E_{0})=(0.5,0.5,0.5)$. For $(\alpha _1,\alpha _2)=(0.7,0.8)$, all eigenvalues are approximated, which gives the minimum of argument: $\min |\arg (\lambda )| =0.1774$. Since $\gamma =\pi /20 = 0.1570$, the equilibrium point is asymptotic stable. For $(\alpha _1,\alpha _2)=(0.8,0.9)$, we have $\min |\arg (\lambda )|$$=0.1563$ so that the equilibrium point is unstable. Figure 4 depicts the stability of the equilibrium point with an initial condition $x(0)=y(0)=0.48$. When $\upsilon$ varies from 0.4 to 0.7, the stability regions with respect to $(\alpha _1,\alpha _2)$ are demonstrated in Fig. 5. It is shown that the area of stability region is decreasing as $\upsilon$ is increasing.

Fig. 5

Stability regions with respect to $(\alpha _1,\alpha _2)$ when $\upsilon$ varies from 0.4 to 0.7

4 Hopf bifurcation analysis

Hopf bifurcation for the integer-order system, $\alpha =1$, was studied in [19]. They chose the economic profit $\upsilon$ as a bifurcation parameter and found that Hopf bifurcation occurs when the economic profit is bigger than a certain threshold. In this section, we will investigate the Hopf bifurcation of the system (1) by considering the economic profit $\upsilon$ and fractional order $\alpha$ as the bifurcation parameters. We point out that Hopf bifurcation in the fractional-order system occurs in complex conditions from those in their integer-order system.

For the integer-order system, it has been known that Hopf bifurcation may occur when the system is stable at a bifurcation parameter ${\upsilon }$. Thus, the roots of the characteristic equation (6) are zero real parts for the local stability. Letting $a_{1}(\upsilon )=0$ gives the bifurcation parameter $\upsilon _0$

$$\begin{aligned} \upsilon _{0}=((px_{0}-c)^{2}/p)(k-y_{0}/(a+x_{0})^{2}). \end{aligned}$$

Then, Hopf bifurcation occurs at the bifurcation parameter $\upsilon _0$ if the following conditions are satisfied

$$\begin{aligned} {Im}[\lambda (\upsilon _{0})]\ne 0, \quad \frac{d}{d\upsilon } \left( {Re}[\lambda (\upsilon _{0})] \right) \ne 0. \end{aligned}$$

However, there are differences in a fractional-order system for the stability conditions compared with those in a integer system as shown in Theorems 1 and 2, Moreover, both economic profit and fractional order are the bifurcation parameters so that it requires a new Hopf bifurcation analysis.

4.1 Hopf bifurcation analysis of commensurate system

For the commensurate fractional-order system (1) with $\alpha _{1}=\alpha _{2}=\alpha ,~0<\alpha < 1$, the stability of equilibrium point depends on the sign of $\alpha \pi / 2-\left| \arg (\lambda _{i})\right| , i=1,2$ in Theorem 1. Let us consider the fractional order $\alpha$ as a bifurcation parameter and define a function f with respect to the fractional order ${\alpha }$

$$\begin{aligned} f(\alpha )=\alpha \pi /2-\left| \arg (\lambda _i )\right| . \end{aligned}$$

By Theorem 1, if $f(\alpha )<0$, then the equilibrium point is locally asymptotically stable; if $f(\alpha )>0$, then it is unstable. Next, we will use the function $f(\alpha )$ to investigate Hopf bifurcation in the fractional-order commensurate system (1) versus the fractional order $\alpha$.

Theorem 3

([12] Existence of Hopf bifurcation versus the fractional order) When bifurcation parameter $\alpha$ passes through the critical value $\alpha ^{*}\in (0,1)$, the fractional-order system (1) undergoes a Hopf bifurcation at the equilibrium point $(x_{0},y_{0},E_{0}),$ if the following conditions hold:

• (i) the Jacobian matrix of the system (1) at the equilibrium point has a pair of complex conjugate eigenvalues $\lambda _{1,2}=\theta \pm i\omega$, where $\theta >0$,

• (ii) $f(\alpha ^{*})=0,$

• (iii) $\displaystyle {\left. \frac{d[f(\alpha )]}{d\alpha }\right| _{\alpha =\alpha ^{*}}\ne 0}$ (transversality condition).

Let us note that the eigenvalues $\lambda$ are given by (12). In order to satisfy the condition (i) in Theorem 3 for all $\alpha \in (0,1)$, the eigenvalues have a positive real part complex numbers. This implies that $3\upsilon -1>0$ and $9\upsilon ^2+2\upsilon -7< 0$. Thus, Hopf bifurcation in system (1) occurs for all $\alpha \in (0,1)$ whenever the economic profit locates in $\upsilon \in (1/3,7/9)$. By the conditions (ii) and (iii), it is easy to see that the Hopf bifurcation occurs along the boundary between the stable and unstable region in Fig. 3.

For $\upsilon =0.5$, the bifurcation value $\alpha ^*$ can be evaluated by solving $f(\alpha ^*)=0$ which gives $\alpha ^* \approx 0.8391$. The transversality condition is satisfied by $\left. \frac{d[f(\alpha )]}{d\alpha }\right| _{\alpha =\alpha ^{*}}=\pi /2$. Thus, Hopf bifurcation occurs at $\alpha =\alpha ^*$. As $\alpha$ increases past $\alpha ^*$, it is shown in Fig. 6 that the phase portraits of x and y have larger limit cycle orbits.

Fig. 6

Bifurcation diagram for x(t) with respect to $\alpha$ (top) and phase portrait (bottom) with $\upsilon =0.5$

Now we consider a economic profit $\upsilon$ as a bifurcation parameter when $\alpha$ is fixed. For the stability of the equilibrium point, let us define a function $g(\upsilon )$ as

$$\begin{aligned} g(\upsilon ) =\alpha \pi /2-\left| \arg (\lambda _i (\upsilon ))\right| . \end{aligned}$$

The equilibrium point $(x_{0},y_{0},E_{0})=(0.5,1-\upsilon ,\upsilon )$ is asymptotic stable if $g(\upsilon )<0$, and it is unstable if $g(\upsilon )>0$. Then we propose the following existence of Hopf bifurcation versus a economic profit $\upsilon$.

Theorem 4

([12] Existence of Hopf bifurcation versus an economic profit) When bifurcation parameter $\upsilon$ passes through the critical value $\upsilon ^{*}$, the fractional-order system (1) undergoes a Hopf bifurcation at the equilibrium point $(x_{0},y_{0},E_{0}),$ if the following conditions hold:

• (i) the Jacobian matrix of the system (1) at the equilibrium point has a pair of complex conjugate eigenvalues $\lambda _{1,2}=\theta (\upsilon )\pm i\omega (\upsilon )$, where $\theta (\upsilon )>0$,

• (ii) $g(\upsilon ^{*})=0,$

• (iii) $\displaystyle {\left. \frac{d[g(\upsilon )]}{d\upsilon }\right| _{\upsilon =\upsilon ^{*}}\ne 0}$ (transversality condition).

The condition (i) implies $\upsilon \in (1/3, 7/9)$. Since the bifurcation value $\upsilon ^*$ is the solution of $g(\upsilon )=0$, it can be evaluated by solving

$$\begin{aligned} \sqrt{7-2\upsilon -9\upsilon ^{2}}+(1-3\upsilon )\tan (\alpha \pi /2)=0, \end{aligned}$$

which gives

$$\begin{aligned} \upsilon ^*=\frac{3 p^2-1 \pm 4\sqrt{3p^2+4}}{9(p^2+1)}, p=\tan \left( \frac{\alpha \pi }{2}\right) . \end{aligned}$$

(13)

The last transversality condition (iii) is equivalent to

$$\begin{aligned} \left. \frac{3\upsilon -5}{2(\upsilon -1) \sqrt{7-2\upsilon -9\upsilon ^2} }\right| _{\upsilon =\upsilon ^{*}}\ne 0. \end{aligned}$$

(14)

Let $\alpha =0.95$. Then, the bifurcation value $\upsilon ^*$ can be computed by (13). Combined with the constraint $\upsilon \in (1/3, 7/9)$, we have $\upsilon ^* \approx 0.3910$. Using (14), the transversality condition is satisfied as $\left. \frac{d[g(\upsilon )]}{d\upsilon }\right| _{\upsilon =\upsilon ^{*}}\approx 1.42 \ne 0$. Thus, Hopf bifurcation occurs at $\upsilon ^*$. Figure 7 depicts the bifurcation diagram versus $\upsilon$. When the economic profit $\upsilon$ increases beyond $\upsilon ^*$, it is shown that the radius of limit cycle orbits also increases.

Fig. 7

Bifurcation diagram for x(t) with respect to $\upsilon$ (top) and phase portrait (bottom) with $\alpha =0.95$

4.2 Hopf bifurcation analysis in a incommensurate system

For the incommensurate fractional-order system, it is also important to find a sign of $\gamma \pi /2-\left| \arg (\lambda _{i})\right| ,$ for the stability of equilibrium point by Theorem 2. Let us note that $\gamma$ depends on all fractional orders $\alpha _i$. Since the characteristic equation (3) may be a higher-order polynomial, all $\left| \arg (\lambda _{i})\right|$ may not be same. Suppose the fractional orders $\alpha _{i},i=1,2,\ldots ,n$ can be chosen as the bifurcation parameters in fractional-order systems. Let us define a function h with respect to $\gamma (\alpha _{1},$$\alpha _{2},\ldots ,\alpha _{n})$

$$\begin{aligned} h(\gamma (\alpha _{1},\alpha _{2},\ldots ,\alpha _{n}))=\frac{\gamma \pi }{ 2}-\min _{i}\left| \arg (\lambda _{i})\right| . \end{aligned}$$

By Theorem 2, if $h(\gamma )<0$, then the equilibrium point is locally asymptotically stable; if $h(\gamma )>0$, then the equilibrium point is unstable. Next, we will use the function $h(\gamma )$ to investigate the existence of Hopf bifurcation in the fractional-order incommensurate system (1) versus the fractional order $\alpha _{1}$ and $\alpha _{2}$.

Theorem 5

(Existence of Hopf bifurcation versus a fractional order $(\alpha _1,\alpha _2)$ in a incommensurate system) When bifurcation parameters $(\alpha _{1}, \alpha _{2})$ pass through the critical values $\alpha _{1}^{*},\alpha _{2}^{*}\in (0,1)$, the fractional-order system (1) undergoes a Hopf bifurcation at the equilibrium point $(x_{0},y_{0},E_{0})$ if the following conditions hold:

• (i) $h(\gamma (\alpha _{1}^{*},\alpha _{2}^{*}))=0,$

• (ii) $\nabla h(\gamma (\alpha _{1}^{*},\alpha _{2}^{*}))\cdot \overrightarrow{d}\ne 0$ (transversality condition), where $\overrightarrow{ d}$ is a directional vector of the curve $h(\gamma (\alpha _1,\alpha _2))=0$ at $(\alpha _{1}^{*},\alpha _{2}^{*})$.

Proof

Let $(\alpha _{1}^{*},\alpha _{2}^{*})$ be the solution of the curve $h(\gamma (\alpha _{1},\alpha _{2}))=0$. Since $h(\gamma (\alpha _1,\alpha _2))$ is continuous, there exists a $\delta$-neighborhood $B_{\delta }(\alpha _{1}^{*},\alpha _{2}^{*})$ such that the sign of $h(\gamma (\alpha _1,\alpha _2))$ changes from positive to negative or from negative to positive in $B_{\delta }(\alpha _{1}^{*},\alpha _{2}^{*})$. Let $\overrightarrow{d}$ be a directional vector of $h(\gamma (\alpha _1,\alpha _2))=0$ at $(\alpha _1^*,\alpha _2^*)$. Since $\nabla h(\gamma (\alpha ^* _{1} ,\alpha ^* _{2}))$ is a normal vector of the curve $h(\gamma (\alpha _1,\alpha _2))=0$ at $(\alpha _{1}^{*},\alpha _{2}^{*})$, $\nabla h(\gamma (\alpha _{1}^{*},\alpha _{2}^{*}))\cdot \overrightarrow{d}\ne 0$ if $\overrightarrow{d}$ is not a tangential vector. Suppose that $\overrightarrow{d} \subset B_{\delta }(\alpha _{1}^{*},\alpha _{2}^{*})$ is a directional vector of the curve $h(\gamma (\alpha _1,\alpha _2))=0$ at $(\alpha _{1}^{*},\alpha _{2}^{*})$ and not a tangential vector. Then when $(\alpha _1,\alpha _2) \in \overrightarrow{d}$ passes through $(\alpha _{1}^{*},\alpha _{2}^{*})$, the sign of h can change. Hence, one can assert that Hopf bifurcation occurs $(\alpha _{1}^{*},\alpha _{2}^{*})$. $\square$

Fig. 8

Stability regions for a incommensurate system with several values of $\upsilon$ (a); a horizontal directional vector for $\upsilon =0.5$ (b) an almost tangential vector for $\upsilon =0.6$

Fig. 9

Bifurcation diagram for x(t) when $\alpha _1$ varies (top) and phase portraits of several values of $\alpha _1$(bottom); $\upsilon =0.5$

Fig. 10

Bifurcation diagrams for x(t) with $\alpha _1=0.8,0.8025$ and 0.805 as $\alpha _2$ varies

Figure 8a shows the stability regions on $(\alpha _1, \alpha _2)$ with several economic profits $\upsilon$. For $\upsilon =0.5$, we find the bifurcation value by solving $h(\gamma (\alpha _{1}^{*},\alpha _{2}^{*})) =0$ with a fixed $\alpha _2^{*}=0.75$ which gives $(\alpha _{1}^{*},\alpha _{2}^{*}) = (0.9078, 0.75)$. When we consider a horizontal line $\alpha _2=0.75$ as the directional vector of $h=0$ at $(\alpha _{1}^{*},\alpha _{2}^{*})$ in Fig. 8b, it is clear that the second condition in Theorem 5 is satisfied because the directional vector is not a tangential vector. Then Hopf bifurcation occurs at $(\alpha _{1}^{*},\alpha _{2}^{*})$ by Theorem 5. It is shown in Fig. 9 that Hopf bifurcation appears at $\alpha _{1}^{*}$. Also when $\alpha _1$ increases past the bifurcation value $\alpha _{1}^{*}$, the corresponding limit cycle has an attractor with a lager radius.

Next, we want to demonstrate that a Hopf bifurcation does not occur along the tangential directional vector. But, it is difficult to obtain an exact tangential vector along the curve $h=0$. Instead, we consider a vertical line ${\hat{\alpha }}_1=0.8025$ as the approximated tangential vector in Fig. 8c. Then, it has a very small stable region in $\alpha _2$ axis when the parameter $\alpha _2$ varies along the ${\hat{\alpha }}_1=0.8025$ since the vertical line is the approximated tangential vector. Here, we choose two vertical lines, $\alpha _1=0.8$ and $\alpha _1=0.805$. The first vertical line is smaller than ${\hat{\alpha }}_1=0.8025$ and it has a stable region $(\alpha ^*_{21}, \alpha ^*_{22})$, where $\alpha ^*_{21} = 0.3450, \alpha ^*_{22} = 0.4275$. But, the second one is bigger than the approximated tangential vector and it does not have a stable region in $\alpha _2$ axis. Figure 10 depicts the extremum of x when $\alpha _2$ varies along the several vertical lines, $\alpha _1=0.8, 0.8025$ and 0.805. As the vertical line is approaching to the tangential vector, the stable region in $\alpha _2$ axis is getting smaller. Thus, it is concluded that the Hopf bifurcation does not occur along the tangential vector which supports Theorem 5.

5 Conclusion

In this work, we have studied the dynamic behavior of a fractional-order prey–predator system with Holling type II functional response from the perspective of local stability and Hopf bifurcation.

In both commensurate and incommensurate systems, we have presented the local stability regions associated with the equilibrium points when the economic profit $\upsilon$ varies. It is shown that numerical examples agree with the local stability theory for each equilibrium point. We also have proposed an existence of Hopf bifurcation versus a fractional order or an economic profit in a commensurate system. For the incommensurate fractional-order system, there are multiple bifurcation parameters such as the fractional orders $\alpha _1$ and $\alpha _2$. Thus, it is required to have a new Hopf bifurcation theory for the multiple bifurcation parameters. We have proposed a new transversality condition for the existence of Hopf bifurcation versus multiple bifurcation parameters by introducing the directional vector along with a bifurcation curve such as $h(\gamma (\alpha _1,\alpha _2))=0$. From the several numerical illustrations, it has been shown that all results confirm the proposed theory.