1 Introduction

Electrical signals are the basis of information transfer in the nervous system. The role of electrical activity of neurons for neuro-protection [1] is an emergent research field. The four-variable Hodgkin–Huxley equations [2] and its modified forms are often used to model the electrical activities in neuron.

When neuron is exposed to electromagnetic radiation, the effect of radiation could be described by an equivalent current in neuronal loop [3] and the corresponding electrical activities could be detected. Clinical effects of transcranial electrical simulation with weak currents [4] helps to understand how different amplitude of electric field affect the ongoing brain activities. Experimental studies of complex electrical activities in cardiac tissues with electromagnetic induction are reported which say that these activities responsible for spiral waves, encounter breakup, and turbulence in electrical activities [5].

Magnetic field or flux storage is always associated with memory. Memory effect can be described by time delay term in neuronal models. Nowadays, the electromagnetic induction studies [6] on neuronal network are carried out where memristor is used to describe the memory effect which remembers the magnetic flux across the membrane of neurons or cells. Memristors (memory \(+\) resistors) are nanoscale devices, where the nonlinear resistance can be memorized indefinitely by controlling the flow of the electrical charge or the magnetic flux [7, 8]. The nonvolatile memory property of a memristor is a consequence of state-dependent ohms law. So it affects the potential difference and may lead to a structural change due to the supplied electrical energy [9]. The ‘on’ state is represented by a memory function. A conservation function gives the time-varying resistance which represents the ‘off’ state [9]. It can be used as a synapse in hardware of artificial neural networks. The Magnetic effect due to memristor is similar to that of atomic-scale magnetic susceptibility exhibited by NMR spectroscopy and of MRI imaging [10].

Memristive neural network studies help to integrate information in different functionally specialized regions of brain. Further, the neuronal synchronization helps to encode information in brain through different coherent states which arise through temporal patterns of neural activity, and it emulates even an optical illusion [11, 12].

Recent studies of coupled networks under electromagnetic induction show that the synchronization of neurons causes enlargement of frequency spectrum and self-induction effect [13]. When external electromagnetic radiation is imposed on the Fitzhugh–Nagumo neuron model [14], it helps to detect the mode transition of electrical activities in a myocardial cell. The simulations confirm that the neurons exposed to external electromagnetic field can induce phase synchronization [15].

Noise also can influence and enhance the synchronization pattern formation in excitable systems [16]. The local magnetic flux density due to neurons is very much less than that of the Earth’s magnetic field. So the surrounding noise always becomes comparable to neuronal magnetic signal. The influence of noise can be studied by changing its frequency or intensity [17]. It is also reported [18] that information processing due to synchrony can be modulated by noise.

Energy is an important parameter which influences the normal behavior of brain and its usage mainly depends on the rate of variation of action potential and also on the fraction used by brain for signaling activity. Various studies [19,20,21] are done on metabolic energy for neural activity, energy efficient neural codes, collective behavior of biological oscillators and its energy cost. It is reported that the energy is much dependent on the mode of electrical activities instead of the external forcing currents directly and a smaller energy occurs under bursting states [22]. The study helps to understand the onset of epilepsy (bursting synchronization induced epilepsy makes energy release). The calculation of Hamilton energy of the neuron systems based on Helmholtz’s theorem can explain neurobiological energy states [23]. It is also observed that an event-based minimum energy input is desirable clinically for brain simulation treatment of neurological diseases (like Parkinson’s disease) [24]. The delayed response of Hamilton energy to external forcing currents confirms that neuron contributes to energy coding [25, 26]. These results prompt for further investigation on energy problems in neuronal network.

Bifurcation analysis [27] of H–R neuron helps to understand the relationship between neural firing patterns which are induced by corresponding modulations in potassium channel of neuron model. Gu et al. [28] experimentally demonstrated the bifurcations from bursting to spiking state predicted by theoretical models. The effect of external forcing current on electrical activities of neuron can be predicted with bifurcation diagram [29]. Transverse Lyapunov exponent plot [30] confirms synchronization stability. Also, to determine the neurocomputational properties of cell, bifurcation analysis is important.

The Hindmarsh–Rose model with fractional order [31] can give an explanation to dynamical properties of neuronal electric activities. It is observed that autapse-modulated neuron model and the time- varying electromagnetic field can modulate the membrane potential of neuron and even the time delay in autapse can suppress the bursting in neuronal behavior [32]. Recent studies [33] show that field coupling is also an effective way to contribute toward electromagnetic induction on neurons, when synaptic coupling is not available. Lu et al. [29] have examined the mode selection in neural activities and has done the corresponding bifurcation analysis under high and low frequency current to study electromagnetic induction of four-variable H–R model with cubic flux-controlled memristor. Their results established that the neuron becomes self-adaptive as it responds to external stimuli. Also, studies of Ge et al. [34] showed that for a magnetic flux driven neuron model, different responses in electrical activities are resulted in under periodic frequency of electromagnetic radiation and in the presence of Gaussian white noise.

Studies of Hudson et al. [35] have identified that the quadratic flux minimizing surfaces can be constructed for toroidal magnetic fields. The memory-based quadratic and exponential flux induction can influence conductance in channels including channel blocking [36]. Also, studies [37] show that mathematical model can interpret the experimental observation of exponential variation of fluxes which permit to evaluate the extent to which the membrane is affected by external flux. Under these contexts, it seems to be relevant to examine influence of quadratic and exponential flux-controlled memristor on neurons.

In the next section the influence of quadratic flux-based memristor on the electric activities properties of improved H–R model is analyzed. The dynamics is examined for periodic and nonperiodic forcing current. Bifurcation diagram of interspike interval versus current and the corresponding Lyapunov exponent for the system is plotted. In Sect. 3, the effect of noise on electromagnetic induction of neuron is examined. Section 4 gives the energy of improved H–R model under quadratic flux and the corresponding numerical analysis. In Sect. 5, the study is extended on coupled neurons under quadratic and exponential flux and the Transverse Lyapunov exponent plot for coupled neurons under quadratic flux is also analyzed.

The studies exhibit the highly interesting rich phenomena such as transitions from the rest state to the firing state and from the spiking state to the bursting states in the four-variable H–R neuron models with these different flux-based memristors. Also, the states exhibit tonic spiking and oscillation deaths under various external conditions. When noise is added to the neuronal model the suppression of these activities is achieved. The mode transitions exhibited are different from that of improved H–R neuron model with cubic flux-controlled memristor in the presence of Gaussian white noise [34, 38].

Numerical analysis of Hamilton energy also supports the different transitions in electrical modes. The energy exhibits discontinuous behavior with respect to the variation of external current. Bifurcation analysis of interspike interval (ISI) versus current also shows difference in behavior when compared to that of ordinary H–R neuron model and improved H–R neuron model with cubic flux-based electromagnetic induction [6]. The irregularity in the behavior of neurons is also examined through Lyapunov exponent plot [39].

For coupled neurons, synchronization behavior of neurons under quadratic flux and noise shows periodic-, chaotic- and tonic-type patterns. The quiescent state and subsequent suppression of oscillations are observed for high values of noise intensity and coupling strength. For exponential flux under noise, the synchronization pattern leads to oscillation death.

2 Electrical activities in an H–R neuron under electromagnetic induction without noise

The general H–R model in an isolated neuron has been extended to an improved model of four variables [6]. The new variable \(\varphi \) incorporate magnetic flux. Hence, this model can be effective to detect the effect of electromagnetic radiation by applying external magnetic flux associated with electromagnetic field on the dynamical equation for magnetic flux.

In this section, the study is done on a four-variable H–R neuron model which is made to interact with quadratic flux-controlled memristor. The memristor magnetic flux is due to the flux arising from the ions.

The four-variable H–R neuron model with quadratic flux can be written as

$$\begin{aligned} \dot{x}_{1}= & {} x_{2} - ax_{1}^{3} + bx_{2}^{2} - x_{3} + I_{\mathrm{ext}} - k\rho \left( \varphi \right) x_{1} \nonumber \\ \dot{x}_{2}= & {} c - \mathrm{d}x_{1}^{2} - x_{2} \nonumber \\ \dot{x}_{3}= & {} r\left( {s\left( {x_{1} - x_{0} } \right) } \right) - x_{3} \nonumber \\ \dot{\varphi }= & {} k_{1} x_{1} - k_{2} \varphi \end{aligned}$$
(1)

Here the variables \(x_1, x_2\) and \(x_3\) represent the membrane potential, slow current recovery variable, and adaption current. The important electrical signal in neurons arises from a big voltage change (of the order of many millivolts) which is termed as action potential or membrane potential (spikes) and it occurs in less than a second for neuron [40]. External forcing current is represented by the term \(I_\mathrm{ext}\) and the magnetic flux across the membrane is denoted by the fourth variable \(\varphi \). The memductance corresponding to the charge \(q\left( \varphi \right) =\alpha \varphi +\beta \varphi ^{3}\) is given by the derivative of q with respect to the flux as \(\alpha +3\beta \varphi ^{2}\) [6, 32]. But it is also appropriate to incorporate the quadratic term dependence for the charge [41], and hence the corresponding memductance after scaling will be \(\alpha \varphi ^{2}+\beta \varphi +\gamma \). It is observed that memductance can affect the conduction of electrons [9] and this term can acts as the influencing magnetic flux on membrane potential of the selected neuron. Also the term \(k\rho \left( \varphi \right) x_1\) denotes induced current and it causes the variation in magnetic flux which in turn generates Faradic current. Relation among induced current, flux and memristor can be understood by Faraday’s law of electromagnetic induction [42] as given below.

$$\begin{aligned} i=\frac{\mathrm{d}q\left( \varphi \right) }{\mathrm{d}t}=\frac{\mathrm{d}q\left( \varphi \right) }{\mathrm{d}\varphi }\frac{\mathrm{d}\varphi }{\mathrm{d}t}=\rho \left( \varphi \right) V=k\rho \left( \varphi \right) x_1 \end{aligned}$$

The parameter values are selected as \(a=1,b=3,c=1,d=5,s=4,r=0.006, x_0 =-1.6\) and \(k_1 x_1\) denotes the changes in magnetic flux induced by membrane potential and \(k_2 \varphi \) represents the leakage of magnetic flux. Also the interaction between membrane potential and magnetic flux is represented by the variables k and \({k}_{2}\). The effect of electromagnetic induction and corresponding modes of electrical activities with memristor could be examined by finding the influence of the magnetic flux on membrane.

2.1 Time series behavior under external nonperiodic current

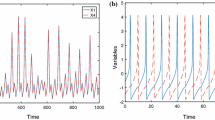
The time series of membrane potential of a neuron is studied under different external forcing current and parameter values. Different electric modes are observed for different external currents. The external current is changed through \(I_\mathrm{ext} =1.5\), 4.5 and 5 mA respectively and the other parameters are chosen as \(k=0.4,k_1 =1\), \(k_2 =0.5,\alpha =0.1, \beta =0.02,\gamma =0.2.\) It is observed that the electrical activity selects different discharge modes under suitable parameter values. The different dynamics resulted are shown through Fig. 1a–d. It is observed that the quiescent states [43] become broadened (Fig. 1b) for the behavior of the membrane potential as the value of external current increases (\(I_\mathrm{ext} = 4.5\,\hbox {mA}\)). Also for higher values of external current \((I_\mathrm{ext} =5\,\hbox {mA})\), the system settles down to oscillation death [6] after a short time (Fig. 1c).

The results of simulations are summarized in Table 1.

2.2 Behavior under external periodic current

To study the influence of periodic external current on neuronal electrical activities, periodic current \(I_\mathrm{ext} =A \cos \,\omega t\) is applied to the system and the dynamics is analyzed. From the plots, it is clear that as external periodic current increases, the action potential shows enhanced quiescent states for the spiking activities and for a higher value of current the neuron system exhibits tonic oscillations in contrast to the suppression of activities observed with the nonperiodic external current described in the previous section. The observation is done for different periodic currents [(a) \(A=0.5,\omega =0.02\), (b) \(A=3,\omega =0.02\) and (c) \(A=5,\omega =0.02\)] and also choosing appropriate parameter values as \(k=1,k_1 =0.9,k_2 =0.5,\alpha =0.4,\beta =0.02\), and \(\gamma =0.2\). Figure 2a shows quiescent state and more quiescent states shows periodic appearances with increase in the intensity of external radiation field (\(A=3,\omega =0.02\)). As external periodic current is increased further (\(A=5,\omega =0.02\)) quiescent state changes to tonic behavior (Fig. 2c).

Fig. 1
figure 1

Variation of action potential with time is plotted for \(I_\mathrm{ext} =1.5\), 4.5 and 5 mA respectively. It is clear from the figure that for high values of external current, the system changes from quiescent state to oscillation suppression behavior

Full size image

The results are summarized in Table 2.

The electrical activities can exhibit different discharge modes by applying external forcing current with appropriate parameter values. The behavior under nonperiodic external current confirmed that neuron can be excited from quiescent state and also states can be suppressed under appropriate intensity of electromagnetic field. The mode transitions in electrical activities can be observed with variation of external periodic current. Here discharge modes even dominated by angular frequency and amplitude. For high amplitude (at \(\omega =0.02\)) the quiescent spiking states give way to tonic behavior.

2.3 Bifurcation diagram and Lyapunov exponent plot

To study the electrical behavior of neurons, it is important to analyze pattern of spikes. The complex bifurcation structures in H–R neuron model [28] mainly help to understand the mechanisms used by the neurons to encode information and its rapid response to stimuli. So bifurcation plot of ISI versus current is important in this respect.

Bifurcation diagram of ISI versus external current of improved H–R neuron model under the influence of quadratic memristor flux is as shown in Fig. 3. Here the pattern of spikes depends on intrinsic property of neurons, nature of input to neurons, and network of interactions.

Table 1 Different types of dynamics of four-variable H–R neuron with quadratic flux under external nonperiodic current
Full size table
Fig. 2
figure 2

Influence of periodic current on membrane potential is shown in figure. Figures are plotted for a \(A=0.5,\omega =0.02\), b \(A=3,\omega =0.02\) and c \(A=5, \omega =0.02\), respectively. The behavior of membrane potential gets changed through quiescent spiking states to tonic behavior as the external periodic current becomes high

Full size image

On Comparing with the study of bifurcation diagram of cubic flux-based improved H–R model [29, 34], it is observed that for improved H–R neuron model with quadratic flux memristor the bifurcation diagram of ISI versus external forcing current is more dense exhibiting the possibility of higher number of periods and hence of more complexity.

The dynamics and hence the anisotropy due to the effect of electromagnetic radiation on neurons is also examined through Lyapunov exponent plot (Fig. 4). Here variation of Lyapunov exponent versus external current is plotted for improved H–R neuron model with quadratic flux-controlled memristor. This plot establishes the chaotic nature of the system. Hence the improved H–R model can produce chaotic electrical modes.

3 Effect of noise on electromagnetic induction of neurons

Noise can affect the transmission of periodic signals by nonlinear systems. Studies show [44] that external noise sources can influence neuronal systems and hence the important parameters like intensity and correlation time of noise can play remarkable role in transmission of signals among the neurons.

Here noise term is added to the fourth variable of Eq. (1). The parameter values are selected as given in Sect. 2. The irregularity of electromagnetic radiation is represented by Gaussian white noise term \(\xi ( t )\) [44]. Here \(\langle \xi ( t )\rangle =0, \langle \xi ( t )\xi ( t' )\rangle = 2D_0 \delta (t-t')\) where \(D_o\) represents the noise intensity.

$$\begin{aligned} \dot{x}_{1}= & {} x_{2} - ax_{1}^{3} + bx_{2}^{2} - x_{3} + I_{\mathrm{ext}} - k\rho ( \varphi )x_{1} \nonumber \\ \dot{x}_{2}= & {} c - \mathrm{d}x_{1}^{2} - x_{2} \nonumber \\ \dot{x}_{3}= & {} r\left( {s\left( {x_{1} - x_{0} } \right) } \right) - x_{3} \nonumber \\ \dot{\varphi }= & {} k_{1} x_{1} - k_{2} \varphi + \xi \left( {t~} \right) \end{aligned}$$
(2)

3.1 Influence of noise under external periodic and nonperiodic currents

Noise term is introduced as given in Eq. (2) keeping all the other parameters the same. For nonperiodic current, the variation of membrane potential with time exhibits the same dynamics as that of noiseless system (Fig. 1a, b). But the magnitude of external current needed to achieve suppression of oscillation gets reduced compared to that of the system without noise (Fig. 1c) and also it occurs at an earlier time. For \({I}_{\mathrm{ext}} =4.2\) mA and for noise intensity \(D_{0}=0.1\) suppression of oscillation takes place (Fig. 5) and same behavior persists for higher noise values.

As the current is changed to the periodic one, for amplitude \(A=1.6\), the resulting oscillations are shown in Fig. 6. Further for the amplitude and frequency \(A=3\) and \(\omega =0.02\), respectively, the addition of noise leads to tonic-type behavior similar to Fig. 2c instead of quiescent states exhibited in Fig. 2b. Hence the discharge modes are highly influenced by the amplitude. So it is important that in contrast to the behavior of the system in noiseless background the effect of noise in the presence of periodic current inhibits the quiescent behavior for low values of amplitude of external current. The system exhibits the tonic-type oscillation in the presence of noise as time progresses. But the presence of noise did not alter the time series plot for the values \(A=0.5,\omega =0.02\) and \(A=5,\omega =0.02\) (Fig. 2a, c).

4 Energy for improved H–R neuron model under the influence of quadratic memristor flux

Hamilton energy can be calculated on chaotic neural systems with different types of attractors [45]. The energy modulation helps to control chaos in various systems. The negative feedback in energy can suppress the phase space and oscillating behaviors, and it in turn can control the chaotic and periodic oscillators. So the calculation and analysis of Hamilton energy in neuronal chaotic and hyperchaotic systems are relevant in this context.

In this section based on the Helmholtz theorem, the Hamilton energy is calculated. It helps to discern the energy dependence on the mode selection of the electric activities of neuron. Here the statistical Hamilton energy [26, 46] is calculated and it can be used to find out the relation among action potential, transition of electric activities of neurons in terms of external forcing and energy. According to Helmholtz theorem, the dynamical equations for neuron can be treated as velocity vector field [47] and this can include sum of two vector fields. These vector fields represent the dissipative and conservative fields. So the system can be represented as sum of two sub-vector fields as shown below

$$\begin{aligned} f\left( r \right) = f_d \left( r \right) + f_c \left( r \right) \end{aligned}$$
(3)

So the dynamical system given by Eq. (1) can be represented written as

$$\begin{aligned} \left( {{\begin{array}{l} {\dot{x}}_1 \\ {\dot{x}}_2 \\ {\dot{x}}_3 \\ \varphi \\ \end{array} }}\right)= & {} [J(x_1 ,x_2 ,x_3 ,\varphi )+R\left( {x_1 ,x_2 ,x_3 ,\varphi } \right) ]\nabla H\nonumber \\= & {} f_c \left( {x_1 ,x_2 ,x_3 ,\varphi } \right) +f_d \left( {x_1 ,x_2 ,x_3 ,\varphi } \right) \end{aligned}$$
(4)

where \(J (x_1 ,x_2 ,x_3 ,\varphi )\) and \(R\left( {x_1 ,x_2 ,x_3 ,\varphi }\right) \) represent skew symmetric matrix which satisfies the Jacobi’s closure condition.

Table 2 Dynamics of four-variable H–R neuron with quadratic flux under external periodic current
Full size table
Fig. 3
figure 3

Bifurcation diagram of ISI versus current for four-variable H–R neuron with quadratic flux-controlled memristor

Full size image
Fig. 4
figure 4

Dynamics of Lyapunov exponent versus parameter for improved H–R neuron model with quadratic flux-controlled memristor

Full size image
Fig. 5
figure 5

Variation of action potential under nonperiodic current and noise. It is observed that when \({I}_{\mathrm{ext}} =4.2\) mA and for noise intensity \(D_{0}=0.1\) suppression of oscillation takes place

Full size image
Fig. 6
figure 6

Variation of action potential under the influence periodic current and noise. It is observed that when \(A=1.6,\omega =0.02\) and noise intensity \(D_0 =0.9\), the quiescent state later on changes to oscillations.

Full size image

So

$$\begin{aligned} f_c \left( {x_1 ,x_2 ,x_3 } \right)= & {} J(x_1 ,x_2 ,x_3 ,\varphi )\nabla H\nonumber \\= & {} \left( {{\begin{array}{c} {x_2 -x_3 +I_\mathrm{ext} -\varphi } \\ {c-\mathrm{d}x_1^2 } \\ {r\left( {s\left( {x_1 -x_0 } \right) } \right) } \\ {k_2 x_1 } \\ \end{array} }} \right) \end{aligned}$$
(5)

and

$$\begin{aligned} f_d \left( {x_1 ,x_2 ,x_3 ,\varphi } \right) = \left( {{\begin{array}{c} {-\,ax_1^3 +bx_1^2 -k\rho \left( \varphi \right) x_1 +\varphi } \\ {-\,x_2 } \\ {-\,rx_3 } \\ {-\,k_3 \varphi } \\ \end{array} }} \right) \end{aligned}$$
(6)

The general Hamilton energy function H is defined by the criterion

$$\begin{aligned} \nabla H^{T}f_c \left( {x_1 ,x_2 ,x_3 ,\varphi } \right)= & {} 0\nonumber \\ \nabla H^{T}f_d \left( {x_1 ,x_2 ,x_3 ,\varphi } \right)= & {} \frac{\mathrm{d}H}{\mathrm{d}t}=\dot{H} \end{aligned}$$
(7)

So energy can be obtained by substituting Eqs. (4) and (5) in Eq. (1) and can be written as

$$\begin{aligned}&(x_2 -x_3 +I_\mathrm{ext} -\varphi )\frac{\partial H}{\partial x_1 }+ \left( {c-\mathrm{d}x_1^2 } \right) \frac{\partial H}{\partial x_2 }\\&\quad +\,rs\left( {x_1 -x_0 } \right) \frac{\partial H}{\partial x_3 }+k_2 x_1 \frac{\partial H}{\partial \varphi }=0 \end{aligned}$$

Solution of above equation can be written as

$$\begin{aligned} H= & {} \frac{2}{3}\mathrm{d}x_1^3 -2cx_1 +rs\left( {x_1 -x_0 } \right) ^{2}\nonumber \\&+\,\left( {x_2 -x_3 +I_\mathrm{ext} -\varphi } \right) ^{2}+k_2 x_1^2 \end{aligned}$$
(8)

Hence time variation of Hamilton energy is given by

$$\begin{aligned} \dot{H}= & {} 2\mathrm{d}x_{1}^{2} \dot{x}_{1} - 2c\dot{x}_{1} + 2rs\left( {x_{1} - x_{0} } \right) \dot{x}_{1} \nonumber \\&+ \,2\left( {x_{2} - x_{3} + I_{\mathrm{ext}} - \varphi }\right) (\dot{x}_{2} - \dot{x}_{3} - \dot{\varphi })+2k_{2} \dot{x}_{1} x_{1}\nonumber \\ \end{aligned}$$
(9)

On substituting the values of \(\dot{x}_{1} ,~\dot{x}_{2} ,~\dot{x}_{3}\) and \(\dot{\varphi }\) in the above equation and rearranging the terms, we get derivative of energy as

$$\begin{aligned} \dot{H}= & {} 2 \mathrm{d}x_1^2 \left( {x_2 -ax_1^3 +bx_1^2 -x_3 +I_\mathrm{ext} -k_1 \rho \left( \varphi \right) x_1 } \right) \nonumber \\&-\,2c\left( {x_2 -ax_1^3 +bx_1^2 -x_3 +I_\mathrm{ext} -k_1 \rho \left( \varphi \right) x_1 } \right) \nonumber \\&+\,2rs\left( {x_1 -x_0 } \right) \left( x_2 -ax_1^3 +bx_1^2 -x_3 +I_\mathrm{ext} \right. \nonumber \\&\left. -\,k_1 \rho \left( \varphi \right) x_1 \right) +2\left( {x_2 -x_3 +I_\mathrm{ext} -\varphi } \right) (c-\mathrm{d}x_1 ^{2}\nonumber \\&-\,x_2 -rs(x_1 -x_0 )+rx_3 -k_2 x_1 +k_3 \varphi \end{aligned}$$
(10)

Again on rearranging the terms in Eq. (10) we get

$$\begin{aligned} \dot{H}= & {} 2\mathrm{d}x_1^2 -2c+2rs\left( {x_1 +1.6} \right) \nonumber \\&+\,2k_2 x_1 \left( {-ax_1^3 +bx_1^2 -k_1 \rho \left( \varphi \right) x_1 +\varphi } \right) \nonumber \\&+\,2\left( {x_2 -x_3 +I_\mathrm{ext} -\varphi } \right) \left( {-x_2 } \right) \nonumber \\&-\,2\left( {x_2 -x_3 +I_\mathrm{ext} -\varphi } \right) \nonumber \\&+\,\left( {-rx_3 } \right) -2\left( {x_2 -x_3 +I_\mathrm{ext} -\varphi } \right) \left( {-k_3 \varphi } \right) \nonumber \\= & {} \nabla H^{T}f_{d} \end{aligned}$$
(11)

The energy function in neuron shows distinct dependence on external forcing current \(I_\mathrm{ext}\) and the action potential \(x_1\) and thus discharge states are obtained. So the Hamilton energy gives the fluctuation of energy function associated with external forcing. This explains why the neuron can give appropriate response to external forcing which supplies continuous energy for neurons.

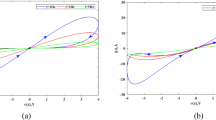
Numerical analysis of system is also done (Fig. 7). The variation of Hamilton energy with external forcing current shows discontinuity in behaviors [47].

Fig. 7
figure 7

a External current variation with time, b variation of average of Hamilton energy with respect to current. Here low value of current gives quiescent state and high value of current leads to tonic-type transitions

Full size image

The plot for the variation of average value of Hamilton energy with current shows a plateau for low values of current which explains the presence of the quiescent state [46, 47] in Fig. 2a. For increased current its behavior get changed through its irregularity and for values high values of external current high frequency tonic-type transitions are obtained. To be specific, when amplitude of external current increases beyond 5 mA, the Hamilton energy increases linearly and hence the appearance of tonic spiking described in Sect. 2.2 is justified.

Fig. 8
figure 8figure 8

Time series for membrane potentials for the two coupled neurons are plotted for different external forcing current. For \(I_\mathrm{ext} =1.5\), 2.5, 3.5, and 4.5 mA the synchronization behavior of the system of neurons changes through periodic, chaotic and finally through tonic-type synchronization

Full size image
Fig. 9
figure 9

Time series for membrane potentials are plotted for fixed external forcing current (\(I_{ext} = 3.5\) mA). The synchronization behavior of the system of neurons is achieved with control parameter values \(g = 1, D = 0\) and the system attains oscillation death state for higher coupling (\(g = 1\) and \(D = 0.9\) ) in the presence of high noise

Full size image
Fig. 10
figure 10

The TLE of coupled improved H–R neuron model with quadratic flux induction

Full size image
Fig. 11
figure 11

Time series for membrane potentials are plotted for different external forcing current \(I_\mathrm{ext} =2.5\,\hbox {mA}\), \(I_\mathrm{ext}=3.5\,\hbox {mA}\) and \(I_\mathrm{ext} =4.5\,\hbox {mA}\). As magnitude of external forcing current increases, the synchronization pattern changes to oscillation death state

Full size image
Fig. 12
figure 12

Time series for membrane potentials are plotted for different coupling strength and noise intensity. Various patterns such as a antiphase (\(g=0.01,D=0.9\)), b chaotic (\(g=0.5, D=1\)) and c periodic (\(g=1, D=0.3\)) behavior are observed for appropriate values of noise intensity and coupling strength

Full size image

5 Synchronization under electromagnetic induction and noise

5.1 Quadratic flux-controlled memristor for coupled neurons

It is possible to control the activity of neurons by magnetic forces which in turn control the flow of ions into specifically targeted cells [48]. Here coupling is introduced to modified four-variable H–R neuron models where quadratic flux-controlled memristor-based electromagnetic radiation is present.

$$\begin{aligned} \dot{x}_{1}= & {} x_{2} - ax_{1}^{3} + bx_{2}^{2} - x_{3} + I_{\mathrm{ext}} - k\rho \left( {\varphi _{1} } \right) x_{1} \nonumber \\&+ \,g\left( {x_{4} - x_{1} } \right) \nonumber \\ \dot{x}_{2}= & {} c - \mathrm{d}x_{1}^{2} - x_{2} \nonumber \\ \dot{x}_{3}= & {} r\left( {s\left( {x_{1} - x_{0} } \right) } \right) - x_{3} \nonumber \\ \dot{\varphi }= & {} k_{1} x_{1} - k_{2} \varphi _{1} + \xi \left( t \right) \nonumber \\ \dot{x}_{4}= & {} x_{5} - ax_{4}^{3} + bx_{5}^{2} - x_{6} + I_{\mathrm{ext}} - \,k\rho \left( {\varphi _{2} } \right) x_{4}\nonumber \\&+ \,g\left( {x_{1} - x_{4} } \right) \nonumber \\ \dot{x}_{5}= & {} c - \mathrm{d}x_{4}^{2} - x_{5} \nonumber \\ \dot{x}_{6}= & {} r\left( {s\left( {x_{5} - x_{o} } \right) } \right) - x_{5}\nonumber \\ \dot{\varphi }= & {} k_{1} x_{4} - k_{2} \varphi _{2} + \xi \left( t \right) \end{aligned}$$
(12)

Here \(x_1 ,x_2 ,x_3\) and \(I_\mathrm{ext}\) represent the membrane potential, slow current associated with the recovery variable, adaptation current term and external forcing current respectively for the first neuron. Similarly \(x_4 ,x_5\) ,and \(x_6\) represent the corresponding variables for the second neuron. The parameter values are selected as \(a=1,b=3,c=1,d=5,r=0.006,s=4,x_0 =-1.6\).

The memristance of quadratic flux-controlled memristor is represented by \(\rho \left( \varphi \right) =\alpha \varphi ^{2}+\beta \varphi +\gamma .\) Since this term is associated with the memory it is used for estimating the effect of feedback regulation on membrane potential when corresponding magnetic flux is changed. The term g represents the coupling intensity between the neurons. Here the irregularity of electromagnetic radiation is represented by Gaussian white noise term \(\xi \left( t \right) \). It is found that the synchronization degree depends on the coupling intensity and the intensity of external electromagnetic radiation.

Time series plots of membrane potentials (\(x_1\) and \(x_4\)) for coupled H–R neurons (Fig. 8) confirm the synchronization pattern. Here the parameter values are \(k=0.4\), \(k_1 =0.8\), \(k_2 =0.5\), \(D_o =0.6\), \(\alpha =0.02,\beta =0.1\), \(\gamma =0.1\), \(g=1\). Depending upon the parameter values and external forcing current \(I_\mathrm{ext},\) various synchronization phenomena are observed. For \(I_\mathrm{ext} =2.5\,\hbox {mA}\), the synchronization behavior of the system shows periodic behavior. Also when the external forcing current is set as \(I_\mathrm{ext} =3.5\,\hbox {mA}\) chaotic synchronization resulted in. The mode transition from chaotic totonic synchronization states are detected by imposing larger external forcing current \((I_\mathrm{ext} =5\,\hbox {mA})\). Hence it is remarkable to note that as the value of external current increases the dynamical behaviors such as periodic-, chaotic-, and tonic-type synchronizations are observed.

In a similar way by keeping the external current fixed as \(I_\mathrm{ext}=3.5\,\hbox {mA}\) and changing the coupling parameter and noise intensity as (a) \(g=0,D=0\), (b) \(g=1,D=0\) and (c) \(g=1\) and \(D=0.9\) various patterns are observed. When there is no influence of coupling (\(g=0\)) and with no noise intensity (\(D=0\)), the two different neurons behave independently as it must be Fig. 9a. The behavior is retained with the case where the noise intensity is raised to maximum (same behavior as that of Fig. 9a). But as the two neurons are coupled, for high value of coupling strength and in absence of noise intensity, synchronization of the system takes place (Fig. 9b). Finally quiescent state and subsequent suppression of oscillation effects are observed for appropriate high values of noise intensity and coupling strength (Fig. 9c).

5.1.1 Transverse Lyapunov plot for quadratic flux-based memristor

The stability of synchronization can be quantified by master stability approach [49]. The synchronization is stable if the master stability function is negative at each of transverse eigenvalues (Fig. 10).

The largest TLE crosses zero and becomes negative indicating synchronized state and its stability.

5.2 Influence of exponential flux-controlled memristor on coupled neurons

The work is extended to examine neuron dynamics under the influence of exponential flux-controlled memristor where the neurons are allowed to interact with each other.

$$\begin{aligned} \dot{x}_{1}= & {} x_{2} - ax_{1}^{3} + bx_{2}^{2} - x_{3} + I_{\mathrm{ext}} - k\rho \left( {\varphi _{1} } \right) x_{1}\nonumber \\&+\, g\left( {x_{4} - x_{1} } \right) \nonumber \\ \dot{x}_{2}= & {} c - \mathrm{d}x_{1}^{2} - x_{2} \nonumber \\ \dot{x}_{3}= & {} r\left( {s\left( {x_{1} - x_{0} } \right) } \right) - x_{3} \nonumber \\ \dot{\varphi }= & {} k_{1} x_{1} - k_{2} \varphi _{1} + \xi \left( t \right) \nonumber \\ \dot{x}_{4}= & {} x_{5} - ax_{4}^{3} + bx_{5}^{2} - x_{6} + I_{\mathrm{ext}} - k\rho \left( {\varphi _{2} } \right) x_{4} \nonumber \\&+ \,g\left( {x_{1} - x_{4} } \right) \nonumber \\ \dot{x}_{5}= & {} c - \mathrm{d}x_{4}^{2} - x_{5} \nonumber \\ \dot{x}_{6}= & {} r\left( {s\left( {x_{5} - x_{0} } \right) } \right) - x_{5}\nonumber \\ \dot{\varphi }= & {} k_{1} x_{4} - k_{2} \varphi _{2} + \xi \left( t \right) \end{aligned}$$
(13)

The parameter values are selected as \(a=1,b=3,c=1,{d}=5,{r}=0.006,s=4,k_1 =0.9, k_2 =0.5\).

The exponential flux-controlled memristor [50] is represented as

$$\begin{aligned} q\left( \varphi \right) =k_3 \left( {a_1 ^{b_1 \varphi }-1} \right) \end{aligned}$$
(14)

where \(a>1\) and \(k_3 b_1 >0\). The memductance of the function is \(\rho \left( \varphi \right) =a_1 ^{b_1 {\upvarphi }}k_3 b_1 lna_1 \). Here \(a_1= e\), \(b_1 =50\log \left( {0.5} \right) \) and \(k_3 =10\).

As the values of external current changes, the synchronization pattern shows various patterns as depicted in Fig. 11a–c. When \(I_\mathrm{ext} =2.5\,\hbox {mA}\) synchronization behavior is resulted in. Also as the magnitude of external forcing current increases (\(I_\mathrm{ext} =3.5\,\hbox {mA}\)), the synchronization pattern shows tonic oscillations. Finally oscillation death state is achieved with appropriate value of external forcing current (\(I_\mathrm{ext} =5\,\hbox {mA}\)).

On comparing with the dynamics corresponding to quadratic flux-controlled memristor, it is interesting to find that for same coupling strength and for same noise intensity (\(g=1\) and \(D_\mathrm{o}=0.6\)), instead of the tonic behavior, the system sets into oscillation death state for higher magnitude of external forcing current in the case of exponential flux-controlled system.

Further by keeping the external current fixed at \(I_\mathrm{ext} =3.5\,\hbox {mA}\) and changing the coupling parameter and noise intensity terms as (a) \(g=0.01,D=0.9\), (b) \(g=0.5, D=1\), and (c) \(g=1,D=0.3\) various patterns are obtained. It is observed that for low values of coupling strength and noise intensity the system exhibits antiphase state (Fig. 12a). The behavior is preserved as noise intensity is stepped up (the pattern is same as that of Fig. 12a). As g is increased to 0.5 keeping the noise intensity as1, the behavior of membrane potential gets changed to chaotic synchronized state (Fig. 12b). But the decrease in intensity of noise to \(D=0.3\), at high coupling strength, causes the time series dynamics to change into that of periodic one (Fig. 12c).

Depending upon the low and high values of noise and coupling parameters antiphase state of the system gives way to chaotic- and then to periodic-type synchronization patterns.

On comparing with the synchronized and oscillation death states found in coupled neurons with quadratic flux-based memristor, the system with exponential flux-based memristor exhibits chaotic- and periodic-type synchronization state.

6 Discussions and concluding remarks

The essence of brain function consists in how the information is being processed, transferred and stored. The neuroelectronynamic model (NED) [51] is an emerging field which describes the intrinsic computational processes by the dynamics and interaction of charges.

Various studies [6, 29, 32, 42] had been carried out on the effect of electromagnetic induction on H–R neuron under the influence of cubic flux-controlled memristor. In the present work influence of quadratic flux and exponential flux-based inductions in four-variable H–R neuron model is studied. In the first part, we analyzed the different modes of electrical activities in single neuron under quadratic memristive term. The system behavior is studied under the influence of external periodic and nonperiodic current. It is observed that for nonperiodic current, as the value of external current increases the quiescent states [43] become broadened and also for higher values of external current, the system settles down to oscillation death state. However, for the periodic current, the action potential shows enhanced quiescent states for the spiking activities and for the higher current the neuron exhibits tonic oscillations in contrast to the suppression of activities observed in nonperiodic case. So in quadratic flux-based mode transition, when compared to cubic flux memristor [6, 29, 34] the suppression of oscillations is an additional feature.

The influence of control parameter like noise on the neurons is also subjected to study. It is found that when noise is added to the system, the oscillation death is achieved for smaller magnitude of external current. Also the presence of noise leads to the inhibition of quiescent activity under periodic current. The Lyapunov exponents are plotted which confirm irregularity in the neuron dynamics.

Energy is calculated in terms of Hamilton energy to understand the neuron response to external forcing current and action potential. It is observed that the plot for Hamilton energy versus current shows discontinuity in behavior. There is a plateau for low values of current which explains the presence of the quiescent states and as current increases tonic behavior is resulted in. Bifurcation of ISI versus current is also plotted, and it shows denser pattern as compared with that of cubic flux-based electromagnetic induction.

The synchronization of coupled neurons also is the focus of study. Under the influence of quadratic flux and noise term the system changes through periodic-, chaotic- and tonic-type synchronization as the current is increased. The variation of noise intensity and coupling strength leads to oscillation death of these coupled neurons under constant current. Transverse Lyapunov exponent plot gives a picture of the stability of the coupled system. The effect of exponential flux-controlled memristor-based electromagnetic induction on neurons when coupled is also examined. With exponential flux-controlled memristor the activity changes to tonic-type synchronization with increase in forcing current. Here the synchronization pattern displays oscillation death, antiphase, periodic, and chaotic transitions.

The work gives a pathway to understand electromagnetic flux influence on the overall activity of neurons. The activity of neurons is examined with quadratic and exponential flux-based memristor. Brain produces an electromagnetic field with specific characteristics. Also Electromagnetic waves are produced due to artificial nanosynapses. The memristor as magnetic flux can also influence neuromorphic quantum computation.

The effect of field coupling under the influence of Levy noise on the electromagnetic properties of neuron with quadratic flux is the future focus of study. In the presence of field coupling and non-Gaussian-type noise like Levy noise, studies may exhibit improved electrical activity of neuronal network with information exchange in the absence of the synapse.