Fourth body gravitation effect on the resonance orbit characteristics of the restricted three-body problem

Abstract

In this paper, the gravitational effect of a fourth body on the resonance orbit defined in the restricted three-body problem (RTBP) is considered. In this regard, Resonance Hamiltonian of the RTBP and the Hamiltonian associated with the fourth gravitational body that perturbs the resonance orbit are computed. The Melnikov approach is utilized as a mean for the detection of chaos in resonance orbit under the influence of the fourth gravitation body. In addition, the numerical simulation of RTBP and bicircular four-body model, time–frequency analysis (TFA), and fast Lyapunov indicator (FLI) are performed to verify the results of the Melnikov approach. The results indicate that for the (2:1) resonance orbit, the Melnikov integral computed over outer loop of separatrix does not cross the zero line, and consequently chaos is unexpected. On the other hand, the Melnikov integral computed over the inner sepratrix loop crosses the zero line indicating a potential for chaos. Similarly, it is shown that inclusion of the fourth body gravitation leads the (3:1) as well as the (4:1) resonance orbits to chaos. Additionally, simulation results indicate that for some initial conditions on the separatrix, the fourth body effect bounds the amplitude of the resonance orbits while diffusing its corresponding trajectory in the bounded phase space. TFA and the FLI verify similar results.

1 Introduction

Chaos in the RTBP has been investigated in a few researches using various approaches. The simplest effective numerical method for chaos detection is through Poincare section [1, 2]. Other numerical methods such as fast Lyapunov indicator (FLI) [3] and time–frequency analysis (TFA) [4] have also been used to detect chaotic regions of the RTBP.

Resonance overlap criterion is among the analytical methods to explore chaos in dynamical system [5]. Resonance overlap for the onset of stochastic behavior has been applied to RTBP with small mass ratios where regions at which two resonances overlap is identified in term of semi-major axis and eccentricity [6]. Unfortunately, many phenomena and concepts observed in RTBP do not remain the same in the four-body problem [7], such as libration point, halo orbit, etc. In other words, equilibrium points (libration) do not exist in the four body, and instantaneous equilibrium points as well as halo orbit geometry are different [8]. A pertinent question of interest is how resonance orbits of RTBP change in the context of the four body problem?

Definition of resonance in the four-body problem (bicircular four body problem) is not simple or similar to that of the three-body problem. In other words, a (p:q:r) resonance should be used instead of (p:q) resonance. At RTBP, for example, (2:1) resonance in Earth–Moon system means that Satellite revolves 2 times around the Earth when Moon revolves 1 time around Earth. In the Sun–Earth–Moon–Satellite four-body problem, the values of the resonance parameters p and q are fixed as (1,12,r), which mean Sun revolves once when Moon revolves 12 times and the Satellite x times around Earth. Instead of defining new resonance parameters, we can implicitly study the effect of a fourth body (Sun) on the resonances defined in the three-body problem (Earth–Moon–Satellite). In the present paper, the Melnikov integral [9], TFA, and fast Lyapunov exponent are utilized to specifically detect an answer to the question of “Can a fourth body gravitational attraction cause resonance orbit of the RTBP to become chaotic.” Results obtained in this study indicate that the fourth body gravitation can cause resonance orbits of the RTBP to become chaotic. And on the other hand, for some initial conditions the fourth body effect can bound the growing motion of the resonance trajectory while diffusing it in the phase space.

This paper is arranged as follows: Sect. 2 presents the derivation of the Hamiltonian of the RTBP in terms of Delaunay variables. In Sect. 3, Zeroth-Order Hamiltonian resonance of the RTBP is derived, and consequently, the Hamiltonian of the fourth body gravitation effect on resonance separatrix equation is obtained in Sect. 4. At Sect. 4.1, Melnikov theory is used for detection of chaotic phenomena for resonance orbit defined in RTBP under influence of fourth gravitational effect. At Sects. 4.2 and 4.3, FLI and TFA have used as another method for detection of chaos in mentioned problem.

2 Restricted three-body problem Hamiltonian

The equation of motion of a negligible mass $P_2$ (Satellite) under the gravitational force of two massive bodies $P_1$ (Earth) and $P_2$ (Moon) rotating in circular orbit around their center of masses, in the Earth centric frame, is presented [10]:

$$\begin{aligned} \frac{\mathrm{d}^{2}r_2}{\mathrm{d}t^{2}}+\mu \frac{r_2}{\rho _2^3} = -\varepsilon \frac{\partial R}{\partial r_2}, \end{aligned}$$

(1)

where

$$\begin{aligned}&R = \frac{\vec {r}_3\cdot \vec {r}_2}{\rho _3^3}-\frac{1}{\left| {\vec {r}_3 -\vec {r}_2}\right| },\nonumber \\&\quad \mu = G(m_1 + m_2), \varepsilon = Gm_3. \end{aligned}$$

(2)

The perturbation term R can be written using the Legendre polynomial [10]:

$$\begin{aligned} R = -\frac{1}{\rho _3}\sum _{j = 2}^\infty {P_j (\cos S) \left( {\frac{\rho _2}{\rho _3}}\right) ^{j}}, \end{aligned}$$

(3)

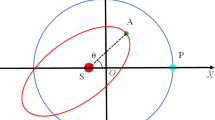
where S is the angle between the Earth–Satellite and Earth–Moon vectors, as shown in Fig. 1. Noting that cosine of S can be written in terms of the orbital parameters $\Omega , \omega$, J, and f [11] as follows:

$$\begin{aligned}&\cos S = \left( {1-\frac{1}{4}\gamma ^{2}}\right) \cos (\psi -\psi _M) \nonumber \\&\quad + \frac{1}{4}\gamma ^{2}\cos (\psi +\psi _M -2\Omega )\nonumber \\&\psi = \Omega +\omega +f = \varpi +f,\quad \psi _M = \Omega +\omega _3\nonumber \\&\quad + f_3 = \varpi _3 + f_3,\;\sin J = \gamma . \end{aligned}$$

(4)

Next the Hamiltonian function of the RTBP is defined. This Hamiltonian consists of the two parts, one independent of the inclination angle, denoted by $H_0$ and another part $H_2$, in terms of $\gamma ^{2}$ as follows:

$$\begin{aligned} H = -\frac{\mu ^{2}}{2L^{2}}-G+\varepsilon R = H_0 +\gamma ^{2}H_2 \end{aligned}$$

(5)

Fig. 1

Restricted three-body problem

In other words, $H_0$ can be considered as the Hamiltonian of the planar motion. Note that $H_0$ and $H_2$ contain terms such as $r_2^i, r_3^j, \cos (k_1 \varpi _3 +k_2 \varpi +k_3 f_3 +k_4 f+k_5 \Omega )$. Through expansion of $\cos (f),r_2$ and $r_3$ in terms of the mean anomalies: $l,l_3$, and eccentricities: $e,e_3$, the system Hamiltonian can be written in term of the Delaunay variables. This Hamiltonian will be a function of $a,a_3,e,e_3,L,G$ as well as the trigonometric function $\cos (i(\omega _3 -\omega )+jl_2 +kl_3)$. Since the mean anomaly motion of the Moon ($P_3$) $l_3$ is smaller than the mean motion of the Satellite, so $l_3$ is neglected in the derived Hamiltonian. Additionally, Moon’s Argument of perigee $\omega _3$ is replaced with mean motion or $\omega _3 = nt$. The non-dimensional Moon mean motion is equal to one, n $=$ 1, in the RTBP. In addition, the following parameters are taken for the current problem:

$$\begin{aligned} a_3 \!=\! 1,\;e_3 = 0.0549006,\;\varepsilon = \frac{\hbox {Moon mass}}{\hbox {Earth mass}} \!=\! 0.0123. \end{aligned}$$

Replacing the eccentricity and the semi-major axis using Eq. (6) makes the Hamiltonian function only in terms of the Delaunay variables.

$$\begin{aligned} e = \sqrt{1-\frac{G^{2}}{L^{2}}}, \quad a = \frac{L^{2}}{\mu } \end{aligned}$$

(6)

3 Zeroth-order resonance Hamiltonian

Resonance occurs when one of the cosine arguments is nearly stationary. Since Hamiltonian is time dependent, the resonance condition will then be [6]

$$\begin{aligned} 0 = -s\omega _l (L,G)+(s+s^{\prime })\left[ {1-\omega _\omega (L,G)}\right] \end{aligned}$$

(7)

In order to obtain Poincare resonance variables, the following canonical transformations are defined:

$$\begin{aligned} \begin{array}{l} \phi = l+\omega -t \\ \psi = -sl+(s+s^{\prime })(t-\omega ) \\ \end{array} \end{aligned}$$

(8)

The generating function of the defined canonical transformation can be written as

$$\begin{aligned} F = \left[ {-sl+(s+s^{\prime })(t-\omega )}\right] \Psi +\left[ {l+\omega -t}\right] \Phi \nonumber \\ \end{aligned}$$

(9)

Finally, by substituting the resonance variables in Hamiltonian and keeping only the trigonometric cosine functions that depend on the slow rate resonance angle $\psi$, we will have the zero-order resonance Hamiltonian.

$$\begin{aligned} H_{ss^{\prime }}^0&= -\frac{1}{2(\Phi -s\Psi )^{2}}+(s+s^{\prime })\Psi \nonumber \\&-\,\Phi -\varepsilon \sum _{i = 1}^\infty {K_i \cos i\psi } \end{aligned}$$

(10)

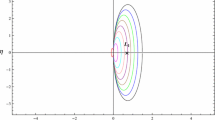
Resonance Hamiltonian is of constant value, and so by assuming constant values for $\Phi$, the resonance behavior of RTBP can be plotted in terms of $\left( {\Psi ,\psi }\right)$ in a 2D-plane (Fig. 2). Zeroth order (2:1) resonance contours for different values of $\Phi$ are shown in Fig. 3, where the separatrix is obtained for $\Phi = 0.98$, shown by dashed lines.

Fig. 2

Zero-order resonance Hamiltonian contours

Fig. 3

Melnikov function of (2:1) resonance for $\Phi =$ 0.98. a inner loop and b outer loop

4 Effect of fourth body gravitation on the resonance separatrix

One can drive the equation of motion [6], if the system is at resonance using the zeroth-order Hamiltonian.

$$\begin{aligned} \dot{\Psi }&= -\frac{\partial H_{ss^{\prime }}^0}{\partial \psi } = -\varepsilon \sum _{i = 1}^\infty {k_i \sin i\psi }\nonumber \\ \dot{\psi }&= \frac{\partial H_{ss^{\prime }}^0}{\partial \Psi } = -\frac{s}{(-s\Psi +\Phi )^{3}}+s+s^{\prime } \end{aligned}$$

(11)

Defining the state vector $x = \left[ {\begin{array}{ll}\Psi &{} \psi \\ \end{array}}\right] ^{T}$, allows one to represent the governing equations of motion (11) in state-space format $\dot{\vec {x}} = f(\vec {x})$. In this form, the Effect of a fourth body (Sun) on the resonance can be considered as a perturbation:

$$\begin{aligned} \dot{\vec {x}} = f(\vec {x})+\varepsilon g(\vec {x},t), \end{aligned}$$

(12)

where $g(\vec {x},t)$ is the perturbation effect of the fourth mass. In the following section, the derivation of $g(\vec {x},t)$ for the bicircular four-body problem is presented. In this regard, pertinent geometry, equation of motion, and its associated Hamiltonian are provided.

Utilizing Newton’s gravitational law, the equation of motion is initially determined. Subsequently, with expansion of the trigonometric parts of the associated Hamiltonian in terms of the Delaunay variables, the perturbation Hamiltonian will be derived in terms of resonance variables. Details of these derivations are presented in the Appendix of this paper.

As for the bicircular four-body Hamiltonian (Eq. 39), $\psi$ and $\phi$ angles are respectively of low and high frequency, magnitudes of $n_S t$ and $l_4$ (Sun mean motion) are smaller with respect to other terms, one can neglect $n_S t$ and $l_4$ and compute the average over the high frequency angle resulting in the average Hamiltonian (for 2:1 resonance) given by Eq. (13):

$$\begin{aligned}&\mathrm{Ham}_{2:1}^\mathrm{fourth} = -\frac{7.068}{\rho _4^2}\Psi ^{2}\Phi ^{2}\Gamma R_S^3\nonumber \\&\quad +\frac{9.15\times 10^{-10}}{\rho _4^2}\Psi ^{2}\cos \left( {6\psi }\right) \Phi ^{2}\Gamma R_S^3\nonumber \\&\quad -\frac{1.13\times 10^{-8}}{\rho _4^2}\Psi ^{2}\cos \left( {2\psi }\right) \Phi ^{2}\Gamma R_S^3\nonumber \\&\quad +\frac{3.31 \times 10^{-9}}{\rho _4^2}\Psi ^{2}\cos \left( {4\psi }\right) \Phi ^{2} \Gamma R_S^3\nonumber \\&\quad +\frac{6.63 \times 10^{-8}}{\rho _4^2}\Psi ^{2}\sqrt{\frac{\Psi \left( {-5\Psi \!+\!2\Phi }\right) }{\left( {-2\Psi \!+\!\Phi }\right) ^{2}}}\nonumber \\&\quad \times \cos \left( \psi \right) \Phi ^{2}\Gamma R_S^3\nonumber \\&\quad -\frac{2.29\times 10^{-8}}{\rho _4^2}\Psi ^{2}\sqrt{\frac{\Psi \left( {-5\Psi \!+\!2\Phi }\right) }{\left( {-2\Psi \!+\!\Phi }\right) ^{2}}} \nonumber \\&\quad \times \cos \left( {3\psi }\right) \Phi ^{2}\Gamma R_S^3\nonumber \\&\quad +\frac{2.18 \times 10^{-9}}{\rho _4^2}\Psi ^{2}\sqrt{\frac{\Psi \left( {-5\Psi \!+\!2\Phi }\right) }{\left( {-2\Psi \!+\!\Phi }\right) ^{2}}}\nonumber \\&\quad \times \cos \left( {5\psi }\right) \Phi ^{2}\Gamma R_S^3 \end{aligned}$$

(13)

So $g\left( x\right)$ in Eq. (12) will be (for resonance 2:1) as follows:

$$\begin{aligned}&g\left( x\right) = \left[ {\begin{array}{l} g_1 (\Psi ,\psi ) \\ g_2 (\Psi ,\psi ) \\ \end{array}}\right] = \left[ {\begin{array}{l} -\frac{\text {d}}{{\text {d}}\psi }{\text {Ham}}_{2:1}^{\text {fourth}} \\ \frac{{\text {d}}}{{\text {d}}\Psi }{\text {Ham}}_{2:1}^{\text {fourth}} \\ \end{array}}\right] \nonumber \\&g_1 (\Psi ,\psi ) = \frac{5.49\times 10^{-9}}{\rho _4^2}\Psi ^{2}\sin \left( {6\psi }\right) \Phi ^{2}\Gamma R_S^3\nonumber \\&\quad -\frac{2.27\times 10^{-8}}{\rho _4^2}\Psi ^{2}\sin \left( {2\psi }\right) \Phi ^{2} \Gamma R_S^3\nonumber \\&\quad +\frac{1.32\times 10^{-8}}{\rho _4^2}\Psi ^{2}\sin \left( {4\psi }\right) \Phi ^{2}\Gamma R_S^3\nonumber \\&\quad +\frac{6.63\times 10^{-8}}{\rho _4^2} \sqrt{\frac{\Psi \left( {-5\Psi +2\Phi }\right) }{\left( {-2\Psi +\Phi }\right) ^{2}}}\nonumber \\&\quad \times \sin \left( \psi \right) \Psi ^{2}\Phi ^{2}\Gamma R_S^3\nonumber \\&\quad -\frac{6.89\times 10^{-8}}{\rho _4^2}\sqrt{\frac{\Psi \left( {-5\Psi +2\Phi }\right) }{\left( {-2\Psi +\Phi }\right) ^{2}}}\nonumber \\&\quad \times \sin \left( {3 \psi }\right) \Psi ^{2}\Phi ^{2}\Gamma R_S^3\nonumber \\&\quad +\frac{1.09\times 10^{-8}}{\rho _4^2}\sqrt{\frac{\Psi \left( {-5\Psi +2\Phi }\right) }{\left( {-2\Psi +\Phi }\right) ^{2}}}\nonumber \\&\quad \times \sin \left( {5 \psi }\right) \Psi ^{2}\Phi ^{2}\Gamma R_S^3 \end{aligned}$$

(14)

In addition, the function $f(x)$ is equal to:

$$\begin{aligned} f(x) = \left[ {\begin{array}{l} f_1 (\Psi ,\psi ) \\ f_2 (\Psi ,\psi ) \\ \end{array}}\right] = \left[ {\begin{array}{l} -\frac{\text {d}}{{\text {d}}\psi }{\text {Ham}}_{2:1}^{\text {RTBP}} \\ \frac{\text {d}}{{\text {d}}\Psi }\mathrm{Ham}_{2:1}^{\text {RTBP}} \\ \end{array}}\right] \end{aligned}$$

(15)

4.1 Melnikov theory

In the current study, Melnikov equation is utilized to detect intersection (if any) stable and unstable manifolds of the separatrix. If stable and unstable manifold intersect then the Melnikov function Eq. (16) becomes zero. Subsequently if the Melnikov function $M(t_0)$ equals to zero, chaos exists. Melnikov integral for the system given by (12) is [12]:

$$\begin{aligned} M(t_0) \!=\! \int \limits _{-\infty }^\infty {\left[ {f\left( {q^{0}(t\!-\!t_0)}\right) \!\wedge \! g\left( {q^{0}\left( {t\!-\!t_0}\right) }\right) ,t}\right] \mathrm{d}t},\nonumber \\ \end{aligned}$$

(16)

where $q^{0}$ is the Separatrix curve. This curve is shown using the dashed lines in Fig. 2 for $\Phi = 0.98$. Through substation of $(\Psi ,\psi )$ values from the separatrix curve, one can compute the Melnikov function. For example this Function value for $\Phi = 0.98$ is shown in Fig. 3. Using figures three through five, it can be concluded that: for the (2:1) resonance, the Melnikov integral computed over the outer loop does not cross the zero line, and so consequently chaos would not exist. On the other hand for the same resonance orbit, when the Melnikov integral is computed over the inner loop, the zero line is crossed that is an indication for potential chaotic motion under the influence of the fourth gravitational body (Figs. 3, 4). In addition for the (3:1) and (4:1) resonances the Melnikov integration over the inner as well as the outer separatrix loop crosses the zero lines, and so one can expect chaos to occur for these resonance orbit trajectories under the influence of a fourth gravitation body. It will be shown in the next sections that performing the numerical simulation for various initial conditions from the separatrix will also verify the above Melnikov based conclusion, see Figs. 6–12. The latter observation is made utilizing the fast Lyapunov indicator (FLI) as well as the Time-Frequency Analysis (TFA) as acceptable means of chaos detection in dynamical systems. As mentioned earlier, Sections 4.2 and 4.3 cover the pertinent details of the FLI and TFA.

Fig. 4

Melnikov function of (3:1) resonance for $\Phi =$ 0.98. a inner loop and b outer loop

Fig. 5

Melnikov function of (4:1) resonance for $\Phi =$ 0.98 (outer loop)

Fig. 6

Resonance (2:1) trajectory (a1, a2), FLI (b1, b2), and time–frequency (c1, c2) in RTBP & bicircular (left inner loop, right outer loop)

Fig. 7

Resonance (2:1) trajectory (a1, a2), FLI (b1, b2), and time–frequency (c1, c2) in RTBP & bicircular (left inner loop, right outer loop)

Fig. 8

Resonance (2:1) trajectory (a), FLI (b), and time–frequency (c) in RTBP & bicircular

Fig. 9

Resonance (3:1) trajectory (a1, a2), FLI (b1, b2), and time–frequency (c1, c2) in RTBP & bicircular (left inner loop, right outer loop)

Fig. 10

Resonance (3:1) trajectory (a1, a2), FLI (b1, b2), and time–frequency (c1, c2) in RTBP & bicircular (left inner loop, right outer loop)

Fig. 11

Resonance (3:1) trajectory (a), FLI (b), and time–frequency (c) in RTBP & bicircular

Fig. 12

Resonance (4:1) trajectory (a1, a2), FLI (b1, b2), and time–frequency (c1, c2) in RTBP& bicircular (outer loop)

4.2 Fast Lyapunov exponent

Consider a trajectory $x(t);\;x(t_0) = x_0$ of a dynamical system of the form $\dot{x} = f(x,t)$, one can propagate a tangent vector $v_0$ along the trajectory by integrating the linearized dynamics, $\dot{v} = Df(x(t)) \cdot v;\; v(t_0) = v_0$. Then the supremum of the norm of $v(t)$ over an integration period $[0,T]$ provides the value of the FLI [3]:

$$\begin{aligned} \hbox {FLI}_n (x_0,\{v_i\},T) = \sup _{i,t_0 \le t\le T} \log \left\| {v_i (t)}\right\| _n \end{aligned}$$

(17)

If the component of $v(t)$ is denoted by $(v_x, v_y, v_z, v_{\dot{x}},v_{\dot{y}}, v_{\dot{z}})$, then $\left\| v\right\| _n \!=\! \sqrt{\frac{1}{r}\left( {v_x^2 \!+\!v_y^2 \!+\!v_z^2}\right) \!+\!\frac{1}{v}\left( {v_{\dot{x}}^2 \!+\!v_{\dot{y}}^2 \!+\!v_{\dot{z}}^2}\right) }$ where $r$ and $v$ represent the Euclidean norms of the position and velocity of the spacecraft state at the current time t, respectively. At Figs. 6–10, $\log \left\| {v_i(t)}\right\| _2$ are displayed for different resonant orbits. As seen in Fig. 6, if one selects an initial condition from the outer separatrix loop, the Melnikov approach predicts no chaos. The FLI method and the bicircular model also verify the same results. On the other hand for initial conditions from the inner separatrix loop,chaos was previously detected, and one can also clearly see a jump in the FLI for both models. The same discussions are generally true for the remaining figures with one exception, see Fig. 10. In this condition, FLI for RTBP is larger than bicircular model, while resonance orbit in bicircular model has increasing amplitude motion (increasing but bounded).

4.3 Time–frequency analysis

A method of TFA based on wavelets is applied to resonance orbit in RTBP and bicircular model [4]. This method is based on the extraction of instantaneous frequencies from the wavelet transform of numerical solution in both model mentioned above. There are mainly two methods to extract instantaneous frequency or the time variation of the frequencies: the Gabor transform and the wavelet transform. At this study, wavelet transform is used. The wavelet transform is defined in terms of a function $\psi$, called the mother wavelet, in the following way [13]

$$\begin{aligned} L_\psi f(a,b) = \frac{1}{\sqrt{a}}\int \limits _{-\infty }^\infty {f(t)\bar{\psi }\left( {\frac{t-b}{a}}\right) \;\mathrm{d}t} \end{aligned}$$

(18)

Mother wavelet must be like a wave with short duration it must have compact support or decay rapidly to 0 for $\left| t\right| \rightarrow \infty$. There exist various wavelet forms used in the open literature, such as the “Mexican hat,” Haar and spline wavelets. In this study the Morlet wavelet, Eq. 19 is used:

$$\begin{aligned} \psi (t) = \frac{1}{\sigma \sqrt{2\pi }}e^{2\pi i\lambda t} e^{-t^{2}/2\sigma ^{2}} \end{aligned}$$

(19)

The wavelet transform also depends on two parameters: a is called the scale and is multiple of the inverse of the frequency; and b is the time parameter that slides the wavelet as a time window. The wavelet transform consists of expansion of a function in terms of wavelet $\psi _{ab}$ that is constructed as dilations and translations of the mother wavelet $\psi$

$$\begin{aligned} \psi _{ab} (t) = \frac{1}{\sqrt{a}}\psi \left( {\frac{t-b}{a}}\right) \; b\in \mathrm{R}\;a>0 \end{aligned}$$

(20)

Let $f(t) = A_f (t)\exp \left[ {i\phi _f (t)}\right]$ be an analytic signal. If the wavelet $\psi$ is an analytic signal itself, and it is written in the form

$$\begin{aligned} \psi (t) = A_\psi (t)\exp \left[ {i\phi _\psi (t)}\right] \end{aligned}$$

(21)

Then the wavelet transform coefficients can be computed as

$$\begin{aligned} L_\psi f(a,b) = \frac{1}{\sqrt{a}}\int \limits _{-\infty }^\infty {M_{ab} (t)\exp \left[ {i\Phi _{ab} (t)}\right] } \;\mathrm{d}t, \end{aligned}$$

(22)

where

$$\begin{aligned}&M_{ab} = A_f (t)A_\psi \left( {\frac{t-b}{a}}\right) \nonumber \\&\Phi _{ab} (t) = \phi _f (t)-\phi _\psi \left( {\frac{t-b}{a}}\right) \end{aligned}$$

(23)

Let $t_0$ be a unique point such that $\Phi ^{\prime }_{ab} (t_0) = 0$ and $\Phi ^{\prime \prime }_{ab} (t_0)\ne 0$. $t_0$ is called a stationary point. We can apply the method of stationary phase to obtain the expression,

$$\begin{aligned} L_\psi f(a,b)&\simeq \frac{1}{\sqrt{a}}f(t_0)\;\bar{{\psi }} \left( {\frac{t_0-b}{a}}\right) \sqrt{\frac{2\pi }{\left| {\Phi ^{\prime \prime }_{ab} (t_0)}\right| }}\nonumber \\&\times e^{i\;\text {sgn}\Phi ^{\prime \prime }_{ab} (t_0)\pi /4} \end{aligned}$$

(24)

Then the equation $t_0 (a,b) = b$ gives a curve in time-scale plane. This leads to the following definition:

Definition 1

The ridge of the wavelet transform is the collection of points for which $t_0 (a,b) = b$

From the equation $\Phi ^{\prime }_{ab} (t_0) = 0$, we have that

$$\begin{aligned} \Phi ^{\prime }_{ab} (t_0) = \phi _f^{\prime } (t_0)-\frac{1}{a} \phi _\psi ^{\prime } \left( {\frac{t_0 -b}{a}}\right) = 0 \end{aligned}$$

(25)

And then, by definition, the points on the ridge satisfy

$$\begin{aligned} \Phi ^{\prime }_{ab} (t_0) = \phi _f^{\prime } (t_0)-\frac{1}{a} \phi _\psi ^{\prime } \left( {\frac{t_0 -b}{a}}\right) = 0 \end{aligned}$$

(26)

Therefore, the instantaneous frequency $\phi _f^{\prime } (b)$ of the function f can be obtained from this equation once we have determined the ridge of the wavelet transform. The ridge of the wavelet transform can be obtained by computing the maximum modulus of the wavelet transform (with respect to scale) for each point in time. Therefore, the maximum in scale for each time t $=$ b corresponds to the instantaneous frequency of $f(t)$. In Figs.  6–10, instantaneous frequency for different resonance orbit has shown. In resonance (2:1) (outer loop, Fig. 6), instantaneous frequencies are similar in RTBP and bicircular model, similarity for Fig. 7 (outer loop). But in Fig. 8, a jump in instantaneous frequencies is appeared, which indicates chaos. But at some of figures, e.g. Fig. 7 (inner loop), same behavior in instantaneous frequencies is seen for both RTBP and bicircular model, while numerical integration of motion indicates that chaos exists in bicircular model (for example).

5 Concluding remarks

Utilizing the Melnikov method, it is proved that the fourth body gravitational effect can cause some of the resonance orbits of the RTBP (Earth–Moon–Satellite) to become chaotic. The results indicate that different resonance orbits exhibit different behaviors under the similar (Sun) gravitational effect. Also it is proved that inner and outer sepratrix loops exhibit different behaviors. It is shown that if we select (2:1) resonance orbit (outer loop sepratrix), then chaotic phenomena do not appear, except in point of conjunction of inner and outer loops. But for resonance (3:1) and (4:1), chaotic motion is appeared under the influence of fourth gravitation body. Also, the obtained result verified using numerical integration, FLI and TFA. Also results also show that fourth body gravitation may reduce amplitude of resonance trajectory relative to numerical integration of trajectory in RTBP, but fourth body diffuse trajectory in bounded phase space.

Appendix

Utilizing Newton’s gravitational law, one obtains that the motion of $P_1$ and $P_4$ in an inertial frame $(\xi _1, \xi _2)$ is described by the following equations:

$$\begin{aligned} \frac{\mathrm{d}^{2}\vec {\xi }_4}{\mathrm{d}t^{2}}&= Gm_1 \;\frac{\vec {\xi }_1 -\vec {\xi }_4}{\left| {\vec {\xi }_1 -\vec {\xi }_4}\right| ^{3}}+ Gm_2 \frac{\vec {\xi }_2 -\vec {\xi }_4}{\left| {\vec {\xi }_2 -\vec {\xi }_4}\right| ^{3}}\nonumber \\&+\,Gm_3\frac{\vec {\xi }_3 -\vec {\xi }_4}{\left| {\vec {\xi }_3 -\vec {\xi }_4}\right| ^{3}}\end{aligned}$$

(27)

$$\begin{aligned} \frac{\mathrm{d}^{2}\vec {\xi }_1}{\mathrm{d}t^{2}}&= Gm_2\;\frac{\vec {\xi }_2 -\vec {\xi }_1}{\left| {\vec {\xi }_2 -\vec {\xi }_1}\right| ^{3}}+ Gm_3 \frac{\vec {\xi }_3 -\vec {\xi }_1}{\left| {\vec {\xi }_3 -\vec {\xi }_1}\right| ^{3}}\nonumber \\&+\,Gm_4\frac{\vec {\xi }_4 -\vec {\xi }_1}{\left| {\vec {\xi }_4 -\vec {\xi }_1}\right| ^{3}} \end{aligned}$$

(28)

Defining the Earth centric frame ($P_1$), the following relative distance are defined:

$$\begin{aligned} \vec {r}_4 = \vec {\xi }_4 -\vec {\xi }_1, \quad \vec {r}_3 = \vec {\xi }_3 -\vec {\xi }_1, \quad \vec {r}_2 = \vec {\xi }_2 -\vec {\xi }_1 \end{aligned}$$

(29)

Thus, the equation of motion for $P_4$ will be

$$\begin{aligned} \frac{\mathrm{d}^{2}\vec {r}_4}{\mathrm{d}t^{2}}&= -\mu \frac{\vec {r}_4}{\rho _4^3}+ \varepsilon \left[ {-\frac{\vec {r}_2}{\rho _2^3}+\frac{\vec {r}_2 -\vec {r}_4}{\left| {\vec {r}_2 -\vec {r}_4}\right| ^{3}}}\right] \nonumber \\&+\, gm_3 \left[ {-\frac{\vec {r}_3}{\rho _3^3}+\frac{\vec {r}_3 -\vec {r}_4}{\left| {\vec {r}_3 -\vec {r}_4}\right| ^{3}}}\right] , \end{aligned}$$

(30)

where

$$\begin{aligned} \mu&= G(m_1 +m_4)\hbox { and}\\ \varepsilon&= Gm_2 \end{aligned}$$

Subsequently, (30) can be rewritten as

$$\begin{aligned} \frac{\mathrm{d}^{2}\vec {r}_4}{\mathrm{d}t^{2}}&= -\mu \frac{\vec {r}_4}{\rho _4^3}+ \varepsilon \left[ {-\frac{\vec {r}_2}{\rho _2^3}+\frac{\vec {r}_2 -\vec {r}_4}{\left| {\vec {r}_2 -\vec {r}_4}\right| ^{3}}}\right] \nonumber \\&+\gamma \left[ {-\vec {r}_3 +R_s^3 \frac{\vec {r}_3 -\vec {r}_4}{\left| {\vec {r}_3 -\vec {r}_4}\right| ^{3}}}\right] , \end{aligned}$$

(31)

where $\gamma = \frac{gm_3}{R_s^3}$

It can be shown that the perturbation terms in the RHS of (31) can be simplified as,

$$\begin{aligned}&-\frac{\vec {r}_2}{\rho _2^3}+\frac{\vec {r}_2 -\vec {r}_4}{\left| {\vec {r}_2 -\vec {r}_4}\right| ^{3}} = \frac{\partial }{\partial r_4}\left( {-\frac{\vec {r}_2\cdot \vec {r}_4}{\rho _2^3}+\frac{1}{\left| {\vec {r}_2 -\vec {r}_4}\right| }}\right) \nonumber \\&-\vec {r}_3 \!+\!R_s^3 \frac{\vec {r}_3 \!-\!\vec {r}_4}{\left| {\vec {r}_3 -\vec {r}_4}\right| ^{3}} \!=\! \frac{\partial }{\partial r_4 } \left( {-\vec {r}_3\cdot \vec {r}_4 +R_s^3 \frac{1}{\left| {\vec {r}_3 -\vec {r}_4}\right| }}\right) \nonumber \\ \end{aligned}$$

(32)

Finally, the equation of motion and the Hamiltonian of the negligible mass (P4) in the bicircular model will be

$$\begin{aligned}&\frac{\mathrm{d}^{2}\vec {r}_4}{\mathrm{d}t^{2}} = -\mu \frac{\vec {r}_4}{\rho _4^3} -\varepsilon \frac{\partial R_1}{\partial \vec {r}_4}-\gamma \frac{\partial R_2}{\partial \vec {r}_4}\end{aligned}$$

(33)

$$\begin{aligned}&H = -\frac{\mu ^{2}}{2L^{2}}+\varepsilon R_1 +\gamma R_2, \end{aligned}$$

(34)

where

$$\begin{aligned} R_1&= \frac{\vec {r}_2\cdot \vec {r}_4}{\rho _2^3}-\frac{1}{\left| {\vec {r}_2 -\vec {r}_4}\right| ^{3}}\nonumber \\ R_2&= \vec {r}_3\cdot \vec {r}_4 -R_s^3 \frac{1}{\left| {\vec {r}_3 -\vec {r}_4}\right| ^{3}} \end{aligned}$$

(35)

One can also express $R_2$ in terms of the resonance variables. Note that $R_2$ can also be defined as posed in Eq. (3),

$$\begin{aligned} R_2 = \sum _{j = 2}^\infty {P_j (\cos S_2) \left( {\frac{\rho _4}{\rho _3}}\right) ^{j}}, \end{aligned}$$

(36)

where $S_2$ is the angle between Earth–Satellite and Earth–Sun vectors, see Fig. 13. Similarly $\cos S_2$ can be defined:

$$\begin{aligned} \cos S_2&= \left( {1-\frac{1}{4}\gamma ^{2}}\right) \cos (\psi -\psi _S)\nonumber \\&+\frac{1}{4}\gamma ^{2}\cos (\psi +\psi _S -2\Omega ) \end{aligned}$$

(37)

Substitution of (37) into (36) with expansion of the trigonometric parts in terms of the Delaunay variables will result in the perturbation Hamiltonian $R_2$ in terms of resonance variables. In Eq. (38), the Hamiltonian associated with the fourth body mass is shown, assuming a zero inclination orbit:

$$\begin{aligned} \mathrm{Ham}_0 = \frac{1}{16384}\frac{1}{\rho _4^4}\left( {\begin{array}{l} -8960\Gamma R_S^3 \rho _4^4 \cos \left( {4\varpi _4 +4f_4 -4\varpi _3 -4f_3}\right) \\ -5120\Gamma R_S^3 \rho _4^4 \cos \left( {2\varpi _4 +2f_4 -2\varpi _3 -2f_3}\right) \\ -10240\Gamma R_S^3 \rho _4^3 \rho _3 \cos \left( {3\varpi _4 +3f_4 -3\varpi _3 -3f_3}\right) \\ -6144\Gamma R_S^3 \rho _4^3 \rho _3 \cos \left( {\varpi _4 +f_4 -\varpi _3 -f_3}\right) \\ -2304\Gamma R_S^3 \rho _4^4 -12288\Gamma R_S^3 \rho _4^2 \rho _3^2 \cos \left( {2\varpi _4 +2f_4 -2\varpi _3 -2f_3}\right) \\ -4096\Gamma R_S^3 \rho _4^2 \rho _3^2 \\ \end{array}}\right) \end{aligned}$$

(38)

Expressing orbital parameters using Delaunay variables and assuming zero eccentricity for the Sun’s orbit and equating higher orders of $\Phi$ and $\Psi$ to zero will yield (39).

Fig. 13

Geometry of the bicircular four-body problem ($P_1 =$ Earth, $P_2 =$ Moon, $P_3 =$ Sun, $P_4 =$ Satellite)

$$\begin{aligned}&\!\!\!\mathrm{Ham}: = -\frac{1}{16384}\frac{1}{\rho _4^4}\nonumber \\&\left( {\begin{array}{l} \left( {\begin{array}{l} 73728\rho _4^2 \cos \left( {2n_S t+2l_4 -2\phi -2t}\right) s^{2}\Psi ^{2}\Phi ^{2} \\ \quad +73728\sqrt{\frac{\Psi s^{\prime }\left( {-2s\Psi -s^{\prime }\Psi +2\Phi }\right) }{\left( {-s\Psi +\Phi }\right) ^{2}}}\,.\,\rho _4^2 \cos \left( {\frac{-2s^{\prime }t-\psi -s\phi +2n_s ts^{\prime }+2l_4 s^{\prime }-3\phi s^{\prime }}{s^{\prime }}}\right) s^{2}\Psi ^{2}\Phi ^{2} \\ \quad -14592\Phi ^{2}\Psi ^{2}s^{\prime 2}\sqrt{\frac{\Psi s^{\prime }\left( {-2s\Psi -\Psi s^{\prime }+2\Phi }\right) }{\left( {-s\Psi +\Phi }\right) ^{2}}}\rho _4^2 \cos \left( {\frac{2l_4 s^{\prime }-2s^{\prime }t+3\psi +3s\phi +s^{\prime }\phi +2n_s ts^{\prime }}{s^{\prime }}}\right) \\ \quad -36864\Psi ^{2}s^{\prime }\rho _4^2 s\Phi ^{2}-403200\Psi ^{2}s^{\prime 2}\rho _4^2 \cos \left( {2n_s t+2l_4 -2\phi -2t}\right) \Phi ^{2} \\ \quad -87552\Phi ^{2}\Psi ^{2}s^{\prime }\sqrt{\frac{\Psi s^{\prime }\left( {-2s\Psi -\Psi s^{\prime }+2\Phi }\right) }{\left( {-s\Psi +\Phi }\right) ^{2}}}\rho _4^2 \cos \left( {\frac{2l_4 s^{\prime }-2s^{\prime }t+3\psi +3s\phi +s^{\prime }\phi +2n_s ts^{\prime }}{s^{\prime }}}\right) s \\ \quad -147456\Psi ^{2}s^{\prime }\rho _4^2 \cos \left( {\frac{2\left( {n_S ts^{\prime }+l_4 s^{\prime }-s^{\prime }t+\psi +s\phi }\right) }{s^{\prime }}}\right) s\Phi ^{2} \\ \quad -32256\Phi ^{2}\Psi ^{2}s^{\prime }\sqrt{\frac{\Psi s^{\prime }\left( {-2s\Psi -\Psi s^{\prime }+2\Phi }\right) }{\left( {-s\Psi +\Phi }\right) ^{2}}}\rho _4^2 \cos \left( {\frac{1}{s^{\prime }}\left( {-2s^{\prime }t+5\psi +5s\phi +2n_S ts^{\prime }+2l_4 s^{\prime }+3\phi s^{\prime }}\right) }\right) s \\ \quad +294912\Phi ^{2}\Psi ^{2}s^{\prime }\sqrt{\frac{\Psi s^{\prime }\left( {-2s\Psi -\Psi s^{\prime }+2\Phi }\right) }{\left( {-s\Psi +\Phi }\right) ^{2}}}\rho _4^2 \cos \left( {\frac{1}{s^{\prime }}\left( {-2s^{\prime }t-3\psi -3s\phi -5\phi s^{\prime }+2n_S ts^{\prime }+2l_4 s^{\prime }}\right) }\right) s \\ \quad +205824\Psi ^{2}s^{\prime 2}\rho _4^2 \cos \left( {\frac{2\left( {n_S ts^{\prime }+s^{\prime }l_4 -s^{\prime }t+\psi +s\phi }\right) }{s^{\prime }}}\right) \Phi ^{2} \\ \quad +207360\Psi ^{2}s^{\prime }\rho _4^2 \cos \left( {2n_S t+2l_4 -2\phi -2t}\right) s\Phi ^{2} \\ \quad -77568\Phi ^{2}\Psi ^{2}s^{\prime 2}\sqrt{\frac{\Psi s^{\prime }\left( {-2s\Psi -\Psi s^{\prime }+2\Phi }\right) }{\left( {-s\Psi +\Phi }\right) ^{2}}}\rho _4^2 \cos \left( {\frac{-2s^{\prime }t-\psi -s\phi +2n_S ts^{\prime }+2l_4 s^{\prime }-3\phi s^{\prime }}{s^{\prime }}}\right) \\ \quad +49152\Phi ^{2}\Psi ^{2}s^{\prime 2}\sqrt{\frac{\Psi s^{\prime }\left( {-2s\Psi -\Psi s^{\prime }+2\Phi }\right) }{\left( {-s\Psi +\Phi }\right) ^{2}}}\rho _4^2 \cos \left( {\frac{-2s^{\prime }t-3\psi -3s\phi -5\phi s^{\prime }+2n_S ts^{\prime }+2l_4 s^{\prime }}{s^{\prime }}}\right) \\ \quad -221184\sqrt{\frac{\Psi s^{\prime }\left( {-2s\Psi -\Psi s^{\prime }+2\Phi }\right) }{\left( {-s\Psi +\Phi }\right) ^{2}}}\rho _4^2 \cos \left( {\frac{-2s^{\prime }l_4 -2s^{\prime }t+\psi +s\phi -\phi s^{\prime }+2n_S ts^{\prime }}{s^{\prime }}}\right) s^{2}\Psi ^{2}\Phi ^{2} \\ \quad +18432\Psi ^{2}s^{\prime }\rho _4^2 \cos \left( {\frac{2\left( {-s^{\prime }t-\psi -s\phi +n_S ts^{\prime }+s^{\prime }l_4 -2s^{\prime }\phi }\right) }{s^{\prime }}}\right) s\Phi ^{2} \\ \quad +346368\Psi ^{2}s^{\prime 2}\rho _4^2 \cos \left( {\frac{2\left( {-s^{\prime }t-\psi -s\phi +n_S ts^{\prime }+s^{\prime }l_4 -2s^{\prime }\phi }\right) }{s^{\prime }}}\right) \Phi ^{2} \\ \quad +69120\Phi ^{2}\Psi ^{2}s^{\prime }\sqrt{\frac{\Psi s^{\prime }\left( {-2s\Psi -\Psi s^{\prime }+2\Phi }\right) }{\left( {-s\Psi +\Phi }\right) ^{2}}}\rho _4^2 \cos \left( {\frac{2s^{\prime }l_4 -2s^{\prime }t+\psi +s\phi -\phi s^{\prime }+2n_S ts^{\prime }}{s^{\prime }}}\right) s \\ \quad -92160\Psi ^{2}s^{\prime 2}\rho _4^2 \cos \left( {\frac{2(s^{\prime }l_4 -s^{\prime }t-2\psi -2s\phi -3\phi s^{\prime }+n_S ts^{\prime })}{s^{\prime }}}\right) \Phi ^{2} \\ \quad +16128\Psi ^{2}s^{\prime 2}\rho _4^2 \cos \left( {\frac{2(n_S s^{\prime }t+l_4 s^{\prime }+3s\phi +2s^{\prime }\phi +3\psi -s^{\prime }t)}{s^{\prime }}}\right) \Phi ^{2} \\ \quad -49152\sqrt{\frac{\Psi s^{\prime }\left( {-2s\Psi -\Psi s^{\prime }+2\Phi }\right) }{\left( {-s\Psi +\Phi }\right) ^{2}}}\cos \left( {\frac{s\phi +s^{\prime }\phi +\psi }{s^{\prime }}}\right) \rho _4^2 s^{2}\Psi ^{2}\Phi ^{2}-6144\Psi ^{2}s^{\prime 2}\rho _4^2 \Phi ^{2} \\ \quad +36864\Psi ^{2}s^{\prime }\rho _4^2 \cos \left( {\frac{2\left( {s\phi +s^{\prime }\phi +\psi }\right) }{s^{\prime }}}\right) s\Phi ^{2}+6144\Psi ^{2}s^{\prime 2}\rho _4^2 \cos \left( {\frac{2\left( {s\phi +s^{\prime }\phi +\psi }\right) }{s^{\prime }}}\right) \Phi ^{2} \\ \quad +24576\rho _4^2 s^{2}\Psi ^{2}\Phi ^{2} \\ \quad +11520\Phi ^{2}\Psi ^{2}s^{\prime 2}\sqrt{\frac{\Psi s^{\prime }\left( {-2s\Psi -\Psi s^{\prime }+2\Phi }\right) }{\left( {-s\Psi +\Phi }\right) ^{2}}}\rho _4^2 \cos \left( {\frac{2l_4 s^{\prime }-2s^{\prime }t+\psi +s\phi -\phi s^{\prime }+2n_S ts^{\prime }}{s^{\prime }}}\right) \\ \quad -465408\Phi ^{2}\Psi ^{2}s^{\prime 2}\sqrt{\frac{\Psi s^{\prime }\left( {-2s\Psi -\Psi s^{\prime }+2\Phi }\right) }{\left( {-s\Psi +\Phi }\right) ^{2}}}\rho _4^2 \cos \left( {\frac{-2s^{\prime }t-\psi -s\phi +2n_S ts^{\prime }+2l_4 s^{\prime }-3\phi s^{\prime }}{s^{\prime }}}\right) s \\ \quad -5376\Phi ^{2}\Psi ^{2}s^{\prime 2}\sqrt{\frac{\Psi s^{\prime }\left( {-2s\Psi -\Psi s^{\prime }+2\Phi }\right) }{\left( {-s\Psi +\Phi }\right) ^{2}}}\rho _4^2 \cos \left( {\frac{-2s^{\prime }t+5\psi +5s\phi +2n_S ts^{\prime }+2l_4 s^{\prime }+3\phi s^{\prime }}{s^{\prime }}}\right) \\ \quad +32256\Psi ^{2}s^{\prime }\rho _4^2 \cos \left( {\frac{2\left( {-s^{\prime }t+2\psi +2s\phi +n_S ts^{\prime }+l_4 s^{\prime }+\phi s^{\prime }}\right) }{s^{\prime }}}\right) s\Phi ^{2} \\ \quad -54528\Psi ^{2}s^{\prime 2}\rho _4^2 \cos \left( {\frac{2\left( {-s^{\prime }t+2\psi +2s\phi +n_S ts^{\prime }+l_4 s^{\prime }+\phi s^{\prime }}\right) }{s^{\prime }}}\right) \Phi ^{2} \\ \quad \end{array}}\right) \cdot \Gamma R_S^3 \\ \\ \end{array}} \right) \end{aligned}$$

(39)