Abstract
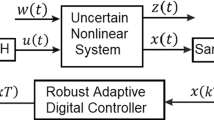
In this paper, an adaptive practical stabilization problem is investigated for a class of nonlinear systems via sampled-data control. The systems under study possess uncertain dynamics and unknown gain functions. During sampled-data controller design procedure, a dynamic signal is introduced to dominate the unmeasured states existed in the external disturbances, and neural networks are adopted to approximate the unknown nonlinear functions. By choosing appropriate sampling period, the designed sampled-data controller can render all states of the resulting closed-loop system to be semi-globally uniformly ultimately bounded. Two examples are given to demonstrate feasibility and efficacy of the proposed methods.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
It is well known that real-world systems are inevitable to contain uncertainties. Driven by practical requirements and theoretical challenges, adaptive controller design of nonlinear systems has become an important research domain recently. An adaptive fault-tolerant tracking control problem of a class of nonlinear systems with multiple delayed state perturbations was investigated in [1]. Adaptive tracking and stabilization problems of the nonlinear large-scale systems with dynamic uncertainties was discussed in [2,3,4,5], where the inverse dynamics of the subsystems considered in [4, 5] were required to be stochastic input-to-state stable. Finite-time stabilization of a class of switched stochastic nonlinear systems under arbitrary switchings was investigated in [6] by adopting the adding a power integrator technique, subsequently, a tracking control method was proposed in [7] for a class of switched stochastic nonlinear systems with unknown dead-zone input by using the common Lyapunov function method. Two additional factors of adaptive control in nonlinear systems were considered in [8, 9], where time delay was considered in [8], and unmeasured dynamic uncertainties was considered in [9]. Adaptive fuzzy output-constrained tracking fault-tolerant control was focused in [10], where the barrier Lyapunov function was used to guarantee that all the signals in the closed-loop system were bounded in probability and the system outputs was constrained in a given compact set. Two novel adaptive finite-time control schemes were developed in [11, 12] for high-order nonlinear systems, where the result presented in [11] was the first time to solve the finite-time control problem of the nonlinear systems with uncertain time-varying control coefficients and unknown nonlinear perturbations. Under some appropriate assumptions, adaptive practical finite-time stabilization for a class of switched nonlinear systems in pure-feedback form was investigated in [13].
However, it should be emphasized that all the aforementioned results were based on continuous-time control. In the past decades, due to the remarkable development in digital technology, it becomes a commonly known standard that sampled-data controllers with analog-to-digital and digital-to-analog devices for interfacing are being digitally implemented into practical systems, such as aircraft systems [14] and multi-robot systems [15]. The three main approaches for the design of sampled-data controllers are (e.g., see [16,17,18]):
-
1.
Design based on a continuous-time plant model plus a controller discretization (the CTD method);
-
2.
Design based on the exact or approximate discrete-time plant model ignoring inter-sample behavior (respectively, the DTD method and the approximate DTD method);
-
3.
Design based on the sampled-data model of the plant which takes into account the inter-sample behavior in the design procedure (the SDD method).
The majority of work for the sampled-data control of nonlinear systems uses the CTD method, and various sampled-data control algorithms for nonlinear systems depicted in continuous dynamics were presented in many existing literature, for example, two sampled-data control schemes were developed in [16, 19] to realize global practical tracking of nonlinear systems, a systematic design scheme was developed in [20] to construct a linear sampled-data output feedback controller that semi-globally asymptotically stabilizes a class of uncertain systems with both higher-order and linear growth nonlinearities. By designing observers, sampled-data control methods were proposed for the nonlinear systems with improved maximum allowable transmission delay [21] and input delay [22]. An observer, which was featured with a special feedforward propagation structure, was constructed in [23] to estimate the unmeasured states of a class of uncertain nonlinear systems with uncontrollable and unobservable linearizations, and global sampled-data stabilization of the nonminimum-phase nonlinear systems were addressed in [24]. Using the small gain approach, a result concerning the sampled-data observer design for a wide classes of nonlinear systems with delayed measurements was considered in [25]. Stabilization for the sampled-data systems under noisy sampling interval was investigated in [26]. A memory sampled-data control scheme which involved a constant signal transmission delay was proposed in [27] for the chaotic systems. Sampled-data stabilization and exponentially synchronization were, respectively, investigated in [28, 29] for the T–S fuzzy systems and the Markovian neural networks. Reliable dissipative control and non-fragile \({H_\infty }\) control for the Markov jump systems were focused in [30, 31].
Although sampled-data control has received much attention, there are few works on sampled-data adaptive practical stabilization for uncertain nonlinear systems, which is mainly due to the complexity arising from the design of adaptive laws for sampled-data controller, that is, under sampled-data situation that system states can only be measured at the sampling points, adaptive laws cannot be constructed like continuous-time control by using system states which are measured everywhere. Thus, an issue naturally arises: under that situation, how to design an adaptive controller to practically stabilize such nonlinear systems by only using the sampled system states? In this paper, we will try to give an answer, and the main contributions can be summarized as follows:
-
(i)
An adaptive practical stabilization problem is considered in this paper for a class of uncertain nonlinear systems via sampled-data control. Different from some existing nonlinear sampled-data control results, such as [16, 19], our scheme can be obtained under a weaker assumption that the diffusion terms of the considered systems are not required to satisfy any linear growth and bounded conditions.
-
(ii)
Unlike existing adaptive continuous-time control schemes of nonlinear systems, such as [2,3,4,5], the adaptive laws in this paper are designed based on the sampled signals due to that the system states can only be measured at the sampling points, and then, we use the sampling values of the adaptive parameters to construct the sampled-data controller to practically stabilize the considered nonlinear systems.
-
(iii)
The sampling period in this paper is non-periodic, which is different from those in [18,19,20,21,22,23,24].
The remainder of the paper is organized as follows: in Sect. 2, we present the problem statements and some preliminaries. An adaptive sampled-data controller design are presented in Sect. 3. The main theorem is shown in Sect. 4, where the stabilization proof is also obtained using the well-known Gronwall–Bellman inequality. Numerical simulations and discussions are shown in Sect. 5 to demonstrate the effectiveness of the proposed method. Finally, conclusions are drawn in Sect. 6.
Notations
R denotes the set of all real numbers; \({R^n}\) indicates the real n-dimension-al space; \({R^{m \times n}}\) denotes the real \(m \times n\) matrix space; \(\left\| \cdot \right\| \) denotes the Euclidean norm; K denotes the set of all functions: \({R^ + } \rightarrow {R^ + }\), which are continuous, strictly increasing and vanish at zero; \(K_{\infty }\) denotes the set of all functions which are class K and unbounded; \({C^i}\) denotes a set of functions whose ith-order derivatives are continuous and differentiable; the argument of the functions will be omitted throughout the paper for simplicity whenever no confusion arises, such as functions \(V,{x_1}\) and \({z_2}\) to be used hereafter.
2 Problem statement and preliminaries
Consider the following uncertain nonlinear system:
where \(x = {[{x_1}, {x_2}, \ldots ,{x_n}]^\mathrm{T}} \in {R^n}\) are the states which can only be measured at the sampling points \({t_k},k = 1,2, \ldots , + \infty \), and \({{{\bar{x}}}_i} = {[{x_1},{x_2}, \ldots ,{x_i}]^\mathrm{T}} \in {R^i},i = 1,2, \ldots ,n; z_0 \in {R^{n_0}}\) is an unmeasured state; \(u \in R\) and \(y \in R\) are the control input and output, respectively; \({f_i}( \cdot ),{g_i}( \cdot ), i = 1,2, \ldots ,n,\) are unknown nonlinear smooth functions, and \({f_i}(0, \ldots ,0) = 0; {\varDelta _i}( \cdot ),i = 1,2, \ldots ,n,\) are external disturbances, and \({\varDelta _i}(0,\ldots ,0) = 0; q(\cdot )\) is an unknown Lipschitz function.
Remark 1
In practical engineering, some nonlinear systems, such as thruster assisted position mooring systems [32], levitated ball systems [33], flexible crane systems [34] and single-link manipulator systems [35], can be described as or converted into system (1). Therefore, it is of importance to investigate system (1).
Remark 2
Note that, for strict-feedback nonlinear systems, the adaptive sampled-data stabilization problem has been addressed in [18] by designing the controller for the systems’ Euler approximate discrete-time model; however, the diffusion terms of the systems considered in [18] are \(\phi _i^\mathrm{T}({{\bar{x}}_i})\theta , i = 1,2, \ldots ,n\), where \(\theta \) is an unknown constant and \(\phi _i(\cdot )\) is a known nonlinear function; furthermore, the control coefficients of the former (\(i-1\)) subsystems’ equations in [18] are 1; thus, system (1) is more general than the systems investigated in [18], and the method proposed in [18] maybe invalid for system (1).
We make the following assumptions.
Assumption 1
[36] The external disturbances \({\varDelta _i}({{\bar{x}}_i},z_0),i = 1,2, \ldots ,n,\) satisfy
where \({\phi _{i1}}( \cdot ) \geqslant 0\) and \({\phi _{i2}}( \cdot ) \geqslant 0\) are unknown continuous functions.
Assumption 2
There exist two unknown constants \(g_i^{\min }\) and \(g_i^{\max }\) such that \(0 < g_i^{\min } \leqslant \left| {{g_i}( \cdot )} \right| \leqslant g_i^{\max }\). Without loss of generality, we assume \(0 < g_i^{\min } \leqslant {{g_i}( \cdot )} \leqslant g_i^{\max }\).
Remark 3
It should be pointed out that continuous-time control of the strict-feedback nonlinear systems has been investigated in [4, 7, 12]; however, in those literature, the upper and lower bounds of the time-varying control coefficients \({g_i}({{\bar{x}}_i}), i = 1,2, \ldots ,n,\) are required to be known.
Assumption 3
[36] The dynamic \(\dot{z}_0 = q(z_0,{x_1})\) is exp-ISPS (exponentially input-state-practically stable), that is, there exists a \({C^1}\) function \({V_0}(z_0)\) such that
where \({{\bar{\alpha }} _1}( \cdot ),{{\bar{\alpha }} _2}( \cdot )\) are class \({K_\infty }\) functions, \(\varGamma ( \cdot )\) is a smooth function with \(\varGamma (0) = 0\), and \(c > 0,d \geqslant 0\) are constants.
Remark 4
In the existing results on sampled-data control [19,20,21,22,23,24], the diffusion terms \({f_i}({{\bar{x}}_i}), i=1,2,\ldots ,n,\) of the considered nonlinear systems are required to satisfy the linear growth condition; however, in system (1), such restriction for the diffusion terms has been relaxed.
Lemma 1
([37], Gronwall–Bellman inequality) Let \(D: = [a,b] \subset R\) be a real region. Suppose \(\mu (t),\rho (t)\) and \(\omega (t) \geqslant 0\) defined in D are real continuous functions. If \(\mu (t)\) satisfies the following inequality
the following holds for \(t \in D\):
Lemma 2
[36] If \({V_0}(z_0)\) is a \(C^1\) function for \(\dot{z}_0 = q(z_0,x_1)\) such that (4a) and (4b) hold, then, for any constant \({\bar{c}} \in (0,c)\), any initial instant \({t_0} > 0\), any initial condition \(z_0({t_0}), {\gamma _0}> 0\), for any continuous function \({{{\bar{\gamma }} (\left| {{x_1}} \right| )}}\) such that \({{{\bar{\gamma }} (\left| {{x_1}} \right| ) \geqslant \varGamma (\left| {{x_1}} \right| )}}\), there exist a finite \({T_0} = \max \left\{ {0,\mathrm{ln} ({V_0}({z_0})/{\gamma _0})/(c - {\bar{c}})} \right\} \geqslant 0\), a function \(D(t,{t_0}) \geqslant 0\) defined for all \(t \geqslant {t_0}\), and a signal described by
such that \(D(t,{t_0}) = 0\) for \(t \geqslant {t_0} + {T_0}\), and \(D(t,{t_0}) = \max \{ 0,{e^{ - c(t - {t_0})}}{V_0}({z_0}) - {e^{ - {\bar{c}}(t - {t_0})}}{\gamma _0}\}\) such that \({V_0}(z_0) \leqslant v(t) + D(t,{t_0})\) for \(\forall t \geqslant {t_0}\). Without loss of generality, we assume \({\bar{\gamma }} (\left| {{x_1}} \right| )= \varGamma (\left| {{x_1}} \right| )\).
Lemma 3
[38] For any real-valued continuous function f(x, y), where \(x \in {R^m},y \in {R^n}\), there exist smooth scalar functions \({\varphi _1}(x)\geqslant 0\) and \({\varphi _2}(y)\geqslant 0\), such that
Lemma 4
([39], Young’s inequality) Let \(x \in {R^n},y \in {R^n}\), and \(p> 1,q > 1\) be two constants, \((p - 1)(q - 1) = 1\), given any real number \(\varepsilon > 1\), the following inequality holds:
Specially, when \(p = q = 2\), we have
Lemma 5
[40] Let H(z) be a continuous function defined on a compact set \(\varOmega _{z}\), then a neural network can be constructed as the following form to approximate it:
where \(T(z) = {[{T_1}(z),\ldots ,{T_l}(z)]^\mathrm{T}} \in {R^l}\) is the basic function vector with the node number \(l\geqslant 1, {W^*} = {[W_1^*,W_2^*, \ldots ,W_l^*]^\mathrm{T}} \in {R^l}\) is the ideal weight vector, D(z) is the approximate error satisfying \(\left| {D(z)} \right| \leqslant D_1^*\) with bound \(D_1^*>0\).
The basic function \({T_i}(z)\) is taken as the Gaussian function, which has the following form:
where \({c_i}\) is the center of the radial basic function vector, and \({\mu _i} > 0\) is the width of the Gaussian function.
The value of the ideal weight vector \({W^*}\) is determined by W that minimizes the approximate error D(z) for all \(z \in {\varOmega _{z}}\):
The objective of the paper is to design the following adaptive sampled-data controller
for nonlinear system (1) such that all states of the resulting closed-loop system to be semi-globally uniformly ultimately bounded.
3 Adaptive sampled-data controller design
In this section, an adaptive sampled-data controller will be constructed by adopting the backstepping technique. The whole design procedure needs n steps, which depends on the following changes of coordinates: \({z_i} = {x_i} - {\alpha _{i - 1}},i = 2,3, \ldots ,n\), where \({\alpha _{i - 1}}\) is a virtual control law.
Step 1 In the first step, we choose the following Lyapunov function candidate:
where \({\eta _1}> 0, {{\bar{\lambda }} _1}>0\) are design parameters, \({{\tilde{\theta }} _1} = {\theta _1} - {{\hat{\theta }} _1}, {{\hat{\theta }} _1}\) is the estimate of \({\theta _1}, {\theta _1}\) will be defined later. From Assumption 1, the time derivative of \(V_1\) satisfies
where \(g_{11}^* = d\displaystyle \sqrt{\displaystyle \frac{2}{{{{{\bar{\lambda }} }_1}}}}\), and \(\displaystyle \Phi ( \cdot )\geqslant 0\) is an unknown smooth function.
According to Assumption 3, Lemmas 2 and 3, we obtain, for \(\forall t \geqslant {t_0}\),
where \({\varphi _{11}}( \cdot ) \geqslant 0\) and \({\varphi _{12}}( \cdot ) \geqslant 0\) are smooth functions. Because \(D(t,{t_0})\) is a bounded function for \(\forall t \geqslant {t_0}\), there exists a constant \(\theta _{12}^* > 0\) such that \({\varphi _{12}}(D(t,{t_0})) \leqslant \theta _{12}^*\) holds, substituting (12) into (11) results in
where \({{{\bar{\phi }} }_1}({X_1})=\displaystyle \frac{{\left| {{f_1}({x_1})} \right| }}{{g_1^{\min }}} + \displaystyle \frac{1}{{g_1^{\min }}}({\varphi _{11}}(v) + \theta _{12}^* + {\phi _{12}}(\left| {{x_1}} \right| )) + \displaystyle \frac{{v\Phi (\left| {{x_1}} \right| )}}{{{}{{{\bar{\lambda }} }_1}}}\) with \({X_1} = {[{x_1},v]^\mathrm{T}}\).
As mentioned in Lemma 5, neural network can approximate any continuous function to any desired accuracy; thus, a neural network is constructed as the following form to approximate \({{\bar{\phi }} _1}({X_1})\):
where \(H_1^*\) is an unknown weight vector, \({S_1}({X_1}) = {[{S_{11}}({X_1}), {S_{12}}({X_1}), \ldots ,{S_{1{L_1}}}({X_1})]^\mathrm{T}} \in {R^{L_1}}\) is a basic function vector and \({S_{1i}}( \cdot ),i = 1,2, \ldots ,L_1,\) are chosen as Gaussian functions, \({\varepsilon _1}({X_1})\) is the approximation error satisfying \(\left| {{\varepsilon _1}({X_1})} \right| \leqslant \varepsilon _1^*\) with \(\varepsilon _1^* > 0\).
Substituting (14) into (13), and using Lemma 4, we arrive at
where \({\theta _1} = {\left\| {H_1^*} \right\| ^2}L\) and \(g_{12}^* = \varepsilon _1^*\sqrt{2g_1^{\min }}+ \sqrt{2g_1^{\min }{\theta _1}}\).
Choose a virtual control law and a “virtual adaptive law” for Step 1 as follows:
where \({c_1} > 0\) is a design parameter. Furthermore, we have the following relation from (10) and (16):
Substituting (16) and (17) into (15) yields
where \(g_{13}^* = {\theta _1}\displaystyle \sqrt{2{\eta _1}}\).
Step 2 Choose a Lyapunov function candidate as the following form:
where \({\eta _2} > 0\) is a design parameter, \({{\tilde{\theta }} _2} = {\theta _2} - {{\hat{\theta }} _2}, {{\hat{\theta }} _2}\) is the estimate of \({\theta _2}, {\theta _2}\) will be defined later. The time derivative of \(V_2\) satisfies
According to Assumption 3, Lemmas 2 and 3, we have, for \(\forall t \geqslant {t_0}\),
where \({\varphi _{21}}( \cdot ) \geqslant 0\) and \({\varphi _{22}}( \cdot ) \geqslant 0\) are two smooth functions. Furthermore, there exists a constant \(\theta _{22}^* > 0\) such that \({\varphi _{22}}(D(t,{t_0}))\leqslant \theta _{22}^*\) holds for \(\forall t \geqslant {t_0}\). Substituting (21) into (20) leads to
where
From Lemma 5, we adopt the following neural network to approximate the unknown nonlinear continuous function \({{\bar{\phi }} _2}({X_2})\):
where \(H_2^*\) is an unknown weight vector, \({S_2}({X_2}) = {[{S_{21}}({X_2}), {S_{22}}({X_2}), \ldots ,{S_{2{L_2}}}({X_2})]^\mathrm{T}} \in {R^{L_2}}\) is a basic function vector, \({\varepsilon _2}({X_2})\) is the approximation error satisfying \(\left| {{\varepsilon _2}({X_2})} \right| \leqslant \varepsilon _2^*\) with \(\varepsilon _2^* > 0\).
Substituting (23) into (22), and using Lemma 4, we have
where \({\theta _2} = {\left\| {H_2^*} \right\| ^2}L\) and \(g_{21}^* = \varepsilon _2^*\displaystyle \sqrt{g_2^{\min }}+\displaystyle \sqrt{2g_2^{\min }{\theta _2}}\).
Take a virtual control law and a “virtual adaptive law” for Step 2 as follows:
where \({c_2} > 0\) is a design parameter.
Substituting (25) into (24) results in
where \(g_1^* = \displaystyle \sum \limits _{i = 1}^3 {g_{1i}^*}+\frac{{g_1^{\max }}}{4}\sqrt{\frac{2}{{g_1^{\min }}}}\) and \(g_{22}^* = {\theta _2}\displaystyle \sqrt{2{\eta _2}}\).
Step \({{\varvec{h}}}(\mathbf{3 } \leqslant {\varvec{h}} \leqslant {\varvec{n}} - \mathbf{1})\) Consider a Lyapunov function candidate as
where \({\eta _h} > 0\) is a design parameter, \({{\tilde{\theta }} _h} = {\theta _h} - {{\hat{\theta }} _h}, {{\hat{\theta }} _h}\) is the estimate of \({\theta _h}, {\theta _h}\) will be given later. From (18), (26) and Assumption 1, the time derivative of \({V_h}\) satisfies
Using Assumption 3, Lemmas 1 and 2, we obtain, for \(\forall t \geqslant {t_0}\),
where \({\varphi _{h1}}( \cdot )\geqslant 0\) and \({\varphi _{h2}}( \cdot )\geqslant 0\) are two smooth functions. Similar to Steps 1 and 2, there exists a constant \(\theta _{h2}^*>0\) such that \({\varphi _{h2}}(D(t,{t_0})) \leqslant \theta _{h2}^*\) holds. Substituting (29) into (28) leads to
where
To approximate the unknown nonlinear continuous function \({{\bar{\phi }} _h}({X_h})\), we adopt the following neural network:
where \(H_h^*\) is an unknown ideal weight vector, \({S_h}({X_h}) = [{S_{h1}}({X_h}),{S_{h2}}({X_h}), \ldots ,{S_{h{L_h}}}({X_h})] \in {R^{L_h}}\) is a basic function vector, \({\varepsilon _h}({X_h})\) is the approximation error satisfying \(\left| {{\varepsilon _h}({X_h})} \right| \leqslant \varepsilon _h^*\) with \(\varepsilon _h^* > 0\).
Substituting (31) into (30), and using Lemma 4, we obtain
where \({\theta _h} = {\left\| {H_h^*} \right\| ^2}L\) and \(g_{h1}^* = \varepsilon _h^*\displaystyle \sqrt{2{{g_h^{\min }}}} + \displaystyle \displaystyle \sqrt{2{{g_h^{\min }}}{\theta _h}}\).
Choose a virtual control law and a “virtual adaptive law” for Step h as follows:
where \({c_h} > 0\) is a design parameter.
Substituting (33) into (32) yields
where \(g_{h - 1}^* = \displaystyle \sum \limits _{i = 1}^2 {g_{h - 1,i}^*} + \displaystyle \frac{{g_{h - 1}^{\max }}}{4}\displaystyle \sqrt{\displaystyle \frac{2}{{g_{h - 1}^{\min }}}}\) and \(g_{h2}^* = {\theta _h}\displaystyle \sqrt{2{\eta _h}}\).
Step \({{\varvec{n}}}\) Consider the following Lyapunov function candidate as
where \({{\tilde{\theta }} _n} = {\theta _n} - {{\hat{\theta }} _n}, {{\hat{\theta }} _n}\) is the estimate of \({\theta _n}, {\theta _n}\) will be given later. From (18), (26) and (34), the time derivative of \({V_n}\) satisfies
Under Assumption 1, for \(\forall t \geqslant {t_0}\), the following inequality holds:
where \({\varphi _{n1}}( \cdot )\geqslant 0\) and \({\varphi _{n2}}( \cdot )\geqslant 0\) are smooth functions.
Note that \(D(t,{t_0})\) is a bounded function for \(\forall t \geqslant {t_0}\), then we can obtain \({\varphi _{n2}}(D(t,{t_0}))\leqslant \theta _{n2}^*\), where \(\theta _{n2}^*>0\) is a constant. Substituting (37) into (36) results in
where
As same as the previous steps, we adopt a neural network to approximate the unknown nonlinear continuous function \({{{\bar{\phi }} }_n}({X_n})\), that is,
where \(H_n^*\) is an unknown ideal weight vector, \({S_n}({X_n}) = [{S_{n1}}({X_n}),{S_{n2}}({X_n}), \ldots ,{S_{n{L_n}}}({X_n})] \in {R^{L_n}}\) is a basic function vector, \({\varepsilon _n}({X_n})\) is the approximation error satisfying \(\left| {{\varepsilon _n}({X_n})} \right| \leqslant \varepsilon _n^*\) with \(\varepsilon _n^* > 0\).
Substituting (39) into (38), and using Lemma 4, we obtain
where \({\theta _n} = {\left\| {H_n^*} \right\| ^2}L\) and \(g_{n1}^* = \varepsilon _n^*\displaystyle \sqrt{{2g_n^{\min }}} + \displaystyle \sqrt{{{2g_n^{\min }{\theta _n}}}}\).
A virtual control law and a “virtual adaptive law” for the last step are chosen as
where \({c_n} > 0\) is a design parameter.
Substituting (41) into (40) results in
where \(g_{n - 1}^* = \displaystyle \sum \limits _{i = 1}^2 {g_{n - 1,i}^*} + \displaystyle \frac{{g_{n - 1}^{\max }}}{4}\displaystyle \sqrt{\displaystyle \frac{2}{{g_{n - 1}^{\min }}}}\) and \(g_n^* = g_{n1}^* + {\displaystyle \theta _n}\displaystyle \sqrt{2{\eta _n}}\).
Note that the states of system (1) are measurable at the sampling points, hence, from (16), (25), (33) and (41), for \(\forall t \in [{t_k},{t_{k + 1}}), k = 0,1, \ldots , + \infty \), we design the adaptive sampled-data controller as
where \(\varrho _l({t_k}) = {x_l}({t_k}) + \varrho _{l-1}({t_k})\big (\displaystyle \sqrt{1 + \mu _{l - 1}^2({t_k})} + {c_{l - 1}}\big ), \varrho _1({t_k}) = {x_1}({t_k})\).
For each sampling interval \(\left[ {{t_k},{t_{k + 1}}} \right) \), relation (42) can be further represented as
where
Remark 5
It should be mentioned that the term \(x_1^2\theta \) in (15) was necessary for the adaptive sampled-data controller design since such term can deal with the uncertainties existed in the first step with virtual controller (16) [see (14)–(18)], and such way to deal with the uncertainties was motivated by the existing literature on the adaptive continuous-time control, such as [2,3,4].
Remark 6
In comparison with the design of adaptive laws in continuous-time control, it can be seen from (43) that the adaptive laws were constructed just based on the sampled values of the system states, which means that the proposed adaptive design can better save the recourses and helps to reduce the computation burden of the controller.
4 Stability analysis
In what follows, the stability of the closed-loop system under sampled-data controller (43) will be demonstrated by using the Gronwall–Bellman inequality.
Theorem 1
Suppose system (1) satisfies Assumptions 1–3, for the given allowable sampling period and any bounded initial condition, sampled-data controller (43) will render all states of the resulting closed-loop system to be semi-globally uniformly ultimately bounded.
Proof
Choose the following Lyapunov function candidate
where \({{\tilde{\mu }} _i} = \mu _i - {\theta _i}, {\beta _i} > 0\) is a design parameter. \(\square \)
Let \(p>0\) be a constant, where \(p \geqslant V({t_0})\); and define a compact set as
next, we will demonstrate that \(V({t})\leqslant p\) is an invariant set for \(\forall t\geqslant t_0\) and \(V({t_0})\leqslant p\).
Under the situation that \(V(t) \leqslant p\), we know that the following derivations hold: according to (45), we have that \({x_1(t)},{z_2(t)},\ldots , {z_n(t)}, {{\hat{\theta }} _1(t)}, {{\hat{\theta }} _2(t)}, \ldots ,{{\hat{\theta }} _n(t)}\) and v(t) are bounded, which implies that there exist constants \({\Xi _1},{\Xi _2}, \ldots ,{\Xi _n},\) \({{\bar{\varDelta }} _1}, {{\bar{\varDelta }} _2}, \ldots , {{\bar{\varDelta }} _n}\) and \({{{\bar{H}}}}\) such that \(\left| {{x_1}(t)} \right| \leqslant {\Xi _1}, \left| {{z_2}(t)} \right| \leqslant {\Xi _2}, \ldots , \left| {{z_n}(t)} \right| \leqslant {\Xi _n}, \left| {{{{\hat{\theta }} }_1}(t)} \right| \leqslant {{\bar{\varDelta }} _1},\left| {{{{\hat{\theta }} }_{2}}(t)} \right| \leqslant {{\bar{\varDelta }} _2}, \ldots ,\left| {{{{\hat{\theta }} }_n}(t)} \right| \leqslant {{\bar{\varDelta }} _n}\) and \(\left| v (t)\right| \leqslant {{{\bar{H}}}}\) hold; furthermore, according to (16), (25), (33) and (41), we know that the virtual control laws are all bounded, noting that \({z_i} = {x_i} - {\alpha _{i - 1}},i = 2,3, \ldots ,n\), we can obtain the boundedness of \({x_1(t)},{x_2(t)}, \ldots ,{x_n(t)}\), i.e., there exist constants \(\sigma _2^*, \sigma _3^*,\ldots , \sigma _n^*\) such that \(\left| {{x_2}(t)} \right| \leqslant \sigma _2^*, \left| {{x_3}(t)} \right| \leqslant \sigma _3^*, \ldots ,\left| {{x_n}(t)} \right| \leqslant \sigma _n^*\) hold; then, for the sampling points, we also have \(\left| {{x_1}({t_k})} \right| \leqslant {\Xi _1}, \left| {{x_2}({t_k})} \right| \leqslant \sigma _2^*, \ldots ,\left| {{x_n}({t_k})} \right| \leqslant \sigma _n^*\).
On the other hand, under the situation that \(V(t) \leqslant p\), the following derivations also hold: from (43), we know that \({\mu _1(t)}\) is bounded by the boundedness of \({x_1}({t_k})\), then the boundedness of \({\mu _1}({t_k})\) can also be guaranteed, which means that \(\left| {{\mu _1}(t)} \right| \leqslant {{\bar{\mu }} _1}\) and \(\left| {{\mu _1}({t_k})} \right| \leqslant {{{\bar{\mu }} }_1}\) hold, where \({{{\bar{\mu }} }_1}>0\) is a constant; since
we can obtain the boundedness of \({\varrho _2}({t_k})\), that is, \(\left| {{\varrho _2}({t_k})} \right| \leqslant {\lambda _2}\) holds, where \({\lambda _2}>0\) is a constant; according to (43) again, we have the boundedness of \({\mu _2(t)}\), equally, \({\mu _2}({t_k})\) is bounded, which means that \(\left| {{\mu _2}(t)} \right| \leqslant {{\bar{\mu }} _2}\) and \(\left| {{\mu _2}({t_k})} \right| \leqslant {{{\bar{\mu }} }_2}\) hold, where \({{{\bar{\mu }} }_2}>0\) is a constant; furthermore, we know that \({\varrho _3}({t_k})\) is bounded due to the boundedness of \({x_3}({t_k}),{\mu _3}({t_k})\) and \({\varrho _2}({t_k})\), i.e., \(\left| {{\rho _3}({t_k})} \right| \leqslant {\lambda _3}\) holds for a constant \({\lambda _3} > 0\); using (43) repeatedly, we can obtain the boundedness of \({\varrho _3}({t_k}), {\varrho _4}({t_k}), \ldots ,{\varrho _n}({t_k}),{\mu _3}({t_k}), \ldots ,{\mu _n}({t_k})\), that is, there exist constants \({\lambda _3}, {\lambda _4}, \ldots , {\lambda _n}, {{{\bar{\mu }} }_3},{{{\bar{\mu }} }_4}, \ldots ,{{{\bar{\mu }} }_n}\) such that \(\left| {{\varrho _3}({t_k})} \right| \leqslant {\lambda _3}, \ldots ,\left| {{\varrho _n}({t_k})} \right| \) \(\leqslant {\lambda _n}, \left| {{\mu _3}(t)} \right| \leqslant {{\bar{\mu }} _3}, \ldots ,\left| {{\mu _n}(t)} \right| \leqslant {{\bar{\mu }} _n}, \left| {{\mu _3}({t_k})} \right| \leqslant {{{\bar{\mu }} }_3}, \ldots ,\left| {{\mu _n}({t_k})} \right| \leqslant {{{\bar{\mu }} }_n}\) hold; furthermore, since x(t) and v(t) are bounded, we know that there exists a constant \({H^*}>0\) such that
holds; then according to (44) and (45), the time derivative of V(t) satisfies the following relation:
where \({d^*} = {\bar{g}} + \Xi _1^2{\eta _1}\displaystyle \sqrt{\frac{2}{{{\beta _1}}}} + \sum \limits _{i = 2}^n {\lambda _i^2}{\eta _i} \sqrt{\displaystyle \frac{2}{{{\beta _i}}}} + \sum \limits _{i = 1}^n {{\eta _i}{\theta _i}} \sqrt{\displaystyle \frac{2}{{{\beta _i}}}}\).
Denote \(\xi (t) = [{\bar{x}}_n^\mathrm{T}(t),{{{\hat{\theta }} }_1}(t),{{{\hat{\theta }} }_2}(t), \ldots ,{{{\hat{\theta }} }_n}(t),{\mu _1}(t), \ldots ,{\mu _n}(t)]^\mathrm{T}\), then we conclude from (16), (25), (33), (41) and (43) that \({\dot{\xi }}(t) = \Psi (\xi (t),\xi ({t_k})),\forall t \in [{t_k},{t_{k + 1}})\). further, from Assumptions 1 and 2, for \(\forall t \in [{t_k},{t_{k + 1}})\), we obtain
where \(\alpha = 2n\max \big \{ \displaystyle \sqrt{{\eta _1}} ,\displaystyle \sqrt{{\eta _2}} , \ldots ,\displaystyle \sqrt{{\eta _n}} \big \}, {g^*} = \max \big \{g_1^{\max }, \ldots ,g_n^{\max }\big \}, \beta ^* = \max \big \{ {\varTheta _1},{\varTheta _2}\big \}\) with
Furthermore, according to Lemma 4, we have the following relation:
where \({\varTheta _3} = \max \left\{ {g^*}\displaystyle \sqrt{6n(n - 2)} ,{g^*}\displaystyle \sqrt{6n(n - 2)}\right. \left. \left( {\Xi _1} + \sum \nolimits _{i = 2}^n {\sigma _i^* + \sum \nolimits _{i = 1}^n {{{{\bar{\mu }} }_i}} } \right) \right\} \).
Substituting (48) into (47), we obtain, for \(\forall t \in [{t_k},{t_{k+1}})\),
where \(\varTheta ^* = {\varTheta _3} + \beta ^*\).
Using Lemma 1, relation (49) can be further rewritten as
where \({\bar{\alpha }} = \max \bigg \{ \displaystyle \sqrt{2g_1^{\min }} ,\displaystyle \sum \limits _{i = 2}^n {\sigma _i^* + \displaystyle \sum \limits _{i = 1}^n {{\bar{\mu }} _i} } + \varTheta ^* \bigg \}\).
Noting that \(\left| {{x_i}(t) - {x_i}({t_k})} \right| \leqslant \left\| {\xi (t) - \xi ({t_k})} \right\| ,i = 1,2, \ldots ,n\), hold for each sampling period, then for \(\forall t \in [{t_k},{t_{k+1}})\), we can deduce from (43) that
where \({b^*} = \displaystyle \sqrt{n} \max \big \{ b_1^*,\ldots ,b_n^*\big \}, b_i^* = \prod \nolimits _{h = i}^n {\bigg (\displaystyle \sqrt{1 + {{\bar{\varDelta }}_h^2}} + {c_i}\bigg )}, i = 1,2, \ldots ,n\); and \({\varTheta _4} > 0\) is a constant.
From (45), (50) and (51), for \(\forall t \in [{t_k},{t_{k+1}})\), we have
where \({\bar{d}} = g_n^{\max }\bigg (2{b^*}\bigg ({\Xi _1} + \displaystyle \sum \nolimits _{i = 2}^n {\sigma _i^*} + \displaystyle \sum \nolimits _{i = 1}^n {{{\bar{\varDelta }} _i}} + \displaystyle \sum \nolimits _{i = 1}^n {{{{\bar{\mu }} }_i}} \bigg ) + {\varTheta _4}\bigg ({\Xi _1} + \displaystyle \sum \nolimits _{i = 2}^n {\sigma _i^*} \bigg )\bigg )\sqrt{\displaystyle \frac{2}{{g_n^{\min }}}}\).
Substituting (52) into (46) results in
Let \(W(t) = \displaystyle \sqrt{V(t)}\), from (53), for \(\forall t \in [{t_k},{t_{k + 1}})\), a straightforward calculation leads to
where \({T_k} = {t_{k + 1}} - {t_k}\) is the sampling period. Choose a constant \({\lambda _0}\) satisfying
where \({\beta _0} = \displaystyle \frac{{{\tilde{c}}}}{{{\tilde{c}}\sqrt{p} - 2({d^*} + {\bar{d}})}} > 0\); and the allowable sampling period \({T_k}\) is given as
Define
then we can obtain the following relations by substituting (55) and (56) into (57):
under which, for \(\forall t \in [{t_0},{t_1})\) and \({{W(t_0) \leqslant {\displaystyle \sqrt{p}}}}\), it can be concluded that
When \(V(t) = p, \forall t \in [{t_0},{t_1})\), then from (59), we have \(\dot{W}(t) \leqslant 0\), which means that \(\{ {W(t) \leqslant {\sqrt{p}}} \}\) is a invariant set for the first sampling period, that is, \(V(t) \leqslant p\) holds for the interval \([{t_0},{t_1})\). Due to that W(t) is a continuous function for \(\forall t \geqslant {t_0}\), we can obtain \(W(t_1^ - ) = W({t_1}) \leqslant \displaystyle \sqrt{p}\); hence, for \(\forall t \in [{t_1},{t_2})\), applying the same analysis approach which is used for the first interval \([{t_0},{t_1})\), we can know that \(V(t) \leqslant p\) also holds, and we equally have \(W(t_2^ - ) = W({t_2}) \leqslant \displaystyle \sqrt{p}\). Following this line of argument, we finally know that \(W(t) \leqslant \sqrt{p}\) holds for every sampling period, that is, \(V(t) \leqslant p\) holds for \(\forall t \geqslant {t_0}\), which has proved that \(V({t})\leqslant p\) is an invariant set for \(\forall t\geqslant t_0\) and \(V({t_0})\leqslant p\). Substituting (56) into (54), and solving the inequality, we obtain, for \(\forall t \in [{t_k},{t_{k + 1}})\),
From (57) and (58), (60) can be further rewritten as
where \({Q^*}(t - {t_k}) = \displaystyle \frac{1}{2} + \displaystyle \frac{1}{2}{e^{ - {\sigma _1}(t - {t_k})}}\). Substituting \(t = {t_{k + 1}}\) into (61) results in
Obviously, \({Q^*}({T_k}) \in (0,1)\), and we can deduce from (62) that
where \(T^*>0\) is a constant.
From (63), it is easy to obtain that
i.e.,
where \({W^*} = \bigg (\displaystyle \frac{1}{{2{\lambda _0}}} +\displaystyle \frac{{{d^*} + {\bar{d}}}}{{{\tilde{c}}}}\bigg )\bigg (\displaystyle \frac{1}{{1 - {Q^*}({T^*})}}\bigg )\). Using (45) and (65), we get
Further, for \(i = 2,3, \ldots ,n\), it can be deduced from (43) and (66) that
Finally, from Assumption 3 and (66), we have the boundedness of \(z_0(t)\) as \(t\rightarrow +\infty \). The proof of Theorem 1 is completed.
Remark 7
Compared with the periodic sampling considered in the existing literature [18,19,20,21,22,23,24], the sampling period in this paper can be chosen freely within an allowable constant [see (56)], which means that the designer can increase the sampling frequency in the initial running stage to make the system to be stable as soon as possible, and decrease the sampling frequency to reduce the computation burden when the system tends to be stable; thus, for the real systems, non-periodic sampling has more advantages than the periodic sampling.
Remark 8
For nonlinear system (1), the adaptive sampled-data controller can be constructed as follows:
Step 1: Determine the constant \(\alpha \) from the parameters \(\eta _i>0, i= 1,2, \ldots ,n\), and choose \({\lambda _0}\) satisfies (55), then work out the allowable sampling period \({T_k}, k = 0,1, \ldots , + \infty \).
Step 2: The adaptive sampled-data controller (43) can be constructed with the design parameters \(c_i>0, i= 1,2, \ldots ,n\), and the sampled values of the system states.
Remark 9
Motivated by the existing literature on sampled-data control, such as [41,42,43,44,45,46,47], the proposed sampled-data control method will be extended to solve the stabilization problem of the Markovian jump systems in the form of (1); furthermore, by choosing appropriate Lyapunov–Krasovskii functional, the proposed sampled-data control method will also be extended to solve the stabilization problem of the systems in the form of (1) with time-varying delays.
5 Simulation examples
In this section, two examples will be provided to show effectiveness of the proposed results.
Example 1
Consider the following second-order nonlinear system
where \({\varDelta _1}({x_1},z_0) = {z_0^2}\sin (z_0) + {\cos ^2}(x_1^2){\sin ^2}(z_0)\) and \({\varDelta _2}({{{\bar{x}}}_2},z_0) = {z_0^2}\cos (z_0)+\sin ({x_1^2}{x_2^2})\cos ({x_2})\).
From (43), for \(\forall t \in [{t_k},{t_{k + 1}})\), we construct the sampled-data controller as
where \({c_1} = 0.2, {c_2} = 0.3\), and \(\mu _1(t_k), \mu _2(t_k)\) can be obtained from the following equations:
where \({\eta _1} = 0.3, {\eta _2} = 0.4\) and \(\varrho _2({t_k}) = {x_1}({t_k}) + {x_1}({t_k})\displaystyle \sqrt{1 + \mu _2^2({t_k})} + {c_1}{x_1}({t_k})\).
Simulation results are shown in Figs. 1, 2, 3 and 4, where \(x(0) = {[0.3, - 0.2]^\mathrm{T}}, {\mu _1}(0) = 0.1, {\mu _2}(0) = 0.2\) and \(z_0(0) = 0.3\), the sampling period is chosen randomly in the interval \((0,0.08\hbox { s})\). It can be seen from Fig. 1 that all states of the resulting closed-loop system converge to a neighborhood of the origin, which demonstrates effectiveness of the proposed sampled-data control method.
Example 2
In the example, a popular benchmark of application example will be provided, that is, the stabilization of an one-link manipulator actuated by a brush dc (BDC) motor, the dynamics of a one-link manipulator actuated by a BDC motor can be expressed as follows [48]:
where \(q(t),\dot{q}(t),\) and \(\ddot{q}(t)\) are the link angular position, velocity, and acceleration, respectively; I(t) is the motor current; \({\varDelta _{I1}}( \cdot )\) is the additive bounded disturbance; \({\varDelta _{I2}}( \cdot )\) is the additive bounded voltage disturbance; \(V_E\) is the input control voltage; M is the armature inductance; Q is the armature resistance; \({K_m}\) is the back-emf coefficient; \(z_0\) is an unmeasured states;
J is rotor inertia; \({R_0}\) is the radius of the load; \({B_0}\) is the coefficient of viscous friction at the joint; m is the link mass; \({L_0}\) is the link length; G is the gravity coefficient, and \({K_\tau }\) is the coefficient which characterizes the electromechanical conversion of armature current to torque; \(q(t),\dot{q}(t)\) and I(t) can only be measured at the sampling points.
In the simulation, the design parameters are selected as \(J = 1.252 \,\times \, {10^{ - 3}}\hbox { kg} \, {\hbox {m}^2}, M = 15.0 \,\times \, {10^{ - 3}}H, {L_0} = 0.205\hbox { m}, Q = 3\;{\Omega }, m= 0.506\hbox { kg}, {M_0} = 0.423\hbox { kg}, {B_0} = 15.25 \times {10^{ - 3}}\hbox { N} \, \hbox {m} \, \hbox {s/rad}, {K_\tau } = 1.5 \times {10^{ - 3}}\hbox { N} \, \hbox {m/A}\), and \({K_m} = 0.7 \hbox { N} \, \hbox {m/A}\).
Now, setting \({x_1}(t) = q(t), {x_2}(t) = \dot{q}(t)\) and \({x_3}(t) = I(t)\), then (71) can be expressed as
where \({\varDelta _{I1}}({{{\bar{x}}}_2},z_0) = {z_0^2}\sin ({x_2}z_0) + \sin (x_1^2x_2^2), {\varDelta _{I2}}({{{\bar{x}}}_3},z_0) = {z_0^2}\cos ({x_1}{x_2}){\sin ^2}({x_3}) + \sin ({x_1}{x_2})\).
To solve the stabilization problem of system (72), we use the following sampled-data controller:
where \({\bar{z}}_i = x_i - {\bar{\alpha }} _{i - 1},i = 2,3\), and \({c_1} = 0.2,{c_2} = 0.3,{c_3} = 0.1\).
According to (43), the adaptive laws are taken as
where \({\eta _1} = 0.3, {\eta _2} = 0.4,{\eta _3} = 0.2\) and
Simulation results are shown in Figs. 5, 6, 7 and 8 with initial conditions \(x(0) = {[0.3, - 0.2,} {0.2]^\mathrm{T}}, \mu _1(0) = 0.1, \mu _2(0) = 0.2, \mu _3(0) = 0.1\) and \(z_0(0) = 0.3\), the sampling period can be chosen randomly in the interval \((0,0.06 \hbox { s})\). It can be seen from Fig. 5 that the link angular position q(t), velocity \(\dot{q}(t)\) and motor current I(t) of system (71) converge to a neighborhood of the origin, which shows effectiveness of the proposed methods.
6 Conclusions
In this paper, an adaptive sampled-data control technique was developed to practically stabilize a class of nonlinear systems in strict-feedback structure with uncertain functions which were not required to satisfy any linear growth condition. During adaptive sampled-data controller design, neural networks were employed to approximate the unknown nonlinear functions, then an adaptive sampled-data controller was constructed by utilizing the virtual control laws and “virtual adaptive laws” which were obtained via the backstepping technique. With the help of Gronwall–Bellman inequality, it was demonstrated that the proposed sampled-data controller can make all states of the resulting closed-loop system to be semi-globally uniformly ultimately bounded with appropriate choice of the sampling period. Finally, two examples were provided to show validness of the obtained results. In addition, the proposed results can be extended to the switched nonlinear systems and multi-agent systems, which is our future work.
References
Wu, L.B., Yang, G.H.: Robust adaptive fault-tolerant tracking control of multiple time-delays systems with mismatched parameter uncertainties and actuator failures. Int. J. Robust Nonlinear Control 25(16), 2922–2938 (2015)
Wang, H., Liu, X., Chen, B., Zhou, Q.: Adaptive fuzzy decentralized control for a class of pure-feedback large-scale nonlinear systems. Nonlinear Dyn. 75(3), 449–460 (2014)
Wang, C., Wen, C., Guo, L.: Decentralized output-feedback adaptive control for a class of interconnected nonlinear systems with unknown actuator failures. Automatica 71, 187–196 (2016)
Wang, Q., Wei, C.: Decentralized robust adaptive output feedback control of stochastic nonlinear interconnected systems with dynamic interactions. Automatica 54, 124–134 (2015)
Zhang, T., Xia, X.: Decentralized adaptive fuzzy output feedback control of stochastic nonlinear large-scale systems with dynamic uncertainties. Inf. Sci. 315, 17–38 (2015)
Huang, S., Xiang, Z.: Finite-time stabilization of a class of switched stochastic nonlinear systems under arbitrary switching. Int. J. Robust Nonlinear Control 26(10), 2136–2152 (2016)
Wang, F., Chen, B., Zhang, Z., Lin, C.: Adaptive tracking control of uncertain switched stochastic nonlinear systems. Nonlinear Dyn. 84(4), 2099–2109 (2016)
Miao, X., Li, L.: Adaptive observer-based control for uncertain nonlinear stochastic systems with time-delay. J. Franklin Inst. 353(14), 3595–3609 (2016)
Zhang, T., Xia, X.: Adaptive output feedback tracking control of stochastic nonlinear systems with dynamic uncertainties. Int. J. Robust Nonlinear Control 25(9), 1282–1300 (2015)
Li, Y., Mao, Z., Tong, S.: Adaptive fuzzy output-constrained fault-tolerant control of nonlinear stochastic large-scale systems with actuator faults. IEEE Trans. Cybern. 47(9), 2362–2376 (2017)
Chen, Y., Du, H., He, Y., Jia, R.: Finite-time tracking control for a class of high-order nonlinear systems and its applications. Nonlinear Dyn. 76(2), 1133–1140 (2014)
Li, D., Cao, J.: Global finite-time output feedback synchronization for a class of high-order nonlinear systems. Nonlinear Dyn. 82(2), 1027–1037 (2015)
Mao, J., Huang, S., Xiang, Z.: Adaptive practical finite-time stabilization for switched nonlinear systems in pure-feedback form. J. Franklin Inst. 354(10), 3971–3994 (2017)
Ma, J., Ni, S., Jie, W., Dong, W.: Deterministic sampling strong tracking filtering algorithms: fast detection and isolation for aircraft actuator fault. Control Theory Appl. 32(6), 734–743 (2015)
Liu, Z., Wang, L., Wang, J., Dong, D., Hu, X.: Distributed sampled-data control of nonholonomic multi-robot systems with proximity networks. Automatica 77, 170–179 (2017)
Wang, Z., Zhai, J., Ai, W., Fei, S.: Global practical tracking for a class of uncertain nonlinear systems via sampled-data control. Appl. Math. Comput. 260, 257–268 (2015)
Nes̆ić, D., Teel, A.R., Kokotović, P.V.: Sufficient conditions for stabilization of sampled-data nonlinear systems via discrete-time approximations. Syst. Control Lett. 38(4), 259–270 (1999)
Wu, B., Ding, Z.: Sampled-data adaptive control of a class of nonlinear systems. Int. J. Adapt. Control Signal Process. 25, 1050–1060 (2011)
Chu, H., Qian, C., Liu, R., Li, S.: Global practical tracking for a class of nonlinear systems via linear sampled-data control. Int. J. Control 88(9), 2667–2672 (2015)
Zhang, C., Jia, R., Qian, C., Li, S.: Semi-global stabilization via linear sampled-data output feedback for a class of uncertain nonlinear systems. Int. J. Robust Nonlinear Control 25(13), 2041–2061 (2015)
Zhang, D., Shen, Y.: Global output feedback sampled-data stabilization for upper-triangular nonlinear systems with improved maximum allowable transmission delay. Int. J. Robust Nonlinear Control 27(2), 212–235 (2017)
Du, H., Qian, C., He, Y., Cheng, Y.: Global sampled-data output feedback stabilisation of a class of upper-triangular systems with input delay. IET Control Theory Appl. 7(10), 1437–1446 (2013)
Qian, C., Du, H., Li, S.: Global stabilization via sampled-data output feedback for a class of linearly uncontrollable and unobservable systems. IEEE Trans. Autom. Control 61(12), 4088–4093 (2016)
Lin, W., Wei, W., Ye, G.: Global stabilization of a class of nonminimum-phase nonlinear systems by sampled-data output feedback. IEEE Trans. Autom. Control 61(10), 3076–3082 (2016)
Tarek, A.A., Iasson, K., Francoise, L.L.: Global exponential sampled-data observers for nonlinear systems with delayed measurements. Syst. Control Lett. 62(7), 539–549 (2013)
Shen, B., Wang, Z., Huang, T.: Stabilization for sampled-data systems under noisy sampling interval. Automatica 63, 162–166 (2016)
Liu, Y., Park, J.H., Guo, B.Z., Sun, Y.: Further results on stabilization of chaotic systems based on fuzzy memory sampled-data control. IEEE Trans. Fuzzy Syst. (2017). https://doi.org/10.1109/TFUZZ.2017.2686364
Wang, B., Cheng, J., Ai-Barakati, A., Fardoun, H.M.: A mismatched membership function approach to sampled-data stabilization for T–S fuzzy systems with time-varying delayed signals. Sig. Process. 140, 161–170 (2017)
Cheng, J., Park, J.H., Karimi, H.R., Shen, H.: A flexible terminal approach to sampled-data exponentially synchronization of Markovian neural networks with time-varying delayed signals. IEEE Trans. Cybern. (2017). https://doi.org/10.1109/TCYB.2017.2729581
Shen, H., Su, L., Wu, Z.G., Park, J.H.: Reliable dissipative control for Markov jump systems using an event-triggered sampling information scheme. Nonlinear Anal. Hybird Syst. 25, 41–59 (2017)
Shen, H., Men, Y., Wu, Z.G., Park, J.H.: Non-fragile \({H_\infty }\) control or fuzzy Markovian jump systems under fast sampling singular perturbation. IEEE Trans. Syst. Man Cybern. Syst. (2017). https://doi.org/10.1009/TSMC.2017.2758381
He, W., Zhang, S., Ge, S.S.: Robust adaptive control of a thruster assisted position mooring system. Automatica 50(7), 1843–1851 (2014)
Krstic, M., Kanellakopoulos, L., Kokotovic, P.V.: Nonlinear and Adaptive Control Design. Wiley, New York, NY (1995)
He, W., Zhang, S., Ge, S.S.: Adaptive control of a flexible crane system with the boundary output constraint. IEEE Trans. Ind. Electron. 61(8), 4126–4133 (2014)
Li, T.S., Wang, D., Feng, G., Tong, S.C.: A DSC approach to robust a NN tracking control for strict-feedback nonlinear systems. IEEE Trans. Syst. Man Cybern. B Cybern. 40(3), 915–927 (2010)
Jiang, Z.P., Praly, L.: Design of robust adaptive controllers for nonlinear systems with dynamic uncertainties. Automatica 34(7), 825–840 (1998)
Apostol, T.: Mathematical Analysis. Addison-Wesley, New Jersey (1974)
Lin, W., Qian, C.: Adaptive control of nonlinearly parameterized systems: the smooth feedback case. IEEE Trans. Autom. Control 47(8), 1249–1266 (2002)
Hardy, G.H., Littlewood, J.E., Pslya, G.: Inequalities. Cambridge University Press, Cambridge (1952)
Sanner, R.M., Slotine, J.J.E.: Gaussian networks for direct adaptive control. IEEE Trans. Neural Netw. 3(6), 837 (1991)
Cheng, J., Park, J.H., Zhang, L., Zhu, Y.: An asynchronous operation approach to event-triggered control for fuzzy Markovian jump systems with general switching policies. IEEE Trans. Fuzzy Syst. (2016). https://doi.org/10.1109/TFUZZ.2016.2633325
Cheng, J., Park, J.H., Karimi, H.R., Zhao, X.: Static output feedback control for nonhomogeneous Markovian jump systems with asychronous time delays. Inf. Sci. 399, 219–238 (2017)
Liang, K., Dai, M., Shen, H., Wang, J., Wang, Z., Chen, B.: \({L_2} - {L_\infty }\) synchronization for singularly perturbed complex networks with semi-Markov jump topology. Appl. Math. Comput. 321, 450–462 (2018)
Lee, T.H., Wu, Z.G., Park, J.H.: Synchronization of a complex dynamical network with coupling time-varying delays via sampled-data control. Appl. Math. Comput. 219(3), 1354–1366 (2012)
Lee, T.H., Park, J.H.: Improved criteria for sampled-data synchronization of chaotic Lur’e systems using two new approaches. Nonlinear Anal. Hybrid Syst. 24, 132–145 (2017)
Lee, T.H., Park, J.H.: Stability analysis of sampled-data systems via free-matrix-based time-dependent discontinuous Lyapunov approach. IEEE Trans. Autom. Control 62(7), 3653–3657 (2017)
Liu, Y., Guo, B.Z., Park, J.H., Lee, S.M.: Event-based reliable dissipative filtering for T–S fuzzy systems with asynchronous constraints. IEEE Trans. Fuzzy Syst. (2017). https://doi.org/10.1109/TFUZZ.2017.2762633
Carroll, J.J., Schneider, M., Dawson, D.M.: Integrator backstepping techniques for the tracking control of permanent magnet brush DC motors. IEEE Trans. Ind. Appl. 31(2), 248–255 (1995)
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Nos. 61273120 and 61673219), Jiangsu Six Talents Peaks Project of Province (No. XNYQC-CXTD-001), Tianjin Major Projects of Science and Technology (No. 15ZXZNGX00250), and Postgraduate Research and Practice Innovation Program of Jiangsu Province (KYCX 17-0365).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
About this article
Cite this article
Mao, J., Xiang, Z., Zhai, G. et al. Adaptive practical stabilization of a class of uncertain nonlinear systems via sampled-data control. Nonlinear Dyn 92, 1679–1694 (2018). https://doi.org/10.1007/s11071-018-4154-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-018-4154-9