A micromechanical mass sensing method based on amplitude tracking within an ultra-wide broadband resonance

Abstract

We propose a mass sensing scheme in which amplitude shifts within a nonlinear ultra-wide broadband resonance serve as indicators for mass detection. To achieve the broad resonance bandwidth, we considered a nonlinear design of the resonator comprised of a doubly clamped beam with a concentrated mass at its center. A reduced-order model of the beam system was constructed in the form of a discrete spring-mass system that contains cubic stiffness due to axial stretching of the beam in addition to linear stiffness (Duffing equation). The cubic nonlinearity has a stiffening effect on the frequency response causing nonlinear bending of the frequency response toward higher frequencies. Interestingly, we found that the presence of the concentrated mass broadens the resonant bandwidth significantly, allowing for an ultra-wide operational range of frequencies and response amplitudes in the proposed mass sensing scheme. A secondary effect of the cubic nonlinearity is strong amplification of the third harmonic in the beam’s response. We computationally study the sensitivity of the first and third harmonic amplitudes to mass addition and find that both metrics are more sensitive than the linearized natural frequency and that in particular, the third harmonic amplitude is most sensitive. This type of open-loop mass sensing avoids complex feedback control and time-consuming frequency sweeping. Moreover, the mass resolution is within a functional range, and the design parameters of the resonator are reasonable from a manufacturing perspective.

1 Introduction

In recent decades, micro- and nanomechanical resonators have drawn considerable attention due to their high sensitivity, portability and relatively low cost. They are currently used for a wide variety of applications including precise frequency generation and timekeeping, and nanoscale imaging and sensor technology [4, 5, 21, 32, 43]. In general, nano/micromechanical resonators have relatively low damping with Q-factors in the range of $10^{2}$–$10^{5}$ and large resonant frequencies ranging from $10^{4}$ to $10^{9}$ Hz. These amazing properties result in sharp resonance peaks at high frequencies, which are extremely sensitive to physical properties like force and mass. For example, such sensors are capable of detecting forces present in intramolecular covalent bonds [17] or even quantifying the mass of a single proton [10].

Among linear resonant mass sensors (also known as “dynamic-mode mass sensors”), there are two different conventional methods typically used for detection. One requires a frequency generator to incrementally sweep the excitation frequency and record the steady-state response amplitude at each frequency, before and after the addition of a discrete mass (the object that is sensed). The resulting resonance curves typically reveal a downward shift in the linear resonant frequency from which the amount of added mass is deduced [5, 32, 43]. This relatively simple, open-loop mass sensing method was among the earliest measurement techniques, commonly used in applications where ultra-high sensitivity is not required [27, 28, 32, 42]. Limitations of this technique include unaccounted-for contributions to the effective stiffness of the resonator; however, recent studies have investigated different ways to approximate the added stiffness [22, 23, 29, 42, 53].

The other common resonant mass sensing technique involves a closed-loop feedback procedure to ensure that as mass is added to the device, the system is always excited at resonance [5, 32]. The advantage of this more complicated closed-loop method is that it eliminates the need for time-consuming frequency sweeps. Also, it allows for the use of ultra-high vacuum (UHV) conditions in which particularly high Q-factors arise, resulting in enhanced sensitivity [20, 21, 36]. The characteristic times associated with the decay of the transient terms are directly proportional to the Q-factor, and for most applications, the decay rate in UHV conditions is so slow that the open-loop approach becomes impractical [21]. For this reason, the closed-loop approach is usually used under UHV conditions to achieve extreme sensitivity, and it is the method required to realize state-of-the-art yoctogram resolution [10, 11, 20, 31, 49, 50]. While closed-loop mass sensing offers the advantages of improved sensitivity and independence from frequency sweeps, it has the disadvantages of requiring sophisticated FM-PLL feedback control, and, typically, extremely small resonator designs and UHV operating conditions.

In the last couple of decades, researchers have studied the advantages of intentional nonlinearity in the design of microresonator mass sensors. A general feature of nano- and microscale resonators is that the relative magnitude of the resonance amplitude is quite large (compared to the device size) and, as a result, these devices often exhibit significant geometric nonlinearity. On the one hand, this limits the operational range for conventional mass sensing methods in which a linear dynamic regime is required. On the other hand, it underscores the potential of intentionally exploiting nonlinear phenomena to improve microresonant sensing technology [6,7,8, 12, 13, 16, 19, 26, 30, 33, 34, 38,39,40,41, 45,46,47, 51, 52, 54, 55]. One such research area is bifurcation-based mass sensing, which utilizes the large changes in amplitudes associated with bifurcations in the nonlinear frequency response of microresonators. Typically, the nonlinear microresonators considered display either a softening frequency response where the frequency response curve bends backward toward lower frequencies, or a hardening response where the frequency response curve bends forward toward higher frequencies. In either case, the bending of the frequency response results in bi-stability, hysteresis and bifurcation points in the frequency response. Bifurcation points associated with a sudden upward shift in the response amplitudes occur at jump-up frequencies and bifurcation points associated with a sudden downward shift in the response amplitude occur at a jump-down frequencies. The addition of mass on the microresonator shifts the entire frequency response toward lower frequencies and hence, the dependence of the jump-up and jump-down frequencies on mass can be exploited in mass detection schemes.

Cho et al. [12] theoretically and experimentally studied a harmonically driven, doubly clamped carbon nanotube resonator and determined that the large resonance bandwidth and jump-down frequency are more sensitive to added mass and damping levels than a the linearized natural frequency of a linear resonator. Zhang et al. [54, 55] studied a single-crystal Si micro-oscillator where fringing-field electrostatic force was used to periodically change the effective stiffness of the resonator and thereby generate parametric harmonic excitation. Shifts in the jump-up frequency were used to detect mass and the jump-up frequency was shown to be 1–2 times more sensitive to mass than the linearized frequency. Kumar et al. [38, 39] studied a piezoelectrically actuated microcantilever probe consisting of a Si cantilever with a piezoelectric layer that was initially designed for scanning probe microscopy. Due to the presence of geometric, material and inertial nonlinearity, both cubic and quadratic terms appear in the reduced-order equation of motion for the microcantilever. Depending on the relative contribution of the different sources of nonlinearity, either a softening or stiffening behavior is observed in the frequency response. In either case, variations in both the jump-up and jump-down frequencies due to mass addition were studied analytically and experimentally. Bouchaala et al. [8] studied an electrostatically actuated beam, which exhibited geometric (cubic) and electrostatic (quadratic) nonlinearity. The contribution of the electrostatic nonlinearity was controlled via the DC voltage, and for low DC voltages, hardening was observed in the frequency response, whereas for large DC voltages, softening was observed in the frequency response. It was shown that in the case of softening, the jump-up event can be used as a switch to detect a threshold amount of added mass and in the case of hardening, changes in the response amplitude prior to the jump-down event can be used to quantify added mass in addition to the jump-down event signaling the addition of a critical amount of mass.

The incorporation of active feedback control in the aforementioned sensing techniques has also been explored. Hiller et al. [26, 40] analytically and experimentally studied amplitude feedback control of a parametrically excited microbeam sensor during parametric resonance. As mass is added to the sensor, the excitation frequency varies in order to maintain a predetermined set-point response amplitude and the resulting frequency shifts are used to quantify the amount of added mass. Interestingly, the operational frequencies and forcing levels considered lie within a parameter space that gives rise to a unique response amplitude (i.e., there is no hysteresis in the operational range considered). Bajaj et al. [7] considered a microscale quarts tuning pitchfork and used feedback control to provide a source of cubic nonlinearity in the dynamics. Due to the feedback, the motion of the pitchfork was well described by the Duffing equation. By varying the gain of the cubic stiffness term from negative, zero to positive, the frequency response behavior varied from softening, linear to hardening, respectively. Analytical and experimental analysis of the bifurcation frequencies in this semi-active Duffing oscillator demonstrated the viability of a tunable, commercially available bifurcation-based sensor.

Fig. 1

a Proposed nonlinear resonator design before (left) and after (right) mass deposition; b steady-state response amplitude at the 1st harmonic versus excitation frequency, before (blue) and after (red) mass deposition and (c) steady-state response amplitude at the 3rd harmonic versus excitation frequency, before (blue) and after (red) mass deposition. In b, c, for drive frequencies lower than a critical value (corresponding to a bifurcation point), there exists a unique, stable response and for drive frequencies larger than this critical value, there co-exist two stable responses denoted by solid lines and one unstable response denoted by a dotted line. (Color figure online)

In this work, we consider a clamped-clamped beam under harmonic base excitation having a concentrated mass at its center. The reduced-order model of the system is that of a Duffing oscillator, which is well known to result in hardening of the fundamental resonance curve. The primary role of the concentrated mass is to enhance the geometric nonlinearity of the system and thereby generate an ultra-wide resonance bandwidth. For a fixed forcing level of the beam, the range of frequencies that constitute the broadband resonance are determined by the linearized frequency (lower bound) and the jump-down frequency (upper bound). However, harmonic base excitation at the two clamped ends of the beam is used in this study and therefore the forcing level is not fixed, rather it is proportional to the square of the excitation frequency. Interestingly, we found that for sufficiently large base excitation amplitudes, there is theoretically no jump-down frequency. Computational results confirm this theoretical prediction, and a physical explanation of the phenomenon is outlined in Appendix. The critical excitation level above which there is no theoretical jump-down event is significantly lowered by the presence of the concentrated mass. In fact, without the concentrated mass, it would not be practically feasible to achieve the no-drop phenomenon, hence its critical role in the beam design. By operating at an excitation amplitude above this critical threshold, we exploit the ultra-wide resonant bandwidth for a mess sensing technique based on amplitude tracking. A secondary effect of the cubic nonlinearity is the strong amplification of the third harmonic, and hence, we track both the first and third harmonic amplitudes as mass is added to the microresonator.

For a fixed excitation frequency within the broadband resonance, as mass is added to the center of the beam, we computationally study the change in the steady-state response amplitudes of the first and third harmonics and find that they show strong sensitivity to mass. The novelty of the proposed mass sensor design is that its ultra-wide resonant bandwidth allows for a considerably larger range of operational frequencies and response amplitudes as compared to other resonant mass sensors incorporating nonlinearity. Additionally, multi-harmonic measurements are considered [18, 24, 44] and while both the first and third harmonic amplitudes prove to be more sensitive to mass than the linearized frequency, the third harmonic amplitude is found to be the most sensitive indicator. Furthermore, the design parameters are reasonable from a manufacturing point of view (beam width and thickness $\sim 100\,\mathrm{nm}$, beam length $\sim 1\,\upmu \mathrm{m}$) and femtogram mass resolution is achieved. This study focuses on developing the analytical and computational framework for the proposed mass sensing technique based on a new resonator design.

Fig. 2

Schematic of the system under consideration: a doubly clamped beam with a concentrated mass at its center under harmonic base excitation

2 Theoretical reduced-order model

In Fig. 2, we depict a schematic of the system under consideration: a thin clamped-clamped beam with a concentrated point mass at its center and harmonic base excitation at its clamped supports. Assuming that plane sections remain plane during the beam vibration, a linear stress–strain constitutive law, and planar motion, one can derive the following equation of motion describing the transverse motion of the beam with nonlinearity due to midplane stretching,

$$\begin{aligned}&\left[ {\rho A+m_\mathrm{c} \delta (x-L)} \right] w_{tt} +(\rho A\omega _1 /Q)w_t +EIw_{xxxx}\nonumber \\&\quad -\,(EA/4L)w_{xx} \int _0^{2L} {w_x^2 \mathrm{d}x=0} \end{aligned}$$

(1)

where $\rho$ is the mass density, A is the cross-sectional area, $m_\mathrm{c}$ is the mass of the concentrated point mass, E is Young’s modulus, I is the area moment of inertia, L is the half-length, Q is the Q-factor, $\omega _1$ is the linearized eigenfrequency of the fundamental flexural mode, $\delta (x)$ is the Dirac delta function, x is the spatial coordinate along the beam, t is time, and w(x, t) is the transverse displacement. The boundary conditions are given by,

$$\begin{aligned}&w\left( {0,t} \right) =w\left( {2L,t} \right) =a\sin \left( {\omega t} \right) ,\nonumber \\&w_x \left( {0,t} \right) =w_x \left( {2L,t} \right) =0 \end{aligned}$$

(2)

By decomposing the displacement into a “pseudo-static” component, $w_s \left( {x,t} \right) =-a\sin \left( {\omega t} \right)$, and a “flexible” component, $w_\mathrm{f} \left( {x,t} \right)$, we can instead consider the following boundary value problem describing the relative transverse motion of the beam with respect to the clamped supports,

$$\begin{aligned}&\left[ {\rho A+m_\mathrm{c} \delta (x-L)} \right] w_{f,tt} +(\rho A\omega _1 /Q)w_{f,t}\nonumber \\&\qquad +\,EIw_{f,{ xxxx}} -(EA/4L)w_{f,xx} \int _0^{2L} {\left( {w_{f,x}} \right) ^{2}\mathrm{d}x}\nonumber \\&\quad =- \left[ {\rho A+m_\mathrm{c} \delta (x-L)} \right] a\omega ^{2}\sin \omega t\nonumber \\&\qquad +\,(\rho A\omega _1 \omega /Q)\cos \omega t \end{aligned}$$

(3a)

$$\begin{aligned}&w_f (0,t)=w_f (2L,t)=0,\nonumber \\&{w_{f,x} (0,t)} =w_{f,x} (2L,t)=0 \end{aligned}$$

(3b)

Finally, by introducing the following normalizations,

$$\begin{aligned}&\tilde{x}=x/2L,\quad {u=w_f /2L,}\quad {\tilde{a}=a/2L,}\nonumber \\&\tilde{\delta }(\tilde{x})=2L\delta (x), \quad {\Theta ^{2}=\frac{EI}{16\rho AL^{4}}} \mu =\frac{m_\mathrm{c} }{2L\rho A},\nonumber \\&{\tau =\Theta t,}\quad {\Omega =\omega /\Theta ,}\quad {\beta =\frac{2AL^{2}}{I}} \end{aligned}$$

(4)

we can write the equation of motion in nondimensional form:

$$\begin{aligned}&\left[ {1+\mu \tilde{\delta }(\tilde{x}-1/2)} \right] u_{\tau \tau } +\frac{\Omega _1 }{Q}u_\tau +u_{\tilde{x}\tilde{x}\tilde{x}\tilde{x}}\nonumber \\&\qquad -\beta u_{\tilde{x}\tilde{x}} \int _0^1 {u_{\tilde{x}}^2 \mathrm{d}\tilde{x}} \nonumber \\&\quad =- \left[ {1+\mu \tilde{\delta }(\tilde{x}-1/2)} \right] \tilde{a}\Omega ^{2}\sin (\Omega \tau )\nonumber \\&\qquad +\frac{\tilde{a}\Omega \Omega _1 }{Q}\cos (\Omega \tau ) \end{aligned}$$

(5a)

$$\begin{aligned}&{u(0,\tau )=u(1,\tau )=0,}\quad {u_{\tilde{x}} (0,\tau )}=u_{\tilde{x}} (1,\tau )=0\nonumber \\ \end{aligned}$$

(5b)

If we assume that the mass-loaded beam vibrates in the fundamental flexural mode of the underlying linear system, we can write the nondimensional displacement along the beam as,

$$\begin{aligned} u\left( {\tilde{x},\tau } \right) =W_1 \left( {\tilde{x}} \right) \varphi _1 \left( \tau \right) \end{aligned}$$

(6)

where $W_1 \left( {\tilde{x}} \right)$ is the fundamental linear mode shape and $\varphi _1 \left( \tau \right)$ is the corresponding modal amplitude. Specifically, $W_1 \left( {\tilde{x}} \right)$ is the solution to the following problem:

$$\begin{aligned}&W_1^{{\prime \prime \prime \prime }} =\left[ {1+\mu \tilde{\delta }(\tilde{x}-1/2)} \right] \Omega _1^2 W_1 \end{aligned}$$

(7a)

$$\begin{aligned}&{W_1 (0)=W_1 (1)=0,}\quad {W_1^{\prime } (0)=W_1^{\prime } (1)=0} \end{aligned}$$

(7b)

where prime denotes differentiation with respect to the normalized spatial variable. The solution can be written in terms of the Green’s function of the system as,

$$\begin{aligned} W_1 =\mu \Omega _1^2 W_1 (1/2)G(\tilde{x};\Omega _1 ) \end{aligned}$$

(8)

where the Green’s function is given by,

$$\begin{aligned} G(\tilde{x};\Omega _1 )=\frac{1}{D(\Omega _1 )}\left\{ \begin{array}{ll} {G_1 (\tilde{x};\Omega _1 ),}&{} \quad {0\le \tilde{x}\le 1/2} \\ {G_2 (\tilde{x};\Omega _2 ),}&{} \quad {1/2\le \tilde{x}\le 1} \\ \end{array}\right. \end{aligned}$$

(9)

where,

$$\begin{aligned} G_1 (\tilde{x};\Omega _1 )= & {} \left\{ \varphi _3 \left( {\Omega _1 /2} \right) \varphi _2 \left( {\Omega _1 } \right) \right. \\&\left. -\,\varphi _2 \left( {\Omega _1 /2} \right) \varphi _3 \left( {\Omega _1 } \right) \right\} \varphi _2 \left( {\Omega _1 \tilde{x}} \right) \\&+\,\left\{ \varphi _2 \left( {\Omega _1 /2} \right) \varphi _2 \left( {\Omega _1 } \right) \right. \\&\left. -\,\varphi _3 \left( {\Omega _1 /2} \right) \varphi _1 \left( {\Omega _1 } \right) \right\} \varphi _3 \left( {\Omega _1 \tilde{x}} \right) \\ G_2 (\tilde{x};\Omega _1 )= & {} \left\{ \varphi _3 \left( {\Omega _1 /2} \right) \varphi _2 \left( {\Omega _1 } \right) \right. \\&\left. -\,\varphi _2 \left( {\Omega _1 /2} \right) \varphi _3 \left( {\Omega _1 } \right) \right\} \varphi _2 \left[ {\Omega _1 \left( {1-\tilde{x}} \right) } \right] \\&+\,\left\{ \varphi _2 \left( {\Omega _1 /2} \right) \varphi _2 \left( {\Omega _1 } \right) \right. \\&\left. -\,\varphi _3 \left( {\Omega _1 /2} \right) \varphi _1 \left( {\Omega _1 } \right) \right\} \varphi _3 \left[ {\Omega _1 \left( {1-\tilde{x}} \right) } \right] \\ D\left( {\Omega _1 } \right)= & {} 4\Omega _1^3 \left( {\cosh \Omega _1 \cos \Omega _1 -1} \right) ,\\ \varphi _2= & {} \cosh \tilde{x}-\cos \tilde{x},\quad \varphi _{1,3} =\sinh \tilde{x}\pm \sin \tilde{x} \\ \end{aligned}$$

Then, by projecting equation (5a) onto the fundamental mode shape and using the following mass-orthogonality and stiffness-orthogonality conditions,

$$\begin{aligned}&\int _0^1 \left[ {1+\mu \tilde{\delta }(\tilde{x}-1/2)} \right] W_1^2 \mathrm{d}\tilde{x}=1, \nonumber \\&\int _0^1 W_1^{{\prime }{\prime }{\prime }{\prime }} W_1 \mathrm{d}\tilde{x}=\Omega _1^2 \end{aligned}$$

(10)

we recover the following Duffing equation describing the fundamental modal amplitude:

$$\begin{aligned}&\ddot{\varphi }_1 +\frac{\Omega _1 }{Q}\left[ {1-\mu W_1^2 \left( {1/2} \right) } \right] \dot{\varphi }_1 +\Omega _1^2 \varphi _1 \nonumber \\&\qquad +\,24\left( {\frac{L}{t}} \right) ^{2}\left\{ -\int _0^1 {W_1^{{\prime }{\prime }} \left( {\tilde{x}} \right) W_1 \left( {\tilde{x}} \right) \mathrm{d}\tilde{x}}\right. \nonumber \\&\qquad \left. \int _0^1 {\left[ {W_1^{\prime } \left( {\tilde{x}} \right) } \right] ^{2}\mathrm{d}\tilde{x}} \right\} \varphi _1^3\nonumber \\&\quad =-\tilde{a}\Omega ^{2}\left[ {\int _0^1 {W_1 \left( {\tilde{x}} \right) \mathrm{d}\tilde{x}} +\mu W_1 \left( {1/2} \right) } \right] \nonumber \\&\qquad \times \,\sin (\Omega \tau )+\tilde{a}\frac{\Omega _1 \Omega }{Q}\left[ {\int _0^1 {W_1 \left( {\tilde{x}} \right) \mathrm{d}\tilde{x}} } \right] \cos (\Omega \tau )\nonumber \\ \end{aligned}$$

(11)

Finally, by introducing the notation $\tilde{z}(\tau )=\varphi _1 (\tau )W_1 \left( {1/2} \right)$, we obtain the single-degree-of-freedom nonlinear reduced-order model,

$$\begin{aligned} {\tilde{\hbox {z}}}''+\tilde{\hbox {c}}_e {\tilde{\hbox {z}}}'+\tilde{k}_e \tilde{z}+\tilde{k}_3 \tilde{z}^{3}=\tilde{b}\Omega ^{2}\sin (\Omega \tau )+\tilde{d}\Omega _1 \Omega \cos (\Omega \tau ) \end{aligned}$$

(12)

where,

$$\begin{aligned} \tilde{c}_e= & {} \frac{\Omega _1 }{Q}\left[ {1-\mu W_1^2 \left( {1/2} \right) } \right] ,\quad {\tilde{k}_e =\Omega _1^2 ,}\nonumber \\ \tilde{b}= & {} - \left[ {\int _0^1 {W_1 \left( {\tilde{x}} \right) \mathrm{d}\tilde{x}} +\mu W_1 \left( {1/2} \right) } \right] \nonumber \\ \tilde{d}= & {} \frac{\tilde{a}}{Q}W_1 \left( {1/2} \right) \int _0^1 {W_1 \left( {\tilde{x}} \right) \mathrm{d}\tilde{x}}\nonumber \\ \tilde{k}_3= & {} \frac{24}{W_1^2 \left( {1/2} \right) }\left( {\frac{L}{t}} \right) ^{2}\left\{ -\int _0^1 {W_1^{{\prime }{\prime }} \left( {\tilde{x}} \right) W_1 \left( {\tilde{x}} \right) \mathrm{d}\tilde{x}}\right. \nonumber \\&\quad \left. \int _0^1 {\left[ {W_1^{\prime } \left( {\tilde{x}} \right) } \right] ^{2}\mathrm{d}\tilde{x}} \right\} \end{aligned}$$

(13)

An interesting observation is that, due to the harmonic base excitation, there are two forcing terms on the right-hand-side of the reduced model (12) depending linearly and quadratically on the forcing frequency $\Omega$. This means that the overall amplitude of the combined forcing terms increases with increasing $\Omega$.

The reduced model (12) is the starting point for the following dynamical analysis. In order to analytically approximate the backbones of the frequency–amplitude curves, we consider the underlying undamped, unforced system and perform harmonic balance using the two-term expansion,

$$\begin{aligned} \tilde{z}(\tau )=\tilde{A}_1 (\tau )\sin \left( {\Omega \tau +\varphi _1 } \right) +\tilde{A}_3 (\tau )\sin \left( {3\Omega \tau +\varphi _3 } \right) \end{aligned}$$

(14)

or, equivalently,

$$\begin{aligned} \tilde{z}(\tau )=\tilde{A}_1 (\tau )\sin \left( \theta \right) +\tilde{A}_3 (\tau )\sin \left( {3\theta +\psi } \right) \end{aligned}$$

(15)

where the two phases are defined as $\theta =\Omega \tau +\varphi _1$ and $\psi =\varphi _3 -3\varphi _1$. The third harmonic is included in the two-term expansion since it is expected that the cubic stiffness nonlinearity of (12) contributes primarily to the amplification of the third harmonic in the response. Upon substitution of (15) into (12) while neglecting damping and forcing (i.e., setting $\tilde{c}_e =\tilde{b}=\tilde{d}=0)$, we recover the coupled, nonlinear equations describing the amplitude–frequency relations for the backbone curves for the first and third harmonics:

$$\begin{aligned}&\tilde{k}_3 \tilde{A}_1^3 +2\tilde{k}_3 \tilde{A}_1 \tilde{A}_3^2 \mp \tilde{k}_3 \tilde{A}_1^2 \tilde{A}_3 +\frac{4}{3}\left( {\Omega _1^2 -\Omega ^{2}} \right) \tilde{A}_1 =0 \end{aligned}$$

(16a)

$$\begin{aligned}&{\mp } \frac{1}{3}\tilde{k}_3 \tilde{A}_1^3 +\frac{4}{3}\left( {\Omega _1^2 -9\Omega ^{2}} \right) \tilde{A}_1 +2\tilde{k}_3 \tilde{A}_3 \tilde{A}_1^2 +\tilde{k}_3 \tilde{A}_3^3 =0 \end{aligned}$$

(16b)

$$\begin{aligned}&\psi =0,\pi \end{aligned}$$

(16c)

We note that since the system has no damping, the phase lag between the two harmonics is either 0 or; $\psi =0$ holds when $\Omega <\Omega _1$, whereas $\psi =\pi$ holds when $\Omega \ge \Omega _1$. Further, the cubic nonlinearity has a hardening effect causing the backbone curves to bend toward higher frequencies so that their domains correspond to $\Omega \ge \Omega _1$ and, hence, it holds that $\psi =\pi$ along the backbone curves.

Fig. 3

Comparison of numerical resonance curves (comprised of forward and backward sweeps) and the analytical backbone curves (resulting from harmonic balancing): a first and b third harmonic components of the steady-state response

3 Computational and analytical fundamental resonances

In Fig. 3, we depict a comparison between computational frequency–amplitude resonance curves and the analytical backbone curves obtained by solving the system (16a)–(16c) for the first and third harmonics. We consider fundamental resonance of the reduced-order model (12), i.e., the forced steady-state responses with dominant harmonic component at the frequency $\Omega$ of the applied harmonic excitation. The computational resonance curves were obtained by numerically integrating the reduced-order model (12) for a specific frequency and amplitude of excitation and specific initial conditions, letting the dynamics reach a steady state and recording the steady-state response. The lumped-parameter model (12) was numerically integrated in Python for several hundreds of cycles into the steady state. Then, a fast Fourier transform (FFT) of the steady-state response was performed to compute the amplitudes of the 1st and 3rd harmonics at each value of the excitation frequency. In order to reduce edge effects in the FFT, the duration of the steady-state segment was set equal to an integer multiple of the drive period. While incrementally increasing or decreasing the drive frequency to simulate a upward or downward frequency sweep, respectively, the initial conditions of a new simulation were set equal to the final conditions of the preceding simulation. Finally, the total simulation time was chosen to be an integer multiple of the drive period to achieve consistency in the initial conditions of the base. The system parameters used to generate all computational and analytical results in this work are listed in Table 1.

Table 1 System parameters used in the computational study of the beam

We note strong agreement between the computational frequency–amplitude curves and the analytical backbone curves. The reason for this strong correlation is twofold: the relatively low damping and forcing level, and the accuracy of the harmonic balance model (14) and (15). Indeed, as the forcing and damping levels approach zero, the frequency–amplitude resonance curves become increasingly narrow and, in the limit of zero damping and forcing, by definition they coincide with the backbone curves. A Q-factor of 100 and a base excitation amplitude of 0.5 nm result in a damping coefficient and forcing levels small enough that, in (12), the harmonic forcing terms and the damping term are dominated by the other terms of the reduced-order model. Additionally, we know a posteriori that most of the energy in the fundamental resonance response is localized in the first and third harmonics and, hence, the two-term approximation used in (14) is appropriate. In particular, we computed the energy partition in the system (i.e., the sum of the kinetic and potential energy of the system) among the first and third harmonics for each excitation frequency considered in Fig. 3 and found that the energy in the first harmonic decreased from 99.99% at the 182 MHz to 97.8% at 500 MHz, whereas the energy in the third harmonic increased from $\sim 0$ at 182 MHz to 0.8% at 500 MHz. If we consider the total energy in both the first and third harmonics, we see that this amount decreases from 99.99% at 182 MHz to 98.6% at 500 MHz and within this range of frequencies, is 99.2% on average. As a result, for the parameter values considered in Table 1, we find that the harmonic balance analysis of the undamped, unforced system approximates well the response of the actual damped, forced system, at least for frequencies not in the immediate vicinity of the linearized natural frequency.

Fig. 4

Comparison of numerical and analytical (resulting from harmonic balance) fundamental resonance amplitude curves versus added mass: a first and b third harmonics of the steady-state response at constant excitation frequency of 250 MHz

More importantly, considering the fundamental resonance branches in Fig. 3, we observe a large broadband resonance of the system encompassing a range of over 270 MHz or 2.5 times the linearized frequency; this broad bandwidth occurs even in the presence of viscous damping in the system. In fact, due to the base excitation and the presence of the concentrated mass at the center of the beam, there is no theoretical jump-down frequency for the excitation level considered (0.5 nm). A detailed analysis and physical explanation of this no-drop phenomenon is presented in “Appendix.” It is shown here that because the excitation level is not fixed, rather it is proportional to the square of the excitation frequency, for sufficiently large excitation amplitudes there should be theoretically no jump-down bifurcation point in the frequency response. The critical excitation amplitude required to achieve the no-drop phenomenon is found to be inversely related to the ratio of the concentrated mass to the beam mass. The role of the concentrated mass in the resonator design is to lower this critical excitation amplitude to a practical level. Specifically, for the system parameters considered in Table 1, the critical excitation amplitude in the absence of the concentrated mass is around 1.1 nm, whereas the critical excitation amplitude for a mass ratio of 4 is 0.1 nm. Hence, the concentrated mass lowers the critical excitation amplitude for the system by an order of magnitude and thereby enhances the feasibility of realizing the ultra-wide broadband.

Physically, of course, it is not possible to truly have no jump-down bifurcation point in the frequency response. In practice, this bifurcation point may occur due to the excitation of higher resonances, perturbations in the initial conditions and/or excitation amplitude caused by noise or, the basin of attraction for the upper branch solution may become impractically small. Indeed noise plays an important role in the dynamics of nonlinear systems near bifurcation points and significant effort has been dedicated to this topic [2, 3, 37, 48]. An experimental study of the dynamics of the proposed resonator and an investigation of the effect that noise has on the dynamics near the jump-down bifurcation are critical to fully characterizing this system, but are beyond the scope of the present work. However, based on the theoretical and numerical analysis shown in “Appendix,” it is reasonable to expect that in practice, for excitation amplitudes larger than the critical excitation amplitude, the resonant bandwidth will be significantly larger than for excitation amplitudes below the threshold.

The ultra-wide broadband resonance could be exploited in a mass sensing application based on amplitude tracking. To place this in context, we recall the mass sensing scenario depicted in Fig. 1. When a foreign mass is attached to the beam, the nonlinear resonance curve (in blue) is shifted toward lower frequencies (in red). For mass sensing, a fixed driving frequency can be randomly chosen within the broad resonance bandwidth as an operating frequency, and the changes of the $1^{\mathrm{st}}$ and 3rd harmonic amplitudes provide the mass sensitivity. Owing to the broad resonance bandwidth, there is no need to adjust the operating frequency, neither by sweeping the frequency around the resonance frequency (as in the open-loop method) nor by modulating the frequency via a PLL (as in the closed-loop method)—as it would be for a linear resonator to follow the moving resonance peak. Further, the ultra-wide broadband allows for a significantly larger range of operational frequencies and amplitudes as compared to other mass sensing techniques relying on nonlinear resonances.

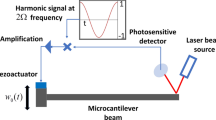
In Fig. 4, we analytically and computationally show how the first and third harmonics vary as mass is added to the center of the resonator at a fixed excitation frequency of 250 MHz. The selection of the frequency of 250 MHz was somewhat arbitrary, and, in fact, any frequency within the broadband (i.e., higher than the linearized frequency) shown in Fig. 3 can be selected as the operational drive frequency. The computational results indicate that tracking the high-amplitude branch as mass is added is indeed feasible despite the perturbations in the concentrated mass. That is to say, the addition of mass in 25 fg increments does not trigger a transition to the lower solution branch. In practice, the excitation frequency would need to be swept up to the target operational frequency initially in order to attract the upper solution branch before mass is added. Once the upper solution branch is realized, the excitation frequency remains constant as mass is added and the upper solution branch is tracked. In other words, the mass sensing procedure would require an initial ramp up of the frequency but would not require frequency sweeping each time a discrete amount of mass is added. The excitation could be applied by a piezoelectric actuator.

Fig. 5

a Sensitivity of the first harmonic amplitude versus excitation frequency versus added mass for an operational frequency range of 182–500 MHz, b sensitivity of the third harmonic amplitude versus excitation frequency versus added mass for an operational frequency range of 182–500 MHz, c zoomed-in image of a for an operational frequency range of 182–200 MHz, d zoomed-in image of b for an operational frequency range of 182–200 MHz, e linearized frequency versus added mass and f sensitivity of the linearized frequency versus added mass. The operational ranges depicted in c, d are indicated by a dashed-blue rectangle in a, b. (Color figure online)

4 Sensitivity and mass resolution

As a way of estimating the efficacy of the proposed resonator design, we introduce the following sensitivities, of the linearized resonant frequency, $S_{\mathrm{lin}}$, the amplitude of the first harmonic, $S_1$, and the amplitude of the third harmonic $S_3$,

$$\begin{aligned} S_{\mathrm{lin}} =\omega _{10} /\omega _1 ,\quad {S_1 =A_1 /A_{10} ,}\quad {S_3 =A_3 /A_{30} }, \end{aligned}$$

(17)

where $\omega _{10} \left( {A_{10} } \right)$ is the linearized resonant frequency (depending on the amplitude of the 1$^{st}$ harmonic, $A_{10} )$ before any mass is added, and $\omega _1 \left( {A_1 } \right)$ is the linearized resonant frequency (depending on the amplitude of the 1st harmonic, $A_1$) after mass is added to the center of the beam, and $A_{30}$ and $A_3$ are the amplitudes of the third harmonics before and after mass is added. As discussed in the previous section, the proposed mass detection scheme relies on changes in the amplitudes at a fixed excitation frequency rather than changes in the linear resonant frequency. However, in the following exposition we include the sensitivity of the linearized frequency for comparison. Since the linearized resonant frequency decreases as mass is added while the amplitudes of the first and third harmonics increase as mass is added, the sensitivities are always greater than or equal to one.

Fig. 6

Analytical backbone curves of the first (a) and third (b) harmonics corresponding to zero damping and zero forcing and resulting from a two-term harmonic balance analysis

In Fig. 5a–b, we plot the sensitivities of the first and third harmonic amplitudes versus excitation frequency and added mass for an operational frequency range of 182–500 MHz. The sensitivities of both the first and third harmonic amplitudes increase significantly in the vicinity of the linearized frequency and for this reason, zoomed-in views of Fig. 5a–b are shown in Fig. 5c–d for an operational frequency range of 182–200 MHz. Due to the broadband resonance, the sensitivities of the steady-state response amplitudes depend on the excitation frequency as well as the added mass. This is due to the fact that the proposed mass sensor offers the advantage of a wide range of operational frequencies, so any excitation frequency that falls within the broad resonant bandwidth of the microresonator can be selected as the excitation frequency. In contrast, the sensitivity of the linearized frequency depends only on added mass (cf. Fig. 5d) since, for a given amount of added mass, there is a unique linearized resonant frequency (cf. Fig. 5c).

All three sensitivities are by construction equal to unity before any mass is added, and they all are directly proportional to the amount of mass added. The reason that the sensitivities increase as added mass increases is because the shift in the linearized frequency and the steady-state response amplitudes is greater for a larger amount of added mass than for a smaller amount of added mass. The peak sensitivity of the linearized frequency is $S_{\mathrm{lin}} =1.28$, the peak sensitivity of the first harmonic amplitude is $S_1 =1.55$, and the peak sensitivity of the third harmonic amplitude is $S_3 =2.95$. In fact, for a given amount of added mass, $S_1$ and $S_3$ are both greater than $S_{\mathrm{lin}}$ at each excitation frequency considered and, in particular, $S_3$ is the largest.

Regarding the dependence of $S_1$ and $S_3$ on the excitation frequency, we clearly see that the sensitivities increase as the excitation frequency decreases. This trend can be understood by considering the analytical backbone curves shown in Fig. 6. Here we plot the backbone curves of the first and third harmonics before any mass is added, $m_{\mathrm{ad}} =0$, and after $m_{\mathrm{ad}} =100\,\mathrm{fg}$ is added to the center. We note that the addition of mass causes the resonance curves to shift toward lower frequencies and, as a result, the steady-state amplitudes increase for a fixed frequency within the broadband. As a representative comparison, consider the cases corresponding to excitation frequencies of 200–400 MHz, denoted by vertical dashed lines in Fig. 6a, b. The increases in the steady-state amplitudes are comparable at these two frequencies; yet the initial amplitudes (i.e., before mass is added—for $m_{\mathrm{ad}} =0)$ are significantly smaller at 200 MHz as compared to 400 MHz. Since the initial amplitudes are smaller at lower frequencies (although the increases in amplitudes with added mass are similar), the sensitivities $S_1$ and $S_3$ increase with decreasing frequency. This is especially true of the third harmonic for operational frequencies in the vicinity of the linearized resonant frequency; since the amplitude of the third harmonic is extremely small ($\sim$10 pm) at the linearized resonant frequency before mass is added, the ratio of the amplitude after mass is deposited to the initial amplitude is quite large for drive frequencies near the linear resonant frequency.

Fig. 7

a Responsivity versus added mass for the linearized frequency, responsivity versus added mass versus excitation frequency of the b first harmonic component, and c third harmonic component and responsivity versus added mass at five particular excitation frequencies of the d first harmonic component, and e third harmonic component. In d, e, the responsivities of the amplitudes of the first and third harmonics are shown at 182 MHz (cyan), 190 MHz (black), 200 MHz (blue), 350 MHz (red) and 500 MHz (green). (Color figure online)

As a final step, we define the responsivities of the linearized frequency,$R_{\mathrm{lin}}$, amplitude of the first harmonic, $R_1$, and amplitude of the third harmonic, $R_3$, as

$$\begin{aligned} {R_{\mathrm{lin}} =\frac{\mathrm{d}\omega _1 }{\mathrm{d}m_{\mathrm{ad}} },}\quad {R_1 =\frac{\mathrm{d}A_1 }{\mathrm{d}m_{\mathrm{ad}} },}\quad {R_3 =\frac{\mathrm{d}A_3 }{\mathrm{d}m_{\mathrm{ad}} }} \end{aligned}$$

(18)

Hence, the responsivities are the derivatives of the corresponding observable (measured) variables with respect to added mass.

As with the sensitivities, the responsivities of the nonlinear steady-state response amplitudes depend on the excitation frequency, as well as the added mass, while the responsivity of the linearized frequency depends only on added mass. In Fig. 7a, we plot $R_{\mathrm{lin}}$ versus added mass, in Fig. 7b (7c) we plot $R_1$ ($R_3$) versus added mass versus excitation frequency, and in Fig. 7d (7e), we plot $R_1$ ($R_3$) versus added mass at five specific drive frequencies, namely 182, 190, 200, 350 and 500 MHz. Since the linearized frequency decreases with increasing added mass, whereas the nonlinear steady-state amplitudes increase, the linear responsivity $R_{\mathrm{lin}}$ is always negative, while the nonlinear responsivities $R_1$ and $R_3$ are positive quantities. Interestingly, we see that $R_1$ is inversely related to the amount of added mass at all excitation frequencies whereas $R_3$ is inversely related to the amount of added mass for excitation frequencies above around 210 MHz and directly proportional to the amount of added mass for frequencies below 210 MHz. Regarding the dependence of the nonlinear responsivities on the operational frequency, $R_1$ decreases as the excitation frequency decreases for frequencies above 251 MHz. At 251 MHz, the trend of $R_1$ with respect to excitation frequency changes and $R_1$ increases sharply as the drive frequency approaches the linearized frequency. In contrast, $R_3$ decreases with decreasing excitation frequency for the entire range of operational frequencies.

Another important mass sensing metric is the minimum detectable mass or mass resolution. For a conventional mass sensor designed to operate in the linear dynamic regime, the mass resolution, $\delta m_{\mathrm{lin}}$, is given by

$$\begin{aligned} \delta m_{\mathrm{lin}} =R_{\mathrm{lin}}^{-1} \delta \omega _1 \end{aligned}$$

(19)

where $\delta \omega _1$ is the minimum detectable shift in the linear resonant frequency. For the proposed nonlinear sensor that tracks shifts in the resonant amplitudes rather than frequency, the mass resolutions are given by

$$\begin{aligned}&\delta m_1 =R_1^{-1} \delta A_1,\end{aligned}$$

(20)

$$\begin{aligned}&\delta m_3 =R_3^{-1} \delta A_3 \end{aligned}$$

(21)

where $\delta m_1$ ($\delta m_3 )$ is the mass resolution that results from tracking shifts in the 1st harmonic (3rd harmonic) amplitude and $\delta A_1$ ($\delta A_3 )$ is the minimum detectable change in 1st harmonic (3rd harmonic) amplitude. The responsivities, $R_{\mathrm{lin}}$, $R_1$ and $R_3$, are deterministic quantities determined by the sensor design while the linear resonant frequency, $\omega _1$, and response amplitudes, $A_1$ and $A_3$, vary stochastically due to the presence of noise in the measurement system. As a result, the minimum detectable shifts in the linear frequency and response amplitudes, and the resulting mass resolutions, are largely influenced by noise [39]. The physical sources of noise are similar for linear and nonlinear sensors, but the primary role that noise plays can be quite different.

As the dissipation-fluctuation theorem states, any source of damping in the system can in turn serve as a source of noise due to thermal fluctuations [25]. This includes the Nyquist–Johnson noise in the readout circuitry and the thermomechanical noise in the resonator itself. In the case of thermomechanical noise, the damping mechanisms present in the resonator’s dynamics induce random forcing along the beam such that the average force is zero, but the mean square amplitude of the resulting motion is nonzero [1, 9, 14, 15, 20, 25]. Additionally, there exist so-called parametric noise sources [15] that are associated with parametric changes in the resonator that do not necessarily result in thermal losses. Examples of parametric noise sources include adsorption and desorption of molecules in the surrounding medium, temperature fluctuations that induce thermal stresses, and defect motion within the resonator [15]. Significant effort has been dedicated to quantifying the minimum detectable frequency shift, $\delta \omega _1$, and resulting mass resolution, $\delta m_{\mathrm{lin}}$, for linear resonators due to the presence of such noise sources [1, 9, 14, 15, 20, 25].

Regarding the effect of noise on nonlinear mass sensors, there are two important distinctions to make in comparison with linear sensors. Within the nonlinear dynamic regime, the signal-to-noise (SNR) is significantly larger due to the relatively large response amplitudes and, as a result, the dissipation-induced amplitude noise is less restrictive in practice. Further, noise has an effect on nonlinear sensors for which there is no counterpart in linear mass sensors. For a nonlinear sensor, in addition to influencing the minimum detectable shift in steady-state amplitudes, noise effects the branch selection within the bi-stable bandwidth by causing perturbations in the initial state of the resonator. Indeed stochastic variations in the response amplitude and phase blur the separatrix between the basins of attraction for the two stable solutions [37] and, as a result, noise may induce undesirable jumping between branches. A detailed study of the variation of the basins of attraction with respect to excitation frequency and its relation to noise is outside the scope of this study but a related discussion is presented by Kozinsky et al. [37].

As a crude estimate for the minimum detectable change in amplitude, the amplitude resolution can be taken to be an order of magnitude larger than the average dissipation-induced amplitude fluctuations (due to thermomechanical noise) near the primary resonance. For the linearized reduced-order model of the doubly clamped beam characterized by the effective stiffeness, $k=\frac{EI}{8L^{3}W_1^2 \left( {1/2} \right) }$, and effective mass, $m=\frac{2\rho AL}{W_1^2 \left( {1/2} \right) }$, the equipartition theorem says that the mean square displacement fluctuations of the center of the beam, $\left\langle {z^{2}_{\mathrm{th}} } \right\rangle$, satisfy $\frac{1}{2}k\left\langle {z_{\mathrm{th}}^2 } \right\rangle =\frac{1}{2}m\omega _1^2 \left\langle {z_{\mathrm{th}}^2 } \right\rangle =\frac{1}{2}k_B T$ near the fundamental bending mode, where $k_B$ is the Boltzmann constant and T is the temperature [25]. Considering the system parameters stated in Table 1 and $T=298\hbox {K}$, we have

$$\begin{aligned} \left\langle {z_{\mathrm{th}}} \right\rangle \approx \sqrt{\frac{k_B T}{k}} \end{aligned}$$

(23)

If the amplitude resolution is assumed to be an order of magnitude larger than $\left\langle {z_{\mathrm{th}} } \right\rangle$, then the minimum detectable shift in amplitude is $\sim$30 pm. Considering the maximum values of $R_1 =0.75\,\hbox {nm/fg}$ and $R_3 =0.026\,\hbox {nm/fg}$ shown in Fig. 7b, c (corresponding to 182 MHz and 500 MHz, respectively, with zero added mass) and using Eqs. 20 and 21, we compute mass resolutions of 0.04 and 1.2 fg for the amplitudes of the first and third harmonics, respectively.

5 Concluding remarks

In this work, we studied the broadband resonance of a doubly clamped thin microbeam with a concentrated mass at its center under harmonic base excitation. By including the effects of geometric nonlinearity in the equation of motion of the beam due to midplane stretching, and considering only the fundamental bending mode, we obtained a single-degree-of-freedom reduced-order model in the form of a Duffing equation (having hardening cubic nonlinearity). We found that for sufficiently large excitation amplitudes, there is no analytically predicted jump-down bifurcation frequency, and we showed computational verification of this no-drop phenomenon. Further, the critical excitation amplitude above which there is no theoretical jump-down bifurcation is lowered by an order of magnitude by the presence of the concentrated mass at the beam’s center, hence its role in the beam design. In practice, there must eventually be a jump-down frequency and therefore, this critical excitation amplitude likely corresponds to a threshold excitation level above which the bandwidth of the nonlinear resonance increases significantly. A two-term harmonic balance analysis was used to analytically predict the backbone curves (i.e., the frequency–amplitude relations of the underlying undamped, unforced system) of the first and third harmonics of the steady-state response of the beam. We also computationally generated frequency–amplitude curves of the damped, forced system and, interestingly, found that they coincide closely with the analytical backbones. The strong correspondence is due to the relatively low-damping and forcing levels of this system, and to the energy localization of the steady-state response in the first and third harmonics.

In order to exploit the large bandwidth for mass sensing, we studied shifts in the steady-state amplitudes of the first and third harmonics resulting from the addition of mass at the center of the beam. We found that tracking the high-amplitude resonant response is indeed feasible and that the steady-state response amplitudes are quite sensitive to added mass. The unique advantage of the proposed resonator deign as compared to other nonlinear mass sensors is its ultra-wide range of operational frequencies and amplitudes owing to the presence of the concentrated mass at the center. The design of the resonator is also simple in terms of fabrication with feature sizes larger than 100 nm. Finally, the first and third harmonic amplitudes demonstrated enhanced sensitivity to mass addition as compared to the linearized frequency, and their mass resolutions were found to be on the femtogram scale. In practice, the presence of electrical and parametric noise would likely increase the minimum detectable shift in amplitude and thereby increase the resulting mass resolutions for the 1st and 3rd harmonics. The primary focus of this study was to introduce the proposed resonator design and develop a theoretical framework for the mass sensing method based on amplitude tracking within ultra-wide resonant bandwidths. Future work includes manufacturing the mass sensor using conventional microfabrication or emerging microassembly [35] techniques, verifying its sensing performance experimentally and studying the effect of noise.

Appendix

The purpose of this appendix is to numerically and analytically illustrate the no-drop phenomenon exhibited by the proposed resonator design (i.e., the absence of a jump-down frequency in the frequency response), which results in an ultra-wide resonant bandwidth. Beginning with the reduced-order model of the beam stated in Eqs. (12) and (13) of the manuscript, we neglect the second term on the right-hand side of equation (12) since it is trivially small compared to the other forcing term present and recover the following equation

$$\begin{aligned} {\tilde{z}}''+\tilde{c}_e {\tilde{z}}'+\tilde{k}_e \tilde{z}+\tilde{k}_3 \tilde{z}^{3}=\tilde{b}\Omega ^{2}\sin \left( {\Omega \tau } \right) \end{aligned}$$

(A1)

Fig. 8

Computational forward frequency sweeps and analytical frequency amplitude curves at excitation amplitudes of a $a=0.03\,\hbox {nm}$, b $a=0.035\,\hbox {nm}$, c $a=0.045\,\hbox {nm}$ and d $a=0.05\,\hbox {nm}.$

Table 2 System parameters used in the computational study of the beam.

The forcing term proportional to $\tilde{d}$ in Eq. (12) is neglected because we restrict our attention to systems with Q-factors on the order of 100 or higher ($\Rightarrow \tilde{d}<<\tilde{b})$. We now take a one term expansion in the displacement at the center of the beam, $\tilde{z}=\tilde{A}\cos \left( {\Omega \tau -\varphi } \right)$ and balance the harmonics to obtain an approximate frequency–amplitude relation in the beam,

$$\begin{aligned} \frac{3}{4}\frac{\tilde{k}_3 }{\Omega _1^2 }\tilde{A}^{3}=\left( {\frac{\Omega ^{2}}{\Omega _1^2 }-1} \right) \tilde{A}+\frac{\tilde{b}\Omega ^{2}}{\Omega _1^2 }\sqrt{1-\frac{\tilde{c}^{2}_e }{\tilde{b}^{2}\Omega ^{2}}\tilde{A}^{2}}\nonumber \\ \end{aligned}$$

(A2)

The backbone curve of the frequency amplitude relation corresponds to the undamped, unforced system and hence is given by

$$\begin{aligned} \frac{3}{4}\frac{\tilde{k}_3 }{\Omega _1^2 }\tilde{A}^{3}=\left( {\frac{\Omega ^{2}}{\Omega _1^2 }-1} \right) \tilde{A} \end{aligned}$$

(A3)

At the intersection of the backbone curve and the frequency amplitude curve, we have the point containing the drop frequency, $\Omega _\mathrm{d}$, and the drop amplitude, $\tilde{A}_\mathrm{d}$, and therefore the drop frequency is given by

$$\begin{aligned} \Omega _\mathrm{d} =\Omega _1 /\sqrt{1-\frac{3\tilde{k}_3 \tilde{b}^{2}}{4\tilde{c}^{2}_e }} \end{aligned}$$

(A4)

which gives real values only for $\tilde{b}\le \sqrt{\frac{4\tilde{c}^{2}_e }{3\tilde{k}_3 }}$, indicating that there is no drop in the frequency amplitude curve for excitation amplitudes larger than a critical amplitude, $\tilde{a}_\mathrm{c}$, given by

$$\begin{aligned} \tilde{a}_\mathrm{c} =\frac{\sqrt{4\tilde{c}^{2}_e }}{\sqrt{3\tilde{k}_3 }W_1 \left( {1/2} \right) \left[ \int _0^1 {W_1\left( {\tilde{x}} \right) \mathrm{d}\tilde{x}} +\mu W_1 \left( {1/2} \right) \right] }\nonumber \\ \end{aligned}$$

(A5)

In order to verify this numerically, we construct computational frequency amplitude curves for the system by using parameters given in Table 2. For the duration of this section, these system parameters will be used in all computational studies. According to Eq. (A5), the critical excitation amplitude above which there is no drop frequency (for this set of parameters) is $a_\mathrm{c} =0.049\,\hbox {nm}$. The analytical and numerical results of forward frequency sweeps corresponding to $a=0.03\,\hbox {nm}$, $a=0.035\,\hbox {nm}$, $a=0.045\,\hbox {nm}$ and $a=0.05\,\hbox {nm}$ are compared in Fig. 8. We see that for $a<a_\mathrm{c}$, there is strong correspondence between the theoretical and computational curves and that indeed there is a drop in the computational frequency amplitude curve as predicted. In contrast for the case of $a>a_\mathrm{c}$, there is no drop frequency within the large range of frequencies considered. This provides some numerical verification of the theoretically predicted no-drop phenomenon resulting from the harmonic balancing analysis.

Fig. 9

Computational frequency amplitude curves for $q_1<q_2<q_3 <q_4$. The corresponding drop frequencies are denoted by $\hbox {f}_\mathrm{d}^i$, where $\hbox {f}_\mathrm{d} \left( q \right) =\frac{\Theta }{2\pi }\Omega _\mathrm{d}$ and $\hbox {f}_\mathrm{d}^i \equiv \hbox {f}_\mathrm{d} (q_i )$

Fig. 10

Drop frequency associated with a fixed forcing level corresponding to $q=\tilde{b}\Omega ^{2}$ versus excitation frequency for several different excitation amplitudes. For $a<a_c =0.049\,\hbox {nm}$, the drop frequency occurs at $\Omega _\mathrm{d} \left( \Omega \right) =\Omega$ and for $a>a_c$, there is no drop frequency

Fig. 11

Amplitude versus frequency curve for $a>a_c$. The quantity $\lambda$ is a measure of the bending of the frequency response curve

In order to gain a physical understanding of this phenomenon, we consider the same system but with harmonic excitation applied directly to the center of the beam rather than the base. The reduced order equation of motion in this case is

$$\begin{aligned} {\tilde{z}}''+\tilde{c}_e {\tilde{z}}'+\tilde{k}_e \tilde{z}+\tilde{k}_3 \tilde{z}^{3}=q\sin \left( {\Omega \tau } \right) \end{aligned}$$

(A6)

where q is the (fixed) nondimensional forcing level. Holding all system parameters fixed, the drop frequency is a function only of q and for each value of q, there exists a drop frequency given by

$$\begin{aligned} \Omega _\mathrm{d} \left( q \right) =\sqrt{\frac{\tilde{k}_e }{2}\left( {1+\sqrt{1+\frac{3\tilde{k}_3 q^{2}}{\Omega _1^4 \tilde{c}_e^2 }}} \right) }. \end{aligned}$$

(A7)

Fig. 12

A measure of the nonlinearity, $\lambda$, versus the mass ratio of the concentrated mass to the mass of the rest of the beam, $\mu$, (a); the half-length of the beam, L, (b); the thickness of the beam, t, (c) and the ratio of the Young’s modulus to the density of the beam, $E/\rho ,$ (d)

An increase in the forcing level results in an increase of the drop frequency as illustrated in Fig. 9. For base excitation, the forcing level is proportional to the square of the excitation frequency, $q=\tilde{b}\Omega ^{2}$, and hence, for a fixed base excitation we can compute the drop frequency as a function of the excitation frequency,

$$\begin{aligned} \Omega _\mathrm{d} \left( {q\left( \Omega \right) } \right) =\Omega _\mathrm{d} \left( \Omega \right) =\sqrt{\frac{\tilde{k}_e }{2}\left( {1+\sqrt{1+\frac{3\tilde{k}_3 \tilde{b}^{2}\Omega ^{4}}{\omega _1^4 \tilde{c}_e^2 }}} \right) }\nonumber \\ \end{aligned}$$

(A8)

In Fig. 10, the drop frequency as a function of the excitation frequency is plotted for several different base excitation amplitudes. In this plot, a drop occurs at $\Omega$ if$\Omega _\mathrm{d} \left( \Omega \right) =\Omega$. Interestingly, we see that for $a<a_c =0.049\hbox {nm}$ there indeed exists an $\Omega$ for which $\Omega _\mathrm{d} \left( \Omega \right) =\Omega$ but for $a>a_c$, $\Omega _\mathrm{d} \left( \Omega \right) >\Omega$ for all $\Omega$ and hence there is no drop frequency.

The next step in our analysis focuses on quantifying the nonlinearity in terms of system parameters. We restrict our attention to the case when $a>a_c$ and introduce the following parameter, $\lambda$, as a measure of the nonlinearity

$$\begin{aligned} \lambda =\frac{\bar{{f}}-f_1 }{A\left( {\bar{{f}}} \right) }=\frac{\hat{{f}}}{A\left( {\bar{{f}}} \right) } \end{aligned}$$

(A9)

where $f_1$ is the linearized frequency, $\bar{{f}}$is some frequency larger than $f_1$, $\hat{{f}}=\bar{{f}}-f_1$ is their difference and $A\left( {\bar{{f}}} \right)$ is the response amplitude at $\bar{{f}}$as depicted in Fig. 11. For simplicity, $A\left( {\bar{{f}}} \right)$ is taken to be the response along the backbone curve, and therefore, we can write $\lambda$ in terms of system parameters as

$$\begin{aligned} \lambda= & {} \frac{\sqrt{6}}{32\pi }\sqrt{\frac{E}{\rho }}\frac{1}{L^{2}}F\left( \mu \right) \sqrt{\frac{\pi \hat{{f}}}{\pi \hat{{f}}+\frac{1}{8\sqrt{3}}\sqrt{\frac{E}{\rho }}\frac{t}{L^{2}}\Omega _1 \left( \mu \right) }},\nonumber \\ F(\mu )= & {} \frac{1}{W_1 \left( {1/2} \right) }\sqrt{-\int _0^1 {W_1^{{\prime }{\prime }} W_1^ \mathrm{d}\tilde{x}} \int _0^1 {\left( {W_1^{\prime } } \right) ^{2}\mathrm{d}\tilde{x}} }\nonumber \\ \end{aligned}$$

(A10)

Notice that $\lambda$ does not depend on w and that it is directly proportional to $\hat{{f}}$. The dependence of $\lambda$ on all other parameters is illustrated in Fig. 12. We see that a decrease in$\lambda$, L and tand an increase in the ratio $E/\rho$ result in an increase of $\lambda$. The relationship between $\lambda$ and $\mu$ raises the question, what is the significance of the concentrated mass? As will be shown, the function of the concentrated mass is to lower the critical excitation amplitude to a level that is physically practical (Fig. 13).

Fig. 13

Critical excitation amplitude above which there is no drop frequency versus the mass ratio of the concentrated mass to the mass of the rest of the beam

The critical excitation amplitude required to achieve the no-drop phenomenon can also be written in terms of the system parameters,

$$\begin{aligned}&a_c =\frac{2}{3\sqrt{2}}\frac{t}{Q}p\left( \mu \right) \nonumber \\&p(\mu )\nonumber \\&\,\,=\frac{\Omega _1 \left( \mu \right) \left[ {1-W_1^2 \left( {1/2} \right) } \right] }{\left[ {\int _0^1 {W_1^ \mathrm{d}\tilde{x}+\mu W_1 } \left( {1/2} \right) } \right] \sqrt{-\int _0^1 {W_1^{{\prime }{\prime }} W_1^ \mathrm{d}\tilde{x}} \int _0^1 {\left( {W_1^{\prime } } \right) ^{2}\mathrm{d}\tilde{x}} }}\nonumber \\ \end{aligned}$$

(A11)

For the thickness and Q-factor considered in this section, the critical amplitude as a function of the mass ratio is shown in Fig. 13. Clearly, the critical amplitude decreases dramatically as the mass ratio increases from 0 to around 10. For a mass ratio of 0 (no concentrated mass), the critical amplitude is nearly 3 nm, which is well above the commonly used excitation amplitudes on the order of 0.1 nm. This means that without the concentrated mass, it would not be physically feasible to achieve the no-drop phenomenon, hence its critical role in the beam design.