Use of independent volume parameters in the development of new large displacement ANCF triangular plate/shell elements

Abstract

In this paper, a new unified kinematic description, obtained from Bezier geometry using linear mapping and position vector gradients associated with three independent parameters, is used to develop large displacement plate/shell finite elements (FE). Contrary to the conventional FE method, in the approach developed in this paper based on the absolute nodal coordinate formulation (ANCF), no distinction is made between plate and shell structures. The proposed ANCF triangular plate/shell elements have 12 coordinates per node: three position coordinates and nine position gradient coordinates that define vectors tangent to coordinate lines at the nodes. The fundamental differences between the conventional FE and the new ANCF parameterizations are highlighted. In this investigation, two different parameterizations, each of which employs independent coordinates, are used. In the first parameterization, called volume parameterization, coordinate lines along the sides of the triangular element in the straight (un-deformed) configuration are used in order to facilitate the development of closed-form cubic shape functions. In the second parameterization, called Cartesian parameterization, coordinate lines along the global axes of the structure (body) coordinate system are used to facilitate the element assembly. The element transformation between the volume and the Cartesian parameterizations is developed and used to define the structure inertia and elastic forces. Three new fully parameterized ANCF triangular plate/shell elements are developed in this investigation: a four-node mixed-coordinate element (FNMC) and two three-node elements (TN1 and TN2). All the elements developed in this investigation lead to a constant mass matrix and zero Coriolis and centrifugal forces. A non-incremental total Lagrangian procedure is used for the numerical solution of the nonlinear equations of motion. The performance of the proposed ANCF triangular plate/shell elements is analyzed by comparison with the ANCF rectangular plate element and conventional three-node linear (TNL) and six-node quadratic (SNQ) triangular plate elements.

1 Introduction

In this section, a brief literature review of conventional plate and shell finite elements, the features of ANCF plate/shell elements that distinguish them from conventional elements, and the goal, scope, and contributions of this investigation are discussed.

1.1 Literature review

In the conventional FE, structural mechanics, and vibration theory formulations; plates and shells are described using different geometric approaches and different displacement fields [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. Noor provided a comprehensive survey of books and monographs on plate and shell elements [1]. Reddy presented a unified treatment of plates and shell elements commonly used in aerospace, automotive, and civil engineering applications [2]. Armenakas et al. [3] used plate and shell elements to study the vibration of thin-walled structures subjected to severe dynamic loading conditions. Ashwell and Gallagher edited a series of conference papers on the FE theory of plate and shell elements and discussed the meshing algorithms for modeling curved geometry [4]. Axelrad used a local approach for the stability analysis of plate/shell large deformations [5]. Bieger used analytical methods based on series expansions to investigate circular cylindrical shells subjected to concentrated loads [6]. Billington studied complex three-dimensional shell structures [7], while Brush et al. [8] examined the buckling and stability of bar, plate, and shell elements using energy methods. Calladine investigated the coupling between the bending and stretching of shell structures under static loading [9]. Cox analyzed the buckling of plate and shell elements using continuum mechanics and energy methods [10]. Dym discussed important elasticity problems applicable to shell theory [11], while Flugge analyzed both plate and shell elements using modern analytical and computational methods [12]. Gould studied thin shell structures using a new FE approach for modeling curved geometric shapes [13,14,15]. Heyman investigated the static equilibrium of thin shell structures with complex curved geometry [16]. Hinton and Owen developed a computer program for the FE solution of static and dynamic problems of thin plate and shell structures considering elastoplastic and geometrically nonlinear anisotropic effects [17]. Huang developed an FE software for the static and dynamic analyses of plate and shell structures using an approach designed for alleviating shear and membrane locking that occurs in degenerated Mindlin curved elements [18]. Hughes and Hinton discussed the plate and shell element technology for developing efficient computational algorithms [19, 20]. Kelkar and Sewell examined fundamental analysis and design issues related to shell structures [21]. Kratzig and Onate edited a series of conference papers on the nonlinear dynamics and the computational mechanics of plate and shell structures [22]. Kraus studied the load-carrying capacity and analyzed the dynamic behavior of thin shell structures [23]. Kuhn examined the stresses of aircraft shell structures using analytical and computational methods [24]. Timoshenko and Woinowsky-Krieger made significant contributions to the development of plate/shell theory of elasticity [25]. Ugural studied the stresses in the case of small and large deformations of plate and shell structures [26]. Werner investigated the complex vibration behavior of plates, shells, curved membranes, rings, and thin structures by using both classical and computational methods [27].

In the classical FE theory, distinction is always made between plates and shells, and shell geometry cannot be systematically obtained from conventional plate element geometry because of the nature of the nodal coordinates and/or polynomial interpolations used. Use of infinitesimal rotations that impose restriction on the magnitude of rotations, employing vector transformations that differ from the transformations used for the gradients required to properly create accurate geometry, and/or treatment of the slopes as vectors and not strictly as gradients are among the reasons that arbitrary initially curved shell geometry cannot be systematically obtained from conventional plate elements. These geometric restrictions can be alleviated by using control points as in the case of computational geometry methods or by using position vector gradients with the proper gradient tensor transformation in order to correctly capture discontinuities.

1.2 Plate/shell elements

It is the objective of this study to introduce a new unified approach, based on the absolute nodal coordinate formulation (ANCF), for modeling three-dimensional triangular plate/shell structures using the same geometric representation and same displacement field. The proposed ANCF triangular plate/shell elements allow for correctly capturing finite rotations, large deformations, and complex geometry that cannot be easily captured using the conventional FE methods; some of which employ infinitesimal rotations as nodal coordinates. Capturing large displacements and complex geometry is necessary for accurate analysis of both structural and multibody system (MBS) applications [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]. MBS computational challenges, in particular, can be addressed using ANCF elements that impose no restrictions on the amount of rotation or deformation within the element, lead to a constant mass matrix and zero centrifugal and Coriolis forces, correctly account for the dynamic coupling between the rigid-body motion and the elastic deformation, and allow for using a non-incremental procedure for the numerical solution of the equations of motion [44]. In recent years, several ANCF elements have been proposed, validated numerically and experimentally, and successfully used in modeling complex MBS applications [45,46,47,48,49,50,51,52,53,54,55,56,57].

1.3 Conventional plate elements

Although a large number of quadrilateral plate and shell elements have been proposed in the conventional FE and ANCF literature [58,59,60], these rectangular elements are not suitable for meshing complex geometry with irregular shapes, and therefore, the development of triangular plate/shell elements becomes necessary. Conventional planar and spatial triangular plate elements are widely used for solving static and dynamic problems [61]. Furthermore, the availability of several automatic meshing algorithms facilitates the development of complex and high fidelity triangular meshes. Another important reason for the popularity of the triangular elements in the analysis of machines and structures is the possibility of performing mesh refinements in regions of stress concentrations that are of particular interest in the FE durability analysis. In structural mechanics, several types of triangular plate elements having transversal gradients as extensible directors are available [62]. While extensible directors are not often treated as position vector gradients throughout the solution algorithms, two conventional triangular plate elements are of particular interest in this investigation and can be distinguished according to their order of interpolation. These triangular plate elements are the three-node linear (TNL) element and the six-node quadratic (SNQ) element. The shape functions of the TNL and SNQ triangular plate elements are presented in the Appendix of the paper. An interesting property of the triangular plate elements that are based on transversal slopes is the fact that their kinematic description allows using a complete set of polynomial functions for the definition of the basis functions expressed in terms of dependent dimensionless volume coordinates with additional linear basis functions expressed in terms of dimensionless thickness coordinate. For a given order of interpolation, this important feature ensures the existence of a linear mapping between the Bezier triangular basis functions and the triangular element shape functions. In this investigation, three new ANCF fully parameterized plate/shell elements are developed using the simple geometric concepts introduced in this section.

1.4 ANCF plate elements

In recent years, several ANCF triangular plate elements have been proposed. Using a set of basis functions originally developed by Specht and Morley [63, 64], Dmitrochenko and Mikkola proposed two new ANCF triangular plate elements by considering an incomplete set of cubic shape functions [65]. The first triangular plate element developed by Dmitrochenko and Mikkola is based on the basis functions proposed by Specht and employs constant coefficients which depend on the geometry of the particular triangular plate element considered [63]. This ANCF triangular plate element can effectively describe large deformations but it can be inefficient for large meshes because the pre-evaluation of the element shape functions at the Gauss quadrature nodes must be repeated for each element in the triangular mesh, resulting in an increased computational cost. The second triangular plate element developed by Dmitrochenko and Mikkola is based on the basis functions proposed by Morley and employs as nodal coordinates absolute displacement vectors and a particular set of slope vectors normal to the sides of the triangular plate element leading to a set of non-conformal shape functions [64]. Because this triangular plate element produces meshes that are non-conformal along the element sides, it can introduce significant errors in predicting large deformations [66]. A new fully parameterized ANCF triangular plate element was also proposed by Mohamed in order to capture the plate thickness deformation as well as the transversal shear deformation [67]. In the ANCF triangular plate element proposed by Mohamed, three additional shape functions were added to the nine shape functions of the ANCF thin triangular plate element proposed by Dmitrochenko and Mikkola [65]. Olshevskiy et al. [68] proposed two new types of three- and four-node planar plate elements obtained from spatial ANCF plate elements. Dmitrochenko and Pogorelov [69] proposed a way to generate new ANCF rectangular and triangular elements employing displacement fields of conventional elements used in structural mechanics. However, all the ANCF triangular plate elements cited above were developed using a kinematic representation based on the conventional triangular plate elements, and have complex shape function expressions. Furthermore, the shape functions of some of these elements are not reported in a compact closed-form and numerical methods were used for their evaluation [70].

In addition to the triangular plate elements obtained from the conventional elements, Chang et al. [71] proposed three new ANCF triangular shell elements based on Bezier triangular patches. These ANCF triangular elements were referred to as the thin triangular shell element, the low-order thick triangular shell element, and the high-order thick triangular shell element. Because, in this case, the basis functions are independent of the nodal Cartesian coordinates in the parametric domain, concise expressions for the shape functions are obtained compared with the triangular elements obtained from the conventional finite elements. However, in the kinematic description of the triangular plate elements proposed by Chang et al. [71], the geometric interpretation of the gradient vectors associated with the parametric coordinates is not obvious. Furthermore, only geometric continuity associated with the tangential direction of the element position field can be imposed at the element interfaces, and consequently, the structural continuity of the position vector gradients cannot be enforced leading to discontinuous strains and stresses at the mesh interface nodes. Recently, new types of planar ANCF triangular elements and spatial ANCF tetrahedral elements with closed-form shape function expressions were developed starting with Bezier basis functions [72, 73]. Using a new approach, the geometric interpretation of the ANCF position vector gradients is utilized in order to facilitate the development of closed-form shape function expressions for these new elements.

1.5 Scope of this investigation

The main goal of this paper is to address challenges associated with the geometric description of the three-dimensional triangular plate elements, propose new ANCF triangular plate/shell elements that differ from the ones presented in the literature, and evaluate the performance of these new elements by comparing with existing conventional and ANCF elements. As shown in this paper, complete cubic polynomials of the triangular plate elements have thirty-nine coefficients, or equivalently thirteen Bezier control points. Therefore, in addition to the position and gradient coordinates, the use of internal middle surface nodes and/or curvature coordinates is required to formulate an ANCF triangular plate element based on a complete set of polynomial basis functions. On the other hand, a lower-order triangular plate element with position and gradient nodal coordinates can be systematically developed by applying linear constraint equations. These constraint equations allow identifying dependent variables and reducing the number of the element coordinates. Alternatively, an incomplete cubic polynomial representation can be employed from the outset for obtaining a lower-order triangular plate element that employs only position and gradient coordinates as nodal coordinates. In this study, these two systematic approaches are used for developing two new lower-order ANCF triangular plate elements and a new high-order ANCF triangular plate element based on Bezier geometry. Specifically, three new ANCF fully parameterized triangular plate elements are developed in this investigation; an ANCF four-node mixed-coordinate triangular plate element (FNMC), a three-node triangular plate element (TN1) obtained from the FNMC element by imposing a set of linear algebraic equations, and another three-node triangular plate element (TN2) obtained by using incomplete polynomials from the outset. All the proposed ANCF triangular plate elements are based on a full parameterization; have global nodal positions and gradient coordinates; ensure continuity of displacement, gradient, and rotation fields at the nodes; allow for easily creating arbitrary shell geometry by simply changing the values of the nodal coordinates in the reference stress-free configuration; and have geometry that is related to B-spline and NURBS (non-uniform rational B-splines) by a linear mapping [74]. The performance of the elements developed in this investigation is also evaluated by comparing their results and convergence characteristics with those of the previously developed conventional linear and quadratic triangular plate elements and the ANCF fully parameterized rectangular plate element available in the general purpose MBS software SIGMA/SAMS.

The structure and organization of this paper are as follows. In Sect. 2, the volume and Cartesian parameterizations used in this investigation to obtain compact and closed-form shape function expressions and to systematically assemble the mesh elements are introduced. The coordinate transformation between the volume and Cartesian gradients is developed in Sect. 3. In Sect. 4, the position field of the new ANCF/FNMC triangular plate element is obtained from a complete cubic Bezier interpolation. In Sect. 5, the lower-order ANCF/TN1 element shape functions are derived by imposing linear constraints on the center node of the ANCF/FNMC element. In Sect. 6, the lower-order ANCF/TN2 element shape functions are directly obtained from an incomplete set of cubic basis functions. The isoparametric properties of the proposed ANCF triangular plate elements are discussed in Sect. 7. In Sect. 8, the procedure for developing the equations of motion of the proposed ANCF elements is described. In Sect. 9, numerical results obtained using different types of triangular plate elements are analyzed and compared in order to evaluate the performance and convergence of the proposed elements. In Sect. 10, summary and conclusions of this investigation are provided.

2 Element parameterization

The continuum mechanics position vector gradients, defined by differentiation of the position vector field with respect to parameters (fibers or coordinate lines), play a fundamental role in the developments presented in this paper. In order to understand the fundamental differences between the triangular plate and shell elements used in the conventional FE literature and the ANCF fully parameterized triangular plate elements developed in this study, the conventional FE coordinate parameterization is analyzed in details in this section. To this end, a set of coordinate lines associated with the material fibers of a continuum defined by the Cartesian parameters $\mathbf{x}=\left[ {{\begin{array}{lll} x&{} y&{} z \\ \end{array} }} \right] ^{T}$ is considered. One can show that the position field of a three-dimensional continuum $\mathbf{r}\left( {\mathbf{x},t} \right) =\left[ {{\begin{array}{ccc} {r_1 }&{} {r_2 }&{} {r_3 } \\ \end{array} }} \right] ^{T}$ can be written as follows:

$$\begin{aligned} \mathbf{r}={} \mathbf{r}(x,y,z)=\left[ {{\begin{array}{ccc} {r_1 (x,y,z)}&{} {r_2 (x,y,z)}&{} {r_3 (x,y,z)} \\ \end{array} }} \right] ^{T}\nonumber \\ \end{aligned}$$

(1)

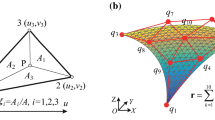
The use of the Cartesian parameterization is necessary to assemble triangular plate elements having gradient vectors as nodal coordinates. On the other hand, it is more convenient to use other dimensionless parameters for describing the element geometry. For this purpose, consider an arbitrary triangular plate element whose corner nodes are ordered counterclockwise and labeled 1, 2, and 3, as shown in Fig. 1. The positions of the element vertices, located on the element mid-surface, are defined in the global coordinate system by the vectors $\mathbf{v}_k =\left[ {{\begin{array}{ccc} {x_k }&{} {y_k }&{} {z_k } \\ \end{array} }} \right] ^{T}, k=1,2,3$, with $x_k , y_k$, and $z_k$ are the Cartesian coordinates at vertex k of the triangular plate element. The Cartesian coordinates $\mathbf{x}$ and the element corner node position vectors $\mathbf{v}_k , k=1,2,3$ are defined in the same global coordinate system. The vector $\mathbf{x}$ can be written in terms of four dimensionless volume coordinates $\varvec{\upxi }{=}\left[ {{\begin{array}{cccc} \xi &{} \eta &{} \zeta &{} \chi \\ \end{array} }} \right] ^{T}$ as

$$\begin{aligned} \mathbf{x}={} \mathbf{x}(\varvec{\upxi })=\left[ {{\begin{array}{ccc} {x(\xi ,\eta ,\zeta ,\chi )}&{} {y(\xi ,\eta ,\zeta ,\chi )}&{} {z(\xi ,\eta ,\zeta ,\chi )} \\ \end{array} }} \right] ^{T}\nonumber \\ \end{aligned}$$

(2)

Fig. 1

Triangular plate element geometry

Fig. 2

Triangular plate element coordinate lines. a Triangular plate element coordinate lines $\xi$. b Triangular plate element coordinate lines $\eta$. c Triangular plate element coordinate lines $\zeta$. d Triangular plate element coordinate lines $\chi$

As shown in Fig. 1, while the first three dimensionless volume coordinates $\xi , \eta$, and $\zeta$ define the coordinates of an arbitrary point on the plate mid-surface, the fourth dimensionless volume coordinate $\chi$ defines the location of an arbitrary plate surface from the mid-surface. It should be noted that the volume coordinates $\xi , \eta$, and $\zeta$, associated with the continuum coordinate lines, are not independent parameters. The dimensionless coordinates are related by the following algebraic equation [58, 61, 62]:

$$\begin{aligned} \xi +\eta +\zeta =1 \end{aligned}$$

(3)

Fig. 3

Triangular plate element isolines and isoplanes. a Triangular plate element isolines $\xi$. b Triangular plate element isolines $\eta$. c Triangular plate element isolines $\zeta$. d Triangular plate element isoplanes $\chi$

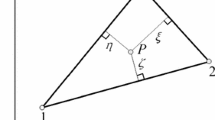
As shown in Fig. 2, each of the dimensionless volume coordinates $\xi , \eta$, and $\zeta$ ranges from zero to one, while the dimensionless volume coordinate $\chi$ ranges from − 1 to $+$ 1. The coordinates $\xi , \eta$, and $\zeta$ form straight lines normal to the sides of the triangular plate element, whereas the coordinate $\chi$ forms straight lines orthogonal to the mid-surface of the element. Furthermore, for a general triangular plate element, the contour lines (isolines) are normal to the coordinate lines $\xi , \eta$, and $\zeta$, while a set of contour planes (isoplanes) is associated with the dimensionless coordinate $\chi$. The equation $\xi =\hbox {c}$, for example, describes a set of straight lines parallel to the triangular plate side identified by the vertices 2 and 3. Similar comments applies to the dimensionless volume coordinates $\eta$ and $\zeta$, as shown in Fig. 3. On the other hand, $\chi =\hbox {c}$ can be geometrically interpreted as a set of straight planes called contour planes (isoplanes) parallel to the triangular plate mid-surface identified by the vertices 1, 2, and 3, as shown in Fig. 3. Let P be an arbitrary point inside the triangular plate whose vertices are relabeled for convenience as A, B, and C, which correspond to the vertex numbers 1, 2, and 3, respectively, as shown in Fig. 4, where $\Delta$ is the volume of the triangular plate element, and $\Delta _1 , \Delta _2$, and $\Delta _3$ represent the volumes of the three triangular plates PBC, PCA, and PAB. The first three volume coordinates $\xi , \eta$, and $\zeta$ can be written, respectively, as $\xi ={\Delta _1 }/\Delta , \eta ={\Delta _2 }/\Delta$, and $\zeta ={\Delta _3 }/\Delta$. Furthermore, considering a triangular plate element of thickness W, one can define a transversal director vector $\mathbf{w}$ orthogonal to the triangular plate mid-surface in the straight (un-deformed) configuration as follows:

$$\begin{aligned} \mathbf{w}=\frac{W}{2}\frac{\mathbf{v}_{2,1} \times \mathbf{v}_{3,1} }{\left| {\mathbf{v}_{2,1} \times \mathbf{v}_{3,1} } \right| } \end{aligned}$$

(4)

Fig. 4

Triangular plate element volume coordinates

where $\mathbf{v}_{2,1} =\mathbf{v}_2 -\mathbf{v}_1 , \mathbf{v}_{3,1} =\mathbf{v}_3 -\mathbf{v}_1$, and $\mathbf{v}_k , k=1,2,3$ are the global position vectors of the triangular plate corner nodes. It is important to note that transversal directors used in the FE literature do not always represent position vector gradients, and the cross product of two position vector gradients does not in general lead to another position vector gradient. The Cartesian coordinates $\mathbf{x}=\left[ {{\begin{array}{ccc} x&{} y&{} z \\ \end{array} }} \right] ^{T}$ and the volume coordinates $\varvec{\upxi }=\left[ {{\begin{array}{cccc} \xi &{} \eta &{} \zeta &{} \chi \\ \end{array} }} \right] ^{T}$ are related by $\mathbf{x}=\xi \mathbf{v}_1 +\eta \mathbf{v}_2 +\zeta \mathbf{v}_3 +\chi \mathbf{w}$, or equivalently:

$$\begin{aligned} \left. \begin{array}{ll} x&{}=x_1 \xi +x_2 \eta +x_3 \zeta +w_1 \chi \\ y&{}=y_1 \xi +y_2 \eta +y_3 \zeta +w_2 \chi \\ z&{}=z_1 \xi +z_2 \eta +z_3 \zeta +w_3 \chi \end{array}\right\} \end{aligned}$$

(5)

where $x_k , y_k$, and $z_k$ represent the Cartesian coordinates of the triangular plate vertex k and $w_i , i=1,2,3$ are the Cartesian components of the transversal director vector $\mathbf{w}$. One can show, using Eq. 5, that the mid-surface triangular plate element corner nodes $\left( {x_1 ,y_1 ,z_1 } \right) , \left( {x_2 ,y_2 ,z_2 } \right)$, and $\left( {x_3 ,y_3 ,z_3 } \right)$ correspond to the volume coordinates $\left( {1,0,0,0} \right) , \left( {0,1,0,0} \right)$, and $\left( {0,0,1,0} \right)$, respectively. Using Eqs. 3 and 5, one can write

$$\begin{aligned} \left[ {{\begin{array}{l} 1 \\ x \\ y \\ z \\ \end{array} }} \right] ={\bar{\mathbf{x}}}=\left[ {{\begin{array}{cccc} 1&{} 1&{} 1&{} 0 \\ {x_1 }&{} {x_2 }&{} {x_3 }&{} {w_1 } \\ {y_1 }&{} {y_2 }&{} {y_3 }&{} {w_2 } \\ {z_1 }&{} {z_2 }&{} {z_3 }&{} {w_3 } \\ \end{array} }} \right] \left[ {{\begin{array}{c} \xi \\ \eta \\ \zeta \\ \chi \\ \end{array} }} \right] =\mathbf{V}{\varvec{\upxi }} \end{aligned}$$

(6)

where ${\bar{\mathbf{x}}}=\left[ {{\begin{array}{cccc} 1&{} x&{} y&{} z \\ \end{array} }} \right] ^{T}$, while $\mathbf{V}$ is the $4\times 4$ matrix

$$\begin{aligned} \mathbf{V}=\left[ {{\begin{array}{cccc} 1&{} 1&{} 1&{} 0 \\ {x_1 }&{} {x_2 }&{} {x_3 }&{} {w_1 } \\ {y_1 }&{} {y_2 }&{} {y_3 }&{} {w_2 } \\ {z_1 }&{} {z_2 }&{} {z_3 }&{} {w_3 } \\ \end{array} }} \right] \end{aligned}$$

(7)

The inverse representation is $\varvec{\upxi }=\mathbf{V}^{-1}{\bar{\mathbf{x}}}$, where

$$\begin{aligned} \mathbf{V}^{-1}=\frac{1}{V}\left[ {{\begin{array}{cccc} {C_1 }&{} {L_{1,1} }&{} {L_{1,2} }&{} {L_{1,3} } \\ {C_2 }&{} {L_{2,1} }&{} {L_{2,2} }&{} {L_{2,3} } \\ {C_3 }&{} {L_{3,1} }&{} {L_{3,2} }&{} {L_{3,3} } \\ {C_4 }&{} {L_{4,1} }&{} {L_{4,2} }&{} {L_{4,3} } \\ \end{array} }} \right] , \end{aligned}$$

(8)

V denotes the volume of the triangular plate element, which is equal to the determinant of the vertex matrix $\mathbf{V}$, and the constant coefficients $C_1 , C_2 , C_3 , C_4 , L_{1,1}, L_{1,2}, L_{1,3} , L_{2,1}$, $L_{2,2}, L_{2,3} , L_{3,1} , L_{3,2} , L_{3,3}, L_{4,1}, L_{4,2}$, and $L_{4,3}$ are the cofactors of the vertex matrix $\mathbf{V}$. The equation $\varvec{\upxi }=\mathbf{V}^{-1}{\bar{\mathbf{x}}}$ leads to

$$\begin{aligned} \left. \begin{array}{ll} \xi &{}=\frac{1}{V}\left( {C_1 +L_{1,1} x+L_{1,2} y+L_{1,3} z} \right) ,\\ \eta &{}=\frac{1}{V}\left( {C_2 +L_{2,1} x+L_{2,2} y+L_{2,3} z} \right) ,\\ \zeta &{}=\frac{1}{V}\left( {C_3 +L_{3,1} x+L_{3,2} y+L_{3,3} z} \right) ,\\ \chi &{}=\frac{1}{V}\left( {C_4 +L_{4,1} x+L_{4,2} y+L_{4,3} z} \right) \end{array}\right\} \end{aligned}$$

(9)

It follows that

$$\begin{aligned} \left. \begin{array}{ll} \mathbf{r}_x &{}=\frac{\partial \mathbf{r}}{\partial x}=\frac{\partial \mathbf{r}}{\partial \xi }\frac{\partial \xi }{\partial x}+\frac{\partial \mathbf{r}}{\partial \eta }\frac{\partial \eta }{\partial x}+\frac{\partial \mathbf{r}}{\partial \zeta }\frac{\partial \zeta }{\partial x}+\frac{\partial \mathbf{r}}{\partial \chi }\frac{\partial \chi }{\partial x}\\ &{}=\frac{1}{V}\left( {\mathbf{r}_\xi L_{1,1} +\mathbf{r}_\eta L_{2,1} +\mathbf{r}_\zeta L_{3,1} +\mathbf{r}_\chi L_{4,1} } \right) \\ \mathbf{r}_y &{}=\frac{\partial \mathbf{r}}{\partial y}=\frac{\partial \mathbf{r}}{\partial \xi }\frac{\partial \xi }{\partial y}+\frac{\partial \mathbf{r}}{\partial \eta }\frac{\partial \eta }{\partial y}+\frac{\partial \mathbf{r}}{\partial \zeta }\frac{\partial \zeta }{\partial y}+\frac{\partial \mathbf{r}}{\partial \chi }\frac{\partial \chi }{\partial y}\\ &{}=\frac{1}{V}\left( {\mathbf{r}_\xi L_{1,2} +\mathbf{r}_\eta L_{2,2} +\mathbf{r}_\zeta L_{3,2} +\mathbf{r}_\chi L_{4,2} } \right) \\ \mathbf{r}_z &{}=\frac{\partial \mathbf{r}}{\partial z}=\frac{\partial \mathbf{r}}{\partial \xi }\frac{\partial \xi }{\partial z}+\frac{\partial \mathbf{r}}{\partial \eta }\frac{\partial \eta }{\partial z}+\frac{\partial \mathbf{r}}{\partial \zeta }\frac{\partial \zeta }{\partial z}+\frac{\partial \mathbf{r}}{\partial \chi }\frac{\partial \chi }{\partial z}\\ &{}=\frac{1}{V}\left( {\mathbf{r}_\xi L_{1,3} +\mathbf{r}_\eta L_{2,3} +\mathbf{r}_\zeta L_{3,3} +\mathbf{r}_\chi L_{4,3} } \right) \end{array}\right\} \nonumber \\ \end{aligned}$$

(10)

This equation can be written compactly as

$$\begin{aligned}&\left[ {{\begin{array}{ccc} {\mathbf{r}_x }&{} {\mathbf{r}_y }&{} {\mathbf{r}_z } \\ \end{array} }} \right] =\frac{1}{V}\left[ {{\begin{array}{cccc} {\mathbf{r}_\xi }&{} {\mathbf{r}_\eta }&{} {\mathbf{r}_\zeta }&{} {\mathbf{r}_\chi } \\ \end{array} }} \right] \nonumber \\&\quad \times \left[ {{\begin{array}{ccc} {L_{1,1} }&{} {L_{1,2} }&{} {L_{1,3} } \\ {L_{2,1} }&{} {L_{2,2} }&{} {L_{2,3} } \\ {L_{3,1} }&{} {L_{3,2} }&{} {L_{3,3} } \\ {L_{4,1} }&{} {L_{4,2} }&{} {L_{4,3} } \\ \end{array} }} \right] =\frac{1}{V}\left[ {{\begin{array}{cccc} {\mathbf{r}_\xi }&{} {\mathbf{r}_\eta }&{} {\mathbf{r}_\zeta }&{} {\mathbf{r}_\chi } \\ \end{array} }} \right] \mathbf{N} \end{aligned}$$

(11)

In this equation $\mathbf{N}$ is

$$\begin{aligned} \mathbf{N}=\left[ {{\begin{array}{ccc} {L_{1,1} }&{} {L_{1,2} }&{} {L_{1,3} } \\ {L_{2,1} }&{} {L_{2,2} }&{} {L_{2,3} } \\ {L_{3,1} }&{} {L_{3,2} }&{} {L_{3,3} } \\ {L_{4,1} }&{} {L_{4,2} }&{} {L_{4,3} } \\ \end{array} }} \right] =\left[ {{\begin{array}{l} {\mathbf{n}_1^T } \\ {\mathbf{n}_2^T } \\ {\mathbf{n}_3^T } \\ {\mathbf{n}_4^T } \\ \end{array} }} \right] \end{aligned}$$

(12)

In the straight (un-deformed) configuration, it can be shown that the vectors $\mathbf{n}_1 =\left[ {{\begin{array}{ccc} {L_{1,1} }&{} {L_{1,2} }&{} {L_{1,3} } \\ \end{array} }} \right] ^{T}, \mathbf{n}_2 =\left[ {{\begin{array}{ccc} {L_{2,1} }&{} {L_{2,2} }&{} {L_{2,3} } \\ \end{array} }} \right] ^{T}$, and $\mathbf{n}_3 =\left[ {{\begin{array}{ccc} {L_{3,1} }&{} {L_{3,2} }&{} {L_{3,3} } \\ \end{array} }} \right] ^{T}$ are normal to the triangular plate sides opposite to the triangular plate vertices 1, 2, and 3, respectively, while the vector $\mathbf{n}_4 =\left[ {{\begin{array}{ccc} {L_{4,1} }&{} {L_{4,2} }&{} {L_{4,3} } \\ \end{array} }} \right] ^{T}$ is a vector normal to the triangular plate mid-surface. As mentioned before, the dependent volume coordinate lines $\xi , \eta$, and $\zeta$ are normal to the element sides, while the independent volume parameter $\chi$ is normal to the plate mid-surface, as it is clear from Eq. 9. For example, using Eq. 9, one can write $\hbox {d}\xi ={\left( {L_{1,1} \hbox {d}x+L_{1,2} \hbox {d}y+L_{1,3} \hbox {d}z} \right) }/V={\mathbf{n}_1^T \hbox {d}\mathbf{x}}/V$, which represents an infinitesimal change of the dimensionless volume parameter $\xi$. Since an infinitesimal change of $\xi$ can be expressed as $\hbox {d}\xi ={\mathbf{n}_1^T \hbox {d}{} \mathbf{x}}/V$, the projection of the Cartesian vector $\hbox {d}{} \mathbf{x}=\left[ {{\begin{array}{ccc} {\hbox {d}x}&{} {\hbox {d}y}&{} {\hbox {d}z} \\ \end{array} }} \right] ^{T}$ along the vector $\mathbf{n}_1 =\left[ {{\begin{array}{ccc} {L_{1,1} }&{} {L_{1,2} }&{} {L_{1,3} } \\ \end{array} }} \right] ^{T}$ is given by $\hbox {d}\xi$ and is orthogonal to the element side defined by the vertices 2 and 3. Similar comments apply to the dimensionless volume coordinates $\eta$ and $\zeta$. On the other hand, using Eq. 9 one can write $\hbox {d}\chi ={\left( {L_{4,1} \hbox {d}x+L_{4,2} \hbox {d}y+L_{4,3} \hbox {d}z} \right) }/V={\mathbf{n}_4^T \hbox {d}\mathbf{x}}/V$, which represents an infinitesimal change of the volume parameter $\chi$. Since one can write $\chi$ in terms of the vectors $\mathbf{n}_4$ and $\hbox {d}{} \mathbf{x}$ as $\hbox {d}\chi ={\mathbf{n}_4^T \hbox {d}\mathbf{x}}/V$, the projection of the Cartesian vector $\hbox {d}{} \mathbf{x}=\left[ {{\begin{array}{ccc} {\hbox {d}x}&{} {\hbox {d}y}&{} {\hbox {d}z} \\ \end{array} }} \right] ^{T}$ along the vector $\mathbf{n}_4 =\left[ {{\begin{array}{ccc} {L_{4,1} }&{} {L_{4,2} }&{} {L_{4,3} } \\ \end{array} }} \right] ^{T}$ is given by $\hbox {d}\chi$ and is orthogonal to the element middle surface. Therefore, using Eqs. 9 and 12, one can write $\hbox {d}\varvec{\upxi }={\mathbf{N}\hbox {d}{} \mathbf{x}}/V$, which demonstrates that the infinitesimal change $\hbox {d}\varvec{\upxi }$ can be defined using the product of $\mathbf{N}$ and $\hbox {d}{} \mathbf{x}$. Because the vectors $\mathbf{n}_1 , \mathbf{n}_2$, and $\mathbf{n}_3$ that form the rows of $\mathbf{N}$ are normal to the element faces, $\mathbf{n}_4$ is normal to the element mid-surface, the volume coordinate lines $\xi , \eta$, and $\zeta$ are normal to the element sides, and $\chi$ is along a direction normal to the element mid-surface; the gradients $\mathbf{r}_\xi , \mathbf{r}_\eta , \mathbf{r}_\zeta$, and $\mathbf{r}_\chi$, tangent to the coordinate lines $\xi , \eta , \zeta$, and $\chi$, are normal to the element sides associated with $\xi , \eta$, and $\zeta$, and to the element mid-surface associated with $\chi$, respectively. As will be discussed in Sect. 3, special definitions of the corner node coordinate lines will be used to facilitate the element assembly.

Fig. 5

Triangular plate element gradients. a Volume and Cartesian gradients of the triangular plate element first node. b Volume and Cartesian gradients of the triangular plate element second node. c Volume and Cartesian gradients of the triangular plate element third node

3 Position vector gradient transformations

In order to be able to use a standard FE assembly procedure with the proposed ANCF triangular plate mesh, a new set of volume parameters must be used to define volume gradient vectors parallel to the triangular plate sides. To be able to develop these position vector gradients, a different geometric definition of the volume coordinate lines is obtained by using the algebraic constraint equation $\xi +\eta +\zeta =1$ to eliminate a dependent volume parameter at each of the three element nodes.

3.1 Node parameterization

Consider the first triangular element node, denoted as node 1 and shown in Fig. 1. The first dimensionless volume coordinate $\xi$ can be written as a linear function of the other two independent volume coordinates $\eta _i$ and $\zeta _i$ as $\xi =1-\eta _i -\zeta _i$, where the subscript i refers to independent parameters. The volume parameter $\chi$, on the other hand, is always considered an independent parameter denoted as $\chi _i$. Eliminating $\xi$ from Eq. 5, one obtains

$$\begin{aligned} \mathbf{x}= & {} \mathbf{v}_1 {+}\eta _i \left( {\mathbf{v}_2 -\mathbf{v}_1 } \right) {+}\zeta _i \left( {\mathbf{v}_3 -\mathbf{v}_1 } \right) {+}\,\chi _i \mathbf{w} \nonumber \\= & {} \mathbf{v}_1 {+}\eta _i \mathbf{v}_{2,1} {+}\zeta _i \mathbf{v}_{3,1} {+}\chi _i \mathbf{w} \end{aligned}$$

(13)

where $\mathbf{v}_{2,1} =\mathbf{v}_2 -\mathbf{v}_1$ and $\mathbf{v}_{3,1} =\mathbf{v}_3 -\mathbf{v}_1$. Equivalently, the preceding equation can be written as

$$\begin{aligned} \left. \begin{array}{ll} x&{}=x_1 +\eta _i a_{2,1} +\zeta _i a_{3,1} +\chi _i w_1\\ y&{}=y_1 +\eta _i b_{2,1} +\zeta _i b_{3,1} +\chi _i w_2\\ z&{}=z_1 +\eta _i c_{2,1} +\zeta _i c_{3,1} +\chi _i w_3 \end{array}\right\} \end{aligned}$$

(14)

where

$$\begin{aligned} \left. \begin{array}{ll} a_{2,1} &{}=x_2 -x_1 ,\quad a_{3,1} =x_3 -x_1 ,\\ b_{2,1} &{}=y_2 -y_1 ,\\ b_{3,1} &{}=y_3 -y_1 ,\quad c_{2,1} =z_2 -z_1 ,\\ c_{3,1} &{}=z_3 -z_1 \end{array}\right\} \end{aligned}$$

(15)

It is important to observe the change of the geometric meaning of the volume parameters as the result of substituting Eq. 3 into Eq. 5. For instance, as shown in Fig. 5, when $\xi$ is eliminated because of the constraint equations between the element volume coordinates, the geometric interpretation of the independent volume parameters $\eta _i$ and $\zeta _i$ changes. This important geometric concept is also described by the equation $\mathbf{x}=\mathbf{v}_1 +\eta _i \mathbf{v}_{2,1} +\zeta _i \mathbf{v}_{3,1} +\chi _i \mathbf{w}$. In this case, $\eta _i$ coordinate lines are a set of straight lines parallel to the element side defined by the vertices 2 and 1 (2–1 side), whereas the $\zeta _i$ coordinate lines are straight lines parallel to the 3 - 1 side. On the other hand, the $\chi _i$ coordinate lines are always a set of straight lines orthogonal to the mid-surface of the plate. Therefore, an infinitesimal change in the Cartesian parameter vector $\mathbf{x}$ is the result of infinitesimal changes in the independent $\eta _i , \zeta _i$, and $\chi _i$ volume parameters along, respectively, the vectors $\mathbf{v}_{2,1} , \mathbf{v}_{3,1}$, and $\mathbf{w}$, which can also be made unit vectors. At the first node, a constant transformation between the volume gradient vectors $\mathbf{r}_{\eta _i } , \mathbf{r}_{\zeta _i }$, and $\mathbf{r}_{\chi _i }$, and the Cartesian gradient vectors $\mathbf{r}_x , \mathbf{r}_y$, and $\mathbf{r}_z$ can be written as

$$\begin{aligned} \left. \begin{array}{ll} \mathbf{r}_{\eta _i } &{}=\frac{\partial \mathbf{r}}{\partial \eta _i }=\frac{\partial \mathbf{r}}{\partial x}\frac{\partial x}{\partial \eta _i }+\frac{\partial \mathbf{r}}{\partial y}\frac{\partial y}{\partial \eta _i }+\frac{\partial \mathbf{r}}{\partial z}\frac{\partial z}{\partial \eta _i }\\ &{}=\mathbf{r}_x a_{2,1} +\mathbf{r}_y b_{2,1} +\mathbf{r}_z c_{2,1}\\ \mathbf{r}_{\zeta _i } &{}=\frac{\partial \mathbf{r}}{\partial \zeta _i }=\frac{\partial \mathbf{r}}{\partial x}\frac{\partial x}{\partial \zeta _i }+\frac{\partial \mathbf{r}}{\partial y}\frac{\partial y}{\partial \zeta _i }+\frac{\partial \mathbf{r}}{\partial z}\frac{\partial z}{\partial \zeta _i }\\ &{}=\mathbf{r}_x a_{3,1} +\mathbf{r}_y b_{3,1} +\mathbf{r}_z c_{3,1}\\ \mathbf{r}_{\chi _i } &{}=\frac{\partial \mathbf{r}}{\partial \chi _i }=\frac{\partial \mathbf{r}}{\partial x}\frac{\partial x}{\partial \chi _i }+\frac{\partial \mathbf{r}}{\partial y}\frac{\partial y}{\partial \chi _i }+\frac{\partial \mathbf{r}}{\partial z}\frac{\partial z}{\partial \chi _i }\\ &{}=\mathbf{r}_x w_1 +\mathbf{r}_y w_2 +\mathbf{r}_z w_3 \end{array}\right\} \end{aligned}$$

(16)

By including the position coordinates, the preceding equation can be written as

$$\begin{aligned} \left. \begin{array}{ll} &{}\mathbf{r}=\mathbf{r}\\ &{}\mathbf{r}_{\eta _i } =\mathbf{r}_x a_{2,1} +\mathbf{r}_y b_{2,1} +\mathbf{r}_z c_{2,1}\\ &{}\mathbf{r}_{\zeta _i } =\mathbf{r}_x a_{3,1} +\mathbf{r}_y b_{3,1} +\mathbf{r}_z c_{3,1}\\ &{}\mathbf{r}_{\chi _i } =\mathbf{r}_x w_1 +\mathbf{r}_y w_2 +\mathbf{r}_z w_3 \end{array}\right\} \end{aligned}$$

(17)

The nodal coordinates at the first node in terms of the volume and Cartesian gradients given by ${\bar{\mathbf{e}}}^{1}=\Big [ {\left( {\mathbf{r}^{1}} \right) ^{T}} {\left( {\mathbf{r}_{\eta _i }^1 } \right) ^{T}} {\left( {\mathbf{r}_{\zeta _i }^1 } \right) ^{T}} {\left( {\mathbf{r}_{\chi _i }^1 } \right) ^{T}} \Big ]^{T}$, and ${\bar{\mathbf{p}}}^{1}=\Big [ {\left( {\mathbf{r}^{1}} \right) ^{T}} {\left( {\mathbf{r}_x^1 } \right) ^{T}} {\left( {\mathbf{r}_y^1 } \right) ^{T}} {\left( {\mathbf{r}_z^1 } \right) ^{T}} \Big ]^{T}$, respectively, are related by ${\bar{\mathbf{e}}}^{1}={\bar{\mathbf{T}}}^{1}{\bar{\mathbf{p}}}^{1}$. In this equation, ${\bar{\mathbf{T}}}^{1}$ is a $12\times 12$ square transformation matrix defined as

$$\begin{aligned} {\bar{\mathbf{T}}}^{1}=\left[ {{\begin{array}{cccc} \mathbf{I}&{} \mathbf{O}&{} \mathbf{O}&{} \mathbf{O} \\ \mathbf{O}&{} {a_{2,1} \mathbf{I}}&{} {b_{2,1} \mathbf{I}}&{} {c_{2,1} \mathbf{I}} \\ \mathbf{O}&{} {a_{3,1} \mathbf{I}}&{} {b_{3,1} \mathbf{I}}&{} {c_{3,1} \mathbf{I}} \\ \mathbf{O}&{} {w_1 \mathbf{I}}&{} {w_2 \mathbf{I}}&{} {w_3 \mathbf{I}} \\ \end{array} }} \right] , \end{aligned}$$

(18)

Fig. 6

ANCF triangular plate elements. a ANCF/FNMC element. b ANCF/TN element

and $\mathbf{I}$ is the $3\times 3$ identity matrix. Using the Cartesian nodal coordinates allows performing a standard FE assembly. On the other hand, using the independent volume parameterization, the vector of Cartesian coordinates can be written as $\mathbf{x}=\mathbf{v}_1 +\eta _i \mathbf{v}_{2,1} +\zeta _i \mathbf{v}_{3,1} +\chi _i \mathbf{w}=\mathbf{v}_1 +\bar{{\eta }}_i \hat{{\mathbf{v}}}_{2,1} +\bar{{\zeta }}_i \hat{{\mathbf{v}}}_{3,1} +\bar{{\chi }}_i \hat{{\mathbf{w}}}$, where $\bar{{\eta }}_i =\eta _i \left| {\mathbf{v}_{2,1} } \right| , \bar{{\zeta }}_i =\zeta _i \left| {\mathbf{v}_{3,1} } \right| , \bar{{\chi }}_i =\chi _i \left| \mathbf{w} \right| , \hat{{\mathbf{v}}}_{2,1} ={\mathbf{v}_{2,1} }/{\left| {\mathbf{v}_{2,1} } \right| }, \hat{{\mathbf{v}}}_{3,1} ={\mathbf{v}_{3,1} }/{\left| {\mathbf{v}_{3,1} } \right| }$, and $\hat{{\mathbf{w}}}=\mathbf{w}/{\left| \mathbf{w} \right| }$. Therefore, an infinitesimal change in the Cartesian coordinates $\mathbf{x}$ is due to infinitesimal changes in the independent volume coordinates $\bar{{\eta }}_i , \bar{{\zeta }}_i$, and $\bar{{\chi }}_i$. These independent infinitesimal changes are, respectively, along the three unit vectors $\hat{{\mathbf{v}}}_{2,1} , \hat{{\mathbf{v}}}_{3,1}$, and $\hat{{\mathbf{w}}}$ which are not necessarily orthogonal unit vectors. The Cartesian gradients associated with the element straight (un-deformed) configuration are $\mathbf{r}_x =\left[ {{\begin{array}{ccc} 1&{} 0&{} 0 \\ \end{array} }} \right] ^{T}, \mathbf{r}_y =\left[ {{\begin{array}{ccc} 0&{} 1&{} 0 \\ \end{array} }} \right] ^{T}$, and $\mathbf{r}_z =\left[ {{\begin{array}{ccc} 0&{} 0&{} 1 \\ \end{array} }} \right] ^{T}$. Therefore, one can write $\left[ {{\begin{array}{ccc} {\mathbf{r}_{\bar{{\eta }}_i } }&{} {\mathbf{r}_{\bar{{\zeta }}_i } }&{} {\mathbf{r}_{\bar{{\chi }}_i } } \\ \end{array} }} \right] =\left[ {{\begin{array}{ccc} {{\partial \mathbf{x}}/{\partial \bar{{\eta }}_i }}&{} {{\partial \mathbf{x}}/{\partial \bar{{\zeta }}_i }}&{} {{\partial \mathbf{x}}/{\partial \bar{{\chi }}_i }} \\ \end{array} }} \right] =\left[ {{\begin{array}{ccc} {\hat{{\mathbf{v}}}_{2,1} }&{} {\hat{{\mathbf{v}}}_{3,1} }&{} {\hat{{\mathbf{w}}}} \\ \end{array} }} \right]$ since it can be shown that $\mathbf{r}_{\bar{{\eta }}_i } =\hat{{\mathbf{v}}}_{2,1} , \mathbf{r}_{\bar{{\zeta }}_i } =\hat{{\mathbf{v}}}_{3,1}$, and $\mathbf{r}_{\bar{{\chi }}_i } =\hat{{\mathbf{w}}}$. This equation demonstrates that, in the straight (un-deformed) configuration, the volume gradients are tangent to the element sides that intersect at node 1 and to the normal of the plate mid-surface, respectively, as shown in Fig. 5. As previously discussed, the dimensionless coordinates $\eta _i$ and $\zeta _i$ are independent volume parameters which can be geometrically interpreted as coordinate lines associated with straight lines parallel to the element sides. Therefore, the geometric meaning of the independent volume parameters used in this investigation is different from the geometric interpretation of the redundant parameters used in the conventional FE literature. Applying the same procedure for nodes 2 and 3, by writing $\eta =1-\zeta _i -\xi _i$ and $\zeta =1-\xi _i -\eta _i$, respectively, one can define, as shown in Fig. 5, the transformation matrices at nodes 2 and 3

$$\begin{aligned} {\bar{\mathbf{T}}}^{2}= & {} \left[ {{\begin{array}{cccc} \mathbf{I}&{} \mathbf{O}&{} \mathbf{O}&{} \mathbf{O} \\ \mathbf{O}&{} {a_{3,2} \mathbf{I}}&{} {b_{3,2} \mathbf{I}}&{} {c_{3,2} \mathbf{I}} \\ \mathbf{O}&{} {a_{1,2} \mathbf{I}}&{} {b_{1,2} \mathbf{I}}&{} {c_{1,2} \mathbf{I}} \\ \mathbf{O}&{} {w_1 \mathbf{I}}&{} {w_2 \mathbf{I}}&{} {w_3 \mathbf{I}} \\ \end{array} }} \right] ,\nonumber \\ {\bar{\mathbf{T}}}^{3}= & {} \left[ {{\begin{array}{cccc} \mathbf{I}&{} \mathbf{O}&{} \mathbf{O}&{} \mathbf{O} \\ \mathbf{O}&{} {a_{1,3} \mathbf{I}}&{} {b_{1,3} \mathbf{I}}&{} {c_{1,3} \mathbf{I}} \\ \mathbf{O}&{} {a_{2,3} \mathbf{I}}&{} {b_{2,3} \mathbf{I}}&{} {c_{2,3} \mathbf{I}} \\ \mathbf{O}&{} {w_1 \mathbf{I}}&{} {w_2 \mathbf{I}}&{} {w_3 \mathbf{I}} \\ \end{array} }} \right] \end{aligned}$$

(19)

where $a_{i,j} =x_i -x_j ,\quad b_{i,j} =y_i -y_j ,\quad c_{i,j} =z_i -z_j ,\quad i=1,2,\ldots ,3,\;j=1,2,\ldots ,3,\;i\ne j$. The transformations obtained in this section, which will facilitate the derivation of closed-form shape functions for the ANCF triangular plate element, also make the geometric interpretation of the gradient vectors used more obvious.

3.2 Element transformation matrix

Using the three transformation matrices developed in this section, and denoting the total vector of volume and Cartesian nodal coordinates as ${\bar{\mathbf{e}}}=\Big [ {\left( {{\bar{\mathbf{e}}}^{1}} \right) ^{T}} {\left( {{\bar{\mathbf{e}}}^{2}} \right) ^{T}} {\left( {{\bar{\mathbf{e}}}^{3}} \right) ^{T}} \Big ]^{T}$, and ${\bar{\mathbf{p}}}=\left[ {\left( {{\bar{\mathbf{p}}}^{1}} \right) ^{T}} {\left( {{\bar{\mathbf{p}}}^{2}} \right) ^{T}}{\left( {{\bar{\mathbf{p}}}^{3}} \right) ^{T}} \right] ^{T}$, respectively, one can write a linear relationship between the vectors of nodal coordinates as ${\bar{\mathbf{e}}}={\bar{\mathbf{T}}\bar{\mathbf{p}}}$. In this equation, the transformation matrix ${\bar{\mathbf{T}}}$ has dimensions $36\times 36$ and is defined in a block diagonal form as

$$\begin{aligned} {\bar{\mathbf{T}}}=\left[ {{\begin{array}{ccc} {{\bar{\mathbf{T}}}^{1}}&{} \mathbf{O}&{} \mathbf{O} \\ \mathbf{O}&{} {{\bar{\mathbf{T}}}^{2}}&{} \mathbf{O} \\ \mathbf{O}&{} \mathbf{O}&{} {{\bar{\mathbf{T}}}^{3}} \\ \end{array} }} \right] \end{aligned}$$

(20)

In the following section, a kinematic description based on Bezier geometry and a set of cubic basis functions are used in the development of the shape functions of the four-node mixed-coordinate (FNMC) ANCF triangular plate element. Using the FNMC shape functions, the shape functions of the three-node ANCF element (TN1) can be derived by using a set of linear constraint equations. Another three-node ANCF triangular plate element (TN2) is developed by using incomplete polynomials from the outset. It can be shown that the proposed FNMC and TN triangular elements are isoparametric, lead to exact representation of the rigid-body motion, define a constant mass matrix, and define complex shell geometry by simply changing the values of the nodal coordinates in the reference configuration thereby eliminating the distinction between plate and shell geometries as it is the case when conventional FE formulations are used.

4 Complete cubic polynomial four-node element

In this section, the shape functions of the ANCF/FNMC triangular plate element shown in Fig. 6 are developed using a special type of a cubic Bezier triangle on which the global position of an arbitrary point can be written as $\mathbf{r}=\sum \nolimits _{k=1}^m {g_k \mathbf{q}^{k}}$, where $m=13, g_k$ are the Bezier triangle basis functions defined in terms of the volume coordinates $\xi , \eta , \zeta$, and $\chi$, and $\mathbf{q}^{k}$ are the Bezier control points. The Bezier polynomial terms $g_k , k=1,2,\ldots ,10$, are the terms which appear in the expansion of $({\xi +\eta +\zeta } )^{3}$, while the Bezier polynomial terms $g_k , k=11,12,13$, are the product of $\xi , \eta$, and $\zeta$ with $\chi$. The cubic Bezier basis functions used in this investigation are

$$\begin{aligned} \left. \begin{array}{ll} g_1 &{}=\xi ^{3},\quad g_2 =\eta ^{3},\quad g_3 =\zeta ^{3},\\ g_4 &{}=3\xi ^{2}\eta ,\quad g_5 =3\xi \eta ^{2},\\ g_6 &{}=3\eta ^{2}\zeta ,\quad g_7 =3\eta \zeta ^{2},\\ g_8 &{}=3\xi ^{2}\zeta ,\quad g_9 =3\xi \zeta ^{2},\\ g_{10} &{}=6\xi \eta \zeta ,\quad g_{11} =\xi \chi ,\\ g_{12} &{}=\eta \chi ,\quad g_{13} =\zeta \chi \end{array}\right\} \end{aligned}$$

(21)

The cubic Bezier triangle description can be used with a constant coordinate transformation to define the FNMC element assumed displacement field. The relationship between the cubic Bezier control points and the FNMC element nodal coordinates can be expressed as

$$\begin{aligned} \left. \begin{array}{ll} \mathbf{r}^{1}&{}=\mathbf{q}^{1},\quad \mathbf{r}_{\eta _i }^1 =3\left( {\mathbf{q}^{4}-\mathbf{q}^{1}} \right) ,\\ \mathbf{r}_{\zeta _i }^1 &{}=3\left( {\mathbf{q}^{8}-\mathbf{q}^{1}} \right) ,\quad \mathbf{r}_{\chi _i }^1 =\mathbf{q}^{11},\\ \mathbf{r}^{2}&{}=\mathbf{q}^{2},\quad \mathbf{r}_{\zeta _i }^2 =3\left( {\mathbf{q}^{6}-\mathbf{q}^{2}} \right) ,\\ \mathbf{r}_{\xi _i }^2 &{}=3\left( {\mathbf{q}^{5}-\mathbf{q}^{2}} \right) ,\quad \mathbf{r}_{\chi _i }^2 =\mathbf{q}^{12},\\ \mathbf{r}^{3}&{}=\mathbf{q}^{3},\quad \mathbf{r}_{\xi _i }^3 =3\left( {\mathbf{q}^{9}-\mathbf{q}^{3}} \right) ,\\ \mathbf{r}_{\eta _i }^3 &{}=3\left( {\mathbf{q}^{7}-\mathbf{q}^{3}} \right) ,\quad \mathbf{r}_{\chi _i }^3 =\mathbf{q}^{13},\\ \mathbf{r}^{4}&{}=\frac{1}{27}\left( \mathbf{q}^{1}+\mathbf{q}^{2}+\mathbf{q}^{3}+3\mathbf{q}^{4}+3\mathbf{q}^{5}\right. \\ &{}\left. +\,3\mathbf{q}^{6}+3\mathbf{q}^{7}+3\mathbf{q}^{8}+3\mathbf{q}^{9}+6\mathbf{q}^{10} \right) \end{array}\right\} \end{aligned}$$

(22)

Using these linear algebraic equations, the FNMC position field is defined as $\mathbf{r}=\mathbf{Se}$, where $\mathbf{S}$ and $\mathbf{e}$ are, respectively, the FNMC shape function matrix and vector of nodal coordinates defined as

$$\begin{aligned} \mathbf{S}= & {} \Big [ {s_1 \mathbf{I}}\quad {s_2 \mathbf{I}}\quad {s_3 \mathbf{I}}\quad {s_4 \mathbf{I}}\quad {s_5 \mathbf{I}}\quad {s_6 \mathbf{I}}\quad {s_7 \mathbf{I}}\quad {s_8 \mathbf{I}}\nonumber \\&\quad {s_9 \mathbf{I}}\quad {s_{10} \mathbf{I}}\quad {s_{11} \mathbf{I}}\quad {s_{12} \mathbf{I}}\quad {s_{13} \mathbf{I}} \Big ] \end{aligned}$$

(23)

and

$$\begin{aligned} \mathbf{e}= & {} \left[ {{\begin{array}{cccccccc} {\left( {\mathbf{r}^{1}} \right) ^{T}}&{} {\left( {\mathbf{r}_{\eta _i }^1 } \right) ^{T}}&{} {\left( {\mathbf{r}_{\zeta _i }^1 } \right) ^{T}}&{} {\left( {\mathbf{r}_{\chi _i }^1 } \right) ^{T}}&{} {\left( {\mathbf{r}^{2}} \right) ^{T}}&{} {\left( {\mathbf{r}_{\zeta _i }^2 } \right) ^{T}}&{} {\left( {\mathbf{r}_{\xi _i }^2 } \right) ^{T}} \\ \end{array} }} \right. \nonumber \\&\left. {{\begin{array}{*{20}c} {\left( {\mathbf{r}_{\chi _i }^2 } \right) ^{T}}&{}{\left( {\mathbf{r}^{3}} \right) ^{T}}&{} {\left( {\mathbf{r}_{\xi _i }^3 } \right) ^{T}}&{} {\left( {\mathbf{r}_{\eta _i }^3 } \right) ^{T}}&{} {\left( {\mathbf{r}_{\chi _i }^3 } \right) ^{T}}&{} {\left( {\mathbf{r}^{4}} \right) ^{T}} \\ \end{array} }} \right] ^{T}\nonumber \\ \end{aligned}$$

(24)

where $\mathbf{I}$ is the $3\times 3$ identity matrix, and $\mathbf{r}_{\xi _i } ={\partial \mathbf{r}}/{\partial \xi _i }, \mathbf{r}_{\eta _i } ={\partial \mathbf{r}}/{\partial \eta _i }, \mathbf{r}_{\zeta _i } ={\partial \mathbf{r}}/{\partial \zeta _i }$, and $\mathbf{r}_{\chi _i } ={\partial \mathbf{r}}/{\partial \chi _i }$ are the nodal gradients defined by differentiation with respect to the independent volume parameters along the element sides and along the normal to the element mid-surface. The FNMC shape functions $s_k ,\;k=1,2,\ldots ,13$, are

$$\begin{aligned} \left. \begin{array}{ll} s_1 &{}=\xi \left( {\xi ^{2}+3\xi \left( {\eta +\zeta } \right) -7\eta \zeta } \right) ,\\ s_2 &{}=\xi \eta \left( {\xi -\zeta } \right) ,\\ s_3 &{}=\xi \zeta \left( {\xi -\eta } \right) , \\ s_4 &{}=\xi \chi ,\quad s_5 =\eta \left( {\eta ^{2}+3\eta \left( {\zeta +\xi } \right) -7\zeta \xi } \right) ,\\ s_6 &{}=\eta \zeta \left( {\eta -\xi } \right) , \\ s_7 &{}=\eta \xi \left( {\eta -\zeta } \right) ,\quad s_8 =\eta \chi ,\\ s_9 &{}=\zeta \left( {\zeta ^{2}+3\zeta \left( {\xi +\eta } \right) -7\xi \eta } \right) , \\ s_{10} &{}=\zeta \xi \left( {\zeta -\eta } \right) ,\quad s_{11} =\zeta \eta \left( {\zeta -\xi } \right) ,\\ s_{12} &{}=\zeta \chi ,\quad s_{13} =27\xi \eta \zeta \end{array}\right\} \end{aligned}$$

(25)

The superscripts 1, 2, and 3 refer to corner nodes in the definition of the nodal coordinate vector, while superscript 4 refers to the FNMC center node as shown in Fig. 6. The element corner nodes are ordered counterclockwise in a manner that follows the right-hand rule. The FNMC nodal coordinates are defined as

$$\begin{aligned} \left. \begin{array}{ll} \mathbf{r}^{1}&{}=\mathbf{r}(1,0,0,0),\quad \mathbf{r}_{\eta _i }^1 =\left. {\mathbf{r}_\eta } \right| _{\xi =1-\eta -\zeta } (1,0,0,0),\\ \mathbf{r}_{\zeta _i }^1 &{}=\left. {\mathbf{r}_\zeta } \right| _{\xi =1-\eta -\zeta } (1,0,0,0),\quad \mathbf{r}_{\chi _i }^1 =\left. {\mathbf{r}_\chi } \right| _{\xi =1-\eta -\zeta } (1,0,0,0) \\ \mathbf{r}^{2}&{}=\mathbf{r}(0,1,0,0),\quad \mathbf{r}_{\zeta _i }^2 =\left. {\mathbf{r}_\zeta } \right| _{\eta =1-\zeta -\xi } (0,1,0,0),\\ \mathbf{r}_{\xi _i }^2 &{}=\left. {\mathbf{r}_\xi } \right| _{\eta =1-\zeta -\xi } (0,1,0,0),\quad \mathbf{r}_{\chi _i }^2 =\left. {\mathbf{r}_\chi } \right| _{\xi =1-\eta -\zeta } (0,1,0,0) \\ \mathbf{r}^{3}&{}=\mathbf{r}(0,0,1,0),\quad \mathbf{r}_{\xi _i }^3 =\left. {\mathbf{r}_\xi } \right| _{\zeta =1-\xi -\eta } (0,0,1,0),\\ \mathbf{r}_{\eta _i }^3 &{}=\left. {\mathbf{r}_\eta } \right| _{\zeta =1-\xi -\eta } (0,0,1,0),\quad \mathbf{r}_{\chi _i }^3 =\left. {\mathbf{r}_\chi } \right| _{\xi =1-\eta -\zeta } (0,0,1,0) \\ \mathbf{r}^{4}&{}=\mathbf{r}(1/3,1/3,1/3,0) \end{array}\right\} \nonumber \\ \end{aligned}$$

(26)

In this equation, the volume gradient partial derivatives are performed using the volume coordinate constraint equation in the Bezier displacement field. The proposed FNMC element is an isoparametric finite element, describes correctly rigid-body motion, and can be used to develop shell geometry by using an appropriate value for the vector $\mathbf{e}$ in the reference configuration.

The linear transformations between the cubic Bezier basis functions $g_k ,\;k=1,2,\ldots ,13$, and the FNMC shape functions $s_k ,\;k=1,2,\ldots ,13$, are given by

$$\begin{aligned} \left. \begin{array}{ll} s_1 &{}=g_1 +g_4 +g_8 -\frac{7}{6}g_{10} , \\ s_2 &{}=\frac{1}{3}g_4 -\frac{1}{6}g_{10} ,\\ s_3 &{}=\frac{1}{3}g_8 -\frac{1}{6}g_{10} ,\quad s_4 =g_{11} , \\ s_5 &{}=g_2 +g_5 +g_6 -\frac{7}{6}g_{10} ,\\ s_6 &{}=\frac{1}{3}g_6 -\frac{1}{6}g_{10} ,\\ s_7 &{}=\frac{1}{3}g_5 -\frac{1}{6}g_{10} ,\quad s_8 =g_{12} , \\ s_9 &{}=g_3 +g_7 +g_9 -\frac{7}{6}g_{10} ,\\ s_{10} &{}=\frac{1}{3}g_9 -\frac{1}{6}g_{10} ,\\ s_{11} &{}=\frac{1}{3}g_7 -\frac{1}{6}g_{10} ,\quad s_{12} =g_{13} , \\ s_{13} &{}=\frac{9}{6}g_{10} \end{array}\right\} \end{aligned}$$

(27)

The FNMC element has 39 nodal coordinates which consist of 12 position coordinates and 27 gradient coordinates. A linear transformation can be used to write the nodal coordinate vector $\mathbf{e}$ in terms of the coordinates $\mathbf{p}$, whose elements contain the Cartesian gradients $\mathbf{r}_x , \mathbf{r}_y$, and $\mathbf{r}_z$, as $\mathbf{e}=\mathbf{Tp}$, where $\mathbf{T}$ is a $39\times 39$ block diagonal constant transformation defined as

$$\begin{aligned} \mathbf{T}=\left[ {{\begin{array}{cccc} {\mathbf{T}^{1}}&{} \mathbf{O}&{} \mathbf{O}&{} \mathbf{O} \\ \mathbf{O}&{} {\mathbf{T}^{2}}&{} \mathbf{O}&{} \mathbf{O} \\ \mathbf{O}&{} \mathbf{O}&{} {\mathbf{T}^{3}}&{} \mathbf{O} \\ \mathbf{O}&{} \mathbf{O}&{} \mathbf{O}&{} {\mathbf{T}^{4}} \\ \end{array} }} \right] \end{aligned}$$

(28)

The matrices on the diagonal of this transformation are $\mathbf{T}^{1}={\bar{\mathbf{T}}}^{1}, \mathbf{T}^{2}={\bar{\mathbf{T}}}^{2}, \mathbf{T}^{3}={\bar{\mathbf{T}}}^{3}, \mathbf{T}^{4}=\mathbf{I}$, where $\mathbf{I}$ is the $3\times 3$ identity matrix.

5 Elimination of the internal node

As discussed in the preceding section, the FNMC complete cubic polynomials have 39 coefficients, or equivalently 13 control points. For this reason, an internal node was introduced to allow for the use of a complete polynomial representation. Nonetheless, a lower-order three-node element can be systematically obtained by writing the position coordinates of the internal node in terms of the coordinates of a set of material point located on the sides of the element. This procedure leads to linear constraint equations that can be written as $\mathbf{r}^{10}=\frac{1}{9}\sum \nolimits _{i=1}^9 {\mathbf{r}^{i}}$, where $\mathbf{r}^{i},i=1,2,\ldots ,9$ are global positions of material points distributed on the sides of the FNMC element and are defined as

$$\begin{aligned} \left. \begin{array}{ll} \mathbf{r}^{1}&{}=\mathbf{r}\left( {1,0,0,0} \right) ,\\ \mathbf{r}^{2}&{}=\mathbf{r}\left( {0,1,0,0} \right) ,\\ \mathbf{r}^{3}&{}=\mathbf{r}\left( {0,0,1,0} \right) \\ \mathbf{r}^{4}&{}=\mathbf{r}\left( {2/3,1/3,0,0} \right) ,\\ \mathbf{r}^{5}&{}=\mathbf{r}\left( {1/3,2/3,0,0} \right) , \\ \mathbf{r}^{6}&{}=\mathbf{r}\left( {2/3,0,1/3,0} \right) , \\ \mathbf{r}^{7}&{}=\mathbf{r}\left( {1/3,0,2/3,0} \right) ,\\ \mathbf{r}^{8}&{}=\mathbf{r}\left( {{0,2}/3,1/3,0} \right) ,\\ \mathbf{r}^{9}&{}=\mathbf{r}\left( {{0,1}/3,2/3,0} \right) \end{array}\right\} \end{aligned}$$

(29)

Using the resulting algebraic constraint equations, a linear transformation can be developed and used to define the TN1 shape functions and position field which can be written as ${\bar{\mathbf{r}}}={\bar{\mathbf{S}}\bar{\mathbf{e}}}$, where ${\bar{\mathbf{S}}}$ and ${\bar{\mathbf{e}}}$ are, respectively, the shape function matrix and vector of nodal coordinates defined as

$$\begin{aligned} {\bar{\mathbf{S}}}=\left[ {{\begin{array}{cccccccccccc} {\bar{{s}}_1 \mathbf{I}}&{}{\bar{{s}}_2 \mathbf{I}}&{}{\bar{{s}}_3 \mathbf{I}}&{}{\bar{{s}}_4 \mathbf{I}}&{}{\bar{{s}}_5 \mathbf{I}}&{}{\bar{{s}}_6 \mathbf{I}}&{}{\bar{{s}}_7 \mathbf{I}}&{}{\bar{{s}}_8 \mathbf{I}}&{}{\bar{{s}}_9 \mathbf{I}}&{}{\bar{{s}}_{10} \mathbf{I}}&{}{\bar{{s}}_{11} \mathbf{I}}&{}{\bar{{s}}_{12} \mathbf{I}} \\ \end{array} }} \right] \nonumber \\ \end{aligned}$$

(30)

and

$$\begin{aligned} {\bar{\mathbf{e}}}= & {} \left[ {{\begin{array}{cccccccc} {\left( {\mathbf{r}^{1}} \right) ^{T}}&{} {\left( {\mathbf{r}_{\eta _i }^1 } \right) ^{T}}&{} {\left( {\mathbf{r}_{\zeta _i }^1 } \right) ^{T}}&{} {\left( {\mathbf{r}_{\chi _i }^1 } \right) ^{T}}&{} {\left( {\mathbf{r}^{2}} \right) ^{T}}&{} {\left( {\mathbf{r}_{\zeta _i }^2 } \right) ^{T}}&{} {\left( {\mathbf{r}_{\xi _i }^2 } \right) ^{T}}&{} {\left( {\mathbf{r}_{\chi _i }^2 } \right) ^{T}} \\ \end{array} }} \right. \nonumber \\&\left. {{\begin{array}{cccc} {\left( {\mathbf{r}^{3}} \right) ^{T}}&{} {\left( {\mathbf{r}_{\xi _i }^3 } \right) ^{T}}&{} {\left( {\mathbf{r}_{\eta _i }^3 } \right) ^{T}}&{} {\left( {\mathbf{r}_{\chi _i }^3 } \right) ^{T}} \\ \end{array} }} \right] ^{T} \end{aligned}$$

(31)

where $\mathbf{I}$ is the $3\times 3$ identity matrix, and $\mathbf{r}_{\xi _i } ={\partial \mathbf{r}}/{\partial \xi _i }, \mathbf{r}_{\eta _i } ={\partial \mathbf{r}}/{\partial \eta _i }, \mathbf{r}_{\zeta _i } ={\partial \mathbf{r}}/{\partial \zeta _i }$, and $\mathbf{r}_{\chi _i } ={\partial \mathbf{r}}/{\partial \chi _i }$ are the element nodal gradients associated with independent volume parameters along the element sides and along the normal to the element mid-surface, as previously discussed. The shape functions $\bar{{s}}_k ,\;k=1,2,\ldots ,12$, of the TN1 element are defined in as

$$\begin{aligned} \left. \begin{array}{ll} \bar{s}_1 &{}=\xi \left( {\xi ^{2}+3\xi \left( {\eta +\zeta } \right) +2\eta \zeta } \right) ,\\ \bar{{s}}_2 &{}=\xi \eta \left( {\xi -\frac{1}{3}\zeta } \right) ,\\ \bar{{s}}_3 &{}=\xi \zeta \left( {\xi -\frac{1}{3}\eta } \right) , \\ \bar{s}_4 &{}=\xi \chi ,\quad \bar{{s}}_5 =\eta \left( {\eta ^{2}+3\eta \left( {\zeta +\xi } \right) +2\zeta \xi } \right) ,\\ \bar{{s}}_6 &{}=\eta \zeta \left( {\eta -\frac{1}{3}\xi } \right) , \\ \bar{s}_7 &{}=\eta \xi \left( {\eta -\frac{1}{3}\zeta } \right) ,\\ \bar{{s}}_8 &{}=\eta \chi ,\\ \bar{{s}}_9 &{}=\zeta \left( {\zeta ^{2}+3\zeta \left( {\xi +\eta } \right) +2\xi \eta } \right) , \\ \bar{s}_{10} &{}=\zeta \xi \left( {\zeta -\frac{1}{3}\eta } \right) ,\\ \bar{{s}}_{11} &{}=\zeta \eta \left( {\zeta -\frac{1}{3}\xi } \right) ,\quad \bar{{s}}_{12} =\zeta \chi \end{array}\right\} \end{aligned}$$

(32)

The TN1 triangular plate element has 36 nodal coordinates which consist of 9 position coordinates and 27 gradient coordinates. The vector of element coordinates ${\bar{\mathbf{e}}}$ which has the volume gradients is related to the vector of structural coordinates ${\bar{\mathbf{p}}}$ which has the Cartesian gradients by the constant transformation ${\bar{\mathbf{e}}}={\bar{\mathbf{T}}\bar{\mathbf{p}}}$, where the transformation ${\bar{\mathbf{T}}}$ is defined in Sect. 3.

The procedure described in this section, in which algebraic equations are used to eliminate the internal node, allows for systematically obtaining a symmetric incomplete polynomial representation without the need for using a trial and error process to identify the appropriate basis functions. As demonstrated in the following section, an alternate set of incomplete cubic Bezier basis functions can be used to obtain directly the shape functions using a linear mapping.

6 Use of incomplete cubic polynomial representation

In order to develop the shape functions of the TN2 element shown in Fig. 6, a special type of Bezier basis functions and a set of control points are used to define the global position vector of an arbitrary point as $\mathbf{r}=\sum \nolimits _{k=1}^{12} {h_k \mathbf{q}^{k}}$, where $h_k$ are the Bezier basis or blending functions defined in terms of the volume coordinates $\xi , \eta , \zeta$, and $\chi$, and $\mathbf{q}^{k}$ are the control points. The incomplete cubic Bezier basis functions used in this investigation are

$$\begin{aligned} \left. \begin{array}{ll} h_1 &{}=\xi ,\quad h_2 =\eta ,\quad h_3 =\zeta ,\quad h_4 =3\xi ^{2}\eta ,\\ h_5 &{}=3\xi \eta ^{2},\quad h_6 =3\eta ^{2}\zeta , \\ h_7 &{}=3\eta \zeta ^{2},\quad h_8 =3\xi ^{2}\zeta ,\quad h_9 =3\xi \zeta ^{2},\\ h_{10} &{}=\xi \chi ,\quad h_{11} =\eta \chi ,\quad h_{12} =\zeta \chi \end{array}\right\} \end{aligned}$$

(33)

In this case, the relationship between the incomplete cubic Bezier control points and the TN2 element nodal coordinates can be written as

$$\begin{aligned} \left. \begin{array}{ll} \mathbf{r}^{1}&{}=\mathbf{q}^{1},\quad \mathbf{r}_{\eta _i }^1 =3\mathbf{q}^{4}+\mathbf{q}^{2}-\mathbf{q}^{1},\\ \mathbf{r}_{\zeta _i }^1 &{}=3\mathbf{q}^{8}+\mathbf{q}^{3}-\mathbf{q}^{1},\quad \mathbf{r}_{\chi _i }^1 =\mathbf{q}^{10},\\ \mathbf{r}^{2}&{}=\mathbf{q}^{2},\quad \mathbf{r}_{\zeta _i }^2 =3\mathbf{q}^{6}+\mathbf{q}^{3}-\mathbf{q}^{2},\\ \mathbf{r}_{\xi _i }^2 &{}=3\mathbf{q}^{5}+\mathbf{q}^{1}-\mathbf{q}^{2},\quad \mathbf{r}_{\chi _i }^2 =\mathbf{q}^{11}, \\ \mathbf{r}^{3}&{}=\mathbf{q}^{3},\quad \mathbf{r}_{\xi _i }^3 =3\mathbf{q}^{9}+\mathbf{q}^{1}-\mathbf{q}^{3},\\ \mathbf{r}_{\eta _i }^3 &{}=3\mathbf{q}^{7}+\mathbf{q}^{2}-\mathbf{q}^{3},\quad \mathbf{r}_{\chi _i }^3 =\mathbf{q}^{12} \end{array}\right\} \end{aligned}$$

(34)

Using these linear algebraic equations, the TN2 position field can be expressed as $\mathbf{r}={\bar{\bar{\mathbf{S}}}\bar{{\bar{\mathbf{e}}}}}$, where ${\bar{\bar{\mathbf{S}}}}$ and ${\bar{\bar{\mathbf{e}}}}$ are the TN2 shape function matrix and vector of nodal coordinates given, respectively, by

$$\begin{aligned} {\bar{\bar{\mathbf{S}}}}=\left[ {{\begin{array}{cccccccccccc} {\bar{{\bar{s}}}_1 \mathbf{I}}&{} {\bar{{\bar{{s}}}}_2 \mathbf{I}}&{} {\bar{{\bar{s}}}_3 \mathbf{I}}&{} {\bar{{\bar{{s}}}}_4 \mathbf{I}}&{} {\bar{{\bar{s}}}_5 \mathbf{I}}&{} {\bar{{\bar{{s}}}}_6 \mathbf{I}}&{} {\bar{{\bar{s}}}_7 \mathbf{I}}&{} {\bar{{\bar{{s}}}}_8 \mathbf{I}}&{} {\bar{{\bar{s}}}_9 \mathbf{I}}&{} {\bar{{\bar{{s}}}}_{10} \mathbf{I}}&{} {\bar{{\bar{s}}}_{11} \mathbf{I}}&{} {\bar{{\bar{{s}}}}_{12} \mathbf{I}} \\ \end{array} }} \right] \nonumber \\ \end{aligned}$$

(35)

Fig. 7

Continuum configurations

and

$$\begin{aligned} {\bar{\bar{\mathbf{e}}}}= & {} \left[ {{\begin{array}{cccccccc} {\left( {\mathbf{r}^{1}} \right) ^{T}}&{} {\left( {\mathbf{r}_{\eta _i }^1 } \right) ^{T}}&{} {\left( {\mathbf{r}_{\zeta _i }^1 } \right) ^{T}}&{} {\left( {\mathbf{r}_{\chi _i }^1 } \right) ^{T}}&{} {\left( {\mathbf{r}^{2}} \right) ^{T}}&{} {\left( {\mathbf{r}_{\zeta _i }^2 } \right) ^{T}}&{} {\left( {\mathbf{r}_{\xi _i }^2 } \right) ^{T}}&{} {\left( {\mathbf{r}_{\chi _i }^2 } \right) ^{T}} \\ \end{array} }} \right. \nonumber \\&\left. {{\begin{array}{cccc} {\left( {\mathbf{r}^{3}} \right) ^{T}}&{} {\left( {\mathbf{r}_{\xi _i }^3 } \right) ^{T}}&{} {\left( {\mathbf{r}_{\eta _i }^3 } \right) ^{T}}&{} {\left( {\mathbf{r}_{\chi _i }^3 } \right) ^{T}} \\ \end{array} }} \right] ^{T} \end{aligned}$$

(36)

where the nodal gradients have the same interpretation as in the case of the TN1 element. The TN2 shape functions $\bar{{\bar{{s}}}}_k ,\;k=1,2,\ldots ,12$, are

$$\begin{aligned} \left. \begin{array}{ll} \bar{{\bar{{s}}}}_1 &{}=\xi ^{2}\left( {\eta +\zeta } \right) +\xi \left( {1-\eta ^{2}-\zeta ^{2}} \right) ,\\ \bar{{\bar{{s}}}}_2 &{}=\xi ^{2}\eta ,\quad \bar{{\bar{{s}}}}_3 =\xi ^{2}\zeta ,\quad \bar{{\bar{{s}}}}_4 =\xi \chi , \\ \bar{{\bar{{s}}}}_5 &{}=\eta ^{2}\left( {\zeta +\xi } \right) +\eta \left( {1-\zeta ^{2}-\xi ^{2}} \right) ,\\ \bar{{\bar{{s}}}}_6 &{}=\eta ^{2}\zeta ,\quad \bar{{\bar{{s}}}}_7 =\eta ^{2}\xi ,\quad \bar{{\bar{{s}}}}_8 =\eta \chi , \\ \bar{{\bar{{s}}}}_9 &{}=\zeta ^{2}\left( {\xi +\eta } \right) +\zeta \left( {1-\xi ^{2}-\eta ^{2}} \right) ,\\ \bar{{\bar{{s}}}}_{10} &{}=\zeta ^{2}\xi ,\quad \bar{{\bar{{s}}}}_{11} =\zeta ^{2}\eta ,\quad \bar{{\bar{{s}}}}_{12} =\zeta \chi \end{array}\right\} \end{aligned}$$

(37)

The linear transformations between the incomplete cubic Bezier basis functions $h_k ,\;k=1,2,\ldots ,12$, and the shape functions of the TN2 triangular plate element $\bar{{\bar{{s}}}}_k ,\;k=1,2,\ldots ,12$, are given by

$$\begin{aligned} \left. \begin{array}{ll} \bar{{\bar{{s}}}}_1 &{}=h_1 +\frac{1}{3}\left( {h_4 +h_8 -h_5 -h_9 } \right) ,\quad \bar{{\bar{{s}}}}_2 =\frac{1}{3}h_4 ,\\ \bar{{\bar{{s}}}}_3 &{}=\frac{1}{3}h_8 ,\quad \bar{{\bar{{s}}}}_4 =h_{10} , \\ \bar{{\bar{{s}}}}_5 &{}=h_2 +\frac{1}{3}\left( {h_5 +h_6 -h_4 -h_7 } \right) ,\quad \bar{{\bar{{s}}}}_6 =\frac{1}{3}h_6 ,\\ \bar{{\bar{{s}}}}_7 &{}=\frac{1}{3}h_5 ,\quad \bar{{\bar{{s}}}}_8 =h_{11} , \\ \bar{{\bar{{s}}}}_9 &{}=h_3 +\frac{1}{3}\left( {h_7 +h_9 -h_6 -h_8 } \right) ,\\ \bar{{\bar{{s}}}}_{10} &{}=\frac{1}{3}h_9 ,\quad \bar{{\bar{{s}}}}_{11} =\frac{1}{3}h_7 ,\quad \bar{{\bar{{s}}}}_{12} =h_{12} \end{array}\right\} \end{aligned}$$

(38)

The TN2 triangular plate element has 36 nodal coordinates; 9 position and 27 gradient coordinates. As in the case of the TN1 element, the coordinate vector ${\bar{\bar{\mathbf{{e}}}}}$ is related to the vector of structural coordinates ${\bar{\bar{\mathbf{{p}}}}}$ by the linear equation ${\bar{\bar{\mathbf{{e}}}}}=\bar{\bar{\mathbf{{T}}}}\bar{{\bar{{\mathbf{p}}}}}$, where ${\bar{\bar{\mathbf{{T}}}}}={\bar{\mathbf{T}}}$.

7 Isoparametric property and shell geometry

In this section, two important features of the higher-order ANCF elements proposed in this investigation are discussed. The first is the isoparametric property and the second is the shell geometry.

7.1 Isoparametric property

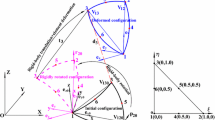
Isoparametric elements, which are capable of describing the element geometry and displacement using the same shape function matrix, correctly describe rigid-body motion and can be used in a non-incremental solution procedure. As shown in Fig. 7, three general configuration of a continuum body can be identified, namely a straight (un-deformed) configuration, a reference (curved) stress-free configuration, and a current (deformed) configuration. In the current configuration, one can write the element position field as $\mathbf{r}=\mathbf{Se}=\mathbf{STp}$, where $\mathbf{e}$ and $\mathbf{p}$ are the coordinate vectors associated with the volume and Cartesian parameterizations, respectively. In the reference configuration, the definition of the element position field is given by $\mathbf{r}_0 =\mathbf{Se}_0 =\mathbf{STp}_0$, where $\mathbf{e}_0$ and $\mathbf{p}_0$ are appropriate coordinate vectors associated with the volume and Cartesian parameterizations, respectively, which define the stress-free reference configuration and allow for describing a general curved geometry. In the straight (un-deformed) configuration, the element position field is $\mathbf{x}=\mathbf{Se}_s =\mathbf{STp}_s$, where $\mathbf{e}_s$ and $\mathbf{p}_s$ are nodal coordinate vectors associated with the volume and Cartesian parameterization, respectively, that define the geometry of the element in the straight (un-deformed) configuration. One can then write $\mathbf{J}=\left( {{\partial \mathbf{r}}/{\partial \mathbf{r}_0 }} \right) =\left( {{\partial \mathbf{r}}/{\partial \mathbf{x}}} \right) \left( {{\partial \mathbf{x}}/{\partial \mathbf{r}_0 }} \right) =\left( {{\partial \mathbf{r}}/{\partial \mathbf{x}}} \right) \left( {{\partial \mathbf{r}_0 }/{\partial \mathbf{x}}} \right) ^{-1}=\mathbf{J}_e \mathbf{J}_0^{-1}$, where $\mathbf{J}$ is the matrix of position vector gradients, and $\mathbf{J}_e ={\partial \mathbf{r}}/{\partial \mathbf{x}}$ and $\mathbf{J}_0 ={\partial \mathbf{r}_0 }/{\partial \mathbf{x}}$, as shown in Fig. 7, are matrices of position vector gradients defined using the straight configuration coordinate lines. A simple example can be used to show that all the ANCF triangular plate elements developed in this investigation are isoparametric. In order to demonstrate the isoparameteric property, consider the straight (un-deformed) configuration of the ANCF/FNMC element shown in Fig. 7. The vectors of nodal coordinates can be expressed as $\mathbf{p}_s =\left[ {{\begin{array}{cccc} {\left( {\mathbf{p}_s^1 } \right) ^{T}}&{} {\left( {\mathbf{p}_s^2 } \right) ^{T}}&{} {\left( {\mathbf{p}_s^3 } \right) ^{T}}&{} {\left( {\mathbf{p}_s^4 } \right) ^{T}} \\ \end{array} }} \right] ^{T}$, where

$$\begin{aligned} \left. \begin{array}{ll} \mathbf{p}_s^1 &{}=\left[ {{\begin{array}{*{20}c} {x_1 }&{} {y_1 }&{} {z_1 }&{} 1&{} 0&{} 0&{} 0&{} 1&{} 0&{} 0&{} 0&{} 1 \\ \end{array} }} \right] ^{T} \\ \mathbf{p}_s^2 &{}=\left[ {{\begin{array}{*{20}c} {x_2 }&{} {y_2 }&{} {z_2 }&{} 1&{} 0&{} 0&{} 0&{} 1&{} 0&{} 0&{} 0&{} 1 \\ \end{array} }} \right] ^{T} \\ \mathbf{p}_s^3 &{}=\left[ {{\begin{array}{*{20}c} {x_3 }&{} {y_3 }&{} {z_3 }&{} 1&{} 0&{} 0&{} 0&{} 1&{} 0&{} 0&{} 0&{} 1 \\ \end{array} }} \right] ^{T} \\ \mathbf{p}_s^4 &{}=\left[ {{\left( {x_1 +x_2 +x_3 } \right) }/3}\, {{\left( {y_1 +y_2 +y_3 } \right) }/3}\right. \\ &{}\left. {{\left( {z_1 +z_2 +z_3 } \right) }/3} \right] ^{T} \end{array}\right\} \end{aligned}$$

(39)

The coordinates $x_k , y_k$, and $z_k$ are the Cartesian coordinates of the vertex k of the element. Using the relation $\xi +\eta +\zeta =1$, the ANCF/FNMC shape functions, and the expression of the transformation matrix $\mathbf{T}$, one can show that

$$\begin{aligned} \mathbf{x}=\mathbf{STp}_s =\left[ {{\begin{array}{*{20}c} {\xi x_1 +\eta x_2 +\zeta x_3 +\chi w_1 } \\ {\xi y_1 +\eta y_2 +\zeta y_3 +\chi w_2 } \\ {\xi z_1 +\eta z_2 +\zeta z_3 +\chi w_3 } \\ \end{array} }} \right] \end{aligned}$$

(40)

In this equation, $w_1 , w_2$, and $w_3$ are the Cartesian coordinates of the triangular plate director vector associated with the element straight (un-deformed) configuration. Equation 40 shows that the element straight (un-deformed) configuration can be represented by the ANCF/FNMC element shape functions using an appropriate set of nodal coordinates. Similar procedures can be used to demonstrate the isoparametric property of the ANCF/TN1 and ANCF/TN2 elements.

Table 1 Examples of complex geometry obtained using the ANCF triangular plate elements

7.2 Shell geometry

In the conventional FE literature, there is a clear distinction between the assumed displacement fields of plates and shells. The main reason for making this distinction is attributed to the fact that most conventional plate and shell elements employ infinitesimal rotations as nodal coordinates. Because of the use of infinitesimal rotations, these plate and shell elements are not isoparametric elements, and as a consequence, their displacement fields cannot be used to describe arbitrary initial curved geometry. Furthermore, because of the use of infinitesimal rotations, the element displacement fields cannot be related to the more accurate computational geometry B-spline and NURBS representations using a linear mapping. Special techniques are often used in the conventional FE literature to develop shell elements [1, 58, 62]. Because the governing partial differential equations of plate and shell bending involve fourth-order derivative with respect to the spatial coordinates, the use of cubic polynomials is important in order to be able to correctly capture the effect of curvature changes within the element. The use of lower-order conventional isoparametric elements which do not ensure the continuity of the rotation field at the nodal points may require the use of a very large number of elements to capture accurately the bending deformations. Nonetheless, even with the use of a very fine mesh, the rotations, stresses, and curvatures remain discontinuous at the nodal points. Another serious limitation of the conventional plate and shell elements is the restriction imposed on the definition of the elastic forces. For the conventional elements, the elastic forces cannot be easily formulated using a general continuum mechanics approach or general material models, and therefore, specialized theories with simplifying assumptions are often used [19, 20, 75].

For the ANCF elements proposed in this investigation, there is no distinction between the assumed displacement fields of plates and shells. By simply changing the values of the nodal coordinates in the reference configuration, initially curved and stress-free shell structures with complex shapes can be obtained. The shell reference configuration can simply be defined by the ANCF displacement field as $\mathbf{X}_s =\mathbf{r}_0 =\mathbf{S}\left( \mathbf{x} \right) \mathbf{e}_0$, where $\mathbf{e}_0$ is the vector of nodal coordinates in the reference configuration. By using the definition $\mathbf{J}=\mathbf{J}_e \mathbf{J}_0^{-1}$, as discussed in the preceding section, a stress-free initially curved configurations can be systematically achieved. Table 1 shows examples of some of the shell geometry that can be obtained with one ANCF triangular plate element. Other complex shell geometries can be created by simply changing the orientation and magnitude of the position vector gradients. Furthermore, the proposed ANCF triangular plate element assumed displacement fields are related to the B-spline and NURBS representations using a linear mapping, and therefore, they can be effectively used in the successful integration of computer-aided design and analysis (I-CAD-A). Furthermore, the generalized ANCF triangular plate element stress forces can be formulated using a general continuum mechanics approach and general material models.

8 Element equations of motion

In this section, the D’Alembert-Lagrange principle is used to develop the FE equations of motion which are based on a total Lagrangian description and allow using non-incremental solution procedure [76]. While the ANCF/FNMC element is used as an example, the same procedure can be used with the ANCF/TN1 and ANCF/TN2 elements.

8.1 Element kinematics

Using the FNMC position field, $\mathbf{r}=\mathbf{Se}=\mathbf{STp}$, one can write $\delta \mathbf{e}=\mathbf{T}\delta \mathbf{p}=\mathbf{ST}\delta \mathbf{p}$. The virtual change in the FNMC Cartesian gradients can be written as

$$\begin{aligned} \left. \begin{array}{ll} \delta \mathbf{r}_x &{}=\frac{1}{V}\left( {L_{1,1} \delta \mathbf{r}_\xi +L_{2,1} \delta \mathbf{r}_\eta +L_{3,1} \delta \mathbf{r}_\zeta +L_{4,1} \delta \mathbf{r}_\chi } \right) \\ &{}=\frac{1}{V}\left( {L_{1,1} \mathbf{S}_\xi +L_{2,1} \mathbf{S}_\eta +L_{3,1} \mathbf{S}_\zeta +L_{4,1} \mathbf{S}_\chi } \right) \mathbf{T}\delta \mathbf{p} \\ \delta \mathbf{r}_y &{}=\frac{1}{V}\left( {L_{1,2} \delta \mathbf{r}_\xi +L_{2,2} \delta \mathbf{r}_\eta +L_{3,2} \delta \mathbf{r}_\zeta +L_{4,2} \delta \mathbf{r}_\chi } \right) \\ &{}=\frac{1}{V}\left( {L_{1,2} \mathbf{S}_\xi +L_{2,2} \mathbf{S}_\eta +L_{3,2} \mathbf{S}_\zeta +L_{4,2} \mathbf{S}_\chi } \right) \mathbf{T}\delta \mathbf{p} \\ \delta \mathbf{r}_z &{}=\frac{1}{V}\left( {L_{1,3} \delta \mathbf{r}_\xi +L_{2,3} \delta \mathbf{r}_\eta +L_{3,3} \delta \mathbf{r}_\zeta +L_{4,3} \delta \mathbf{r}_\chi } \right) \\ &{}=\frac{1}{V}\left( {L_{1,3} \mathbf{S}_\xi +L_{2,3} \mathbf{S}_\eta +L_{3,3} \mathbf{S}_\zeta +L_{4,3} \mathbf{S}_\chi } \right) \mathbf{T}\delta \mathbf{p}\\ \end{array}\right\} \end{aligned}$$

(41)

or equivalently $\delta \mathbf{r}_x =\mathbf{S}_x \mathbf{T}\delta \mathbf{p}, \delta \mathbf{r}_y =\mathbf{S}_y \mathbf{T}\delta \mathbf{p}$, and $\delta \mathbf{r}_z =\mathbf{S}_z \mathbf{T}\delta \mathbf{p}$, where:

$$\begin{aligned} \left. \begin{array}{ll} \mathbf{S}_x &{}=\frac{1}{V}\left( {L_{1,1} \mathbf{S}_\xi +L_{2,1} \mathbf{S}_\eta +L_{3,1} \mathbf{S}_\zeta +L_{4,1} \mathbf{S}_\chi } \right) \\ \mathbf{S}_y &{}=\frac{1}{V}\left( {L_{1,2} \mathbf{S}_\xi +L_{2,2} \mathbf{S}_\eta +L_{3,2} \mathbf{S}_\zeta +L_{4,2} \mathbf{S}_\chi } \right) \\ \mathbf{S}_z &{}=\frac{1}{V}\left( {L_{1,3} \mathbf{S}_\xi +L_{2,3} \mathbf{S}_\eta +L_{3,3} \mathbf{S}_\zeta +L_{4,3} \mathbf{S}_\chi } \right) \\ \end{array}\right\} \end{aligned}$$

(42)

where $\mathbf{S}_x , \mathbf{S}_y$, and $\mathbf{S}_z$ are, respectively, the spatial derivatives of the matrix of shape functions with respect to the Cartesian coordinates x, y, and z. The evaluation of the Cartesian derivatives $\mathbf{S}_x , \mathbf{S}_y$, and $\mathbf{S}_z$ is necessary for the formulation of the element elastic forces.

8.2 Element mass matrix

The virtual work of the FNMC element inertia forces is defined as $\delta W_i =-\int _V {\rho \ddot{\mathbf{r}}^{T}\delta \mathbf{r}\left| {\mathbf{J}_0 } \right| \hbox {d}V}$, where $\rho$ is the element mass density defined in the stress-free reference configuration, $\ddot{\mathbf{r}}$ is the absolute acceleration vector of an arbitrary element material point, $\left| {\mathbf{J}_0 } \right|$ is the determinant of the gradient matrix defined in the stress-free reference configuration, and V is the volume in the straight (un-deformed) configuration. By using the FNMC kinematic equations, one can write:

$$\begin{aligned} \delta W_i= & {} -\int _V {\rho \ddot{\mathbf{r}}^{T}\delta \mathbf{r}\left| {\mathbf{J}_0 } \right| \hbox {d}V} \nonumber \\= & {} -\,\ddot{\mathbf{p}}^{T}\mathbf{T}^{T}\left( {\int _V {\rho \mathbf{S}^{T}{} \mathbf{S}\left| {\mathbf{J}_0 } \right| \hbox {d}V} } \right) \mathbf{T}\delta \mathbf{p}\nonumber \\= & {} -\left( {\mathbf{M}\ddot{\mathbf{p}}} \right) ^{T}\delta \mathbf{p} \end{aligned}$$

(43)

where the element mass matrix $\mathbf{M}=\mathbf{T}^{T}\left( \int _V \rho \mathbf{S}^{T}{} \mathbf{S}\left| \mathbf{J}_0 \right| \hbox {d}V \right) \mathbf{T}$ is a constant, symmetric, and positive definite matrix, and consequently, the centrifugal and Coriolis inertia forces are identically zero. The definition of the element mass matrix associated with the Cartesian coordinate vector allows for performing a standard FE assembly to obtain the mesh mass matrix.

8.3 Element external forces

One can write the virtual work of the external forces as $\delta W_e =\int _V {\mathbf{f}_e^T \delta \mathbf{r}\left| {\mathbf{J}_0 } \right| \hbox {d}V}$, where $\mathbf{f}_e$ is a vector of body forces such as the gravity and magnetic forces. Using the FNMC kinematic equations, the virtual work of the external forces can be rewritten as

$$\begin{aligned} \delta W_e= & {} \int _V {\mathbf{f}_e^T \delta \mathbf{r}\left| {\mathbf{J}_0 } \right| \hbox {d}V} \nonumber \\= & {} \left( {\int _V {\mathbf{f}_e^T \mathbf{S}\left| {\mathbf{J}_0 } \right| \hbox {d}V} } \right) \mathbf{T}\delta \mathbf{p}\nonumber \\= & {} \mathbf{Q}_e^T \delta \mathbf{p} \end{aligned}$$

(44)

where $\mathbf{Q}_e =\mathbf{T}^{T}\left( {\int _V {\mathbf{S}^{T}{} \mathbf{f}_e \left| {\mathbf{J}_0 } \right| \hbox {d}V} } \right)$ defines the vector of generalized external forces associated with the element generalized nodal coordinates. The use of the Cartesian gradients in the coordinate vector $\mathbf{p}$ allows for a standard FE generalized force assembly.

8.4 Element elastic forces

Using a general continuum mechanics approach, one can write the virtual work of the element elastic forces as $\delta W_s =-\int _V {\varvec{\upsigma }:\delta \varvec{\upvarepsilon }\left| {\mathbf{J}_0 } \right| \hbox {d}V}$, where $\varvec{\upsigma }$ denotes the symmetric second Piola–Kirchhoff stress tensor, $\varvec{\upvarepsilon }$ represents the symmetric Green-Lagrange strain tensor, and the symbol  :  defines tensor double contraction. All the elements proposed in this investigation allow using general constitutive models in the elastic force formulation. Using the FNMC kinematics, one can write the virtual work of the elastic forces as

$$\begin{aligned} \delta W_s= & {} -\int _V {\varvec{\upsigma }:\delta \varvec{\upvarepsilon }\left| {\mathbf{J}_0 } \right| \hbox {d}V} \nonumber \\= & {} -\left( {\int _V {\varvec{\upsigma }:\frac{\partial \varvec{\upvarepsilon }}{\partial \mathbf{e}}\left| {\mathbf{J}_0 } \right| \hbox {d}V} } \right) \mathbf{T}\delta \mathbf{p}=\mathbf{Q}_s^T \delta \mathbf{p} \end{aligned}$$

(45)

where $\mathbf{Q}_s =-\mathbf{T}^{T}\left( {\int _V {\left( {\varvec{\upsigma }:\frac{\partial \varvec{\upvarepsilon }}{\partial \mathbf{e}}} \right) ^{T}\left| {\mathbf{J}_0 } \right| \hbox {d}V} } \right)$ is the nonlinear vector of the element generalized elastic forces which can be evaluated using Gauss quadrature rules. A standard FE assembly procedure can be adopted to define the body elastic forces because of the use of Cartesian gradients in $\mathbf{p}$.

Fig. 8

Location of the Gauss integration points

8.5 System equations of motion

The system equations of motion of the ANCF/FNMC element mesh can be developed using the principle of virtual work which can be stated as $\delta W_i\, +\,\delta W_e\, +\,\delta W_s =0$, where $\delta W_i$ is the virtual work of the element inertia forces, $\delta W_e$ is the virtual work of the element external forces, and $\delta W_s$ is the virtual work of the element elastic forces. Applying this principle, the element equations of motion can be written as $\mathbf{M}\ddot{\mathbf{p}}=\mathbf{Q}_e +\mathbf{Q}_s$. As mentioned previously, the use of the Cartesian gradients $\mathbf{r}_x , \mathbf{r}_y$, and $\mathbf{r}_z$ in the generalized coordinate vector $\mathbf{p}$ allows for standard FE assembly of the element vectors and matrices.

9 Numerical results and discussion

In this section, several FE models are developed in order to demonstrate the use and evaluate the performance of the proposed FNMC, TN1, and TN2 elements. The numerical results obtained using these elements are compared with the results of the conventional three-node linear (TNL) and six-node quadratic (SNQ) triangular plate elements [77]. The shape functions of the conventional TNL and SNQ elements are presented in the Appendix of the paper. While these conventional elements ensure only the continuity of the position field at the nodes, the proposed ANCF elements guarantee the continuity of both the position and gradient fields, and therefore, the continuity of the rotation, strain, and stress fields is also ensured. The conventional TNL and SNQ elements are implemented using a total Lagrangian approach and the results are obtained using a non-incremental solution procedure [78, 79]. Additionally, the numerical results obtained using the proposed ANCF triangular plate elements are compared with the numerical results of the ANCF fully parameterized rectangular plate element developed by Mikkola and Shabana [34] and implemented in the general purpose MBS computer program SIGMA/SAMS (Systematic Integration of Geometric Modeling and Analysis for the Simulation of Articulated Mechanical Systems). It is important, however, to point out that because of the low-order of polynomial interpolation of the conventional elements, the curvature within these elements is either constant or identically zero, and therefore, these conventional elements are not suitable for describing large deformations and extreme bending scenarios.

Table 2 Volume coordinates and weights of the Gauss quadrature nodes

In this investigation, a MATLAB computer program was developed in order to obtain the numerical results presented in this section for the conventional and proposed ANCF elements. In order to correctly capture geometric nonlinearities, a general continuum mechanics approach is employed for evaluating the generalized elastic forces. The Saint Venant–Kirchhoff hyper-elastic constitutive law and a standard Gauss quadrature procedure based on a full integration scheme are used for the evaluation of the generalized elastic forces [58]. For the ANCF elements developed in this investigation, full integration requires combination of 12 triangular Gauss integration points distributed along the plate mid-surface; this corresponds to the standard sixth-order Gauss integration quadrature scheme for triangular elements, with 2 linear Gauss integration points along the thickness, which corresponds to the standard third-order Gauss integration quadrature scheme for linear elements. The choice of the type and number of integration points was made based on numerical experimentation. It was found that using a larger number of quadrature points does not improve the accuracy of the numerical results, whereas using a smaller number of integration points can lead to less accurate results. The locations of the Gauss integration points used for performing the numerical integration of the proposed ANCF fully parameterized triangular plate elements are shown in Fig. 8, while the corresponding quadrature nodes and weights are presented in Table 2. The numerical integration of the equations of motion is performed using the explicit multistep fourth-order Adams–Bashforth numerical integration method with a constant time step [80].

9.1 Rigid-body motion

Fig. 9

Plate pendulum

Fig. 10

Triangular plate mesh for the stiff pendulum

Fig. 11

Triangular plate asymmetric rectangular macro-element

Fig. 12

Vertical displacement of the rigid pendulum tip (

TNL element,

SNQ element,

TN1 element,

TN2 element,

FNMC element,

rigid-body)

The stiff rectangular pendulum example shown in Fig. 9 is used to demonstrate that both the conventional and the proposed ANCF elements can correctly describe rigid-body motion. The rectangular pendulum is subjected to a constant gravitational force field and is assumed to be initially in a horizontal configuration. The pendulum has length $L=0.1\;\hbox {m}$, width $H=0.1\;\hbox {m}$, thickness $W=0.01\;\hbox {m}$, mass density $\rho =7860\;{\hbox {kg}}/{\hbox {m}^{\mathrm {3}}}$, Poisson ratio $\nu =0.27$, and Young’s modulus $E=2.1\times 10^{9}\;\hbox {N}/{\hbox {m}^{\mathrm {2}}}$. The gravity acceleration considered is $g=9.81\;\hbox {m}/{\hbox {s}^{\mathrm {2}}}$. Based on the assumed inertia and geometry properties, the pendulum has a mass $m=0.786\;\hbox {kg}$ and principal mass moments of inertia $I_{xx} =\hbox {6.6155}\times 10^{-4}\;\hbox {kg}\;\hbox {m}^{\mathrm {2}}, I_{yy} =\hbox {6.6155}\times 10^{-4}\;\hbox {kg}\;\hbox {m}^{\mathrm {2}}$, and $I_{zz} =\hbox {1.3}\times 10^{-3}\;\hbox {kg}\;\hbox {m}^{\mathrm {2}}$. In order to compare the results of this numerical example with the results obtained using a rigid-body pendulum model, a large elastic modulus is used for the flexible pendulum models. Figure 10 shows the FE mesh used for modeling the stiff pendulum system. Only one rectangular macro-element, shown in Fig. 11, which consists of two triangular plate elements, is used. As shown in Fig. 10, two revolute joints located at the points $A_1$ and $A_2$ are used to constrain the flexible pendulum motion with respect to the ground. On the other hand, a revolute joint having a joint axis passing through the two points $A_1$ and $A_2$ is used to constrain the motion of the rigid pendulum. The constraint equations for the flexible pendulum are linear algebraic equations, and therefore, are systematically eliminated at a preprocessing stage. In addition to the proposed FNMC, TN1, and TN2 element models, two other models based on the conventional TNL and SNQ elements are developed. The duration of the dynamic simulation is assumed $T=1.0\;\hbox {s}$, while the minimum time step used in the numerical integration algorithm is $\Delta t=5.0\times 10^{-6}\;\hbox {s}$. The vertical displacement of the plate pendulum tip point B obtained using the stiff flexible and rigid-body models is shown in Fig. 12. The results presented in this figure show a good agreement, demonstrating that the ANCF elements developed in this investigation can correctly describe rigid-body motion.

9.2 Patch test

In order to perform the patch test [58, 62], the rectangular plate shown in Fig. 13 with a mesh of 10 triangular plate elements, shown in Fig. 14, is used. The model geometric and material properties are the same as previously presented in this section and the nodal coordinates considered are shown in Table 3. In order to eliminate all the rigid-body modes, a minimum set of displacement and gradient boundary conditions are used for constraining the rectangular plate to the ground at the points $A_1$ and $A_2$. A modal analysis was performed in order to obtain the natural frequencies, and no zero spurious eigenvalues were found. Therefore, the states of constant strain can be correctly captured by all the triangular plate elements considered in this investigation. This simple example demonstrates that the ANCF elements developed in this paper pass the patch test, are compatible elements, and converge when the number of elements is properly increased [61].

Fig. 13

Rectangular plate

Fig. 14

Plate mesh for the patch test

Table 3 Node Cartesian coordinates of the patch test mesh

Fig. 15

Plate mesh for the flexible pendulum

Fig. 16

Symmetric rectangualr macro-element

Table 4 TNL triangular plate element convergence analysis

Table 5 SNQ triangular plate element convergence analysis

9.3 Convergence analysis

In order to check the element convergence in the case of finite rotations and large displacements, the initially straight flexible rectangular pendulum shown in Fig. 9 is considered. The pendulum length, width, thickness, and modulus of elasticity considered in this numerical example are $L=1.0\;\hbox {m}, H=1.0\;\hbox {m}, W=0.1\;\hbox {m}$, and $E=2.1\times 10^{6}\;\hbox {N}/{\hbox {m}^{\mathrm {2}}}$, respectively, while the other model data are the same as previously used. The numerical simulation is performed using a time interval and a minimum time step size $T=1.0\;\hbox {s}$ and $\Delta t=5.0\times 10^{-5}\;\hbox {s}$, respectively. Figures 15 and 16 show, respectively, the FE mesh and the rectangular macro-element used. The TNL, SNQ, TN1, TN2, and FNMC element models are developed using a symmetric mesh made of rectangular macro-elements. The total number of triangular plate elements that form each mesh is $N_e =8N_m^2$, where $N_m$ is the number of macro-elements, each of which is constructed from 8 triangular plate elements. Because the convergence rate is not the same for the five types of triangular plate elements considered, different numbers of elements are used to obtain convergent solutions for different plate models. It was found that the displacement and strain convergence requires a 16 macro-element ($N_e =8\times 16^{2}=2048)$ for the TNL element; a 14 macro-element ($N_e =8\times 14^{2}=1568)$ for the SNQ element; a 14 macro-element mesh ($N_e =8\times 14^{2}=1568)$ for the TN1 element; a 14 macro-element mesh ($N_e =8\times 14^{2}=1568)$ for the TN2 element; and a 12 macro-element mesh ($N_e =8\times 12^{2}=1152)$ for the FNMC element. However, in the case of the conventional TNL and SNQ models, finer meshes cannot achieve geometric convergence because of the gradient discontinuities at the element interface nodes that lead to rotation, strain, and stress discontinuities. In order to perform a comparative convergence rate study of the elements considered in this investigation, the root-mean-square errors of the numerical results are evaluated considering a set of reference solutions and the resulting normalized values are reported in Tables 4, 5, 6, 7, and 8. The normalized root-mean-square errors of the numerical results are computed for the complete simulation interval considering the displacements and the normal strains $\varepsilon _{xx} , \varepsilon _{yy}$, and $\varepsilon _{zz}$. The reference solution corresponds to the 16 macro-element mesh for the TNL element; 14 macro-element mesh for the SNQ element; 14 macro-element mesh for the TN1 element; 14 macro-element mesh for the TN2 element; and 12 macro-element mesh for the FNMC element. As expected, for all elements considered, the normalized root-mean-square errors decrease as the number of elements increases. The TNL element has the slowest convergence rate, while the TN1 and TN2 elements have a convergence rate comparable with the convergence rate of the SNQ element. The FNMC element, on the other hand, has the fastest convergence rate. The difference in the convergence rates can be attributed to the fact that the TN1 and TN2 elements are based on an incomplete set of cubic polynomials, whereas the shape functions of the FNMC element are obtained from a complete set of cubic polynomial basis functions.

Table 6 TN1 triangular plate element convergence analysis

Table 7 TN2 triangular plate element convergence analysis

Table 8 FNMC triangular plate element convergence analysis

Fig. 17

Vertical displacement of the flexible pendulum tip (

ANCF element,

TNL element,

SNQ element)

Fig. 18

Normal strain $\varepsilon _{xx}$ at the flexible pendulum center (

ANCF element,

TNL element,

SNQ element)

Fig. 19

Normal strain $\varepsilon _{yy}$ at the flexible pendulum center (

ANCF element,

TNL element,

SNQ element)

Fig. 20

Normal strain $\varepsilon _{zz}$ at the flexible pendulum center (

ANCF element,

TNL element,

SNQ element)

Fig. 21

Vertical displacement of the flexible pendulum tip (

ANCF element,

TN1 element,

TN2 element,

FNMC element)

Fig. 22

Normal strain $\varepsilon _{xx}$ at the flexible pendulum center (

ANCF element,

TN1 element,

TN2 element,

FNMC element)

Fig. 23

Normal strain $\varepsilon _{yy}$ at the flexible pendulum center (

ANCF element,

TN1 element,

TN2 element,

FNMC element)

Fig. 24

Normal strain $\varepsilon _{zz}$ at the flexible pendulum center (

ANCF element,

TN1 element,

TN2 element,

FNMC element)

The numerical results obtained using the proposed ANCF elements are also compared with the numerical results obtained using the ANCF rectangular plate element developed by Mikkola and Shabana [34]. To this end, a $10\times 10$ mesh, a $12\times 12$ mesh, and a $14\times 14$ mesh made of ANCF rectangular plate elements are developed and it was found that the displacement and strain convergence is achieved for this ANCF element using the $14\times 14$ element model. Figures 17, 18, 19, and 20 show, respectively, the vertical displacement of point B on the pendulum under the effect of gravity, and the normal strains $\varepsilon _{xx} , \varepsilon _{yy}$, and $\varepsilon _{zz}$ at the pendulum center point C when convergence is achieved for the TNL and SNQ element models. Because nodal strain continuity is not ensured by the conventional triangular plate elements, averaging techniques were adopted to improve the accuracy of the strain results of these conventional elements. Figures 21, 22, 23, and 24 show, respectively, the point B vertical displacement under the effect of gravity, and the normal strains $\varepsilon _{xx} , \varepsilon _{yy}$, and $\varepsilon _{zz}$ at the pendulum center point C when convergence is achieved for the ANCF rectangular plate, TN1, TN2, and FNMC element models. Since the ANCF triangular plate elements guarantee the continuity of the rotation, strain, and stress fields at the nodes, there is no need for using strain averaging techniques. The numerical results presented in this section demonstrate that there is, in general, a good agreement between the numerical solutions obtained using different triangular plate element models. However, the strain results obtained using the TNL and SNQ element models show slightly different trends because such elements do not guarantee the continuity of the rotation, strain, and stress fields at the nodal points.

9.4 Continuity conditions

In order to demonstrate the gradient and strain continuity that characterize ANCF elements, the flexible straight rectangular pendulum shown in Fig. 25 is modeled using a mesh of one macro-element composed of eight FNMC triangular plate elements. The dynamic simulation is carried out using the geometric and material properties previously used. Figures 26, 27, and 28 show the normal strains $\varepsilon _{xx} , \varepsilon _{yy}$, and $\varepsilon _{zz}$ at the pendulum center point C, while Figs. 29, 30, and 31 show the normal stresses $\sigma _{xx} , \sigma _{yy}$, and $\sigma _{zz}$ at the same point C predicted using the coordinates of all the eight FNMC elements of the rectangular macro-element. The numerical results presented in Figs. 26, 27, 28, 29, 30, and 31 clearly demonstrate the continuity of the normal strains and stresses; similar continuity results are obtained for the shear strains and stresses. The proposed TN1 and TN2 elements also ensure the gradient, strain, and stress continuity at the nodes.

9.5 Quasi-periodic motion

In order to demonstrate that the proposed ANCF elements can capture the quasi-periodic motion that characterizes the dynamic simulation of the flexible pendulum system, the straight rectangular pendulum shown in Fig. 9 is modeled using a mesh of one macro-element composed of eight FNMC triangular plate elements. The dynamic simulation is carried out using the geometric and material properties used previously except for the elasticity modulus and the time interval which are assumed to be $E=2.1\times 10^{7}\;\hbox {N}/{\hbox {m}^{\mathrm {2}}}$ and $T=10.0\;\hbox {s}$. Figure 32 shows the vertical displacement of point B under the effect of gravity. Figures 33, 34, and 35 show the normal strains $\varepsilon _{xx} , \varepsilon _{yy}$, and $\varepsilon _{zz}$, respectively, at the pendulum center point C. These figures clearly show that the flexible pendulum meshed using the proposed FNMC element exhibits the expected quasi-periodic motion. The proposed TN1 and TN2 elements also show a similar dynamic response.

Fig. 25

Flexible pendulum $2\times 2$ mesh

Fig. 26

Normal strain $\varepsilon _{xx}$ at the flexible pendulum center using an FNMC $2\times 2$ mesh (

element 1,

element 2,

element 3,

element 4,

element 5,

element 6,

element 7,

element 8)

Fig. 27

Normal strain $\varepsilon _{yy}$ at the flexible pendulum center using an FNMC $2\times 2$ mesh (

element 1,

element 2,

element 3,

element 4,

element 5,

element 6,

element 7,

element 8)

Fig. 28

Normal strain $\varepsilon _{zz}$ at the flexible pendulum center using an FNMC $2\times 2$ mesh (

element 1,

element 2,

element 3,

element 4,

element 5,

element 6,

element 7,

element 8)

Fig. 29

Normal stress $\sigma _{xx}$ at the flexible pendulum center using an FNMC $2\times 2$ mesh (

element 1,

element 2,

element 3,

element 4,

element 5,

element 6,

element 7,

element 8)

Fig. 30

Normal stress $\sigma _{yy}$ at the flexible pendulum center using an FNMC $2\times 2$ mesh (

element 1,

element 2,

element 3,

element 4,

element 5,

element 6,

element 7,

element 8)

Fig. 31

Normal stress $\sigma _{zz}$ at the flexible pendulum center using an FNMC $2\times 2$ mesh (

element 1,

element 2,

element 3,

element 4,

element 5,

element 6,

element 7,

element 8)

Fig. 32

Vertical displacement of the flexible pendulum tip (FNMC element)

Fig. 33

Normal strain $\varepsilon _{xx}$ at the flexible pendulum center (FNMC element)

Fig. 34

Normal strain $\varepsilon _{yy}$ at the flexible pendulum center (FNMC element)

Fig. 35

Normal strain $\varepsilon _{zz}$ at the pendulum center (FNMC element)

10 Summary and conclusions

In the conventional FE literature, distinction is often made between plate and shell elements as the results of using rotations as nodal coordinates. The use of this non-isoparametric element description does not allow for obtaining complex geometric shapes by changing the value of the nodal coordinates. In this investigation, three new ANCF triangular plate/shell elements are developed, namely four-node mixed-coordinate element (FNMC) obtained using a complete cubic polynomial representation, three-node triangular plate element (TN1) obtained from the FNMC element by eliminating the internal node, and three-node element (TN2) obtained by using an incomplete cubic polynomial representation from the outset. A cubic polynomial interpolation and a constant transformation between the ANCF nodal coordinates and the Bezier control points are used to develop the ANCF fully parameterized triangular plate elements developed in this study. All the proposed ANCF elements are isoparametric; describe correctly arbitrary rigid-body motion; lead to constant mass matrix and zero Coriolis and centrifugal forces; allow for consistently representing large finite rotations; ensure continuity of the gradients, rotations, strains, and stresses at the nodal points; and impose no restrictions on the value of the deformation within the finite element. Two coordinate parameterizations are used for describing the kinematics of the proposed elements, namely volume and Cartesian parameterizations. In order to be able to use a standard FE assembly procedure, the volume position vector gradients are first used to develop closed-form and compact element shape function expressions. The numerical results obtained using the proposed elements are compared with the numerical results obtained using the conventional elements (TNL and SNQ) as well as an ANCF fully parameterized rectangular plate element. The results obtained in this study using the proposed elements showed, in general, good convergence characteristics.

Appendix

In this appendix, the shape functions of the TNL and SNQ elements that use extensible directors are presented [77]. Considering a general node k, both the TNL and SNQ elements have the nodal position vector $\mathbf{r}^{k}$ and the slope vector $\mathbf{r}_z^k$ as nodal coordinates. The linear shape functions $s_k ,k=1,2,\ldots ,6$, of the conventional TNL element can be explicitly written in terms of the set of volume coordinates $\xi , \eta , \zeta$, and $\chi$ as follows:

$$\begin{aligned} \left. \begin{array}{ll} s_1 &{}=\xi ,\quad s_2 =\frac{W}{2}\xi \chi ,\quad s_3 =\eta ,\quad s_4 =\frac{W}{2}\eta \chi ,\\ s_5 &{}=\zeta ,\quad s_6 =\frac{W}{2}\zeta \chi \end{array}\right\} \end{aligned}$$

(A.1)

where W is the TNL element thickness. The pairs of shape functions $s_i$ and $s_j , i=1,3,5, j=2,4,6$, are, respectively, associated with the TNL nodal positions and slopes of the corner nodes $k, k=1,2,3$.

The quadratic shape functions $s_k ,k=1,2,\ldots ,12$, of the SNQ element can be written in terms of the set of volume coordinates $\xi , \eta , \zeta$, and $\chi$ as

$$\begin{aligned} \left. \begin{array}{ll} s_1 &{}=\xi \left( {\xi -\left( {\eta +\zeta } \right) } \right) ,\quad s_2 =\frac{W}{2}\xi \chi \left( {1-2\left( {\eta +\zeta } \right) } \right) ,\\ s_3 &{}=\eta \left( {\eta -\left( {\zeta +\xi } \right) } \right) , \\ s_4 &{}=\frac{W}{2}\eta \chi \left( {1-2\left( {\zeta +\xi } \right) } \right) ,\\ s_5 &{}=\zeta \left( {\zeta -\left( {\xi +\eta } \right) } \right) ,\quad s_6 =\frac{W}{2}\zeta \chi \left( {1-2\left( {\xi +\eta } \right) } \right) , \\ s_7 &{}=4\xi \eta ,\quad s_8 =2W\xi \eta \chi ,\\ s_9 &{}=4\eta \zeta ,\quad s_{10} =2W\eta \zeta \chi ,\\ s_{11} &{}=4\zeta \xi ,\quad s_{12} =2W\zeta \xi \chi \end{array}\right\} \end{aligned}$$

(A.2)

where W is the SNQ element thickness. While the pairs of shape functions $s_i$ and $s_j , i=1,3,5, j=2,4,6$, are, respectively, associated with the SNQ nodal positions and slopes of the corner node $k, k=1,2,3$, the pairs of shape functions $s_i$ and $s_j , i=7,9,11, j=8,10,12$, are, respectively, associated with the nodal positions and slopes of the middle node $k, k=4,5,6$, on the sides of the element.