1 Introduction

In recent years, triaxial gyroscope based on micro electro mechanical systems (MEMS) technology has been receiving increasing attention in automotive navigation, the attitude measuring of satellite and control stabilization due to its compact size, cheapness and much more energy efficient devices than conventional macro-sized devices [1–5]. However, in practical applications, the performance of the MEMS gyroscope can be affected or degraded by electromagnetic interference, time-varying parameters and mechanical coupling terms between the axes. And input-signal (current/voltage) of gyroscope systems is frequently subject to nonlinearity as a result of physical limitations. It has been shown that input nonlinearity, including saturation and dead-zone, can cause a serious degradation of the system performance, a reduced rate of response, system failure if the design of controller does not consider input nonlinearity in practical applications. Therefore, the MEMS gyroscope system should be capable and reliable enough to withstand such undesirable conditions and operate in an acceptable manner even in the presence of disturbances, time-varying parameters, and input nonlinearity.

Recently, various control strategies have been proposed. In [6], a novel single-mass adaptively controlled triaxial angular rate sensor has been presented. In [7], a new adaptive force-balancing control with a trajectory-switching algorithm is proposed to drive both axes of vibration and controls the entire operation of the gyroscope. Fei and Zhou [8] present a robust adaptive control strategy with a fuzzy compensator for the tracking control of MEMS triaxial gyroscope. Antonello et al. [9] introduced extremum-seeking control to automatically match the vibration mode in MEMS vibrating gyroscopes. A new control method is presented [10] to drive the drive axis of a MEMS gyroscope to resonance and to regulate the output amplitude of the axis to a fixed level. These results provide a basic tool for stabilization of MEMS triaxial gyroscope. In [11], a dynamical model of MEMS vibratory gyroscope with unknown dead-zone is analyzed, and an adaptive fuzzy control of dead-zone compensation strategy is proposed. Different form the referenced literature [11], in this paper, the input nonlinearity includes both input saturation and unknown dead-zone. Hence, the effectiveness design of the control input signal with saturation and dead-zone is becoming a very challenging task. And the proposed control algorithm based on adaptive dynamic surface control strategy is used to eliminate the effect of input nonlinearity and fuzzy approximation error.

The backstepping control has been an important tool for nonlinear system analysis and control owing to the recursive and systematic controller design procedure for strict-feedback systems. A number of applications of backstepping method have been addressed over the past few decades. Although backstepping method can be applied to a wide range of nonlinear systems, however, the conventional backstepping method suffers from the problem of explosion of complexity. To solve this problem, the dynamic surface control strategy [12–17] was proposed by introducing first-order filter of the synthetic virtual control input at each step of the conventional backstepping. A adaptive robust DSC strategy was proposed in [18], where the model uncertainties can be estimated by a radial basis function neural network. Furthermore, an observer-based adaptive robust controller was developed via DSC techniques to achieve high performance servo mechanisms with unmeasurable states [19].

So far, to the best of authors’ knowledge, it is the first time in the literature that the nonlinear input including dead-zone and saturation constraint is considered for the regulating problem of MEMS gyroscope with external disturbance and uncertainty. The study is focused on developing an on-line adaptive control technique to possibly resonance and to regulate the output amplitude of the axis to a fixed level in spite of the existence of uncertainty, external disturbance, and input nonlinearity. We employ a fuzzy logic system to approximate the uncertainty, therefore, it relax the requirement of the exact model. The proposed control scheme can guarantee that the trajectory of tracking-error converges to the small neighborhood of equilibrium point. Finally, numerical simulation results demonstrate the effectiveness of the proposed control scheme (Fig. 1).

Fig. 1
figure 1

Model of MEMS triaxial gyroscope

Full size image

2 System description and preliminaries

2.1 Model of MEMS triaxial gyroscope

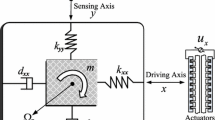
The MEMS triaxial gyroscope is a highly nonlinear and strongly coupled system with multi-input and multi-output. The mathematical model of the triaxial gyroscope system is given by [6].

$$\begin{aligned}&\ddot{x}+\lambda _{xx}\dot{x}+\lambda _{xy}\dot{y}+\lambda _{xz}\dot{z}+k_{xx}x+k_{xy}y+k_{xz}z\nonumber \\&\quad +\,2(\varOmega _y\dot{z}-\varOmega _z\dot{y})=u_1.\end{aligned}$$
(1)
$$\begin{aligned}&\ddot{y}+\lambda _{xy}\dot{x}+\lambda _{yy}\dot{y}+\lambda _{yz}\dot{z}+k_{xy}x+k_{yy}y+k_{yz}z\nonumber \\&\quad +\,2(\varOmega _x\dot{z}-\varOmega _z\dot{y})=u_2.\end{aligned}$$
(2)
$$\begin{aligned}&\ddot{z}+\lambda _{xz}\dot{x}+\lambda _{yz}\dot{y}+\lambda _{zz}\dot{z}+k_{xz}x+k_{yz}y+k_{zz}z\nonumber \\&\quad +\,2(\varOmega _x\dot{z}-\varOmega _y\dot{x})=u_3. \end{aligned}$$
(3)

where the \(\lambda _{xx}\), \(\lambda _{xy}\), \(\lambda _{xz}\), \(\lambda _{yy}\), \(\lambda _{yz}\) and \(\lambda _{zz}\) are damping term; the \(k_{xx}\), \(k_{xy}\), \(k_{xz}\), \(k_{yy}\), \(k_{yz}\) and \(k_{zz}\) are stiffness parameters; \(\varOmega _{x}\), \(\varOmega _{y}\) and \(\varOmega _{z}\) are angular velocities in the \(x-\), \(y-\) and \(z-\) directions, respectively; \(u_{1}\), \(u_{2}\) and \(u_{3}\) are the control signals in the \(x\)-, \(y\)- and \(z\)-directions, respectively;

From the practical point of view, the external disturbances, parameter uncertainty and the system uncertainty always exist in application. The input signal of MEMS gyroscope is usually subject to input nonlinearity as a result of physical limitations. In this literarure, we will consider these problems.

Assumption 1

Control input nonlinearity \(\sigma _{i}(u_{i})\) \((i=1,2,3)\) (such as saturation and dead-zones) and \(u_{i}\) are all constrained by saturation value (\(u_\mathrm{up}>0\) and \(u_\mathrm{down}>0\)) and dead-zone value (unknown right dead-zone \(u_\mathrm{irdz}>0\) and unknown left dead-zone \(u_\mathrm{ildz}<0\)), expressed by

$$\begin{aligned} \bigg \{\begin{array}{lll} \ u_{i}-u_\mathrm{irdz}\leqslant {u_\mathrm{up}},&{}\quad \hbox {for}\quad u_{i}\geqslant {u_\mathrm{irdz}}\\ \ u_{i}-u_\mathrm{ildz}\geqslant {-u_\mathrm{down}},&{}\quad \hbox {for}\quad u_{i}\leqslant {u_\mathrm{ildz}} \end{array} \end{aligned}$$
(4)

and

$$\begin{aligned} \sigma _{i}(u_{i})\!=\! {\left\{ \begin{array}{ll} \ \iota _{i}\cdot (u_{i}-u_\mathrm{irdz}),&{}\!\quad \!\hbox {for}\quad \! u_{i}\geqslant {u_\mathrm{irdz}}\\ \ \iota _{i}\cdot (u_{i}-u_\mathrm{ildz}),&{}\!\quad \!\hbox {for}\!\quad \! u_{i}\leqslant {u_\mathrm{ildz}}\\ \ 0, &{}\!\quad \!\hbox {for}\quad \! u_\mathrm{ildz}<u_{i}<u_\mathrm{irdz} \end{array}\right. } \end{aligned}$$
(5)

where

$$\begin{aligned} \iota _{i}\!=\! {\left\{ \begin{array}{ll} \ \frac{u_\mathrm{up}}{u_{i}-u_\mathrm{irdz}},&{}\quad \hbox {for}\quad u_{i}-u_\mathrm{irdz}\geqslant {u_{up}}\\ \ 1, &{}\quad \hbox {for}\quad u_\mathrm{irdz}\leqslant {u_{i}}\leqslant {u_\mathrm{up}+u_\mathrm{irdz}}\\ \ 1, &{}\quad \hbox {for}\quad \!-u_{down}+u_\mathrm{ildz}\!\leqslant \!{u_{i}}\!\leqslant \!{u_\mathrm{ildz}}\\ \ \frac{-u_\mathrm{down}}{u_{i}-u_\mathrm{ildz}}, &{}\quad \hbox {for}\quad u_{i}-u_\mathrm{ildz}\leqslant {-u_\mathrm{down}}\\ \end{array}\right. } \end{aligned}$$
(6)

Considering control input nonlinearity as shown in Fig. 2. From the Eq. (6), we can easily know that \(0<{\iota _{i}}\leqslant {1}\). According to analysis above, the Eqs. (1)–(3) can be written as

$$\begin{aligned}&\ddot{x}\!+\!(\varDelta \lambda _{xx}\!+\!\lambda _{xx})\dot{x}\!+\!(\varDelta \lambda _{xy}\!+\!\lambda _{xy})\dot{y}\!+\!(\varDelta \lambda _{xz}+\lambda _{xz})\dot{z}\\&\quad +(\varDelta {k_{xx}}+k_{xx})x+(\varDelta {k_{xy}}+k_{xy})y+(\varDelta {k_{xz}}+k_{xz})z\\&\quad +2(\varOmega _y\dot{z}-\varOmega _z\dot{y})+d_1=\sigma _{1}(u_1)\\&\ddot{y}\!+\!(\varDelta \lambda _{xy}\!+\!\lambda _{xy})\dot{x}\!+\!(\varDelta \lambda _{yy}\!+\!\lambda _{yy})\dot{y}\!+\!(\varDelta \lambda _{yz}+\lambda _{yz})\dot{z}\\&\quad +\,(\varDelta {k_{xy}}+k_{xy})x+(\varDelta {k_{yy}}+k_{yy})y+(\varDelta {k_{yz}}+k_{yz})z\\&\quad +2(\varOmega _x\dot{z}-\varOmega _z\dot{y})+d_2=\sigma _{2}(u_2)\\&\ddot{z}\!+\!(\varDelta \lambda _{xz}\!+\!\lambda _{xz})\dot{x}\!+\!(\varDelta \lambda _{yz}\!+\!\lambda _{yz})\dot{y}\!+\!(\varDelta \lambda _{zz}\!+\!\lambda _{zz})\dot{z}\\&\quad +(\varDelta {k_{xz}}+k_{xz})x+(\varDelta {k_{yz}}+k_{yz})y+(\varDelta {k_{zz}}+k_{zz})z\\&\quad +2(\varOmega _x\dot{y}-\varOmega _y\dot{x})+d_3=\sigma _{3}(u_3) \end{aligned}$$

where \(\varDelta \lambda _{xx}\), \(\varDelta \lambda _{xy}\), \(\varDelta \lambda _{xz}\), \(\varDelta \lambda _{yy}\), \(\varDelta \lambda _{yz}\), \(\varDelta \lambda _{zz}\), \(\varDelta {k_{yy}}\) and \(\varDelta {k_{yz}}\) \(\varDelta {k_{xx}}\), \(\varDelta {k_{xy}}\), \(\varDelta {k_{xz}}\),are uncertainty parameters; \(d_{i}\) are external disturbance. Note that the gyroscope control system can be regarded as three individual sub-systems and we can control coordinates independently. Let \(\varpi =[x_1, x_2, x_3, x_4, \) \(x_5, x_6]=[x, \dot{x}, y, \dot{y}, z, \dot{z}]\), then the MEMS gyroscope with uncertainty parameters and external disturbance is described as follows:

$$\begin{aligned} \bigg \{\begin{array}{lll} \ \dot{x}_{2i-1}&{}=x_{2i} \\ \ \dot{x}_{2i}&{}=f_i(\varpi )+\sigma _{i}(u_i)-d_i \end{array} \end{aligned}$$
(7)

where \(i=1,2,3\), and

\(f_1=-(\varDelta \lambda _{xx}+\lambda _{xx})\dot{x}-(\varDelta \lambda _{xy}+\lambda _{xy})\dot{y} -(\varDelta \lambda _{xz}+\lambda _{xz})\dot{z} -(\varDelta {k_{xx}}+k_{xx})x-(\varDelta {k_{xy}}+k_{xy})y-(\varDelta {k_{xz}}+k_{xz})z -2(\varOmega _y\dot{z}-\varOmega _z\dot{y})\),

\(f_2=-(\varDelta \lambda _{xy}+\lambda _{xy})\dot{x}-(\varDelta \lambda _{yy}+\lambda _{yy})\dot{y} -(\varDelta \lambda _{yz}+\lambda _{yz})\dot{z} -(\varDelta {k_{xy}}+k_{xy})x-(\varDelta {k_{yy}}+k_{yy})y-(\varDelta {k_{yz}}+k_{yz})z -2(\varOmega _x\dot{z}-\varOmega _z\dot{y})\),

\(f_3=-(\varDelta \lambda _{xz}+\lambda _{xz})\dot{x}-(\varDelta \lambda _{yz}+\lambda _{yz})\dot{y} -(\varDelta \lambda _{zz}+\lambda _{zz})\dot{z} -(\varDelta {k_{xz}}+k_{xz})x-(\varDelta {k_{yz}}+k_{yz})y-(\varDelta {k_{zz}}+k_{zz})z-2(\varOmega _x\dot{y}-\varOmega _y\dot{x})\) are unknown nonlinear function.

Fig. 2
figure 2

Control input nonlinearity model

Full size image

Without loss of generality, the technical assumptions are made to pose the problem in a tractable manner.

Assumption 2

The desired command signal and their first and second time derivatives are bounded.

Assumption 3

There exist a positive constant \(u_\mathrm{idz}^{*}\) such that the \(\max \{{u_\mathrm{irdz},|u_\mathrm{ildz}|}\}\leqslant {u_\mathrm{idz}^{*}}\).

2.2 Fuzzy logic system

A fuzzy logic system (FLS) consists of four parts: the knowledge base, the fuzzifier, the fuzzy inference engine working on fuzzy rules, and the defuzzifier. The knowledge base for FLS comprised a collection of fuzzy If-then rules of the following form:

$$\begin{aligned} y(x)=\frac{\sum _{i=1}^N\overline{\varPhi _{i}}\Pi _{j=1}^n \mu _{F_{j}^{i}}(x_j)}{\sum _{i=1}^N\Pi _{j=1}^n\mu _{F_{j}^{i}}(x_j)} \end{aligned}$$

where \(x=[x_1, x_2, \ldots , x_n]^{T}\in {R^{n}}\), \(\mu _{F_{j}^{i}}(x_j)\) is the membership of \(F_{j}^{i}\) and \(\overline{\varPhi _{i}}=\max {\mu _{B^{i}}(y)}\). Let

$$\begin{aligned} \xi _{i}(x)=\frac{\Pi _{j=1}^N\mu _{F_{j}^{i}}(x_j)}{\sum _{i=1}^N\Pi _{j=1}^n \mu _{F_{j}^{i}}(x_j)} \end{aligned}$$

Then, the fuzzy logic system can be rewritten as \(y_i(x)=\varPhi \xi _{i}(x)=[\overline{\varPhi _{i1}}, \overline{\varPhi _{i2}}, \ldots , \overline{\varPhi _{in}}][\xi _{i1}, \xi _{i2}, \ldots , \xi _{in}]^{T}\). To begin with the design procedure of the proposed control strategy, we define \(\alpha _{i}^{*}=\Vert \varPhi _{i}\Vert ^{2} (i=1, 2,\ldots , n)\).

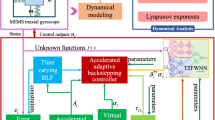
The purpose of this paper is to present a design methodology of adaptive dynamic surface control to regulate and track the output amplitude of the axis to a fixed level so that the trajectory of tracking-error converges to the small neighborhood of equilibrium point. The adaptive dynamic surface control strategy is shown in Fig. 3, and the design procedure will be described step by step as follows

Fig. 3
figure 3

Block diagram of control system

Full size image

3 Design of adaptive dynamic surface control strategy

3.1 Controller design

Step 1: We define the tracking-error

$$\begin{aligned} e_{i1}=x_{2i-1}-x_{(2i-1)d} \end{aligned}$$
(8)

where \(x_{(2i-1)d}\) is a desired command signal (fixed level). Taking the derivative of Eq. (8), it yield

$$\begin{aligned} \dot{e}_{i1}=\dot{x}_{2i-1}-\dot{x}_{(2i-1)d}=x_{2i}-\dot{x}_{(2i-1)d} \end{aligned}$$
(9)

A virtual control term \(\bar{\varphi _{i}}\) is selected to stabilize the surface \(e_{i1}\):

$$\begin{aligned} \bar{\varphi }_{i}=-\,k_{i1}e_{i1}+\dot{x}_{(2i-1)d} \end{aligned}$$
(10)

where \(k_{i1}>1\) is design parameter.

Conventional backstepping algorithm has a drawback called the explosion of complexity which is caused by the repeated differentiations of virtual controllers. In order to solve this drawback, a auxiliary filter term is introduced to simplify the process of controller design. The auxiliary filter term is built according to the following:

$$\begin{aligned} \dot{\varphi }_{i}=-\frac{\varphi _{i}- \overline{\varphi _{i}}}{\tau _{i}}-\frac{\kappa _{i}(\varphi _{i}- \overline{\varphi _{i}})}{|\varphi _{i}-\overline{\varphi _{i}}|+\delta _i} \end{aligned}$$
(11)

where \(0<\tau _{i}<2\), \(\delta _{i}>0\), \(\kappa _{i}=\theta \cdot \hat{\gamma }_{i}\) with \(\theta >1\), and \(\hat{\gamma }_{i}\) is updated by Eq. (30).

Remark 1

In fact, Eq. (11) can be written as

$$\begin{aligned} \dot{\varphi _{i}}=-\left( \overbrace{{\frac{1}{\tau _{i}}+\frac{\kappa _{i}}{|\varphi _{i}- \overline{\varphi _{i}}|+\delta _{i}}}}^{1/T}\right) \cdot (\varphi _{i}-\overline{\varphi _{i}}), \end{aligned}$$

obviously, the auxiliary filter term is also a classical integral filter; it should be pointed out that the auxiliary term will be analytically studied during the stability analysis.

Step 2: The second dynamic surface is defined as follows:

$$\begin{aligned} e_{i2}=x_{2i}-\varphi _i \end{aligned}$$
(12)

Then the derivative of \(e_{i2}\) can be obtained as

$$\begin{aligned} \dot{e}_{i2}= \dot{x}_{2i}-\dot{\varphi _i}=f_{i}(x)+d_i-\dot{\varphi _{i}}+\sigma _{i}(u_{i}) \end{aligned}$$
(13)

We introduce a auxiliary term \(\Xi _{i}=f_{i}(x)-\dot{\varphi _{i}}+(k_{i2}+1/2)e_{i2}\) with \(k_{i2}\) is design parameter, then the Eq. (13) can be rewritten as

$$\begin{aligned} \dot{e}_{i2}=\Xi _{i}-(k_{i2}+1/2)e_{i2}+d_{i}+\sigma _{i}(u_{i}) \end{aligned}$$
(14)

Obviously, the \(\Xi _{i}\) contain the uncertainty nonlinear part \(f_{i}\), and it is difficult to design controller. Thus, we utilize fuzzy logic system to approximate \(\Xi _{i}\) such that \(\Xi _{i}=\varPhi _{i}\xi _{i}+\varepsilon _{i}\), where \(\varepsilon _{i}\) is approximate error. And then, the following relationship can be established

$$\begin{aligned} e_{i2}(\varPhi _{i}\xi _{i}+\varepsilon _{i}) \leqslant {\frac{e_{i2}^{2}\alpha _{i}^{*}\Vert \xi _{i}\Vert ^{2}}{2\upsilon ^{2}} +\frac{\upsilon ^{2}}{2}+e_{i2}\varepsilon _{i}} \end{aligned}$$
(15)

where \(\upsilon \) is positive design parameter.

Assumption 4

There exist unknown positive constants \(\psi _{i}^{*}\) such that \(|d_{i}+\varepsilon _{i}|\leqslant {\psi _{i}^{*}}\).

For the convenience of analysis, define \({\psi _{i}^{*}}^{2}=\beta _{i}^{*}\). Then, we can obtain

$$\begin{aligned} e_{i2}(d_{i}+\varepsilon _{i}) \leqslant {\frac{1}{2\upsilon ^{2}}e_{i2}^{2}\beta _{i}^{*}+\frac{\upsilon ^{2}}{2}} \end{aligned}$$
(16)

Combining (14), (15) with (16), yielding

$$\begin{aligned} e_{i2}\dot{e}_{i2}&\leqslant \frac{e_{i2}^{2}\alpha _{i}^{*}\Vert \xi _{i}\Vert ^{2}}{2\upsilon ^{2}} +\frac{1}{2\upsilon ^{2}}e_{i2}^{2}\beta _{i}^{*}+\upsilon ^2\nonumber \\&\quad -\,(k_{i2}+1/2)e_{i2}^{2}+e_{i2}\sigma _{i}(u_{i}) \end{aligned}$$
(17)

In order to achieve control objectives, the proposed control scheme is designed as

$$\begin{aligned} u_{i}\!=\! {\left\{ \begin{array}{ll} \frac{-1}{2\upsilon ^{2}}(\hat{\alpha }_{i}\Vert \xi _{i}\Vert ^{2}\!+\!\hat{\beta }_{i})e_{i2}\!+\!\hat{u}_\mathrm{idz}, &{}\!\quad \!\hbox {if}\!\quad \! e_{i2}\!<\!0\\ \ 0, &{}\!\quad \!\hbox {if}\!\quad \! e_{i2}=0\\ \frac{-1}{2\upsilon ^{2}}(\hat{\alpha }_{i}\Vert \xi _{i}\Vert ^{2} \!+\!\hat{\beta }_{i})e_{i2}\!-\!\hat{u}_\mathrm{idz}, &{}\!\quad \!\hbox {if}\!\quad \! e_{i2}\!>\!0\\ \end{array}\right. } \end{aligned}$$
(18)

where \(\hat{u}_\mathrm{idz}\) is the estimate of the \(u_\mathrm{idz}^{*}\), and the \(\tilde{u}_\mathrm{idz}=u_\mathrm{idz}^{*}-\hat{u}_\mathrm{idz}\) is defined as estimate error. The corresponding adaption laws are chosen as

$$\begin{aligned}&\dot{\hat{\alpha }}_{i}= {\left\{ \begin{array}{ll} \frac{a_{i1}}{2\upsilon ^{2}}e_{i2}^{2}\Vert \xi _{i}\Vert ^{2}-a_{i1}\nu _{i}\hat{\alpha }_{i},&{}\quad \hbox {if}\quad |e_{i1}|>\varsigma \\ 0, &{}\quad \hbox {if}\quad |e_{i1}|\leqslant \varsigma \end{array}\right. }\end{aligned}$$
(19)
$$\begin{aligned}&\dot{\hat{\beta }}_{i}= {\left\{ \begin{array}{ll} \ \frac{a_{i2}}{2\upsilon ^{2}}e_{i2}^{2}-a_{i2} \nu _{i}\hat{\beta }_{i}, &{}\quad \hbox {if}\quad |e_{i1}|>\varsigma \\ \ 0, &{}\quad \hbox {if}\quad |e_{i1}|\leqslant \varsigma \end{array}\right. }\end{aligned}$$
(20)
$$\begin{aligned}&\dot{\hat{u}}_\mathrm{idz}={\left\{ \begin{array}{ll} \ a_{i4}|e_{i2}|-a_{i4}c\hat{u}_\mathrm{idz}, &{}\quad \hbox {if}\quad |e_{i1}|>\varsigma \\ \ 0, &{}\quad \hbox {if}\quad |e_{i1}|\leqslant \varsigma \end{array}\right. } \end{aligned}$$
(21)

where \(\hat{\alpha }_{i}(0)>0\), \(\hat{\beta }_{i}(0)>0\), \(\hat{u}_\mathrm{idz}(0)>0\), and \(\varsigma \) is a small positive constant. Note that the adaptation speed of \(\hat{\alpha }_{i}\), \(\hat{\beta }_{i}\) and \(\hat{u}_\mathrm{idz}\) can be turned by \(a_{i1}>0\), \(a_{i2}>0\), \(a_{i4}>0\), \(\nu _{i}>0\) and \(c>0\). Choosing a suitable adaptation parameters can also effectively avoid high control activity. Next, lemma1 will be presented to develop the adaptive dynamic surface control design.

Lemma 1

For all the input nonlinearities \(\sigma _{i}(u_{i})\) satisfying Assumption 1, the following relationship can be established.

$$\begin{aligned} e_{i2}\sigma _{i}(u_{i})\leqslant \frac{-\eta (\hat{\alpha }_{i} \Vert \xi _{i}\Vert ^{2}+\hat{\beta }_{i})}{2\upsilon ^{2}}e_{i2}^{2}+\eta |e_{i2}|\tilde{u}_\mathrm{idz} \end{aligned}$$
(22)

where \(0<\eta \leqslant \iota _{i}\leqslant 1\)

Proof

According to (18), for \(u_{i}>\hat{u}_\mathrm{irdz}\geqslant u_\mathrm{irdz}\) or \(u_{i}> u_\mathrm{irdz}\geqslant \hat{u}_\mathrm{irdz}\), it implies that \(e_{i2}<0\). Thus, yielding

$$\begin{aligned}&\frac{-(\hat{\alpha }_{i}\Vert \xi _{i}\Vert ^{2}+\hat{\beta }_{i})}{2\upsilon ^{2}}e_{i2}\sigma _{i}(u_{i})\nonumber \\&\quad \quad \geqslant \frac{-\eta (\hat{\alpha }_{i}\Vert \xi _{i}\Vert ^{2}+\hat{\beta }_{i})}{2\upsilon ^{2}}e_{i2}\eta \nonumber \\&\quad \quad \quad \cdot (u_{i}-\hat{u}_\mathrm{idz}+\hat{u}_\mathrm{idz}-u_\mathrm{idz}^{*}+u_\mathrm{idz}^{*}-u_\mathrm{irdz})\nonumber \\&\quad \quad \geqslant \frac{-\eta (\hat{\alpha }_{i}\Vert \xi _{i}\Vert ^{2}+\hat{\beta }_{i})}{2\upsilon ^{2}}e_{i2}\eta \cdot \nonumber \\&(u_{i}-\hat{u}_\mathrm{idz}+\hat{u}_\mathrm{idz}-u_\mathrm{idz}^{*})=\eta \bigg \{\frac{(\hat{\alpha }_{i}\Vert \xi _{i}\Vert ^{2}+\hat{\beta }_{i})}{2\upsilon ^{2}}\bigg \}^{2}e_{i2}^{2}\nonumber \\&\quad \quad +\frac{(\hat{\alpha }_{i}\Vert \xi _{i}\Vert ^{2}+\hat{\beta }_{i})\eta e_{i2}}{2\upsilon ^{2}}\tilde{u}_\mathrm{idz}, ~i.e. \nonumber \\&\quad \quad e_{i2}\sigma _{i}(u_{i})\leqslant \frac{-\eta (\hat{\alpha }_{i}\Vert \xi _{i}\Vert ^{2}+\hat{\beta }_{i})}{2\upsilon ^{2}}e_{i2}^{2}-\eta e_{i2}\tilde{u}_\mathrm{idz}\nonumber \\&\quad \quad =\frac{-\eta (\hat{\alpha }_{i}\Vert \xi _{i}\Vert ^{2}+\hat{\beta }_{i})}{2\upsilon ^{2}}e_{i2}^{2}+\eta |e_{i2}|\tilde{u}_\mathrm{idz} \end{aligned}$$
(23)

Where as for \(u_{i}<-\hat{u}_\mathrm{ildz}\leqslant u_\mathrm{ildz}\) or \(u_{i}< u_\mathrm{ildz}\leqslant \hat{u}_\mathrm{ildz}\), it implies that \(e_{i2}>0\), we can obtain

$$\begin{aligned}&\frac{-(\hat{\alpha }_{i}\Vert \xi _{i}\Vert ^{2}+\hat{\beta }_{i})}{2\upsilon ^{2}}e_{i2}\sigma _{i}(u_{i})\nonumber \\&\quad \geqslant \frac{-\eta (\hat{\alpha }_{i}\Vert \xi _{i}\Vert ^{2}+\hat{\beta }_{i})}{2\upsilon ^{2}}e_{i2}\nonumber \\&\quad \cdot (u_{i}+\hat{u}_\mathrm{idz}-\hat{u}_\mathrm{idz}-u_\mathrm{idz}^{*}+u_\mathrm{idz}^{*}-u_\mathrm{ildz})\nonumber \\&\quad =\eta \bigg \{\frac{(\hat{\alpha }_{i}\Vert \xi _{i}\Vert ^{2}+\hat{\beta }_{i})}{2\upsilon ^{2}}\bigg \}^{2}e_{i2}^{2}\nonumber \\&\qquad -\,\frac{(\hat{\alpha }_{i}\Vert \xi _{i}\Vert ^{2}+\hat{\beta }_{i})\eta e_{i2}}{2\upsilon ^{2}}\cdot (\tilde{u}_\mathrm{idz}-u_\mathrm{ildz}-u_\mathrm{idz}^{*}),~i.e.\nonumber \\&e_{i2}\sigma _{i}(u_{i})\leqslant \frac{-\eta (\hat{\alpha }_{i}\Vert \xi _{i}\Vert ^{2}+\hat{\beta }_{i})}{2\upsilon ^{2}}e_{i2}^{2}\nonumber \\&\qquad \qquad +\eta e_{i2}(\tilde{u}_\mathrm{idz}-u_\mathrm{ildz}-u_\mathrm{idz}^{*})\nonumber \\&\quad \quad \leqslant \frac{-\eta (\hat{\alpha }_{i}\Vert \xi _{i}\Vert ^{2}+\hat{\beta }_{i})}{2\upsilon ^{2}}e_{i2}^{2}+\eta |e_{i2}|\tilde{u}_\mathrm{idz} \end{aligned}$$
(24)

From (23) and (24), the conclusion is held.

3.2 Stability analysis

In this subsection, we will testify the feasibility of the control strategy. First, define the boundary layer error as.

$$\begin{aligned} z_{i}=\varphi _{i}-\bar{\varphi }_{i} \end{aligned}$$
(25)

Then, we describe the derivative of the surface errors to represent the closed-loop system as follows:

$$\begin{aligned} \dot{e}_{i1}&= x_{2i}-\dot{x}_{(2i-1)d}=e_{i2}+\varphi _{i}-\dot{x}_{(2i-1)d}\nonumber \\&= e_{i2}+z_{i}+\bar{\varphi }_{i}-\dot{x}_{(2i-1)d}\nonumber \\&= e_{i2}+z_{i}-k_{i1}e_{i1} \end{aligned}$$
(26)

Therefore, we obtain

$$\begin{aligned} e_{i1}\dot{e}_{i1}&= -\,k_{i1}e_{i1}^{2}+e_{i1}e_{i2}+z_{i}e_{i1}\nonumber \\&\leqslant -\,k_{i1}e_{i1}^{2}+|e_{i1}||e_{i2}|+|z_{i}||e_{i1}|\nonumber \\&\leqslant -\,k_{i1}e_{i1}^{2}+e_{i1}^{2}+e_{i2}^{2}/2+z_{i}^{2}/2 \end{aligned}$$
(27)

Considering the derivative of Eq. (25), yielding

$$\begin{aligned} \dot{z}_{i}=-\frac{z_{i}}{\tau _{i}}- \frac{\kappa _{i}z_{i}}{|z_{i}|+\delta _{i}}-\dot{\bar{\varphi }}_{i} \end{aligned}$$
(28)

And then, we have

$$\begin{aligned} z_{i}\dot{z}_{i}=-\frac{z_{i}^{2}}{\tau _{i}}-z_{i}\left( \frac{\kappa _{i}z_{i}}{|z_{i}|+\delta _{i}}+\dot{\bar{\varphi }}_{i}\right) \end{aligned}$$
(29)

In this study, we assume that the \(\dot{\bar{\varphi }}_{i}\) is bounded with a large enough unknown positive number \(\gamma _{i}^{*}\), i.e. ,\(|\dot{\bar{\varphi }}_{i}|\leqslant \gamma _{i}^{*}\), and \(\hat{\gamma }_{i}\) is used to estimate \(\gamma _{i}^{*}\) where \(\tilde{\gamma }_{i}=\hat{\gamma }_{i}-\gamma _{i}^{*}\) is estimation error. The corresponding adaption law is chosen as

$$\begin{aligned} \dot{\hat{\gamma }}_{i}=a_{i3}|z_{i}| \left( \frac{\theta |z_{i}|}{|z_{i}|+\delta _{i}}\right) +a_{i3}\nu _{i}\hat{\gamma }_{i} \end{aligned}$$
(30)

where \(\theta >1\) is a design parameter. The stability of the closed-loop system will be stated in the following theorem.

Theorem 1

Suppose that the system (7) with uncertainties, external disturbance, and input nonlinearity is controlled by the proposed control scheme (18) with update laws in (19), (20), (21) and (30). In addition, if the proposed control system satisfies Assumptions 1–3. Then, whenever the tracking-error starts from any initial point, it can asymptotically reach the small neighborhood of equilibrium point.

Proof

In the case of \(e_{i2}\ne 0\). Define the following Lyapunov candidate function:

$$\begin{aligned} V_\mathrm{g}\!=\!\frac{e_{i1}^{2}\!+\!e_{i2}^{2}\!+\!z_{i}^{2}}{2}\!+\!\frac{\tilde{\alpha }_{i}^{2}}{2\eta a_{i1}}\!+\!\frac{\tilde{\beta }_{i}^{2}}{2\eta a_{i2}}\!+\!\frac{\tilde{\gamma }_{i}^{2}}{2a_{i3}}\!+\!\eta \frac{\tilde{u}_\mathrm{idz}^{2}}{2a_{i4}}\nonumber \\ \end{aligned}$$
(31)

where \(\tilde{\alpha }_{i}=\alpha _{i}^{*}-\eta \hat{\alpha }_{i}\), \(\tilde{\beta }_{i}=\beta _{i}^{*}-\eta \hat{\beta }_{i}\) and \(\tilde{\gamma }_{i}=\gamma _{i}^{*}-\hat{\gamma }_{i}\). From (17), (22), (27) and (29), the derivative of \(V_\mathrm{g}\) can be obtained as

$$\begin{aligned} \dot{V}_\mathrm{g}&\leqslant -\,(k_{i1}-1)e_{i1}^{2}-k_{i2}e_{i2}^{2}-\frac{(2-\tau _{i})z_{i}^{2}}{2\tau _{i}}+\frac{\alpha _{i}^{*}\Vert \xi _{i}\Vert ^{2}e_{i2}^{2}}{2\upsilon ^{2}}\nonumber \\&+\,\frac{\beta _{i}^{*}e_{i2}^{2}}{2\upsilon ^{2}}-z_{i}\Bigg (\frac{\kappa _{i}z_{i}}{|z_{i}|+\delta _{i}}+\dot{\bar{\varphi }}_{i}\Bigg )-\eta \frac{(\hat{\alpha }_{i}\Vert \xi _{i}\Vert ^{2}+\hat{\beta }_{i})e_{i2}^{2}}{2\upsilon ^{2}}\nonumber \\&+\,\eta |e_{i2}|\tilde{u}_\mathrm{idz}+\upsilon ^{2}-\frac{\tilde{\alpha }_{i}\dot{\hat{\alpha }}_{i}}{a_{i1}}-\frac{\tilde{\beta }_{i}\dot{\hat{\beta }}_{i}}{a_{i2}} -\frac{\tilde{\gamma }_{i}\dot{\hat{\gamma }}_{i}}{a_{i3}}-\frac{\eta \tilde{u}_\mathrm{idz}\dot{\hat{u}}_\mathrm{idz}}{a_{i4}}\nonumber \\&\leqslant -\,(k_{i1}-1)e_{i1}^2-k_{i2}e_{i2}^{2}-\frac{(2-\tau _{i})z_{i}^{2}}{2\tau _{i}}+\frac{\tilde{\alpha }_{i}\Vert \xi _{i}\Vert ^{2}e_{i2}^{2}}{2\upsilon ^{2}}\nonumber \\&+\,\frac{\tilde{\beta }_{i}e_{i2}^{2}}{2\upsilon ^{2}}-|z_{i}|\Bigg (\frac{\kappa _{i}|z_{i}|}{|z_{i}|+\delta _{i}}-\gamma _{i}^{*}\Bigg )+\eta |e_{i2}|\tilde{u}_\mathrm{idz}+\upsilon ^{2}\nonumber \\&-\,\frac{\tilde{\alpha }_{i}\dot{\hat{\alpha }}_{i}}{a_{i1}}-\frac{\tilde{\beta }_{i}\dot{\hat{\beta }}_{i}}{a_{i2}} -\frac{\tilde{\gamma }_{i}\dot{\hat{\gamma }}_{i}}{a_{i3}}-\frac{\eta \tilde{u}_\mathrm{idz}\dot{\hat{u}}_\mathrm{idz}}{a_{i4}} \end{aligned}$$
(32)

Substitute adaptive laws \(\dot{\hat{\alpha }}_{i}\), \(\dot{\hat{\beta }}_{i}\), \(\dot{\hat{\gamma }}_{i}\), \(\dot{\hat{u}}_\mathrm{idz}\), and \(\kappa _{i}=\theta \hat{\gamma }_{i}\) into Eq. (32), we obtain

$$\begin{aligned} \dot{V}_\mathrm{g}&\leqslant -\,(k_{i1}-1)e_{i1}^2-k_{i2}e_{i2}^{2}-\frac{(2-\tau _{i})z_{i}^{2}}{2\tau _{i}}\nonumber \\&-\,\frac{\theta |z_{i}|^{2}}{|z_{i}|+\delta _{i}}\tilde{\gamma }_{i}-|z_{i}|\Bigg (\frac{\theta \hat{\gamma }_{i}|z_{i}|}{|z_{i}|+\delta _{i}}-\gamma _{i}^{*}\Bigg )+\nu _{i}\tilde{\alpha }_{i}\hat{\alpha }_{i} \nonumber \\&+\,\nu _{i}\tilde{\beta }_{i}\hat{\beta }_{i}+\nu _{i}\tilde{\gamma }_{i}\hat{\gamma }_{i}+c\eta \tilde{u}_\mathrm{idz}\hat{u}_\mathrm{idz}+\upsilon ^{2} \end{aligned}$$
(33)

Due to \(\tilde{\alpha }_{i}=\alpha _{i}^{*}-\eta \hat{\alpha }_{i}\), \(\tilde{\beta }_{i}=\beta _{i}^{*}-\eta \hat{\beta }_{i}\), \(\tilde{\gamma }_{i}=\gamma _{i}^{*}-\hat{\gamma }_{i}\) and \(\tilde{u}_\mathrm{idz}=u_\mathrm{idz}^{*}-\hat{u}_\mathrm{idz}\), we can get the following relationship

$$\begin{aligned}&-|z_{i}|\left( \frac{\theta \hat{\gamma }_{i}|z_{i}|}{|z_{i}|+\delta _{i}}-\gamma _{i}^{*}\right) -\frac{\theta |z_{i}|^{2}}{|z_{i}|+\delta _{i}}\tilde{\gamma }_{i}\nonumber \\&=-|z_{i}|\gamma _{i}^{*}\left( \frac{\theta |z_{i}|}{|z_{i}|+\delta _{i}}-1\right) \end{aligned}$$
(34)

and

$$\begin{aligned} \nu _{i}\tilde{\alpha }_{i}\hat{\alpha }_{i}&= -\frac{\nu _{i}}{\eta }(\alpha _{i}^{*}-\eta \hat{\alpha }_{i})(\alpha _{i}^{*}-\eta \hat{\alpha }_{i}-\alpha _{i}^{*})\nonumber \\&\leqslant \frac{\nu _{i}}{\eta }\left( -(\alpha _{i}^{*}\!-\!\eta \hat{\alpha }_{i})^{2}\!+\!\frac{(\alpha _{i}^{*}\!-\!\eta \hat{\alpha }_{i})^{2}}{2}\!+\!\frac{(\alpha _{i}^{*})^2}{2} \right) \nonumber \\&= -\frac{\nu _{i}(\alpha _{i}^{*}-\eta \hat{\alpha }_{i})^{2}}{2\eta }+\frac{\nu _{i}(\alpha _{i}^{*})^{2}}{2\eta } \end{aligned}$$
(35)

Similarly to (35), we can get

$$\begin{aligned} \nu _{i}\tilde{\beta }_{i}\hat{\beta }_{i}&\leqslant -\frac{\nu _{i}(\beta _{i}^{*}-\eta \hat{\beta }_{i})^{2}}{2\eta }+\frac{\nu _{i}(\beta _{i}^{*})^{2}}{2\eta }\end{aligned}$$
(36)
$$\begin{aligned} \nu _{i}\tilde{\gamma }_{i}\hat{\gamma }_{i}&\leqslant -\frac{\nu _{i}(\gamma _{i}^{*}-\hat{\gamma }_{i})^{2}}{2}+\frac{\nu _{i}(\gamma _{i}^{*})^{2}}{2}\end{aligned}$$
(37)
$$\begin{aligned} c\eta \tilde{u}_\mathrm{idz} \hat{u}_\mathrm{idz}&\leqslant -\frac{c\eta (u_\mathrm{idz}^{*}-\hat{u}_\mathrm{idz})^{2}}{2}+\frac{c\eta (u_\mathrm{idz}^{*})^{2}}{2} \end{aligned}$$
(38)

By noticing Eq. (34), if \(|z_{i}|>\frac{\delta _{i}}{\theta -1}\), then \(-|z_{i}|\gamma _{i}^{*}\big (\frac{\theta |z_{i}|}{|z_{i}|+\delta _{i}}-1\big )<0\).  If \(|z_{i}|\leqslant \frac{\delta _{i}}{\theta -1}\), then \(-|z_{i}|\gamma _{i}^{*}\big (\frac{\theta |z_{i}|}{|z_{i}|+\delta _{i}}-1\big ) \leqslant \frac{\delta _{i}\gamma _{i}^{*}}{\theta -1}\). Thus, relationship \(-|z_{i}|\gamma _{i}^{*} \big (\frac{\theta |z_{i}|}{|z_{i}|+\delta _{i}}-1\big )\leqslant \frac{\delta _{i}\gamma _{i}^{*}}{\theta -1}\) can be established.

With the knowledge above, Eq. (33) is expressed as follows:

$$\begin{aligned} \dot{V}_\mathrm{g}&\leqslant -(k_{i1}-1)e_{i1}^2-k_{i2}e_{i2}^{2}-\frac{(2-\tau _{i})z_{i}^{2}}{2\tau _{i}}-|z_{i}|\gamma _{i}^{*}\nonumber \\&\cdot \left( \frac{\theta |z_{i}|}{|z_{i}|+\delta _{i}}-1\right) -\frac{\nu _{i}(\alpha _{i}^{*}-\eta \hat{\alpha }_{i})^{2}}{2\eta }+\frac{\nu _{i}(\alpha _{i}^{*})^{2}}{2\eta }\nonumber \\&-\frac{\nu _{i}(\beta _{i}^{*}-\eta \hat{\beta }_{i})^{2}}{2\eta }+\frac{\nu _{i}(\beta _{i}^{*})^{2}}{2\eta }-\frac{\nu _{i}(\gamma _{i}^{*}-\hat{\gamma }_{i})^{2}}{2}\nonumber \\&+\frac{\nu _{i}(\gamma _{i}^{*})^{2}}{2}-\frac{c\eta (u_\mathrm{idz}^{*}-\hat{u}_\mathrm{idz})^{2}}{2}+\frac{c\eta (u_\mathrm{idz}^{*})^{2}}{2}+\upsilon ^{2}\nonumber \\&\leqslant -\mu _1 V_\mathrm{g}+\frac{\delta _{i}\gamma _{i}^{*}}{\theta -1}+\frac{\nu _{i}}{2\eta }\big [(\alpha _{i}^{*})^{2}+(\beta _{i}^{*})^{2}+\eta (\gamma _{i}^{*})^{2}\nonumber \\&+\,\eta c(u_\mathrm{idz}^{*})^{2}\big ]+\upsilon ^{2}=-\mu _1 V_\mathrm{g}+\varDelta _1 \end{aligned}$$
(39)

where \(\mu _1=\min \big \{2(k_{i1}-1), 2k_{i2}, \frac{2-\tau _{i}}{\tau _{i}}, \nu _{i}a_{i1}, \nu _{i}a_{i2}, \nu _{i}a_{i3}, ca_{i4}\big \}\), \(\varDelta _1=\frac{\delta _{i}\gamma _{i}^{*}}{\theta -1}+\frac{\nu _{i}}{2\eta } \big [(\alpha _{i}^{*})^{2}+(\beta _{i}^{*})^{2} +\eta (\gamma _{i}^{*})^{2}+c\eta (u_\mathrm{idz}^{*})^{2}\big ]+\upsilon ^{2}\). Furthermore, we can obtain

$$\begin{aligned} \dot{V}_\mathrm{g}\leqslant -\zeta \mu _1 V_\mathrm{g}-(1-\zeta )\mu _1 V_\mathrm{g}+\varDelta _1 \end{aligned}$$
(40)

where \(0<\zeta <1\). Obviously, if \(V_\mathrm{g}>\frac{\varDelta _1}{(1-\zeta )\mu _1}\) , then (40) can be written as \(\dot{V}_\mathrm{g}<-\zeta \mu _1 V_\mathrm{g}\). The decrease of \(V_\mathrm{g}\) enforce the trajectories of the closed loop system into \(V_\mathrm{g}\leqslant \frac{\varDelta _1}{(1-\zeta )\mu _1}\). Thus, the trajectories of the closed loop system is bounded, i.e. \(\underset{t\rightarrow T}{\lim } e_{i1}\in \big (|e_{i1}|\leqslant \sqrt{\frac{2\varDelta _1}{(1-\zeta )\mu _1}}\big )\).

In the case of \(e_{i2}=0\), the derivative of \(V_\mathrm{g}\) satisfies

$$\begin{aligned} \dot{V}_\mathrm{g}&\leqslant -(k_{i1}-1)e_{i1}^2-\frac{(2-\tau _{i})z_{i}^{2}}{2\tau _{i}}-\frac{\theta |z_{i}|^{2}}{|z_{i}|+\delta _{i}}\tilde{\gamma }_{i}\nonumber \\&-\,|z_{i}|\left( \frac{\theta \hat{\gamma }_{i}|z_{i}|}{|z_{i}|+\delta _{i}}-\gamma _{i}^{*}\right) +\nu _{i}\tilde{\alpha }_{i}\hat{\alpha }_{i} +\nu _{i}\tilde{\beta }_{i}\hat{\beta }_{i}\nonumber \\&+\,\nu _{i}\tilde{\gamma }_{i}\hat{\gamma }_{i}+c\eta \tilde{u}_\mathrm{idz}\hat{u}_\mathrm{idz} \end{aligned}$$
(41)

Similar to the process of (33), we can also obtain \(V_\mathrm{g}\!\leqslant \!-\mu _2V_\mathrm{g}\!+\!\varDelta _2\), where \(\mu _2\!=\!\min \big \{2(k_{i1}-1), \frac{2-\tau _{i}}{\tau _{i}}, \nu _{i}a_{i1}, \nu _{i}a_{i2}, \nu _{i}a_{i3}, ca_{i4}\big \}\), \(\varDelta _2\!=\!\frac{\delta _{i}\gamma _{i}^{*}}{\theta -1}\!+\! \frac{\nu _{i}}{2\eta }\big [(\alpha _{i}^{*})^{2}+(\beta _{i}^{*})^{2} +\eta (\gamma _{i}^{*})^{2}+c\eta (u_\mathrm{idz}^{*})^{2}\big ]\), and the error trajectories is bounded, i.e. \(\underset{t\rightarrow T}{\lim } e_{i1}\in \big (|e_{i1}|\leqslant \sqrt{\frac{2\varDelta _2}{(1-\zeta )\mu _2}}\big )\). Therefore, we can conclude from case \(e_{i2}\ne 0\) and \(e_{i2}=0\) that all the closed-loop errors are bounded.

Remark 2

Practically, in (30), the \(|z_{i}|\) cannot become exactly zero and thus the adaptive parameter \(\hat{\gamma }\) may increase boundlessly. In order to avoid the issue, we modify the update law as

$$\begin{aligned} \dot{\hat{\gamma }}_{i}= {\left\{ \begin{array}{ll} \ a_{i3}|z_{i}|\left( \frac{\theta |z_{i}|}{|z_{i}|+\delta _{i}}\right) +a_{i3}\nu _{i}\hat{\gamma }_{i},&{}\quad \hbox {if}\quad |e_{i1}|>\varsigma \\ \ 0, &{}\quad \hbox {if}\quad |e_{i1}|\leqslant \varsigma \\ \end{array}\right. }\nonumber \\ \end{aligned}$$
(42)

where  \(\hat{\gamma }_{i}(0)\!>\!0\), and \(a_{i3}\) is a positive design parameter

Remark 3

From the proof of the Theorem 1, it implies that the \(\hat{\alpha }_{i}\), \(\hat{\beta }_{i}\), \(\hat{\gamma }_{i}\), \(\hat{u}_\mathrm{idz}\), and \(e_{i2}\) are all bounded over \(t \in [0, \infty )\) . For the right-hand side of (18) is also bounded, therefore we conclude that \(u_{i}\) is bounded for all \(t \in [0, \infty )\).

Remark 4

The proposed controller (18) can be applied without any prior knowledge of MEMS triaxial gyroscope such as exact model, external disturbance, and unknown dead zone. On the other hand, the control scheme (18) not only compensates for external disturbance and uncertainties, but also trajectory of tracking-error converges to the small neighborhood of equilibrium point, even in the presence of nonlinear input. Accordingly, it is indeed an adaptive control.

4 Numerical simulations

In this section, the numerical simulation demonstrates the effectiveness of the proposed control scheme. The desired trajectory are given as \(x_{1d}=0.1sin(\pi t)\), \(x_{2d}=0.1cos(\pi t)\) and \(x_{3d}=0.1sin(\pi t)\cdot cos(t)\). The sampling time/interval \(T_{time}\) is 0.001s. Note that the tracking signals can be obtained by signal catching devices in practice. In the simulation, the parameters of the control law are selected as \(k_{11}=k_{21}=k_{31}=5.2\), \(a_{11}=a_{21}=a_{31}=8\), \(a_{12}=a_{22}=3.4\), \(a_{41}=6.5\), \(a_{13}=a_{23}=a_{33}=4\), \(a_{24}=a_{42}=a_{43}=1.5\), \(\theta =2.2\), \(\upsilon =0.05\), \(\delta _{i}=1\), \(\nu _{i}=0.02\), \(c=0.01\), \(\varsigma =0.03\). The \(\hat{\alpha }_{i}(0)=0.01\), \(\hat{\beta }_{i}(0)=0.01\), \(\hat{u}_\mathrm{idz}(0)=0.01\). The nonlinearities input \(\sigma _{i}(u_{i})\) is taken as saturation, the saturated value and dead-band value are 1.7 and \((u_\mathrm{ildz}=-0.3, u_\mathrm{irdz}=0.7)\), respectively. The disturbance is \(d_{1}=d_{2}=d_{3}=0.8sin(\pi t)cos(2\pi t)\). To implement the fuzzy logic system, membership functions are given as: \(\mu _{F_{i}^{1}}(x_{i})=\exp \big [-\big (\frac{(x_{i}+\pi /6)}{(\pi /24)}\big )^{2}\big ]\), \(\mu _{F_{i}^{2}}(x_{i})=\exp \big [-\big (\frac{(x_{i}+\pi /12)}{(\pi /24)}\big )^{2}\big ]\), \(\mu _{F_{i}^{3}}(x_{i})=\exp \big [-\big (\frac{x_{i}}{(\pi /24)}\big )^{2}\big ]\), \(\mu _{F_{i}^{4}}(x_{i})=\exp \big [-\big (\frac{(x_{i}-\pi /12)}{(\pi /24)}\big )^{2}\big ]\), \(\mu _{F_{i}^{5}}(x_{i})=\exp \big [-\big (\frac{(x_{i}-\pi /6)}{(\pi /24)}\big )^{2}\big ]\). In addition, the parameters of MEMS gyroscope system are randomly selected within \(20\,\%\) of their nominal values in all the simulations.

The response curves of the tracking trajectories are illustrated in Figs. 4, 5 and 6. As indicated in Figs. 4, 5 and 6, as expected, the proposed control scheme could guarantee the achieved system states track the desired signals effectively, even in the presence of the uncertainties and input uncertainty. Moreover, the tracking-error achieves its maximum at the beginning of the engagement, and stays at a small neighborhood of equilibrium point at the rest. It can be concluded that the MEMS gyroscope can maintain the proof mass to oscillate in the \(x\)-, \(y\)-, and \(z\)-directions at a given frequency and amplitude with the adaptive mechanism, and the control objective is well accomplished because the proposed controller has a strong ability to compensate both the system nonlinearities and disturbance. From Fig. 7, we can see that the control inputs are saturated in the initialization transient phase. The dead-zone parameters are provided in Fig. 8. As can be seen, adaptive compensators for dead-zone in the closed-loop are bounded. Moreover, the adaptive parameters can estimate the upper bound value of the dead zone. And the adaptive compensators \(\hat{u}_\mathrm{idz}\) and adaptive control term \(-e_{i2}(\hat{\alpha }_{i}\Vert \xi _{i}\Vert ^{2}+\hat{\beta }_{i})/2\upsilon \) work in a cooperative manner. That is, if one works more, the other one works less, and vice versa. The advantage of the idea is that we need not a perfect dead-zone compensator. These simulation results show that good tracking performance can be obtained under the proposed adaptive control.

Fig. 4
figure 4

Tracking (\(x_1-x_1d\)) by using proposed controller

Full size image
Fig. 5
figure 5

Tracking (\(x_2-x_2d\)) by using proposed controller

Full size image
Fig. 6
figure 6

Tracking (\(x_3-x_3d\)) by using proposed controller

Full size image
Fig. 7
figure 7

Control input signal

Full size image
Fig. 8
figure 8

Estimate \(u_{idz}^{*}\)

Full size image

5 Conclusion

In this paper, a novel adaptive dynamic surface controller is presented for MEMS gyroscope system with disturbance, uncertainty, and input nonlinearity. The proposed control scheme can guarantee that the trajectory of tracking-error converges to the small neighborhood of equilibrium point. The controller with adaptive mechanism does not depend on accurate mathematical models. Moreover, it has been demonstrated good performance and still holds robustness and stability in the presence environmental disturbance, uncertainties and input nonlinearity. Numerical simulations are included to support the above analysis, and the results demonstrate that the proposed control strategy has good tracking performance and robustness for uncertainties.