Parametric instability of a Jeffcott rotor with rotationally asymmetric inertia and transverse crack

Abstract

Both the rotationally asymmetric inertia and transverse crack frequently appear in the rotor system. The parametric excitations induced by this two features cause instability and severe vibration under certain operating conditions. Thus, the parametric instability of a Jeffcott rotor with asymmetric disk and open transverse crack is studied analytically. The vibration equations of four degrees-of-freedom of the system are established, and the stiffness coefficients of cracked rotor shaft are derived based upon the compliance method and strain energy release rate method. Then, utilizing the harmonic balance method and Taylor expansion technique, the unstable widths of simple and combination instability regions (SIR and CIR) are solved approximately. For a practical rotor system, the approximate unstable widths are verified by the Floquet numerical analysis. The effects of crack depth and position upon the unstable widths are discussed, and the conditions for zero unstable points (ZUPs) are given: Besides the asymmetric angle should be π/2 (for SIR) or 0 (for CIR), the relationships between the inertia asymmetry and crack parameters (depth and position) are also presented analytically. These results would be useful for crack detection and instability control of the asymmetric rotor-bearing system.

1 Introduction

Rotary inertia inequality is a common feature of the rotor system. A two-blade propeller, a fan or pump impeller, a teetered wind turbine, a cam shaft, and a rotary plow all have unequal rotary inertia about two principal axes of the rotating disk. Transverse cracks frequently appear in rotating machinery due to manufacturing flaws or cyclic loading. Either the asymmetric inertia or transverse crack will cause parametric excitations, and then alters the vibrational behavior of the rotor. The parametric excitation from the asymmetric inertia causes instability and severe vibration under certain operating conditions. Determination of operating conditions of parametric instability is crucial to the design and usage of the asymmetric rotor system.

Many studies focused on the instability behavior of systems with asymmetric inertia. In the 1960s–1970s, Crandall and Brosens [1] and Yamamoto et al. [2, 3], respectively, carried out a series of in-depth theoretical and experimental studies on the unstable vibrations of a rotating shaft carrying an unsymmetrical rotor. Ardayfio and Frohrib [4] extended the four degree-of-freedom rotor system of Yamamoto and Ota [2] to include flexibility in the bearing supports. During this period, the lumped parameter model was mainly considered. In the 1980s–1990s, Genta [5] first derived the finite element equations of motion for the general asymmetric rotor system. Then, both deviatoric inertia and stiffness due to the asymmetry of flexible shaft and multiple disks were considered in the finite element model by Kang et al. [6]. The effects of asymmetric disks were included to study the transition curves of stable and unstable regions of a rotating asymmetric shaft supported by isotropic bearings [7]. Takashi and Murakami [8] considered the influence of flexible base on the dynamic stability of an asymmetric rotor system near the major and secondary critical speeds. Recently, Nriot et al. [9] applied stochastic methods dealing with uncertain inertia parametric excitation to rotating machines with constant rotating speed subjected to a base translational motion. Ishida and Lin [10] proposed a simple passive control method utilizing discontinuous spring characteristics to eliminate the unstable ranges of an inertia asymmetrical rotor system. Hsieh et al. [11] developed an extended transfer matrix method for analyzing the coupled lateral and torsional vibration responses of asymmetric rotor-bearing system.

The parametric instability induced by the transverse crack also has been concerned for many years. The stability and the stability degree of a cracked Jeffcott rotor supported on different kinds of journal bearings were investigated by Meng and Gasch [12]. Gasch [13] presented an overview stability diagram of a Laval rotor having a transverse crack. Nonlinear dynamic stability analysis of a rotating shaft-disk system with a transverse crack was conducted by Fu et al. [14], Dai and Chen [15] and Chen et al. [16], respectively. In their model, the mass of elastic shaft, the additional displacements caused by the crack, the geometric nonlinearity of the shaft, and asymmetrical viscoelastic supports were taken into account based upon the energy theorem and Lagrange equation. Simple systems with few degrees-of-freedom were utilized in the above analysis. With the widespread adoption of finite element model in rotor dynamic analysis, the parametric instability analysis was also extended to finite element cracked rotor-bearing systems [17–19]. Sekhar and Dey [17] studied the variation of the first stability threshold limit with crack parameters and shaft internal damping. Sinou [18] conducted the stability analysis by applying a perturbation to the non-linear periodic solution, and analyzed the effect of crack on the first three instability regions. Ricci and Pennacchi [19] evaluated the stability of a steam turbo generator rotor for different values of rotating speed and crack depth.

As the above literature shows, extensive efforts have been devoted to study the parametric instability behaviors of rotor-bearing systems with asymmetric disks or transverse cracks separately. When both of them appear in a rotor system, the dynamic characteristics of the system have not gained sufficient attention. A complex modal analysis for the asymmetric rotor system consider a transverse crack on the shaft was proposed by Han [20], and the reverse frequency response functions were defined to identify the transverse crack. Very recently, based upon the finite element model, the effect of transverse crack upon parametric instability of a rotor-bearing system with an asymmetric disk was analyzed by the authors [21]. It is shown that the interaction of both asymmetric disk and transverse crack certainly brings significant influence on the parametric instability of the rotor system. Due to the utilization of finite element model, it is difficult to conduct parametric analysis. Moreover, the analytical expressions for describing the effects of two parametric excitations upon the unstable regions are not given.

Thus, in this paper, a Jeffcott rotor model with rotationally asymmetric inertia and open transverse crack is established. The stiffness coefficients of cracked rotor shaft are derived based upon the compliance method and strain energy release rate method. Then, utilizing the harmonic balance method and Taylor expansion technique, the unstable widths for various unstable regions are solved approximately. For a practical rotor system, the approximate unstable widths are verified by the Floquet numerical analysis. The effects of crack depth and position upon the unstable widths are discussed. Finally, some useful conclusions are obtained.

2 Equations of motion for the asymmetric rotor with transverse crack

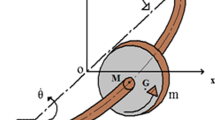
A simply supported rotor system, as shown in Fig. 1(a), consists of a light shaft and an asymmetric disk without any static and dynamic unbalance. The angular rotating velocity is Ω. Without considering the axial and torsional vibrations, the x,y,θ _y ,θ _x are respectively utilized to describe the transversal and angle vibration displacements of the asymmetric disk. Thus, the vibratory system has four degrees-of- freedom. L, l _d, and l _c denote the rotor span and the distances to the disk and crack from the left support of the shaft. The relative position between the asymmetric and transverse crack in the circumference is shown in Fig. 1(b). The angles between the major axes of the disk/crack and the shaft are denoted by ϕ _d and ϕ _c. Without loss of generality, the ϕ _d is assumed to be zero, and the ϕ _c=ϕ is also called the asymmetric angle in the paper. In the following, one would see that the asymmetric angle ϕ is an important factor in the parametric instability of the rotor system.

Fig. 1

Schematic diagram of the rotor bearing system with asymmetric disk and open transverse crack (a) and the relative position between the disk and crack in the circumference direction (b)

2.1 Asymmetric disk

The nodal displacement vector of the asymmetric disk is q=[x y θ _y θ _x ]^T. The mass of the disk is m _d. Besides, three (one polar and two diametral) moments of inertia about the z-coordinate, x-coordinate, and y-coordinates are represented by I _dp , I _dx , and I _dy . For the inertia unsymmetrical disk, I _dx ≠I _dy . Without considering the mass unbalance and self-gravity force, the equation of motion of the disk in the fixed coordinates is written as [6]

(1)

in which m ^d and g ^d are the classical mass and gyroscopic matrices of the disk without unsymmetrical inertia, $\mathbf{m}_{\mathrm{c}}^{\mathrm{d}}$ and $\mathbf{m}_{\mathrm{s}}^{\mathrm{d}}$ are the coefficient matrices due to the inertia asymmetry. By introducing the mean value of the diametral moments of inertia I _d=(I _dx +I _dy )/2 and the relative inertia asymmetry of the disk $\varDelta _{\mathrm{d}}=\frac {I_{\mathrm{d}x}-I_{\mathrm{d}y}}{2I_{\mathrm{d}}}$, these matrices could be written as follows:

(2a)

(2b)

Obviously, due to the inertia asymmetry, the mass and gyroscopic matrices of the disk are all sinusoidal time-periodic, and the frequency is twice of the rotating speed.

2.2 Massless shaft with an open transverse crack

The massless shaft is modeled by Euler–Bernoulli beam. The elastic restoring forces induced by the massless shaft could be expressed as

$$ \mathbf{v}= \mathbf{R}^T\mathbf{f}^{-1}\mathbf{R}\mathbf{q} $$

(3)

in which R is the transformation matrix. Considering the asymmetric angle, it could be expressed as

(4)

f is the flexibility matrix in the rotating reference frame, and one has [22]

(5)

where

(6a)

(6b)

(6c)

(6d)

(6e)

(6f)

The f _ij (i,j=1,2,…,4) denote the elements of compliance matrix of an uncracked engineering Euler beam, and are computed as

$$ f_{ij}=\int_z\frac{M_j^0(z)M_i^0(z)}{EI_{\mathrm{s}}}\,\mathrm{d}z $$

(7)

where $M_{i}^{0}(z)$ and $M_{j}^{0}(z)$ are the bending moment distributions due to the unit load at the ith and jth nodes, respectively. The Young’s modulus and moment of inertia of the shaft cross-section are denoted by E and I _s. The $M_{i}^{0}(z)$ and $M_{j}^{0}(z)$ for a simply supported beam under concentrated force or bending moment are easily obtained, and the f _ij could be solved. The c _ij (i=j=1,2,3,4) denote the additional flexibility coefficients due to the transverse crack for the shaft under shear force and bending moments. The cracked shaft cross-section with radius R and crack depth a is shown in Fig. 2. The nondimensional crack depth is defined as σ=a/R. According to the strain energy release rate method (SERR), the c _ij are determined by [23]

(8a)

(8b)

(8c)

(8d)

in which F ₁, F ₂, F _II, F _III are the geometrical factors for the stress intensity factors (SIFs) when the crack is in Mode I (opening mode), Mode II (sliding mode), and Mode III (tearing mode). The dimensionless parameters: $\bar{\xi}=\xi/R$, $\bar{\mu}=\mu/R$ where ξ and μ are given in Fig. 2. The double integration limits are expressed as: $\bar{a}=\sqrt{1-\bar {\xi}^{2}}-1+\sigma$ and $\bar{b}=\sqrt{1-(1-\sigma)^{2}}$.

Fig. 2

Cross-section of the open transverse crack for flexibility computations

Considering Eqs. (4–8d), the stiffness matrix of a rotating shaft with fully open transverse crack is rewritten as

(9)

where

(10a)

(10b)

(10c)

In these equations, the “+” is for the former variable and “−” for the latter one.

2.3 Nondimensional equation

A reference displacement and angular velocity are introduced as $x_{\mathrm{s}\,t}=\sqrt{I_{\mathrm{d}}/m_{\mathrm{d}}}$ and $\omega_{\mathrm{s}\,t}=\sqrt {k_{tt}/m_{\mathrm{d}}}$. Then the transverse displacements, time, and rotating velocity could be written in nondimensional forms as: x′=x/x _s t , y′=y/x _s t , t′=ω _s t t, and Ω′=Ω/ω _s t . For convenience sake, the primes on the dimensionless quantities are omitted in the following.

By substituting the above dimensionless quantities into Eq. (1), Eq. (3), and Eq. (9), and defining some parameters, including: inertia ratio β=I _dp /I _d, time-invariant stiffness coefficients $\gamma=k_{tm}/(m_{\mathrm{d}}x_{\mathrm{s}\,t}\omega_{\mathrm{s}\,t}^{2})$, and $\delta=k_{mm}/(I_{\mathrm{d}}\omega_{\mathrm{s}\,t}^{2})$, and relative amplitudes of time-varying stiffness due to the open transverse crack $\epsilon _{1}=\varDelta k_{tt}/(m_{\mathrm{d}}\omega_{\mathrm{s}\,t}^{2})$, ϵ ₂=Δk _mm /k _mm , and ϵ ₁₂=Δk _tm /k _tm , one gets the dimensionless form of the vibrational differential equations for the cracked rotor system

(11)

where

(12a)

(12b)

(12c)

(12d)

The nondimensional form of the system equation (Eq. (11)) will be mainly considered in the following instability analysis.

3 Parametric instability analysis

3.1 Without asymmetry and open transverse crack

Before instability analysis, the whirling characteristics of the rotor system without asymmetric disk and transverse crack should be studied. Setting Δ _d=ϵ ₁=ϵ ₂=ϵ ₁₂=0, the frequency equation is expressed as

(13)

in which ω ₁>1>ω ₂>0>ω ₃>−1>ω ₄ and ω _i (i=1,2,3,4) are the whirling frequencies of the system consisting a symmetric disk and a uncracked shaft with stiffness k _tt , k _mm , k _tm .

There are two types of instability regions: simple instability regions (SIRs) and combination instability regions (CIRs). Considering the parametric frequency of the rotor system is 2Ω, the starting points of these instability regions in the rotating speed axis could be expressed as [24]

$$ \left \{ \begin{array}{l@{\quad}l} \varOmega=\frac{1}{n}\omega_i, & \hbox{$n=1,2,\ldots$ for SIRs;} \\[6pt] \varOmega=\frac{1}{2m}(\omega_i+\omega_j), & \hbox{$i\neq j$, $m=1,2,\ldots$ for CIRs} \end{array} \right . $$

(14)

where ω _i and ω _j are the ith and jth whirling frequencies of the time-invariant system. Only the values of ω ₁ and ω ₂ are bigger than zero. As the instability regions with n=1 (or m=1) would have greater ranges compared with the other instability regions, so the SIR with starting point of Ω _s=ω ₂ and CIR with a starting point of Ω _c=(ω ₁+ω ₂)/2 are mainly considered, and denoted by U _s and U _c, respectively. By putting ω=Ω in Eq. (13) and considering the inertia ratio β>1, one obtains

(15)

For the starting point of CIR Ω _c, Yamamoto et al. presented the analytical form as

(16)

In following section, the widths λ _s, λ _c of U _s, and U _c will be solved analytically.

3.2 Unstable width

Based upon the parametric instability theory and the Taylor expansion technique, an approximate method is introduced to compute the width of the unstable regions U _s and U _c. Without considering system damping, there are two frequency components ω and ϖ (ϖ=2Ω−ω) in the free response of the rotor system due to inertia asymmetry and transverse crack. Thus, the free response of the system could be expressed as follows:

$$ \left \{ \begin{array}{l} x= E_1\cos\omega t+A_1\sin\omega t+F_1\cos\varpi t+B_1\sin\varpi t \\[6pt] y= A_1\cos\omega t-E_1\sin\omega t+B_1\cos\varpi t-F_1\sin\varpi t \\[6pt] \theta_y= G_1\cos\omega t+C_1\sin\omega t+H_1\cos\varpi t\\ \hphantom{\theta_y=} {}+D_1\sin \varpi t \\[6pt] \theta_x= C_1\cos\omega t-G_1\sin\omega t+D_1\cos\varpi t\\[6pt] \hphantom{\theta_x=} {}-H_1\sin \varpi t \end{array} \right . $$

(17)

in which A ₁,B ₁,C ₁,D ₁,E ₁,F ₁,G ₁,H ₁ are the unknown constant coefficients. Substituting Eq. (17) into Eq. (11) and taking the coefficients of the harmonic function to be zero, one can obtain the linear algebraic equations about the unknown constant coefficients as

(18)

in which

(19)

(20)

(21)

Thus, by taking the determinant of Eq. (18) to be zero, one can obtain a equation in form of Φ ²=0, and finally the following frequency equation is obtained as

(22)

where

(23)

After simplification, Eq. (22) can be rewritten in the form

$$ \varPhi=f_n \bar{f}_n-\varGamma/(H\bar{H})+\varPsi=0 $$

(24)

in which

(25a)

(25b)

(25c)

(25d)

The term Ψ is of fourth-order asymmetries Δ _d,ϵ ₁,ϵ ₁₂,ϵ ₂. Hence, it is negligibly small.

As the ω _i (i=1,2) and Ω _s(c) are the forward whirling frequency and unstable rotating speed of the rotor system with zero asymmetries, so f _n (ω _i ,Ω _s(c))=0, $\bar{f}_{n}(\omega _{i}, \varOmega_{\mathrm{s}(\mathrm{c})})=0$ and $\varPhi(\omega_{i}, \varOmega_{\mathrm{s}(\mathrm{c})})=-\varGamma/(H\bar {H})$. When the asymmetries are greater than zero, the unstable region is around the point (ω _i ,Ω _s(c)). Thus, the width of unstable region could be obtained through the Taylor expansion of Φ at the point (ω=ω _i +ς,Ω=Ω _s(c)+ϑ). Assuming ς,ϑ and Δ _d,ϵ ₁,ϵ ₁₂,ϵ ₂ to be small, one has

(26)

From Eq. (24), one can obtain: $\frac{\partial \varPhi}{\partial\omega}=f_{n}\frac{\partial\bar{f}_{n}}{\partial\omega}+\bar {f}_{n}\frac{\partial f_{n}}{\partial\omega}=0$, $\frac{\partial\varPhi }{\partial\varOmega}=f_{n}\frac{\partial\bar{f}_{n}}{\partial\varOmega}+\bar {f}_{n}\frac{\partial f_{n}}{\partial\varOmega}=0$, $\frac{\partial^{2}\varPhi }{\partial\omega^{2}}=2\frac{\partial f_{n}}{\partial\omega}\frac{\partial \bar{f}_{n}}{\partial\omega}$, $\frac{\partial^{2}\varPhi}{\partial\varOmega ^{2}}=2\frac{\partial f_{n}}{\partial\varOmega}\frac{\partial\bar {f}_{n}}{\partial\varOmega}$, and $\frac{\partial^{2}\varPhi}{\partial\omega\varOmega }=\frac{\partial f_{n}}{\partial\omega}\frac{\partial\bar{f}_{n}}{\partial \varOmega}+\frac{\partial f_{n}}{\partial\varOmega}\frac{\partial\bar {f}_{n}}{\partial\omega}$. By substituting these relations into Eq. (26) and simplifying, we have

(27)

Solving the quadratic equation about ς, one can obtain

$$ \varsigma=\frac{- (\frac{\partial f_n}{\partial\omega}\frac{\partial \bar{f}_n}{\partial\varOmega}\vartheta+\frac{\partial f_n}{\partial\varOmega }\frac{\partial\bar{f}_n}{\partial\omega}\vartheta )\pm\sqrt{ (\frac{\partial f_n}{\partial\omega}\frac{\partial\bar{f}_n}{\partial \varOmega}\vartheta-\frac{\partial f_n}{\partial\varOmega}\frac{\partial\bar {f}_n}{\partial\omega}\vartheta )^2-4 (\frac{\partial f_n}{\partial\omega}\frac{\partial\bar{f}_n}{\partial\omega} ) (-\frac{\varGamma}{H\bar{H}} )}}{2 (\frac{\partial f_n}{\partial \omega}\frac{\partial\bar{f}_n}{\partial\omega} )} $$

(28)

When the system is in the unstable region, the ς is a complex number, whose imaginary part characterizes the intensity of the parametric instability. The absolute value of the imaginary part of ς is denoted by κ, and

$$ \kappa=\frac{1}{2}\sqrt{4 \biggl(-\frac{\varGamma}{H\bar{H}} \biggr) / \biggl( \frac{\partial f_n}{\partial\omega}\frac{\partial\bar{f}_n}{\partial \omega} \biggr)- \biggl(\frac{\partial\bar{f}_n}{\partial\varOmega} / \frac {\partial\bar{f}_n}{\partial\omega}-\frac{\partial f_n}{\partial\varOmega } /\frac{\partial f_n}{\partial\omega} \biggr)^2 \vartheta^2} $$

(29)

When κ=0, the system is at the unstable boundary, and we get

(30)

Thus, the width λ _s(c) of the unstable region U _s(c) could be obtained as

(31)

Based upon the parametric instability and Taylor expansion technique, the widths of unstable region are solved approximately utilizing Eq. (31).

4 Computations and discussions

The values of rotor parameters are: m _d=10.43 kg, I _d=0.1397 kgm², I _p=0.2096 kgm², R=0.01188 m, L=0.5045 m. Thus, the inertia ratio β=I _p/I _d=1.5. The Young’s modulus of the shaft is E=2.0×10¹¹ N/m², Poisson’s ratio ν=0.3.

4.1 Validation

The disk location is at l _d=0.25L. Without considering the inertia asymmetry and transverse crack, Fig. 3 gives the four whirling frequencies ω _i varying with the rotating angular velocity Ω in the range of 0–4. According to the definitions in Eq. (14), the intersections between the speed lines of ω=Ω, ω=2Ω−ω ₂ and the first forward whirling frequency line are just the Ω _s and Ω _c, as marked in the figure. The values of these angular velocities are gained analytically using Eq. (15) and Eq. (16), respectively.

Fig. 3

Whirling frequencies of rotor system with l _d=0.25L

When the parametric excitations are considered, the widths of unstable regions could be solved approximately by the harmonic balance method and Taylor expansion technique. In order for the validation, a numerical method based upon the Floquet theory is also utilized, and the detailed solution process is presented in the Appendix. For inertia asymmetry Δ _d=0.2, crack depth σ=0.2 and crack location l _c=0.5L, both the approximate and numerical results of λ _s and λ _c varying with the asymmetric angle ϕ are plotted in Fig. 4, respectively. It is shown that the approximate results are in good agreement with the numerical results. Thus, the approximate method developed in this paper is verified to be reasonable. With the increasing of ϕ, the λ _s is significantly reduced, and reaches the minimum value for ϕ=π/2. However, the variation of λ _c with ϕ is just opposite with that of λ _s, as shown in Fig. 4(b). In this case, the minimum value of λ _c is obtained at ϕ=0. The effects of transverse crack parameters upon the unstable widths are analyzed in the next section.

Fig. 4

Comparisons for the unstable widths obtained by approximate and numerical methods: (a) widths of SIR λ _s; (b) widths of CIR λ _c

4.2 Effects of transverse crack parameters

Two transverse crack parameters are considered in the analysis: crack depth σ and crack position l _c. The stiffness coefficients of a cracked shaft varying with a crack depth for l _c=0.5L is plotted in Fig. 5. It is shown that the values of ϵ ₁,ϵ ₁₂,ϵ ₂ are increasing with σ, while the coupled stiffness coefficient δ is slightly reduced with the increasing of σ.

Fig. 5

The stiffness coefficients of the cracked rotor system with l _c=0.5L: (a) time-invariant stiffness γ,δ; (b) relative amplitudes of time-varying stiffness ϵ ₁,ϵ ₁₂,ϵ ₂

Here, the relative inertia asymmetry is fixed Δ _d=0.2. With the crack position l _c=0.5L and four values of crack depth (σ=0.1,0.2,0.25,0.3), the variations of λ _s and λ _c with ϕ are given in Fig. 6. For the smaller crack depth (σ=0.1), the varying of ϕ has little effect upon the unstable widths. Increasing the crack depth, i.e., σ=0.2,0.25, increasing ϕ from 0 to π/2 would reduce (for λ _s) or increase (for λ _c) the values of unstable width distinctly. Especially for σ=0.25, the λ _s with ϕ=π/2 (or λ _c with ϕ=0) would have the minimum value. Continuing to increase the crack depth (σ=0.3), the system could not gain the minimum unstable widths; even the ϕ is adjusted to π/2 or 0. This means that as long as the Δ _d and l _c are given, there are specific crack depths to make the λ _s and λ _c minimum (even zero). The specific crack depths corresponding to the zero unstable points (ZUPs) are of interest as they could be used for crack identification and instability control of an actual asymmetric rotor-bearing system.

Fig. 6

Effects of crack depth upon the unstable widths: (a) widths of SIR λ _s; (b) widths of CIR λ _c

For the σ=0.2, the effect of crack position (l _c=0.3L,0.4L,0.5L) upon the unstable widths is shown in Fig. 7. One can see that with the l _c moving from the middle point of rotor span to the left support point, the influence of transverse crack is reduced gradually. This is explained as the following: The first whirling mode has a greater modal deflection at the middle point of the rotor span. At this point, the parametric excitation induced by the open transverse crack would bring a significant effect to the rotor system. At other points of the rotor, the impact of the transverse crack becomes weakened. Obviously, the crack position also affects the values of crack depth of ZUPs. The quantitative analysis will be conducted in the next section.

Fig. 7

Effects of crack position upon the unstable widths: (a) widths of SIR λ _s; (b) widths of CIR λ _c

4.3 Zero unstable points (ZUPs)

In order to get the ZUPs, the Γ should be equal to zero, i.e., Γ=0, as shown in Eq. (31). For the SIR, the Θ ₁>0,Θ ₂>0 as the ω ₁>1>ω ₂. According to Eqs. (25a)–(25d), one condition for Γ=0 is ϕ=π/2. When the CIR is considered, the Θ ₁>0 but Θ ₂<0. In this case, the ϕ=0 is the requirement of Γ=0. Therefore, the relationships between the inertia asymmetry Δ _d and cracked shaft stiffness coefficients (determined by σ and l _c) for the ZUPs could be expressed as follows:

$$ \varDelta _{\mathrm{d}}=\pm \bigl(\epsilon_1 \gamma^2-\epsilon_{12}\gamma ^2(H+\bar{H})+ \epsilon_2\delta H\bar{H} \bigr) / (\omega\varpi H\bar{H} ) $$

(32)

where the “+” is for the SIR and the “−” is for CIR. Utilizing Eq. (32), the crack depth corresponding to ZUPs for certain inertia asymmetry could be solved analytically. Figures 8 and 9 give the relationships between σ and Δ _d in order for the ZUPs of SIR and CIR, respectively. Three values of crack position are considered. It is shown that the Δ _d is nonlinear proportional to the σ. With the l _c varying from 0.5L to 0.3L, the relation curve becomes flatter, and the slops are reduced. Under certain Δ _d, in order for the ZUPs, the transverse crack is required to be deeper. It is reasonable because the parametric excitation induced by transverse crack becomes weaker. Moreover, utilizing Figs. 8 and 9, the actual value of crack depth could be determined with certain inertia asymmetry. For Δ _d=0.2 and l _c=0.5L, just the case of Fig. 6 in the previous section, the actual values of σ corresponding to the ZUPs of SIR and CIR are 0.231 and 0.265, which are marked in the figures, respectively. Basically, the required crack depth of CIR is greater than that of the SIR (i.e., 0.265>0.231), indicating that the CIR is more “difficult” to clear away under the same Δ _d.

Fig. 8

The relationship between σ and Δ _d in order for the ZUPs of SIR

Fig. 9

The relationship between σ and Δ _d in order for the ZUPs of CIR

5 Conclusions

Based upon the harmonic balance method and Taylor expansion technique, the unstable widths of a Jeffcott rotor with rotationally asymmetric inertia and open transverse crack are derived approximately and verified by Floquet numerical analysis. Two types of unstable regions, SIR and CIR, are considered and the conditions for ZUPs are given. Besides, the asymmetric angle should be π/2 (for SIR) or 0 (for CIR), and the relationships between the inertia asymmetry and crack parameters (depth and position) are also presented analytically. These results would be useful for crack detection and instability control of the asymmetric rotor-bearing system. In future study, the rotor damping and breathing crack will be taken into account to show their effects upon the parametric instability.

Appendix: Numerical determination of unstable regions based upon the Floquet theory

By taking $\mathbf{y}(t)=[\dot{\mathbf{q}}(t)\ \mathbf{q}(t)]^{T}$, Eq. (11) could be transformed into the state space as

$$ \mathbf{A}(t)\dot{\mathbf{y}}=\mathbf{B}(t)\mathbf{y} $$

(33)

in which the coefficient matrices A(t) and B(t) are expressed as

(34)

(35)

where

(36a)

(36b)

(36c)

The classical method to study the parametric stability uses the Floquet theory. To avoid the additional time domain processing and to keep the inherent advantages of the frequency method (low computational cost and speed compared with the direct integration), it is recommended to use a frequency method for the determination of the stability. According to the Floquet theory, a solution of Eq. (33) can be written as a product of an exponential part and 2π/(2Ω)=π/Ω periodic part. Representing the periodic part by its complex Fourier series expansion, this solution can be written as

$$ \mathbf{y}(t)=\textrm{e}^{2\rho\varOmega t} \sum_{k=-\infty}^{\infty}\textbf {y}_k \textrm{e}^{2\textrm{i}k\varOmega t} $$

(37)

where $\textrm{i}=\sqrt{-1}$, ρ represents the Floquet (or characteristic) exponent and y _k are the complex Fourier coefficients’ vectors. Considering the coefficient matrices A(t) and B(t) are periodic with single harmonic frequency 2Ω, thus they could be rewritten by finite complex Fourier series

(38)

(39)

Substituting Eqs. (37)–(39) into Eq. (33), and simplifying by setting the same harmonic coefficients zero, then one can obtain the following infinite-dimensional eigenvalue problems about ρ as

$$ (\boldsymbol{\varLambda}+\rho\boldsymbol{\varUpsilon})\textbf{Y}=\mathbf{0} $$

(40)

in which

$$\textbf{Y}= \bigl[\cdots\quad\mathbf{y}_{-4}^T\quad \mathbf{y}_{-3}^T\quad\mathbf{y}_{-2}^T\quad\mathbf{y}_{-1}^T\quad \mathbf{y}_{0}^T\quad\mathbf{y}_{1}^T\quad\mathbf{y}_{2}^T\quad \mathbf{y}_{3}^T\quad\mathbf{y}_{4}^T\quad\cdots \bigr]^T, $$

and

(41)

(42)

where $\boldsymbol{\varLambda}^{(0)}_{k}=-\mathbf{B}_{0}+\textrm{i}2k\varOmega \mathbf{A}_{0}$, $\boldsymbol{\varLambda}^{(1)}_{k}=-\mathbf{B}_{-2} + \textrm{i}2k\varOmega\mathbf{A}_{-2}$ and $\boldsymbol{\varLambda}^{(2)}_{k}=- \mathbf{B}_{2}+\textrm{i}2k\varOmega\mathbf{A}_{2}$ (k=…,−1,0,1,…). In order to get approximate numerical eigenvalues for the stability analysis, Eq. (40) should be truncated into a finite-dimensional one. In practice, the first few harmonics are needed to meet the precision requirements. The eigenvalues of Eq. (40) are complex. If the system is stable, the real part of all eigenvalues ρ is negative and the exponential part diminishes as the time passes. On the other hand, if at least one of the eigenvalues has a positive part, the system is unstable.