1 Introduction

Synchronization between interacted elements is very popular in nature and social systems [1,2,3,4]. Particularly in the field of neuroscience, the synchronized firing rhythm, as a form of temporal relationship among neurons, can underline the formation of brain, which contributes to encode memory processes and other cognitive functions [5,6,7,8]. Note that spiking and bursting are two basic timescales for neuronal firing activity. A neuron is thought to be in bursting state when its firing activity alternates between a rest state and repetitive spikes. Synchronous patterns of bursting neurons are diverse, such as spiking synchronization, bursting synchronization and complete synchronization.

At present, there has been a growing interest in bursting synchronization in neuronal network. Several ingredients consisting of heterogeneous delays, noises, autapse and connection topology have been witnessed by their significance in shaping bursting synchronization. For example, Wang et al. have identified the mechanisms of synchronous bursts and desynchronized bursts on the neuronal networks in the presence of time delays [9,10,11]. Burić et al. [12] have discussed the influence of white noise on the synchronization between a pair of electrically coupled Hindmarsh–Rose bursting neurons. Zheng and Lu [13] have found that chaotic burst synchronization can be observed if the link probability and the coupling strength are large enough. Guo et al. have discussed how the self-back autaptic transmission tames and modulates neural firing dynamics [14, 15]. Recent experiment has revealed that connectivity between regions of cerebral cortex in macaque monkeys and cats possesses a modular structure [16, 17]. Modular neuronal network may be a good candidate model for numerical simulation of brain neuronal network, which has been believed to understand the brain’s cognitive function better. Some attention has been shifted to the collective dynamics of bursting neurons on modular neuronal network [18,19,20]. For example, Yang and Wang [18] have explored the development of global burst synchronization in a modular neuronal network from the mesoscopic viewpoint. Batista at al. [19] have discussed that how the coupling strength as well as the probabilities of intra-cluster and inter-cluster connections influences bursting synchronization in the modular neuronal networks.

On the other hand, there has been a resurgence of interest in the topic of synaptic plasticity, which is helpful to describe the property of changed synaptic weights among coupled neurons. It is shown that for discrete neural circuits including the hippocampus and amygdala synaptic plasticity is a popular feature, which regulates synaptic efficacy as various timescales from milliseconds to minutes [21, 22]. As a matter of fact, in the growth of neurons together with the learning and memorizing processes, the weights of synapses among connected neurons keep updated rather than hold constant [23,24,25,26,27]. Till now, many learning rules regulating synaptic weights, such as Hebbian rule [28], Oja’s rule [23, 24, 29,30,31,32] and spike-timing-dependent plasticity rule [33, 34], have been proposed to describe synaptic plasticity. Recently, some heuristic firing dynamics induced by synaptic plasticity have been reported in neuronal network. For example, Han et al. [23] have revealed that synaptic plasticity regulated by Oja’s rule can help synchronization in the electrically coupled network but impair synchronization in the chemically coupled one. Zheng et al. [24] have found that there exists an optimal learning rate which makes the excitement of neuronal network strongest. Kube et al. [33] have reported that the introduction of spike-timing-dependent plasticity can modify the weights of synaptic connection in such a way that synchronization of neuronal activity is considerably weakened. Zhang et al. [35] have investigated the impact of short-term synaptic plasticity on spike propagation in neuronal network.

Now how the synaptic plasticity influences the firing dynamics of neuronal network is becoming a great concern. However, in most of the researches on neurodynamics in the literature, for the purpose of simplicity and clarity, the synaptic plasticity is ignored and the weights of synapses among neurons are kept unchanged. For the objectivity of synaptic plasticity in neuronal network, exploring the relationship between synaptic plasticity and the firing dynamics is of great realistic significance. The focus of this study will be on the collective bursting dynamics in a modular neuronal network with synaptic plasticity. To the best of our knowledge, there is no attention devoted to this issue until now. The rest of this study is organized as follows: Sect. 2 introduces a model of modular neuronal network and quantitative measurements for bursting synchronization. Section 3 illustrates the main numerical results. The conclusion is presented in Sect. 4.

2 Model presentation and synchronization measurements

In this section, constructing a modular neuronal network with synaptic plasticity is firstly presented and then quantitative measurements for bursting synchronization are followed.

2.1 Model presentation

The considered modular network consists of M sub-networks, each of which is possessed of small-world property. The sub-network obeys the procedure proposed by Newman and Watts [36], i.e., starting from a regular ring of N nodes with periodic boundary condition where each node is connected to its k nearest neighbors, and then adding shortcuts between non-nearest nodes with intra-connection probability \(p_{\mathrm{intra}} \). After generating all the sub-networks, we choose some pairs of nodes from different sub-networks with interconnection probability \(p_{\mathrm{inter}}\) and then add links between them. By doing this, a modular network is constructed. Without loss of generality, the parameters of network configuration are fixed at \(M = 2,N = 80,k = 6, p_{\mathrm{intra1}} = 0.1, p_{\mathrm{intra2}} = 0.09, p_{\mathrm{inter}} = 0.019\) in this study. \(p_{\mathrm{intra1}}\) and \(p_{\mathrm{intra2}}\) denote the intra-connection probability for the two sub-networks, respectively.

When employing the Rulkov map [37] to simulate the local dynamics of individual neurons, the modular neuronal network with synaptic plasticity can be described by the following set of discrete equations:

$$\begin{aligned} \left\{ \begin{array}{l} x_{I,i} (n+1)=\alpha /(1+x_{I,i}^2 (n))+y_{I,i} (n)\\ \quad +\varepsilon \sum _{J=1}^M \sum _{j=1}^N {A_{I,J} (i,j)} w_{I,J} (i,j,n)H(x_{J,j} (n)-\Theta )\\ y_{I,i} (n+1)=y_{I,i} (n)-\beta x_{I,i} (n)-\gamma \\ \Delta w_{I,J} (i,j)=L*\arctan \{x_{I,i} (n)[x_{J,j} (n)\\ \quad -x_{I,i} (n)w_{I,J} (i,j,n)]\} \end{array}\right. \end{aligned}$$
(1)

in which \(x_{I,i} (n)(i=1,2,\ldots ,N,I=1,\ldots ,M)\) represents the membrane potential of neuron i in Ith sub-network and \(y_{I,i} (n)\) is the corresponding recovery variable. The dynamical parameter \(\alpha \) directly affects the spiking-bursting activities of neurons. \(\beta \) and \(\gamma \) describe the slow time scale. To make the isolated neuron produce chaotic bursting behavior, the parameters of Rulkov map are chosen as: \({\alpha \in [4.1,4.4]},\beta = \gamma = 0.001.\, \varepsilon {>}0\) is the global coupling strength. \(H(x)=\left\{ \begin{array}{l} {0,x\le 0} \\ {1,x>0} \\ \end{array}\right. \) and the synaptic threshold is selected as \(\Theta =0.0\). \(A_{\textit{I,J}} (\textit{i,j})\) is a connectivity matrix. In detail, \(A_{\textit{I,J}} (i,j) = A_{\textit{J,I}} (\textit{j,i})=1\) if neuron i in Ith sub-network is connected with neuron j in Jth sub-network, otherwise \(A_{\textit{I,J}} (\textit{i,j}) = A_{\textit{J,I}} (\textit{j,i}) = 0\) and \(A_{\textit{I,I}} (\textit{i,i})=0\). \(w_{\textit{I,J}} (\textit{i,j,n})\) denotes the updated synaptic weights between neuron i in Ith sub-network and neuron j in Jth sub-network. Specifically, \(w_{\textit{I,J}} (\textit{i,j,n})\ne w_{\textit{J,I}} (\textit{j,i,n})\) if there is a connection between neuron i in Ith sub-network and neuron \(j(i\ne j)\) in Jth sub-network, \(w_{\textit{I,J}} (\textit{i,j,n}) = w_{\textit{J,I}} (\textit{j,i,n})=0\) otherwise. There is no self-connection for all neurons, i.e., \(w_{\textit{I,I}} (\textit{i,i,n}) = 0\). \(\Delta w_{\textit{I,J}} (\textit{i,j})\) denotes the change in synaptic weight from neuron i in Ith sub-network to neuron j in Jth sub-network. Here a modified Oja’s learning rule is implemented in this modular network through changes in the strength of synaptic weight between neurons. L represents the learning rate, which reflects how quickly the synaptic weights update in response to neuron activation [21, 28].

Fig. 1
figure 1

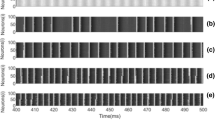
Spatiotemporal patterns of the modular network for different values \(\varepsilon \) when \(\alpha =4.2\) and \(L=0.0\): a \(\varepsilon =0.0\), b \(\varepsilon =0.003\), c \(\varepsilon =0.03\), d \(\varepsilon =0.07\), e \(\varepsilon =0.1\). The neurons in the modular neuronal network gradually burst consistently as the coupling strength \(\varepsilon \) is increased

Full size image

2.2 Synchronization measurements

To quantitatively describe the degree of bursting synchronization in the modular neuronal network, the order parameter R is introduced as follows:

$$\begin{aligned} R=\frac{1}{MN}\left| {\sum _{J=1}^M {\sum _{j=1}^N {e^{i\phi _{J,j} (n)}} } } \right| \end{aligned}$$
(2)

where \(\phi _{J,j} (n)\) indicates the burst phase for neuron j in the Jth sub-network at time n. The burst phase \(\phi _{J,j} (n)\) is defined as

$$\begin{aligned}&\phi _{J,j} (n) =2\pi k\nonumber \\&\quad +\,2\pi \frac{n-n_{J,j,k} }{n_{J,j,k+1} -n_{J,j,k} }(n_{J,j,k} \le n\le n_{J,j,k+1} ) \end{aligned}$$
(3)

in which \(n_{J,j,k}\) denotes the moment of the kth burst for neuron j in the Jth sub-network. For the synchronized state, the burst phases nearly coincide; thus, R tends to unity. In contrast, \(R\approx 0\) when the burst phases are weakly correlated. Clearly, larger R implies a higher degree of bursting synchronization of interacted neurons.

In addition, the mean field \(X(n)=\frac{1}{MN}\sum _{J=1}^M \sum _{j=1}^N {x_{J,j}} (n)\) can describe the mean membrane potential of neurons in the modular neuronal network. Higher degree of bursting synchronization is characterized by large-amplitude oscillation of mean field, which results in larger variance \({\hbox {Var}}(X)\) of the mean field X(n). On the contrary, small-amplitude fluctuation of the mean field X(n) as well as the smaller variance \({\hbox {Var}}(X)\) indicates lower degree of bursting synchronization. Therefore, the mean field X(n) together with its variance \({\hbox {Var}}(X)\) can be also employed to quantitatively depict the degree of bursting synchronization.

3 Simulation results

In what follows, how the coupling strength influences bursting synchronization in the modular neuronal network is firstly investigated when the synaptic weights among neurons keep constant, then the effect of synaptic plasticity on bursting dynamics, particularly the excitability and synchronizability of bursting neurons, is discussed. Setting initial conditions of Eq. (1) randomly distributing in the interval of [0,1], numerical integration of the considered modular neuronal network is carried out by the explicit Euler technique. To guarantee statistical accuracy, all the following numerical results, except for the spatiotemporal patterns of the modular network, are obtained by averaging over 20 different realizations.

3.1 Coupling-induced bursting synchronization in the modular network

Coupling strength can have a dramatic effect on bursting synchronization of interacted neurons. To describe how the coupling strength affects the neuronal bursting dynamics vividly, Fig. 1 illustrates some typical spatiotemporal patterns of the modular network when the synaptic weights among neurons keep constant, i.e., the learning rate \(L=0.0\). When neurons are uncoupled (i.e., \(\varepsilon = 0.0)\), the spatiotemporal behavior of the modular network, displayed in Fig. 1a, presents a de-synchronous state for the reason that all the bursting neurons behave chaotic independently in the absence of coupling. When the coupling is present (e.g., \(\varepsilon =0.003)\), as shown in Fig. 1b, some neurons in the modular neuronal network start to burst consistently. With the further increase in coupling strength (e.g., \(\varepsilon =\hbox {0.03, }0.07,\hbox {0.1})\), the spatiotemporal patterns, displayed in Fig. 1c–e, indicate a near coincidence between the times when the neurons start bursting and end bursting, which is a characteristic feature of bursting synchronization.

The qualitative analysis in Fig. 1 implies that coupling strength can induce bursting synchronization in the modular neuronal network. To account for this phenomenon quantitatively, Fig. 2a depicts the evolution of order parameter R during the course of coupling strength \(\varepsilon \). From this figure, one can see that R increases rapidly as \(\varepsilon \) is increased, and it approaches 1 when \(\varepsilon \) exceeds a critical value (\(\varepsilon \approx 0.03\)). Meanwhile, the dependence of variance \({\hbox {Var}}(X)\) of the mean field X(n) on coupling strength \(\varepsilon \) is illustrated in Fig. 2b. As \(\varepsilon \) is increased, the increasing trend of \({\hbox {Var}}(X)\) also verifies that the coupling is greatly beneficial to induce bursting synchronization in the modular neuronal network.

Fig. 2
figure 2

a The order parameter R and b the variance \({\hbox {Var}}(X)\) as the function of coupling strength \(\varepsilon \) when \(\alpha =4.2\) and \(L=0.0\). Upon increasing \(\varepsilon \), R and \({\hbox {Var}}(X)\) increase and R approaches 1 when \(\varepsilon \) exceeds a critical value

Full size image

The above result is obtained when the local dynamical parameter of Rulkov map is fixed at \(\alpha =4.2\). Furthermore, Fig. 3 shows the dependence of R and \({\hbox {Var}}(X)\) on \(\varepsilon \) for other values of dynamical parameter such as \(\alpha =4.15,4.25,4.3\). It is clear that, for various values of \(\alpha \) lying in the interval [4.1, 4.4], the variations of R and \({\hbox {Var}}(X)\) with respect to \(\varepsilon \) are similar to the case of \(\alpha =4.2\). That is to say, the coupling strength can induce bursting synchronization in the modular network, which has certain robustness to the change of the local dynamical parameter \(\alpha \).

Fig. 3
figure 3

a The order parameter R and b the variance \({\hbox {Var}}(X)\) as the function of coupling strength \(\varepsilon \) when\(\alpha =4.15,4.25,4.3\) and \(L=0.0\). It is clear that the variations of R and \({\hbox {Var}}(X)\) with respect to \(\varepsilon \) are similar to the case of \(\alpha =4.2\) displayed in Fig. 2

Full size image

3.2 Effects of synaptic plasticity on excitability and synchronizability of bursting neurons

Section 3.1 states that coupling strength can make all the bursting neurons get synchronized when the synaptic weights in the modular neuronal network hold constant. How will the collective bursting dynamics be changed when the synaptic weights keep updated, i.e., the learning rate \(L\ne 0.0\)? To solve this problem, we fix the dynamical parameter \(\alpha =4.2\) and the coupling strength at \(\varepsilon =0.0\hbox {7}\), and then illustrate some typical spatiotemporal patterns together with its corresponding mean field X for different learning rates L. For comparity, the case for \(L=0.0\), just as shown in Figs. 4a and 5a, is also employed. Figures 4b–f and 5b–f depict the spatiotemporal patterns and the corresponding mean fields of the modular neuronal network when the learning rate is \(L=0.02,0.05,0.08\) and 0.1, respectively. A characteristic feature of Figs. 4 and 5 is that more and more bursts appear, and thus the bursting rhythms of neurons are obviously accelerated upon increasing learning rate. This result implies the excitability of bursting neurons is obviously enhanced by the updated synaptic weights in the modular neuronal network.

Fig. 4
figure 4

Spatiotemporal patterns of the modular network for different learning rates when \(\varepsilon =0.07\): a \(L=0.0\), b \(L=0.02\), c \(L=0.05\), d \(L=0.08\), e \(L=0.1\). As the L increases, the spatiotemporal behaviors of the modular network present more de-synchronous state and the bursting rhythms of neurons are obviously accelerated

Full size image
Fig. 5
figure 5

Mean field of the modular network for different learning rates when \(\varepsilon =0.07\): a \(L=0.0\), b \(L=0.02\), c \(L=0.05\), d \(L=0.08\), e \(L=0.1\). As L increases, the amplitude of mean field gets smaller and the bursting rhythms of neurons are obviously accelerated

Full size image
Fig. 6
figure 6

Dependence of a the average bursting rate \(\Omega \)and b the average bursting period \({<}\)ISI\({>}\) on the learning rate L when \(\varepsilon =0.07\). Upon increasing L, \(\Omega \) increases and \({<}\)ISI\({>}\) decreases gradually; moreover, both of them wander at a certain value

Full size image

Excitability of neurons can reflect how active the neuronal network is to some extent. In order to explore the influence of synaptic learning rate on the degree of neuronal excitability in the modular neuronal network quantitatively, two excitability indexes, i.e., the average bursting frequency \(\Omega =\frac{1}{MN}\sum _{J=1}^M {\sum _{j=1}^N {\mathop {[\lim }\limits _{n\rightarrow \infty } } (\phi _{J,j} (n)-\phi _{J,j} (0))/n]} \) and the average bursting period \({<}ISI{>}\,=\,\frac{1}{MN}\sum _{J=1}^M \sum _{j=1}^N {T_{J,j}}\), are introduced. Here \(\phi _{J,j} (n)\) and \(T_{J,j} \) denote the burst phase and the inter-burst interval in the considered modular neuronal network, respectively. Obviously, the larger the average bursting frequency or the smaller average bursting period, the more excited the neuronal network is.

Figure 6 depicts the dependence of the two mentioned excitability indexes \(\Omega \) and \({<}\)ISI\({>}\) on the learning rate L with the coupling strength \(\varepsilon \) being fixed, respectively. It is clear that along with the increase in L, the average bursting frequency \(\Omega \) gradually increases and then fluctuates around a certain value. Correspondingly, the average bursting period \({<}\)ISI\({>}\) gradually decreases and also wanders at a certain value with increasing L. It means that the excitability of neuronal can be enhanced by the incorporation of changed synaptic weights; moreover, the excitability level can be gradually maintained in a plausible context. The biological implication of this phenomenon could be understood as follows. In biological neuronal networks, the efficacy of synapses is governed by some complex mechanisms such that it keeps changing in the growth of neurons together with the learning and memorizing processes. The modified Oja’s learning rule contained in Eq. 1 indicates that the change of synaptic weights in response to neuron activation is dependent on the synaptic learning rate. During the initial development period of the brain, the bursting activities of neurons could be enhanced by the increase in synaptic learning rate, that is, the updated synaptic weights improve the excitability of neurons. Meanwhile, the firing activities of glial neurons regulated by the synaptic learning rate can suppress excitability of neurons to prevent over-excitability [23, 38]. Thus, the excitability level of neuronal network can be maintained in a plausible context under the modulation of changed synaptic weights. This phenomenon could accord with the brain’s character and imply that synaptic plasticity is beneficial to the maturation of brain [23, 24, 38].

Fig. 7
figure 7

a The order parameter R as a function of coupling strength \(\varepsilon \) for various L. One can see that the larger L, the lower the R–\(\varepsilon \) curve. b–d The order parameter R as a function of learning rate L for fixed coupling strength \(\varepsilon \). R is basically decreased with the increase in L

Full size image

On the other hand, through a careful inspection of Fig. 4a, one can observe that all bursting neurons are in a fairly good synchronized state when the synaptic plasticity is absent. However, the status of bursting synchronization is a little depressed with the presence of synaptic plasticity, as shown in Fig. 4b–e. This phenomenon is also verified by the corresponding mean field. Compared with the large amplitude of mean field in the absence of synaptic plasticity, as shown in Fig. 5a, the relative small amplitude of mean field in the case of different learning rates, as displayed in Fig. 5b–d, further implies that the updated synaptic weights are a little disadvantageous to bursting synchronization.

In what follows, the adverse influence of synaptic plasticity on bursting synchronization is discussed detailedly. Figure 7a illustrates the dependence of R on coupling \(\varepsilon \) for different learning rates such as \(L=0.02,0.05,0.08\) and 0.1. From these figures, one can see that the order parameter R in the presence of synaptic plasticity is no more than that in the absence of synaptic plasticity. That is to say, the R–\(\varepsilon \) curve in the case of \(L=\hbox {0.0}\) is not lower than the R–\(\varepsilon \) curve in the case of \(L\ne \hbox {0.0}\); moreover, the larger the learning rate L, the lower the R–\(\varepsilon \) curve. In order to get a good visual effect, we fix coupling strength (e.g., \(\varepsilon =0.0\hbox {3})\) and depict the relationship of the order parameter R and the learning rate L in Fig. 7b. Obviously, the order parameter R is basically decreased with the increase in learning rate L. As shown in Fig. 7c, d, this phenomenon still appears when the coupling is altered to other values such as \(\varepsilon =0.05,0.07\). The above result indeed implies that the larger learning rate is not favorable to bursting synchronization in this modular neuronal network. The less synchronizability of bursting neuron could be explained as follows. It has been evidenced that excitability of bursting neuron is enhanced by the increase in synaptic learning rate, which might consume more energy and in turn result in not enough energy to preserve a fairly good synchronization in the modular network. In fact, some neurological diseases such as Parkinson and epilepsy are caused by the pathologically strong synchronization of bursting neurons. Hence, the updated synaptic weight may have great significance to modulate such undesirable synchronized behavior of the neuron population.

4 Conclusion

Note that most of research work on neurodynamics in the literature has neglected synaptic plasticity and kept synaptic weights unchanged for simplicity. Thus, the issue concerning how the synaptic plasticity influences the firing dynamics of neuronal network is puzzled until now. This study, by constructing a modular neuronal network with NW small-world sub-networks, has explored the influence of synaptic plasticity on the collective bursting dynamics of interacted bursting neurons. The considered synaptic plasticity is described by a modified Oja’s learning rule. To measure bursting synchronization and firing excitability, we numerically simulate several key indexes such as the order parameter and the average bursting frequency, and the results reveal that the learning rate together with the coupling strength can have remarkable influences on the bursting dynamics of modular neuronal network. When the synaptic weights among neurons keep constant, the results evidence that large coupling strength can induce bursting synchronization in the modular network, which has certain robustness to the change of local dynamical parameter. With the incorporation of synaptic plasticity into the modular neuronal network, i.e., the synaptic weights keep updated, it has been found that synaptic learning rate can regulate both excitability and synchronizability of bursting neurons. In detail, the coupling strength induced bursting synchronization is a little depressed by the addition of learning rate, i.e., the synchronizability of bursting neurons is gradually degraded as the learning rate is increased. Meanwhile, the excitability of neurons is found to be enhanced by the increase in learning rate; moreover, the excitability level can be maintained in a plausible context. The above phenomena indicate that the emergence of synaptic plasticity can shape the bursting dynamics in this modular neuronal network significantly. These findings could be expected to understand the important role of synaptic plasticity on neural coding in biological neural networks.