Flexural–flexural–extensional–torsional vibration analysis of composite spinning shafts with geometrical nonlinearity

Abstract

In this paper, nonlinear dynamics of an unbalanced composite spinning shaft are studied. Extensional–flexural–flexural–torsional equations of motion are derived via utilizing the three-dimensional constitutive relations of the material and Hamilton’s principle. The gyroscopic effects, rotary inertia and coupling due to material anisotropy are included, while the shear deformation is neglected. To analyze the rotor dynamic behavior, the full form of the equations without any simplification assumption (e.g., stretching or shortening assumption) is used. The method of multiple scales is applied to the discretized equations. An analytical expression as a function of the system parameters describing the forced vibration of a spinning composite shaft in the neighborhood of the primary resonance is obtained. The discretization is done with both one and two modes, and the results are compared. It is shown that although the excitation is tuned in the neighborhood of the first mode, one-mode discretization is not sufficient and it leads to inaccurate results. It shows the necessity of employing at least two modes in discretization due to the coupling in the equations. The effects of the external damping, eccentricity and the lamination angle on the vibration amplitude are investigated. In addition, the effect of the extensional–torsional coupling on the frequency response curves is investigated. To validate the perturbation results, numerical simulation is used.

1 Introduction

Without doubt, spinning shafts can be considered as a vital part in various mechanical devices such as automobiles and helicopters in a long range of history up to now. Composite material shafts have also been investigated in recent decades as a new reliable potential candidates for replacement of conventional metallic shafts in a vast area of applications. A composite shaft not only has a great strength-to-weight ratio, but also has a lower vibration level and a longer service life compared to its metallic counterpart. According to these considerable benefits, various investigations have been carried out to analyze these shafts which have led to different mathematical models describing dynamic behavior of composite material shafts.

Symonds and Zinberg [1], for example, used an equivalent modules beam theory (EMBT) to model composite shaft and compared the critical speed with those of the tests they had performed. dos Reis et al. [2] considered Timoshenko beam theory with the Donnell thin shell theory to derive the stiffness matrix. They employed an approximate finite element of Ruhl and Booker [3] to derive the equations of motion of the shaft. The model was used to calculate the critical speed. Bert [4] later in 1992 used Euler–Bernoulli beam theory to present a model which include gyroscopic as well as bending–torsion coupling effect. Kim and Bert [5] employed a shell theory of first-order approximation to derive the equation of motion. They used their model to obtain the critical speed. Bert and Kim [6] adopted Bresse–Timoshenko beam theory to derive the governing equations. They had shown that the transverse shear deformation effect is important in the determination of the critical speed of short shafts. Singh and Gupta [7] presented two models by invoking EMBT and layer-wise beam theory for each one of them. The model included bending and stretching deformation effects. It was shown that two models result in different critical speed in the case of asymmetric lamination. Chen and Peng [8] adopted a Timoshenko beam theory to obtain the equations of motion. They studied the stability condition of a composite shaft under periodic axial compressive load by employing the finite element method. In 2001, Song et al. [9] further developed a model for thin-walled composite shaft based on a thin-walled beam theory. The model was used to investigate the natural frequencies and stability in the case of axial edge loads and variation of lamination angle. Chang et al. [10] presented a model based on first-order Timoshenko beam theory and adopted finite element method to derive the governing equations. The model was used to investigate the critical speed, natural frequencies, mode shapes and the transient response caused by unbalance force. Chang et al. [11] analyzed the vibration of a composite shaft containing randomly oriented reinforcement. They adopted the Mori–Tanaka mean-field theory to account for the interactions at finite concentrations of reinforcements in the composite material. The finite element method was used to investigate the natural frequencies of the stationary shafts, and the whirling speeds as well as the critical speeds of rotating shafts. Banerjee and Su [12] developed the dynamic stiffness matrix of a spinning composite beam to analyze free vibration of a composite shaft. Hamilton’s principle was used to derive the governing equations. They applied Wittrick–Williams algorithm to the resulting dynamic stiffness matrix to obtain the natural frequencies. The model also included torsion–bending coupling effect. Sino et al. [13] introduced a simplified homogenized beam theory (SHBT) to evaluate natural frequencies and instability thresholds. Badi et al. [14] employed finite element analysis (FEA) to examine the effects of fiber orientation angles and stacking sequence on the torsional stiffness, natural frequencies, bending strength fatigue, life and failure modes of composite tubes. Experimental tests were carried out on a composite drive shaft to validate the FEA model. Montagnier and Hochard [15] considered Timoshenko beam model to develop a formulation for the flexural vibration of a composite driveshaft mounted on viscoelastic supports. They studied the optimization by invoking the genetic algorithm. Montagnier and Hochard [16] later used the Rayleigh–Timoshenko equation to study the dynamic of a supercritical composite shaft mounted on viscoelastic supports to predict instabilities. They investigated the effects of different factors such as rotary inertia, gyroscopic forces, transverse shear and the supports stiffness. They also included hysteric damping in their analysis. The most effective factors were the transverse shear and supports stiffness. The effects of composite stacking sequence, the shaft length and supports stiffness on the threshold speed were studied in the paper. Yongshen et al. [17] employed variational asymptotic method (VAM) and Hamilton’s principle to derive the equations of motion of a composite shaft. The effects of fiber orientation, ratios of length over radius, ratios of radius over thickness and shear deformation on natural frequency and critical speeds were investigated. The next year Yan Qing Wang [18] studied the large-amplitude (geometrically nonlinear) vibrations of rotary laminated composite circular cylindrical shells. The shell was subjected to radial harmonic excitation in the neighborhood of the lowest resonance. The Donnell’s nonlinear shallow shell theory was utilized to consider nonlinearities due to the large-amplitude shell motion. The method of harmonic balance was applied to investigate the forced vibration response of the two-degrees-of-freedom system. The stability of analytical steady-state solution was analyzed. The effect of rotating speed on the nonlinear dynamic response of the system was also investigated. Yongshen et al. [19] investigated the primary resonances of a composite nonlinear shaft using thin-walled beam theory. Nonlinearity was due to von Karman effect. All coupling terms were neglected, and equations were reduced to flexural–flexural ones.

Using accurate analytical solution results in a good prediction of the system’s behavior and could definitely cause the performance of the shafts made of composite materials to improve and provides a better understanding of underlying physics concepts and highly complex interactions of the system encountered in cases of nonlinear vibration phenomena. However, the usual procedure in composite shaft vibration analysis in nonlinear cases is numeric. The model is usually assumed linear when the problem is solved analytically. There are some nonlinear analytical investigations considering vibrations of spinning metallic shafts. For example, Hosseini and Khadem [20] used the multiple scales method to analyze the free vibration of a rotating shaft with nonlinearity in curvature and inertia. They found that both forward and backward natural frequencies were excited. An analytical expression for transverse vibration in two planes was obtained. Later same authors [21] investigated combination resonances in a rotating shaft. They used the harmonic balance method to analyze the system and obtained the frequency response curve. The effects of mass moment of inertia, eccentricity and external damping coefficient were studied. The loci of saddle node bifurcation points were also investigated. Khadem et al. [22] adopted the method of multiple scales to analyze the primary resonances of a simply supported in-extensional rotating shaft with large amplitudes. The effects of diametrical mass moment of inertia, eccentricity and external damping as well as bifurcation points were investigated. Shahgholi and Khadem [23] studied primary and parametric resonances of a nonlinear rotating asymmetrical shaft with unequal mass moments of inertia and bending stiffness in the direction of principle axes. The method of multiple scales was applied. The influences of inequality of mass moments of inertia and bending stiffness and inequality between two eccentricities both corresponding to the principle axes were investigated. Hosseini and Zamanian [24] studied the free vibration of a simply supported rotating shaft with stretching nonlinearity. Rotary inertia and gyroscopic effects were included, but shear deformation was neglected. The equations of motion were derived with the aid of the Hamilton’s principle. The method of multiple scales was applied directly to the complex form of the equations to analyze the free vibration. An analytical solution describing the nonlinear vibration in two transverse planes was obtained. Again it was shown that both forward and backward natural frequencies were excited. The results were validated with numerical simulation. Pai et al. [25] analyzed dynamic characteristic of a downward vertical spinning Rayleigh beams with six different sets of boundary conditions in both linear and nonlinear methods. They showed that an important linear term was missing in many reports in the literature because of inconsistent use of nonlinear terms in derivation. The influences of rotary inertia, spinning speed, Coriolis and centrifugal forces, slenderness and gravity on forward and backward whirling speeds, whirling mode shapes and critical speeds were investigated. They found that there are infinite forward and backward critical speeds for a spinning Rayleigh beam. Hosseini [26] investigated the stability and bifurcations in a simply supported rotating shaft. The shaft was modeled as an in-extensional spinning beam with large amplitude. The bifurcations considered was Hopf and double zero eigenvalues. Center manifold theory and the method of normal form were used to obtain analytical expression. Hosseini et al. [27] investigated free vibration of an in-extensional spinning beam with six general boundary conditions. Nonlinearities were due to curvature and inertia. Rotary inertia and gyroscopic effects were included, while shear deformation was neglected. The method of multiple scales was used to obtain an analytical expression for lateral vibration in two planes. Shahgholi and Khadem [28] studied the Hopf and double bifurcations analysis of an asymmetrical rotating shaft with stretching nonlinearity. The shaft was composed of viscoelastic material which was modeled using a Kelvin–Voigt model. The center manifold theory was utilized to study the dynamic of the system. Zhu and Chung [29] developed new nonlinear model based on Bernoulli–Euler and von Karman nonlinear strain theory for a spinning beam. Extensional–flexural coupling was included.

There are also a number of researches that have dealt with cylindrical shell. For example, Wang et al. [30] studied nonlinear travelling wave response of a cantilever circular cylindrical shell. The shell was subjected to a concentrated harmonic force moving in a concentric circular path at a constant velocity. They used Donnell’s shallow shell theory to analyze moderately large vibration. The method of harmonic balance was adopted to investigate the nonlinear dynamic response in forced oscillation of the system. They also studied the stability of period solution. Wang et al. [31, 32] analyzed nonlinear dynamic response of a cantilever rotating circular cylindrical shell with precession of vibrating shape subjected to a harmonic excitation. They used Donnell’s shallow shell theory. Wang et al. [33] studied the nonlinear vibration of a cantilever cylindrical shell under a concentrated harmonic excitation moving in a concentric circular path. They developed the method of averaging to study the nonlinear traveling wave responses of the multi-degrees-of-freedom system. They used the averaged system to investigate the bifurcation phenomenon. Wang et al. [34] studied the nonlinear vibration of a thin laminated composite cylindrical shell moving in axial direction having internal resonances. They developed an improved nonlinear model and used harmonic balance method to analyze the nonlinear dynamic response.

Fig. 1

Principal coordinate axes on an arbitrary layer of the shaft

The shaft models which were mentioned above have an acceptable accuracy in small amplitude, but none of them has dealt with large amplitude except for those of the metallic shafts. Most researchers have also used numeric methods for dealing with nonlinear problems in composite rotors. In this paper, a new set of nonlinear equations is derived for composite spinning shafts based on Bernoulli–Euler theory. Of particular interest in this study is that the governing equations include the extensional–flexural–flexural–torsional vibrations of the spinning shaft with geometrical nonlinearity and linear couplings due to the material anisotropy. Without any simplifying assumption (e.g., shortening or stretching assumption), these equations are employed to investigate the nonlinear dynamics behavior using perturbation theory. Noted that in previous works [20,21,22,23,24], with employing these assumptions, the equations were reduced to flexural–flexural ones. But, in the present paper, due to coupling presence, full version of the equations is used. The equations include gyroscopic as well as extensional–flexural–torsional coupling effects. Shear deformation is neglected due to the assumption that the shaft is slender. The equations of motion are derived by employing the Hamilton’s principle. To study the forced vibration of the spinning composite shaft, it is assumed that there is an unbalance force due to the imperfection in the composite shaft geometry and the shaft is hinged at both ends. The equations are discretized using the Galerkin method, and then, the method of multiple scales is used to analyze the primary resonance. Although the spin is tuned in the neighborhood of the first mode, one-mode discretization is not sufficient due to the second-order nonlinear terms existing in the equations of motion. The discretization is done with both one mode and two modes, and the results are compared which shows discrepancy between amplitudes in the neighborhood of the primary resonance. This is an important result showing that the one-mode discretization is not always accurate. A comparison is made between amplitude variations of these two cases. There is no assumption in the stacking sequence which means lamination can be either symmetric or asymmetric. The effects of the external damping, eccentricity and the lamination angle on the vibration amplitude are investigated. Each result is compared with numerical simulation to validate the solution.

2 Equations of motion

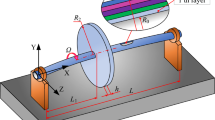
Figure 1 shows a composite hollow shaft made of boron/epoxy laminas that has ten layers, each one with a specific fiber orientation angle $\eta$. The shaft is spinning with a constant angular velocity $\Omega$ about its longitudinal axis (i.e., X-axis) and has a length of l. The bearings are stiff in comparison with the shaft so the boundary conditions can be assumed as hinge. The layup is $[90^{\circ }/45^{\circ }/-45^{\circ }/0^{\circ }_6 /90^{\circ }]$ starting from the inside surface of the shaft. In this section, extensional–flexural–flexural–torsional equations of the shaft are derived. The nonlinearity due to the large deformation is considered in the equations.

Figure 1 shows a composite shaft with the cylindrical and principal coordinates systems attached to it. Cylindrical coordinate system denoted by $x-r-\tau$ shows the general direction of the shaft, but the principal coordinate system denoted by 1-2-3 is attached to an arbitrary lamina and depicts the principal directions of the material.

2.1 Kinetic and strain energies

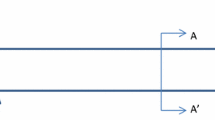
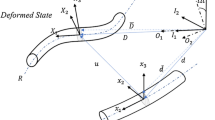
Here, the kinetic and strain energies will be derived. Figure 2 shows a schematic of a deformed rotating composite shaft. There are two coordinate systems. The frame $X{-}Y{-}Z$ is an inertial coordinate system positioned at point O, and frame $x{-}y{-}z$ is a local coordinate system fixed to the centerline of the shaft.

The following assumptions are made concerning the description of the composite shaft motion:

• 1. The rotating shaft is hinged at both ends. Indeed, it is assumed that the bearings are much stiffer than of the shaft; so, the compliance of the bearing is negligible.

• 2. The shaft is hollow and has a uniform annular cross section.

• 3. The shaft is spinning at a constant angular velocity about the axial coordinate.

• 4. The shaft is slender; so, the gyroscopic effects is included, but shear deformation is neglected.

• 5. Amplitude is large, and this leads to geometrical nonlinearity.

• 6. Dissipation in the shaft is modeled as viscous damping.

• 7. The material in every layer is linear elastic and macroscopic. The shaft is modeled with orthotropic material property.

Fig. 2

A schematic of the deformed shaft and the local coordinates, $x{-}y{-}z$

The kinetic energy of the shaft can be expressed as [20]

$$\begin{aligned} T= & {} \frac{1}{2}\int _0^l I_0 (\dot{u}^{2}+\dot{v}^{2}+\dot{w}^{2})+I_{\mathrm{P}} \omega _1^2 \nonumber \\&+I_2 (\omega _2^2 +\omega _3^2 )\mathrm{d}x \end{aligned}$$

(1)

where $\omega _i (i=1,2,3)$ are angular velocities of local frame $x{-}y{-}z$ with respect to frame $X{-}Y{-}Z$ and u, v and w are the displacements of the local frame $x{-}y{-}z$ in X, Y and Z directions, respectively. In addition,

$$\begin{aligned} I_0= & {} \pi \sum _{i=1}^n \rho _i (r_{i+1}^2 -r_i^2 ),\nonumber \\ I_{\mathrm{P}}= & {} \frac{\pi }{2}\sum _{i=1}^n {\rho _i (r_{i+1}^4 -r_i^4 )} , \nonumber \\ I_2= & {} \frac{\pi }{4}\sum _{i=1}^n {\rho _i (r_{i+1}^4 -r_i^4 )} \end{aligned}$$

(2)

in which n is the number of layers in the laminate, $\rho _i$ is the density of the ith layer, and $r_i$ and $r_{i+1}$ are inner and outer radii of the ith layer, respectively. In the above, $I_0$ is mass per unit length, $I_{\mathrm{P}}$, and $I_2$ are polar and diametrical mass moment of inertia, respectively.

To obtain the orientation of the local frame $x{-}y{-}z$ with respect to frame $X{-}Y{-}Z$, Euler angles are used. Figure 3 shows how inertial frame $X{-}Y{-}Z$ with three successive rotations $\psi , \theta$ and $\beta$ coincide with the local frame $x{-}y{-}z$. First, frame $X{-}Y{-}Z$ rotates about Z-axis with angle $\psi$ to coincide with frame $X_1 {-}Y_1 -Z$. This frame rotates about $Y_1$-axis with angle $\theta$ to coincide with frame $X_2 {-}Y_1 {-}Z_2$, and finally, this frame rotates about $X_2$-axis with angle $\beta$ to coincide with frame $x{-}y{-}z$.

By use of the aforementioned Euler angles, angular velocity of the local frame $x{-}y{-}z$ with respect to the inertial frame $X{-}Y{-}Z$ becomes [20]

$$\begin{aligned} {{\varvec{\upomega }}}= & {} \omega _1 \mathbf{e}_1 +\omega _2 \mathbf{e}_2 +\omega _3 \mathbf{e}_3 \nonumber \\= & {} (\dot{\beta }-\dot{\psi }\sin \theta )\mathbf{e}_1 +(\dot{\psi }\sin \beta \cos \theta +\dot{\theta }\cos \beta )\mathbf{e}_2\nonumber \\&+(\dot{\psi }\cos \beta \cos \theta -\dot{\theta }\sin \beta )\mathbf{e}_3 \end{aligned}$$

(3)

Fig. 3

Euler angles and the frames rotation sequence

For a constant spin rate, the rotation angle $\beta$ can be resolved as $\beta =\phi +\Omega t$; the variable $\phi$ is the angular displacement of the cross section due to shaft torsional deformation, and $\Omega t$ is rigid body rotation of the shaft about x-axis.

The kinetic energy $T_\mathrm{e}$, which is due to the eccentricity, can be written as [21]

$$\begin{aligned} T_\mathrm{e}= & {} \frac{1}{2}\int _0^l I_0 \Omega ^{2}\left[ e_\mathrm{y}^2 (x)+e_\mathrm{z}^2 (x)\right] \nonumber \\&-2I_0 \Omega \left\{ \left[ e_\mathrm{z} (x)\dot{v}+e_\mathrm{y} (x)\dot{w}\right] \sin \beta \right. \nonumber \\&\left. +\left[ e_\mathrm{y} (x)\dot{v}-e_\mathrm{z} (x)\dot{w}\right] \cos \beta \right\} \mathrm{d}x \end{aligned}$$

(4)

where $e_y (x)$ and $e_z (x)$ denote the eccentricities with respect to y- and z-axes, respectively.

The following form of the strain expression of the shaft is assumed in order to derive the strain energy [20]

$$\begin{aligned} \varepsilon _{xx}= & {} e+z\rho _y -y\rho _z \nonumber \\ \gamma _{xy}= & {} -z\rho _x \nonumber \\ \gamma _{xz}= & {} y\rho _x \end{aligned}$$

(5)

where $\rho$ is the curvature of the shaft and in the local frame ($x{-}y{-}z$) computed as

$$\begin{aligned} \rho= & {} \rho _x e_x +\rho _y e_y +\rho _z e_z \nonumber \\= & {} \left( {\varphi }'-{\psi }'\sin \theta \right) e_x +({\psi }'\sin \varphi \cos \theta \nonumber \\&+{\theta }'\cos \varphi )e_y +\left( {\psi }'\cos \varphi \cos \theta -{\theta }'\sin \varphi \right) e_z \end{aligned}$$

(6)

If shear deformation is neglected, angles $\psi$ and $\theta$ can be related to the displacements as [20]

$$\begin{aligned} \psi= & {} \sin ^{-1}\left( \frac{{v}'}{\sqrt{(1+{u}')^{2}+{v}'^{2}}}\right) \nonumber \\ \theta= & {} \sin ^{-1}\left( \frac{-{w}'}{\sqrt{(1+{u}')^{2}+{v}'^{2}+{w}'^{2}}}\right) \end{aligned}$$

(7)

It is more convenient to express the stress–strain relation in cylindrical coordinate. To meet the requirement, a transformation matrix is employed as follows [10]

$$\begin{aligned} \left\{ {{\begin{array}{l} {\varepsilon _{xx} } \\ {\varepsilon _{\tau \tau } } \\ {\varepsilon _{rr} } \\ {\gamma _{x\tau } } \\ {\gamma _{r\tau } } \\ {\gamma _{xr} } \\ \end{array} }} \right\} =\left[ {{\begin{array}{llllll} 1&{} 0&{} 0&{} 0&{} 0&{} 0 \\ 0&{} {n^{2}}&{} {m^{2}}&{} 0&{} {-2mn}&{} 0 \\ 0&{} {m^{2}}&{} {n^{2}}&{} 0&{} {2mn}&{} 0 \\ 0&{} 0&{} 0&{} {-n}&{} 0&{} m \\ 0&{} {-mn}&{} {mn}&{} 0&{} {m^{2}-n^{2}}&{} 0 \\ 0&{} 0&{} 0&{} m&{} 0&{} n \\ \end{array} }} \right] \left\{ {{\begin{array}{l} {\varepsilon _{xx} } \\ {\varepsilon _{yy} } \\ {\varepsilon _{zz} } \\ {\gamma _{xy} } \\ {\gamma _{yz} } \\ {\gamma _{xz} } \\ \end{array} }} \right\} \nonumber \\ \end{aligned}$$

(8)

where $m=\cos (\tau )$ and $n=\sin (\tau )$.

Substituting Eq. (5) into Eq. (8) and letting $y=r\cos (\tau )$ and $z=r\sin (\tau )$, it is found

$$\begin{aligned} \varepsilon _{xx}= & {} e-r\cos (\tau )\rho _z +r\sin (\tau )\rho _y \nonumber \\ \varepsilon _{x\tau }= & {} r\rho _x \nonumber \\ \varepsilon _{\tau \tau }= & {} \varepsilon _{rr} =\varepsilon _{r\tau } =\varepsilon _{xr} =0 \end{aligned}$$

(9)

Finally, the stress–strain relation can be written as follows

$$\begin{aligned} \sigma _{xx}= & {} \bar{{Q}}_{11} \varepsilon _{xx} +\bar{{Q}}_{16} \gamma _{x\tau } \nonumber \\ \tau _{x\tau }= & {} \bar{{Q}}_{16} \varepsilon _{xx} +\bar{{Q}}_{66} \gamma _{x\tau } \end{aligned}$$

(10)

The strain energy for a composite shaft can be expressed as

$$\begin{aligned} U_s= & {} \frac{1}{2}\int _v \left( \sigma _{xx} \varepsilon _{xx} +\sigma _{rr} \varepsilon _{rr} +\sigma _{\tau \tau } \varepsilon _{\tau \tau } \right. \nonumber \\&\left. +\tau _{xr} \gamma _{xr} +\tau _{x\tau } \gamma _{x\tau } +\tau _{r\tau } \gamma _{r\tau } \right) dV \end{aligned}$$

(11)

By substituting Eqs. (9) and (10) into Eq. (11), the strain energy becomes

$$\begin{aligned} U_s= & {} \frac{1}{2}\left[ A_{11} \mathrm{e}^{2}+D_{11} (\rho _z^2 +\rho _y^2 )\right. \nonumber \\&\left. +D_{66} \rho _x^2 +2B_{16} \rho _x e\right] \end{aligned}$$

(12)

where

$$\begin{aligned} A_{11}= & {} \pi \sum _{i=1}^n {\overline{Q} _{11i} (r_{i+1}^2 -r_i^2 )} , \nonumber \\ B_{16}= & {} \frac{2\pi }{3}\sum _{i=1}^n {\overline{Q} _{16i} (r_{i+1}^3 -r_i^3 )} \nonumber \\ D_{11}= & {} \frac{\pi }{4}\sum _{i=1}^n {\overline{Q} _{11i} (r_{i+1}^4 -r_i^4 )} , \nonumber \\ D_{66}= & {} \frac{\pi }{2}\sum _{i=1}^n {\overline{Q} _{66i} (r_{i+1}^4 -r_i^4 )} \end{aligned}$$

(13)

where $A_{11}$ is longitudinal stiffness, $D_{11}$ is bending stiffness, $D_{66}$ is torsional rigidity and $B_{16}$ is extensional–torsional coupling term. Parameters $Q_{11} , Q_{16}$ and $Q_{66}$ are presented in “Appendix 1.”

2.2 Derivation of equations of motion

Considering the kinetic and strain energy expressions obtained above, the equations of motion can be derived by invoking the Hamilton’s principle. First, Eq. (7) is substituted into Eqs. (3) and (6) to compute the curvature and angular velocity. Then, the results are substituted into the kinetic and strain energies, expanded to Taylor series and only the terms which are up to $O(\varepsilon ^{3})$ are retained. Finally, by applying Hamilton’s principle to the computed kinetic and strain energies, the following is obtained

$$\begin{aligned}&I_0 \ddot{u}-A_{11} \left( {v}'{v}''+{w}'{w}''-{v}'^{2}{u}''-{w}'^{2}{u}''\right. \nonumber \\&\qquad \left. +{u}''-2{v}'{u}'{v}''-2{w}'{u}'{w}''\right) \nonumber \\&\qquad -B_{16} \left( -6{u}'{v}'''{w}'+2{w}''{v}'{u}''-6{u}''{v}''{w}' \right. \nonumber \\&\qquad +2{v}''{w}''-4{u}'{v}''{w}''-2{w}'{\phi }'{w}''-2{\phi }'{v}'{v}''\nonumber \\&\qquad -{w}'^{2}{\phi }''-{\phi }''{v}'^{2}+2{u}'{w}'''{v}'\nonumber \\&\qquad \left. +2{v}'''{w}'+2{\phi }''\right) -D_{11} \left( -5{v}'{u}''{v}''' \right. \nonumber \\&\qquad -4{v}'{u}'''{v}''-3{v}''{u}'{v}'''-3{w}''{u}'{w}'''+{v}'v^{(IV)}\nonumber \\&\qquad -5{w}'''{w}'{u}''-3w^{(IV)}{w}'{u}'-4{w}''{w}'{u}'''\nonumber \\&\qquad -2{v}''^{2}{u}''+w^{(IV)}{w}'+{v}''{v}'''-{v}'^{2}u^{(IV)}\nonumber \\&\qquad \left. -{w}'^{2}u^{(IV)}-2{w}''^{2}{u}''-3{v}'{u}'v^{(IV)}+{w}''{w}'''\right) \nonumber \\&\qquad -D_{66}\left( {\phi }'{w}'''{v}'+2{\phi }''{w}''{v}'-{\phi }'{v}'''{w}'\right. \nonumber \\&\qquad \left. +{\phi }'''{w}'{v}'\right) -I_2 \left( -\ddot{w}'{w}''-\ddot{v}''{v}'\right. \nonumber \\&\qquad -\ddot{v}'{v}''-\ddot{w}''{w}'+{v}'^{2}\ddot{u}''\nonumber \\&\qquad +{w}'^{2}\ddot{u}''+2{w}'\dot{w}''\dot{u}'+2{w}'\dot{w}'\dot{u}''\nonumber \\&\qquad +3\ddot{v}''{v}'{u}'+3\ddot{v}'{v}''{u}' \nonumber \\&\qquad +3\ddot{v}'{v}'{u}''+2{v}''\dot{v}'\dot{u}'+2{v}'\dot{v}''\dot{u}'\nonumber \\&\qquad +2{v}'\dot{v}'\dot{u}''+2{w}''\dot{w}'\dot{u}'+3\ddot{w}''{w}'{u}'\nonumber \\&\qquad +3\ddot{w}'{w}''{u}'+3\ddot{w}'{w}'{u}''+2{v}'\ddot{u}'{v}''+2{w}'\ddot{u}'{w}'') \nonumber \\&\qquad -I_\mathrm{p} \left( \Omega \left( 3{v}'{u}'\dot{w}'-3\dot{v}'{w}'{u}''+\dot{v}''{w}'+\dot{v}'{w}''\right. \right. \nonumber \\&\qquad -3\dot{v}''{w}'{u}'-3\dot{v}'{w}''{u}'-{v}'\dot{w}''+3{v}''{u}'\dot{w}'\nonumber \\&\qquad \left. +3{v}'{u}''\dot{w}'-{v}''\dot{w}'\right) \nonumber \\&\qquad -\ddot{\phi }{v}''{w}'-\dot{\phi }{v}''\dot{w}'-\ddot{\phi }{v}'{w}''-{\ddot{\phi }}'{v}'{w}'-{\dot{\phi }}'{v}'\dot{w}'\nonumber \\&\qquad +\dot{\phi }\dot{v}''{w}'+\dot{\phi }\dot{v}'{w}'' \left. -\dot{\phi }{v}'\dot{w}''+\dot{{\phi }'}\dot{v}'{w}'\right) =0 \end{aligned}$$

(14)

$$\begin{aligned}&I_0 \ddot{v}+c\dot{v}-A_{11}\left( {w}'{v}'{w}''+{v}'{u}''+{v}''{u}'\right. \nonumber \\&\qquad +\frac{3}{2}{v}'^{2}{v}''+\frac{1}{2}{w}'^{2}{v}''-2{v}'{u}'{u}''\nonumber \\&\qquad \left. -{v}''{u}'^{2}\right) -B_{16}(6{w}'{u}'{u}'''+6{w}'{u}''^{2} \nonumber \\&\qquad +14{w}''{u}'{u}''-4{u}''{w}''-2{w}''{v}''{v}'+2{\phi }''{v}'\nonumber \\&\qquad +2{\phi }'{v}''-6{w}'{w}''^{2}-2{u}'{w}'''-2{u}'''{w}'\nonumber \\&\qquad -3{w}'^{2}{w}'''-{w}'''{v}'^{2}+4{u}'^{2}{w}'''\nonumber \\&\qquad -2{\phi }''{v}'{u}'-2{\phi }'{v}''{u}'-2{\phi }'{v}'{u}'')\nonumber \\&\qquad -D_{11} (w^{(IV)}{w}'{v}'+8{v}''{v}'{v}'''+3{w}'{v}''{w}'''\nonumber \\&\qquad +{w}''{v}'{w}'''+{v}'u^{(IV)}+2v^{(IV)}{u}'\nonumber \\&\qquad +{w}'^{2}v^{(IV)}+2v^{(IV)}{v}'^{2}+2{w}''^{2}{v}''+4{v}'''{u}''\nonumber \\&\qquad +4{w}'{v}'''{w}''+2{v}''^{3}+3{v}''{u}'''-v^{(IV)}\nonumber \\&\qquad -3v^{(IV)}{u}'^{2}-7{v}'{u}''{u}'''\nonumber \\&\qquad -12{u}'{u}''{v}'''-9{u}'{u}'''{v}''-8{v}''{u}''^{2}-3{v}'{u}'u^{(IV)})\nonumber \\&\qquad -D_{66} (-4{w}'{v}'''{w}''-2{\phi }''{w}''-{\phi }'''{w}'-2{w}''^{2}{v}'' \nonumber \\&\qquad -{w}'^{2}v^{(IV)}-2{w}'{v}''{w}'''-{\phi }'{w}'''+{\phi }'{w}'{u}'''\nonumber \\&\qquad +3{\phi }''{w}'{u}''-{w}'^{2}v^{(IV)}+4{\phi }''{w}''{u}'+2{\phi }'{w}'''{u}'\nonumber \\&\qquad +3{\phi }'{w}''{u}''+2{\phi }'''{w}'{u}') \nonumber \\&\qquad -I_2 (-2{w}'\ddot{v}'{w}''-4\dot{v}'{v}'\dot{v}''\nonumber \\&\qquad -2{w}'\dot{v}''\dot{w}'-4\ddot{v}'{v}'{v}''-\ddot{w}'{w}''{v}'\nonumber \\&\qquad -\ddot{w}'{w}'{v}''-2{w}'\dot{v}'\dot{w}''-2\dot{w}'\dot{v}'{w}''\nonumber \\&\qquad -2\dot{u}'\dot{v}'' \nonumber \\&\qquad -2\dot{v}'^{2}{v}''-2\dot{u}''\dot{v}'-2\ddot{v}''{v}'^{2}\nonumber \\&\qquad -{v}''\ddot{u}'-{v}'\ddot{u}''-2\ddot{v}''{u}'-2\ddot{v}'{u}''-\ddot{w}''{w}'{v}'\nonumber \\&\qquad -{w}'^{2}\ddot{v}''+\ddot{v}''+3{v}'{u}'\ddot{u}''+3\ddot{v}''{u}'^{2} \nonumber \\&\qquad +2{v}''\dot{u}'^{2}-2\dot{v}'\dot{u}''+6\ddot{v}'{u}'{u}''\nonumber \\&\qquad +4{v}'\dot{u}'\dot{u}''+6\dot{v}''{u}'\dot{u}'+6\dot{v}'{u}''\dot{u}'+6\dot{v}'{u}'\dot{u}''\nonumber \\&\qquad +3{v}''{u}'\ddot{u}'+3{v}'{u}''\ddot{u}')-I_\mathrm{p} (\Omega (-{w}'\dot{u}'' \nonumber \\&\qquad -\frac{3}{2}{w}'^{2}\dot{w}''-3{w}'{w}''\dot{w}'-{w}''\dot{u}'-3\dot{w}'{v}'{v}''+\dot{w}''\nonumber \\&\qquad -\frac{3}{2}\dot{w}''{v}'^{2}-2\dot{w}''{u}'-2\dot{w}'{u}''+3\dot{w}''{u}'^{2}\nonumber \\&\qquad +3{w}'{u}''\dot{u}'+3{w}''{u}'\dot{u}' \nonumber \\&\qquad +6\dot{w}'{u}'{u}''+3{w}'{u}'\dot{u}'')+\dot{\phi }\dot{w}''\nonumber \\&\qquad +\dot{{\phi }'}\dot{w}'+\ddot{\phi }{w}''+2\dot{w}'\dot{v}'{w}''+{w}'^{2}\ddot{v}''\nonumber \\&\qquad +\ddot{{\phi }'}{w}'+2{w}'\dot{v}''\dot{w}'+2{w}'\ddot{v}'{w}''+2{w}'\dot{v}'\dot{w}'' \nonumber \\&\qquad -2{\phi }''{w}'{u}''-2\dot{\phi }\dot{w}'{u}''-{w}'\dot{\phi }\dot{u}''\nonumber \\&\qquad -2\ddot{{\phi }'}{w}'{u}'-{w}''\dot{\phi }\dot{u}'-{w}'\dot{{\phi }'}\dot{u}'-2\dot{\phi }\dot{w}''{u}'\nonumber \\&\qquad -2\dot{{\phi }'}\dot{w}'{u}'-2\ddot{\phi }{w}''{u}') \nonumber \\&\quad =\Omega ^{2}I_0 (e_\mathrm{y} (x)\cos (\Omega t)-e_\mathrm{z} (x)\sin (\Omega t)) \end{aligned}$$

(15)

$$\begin{aligned}&I_0 \ddot{w}+c\dot{w}-A_{11}({w}'{v}'{v}''+{w}'{u}''+{w}''{u}'\nonumber \\&\qquad +\frac{3}{2}{w}'^{2}{w}''+\frac{1}{2}{v}'^{2}{w}''-2{w}'{u}'{u}''\nonumber \\&\qquad -{w}''{u}'^{2})-B_{16}(2{u}''{v}''+6{w}''{v}''{w}' \nonumber \\&\qquad +2{\phi }''{w}'+2{\phi }'{w}''+2{v}'{v}''^{2}+2{u}'{v}'''\nonumber \\&\qquad +{v}'^{2}{v}'''+3{v}'''{w}'^{2}-2{w}'{\phi }''{u}'-4{u}'^{2}{v}'''\nonumber \\&\qquad -2{v}'{u}''^{2}-2{w}''{\phi }'{u}'-2{w}'{\phi }'{u}'' \nonumber \\&\qquad -10{v}''{u}'{u}''-2{v}'{u}'{u}''')-D_{11}(2w^{(IV)}{u}'\nonumber \\&\qquad +2w^{(IV)}{w}'^{2}+v^{(IV)}{w}'{v}'+4{w}'''{v}'{v}''\nonumber \\&\qquad +2{w}''{v}''^{2}+4{u}''{w}'''+{w}'{v}''{v}'''\nonumber \\&\qquad -w^{(IV)}+3{w}''{v}'{v}'''+8{w}''{w}'{w}'''+w^{(IV)}{v}'^{2}\nonumber \\&\qquad +{w}'u^{(IV)}+3{u}'''{w}''+2{w}''^{2}-7{w}'{u}''{u}'''\nonumber \\&\qquad -3{w}'{u}'u^{(IV)}-8{w}''{u}''^{2}-12{w}'''{u}'{u}''\nonumber \\&\qquad -9{w}''{u}'{u}'''-3w^{(IV)}{u}'^{2})-D_{66} ({\phi }''{v}''\nonumber \\&\qquad +{v}''^{2}{w}''+2{w}'{v}''{v}'''+{\phi }'{v}'''\nonumber \\&\qquad -{\phi }''{v}'{u}''-2{\phi }'{v}'''{u}' \nonumber \\&\qquad -2{\phi }''{v}''{u}'-3{\phi }'{v}''{u}''-{\phi }'{v}'{u}''')\nonumber \\&\qquad -I_2 (-2\dot{w}'^{2}{w}''-2\dot{u}'\dot{w}''-2\dot{u}''\dot{w}'-{w}''\ddot{u}'\nonumber \\&\qquad +\ddot{w}''-\ddot{w}''{v}'^{2}-2\ddot{w}''{w}'^{2}-2\ddot{w}'{u}'' \nonumber \\&\qquad -4\dot{w}'{w}'\dot{w}''-2\ddot{w}''{u}'-2{v}''\dot{w}'\dot{v}'\nonumber \\&\qquad -2{v}'\dot{w}''\dot{v}'-2{v}'\dot{w}'\dot{v}''-4\ddot{w}'{w}'{w}''\nonumber \\&\qquad -{v}''{w}'\ddot{v}'-{v}'{w}''\ddot{v}'-{v}'{w}'\ddot{v}''-2\ddot{w}'{v}'{v}'' \nonumber \\&\qquad -{w}'\ddot{u}''+2{w}''\dot{u}'^{2}-3\ddot{w}''{u}'^{2}\nonumber \\&\qquad +4{w}'\dot{u}'\dot{u}''+3{w}''{u}'\ddot{u}'+3{w}'{u}''\ddot{u}'\nonumber \\&\qquad +3{w}'{u}'\ddot{u}''+6\ddot{w}'{u}'{u}''+6\dot{w}''{u}'\dot{u}'\nonumber \\&\qquad +6\dot{w}'{u}''\dot{u}' \nonumber \\&\qquad +6\dot{w}'{u}'\dot{u}'')-I_\mathrm{p} (\Omega (3\dot{v}'{w}'{w}''+{v}'\dot{u}''\nonumber \\&\qquad +3\dot{v}'{v}'{v}''+{v}''\dot{u}'-\dot{v}''+2\dot{v}''{u}'+2\dot{v}'{u}''\nonumber \\&\qquad +\frac{3}{2}\dot{v}''{w}'^{2}+\frac{3}{2}\dot{v}''{v}'^{2}-3{v}'{u}'\dot{u}'' \nonumber \\&\qquad -3{v}''{u}'\dot{u}'-6\dot{v}'{u}'{u}''-3{v}'{u}''\dot{u}'-3\dot{v}''{u}'^{2})\nonumber \\&\qquad -\dot{\phi }\dot{v}''-\dot{{\phi }'}\dot{v}'-{w}''\dot{v}'^{2}-2{w}'\dot{v}'\dot{v}''+2\dot{{\phi }'}\dot{v}'{u}'\nonumber \\&\qquad +2\dot{\phi }\dot{v}''{u}'+2\dot{\phi }\dot{v}'{u}'' \nonumber \\&\qquad -2{w}'\dot{v}'\dot{v}''+{v}'\dot{{\phi }'}\dot{u}'+{v}'\dot{\phi }\dot{u}''\nonumber \\&\qquad +{v}''\dot{\phi }\dot{u}')=\Omega ^{2}I_0 (e_\mathrm{z} (x)\cos (\Omega t)\nonumber \\&\qquad +e_\mathrm{y} (x)\sin (\Omega t)) \end{aligned}$$

(16)

$$\begin{aligned}&B_{16}\left( 2{u}''+2{w}'{w}''+2{v}'{v}''\right. \nonumber \\&\qquad \left. -2{v}'{u}'{v}''-2{w}'{u}'{w}''-{w}'^{2}{u}''-{v}'^{2}{u}''\right) \nonumber \\&\qquad +D_{66} \left( {v}''{w}''+{\phi }''+{v}'''{w}'-{w}''{v}'{u}''\right. \nonumber \\&\qquad \left. -3{u}''{v}''{w}'-2{u}'{v}''{w}''-2{u}'{v}'''{w}'-{w}'{v}'{u}'''\right) \nonumber \\&\qquad +I_\mathrm{p} \left( -\ddot{\phi }-\ddot{v}'{w}'-\dot{v}'\dot{w}'+3\dot{v}'{w}'\dot{u}'\right. \nonumber \\&\qquad \left. +\dot{w}'{v}'\dot{u}'+2\dot{v}'\dot{w}'{u}'+{w}'{v}'\ddot{u}'+2\ddot{v}'{w}'{u}'\right) =0\nonumber \\ \end{aligned}$$

(17)

Note that in Eqs. (14)–(17), dot (.) and prime (${}^{'}$) denote derivative with respect to time and spatial variables, respectively. A simplified procedure for derivation of the above equations is presented in “Appendix 2.”

These are full equations governing the extensional–flexural–flexural–torsional vibration of the composite shaft with geometrical nonlinearity. Equations show linear as well as nonlinear couplings. Linear coupling is due to anisotropy properties in composite material, and nonlinear coupling is due to the large deformation of the shaft. In previous researches (e.g., [20]), the equations were reduced by application of in-extensionality assumption and neglect of torsional inertia to a flexural–flexural one. In addition, in some cases (e.g., [22]), the equations were again reduced to flexural–flexural one by neglecting the axial and torsional inertias. But, in the above equations due to linear extensional–torsional coupling, these kinds of reduction are not acceptable and full version of equations are employed. Later, it will be shown that the neglecting of couplings leads to inaccurate results.

The equations of motion presented in the literature are either linear (with anisotropic material) or for a metallic shaft (with nonlinear effects), but equations derived here are nonlinear equations of motion of a composite shaft based on the Bernoulli–Euler theory. If the material is assumed isotropic, the composite coupling coefficient $B_{16}$ vanishes, while the other coefficients are changed accordingly, which finally yields the equations governing the motion of a metallic shaft as in references [20, 30]. In addition, if the terms resulting from Timoshenko theory are removed from equations of motion presented in reference [10], which is derived for a spinning composite shaft, then its equations will reduce to the equations obtained here. This confirms partially the validity of equations obtained in this paper.

For a slender composite shaft, bending stiffness $D_{11}$ and torsional rigidity $D_{66}$ are much smaller than the longitudinal stiffness $A_{11}$; so their nonlinear coefficients (power or product of them) can be neglected. The same strategy is taken into account for rotary inertia $I_2$ and coupling term, $B_{16}$.

Applying these simplifications, and using the following dimensionless quantities

$$\begin{aligned}&\bar{{v}}=\frac{v}{l}, \bar{{w}}=\frac{w}{l}, \bar{{u}}=\frac{u}{l}, \bar{{e}}_y =\frac{e_y }{l}, \bar{{e}}_z =\frac{e_z }{l}, \nonumber \\&\bar{{x}}=\frac{x}{l}, \bar{{t}}=t\omega , \bar{{\Omega }}=\frac{\Omega }{\omega }, \bar{{B}}_{16} =\frac{B_{16} }{\omega ^{2}I_0 l^{3}} \nonumber \\&\bar{{D}}_{66} =\frac{D_{66} }{\omega ^{2}I_0 l^{4}}, \bar{{D}}_{11} =\frac{D_{11} }{\omega ^{2}I_0 l^{4}}, \bar{{A}}_{11} =\frac{A_{11} }{\omega ^{2}I_0 l^{2}},\nonumber \\&\bar{{I}}_2 =\frac{I_2 }{I_0 l^{2}}, \bar{{I}}_\mathrm{p} =\frac{I_\mathrm{p} }{I_0 l^{2}} , \bar{{c}}=\frac{c}{\omega I_0 } \end{aligned}$$

(18)

the final dimensionless equations of motion in a simplified form are found as

$$\begin{aligned}&\ddot{\bar{{u}}}-\bar{{B}}_{16} \bar{{{\phi }''}}-\bar{{A}}_{11} \left( \bar{{{v}'}}\bar{{{v}''}}+\bar{{{w}'}}\bar{{{w}''}}\right. \nonumber \\&\qquad -\,\bar{{{v}'}}^{2}\bar{{{u}''}}-\bar{{{w}'}}^{2}\bar{{{u}''}}+\bar{{{u}''}}\nonumber \\&\qquad \left. -\,2\bar{{{v}'}}\bar{{{u}'}}\bar{{{v}''}}-2\bar{{{w}'}}\bar{{{u}'}}\bar{{{w}''}}\right) =0 \end{aligned}$$

(19)

$$\begin{aligned}&\ddot{\bar{{v}}}+\bar{{c}}\dot{\bar{{v}}}-\bar{{D}}_{11} (-\bar{{v}}^{(IV)})\nonumber \\&\qquad -\,\bar{{I}}_\mathrm{p} \Omega \dot{\bar{{{w}''}}}-\bar{{A}}_{11}\left( \bar{{{w}'}}\bar{{{v}'}}\bar{{{w}''}}+\bar{{{v}'}}\bar{{{u}''}}\right. \nonumber \\&\qquad +\,\bar{{{v}''}}\bar{{{u}'}}+\frac{3}{2}\bar{{{v}'}}^{2}\bar{{{v}''}}+\frac{1}{2}\bar{{{w}'}}^{2}\bar{{{v}''}}\nonumber \\&\qquad \left. -\,2\bar{{{v}'}}\bar{{{u}'}}\bar{{{u}''}}-\bar{{{v}''}}\bar{{{u}'}}^{2}\right) \nonumber \\&\quad =\bar{{\Omega }}^{2}(\bar{{e}}_y (\bar{{x}})\cos (\bar{{\Omega }}\bar{{t}})-\bar{{e}}_z (\bar{{x}})\sin (\bar{{\Omega }}\bar{{t}})) \end{aligned}$$

(20)

$$\begin{aligned}&\ddot{\bar{{w}}}+\bar{{c}}\dot{\bar{{w}}}-\bar{{D}}_{11}\left( -\bar{{w}}^{(IV)}\right) -\bar{{I}}_\mathrm{p} \Omega \dot{\bar{{{v}''}}}\nonumber \\&\qquad -\,\bar{{A}}_{11}\left( \bar{{{w}'}}\bar{{{v}'}}\bar{{{v}''}}+\bar{{{w}'}}\bar{{{u}''}}+\bar{{{w}''}}\bar{{{u}'}}\right. \nonumber \\&\qquad +\,\frac{3}{2}\bar{{{w}'}}^{2}\bar{{{w}''}}+\frac{1}{2}\bar{{{v}'}}^{2}\bar{{{w}''}}\nonumber \\&\qquad \left. -\,2\bar{{{w}'}}\bar{{{u}'}}\bar{{{u}''}}-\bar{{{w}''}}\bar{{{u}'}}^{2}\right) \nonumber \\&\quad =\bar{{\Omega }}^{2}(\bar{{e}}_\mathrm{z} (\bar{{x}})\cos (\bar{{\Omega }}\bar{{t}})+\bar{{e}}_\mathrm{y} (\bar{{x}})\sin (\bar{{\Omega }}\bar{{t}})) \end{aligned}$$

(21)

$$\begin{aligned}&\bar{{I}}_\mathrm{p} \ddot{\bar{{\phi }}}-\bar{{B}}_{16} 2\bar{{{u}''}}-\bar{{D}}_{66} \left( \bar{{{v}''}}\bar{{{w}''}}\right. \nonumber \\&\qquad +\,\bar{{{\phi }''}}+\bar{{{v}'''}}\bar{{{w}'}}-\bar{{{w}''}}\bar{{{v}'}}\bar{{{u}''}}-3\bar{{{u}''}}\bar{{{v}''}}\bar{{{w}'}}\nonumber \\&\qquad \left. -\,2\bar{{{u}'}}\bar{{{v}''}}\bar{{{w}''}}-2\bar{{{u}'}}\bar{{{v}'''}}\bar{{{w}'}}-\bar{{{w}'}}\bar{{{v}'}}\bar{{{u}'''}}\right) =0 \end{aligned}$$

(22)

As mentioned earlier, the bearings are much stiffer than the shaft itself which let the shaft to rotate freely but limits the transverse movement of the shaft at the bearings. In fact, bearings can be modeled as hinged boundaries. So the boundary conditions are

$$ \begin{aligned} \bar{{u}}= & {} 0, \bar{{v}}=0, \bar{{{v}''}}=0, \bar{{w}}=0, \bar{{{w}''}}=0,\nonumber \\ \bar{{{\phi }'}}= & {} 0 \,\,@ \bar{{x}}=0\,\, \& \,\,\bar{{x}}=1 \end{aligned}$$

(23)

where $\omega$ is the shaft linear natural frequency. In the above equations, $\bar{{B}}_{16}$ is the extensional–torsional coupling coefficient and $\bar{{I}}_\mathrm{p} \Omega {\dot{\bar{{w}}}}''$ and $\bar{{I}}_\mathrm{p} \Omega {\dot{\bar{{v}}}}''$ are gyroscopic terms which couple the two transverse motions linearly. For the ease of notation, the bars are dropped from equations hereafter. Equations (19)–(22) can be generally used for any kinds of boundary condition.

To verify the aforementioned simplification, analytical method (perturbation method in the next section) was applied to full equations (14)–(17) and simplified version (19)–(22). It was observed that the results are practically equal. This shows that the omitted terms are really negligible and the simplified form of the equations are sufficient for the analysis.

Equations (19)–(22) and the perturbation theory are used in the next section to investigate the shaft dynamics in the neighborhood of the primary resonance. Due to the extensional–torsional coupling, further reduction of equations is not possible. It should be noted that, in previous works [18,19,20,21,22], the equations corresponding to extension and torsion were solved in terms of flexural variables with some assumptions (e.g., stretching or shortening) due to the lack of coupling, and finally the reduced flexural–flexural equations of motion were obtained and analyzed. But here, these reductions are not applied and extensional–flexural–flexural–torsional equations of motion are used.

3 Method of multiple scales

The method of multiple scales [36] is a powerful perturbation method. In this method, the independent variable t is split up into several new independent variables, $T_0 ,T_1 ,\ldots$. Although these new variables are not perfectly independent and can be related to each other by means of a bookkeeping parameter, they are treated as independent variables in the solution procedure. Here, the multiple scales method is used to analyze the forced vibration of the system. Before application of the multiple scales method, the partial differential equations of motion should be discretized with a suitable method. In this paper, the equations are discretized using Galerkin method by taking suitable shape functions. It is usually common in nonlinear vibration [37] that if the excitation is tuned in the neighborhood of a specific mode and this mode does not involve in an internal resonance, then other modes are decayed with the passage of time and one-mode discretization is sufficient for steady-state analysis. Here, this is not the case. Although the excitation (i.e., spin) is tuned in the neighborhood of the first mode and the first mode does not involve in an internal resonance with other modes, it will be shown that one-mode discretization is not sufficient. Here both one-mode discretization and two-mode discretization are implemented, and a comparison is made between the results. To investigate the effect of the mode number on the convergence of the solution, three-mode discretization was also applied (the results are not presented here). Numerical solutions of three-mode and two-mode discretization show that the results (steady-state solutions) are equal and two-mode discretization is sufficient for the present problem. So, our analysis concentrates on one-mode and two-mode discretization methods.

3.1 Primary resonances with one-mode discretization

In order to use the Galerkin method with one mode, the following form may be assumed

$$\begin{aligned} u(x,t)= & {} \nu _n (x)U(t) \nonumber \\ v(x,t)= & {} \psi _n (x)V(t) \nonumber \\ w(x,t)= & {} \xi _n (x)W(t) \nonumber \\ \phi (x,t)= & {} \zeta _n (x)\varphi (t) \end{aligned}$$

(24)

where $\nu , \psi , \xi$ and $\zeta$ are the mode shapes obtained by solving linear form of the existing equations [i.e., Eqs. (14)–(17)] considering the boundary conditions in (23) and n is the mode number:

$$\begin{aligned} \nu _n= & {} \sqrt{2}\sin (n\pi x) \nonumber \\ \psi _n= & {} \sqrt{2}\sin (n\pi x) \nonumber \\ \xi _n= & {} \sqrt{2}\sin (n\pi x) \nonumber \\ \zeta _n= & {} \sqrt{2}\cos (n\pi x) \end{aligned}$$

(25)

Substituting Eq. (24) into Eqs. (19)–(22) and multiplying each equation by its corresponding mode shape, finally the discretized equations are obtained in the following form by using the orthogonality relation [38]

$$\begin{aligned}&\frac{3}{2}A_{11} V(t)^{2}\pi ^{4}U(t)+\frac{3}{2}A_{11}W(t)^{2}\pi ^{4}U(t)\nonumber \\&\qquad -\,A_{11} U(t)\pi ^{2}-\frac{\mathrm{d}^{2}}{\mathrm{d}t^{2}}U(t)=0 \end{aligned}$$

(26)

$$\begin{aligned}&-\frac{3}{4}A_{11} W(t)^{2}\pi ^{4}V(t)+\frac{3}{2}A_{11} V(t)\pi ^{4}U(t)^{2}\nonumber \\&\qquad -\,\frac{3}{4}A_{11} V(t)^{3}\pi ^{4}-D_{11} V(t)\pi ^{4}\nonumber \\&\qquad -\,I_\mathrm{p} \Omega \frac{\mathrm{d}}{\mathrm{d}t}W(t)\pi ^{2}-\frac{\mathrm{d}^{2}}{\mathrm{d}t^{2}}V(t) \nonumber \\&\qquad -\,c\frac{\mathrm{d}}{\mathrm{d}t}V(t)+\Omega ^{2}e_2 \cos (\Omega t)\nonumber \\&\qquad -\,\Omega ^{2}e_1 \sin (\Omega t)=0 \end{aligned}$$

(27)

$$\begin{aligned}&-\frac{3}{4}A_{11} V(t)^{2}\pi ^{4}W(t)+\frac{3}{2}A_{11} W(t)\pi ^{4}U(t)^{2}\nonumber \\&\qquad -\,\frac{3}{4}A_{11} W(t)^{3}\pi ^{4}-D_{11}W(t)\pi ^{4}+I_\mathrm{p} \Omega \frac{\mathrm{d}}{\mathrm{d}t}V(t)\pi ^{2}\nonumber \\&\qquad -\,\frac{\mathrm{d}^{2}}{\mathrm{d}t^{2}}W(t) -c\frac{\mathrm{d}}{\mathrm{d}t}W(t)+\Omega ^{2}e_1 \cos (\Omega t)\nonumber \\&\qquad +\,\Omega ^{2}e_2 \sin (\Omega t)=0 \end{aligned}$$

(28)

$$\begin{aligned}&\frac{3}{2}D_{66} V(t)\pi ^{5}W(t)U(t)-D_{66} \varphi (t)\pi ^{2}\nonumber \\&\qquad -\,\frac{\mathrm{d}^{2}}{\mathrm{d}t^{2}}\varphi (t)=0 \end{aligned}$$

(29)

where $e_1 =\int _0^1 {[\sqrt{2}e_y (x)\sin (\pi x)]\mathrm{d}dx}$ and $e_2 =\int _0^1 {[\sqrt{2}e_z (x)\sin (\pi x)]\mathrm{d}x}$. Here, the analysis is carried out for the first mode, although the procedure is applicable in similar fashion to other modes.

Now, dependent variables are expanded in the following form in order to apply the multiple scales method

$$\begin{aligned} U(t)= & {} \varepsilon U_1 (T_0 ,T_1 ,T_2 )+\varepsilon ^{2}U_2 (T_0 ,T_1 ,T_2 )\nonumber \\&+\varepsilon ^{3}U_3 (T_0 ,T_1 ,T_2 ) \nonumber \\ V(t)= & {} \varepsilon V_1 (T_0 ,T_1 ,T_2 )+\varepsilon ^{2}V_2 (T_0 ,T_1 ,T_2 )\nonumber \\&+\varepsilon ^{3}V_3 (T_0 ,T_1 ,T_2 ) \nonumber \\ W(t)= & {} \varepsilon W_1 (T_0 ,T_1 ,T_2 )+\varepsilon ^{2}W_2 (T_0 ,T_1 ,T_2 )\nonumber \\&+\varepsilon ^{3}W_3 (T_0 ,T_1 ,T_2 ) \nonumber \\ \varphi (t)= & {} \varepsilon \varphi _1 (T_0 ,T_1 ,T_2 )+\varepsilon ^{2}\varphi _2 (T_0 ,T_1 ,T_2 )\nonumber \\&+\varepsilon ^{3}\varphi _3 (T_0 ,T_1 ,T_2 ) \end{aligned}$$

(30)

where $T_0 =t, T_1 =\varepsilon t$ and $T_2 =\varepsilon ^{2}t$ are different time scales and $\varepsilon$ is a small dimensionless bookkeeping parameter. Damping c and unbalance parameters $e_j (j=1,2)$ are scaled as $c\varepsilon ^{2}$ and $e_j \varepsilon ^{3}$ so that their effects are balanced with the third-order nonlinearities.

Using the chain rule, time derivatives, in terms of $T_0$, $T_1$ and $T_2$, become

$$\begin{aligned} \frac{\partial }{\partial t}= & {} D_0 +\varepsilon D_1 +\varepsilon ^{2}D_2 \nonumber \\ \frac{\partial }{\partial t^{2}}= & {} D_0^2 +2\varepsilon D_0 D_1 +\varepsilon ^{2}D_1^2 +2\varepsilon ^{2}D_0 D_2 \end{aligned}$$

(31)

where $D_n =\frac{\partial }{\partial T_n },(n=0,1,2)$. Substituting Eqs. (30) and (31) into Eqs. (26)–(29) and equating coefficients of like power of $\varepsilon$, the equations in different orders are obtained in the following form

$$\begin{aligned}&O(\varepsilon ) \nonumber \\&\qquad \pi ^{2}A_{11} U_1 (T_0 ,T_1 ,T_2 )+\frac{\partial ^{2}}{\partial T_0^2 }U_1 (T_0 ,T_1 ,T_2 )=0 \nonumber \\&\qquad \pi ^{4}D_{11} V_1 (T_0 ,T_1 ,T_2 )+\frac{\partial ^{2}}{\partial T_0^2 }V_1 (T_0 ,T_1 ,T_2 )\nonumber \\&\quad \qquad +\pi ^{2}\Omega I_{\mathrm{P}} \frac{\partial }{\partial T_0 }W_1 (T_0 ,T_1 ,T_2 )=0 \nonumber \\&\qquad \pi ^{4}D_{11} W_1 (T_0 ,T_1 ,T_2 )+\frac{\partial ^{2}}{\partial T_0^2 }W_1 (T_0 ,T_1 ,T_2 )\nonumber \\&\qquad \quad -\pi ^{2}\Omega I_{\mathrm{P}} \frac{\partial }{\partial T_0 }V_1 (T_0 ,T_1 ,T_2 )=0 \nonumber \\&\qquad \pi ^{2}D_{66} \varphi _1 (T_0 ,T_1 ,T_2 )+\frac{\partial ^{2}}{\partial T_0^2 }\varphi _1 (T_0 ,T_1 ,T_2 )=0\nonumber \\ \end{aligned}$$

(32)

$$\begin{aligned}&O(\varepsilon ^{2}) \nonumber \\&\pi ^{4}D_{11} V_2 (T_0 ,T_1 ,T_2 )+\frac{\partial ^{2}}{\partial T_0^2 }V_2 (T_0 ,T_1 ,T_2 )\nonumber \\&\qquad +\pi ^{2}\Omega I_{\mathrm{P}} \frac{\partial }{\partial T_0 }W_2 (T_0 ,T_1 ,T_2 ) \nonumber \\&\quad =-2\frac{\partial ^{2}}{\partial T_0 \partial T_1 }V_1 (T_0 ,T_1 ,T_2 )\nonumber \\&\qquad -\pi ^{2}\Omega I_{\mathrm{P}} \frac{\partial }{\partial T_1 }W_1 (T_0 ,T_1 ,T_2 ) \nonumber \\&\pi ^{4}D_{11} W_2 (T_0 ,T_1 ,T_2 )+\frac{\partial ^{2}}{\partial T_0^2 }W_2 (T_0 ,T_1 ,T_2 )\nonumber \\&\qquad -\pi ^{2}\Omega I_{\mathrm{P}} \frac{\partial }{\partial T_0 }V_2 (T_0 ,T_1 ,T_2 ) \nonumber \\&\quad =-2\frac{\partial ^{2}}{\partial T_0 \partial T_1 }W_1 (T_0 ,T_1 ,T_2 )\nonumber \\&\qquad +\pi ^{2}\Omega I_{\mathrm{P}} \frac{\partial }{\partial T_1 }V_1 (T_0 ,T_1 ,T_2 ) \nonumber \\&\pi ^{2}A_{11} U_2 (T_0 ,T_1 ,T_2 )+\frac{\partial ^{2}}{\partial T_0^2 }U_2 (T_0 ,T_1 ,T_2 )\nonumber \\&\quad =-2\frac{\partial ^{2}}{\partial T_0 \partial T_1 }U_1 (T_0 ,T_1 ,T_2 ) \nonumber \\&\pi ^{2}D_{66} \varphi _2 (T_0 ,T_1 ,T_2 )+\frac{\partial ^{2}}{\partial T_0^2 }\varphi _2 (T_0 ,T_1 ,T_2 )\nonumber \\&\quad =-2\frac{\partial ^{2}}{\partial T_0 \partial T_1 }\varphi _1 (T_0 ,T_1 ,T_2 ) \end{aligned}$$

(33)

$$\begin{aligned}&O\left( \varepsilon ^{3}\right) \nonumber \\&D_{11} \pi ^{4}V_3 \left( T_0 ,T_1 ,T_2 \right) +\frac{\partial ^{2}}{\partial T_0^2 }V_3 \left( T_0 ,T_1 ,T_2 \right) \nonumber \\&\qquad +I_{\mathrm{P}} \Omega \pi ^{2}\frac{\partial }{\partial T_0 }W_3 \left( T_0 ,T_1 ,T_2 \right) \nonumber \\&\quad =-c\frac{\partial }{\partial T_0 }V_1 \left( T_0 ,T_1 ,T_2 \right) \nonumber \\&\qquad +A_{11} \left[ \frac{3}{2}\pi ^{4}V_1 \left( T_0 ,T_1 ,T_2 \right) U_1 (T_0 ,T_1 ,T_2 )^{2}\right. \nonumber \\&\qquad \quad -\frac{3}{4}\pi ^{4}V_1 \left( T_0 ,T_1 ,T_2 \right) ^{3}\nonumber \\&\qquad \left. -\frac{3}{4}\pi ^{4}W_1 \left( T_0 ,T_1 ,T_2 \right) ^{2}V_1 \left( T_0 ,T_1 ,T_2 \right) \right] \nonumber \\&\qquad -2\frac{\partial ^{2}}{\partial T_1 \partial T_0 }V_2 (T_0 ,T_1 ,T_2 )\nonumber \\&\qquad -2\frac{\partial ^{2}}{\partial T_2 \partial T_0 }V_1 (T_0 ,T_1 ,T_2 )\nonumber \\&\qquad -\frac{\partial ^{2}}{\partial T_1^2 }V_1 (T_0 ,T_1 ,T_2 )\nonumber \\&\qquad -I_{\mathrm{P}} \Omega \pi ^{2}\left[ \frac{\partial }{\partial T_1 }W_2 \left( T_0 ,T_1 ,T_2 \right) \right. \nonumber \\&\qquad \left. +\frac{\partial }{\partial T_2 }W_1 \left( T_0 ,T_1 ,T_2 \right) \right] -\Omega ^{2}e_1 \sin (\Omega T_0 )\nonumber \\&\qquad +\Omega ^{2}e_2 \cos (\Omega T_0 ) \nonumber \\&D_{11} \pi ^{4}W_3 (T_0 ,T_1 ,T_2 )+\frac{\partial ^{2}}{\partial T_0^2 }W_3 (T_0 ,T_1 ,T_2 )\nonumber \\&\qquad -I_{\mathrm{P}} \Omega \pi ^{2}\frac{\partial }{\partial T_0 }V_3 (T_0 ,T_1 ,T_2 )\nonumber \\&\quad =-c\frac{\partial }{\partial T_0 }W_1 (T_0 ,T_1 ,T_2 ) \nonumber \\&\qquad +A_{11} \left[ \frac{3}{2}\pi ^{4}W_1 (T_0 ,T_1 ,T_2 )U_1 (T_0 ,T_1 ,T_2 )^{2}\right. \nonumber \\&\qquad -\frac{3}{4}\pi ^{4}W_1 (T_0 ,T_1 ,T_2 )^{3}\nonumber \\&\qquad \left. -\frac{3}{4}\pi ^{4}V_1 (T_0 ,T_1 ,T_2 )^{2}W_1 \left( T_0 ,T_1 ,T_2 \right) \right] \nonumber \\&\qquad -2\frac{\partial ^{2}}{\partial T_1 \partial T_0 }W_2 \left( T_0 ,T_1 ,T_2 \right) \nonumber \\&\qquad -2\frac{\partial ^{2}}{\partial T_2 \partial T_0 }W_1 \left( T_0 ,T_1 ,T_2 \right) \nonumber \\&\qquad -\frac{\partial ^{2}}{\partial T_1^2 }W_1 (T_0 ,T_1 ,T_2 )\nonumber \\&\qquad +I_{\mathrm{P}} \Omega \pi ^{2}\left[ \frac{\partial }{\partial T_1 }V_2 (T_0 ,T_1 ,T_2 ) \right. \nonumber \\&\qquad \left. +\frac{\partial }{\partial T_2 }V_1 (T_0 ,T_1 ,T_2 )\right] +\Omega ^{2}e_2 \sin (\Omega T_0 )\nonumber \\&\qquad +\Omega ^{2}e_1 \cos (\Omega T_0 ) \nonumber \\&A_{11} \pi ^{2}U_3 (T_0 ,T_1 ,T_2 )+\frac{\partial ^{2}}{\partial T_0^2 }U_3 (T_0 ,T_1 ,T_2 )\nonumber \\&\quad =A_{11} \left[ \frac{3}{2}\pi ^{4}W_1 (T_0 ,T_1 ,T_2 )^{2}U_1 (T_0 ,T_1 ,T_2 ) \right. \nonumber \\&\qquad \left. +\frac{3}{2}\pi ^{4}V_1 (T_0 ,T_1 ,T_2 )^{2}U_1 (T_0 ,T_1 ,T_2 )\right] \nonumber \\&\qquad -2\frac{\partial ^{2}}{\partial T_1 \partial T_0 }U_2 (T_0 ,T_1 ,T_2 )-\frac{\partial ^{2}}{\partial T_1^2 }U_1 (T_0 ,T_1 ,T_2 ) \nonumber \\&D_{66} \pi ^{2}\varphi _3 (T_0 ,T_1 ,T_2 )+\frac{\partial ^{2}}{\partial T_0^2 }\varphi _3 (T_0 ,T_1 ,T_2 )\nonumber \\&\quad =D_{66} \left[ \frac{3}{2}\pi ^{5}V_1 \left( T_0 ,T_1 ,T_2 \right) W_1 \left( T_0 ,T_1 ,T_2 \right) \right. \nonumber \\&\qquad \left. U_1 \left( T_0 ,T_1 ,T_2 \right) \right] -\frac{\partial ^{2}}{\partial T_1^2 }\varphi _1 (T_0 ,T_1 ,T_2 )\nonumber \\&\qquad -2\frac{\partial ^{2}}{\partial T_1 \partial T_0 }\varphi _2 (T_0 ,T_1 ,T_2 ) {-}2\frac{\partial ^{2}}{\partial T_2 \partial T_0 }\varphi _1 (T_0 ,T_1 ,T_2 )\nonumber \\ \end{aligned}$$

(34)

The general solution of (32) can be expressed as

$$\begin{aligned} V_1 (T_0 ,T_1 ,T_2 )= & {} F_1 (T_1 ,T_2 )\hbox {e}^{\beta _f T_0 i}\nonumber \\&\quad +F_2 (T_1 ,T_2 )\hbox {e}^{\beta _b T_0 i}\nonumber \\&\quad +\bar{{F}}_1 (T_1 ,T_2 )\hbox {e}^{-\beta _f T_0 i}\nonumber \\&\quad +\bar{{F}}_2 (T_1 ,T_2 )\hbox {e}^{-\beta _b T_0 i} \nonumber \\ W_1 (T_0 ,T_1 ,T_2 )= & {} \alpha iF_1 (T_1 ,T_2 )\hbox {e}^{\beta _f T_0 i}\nonumber \\&\quad +\delta iF_2 (T_1 ,T_2 )\hbox {e}^{\beta _b T_0 i}\nonumber \\&\quad -\alpha i\bar{{F}}_1 (T_1 ,T_2 )\hbox {e}^{-\beta _f T_0 i}\nonumber \\&\quad -\delta i\bar{{F}}_2 (T_1 ,T_2)\hbox {e}^{-\beta _b T_0 i} \nonumber \\ U_1 (T_0 ,T_1 ,T_2 )= & {} \frac{1}{2}H_1 (T_1 ,T_2 )\hbox {e}^{-\beta _u T_0 i}\nonumber \\&\quad +\frac{1}{2}\bar{{H}}_1 (T_1 ,T_2 )\hbox {e}^{\beta _u T_0 i} \nonumber \\ \varphi _1 (T_0 ,T_1 ,T_2 )= & {} \frac{1}{2}G_1 (T_1 ,T_2 )\hbox {e}^{-\beta _\varphi T_0 i}\nonumber \\&\quad +\frac{1}{2}\bar{{G}}_1 (T_1 ,T_2 )\hbox {e}^{\beta _\varphi T_0 i} \end{aligned}$$

(35)

where $F_i (T_1 ,T_2 )$, $G_1 (T_1 ,T_2 )$ and $H_1 (T_1 ,T_2 )$, $(i=1,2)$ are complex functions which will be determined at the third order of approximation. $\beta _f$ and $\beta _b$ are forward and backward natural frequencies corresponding to flexural modes. The solution in this form is due to the existence of the gyroscopic term. Also, $\beta _u$ and $\beta _\varphi$ are natural frequencies corresponding to extensional–torsional modes. They are computed as

$$\begin{aligned} \beta _f= & {} -\frac{1}{2}\sqrt{2\sqrt{\pi ^{8}I_{\mathrm{p}} ^{2}\Omega ^{2}(I_{\mathrm{p}} ^{2}\Omega ^{2}+4D_{11} )}+(4D_{11} +2\pi ^{4}I_{\mathrm{p}} ^{2}\Omega ^{2})} \nonumber \\ \beta _b= & {} -\frac{1}{2}\sqrt{-2\sqrt{\pi ^{8}I_{\mathrm{p}} ^{2}\Omega ^{2}(I_{\mathrm{p}} ^{2}\Omega ^{2}+4D_{11} )}+(4D_{11} +2\pi ^{4}I_{\mathrm{p}} ^{2}\Omega ^{2})} \nonumber \\ \beta _u= & {} \pi \sqrt{A_{11} } \nonumber \\ \beta _\varphi= & {} \pi \sqrt{D_{66} } \end{aligned}$$

(36)

where $\alpha$ and $\delta$ are coefficients computed as

$$\begin{aligned} \alpha= & {} -\frac{1}{2}i\left( {\frac{(-2\sqrt{\pi ^{8}I_{\mathrm{p}} ^{2}\Omega ^{2}(I_{\mathrm{p}} ^{2}\Omega ^{2}+4D_{11} )}+(-4D_{11} -2\pi ^{4}I_{\mathrm{p}} ^{2}\Omega ^{2}))^{\frac{3}{2}}}{I_{\mathrm{p}} \Omega \pi ^{6}D_{11} }} \right. \nonumber \\&\left. +{\frac{\pi ^{4}(I_{\mathrm{p}} ^{2}\Omega ^{2}+D_{11} )\sqrt{-2\sqrt{\pi ^{8}I_{\mathrm{p}} ^{2}\Omega ^{2}(I_{\mathrm{p}} ^{2}\Omega ^{2}+4D_{11} )}+(-4D_{11} -2\pi ^{4}I_{\mathrm{p}} ^{2}\Omega ^{2})}}{I_{\mathrm{p}} \Omega \pi ^{6}D_{11} }} \right) \nonumber \\ \delta= & {} -\frac{1}{2}i\left( {\frac{(2\sqrt{\pi ^{8}I_{\mathrm{p}} ^{2}\Omega ^{2}(I_{\mathrm{p}} ^{2}\Omega ^{2}+4D_{11} )}+(-4D_{11} -2\pi ^{4}I_{\mathrm{p}} ^{2}\Omega ^{2}))^{\frac{3}{2}}}{I_{\mathrm{p}} \Omega \pi ^{6}D_{11} }} \right. \nonumber \\&\left. +{\frac{\pi ^{4}(I_{\mathrm{p}} ^{2}\Omega ^{2}+D_{11} )\sqrt{2\sqrt{\pi ^{8}I_{\mathrm{p}} ^{2}\Omega ^{2}(I_{\mathrm{p}} ^{2}\Omega ^{2}+4D_{11} )}+(-4D_{11} -2\pi ^{4}I_{\mathrm{p}} ^{2}\Omega ^{2})}}{I_{\mathrm{p}} \Omega \pi ^{6}D_{11} }} \right) \end{aligned}$$

(37)

Substituting Eqs. (35) into (33) yields

$$\begin{aligned}&\pi ^{4}D_{11} V_2 (T_0 ,T_1 ,T_2 )+\frac{\partial ^{2}}{\partial T_0^2 }V_2 (T_0 ,T_1 ,T_2 )\nonumber \\&\qquad +\pi ^{2}\Omega I_{\mathrm{P}} \frac{\partial }{\partial T_0 }W_2 (T_0 ,T_1 ,T_2 ) \nonumber \\&\quad =i(2\beta _f +I_{\mathrm{p}} \Omega \pi ^{2}\alpha )\frac{\partial }{\partial T_1 }F_1 (T_1 ,T_2 )\mathrm{e}^{i\beta _f T_0 }\nonumber \\&\qquad +i(2\beta _b +I_{\mathrm{p}} \Omega \pi ^{2}\delta )\frac{\partial }{\partial T_1 }F_2 (T_1 ,T_2 )\mathrm{e}^{i\beta _b T_0 }+cc \nonumber \\&\pi ^{4}D_{11} W_2 (T_0 ,T_1 ,T_2 )+\frac{\partial ^{2}}{\partial T_0^2 }W_2 (T_0 ,T_1 ,T_2 )\nonumber \\&\qquad -\pi ^{2}\Omega I_{\mathrm{P}} \frac{\partial }{\partial T_0 }V_2 (T_0 ,T_1 ,T_2 ) \nonumber \\&\quad =(2\alpha \beta _f +I_{\mathrm{p}} \Omega \pi ^{2})\frac{\partial }{\partial T_1 }F_1 (T_1 ,T_2 )\mathrm{e}^{i\beta _f T_0 }\nonumber \\&\qquad +(2\delta \beta _b +I_{\mathrm{p}} \Omega \pi ^{2})\frac{\partial }{\partial T_1 }F_2 (T_1 ,T_2 )\mathrm{e}^{i\beta _b T_0 }+cc \nonumber \\&\pi ^{2}A_{11} U_2 (T_0 ,T_1 ,T_2 )+\frac{\partial ^{2}}{\partial T_0^2 }U_2 (T_0 ,T_1 ,T_2 )\nonumber \\&\quad =-\frac{\partial ^{2}}{\partial T_0 \partial T_1 }\bar{{H}}_1 (T_1 ,T_2 )\mathrm{e}^{i\beta _u T_0 }+cc \nonumber \\&\pi ^{2}D_{66} \varphi _2 (T_0 ,T_1 ,T_2 )+\frac{\partial ^{2}}{\partial T_0^2 }\varphi _2 (T_0 ,T_1 ,T_2 )\nonumber \\&\quad =-\frac{\partial ^{2}}{\partial T_0 \partial T_1 }\bar{{G}}_1 (T_1 ,T_2 )\mathrm{e}^{i\beta _\varphi T_0 }+cc \end{aligned}$$

(38)

where cc stands for the complex conjugate terms. As Eq. (38) show, no non-secular term exists at this order, so the inhomogeneous solution of Eq. (38) yields

$$\begin{aligned} U_2 (T_0 ,T_1 ,T_2 )= & {} 0,V_2 (T_0 ,T_1 ,T_2 )=0,\nonumber \\ W_2 (T_0 ,T_1 ,T_2)= & {} 0,\varphi _2 (T_0 ,T_1 ,T_2 )=0 \end{aligned}$$

(39)

The solvability conditions are satisfied if the terms that lead to secular terms are eliminated. Because the first two equations in (38) are coupled, the solvability condition can be obtained through a procedure explained in the following. To find the solvability conditions, solution of the first two equations in (38) is assumed in following form [35]

$$\begin{aligned} V_2 (T_0 ,T_1 ,T_2 )= & {} F_{11} (T_1 ,T_2 )\mathrm{e}^{i\beta _f T_0 }\nonumber \\&+F_{12} (T_1 ,T_2 )\mathrm{e}^{i\beta _b T_0 } \nonumber \\ W_2 (T_0 ,T_1 ,T_2 )= & {} F_{21} (T_1 ,T_2 )\mathrm{e}^{i\beta _f T_0 }\nonumber \\&+F_{22} (T_1 ,T_2 )\mathrm{e}^{i\beta _b T_0 } \end{aligned}$$

(40)

By substituting Eqs. (40) into (38) and equating the coefficients of $\mathrm{e}^{i\beta _f T_0 }$ and $\mathrm{e}^{i\beta _b T_0 }$ from both sides of the result, one can obtain

$$\begin{aligned}&{[}(\pi ^{4}D_{11} -\beta _f^2 )F_{11} (T_1 ,T_2 )+iI_{\mathrm{p}} \Omega \pi ^{2}\beta _f F_{21} (T_1 ,T_2 )]\mathrm{e}^{i\beta _f T_0 }\nonumber \\&\quad =i(2\beta _f +I_{\mathrm{p}} \Omega \pi ^{2}\alpha )\frac{\partial }{\partial T_1 }F_1 (T_1 ,T_2 )\mathrm{e}^{i\beta _f T_0 } \nonumber \\&{[}(\pi ^{4}D_{11} -\beta _b^2 )F_{12} (T_1 ,T_2 )+iI_{\mathrm{p}} \Omega \pi ^{2}\beta _b F_{22} (T_1 ,T_2 )]\mathrm{e}^{i\beta _b T_0 }\nonumber \\&\quad =i(2\beta _b +I_{\mathrm{p}} \Omega \pi ^{2}\delta )\frac{\partial }{\partial T_1 }F_2 (T_1 ,T_2 )\mathrm{e}^{i\beta _b T_0 } \nonumber \\&{[}-iI_{\mathrm{p}} \Omega \pi ^{2}\beta _f F_{11} (T_1 ,T_2 )+(\pi ^{4}D_{11} -\beta _f^2 )F_{21} (T_1 ,T_2 )]\mathrm{e}^{i\beta _f T_0 }\nonumber \\&\quad =(2\alpha \beta _f +I_{\mathrm{p}} \Omega \pi ^{2})\frac{\partial }{\partial T_1 }F_1 (T_1 ,T_2 )\mathrm{e}^{i\beta _f T_0 } \nonumber \\&{[}-iI_{\mathrm{p}} \Omega \pi ^{2}\beta _b F_{12} (T_1 ,T_2 )+(\pi ^{4}D_{11} -\beta _b^2 )F_{22} (T_1 ,T_2 )]\mathrm{e}^{i\beta _b T_0 }\nonumber \\&\quad =(2\delta \beta _b +I_{\mathrm{p}} \Omega \pi ^{2})\frac{\partial }{\partial T_1 }F_2 (T_1 ,T_2 )\mathrm{e}^{i\beta _b T_0 } \end{aligned}$$

(41)

Equation (41) forms two systems of equations and they both have non-trivial solution if

$$\begin{aligned}&\left| {{\begin{array}{ll} {(\pi ^{4}D_{11} -\beta _f^2 )}&{} {i(2\beta _f +I_{\mathrm{p}} \Omega \pi ^{2}\alpha )\frac{\partial }{\partial T_1 }F_1 (T_1 ,T_2 )} \\ \quad {-iI_{\mathrm{p}} \Omega \pi ^{2}\beta _f }&{} {(2\alpha \beta _f +I_{\mathrm{p}} \Omega \pi ^{2})\frac{\partial }{\partial T_1 }F_1 (T_1 ,T_2 )} \\ \end{array} }} \right| =0 \nonumber \\&\left| {{\begin{array}{ll} {(\pi ^{4}D_{11} -\beta _b^2 )}&{} {i(2\beta _b +I_{\mathrm{p}} \Omega \pi ^{2}\delta )\frac{\partial }{\partial T_1 }F_2 (T_1 ,T_2 )} \\ \quad {-iI_{\mathrm{p}} \Omega \pi ^{2}\beta _f }&{} {(2\delta \beta _b +I_{\mathrm{p}} \Omega \pi ^{2})\frac{\partial }{\partial T_1 }F_2 (T_1 ,T_2 )} \\ \end{array} }} \right| =0\nonumber \\ \end{aligned}$$

(42)

So, the solvability conditions for the second order become

$$\begin{aligned}&\left[ (\pi ^{4}D_{11} -\beta _f^2 )(2\alpha \beta _f +I_{\mathrm{p}} \Omega \pi ^{2})\right. \nonumber \\&\qquad \left. -I_{\mathrm{p}} \Omega \pi ^{2}\beta _f (2\beta _f +I_{\mathrm{p}} \Omega \pi ^{2}\alpha )\right] \frac{\partial }{\partial T_1 }F_1 (T_1 ,T_2 )=0 \nonumber \\&\left[ (\pi ^{4}D_{11} -\beta _b^2 )(2\delta \beta _b +I_{\mathrm{p}} \Omega \pi ^{2})\right. \nonumber \\&\qquad \left. -I_{\mathrm{p}} \Omega \pi ^{2}\beta _f (2\beta _b +I_{\mathrm{p}} \Omega \pi ^{2}\delta )\right] \frac{\partial }{\partial T_1 }F_2 (T_1 ,T_2 )=0\nonumber \\ \end{aligned}$$

(43)

which demand that $F_1 (T_1 ,T_2 )$ and $F_2 (T_1 ,T_2 )$ to be function of only $T_2$. To satisfy the solvability conditions for the last two equations in (38), their secular terms are directly eliminated due to the decoupling of the equations. Thus, it can be written

$$\begin{aligned} \frac{\partial }{\partial T_1 }\bar{{H}}_1 (T_1 ,T_2 )= & {} 0 \nonumber \\ \frac{\partial }{\partial T_1 }\bar{{G}}_1 (T_1 ,T_2 )= & {} 0 \end{aligned}$$

(44)

Again the solvability conditions demand that $H_1 (T_1 ,T_2 )$ and $G_1 (T_1 ,T_2 )$ to be function of only $T_2$. Finally, Eq. (35) can be rewritten as

$$\begin{aligned} V_1 (T_0 ,T_2 )= & {} F_1 (T_2 )\hbox {e}^{\beta _f T_0 i}+F_2 (T_2 )\hbox {e}^{\beta _b T_0 i}\nonumber \\&+\,\bar{{F}}_1 (T_2 )\hbox {e}^{-\beta _f T_0 i}+\bar{{F}}_2 (T_2 )\hbox {e}^{-\beta _b T_0 i} \nonumber \\ W_1 (T_0 ,T_2 )= & {} \alpha iF_1 (T_2 )\hbox {e}^{\beta _f T_0 i}+\delta iF_2 (T_2 )\hbox {e}^{\beta _b T_0 i}\nonumber \\&-\,\alpha i\bar{{F}}_1 (T_2 )\hbox {e}^{-\beta _f T_0 i}\!-\!\delta i\bar{{F}}_2 (T_2 )\hbox {e}^{-\beta _b T_0 i} \nonumber \\ U_1 (T_0 ,T_2 )= & {} \frac{1}{2}H_1 (T_2 )\hbox {e}^{-\beta _u T_0 i} +\frac{1}{2}\bar{{H}}_1 (T_2 )\hbox {e}^{\beta _u T_0 i} \nonumber \\ \varphi _1 (T_0 ,T_2 )= & {} \frac{1}{2}G_1 (T_2 )\hbox {e}^{-\beta _\varphi T_0 i}+\frac{1}{2}\bar{{G}}_1 (T_2 )\hbox {e}^{\beta _\varphi T_0 i}\nonumber \\ \end{aligned}$$

(45)

The third order is treated in the same procedure to compute solvability conditions. To express the nearness of the excitation frequency to the natural frequency, a detuning parameter $\sigma$ is introduced which is defined as

$$\begin{aligned} \Omega =\beta _f +\varepsilon ^{2}\sigma \end{aligned}$$

(46)

Again, solvability conditions for the first two equations in (34) must be obtained through a system of equations because of the existence of the gyroscopic coupling in the equations. So one may assume

$$\begin{aligned} V_3 (T_0 ,T_1 ,T_2 )= & {} P_{11} (T_1 ,T_2 )\mathrm{e}^{i\beta _f T_0 }\nonumber \\&+P_{12} (T_1 ,T_2 )\mathrm{e}^{i\beta _b T_0 } \nonumber \\ W_3 (T_0 ,T_1 ,T_2 )= & {} P_{21} (T_1 ,T_2 )\mathrm{e}^{i\beta _f T_0 }\nonumber \\&+P_{22} (T_1 ,T_2 )\mathrm{e}^{i\beta _b T_0 } \end{aligned}$$

(47)

By substituting Eqs. (39), (45)–(47) into (34) and equating the coefficients of $\mathrm{e}^{i\beta _f T_0 }$ and $\mathrm{e}^{i\beta _f T_0 }$ from both side of it one can obtain

$$\begin{aligned}&\left[ (\pi ^{4}D_{11} -\beta _f^2 )P_{11} (T_1 ,T_2 )\right. \nonumber \\&\qquad \left. +iI_{\mathrm{p}} \Omega \pi ^{2}\beta _f P_{21} (T_1 ,T_2 )\right] \mathrm{e}^{i\beta _f T_0 } \nonumber \\&\quad =\left[ A_{11} \pi ^{4}\left( -\left( \frac{9}{2}+\frac{3}{2}\delta ^{2}\right) F_1 (T_2 )F_2 (T_2 )\bar{{F}}_2 (T_2 )\right. \right. \nonumber \\&\qquad -\left( \frac{9}{4}+\frac{3}{4}\alpha ^{2}\right) F_1 (T_2 )^{2}\bar{{F}}_1 (T_2 )\nonumber \\&\qquad \left. +\frac{3}{4}F_1 (T_2 )H_1 (T_2 )\bar{{H}}_1 (T_2 )\right) \nonumber \\&\qquad +i(-2\beta _f -I_{\mathrm{p}} \Omega \pi ^{2}\alpha )\frac{\mathrm{d}}{\mathrm{d}T_2 }F_1 (T_2 )\nonumber \\&\qquad \left. -ic\beta _f F_1 (T_2 )+\frac{1}{2}\Omega ^{2}(ie_1 +e_2 )\mathrm{e}^{i\sigma T_2 }\right] \mathrm{e}^{i\beta _f T_0 } \nonumber \\&\left[ (\pi ^{4}D_{11} -\beta _b^2 )P_{12} (T_1 ,T_2 )\right. \nonumber \\&\qquad \left. +iI_{\mathrm{p}} \Omega \pi ^{2}\beta _b P_{22} (T_1 ,T_2 )\right] \mathrm{e}^{i\beta _b T_0 } \nonumber \\&\quad =\bigg [A_{11} \pi ^{4}\left( -\left( \frac{9}{2}+\frac{3}{2}\alpha ^{2}\right) F_1 (T_2 )F_2 (T_2 )\bar{{F}}_1 (T_2 )\right. \nonumber \\&\qquad -\left( \frac{9}{4}+\frac{3}{4}\delta ^{2}\right) F_2 (T_2 )^{2}\bar{{F}}_2 (T_2 ) \nonumber \\&\qquad \left. +\frac{3}{4}F_2 (T_2 )H_1 (T_2 )\bar{{H}}_1 (T_2 )\right) +\,i(-2\beta _b \nonumber \\&\qquad +I_{\mathrm{p}} \Omega \pi ^{2}\delta )\frac{\mathrm{d}}{\mathrm{d}T_2 }F_2 (T_2 ) -ic\beta _b F_2 (T_2 )\bigg ]\mathrm{e}^{i\beta _b T_0 } \nonumber \\&\qquad \left[ -iI_{\mathrm{p}} \Omega \pi ^{2}\beta _f P_{11} (T_1 ,T_2 )\right. \nonumber \\&\qquad \left. +(\pi ^{4}D_{11} -\beta _f^2 )P_{21} (T_1 ,T_2 )\right] \mathrm{e}^{i\beta _f T_0 } \nonumber \\&\quad =\left[ A_{11} i\pi ^{4}\left( -\left( \frac{9}{2}\alpha \delta ^{2}\right. \right. \right. \nonumber \\&\qquad \left. +\frac{3}{2}\alpha \right) F_1 (T_2 )F_2 (T_2 )\bar{{F}}_2 (T_2)\nonumber \\&\qquad -\left( \frac{9}{4}\alpha ^{3}+\frac{3}{4}\alpha \right) F_1 (T_2 )^{2}\bar{{F}}_1 (T_2 )\nonumber \\&\qquad \left. +\frac{3}{4}\alpha F_1 (T_2 )H_1 (T_2 )\bar{{H}}_1 (T_2 )\right) \nonumber \\&\qquad +(2\alpha \beta _f +I_{\mathrm{p}} \Omega \pi ^{2})\frac{\mathrm{d}}{\mathrm{d}T_2 }F_1 (T_2 )+c\alpha \beta _f F_1 (T_2 )\nonumber \\&\qquad \left. +\frac{1}{2}\Omega ^{2}(e_1 -ie_2 )\mathrm{e}^{i\sigma T_2 }\right] \mathrm{e}^{i\beta _f T_0 } \nonumber \\&\left[ -iI_{\mathrm{p}} \Omega \pi ^{2}\beta _b P_{12} (T_1 ,T_2 )\right. \nonumber \\&\qquad \left. +(\pi ^{4}D_{11} -\beta _b^2 )P_{22} (T_1 ,T_2 )\right] \mathrm{e}^{i\beta _b T_0 } \nonumber \\&\quad =\left[ A_{11} i\pi ^{4}\left( -\left( \frac{9}{2}\alpha ^{2}\delta +\frac{3}{2}\delta \right) \right. \right. \nonumber \\&\qquad F_1 (T_2 )F_2 (T_2 )\bar{{F}}_1 (T_2 )\nonumber \\&\qquad -\left( \frac{9}{4}\delta ^{3}+\frac{3}{4}\delta \right) F_2 (T_2 )^{2}\bar{{F}}_2 (T_2 ) \nonumber \\&\qquad \left. +\frac{3}{4}\delta F_2 (T_2 )H_1 (T_2 )\bar{{H}}_1 (T_2 )\right) \nonumber \\&\qquad +(2\delta \beta _f +I_{\mathrm{p}} \Omega \pi ^{2})\frac{\mathrm{d}}{\mathrm{d}T_2 }F_2 (T_2 )\nonumber \\&\qquad \left. +c\delta \beta _b F_2 (T_2 )\right] \mathrm{e}^{i\beta _b T_0 } \end{aligned}$$

(48)

The solvability conditions are computed in the following form as

$$\begin{aligned}&\left| {{\begin{array}{ll} {(\pi ^{4}D_{11} -\beta _f^2 )}&{} {\begin{array}{l} A_{11} \pi ^{4}\left( -\left( \frac{9}{2}+\frac{3}{2}\delta ^{2}\right) F_1 (T_2 )F_2 (T_2 )\bar{{F}}_2 (T_2 )-\left( \frac{9}{4}+\frac{3}{4}\alpha ^{2}\right) F_1 (T_2 )^{2}\bar{{F}}_1 (T_2 ) \right. \\ \quad +\,\frac{3}{4}F_1 (T_2 )H_1 (T_2 )\bar{{H}}_1 (T_2 ))+i\left( -2\beta _f -I_{\mathrm{p}} \Omega \pi ^{2}\alpha \right) \frac{\mathrm{d}}{\mathrm{d}T_2 }F_1 (T_2 )-ic\beta _f F_1 (T_2 )+\frac{1}{2}\Omega ^{2}(ie_1 +e_2 )\mathrm{e}^{i\sigma T_2 } \\ \end{array}} \\ {-iI_{\mathrm{p}} \Omega \pi ^{2}\beta _f }&{} {\begin{array}{l} A_{11} i\pi ^{4}\left( -\left( \frac{9}{2}\alpha \delta ^{2}+\frac{3}{2}\alpha \right) F_1 (T_2 )F_2 (T_2 )\bar{{F}}_2 (T_2 )-\left( \frac{9}{4}\alpha ^{3}+\frac{3}{4}\alpha \right) F_1 (T_2 )^{2}\bar{{F}}_1 (T_2 ) \right. \\ \quad +\,\frac{3}{4}\alpha F_1 (T_2 )H_1 (T_2 )\bar{{H}}_1 (T_2 ))+(2\alpha \beta _f +I_{\mathrm{p}} \Omega \pi ^{2})\frac{\mathrm{d}}{\mathrm{d}T_2 }F_1 (T_2 )+c\alpha \beta _f F_1 (T_2 ) \\ \end{array}} \\ \end{array} }} \right| =0 \nonumber \\&\left| {{\begin{array}{ll} {(\pi ^{4}D_{11} -\beta _b^2 )}&{} {\begin{array}{l} A_{11} \pi ^{4}\left( -\left( \frac{9}{2}+\frac{3}{2}\alpha ^{2}\right) F_1 (T_2 )F_2 (T_2 )\bar{{F}}_1 (T_2 )-\left( \frac{9}{4}+\frac{3}{4}\delta ^{2}\right) F_2 (T_2 )^{2}\bar{{F}}_2 (T_2 ) \right. \\ \quad +\,\frac{3}{4}F_2 (T_2 )H_1 (T_2 )\bar{{H}}_1 (T_2 ))+i(-2\beta _b +I_{\mathrm{p}} \Omega \pi ^{2}\delta )\frac{\mathrm{d}}{\mathrm{d}T_2 }F_2 (T_2 )-ic\beta _b F_2 (T_2 )+\frac{1}{2}\Omega ^{2}(e_1 -ie_2 )\mathrm{e}^{i\sigma T_2 } \\ \end{array}} \\ {-iI_{\mathrm{p}} \Omega \pi ^{2}\beta _b }&{} {\begin{array}{l} A_{11} i\pi ^{4}\left( -\left( \frac{9}{2}\alpha ^{2}\delta +\frac{3}{2}\delta \right) F_1 (T_2 )F_2 (T_2 )\bar{{F}}_1 (T_2 )-\left( \frac{9}{4}\delta ^{3}+\frac{3}{4}\delta \right) F_2 (T_2 )^{2}\bar{{F}}_2 (T_2 )\right. \\ \quad +\,\frac{3}{4}\delta F_2 (T_2 )H_1 (T_2 )\bar{{H}}_1 (T_2 ))+(2\delta \beta _f +I_{\mathrm{p}} \Omega \pi ^{2})\frac{\mathrm{d}}{\mathrm{d}T_2 }F_2 (T_2 )+c\delta \beta _b F_2 (T_2 ) \\ \end{array}} \\ \end{array} }} \right| =0\nonumber \\ \end{aligned}$$

(49)

which can be rewritten as

$$\begin{aligned}&i\Gamma _1 F_1 (T_2 )F_2 (T_2 )\bar{{F}}_2 (T_2 )+i\Lambda _1 F_1 (T_2 )^{2}\bar{{F}}_1 (T_2 )\nonumber \\&\qquad +i\Psi _1 F_1 (T_2 )H_1 (T_2 )\bar{{H}}_1 (T_2 )+\Phi _1 D_2 F_1 (T_2 ) \nonumber \\&\qquad +\left( {-\pi ^{4}D_{11} \alpha \beta _1 +\beta _1 ^{3}\alpha -\beta _1 ^{2}I_{\mathrm{p}} \Omega \pi ^{2}} \right) cF_1 (T_2 ) \nonumber \\&\qquad +1/2\left( -\beta _1 ^{2}-I_{\mathrm{p}} \pi ^{2}\Omega \beta _1 \right. \nonumber \\&\qquad \left. +\pi ^{4}D_{11} \right) \hbox {e}^{i\sigma T_2 }\left( {-e_1 +ie_2 } \right) \Omega ^{2}=0 \nonumber \\&i\Gamma _2 F_2 (T_2 )F_1 (T_2 )\bar{{F}}_1 (T_2 )+i\Lambda _2 F_2 (T_2 )^{2}\bar{{F}}_2 (T_2 )\nonumber \\&\qquad +i\Psi _2 F_2 (T_2 )H_1 (T_2 )\bar{{H}}_1 (T_2 )+\Phi _2 D_2 F_2 (T_2 ) \nonumber \\&\qquad +\left( -\beta _2 ^{2}I_{\mathrm{p}} \Omega \pi ^{2}-\pi ^{4}D_{11} \delta \beta _2 \right. \nonumber \\&\qquad \left. +\beta _2 ^{3}\delta \right) cF_2 (T_2 )=0 \end{aligned}$$

(50)

where $\Gamma _i ,\Lambda _i ,\Psi _i ,\Phi _i , (i=1,2)$ are the coefficients expressed in “Appendix 3” in more details. For the last two equations of (34), again the solvability conditions are obtained by substituting Eqs. (39) and (45), and eliminating the secular terms directly:

$$\begin{aligned}&\mathrm{X}F_2 (T_2 )\bar{{F}}_2 (T_2 )\bar{{H}}_1 (T_2 )+\Delta F_1 (T_2 )\bar{{F}}_1 (T_2 )\bar{{H}}_1 (T_2 )\nonumber \\&\qquad -i\beta _3 D_2 \bar{{H}}_1 (T_2 )=0 -i\beta _4 D_2 \bar{{G}}_1 (T_2 )=0 \end{aligned}$$

(51)

where

$$\begin{aligned} \mathrm{X}=\left( {1+\delta ^{2}} \right) \frac{3}{2}\pi ^{4}A_{11}\qquad \Delta =\left( {1+\alpha ^{2}} \right) \frac{3}{2}\pi ^{4}A_{11}\nonumber \\ \end{aligned}$$

(52)

It is seen from the second equation of (51) that the steady-state solution corresponding to $\bar{{G}}_1$ is zero. So, complex-valued functions $F_1 (T_2 ), F_2 (T_2 )$ and $H_1 (T_2 )$ are expressed in the polar form as

$$\begin{aligned} F_1 (T_2)= & {} \frac{1}{2}a_{f1} (T_2 )\mathrm{e}^{i\theta _{f1} (T_2 )}, \nonumber \\ F_2 (T_2)= & {} \frac{1}{2}a_{f2} (T_2 )\mathrm{e}^{i\theta _{f2} (T_2 )}, \nonumber \\ H_1 (T_2)= & {} \frac{1}{2}a_{h1} (T_2 )\mathrm{e}^{i\theta _{h1} (T_2 )} \end{aligned}$$

(53)

where real-valued quantities $a_i (T_2 )$ and $\theta _i (T_2 )$, $(i=f1,f2,k1)$ are amplitude and phase angle of the responses, respectively. Substituting Eq. (53) into Eq. (50) and the first equation in (51) and separating real and imaginary parts, the modulation equations are computed as

$$\begin{aligned}&\frac{1}{2}\left( {\pi ^{4}D_{11} \beta _1 -\beta _1 ^{2}I_{\mathrm{p}} \Omega \pi ^{2}-\beta _1 ^{3}} \right) ca_{f1} +\frac{1}{2}\Phi _1 D_2 a_{f1} \nonumber \\&\quad =\frac{1}{2}\Omega ^{2}\left( {e_2 \sin \left( {\gamma _1 } \right) -\cos \left( {\gamma _1 } \right) e_1 } \right) \left( -\beta _1 ^{2}\right. \nonumber \\&\qquad \left. -I_{\mathrm{p}} \pi ^{2}\Omega \beta _1 +\pi ^{4}D_{11} \right) \frac{1}{8}a_{f1} \left( \Gamma _1 a_{f2} ^{2}+\Psi _1 a_{h1} ^{2}\right. \nonumber \\&\qquad \left. +\,4\Phi _1 \sigma +a_{f1} ^{2}\Lambda _1 \right) \nonumber \\&\quad =\frac{1}{2}\Omega ^{2}\left( e_1 \sin \left( {\gamma _1 } \right) \right. \nonumber \\&\qquad \left. +\cos \left( {\gamma _1 } \right) e_2 \right) \left( {-\beta _1 ^{2}-I_{\mathrm{p}} \pi ^{2}\Omega \beta _1 +\pi ^{4}D_{11} } \right) \nonumber \\&\qquad \times \frac{1}{8}\Gamma _2 a_{f2} a_{f1} ^{2}+\frac{1}{8}\Lambda _2 a_{f2} ^{3}+\frac{1}{8}\Psi _2 a_{f2} a_{h1} ^{2} \nonumber \\&\qquad +\frac{1}{2}a_{f2} \Phi _2 \sigma \nonumber \\&\quad =0\frac{1}{2}\Phi _2 D_2 a_{f2} \nonumber \\&\qquad +\frac{1}{2}ca_{f2} \left( {-\pi ^{4}D_{11} \beta _2 +\beta _2 ^{3}-\beta _2 ^{2}I_{\mathrm{p}} \Omega \pi ^{2}} \right) =0 \nonumber \\&\qquad \times \frac{1}{8}\mathrm{X} a_{f2} ^{2}a_{h1} +\frac{1}{8}\Delta a_{f1} ^{2}a_{h1} -\frac{1}{2}\beta _3 a_{h1} D_2 \theta _{h1} =0 \nonumber \\&\qquad -\frac{1}{2}\beta _3 D_2 a_{h1} =0 \end{aligned}$$

(54)

where $\gamma _i =\sigma _1 T_2 -\theta _i ,(i=1,2)$. To investigate the steady-state response, the time derivatives in (54) must vanish, which results in $a_{f2} (T_2 )=0$ and $a_{h1} (T_2 )=0$ that means the unbalance force does not excite backward whirling and extensional vibration mode; so they vanish at this stage. By substituting $a_{f2} (T_2 )=0$ and $a_{h1} (T_2 )=0$ into equations of (54) and eliminating $\gamma$ between the remaining equations finally, the following modulation equation is obtained

$$\begin{aligned}&\lambda _1 a_{f1} ^{6}+\lambda _2 a_{f1} ^{4}+\lambda _3 a_{f1} ^{2}\nonumber \\&\quad =\frac{1}{4}\Omega ^{4}e_t^2 \left( {-\beta _1 ^{2}-I_{\mathrm{p}} \pi ^{2}\Omega \beta _1 +\pi ^{4}D_{11} } \right) ^{2} \end{aligned}$$

(55)

where

$$\begin{aligned} \lambda _1= & {} \frac{1}{64}\Lambda _1 ^{2} \nonumber \\ \lambda _2= & {} \frac{1}{8}\Phi _1 \sigma \Lambda _1 \nonumber \\ \lambda _3= & {} \frac{1}{4}c^{2}\beta _1 ^{6}\alpha ^{2}-\frac{1}{2}c^{2}\beta _1 ^{4}\alpha ^{2}\pi ^{4}D_{11}\nonumber \\&-\frac{1}{2}c^{2}\beta _1 ^{5}\alpha I_{\mathrm{p}} \Omega \pi ^{2}+\frac{1}{4}c^{2}\pi ^{8}D_{11} ^{2}\alpha ^{2}\beta _1 ^{2} \nonumber \\&+\frac{1}{2}c^{2}\pi ^{6}D_{11} \alpha \beta _1 ^{3}I_{\mathrm{p}} \Omega \!+\!\frac{1}{4}c^{2}\beta _1 ^{4}I_{\mathrm{p}} ^{2}\Omega ^{2}\pi ^{4}\!+\!\frac{1}{4}\Phi _1 ^{2}\sigma ^{2} \nonumber \\ e_t= & {} \sqrt{e_1^2 +e_2^2 } \end{aligned}$$

(56)

Equation (55) gives an analytical expression explaining the amplitude variation versus different parameter changes, such as detuning parameter, damping coefficient and other parameters.

3.2 Primary resonances with two-mode discretization

In this section, the method of multiple scales is applied to the governing equations like the previous section, but here the discretization is done using two modes, so the main procedure is similar to the previous section.

Using Eqs. (24)–(25) and expanding for two modes, it is obtained

$$\begin{aligned} u(x,t)= & {} U1(t)\sqrt{2}\sin (\pi x)+U2(t)\sqrt{2}\sin (2\pi x) \nonumber \\ v(x,t)= & {} V1(t)\sqrt{2}\sin (\pi x)+V2(t)\sqrt{2}\sin (2\pi x) \nonumber \\ w(x,t)= & {} W1(t)\sqrt{2}\sin (\pi x)+W2(t)\sqrt{2}\sin (2\pi x) \nonumber \\ \phi (x,t)= & {} \varphi 1(t)\sqrt{2}\cos (\pi x)+\varphi 2(t)\sqrt{2}\cos (2\pi x)\nonumber \\ \end{aligned}$$

(57)

Again using Eq. (57) and the orthogonality relation, the discretized equations are obtained as

$$\begin{aligned}&\frac{\mathrm{d}^{2}}{\mathrm{d}t^{2}}U1\left( t \right) -\frac{32}{3}B_{16} \varphi 2\left( t \right) \pi \nonumber \\&\qquad -A_{11} \left[ \sqrt{2}V1\left( t \right) \pi ^{3}V2\left( t \right) \right. \nonumber \\&\qquad +\sqrt{2}W1\left( t \right) \pi ^{3}W2\left( t \right) +U1\left( t \right) \pi ^{2} \nonumber \\&\qquad -8 V1\left( t \right) \pi ^{4}V2\left( t \right) U2\left( t \right) \nonumber \\&\qquad -8 W1\left( t \right) \pi ^{4}W2\left( t \right) U2\left( t \right) -4\left( {V2\left( t \right) } \right) ^{2}\pi ^{4}U1\left( t \right) \nonumber \\&\qquad -\frac{3}{2}\left( {V1\left( t \right) } \right) ^{2}\pi ^{4}U1\left( t \right) -4\left( {W2\left( t \right) } \right) ^{2}\pi ^{4}U1\left( t \right) \nonumber \\&\qquad \left. -\frac{3}{2}\left( {W1\left( t \right) } \right) ^{2}\pi ^{4}U1\left( t \right) \right] =0 \nonumber \\&\frac{\mathrm{d}^{2}}{\mathrm{d}t^{2}}U2\left( t \right) +\frac{16}{3}B_{16} P1\left( t \right) \pi \nonumber \\&\qquad -A_{11} \left[ 4\left( {W1\left( t \right) } \right) ^{2}\pi ^{4}U2\left( t \right) \right. \nonumber \\&\qquad -8W1\left( t \right) \pi ^{4}W2\left( t \right) U1\left( t \right) \nonumber \\&\qquad -24\left( {W2\left( t \right) } \right) ^{2}\pi ^{4}U2\left( t \right) \nonumber \\&\qquad -4\left( {V1\left( t \right) } \right) ^{2}\pi ^{4}U2\left( t \right) +\frac{1}{2}\sqrt{2}\left( {V1\left( t \right) } \right) ^{2}\pi ^{3} \nonumber \\&\qquad -8V1\left( t \right) \pi ^{4}V2\left( t \right) U1\left( t \right) +\frac{1}{2}\sqrt{2}\left( {W1\left( t \right) } \right) ^{2}\pi ^{3}\nonumber \\&\qquad \left. +4U2\left( t \right) \pi ^{2}-24\left( {V2\left( t \right) } \right) ^{2}\pi ^{4}U2\left( t \right) \right] =0 \end{aligned}$$

(58)

$$\begin{aligned}&A_{11} \left[ \sqrt{2}V2\left( t \right) \pi ^{3}U1\left( t \right) +6V1\left( t \right) \pi ^{4}\left( {V2\left( t \right) } \right) ^{2}\right. \nonumber \\&\qquad +\sqrt{2}V1\left( t \right) \pi ^{3}U2\left( t \right) +2\left( {W2\left( t \right) } \right) ^{2}\pi ^{4}V1\left( t \right) \nonumber \\&\qquad -8V2\left( t \right) \pi ^{4}U1\left( t \right) U2\left( t \right) -\frac{3}{2}V1\left( t \right) \pi ^{4}\left( {U1\left( t \right) } \right) ^{2}\nonumber \\&\qquad -4V1\left( t \right) \pi ^{4}\left( {U2\left( t \right) } \right) ^{2}+\frac{3}{4}\left( {V1\left( t \right) } \right) ^{3}\pi ^{4} \nonumber \\&\qquad \left. +\frac{3}{4}\left( {W1\left( t \right) } \right) ^{2}\pi ^{4}V1\left( t \right) +4W1\left( t \right) \pi ^{4}V2\left( t \right) W2\left( t \right) \right] \nonumber \\&\qquad +I_{\mathrm{p}} \Omega \pi ^{2}\left( {\frac{\mathrm{d}}{\mathrm{d}t}W1\left( t \right) } \right) +D_{11} V1\left( t \right) \pi ^{4} \nonumber \\&\qquad +c\frac{\mathrm{d}}{\mathrm{d}t}V1\left( t \right) +\frac{\mathrm{d}^{2}}{\mathrm{d}t^{2}}V1\left( t \right) \nonumber \\&\quad =\Omega ^{2}\left[ e_2 \cos \left( {\Omega t} \right) -e_1 \sin \left( {\Omega t} \right) \right] \nonumber \\&A_{11} \left[ 12\left( {W2\left( t \right) } \right) ^{2}\pi ^{4}V2\left( t \right) -24V2\left( t \right) \pi ^{4}\left( {U2\left( t \right) } \right) ^{2}\right. \nonumber \\&\qquad +4W1\left( t \right) \pi ^{4}V1\left( t \right) W2\left( t \right) +6\left( {V1\left( t \right) } \right) ^{2}\pi ^{4}V2\left( t \right) \nonumber \\&\qquad -8V1\left( t \right) \pi ^{4}U2\left( t \right) U1\left( t \right) +12\left( {V2\left( t \right) } \right) ^{3}\pi ^{4}\nonumber \\&\qquad +\sqrt{2}V1\left( t \right) \pi ^{3}U1\left( t \right) -4V2\left( t \right) \pi ^{4}\left( {U1\left( t \right) } \right) ^{2} \nonumber \\&\qquad \left. +2\left( {W1\left( t \right) } \right) ^{2}\pi ^{4}V2\left( t \right) \right] +16D_{11} V2\left( t \right) \pi ^{4}\nonumber \\&\qquad +c\frac{\mathrm{d}}{\mathrm{d}t}V2\left( t \right) +\frac{\mathrm{d}^{2}}{\mathrm{d}t^{2}}V2\left( t \right) \nonumber \\&\qquad +4I_{\mathrm{p}} \Omega \pi ^{2}\left( {\frac{\mathrm{d}}{\mathrm{d}t}W2\left( t \right) } \right) =0 \end{aligned}$$

(59)

$$\begin{aligned}&A_{11} \left[ \frac{3}{4}\pi ^{4}W1\left( t \right) \left( {V1\left( t \right) } \right) ^{2}+6\pi ^{4}W1\left( t \right) \left( {W2\left( t \right) } \right) ^{2}\right. \nonumber \\&\qquad +2\pi ^{4}W1\left( t \right) \left( {V2\left( t \right) } \right) ^{2}-\frac{3}{2}\pi ^{4}W1\left( t \right) \left( {U1\left( t \right) } \right) ^{2} \nonumber \\&\qquad -4\pi ^{4}W1\left( t \right) \left( {U2\left( t \right) } \right) ^{2}+4\pi ^{4}W2\left( t \right) V1\left( t \right) V2\left( t \right) \nonumber \\&\qquad +\sqrt{2}\pi ^{3}W2\left( t \right) U1\left( t \right) +\sqrt{2}\pi ^{3}W1\left( t \right) U2\left( t \right) \nonumber \\&\qquad \left. -8\pi ^{4}W2\left( t \right) U2\left( t \right) U1\left( t \right) +\frac{3}{4}\pi ^{4}\left( {W1\left( t \right) } \right) ^{3}\right] \nonumber \\&\qquad -\Omega I_{\mathrm{p}} \pi ^{2}\left( {\frac{\mathrm{d}}{\mathrm{d}t}V1\left( t \right) } \right) +D_{11 } \pi ^{4}W1\left( t \right) +c\frac{\mathrm{d}}{\mathrm{d}t}W1\left( t \right) \nonumber \\&\qquad +\frac{\mathrm{d}^{2}}{\mathrm{d}t^{2}}W1\left( t \right) =\Omega ^{2}e_1 \cos \left( {\Omega t} \right) +\Omega ^{2}e_2 \sin \left( {\Omega t} \right) \nonumber \\&A_{11} \left[ -4W2\left( t \right) \pi ^{4}\left( {U1\left( t \right) } \right) ^{2}+6\left( {W1\left( t \right) } \right) ^{2}\pi ^{4}W2\left( t \right) \right. \nonumber \\&\qquad +12\left( {W2\left( t \right) } \right) ^{3}\pi ^{4}+\sqrt{2}W1\left( t \right) \pi ^{3}U1\left( t \right) \nonumber \\&\qquad -8W1\left( t \right) \pi ^{4}U1\left( t \right) U2\left( t \right) -24W2\left( t \right) \pi ^{4}\left( {U2\left( t \right) } \right) ^{2}\nonumber \\&\qquad +4W1\left( t \right) \pi ^{4}V2\left( t \right) V1\left( t \right) +2W2\left( t \right) \pi ^{4}\left( {V1\left( t \right) } \right) ^{2} \nonumber \\&\qquad \left. +12W2\left( t \right) \pi ^{4}\left( {V2\left( t \right) } \right) ^{2}\right] +c\frac{\mathrm{d}}{\mathrm{d}t}W2\left( t \right) \nonumber \\&\qquad +16D_{11} W2\left( t \right) \pi ^{4}\nonumber \\&\qquad -4\Omega Ipp\left( {\frac{\mathrm{d}}{\mathrm{d}t}V2\left( t \right) } \right) \pi ^{2}+\frac{\mathrm{d}^{2}}{\mathrm{d}t^{2}}W2\left( t \right) =0 \nonumber \\ \end{aligned}$$

(60)

$$\begin{aligned}&D_{66} \left[ -8\pi ^{5}W2\left( t \right) V1\left( t \right) U2\left( t \right) \right. \nonumber \\&\qquad -4\pi ^{5}W2\left( t \right) V2\left( t \right) U1\left( t \right) \nonumber \\&\qquad +\varphi 1\left( t \right) \pi ^{2}-\pi ^{4}\sqrt{2}V1\left( t \right) W2\left( t \right) \nonumber \\&\qquad +2\pi ^{4}\sqrt{2}V2\left( t \right) W1\left( t \right) \nonumber \\&\qquad \left. -\frac{3}{2}\pi ^{5}W1\left( t \right) V1\left( t \right) U1\left( t \right) \right] \nonumber \\&\qquad +\frac{64}{3}\pi B_{16} U2\left( t \right) +\frac{\mathrm{d}^{2}}{\mathrm{d}t^{2}}\varphi 1\left( t \right) =0 \nonumber \\&D_{66} \left[ -48\pi ^{5} W2\left( t \right) V2\left( t \right) U2\left( t \right) \right. \nonumber \\&\qquad -8\pi ^{5} U2\left( t \right) V1\left( t \right) W1\left( t \right) +4\pi ^{2} \varphi 2\left( t \right) \nonumber \\&\qquad +\pi ^{4}\sqrt{2} V1\left( t \right) W1\left( t \right) \nonumber \\&\qquad \left. -16\pi ^{5}U1\left( t \right) V2\left( t \right) W1\left( t \right) \right] \nonumber \\&\qquad +\frac{\mathrm{d}^{2}}{\mathrm{d}t^{2}}\varphi 2\left( t \right) -\frac{8}{3}\pi B_{16} U1\left( t \right) =0 \end{aligned}$$

(61)

Expanding the dependent variable in the following form

$$\begin{aligned} \begin{array}{l} Ui(T_0 ,T_2 )\!=\!\varepsilon Ui_1 (T_0 ,T_2 )\!+\!\varepsilon ^{2}Ui_2 (T_0 ,T_2 ) \!+\!\varepsilon ^{3}Ui_3 (T_0 ,T_2 ) \\ Vi(T_0 ,T_2 )\!=\!\varepsilon Vi_1 (T_0 ,T_2 )\!+\!\varepsilon ^{2}Vi_2 (T_0 ,T_2 )\!+\!\varepsilon ^{3}Vi_3 (T_0 ,T_2 ) \\ Wi(T_0 ,T_2 )\!=\!\varepsilon Wi_1 (T_0 ,T_2 )\!+\!\varepsilon ^{2}Wi_2 (T_0 ,T_2 ) \!+\!\varepsilon ^{3}Wi_3 (T_0 ,T_2 ) \\ \varphi i(T_0 ,T_2 )\!=\!\varepsilon \varphi i_1 (T_0 ,T_2 )\!+\!\varepsilon ^{2}\varphi i_2 (T_0 ,T_2 )\!+\!\varepsilon ^{3}\varphi i_3 (T_0 ,T_2 ) \\ \end{array} \qquad (i=1,2)\nonumber \\ \end{aligned}$$

(62)

Using chain rule [i.e., Eq. (31)] for Eqs. (58)–(61) and equating coefficients of like power of $\varepsilon$, the equations are obtained in the following form

$$\begin{aligned}&O(\varepsilon ) \nonumber \\&\frac{\partial ^{2}}{\partial T_0 ^{2}}U1_1 \left( {T_0 ,T_2 } \right) +A_{11} \pi ^{2} U1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\quad \qquad -\,\frac{32}{3}B_{16} \pi \varphi 2_1 \left( {T_0 ,T_2 } \right) =0 \nonumber \\&\frac{\partial ^{2}}{\partial T_0 ^{2}}U2_1 \left( {T_0 ,T_2 } \right) +4A_{11} \pi ^{2}U2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\quad \qquad +\,\frac{16}{3}B_{16} \pi \varphi 1_1 \left( {T_0 ,T_2 } \right) =0 \nonumber \\&\frac{\partial ^{2}}{\partial T_0 ^{2}}V1_1 \left( {T_0 ,T_2 } \right) +D_{11} \pi ^{4}V1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,I_{\mathrm{p}} \Omega \pi ^{2}\frac{\partial }{\partial T_0 }W1_1 \left( {T_0 ,T_2 } \right) =0 \nonumber \\&\frac{\partial ^{2}}{\partial T_0 ^{2}}V2_1 \left( {T_0 ,T_2 } \right) +16D_{11} \pi ^{4}V2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,4I_{\mathrm{p}} \Omega \pi ^{2}\frac{\partial }{\partial T_0 }W2_1 \left( {T_0 ,T_2 } \right) =0 \nonumber \\&\frac{\partial ^{2}}{\partial T_0 ^{2}}W1_1 \left( {T_0 ,T_2 } \right) +D_{11} \pi ^{4}W1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -\,I_{\mathrm{p}} \Omega \pi ^{2}\frac{\partial }{\partial T_0 }V1_1 \left( {T_0 ,T_2 } \right) =0 \nonumber \\&\frac{\partial ^{2}}{\partial T_0 ^{2}}W2_1 \left( {T_0 ,T_2 } \right) +16D_{11} \pi ^{4}W2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -\,4I_{\mathrm{p}} \Omega \pi ^{2}\frac{\partial }{\partial T_0 }V2_1 \left( {T_0 ,T_2 } \right) =0 \nonumber \\&\frac{\partial ^{2}}{\partial T_0 ^{2}}\varphi 1_1 \left( {T_0 ,T_2 } \right) +D_{66} \pi ^{2}\varphi 1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,\frac{64}{3}B_{16} \pi U2_1 \left( {T_0 ,T_2 } \right) =0 \nonumber \\&\frac{\partial ^{2}}{\partial T_0 ^{2}}\varphi 2_1 \left( {T_0 ,T_2 } \right) +4D_{66} \pi ^{2}\varphi 2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -\,\frac{8}{3}B_{16} \pi U1_1 \left( {T_0 ,T_2 } \right) =0 \end{aligned}$$

(63)

$$\begin{aligned}&O(\varepsilon ^{2}) \nonumber \\&\frac{\partial ^{2}}{\partial T_0 ^{2}}U1_2 \left( {T_0 ,T_2 } \right) -\frac{32}{3}B_{16} \pi \varphi 2_2 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,A_{11} \pi ^{2}U1_2 \left( {T_0 ,T_2 } \right) \nonumber \\&\quad =-\sqrt{2}A_{11} \pi ^{3}\left[ W1_1 \left( {T_0 ,T_2 } \right) W2_1 \left( {T_0 ,T_2 } \right) \right. \nonumber \\&\qquad \left. +\,V1_1 \left( {T_0 ,T_2 } \right) V2_1 \left( {T_0 ,T_2 } \right) \right] \nonumber \\&\frac{\partial ^{2}}{\partial T_0 ^{2}}U2_2 \left( {T_0 ,T_2 } \right) +\frac{16}{3}B_{16} \pi \varphi 1_2 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,4A_{11} \pi ^{2}U2_2 \left( {T_0 ,T_2 } \right) \nonumber \\&\quad =-\frac{1}{2}\sqrt{2}A_{11} \pi ^{3}\left[ \left( {W1_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}\right. \nonumber \\&\qquad \left. +\,\left( {V1_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}\right] \nonumber \\&\frac{\partial ^{2}}{\partial T_0 ^{2}}V1_2 \left( {T_0 ,T_2 } \right) +D_{11} \pi ^{4}V1_2 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,I_{\mathrm{p}} \Omega \pi ^{2}\frac{\partial }{\partial T_0 }W1_2 \left( {T_0 ,T_2 } \right) \nonumber \\&\quad =-\sqrt{2}A_{11} \pi ^{3}\left[ V1_1 \left( {T_0 ,T_2 } \right) U2_1 \left( {T_0 ,T_2 } \right) \right. \nonumber \\&\qquad \left. +\,V2_1 \left( {T_0 ,T_2 } \right) U1_1 \left( {T_0 ,T_2 } \right) \right] \nonumber \\&\frac{\partial ^{2}}{\partial T_0 ^{2}}V2_2 \left( {T_0 ,T_2 } \right) +16D_{11} \pi ^{4}V2_2 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +4I_{\mathrm{p}} \Omega \pi ^{2}\frac{\partial }{\partial T_0 }W2_2 \left( {T_0 ,T_2 } \right) \nonumber \\&\quad =-\sqrt{2}A_{11} \pi ^{3}V1_1 \left( {T_0 ,T_2 } \right) U1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\frac{\partial ^{2}}{\partial T_0 ^{2}}W1_2 \left( {T_0 ,T_2 } \right) +D_{11} \pi ^{4}W1_2 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -I_{\mathrm{p}} \Omega \pi ^{2}\frac{\partial }{\partial T_0 }V1_2 \left( {T_0 ,T_2 } \right) \nonumber \\&\quad =-\sqrt{2}A_{11} \pi ^{3}\left[ W2_1 \left( {T_0 ,T_2 } \right) U1_1 \left( {T_0 ,T_2 } \right) \right. \nonumber \\&\qquad \left. +\,W1_1 \left( {T_0 ,T_2 } \right) U2_1 \left( {T_0 ,T_2 } \right) \right] \nonumber \\&\qquad \frac{\partial ^{2}}{\partial T_0 ^{2}}W2_2 \left( {T_0 ,T_2 } \right) +16D_{11} \pi ^{4}W2_2 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -4I_{\mathrm{p}} \Omega \pi ^{2}\frac{\partial }{\partial T_0 }V2_2 \left( {T_0 ,T_2 } \right) \nonumber \\&\quad =\sqrt{2}A_{11} \pi ^{3}W1_1 \left( {T_0 ,T_2 } \right) U1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad \frac{\partial ^{2}}{\partial T_0 ^{2}}\varphi 1_2 \left( {T_0 ,T_2 } \right) +\frac{64}{3}B_{16} \pi U2_2 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +D_{66} \pi ^{2}\varphi 1_2 \left( {T_0 ,T_2 } \right) \nonumber \\&\quad =\sqrt{2}D_{66} \pi ^{4}\left[ W2_1 \left( {T_0 ,T_2 } \right) V1_1 \left( {T_0 ,T_2 } \right) \right. \nonumber \\&\qquad \left. -2W1_1 \left( {T_0 ,T_2 } \right) V2_1 \left( {T_0 ,T_2 } \right) \right] \nonumber \\&\qquad \frac{\partial ^{2}}{\partial T_0 ^{2}}P2_2 \left( {T_0 ,T_2 } \right) -\frac{8}{3}B_{16} \pi U1_2 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +4D_{66} \pi ^{2}P2_2 \left( {T_0 ,T_2 } \right) \nonumber \\&\quad =-\sqrt{2}D_{66} \pi ^{4}W1_1 \left( {T_0 ,T_2 } \right) V1_1 \left( {T_0 ,T_2 } \right) \end{aligned}$$

(64)

$$\begin{aligned}&O(\varepsilon ^{3}) \nonumber \\&\frac{\partial ^{2}}{\partial T_0 ^{2}}U1_3 \left( {T_0 ,T_2 } \right) +A_{11} \pi ^{2}U1_3 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -\,\frac{32}{3}B_{16} \pi P2_3 \left( {T_0 ,T_2 } \right) \nonumber \\&\quad =\frac{3}{2}A_{11} \pi ^{3}\left\{ \pi \left[ \left( {V1_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}U1_1 \left( {T_0 ,T_2 } \right) \right. \right. \nonumber \\&\qquad +\,\frac{3}{2}\left( {W1_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}U1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,4 \left( {W2_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}U1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,8 W1_1 \left( {T_0 ,T_2 } \right) W2_1 \left( {T_0 ,T_2 } \right) U2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,8V1_1 \left( {T_0 ,T_2 } \right) V2_1 \left( {T_0 ,T_2 } \right) U2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad \left. +\,4\left( {V2_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}U1_1 \left( {T_0 ,T_2 } \right) \right] \nonumber \\&\qquad -\,\sqrt{2} W1_1 \left( {T_0 ,T_2 } \right) W2_2 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -\,\sqrt{2}W1_2 \left( {T_0 ,T_2 } \right) W2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -\,\sqrt{2} V1_2 \left( {T_0 ,T_2 } \right) V2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad \left. -\,\sqrt{2} V1_1 \left( {T_0 ,T_2 } \right) V2_2 \left( {T_0 ,T_2 } \right) \right\} \nonumber \\&\qquad -\,2\frac{\partial ^{2}}{\partial T_2 \partial T_0 }U1_1 \left( {T_0 ,T_2 } \right) \nonumber \end{aligned}$$

$$\begin{aligned}&\frac{\partial ^{2}}{\partial T_0 ^{2}}U2_3 \left( {T_0 ,T_2 } \right) +\frac{16}{3}B_{16} \pi P1_3 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,4A_{11} \pi ^{2}U2_3 \left( {T_0 ,T_2 } \right) \nonumber \\&\quad =4A_{11} \pi ^{3}\left\{ \pi \left[ \left( {W1_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}U2_1 \left( {T_0 ,T_2 } \right) \right. \right. \nonumber \\&\qquad +\,24\left( {W2_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}U2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,8W1_1 \left( {T_0 ,T_2 } \right) W2_1 \left( {T_0 ,T_2 } \right) U1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,4\left( {V1_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}U2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,24\left( {V2_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}U2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad \left. +\,8V1_1 \left( {T_0 ,T_2 } \right) V2_1 \left( {T_0 ,T_2 } \right) U1_1 \left( {T_0 ,T_2 } \right) \right] \nonumber \\&\qquad -\,\sqrt{2}V1_1 \left( {T_0 ,T_2 } \right) V1_2 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad \left. -\,\sqrt{2}W1_1 \left( {T_0 ,T_2 } \right) W1_2 \left( {T_0 ,T_2 } \right) \right\} \nonumber \\&\qquad -\,2\frac{\partial ^{2}}{\partial T_2 \partial T_0 }U2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&D_{11} \pi ^{4}V1_3 \left( {T_0 ,T_2 } \right) +I_{\mathrm{p}} \Omega \pi ^{2}\frac{\partial }{\partial T_0 }W1_3 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,\frac{\partial ^{2}}{\partial T_0 ^{2}}V1_3 \left( {T_0 ,T_2 } \right) \nonumber \\&\quad =6A_{11} \pi ^{3}\left\{ \pi \left[ -\left( {V2_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}V1_1 \left( {T_0 ,T_2 } \right) \right. \right. \nonumber \\&\qquad +\,\frac{3}{2}V1_1 \left( {T_0 ,T_2 } \right) \left( {U1_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}\nonumber \\&\qquad -\,\frac{3}{4}\left( {V1_1 \left( {T_0 ,T_2 } \right) } \right) ^{3}\nonumber \\&\qquad +\,8V2_1 \left( {T_0 ,T_2 } \right) U2_1 \left( {T_0 ,T_2 } \right) U1_1 \left( {T_0 ,T_2 } \right) \end{aligned}$$

$$\begin{aligned}&\qquad -\,4W2_1 \left( {T_0 ,T_2 } \right) V2_1 \left( {T_0 ,T_2 } \right) W1_1 \left( {T_0 ,T_2 } \right) \nonumber \end{aligned}$$

$$\begin{aligned}&\qquad +\,4V1_1 \left( {T_0 ,T_2 } \right) \left( {U2_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}\nonumber \\&\qquad -\,2 \left( {W2_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}V1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad \left. -\,\frac{3}{4}\left( {W1_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}V1_1 \left( {T_0 ,T_2 } \right) \right] \nonumber \\&\qquad -\,\sqrt{2} V2_2 \left( {T_0 ,T_2 } \right) U1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -\,\sqrt{2} V1_2 \left( {T_0 ,T_2 } \right) U2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -\,\sqrt{2} V1_1 \left( {T_0 ,T_2 } \right) U2_2 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad \left. -\,\sqrt{2} V2_1 \left( {T_0 ,T_2 } \right) U1_2 \left( {T_0 ,T_2 } \right) \right\} \nonumber \\&\qquad +\,\Omega ^{2}\left[ -e_1 \sin \left( {\Omega T_0 } \right) +e_2 \cos \left( {\Omega T_0 } \right) \right] \nonumber \\&\qquad -\,c\frac{\partial }{\partial T_0 }V1_1 \left( {T_0 ,T_2 } \right) -I_{\mathrm{p}} \Omega \pi ^{2}\frac{\partial }{\partial T_2 }W1_1 \left( {T_0 ,T_2 } \right) \nonumber \end{aligned}$$

$$\begin{aligned}&\qquad -\,2\frac{\partial ^{2}}{\partial T_2 \partial T_0 }V1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -\,16D_{11} \pi ^{4}V2_3 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,4I_{\mathrm{p}} \Omega \pi ^{2}\frac{\partial }{\partial T_0 }W2_3 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,\frac{\partial ^{2}}{\partial T_0 ^{2}}V2_3 \left( {T_0 ,T_2 } \right) \nonumber \\&\quad =12A_{11} \pi ^{3}\left\{ \pi \left[ -\left( {V2_1 \left( {T_0 ,T_2 } \right) } \right) ^{3} \right. \right. \nonumber \\&\qquad +\,24V2_1 \left( {T_0 ,T_2 } \right) \left( {U2_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}\nonumber \\&\qquad -\,4 W1_1 \left( {T_0 ,T_2 } \right) V1_1 \left( {T_0 ,T_2 } \right) W2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -\,6\left( {V1_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}V2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,8V1_1 \left( {T_0 ,T_2 } \right) U1_1 \left( {T_0 ,T_2 } \right) U2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -\,12\left( {W2_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}V2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,4 V2_1 \left( {T_0 ,T_2 } \right) \left( {U1_1 \left( {T_0 ,T_2 } \right) } \right) ^{2} \nonumber \end{aligned}$$

$$\begin{aligned}&\qquad \left. -\,2\left( {W1_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}V2_1 \left( {T_0 ,T_2 } \right) \right] \nonumber \\&\qquad -\,\sqrt{2} V1_2 \left( {T_0 ,T_2 } \right) U1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad \left. -\,\sqrt{2} V1_1 \left( {T_0 ,T_2 } \right) U1_2 \left( {T_0 ,T_2 } \right) \right\} \nonumber \\&\qquad -\,4I_{\mathrm{p}} \Omega \pi ^{2}\frac{\partial }{\partial T_2 }W2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -\,c\frac{\partial }{\partial T_0 }V2_1 \left( {T_0 ,T_2 } \right) -2\frac{\partial ^{2}}{\partial T_2 \partial T_0 }V2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -\,I_{\mathrm{p}} \Omega \pi ^{2}\frac{\partial }{\partial T_0 }V1_3 \left( {T_0 ,T_2 } \right) +D_{11} \pi ^{4}W1_3 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,\frac{\partial ^{2}}{\partial T_0 ^{2}}W1_3 \left( {T_0 ,T_2 } \right) =A_{11} \pi ^{3}\nonumber \\&\qquad \left\{ \pi \left[ -\frac{3}{4}\left( {W1_1 \left( {T_0 ,T_2 } \right) } \right) ^{3}\right. \right. \nonumber \end{aligned}$$

$$\begin{aligned}&\qquad +\,\frac{3}{2}W1_1 \left( {T_0 ,T_2 } \right) \left( {U1_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}\nonumber \\&\qquad +\,8W2_1 \left( {T_0 ,T_2 } \right) U1_1 \left( {T_0 ,T_2 } \right) U2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -\,2W1_1 \left( {T_0 ,T_2 } \right) \left( {V2_1 \left( {T_0 ,T_2 } \right) } \right) ^{2} \nonumber \\&\qquad -\,4W2_1 \left( {T_0 ,T_2 } \right) V1_1 \left( {T_0 ,T_2 } \right) V2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,4W1_1 \left( {T_0 ,T_2 } \right) \left( {U2_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}\nonumber \\&\qquad -\,\frac{3}{4}W1_1 \left( {T_0 ,T_2 } \right) \left( {V1_1 \left( {T_0 ,T_2 } \right) } \right) ^{2} \nonumber \\&\qquad \left. -\,6\left( {W2_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}W1_1 \left( {T_0 ,T_2 } \right) \right] \nonumber \\&\qquad -\,\sqrt{2}W2_2 \left( {T_0 ,T_2 } \right) U1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -\,\sqrt{2}W1_2 \left( {T_0 ,T_2 } \right) U2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -\,\sqrt{2}W2_1 \left( {T_0 ,T_2 } \right) U1_2 \left( {T_0,T_2 } \right) \nonumber \end{aligned}$$

$$\begin{aligned}&\qquad \left. -\,\sqrt{2}W1_1 \left( {T_0 ,T_2 } \right) U2_2 \left( {T_0 ,T_2 } \right) \right\} \nonumber \\&\qquad -\,c\frac{\partial }{\partial T_0 }W1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,I_{\mathrm{p}} \Omega \pi ^{2}\frac{\partial }{\partial T_2 }V1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -\,2\frac{\partial ^{2}}{\partial T_2 \partial T_0 }W1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,\Omega ^{2}\left[ e_1 \cos \left( {\Omega T_0 } \right) +e_2 \sin \left( {\Omega T_0 } \right) \right] \nonumber \\&16D_{11} \pi ^{4}W2_3 \left( {T_0 ,T_2 } \right) +\frac{\partial ^{2}}{\partial T_0 ^{2}}W2_3 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -\,4I_{\mathrm{p}} \Omega \pi ^{2}\frac{\partial }{\partial T_0 }V2_3 \left( {T_0 ,T_2 } \right) \nonumber \\&\quad =A_{11} \pi ^{3}\left\{ \pi \left[ -12\left( {W2_1 \left( {T_0 ,T_2 } \right) } \right) ^{3} \right. \right. \nonumber \\&\qquad -2W2_1 \left( {T_0 ,T_2 } \right) \left( {V1_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}\nonumber \\&\qquad +\,4 W2_1 \left( {T_0 ,T_2 } \right) \left( {U1_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}\nonumber \\&\qquad +\,8 W1_1 \left( {T_0 ,T_2 } \right) U1_1 \left( {T_0 ,T_2 } \right) U2_1 \left( {T_0 ,T_2 } \right) \nonumber \end{aligned}$$

$$\begin{aligned}&\qquad +\,24W2_1 \left( {T_0 ,T_2 } \right) \left( {U2_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}\nonumber \\&\qquad -\,6\left( {W1_1 \left( {T_0 ,T_2 } \right) } \right) ^{2}W2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -\,12W2_1 \left( {T_0 ,T_2 } \right) \left( {V2_1 \left( {T_0 ,T_2 } \right) } \right) ^{2} \nonumber \\&\qquad \left. -\,4 W1_1 \left( {T_0 ,T_2 } \right) V2_1 \left( {T_0 ,T_2 } \right) V1_1 \left( {T_0 ,T_2 } \right) \right] \nonumber \\&\qquad -\,\sqrt{2} W1_2 \left( {T_0 ,T_2 } \right) U1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad \left. -\,\sqrt{2} W1_1 \left( {T_0 ,T_2 } \right) U1_2 \left( {T_0 ,T_2 } \right) \right\} \nonumber \\&\qquad +\,4I_{\mathrm{p}} \Omega \pi ^{2}\frac{\partial }{\partial T_2 }V2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -\,c\frac{\partial }{\partial T_0 }W2_1 \left( {T_0 ,T_2 } \right) -2\frac{\partial ^{2}}{\partial T_2 \partial T_0 }W2_1 \left( {T_0 ,T_2 } \right) \nonumber \end{aligned}$$

$$\begin{aligned}&\frac{64}{3}B_{16} \pi U2_3 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,\frac{\partial ^{2}}{\partial T_0 ^{2}}P1_3 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,D_{66} \pi ^{2}P1_3 \left( {T_0 ,T_2 } \right) \nonumber \\&\quad =D_{66} \pi ^{4}\left\{ -2\sqrt{2}W1_1 \left( {T_0 ,T_2 } \right) V2_2 \left( {T_0 ,T_2 } \right) \right. \nonumber \\&\qquad +\,\sqrt{2} W2_1 \left( {T_0 ,T_2 } \right) V1_2 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad -2\sqrt{2} W1_2 \left( {T_0 ,T_2 } \right) V2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,\sqrt{2} W2_2 \left( {T_0 ,T_2 } \right) V1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,\pi \left[ \frac{3}{2}V1_1 \left( {T_0 ,T_2 } \right) U1_1 \left( {T_0 ,T_2 } \right) W1_1 \left( {T_0 ,T_2 } \right) \right. \nonumber \\&\qquad +\,8 V1_1 \left( {T_0 ,T_2 } \right) U2_1 \left( {T_0 ,T_2 } \right) W2_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad \left. \left. +\,4 V2_1 \left( {T_0 ,T_2 } \right) U1_1 \left( {T_0 ,T_2 } \right) W2_1 \left( {T_0 ,T_2 } \right) \right] \right\} \nonumber \\&\qquad -2\frac{\partial ^{2}}{\partial T_2 \partial T_0 }P1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\frac{\partial ^{2}}{\partial T_0 ^{2}}P2_3 \left( {T_0 ,T_2 } \right) +4D_{66} \pi ^{2}P2_3 \left( {T_0 ,T_2 } \right) \nonumber \end{aligned}$$

$$\begin{aligned}&\qquad -\,\frac{8}{3}B_{16} \pi U1_3 \left( {T_0 ,T_2 } \right) \nonumber \\&\quad =D_{66} \pi ^{4}\left\{ -\sqrt{2}W1_1 \left( {T_0 ,T_2 } \right) V1_2 \left( {T_0 ,T_2 } \right) \right. \nonumber \\&\qquad -\,\sqrt{2}W1_2 \left( {T_0 ,T_2 } \right) V1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad +\,\pi \left[ 48V2_1 \left( {T_0 ,T_2 } \right) U2_1 \left( {T_0 ,T_2 } \right) W2_1 \left( {T_0 ,T_2 } \right) \right. \nonumber \\&\qquad +\,16V2_1 \left( {T_0 ,T_2 } \right) U1_1 \left( {T_0 ,T_2 } \right) W1_1 \left( {T_0 ,T_2 } \right) \nonumber \\&\qquad \left. \left. +\,8V1_1 \left( {T_0 ,T_2 } \right) U2_1 \left( {T_0 ,T_2 } \right) W1_1 \left( {T_0 ,T_2 } \right) \right] \right\} \nonumber \\&\qquad -2\frac{\partial ^{2}}{\partial T_2 \partial T_0 }P2_1 \left( {T_0 ,T_2 } \right) \end{aligned}$$

(65)

The general solution of (63) can be expressed as

$$\begin{aligned} V1_1 (T_0 ,T_2 )= & {} F_1 (T_2 )\hbox {e}^{\beta _f T_0 i}+F_2 (T_2 )\hbox {e}^{\beta _b T_0 i}\nonumber \\&+\bar{{F}}_1 (T_2 )\hbox {e}^{-\beta _f T_0 i}+\bar{{F}}_2 (T_2 )\hbox {e}^{-\beta _b T_0 i} \nonumber \\ W1_1 (T_0 ,T_2 )= & {} \alpha iF_1 (T_2 )\mathrm{e}^{\beta _f T_0 i}+\delta iF_2 (T_2 )\mathrm{e}^{\beta _b T_0 i}\nonumber \\&-\alpha i\bar{{F}}_1 (T_2 )\mathrm{e}^{-\beta _f T_0 i}-\delta i\bar{{F}}_2 (T_2 )\mathrm{e}^{-\beta _b T_0 i} \nonumber \\ V2_1 (T_0 ,T_2 )= & {} Y_1 (T_2 )\mathrm{e}^{4\beta _f T_0 i}+Y_2 (T_2 )\mathrm{e}^{4\beta _b T_0 i}\nonumber \\&+\bar{{Y}}_1 (T_2 )\mathrm{e}^{-4\beta _f T_0 i}+\bar{{Y}}_2 (T_2 )\mathrm{e}^{-4\beta _b T_0 i} \nonumber \\ W2_1 (T_0 ,T_2 )= & {} \alpha iY_1 (T_2 )\mathrm{e}^{4\beta _f T_0 i}+\delta iY_2 (T_2 )\mathrm{e}^{4\beta _b T_0 i}\nonumber \\&-\alpha i\bar{{Y}}_1 (T_2 )\mathrm{e}^{-4\beta _f T_0 i}-\delta i\bar{{Y}}_2 (T_2 )\mathrm{e}^{-4\beta _b T_0 i} \nonumber \\ U1_1 (T_0 ,T_2 )= & {} \zeta H_1 (T_2 )\mathrm{e}^{\beta _{u1} T_0 i}+\zeta \bar{{H}}_1 (T_2 )\mathrm{e}^{-\beta _{u1} T_0 i}\nonumber \\&+\lambda H_2 (T_2 )\mathrm{e}^{\beta _{\varphi 2} T_0 i}+\lambda \bar{{H}}_2 (T_2 )\mathrm{e}^{-\beta _{\varphi 2} T_0 i} \nonumber \\ \varphi 2_1 (T_0 ,T_2 )= & {} H_1 (T_2 )\mathrm{e}^{\beta _{u1} T_0 i}+\bar{{H}}_1 (T_2 )\mathrm{e}^{-\beta _{u1} T_0 i}\nonumber \\&+H_2 (T_2 )\mathrm{e}^{\beta _{\varphi 2} T_0 i}+\bar{{H}}_2 (T_2 )\mathrm{e}^{-\beta _{\varphi 2} T_0 i} \nonumber \\ U2_1 (T_0 ,T_2 )= & {} \eta G_1 (T_2 )\mathrm{e}^{\beta _{u2} T_0 i}+\eta \bar{{G}}_1 (T_2 )\mathrm{e}^{-\beta _{u2} T_0 i}\nonumber \\&+\mu G_2 (T_2 )\mathrm{e}^{\beta _{\varphi 1} T_0 i}+\mu \bar{{G}}_2 (T_2 )\mathrm{e}^{-\beta _{\varphi 1} T_0 i} \nonumber \\ \varphi 1_1 (T_0 ,T_2 )= & {} G_1 (T_2 )\mathrm{e}^{\beta _{u2} T_0 i}+\bar{{G}}_1 (T_2 )\mathrm{e}^{-\beta _{u2} T_0 i}\nonumber \\&+G_2 (T_2 )\mathrm{e}^{\beta _{\varphi 1} T_0 i}+\bar{{G}}_2 (T_2 )\mathrm{e}^{-\beta _{\varphi 1} T_0 i} \end{aligned}$$

(66)

Note that the first mode’s solution of U is coupled with the second mode’s solution of $\varphi$ and vice versa. $F_i (T_2 ), Y_i (T_2 ), H_i (T_2 )$ and $G_i (T_2 ), (i=1,2)$ are complex functions which will be determined at the third order of approximation. $\beta _f$ and $\beta _b$ are forward and backward natural frequencies, and $\beta _{u1} , \beta _{\varphi 1} , \beta _{u2}$ and $\beta _{\varphi 2}$ are corresponding natural frequencies for the first and second modes in u and $\varphi$ directions. So

$$\begin{aligned} \beta _f= & {} -\frac{1}{2}i\sqrt{-2\sqrt{\pi ^{8}I_{\mathrm{p}} ^{2}\Omega ^{2}\left( {I_{\mathrm{p}} ^{2}\Omega ^{2}+4D_{11} } \right) }+\left( {-4D_{11} -2I_{\mathrm{p}} ^{2}\Omega ^{2}} \right) \pi ^{4}} \nonumber \\ \beta _b= & {} -\frac{1}{2}i\sqrt{2\sqrt{\pi ^{8}I_{\mathrm{p}} ^{2}\Omega ^{2}\left( {I_{\mathrm{p}} ^{2}\Omega ^{2}+4D_{11} } \right) }+\left( {-4D_{11} -2I_{\mathrm{p}} ^{2}\Omega ^{2}} \right) \pi ^{4}} \nonumber \\ \beta _{u1}= & {} -\frac{1}{6}i\sqrt{-6\sqrt{9}\sqrt{\left( {\left( {A_{11} -4D_{66} } \right) ^{2}\pi ^{2}+\frac{1024}{9}B_{16} ^{2}} \right) \pi ^{2}}+\left( {-72D_{66} -18A_{11} } \right) \pi ^{2}} \nonumber \\ \beta _{u2}= & {} -\frac{1}{6}i\sqrt{-6\sqrt{144}\sqrt{\left( {\left( {A_{11} -\frac{1}{4}D_{66} } \right) ^{2}\pi ^{2}+\frac{256}{9}B_{16} ^{2}} \right) \pi ^{2}}+\left( {-18D_{66} -72A_{11} } \right) \pi ^{2}} \nonumber \\ \beta _{\varphi 1}= & {} -\frac{1}{6}i\sqrt{6\sqrt{144}\sqrt{\left( {\left( {A1-\frac{1}{4}D_{66} } \right) ^{2}\pi ^{2}+\frac{256}{9}B_{16} ^{2}} \right) \pi ^{2}}+\left( {-18D_{66} -72A_{11} } \right) \pi ^{2}} \nonumber \\ \beta _{\varphi 2}= & {} -\frac{1}{6}i\sqrt{6\sqrt{9}\sqrt{\left( {\left( {A_{11} -4D_{66} } \right) ^{2}\pi ^{2}+\frac{1024}{9}B_{16} ^{2}} \right) \pi ^{2}}+\left( {-72D_{66} -18A_{11} } \right) \pi ^{2}} \end{aligned}$$

(67)

$\alpha , \delta ,\zeta ,\lambda , \eta$ and $\mu$ are coefficients presented in “Appendix 4.” Substituting Eq. (66) into Eq. (64) and solving for the inhomogeneous solution, one can obtain $U1_2 (T_0, T_2 ), U2_2 (T_0,T_2 ) V1_2 (T_0, T_2 ), V2_2 (T_0,T_2 ), W1_2 (T_0 ,T_2 )$, $W2_2 (T_0 ,T_2 ),\,\,\varphi 1_2 (T_0 ,T_2 )$ and $\varphi 2_2 (T_0,T_2 )$; the general form of the solutions can be found in “Appendix 5,” and the detailed expressions are presented in [39] for the sake of simplicity.

The solvability conditions are obtained in the same manner as one mode, but here only the number of operations is doubled. Again, to express the nearness of excitation frequency to the natural frequency, Eq. (46) is used. The following form is assumed in order to obtain a system of equation and compute the solvability conditions for v and w,  in both the first and second modes:

$$\begin{aligned} V1_3 (T_0 ,T_1 ,T_2 )= & {} P_{11} (T_1 ,T_2 )\mathrm{e}^{i\beta _f T_0 }\nonumber \\&+P_{12}(T_1 ,T_2 )\mathrm{e}^{i\beta _b T_0 } \nonumber \\ W1_3 (T_0 ,T_1 ,T_2 )= & {} P_{21} (T_1 ,T_2 )\mathrm{e}^{i\beta _f T_0 }\nonumber \\&+P_{22}(T_1 ,T_2 )\mathrm{e}^{i\beta _b T_0 } \end{aligned}$$

(68)

Substituting Eqs. (46), (66), the found inhomogeneous solution and (68) into (65) and equating the coefficients of $\mathrm{e}^{i\beta _f T_0 }$ and $\mathrm{e}^{i\beta _b T_0 }$ on both sides, the solvability conditions are computed in the following form

$$\begin{aligned}&\Gamma _v^1 F_1 (T_2 )H_1 (T_2 )\bar{{H}}_1 (T_2 )+\Phi _v^1 F_1 (T_2 )H_2 (T_2 )\bar{{H}}_2 (T_2 )\nonumber \\&\qquad +\Delta _v^1 F_1 (T_2 )G_1 (T_2 )\bar{{G}}_1 (T_2 )+\Psi _v^1 F_1 (T_2 )G_2 (T_2 )\bar{{G}}_2 (T_2 ) \nonumber \\&\qquad +\Lambda _v^1 F_1 (T_2 )Y_1 (T_2 )\bar{{Y}}_1 (T_2 )+\mathrm{K}_v^1 F_1 (T_2 )Y_2 (T_2 )\bar{{Y}}_2 (T_2 )\nonumber \\&\qquad +\mathrm{Z}_v^1 F_1 (T_2 )F_2 (T_2 )\bar{{F}}_2 (T_2 )+\Theta _v^1 F_1 (T_2 )^{2}\bar{{F}}_1 (T_2 ) \nonumber \\&\qquad +\mathrm{X}_v^1 D_2 F_1 (T_2 )+\left( \beta _1 ^{3}\alpha -D_{11} \pi ^{4}\alpha \beta _1 \right. \nonumber \\&\qquad \left. -I_{\mathrm{p}} \Omega \pi ^{2}\beta _1 ^{2} \right) cF_1 (T_2 )=\frac{1}{2}\left( -\beta _1 ^{2}-I_{\mathrm{p}} \Omega \pi ^{2}\beta _1 \right. \nonumber \\&\qquad \left. +D_{11} \pi ^{4} \right) \left( {e_1 -ie_2 } \right) \Omega ^{2}\hbox {e}^{i\sigma _1 T_2 } \nonumber \\&\Gamma _w^1 F_2 (T_2 )H_1 (T_2 )\bar{{H}}_1 (T_2 )+\Phi _w^1 F_2 (T_2 )H_2 (T_2 )\bar{{H}}_2 (T_2 )\nonumber \\&\qquad +\Delta _w^1 F_2 (T_2 )G_1 (T_2 )\bar{{G}}_1 (T_2 )+\Psi _w^1 F_2 (T_2 )G_2 (T_2 )\bar{{G}}_2 (T_2 ) \nonumber \\&\qquad +\Lambda _w^1 F_2 (T_2 )Y_1 (T_2 )\bar{{Y}}_1 (T_2 )+\mathrm{K}_w^1 F_2 (T_2 )Y_2 (T_2 )\bar{{Y}}_2 (T_2 )\nonumber \\&\qquad +\mathrm{Z}_w^1 F_2 (T_2 )F_1 (T_2 )\bar{{F}}_1 (T_2 )+\Theta _w^1 F_2 (T_2 )^{2}\bar{{F}}_2 (T_2 ) \nonumber \\&\qquad +\mathrm{X}_w^1 D_2 F_2 (T_2 )+\left( \delta \beta _2 ^{3}-D_{11} \pi ^{4}\delta \beta _2 \right. \nonumber \\&\qquad \left. -I_{\mathrm{p}} \Omega \pi ^{2}\beta _2 ^{2} \right) cF_2 (T_2 )=0 \end{aligned}$$

(69)

Through the same procedure, solvability conditions corresponding to the second mode are computed as

$$\begin{aligned}&\Gamma _v^2 Y_1 (T_2 )H_1 (T_2 )\bar{{H}}_1 (T_2 )+\Phi _v^2 Y_1 (T_2 )H_2 (T_2 )\bar{{H}}_2 (T_2 )\nonumber \\&\qquad +\Delta _v^2 Y_1 (T_2 )G_1 (T_2 )\bar{{G}}_1 (T_2 )\nonumber \\&\qquad +\Psi _v^2 Y_1 (T_2 )G_2 (T_2 )\bar{{G}}_2 (T_2 ) \nonumber \\&\qquad +\Lambda _v^2 Y_1 (T_2 )F_1 (T_2 )\bar{{F}}_1 (T_2 )\nonumber \\&\qquad +\mathrm{K}_v^2 Y_1 (T_2 )F_2 (T_2 )\bar{{F}}_2 (T_2 )\nonumber \\&\qquad +\mathrm{Z}_v^2 Y_1 (T_2 )Y_2 (T_2 )\bar{{Y}}_2 (T_2 )+\Theta _v^2 Y_1 (T_2 )^{2}\bar{{Y}}_1 (T_2 ) \nonumber \\&\qquad \mathrm{X}_v^2 D_2 Y_1 (T_2 )+\left( -\beta _1 ^{3}\alpha +D_{11} \pi ^{4}\alpha \beta _1 \right. \nonumber \\&\qquad \left. +I_{\mathrm{p}} \Omega \pi ^{2}\beta _1 ^{2} \right) 64cY_1 (T_2 )=0 \nonumber \\&\Gamma _w^2 Y_2 (T_2 )H_1 (T_2 )\bar{{H}}_1 (T_2 )+\Phi _w^2 Y_2 (T_2 )H_2 (T_2 )\bar{{H}}_2 (T_2 )\nonumber \\&\qquad +\Delta _w^2 Y_2 (T_2 )G_1 (T_2 )\bar{{G}}_1 (T_2 )\nonumber \\&\qquad +\Psi _w^2 Y_2 (T_2 )G_2 (T_2 )\bar{{G}}_2 (T_2 ) \nonumber \\&\qquad +\Lambda _w^2 Y_2 (T_2 )F_1 (T_2 )\bar{{F}}_1 (T_2 )\nonumber \\&\qquad +\mathrm{K}_w^2 Y_2 (T_2 )F_2 (T_2 )\bar{{F}}_2 (T_2 )\nonumber \\&\qquad +\mathrm{Z}_w^2 Y_2 (T_2 )Y_1 (T_2 )\bar{{Y}}_1 (T_2 )+\Theta _w^2 Y_2 (T_2 )^{2}\bar{{Y}}_2 (T_2 ) \nonumber \\&\qquad \mathrm{X}_w^2 D_2 Y_2 (T_2 )+\left( -\beta _2 ^{3}\delta +D_{11} \pi ^{4}\delta \beta _2 \right. \nonumber \\&\qquad \left. +I_{\mathrm{p}} \Omega \pi ^{2}\beta _2 ^{2} \right) 64cY_2 (T_2 )=0 \end{aligned}$$

(70)

where $\Gamma _j^i ,\Phi _j^i ,\Delta _j^i ,\Psi _j^i ,\Lambda _j^i ,\mathrm{K}_j^i ,\mathrm{Z}_j^i ,\Theta _j^i ,\mathrm{X}_j^i$, $(i\!=\!1,2), (j=v,w)$ are the coefficients presented in numeric form for the special case studied in Sect. 4 because unfortunately they are too large to be expressed in analytical form. For the two equations of motion corresponding to the u and $\varphi$, the solvability conditions are obtained by substituting (66) and the second-order solution into (65) and following the same procedure as previous section to find for the first mode as

$$\begin{aligned}&\Gamma _u^1 H_1 (T_2 )Y_1 (T_2 )\bar{{Y}}_1 (T_2 )+\Phi _u^1 H_1 (T_2 )Y_2 (T_2 )\bar{{Y}}_2 (T_2 )\nonumber \\&\qquad +\Lambda _u^1 H_1 (T_2 )F_1 (T_2 )\bar{{F}}_1 (T_2 ) \nonumber \\&\qquad +\mathrm{K}_u^1 H_1 (T_2 )F_2 (T_2 )\bar{{F}}_2 (T_2 )+\mathrm{X}_u^1 D_2 H_1 (T_2 )=0 \nonumber \\&\Gamma _\varphi ^2 H_2 (T_2 )Y_1 (T_2 )\bar{{Y}}_1 (T_2 )+\Phi _\varphi ^2 H_2 (T_2 )Y_2 (T_2 )\bar{{Y}}_2 (T_2 )\nonumber \\&\qquad +\Lambda _\varphi ^2 H_2 (T_2 )F_1 (T_2 )\bar{{F}}_1 (T_2 ) \nonumber \\&\qquad +\mathrm{K}_\varphi ^2 H_2 (T_2 )F_2 (T_2 )\bar{{F}}_2 (T_2 )+\mathrm{X}_\varphi ^2 D_2 H_2 (T_2 )=0\nonumber \\ \end{aligned}$$

(71)

and for the second mode as

$$\begin{aligned}&\Gamma _u^2 G_1 (T_2 )Y_1 (T_2 )\bar{{Y}}_1 (T_2 )+\Phi _u^2 G_1 (T_2 )Y_2 (T_2 )\bar{{Y}}_2 (T_2 )\nonumber \\&\qquad +\Lambda _u^2 G_1 (T_2 )F_1 (T_2 )\bar{{F}}_1 (T_2 ) \nonumber \\&\qquad +\mathrm{K}_u^2 G_1 (T_2 )F_2 (T_2 )\bar{{F}}_2 (T_2 )+\mathrm{X}_u^2 D_2 G_1 (T_2 )=0 \nonumber \\&\Gamma _\varphi ^1 G_2 (T_2 )Y_1 (T_2 )\bar{{Y}}_1 (T_2 )+\Phi _\varphi ^1 G_2 (T_2 )Y_2 (T_2 )\bar{{Y}}_2 (T_2 )\nonumber \\&\qquad +\Lambda _\varphi ^1 G_2 (T_2 )F_1 (T_2 )\bar{{F}}_1 (T_2 ) \nonumber \\&\qquad +\mathrm{K}_\varphi ^1 G_2 (T_2 )F_2 (T_2 )\bar{{F}}_2 (T_2 )+\mathrm{X}_\varphi ^1 D_2 G_2 (T_2 )=0\nonumber \\ \end{aligned}$$

(72)

where $\Gamma _j^i , \Phi _j^i , \Lambda _j^i , \mathrm{K}_j^i , \mathrm{X}_j^i$, $(i=1,2), (j=u,\varphi )$ are the coefficients and are treated in the same way as before. Expressing the complex-valued functions $F_i (T_2 ), H_i (T_2 ), G_i (T_2 ), (i=1,2)$ in the polar form

$$\begin{aligned} F_1 (T_2 )= & {} \frac{1}{2}a_{f1} (T_2 )\mathrm{e}^{i\theta _{f1} (T_2 )},\nonumber \\ F_2 (T_2 )= & {} \frac{1}{2}a_{f2} (T_2 )\mathrm{e}^{i\theta _{f2} (T_2 )},\nonumber \\ H_1 (T_2 )= & {} \frac{1}{2}a_{h1} (T_2 )\mathrm{e}^{i\theta _{h1} (T_2 )} \nonumber \\ H_2 (T_2 )= & {} \frac{1}{2}a_{h2} (T_2 )\mathrm{e}^{i\theta _{h2} (T_2 )},\nonumber \\ G_1 (T_2 )= & {} \frac{1}{2}a_{g1} (T_2 )\mathrm{e}^{i\theta _{g1} (T_2 )},\nonumber \\ G_2 (T_2 )= & {} \frac{1}{2}a_{g2} (T_2 )\mathrm{e}^{i\theta _{g2} (T_2 )} \end{aligned}$$

(73)

where real-valued quantities $a_i (T_2 )$ and $\theta _i (T_2 )$, $(i=f1,f2,h1,h2,g1,g2)$ are the amplitudes and phase angles of the response, respectively. Substituting Eq. (73) into (69)–(72) and separating real and imaginary parts, the modulation equations are computed for the first mode as

$$\begin{aligned}&\mathrm{X}_v^1 D_2 a_{f1} +ca_{f1} \left[ \alpha \beta _1 ^{3}-D_{11} \pi ^{4}\alpha \beta _1 \right. \nonumber \\&\qquad \left. -I_{\mathrm{p}} \Omega \pi ^{2}\beta _1 ^{2}\right] \nonumber \\&\quad =\Omega ^{2}\left( {\sin \left( {\gamma _1 } \right) e_2 +e_1 \cos \left( {\gamma _1 } \right) } \right) \left( -\beta _1 ^{2}\right. \nonumber \\&\qquad \left. -I_{\mathrm{p}} \Omega \pi ^{2}\beta _1 +D_{11} \pi ^{4} \right) \nonumber \\&\frac{1}{4}a_{f1} \left[ 4\sigma \mathrm{X}_v^1 -4\mathrm{X}_v^1 D_2 \gamma _1 +\mathrm{Z}_v^1 a_{f2} ^{2}\right. \nonumber \\&\qquad +\mathrm{K}_v^1 a_{y2} ^{2}+\Lambda _v^1 a_{y1} ^{2}+\Psi _v^1 a_{g2} ^{2} \nonumber \\&\qquad +\Delta _v^1 a_{g1} ^{2}+\Phi _v^1 a_{h2} ^{2}\nonumber \\&\qquad \left. +\Theta _v^1 a_{f1} ^{2}+\Gamma _v^1 a_{h1} ^{2}\right] \nonumber \\&\quad =\Omega ^{2}\left( -\beta _1 ^{2}-I_{\mathrm{p}} \Omega \pi ^{2}\beta \right. _1 \nonumber \\&\qquad \left. +D_{11} \pi ^{4} \right) \left( {e_1 \sin \left( {\gamma _1 } \right) -e_2 \cos \left( {\gamma _1 } \right) } \right) \nonumber \\&\mathrm{X}_w^1 D_2 a_{f2} +ca_{f2} \left[ \delta \beta _2 ^{3}\right. \nonumber \\&\qquad \left. -D_{11} \pi ^{4}\delta \beta _2 -I_{\mathrm{p}} \Omega \pi ^{2}\beta _2 ^{2}\right] =0 \nonumber \\&\qquad a_{f2} \left[ 4\mathrm{X}_w^1 \sigma -4\mathrm{X}_w^1 D_2 \gamma _2 +\Theta _w^1 a_{f2} ^{2}\right. \nonumber \\&\qquad +\mathrm{K}_w^1 a_{y2} ^{2}+\Lambda _w^1 a_{y1} ^{2}+\Psi _w^1 a_{g2} ^{2} \nonumber \\&\qquad +\Delta _w^1 a_{g1} ^{2}+\Phi _w^1 a_{h2} ^{2}\nonumber \\&\qquad \left. +\Gamma _w^1 a_{h1} ^{2}+\mathrm{Z}_w^1 a_{f1} ^{2}\right] =0 \end{aligned}$$

(74)

$$\begin{aligned}&\frac{1}{4}\left[ \Gamma _u^1 a_{h1} a_{y1} ^{2}+\Phi _u^1 a_{h1} a_{y2} ^{2}\right. \nonumber \\&\qquad \left. +\Lambda _u^1 a_{h1} a_{f1} ^{2}+\mathrm{K}_u^1 a_{h1} a_{f2} ^{2}\right] -\mathrm{X}_u^1 a_{h1} D_2 \theta _{h1} =0 \nonumber \\&\mathrm{X}_u^1 D_2 a_{h1} =0 \nonumber \\&\frac{1}{4}\left[ \Gamma _\varphi ^2 a_{h2} a_{y1} ^{2}+\Phi _\varphi ^2 a_{h2} a_{y2} ^{2}\right. \nonumber \\&\qquad \left. +\Lambda _\varphi ^2 a_{h2} a_{f1} ^{2}+\mathrm{K}_\varphi ^2 a_{h2} a_{f2} ^{2}\right] -\mathrm{X}_\varphi ^2 a_{h2} D_2 \theta _{h2} =0 \nonumber \\&\qquad \mathrm{X}_\varphi ^2 D_2 a_{h2} =0 \end{aligned}$$

(75)

where $\gamma _i =\sigma T_2 -\theta _i ,(i=1,2)$. For the second mode it is obtained as

$$\begin{aligned}&\frac{1}{2}\mathrm{X}_v^2 D_2 a_{y1} +32c\,a_{y1} \left[ -\alpha \beta _1 ^{3}\right. \nonumber \\&\qquad \left. +D_{11} \pi ^{4}\alpha \beta _1 +I_{\mathrm{p}} \Omega \pi ^{2}\beta _1 ^{2}\right] =0 \nonumber \\&\frac{1}{4}\left[ \Psi _v^2 a_{y1} a_{g2} ^{2}+\mathrm{Z}_v^2 a_{y1} a_{y2} ^{2}\right. \nonumber \\&\qquad +\Lambda _v^2 a_{y1} a_{f1} ^{2}+\mathrm{K}_v^2 a_{y1} a_{f2} ^{2}+\Delta _v^2 a_{y1} a_{g1} ^{2} \nonumber \\&\qquad +\Phi _v^2 a_{y1} a_{h2} ^{2}+\Theta _v^2 a_{y1} ^{3}\nonumber \\&\qquad \left. +\Gamma _v^2 a_{y1} a_{h1} ^{2}\right] +\mathrm{X}_v^2 a_{y1} D_2 \theta _{y1} =0 \nonumber \\&\frac{1}{2}\mathrm{X}_w^2 D_2 a_{y2} -32ca_{y2} \left[ \delta \beta _2 ^{3}\right. \nonumber \\&\qquad \left. +D_{11} \pi ^{4}\delta \beta _2 +I_{\mathrm{p}} \Omega \pi ^{2}\beta _2 ^{2}\right] =0 \nonumber \\&\frac{1}{4}\left[ \Lambda _w^2 a_{y2} a_{f1} ^{2}+\Psi _w^2 a_{y2} a_{g2} ^{2}\right. \nonumber \\&\qquad +\mathrm{Z}_w^2 a_{y2} a_{y1} ^{2}+\Delta _w^2 a_{y2} a_{g1} ^{2}+\mathrm{K}_w^2 a_{y2} a_{f2} ^{2} \nonumber \\&\qquad \left. +\Theta _w^2 a_{y2} ^{3}+\Gamma _w^2 a_{y2} a_{h1} ^{2}+\Phi _w^2 a_{y2} a_{h2} ^{2}\right] \nonumber \\&\qquad +\mathrm{X}_w^2 a_{y2} D_2 \theta _{y2} =0 \end{aligned}$$

(76)

$$\begin{aligned}&\frac{1}{4}a_{g1} \left[ \Gamma _u^2 a_{y1} ^{2}+\Phi _u^2 a_{y2} ^{2}\right. \nonumber \\&\qquad \left. +\Lambda _u^2 a_{f1} ^{2}+\mathrm{K}_u^2 a_{f2} ^{2}\right] -\mathrm{X}_u^2 a_{g1} D_2 \theta _{g1} =0 \nonumber \\&\mathrm{X}_u^2 D_2 a_{g1} =0 \nonumber \\&\frac{1}{4}a_{g2} \left[ \Gamma _\varphi ^1 a_{y1} ^{2}+\Phi _\varphi ^1 a_{y2} ^{2}\right. \nonumber \\&\qquad \left. +\Lambda _\varphi ^1 a_{f1} ^{2}+\mathrm{K}_\varphi ^1 a_{f2} ^{2}\right] -\mathrm{X}_\varphi ^1 a_{g2} D_2 \theta _{g2} =0\nonumber \\&\qquad \mathrm{X}_\varphi ^1 D_2 a_{g2} =0 \end{aligned}$$

(77)

For steady-state solution, the time derivatives in (74)–(77) are set to zero which results in

$$\begin{aligned} a_{f2} =a_{y1} =a_{y2} =a_{g1} =a_{g2} =a_{h1} =a_{h2} =0 \end{aligned}$$

(78)

Substituting Eq. (78) into Eqs. (74)–(77) and eliminating $\gamma _i$ between the remaining equations finally yield

$$\begin{aligned}&\vartheta _1 a_{f1}^6 +\vartheta _2 a_{f1}^4 +\vartheta _3 a_{f1}^2\nonumber \\&\quad =\frac{1}{4}\Omega ^{4}e_t^2 \left( {-\beta _1 ^{2}-I_{\mathrm{p}} \Omega \pi ^{2}\beta _1 +D_{11} \pi ^{4}} \right) ^{2} \end{aligned}$$

(79)

where

$$\begin{aligned} \vartheta _1= & {} \frac{1}{64}\Theta _v^{12} \nonumber \\ \vartheta _2= & {} \frac{1}{8}\mathrm{X}_v^1 \sigma \Theta _v^1 \nonumber \\ \vartheta _3= & {} \frac{1}{4}c^{2}\beta _1 ^{2}\left( {-\beta _1 ^{2}\alpha +D_{11} \pi ^{4}\alpha +I_{\mathrm{p}} \Omega \pi ^{2}\beta _1 } \right) ^{2}\nonumber \\&+\frac{1}{4}(\mathrm{X}_v^1 )^{2}\sigma ^{2} \nonumber \\ e_t= & {} \sqrt{e_1^2 +e_2^2 } \end{aligned}$$

(80)

Here an explanation about the effect of the second mode in the solution is presented. It was assumed that the excitation was tuned in the neighborhood of the first mode. Consequently, the excitation does not actuate the second mode directly; so the linear amplitudes (first-order solution) of the second mode are all zero which means there is no first-order solution for the second mode (i.e., $a_{f2} =a_{y2} =a_{g2} = a_{h2} =0)$, but, meanwhile, the second-order solution (i.e., the solution of (71)) corresponding to the second mode which consists of nonlinear terms are nonzero due to inhomogeneous parts appearing in the right-hand side of the equations in second order of the second mode. So, this fact explains although linear solution to the second mode vanishes, nonlinear solution remains, so its components must be kept till the last steps of the calculations.

Fig. 4

Frequency response curves for different eccentricity and one-mode discretization

Fig. 5

Frequency response curves for different eccentricity and two-mode discretization

4 Numerical examples

In this section, numerical examples are studied to examine forced vibration of the composite shaft with the following dimensionless parameters [10]

$$\begin{aligned} I_{\mathrm{p}}= & {} 0.000657\,\,I_2 =0.000328\,\,D_{66} =0.0224\nonumber \\ D_{11}= & {} 0.101 \nonumber \\ A_{11}= & {} 307.754\,\,B_{16} =-0.00105\,\,c=0.05 \end{aligned}$$

(81)

The layup is $[90^{\circ }/45^{\circ }/{-}45^{\circ }/0^{\circ }_6 /90^{\circ }]$ starting from inside surface of the hollow shaft. By substituting parameters (81) and Eq. (80) into Eq. (79), one can obtain the equation for two-mode as

$$\begin{aligned}&937446.506 a_{f1} ^{6}-786.524 a_{f1} ^{4}\sigma \nonumber \\&\quad +(0.164 \sigma ^{2}+0.041c) a_{f1} ^{2}=0.413e_t ^{2} \end{aligned}$$

(82)

and for one-mode discretization, the equation is

$$\begin{aligned}&2109255.490 a_{f1} ^{6}-1179.786636 a_{f1} ^{4}\sigma \nonumber \\&\quad +(0.164 \sigma ^{2}+0.041c) a_{f1} ^{2}=0.413e_t ^{2} \end{aligned}$$

(83)

These expressions are amplitude–frequency relations (bifurcation diagram) for one- and two-mode discretization methods. These relations clearly show the differences between two methods of discretization. Note that the amplitude presented here is total displacement of the shaft cross section central point in y–z plane (see Eqs. 45 and 53). In other words, the term amplitude is used here for shaft whirl radius.

Fig. 6

Comparison of frequency response curves for one- and two-mode discretization

Figures 4 and 5 show the frequency response curves of the composite shaft for one-mode and two-mode discretization, respectively. These figures are plotted for different values of eccentricities. As Figs. 4 and 5 show the curves are bent to the right in regions near the peak which means that the effective nonlinearity here is of hardening type. For some ranges of $\sigma$, there is one solution, and for some others, three solutions exist, including one unstable; so jump and bifurcation phenomena happen. In addition, it is observed that for small eccentricity, all solution branches are stable. By increasing the eccentricity, the amplitude grows up, and unstable branches appear. The unstable regions were identified using a Jacobian matrix constructed for this case. As Figs. 4 and 5 show, the amplitude increases as excitation frequency gets closer to the natural frequency and decreases as excitation frequency goes upper than natural frequency so a peak is formed in the curves. It should be noted that in the linear analysis, the peak must lead straight upward, while here in nonlinear analysis, the peak is bent to the right which shows that maximum amplitude is achieved in a frequency more than linear natural frequency which means that more energy is needed to raise the amplitude to its maximum amount and that is called hardening. It means that the system is harder than what is estimated by linear methods; meanwhile, the two-mode discretization can estimate the response with more accuracy which is a softer system in result. To verify the perturbation solution for both one-mode discretization and two-mode discretization, numerical simulations are applied in these figures using the Runge–Kutta–Fehlberg method. It is seen that the results agree well. So, it is concluded that the perturbation results are valid.

Figure 6 compares frequency response curves for one-mode and two-mode discretization which shows a considerable difference especially near the peak. It is obvious from the figure that peak values for both cases are approximately equal. But this peak occurs in different frequencies. These differences increase when amplitude increases. This difference is important. For example, for $\sigma =0.2$, one-mode response predicts two stable solution branches, while two-mode response predicts one stable solution branch.

Fig. 7

Amplitude versus total eccentricity for one-mode discretization

Fig. 8

Amplitude versus total eccentricity for two-mode discretization

The figure shows that the one-mode discretization has harder nonlinearity, while two-mode nonlinearity is softer. The presented result is interesting. Although the excitation (i.e., spin) is tuned in the neighborhood of the first flexural mode and this mode does not involve in an internal resonance with other modes, the presented result shows that one-mode discretization is not sufficient. This is in contrast to usual idea in nonlinear vibration [37] that if the excitation is tuned in the neighborhood of a mode and this mode does not involve in an internal resonance, then other modes are decayed with passing of time and one-mode discretization is sufficient for steady-state analysis. Here, the reason is the existence of the second-order nonlinear terms. In discretization procedure, when one-mode discretization is employed, some second-order nonlinear terms existing in extensional and torsional equations of motion (26 and 29) vanish. So, their effects are not observed in the solution. On the other hand, with application of two-mode discretization, the effects of these terms are included in the solution.

Fig. 9

Comparison of amplitude–total eccentricity curves for one- and two-mode discretization

Fig. 10

Amplitude versus external damping for one-mode discretization

Fig. 11

Amplitude versus external damping for two-mode discretization

Figures 7 and 8 show amplitude versus total eccentricity for one-mode and two-mode discretization, respectively, for various values of $\sigma$. For some values of $\sigma$, jump phenomenon happens. For some values of $\sigma$ and a certain range of $e_t$, the curve consists of three parts including one unstable. For example, in Fig. 8 when $\sigma =0.3$ for $e_t <0.00082$, curve has three parts, and for $e_t >0.00082$, the curve is one part. Figure 9 makes a comparison between Figs. 7 and 8. The figure shows that the differences between one-mode and two-mode discretization increase with increasing eccentricity. All the parameters are the same as introduced earlier in this section.

Figures 10 and 11 show amplitude versus damping coefficient. Again for some values of $\sigma$, the curve becomes multi-valued. For example, in Fig. 11 when $\sigma =-0.1$ for every value of c the curve is single valued but when $\sigma =0.3$ for $c<0.2$, the curve consists of three parts which one of them is unstable, and for $c>0.2$, the curve is again single valued. All parameters used here are the same as before except for the eccentricity which is assumed to be 0.0005, i.e., $e_1 =e_2 =0.0005$. It should be noted that Figs. 10 and 11 are for the one-mode and two-mode discretization, respectively, and Fig. 12 is the comparison between these two results. Figure 12 shows again that two methods of discretization for different damping coefficient values lead to large differences.

Fig. 12

Comparison between amplitude–damping curves for one- and two-mode discretization

Fig. 13

$\sigma _{\mathrm{bifurcation}}$ versus damping coefficient; one-mode discretization

Because bifurcation phenomenon happens, it would be useful to plot loci of bifurcation points versus damping coefficient and eccentricity. Here, the bifurcation points are shown with $\sigma _\mathrm{bifurcation}$ which denotes the coordinate that a bifurcation occur (e.g., distance from the origins of Figs. 4 and 5). The first bifurcation point is lower saddle point, and the second bifurcation point is upper one. Saddle node bifurcation is one of three static bifurcation points which occurs at the meeting point of fixed points’ branches [40]. As Figs. 4 and 5 show, when detuning parameter and consequently the spinning speed increases (see Eq. 46), the solution becomes multi-valued. Specifically, we consider Fig. 4. In the left-hand side of point A, there is no fixed point. In point A, there is one fixed point and in the right-hand side of this point, there are two branches of fixed points: one stable and the other unstable. So, in point A, there are two branches of fixed points. This scenario is a saddle node bifurcation [40]. Similarly, this bifurcation occurs in the neighborhood of point B. To analytically determine the type of bifurcation, Jacobian matrix of modulation of Eq. (54) and its partial derivative with respect to control parameter must be computed. In the saddle node bifurcation, the vector of partial derivative does not belong to the range of Jacobian matrix. This can be checked by the range of augmented matrix [40].

Fig. 14

$\sigma _{\mathrm{bifurcation}}$ versus damping coefficient; two-mode discretization

Fig. 15

Comparison between one- and two-mode discretization for $\sigma _{\mathrm{bifurcation}}$ versus damping coefficient

Fig. 16

$\sigma _{\mathrm{bifurcation}}$ versus total eccentricity; one-mode discretization

Fig. 17

$\sigma _{\mathrm{bifurcation}}$ versus total eccentricity; two-mode discretization

Fig. 18

Comparison between one- and two-mode discretization for $\sigma _{\mathrm{bifurcation}}$ versus total eccentricity

Fig. 19

Frequency response curves for different lamination angles; $e_{1}=e_{2}=0.0003$

Figures 13 and 14 show loci of bifurcation points versus damping coefficient for one-mode and two-mode discretization. These figures show that the first saddle node bifurcation point is approximately constant with variation of damping. But the variation of second one is large. Figure 15 shows a comparison between these two results. Again, the difference between two methods of discretization is considerable. It should be noted that in Figs. 13 and 14, all the parameters are the same as introduced earlier in this section and the eccentricity has the value of 0.0003 in both one-mode and two-mode discretization methods.

Figures 16 and 17 show the loci of bifurcation points versus total eccentricity. In contrast to previous figures, both the first and second bifurcation points vary with the variation of eccentricity. However, the variation for the second bifurcation point is larger which is confirmed by Figs. 4 and 5. In addition, it is seen that $\sigma _{{ bifurcation}}$ is ascending with increasing $e_t$, in contrast to Figs. 13 and 14 which show descending trend upon increasing c. The two points get farther from each other as the eccentricity increases which is confirmed by Figs. 4 and 5. Figure 18 makes a comparison between Figs. 16 and 17. This figure shows a considerable error with use of one-mode discretization. It should be noted that the more the eccentricity, the more error is produced, and this confirms the undeniable role of nonlinear terms which would be kept through two-mode discretization method. All parameters are the same as before for the diagrams presented in Figs. 16 and 17.

Figure 19 shows the frequency response curves for a fixed value of eccentricity and different lamination angles, for two-mode discretization. This figure shows that for three present lamination patterns, the bifurcation diagrams are not so different. If lamination angle increases with respect to the longitudinal axis of the shaft, system responses in a softer manner.

One of the interesting aspects of this paper is that the derived equations of motion are used in the analysis without any reduction (i.e., neglecting coupling terms). They consist of extensional–flexural–flexural–torsional coupling, while in some works such as [18], coupling effects are neglected. Here, the effect of coupling in the results is considered.

Actually, this coupling is associated with longitudinal and torsional motions. Its effect is reflected in the coefficient $B_{16}$. This coupling vanishes when the fibers have an orientation angle equal to $0^{\circ }$ and $90^{\circ }$ (i.e., cross-ply lamination). In angle-ply lamination, the coefficient $B_{16}$ is nonzero. Now, in angle-ply lamination, according to the symmetry in stacking sequence the problem divides into two cases: symmetric layup and asymmetric layup.

It must be noted that symmetric layup here is defined as a layup which consists of both $\theta$ and $-\theta$ orientation angle, while in asymmetric layup, any fiber orientation angle can be considered without its negative counterpart. So, the first layup mentioned in this paper is considered as symmetric according to the assumption made in this paper, and the following layup is considered as asymmetric.

In case 1 (symmetric layup), because the fibers are plied with both $\theta$ and $-\theta$ orientation and considering the small thickness nature of composite layers, each pair of fibers with opposite angle approximately neutralize each other’s effect; so in this case, coupling coefficient $(B_{16} )$ does not vanish but has a small value. In case 2 (asymmetric layup), the effect of coupling is considerable due to the asymmetry in stacking sequence. So, consider the coupling is necessary in response analysis. The following explanation confirms this claim.

Fig. 20

Frequency curve obtained including and excluding extensional–torsional coupling for one-mode discretization

In order to investigate the effect of the extensional–torsional coupling, a numerical example considering an asymmetric layup is studied with these equations. Finally, the results are compared with those of a shaft with previous data, but it is obtained using the firstly derived equations in this paper. Omitting extensional–torsional coupling in Eqs. (19)–(22), the new equations of motion become

$$\begin{aligned}&\ddot{\bar{{u}}}-\bar{{A}}_{11}(\bar{{{v}'}}\bar{{{v}''}}+\bar{{{w}'}}\bar{{{w}''}}\nonumber \\&\qquad -\bar{{{v}'}}^{2}\bar{{{u}''}}-\bar{{{w}'}}^{2}\bar{{{u}''}}+\bar{{{u}''}}\nonumber \\&\qquad -2\bar{{{v}'}}\bar{{{u}'}}\bar{{{v}''}}-2\bar{{{w}'}}\bar{{{u}'}}\bar{{{w}''}})=0 \end{aligned}$$

(84)

$$\begin{aligned}&\ddot{\bar{{v}}}+\bar{{c}}\dot{\bar{{v}}}-\bar{{D}}_{11}(-\bar{{v}}^{(IV)})\nonumber \\&\qquad -\bar{{I}}_p \Omega \dot{\bar{{{w}''}}}-\bar{{A}}_{11}(\bar{{{w}'}}\bar{{{v}'}}\bar{{{w}''}}\nonumber \\&\qquad +\bar{{{v}'}}\bar{{{u}''}}+\bar{{{v}''}}\bar{{{u}'}}\nonumber \\&\qquad +\frac{3}{2}\bar{{{v}'}}^{2}\bar{{{v}''}}+\frac{1}{2}\bar{{{w}'}}^{2}\bar{{{v}''}}-2\bar{{{v}'}}\bar{{{u}'}}\bar{{{u}''}}-\bar{{{v}''}}\bar{{{u}'}}^{2})\nonumber \\&\quad =\bar{{\Omega }}^{2}(\bar{{e}}_y (\bar{{x}})\cos (\bar{{\Omega }}\bar{{t}})-\bar{{e}}_\mathrm{z} (\bar{{x}})\sin (\bar{{\Omega }}\bar{{t}})) \end{aligned}$$

(85)

$$\begin{aligned}&\ddot{\bar{{w}}}+\bar{{c}}\dot{\bar{{w}}}-\bar{{D}}_{11}(-\bar{{w}}^{(IV)})-\bar{{I}}_p \Omega \dot{\bar{{{v}''}}}\nonumber \\&\qquad -\bar{{A}}_{11}(\bar{{{w}'}}\bar{{{v}'}}\bar{{{v}''}}+\bar{{{w}'}}\bar{{{u}''}}+\bar{{{w}''}}\bar{{{u}'}}\nonumber \\&\qquad +\frac{3}{2}\bar{{{w}'}}^{2}\bar{{{w}''}}+\frac{1}{2}\bar{{{v}'}}^{2}\bar{{{w}''}}-2\bar{{{w}'}}\bar{{{u}'}}\bar{{{u}''}}-\bar{{{w}''}}\bar{{{u}'}}^{2}) \nonumber \\&\quad =\bar{{\Omega }}^{2}(\bar{{e}}_\mathrm{z} (\bar{{x}})\cos (\bar{{\Omega }}\bar{{t}})+\bar{{e}}_\mathrm{y} (\bar{{x}})\sin (\bar{{\Omega }}\bar{{t}})) \end{aligned}$$

(86)

$$\begin{aligned}&\bar{{I}}_p \ddot{\bar{{\phi }}}-\bar{{D}}_{66} (\bar{{{v}''}}\bar{{{w}''}}\nonumber \\&\qquad +\bar{{{\phi }''}}+\bar{{{v}'''}}\bar{{{w}'}}-\bar{{{w}''}}\bar{{{v}'}}\bar{{{u}''}}-3\bar{{{u}''}}\bar{{{v}''}}\bar{{{w}'}}-2\bar{{{u}'}}\bar{{{v}''}}\bar{{{w}''}}\nonumber \\&\qquad -2\bar{{{u}'}}\bar{{{v}'''}}\bar{{{w}'}}-\bar{{{w}'}}\bar{{{v}'}}\bar{{{u}'''}})=0 \end{aligned}$$

(87)

Fig. 21

Frequency curve obtained including and excluding extensional–torsional coupling for two-mode discretization

The solution procedure is the same as before. The frequency response curve is obtained for the shaft in Sect. 4 but with an asymmetric stacking sequence as below

$$\begin{aligned} \left[ 90^{\circ },45^{\circ },45^{\circ },30^{\circ },60^{\circ },0^{\circ },0^{\circ },0^{\circ },0^{\circ },90^{\circ }\right] \end{aligned}$$

(88)

So the new dimensionless parameters are

$$\begin{aligned} A_{11}= & {} 253.20, \,\, D_{11} = 0.08359, \,\,D_{66} = 0.03233, \nonumber \\ I_2= & {} 0.000328, I_{\mathrm{p}} = 0.000657,\,\,B_{16} = .937, \nonumber \\ c= & {} 0.05 \end{aligned}$$

(89)

and the eccentricity is $e_1 =e_2 =0.0003$. As it can be seen in (89), the extensional–torsional coupling obtained with asymmetric layup assumption is much bigger than what was calculated before with symmetric layup.

Using the parameters obtained above, the final equation for one mode and without coupling is as follows

$$\begin{aligned}&2109255.49 a_{f1} ^{6}-1179.786 a_{f1} ^{4}\sigma \nonumber \\&\quad +(0.165\sigma ^{2}+0.0001)a_{f1} ^{2}=0.412e_t ^{2} \end{aligned}$$

(90)

and the equation for two-mode discretization and without coupling becomes

$$\begin{aligned}&523080.744 a_{f1} ^{6}-484.149 a_{f1} ^{4}\sigma \nonumber \\&\quad +(0.112 \sigma ^{2}+0.000065)a_{f1} ^{2}=0.34e_t ^{2} \end{aligned}$$

(91)

For one- and two-mode discretization including coupling, the equation is, respectively,

$$\begin{aligned}&1176931.678 a_{f1} ^{6}-726.224 a_{f1} ^{4}\sigma \nonumber \\&\quad +(0.112\sigma ^{2}+0.000066) a_{f1} ^{2}=0.34e_t ^{2}\nonumber \\&314961.871 a_{f1} ^{6}-375.685 a_{f1} ^{4}\sigma \nonumber \\&\quad +(0.112\sigma ^{2}+0.000066) a_{f1} ^{2}=0.34e_t ^{2} \end{aligned}$$

(92)

Fig. 22

A comparison between one-mode and two-mode discretization including and excluding extensional–torsional coupling

Figures 20 and 21 show the frequency curve for the composite shaft with aforementioned asymmetric stacking sequence obtained with and without extensional–torsional coupling for one-mode and two-mode discretization. As it can be seen, inclusion of coupling term results in more accurate frequency response curves. The difference between two cases is considerable in the resonance tip. A comparison between response curves in Figs. 20 and 21 shows that the coupling term has softening nonlinearity effect on the response.

Figure 22 shows a comparison between one-mode and two-mode discretization with and without inclusion of extensional–torsional coupling. This figure shows the combination effect of the linear coupling and number of modes. It is observed that the effect of linear coupling in one-mode discretization is negligible. The reason is that the coupling coefficient affects the second-order nonlinear terms, and these terms vanish when one-mode discretization is employed. So, the effect of coupling in one-mode discretization is small and is completely due to the few remaining linear terms associated with this coupling. On the other hand, in the case of two-mode discretization, the second-order nonlinear terms do not vanish and consequently coupling coefficient has an important effect on the response. In this case, the coupling can affect the response through both the second-order nonlinear terms and few linear terms associated with coupling so as it can be seen the effect of coupling in two-mode discretization is more than that of one mode. This figure clearly shows the order of error induced in the case of one-mode discretization and neglecting of coupling terms.

5 Summary and conclusion

In this paper, nonlinear forced vibration of a rotating composite shaft under the excitation due to the eccentricity was studied. The flexural–flexural–extensional–torsional equations of motion were derived via utilizing the three-dimensional constitutive relations of the material and application of the Hamilton’s principle. Rotary inertia and gyroscopic effects were included, but the shear deformation was neglected due to the slenderness of the shaft. To analyze the equations, the method of multiple scales was applied to the discrete equations with inclusion of one and two modes. Although the excitation was tuned in the neighborhood of the first mode, one-mode discretization resulted in inaccurate results, and at least two modes are necessary in the analysis. The effects of external damping, total eccentricity and lamination angle were considered on the response of the shaft. All the results were obtained for both one-mode discretization and two-mode discretization, and the results were compared. The nonlinearity effect due to the large deformation of the shaft is of the hardening type. There is jump phenomenon, and the bifurcation points are affected by the external damping and the eccentricity. Lamination angle does not affect bifurcation point, while it can soften the system as lamination angle increases with respect to the longitudinal axis of the shaft. Finally, the effect of extensional–torsional coupling on the frequency curves was investigated, and it was shown that when the stacking sequence is asymmetric, the coupling should be considered in the analysis to obtain more accurate results.

Appendices

Appendix 1

$$\begin{aligned} \left\{ {\begin{array}{l} \sigma _{11} \\ \sigma _{22} \\ \sigma _{33} \\ \tau _{23} \\ \tau _{31} \\ \tau _{12} \\ \end{array}} \right\}= & {} \left[ {{\begin{array}{cccccc} {Q_{11} }&{} {Q_{12} }&{} {Q_{13} }&{} 0&{} 0&{} 0 \\ {Q_{12} }&{} {Q_{22} }&{} {Q_{23} }&{} 0&{} 0&{} 0 \\ {Q_{13} }&{} {Q_{23} }&{} {Q_{33} }&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} {Q_{44} }&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 0&{} {Q_{55} }&{} 0 \\ 0&{} 0&{} 0&{} 0&{} 0&{} {Q_{66} } \\ \end{array} }} \right] \left\{ {\begin{array}{l} \varepsilon _{11} \\ \varepsilon _{22} \\ \varepsilon _{33} \\ \gamma _{23} \\ \gamma _{31} \\ \gamma _{12} \\ \end{array}} \right\} \\ \left\{ {\begin{array}{l} \sigma _{xx} \\ \sigma _{\theta \theta } \\ \sigma _{rr} \\ \tau _{r\theta } \\ \tau _{xr} \\ \tau _{x\theta } \\ \end{array}} \right\}= & {} \left[ {{\begin{array}{cccccc} {\overline{Q} _{11} }&{} {\overline{Q} _{12} }&{} {\overline{Q} _{13} }&{} 0&{} 0&{} {\overline{Q} _{16} } \\ {\overline{Q} _{12} }&{} {\overline{Q} _{22} }&{} {\overline{Q} _{23} }&{} 0&{} 0&{} {\overline{Q} _{26} } \\ {\overline{Q} _{13} }&{} {\overline{Q} _{23} }&{} {\overline{Q} _{33} }&{} 0&{} 0&{} {\overline{Q} _{36} } \\ 0&{} 0&{} 0&{} {\overline{Q} _{44} }&{} {\overline{Q} _{45} }&{} 0 \\ 0&{} 0&{} 0&{} {\overline{Q} _{45} }&{} {\overline{Q} _{55} }&{} 0 \\ {\overline{Q} _{16} }&{} {\overline{Q} _{26} }&{} {\overline{Q} _{36} }&{} 0&{} 0&{} {\overline{Q} _{66} } \\ \end{array} }} \right] \left\{ {\begin{array}{l} \varepsilon _{xx} \\ \varepsilon _{\theta \theta } \\ \varepsilon _{rr} \\ \gamma _{r\theta } \\ \gamma _{xr} \\ \gamma _{x\theta } \\ \end{array}} \right\} \\ \left[ {\bar{{Q}}} \right]= & {} \left[ T \right] ^{-1}\left[ Q \right] \left[ T \right] ^{-T} \end{aligned}$$

where $\bar{{Q}}$ is the stiffness matrix of the layer in which

$$\begin{aligned} \left[ T \right]= & {} \left[ {{\begin{array}{cccccc} {m^{2}}&{} {n^{2}}&{} 0&{} 0&{} 0&{} {2mn} \\ {n^{2}}&{} {m^{2}}&{} 0&{} 0&{} 0&{} {-2mn} \\ 0&{} 0&{} 1&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} m&{} {-n}&{} 0 \\ 0&{} 0&{} 0&{} n&{} m&{} 0 \\ {-mn}&{} {mn}&{} 0&{} 0&{} 0&{} {m^{2}-n^{2}} \\ \end{array} }} \right] \\ m= & {} \cos \eta , n=\sin \eta \end{aligned}$$

where $\eta$ is shown in Fig. 1.

$$\begin{aligned} Q_{11}= & {} \frac{E_1 }{1-\frac{\nu _{12}^2 E_2 }{E_1 }}, Q_{12} =\frac{E_2 \nu _{12} }{1-\frac{\nu _{12}^2 E_2 }{E_1 }},\\ Q_{22}= & {} \frac{E_2 }{1-\frac{\nu _{12}^2 E_2 }{E_1 }}, Q_{44} =G_{23} , Q_{55} =G_{13} , \\ Q_{66}= & {} G_{12} ,Q_{13} =Q_{23} =Q_{33} =0 \end{aligned}$$

Appendix 2

Derivation of equations of motion

Kinetic energy

$$\begin{aligned} T= & {} \frac{1}{2}I_0 \left( {\left( {\frac{\partial }{\partial t}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial t}v(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial t}w(s,t)} \right) ^{2}} \right) \\&+\frac{1}{2}\frac{I_2 \left( {\frac{\frac{\partial ^{2}}{\partial t\partial s}v(s,t)}{1+\frac{\partial }{\partial s}u(s,t)}-\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial t\partial s}u(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) }{\left( {1+\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) ^{2}\left( {1+\frac{\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}} \right) }\\&+\frac{1}{2}\frac{I_2 \left( {\frac{\frac{\partial ^{2}}{\partial t\partial s}w(s,t)}{\sqrt{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}}-\frac{0.5\left( {\frac{\partial }{\partial s}w(s,t)} \right) \left( {2\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial t\partial s}u(s,t)} \right) +2\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial t\partial s}v(s,t)} \right) } \right) }{\sqrt{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}}} \right) ^{2}}{\left( {1+\frac{\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}} \right) ^{2}}\\&+\frac{1}{2}I_{\mathrm{p}} \left( {\frac{\partial }{\partial s}\phi (s,t)} \right) ^{2}+I_{\mathrm{p}} \Omega \left( {\frac{\partial }{\partial s}\phi (s,t)} \right) +\frac{1}{2}I_{\mathrm{p}} \Omega ^{2}\\&+\frac{I_{\mathrm{p}} \left( {\frac{\partial }{\partial s}\phi (s,t)} \right) \left( {\frac{\frac{\partial ^{2}}{\partial t\partial s}v(s,t)}{1+\frac{\partial }{\partial s}u(s,t)}-\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial t\partial s}u(s,t)} \right) }{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) \left( {\frac{\partial }{\partial s}w(s,t)} \right) }{\left( {1+\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) \sqrt{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}\sqrt{1+\frac{\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}}}\\&+\frac{I_{\mathrm{p}} \Omega \left( {\frac{\frac{\partial ^{2}}{\partial t\partial s}v(s,t)}{1+\frac{\partial }{\partial s}u(s,t)}-\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial t\partial s}u(s,t)} \right) }{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) \left( {\frac{\partial }{\partial s}w(s,t)} \right) }{\left( {1+\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) \sqrt{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}\sqrt{1+\frac{\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}}}\\&+\frac{1}{2}\frac{I_{\mathrm{p}} \left( {\frac{\frac{\partial ^{2}}{\partial t\partial s}v(s,t)}{1+\frac{\partial }{\partial s}u(s,t)}-\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial t\partial s}u(s,t)} \right) }{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) ^{2}}{\left( {1+\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) ^{2}}-\frac{1}{2}\frac{I_{\mathrm{p}} \left( {\frac{\frac{\partial ^{2}}{\partial t\partial s}v(s,t)}{1+\frac{\partial }{\partial s}u(s,t)}-\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial t\partial s}u(s,t)} \right) }{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) ^{2}}{\left( {1+\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) ^{2}\left( {1+\frac{\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}} \right) }\\ \end{aligned}$$

Potential energy

$$\begin{aligned} U= & {} \frac{1}{2}A_{11} \left( {\sqrt{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}-1} \right) ^{2}\\&+2B_{16} \left( {\sqrt{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}-1} \right) \\&\left( {\frac{\partial }{\partial s}\phi (s,t)+\frac{\left( {\frac{\frac{\partial ^{2}}{\partial s^{2}}v(s,t)}{1+\frac{\partial }{\partial s}u(s,t)}-\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial s^{2}}u(s,t)} \right) }{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) \left( {\frac{\partial }{\partial s}w(s,t)} \right) }{\left( {1+\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) \sqrt{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}\sqrt{1+\frac{\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}}}} \right) \\&+\frac{1}{2}D_{11} \left( {\begin{array}{l} \frac{\left( {\frac{\frac{\partial ^{2}}{\partial s^{2}}v(s,t)}{1+\frac{\partial }{\partial s}u(s,t)}-\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial s^{2}}u(s,t)} \right) }{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) ^{2}}{\left( {1+\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) ^{2}\left( {1+\frac{\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}} \right) }+ \\ \frac{\left( {\frac{\frac{\partial ^{2}}{\partial s^{2}}w(s,t)}{\sqrt{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}}-\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial s^{2}}u(s,t)} \right) +\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial s^{2}}v(s,t)} \right) } \right) }{\sqrt{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}}} \right) ^{2}}{\left( {1+\frac{\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}} \right) ^{2}} \\ \end{array}} \right) \\&+\frac{1}{2}D_{66} \left( {\frac{\partial }{\partial s}\phi (s,t)+\frac{\left( {\frac{\frac{\partial ^{2}}{\partial s^{2}}v(s,t)}{1+\frac{\partial }{\partial s}u(s,t)}-\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) \left( {\frac{\partial ^{2}}{\partial s^{2}}u(s,t)} \right) }{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) \left( {\frac{\partial }{\partial s}w(s,t)} \right) }{\left( {1+\frac{\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}}} \right) \sqrt{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}\sqrt{1+\frac{\left( {\frac{\partial }{\partial s}w(s,t)} \right) ^{2}}{\left( {1+\frac{\partial }{\partial s}u(s,t)} \right) ^{2}+\left( {\frac{\partial }{\partial s}v(s,t)} \right) ^{2}}}}} \right) \end{aligned}$$

First the above kinetic and potential energies are expanded in Taylor series up to order four and then Hamilton’s principle

$$\begin{aligned} \int _{t_1 }^{t_2 } {\left[ {\delta (T)-\delta U} \right] \mathrm{d}t=0} \end{aligned}$$

is applied to obtain Eqs. (14)–(17).

Appendix 3

$$\begin{aligned} \Gamma _1= & {} \left( -\frac{9}{2}\beta _1 ^{2}\pi ^{4}\alpha \delta ^{2}+\frac{9}{2}I_{\mathrm{p}} \Omega \pi ^{6}\beta _1 +\frac{9}{2}\pi ^{8}D_{11} \alpha \delta ^{2}\right. \nonumber \\&\left. +\frac{3}{2}I_{\mathrm{p}} \Omega \pi ^{6}\beta _1 \delta ^{2}-\frac{3}{2}\beta _1 ^{2}\pi ^{4}\alpha +\frac{3}{2}\pi ^{8}D_{11} \alpha \right) A_{11}\nonumber \\ \Lambda _1= & {} \left( \frac{3}{4}\pi ^{8}D_{11} \alpha +\frac{9}{4}I_{\mathrm{p}} \Omega \pi ^{6}\beta _1 -\frac{9}{4}\beta _1 ^{2}\pi ^{4}\alpha ^{3}\right. \nonumber \\&\left. +\frac{3}{4}I_{\mathrm{p}} \Omega \pi ^{6}\beta _1 \alpha ^{2}+\frac{9}{4}\pi ^{8}D_{11} \alpha ^{3}-\frac{3}{4}\beta _1 ^{2}\pi ^{4}\alpha \right) A_{11} \end{aligned}$$

$$\begin{aligned} \Psi _1= & {} \left( \frac{3}{4}\beta _1 ^{2}\pi ^{4}\alpha -\frac{3}{4}\pi ^{8}D_{11} \alpha -\frac{3}{4}I_{\mathrm{p}} \Omega \pi ^{6}\beta _1 \right) A_{11} \\ \Phi _1= & {} -2\pi ^{4}D_{11} \alpha \beta _1 -I_{\mathrm{p}} ^{2}\Omega ^{2}\pi ^{4}\beta _1 \alpha \nonumber \\&+2\beta _1 ^{3}\alpha -\beta _1 ^{2}I_{\mathrm{p}} \Omega \pi ^{2}-\pi ^{6}D_{11} I_{\mathrm{p}} \Omega \\ \Gamma _2= & {} \left( \frac{9}{2}I_{\mathrm{p}} \Omega \pi ^{6}\beta _2 -\frac{3}{2}\beta _2 ^{2}\pi ^{4}\delta -\frac{9}{2}\beta _2 ^{2}\pi ^{4}\alpha ^{2}\delta \right. \nonumber \\&\left. +\frac{3}{2}I_{\mathrm{p}} \Omega \pi ^{6}\beta _2 \alpha ^{2}\!+\!\frac{9}{2}\pi ^{8}D_{11} \alpha ^{2}\delta \!+\!\frac{3}{2}\pi ^{8}D_{11} \delta \!\right) A_{11} \\ \Lambda _2= & {} \left( \frac{3}{4}I_{\mathrm{p}} \Omega \pi ^{6}\beta _2 \delta ^{2}+\frac{9}{4}I_{\mathrm{p}} \Omega \pi ^{6}\beta _2 \right. \nonumber \\&+\frac{3}{4}\pi ^{8}D_{11} \delta +\frac{9}{4}\pi ^{8}D_{11} \delta ^{3}-\frac{3}{4}\beta _2 ^{2}\pi ^{4}\delta \nonumber \\&\left. -\frac{9}{4}\beta _2 ^{2}\pi ^{4}\delta ^{3} \right) A_{11} \\ \Psi _2= & {} \left( {-\frac{3}{4}I_{\mathrm{p}} \Omega \pi ^{6}\beta _2 +\frac{3}{4}\beta _2 ^{2}\pi ^{4}\delta -\frac{3}{4}\pi ^{8}D_{11} \delta } \right) A_{11} \\ \Phi _2= & {} 2\beta _2 ^{3}\delta -\beta _2 ^{2}I_{\mathrm{p}} \Omega \pi ^{2}-I_{\mathrm{p}} ^{2}\Omega ^{2}\pi ^{4}\beta _2 \delta -\pi ^{6}D_{11} I_{\mathrm{p}} \Omega \nonumber \\&-2\pi ^{4}D_{11} \delta \beta _2 \end{aligned}$$

Appendix 4

$$\begin{aligned} \alpha= & {} -\frac{i\left( {\left( {-2\sqrt{\pi ^{8}\Omega ^{2}I_{\mathrm{p}} ^{2}\left( {\Omega ^{2}I_{\mathrm{p}} ^{2}+4D_{11} } \right) }+\left( {-4D_{11} -2\Omega ^{2}I_{\mathrm{p}} ^{2}} \right) \pi ^{4}} \right) ^{3/2}} \right) }{8I_{pp} \Omega \pi ^{6}D_{11} } \\&-\frac{i\left( {\pi ^{4}\left( {\Omega ^{2}I_{\mathrm{p}} ^{2}+D_{11} } \right) \sqrt{-2\sqrt{\pi ^{8}\Omega ^{2}I_{\mathrm{p}} ^{2}\left( {\Omega ^{2}I_{\mathrm{p}} ^{2}+4D_{11} } \right) }+\left( {-4D_{11} -2\Omega ^{2}I_{\mathrm{p}} ^{2}} \right) \pi ^{4}}} \right) }{2I_{pp} \Omega \pi ^{6}D_{11} } \\ \delta= & {} \frac{-i\left( {\left( {2\sqrt{\pi ^{8}\Omega ^{2}I_{\mathrm{p}} ^{2}\left( {\Omega ^{2}I_{\mathrm{p}} ^{2}+4D_{11} } \right) }+\left( {-4D_{11} -2\Omega ^{2}I_{\mathrm{p}} ^{2}} \right) \pi ^{4}} \right) ^{3/2}} \right) }{8I_{\mathrm{p}} \Omega \pi ^{6}D_{11} } \\&\frac{-i\left( {\pi ^{4}\left( {\Omega ^{2}I_{\mathrm{p}} ^{2}+D_{11} } \right) \sqrt{2\sqrt{\pi ^{8}\Omega ^{2}I_{\mathrm{p}} ^{2}\left( {\Omega ^{2}I_{\mathrm{p}} ^{2}+4D_{11} } \right) }+\left( {-4D_{11} -2\Omega ^{2}I_{\mathrm{p}} ^{2}} \right) \pi ^{4}}} \right) }{2I_{\mathrm{p}} \Omega \pi ^{6}D_{11} } \\ \zeta= & {} -\frac{3\left( {\frac{1}{3}\sqrt{9}\sqrt{\pi ^{2}\left( {\left( {A_{11} -4D_{66} } \right) ^{2}\pi ^{2}+\frac{1024}{9}B_{16} ^{2}} \right) }+\pi ^{2}\left( {A_{11} -4D_{66} } \right) } \right) }{16B_{16} \pi } \\ \lambda= & {} -\frac{3\left( {-\frac{1}{3}\sqrt{9}\sqrt{\pi ^{2}\left( {\left( {A_{11} -4D_{66} } \right) ^{2}\pi ^{2}+\frac{1024}{9}B_{16} ^{2}} \right) }+\pi ^{2}\left( {A_{11} -4D_{66} } \right) } \right) }{16B_{16} \pi } \\ \eta= & {} \frac{3\left( {\frac{1}{12}\sqrt{144}\sqrt{\left( {\left( {A_{11} -\frac{1}{4}D_{66} } \right) ^{2}\pi ^{2}+\frac{256}{9}B_{16} ^{2}} \right) \pi ^{2}}+\left( {A_{11} -\frac{1}{4}D_{66} } \right) \pi ^{2}} \right) }{32B_{16} \pi } \\ \mu= & {} \frac{3\left( {-\frac{1}{12}\sqrt{144}\sqrt{\left( {\left( {A_{11} -\frac{1}{4}D_{66} } \right) ^{2}\pi ^{2}+\frac{256}{9}B_{16} ^{2}} \right) \pi ^{2}}+\left( {A_{11} -\frac{1}{4}D_{66} } \right) \pi ^{2}} \right) }{32B_{16} \pi } \end{aligned}$$

Appendix 5

$$\begin{aligned}&U1_2 \left( {T_0 ,T_1 ,T_2 } \right) =\Pi 1_{u\phi 1} \left( {T_2 } \right) \hbox {e}^{-5i\beta _1 T_0 }\nonumber \\&\quad +\Pi 1_{u\phi 2} \left( {T_2 } \right) \hbox {e}^{-5i\beta _2 T_0 }+\Pi 1_{u\phi 3} \left( {T_2 } \right) \hbox {e}^{-3i\beta _1 T_0 }\nonumber \\&\quad +\Pi 1_{u\phi 4} \left( {T_2 } \right) \hbox {e}^{-3i\beta _2 T_0 } +\Pi 1_{u\phi 5} \left( {T_2 } \right) \hbox {e}^{-2i\beta _1 T_0 }\nonumber \\&\quad +\Pi 1_{u\phi 6} \left( {T_2 } \right) \hbox {e}^{-2i\beta _2 T_0 }+\Pi 1_{u\phi 7} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-4\beta _2 +\beta _1 } \right) }\nonumber \\&\quad +\Pi 1_{u\phi 8} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-\beta _2 +\beta _1 } \right) } +\Pi 1_{u\phi 9} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-\beta _2 +4\beta _1 } \right) }\nonumber \\&\quad +\Pi 1_{u\phi 10} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _1 } \right) }+\Pi 1_{u\phi 11} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +4\beta _1 } \right) }\nonumber \\&\quad +\Pi 1_{u\phi 12} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {4\beta _2 +\beta _1 } \right) } +\Pi 1_{u\phi 13} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-4\beta _2 +\beta _1 } \right) }\nonumber \\&\quad +\Pi 1_{u\phi 14} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-\beta _2 +\beta _1 } \right) }+\Pi 1_{u\phi 15} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-\beta _2 +4\beta _1 } \right) }\nonumber \\&\quad +\Pi 1_{u\phi 16} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +\beta _1 } \right) } +\Pi 1_{u\phi 17} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +4\beta _1 } \right) }\nonumber \\&\quad +\Pi 1_{u\phi 18} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {4\beta _2 +\beta _1 } \right) }+\Pi 1_{u\phi 19} \left( {T_2 } \right) \hbox {e}^{2i\beta _1 T_0 }\nonumber \\&\quad +\Pi 1_{u\phi 20} \left( {T_2 } \right) \hbox {e}^{2i\beta _2 T_0 }+\Pi 1_{u\phi 21} \left( {T_2 } \right) \hbox {e}^{3i\beta _1 T_0 } \\&\quad +\Pi 1_{u\phi 22} \left( {T_2 } \right) \hbox {e}^{3i\beta _2 T_0 }+\Pi 1_{u\phi 23} \left( {T_2 } \right) \hbox {e}^{5i\beta _1 T_0 }\nonumber \\&\quad +\Pi 1_{u\phi 24} \left( {T_2 } \right) \hbox {e}^{5i\beta _2 T_0 } \\&\varphi 2_2 \left( {T_0 ,T_1 ,T_2 } \right) =\Theta 2_{u\phi 1} \left( {T_2 } \right) \hbox {e}^{-5i\beta _1 T_0 }\nonumber \\&\quad +\Theta 2_{u\phi 2} \left( {T_2 } \right) \hbox {e}^{-5i\beta _2 T_0 }+\Theta 2_{u\phi 3} \left( {T_2 } \right) \hbox {e}^{-3i\beta _1 T_0 }\nonumber \\&\quad +\Theta 2_{u\phi 4} \left( {T_2 } \right) \hbox {e}^{-3i\beta _2 T_0 } +\Theta 2_{u\phi 5} \left( {T_2 } \right) \hbox {e}^{-2i\beta _1 T_0 }\nonumber \\&\quad +\Theta 2_{u\phi 6} \left( {T_2 } \right) \hbox {e}^{-2i\beta _2 T_0 } +\Theta 2_{u\phi 7} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-4\beta _2 +\beta _1 } \right) }\nonumber \\&\quad +\Theta 2_{u\phi 8} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-\beta _2 +\beta _1 } \right) }+\Theta 2_{u\phi 9} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-\beta _2 +4\beta _1 } \right) }\nonumber \\&\quad +\Theta 2_{u\phi 10} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _1 } \right) }+\Theta 2_{u\phi 11} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +4\beta _1 } \right) }\nonumber \\&\quad +\Theta 2_{u\phi 12} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {4\beta _2 +\beta _1 } \right) } +\Theta 2_{u\phi 13} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-4\beta _2 +\beta _1 } \right) }\nonumber \\&\quad +\Theta 2_{u\phi 14} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-\beta _2 +\beta _1 } \right) }+\Theta 2_{u\phi 15} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-\beta _2 +4\beta _1 } \right) }\nonumber \\&\quad +\Theta 2_{u\phi 16} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +\beta _1 } \right) } +\Theta 2_{u\phi 17} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +4\beta _1 } \right) }\nonumber \\&\quad +\Theta 2_{u\phi 18} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {4\beta _2 +\beta _1 } \right) }+\Theta 2_{u\phi 19} \left( {T_2 } \right) \hbox {e}^{2i\beta _1 T_0 }\nonumber \\&\quad +\Theta 2_{u\phi 20} \left( {T_2 } \right) \hbox {e}^{2i\beta _2 T_0 } +\Theta 2_{u\phi 21} \left( {T_2 } \right) \hbox {e}^{3i\beta _1 T_0 }\nonumber \\&\quad +\Theta 2_{u\phi 22} \left( {T_2 } \right) \hbox {e}^{3i\beta _2 T_0 }+\Theta 2_{u\phi 23} \left( {T_2 } \right) \hbox {e}^{5i\beta _1 T_0 }\nonumber \\&\quad +\Theta 2_{u\phi 24} \left( {T_2 } \right) \hbox {e}^{5i\beta _2 T_0 } \\ \end{aligned}$$

$$\begin{aligned}&U2_2 \left( {T_0 ,T_2 } \right) =\Pi 2_{u\phi 1} \left( {T_2 } \right) \hbox {e}^{-5i\beta _1 T_0 }\nonumber \\&\quad +\Pi 2_{u\phi 2} \left( {T_2 } \right) \hbox {e}^{-5i\beta _2 T_0 }+\Pi 2_{u\phi 3} \left( {T_2 } \right) \hbox {e}^{-3i\beta _1 T_0 }\nonumber \\&\quad +\Pi 2_{u\phi 4} \left( {T_2 } \right) \hbox {e}^{-3i\beta _2 T_0 } +\Pi 2_{u\phi 5} \left( {T_2 } \right) \hbox {e}^{-2i\beta _1 T_0 } \nonumber \\&\quad +\Pi 2_{u\phi 6} \left( {T_2 } \right) \hbox {e}^{-2i\beta _2 T_0 }+\Pi 2_{u\phi 7} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-4\beta _2 +\beta _1 } \right) }\nonumber \\&\quad +\Pi 2_{u\phi 8} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-\beta _2 +\beta _1 } \right) } +\Pi 2_{u\phi 9} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-\beta _2 +4\beta _1 } \right) }\nonumber \\&\quad +\Pi 2_{u\phi 10} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _1 } \right) }+\Pi 2_{u\phi 11} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +4\beta _1 } \right) }\nonumber \\&\quad +\Pi 2_{u\phi 12} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {4\beta _2 +\beta _1 } \right) } \\&\quad +\Pi 2_{u\phi 13} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-4\beta _2 +\beta _1 } \right) }+\Pi 2_{u\phi 14} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-\beta _2 +\beta _1 } \right) }\nonumber \\&\quad +\Pi 2_{u\phi 15} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-\beta _2 +4\beta _1 } \right) }+\Pi 2_{u\phi 16} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +\beta _1 } \right) } \\&\quad +\Pi 2_{u\phi 17} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +4\beta _1 } \right) }+\Pi 2_{u\phi 18} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {4\beta _2 +\beta _1 } \right) }\nonumber \\&\quad +\Pi 2_{u\phi 19} \left( {T_2 } \right) \hbox {e}^{2i\beta _1 T_0 }+\Pi 2_{u\phi 20} \left( {T_2 } \right) \hbox {e}^{2i\beta _2 T_0 } \\&\quad +\Pi 2_{u\phi 21} \left( {T_2 } \right) \hbox {e}^{3i\beta _1 T_0 }+\Pi 2_{u\phi 22} \left( {T_2 } \right) \hbox {e}^{3i\beta _2 T_0 }\nonumber \\&\quad +\Pi 2_{u\phi 23} \left( {T_2 } \right) \hbox {e}^{5i\beta _1 T_0 }+\Pi 2_{u\phi 24} \left( {T_2 } \right) \hbox {e}^{5i\beta _2 T_0 } \\&\varphi 1_2 \left( {T_0 ,T_2 } \right) =\Theta 1_{u\phi 1} \left( {T_2 } \right) \hbox {e}^{-5i\beta _1 T_0 }+\Theta 1_{u\phi 2} \left( {T_2 } \right) \hbox {e}^{-5i\beta _2 T_0 }\nonumber \\&\quad +\Theta 1_{u\phi 3} \left( {T_2 } \right) \hbox {e}^{-3i\beta _1 T_0 }+\Theta 1_{u\phi 4} \left( {T_2 } \right) \hbox {e}^{-3i\beta _2 T_0 } \\&\quad +\Theta 1_{u\phi 5} \left( {T_2 } \right) \hbox {e}^{-2i\beta _1 T_0 }+\Theta 1_{u\phi 6} \left( {T_2 } \right) \hbox {e}^{-2i\beta _2 T_0 }\nonumber \\&\quad +\Theta 1_{u\phi 7} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-4\beta _2 +\beta _1 } \right) }+\Theta 1_{u\phi 8} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-\beta _2 +\beta _1 } \right) } \\&\quad +\Theta 1_{u\phi 9} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {-\beta _2 +4\beta _1 } \right) }+\Theta 1_{u\phi 10} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _1 } \right) }\nonumber \\&\quad +\Theta 1_{u\phi 11} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +4\beta _1 } \right) }+\Theta 1_{u\phi 12} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {4\beta _2 +\beta _1 } \right) } \\&\quad +\Theta 1_{u\phi 13} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-4\beta _2 +\beta _1 } \right) }+\Theta 1_{u\phi 14} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-\beta _2 +\beta _1 } \right) }\nonumber \\&\quad +\Theta 1_{u\phi 15} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {-\beta _2 +4\beta _1 } \right) }+\Theta 1_{u\phi 16} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +\beta _1 } \right) } \\&\quad +\Theta 1_{u\phi 17} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +4\beta _1 } \right) }+\Theta 1_{u\phi 18} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {4\beta _2 +\beta _1 } \right) }\nonumber \\&\quad +\Theta 1_{u\phi 19} \left( {T_2 } \right) \hbox {e}^{2i\beta _1 T_0 }+\Theta 1_{u\phi 20} \left( {T_2 } \right) \hbox {e}^{2i\beta _2 T_0 }\nonumber \\&\quad +\Theta 1_{u\phi 21} \left( {T_2 } \right) \hbox {e}^{3i\beta _1 T_0 } \\&\quad +\Theta 1_{u\phi 22} \left( {T_2 } \right) \hbox {e}^{3i\beta _2 T_0 }+\Theta 1_{u\phi 23} \left( {T_2 } \right) \hbox {e}^{5i\beta _1 T_0 }\\&\quad +\Theta 1_{u\phi 24} \left( {T_2 } \right) \hbox {e}^{5i\beta _2 T_0 } \\ \end{aligned}$$

$$\begin{aligned}&V1_2 (T_0 ,T_2 )=\Pi 1_{vw1} \hbox {e}^{-iT_0 \left( {\beta _1 -\beta _{32} } \right) }\nonumber \\&\quad +\Pi 1_{vw2} \hbox {e}^{-iT_0 \left( {\beta _1 +\beta _{32} } \right) }\nonumber \\&\quad +\Pi 1_{vw3} \hbox {e}^{-iT_0 \left( {\beta _1 -\beta _\phi } \right) }+\Pi 1_{vw4} \hbox {e}^{-iT_0 \left( {\beta _1 +\beta _\phi } \right) } \\&\quad +\Pi 1_{vw5} \hbox {e}^{-iT_0 \left( {4\beta _1 -\beta _{31} } \right) }+\Pi 1_{vw6} \hbox {e}^{-iT_0 \left( {\beta _2 -\beta _{32} } \right) }\nonumber \\&\quad +\Pi 1_{vw7} \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _{32} } \right) }+\Pi 1_{vw8} \hbox {e}^{-iT_0 \left( {\beta _2 -\beta _\phi } \right) }\nonumber \\&\quad +\Pi 1_{vw9} \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _\phi } \right) }+\Pi 1_{vw10} \hbox {e}^{-iT_0 \left( {4\beta _2 -\beta _{2\phi } } \right) } \\&\quad +\Pi 1_{vw11} \hbox {e}^{-iT_0 \left( {-\beta _{31} +4\beta _2 } \right) }+\Pi 1_{vw12} \hbox {e}^{-iT_0 \left( {\beta _{31} +4\beta _1 } \right) }\nonumber \\&\quad +\Pi 1_{vw13} \hbox {e}^{-iT_0 \left( {\beta _{31} +4\beta _2 } \right) }+\Pi 1_{vw14} \hbox {e}^{-iT_0 \left( {-\beta _{2\phi } +4\beta _1 } \right) } \\&\quad +\Pi 1_{vw15} \hbox {e}^{-iT_0 \left( {\beta _{2\phi } +4\beta _1 } \right) }+\Pi 1_{vw16} \hbox {e}^{-iT_0 \left( {\beta _{2\phi } +4\beta _2 } \right) }\nonumber \\&\quad +\Pi 1_{vw17} \hbox {e}^{iT_0 \left( {\beta _1 -\beta _{32} } \right) }+\Pi 1_{vw18} \hbox {e}^{iT_0 \left( {\beta _1 +\beta _{32} } \right) } \\&\quad +\Pi 1_{vw19} \hbox {e}^{iT_0 \left( {\beta _1 -\beta _\phi } \right) }+\Pi 1_{vw20} \hbox {e}^{iT_0 \left( {\beta _1 +\beta _\phi } \right) }\nonumber \\&\quad +\Pi 1_{vw21} \hbox {e}^{iT_0 \left( {4\beta _1 -\beta _{31} } \right) }+\Pi 1_{vw22} \hbox {e}^{iT_0 \left( {\beta _2 -\beta _{32} } \right) } \\&\quad +\Pi 1_{vw23} \hbox {e}^{iT_0 \left( {\beta _2 +\beta _{32} } \right) }+\Pi 1_{vw24} \hbox {e}^{iT_0 \left( {\beta _2 -\beta _\phi } \right) }\nonumber \\&\quad +\Pi 1_{vw25} \hbox {e}^{iT_0 \left( {\beta _2 +\beta _\phi } \right) }+\Pi 1_{vw26} \hbox {e}^{iT_0 \left( {4\beta _2 -\beta _{2\phi } } \right) }\nonumber \\&\quad +\Pi 1_{vw27} \hbox {e}^{iT_0 \left( {-\beta _{31} +4\beta _2 } \right) }+\Pi 1_{vw28} \hbox {e}^{iT_0 \left( {\beta _{31} +4\beta _1 } \right) } \\&\quad +\Pi 1_{vw29} \hbox {e}^{iT_0 \left( {\beta _{31} +4\beta _2 } \right) }+\Pi 1_{vw30} \hbox {e}^{iT_0 \left( {-\beta _{2\phi } +4\beta _1 } \right) }\nonumber \\&\quad +\Pi 1_{vw31} \hbox {e}^{iT_0 \left( {\beta _{2\phi } +4\beta _1 } \right) }+\Pi 1_{vw32} \hbox {e}^{iT_0 \left( {\beta _{2\phi } +4\beta _2 } \right) } \\ \end{aligned}$$

$$\begin{aligned}&W1_2 (T_0 ,T_2 )=\Theta 1_{vw1} \hbox {e}^{-iT_0 \left( {\beta _1 -\beta _{32} } \right) }\nonumber \\&\quad +\Theta 1_{vw2} \hbox {e}^{-iT_0 \left( {\beta _1 +\beta _{32} } \right) }+\Theta 1_{vw3} \hbox {e}^{-iT_0 \left( {\beta _1 -\beta _\phi } \right) }\nonumber \\&\quad +\Theta 1_{vw4} \hbox {e}^{-iT_0 \left( {\beta _1 +\beta _\phi } \right) }+\Theta 1_{vw5} \hbox {e}^{-iT_0 \left( {4\beta _1 -\beta _{31} } \right) } \\&\quad +\Theta 1_{vw6} \hbox {e}^{-iT_0 \left( {\beta _2 -\beta _{32} } \right) }+\Theta 1_{vw7} \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _{32} } \right) }\nonumber \\&\quad +\Theta 1_{vw8} \hbox {e}^{-iT_0 \left( {\beta _2 -\beta _\phi } \right) }+\Theta 1_{vw9} \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _\phi } \right) }\nonumber \\&\quad +\Theta 1_{vw10} \hbox {e}^{-iT_0 \left( {4\beta _2 -\beta _{2\phi } } \right) } \\&\quad +\Theta 1_{vw11} \hbox {e}^{-iT_0 \left( {-\beta _{31} +4\beta _2 } \right) }+\Theta 1_{vw12} \hbox {e}^{-iT_0 \left( {\beta _{31} +4\beta _1 } \right) }\nonumber \\&\quad +\Theta 1_{vw13} \hbox {e}^{-iT_0 \left( {\beta _{31} +4\beta _2 } \right) }+\Theta 1_{vw14} \hbox {e}^{-iT_0 \left( {-\beta _{2\phi } +4\beta _1 } \right) } \\&\quad +\Theta 1_{vw15} \hbox {e}^{-iT_0 \left( {\beta _{2\phi } +4\beta _1 } \right) }\nonumber \\&\quad +\Theta 1_{vw16} \hbox {e}^{-iT_0 \left( {\beta _{2\phi } +4\beta _2 } \right) }+\Theta 1_{vw17} \hbox {e}^{iT_0 \left( {\beta _1 -\beta _{32} } \right) }\nonumber \\&\quad +\Theta 1_{vw18} \hbox {e}^{iT_0 \left( {\beta _1 +\beta _{32} } \right) }+\Theta 1_{vw19} \hbox {e}^{iT_0 \left( {\beta _1 -\beta _\phi } \right) } \\&\quad +\Theta 1_{vw20} \hbox {e}^{iT_0 \left( {\beta _1 +\beta _\phi } \right) }+\Theta 1_{vw21} \hbox {e}^{iT_0 \left( {4\beta _1 -\beta _{31} } \right) }\nonumber \\&\quad +\Theta 1_{vw22} \hbox {e}^{iT_0 \left( {\beta _2 -\beta _{32} } \right) }+\Theta 1_{vw23} \hbox {e}^{iT_0 \left( {\beta _2 +\beta _{32} } \right) }\nonumber \\&\quad +\Theta 1_{vw24} \hbox {e}^{iT_0 \left( {\beta _2 -\beta _\phi } \right) } \\&\quad +\Theta 1_{vw25} \hbox {e}^{iT_0 \left( {\beta _2 +\beta _\phi } \right) }+\Theta 1_{vw26} \hbox {e}^{iT_0 \left( {4\beta _2 -\beta _{2\phi } } \right) }\nonumber \\&\quad +\Theta 1_{vw27} \hbox {e}^{iT_0 \left( {-\beta _{31} +4\beta _2 } \right) }+\Theta 1_{vw28} \hbox {e}^{iT_0 \left( {\beta _{31} +4\beta _1 } \right) }\nonumber \\&\quad +\Theta 1_{vw29} \hbox {e}^{iT_0 \left( {\beta _{31} +4\beta _2 } \right) } +\Theta 1_{vw30} \hbox {e}^{iT_0 \left( {-\beta _{2\phi } +4\beta _1 } \right) }\nonumber \\&\quad +\Theta 1_{vw31} \hbox {e}^{iT_0 \left( {\beta _{2\phi } +4\beta _1 } \right) }+\Theta 1_{vw32} \hbox {e}^{iT_0 \left( {\beta _{2\phi } +4\beta _2 } \right) } \\ \end{aligned}$$

$$\begin{aligned}&V2_2 \left( {T_0 ,T_2 } \right) =\Pi 2_{vw1} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _1 -\beta _{31} } \right) }\\&\quad +\Pi 2_{vw2} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _1 +\beta _{u1} } \right) }\nonumber \\&\quad +\Pi 2_{vw3} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _1 -\beta _{\phi 2} } \right) } \\&\quad +\Pi 2_{vw4} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _1 +\beta _{\phi 2} } \right) }\nonumber \\&\quad +\Pi 2_{vw5} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 -\beta _{u1} } \right) }\\&\quad +\Pi 2_{vw6} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _{u1} } \right) }\nonumber \\&\quad +\Pi 2_{vw7} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 -\beta _{\phi 2} } \right) } \\&\quad +\Pi 2_{vw8} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _{\phi 2} } \right) }\nonumber \\&\quad +\Pi 2_{vw9} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _1 -\beta _{u1} } \right) }\nonumber \\&\quad +\Pi 2_{vw10} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _1 +\beta _{u1} } \right) }\nonumber \\&\quad +\Pi 2_{vw11} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _1 -\beta _{\phi 2} } \right) } \\&\quad +\Pi 2_{vw12} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _1 +\beta _{\phi 2} } \right) }\nonumber \\&\quad +\Pi 2_{vw13} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 -\beta _{u1} } \right) }\nonumber \\&\quad +\Pi 2_{vw14} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +\beta _{u1} } \right) }\nonumber \\&\quad +\Pi 2_{vw15} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 -\beta _{\phi 2} } \right) } \\&\quad +\Pi 2_{vw16} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +\beta _{\phi 2} } \right) } \\&W2_2 \left( {T_0 ,T_2 } \right) =\Theta 2_{vw1} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _1 -\beta _{31} } \right) }\nonumber \\&\quad +\Theta 2_{vw2} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _1 +\beta _{u1} } \right) }+\Theta 2_{vw3} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _1 -\beta _{\phi 2} } \right) } \\&\quad +\Theta 2_{vw4} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _1 +\beta _{\phi 2} } \right) }+\Theta 2_{vw5} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 -\beta _{u1} } \right) }\nonumber \\&\quad +\Theta 2_{vw6} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _{u1} } \right) }+\Theta 2_{vw7} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 -\beta _{\phi 2} } \right) } \\&\quad +\Theta 2_{vw8} \left( {T_2 } \right) \hbox {e}^{-iT_0 \left( {\beta _2 +\beta _{\phi 2} } \right) }+\Theta 2_{vw9} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _1 -\beta _{u1} } \right) }\nonumber \\&\quad +\Theta 2_{vw10} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _1 +\beta _{u1} } \right) }+\Theta 2_{vw11} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _1 -\beta _{\phi 2} } \right) } \\&\quad +\Theta 2_{vw12} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _1 +\beta _{\phi 2} } \right) }+\Theta 2_{vw13} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 -\beta _{u1} } \right) }\nonumber \\&\quad +\Theta 2_{vw14} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +\beta _{u1} } \right) }+\Theta 2_{vw15} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 -\beta _{\phi 2} } \right) } \\&\quad +\Theta 2_{vw16} \left( {T_2 } \right) \hbox {e}^{iT_0 \left( {\beta _2 +\beta _{\phi 2} } \right) } \\ \end{aligned}$$