Nonlinear modal interactions and bifurcations of a piezoelectric nanoresonator with three-to-one internal resonances incorporating surface effects and van der Waals dissipation forces

Abstract

This paper investigates the nonlinear dynamics of a doubly clamped piezoelectric nanobeam subjected to a combined AC and DC loadings in the presence of three-to-one internal resonance. Surface effects are taken into account in the governing equation of motion to incorporate the associated size effects at nanoscales. The reduced-order model equation (ROM) is obtained based on the Galerkin method. The multiple scales method is applied directly to the nonlinear equation of motion and associated boundary conditions to obtain the modulation equations. The equilibrium solutions of the modulation equations and the dynamic solutions of the ROM equation are investigated in the case of primary and principal parametric resonances of the first mode. Stability, bifurcations and frequency response curves of the nanobeam are investigated. Dynamic behaviors of the motion are shown in the form of time traces, phase portraits, Poincare sections and fast Fourier transforms. The results indicate rich dynamic behaviors such as Hopf bifurcations, periodic and quasiperiodic motions in both directly and indirectly excited modes illustrating the influence of modal interactions on the response.

1 Introduction

In recent years, nanoelectromechanical systems (NEMSs) have been the focus of attention of vast majority of researchers. Thanks to their inherent characteristics, NEMSs are being used in a wide variety of applications such as capacitive sensors, actuators, narrow band filtering, mass and force detection and atomic-force microscopes. NEMS resonators excited electrostatically could experience different sources of nonlinearity such as molecular interactions (Casimir and van der Waals forces) and nonlinear electrostatic forces. This reveals the importance of the nonlinear dynamics in modeling a NEMS-based resonator under electrostatic actuation. Many studies have been carried out in the literature on the nonlinear behavior of the NEMS/MEMS resonators. Nonlinear dynamics of NEMS-based sensors under superharmonic resonance was investigated by Kacem et al. [1] using the method of multiple scales. They obtained a way to retard the pull-in voltage by decreasing the AC voltage. Ouakad and Younis [2] studied nonlinear dynamics of an electrostatically actuated carbon nanotube (CNT) resonator. Primary and secondary resonances were studied using shooting method [3, 4]. Several nonlinear phenomena have been reported such as hysteresis [5, 6], dynamic pull-in [7,8,9], hardening behavior [8] and softening behavior [10]. In a series of works [11,12,13,14], they investigated the nonlinear dynamics of a CNT resonator in the presence of the initial curvature. They studied the effect of DC electrostatic force and the slack level on the CNT natural frequencies and mode shapes. Rasekh and Khadem [15] investigated pull-in instability of a CNT cantilever using direct numerical integration. Curvature and inertia nonlinearities were also taken into account. Asemi et al. [16] obtained a nonlinear continuum model for the large amplitude vibration of nanoelectromechanical resonators using piezoelectric nanofilms (PNFs) under external electric voltage. Ke et al. [17] investigated nonlinear vibration of the piezoelectric nanobeams based on the nonlocal and Timoshenko beam theories using the DQM. They studied the effect of nonlocal parameter and piezoelectric voltage on the nanobeam behavior. Hajnayeb and Khadem [18, 19] investigated in depth the stability and the nonlinear vibrations of single-walled and double-walled CNTs under electrostatic actuations. Primary and secondary resonances and bifurcation points under different values of DC and AC voltages were studied using the multiple scales method. Rhoads et al. [20] explored the nonlinear dynamics of an electromagnetically actuated microcantilever under parametric excitations. The fifth-order nonlinearity was investigated using the perturbation methods. Abdel-Rahman and Nayfeh [21] investigated secondary resonances of electrically actuated resonant microsensors analytically using the method of the multiple scales. Xu and Younis [22] investigated the nonlinear dynamics of a CNT actuated under large electrostatic forces. They expanded the nonlinear electrostatic term into enough number of terms of the Taylor series. Younis and Nayfeh [23] studied nonlinear dynamics of an electrically actuated microbeam using the method of multiple scales. They explored the three-to-one resonance between the first and second modes. They showed that internal resonance cannot be activated between the considered modes. Vyas et al. [24] designed a T-beam microresonator based on the nonlinear 1:2 internal resonance. They used asymptotic averaging method to analyze dynamic responses of the system. It is beneficial to mention that reducing the size to nanoscale leads to size-dependent behaviors of nanostructures [25, 26]. Moreover, large surface area-to-volume ratio is an important consequence of the scale-down. Large surface-to-bulk ratio at nanoscales results in an increase in the surface energy [27]. Many studies have been carried out by researchers to investigate the influence of the surface effects on nanostructures. Pourkiaee et al. [28, 29] investigated nonlinear vibrations of a piezoelectric nanobeam considering surface effects and intermolecular interactions. They explored the effect of different parameters such as surface effects and piezoelectric voltage on static equilibria, pull-in voltages and primary and secondary resonances of the nanobeam. Wang and Wang [30] studied the effect of surface energy on free vibration of a cracked nanobeam. They showed that the natural frequencies of the nanobeam have dramatic dependence on surface stresses. Eltaher et al. [31] investigated coupling effects of nonlocal and surface energy on vibration of nanobeams using Galerkin finite element technique. There are also numerous papers in the literature which have reported the influence of surface energy on pull-in instability [32,33,34], buckling [35, 36] and free vibration [37] of nanostructures. According to the literature, it can be found that internal resonance in MEMS-/NEMS-based resonators has not been explored so far. The present study aims to investigate the nonlinear dynamics of a piezoelectric nanoresonator in the presence of internal resonance, while physical behaviors peculiar to the nanosized systems are considered in the model. Accordingly, surface effects and intermolecular van der Waals forces are taken into account, due to the size effects and the small initial gap between the electrodes. For specific combination of system parameters, natural frequency of the second symmetric mode (third mode) is approximately three times that of the first one, a situation which results in nonlinear modal interaction between the associated modes through the three-to-one internal resonance. In-depth study of nonlinear oscillations of the nanobeam under small AC loads is presented using the multiple scales method. Stability, bifurcations and frequency response curves of the nanobeam are investigated. Dynamic behaviors of the motion are shown in the form of time traces, phase portraits, Poincare sections and FFT diagrams. The results indicate rich dynamic behaviors such as Hopf bifurcations and quasiperiodic motions in both directly and indirectly excited modes illustrating the influence of modal interactions on the stability and the response of the nanoresonator.

Fig. 1

Schematic diagram of an electrically actuated clamped–clamped piezoelectric nanobeam

2 Problem formulation

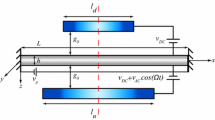
Consider a clamped–clamped piezoelectric nanoresonator of length L, width b, thickness h, surrounded between two conductive electrodes of different lengths, as illustrated in Fig. 1. The xyz inertial coordinate system passes through the centroid of the cross section $(y=0,z=0)$ and is located at the left clamped end of the nanobeam. The vertical displacement of the nanobeam centerline along the z-axis is denoted by w(x, t).

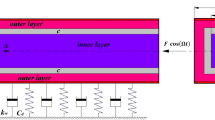
The piezoelectric nanobeam is actuated by the electric load $V_\mathrm{DC} +V_\mathrm{AC} \cos (\Omega t)$ through the lower electrode and the $V_\mathrm{DC}$ load through the upper electrode, where $V_\mathrm{DC}$, $V_\mathrm{AC}$ and $\Omega$ are DC bias voltage, amplitude and frequency of AC voltage, respectively. In addition, the piezoelectric nanobeam is actuated by the direct current polarization voltage $V_\mathrm{P}$, which is applied along the height of the nanobeam. The initial capacitor gap width $g_0$ is assumed to be under 20 nm, such that the van der Waals force becomes dominant as an intermolecular interaction between the electrodes [38]. Note here that the initial gap is comparable to the nanobeam width; consequently, the fringing field effects are also considered in this study. Moreover, due to the large surface-to-bulk ratio at the nanoscale, the surface energies are taken into account [27, 28]. To incorporate the surface effects, it is assumed that the surface layer has a mathematically zero thickness that is perfectly bonded to the bulk material and there is no slipping between the bulk and the surface. Assuming the Euler–Bernoulli beam model and defining $V_\mathrm{D} =V_\mathrm{DC} -V_\mathrm{P}$, the nondimensional equation of motion governing the transverse vibration of the piezoelectric nanobeam considering surface effects and van der Walls force distribution is given by [28]:

$$\begin{aligned}&\frac{\partial ^{4}w}{\partial x^{4}}+\frac{\partial ^{2}w}{\partial t^{2}}-\left[ {\alpha _1 +\alpha _2 +\alpha _3 \Gamma (w,w)} \right] \frac{\partial ^{2}w}{\partial x^{2}}\nonumber \\&\qquad +\, \alpha _4 \frac{\partial ^{4}w}{\partial x^{2}\partial t^{2}}+\alpha _5 \frac{\partial w}{\partial t} \nonumber \\&\quad =\alpha _6 \frac{\left[ {V_\mathrm{D} +V_\mathrm{AC} \cos (\Omega t)} \right] ^{2}}{\left( {1-w} \right) ^{2}}H_1 (x)\nonumber \\&\qquad -\,\alpha _6 \frac{V_\mathrm{D} ^{2}}{\left( {1+w} \right) ^{2}}H_2 (x)\nonumber \\&\qquad +\,\alpha _7 \frac{H_1 (x)}{\left( {1-w} \right) ^{3}}-\alpha _7 \frac{H_2 (x)}{\left( {1+w} \right) ^{3}} \end{aligned}$$

(1)

$$\begin{aligned}&w(0,t)=w(1,t)=0, \frac{\partial w(0,t)}{\partial x}=\frac{\partial w(1,t)}{\partial x}=0 \end{aligned}$$

(2)

The functions $\Gamma$, $H_{i=1,2} \left( x \right)$ and the nondimensional parameters in Eq. (1) are defined in “Appendix 1.” The nanobeam deflection under electrostatic excitation is composed of the dynamic component u(x, t), due to the AC voltage, and the static component $w_s (x)$, due to the DC voltage:

$$\begin{aligned} w(x,t)=w_s (x)+u(x,t) \end{aligned}$$

(3)

To calculate the static deflection and boundary conditions, all time-varying terms in Eqs. (1) and (2) are set equal to zero and the following results are obtained:

$$\begin{aligned}&w_s^{IV} (x)-\left[ {\alpha _1 +\alpha _2 +\alpha _3 \Gamma (w_s ,w_s )} \right] {w}''_s \nonumber \\&\quad =\alpha _6 \frac{V_\mathrm{D}^2 }{\left( {1-w_s } \right) ^{2}}H_1 (x) -\alpha _6 \frac{V_\mathrm{D}^2 }{\left( {1+w_s } \right) ^{2}}H_2 (x) \nonumber \\&\qquad +\, \alpha _7 \frac{H_1 (x)}{\left( {1-w_s } \right) ^{3}}-\alpha _7 \frac{H_1 (x)}{\left( {1+w_s } \right) ^{3}} \end{aligned}$$

(4)

$$\begin{aligned}&w_s (x=0,1)=0 \hbox { and } w_s ^{\prime }(x=0,1)=0 \end{aligned}$$

(5)

where the prime denotes the derivative with respect to x. Substituting Eq. (3) into Eqs. (1) and (2) and using Eqs. (4) and (5) to eliminate the static equilibrium position, and expanding the electrostatic and dispersion forces around the stability point, yields nondimensional equations and boundary conditions governing the dynamic behavior of the nanobeam:

$$\begin{aligned}&\ddot{u}+\alpha _5 \dot{u}+u^{IV}-\left[ {\alpha _1 +\alpha _2 +\alpha _3 \Gamma (w_s ,w_s )} \right] {u}''\nonumber \\&\qquad -\, 2\alpha _3 \Gamma (w_s ,u)u -2\alpha _3 \Gamma (w_s ,u){w}''_s -\alpha _3 \Gamma (u,u){w}''_s\nonumber \\&\qquad -\, \alpha _3 \Gamma (u,u){u}''+\alpha _4 {\ddot{u}}'' \nonumber \\&\quad =\alpha _{61} \left( {\begin{array}{l} \frac{2V_\mathrm{D}^2 }{\left( {1-w_s } \right) ^{3}}u+\frac{3V_\mathrm{D}^2 }{\left( {1-w_s } \right) ^{4}}u^{2}+\frac{4V_\mathrm{D}^2 }{\left( {1-w_s } \right) ^{5}}u^{3} \\ +\frac{2V_\mathrm{D} V_\mathrm{AC} \cos (\Omega t)}{\left( {1-w_s } \right) ^{2}}+\frac{4V_\mathrm{D} V_\mathrm{AC} \cos (\Omega t)}{\left( {1-w_s } \right) ^{3}}u \\ \end{array}} \right) \nonumber \\&\qquad -\, \alpha _{62} \left( {\frac{-2V_\mathrm{D}^2 }{\left( {1+w_s } \right) ^{3}}u+\frac{3V_\mathrm{D}^2 }{\left( {1+w_s } \right) ^{4}}u^{2}-\frac{4V_\mathrm{D}^2 }{\left( {1+w_s } \right) ^{5}}u^{3}} \right) \nonumber \\&\qquad +\, \alpha _{71} \left( {\frac{3}{\left( {1-w_s } \right) ^{4}}u+\frac{6}{\left( {1-w_s } \right) ^{5}}u^{2}+\frac{10}{\left( {1-w_s } \right) ^{6}}u^{3}} \right) \nonumber \\&\qquad -\, \alpha _{72} \left( {\frac{-3}{\left( {1+w_s } \right) ^{4}}u+\frac{6}{\left( {1+w_s } \right) ^{5}}u^{2}-\frac{10}{\left( {1+w_s } \right) ^{6}}u^{3}} \right) \nonumber \\ \end{aligned}$$

(6)

$$\begin{aligned}&u(x=0,1)=0 \hbox { and } u^{\prime }(x=0,1)=0 \end{aligned}$$

(7)

where the dot denotes the derivative with respect to t. The nondimensional parameters in Eq. (6) are defined in “Appendix 1.” According to Ref. [23], $V_\mathrm{AC}^2$ is dropped due to the fact $V_\mathrm{AC}^2 \ll V_\mathrm{D}^2$.

Table 1 Variation of the natural frequencies of the two first symmetric modes with the piezoelectric actuation voltage for two different levels of DC voltage

3 The reduced-order model

The linear natural frequencies of the nanobeam resonator differ with the variation of the system parameters such as DC voltage load, piezoelectric actuation voltage and the initial gap width. For specific combination of system parameters, natural frequencies of specific modes could become commensurable, a situation which may result in nonlinear interactions between the associated modes through the internal resonance. To generate the reduced-order model of the system using the Galerkin discretization method, the nanobeam deflection is approximated as:

$$\begin{aligned} u(x,t)=\sum _{i=1}^n {q_i (t)\varphi _i (x)} \end{aligned}$$

(8)

where $q_i (t)$ is the ith time-dependent generalized coordinate and $\varphi _{i=1,3,5,\ldots } (x)$ is the ith symmetric eigenfuction of the clamped–clamped linear undamped nanobeam, considering the surface effects and axial load due to piezoelectric actuation [28]. It is worth mentioning that there would be no energy exchange between the symmetric and antisymmetric modes (the antisymmetric modes would not be activated in the case of beams with symmetric properties and forces) [23]. To obtain the ROM, first the nonlinear electrostatic and van der Waals forces are expanded in Taylor series up to the forth order. Taylor series expansion is used to avoid the strong nonlinearities, and the truncated expansion is valid under the small motion assumption. Substituting Eq. (8) into Eq. (6), multiplying the resulting equation by $\varphi _i$, and integrating the outcome from $x=0$ to 1 would reduce to the following nonlinear differential equations in terms of generalized coordinates $q_j (t)$:

$$\begin{aligned}&\sum _{j=1}^n {M_{ij} \ddot{q}_j }+ \sum _{j=1}^n {C_{ij} \dot{q}_j }+ \sum _{j=1}^n {K_{ij} q_j }+ \sum _{j=1}^n {\sum _{k=1}^n {K_{ijk} q_j } } q_k\nonumber \\&\quad +\sum _{j=1}^n {\sum _{k=1}^n {\sum _{l=1}^n {K_{ijkl} q_j } } q_k } q_l =F_i (t) \end{aligned}$$

(9)

The coefficients of Eq. (9) are defined in “Appendix 2.” This study investigates the special case of three-to-one internal resonance $(\omega _3 \approx 3\omega _1 )$, and it is assumed that there are no other commensurate frequencies in the higher modes; hence, just the two first symmetric modes are considered to obtain the ROM. Equation (9) can be numerically integrated using the Runge–Kutta technique to simulate the dynamic behavior of the nanobeam.

4 Perturbation analysis

It follows from Table 1 that for some specific values of system parameters, there is a commensurable relation between the first and the third natural frequencies $(\omega _3 \approx 3\omega _1 )$, indicating the possibility of activating a 1:3 internal resonance between the first and third (second symmetric) modes. In order to determine approximate solution of the nonlinear distributed parameter system, the multiple scales method is directly applied to the partial differential equation of motion and associated boundary conditions. Therefore, the second-order uniform solution is expressed in the form of [39]:

$$\begin{aligned} u(x,t;\varepsilon )= & {} \varepsilon u_1 (x,T_0 ,T_1 ,T_2 )+\varepsilon ^{2}u_2 (x,T_0 ,T_1 ,T_2 )\nonumber \\&+\, \varepsilon ^{3}u_3 (x,T_0 ,T_1 ,T_2 )+\cdot \cdot \cdot \end{aligned}$$

(10)

where $\varepsilon$ is a small dimensionless book-keeping parameter and $T_0 =t$, $T_1 =\varepsilon t$ and $T_2 =\varepsilon ^{2}t$ are different timescales. Using chain rule, time derivatives can be written as:

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}= & {} D_0 +\varepsilon D_1 +\varepsilon ^{2}D_2 +\cdot \cdot \cdot \nonumber \\ \frac{\hbox {d}^{2}}{\hbox {d}t^{2}}= & {} D_0 +2\varepsilon D_0 D_1 +\varepsilon ^{2}\left( {D_1^2 +2D_0 D_2 } \right) +\cdot \cdot \cdot \nonumber \\ \end{aligned}$$

(11)

where $D_n =\partial /{\partial T_n }$.

Next, we consider primary and principal parametric resonances of the first mode separately.

4.1 Primary resonances of the first mode

In order to investigate the case of primary resonance involving the two first symmetric modes, the damping coefficient and the excitation amplitude are scaled as:

$$\begin{aligned} C=\varepsilon ^{2}C, V_\mathrm{AC} =\varepsilon ^{3}V_\mathrm{AC} \end{aligned}$$

(12)

Substituting Eqs. (10–12) into Eq. (6) and equating the terms of like powers of $\varepsilon$, the following results are achieved:

$$\begin{aligned} O(\varepsilon ):&\nonumber \\ L(u_1 )&=D_0^2 u_1 +u_1^{IV} +\alpha _4 {\ddot{u}}''_1\nonumber \\&\quad -\, \left[ {\alpha _1 +\alpha _2 +\alpha _3 \Gamma \left( {w_s ,w_s } \right) } \right] {u}''_1 -2\alpha _3 \Gamma \left( {w_s ,u_1 } \right) w_s ^{\prime \prime }\nonumber \\&\quad -\, \frac{2\alpha _{61} V_\mathrm{D}^2 }{\left( {1-w_s } \right) ^{3}}u_1 -\frac{2\alpha _{62} V_\mathrm{D} ^{2}}{\left( {1+w_s } \right) ^{3}}u_1\nonumber \\&\quad -\, \frac{3\alpha _{71} }{\left( {1-w_s } \right) ^{4}}u_1 -\frac{3\alpha _{72} }{\left( {1+w_s } \right) ^{4}}u_1 =0 \end{aligned}$$

(13)

$$\begin{aligned} O(\varepsilon ^{2}):&\nonumber \\ L(u_2 )&=-2D_0 D_1 u_1 -2\alpha _4 D_0 D_1 u_1 ^{\prime \prime }\nonumber \\&\quad +\, 2\alpha _3 \Gamma \left( {w_s ,u_1 } \right) u_1 ^{\prime \prime } +\alpha _3 \Gamma \left( {u_1 ,u_1 } \right) w_s ^{\prime \prime }\nonumber \\&\quad +\, \frac{3\alpha _{61} V_\mathrm{D}^2 }{\left( {1-w_s } \right) ^{4}}u_1^2 -\frac{3\alpha _{62} V_\mathrm{D} ^{2}}{\left( {1+w_s } \right) ^{4}}u_1 ^{2}+\frac{6\alpha _{71} }{\left( {1-w_s } \right) ^{5}}u_1 ^{2}\nonumber \\&\quad -\, \frac{6\alpha _{72} }{\left( {1+w_s } \right) ^{5}}u_1 ^{2} \end{aligned}$$

(14)

$$\begin{aligned} O(\varepsilon ^{3}):&\nonumber \\ L(u_3 )&=-2D_0 D_1 u_2 -D_1^2 u_1 -2D_0 D_2 u_1 -CD_0 u_1\nonumber \\&\quad -\, \alpha _4 \left( {2D_0 D_1 {u}''_2 +2D_0 D_2 {u}''_1 +D_1^2 {u}''_1 } \right) \nonumber \\&\quad +\, 2\alpha _3 \Gamma \left( {u_1 ,u_2 } \right) w_s ^{\prime \prime }+\alpha _3 \Gamma \left( {u_1 ,u_1 } \right) {u}''_1\nonumber \\&\quad +\, 2\alpha _3 \Gamma \left( {w_s ,u_1 } \right) u_2 ^{\prime \prime }+2\alpha _3 \Gamma \left( {w_s ,u_2 } \right) u_1 ^{\prime \prime }\nonumber \\&\quad +\, \frac{6\alpha _{61} V_\mathrm{D}^2 }{\left( {1-w_s } \right) ^{4}}u_1 u_2 -\frac{6\alpha _{62} V_\mathrm{D} ^{2}}{\left( {1+w_s } \right) ^{4}}u_1 u_2\nonumber \\&\quad +\,\frac{12\alpha _{71} }{\left( {1-w_s } \right) ^{5}}u_1 u_2 -\frac{12\alpha _{72} }{\left( {1+w_s } \right) ^{5}}u_1 u_2\nonumber \\&\quad +\, \frac{4\alpha _{61} V_\mathrm{D}^2 }{\left( {1-w_s } \right) ^{5}}u_1^3 + \frac{4\alpha _{62} V_\mathrm{D} ^{2}}{\left( {1+w_s } \right) ^{5}}u_1 ^{3}+\frac{10\alpha _{71} }{\left( {1-w_s } \right) ^{6}}u_1 ^{3}\nonumber \\&\quad +\, \frac{10\alpha _{72} }{\left( {1+w_s } \right) ^{6}}u_1 ^{3}+2P_1 (x)\cos (\Omega T_0 ) \end{aligned}$$

(15)

where

$$\begin{aligned} P_1 (x)=\frac{\alpha _{61} V_\mathrm{D} V_\mathrm{AC} }{\left( {1-w_s } \right) ^{2}} \end{aligned}$$

(16)

The boundary conditions are similar for all orders and are given by:

$$\begin{aligned} u_i (x=0,1)=0 \hbox { and } u_i ^{\prime }(x=0,1)=0,\quad i=1,2,3\nonumber \\ \end{aligned}$$

(17)

It is assumed that neither of the considered modes are involved in the modal interaction with higher modes. Therefore, in the presence of the damping, all other modes except the directly or indirectly excited modes decay with time. Consequently, the general solution of Eq. (13) and the associated boundary conditions, consisting of the two first symmetric modes, can be expressed as:

$$\begin{aligned} u_1= & {} A_1 (T_1 ,T_2 )e^{i\omega _1 T_0 }\phi _1 (x)\nonumber \\&+\, A_3 (T_1 ,T_2 )e^{i\omega _3 T_0 }\phi _3 (x)+cc \end{aligned}$$

(18)

where $\phi _j (x)$ and $\omega _j$ are the mode shapes and the corresponding natural frequencies for the considered modes, respectively, and cc denotes the complex conjugate of prior terms. Substituting Eq. (18) into Eq. (14) and considering the solvability condition, one realizes that $A_j$ are just the slow timescale complex-valued functions (i.e., $A_1 =A_1 (T_2 )$, $A_3 =A_3 (T_2 ))$, which can be obtained by applying the solvability conditions at third order. By eliminating the secular terms, the second-order equation reduces to:

$$\begin{aligned} L(u_2 )= & {} \left( {A_1 ^{2}\hbox {e}^{2i\omega _1 T_0 }+A_1 \bar{{A}}_1 } \right) h_{11} (x)\nonumber \\&+\left( {A_3 ^{2}\hbox {e}^{2i\omega _3 T_0 }+A_3 \bar{{A}}_3 } \right) h_{13} (x)\nonumber \\&+ \left( A_3 A_1 \hbox {e}^{i(\omega _3 +\omega _1 )T_0 }\right. \nonumber \\&\left. +\, A_3 \bar{{A}}_1 \hbox {e}^{i(\omega _3 -\omega _1 )T_0 } \right) H_{31} (x) \end{aligned}$$

(19)

where $h_{1j} (x)$ and $H_{31} (x)$ are defined as follows:

$$\begin{aligned} h_{1j} (x)= & {} 2\alpha _3 \Gamma \left( {w_s ,\phi _j } \right) \phi _j ^{\prime \prime }+\alpha _3 \Gamma \left( {\phi _j ,\phi _j } \right) w_s ^{\prime \prime }\nonumber \\&+\, \frac{3\alpha _{61} V_\mathrm{D}^2 }{\left( {1-w_s } \right) ^{4}}\phi _j ^{2}-\frac{3\alpha _{62} V_\mathrm{D} ^{2}}{\left( {1+w_s } \right) ^{4}}\phi _j ^{2}\nonumber \\&+\, \frac{6\alpha _{71} }{\left( {1-w_s } \right) ^{5}}\phi _j ^{2} -\frac{6\alpha _{72} }{\left( {1+w_s } \right) ^{5}}\phi _j ^{2} \end{aligned}$$

(20)

$$\begin{aligned} H_{31} (x)= & {} 2\alpha _3 \Gamma \left( {\phi _1 ,\phi _3 } \right) w_s ^{\prime \prime }+2\alpha _3 \Gamma \left( {w_s ,\phi _1 } \right) \phi _3 ^{\prime \prime }\nonumber \\&+\, 2\alpha _3 \Gamma \left( {w_s ,\phi _3 } \right) \phi _1 ^{\prime \prime } + \frac{6\alpha _{61} V_\mathrm{D}^2 }{\left( {1-w_s } \right) ^{4}}\phi _1 \phi _3\nonumber \\&-\, \frac{6\alpha _{62} V_\mathrm{D} ^{2}}{\left( {1+w_s } \right) ^{4}}\phi _1 \phi _3 +\frac{12\alpha _{71} }{\left( {1-w_s } \right) ^{5}}\phi _1 \phi _3\nonumber \\&-\,\frac{12\alpha _{72} }{\left( {1+w_s } \right) ^{5}}\phi _1 \phi _3 \end{aligned}$$

(21)

The solution of the second-order equation can be found in the form of:

$$\begin{aligned} u_2= & {} \psi _{11} (x)A_1 ^{2}\hbox {e}^{2i\omega _1 T_0 }+\psi _{13} (x)A_3 ^{2}\hbox {e}^{2i\omega _3 T_0 }\nonumber \\&+\, \psi _3 (x)A_3 A_1 \hbox {e}^{i(\omega _3 +\omega _1 )T_0 } \nonumber \\&\times \,\psi _4 (x)A_3 \bar{{A}}_1 \hbox {e}^{i(\omega _3 -\omega _1 )T_0 }+\psi _{21} (x)A_1 \bar{{A}}_1\nonumber \\&+\, \psi _{23} (x)A_3 \bar{{A}}_3 +cc \end{aligned}$$

(22)

where $\psi _{ij} (x)$ and $\psi _j (x)$ are the solutions of the following boundary value problems [23]:

$$\begin{aligned} \vartheta (\psi _{1j} ,2\omega _j )= & {} h_{1j} (x) \end{aligned}$$

(23a)

$$\begin{aligned} \vartheta (\psi _{1j} ,2\omega _j )= & {} h_{1j} (x) \end{aligned}$$

(23b)

$$\begin{aligned} \vartheta (\psi _3 ,\omega _3 +\omega _1 )= & {} H_{31} (x) \end{aligned}$$

(23c)

$$\begin{aligned} \vartheta (\psi _4 ,\omega _3 -\omega _1 )= & {} H_{31} (x) \end{aligned}$$

(23d)

$$\begin{aligned} \psi (x=0,1)=0 \hbox { and } \psi ^{\prime }(x=0,1)=0 \end{aligned}$$

(24)

The linear differential operator $\vartheta (\psi ,\omega )$ is defined as:

$$\begin{aligned} \vartheta (\psi ,\omega )= & {} \psi ^{IV}-\omega ^{2}\psi -\alpha _4 \omega ^{2}{\psi }''\nonumber \\&-\left[ {\alpha _1 +\alpha _2 +\alpha _3 \Gamma \left( {w_s ,w_s } \right) } \right] {\psi }''\nonumber \\&- 2\alpha _3 \Gamma \left( {w_s ,\psi } \right) w_s ^{\prime \prime }-\frac{2\alpha _{61} V_\mathrm{D}^2 }{\left( {1-w_s } \right) ^{3}}\psi \nonumber \\&-\frac{2\alpha _{62} V_\mathrm{D} ^{2}}{\left( {1+w_s } \right) ^{3}}\psi \nonumber \\&-\frac{3\alpha _{71} }{\left( {1-w_s } \right) ^{4}}\psi -\frac{3\alpha _{72} }{\left( {1+w_s } \right) ^{4}}\psi \end{aligned}$$

(25)

Substituting Eqs. (18) and (22) into Eq. (15) yields:

$$\begin{aligned} L(u_3 )= & {} \left[ -i\omega _1 \left( {2{A}'_1 \left( {\phi _1 +\alpha _4 {\phi }''_1 } \right) +A_1 C\phi _1 } \right) \right. \nonumber \\&\left. +\,\chi _{11} (x)A_1 ^{2}\bar{{A}}_1 +\zeta _{13} (x)A_1 A_3 \bar{{A}}_3 \right] e^{i\omega _1 T_0 } \nonumber \\&\times \left[ -i\omega _3 \left( {2{A}'_3 \left( {\phi _3 +\alpha _4 {\phi }''_3 } \right) +A_3 C\phi _3 } \right) \right. \nonumber \\&\left. +\, \chi _{13} (x)A_3 ^{2}\bar{{A}}_3 +\zeta _{31} (x)A_3 A_1 \bar{{A}}_1 \right] e^{i\omega _3 T_0 } \nonumber \\&+\, \chi _5 (x)A_1^3 e^{3i\omega _1 T_0 }+\chi _6 (x)A_3 \bar{{A}}_1 ^{2}e^{i(\omega _3 -2\omega _1 )T_0 }\nonumber \\&+\, P_1 (x)e^{i\Omega T_2 }+cc+NST \end{aligned}$$

(26)

where ${A}'_j$ is the derivative of $A_j$ with respect to $T_2$ and NST denotes nonsecular terms. The functions $\chi _{1j}$, $\chi _j$ and $\zeta _{ij}$ are defined in “Appendix 3.” In the case of internal resonance and primary resonance of the first mode, to show the nearness of $\omega _3$ to $3\omega _1$ and $\Omega$ to $\omega _1$, detuning parameters $\sigma _1$ and $\sigma _2$ are described as:

$$\begin{aligned} \omega _3 =3\omega _1 +\varepsilon ^{2}\sigma _1 , \Omega =\omega _1 +\varepsilon ^{2}\sigma _2 \end{aligned}$$

(27)

Since the corresponding homogeneous problem of Eq. (26) has a nontrivial solution, the nonhomogeneous problem has a solution only if the right-hand side of Eq. (26) is orthogonal to every solution of the adjoint homogeneous problem governing $u_3$ [23]. Introducing Eq. (27) into Eq. (26), multiplying the right-hand side of the resulting equation by $\phi _1 (x)e^{-i\omega _1 T_0 }$ and $\phi _3 (x)e^{-i\omega _3 T_0 }$, respectively, and integrating the outcome from $x=0$ to $x=1$, the solvability conditions can be obtained as follows:

$$\begin{aligned}&2i\omega _1 \left( {m_1 {A}'_1 +\mu _1 A_1 } \right) -8S_{11} A_1 ^{2}\bar{{A}}_1 -8S_{13} A_1 A_3 \bar{{A}}_3\nonumber \\&\quad -\, 8\Lambda _1 A_3 \bar{{A}}_1^2 e^{i\sigma _1 T_2 }+Fe^{i\sigma _2 T_2 }=0 \end{aligned}$$

(28)

$$\begin{aligned}&2i\omega _3 \left( {m_3 {A}'_3 +\mu _3 A_3 } \right) -8S_{33} A_3 ^{2}\bar{{A}}_3\nonumber \\&\quad -\, 8S_{31} A_3 A_1 \bar{{A}}_1 -8\Lambda _3 A_1^3 e^{-i\sigma _1 T_2 }=0 \end{aligned}$$

(29)

where

$$\begin{aligned} \mu _j= & {} \frac{1}{2}\int _0^1 {C\phi _j ^{2}(x)\hbox {d}x} ,\nonumber \\ m_j= & {} \int _0^1 {\left( {\phi _j ^{2}(x)+\alpha _4 {\phi }''_j (x)\phi _j (x)} \right) } \hbox {d}x,\nonumber \\ S_{jj}= & {} \frac{1}{8}\int _0^1 {\chi _{1j} (x)\phi _j (x)\hbox {d}x} ,\nonumber \\ S_{ij}= & {} \frac{1}{8}\int _0^1 {\zeta _{ij} (x)\phi _i (x)\hbox {d}x} {\begin{array}{ll} &{} {i\ne j} \\ \end{array} },\nonumber \\ \Lambda _1= & {} \frac{1}{8}\int _0^1 {\chi _6 (x)\phi _1 (x)\hbox {d}x} ,\nonumber \\ \Lambda _3= & {} \frac{1}{8}\int _0^1 {\chi _5 (x)\phi _3 (x)\hbox {d}x} ,\nonumber \\ F= & {} \int _0^1 {P_1 (x)\phi _1 (x)\hbox {d}x}. \end{aligned}$$

(30)

We express $A_n$ in the polar form as follows:

$$\begin{aligned} A_n =\frac{1}{2}a_n (T_2 )e^{i\beta _n (T_2 )} \end{aligned}$$

(31)

where $a_n$ and $\beta _n$ are real-valued functions of $T_2$ representing the amplitude and the phase of the response, respectively. Substituting Eq. (31) into Eqs. (28) and (29), separating the real and imaginary parts, and introducing $\gamma _1 =\sigma _1 T_2 -3\beta _1 +\beta _2$ and $\gamma _3 =\sigma _2 T_2 -\beta _1$, the modulation equations can be expressed as:

$$\begin{aligned} \dot{a}_1= & {} -\frac{\mu _1 a_1 }{m_1 }+\frac{\Lambda _1 a_3 a_1 ^{2}}{\omega _1 m_1 }\sin \left( {\gamma _1 } \right) +\frac{F}{\omega _1 m_1 }\sin \left( {\gamma _3 } \right) \nonumber \\ \end{aligned}$$

(32)

$$\begin{aligned} \dot{a}_3= & {} -\frac{\Lambda _3 a_1 ^{3}}{\omega _3 m_3 }\sin \left( {\gamma _1 } \right) -\frac{\mu _3 a_3 }{m_3 } \end{aligned}$$

(33)

$$\begin{aligned} \dot{\gamma }_1= & {} \frac{3a_1 ^{2}S_{11} }{\omega _1 m_1 }-\frac{a_1 ^{2}S_{31} }{\omega _3 m_3 }+\frac{3a_3 ^{2}S_{13} }{\omega _1 m_1 }-\frac{a_3 ^{2}S_{33} }{\omega _3 m_3 }\nonumber \\&-\, \frac{\Lambda _3 a_1 ^{3}}{a_3 m_3 \omega _3 }\cos \left( {\gamma _1 } \right) +\frac{3\Lambda _1 a_3 a_1 }{\omega _1 m_1 }\cos \left( {\gamma _1 } \right) \nonumber \\&+\, \frac{3F_1 }{a_1 m_1 \omega _1 }\cos \left( {\gamma _3 } \right) +\sigma _1 \end{aligned}$$

(34)

$$\begin{aligned} \dot{\gamma }_3= & {} \frac{a_1 ^{2}S_{11} }{\omega _1 m_1 }+\frac{a_3 ^{2}S_{13} }{\omega _1 m_1 }+\frac{\Lambda _1 a_3 a_1 }{\omega _1 m_1 }\cos \left( {\gamma _1 } \right) \nonumber \\&+\, \frac{F_1 }{a_1 m_1 \omega _1 }\cos \left( {\gamma _3 } \right) +\sigma _2 \end{aligned}$$

(35)

where $({}^{\cdot } )$ stands for derivative with respect to $T_2$. The steady-state response can be calculated by numerically integrating Eqs. (32)–(35) or instead using the fact that $a_1$, $a_3$, $\gamma _1$ and $\gamma _3$ are constants in the steady state. Hence, the fixed points of Eqs. (32)–(35) are determined by letting $\dot{a}_1 =\dot{a}_3 =\dot{\gamma }_1 =\dot{\gamma }_3 =0$ and solving the consequent four algebraic equations numerically for $a_1$, $a_3$, $\gamma _1$ and $\gamma _3$. The stability of equilibrium solutions can be determined by evaluating the eigenvalues of the Jacobian matrix of the modulation equations at fixed points.

4.2 Principal parametric resonances of the first mode

This section investigates the principal parametric resonances of the first mode. In order to apply the method of multiple scales, the damping coefficient and the excitation amplitude are scaled as:

$$\begin{aligned} C=\varepsilon ^{2}C, \quad V_\mathrm{AC} =\varepsilon ^{2}V_\mathrm{AC} \end{aligned}$$

(36)

Substituting Eqs. (10), (11) and (36) into Eq. (6) and equating the terms of like powers of $\varepsilon$, the following results are achieved:

$$\begin{aligned}&O(\varepsilon ): \nonumber \\&L(u_1 )=D_0^2 u_1 +u_1^{IV} +\alpha _4 {\ddot{u}}''_1 -\left[ \alpha _1 +\alpha _2\right. \nonumber \\&\quad \left. +\, \alpha _3 \Gamma \left( {w_s ,w_s } \right) \right] {u}''_1 -2\alpha _3 \Gamma \left( {w_s ,u_1 } \right) w_s ^{\prime \prime }\nonumber \\&\quad -\, \frac{2\alpha _{61} V_\mathrm{D}^2 }{\left( {1-w_s } \right) ^{3}}u_1 -\frac{2\alpha _{62} V_\mathrm{D} ^{2}}{\left( {1+w_s } \right) ^{3}}u_1\nonumber \\&\quad -\,\frac{3\alpha _{71} }{\left( {1-w_s } \right) ^{4}}u_1 -\frac{3\alpha _{72} }{\left( {1+w_s } \right) ^{4}}u_1 =0 \end{aligned}$$

(37)

$$\begin{aligned}&O(\varepsilon ^{2}): \nonumber \\&L(u_2 )=-2D_0 D_1 u_1 -2\alpha _4 D_0 D_1 u_1 ^{\prime \prime }\nonumber \\&\quad +\, 2\alpha _3 \Gamma \left( {w_s ,u_1 } \right) u_1 ^{\prime \prime } +\alpha _3 \Gamma \left( {u_1 ,u_1 } \right) w_s ^{\prime \prime }\nonumber \\&\quad +\, \frac{3\alpha _{61} V_\mathrm{D}^2 }{\left( {1-w_s } \right) ^{4}}u_1^2 -\frac{3\alpha _{62} V_\mathrm{D} ^{2}}{\left( {1+w_s } \right) ^{4}}u_1 ^{2}+\frac{6\alpha _{71} }{\left( {1-w_s } \right) ^{5}}u_1 ^{2}\nonumber \\&\quad -\, \frac{6\alpha _{72} }{\left( {1+w_s } \right) ^{5}}u_1 ^{2}+2P_1 (x)\cos (\Omega T_0 ) \end{aligned}$$

(38)

$$\begin{aligned}&O(\varepsilon ^{3}): \nonumber \\&L(u_3 )=-2D_0 D_1 u_2 -D_1^2 u_1 -2D_0 D_2 u_1 \nonumber \\&\quad -\, CD_0 u_1 -\alpha _4 \left( {2D_0 D_1 {u}''_2 +2D_0 D_2 {u}''_1 +D_1^2 {u}''_1 } \right) \nonumber \\&\quad +\, 2\alpha _3 \Gamma \left( {u_1 ,u_2 } \right) w_s ^{\prime \prime } +\alpha _3 \Gamma \left( {u_1 ,u_1 } \right) {u}''_1 \nonumber \\&\quad +\, 2\alpha _3 \Gamma \left( {w_s ,u_1 } \right) u_2 ^{\prime \prime }+2\alpha _3 \Gamma \left( {w_s ,u_2 } \right) u_1 ^{\prime \prime }\nonumber \\&\quad +\, \frac{6\alpha _{61} V_\mathrm{D}^2 }{\left( {1-w_s } \right) ^{4}}u_1 u_2 -\frac{6\alpha _{62} V_\mathrm{D} ^{2}}{\left( {1+w_s } \right) ^{4}}u_1 u_2 \nonumber \\&\quad +\, \frac{12\alpha _{71} }{\left( {1-w_s } \right) ^{5}}u_1 u_2 -\frac{12\alpha _{72} }{\left( {1+w_s } \right) ^{5}}u_1 u_2 \nonumber \\&\quad +\, \frac{4\alpha _{61} V_\mathrm{D}^2 }{\left( {1-w_s } \right) ^{5}}u_1^3+ \frac{4\alpha _{62} V_\mathrm{D} ^{2}}{\left( {1+w_s } \right) ^{5}}u_1 ^{3}+\frac{10\alpha _{71} }{\left( {1-w_s } \right) ^{6}}u_1 ^{3}\nonumber \\&\quad +\, \frac{10\alpha _{72} }{\left( {1+w_s } \right) ^{6}}u_1 ^{3}+4P_2 (x)\cos (\Omega T_0 ) \end{aligned}$$

(39)

where

$$\begin{aligned} P_2 \left( x \right) =\frac{\alpha _{61} V_\mathrm{D} V_\mathrm{AC} }{\left( {1-w_s } \right) ^{3}} \end{aligned}$$

(40)

The modulation equations can be found by implementing the procedure similar to that in Sect. 4.1. To avoid repetition and also for the sake of brevity, the complete scheme is not stated here (see the details in “Appendix 4”). The modulation equations in the presence of the principal parametric resonances of the first mode can be expressed as:

$$\begin{aligned} \dot{a}_1= & {} -\frac{\mu _1 a_1 }{m_1 }+\frac{\Lambda _1 a_3 a_1 ^{2}\sin \left( {\gamma _1 } \right) }{m_1 \omega _1 }+\frac{K_1 a_1 \sin \left( {\gamma _3 } \right) }{m_1 \omega _1 }\nonumber \\&-\, \frac{K_2 a_3 \sin \left( {\gamma _3 } \right) \cos \left( {\gamma _1 } \right) }{m_1 \omega _1 } + \frac{K_2 a_3 \cos \left( {\gamma _3 } \right) \sin \left( {\gamma _1 } \right) }{m_1 \omega _1 }\nonumber \\ \end{aligned}$$

(41)

$$\begin{aligned} \dot{a}_3= & {} -\frac{\mu _3 a_3 }{m_3 }-\frac{\Lambda _2 a_1 ^{3}\sin \left( {\gamma _1 } \right) }{\omega _3 m_3 }+\frac{K_3 a_1 \sin \left( {\gamma _3 } \right) \cos \left( {\gamma _1 } \right) }{\omega _3 m_3 }\nonumber \\&-\, \frac{K_3 a_1 \cos \left( {\gamma _3 } \right) \sin \left( {\gamma _1 } \right) }{\omega _3 m_3 } \end{aligned}$$

(42)

$$\begin{aligned} \dot{\gamma }_1= & {} 3\frac{a_1 ^{2}S_{11} }{m_1 \omega _1 }-\frac{a_1 ^{2}S_{31} }{\omega _3 m_3 }+3\frac{a_3 ^{2}S_{13} }{m_1 \omega _1 }-\frac{a_3 ^{2}S_{33} }{\omega _3 m_3 }\nonumber \\&-\, \frac{\Lambda _3 a_1 ^{3}\cos \left( {\gamma _1 } \right) }{a_3 m_3 \omega _3 }+3\frac{a_3 a_1 \cos \left( {\gamma _1 } \right) \Lambda _1 }{m_1 \omega _1 }\nonumber \\&+\, 3\frac{K_1 \cos \left( {\gamma _3 } \right) }{m_1 \omega _1 }+3\frac{K_2 a_3 \cos \left( {\gamma _3 } \right) \cos \left( {\gamma _1 } \right) }{a_1 m_1 \omega _1 }\nonumber \\&+\, 3\frac{K_2 a_3 \sin \left( {\gamma _3 } \right) \sin \left( {\gamma _1 } \right) }{a_1 m_1 \omega _1 }- \frac{K_3 a_1 \cos \left( {\gamma _3 } \right) \cos \left( {\gamma _1 } \right) }{a_3 m_3 \omega _3 }\nonumber \\&-\, \frac{K_3 a_1 \sin \left( {\gamma _3 } \right) \sin \left( {\gamma _1 } \right) }{a_3 m_3 \omega _3 }+\sigma _1 \end{aligned}$$

(43)

$$\begin{aligned} \dot{\gamma }_3= & {} 2\frac{a_3 a_1 \cos \left( {\gamma _1 } \right) \Lambda _1 }{m_1 \omega _1 }+2\frac{a_1 ^{2}S_{11} }{m_1 \omega _1 }\nonumber \\&+\, 2\frac{a_3 ^{2}S_{13} }{m_1 \omega _1 }+\sigma _2 +2\frac{K_1 \cos \left( {\gamma _3 } \right) }{m_1 \omega _1 }\nonumber \\&+\, 2\frac{K_2 a_3 \cos \left( {\gamma _3 } \right) \cos \left( {\gamma _1 } \right) }{a_1 m_1 \omega _1 } +2\frac{K_2 a_3 \sin \left( {\gamma _3 } \right) \sin \left( {\gamma _1 } \right) }{a_1 m_1 \omega _1 }\nonumber \\ \end{aligned}$$

(44)

where $({}^{\cdot })$ stands for derivative with respect to $T_2$. According to the modulation equations, there are two possibilities of solutions: trivial response and nontrivial response. The stability of the nontrivial periodic solutions can be determined by evaluating the eigenvalues of the Jacobian matrix of modulation equations at fixed points. It is convenient to determine the stability of the trivial fixed points from the Cartesian form of the modulation equation rather than the polar form. Introducing $A_n =\frac{1}{2}\left( {p_n (T_2 )-iq_n (T_2 )} \right) e^{i\nu _n (T_2 )}$ into Eqs. (55) and (56) and separating the real and imaginary parts, modulation equation in the Cartesian form can be obtained as:

$$\begin{aligned} \dot{p}_1= & {} -\frac{\mu _1 p_1 }{m_1 }+\frac{K_1 q_1 }{m_1 \omega _1 }-\frac{K_2 q_3 }{m_1 \omega _1 }+2\frac{\Lambda _1 q_1 p_1 p_3 }{m_1 \omega _1 }\nonumber \\&-\, \nu _1 q_1 -\frac{S_{11} q_1 }{m_1 \omega _1 }\left( {p_1 ^{2}+q_1 ^{2}} \right) \nonumber \\&-\, \frac{S_{13} q_1 }{m_1 \omega _1 }\left( {p_3 ^{2}+q_3 ^{2}} \right) -\frac{q_3 \Lambda _1 }{m_1 \omega _1 }\left( {p_1 ^{2}-q_1 ^{2}} \right) \end{aligned}$$

(45)

$$\begin{aligned} \dot{q}_1= & {} -\frac{\mu _1 q_1 }{m_1 }+\frac{K_1 p_1 }{m_1 \omega _1 }+\frac{p_3 K_2 }{m_1 \omega _1 }+2\frac{q_3 \Lambda _1 q_1 p_1 }{m_1 \omega _1 }\nonumber \\&+\, \nu _1 p_1 +\frac{S_{11} p_1 }{m_1 \omega _1 }\left( {p_1 ^{2}+q_1 ^{2}} \right) \nonumber \\&+\, \frac{S_{13} p_1 }{m_1 \omega _1 }\left( {p_3 ^{2}+q_3 ^{2}} \right) +\frac{p_3 \Lambda _1 }{m_1 \omega _1 }\left( {p_1 ^{2}+q_1 ^{2}} \right) \end{aligned}$$

(46)

$$\begin{aligned} {} \dot{p}_3= & {} -\frac{\mu _3 p_3 }{m_3 }-\frac{K_3 q_1 }{\omega _3 m_3 }-\nu _3 q_2 -\frac{S_{31} q_3 }{\omega _3 m_3 }\left( {p_1 ^{2}+q_1 ^{2}} \right) \nonumber \\&-\, \frac{S_{33} q_3 }{\omega _3 m_3 }\left( {p_3 ^{2}+q_3 ^{2}} \right) - \frac{\Lambda _2 q_1 }{\omega _3 m_3 }\left( {3p_1 ^{2}-q_1 ^{2}} \right) \end{aligned}$$

(47)

$$\begin{aligned} \dot{q}_3= & {} -\frac{\mu _3 q_3 }{m_3 }+\frac{K_3 p_1 }{\omega _3 m_3 }+\nu _3 p_3 +\frac{\Lambda _3 p_1 }{\omega _3 m_3 }\left( {p_1 ^{2}-3q_1 ^{2}} \right) \nonumber \\&+\, \frac{S_{31} p_3 }{\omega _3 m_3 }\left( {p_1 ^{2}+q_1 ^{2}} \right) + \frac{S_{33} p_3 }{\omega _3 m_3 }\left( {p_3 ^{2}+q_3 ^{2}} \right) \end{aligned}$$

(48)

where $\nu _1 =\frac{1}{2}\sigma _2$ and $\nu _3 =\frac{3}{2}\sigma _2 -\sigma _1$. The stability of the trivial fixed points can be determined by evaluating the eigenvalues of the Jacobian matrix of Eqs. (45)–(48) at trivial state $p_1 =q_1 =p_3 =q_3 =0$.

5 Results and discussion

In this section, the numerical results are presented. The numerical simulations are performed for the case study of the PZT-5H nanobeam of $L=108\hbox { nm}$, $b=6\hbox { nm}$, $h=5\hbox { nm}$, $l_u =80\hbox { nm}$, $l_d =5\hbox { nm}$, $g_0 =4\hbox { nm}$. The mechanical properties of the case study nanobeam are adopted from [28]. The nondimensional natural frequencies of the considered nanoresonator are evaluated as functions of piezoelectric actuation voltage, for specific values of DC voltages and system parameters (the dependency of the nanobeam natural frequency on the DC and the piezoelectric actuation voltages is also apparent from the $K_{ij}$ expression; “Appendix 2”). The results are illustrated in Table 1 for the two first symmetric modes.

In addition, the variation of the natural frequencies ratio of the two first symmetric modes with piezoelectric actuation voltage is illustrated in Fig. 2.

Fig. 2

Variations of two first symmetric mode natural frequencies ratio $(\omega _{3}/\omega _{1})$ with piezoelectric actuation voltage, for $V_\mathrm{DC}=1v$ and $V_\mathrm{DC}=1.5v$

It is noticed that a three-to-one internal resonance (i.e., $\omega _3 \approx 3\omega _1$; the highlighted narrow zone in Fig. 2) is tuned for two different sets of system parameters $V_\mathrm{DC} =1\hbox { v}$, $V_\mathrm{P} =0.2\hbox { v}$ and $V_\mathrm{DC} =1.5\hbox { v}$, $V_\mathrm{P} =0.239\hbox { v}$. For these values of parameters, it is assumed that there are no other nonlinear interactions among the higher modes and the investigation is limited to the following resonances of the first mode in the presence of internal resonance: (a) primary resonance (i.e., $\Omega \approx \omega _1 )$ and (b) principal parametric resonance (i.e., $\Omega \approx 2\omega _1 )$. The equilibrium and dynamic solutions are obtained by numerically solving the modulation and the ROM equations of motion, respectively. Specifically, the frequency/force response curves are provided by finding the stationary values of the modulation equations obtained from the direct perturbation technique and the dynamic solutions in terms of time histories, phase portraits, Poincare sections and FFT diagrams are provided by direct time integration of ROM equations obtained from Galerkin method.

5.1 The case of $\Omega \approx \omega _{1}$

Figures 3 and 4 illustrate the typical frequency response curves for the first and second symmetric modes of the nanoresonator as functions of detuning parameter $\sigma _2$, near the primary resonance of the first mode. The corresponding system parameters are $V_\mathrm{DC} =1\hbox { v}$, $V_\mathrm{P} =0.2\hbox { v}$, $V_\mathrm{AC} =0.09\hbox { v}$ and $\sigma _1 =0.2463$. It is noted that the quality factor is equal to $Q=1000$ and is related to damping coefficient by $Q={\omega _1 }/C$. In these figures, the solid lines and the blue dotted lines represent the stable and the unstable response branches, respectively, and the small red circles denote unstable foci. An enlarged part of Fig. 3 is also presented to provide a detailed frequency response diagram.

Fig. 3

Frequency response curve of the first mode in the presence of internal resonance when $\Omega \approx \omega _1$, and for system parameters $V_\mathrm{DC} =1\hbox { v}$, $V_\mathrm{P} =0.2\hbox { v}$, $V_\mathrm{AC} =0.09\hbox { v}$ and $\sigma _1 =0.2463$. Solid lines represent stable solutions, blue dotted lines represent saddle-nodes, and red circles represent unstable foci. (Color figure online)

Fig. 4

Frequency response curve of the second symmetric mode in the presence of internal resonance when $\Omega \approx \omega _1$, and for system parameters $V_\mathrm{DC} =1\hbox { v}$, $V_\mathrm{P} =0.2\hbox { v}$, $V_\mathrm{AC} =0.09\hbox { v}$ and $\sigma _1 =0.2463$. Solid lines represent stable solutions, blue dotted lines represent saddle-nodes, and red circles represent unstable foci. (Color figure online)

The figures exhibit a hardening spring-type behavior. According to the figures, there are multiple solutions in the frequency response curves when $0.3937<\sigma _2 <3.4301$. The response of the nanoresonator settles on either of the stable branches depending on the initial conditions. Hence, the system may experience nonlinear dynamic phenomena such as jump and hysteresis in this region. As the detuning parameter $\sigma _2$ increases from small values, the amplitude of the stable response increases monotonically in both modes until it reaches the value of $\sigma _2 \approx 0.39$, where the amplitude of the first mode drops slowly until it reaches the point A. On the other hand, Fig. 4 shows a rise in the amplitude of the second symmetric mode response over the same detuning parameter range. A steady increase in amplitude of the third mode coincided with a decrease in first mode amplitude and exhibits an energy transfer from the first mode to the third mode due to the internal resonance. At point A $(\sigma _2 =\hbox {0.4738})$, the solution loses its stability through a saddle-node bifurcation. With further decrease in the detuning parameter, the unstable solution regains stability through the saddle-node bifurcation point B $(\sigma _2 =\hbox {0.417}1)$. For increasing $\sigma _2$ beyond point B, the amplitude of the first mode rises steadily, while the amplitude of the third mode drops continuously. It is noted that, in this region, the energy is transferred back from the second symmetric mode to the first symmetric mode. As $\sigma _2$ increases beyond the point C $(\sigma _2 =\hbox {0.5190})$, the system response loses its stability via a Hopf bifurcation where one pair of complex conjugate eigenvalues of the Jacobian matrix crosses the imaginary axis into the right-half plane. The unstable solution branch regains its stability via a reverse Hopf bifurcation at point D $(\sigma _2 =\hbox {0.5881})$. It is worth mentioning that numerous numerical simulations are needed to reveal the characteristic of the response in this region. The numerical results are presented in the following sections to highlight the dynamical features of this region. As the detuning parameter is increased further, this new stable equilibrium solution encounters a saddle-node bifurcation point at E $(\sigma _2 =\hbox {3.430}1)$ and loses its stability where the response jumps to the lower stable equilibrium manifold. With further decrease in $\sigma _2$, the motion regains stability at point F $(\sigma _2 =0.3937)$, where a saddle-node bifurcation takes place. It is noted that the directly excited first mode dominates the indirectly excited second mode. Frequency response curves of the nanoresonator near the primary resonance of the first mode for the system parameters $V_\mathrm{DC} =1.5\hbox { v}$, $V_\mathrm{P} =0.239\hbox { v}$, $V_\mathrm{AC} =0.09\hbox { v}$ and $\sigma _1 =0.2403$ are shown in Figs. 5 and 6.

Fig. 5

Frequency response curve of the first mode in the presence of internal resonance when $\Omega \approx \omega _1$, and for system parameters $V_\mathrm{DC} =1.5\hbox { v}$, $V_\mathrm{P} =0.239\hbox { v}$, $V_\mathrm{AC} =0.09\hbox { v}$ and $\sigma _1 =0.2403$. Solid lines represent stable solutions, blue dotted lines represent saddle-nodes, and red circles represent unstable foci. (Color figure online)

Fig. 6

Frequency response curve of the second symmetric mode in the presence of internal resonance when $\Omega \approx \omega _1$, and for system parameters $V_\mathrm{DC} =1.5\hbox { v}$, $V_\mathrm{P} =0.239\hbox { v}$, $V_\mathrm{AC} =0.09\hbox { v}$ and $\sigma _1 =0.2403$. Solid lines represent stable solutions, blue dotted lines represent saddle-nodes, and red circles represent unstable foci. (Color figure online)

As it is seen, the frequency response curves are totally different from the curves of Figs. 3 and 4. Overall, frequency response curves are tilted to the right, which represents a hardening-like behavior and the nonlinear response includes two-mode solution. It is noted that there exist four stable two-mode branches in the frequency range $0.4069<\sigma _2 <{3.3513}$, which results in a relatively wide multivalued region. The response settles on either of the stable branches depending on the initial conditions. Referring to Figs. 5 and 6, as the detuning parameter $\sigma _2$ increases, the response amplitude increases steadily for both modes until it reaches the first saddle-node bifurcation point A $(\sigma _2 ={3.35})$ and loses stability. The amplitude of this unstable branch decreases continuously for the first mode until the second saddle-node bifurcation point occurs at B $(\sigma _2 =1{.17})$, and the motion regains its stability, whereas the amplitude of the second symmetric mode increases steadily in this frequency range. The stable two-mode solution loses stability via a Hopf bifurcation at C $(\sigma _2 =1{.21})$ and retrieves stability via a reverse Hopf Bifurcation at D $(\sigma _2 =1.32)$. In the frequency range between the Hopf bifurcation points C and D, a more precise investigation is required to characterize the dynamic behavior of the motion. With further increase in $\sigma _2$, the stable manifold loses stability through the saddle-node bifurcation E $(\sigma _2 =2{.65})$. As the detuning parameter decreases even further, the amplitude of the unstable branch decreases accordingly until the saddle-node point F is reached at $\sigma _2 =0.41$, and the motion recovers its stability. It is noted that the contribution of the indirectly excited mode to the nonlinear response is considerable in this case which highlights the role of the three-to-one internal resonance.

Figure 7 shows the effect of DC voltage actuation on the internal resonance of the nanobeam in the neighborhood of primary resonance of the first mode for the system parameters $V_\mathrm{P} =0.2\hbox { v}$ and $V_\mathrm{AC} =0.09\hbox { v}$. Frequency response curves in the case of lower DC voltage actuation $V_\mathrm{DC} =0.9\hbox { v}$ and $\sigma _1 =-0.1293$ are shown in Fig. 7a, b for the first and the second symmetric modes, respectively.

Fig. 7

Influence of the DC voltage level on the frequency response curves in the presence of internal resonance when $\Omega \approx \omega _1$, $V_\mathrm{P} =0.2\hbox { v}$ and $V_\mathrm{AC} =0.09\hbox { v}$: a, b two first symmetric modes with system parameters $V_\mathrm{DC} =0.9\hbox { v}$ and $\sigma _1 =-0.1293$; c, d two first symmetric modes with system parameters $V_\mathrm{DC} =1.1\hbox { v}$ and $\sigma _1 =0.6778$. Solid lines represent stable solutions, blue dotted lines represent saddle-nodes, and red circles represent unstable foci. (Color figure online)

Fig. 8

Influence of the piezoelectric actuation voltage on the frequency response curves in the presence of internal resonance when $\Omega \approx \omega _1$, $V_\mathrm{DC} =1\hbox { v}$ and $V_\mathrm{AC} =0.09\hbox { v}$: a, b two first symmetric modes with system parameters $V_\mathrm{P} =0.17\hbox { v}$ and $\sigma _1 =2.2853$; c, d two first symmetric modes with system parameters $V_\mathrm{P} =0.23\hbox { v}$ and $\sigma _1 =-1.7972$. Solid lines represent stable solutions, and blue dotted lines represent saddle-nodes. (Color figure online)

It follows that decreasing the DC voltage load significantly alters the locus of the bifurcation points (significantly shifted toward the $\sigma _2 =0)$. Besides, the hysteresis loop narrows $(0.37<\sigma _2 <2.83)$ and jump phenomena take place at lower values of detuning parameter. It is noted that the Hopf bifurcation points totally vanish in the upper stable branch. As it is seen, the amplitude of the both directly and indirectly excited modes are reduced in this case. It could be due to the fact that decreasing the DC voltage load weakens the effect of nonlinear electrostatic term and increases the geometric nonlinearity effect. In more general sense, changing the DC voltage will alter the natural frequencies of the nanobeam, and as a result, it alters the detuning parameter $\sigma _1$ and consequently the nonlinear response of the nanobeam. Frequency response curves in the case of higher DC voltage actuation $V_\mathrm{DC} =1.1\hbox { v}$ and $\sigma _1 =0.6778$ are shown in Fig. 7c, d for the first and the second symmetric modes, respectively. While these curves are similar in shape to that of the lower DC voltage load (Figs. 3, 4), all the bifurcation points take place at higher values of detuning parameter $\sigma _2$. The unstable interval between the two Hopf bifurcation points is also increased $(0.8009<\sigma _2 <{1.049}2)$. It is evident that the multivalued region of the response takes place in a wider range of the detuning parameter $({0.4161}<\sigma _2 <{3.9289})$. As it is seen, the amplitude of the both directly and indirectly excited modes is amplified and the nonlinear interaction due to the three-to-one internal resonance is strengthened compared to the case of $V_\mathrm{DC} =1\hbox { v}$ (Figs. 3 and 4). It is also due to the fact that changing the detuning parameter $\sigma _1$ directly modifies the nonlinear behavior of the response.

Fig. 9

Force response curves of the a first mode and b second symmetric mode in the presence of internal resonance when $\Omega \approx \omega _1$ and for system parameters $V_\mathrm{DC} =1\hbox { v}$, $V_\mathrm{P} =0.2\hbox { v}$, $\sigma _1 =0.2463$ and $\sigma _2 =1$. Solid lines represent stable solutions, blue dotted lines represent saddle-nodes, and red circles represent unstable foci. (Color figure online)

Figure 8 illustrates the influence of the piezoelectric actuation voltage on the frequency response curves of the two first symmetric modes when $\Omega \approx \omega _1$ and system parameters are $V_\mathrm{DC} =1\hbox { v}$ and $V_\mathrm{AC} =0.9\hbox { v}$. Frequency response curves in the case of lower piezoelectric voltage actuation $V_\mathrm{P} =0.17\hbox { v}$ and $\sigma _1 =2.2853$ are shown in Fig. 8a, b. As it is seen, the response of the both modes resembles those of the case with the absence of modal interaction with the exception of the emergence of a very small region in the response of the indirectly excited mode in the range of ${0.7}<\sigma _2 <0{.85}$ which depicts the slight role of the three-to-one internal resonance. It is due to the fact that changing the piezoelectric actuation voltage alters the detuning parameter $\sigma _1$ and consequently violates the perfect conditions of internal resonance. It is noted that the response amplitude of the directly excited mode is decreased, while the response amplitude of the indirectly excited mode is increased compared to the case of Figs. 3 and 4. It follows from Fig. 8 that decreasing the piezoelectric actuation voltage vanishes the small multivalued region and saddle-node bifurcation points in the upper stable branch of the response and makes the hysteresis loop narrower. Another significant difference is disappearance of the Hopf bifurcation points C and D and the associated unstable region.

Frequency response curves in the case of higher piezoelectric voltage actuation $V_\mathrm{P} =0.23\hbox { v}$ and $\sigma _1 =-1.7972$ are shown in Fig. 8c, d for the first and the second symmetric modes, respectively. While these curves are similar in nature and shape to those of lower piezoelectric actuation load $(V_\mathrm{DC} =0.17\hbox { v})$, the response amplitude of the both directly and indirectly excited modes is decreased compared to the case of Figs. 3 and 4. It follows that the response amplitude of the second symmetric mode is decreased more profoundly compared to the first mode. As it is seen, the hysteresis loop range is influenced much less in this case compared to the previous case. According to Fig. 8, piezoelectric excitation amplitude significantly affects modal interactions. It is seen that any slight variation of the piezoelectric actuation voltage could cause drastic changes in the overall system response, since it directly alters the internal resonance detuning parameter $\sigma _1$ which could violate the perfect internal resonance conditions. Thus, it could be considered as a powerful design parameter to control internal resonances of a piezoelectric NEMS resonator.

Figure 9 shows the characteristic curves of the response amplitude versus the excitation amplitude $V_\mathrm{AC}$ corresponding to static loading of Fig. 3 and $\sigma _2 =1$ for the two first symmetric modes. As the excitation amplitude $V_\mathrm{AC}$ increases from small values, the amplitude of the stable response increases steadily for both modes until it reaches point A $(V_\mathrm{AC} =0.36\hbox { v})$, where the response loses its stability through a saddle-node bifurcation and jumps to one of the two other branches of stable equilibrium solutions depending on the initial conditions.

The stability is regained at saddle-node bifurcation B $(V_\mathrm{AC} =0.049\hbox { v})$. With further increase of excitation amplitude, the stable response loses stability via a Hopf bifurcation at C $(V_\mathrm{AC} =0.21\hbox { v})$ and recovers stability via a reverse Hopf bifurcation at D $(V_\mathrm{AC} =0.31\hbox { v})$. As $V_\mathrm{AC}$ amplitude is increased further, the new stable solution loses stability at saddle-node bifurcation E $(V_\mathrm{AC} =0.48\hbox { v})$, where a sudden jump takes place to the other stable solution. As the excitation amplitude decreases from high values, the response settles on the stable branch. With further decrease in $V_\mathrm{AC}$ amplitude, the response loses stability at saddle-node bifurcation point F $(V_\mathrm{AC} =0.24\hbox { v})$ where it jumps to one of the two other branches of stable equilibrium solutions depending on initial conditions. It is noted that there is an upper bound for the response of the indirectly excited mode, while there is no limit for the response of the directly excited mode which could result in dynamic pull-in for higher values of $V_\mathrm{AC}$.

Figure 10 illustrates the typical force response curves of the two first symmetric modes with $\sigma _2 =2$ and static loading of Fig. 5. As the excitation amplitude $V_\mathrm{AC}$ increases from small values, the amplitude of the stable response increases for both modes until it reaches point A $(V_\mathrm{AC} =0.97\hbox { v})$, where the response loses stability through a saddle-node bifurcation and jumps to the upper stable branch.

Fig. 10

Force response curves of the a first mode and b second symmetric mode in the presence of internal resonance when $\Omega \approx \omega _1$ and for system parameters $V_\mathrm{DC} =1.5\hbox { v}$, $V_\mathrm{P} =0.239\hbox { v}$, $\sigma _1 =0.2403$ and $\sigma _2 =2$. Solid lines represent stable solutions, and blue dotted lines represent saddle-nodes. (Color figure online)

As the excitation amplitude decreases from high values, the stable response amplitude decreases continuously until the saddle-node bifurcation point D $(V_\mathrm{AC} =0.07\hbox { v})$ is reached, where the response jumps to one of the two other branches of stable equilibrium solutions depending on the initial conditions. It is noted that a segment of stable solution $(0.11\hbox { v}<V_\mathrm{AC} \hbox {<0.15 v})$ is separated by two saddle-node bifurcations at B and C. It follows from Fig. 10 that there is an upper bound for response of the indirectly excited mode, while there is no bound for response of the directly excited mode in this case.

Figure 11 illustrates typical system response in terms of time traces, phase portraits and Poincare sections at $\sigma _2 =0.2$ for system parameters $V_\mathrm{DC} =1\hbox { v}$, $V_\mathrm{P} =0.2\hbox { v}$, $V_\mathrm{AC} =0.09\hbox { v}$, and $\sigma _1 =0.2463$ corresponding to a point on the stable branch of frequency response curves of Figs. 3 and 4.

Fig. 11

Mixed response in the two first symmetric modes in the presence of internal resonance when $\Omega \approx \omega _1$, and for system parameters $V_\mathrm{DC} =1\hbox { v}$, $V_\mathrm{P} =0.2\hbox { v}$, $V_\mathrm{AC} =0.09\hbox { v}$, $\sigma _1 =0.2463$ and $\sigma _2 =0.2$: a, b time traces of the $q_1$ and $q_3$, respectively; c, d phase portraits of the $q_1$ and $q_3$ respectively; e, f Poincare maps of the $q_1$ and $q_3$, respectively

This figure reveals that after long transients, system experiences a mixed response, periodic behavior in the first symmetric mode and quasiperiodic in the second symmetric mode. It is noted that the quasiperiodic nature of the second symmetric mode is indicated by the mild beating effect of the time history and the closed loop form of the Poincare map (Fig. 11f). Further along the same branch of the frequency response curves, at $\sigma _2 =0.52$ in the vicinity of the Hopf bifurcation point C, the response becomes quasiperiodic as shown in Fig. 12. This figure depicts time histories, phase portraits, Poincare sections and FFTs of the two first symmetric modes.

Fig. 12

Quasiperiodic response in the two first symmetric modes in the presence of internal resonance when $\Omega \approx \omega _1$, and for system parameters $V_\mathrm{DC} =1\hbox { v}$, $V_\mathrm{P} =0.2\hbox { v}$, $V_\mathrm{AC} =0.09\hbox { v}$, $\sigma _1 =0.2463$ and $\sigma _2 =0.52$: a, b time traces of the $q_1$ and $q_3$, respectively; c, d phase portraits of the $q_1$ and $q_3$ respectively; e, f Poincare maps of the $q_1$ and $q_3$, respectively; g, h FFTs of the $q_1$ and $q_3$, respectively

The quasiperiodic behavior of the response is more prominent in the second symmetric mode as it is shown in the time traces (Fig. 12a, b) and phase portraits (Fig. 12c, d). The system response exhibits beating phenomenon in the both modes as shown in the time traces which results in a continuous energy exchange between the associated modes. Moreover, FFTs of the response indicate that $\omega _1$ is the dominant resonance frequency in the response of the directly excited mode, and $3\omega _1$ is the dominant resonance frequency in the response of the indirectly excited mode. Furthermore, the FFT shows asymmetric sideband frequencies near the dominant peaks indicating nonlinear interactions and presence of modulated quasiperiodic motions in the system. It is worth mentioning that FFT power spectra of the response show some other harmonics in the response (due to quasiperiodic behavior of the motion) which is not presented in this paper. For the higher values of the detuning parameter, the response remains quasiperiodic in both modes, and a similar behavior is noticed in the region between the Hopf bifurcation points C and D (the results have not been presented to avoid repetition).

Figure 13 shows the system behavior at $\sigma _2 =0.2$ for system parameters $V_\mathrm{DC} =1.5\hbox { v}$, $V_\mathrm{P} =0.239\hbox { v}$, $V_\mathrm{AC} =0.09\hbox { v}$ and $\sigma _1 =0.2403$ corresponding to the typical frequency response curves shown in Figs. 5 and 6, in terms of time traces, phase portraits and Poincare maps. The system experiences a mixed behavior in this case.

Fig. 13

Mixed response in the two first symmetric modes in the presence of internal resonance when $\Omega \approx \omega _1$, and for system parameters $V_\mathrm{DC} =1.5\hbox { v}$, $V_\mathrm{P} =0.239\hbox { v}$, $V_\mathrm{AC} =0.09\hbox { v}$, $\sigma _1 =0.2403$ and $\sigma _2 =0.2$: a, b time traces of the $q_1$ and $q_3$, respectively; c, d phase portraits of the $q_1$ and $q_3$, respectively; e, f Poincare maps of the $q_1$ and $q_3$, respectively

The response is periodic in the first symmetric mode while a beating effect in the time history (Fig. 13b), and a closed loop curve in the Poincare map (Fig. 13f) exhibits a quasiperiodic behavior in the second symmetric mode. It is noted that, further along a same branch, the response remains periodic in the first mode and quasiperiodic in the second symmetric mode. For instance, at $\sigma _2 =1.9598$ (corresponding to a point on the stable branch, settled between the bifurcation points D and E), system exhibits a mixed behavior, a periodic response in the directly excited mode and a quasiperiodic response in the indirectly excited mode as shown in Fig. 14. It is worth mentioning that time history apparently shows a beating effect in the second symmetric mode. The rich dynamic behaviors (periodic, quasiperiodic and mixed response) observed in the motion illustrate the intense effect of the modal interactions on the system response.

Fig. 14

Mixed response in the two first symmetric modes in the presence of internal resonance when $\Omega \approx \omega _1$, and for system parameters $V_\mathrm{DC} =1.5\hbox { v}$, $V_\mathrm{P} =0.239\hbox { v}$, $V_\mathrm{AC} =0.09\hbox { v}$, $\sigma _1 =0.2403$ and $\sigma _2 =1.9598$: a, b time traces of the $q_1$ and $q_3$, respectively; c, d phase portraits of the $q_1$ and $q_3$, respectively; e, f Poincare maps of the $q_1$ and $q_3$, respectively; g, h FFTs of the $q_1$ and $q_3$, respectively

5.2 The case of $\Omega \approx$ 2$\omega _{1}$

Frequency response curves of the piezoelectric nanobeam near the principal parametric resonance of the first mode are depicted in Figs. 15 and 16 for the first and second symmetric modes, respectively. Response of the nanoresonator is investigated for $V_\mathrm{DC} =1\hbox { v}$, $V_\mathrm{P} =0.2\hbox { v}$, $V_\mathrm{AC} =0.9\hbox { v}$, and $\sigma _1 =0.2463$. The parametric frequency response curves consist of one trivial branch and two nontrivial steady-state branches, and they represent a hardening-like behavior. As it is seen, there exists a sharp transition between the trivial response and the large amplitude subharmonic responses due to the parametric excitation. As detuning parameter $\sigma _2$ increases from small values, the response of the system remains trivial until it reaches the supercritical pitchfork bifurcation point A ($\sigma _2 =-1.08)$ where the parametric response is activated.

At this point, the trivial solution loses stability and the solution jumps up to the new stable nontrivial branch. As $\sigma _2$ increases further, the response amplitude increases along the nontrivial branch until the saddle-node bifurcation B $(\sigma _2 =3.29)$ is reached and the stability gets lost. As the detuning parameter decreases, the response turns stable through the saddle-node bifurcation C $(\sigma _2 =1.95)$. With further increase in detuning parameter, the stable branch loses stability through a Hopf bifurcation at D $(\sigma _2 =5.07)$ and regains stability through a reverse Hopf bifurcation at E $(\sigma _2 =5.22)$. As it is seen, the trivial solution turns stable through the supercritical bifurcation point F $(\sigma _2 =1.08)$, and another unstable nontrivial solution appears in the response. For high values of the detuning parameter, there is no bound for the amplitude of the directly excited mode and the amplitude increases steadily until a dynamic pull-in takes place in the system. However, the amplitude of the indirectly excited mode is almost around an upper bound. It is noted that the applied methods in this paper (bifurcation techniques and Taylor series expansion) are not capable of accurate investigation of the system response near the dynamic pull-in.

In Figs. 17 and 18, the frequency response curves of the two first symmetric modes were obtained for $V_\mathrm{DC} =1.5\hbox { v}$, $V_\mathrm{P} =0.239\hbox { v}$, $V_\mathrm{AC} =0.9\hbox { v}$, and $\sigma _1 =0.2403$ while $\Omega \approx 2\omega _1$. As it is seen, the response of the both modes resembles those of the case with the absence of internal resonance with the exception of the interaction of the stable and unstable nontrivial branches in the response of the indirectly excited mode at $\sigma _2 =4.65$. As the detuning parameter $\sigma _2$ increases from small values, amplitude of the both modes increases steadily and there is no bound for the response amplitudes. It is noted that the directly excited mode dominates the indirectly excited mode, and the role of the three-to-one internal resonance is ignorable in this case.

Figure 19 shows the effect of DC voltage actuation on the principal parametric resonance of the nanobeam in the presence of the internal resonance for the system parameters $V_\mathrm{P} =0.2\hbox { v}$ and $V_\mathrm{AC} =0.09\hbox { v}$. Frequency response curves in the case of lower DC voltage actuation $V_\mathrm{DC} =0.9\hbox { v}$ and $\sigma _1 =-0.1293$ are shown in Fig. 19a, b for the first and the second symmetric modes, respectively.

These figures show that decreasing the DC voltage level narrows the trivial solution instability range $(-0.94<\sigma _2 <0.94)$ and affects the pitchfork bifurcation points’ loci. It is noted that the Hopf bifurcation points totally vanish in the nontrivial stable branch. As it is seen, the amplitude of the parametric response of both directly and indirectly excited modes is reduced and nonlinear interactions are weakened compared to the case of $V_\mathrm{DC} =1\hbox { v}$ (Figs. 15, 16). Frequency response curves in the case of higher DC voltage actuation $V_\mathrm{DC} =1.1\hbox { v}$ and $\sigma _1 =0.6778$ are shown in Fig. 19c, d for the two first symmetric modes. While these curves are similar in shape to that of Figs. 15 and 16, all the bifurcation points take place at higher values of detuning parameter $\sigma _2$.

Fig. 15

Frequency response curve of the first mode in the presence of internal resonance when $\Omega \approx 2\omega _1$ and for system parameters $V_\mathrm{DC} =1\hbox { v}$, $V_\mathrm{P} =0.2\hbox { v}$, $V_\mathrm{AC} =0.9\hbox { v}$ and $\sigma _1 =0.2463$. Solid lines represent stable solutions, blue dotted lines represent saddle-nodes, and red circles represent unstable foci. (Color figure online)

Fig. 16

Frequency response curve of the second symmetric mode in the presence of internal resonance when $\Omega \approx 2\omega _1$ and for system parameters $V_\mathrm{DC} =1\hbox { v}$, $V_\mathrm{P} =0.2\hbox { v}$, $V_\mathrm{AC} =0.9\hbox { v}$ and $\sigma _1 =0.2463$. Solid lines represent stable solutions, blue dotted lines represent saddle-nodes, and red circles represent unstable foci. (Color figure online)

Fig. 17

Frequency response curve of the first mode in the presence of internal resonance when $\Omega \approx 2\omega _1$ and for system parameters $V_\mathrm{DC} =1.5\hbox { v}$, $V_\mathrm{P} =0.239\hbox { v}$, $V_\mathrm{AC} =0.9\hbox { v}$ and $\sigma _1 =0.2403$. Solid lines represent stable solutions, and blue dotted lines represent saddle-nodes. (Color figure online)

Fig. 18

Frequency response curve of the second symmetric mode in the presence of internal resonance when $\Omega \approx 2\omega _1$, and for system parameters $V_\mathrm{DC} =1.5\hbox { v}$, $V_\mathrm{P} =0.239\hbox { v}$, $V_\mathrm{AC} =0.9\hbox { v}$ and $\sigma _1 =0.2403$. Solid lines represent stable solutions, and blue dotted lines represent saddle-nodes. (Color figure online)

The trivial solution instability range is broadened in this case $(-1.23<\sigma _2 <1.23)$. Moreover, the unstable interval between the two Hopf bifurcation points is also increased $(7.2<\sigma _2 <7{.81})$. It is evident that the multivalued region of the response takes place in a wider range of the detuning parameter. As it is seen, the amplitude of both directly and indirectly excited modes are amplified, and nonlinear interactions due to the three-to-one internal resonance are enhanced compared to the case of $V_\mathrm{DC} =1\hbox { v}$.

Fig. 19

Influence of the DC voltage level on the frequency response curves in the presence of internal resonance when $\Omega \approx 2\omega _1$, $V_\mathrm{P} =0.2\hbox { v}$ and $V_\mathrm{AC} =0.9\hbox { v}$: (a, b) two first symmetric modes with system parameters $V_\mathrm{DC} =0.9\hbox { v}$ and $\sigma _1 =-0.1293$; (c, d) two first symmetric modes with system parameters $V_\mathrm{DC} =1.1\hbox { v}$ and $\sigma _1 =0.6778$. Solid lines represent stable solutions, blue dotted lines represent saddle-nodes, and red circles represent unstable foci. (Color figure online)

Figure 20 illustrates the influence of the piezoelectric actuation voltage on the frequency response curves of the two first symmetric modes in the presence of the internal resonance when $\Omega \approx 2\omega _1$ and system parameters are $V_\mathrm{DC} =1\hbox { v}$ and $V_\mathrm{AC} =0.9\hbox { v}$. Frequency response curves in the case of lower piezoelectric voltage actuation $V_\mathrm{P} =0.17\hbox { v}$ and $\sigma _1 =2.2853$ are shown in Fig. 20a, b. As it is seen, the response of both modes is similar to those of Figs. 15 and 16 with the exception of the emergence of a very small region in the unstable nontrivial branch of the indirectly excited mode in the range of $2.18<\sigma _2 <2.55$ which highlights the role of the three-to-one internal resonance in this case. It is noted that the response amplitude of the both directly and indirectly excited modes increases compared to the case of Figs. 15 and 16. These figures show that decreasing the piezoelectric actuation voltage enhances the modal interaction in the presence of the three-to-one internal resonance. It is noted that decreasing the piezoelectric voltage level broadens the multivalued region in the upper nontrivial branch $(5.45<\sigma _2 <9.26)$ and increases the unstable response range between the two Hopf bifurcation points $(8.12<\sigma _2 <10.01)$. Frequency response curves in the case of higher piezoelectric voltage actuation $V_\mathrm{DC} =0.23\hbox { v}$ and $\sigma _1 =-1.7972$ are shown in Fig. 20c, d for the first and the second symmetric modes, respectively.

Fig. 20

Influence of the piezoelectric actuation voltage on the frequency response curves in the presence of internal resonance when $\Omega \approx 2\omega _1$, $V_\mathrm{DC} =1\hbox { v}$ and $V_\mathrm{AC} =0.9\hbox { v}$: a, b two first symmetric modes with system parameters $V_\mathrm{P} =0.17\hbox { v}$ and $\sigma _1 =2.2853$; c, d two first symmetric modes with system parameters $V_\mathrm{P} =0.23\hbox { v}$ and $\sigma _1 =-1.7972$. Solid lines represent stable solutions, blue dotted lines represent saddle-nodes, and red circles represent unstable foci. (Color figure online)

Fig. 21

Amplitude versus coefficient $K_1$ of the a first mode and b second symmetric mode in the presence of internal resonance when $\Omega \approx 2\omega _1$ and for system parameters $V_\mathrm{DC} =1\hbox { v}$, $V_\mathrm{P} =0.2\hbox { v}$, $\sigma _1 =0.2463$ and $\sigma _2 =2$. Solid lines represent stable solutions, and blue dotted lines represent saddle-nodes. (Color figure online)

The response of both modes resembles those of the case with the absence of modal interaction with the exception of the emergence of a very small region in the response of the indirectly excited mode in the range of $-1.04<\sigma _2 <-0.9$ which shows the minor role of the three-to-one internal resonance. It is noted that the response amplitude of the directly excited mode is not influenced very much, while the response amplitude of the indirectly excited mode is decreased remarkably compared to the case of Figs. 15 and 16. It follows that increasing the piezoelectric actuation voltage vanishes the small multivalued region and saddle-node bifurcation points in the stable nontrivial branch of the response. Another significant difference is disappearance of the Hopf bifurcation points C and D and the associated unstable region. This figure shows that increasing the piezoelectric actuation voltage weakens the modal interaction in the presence of the three-to-one internal resonance. It is also due to the fact that changing the piezoelectric actuation voltage can directly change the natural frequencies of the nanobeam and consequently the internal detuning parameter $\sigma _1$. According to Fig. 20, piezoelectric excitation amplitude significantly affects modal interactions. It is seen that the variation of the piezoelectric actuation voltage significantly affects the system parametric response. Thus, it could be considered as a powerful design parameter to control parametric internal resonances of a piezoelectric NEMS resonator.

Figure 21 shows the characteristic curves of the response amplitude versus $K_1$ corresponding to static loading of Fig. 15 and $\sigma _2 =2$ for the two first symmetric modes. It is worth mentioning that $K_1$ denotes the terms produced due to external harmonic load (see “Appendix 3”).

As $K_1$ increases from small values, the amplitude remains zero until it reaches a subcritical pitchfork bifurcation at $K_1 =52.18$ where the parametric response is activated and a sudden jump takes place from this point to the upper stable branch. By reversing this procedure, the solution decreases slowly along the upper branch as it reaches the saddle-node bifurcation point ($K_1 =17.59)$, where it experiences a jump to a stable branch depending on the initial conditions. It is noted that there exists a multivalued region in the upper stable branch confined between two saddle-node bifurcation points in the range of $17.59<K_1 <29.26$ which highlights the effect of three-to-one internal resonance.

According to the figure, there is an upper bound for the response of the indirectly excited mode, while there is no limit for the response of the directly excited mode for high values of $K_1$.

Figure 22 shows system response in terms of time traces, phase portraits, Poincare sections and FFT diagrams at $\sigma _2 =1$ for system parameters $V_\mathrm{DC} =1\hbox { v}$, $V_\mathrm{P} =0.2\hbox { v}$, $V_\mathrm{AC} =0.9\hbox { v}$, and $\sigma _1 =0.2463$ corresponding to a point on the stable nontrivial branch of parametric frequency response curves of Figs. 15 and 16.

Fig. 22

Quasiperiodic response in the two first symmetric modes in the presence of internal resonance when $\Omega \approx 2\omega _1$ and for system parameters $V_\mathrm{DC} =1\hbox { v}$, $V_\mathrm{P} =0.2\hbox { v}$, $V_\mathrm{AC} =0.9\hbox { v}$, $\sigma _1 =0.2463$ and $\sigma _2 =1$: a, b time traces of the $q_1$ and $q_3$, respectively; c, d phase portraits of the $q_1$ and $q_3$, respectively; e, f Poincare maps of the $q_1$ and $q_3$, respectively; g, h FFTs of the $q_1$ and $q_3$, respectively

The system illustrates a quasiperiodic response in both modes. While the time history and phase portrait of the first mode do not indicate much about the response nature, Poincare section and FFT diagram (Fig. 22e, g) show a mild quasiperiodic motion in this mode. The quasiperiodic behavior of the second symmetric mode is dominant, and it is apparent from the beating effect of the time history (Fig. 22b). For higher values of the detuning parameter, typically at $\sigma _2 =3.5$, response becomes periodic in the first mode, while it remains quasiperiodic in the second symmetric mode, as shown in Fig. 23. It is noted that increasing the detuning parameter $\sigma _2$ weakens the strength of the quasiperiodic motion, as it makes the response of the first mode periodic and weakens the quasiperiodic nature of the second symmetric mode (Fig. 23b, e).

Fig. 23

Mixed response in the two first symmetric modes in the presence of internal resonance when $\Omega \approx 2\omega _1$ and for system parameters $V_\mathrm{DC} =1\hbox { v}$, $V_\mathrm{P} =0.2\hbox { v}$, $V_\mathrm{AC} =0.9\hbox { v}$, $\sigma _1 =0.2463$ and $\sigma _2 =3.5$: a, b time traces of the $q_1$ and $q_3$, respectively; c, d phase portraits of the $q_1$ and $q_3$, respectively; e, f Poincare maps of the $q_1$ and $q_3$, respectively; g, h FFTs of the $q_1$ and $q_3$, respectively

Fig. 24

Quasiperiodic response in the two first symmetric modes in the presence of internal resonance when $\Omega \approx 2\omega _1$ and for system parameters $V_\mathrm{DC} =1.5\hbox { v}$, $V_\mathrm{P} =0.239\hbox { v}$, $V_\mathrm{AC} =0.9\hbox { v}$, $\sigma _1 =0.2403$ and $\sigma _2 =0.5$: a, b time traces of the $q_1$ and $q_3$, respectively; c, d phase portraits of the $q_1$ and $q_3$, respectively; e, f Poincare maps of the $q_1$ and $q_3$, respectively; g, h FFTs of the $q_1$ and $q_3$, respectively

Figure 24 shows the system behavior at $\sigma _2 =0.5$ for system parameters $V_\mathrm{DC} =1.5\hbox { v}$, $V_\mathrm{P} =0.239\hbox { v}$, $V_\mathrm{AC} =0.9\hbox { v}$ and $\sigma _1 =0.2403$ corresponding to the typical parametric frequency response curves shown in Figs. 17 and 18, in terms of time traces, phase portraits, Poincare maps and FFT diagrams. As it is seen, the system experiences a quasiperiodic motion. The quasiperiodic behavior of the response is more prominent in the second symmetric mode as it is shown in the time traces (Fig. 24a, b) and phase portraits (Fig. 24c, d). It is noted that there exists an energy exchange between the two modes due to the beating phenomenon. It follows from the FFT diagram (Fig. 24h) that the energy in the second symmetric mode is mostly concentrated around the first and the third resonance frequencies.

6 Conclusions

In this paper, the nonlinear oscillations of an electrostatically actuated clamped–clamped piezoelectric nanoresonator in the presence of the three-to-one resonance were studied. The governing equation of motion incorporating surface effects and van der Waals forces was discretized using the Galerkin method. The multiple scales method was applied directly to the nonlinear equation of motion and associated boundary conditions to obtain the modulation equations of the amplitudes and phases of the two first symmetric modes, while the first mode was excited through the primary and principal parametric resonance, respectively. Frequency response and force response curves were obtained in the presence of three-to-one internal resonance for different system parameters. Stability and bifurcations of equilibrium solutions were investigated for each case. Results show different dynamic phenomena such as hardening type behaviors, jumps, fold and pitchfork bifurcations in the system response. Furthermore, existence of Hopf bifurcations, and also complex multivalued regions in the equilibrium solutions, highlights the role of internal resonance on the system response. A detailed study was carried out to investigate the influence of different parameters on the internal resonance. Results illustrate that decreasing the DC voltage level weakens the internal resonance, while increasing the DC voltage level enhances the modal interactions. Moreover, it was shown that any variation of the piezoelectric actuation voltage weakens the strength of modal interactions, while the primary resonance is activated. The results also revealed that, in the case of principal parametric resonance, decreasing the piezoelectric actuation voltage increases the modal interactions due to internal resonance. Alternatively, increasing the piezoelectric actuation voltage decreases the strength of modal interactions. These are due to the fact that changing the DC and piezoelectric actuation voltages changes the natural frequencies of the nanobeam which directly alters the internal detuning parameter $\sigma _1$. This could either violate or enhance the perfect conditions of internal resonance. It was shown that the piezoelectric actuation voltage could be considered as a powerful design parameter to control the internal resonances of a piezoelectric NEMS resonator. Different dynamic behaviors of the system were presented in terms of time traces, phase portraits, Poincare maps and FFT diagrams. Periodic, quasiperiodic and mixed responses were observed in the motion which highlights the role of modal interactions due to internal resonance. The presented modeling approach can be used in the design and optimization of novel NEMS resonators, and also the provided results can give an insight into how modal interactions can affect the stability and the resonant responses of NEMS resonators.

Appendices

Appendix 1

$$\begin{aligned}&\Gamma \left( {f_1 (x,t),f_2 (x,t)} \right) =\int _0^1 {\frac{\partial f_1 }{\partial x}\cdot \frac{\partial f_2 }{\partial x}\hbox {d}x} , \\&\alpha _1 =\frac{F_p L^{2}}{({\textit{EI}})_\mathrm{eff} },\alpha _2 =\frac{F_S L^{2}}{({\textit{EI}})_\mathrm{eff} }, \alpha _3 =\frac{({\textit{EI}})_\mathrm{eff} g_0 }{2({\textit{EI}})_\mathrm{eff} },\\&\alpha _4 =\frac{2\nu I\rho ^{s}}{hL^{2}(\rho A)_\mathrm{eff} }, \alpha _5 =\frac{cL^{2}}{\sqrt{(\rho A)_\mathrm{eff} ({\textit{EI}})_\mathrm{eff} }},\\&\alpha _6 =\frac{1}{2}\frac{\varepsilon bC_n L^{4}}{g_0^3 ({\textit{EI}})_\mathrm{eff} }, \alpha _7 =\frac{\tilde{A}bL^{4}}{6\pi g_0^4 ({\textit{EI}})_\mathrm{eff} },\\&H_1 (x)=H \left( x-\frac{L-l_u }{2L}\right) -H \left( x-\frac{L+l_u }{2L}\right) ,\\&H_2 (x)=H \left( x-\frac{L-l_d }{2L}\right) -H\left( x-\frac{L+l_d }{2L}\right) ,\\&\alpha _{61} =\alpha _6 H_1 (x), \alpha _{62} =\alpha _6 H_2 (x),\\&\alpha _{71} =\alpha _7 H_1 (x), \alpha _{72} =\alpha _7 H_2 (x) \end{aligned}$$

where $\tilde{A}$ is the Hamaker constant and H(x) is the Heaviside function. $F_p$ and $F_S$ are axial forces due to piezoelectric actuation and surface effects, respectively. $C_n$ is a nondimensional coefficient to consider the fringing field effects. For more details, one may see Ref. [28].

Appendix 2

$$\begin{aligned} M_{ij}= & {} \int _0^1 {\varphi _i \varphi _j } \hbox {d}x+\alpha _4 \int _0^1 {\varphi _i {\varphi }''_j } \hbox {d}x\\ C_{ij}= & {} \alpha _5 \int _0^1 {\varphi _i \varphi _j } \hbox {d}x\\ K_{ij}= & {} \int _0^1 \varphi _i \varphi _j^{IV} \hbox {d}x-\left[ {\alpha _1 +\alpha _2 +\alpha _3 \Gamma \left( {w_s ,w_s } \right) } \right] \\&\int _0^1 \varphi _i {\varphi }''_j \hbox {d}x -2\alpha _3 \Gamma \left( {w_s ,\varphi _j } \right) \\&\int _0^1 \varphi _i {w}''_s \hbox {d}x-2\alpha _6 V_\mathrm{D} ^{2}\\&\times \int _{lba}^{uba}\frac{\varphi _i \varphi _j }{\left( {1-w_s } \right) ^{3}}\hbox {d}x-2\alpha _6 V_\mathrm{D} ^{2}\int _{lbd}^{ubd} \frac{\varphi _i \varphi _j }{\left( {1+w_s } \right) ^{3}}\hbox {d}x \\&-\, 3\alpha _7 \int _{lba}^{uba} \frac{\varphi _i \varphi _j }{\left( {1-w_s } \right) ^{4}}\hbox {d}x-3\alpha _7 \int _{lbd}^{ubd} \frac{\varphi _i \varphi _j }{\left( {1+w_s } \right) ^{4}}\hbox {d}x \\ K_{ijk}= & {} -2\alpha _3 \Gamma \left( {w_s ,\varphi _j } \right) \int _0^1 \varphi _i {\varphi }''_k \hbox {d}x\\&-\, \alpha _3 \Gamma \left( {\varphi _j ,\varphi _k } \right) \int _0^1 \varphi _i {w}''_s\hbox {d}x\\&-3\alpha _6 V_\mathrm{D} ^{2}\int _{lba}^{uba} \frac{\varphi _i \varphi _j \varphi _k }{\left( {1-w_s } \right) ^{4}}\hbox {d}x\\&+\, 3\alpha _6 V_\mathrm{D} ^{2}\int _{lbd}^{ubd} \frac{\varphi _i \varphi _j \varphi _k }{\left( {1+w_s } \right) ^{4}}\hbox {d}x\\&-\, 6\alpha _7 \int _{lba}^{uba} \frac{\varphi _i \varphi _j \varphi _k }{\left( {1-w_s } \right) ^{5}}\hbox {d}x+6\alpha _7 \int _{lbd}^{ubd} \frac{\varphi _i \varphi _j \varphi _k }{\left( {1+w_s } \right) ^{5}}\hbox {d}x \\ K_{ijkl}= & {} -\alpha _3 \Gamma \left( {\varphi _j ,\varphi _k } \right) \int _0^1 \varphi _i {\varphi }''_l \hbox {d}x-4\alpha _6 V_\mathrm{D} ^{2}\\&\times \int _{lba}^{uba}\frac{\varphi _i \varphi _j \varphi _k \varphi _l }{\left( {1-w_s } \right) ^{5}}\hbox {d}x -4\alpha _6 V_\mathrm{D} ^{2}\int _{lbd}^{ubd} \frac{\varphi _i \varphi _j \varphi _k \varphi _l }{\left( {1+w_s } \right) ^{5}}\hbox {d}x\\&-\, 10\alpha _7 \int _0^1\frac{\varphi _i \varphi _j \varphi _k \varphi _l }{\left( {1-w_s } \right) ^{6}}\hbox {d}x-10\alpha _7 \int _0^1 \frac{\varphi _i \varphi _j \varphi _k \varphi _l }{\left( {1+w_s } \right) ^{6}}\hbox {d}x \\ F_i (t)= & {} 2\alpha _6 V_\mathrm{D} V_\mathrm{AC} \cos (\Omega t)\int _{lba}^{uba} \frac{\varphi _i }{\left( {1-w_s } \right) ^{2}}\hbox {d}x\\&+\, 4\alpha _6 V_\mathrm{D} V_\mathrm{AC} \cos (\Omega t)\sum _{j=1}^n {\left( {q_j \int _{lbd}^{ubd} \frac{\varphi _j \varphi _i }{\left( {1-w_s } \right) ^{3}}\hbox {d}x} \right) }. \end{aligned}$$

Appendix 3

$$\begin{aligned} \chi _{1j}= & {} 2\alpha _3 \Gamma \left( {\psi _{1j} ,\varphi _j } \right) {w}''_s +4\alpha _3 \Gamma \left( {\psi _{2j} ,\varphi _j } \right) {w}''_s\\&+\, 2\alpha _3 \Gamma \left( {w_s ,\psi _{1j} } \right) {\varphi }''_j +4\alpha _3 \Gamma \left( {w_s ,\psi _{2j} } \right) {\varphi }''_j\\&+\, 3\alpha _3 \Gamma \left( {\varphi _j ,\varphi _j } \right) {\varphi }''_j +2\alpha _3 \Gamma \left( {w_s ,\varphi _j } \right) {\psi }''_{1j}\\&+\, 4\alpha _3 \Gamma \left( {w_s ,\varphi _j } \right) {\psi }''_{2j} +6\alpha _{61} V_\mathrm{D} ^{2}\frac{\varphi _1 \psi _{1j} }{\left( {1-w_s } \right) ^{4}}\\&+\, 12\alpha _{61} \frac{\varphi _j \psi _{2j} }{\left( {1-w_s } \right) ^{4}}+12\alpha _{61} V_\mathrm{D} ^{2}\frac{\varphi _j^3 }{\left( {1-w_s } \right) ^{5}}\\&-\, 6\alpha _{62} V_\mathrm{D} ^{2}\frac{\varphi _j \psi _{1j} }{\left( {1+w_s } \right) ^{4}}-12\alpha _{62} V_\mathrm{D} ^{2}\frac{\varphi _j \psi _{2j} }{\left( {1+w_s } \right) ^{4}} \\&+\, 12\alpha _{62} V_\mathrm{D} ^{2}\frac{\varphi _j^3 }{\left( {1+w_s } \right) ^{5}}+12\alpha _{71} \frac{\varphi _j \psi _{1j} }{\left( {1-w_s } \right) ^{5}}\\&+\, 24\alpha _{71} \frac{\varphi _j \psi _{2j} }{\left( {1-w_s } \right) ^{5}}\\&+\, 30\alpha _{71} \frac{\varphi _j^3 }{\left( {1-w_s } \right) ^{6}}-12\alpha _{72} \frac{\varphi _j \psi _{1j} }{\left( {1+w_s } \right) ^{5}} \\&-\, 24\alpha _{72} \frac{\varphi _j \psi _{2j} }{\left( {1+w_s } \right) ^{5}} +30\alpha _{72} \frac{\varphi _j^3 }{\left( {1+w_s } \right) ^{6}} \end{aligned}$$

$$\begin{aligned} \zeta _{ij}= & {} 2\alpha _3 \Gamma \left( {\psi _3 ,\varphi _j } \right) {w}''_s +2\alpha _3 \Gamma \left( {\psi _4 ,\varphi _j } \right) {w}''_s\\&+\, 4\alpha _3 \Gamma \left( {\psi _{2j} ,\varphi _i } \right) {w}''_s +2\alpha _3 \Gamma \left( {w_s ,\psi _3 } \right) {\varphi }''_j \\&2\alpha _3 \Gamma \left( {w_s ,\psi _4 } \right) {\varphi }''_j +4\alpha _3 \Gamma \left( {w_s ,\psi _{2j} } \right) {\varphi }''_i\\&+\, 2\alpha _3 \Gamma \left( {w_s ,\varphi _j } \right) {\psi }''_3 +2\alpha _3 \Gamma \left( {w_s ,\varphi _j } \right) {\psi }''_4 \\&+\, 4\alpha _3 \Gamma \left( {w_s ,\varphi _i } \right) {\psi }''_{2j} +2\alpha _3 \Gamma \left( {\varphi _j ,\varphi _j } \right) \varphi _i\\&+\, 4\alpha _3 \Gamma \left( {\varphi _i ,\varphi _j } \right) \varphi _j +6\alpha _{61} V_\mathrm{D} ^{2}\frac{\varphi _j \psi _3 }{\left( {1-w_s } \right) ^{4}}\\&+\, 6\alpha _{61} V_\mathrm{D} ^{2}\frac{\varphi _j \psi _4 }{\left( {1-w_s } \right) ^{4}}+12\alpha _{61} V_\mathrm{D} ^{2}\frac{\varphi _i \psi _{2j} }{\left( {1-w_s } \right) ^{4}}\\&+\, 24\alpha _{61} V_\mathrm{D} ^{2}\frac{\varphi _j^2 \varphi _i }{\left( {1-w_s } \right) ^{5}}-6\alpha _{62} V_\mathrm{D} ^{2}\frac{\varphi _j \psi _3 }{\left( {1+w_s } \right) ^{4}}\\&-\, 6\alpha _{62} V_\mathrm{D} ^{2}\frac{\varphi _j \psi _4 }{\left( {1+w_s } \right) ^{4}}-12\alpha _{62} V_\mathrm{D} ^{2}\frac{\varphi _i \psi _{2j} }{\left( {1+w_s } \right) ^{4}}\\&+\, 24\alpha _{62} V_\mathrm{D} ^{2}\frac{\varphi _j^2 \varphi _i }{\left( {1+w_s } \right) ^{5}}+12\alpha _{71} V_\mathrm{D} ^{2}\frac{\varphi _j \psi _3 }{\left( {1-w_s } \right) ^{5}}\\&+\, 12\alpha _{71} V_\mathrm{D} ^{2}\frac{\varphi _j \psi _4 }{\left( {1-w_s } \right) ^{5}}+24\alpha _{71} V_\mathrm{D} ^{2}\frac{\varphi _i \psi _{2j} }{\left( {1-w_s } \right) ^{5}}\\&+\, 60\alpha _{71} V_\mathrm{D} ^{2}\frac{\varphi _j^2 \varphi _i }{\left( {1-w_s } \right) ^{6}}-12\alpha _{72} V_\mathrm{D} ^{2}\frac{\varphi _j \psi _3 }{\left( {1+w_s } \right) ^{5}}\\&-\, 12\alpha _{72} V_\mathrm{D} ^{2}\frac{\varphi _j \psi _4 }{\left( {1+w_s } \right) ^{5}}-24\alpha _{72} V_\mathrm{D} ^{2}\frac{\varphi _i \psi _{2j} }{\left( {1+w_s } \right) ^{5}}\\&+\, 60\alpha _{72} V_\mathrm{D} ^{2}\frac{\varphi _j^2 \varphi _i }{\left( {1+w_s } \right) ^{6}} \\ \chi _5= & {} 2\alpha _3 \Gamma \left( {\psi _{11} ,\varphi _1 } \right) {w}''_s +2\alpha _3 \Gamma \left( {w_s ,\psi _{11} } \right) {\varphi }''_1\\&+\, 2\alpha _3 \Gamma \left( {w_s ,\varphi _1 } \right) {\psi }''_{11} +\alpha _3 \Gamma \left( {\varphi _1 ,\varphi _1 } \right) {\varphi }''_1 \\&+\, 6\alpha _{61} V_\mathrm{D} ^{2}\frac{\varphi _1 \psi _{11} }{\left( {1-w_s } \right) ^{4}}+4\alpha _{61} V_\mathrm{D} ^{2}\frac{\varphi _1^3 }{\left( {1-w_s } \right) ^{5}}\\&-\, 6\alpha _{62} V_\mathrm{D} ^{2}\frac{\varphi _1 \psi _{11} }{\left( {1+w_s } \right) ^{4}}+4\alpha _{62} V_\mathrm{D} ^{2}\frac{\varphi _1^3 }{\left( {1+w_s } \right) ^{5}} \\&+\, 12\alpha _{71} V_\mathrm{D} ^{2}\frac{\varphi _1 \psi _{11} }{\left( {1-w_s } \right) ^{5}}+10\alpha _{71} V_\mathrm{D} ^{2}\frac{\varphi _1^3 }{\left( {1-w_s } \right) ^{6}}\\&-\, 12\alpha _{72} V_\mathrm{D} ^{2}\frac{\varphi _1 \psi _{11} }{\left( {1+w_s } \right) ^{5}}+10\alpha _{72} V_\mathrm{D} ^{2}\frac{\varphi _1^3 }{\left( {1+w_s } \right) ^{6}} \\ \chi _6= & {} 2\alpha _3 \Gamma \left( {\psi _4 ,\varphi _1 } \right) {w}''_s\\&+\, 2\alpha _3 \Gamma \left( {\psi _{11} ,\varphi _3 } \right) {w}''_s +2\alpha _3 \Gamma \left( {w_s ,\psi _4 } \right) {\varphi }''_1\\&+\, 2\alpha _3 \Gamma \left( {w_s ,\psi _{11} } \right) {\varphi }''_3 +2\alpha _3 \Gamma \left( {w_s ,\varphi _1 } \right) {\psi }''_4 \\&+\, 2\alpha _3 \Gamma \left( {w_s ,\varphi _3 } \right) {\psi }''_{11}\\&+\, \alpha _3 \Gamma \left( {\varphi _1 ,\varphi _1 } \right) {\varphi }''_3 +\alpha _3 \Gamma \left( {\varphi _3 ,\varphi _1 } \right) {\varphi }''_1\\&+\, 6\alpha _{61} V_\mathrm{D} ^{2}\frac{\varphi _1 \psi _4 }{\left( {1-w_s } \right) ^{4}}+6\alpha _{61} V_\mathrm{D} ^{2}\frac{\varphi _3 \psi _{11} }{\left( {1-w_s } \right) ^{4}} \\&+\, 12\alpha _{61} V_\mathrm{D} ^{2}\frac{\varphi _3 \varphi _1^2 }{\left( {1-w_s } \right) ^{5}}-6\alpha _{62} V_\mathrm{D} ^{2}\frac{\varphi _1 \psi _4 }{\left( {1+w_s } \right) ^{4}}\\&-\, 6\alpha _{62} V_\mathrm{D} ^{2}\frac{\varphi _3 \psi _{11} }{\left( {1+w_s } \right) ^{4}}+12\alpha _{62} V_\mathrm{D} ^{2}\frac{\varphi _3 \varphi _1^2 }{\left( {1+w_s } \right) ^{5}} \\&+\, 12\alpha _{71} V_\mathrm{D} ^{2}\frac{\varphi _1 \psi _4 }{\left( {1-w_s } \right) ^{5}}+12\alpha _{71} V_\mathrm{D} ^{2}\frac{\varphi _3 \psi _{11} }{\left( {1-w_s } \right) ^{5}}\\&+\, 30\alpha _{71} V_\mathrm{D} ^{2}\frac{\varphi _3 \varphi _1^2 }{\left( {1-w_s } \right) ^{6}}-12\alpha _{72} V_\mathrm{D} ^{2}\frac{\varphi _1 \psi _4 }{\left( {1+w_s } \right) ^{5}}\\&-\, 12\alpha _{72} V_\mathrm{D} ^{2}\frac{\varphi _3 \psi _{11} }{\left( {1+w_s } \right) ^{5}}+30\alpha _{72} V_\mathrm{D} ^{2}\frac{\varphi _3 \varphi _1^2 }{\left( {1+w_s } \right) ^{6}} \end{aligned}$$

$$\begin{aligned} k_1= & {} 2\alpha _3 \Gamma \left( {w_s ,\varphi _1 } \right) {\psi }''_5\\&+\, 2\alpha _3 \Gamma \left( {w_s ,\psi _5 } \right) {\varphi }''_1 +2\alpha _3 \Gamma \left( {\psi _5 ,\varphi _1 } \right) {w}''_s\\&+\, 2\alpha _{61} \frac{V_\mathrm{D} V_\mathrm{AC} \varphi _1 }{\left( {1-w_s } \right) ^{3}}+6\alpha _{61} \frac{\varphi _1 \psi _5 }{\left( {1-w_s } \right) ^{4}}\\&-\, 6\alpha _{62} \frac{\varphi _1 \psi _5 }{\left( {1+w_s } \right) ^{4}}+12\alpha _{71} \frac{\varphi _1 \psi _5 }{\left( {1-w_s } \right) ^{5}}\\&-\, 12\alpha _{71} \frac{\varphi _1 \psi _5 }{\left( {1+w_s } \right) ^{5}} \\ k_2= & {} 2\alpha _3 \Gamma \left( {w_s ,\varphi _3 } \right) {\psi }''_5\\&+\, 2\alpha _3 \Gamma \left( {w_s ,\psi _5 } \right) {\varphi }''_3 +2\alpha _3 \Gamma \left( {\psi _5 ,\varphi _3 } \right) {w}''_s\\&+2\alpha _{61} \frac{V_\mathrm{D} V_\mathrm{AC} \varphi _3 }{\left( {1-w_s } \right) ^{3}}+6\alpha _{61} \frac{\varphi _3 \psi _5 }{\left( {1-w_s } \right) ^{4}} \\&-\, 6\alpha _{62} \frac{\varphi _3 \psi _5 }{\left( {1+w_s } \right) ^{4}}+12\alpha _{71} \frac{\varphi _3 \psi _5 }{\left( {1-w_s } \right) ^{5}}\\&-\, 12\alpha _{71} \frac{\varphi _3 \psi _5 }{\left( {1+w_s } \right) ^{5}}. \end{aligned}$$

Appendix 4

The boundary conditions at all orders are identical to that obtained in Eq. (17). The first-order equation given in Eq. (37) is similar to Eq. (13); thus, the general solution of $u_1$ can be expressed as in Eq. (18). By introducing Eq. (18) in Eq. (38), the second-order equation reduces to:

$$\begin{aligned} L(u_2 )= & {} \left( {A_1 ^{2}\hbox {e}^{2i\omega _1 T_0 }+A_1 \bar{{A}}_1 } \right) h_{11} (x)\nonumber \\&+\left( {A_3 ^{2}\hbox {e}^{2i\omega _3 T_0 }+A_3 \bar{{A}}_3 } \right) h_{13} (x)\nonumber \\&+ \left( {A_3 A_1 \hbox {e}^{i(\omega _3 +\omega _1 )T_0 }+A_3 \bar{{A}}_1 \hbox {e}^{i(\omega _3 -\omega _1 )T_0 }} \right) \nonumber \\&\times H_{31} (x) +2P_1 (x)\cos (\Omega T_0 ) \end{aligned}$$

(49)

where $h_{1j} (x)$ and $H_{31} (x)$ are defined in Eqs. (20) and (21). The solution of the second-order equation can be found in the form of:

$$\begin{aligned} u_2= & {} \psi _{11} (x)A_1 ^{2}\hbox {e}^{2i\omega _1 T_0 }\nonumber \\&+\, \psi _{13} (x)A_3 ^{2}\hbox {e}^{2i\omega _3 T_0 }+\psi _3 (x)A_3 A_1 \hbox {e}^{i(\omega _3 +\omega _1 )T_0 } \nonumber \\&\times \psi _4 (x)A_3 \bar{{A}}_1 \hbox {e}^{i(\omega _3 -\omega _1 )T_0 }+\psi _{21} (x)A_1 \bar{{A}}_1\nonumber \\&+\,\psi _{23} (x)A_3 \bar{{A}}_3 +\psi _5 (x)\left( {\hbox {e}^{i\Omega T_0 }+\hbox {e}^{-i\Omega T_0 }} \right) +cc\nonumber \\ \end{aligned}$$

(50)

where $\psi _{ij} (x)$, $\psi _3 (x)$ and $\psi _4 (x)$ are the solutions of Eqs. (23a) and (24) and $\psi _5 (x)$ is the solution of following boundary value problem:

$$\begin{aligned}&\psi _5^{IV} -\Omega ^{2}\psi _5 -\alpha _4 \Omega ^{2}{\psi }''_5\nonumber \\&\quad -\, \left[ {\alpha _1 +\alpha _2 +\alpha _3 \Gamma \left( {w_s ,w_s } \right) } \right] \nonumber \\&\quad \times {\psi }''_5 -2\alpha _3 \Gamma \left( {w_s ,\psi _5 } \right) w_s ^{\prime \prime }\nonumber \\&\quad -\, \frac{2\alpha _{61} V_\mathrm{D}^2 }{\left( {1-w_s } \right) ^{3}}\psi _5 -\frac{2\alpha _{62} V_\mathrm{D}^{2}}{\left( {1+w_s } \right) ^{3}}\psi _5\nonumber \\&\quad -\, \frac{3\alpha _{71} }{\left( {1-w_s } \right) ^{4}}\psi _5 -\frac{3\alpha _{72} }{\left( {1+w_s } \right) ^{4}}\psi _5 =P_1 (x) \end{aligned}$$

(51)

$$\begin{aligned}&\psi _5 (x=0,1)=0 \hbox { and }\psi _5 ^{\prime }(x=0,1)=0 \end{aligned}$$

(52)

Substituting Eqs. (18) and (50) into Eq. (39) yields:

$$\begin{aligned} L(u_3 )= & {} \left[ -i\omega _1 \left( {2{A}'_1 \left( {\phi _1 +\alpha _4 {\phi }''_1 } \right) +A_1 C\phi _1 } \right) \right. \nonumber \\&\left. +\, \chi _{11} (x)A_1 ^{2}\bar{{A}}_1 +\zeta _{13} (x)A_1 A_3 \bar{{A}}_3 \right] e^{i\omega _1 T_0 } \nonumber \\&\times \left[ -i\omega _3 \left( {2{A}'_3 \left( {\phi _3 +\alpha _4 {\phi }''_3 } \right) +A_3 C\phi _3 } \right) \right. \nonumber \\&\left. +\, \chi _{13} (x)A_3 ^{2}\bar{{A}}_3 +\zeta _{31} (x)A_3 A_1 \bar{{A}}_1 \right] e^{i\omega _3 T_0 }\nonumber \\&+\, \chi _5 (x)A_1^3 e^{3i\omega _1 T_0 }+\chi _6 (x)A_3 \bar{{A}}_1 ^{2}e^{i(\omega _3 -2\omega _1 )T_0 }\nonumber \\&+\, k_1 (x)\bar{{A}}_1 e^{i(\Omega -\omega _1 )T_2 }+k_2 (x)A_3 e^{-i(\Omega -\omega _3 )T_2 }\nonumber \\&+\, k_1 (x)A_1 e^{i(\Omega +\omega _1 )T_2 }+cc+NST \end{aligned}$$

(53)

where $k_1 (x)$ and $k_2 (x)$ are defined in “Appendix 3.” The other functions in Eq. (53) are identical to those arising from Eq. (26). In the case of internal resonances and principal parametric resonances of the first mode, to show the nearness of $\omega _3$ to $3\omega _1$ and $\Omega$ to $2\omega _1$, detuning parameters $\sigma _1$ and $\sigma _2$ are described as:

$$\begin{aligned} \omega _3 =3\omega _1 +\varepsilon ^{2}\sigma _1 , \Omega =2\omega _1 +\varepsilon ^{2}\sigma _2 \end{aligned}$$

(54)

It is worth mentioning that $\Omega =\omega _3 -\omega _1 +\varepsilon ^{2}(\sigma _2 -\sigma _1 )$; hence, a combination parametric resonance of the difference type would also be activated. The corresponding homogeneous problem of Eq. (53) has a nontrivial solution; it follows that the nonhomogeneous problem has a solution only if the right-hand side of Eq. (53) is orthogonal to every solution of the adjoint homogeneous problem governing $u_3$. Introducing Eq. (54) in Eq. (53), multiplying the right-hand side of the resulting equation by $\phi _1 (x)e^{-i\omega _1 T_0 }$ and $\phi _3 (x)e^{-i\omega _3 T_0 }$, respectively, and integrating the outcome from $x=0$ to $x=1$, the solvability conditions can be obtained as follows:

$$\begin{aligned}&2i\omega _1 \left( {m_1 {A}'_1 +\mu _1 A_1 } \right) -8S_{11} A_1 ^{2}\bar{{A}}_1 -8S_{13} A_1 A_3 \bar{{A}}_3\nonumber \\&\quad -\, 8\Lambda _1 A_3 \bar{{A}}_1^2 e^{i\sigma _1 T_2 }-2K_1 \bar{{A}}_1 e^{i\sigma _2 T_2 } \nonumber \\&\quad -\, 2K_2 A_3 e^{i(\sigma _1 -\sigma _2 )T_2 }=0 \end{aligned}$$

(55)

$$\begin{aligned}&2i\omega _3 \left( {m_3 {A}'_3 +\mu _3 A_3 } \right) -8S_{33} A_3 ^{2}\bar{{A}}_3 -8S_{31} A_3 A_1 \bar{{A}}_1\nonumber \\&\quad -\, 8\Lambda _3 A_1^3 e^{-i\sigma _1 T_2 }-2K_3 A_1 e^{i(\sigma _2 -\sigma _1 )T_2 }=0 \end{aligned}$$

(56)

where

$$\begin{aligned}&K_1 =\frac{1}{2}\int _0^1 {k_1 (x)\phi _1 (x)\hbox {d}x} ,\nonumber \\&K_2 =\frac{1}{2}\int _0^1 {k_2 (x)\phi _1 (x)\hbox {d}x} ,\nonumber \\ \quad&K_3 =\frac{1}{2}\int _0^1 {k_1 (x)\phi _3 (x)\hbox {d}x} \end{aligned}$$

(57)

The other terms of Eqs. (55) and (56) are identical to those defined in Eq. (30). Expressing $A_j$ in a polar form, as in Eq. (31), substituting the resulting equations into Eqs. (55) and (56), separating the real and imaginary parts, and introducing $\gamma _1 =\sigma _1 T_2 -3\beta _1 +\beta _2$ and $\gamma _3 =\sigma _2 T_2 -2\beta _1$, the modulation equations can be expressed as Eqs. (41)–(44).