Dynamics of a predator–prey model with double Allee effects and impulse

Abstract

In this paper, a predator–prey model with double Allee effects and impulse is studied. The existence and stability of the prey-free periodic solution are investigated. The sufficient conditions for global stability of the prey-free periodic solution are obtained. We also find a critical threshold that the predator and prey populations will coexist. The existence of the transcritical bifurcations is considered by means of the bifurcation theory when the prey population is not subject to Allee effect. Combining mathematical analysis and numerical simulations, we show that the double Allee effects and impulse greatly alter the outcome of the survival of both species.

1 Introduction

In 1931, Warder Clyde Allee observed that the per capita growth rate increases initially as population size gets larger and then declines thereafter. Such a biological phenomenon is referred to as an Allee effect. It is characterized by a positive correlation between population size and the mean individual fitness of a population. There are two main types of Allee effect: the strong Allee effect and the weak Allee effect. The strong Allee effect implies that there exists a critical population size under which the population growth rate becomes negative. The weak Allee effect, however, implies a reduced per capita growth rate at low population size but never becomes negative. Allee effects can be caused by several causes, such as difficulties in finding mates, social dysfunction and inbreeding depression. There are quite a few real-world examples exhibiting presence of Allee effects. Therefore, analysis of systems involving Allee effect has gained lots of concerns in various fields such as conservation biology [1, 2], sustainable harvesting [3], population management [4], biological invasions [5], interacting species [6].

The Allee effect has numerous impacts on population dynamics, distribution and conservation, and attracts much attention in biomathematics. Recently, the systems with the space and Allee effect have been studied in ecosystems [7,8,9,10,11,12]. Meanwhile, epidemic systems are also related to this topic [13,14,15]. Furthermore, Allee effects in ecological models have been reviewed in [16]. Especially, in predator–prey systems, many authors have considered the Allee effect in the prey [17,18,19,20,21,22,23,24,25,26]. For example, in [17], the authors considered a predator–prey system with the Allee effect in the prey and Holling type III functional response. It was shown that the Allee effect could promote system collapse. In [18], a predator–prey model with Holling II type functional response and the Allee effect in the prey was investigated. The authors found that the Allee effect of prey species increased the extinction risk of both the predator and prey populations and could lead to unstable periodical oscillation. The predator–prey systems with Allee effect for the predator have been also developed in the literature [19, 27, 28].

However, as far as we are aware, there have only been a few studies that consider predator–prey models with Allee effect for both predator and prey (for example, see [29,30,31]). In [29], Alan J. Terry considered the following predator–prey model:

$$\begin{aligned} \left\{ \begin{array}{l} x'(t)=x\left( \displaystyle \frac{bx}{a+x}-d_{1}-mx\right) -\frac{rxy}{1+k_{1}x+k_{2}y},\\ y'(t)=\displaystyle \frac{crxy}{1+k_{1}x+k_{2}y}\left( \frac{y}{h+y}\right) -d_{2}y, \end{array} \right. \end{aligned}$$

(1.1)

where x(t) and y(t) denote the population densities of prey and predator at time t, respectively, $b>0$ is the per capita maximum fertility rate of the prey, $k_{1}, d_{1}, d_{2}, m$ are positive constants, $k_{2}$ is a non-negative constant, $r>0$ is the predation of predator, $c>0$ is the conversion efficiency of prey into predator, m denotes the strength of intra-competition of prey population, $d_{1}$ and $d_{2}$ are the death rates of prey and predator, respectively. $x/(a+x)$ and $y/(h+y)$ are the terms for the Allee effect in prey and predator populations, a and h are the Allee effect constants imposed on prey and predator populations, respectively. The author derived conditions for stable coexistence of the predator and prey and proved that there was always a minimum viable predator population level, that was, a strong Allee effect held for the predator. The sufficient conditions for prey resurgence were obtained.

However, in [29], the author assumed their model holds in a single region, where immigration of the predator into or out of this region was considered negligible and did not contribute terms to their model. However, as Cushing [32] pointed out, it is necessary and important to consider models with perturbations which might be quite naturally exposed. For example, consider the interaction between crops and locusts in a local region. Once a year or once several years, a large amount of locusts may invade into the region and cause damages to the crops together with the local locusts. This has often been seen in recent years in the northwest of Xinjiang Province and Inner Mongolia in China. Systems with such sudden perturbations are involving in impulsive equations. Wang et al. [33] considered a Beddington–DeAngelis interference model with impulsive biological control:

$$\begin{aligned} \left\{ \begin{array}{l l} \left. \begin{array}{l} x'(t)=x(b-mx)-\displaystyle \frac{rxy}{1+k_{1}x+k_{2}y},\\ y'(t)=\displaystyle \frac{crxy}{1+k_{1}x+k_{2}y}-d_{2}y, \end{array} \right\} t\ne nT,\\ \left. \begin{array}{l} \Delta x(t)=0, \\ \Delta y(t)=\mu T, \end{array} \right\} t=nT,\\ \end{array} \right. \end{aligned}$$

(1.2)

where $\mu$ represents the rate of predator release per unit time and T is the release period. The author found that the prey-free periodic solution was local asymptotically stable if the impulsive control rate was larger than a critical value or the release period was smaller than another critical value. Conditions for permanence of the model were established. The existence of nontrivial periodic solution was investigated.

The above discussion leads naturally to the following two problems:

• 1. How the dynamics of system (1.1) will change when we take the impulse into consideration in system (1.1)?

• 2. How do Allee effects affect the dynamics of both the prey and the predator if we incorporate the Allee effects for both the prey and the predator into impulsive system (1.2)?

The goal in this paper is to try to answer the questions raised above. To this aim, we consider the following predator–prey system with double Allee effects and periodic constant impulsive immigration of predator:

$$\begin{aligned} \left\{ \begin{array}{l l} \left. \begin{array}{l} x'(t)=x\left( \displaystyle \frac{bx}{a+x}-d_{1}-mx\right) -\displaystyle \frac{rxy}{1+k_{1}x+k_{2}y},\\ y'(t)=\displaystyle \left( \frac{crxy}{1+k_{1}x+k_{2}y}\right) \left( \frac{y}{h+y}\right) -d_{2}y, \end{array}\right\} t\ne nT,\\ \left. \begin{array}{l} \Delta x(t)=0, \\ \Delta y(t)=p, \end{array} \right\} t=nT,\\ \end{array} \right. \end{aligned}$$

(1.3)

where $p>0$ denotes periodic constant impulsive immigration of predator. The other parameters are defined as system (1.1) and (1.2), respectively.

The remaining part of this paper is organized as follows. In the next section, we discuss the existence and stability of the prey-free periodic solution of system (1.3). In Sect. 3, the coexistence of the predator and prey populations of system (1.3) is considered. In Sect. 4, the existence of transcritical bifurcations in system (1.3) is discussed by means of the bifurcation theory when the prey population is not subject to Allee effect. In Sect. 5, some numerical simulations are given to illustrate our results. Finally, some concluding remarks are given.

2 The existence and stability of the prey-free periodic solution

Due to the biological meaning, we may define the state space of (1.3) as $X=\{(x,y)\in {\mathbb {R}}_{+}^{2}\}.$

In this section, we investigate the existence of the prey-free periodic solution of system (1.3). In this case, the prey population is entirely absent from the population permanently, ie., $x(t)=0, t\ge 0.$ system (1.3) yields

$$\begin{aligned} \left\{ \begin{aligned}&y'(t)=-d_{2}y,&t\ne nT,\\&\Delta y(t)=p,&t=nT, \\&y(0+)=y_{0}\ge 0. \end{aligned} \right. \end{aligned}$$

(2.1)

Lemma 2.1

[34] System (2.1) has a positive periodic solution $y^{*}(t)$ and for any solution y(t) of (2.1), $|y(t)-y^{*}(t)|\rightarrow 0$ as $t\rightarrow \infty .$ Moreover, $y(t)\ge y^{*}(t)$ if $y_{0}\ge y^{*}(0+)$ and $y(t)< y^{*}(t)$ if $y_{0}< y^{*}(0+),$ where

$$\begin{aligned} y^{*}(t)=y^{*}(0+)e^{-d_{2}(t-nT)}, nT<t\le (n+1)T, \end{aligned}$$

(2.2)

and

$$\begin{aligned} y^{*}(0+)=\frac{p}{1-e^{-d_{2}T}}. \end{aligned}$$

(2.3)

Lemma 2.2

${\mathbb {R}}_{+}^{2}=\{(x,y) \mid x>0, y>0\}$ is the positive invariant set of system (1.3).

Proof

For any $t>0$, there exists a $n \in {\mathbb {N}},$ such that $t \in (nT, (n+1)T],$ hence we have

$$\begin{aligned}&x(t) = x\left( nT^{+}\right) \exp \left( \int _{nT}^{t}\left( \displaystyle \frac{bx}{a+x}-d_{1}-mx \right. \right. \\&\quad \left. \left. -\displaystyle \frac{ry}{1+k_{1}x+k_{2}y}\right) \,\mathrm {d}s\right) \\&y(t) = y\left( nT^{+}\right) \exp \left( \displaystyle \int _{nT}^{t}\left( \left( \frac{crx}{1+k_{1}x+k_{2}y}\right) \left( \frac{y}{h+y}\right) \right. \right. \\&\quad \left. \left. -d_{2}\right) \,\mathrm {d}s\right) \\&x\left( nT^{+}\right) = x\left( nT\right) , \ y\left( nT^{+}\right) = y\left( nT\right) +p. \end{aligned}$$

Thus

$$\begin{aligned} y(t)&=y\left( nT^{+}\right) \exp \left( \displaystyle \int _{nT}^{t}\left( \left( \frac{crx}{1+k_{1}x+k_{2}y}\right) \left( \frac{y}{h+y}\right) \right. \right. \\&\quad \left. \left. -d_{2}\right) \,\mathrm {d}s\right) \\&\ge y\left( nT\right) \exp \left( \displaystyle \int _{nT}^{t}\left( \left( \frac{crx}{1+k_{1}x+k_{2}y}\right) \left( \frac{y}{h+y}\right) \right. \right. \\&\quad \left. \left. -d_{2}\right) \,\mathrm {d}s\right) . \end{aligned}$$

Then we get

$$\begin{aligned} x(t)&=x\left( 0^{+}\right) \exp \left( \int _{nT}^{t}\left( \displaystyle \frac{bx}{a+x}-d_{1}-mx \right. \right. \\&\quad \left. \left. -\displaystyle \frac{ry}{1+k_{1}x+k_{2}y}\right) \,\mathrm {d}s\right) \\ y(t)&\ge y\left( 0^{+}\right) \exp \left( \displaystyle \int _{nT}^{t}\left( \left( \frac{crx}{1+k_{1}x+k_{2}y}\right) \left( \frac{y}{h+y}\right) \right. \right. \\&\quad \left. \left. -d_{2}\right) \,\mathrm {d}s\right) . \end{aligned}$$

Therefore, $x(t)>0, y(t)>0$. So ${\mathbb {R}}_{+}^{2}=\{(x,y) \mid x>0, y>0\}$ is the positive invariant set of system (1.3). $\square$

According to Lemma 2.1, we obtain the following result:

Theorem 2.1

System (1.3) has a prey-free periodic solution $(0,y^{*}(t))$.

Next, we will discuss the stability of the periodic solution $(0,y^{*}(t))$.

Suppose that (x(t), y(t)) be any solution of system (1.3). Let

$$\begin{aligned} x_{1}(t)=x(t), y_{1}(t)=y(t)-y^{*}(t). \end{aligned}$$

(2.4)

Substituting (2.4) into (1.3), we obtain the linearization of the system (1.3) as follows

$$\begin{aligned} \left\{ \begin{array}{l l} \left. \begin{array}{l} x_{1}'(t)=(-d_{1}-ry^{*}(t)) x_{1}(t),\\ y_{1}'(t)=\displaystyle \frac{cr(y^{*}(t))^{2}}{(1+k_{2}y^{*}(t))(h+y^{*}(t))}x_{1}(t)-d_{2}y_{1}(t),\\ \end{array}\right\} t\ne nT,\\ \left. \begin{array}{l} \Delta x_{1}(t)= 0, \\ \Delta y_{1}(t)=0,\\ \end{array} \right\} t=nT.\\ \end{array} \right. \end{aligned}$$

Therefore, for $0\le t<T,$ we have

$$\begin{aligned} \begin{pmatrix} x_{1}(t)\\ y_{1}(t) \end{pmatrix}=\phi (t) \begin{pmatrix} x_{1}(0)\\ y_{1}(0) \end{pmatrix}, \end{aligned}$$

where $\phi (t)$ satisfies

$$\begin{aligned} \phi '(t)=\begin{pmatrix} -d_{1}-ry^{*}(t) &{} 0\\ \displaystyle \frac{cr(y^{*}(t))^{2}}{(1+k_{2}y^{*}(t))(h+y^{*}(t))} &{} -d_{2} \end{pmatrix}\phi (t), \end{aligned}$$

$\phi (0)=I,$ the identity matrix.

$$\begin{aligned} \begin{pmatrix} x_{1}(T^{+})\\ y_{1}(T^{+}) \end{pmatrix}= \begin{pmatrix} 1 &{} 0 \\ 0 &{} 1 \end{pmatrix} \begin{pmatrix} x_{1}(T)\\ y_{1}(T) \end{pmatrix}. \end{aligned}$$

The stability of the periodic solution $(0,y^{*}(t))$ is determined by the eigenvalues of the following matrix

$$\begin{aligned} M= \begin{pmatrix} 1 &{} 0 \\ 0 &{} 1 \end{pmatrix}\phi (T). \end{aligned}$$

When $a>0$, the eigenvalues of the matrix M are

$$\begin{aligned} \lambda _{1}= & {} \exp \left( \int ^{T}_{0}\left( -d_{1}-ry^{*}\left( t\right) \right) \,\mathrm {d}t\right)<1, \\ \lambda _{2}= & {} e^{-d_{2}T}<1. \end{aligned}$$

Therefore, we have the following theorem:

Theorem 2.2

If $a>0$, then the prey-free periodic solution $(0,y^{*}(t))$ of system (1.3) is locally asymptotically stable.

Similarly, we obtain the following result when $a=0$:

Theorem 2.3

If $a=0$ and $p>\frac{d_{2}T}{r}(b-d_{1})\triangleq {\bar{p}}$, then the prey-free periodic solution $(0,y^{*}(t))$ of system (1.3) is locally asymptotically stable.

Remark 2.1

From Theorem 2 in [29], we know that the predator of system (1.1) will become extinct if the population density of predator becomes low or the prey goes extinct. However, it follows from Theorems 2.2 and 2.3 that the predator of system (1.3) would not go extinct. Thus, the periodic impulsive immigration of predator increases the survivability of predator. In addition, by Theorem 2.3, we obtain that the prey may become extinct if $p>{\bar{p}}.$ Hence, the periodic impulsive immigration of predator increases the extinction risk of prey.

Remark 2.2

By Theorem 2.2, we find that if the population density of prey becomes low, then prey will go extinct. Therefore, the Allee effect of prey population increases the extinction risk of prey.

Next, we will prove that the prey-free periodic solution $(0,y^{*}(t))$ of system (1.3) is globally attractive.

Lemma 2.3

All the solutions $(x(t),y(t))\in X$ of the system (1.3) are uniformly upper bounded.

Proof

Suppose that $a>0$. From the first equation of (1.3), we have

$$\begin{aligned} x'(t)\le & {} {} x\left( \frac{bx}{a+x}-d_{1}-mx\right) \nonumber \\= & {} -\frac{x}{a+x}\left( mx^{2}+(am+d_{1}-b)x+ad_{1}\right) .\nonumber \\ \end{aligned}$$

(2.5)

It’s clear that if $am+d_{1}-b\ge 0,$ then $x'(t)<0.$ Thus $x(t)<x(0+), t>0.$ By (2.5) we get

$$\begin{aligned} x(t)\le x(0+)\exp \left\{ \int _{0}^{t}G(x(s))\,\mathrm {d}s\right\} ,\ t\ge 0, \end{aligned}$$

where

$$\begin{aligned} G(x(s))&=\displaystyle -\frac{1}{a+x}(mx^{2}+(am+d_{1}-b)x+ad_{1}) \\&\le \displaystyle -\frac{1}{a+x}(ad_{1}) \\&\le \displaystyle -\frac{ad_{1}}{a+x(0+)}\\&\triangleq \eta _{1} <0. \end{aligned}$$

Therefore, $x(t)\le x(0+)e^{\eta _{1} t}.$ It is clear that $x(t)\rightarrow 0$ as $t\rightarrow \infty .$ It is obvious that the prey is uniformly upper bounded.

Now suppose $am+d_{1}-b<0.$ Denote $\Delta =(am+d_{1}-b)^{2}-4amd_{1}, f(x)=mx^{2}+(am+d_{1}-b)x+ad_{1}.$ If $\Delta <0,$ then Eq. $f(x)=0$ has no real root. Obviously, $x'(t)<0, t>0.$ Thus, $x(t)<x(0+), t>0.$ By (2.5) we get

$$\begin{aligned} x(t)\le x(0+)\exp \left\{ \int _{0}^{t}G(x(s))\,\mathrm {d}s\right\} ,\ t\ge 0, \end{aligned}$$

where

$$\begin{aligned} G\left( x\left( s\right) \right)&=\displaystyle -\frac{1}{a+x}\left( mx^{2}+\left( am+d_{1}-b\right) x+ad_{1}\right) \\&=\displaystyle -\frac{m}{a+x}\left[ \left( x+\frac{1}{2m}\left( am+d_{1}-b\right) \right) ^{2}\right. \\&\quad \left. -\frac{1}{4m^{2}}\left( am+d_{1}-b\right) ^{2}+\frac{ad_{1}}{m}\right] \\&\le \displaystyle \frac{m}{a+x}\left[ \frac{1}{4m^{2}}\left( (am+d_{1}-b)^{2}-4amd_{1}\right) \right] \\&= \frac{\Delta }{4m\left( a+x\right) } \\&<\frac{\Delta }{4m\left( a+x\left( 0+\right) \right) } \\&\triangleq \eta _{2} <0. \end{aligned}$$

Therefore, $x(t)\le x(0+)e^{\eta _{2} t}.$ It is clear that $x(t)\rightarrow 0$ as $t\rightarrow \infty .$

If $\Delta =0,$ then Eq. $f(x)=0$ has a unique root $x_{1},$ where $x_{1}= \displaystyle \frac{am+d_{1}-b}{2m}.$ Thus,

$$\begin{aligned} x'(t)\le \displaystyle -\frac{x}{a+x}(x-x_{1})^{2}\le 0. \end{aligned}$$

(2.6)

We hope to obtain that for all t large enough, $x(t)\le x_{1}+\epsilon ,$ where $\epsilon >0$ is small enough. From (2.6), we find that for $x>x_{1}, x'(t)<0, t\ge 0.$ Next, we consider the case $x>x_{1}$. Suppose that there is a $l>x_{1}$ such that $\lim _{t\rightarrow +\infty }x(t)=l$. Obviously, $x(t)\ge l$ for all $t\ge 0$. By (2.6), we get

$$\begin{aligned} x'(t)\le \displaystyle -\frac{l}{a+l}(l-x_{1})^{2}\triangleq -{\bar{B}}, \end{aligned}$$

(2.7)

where ${\bar{B}}=\frac{l}{a+l}(l-x_{1})^{2}.$ Thus, by (2.7), we find that $x(t)\le x(0)-{\bar{B}}t.$ It’s clear that $x(t)\rightarrow -\infty$ as $t\rightarrow +\infty ,$ which is a contradiction. So, $x(t)\rightarrow x_{1}$ or $x(t)<x_{1},$ as $t\rightarrow +\infty .$ Then there exists $\epsilon >0$ small enough such that for all t large enough, $x(t)\le x_{1}+\epsilon .$

If $\Delta >0,$ then Eq. $f(x)=0$ has two roots $x_{2}, x_{3},$ where

$$\begin{aligned} x_{2}= & {} \frac{-(am+d_{1}-b)-\sqrt{\Delta }}{2m},\nonumber \\ x_{3}= & {} \frac{-(am+d_{1}-b)+\sqrt{\Delta }}{2m}. \end{aligned}$$

(2.8)

Since $\Delta =(am+d_{1}-b)^{2}-4amd_{1}<(am+d_{1}-b)^{2}$ and $am+d_{1}-b<0, x_{3}<\frac{1}{m}(b-am-d_{1})<\frac{b}{m}.$

Therefore, for $x>\frac{b}{m},$ we have $x'(t)\le \displaystyle -\frac{x}{a+x}(x-x_{2})(x-x_{3})< 0.$ Similar to the above analysis, we obtain that for all t large enough, $x(t)\le \frac{b}{m}.$

Synthesizing the above analysis, we obtain that there are two positive constants $M_{1}$ and T such that $x(t)\le M_{1}$ for $t>T$.

Now, we discuss the upper bound of y(t). Let $V(t)=cx(t)+y(t).$ Then

$$\begin{aligned} D^{+}V(t)&=cx\left( \displaystyle \frac{bx}{a+x}-d_{1}-mx\right) \\&\quad -\displaystyle \left( \frac{crxy}{1+k_{1}x+k_{2}y}\right) \left( 1-\frac{y}{h+y}\right) -d_{2}y, \\&\le -\frac{cx}{a+x}\left( mx^{2}+\left( am+d_{1}-b\right) x+ad_{1}\right) \\&\quad -d_{2}y. \end{aligned}$$

Observe that f(x) is a quadratic in x and is easily seen to have a global minimum, namely $ad_{1}-\displaystyle \frac{(am+d_{1}-b)^{2}}{4m}\triangleq m_{1}.$ If $m_{1}\ge 0,$ then $f(x)\ge m_{1}\ge 0.$ Thus, for $t>T$,

$$\begin{aligned} D^{+}V(t)\le & {} -d_{2}y=cd_{2}x-d_{2}(cx+y) \nonumber \\\le & {} cd_{2}M_{1}-d_{2}V(t). \end{aligned}$$

(2.9)

If $m_{1}<0$, then $D^{+}V(t)\le \displaystyle -\frac{cm_{1}x}{a+x}-d_{2}y.$ Hence, for $t>T$,

$$\begin{aligned} D^{+}V(t)&\le -\frac{cm_{1}M_{1}}{a+M_{1}}-d_{2}y = -\frac{cm_{1}M_{1}}{a+M_{1}}\nonumber \\&\quad +cd_{2}x-d_{2}(cx+y) \nonumber \\&\le -\frac{cm_{1}M_{1}}{a+M_{1}}+cd_{2}M_{1}-d_{2}V(t). \end{aligned}$$

(2.10)

Denote $M_{2}=\max \{cd_{2}M_{1}, cd_{2}M_{1}- \displaystyle \frac{cm_{1}M_{1}}{a+M_{1}}\}.$ By the inequalities (2.9) and (2.10), we get

$$\begin{aligned} \left\{ \begin{aligned}&D^{+}V(t)\le M_{2}-d_{2}V(t),&t\ne nT,\\&V(nT^{+})=V(nT)+p,&t=nT. \end{aligned} \right. \end{aligned}$$

By the comparison theorem of impulsive differential equation, for $t\in (nT, (n+1)T],$ we have

$$\begin{aligned} V(t)\le & {} \left( V\left( 0+\right) -\frac{M_{2}}{d_{2}}\right) e^{-d_{2}t}\\&+\frac{p\left( 1-e^{-nd_{2}T}\right) }{1-e^{-d_{2}T}}e^{-d_{2}\left( t-nT\right) }+\frac{M_{2}}{d_{2}}. \end{aligned}$$

Therefore, V(t) is ultimately bounded by a constant and there exists a constant $M>0$ such that for all t large enough, $x(t)\le M, y(t)\le M.$

Let

$$\begin{aligned} R_{1}&= \int ^{T}_{0}\left( \frac{b^{2}}{am+b}-d_{1}-\frac{rmy^{*}(t)}{m+bk_{1}+mk_{2}y^{*}(t)}\right) \,\mathrm {d}t \nonumber \\&= \frac{b^{2}T}{am+b}-d_{1}T\nonumber \\&\quad -\frac{r}{k_{2}d_{2}}\ln \frac{k_{2}pm+\left( m+bk_{1}\right) \left( 1-e^{-d_{2}T}\right) }{k_{2}pme^{-d_{2}T}+\left( m+bk_{1}\right) \left( 1-e^{-d_{2}T}\right) }. \end{aligned}$$

(2.11)

$\square$

Theorem 2.4

The prey-free periodic solution $(0,y^{*}(t))$ of system (1.3) is global attractive if one of the following conditions is satisfied

• (1) $am+d_{1}-b\ge 0,$

• (2) $am+d_{1}-b< 0, \Delta <0,$

• (3) $am+d_{1}-b< 0, \Delta \ge 0, R_{1}<0,$

where $\Delta =(am+d_{1}-b)^{2}-4amd_{1}.$

Proof

By the above analysis, it is obvious that if $am+d_{1}-b\ge 0$, or $am+d_{1}-b< 0$ and $\Delta <0,$ then $x(t)\rightarrow 0$ as $t\rightarrow \infty .$ Now suppose $am+d_{1}-b< 0, \Delta \ge 0.$

Since $R_{1}<0,$ one can choose $\epsilon >0$ small enough such that

$$\begin{aligned} \sigma= & {} \int ^{T}_{0}\left( \frac{b^{2}}{am+b}-d_{1}\right. \\&\left. -\frac{rm\left( y^{*}(t)-\epsilon \right) }{m+bk_{1}+mk_{2}\left( y^{*}(t)-\epsilon \right) }\right) \,\mathrm {d}t<0. \end{aligned}$$

By the above analysis, there exists $T_{1}>0$ such that for $t>T_{1}, x(t)\le x_{3}.$

By the second and fourth equations of system (1.3), we obtain

$$\begin{aligned} \left\{ \begin{aligned}&y'(t)\ge -d_{2}y,&t\ne nT,\\&\Delta y(t)=p,&t=nT. \end{aligned} \right. \end{aligned}$$

Consider the following impulsive comparison system

$$\begin{aligned} \left\{ \begin{aligned}&z'(t)= -d_{2}z,&t\ne nT,\\&\Delta z(t)=p,&t=nT. \end{aligned} \right. \end{aligned}$$

(2.12)

According to Lemma 2.1, we obtain that system (2.12) has a globally asymptotically stable periodic solution $y^{*}(t),$ where $y^{*}(t)$ is shown in (2.2). By the comparison principle, there exists $T_{2}>0$ such that for $t>T_{2},$

$$\begin{aligned} y(t)\ge z(t)\ge y^{*}(t)-\epsilon . \end{aligned}$$

(2.13)

From the first equation of system (1.3), we get

$$\begin{aligned} x'(t)&\le \displaystyle \left( \frac{b\frac{b}{m}}{a+\frac{b}{m}}-d_{1} -\frac{r\left( y^{*}(t)-\epsilon \right) }{1+k_{1}\frac{b}{m}+k_{2}\left( y^{*}(t)-\epsilon \right) }\right) x \nonumber \\&= \displaystyle \left( \frac{b^{2}}{am+b}-d_{1}-\frac{rm\left( y^{*}(t)-\epsilon \right) }{m+bk_{1}+mk_{2}\left( y^{*}(t)-\epsilon \right) }\right) x, \end{aligned}$$

(2.14)

for all t large enough, which leads to

$$\begin{aligned} x\left( \left( n+1\right) T\right)&\le x\left( nT^{+}\right) \exp \left( \frac{b^{2}T}{am+b}-d_{1}T \right. \\&\quad \left. -\int ^{\left( n+1\right) T}_{nT}\frac{rm\left( y^{*}(t)-\epsilon \right) }{m+bk_{1}+mk_{2}\left( y^{*}(t)-\epsilon \right) }\,\mathrm {d}t\right) \\&= x\left( nT^{+}\right) e^{\sigma }. \end{aligned}$$

Therefore, $x(nT)\le x(0+)e^{n\sigma }$ and $x(nT)\rightarrow 0$ as $n\rightarrow \infty$. From (2.14), for $t\in (nT, (n+1)T],$ we obtain

$$\begin{aligned} x(t)&\le x\left( nT^{+}\right) \exp \left( \int ^{t}_{nT}\left( \frac{b^{2}}{am+b} \right. \right. \\&\quad \left. \left. -\,d_{1}-\frac{rm\left( y^{*}(t)-\epsilon \right) }{m+bk_{1}+mk_{2}\left( y^{*}(t)-\epsilon \right) }\right) \,\mathrm {d}t\right) \\&\le x\left( nT^{+}\right) \exp \left( \frac{b^{2}T}{am+b}\right) . \end{aligned}$$

Hence, $x(t)\rightarrow 0$ as $t\rightarrow \infty$. Without loss of generality, we may assume that for any $\epsilon _{1}>0$ and $t\ge 0, 0<x(t)<\epsilon _{1}.$

From the second and fourth equations of system (1.3), we get

$$\begin{aligned} \left\{ \begin{aligned}&y'(t)\le \left( crx-d_{2}\right) y \le \left( cr\epsilon _{1}-d_{2}\right) y,&t\ne nT,\\&\Delta y(t)=p,&t=nT. \end{aligned} \right. \end{aligned}$$

Consider the following impulsive comparison system

$$\begin{aligned} \left\{ \begin{aligned}&z'_{1}(t)= (cr\epsilon _{1}-d_{2})z_{1},&t\ne nT,\\&\Delta z_{1}(t)=p,&t=nT. \end{aligned} \right. \end{aligned}$$

(2.15)

According to Lemma 2.1, we obtain that system (2.15) has a globally asymptotically stable periodic solution $z_{1}^{*}(t),$ where

$$\begin{aligned}&z_{1}^{*}(t)=\frac{p\exp \left( -\left( cr\epsilon _{1}-d_{2}\right) \left( t-nT\right) \right) }{1-\exp \left( -\left( cr\epsilon _{1}-d_{2}\right) T\right) },\\&\quad nT<t\le \left( n+1\right) T. \end{aligned}$$

Obviously, $z_{1}^{*}(t)\rightarrow y^{*}(t)$ as $\epsilon _{1}\rightarrow 0$. By the comparison theorem of impulsive differential equation, we get

$$\begin{aligned} y(t)\le z_{1}(t)\le z_{1}^{*}(t)+\epsilon . \end{aligned}$$

(2.16)

for all t large enough. Since $z_{1}^{*}(t)-y^{*}(t)\rightarrow 0$ as $\epsilon _{1}\rightarrow 0$, from (2.13) and (2.16), we obtain that for any $\epsilon _{2} >0$ and all t large enough, $y^{*}(t)-\epsilon _{2}\le y(t)\le y^{*}(t)+\epsilon _{2},$ which implies $y(t)-y^{*}(t)\rightarrow 0$ as $t\rightarrow \infty$. So the prey-free periodic solution $(0,y^{*}(t))$ of system (1.3) is globally attractive. The proof is completed. $\square$

Synthesizing Theorems 2.2, 2.3 and 2.4 , we obtain the following results

Corollary 2.1

Assume $a>0.$ Then the prey-free periodic solution $(0,y^{*}(t))$ of system (1.3) is global asymptotically stable if one of the following conditions is satisfied

• (1) $am+d_{1}-b\ge 0,$

• (2) $am+d_{1}-b< 0, \Delta <0,$

• (3) $am+d_{1}-b< 0, \Delta \ge 0, R_{1}<0,$

where $\Delta =(am+d_{1}-b)^{2}-4amd_{1}.$

Corollary 2.2

Assume $a=0.$ Then the prey-free periodic solution $(0,y^{*}(t))$ of system (1.3) is global asymptotically stable if one of the following conditions is satisfied

• (1) $b\le d_{1},$

• (2) $b> d_{1}, {\bar{R}}_{1} <0,$

where ${\bar{R}}_{1}=(b-d_{1})T-\displaystyle \frac{r}{k_{2}d_{2}}\ln \frac{mk_{2}p+(m+k_{1}(b-d_{1}))(1-e^{-d_{2}T})}{mk_{2}pe^{-d_{2}T}+(m+k_{1}(b-d_{1}))(1-e^{-d_{2}T})}$.

3 The coexistence of the predator and prey

In this section, we discuss the coexistence of the predator and prey for system (1.3). The following theorem reveals that the prey can persist in system (1.3) even when the prey-free periodic solution is locally stable.

Theorem 3.1

(1) Assume $a>0.$ If the following conditions

(H1):

$b>am+d_{1}+2\sqrt{amd_{1}},$

(H2):

$bcr<d_{2}(m+bk_{1}),$

(H3):

$r+k_{2}d_{1}-k_{2}b>0$,

hold, then there exists a positive constant $L_{x}\in (x_{2}, x_{3})$ and solutions (x(t), y(t)) of system (1.3) with $x(0^{+})> L_{x}$ and

$$\begin{aligned} 0<y\left( 0^{+}\right) <\frac{\left( \frac{bL_{x}}{a+L_{x}}-d_{1}-mL_{x}\right) \left( 1+k_{1}L_{x}\right) }{r+k_{2}d_{1}+mk_{2}L_{x}-bk_{2}}-p, \end{aligned}$$

such that $x(t)\ge L_{x}$ for $t\ge 0,$ where $x_{2}, x_{3}$ are defined in (2.8).

(2) Assume $a=0.$ If the following conditions

$({\bar{H}}1)$ :

$b>d_{1},$

$({\bar{H}}2)$ :

$\frac{cr(b-d_{1})}{m+k_{1}(b-d_{1})}-d_{2}<0,$

$({\bar{H}}3)$ :

$r+k_{2}d_{1}>bk_{2}$,

hold, then there exists a positive constant $l_{x}\in (0, \frac{b-d_{1}}{m})$ and solutions (x(t), y(t)) of system (1.3) with $x(0^{+})> l_{x}$ and

$$\begin{aligned} 0<y\left( 0^{+}\right) <\frac{\left( b-d_{1}-ml_{x}\right) \left( 1+k_{1}l_{x}\right) }{r+k_{2}d_{1}+mk_{2}l_{x}-bk_{2}}-p, \end{aligned}$$

such that $x(t)\ge l_{x}$ for $t\ge 0.$

Proof

Firstly, we will prove case (1). According to the proof Theorem 2.4, there exist two positive constants $x_{2}, x_{3}$ if $b>am+d_{1}+2\sqrt{amd_{1}}$ such that

$$\begin{aligned} x'(t)&\le x\left( \frac{bx}{a+x}-d_{1}-mx\right) \\&= -\frac{x}{a+x}(x-x_{2})(x-x_{3}). \end{aligned}$$

So $x'(t)<0$ for $x>\frac{b}{m}.$ Assume $x_{2}<x(0^{+})\le \frac{b}{m}.$ Then x(t) is bounded above by $\frac{b}{m}$ for $t\ge 0$.

Using the second equation of system (1.3), we have

$$\begin{aligned} y'(t)\le&\displaystyle \left( \frac{cr\frac{b}{m}}{1+k_{1}\frac{b}{m}}-d_{2}\right) y \\ =&\displaystyle \left( \frac{bcr}{m+bk_{1}}-d_{2}\right) y \\ \triangleq&{\bar{M}}y, \end{aligned}$$

where ${\bar{M}}=\displaystyle \frac{bcr}{m+bk_{1}}-d_{2}<0.$ Hence, by the comparison principle, we see that for $t\in (nT, (n+1)T],$

$$\begin{aligned} y(t)\le y(nT^{+})e^{{\bar{M}}(t-nT)}. \end{aligned}$$

(3.1)

Thus,

$$\begin{aligned} y((n+1)T^{+})\le y(nT^{+})e^{{\bar{M}}T}+p. \end{aligned}$$

(3.2)

Using (3.2), it is easily established by induction that

$$\begin{aligned}&y(nT^{+})\le y(0^{+})e^{n{\bar{M}}T}\\&\quad +p\left( 1+e^{{\bar{M}}T}+\cdots +e^{(n-1){\bar{M}}T}\right) . \end{aligned}$$

Let $S_{n}=1+e^{{\bar{M}}T}+\cdots +e^{(n-1){\bar{M}}T}.$ If ${\bar{M}}<0,$ then $0<e^{{\bar{M}}T}<1$ and $S_{n}$ is bounded above by $(1-e^{{\bar{M}}T})^{-1}>0.$ Therefore, assuming ${\bar{M}}<0$, we will have

$$\begin{aligned} y(nT^{+})\le y(0^{+})+\frac{p}{1-e^{{\bar{M}}T}}. \end{aligned}$$

(3.3)

Using (3.1) and (3.3), for $t\ge 0,$ we get

$$\begin{aligned} y(t)\le y(0^{+})+\frac{p}{1-e^{{\bar{M}}T}}\le y(0^{+})+p \triangleq {\bar{M}}_{1}. \end{aligned}$$

(3.4)

Now, let us ask for $L_{x}$ such that

$$\begin{aligned} x_{2}<L_{x}<x_{3}. \end{aligned}$$

(3.5)

and for $t>0, t\ne nT,$

$$\begin{aligned} x'(t)|_{x=L_{x}}>0. \end{aligned}$$

(3.6)

Assume that (3.5) holds. In view of (3.4), we have

$$\begin{aligned}&x'(t)|_{x=L_{x}}\\&\quad = L_{x}\left( \frac{bL_{x}}{a+L_{x}}-d_{1}-mL_{x}-\frac{ry}{1+k_{1}L_{x}+k_{2}y}\right) \\&\quad \ge L_{x}\left( \frac{bL_{x}}{a+L_{x}}-d_{1}-mL_{x}-\frac{r{\bar{M}}_{1}}{1+k_{1}L_{x}+k_{2}{\bar{M}}_{1}}\right) . \end{aligned}$$

It’s clear that $x'(t)|_{x=L_{x}}>0$ if

$$\begin{aligned}&\left( \frac{bL_{x}}{a+L_{x}}-d_{1}-mL_{x}\right) \left( 1+k_{1}L_{x}\right) \nonumber \\&\quad> {\bar{M}}_{1}\left( r+k_{2}d_{1}+mk_{2}L_{x}-\frac{bk_{2}L_{x}}{a+L_{x}}\right) \nonumber \\&\quad >{\bar{M}}_{1}\left( r+k_{2}d_{1}+mk_{2}L_{x}-bk_{2}\right) . \end{aligned}$$

(3.7)

Since $x_{2}<L_{x}<x_{3}, \ \frac{bL_{x}}{a+L_{x}}-d_{1}-mL_{x}>0.$ It is clear that if $r+k_{2}d_{1}-bk_{2}>0,$ then $r+k_{2}d_{1}+mk_{2}L_{x}-bk_{2}>0.$ Thus, from (3.7), we obtain

$$\begin{aligned}&y\left( 0^{+}\right) +p \nonumber \\&\quad = {\bar{M}}_{1}<\frac{\left( \frac{bL_{x}}{a+L_{x}}-d_{1}-mL_{x}\right) \left( 1+k_{1}L_{x}\right) }{r+k_{2}d_{1}+mk_{2}L_{x}-bk_{2}}, \end{aligned}$$

(3.8)

provided that

$$\begin{aligned} r+k_{2}d_{1}-bk_{2}>0. \end{aligned}$$

(3.9)

Combining our observations, we see that if (3.5), (3.8), (3.9) and ${\bar{M}}<0$ hold, then any trajectory with the initial condition $(x(0^{+}), y(0^{+}))$, where

$$\begin{aligned} x(0^{+})\in [L_{x}, x_{3}], \end{aligned}$$

(3.10)

will exist and satisfy $x(t)\ge L_{x}$ for $t\ge 0,$ since (3.6) will hold and x(t) is not changed at the time nT. In other word, we have derived conditions such that the case (1) in the statement of Theorem 3.1 holds.

Therefore, Theorem 3.1 will be true if (3.5), (3.8), (3.9) and the conditions $b>am+d_{1}+2\sqrt{amd_{1}}, {\bar{M}}<0$ can hold simultaneously. But we may easily satisfy these conditions simultaneously if we choose parameters and initial conditions according to the following procedure

• (1) Choose $a>0, m>0, d_{1}>0, r>0, k_{2}>0, am+d_{1}+2\sqrt{amd_{1}}<b<d_{1}+\frac{r}{k_{2}}.$

• (2) Choose $L_{x}$ such that $x_{2}<L_{x}<x_{3}.$ Choose $y(0+)>0, p>0, T>0.$ Choose $k_{1}$ large enough to satisfy (3.8) and ${\bar{M}}<0$, where $x_{2}, x_{3}$ are defined in (2.8). This is clearly possible.

• (3) Choose $x(0^{+})$ to satisfy (3.10).

Similarly, we may prove the case (2), ie., $a=0.$ The proof is completed. $\square$

Remark 3.1

It follows from Theorem 3.1 that under the conditions of Theorem 3.1, there exists a critical threshold $L_{x}>0$ (or $l_{x}>0$) such that the prey population will become persistent if the population density of prey is greater than the threshold $L_{x}$ (or $l_{x}$). Of course, if the population density of prey is smaller than the threshold $L_{x}$ (or $l_{x}$), then the prey population will go extinct. Therefore, the threshold $L_{x}$ (or $l_{x}$) is very important for the conservation of the endangered species. It is obvious that there does not exist the critical threshold $L_{x}$ (or $l_{x}$) for model (1.2).

4 The existence of transcritical bifurcations

In Sect. 2, we find that for the predator–prey model (1.3) with Allee effect in the prey, ie., $a>0,$ the prey-free periodic solution $(0,y^{*}(t))$ is always locally stable. Hence, the transcritical bifurcations do not occur. However, for model (1.3) without Allee effect in the prey, ie., $a=0,$ one of the eigenvalues of the prey-free periodic solution $(0,y^{*}(t))$ is 1 if $bT=d_{1}T+r\int _{0}^{T}y^{*}(t)\,\mathrm {d}t$. Hence, the transcritical bifurcations may occur. Therefore, we can see that Allee effect in the prey can extinct the transcritical bifurcations.

Next, we will discuss the existence of transcritical bifurcations of model (1.3) without Allee effect in the prey, ie., $a=0,$ by means of the bifurcation theory.

4.1 The Poincaré map

Suppose the prey-free periodic solution $(0,y^{*}(t))$ with the initial point $A_{0}(0, y^{*}(0^{+}))$ and period T passes through the points $A_{0}$ and $B_{0}(0,y^{*}(T))$ at time T, then jumps to the point $A_{1}(0,y^{*}(T^{+}))$ due to the pulse. Thus, $y^{*}(T^{+})=y^{*}(0^{+}).$

Consider another solution $(x_{1}(t),y_{1}(t))$ of system (1.3) with the initial point $A_{k}(x_{k},y^{*}(0^{+})+y_{k})$. This disturbed trajectory starting from the point $A_{k}$ reaches the point $B_{k}(x_{1}(T),y_{1}(T))$ at time T, then jumps to the point $A_{k+1}(x_{k+1}, y^{*}(0^{+})+y_{k+1})$. Thus, $x_{k+1}=x_{1}(T^{+}), \ y^{*}(0^{+})+y_{k+1}=y_{1}(T^{+}).$

Denote $x(t)=x_{1}(t), y(t)=y_{1}(t)-y^{*}(t)$, then $x(0)=x_{k},y(0)=y_{k}$. Let

$$\begin{aligned} F_{1}\left( x,y\right)&=x\left( b-d_{1}-mx\right) -\displaystyle \frac{rxy}{1+k_{1}x+k_{2}y},\\ F_{2}\left( x,y\right)&= \displaystyle \left( \frac{crxy}{1+k_{1}x+k_{2}y}\right) \left( \frac{y}{h+y}\right) -d_{2}y. \end{aligned}$$

Then system (1.3) may be written as

$$\begin{aligned} \left\{ \begin{array}{l l} \left. \begin{array}{l} x'(t)=F_{1}(x,y+y^{*})\triangleq G_{1}(x,y),\\ y'(t)=F_{2}(x,y+y^{*})-F_{2}(0,y^{*})\triangleq G_{2}(x,y),\\ \end{array} \right\} t\ne nT,\\ \left. \begin{array}{l} \Delta x(t)=0,\\ \Delta y(t)=0,\\ \end{array} \right\} t=nT.\\ \end{array} \right. \end{aligned}$$

(4.1)

By the Taylor expansion, we have

$$\begin{aligned} \left\{ \begin{aligned} G_{1}\left( x,y\right)&=A_{1}(t)x+A_{3}(t)x^{2}+A_{4}(t)xy\\&\quad +o\left( \left( |x|+|y|\right) ^{3}\right) ,\\ G_{2}\left( x,y\right)&= B_{1}(t)x+B_{2}(t)y+B_{3}(t)x^{2}+B_{4}(t)xy\\&\quad +o\left( \left( |x|+|y|\right) ^{3}\right) . \end{aligned} \right. \end{aligned}$$

(4.2)

where

$$\begin{aligned} A_{1}(t)&=b-d_{1}-\frac{ry^{*}(t)}{1+k_{2}y^{*}(t)},\\ A_{3}(t)&=-m+\frac{rk_{1}y^{*}(t)}{\left( 1+k_{2}y^{*}(t)\right) ^{2}},\\ A_{4}(t)&=-\frac{r}{\left( 1+k_{2}y^{*}(t)\right) ^{2}},\\ B_{1}(t)&=\frac{cr\left( y^{*}(t)\right) ^{2}}{\left( h+y^{*}(t)\right) \left( 1+k_{2}y^{*}(t)\right) },\\ B_{2}(t)&=-d_{2},\\ B_{3}(t)&= \frac{crk_{1}\left( y^{*}(t)\right) ^{2}}{\left( h+y^{*}(t)\right) \left( 1+k_{2}y^{*}(t)\right) ^{2}},\\ B_{4}(t)&=\frac{cry^{*}(t)\left( 2h+y^{*}(t)+hk_{2}y^{*}(t)\right) }{\left( h+y^{*}(t)\right) ^{2}\left( 1+k_{2}y^{*}(t)\right) ^{2}}. \end{aligned}$$

For $0<t\le T,$ let

$$\begin{aligned} \left\{ \begin{aligned} x(t)&=a_{1}(t)x_{k}+a_{2}(t)y_{k}+a_{3}(t)x_{k}^{2}+a_{4}(t)x_{k}y_{k}\\&\quad +a_{5}(t)y_{k}^{2} +o\left( \left( |x_{k}|+|y_{k}|\right) ^{3}\right) ,\\ y(t)&=b_{1}(t)x_{k}+b_{2}(t)y_{k}+b_{3}(t)x_{k}^{2}+b_{4}(t)x_{k}y_{k}\\&\quad +b_{5}(t)y_{k}^{2} +o\left( \left( |x_{k}|+|y_{k}|\right) ^{3}\right) , \end{aligned} \right. \end{aligned}$$

(4.3)

where

$$\begin{aligned} a_{1}(0)= & {} 1, a_{2}(0)=a_{3}(0)=a_{4}(0)=a_{5}(0)=0,\\ b_{2}(0)= & {} 1, b_{1}(0)=b_{3}(0)=b_{4}(0)=b_{5}(0)=0. \end{aligned}$$

From system (4.1), (4.2) and (4.3), we get

$$\begin{aligned} a_{1}(t)&=\exp \left( \int _{0}^{t}A_{1}\left( s\right) \,\mathrm {d}s\right) , a_{2}(t)=0, \\ a_{3}(t)&= \exp \left( \int _{0}^{t}A_{1}\left( s\right) \,\mathrm {d}s\right) \int _{0}^{t}\left( A_{3}\left( s\right) a_{1}^{2}\left( s\right) \right. \\&\quad \left. +A_{4}\left( s\right) a_{1}\left( s\right) b_{1}\left( s\right) \right) \\&\quad \times \exp \left( -\int _{0}^{s}A_{1}\left( \tau \right) \,\mathrm {d}\tau \right) \,\mathrm {d}s,\\ a_{4}(t)&= \exp \left( \int _{0}^{t}A_{1}\left( s\right) \,\mathrm {d}s\right) \int _{0}^{t}A_{4}\left( s\right) a_{1}\left( s\right) b_{2}\left( s\right) \\&\quad \times \exp \left( -\int _{0}^{s}A_{1}\left( \tau \right) \,\mathrm {d}\tau \right) \,\mathrm {d}s, \\ a_{5}(t)&=0, b_{1}(t)=e^{-d_{2}t}\int _{0}^{t}B_{1}\left( s\right) a_{1}\left( s\right) e^{d_{2}s}\,\mathrm {d}s, b_{2}(t)\\&=e^{-d_{2}t}, \\ b_{3}(t)&=e^{-d_{2}t}\int _{0}^{t}\left( B_{1}\left( s\right) a_{3}\left( s\right) \right. \\&\quad \left. +B_{3}\left( s\right) a_{1}^{2}\left( s\right) +B_{4}\left( s\right) a_{1}\left( s\right) b_{1}\left( s\right) \right) e^{d_{2}s}\,\mathrm {d}s, \\ b_{4}(t)&=e^{-d_{2}t}\int _{0}^{t}\left( B_{1}\left( s\right) a_{4}\left( s\right) \right. \\&\quad \left. +B_{4}\left( s\right) a_{1}\left( s\right) b_{2}\left( s\right) \right) e^{d_{2}s}\,\mathrm {d}s, b_{5}(t)=0. \end{aligned}$$

It follows from system (4.3) that

$$\begin{aligned} \left\{ \begin{aligned}&x(T)= a_{1}(T)x_{k}+a_{3}(T)x_{k}^{2}+a_{4}(T)x_{k}y_{k}\\&\quad +o\left( \left( |x_{k}|+|y_{k}|\right) ^{3}\right) ,\\&y(T)= b_{1}(T)x_{k}+b_{2}(T)y_{k}+b_{3}(T)x_{k}^{2}+b_{4}(T)x_{k}y_{k}\\&\quad +o\left( \left( |x_{k}|+|y_{k}|\right) ^{3}\right) , \end{aligned} \right. \end{aligned}$$

(4.4)

and

$$\begin{aligned} \left\{ \begin{aligned} x(T^{+})&=x(T),\\ y(T^{+})&=y(T). \end{aligned} \right. \end{aligned}$$

(4.5)

From (4.4) and (4.5), the following Poincaré map is obtained

$$\begin{aligned} \left\{ \begin{aligned} x_{k+1}&= a_{1}(T)x_{k}+a_{3}(T)x_{k}^{2}+a_{4}(T)x_{k}y_{k}\\&\quad +o\left( (|x_{k}|+|y_{k}|)^{3}\right) ,\\ y_{k+1}&= b_{1}(T)x_{k}+b_{2}(T)y_{k}+b_{3}(T)x_{k}^{2}+b_{4}(T)x_{k}y_{k}\\&\quad +o\left( (|x_{k}|+|y_{k}|)^{3}\right) . \end{aligned} \right. \end{aligned}$$

(4.6)

4.2 Transcritical bifurcation

In this subsection, we discuss the existence of a transcritical bifurcation by means of map (4.6).

The fixed point (0, 0) of map (4.6) corresponds to the prey-free periodic solution $(0,y^{*}(t))$ of system (1.3). The associated eigenvalues of the fixed point (0, 0) is given by

$$\begin{aligned} \lambda _{1}&= a_{1}(T)=\exp \left( \int _{0}^{T}\left( b-d_{1}-\frac{ry^{*}(s)}{1+k_{2}y^{*}(s)}\right) \,\mathrm {d}s\right) ,\\ \lambda _{2}&= b_{2}(T)=e^{-d_{2}T}<1, \end{aligned}$$

where $y^{*}(t)$ is defined in (2.2).

Denote

$$\begin{aligned} p_{0}=\frac{\left( 1-\exp \left( -d_{2}T\right) \right) \left( 1-\exp \left( -\frac{\left( b-d_{1}\right) k_{2}d_{2}T}{r}\right) \right) }{k_{2}\left( \exp \left( -\frac{\left( b-d_{1}\right) k_{2}d_{2}T}{r}\right) -\exp \left( -d_{2}T\right) \right) }. \end{aligned}$$

(4.7)

If $0<(b-d_{1})k_{2}<r$, then $p_{0}>0.$ So $\lambda _{1} \mid _{p=p_{0}}=1.$

By the above analysis, we find that one of the eigenvalues of the fixed point (0, 0) is 1. An eigenvalue with 1 is associated with a transcritical bifurcation in the map (4.6). Hence, $(0,0,p_{0})$ is a candidate for a transcritical bifurcation point in the map (4.6).

Let

$$\begin{aligned} E&=\int _{0}^{T}\left( -m+\frac{rk_{1}y^{*}\left( s\right) }{\left( 1+k_{2}y^{*}\left( s\right) \right) ^{2}}\right) \exp \left( \int _{0}^{s}\left( b-d_{1}\right. \right. \\&\quad \left. \left. -\frac{ry^{*}\left( \tau \right) }{1+k_{2}y^{*}\left( \tau \right) }\right) \,\mathrm {d}\tau \right) \,\mathrm {d}s. \end{aligned}$$

Theorem 4.1

Assume $0<(b-d_{1})k_{2}<r.$ If $E\le 0$, then a subcritical bifurcation occurs at $p=p_{0}$ in system (1.3).

Proof

Let $p=p_{0}+p_{1}$, then map (4.6) can be rewritten as

$$\begin{aligned}&F:{x \atopwithdelims ()y} \rightarrow \displaystyle {1 \, 0 \atopwithdelims ()f_{1} \, f_{2}} {x \atopwithdelims ()y}\nonumber \\&\quad + \displaystyle {e_{1}p_{1}x+e_{2}x^{2}+e_{3}xy \atopwithdelims ()f_{3}p_{1}x+f_{4}p_{1}y+f_{5}x^{2}+f_{6}xy} \nonumber \\&\quad +\displaystyle {o\left( \left( |p_{1}|+|x|+|y|\right) ^{3}\right) \atopwithdelims ()o\left( \left( |p_{1}|+|x|+|y|\right) ^{3}\right) }, \end{aligned}$$

(4.8)

where

$$\begin{aligned} e_{1}= & {} \frac{\partial a_{1}(T)}{\partial p}|_{p=p_{0}}, e_{2}=a_{3}(T)|_{p=p_{0}}, e_{3}=a_{4}(T)|_{p=p_{0}}, \\ f_{1}= & {} b_{1}(T)|_{p=p_{0}}, f_{2}=b_{2}(T)|_{p=p_{0}}, f_{3}=\frac{\partial b_{1}(T)}{\partial p}|_{p=p_{0}},\\ f_{4}= & {} \frac{\partial b_{2}(T)}{\partial p}|_{p=p_{0}}, f_{5}=b_{3}(T)|_{p=p_{0}}, f_{6}=b_{4}(T)|_{p=p_{0}}. \end{aligned}$$

According to map (4.8), we may let

$$\begin{aligned} J=\begin{pmatrix} 1 &{} 0 \\ \displaystyle \frac{f_{1}}{1-f_{2}} &{} 1 \end{pmatrix} \end{aligned}$$

and use the translation $\displaystyle {x\atopwithdelims ()y}=J{u\atopwithdelims ()v}$, then map (4.8) becomes

$$\begin{aligned}&{u\atopwithdelims ()v} \rightarrow \displaystyle {1\,0 \atopwithdelims ()0\,f_{2}} {u\atopwithdelims ()v}\nonumber \\&\quad +\displaystyle {h_{1}(u,v,p_{1})+o\left( (|p_{1}|+|u|+|v|)^{3}\right) \atopwithdelims ()h_{2}(u,v,p_{1})+o\left( (|p_{1}|+|u|+|v|)^{3}\right) }, \end{aligned}$$

(4.9)

where

$$\begin{aligned}&h_{1}(u,v,p_{1}) = e_{1}p_{1}u+(e_{2}+\frac{e_{3}f_{1}}{1-f_{2}})u^{2}+e_{3}uv,\\&h_{2}(u,v,p_{1}) = E_{1}p_{1}u+E_{2}p_{1}v+E_{3}u^{2}+E_{4}uv,\\&E_{1} = f_{3}+\frac{f_{1}(f_{4}-e_{1})}{1-f_{2}}, E_{2}=f_{4}, \\&E_{3} =f_{5}+\frac{f_{1}(f_{6}-e_{2})}{1-f_{2}}-\frac{e_{3}f_{1}^{2}}{(1-f_{2})^{2}},\\&E_{4} =f_{6}-\frac{f_{1}e_{3}}{1-f_{2}}. \end{aligned}$$

Now the center manifold theorem is used to determine the nature of the bifurcations of the fixed point (0, 0) at $p_{1}=0$. There exists a center manifold for  (4.9) which can be locally represented as follows

$$\begin{aligned} w^{c}(0)= & {} \{(u,v,p_{1})\in R^{3}\mid v=f(u,p_{1}), f(0,0)\\= & {} Df(0,0)=0\}. \end{aligned}$$

Letting $v=f(u,p_{1})=g_{1}u^{2}+g_{2}up_{1}+g_{3}p_{1}^{2}+o((|u|+|p_{1}|)^{3}),$ and substituting v into (4.9) yields $f(u+h_{1}(u,v,p_{1}),p_{1})=f_{2}v+h_{2}(u,v,p_{1}).$ Equating term of like powers to zero gives

$$\begin{aligned} g_{1}=\frac{E_{3}}{1-f_{2}},g_{2}=\frac{E_{1}}{1-f_{2}},g_{3}=0. \end{aligned}$$

Then

$$\begin{aligned} v=\frac{E_{3}}{1-f_{2}}u^{2}+\frac{E_{1}}{1-f_{2}}up_{1}+o((|u|+|p_{1}|)^{3}). \end{aligned}$$

Hence, the map (4.9) restricted to the center manifold is given by

$$\begin{aligned}&H:u \rightarrow u+e_{1}p_{1}u+\left( \frac{e_{3}f_{1}}{1-f_{2}}+e_{2}\right) u^{2}\\&\quad +o((|u|+|p_{1}|)^{3})=u{\bar{h}}(u,p_{1}), \end{aligned}$$

where

$$\begin{aligned} {\bar{h}}(u,p_{1})= & {} 1+e_{1}p_{1}+\left( \frac{e_{3}f_{1}}{1-f_{2}}+e_{2}\right) u\\&+\,o((|u|+|p_{1}|)^{2}). \end{aligned}$$

Then we consider the following equation

$$\begin{aligned} {\bar{h}}(u,p_{1})=1. \end{aligned}$$

(4.10)

We find

$$\begin{aligned} \frac{\partial {\bar{h}}(0,0)}{\partial u}=\frac{e_{3}f_{1}}{1-f_{2}}+e_{2}. \end{aligned}$$

From above analysis and $\lambda _{1} \mid _{p=p_{0}}=1$, we obtain

$$\begin{aligned} \frac{e_{3}f_{1}}{1-f_{2}}+e_{2}&= \int _{0}^{T}\left( -m+\frac{rk_{1}y^{*}(t)}{\left( 1+k_{2}y^{*}(t)\right) ^{2}}\right) a_{1}(t)\,\mathrm {d}t \nonumber \\&\quad -\int _{0}^{T}\frac{re^{-d_{2}t}}{\left( 1+k_{2}y^{*}(t)\right) ^{2}}\left[ \int _{0}^{t}D\left( s\right) \,\mathrm {d}s \right. \nonumber \\&\quad \left. +\int _{0}^{T}D(t)\,\mathrm {d}t\right] \,\mathrm {d}t \mid _{p=p_{0}}. \end{aligned}$$

(4.11)

where

$$\begin{aligned} D(t)&=\frac{cre^{d_{2}t}\left( y^{*}(t)\right) ^{2}}{\left( h+y^{*}(t)\right) \left( 1+k_{2}y^{*}(t)\right) }\exp \left( \int _{0}^{t}\left( b-d_{1}\right. \right. \nonumber \\&\quad \left. \left. -\frac{ry^{*}\left( s\right) }{1+k_{2}y^{*}(t)}\right) \,\mathrm {d}s\right) . \end{aligned}$$

(4.12)

It is obvious that if

$$\begin{aligned} \int _{0}^{T}\left( -m+\frac{rk_{1}y^{*}(t)}{\left( 1+k_{2}y^{*}(t)\right) ^{2}}\right) a_{1}(t)\,\mathrm {d}t\le 0, \end{aligned}$$

then $\frac{\partial {\bar{h}}(0,0)}{\partial u}<0.$ Thus, by the implicit function theorem, there exists $\epsilon >0$ and continuously differentiable function $\beta :(-\epsilon ,\epsilon )\rightarrow R$, such that

$$\begin{aligned} {\bar{h}}(\beta (p_{1}), p_{1})=1, \end{aligned}$$

(4.13)

where $|p_{1}|<\epsilon , \beta (0)=0.$

Let $u=\beta (p_{1})=p_{1}k$ where $k=k(p_{1}),$ then Eq. (4.13) can be written as

$$\begin{aligned} e_{1}+\frac{\partial {\bar{h}}(0,0)}{\partial u}k+o(|p_{1}k|+|p_{1}|)=0. \end{aligned}$$

(4.14)

It is easy to see that

$$\begin{aligned} e_{1}=-\int _{0}^{T}\frac{re^{-d_{2}s}}{(1-e^{-d_{2}T})(1+k_{2}y^{*}(t))^{2}}\,\mathrm {d}t|_{p=p_{0}}<0. \end{aligned}$$

Therefore, $e_{1}\frac{\partial {\bar{h}}(0,0)}{\partial u}>0.$ Hence, Eq. (4.14) has a negative root $k=k(p_{1})$ if $p_{1}$ is small enough. However, $u=p_{1}k>0.$ So, $p_{1}<0.$ Thus, system (1.3) undergoes a subcritical bifurcation at $p=p_{0}$. $\square$

Remark 4.1

Using (4.7), we find that the critical threshold $p_{0}$ always exists if $0<(b-d_{1})k_{2}<r$. In this case, once the periodic impulsive immigration of predator crosses the threshold $p_{0}$, a transcritical bifurcation will occur. It follows that the prey population will go extinct or resurge. Hence, the periodic impulsive immigration of predator has an important impact on the dynamics of the ecosystem.

Remark 4.2

It follows from Theorem 3.1 in [33] that if we let $\mu$ be the bifurcation parameter, then for a fixed T, there exist a sufficiently small $\epsilon$ and $\mu =\mu _{1}(T)-\epsilon$ such that system (1.2) has a positive periodic solution. That is to say, once there exists a critical threshold $\mu _{1}(T)$ and the parameter $\mu$ crosses this threshold, a transcritical bifurcation will occur. However, from Theorem 4.1, we find that it is not sufficient for the existence of a transcritical bifurcation in system (1.3). Thus, the Allee effect in the predator makes the transcritical bifurcation occur more difficultly.

5 Numerical simulation

In this section, we will give phase portraits and bifurcation diagrams of system (1.3) to illustrate the above theoretical analyses and find new interesting complex dynamical behaviors by using numerical simulations. Our simulation results are created using MATLAB. We consider the following three cases.

(1) The impact of Allee effect in the prey for system (1.3).

Fig. 1

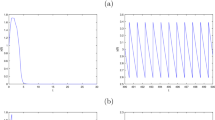
Time series of the solutions of system (1.3). a Time series of the solution with $a=0$. b Time series of the solution with $a=1.2$

Fig. 2

Time series of the solutions of system (1.3) with $a=1.2$

Fig. 3

Time series of the solutions of system (1.3). a Time series of x and y with $a=0.4$ and the initial point (0.1, 0.2). b Time series of x and y with $a=0.4$ and the initial point (0.12, 0.2). c Time series of x and y with $a=0.8$ and the initial point (0.22, 0.2). d Time series of x and y with $a=0.8$ and the initial point (0.23, 0.2). e Time series of x and y with $a=1.2$ and the initial point (0.38, 0.2). f Time series of x and y with $a=1.2$ and the initial point (0.39, 0.2)

Fig. 4

The solutions of system (1.3) with $a=1.2$. a Time series of y with $h=0$ and $p=0$. b Time series of y with $h=1$ and $p=0$. c Time series of the solution with $h=0$ and $p=0.2$. d Time series of the solution with $h=1.2$ and $p=0.2$. e Phase portraits with $h=1$ and $p=0.1$

Fig. 5

Bifurcation diagrams of system (1.3) with $a>0$ and the initial point (0.3, 0.2) with respect to h

Fig. 6

Bifurcation diagrams of system (1.3) with $a>0$ and the initial point (0.8, 0.2) with respect to h

Fig. 7

Bifurcation diagrams of system (1.3) with $a=0$ and $m=4.2$ with respect to h

Fig. 8

Bifurcation diagrams of system (1.3) with $a=0$ with respect to p

Fig. 9

Bifurcation diagrams of system (1.3) with $a=0.01$ with respect to p

Consider the following set of parameters

$$\begin{aligned} b= & {} 0.8, d_{1}=0.1, m=0.1, r=0.2, k_{1}=0.1, k_{2}{=}2, \\ c= & {} 0.8, h=0.2, d_{2}=0.2, T=1, p=0.2. \end{aligned}$$

Time series of the solutions (x(t), y(t)) of system (1.3) from the initial points (0.2, 0.2) are drawn in Fig. 1. Figure 1 shows that Allee effect of the prey population increases the extinction risk of prey.

Time series of the solutions (x(t), y(t)) of system (1.3) from the initial points $(0.2,0.2), (0.25,0.2), (0.3,0.2), (0.35,0.2), (0.4,0.2), (0.45,0.2)$ and $(0.5,0.2)$ with $a=1.2$ are drawn in Fig. 2. Figure 2 shows that there exists a positive constant $L_{x}$ such that the solutions (x(t), y(t)) of system (1.3) with the initial point $(x(0^{+}), y(0^{+}))$ tends to a prey-free periodic solution when t increases if $x(0^{+})<L_{x}$ and tends to a positive periodic solution when t increases if $x(0^{+})>L_{x}.$

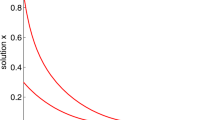
Time series of the solutions (x(t), y(t)) of system (1.3) from the initial points (0.1, 0.2) and (0.12, 0.2) with $a=0.4$ are drawn in Fig. 3a, b. By Fig. 3a, b, we have $0.1<L_{x}<0.12.$ Similarly, from Fig. 3c–f, we find $0.22<L_{x}<0.23$ for $a=0.8$ and $0.38<L_{x}<0.39$ for $a=1.2$. It is obvious that the threshold value $L_{x}$ increases when the parameter a increases.

(2) The impact of Allee effect in the predator for system (1.3).

Case $(A): a > 0.$

In this case, we let $a=1.2.$ The other parameters are the same as case (1). By Fig. 4a, b, we see that Allee effect in the predator may cause the predator of system (1.3) without the periodic constant impulsive immigration of predator to die out. However, from Fig. 4e, we find that predator and prey populations of system (1.3) with impulse coexist. So the impact of Allee effect in the predator can be eliminated by the impulse. Hence the periodic constant impulsive immigration for the predator is beneficial. Fig. 4c, d shows that Allee effect in the predator may make the densities of the predator decrease. However, the predator cannot become extinct since there exists the periodic constant impulsive immigration of predator.

Similar to case (1), we may find that there exists a positive constant $L_{x1}\in (0.34,0.35)$ such that the solution (x(t), y(t)) of system (1.3) with $h=0$ and the initial point $(x(0^{+}), y(0^{+}))$ tends to a prey-free periodic solution when t increases if $x(0^{+})<L_{x1}$ and tends to a positive periodic solution when t increases if $x(0^{+})>L_{x1}.$ Next, we let $x(0^{+})=0.3, 0.8$ and investigate the impact of Allee effect in the predator for system (1.3). The bifurcation diagram of system (1.3) with respect to h is presented in Fig. 5. It is seen from the bifurcation diagram that the solution of system (1.3) with the initial point (0.3, 0.2) always tends to a prey-free periodic solution for $h\in (0,100)$. Figure 6 shows that the solution of system (1.3) with the initial point (0.8, 0.2) always tends to a positive periodic solution for $h\in (0,100)$. Thus, we may predict that Allee effect for the predator does not affect the threshold value $L_{x1}.$

Case $(B): a=0.$

Consider the following set of parameters [34]

$$\begin{aligned}&b=8.1, d_{1}=0.1, m=5, r=1, k_{1}=1, k_{2}=0.01, \\&c=0.95, d_{2}=0.2, T=4, h=1, p=3. \end{aligned}$$

The bifurcation diagram of system (1.3) with respect to h is presented in Fig. 7. System (1.3) presents complicated dynamics in this case. From Fig. 7, we can see that there exist the chaotic regions and period orbits as the parameter h varying. Figure 7 depicts that there are T, 2T-periodic windows.

(3) The impact of the impulse for system (1.3).

The bifurcation diagram of system (1.3) with respect to p is presented in Fig. 8. It is seen from the bifurcation diagram that the prey-free periodic solution is stable for $p\in (7.01, +\infty )$ and unable for $p\in (0,7.01)$. A positive T-periodic solution bifurcates from the prey-free periodic solution at $p\approx 7.01$ through transcritical bifurcation. This positive T-periodic solution is stable for $p\in (4.21, 7.01)$ and unable for $p\in (0, 4.21)$. A positive 2T-periodic solution bifurcates from the positive T-periodic solution at $p\approx 4.21$ through flip bifurcation.

The bifurcation diagram of system (1.3) with $a=0.01$ with respect to p is presented in Fig. 9. From Fig. 8, we may see that there exists a positive T-periodic solution of system (1.3) for $a=0$ and $p\in (0, 1)$. However, if we take $a=0.01,$ then Fig. 9 shows that system (1.3) experiences a complicated process. Thus, the Allee effect in the prey has a greatly effect on the dynamical behaviors of system (1.3).

6 Discussion

In this paper, we mainly discuss the impact of Allee effect and impulse on system (1.3). Using theoretical analyses, we find that the strong Allee effect of the prey population increases the extinction risk of prey. This is the same as the continuous systems with the strong Allee effect in the prey. However, in this case, we may still make the predator and prey coexist by Theorem 3.1. By numerical simulations, we may see that there may be a positive periodic solution which is locally stable. Of course, how do we prove the existence of a positive periodic solution. It will be our future work. Additionally, since the prey-free periodic solution of system (1.3) is always locally asymptotically stable, the transcritical bifurcation does not exist. Hence, the strong Allee effect of the prey population can extinct the transcritical bifurcation. By numerical simulations, we may see that the threshold value $L_{x}$ always exists and will be larger when Allee effect in the prey becomes stronger. Depending on the Allee effect in the predator population, the predator may survive or be driven to extinction as well for the continuous systems. However, if we incorporate the periodic constant impulsive immigration for the predator, then the predator will survive. Hence, the periodic constant impulsive immigration for the predator can extinct the impact of Allee effect on the predator. By numerical simulations, we may predict that Allee effect for the predator does not affect the threshold value $L_{x}.$ For theoretical analyses, it will be our future work. In contrast, whether Allee effect in the predator becomes stronger or not when Allee effect in the prey becomes stronger. It is very interesting. In a word, we can say that the Allee effect of prey species may be a destabilizing force in the system (1.3). Weather it may affect the stability of a positive periodic solution or not, it will be a challenging work which is different from the continuous systems. It is clear that the impact of Allee effect of predator species is relatively small since there exists the periodic constant impulsive immigration for the predator.