1 Introduction

Networked control systems (NCSs) are a special kind of feedback control systems with control loops closed through a real-time network [8, 17, 33]. Roughly speaking, a typical networked control system consists of four fundamental components: (a) plants; (b) sensors/actuators; (c) controllers/filters; and (d) a shared communication network. More specifically, the information from control system components is transmitted through a communication network in NCSs. It has been recognized that there exist many advantages of NCSs compared to traditional ones, such as reducing system wiring, the low installation and maintenance costs, increasing system flexibility and high reliability. Therefore, it is easy to explain why NCSs have been attracting considerable attention and successfully applied in practice in several areas. Examples range from manufacturing, industrial process control, automation, to robotics. For more details, we refer readers to [1, 2, 37].

A fact in NCSs is that the communication bandwidth resource becomes more and more limited as the complexity of the network increases [12, 15]. As a consequence, some phenomena include, but are not limited to, congestion, quantization errors, network-induced delays, packet dropouts, inevitably exist in the applications of NCSs, which lead to some unfavorable factors for system performance or even instability [10, 11, 20, 22, 23, 38]. How to overcome such a difficulty is therefore a hot topic in the study of NCSs. Taking limited communication capacity into consideration, the last decades have witnessed a rapid growth in investigating data sampling schemes in the development of NCSs. Usually, there are two typical schemes to be applied, i.e., the time-triggered sampling scheme and the event-triggered one. The former has advantages of reducing the complexity and difficulty of analysis and design, and then has been extensively used to address the problem of state estimation or control for NCSs. It should be pointed out that the time-triggered scheme with the fixed sampling interval cannot perform the case when the measurement signals have little fluctuating [19]. Thankfully, the latter, i.e., the event-triggered scheme (ETS) has been proposed to screen the unnecessary information, which the trigger condition of transferring information is determined by the occurrence of an “event.” Its superiority in reducing the utilization of the scarce communication resource has been demonstrated in many works, e.g., see in [37] and [19]. It is hardly surprising that the design issue of NCSs based on the ETS has been widely concerned and an abundance of the literature has emerged in recent years. For instance, the problem of distributed event-triggered \(H_{\infty }\) filtering was presented in [4] for sensor networks, where each sensor node could be capable of determining whether or not to transmit the current sample information; the distributed event-triggered fuzzy filter was designed for a class of nonlinear networked control systems in [29]; the event-triggered \(H_{\infty }\) controller was designed for NCSs in [36], where a delayed system method was constructed.

On the other hand, it is known that Markov jump model has long enjoyed a good reputation for modeling many networked-induced phenomena, such as the random time delays and the packet dropouts [5, 9, 14, 24,25,26, 30,31,32] . Within the Markov jump systems (MJSs) framework, the problem of discrete-time \(H_{2}\) output tracking control for wireless NCSs was considered in [35], where the Markov chains were used to model the time delays; the \(H_{\infty }\) fault detection filter was designed in [16], in which NCSs were modeled by MJSs via using the multirate sampling method and the augmented state matrix method. As stated as previous, the event-triggered mechanism has a huge advantage in reducing the utilization of the communication resource; therefore, it is an interesting problem that the event-triggered mechanism is considered in the NCSs with Markov jump parameters [28]. However, in [5, 9, 14, 16, 24,25,26, 28, 30, 32] , the sojourn time between two successive jumps was assumed to obey the exponential probability distribution. Owing to the memoryless property of the exponential probability distribution, the transition rates of MJSs were required to be constant and independent of the past. Such a requirement may be unreasonable in many practical situation. In order to relax the limitation, the semi-Markov process has been introduced and a large quantify of results on semi-Markov jump systems (sMJSs) have been published. To name a few, the design of \(H_{\infty }\) controller for a class of sMJSs was presented in [6], where a sufficient condition for the existence of the controller was proposed; the analysis of the robust stochastic stability and the problem of robust control design for sMJSs were considered in [7, 39]. However, it is worthy noting that most of the existing results on networked MJSs have been reported based on the time-triggered sampling scheme, there are no attempts to the issue of dissipative filtering for networked sMJSs, and few efforts forward the co-design approach for the event-triggered mechanism and the dissipative filter for the underlying systems, which motivates the recent work.

In this paper, we are interested in coping with the problem of the event-triggered dissipative filtering for a class of networked sMJSs. An event-triggered mechanism is introduced as a sampling scheme aiming at the benefit of saving the limited network resources. A Markov switched Lyapunov functional is used to derive conditions of the existence of the desired filter. A networked mass-spring system model is provided to show the availability of the proposed approach. The main contributions of this paper are summarized as two following folds: (1) As a first attempt, a new class of filters named event-triggered dissipative filters are developed to reflect the limited communication links between the plant and the desired filter for networked sMJSs; (2) The improved delayed system approach is employed to deal with the event-triggered filtering problem by using some novel integral inequalities. As a result, the less conservative conditions are established than the existing ones, which is shown in Example 1 in Sect. 4.

The rest of this paper is outlined as follows. The formulation of problem under consideration is presented in Sect. 2. In Sect. 3, the dissipative filtering performance analysis and filter design are given. Two examples are provided to illustrate the efficiency of the proposed method in Sect. 4. Finally, conclusion is given in Sect. 5.

Notation Throughout this paper, \( \mathbb {R} ^{n}\) denotes the n-dimensional Euclidean space; for symmetric matrices P, the notation \(P\ge 0\) (respectively, \(P>0\)) means that the matrix P is positive semi-definite (respectively, positive definite); I and 0 represent the identity matrix and zero matrix with appropriate dimension, respectively. \(\mathcal {E}\left\{ \cdot \right\} \) denotes the expectation operator; the notation \(M^\mathrm{T}\) represents the transpose of the matrix M, and \(\mathrm{sym}\{M\}\) stands for \(M+M^\mathrm{T}\). \( \mathcal {L}_{2}\left[ 0,\infty \right) \) is the space of square-summable infinite vector sequences over \(\left[ 0,\infty \right) \). In symmetric block matrices or complex matrix expressions, an asterisk \((*)\) is employed to represent a term that is induced by symmetry. Matrices, if not explicitly stated, are assumed to have compatible dimensions.

2 Problem formulation

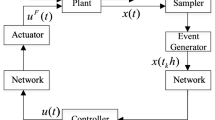
The networked system with an event-triggered communication scheme, as depicted in Fig. 1, contains a linear continuous-time system, a sensor, a sampler, an event detector, a zero-order hold (ZOH), a filter and a communication network. Indeed, the output signal of plant \(y\left( t\right) \) is transmitted over a communication network, where a networked dissipative filter will be designed to estimate the \(z\left( t\right) .\)

Fig. 1
figure 1

A framework of networked filter with an event-triggered communication scheme

Full size image

Considering the following plant which is characterized as a semi-Markov jump system represented by

$$\begin{aligned} \left( \Sigma \right) :\left\{ \begin{array}{l} \dot{x}\left( t\right) =A\left( \beta \left( t\right) \right) x\left( t\right) +B\left( \beta \left( t\right) \right) \omega \left( t\right) , \\ y\left( t\right) =L\left( \beta \left( t\right) \right) x\left( t\right) ,\\ z\left( t\right) =C\left( \beta \left( t\right) \right) x\left( t\right) +D\left( \beta \left( t\right) \right) \omega \left( t\right) , \end{array} \right. \end{aligned}$$
(1)

where \(x\left( t\right) \in \mathbb {R}^{n}\) is the system state, \(y\left( t\right) \in \mathbb {R}^{m}\) is the measurement output and \(z\left( t\right) \in \mathbb {R}^{q}\) is the signal to be estimated, \(\omega \left( t\right) \in \mathbb {R}^{p}\) is assumed to be an arbitrary noise signal, and \(\omega \left( t\right) \in \mathcal {L}_{2}\left[ 0,\infty \right) \). \(A\left( \beta \left( t\right) \right) \), \(B\left( \beta \left( t\right) \right) \), \( C\left( \beta \left( t\right) \right) \), \(D\left( \beta \left( t\right) \right) \) and \(L\left( \beta \left( t\right) \right) \) are known real constant matrices with appropriate dimensions for each \(\beta \left( t\right) \in \mathcal {S}=\left\{ 1,2,\ldots ,r\right\} \). Fixed a probability space \(( \Omega ,\mathcal {F},\mathcal {P})\), where \( \Omega \) is a sample space, \(\mathcal {F}\) is the \(\sigma \)-algebra of subsets of the sample space and \(\mathcal {P}\) is the probability measure on \(\mathcal {F} \). The random variable \(\left\{ \beta \left( t\right) ,t\geqslant 0\right\} \) stands for a continuous-time discrete-state semi-Markov process and taking discrete values in a given finite set \(\mathcal {S}\) with transition probability matrix \(\prod \overset{\triangle }{=}\left\{ \pi _{ij}\left( \triangle \right) \right\} \) given by [13]

$$\begin{aligned}&\Pr \left\{ \beta \left( t+\triangle \right) =j\left| \beta \left( t\right) =i\right. \right\} \nonumber \\&\quad =\left\{ \begin{array}{l} \pi _{ij}\left( \triangle \right) \triangle +o\left( \triangle \right) ,\quad i\ne j \\ 1+\pi _{ii}\left( \triangle \right) \triangle +o\left( \triangle \right) ,\quad i=j \end{array},\right. \end{aligned}$$
(2)

where \(\triangle >0\) is the sojourn time, lim\(_{\triangle \rightarrow 0}\left( o\left( \triangle \right) /\triangle \right) =0\) and \(\pi _{ij}\left( \triangle \right) \ge 0,\) for \(j\ne i,\) is the transition rate from mode i at time t to mode j at time \(t+\triangle \) and

$$\begin{aligned} \pi _{ii}\left( \triangle \right) =-\sum _{j\in \mathcal {S}\text {,}j\ne i}\pi _{ij}\left( \triangle \right) . \end{aligned}$$

In this paper, we are interested in designing a Markov switched filter described by the following state-space realization

$$\begin{aligned} \dot{x}_{f}\left( t\right)= & {} A_{f}\left( \beta \left( t\right) \right) x_{f}\left( t\right) +B_{f}\left( \beta \left( t\right) \right) \overset{\_}{ y}(t), \nonumber \\ z_{f}\left( t\right)= & {} C_{f}\left( \beta \left( t\right) \right) x_{f}\left( t\right) +D_{f}\left( \beta \left( t\right) \right) \overset{\_}{ y}(t), \end{aligned}$$
(3)

where \(x_{f}\left( t\right) \) is the filter state vector, \(z_{f}\left( t\right) \) is the filter output vector, \(\bar{y}(t)\) is input signal of filter which from ZOH. \(A_{f}\left( \beta \left( t\right) \right) \), \(B_{f}\left( \beta \left( t\right) \right) \), \(C_{f}\left( \beta \left( t\right) \right) \) and \(D_{f}\left( \beta \left( t\right) \right) \) are the parameters of the filter to be determined. For brevity, we denote \( A_{i}=A\left( \beta \left( t\right) \right) \) and \(A_{fi}\) \(=A_{f}\left( \beta \left( t\right) \right) \) for each \(\beta \left( t\right) =i\in \mathcal {S}\), and the other symbols are similarly denoted.

Remark 1

In the time-triggered scheme, all the sampled data packets will be sent to ZOH for the filter designed. As a matter of fact, there is no need to transmit those data packets which carry little new information. In this case, how to obtain the threshold conditions to determine whether the current sampled data packets should be transmitted or not is a key question. It is obvious that the limited network bandwidth resources can be saved if we can only transmit the available sampled data packets. Fortunately, event-triggered scheme (ETS) could be applied as an effective solution to screen the unnecessary data packet transmission.

In this paper, an ETS is proposed, where the event detector is used to determine whether the newly sampled data packet \(\left( t_{k}+n,y\left( t_{k}h+nh\right) \right) \) should be stored and sent out to the filter at the same time by using the following threshold condition [36]:

$$\begin{aligned}&\left[ y\left( \left( t_{k}+n\right) h\right) -y\left( t_{k}h\right) \right] ^\mathrm{T}\Lambda _{i}\left[ y\left( \left( t_{k}+n\right) h\right) \right. \nonumber \\&\left. \quad -y\left( t_{k}h\right) \right] <\lambda _{i}y^\mathrm{T}\left( t_{k}h\right) \Lambda _{i}y\left( t_{k}h\right) , \end{aligned}$$
(4)

where \(h\ \)is a constant sampling period, \(t_{k}h\) \(\left( k\in \mathbb {N} \right) \) is the triggered instant (or release instant), \(n=1,2,\cdots ,\rho _{k}\) with \(\rho _{k}=t_{k+1}-t_{k}-1\), \(\lambda _{i}\in \left[ 0,1\right) \) are the given scalar parameters that set the detection thresholds for each \( i\in \mathcal {S}\), \(\Lambda _{i}>0\) are the event-triggered matrices to be determined in the co-design.

Observe that the transmission delay phenomenon and the property of ZOH, we obtain

$$\begin{aligned} \overset{\_}{y}(t)=y\left( t_{k}h\right) ,t\in \left[ t_{k}h+\tau _{t_{k}},t_{k+1}h+\tau _{t_{k+1}}\right) . \end{aligned}$$

Furthermore, under the ZOH, the interval \([ t_{k}h+\tau _{t_{k}}, t_{k+1}h+\tau _{t_{k+1}}) \) can be written as

$$\begin{aligned} \left[ t_{k}h+\tau _{t_{k}},t_{k+1}h+\tau _{t_{k+1}}\right) =\overset{\rho _{k}}{\underset{n=0}{\bigcup }}\mathcal {I}_{n}, \end{aligned}$$

where

$$\begin{aligned} \mathcal {I}_{n}=\left[ t_{k}h+nh+\hat{\tau },t_{k}h+nh+h+\hat{\tau }\right) , \end{aligned}$$

with \(n=1,2,\cdots ,\rho _{k}-1\), \(\mathcal {I}_{0}=\left[ t_{k}h+\tau _{t_{k}},t_{k}h+h+\hat{\tau }\right) \), and \(\mathcal {I}_{\rho _{k}}=\left[ t_{k}h+\rho _{k}h+\hat{\tau },t_{k+1}h+\tau _{t_{k+1}}\right) \), the network-induced delays \(\tau _{t_{k}}\in (0,\hat{\tau }]\), \(\hat{\tau }\) is the upper bound of \(\tau _{t_{k}},\rho _{k}\) is a positive integer.

Define the network delay \(\tau \left( t\right) \) and the error \(e_{k}\left( t\right) \) between the latest transmission data and the current sampled data as

$$\begin{aligned} \tau \left( t\right)= & {} t-t_{k}h-nh, \quad t\in \mathcal {I}_{n}, \\ e_{k}\left( t\right)= & {} y\left( t_{k}h\right) -y\left( t_{k}h+nh\right) , \quad t\in \mathcal {I}_{n}, \end{aligned}$$

then, we have

$$\begin{aligned} 0<h_{1}\leqslant \tau _{t_{k}}\leqslant \tau \left( t\right) <h+\hat{\tau } \overset{\Delta }{=}h_{2},h_{1}=\inf \{\tau _{t_{k}}\}, \end{aligned}$$

and \(\overset{\_}{y}(t)=\) \(y\left( t_{k}h\right) =e_{k}\left( t\right) +y\left( t-\tau \left( t\right) \right) .\)

Augmenting the system \(\left( \Sigma \right) \) to include the filter system (3), we can get the following filtering error system

$$\begin{aligned} \left( \tilde{\Sigma }\right) :\left\{ \begin{array}{l} \overset{\cdot }{\tilde{x}}\left( t\right) =\tilde{A}_{i}\tilde{x}\left( t\right) +\tilde{B}_{i}x\left( t-\tau \left( t\right) \right) +\tilde{C} _{i}\omega \left( t\right) \\ \quad +\,\tilde{D}_{i}e_{k}\left( t\right) , \\ e\left( t\right) =\tilde{S}_{i}\tilde{x}\left( t\right) +D_{i}\omega \left( t\right) \\ \quad -D_{fi}L_{i}x\left( t-\tau \left( t\right) \right) -D_{fi}e_{k}\left( t\right) , \end{array} \right. \end{aligned}$$
(5)

where

$$\begin{aligned} \begin{aligned}&\tilde{x}\left( t\right) =\left[ \begin{array}{c} x\left( t\right) \\ x_{f}\left( t\right) \end{array} \right] ,e\left( t\right) =z\left( t\right) -z_{f}\left( t\right) ,\\&\tilde{A} _{i}=\left[ \begin{array}{cc} A_{i} &{}\quad 0 \\ 0 &{}\quad A_{fi} \end{array} \right] , \\&\tilde{B}_{i}=\left[ \begin{array}{c} 0 \\ B_{fi}L_{i} \end{array} \right] ,\tilde{D}_{i}=\left[ \begin{array}{c} 0 \\ B_{fi} \end{array} \right] ,\\ {}&\tilde{S}_{i}=\left[ \begin{array}{cc} C_{i}&\quad -C_{fi} \end{array} \right] ,\tilde{C}_{i}=\left[ \begin{array}{c} B_{i} \\ 0 \end{array} \right] , \end{aligned} \end{aligned}$$

and the error \(e_{k}\left( t\right) \) satisfies the following threshold condition

$$\begin{aligned} e_{k}^\mathrm{T}\left( t\right) \Lambda _{i}e_{k}\left( t\right)< & {} \lambda _{i}\left[ e_{k}\left( t\right) +L_{i}x\left( t-\tau \left( t\right) \right) \right] ^\mathrm{T}\nonumber \\&\Lambda _{i}\left[ e_{k}\left( t\right) +L_{i}x\left( t-\tau \left( t\right) \right) \right] , \end{aligned}$$
(6)

which is obtained from the triggering condition (4).

Definition 1

Given a scalar \(\alpha >0\), real matrices \(W_{1}^\mathrm{T}=W_{1}=-\bar{W} _{1}^\mathrm{T}\bar{W}_{1}\leqslant 0\), \(W_{2}\) and \(W_{3}=W_{3}^\mathrm{T}>0\), the system \(\left( 5 \right) \) is said to be stochastically stable and strictly \( \left( W_{1},W_{2},W_{3}\right) -\alpha -\)dissipative. Then, the following conditions are satisfied:

  1. 1.

    the system \(\left( 5 \right) \) with \(\omega (t)=0\) is stochastically stable;

  2. 2.

    under zero initial condition, the following condition is satisfied:

    $$\begin{aligned}&\mathcal {E}\left\{ \int _{0}^{\gamma }e^\mathrm{T}\left( t\right) W_{1}e\left( t\right) +\mathrm{sym}\left( e^\mathrm{T}\left( t\right) W_{2}\omega \left( t\right) \right) \right. \nonumber \\&\quad \left. +\,\omega ^\mathrm{T}\left( t\right) W_{3}\omega \left( t\right) \mathrm{d}t\right\} \geqslant \alpha \int _{0}^{\gamma }\left[ \omega ^\mathrm{T}\left( t\right) \omega \left( t\right) \right] \mathrm{d}t,\nonumber \\ \end{aligned}$$
    (7)

    for any \(\gamma \geqslant 0\) and any nonzero \(\omega \left( t\right) \in \mathcal {L}_{2}\left[ 0,\infty \right) \).

Remark 2

By changing \(W_{1}\) and \(W_{2}\), the condition of (7) can degrade into the \(H_{\infty }\) performance index and the passive performance index as follows:

  1. 1.

    when letting \(W_{1}=-I\), \(W_{2}=0\), and \(W_{3}>\alpha I\), the condition of (7) reduces to the \(H_{\infty }\) performance index;

  2. 2.

    when letting \(W_{1}=0\), \(W_{2}=I\), and \(W_{3}>\alpha I\), the condition of (7) turns into the passive performance index.

Lemma 1

[18] Let \(f_{1},f_{2},\ldots ,f_{N}:\mathbb {R}^{m}\longrightarrow \mathbb {R}\) have positive values in an open subset \( \mathsf {A}\) of \(\mathbb {R}^{m}\). Then, the reciprocally convex combination of \(f_{i}\) over \(\mathsf {A}\) satisfies

$$\begin{aligned}&\underset{\left\{ \theta _{i}\left| \theta _{i}>0,\underset{i}{\sum } \theta _{i}=1\right. \right\} }{\min }\underset{i}{\sum }\frac{1}{\theta _{i} }f_{i}\left( t\right) \nonumber \\&\quad =\underset{i}{\sum }f_{i}\left( t\right) +\underset{ g_{i,j}\left( t\right) }{\max }\underset{i\ne j}{\sum }g_{i,j}\left( t\right) \end{aligned}$$
(8)

subject to

$$\begin{aligned}&\left\{ g_{i,j}:\mathbb {R}^{m}\longrightarrow \mathbb {R},g_{j,i}\left( t\right) \triangleq g_{i,j}\left( t\right) ,\right. \nonumber \\&\quad \left. \left[ \begin{array}{cc} f_{i}\left( t\right) &{}\quad g_{i,j}\left( t\right) \\ g_{i,j}\left( t\right) &{}\quad f_{j}\left( t\right) \end{array} \right] \geqslant 0\right\} . \end{aligned}$$

Lemma 2

[21] For scalars \(0<h_{1}<h_{2}\) and matrices \( Z_{1}\in \mathbb {R}^{n\times n}\) and \(X=\left[ \begin{array}{cc} X_{11} &{}\quad X_{12} \\ X_{21} &{}\quad X_{22} \end{array} \right] \in \mathbb {R}^{2n\times 2n}\) satisfying

$$\begin{aligned} \Phi \triangleq \left[ \begin{array}{cc} \mathrm {diag}\left\{ Z_{1},3Z_{1}\right\} &{}\quad X \\ *&{}\quad \mathrm {diag}\left\{ Z_{1},3Z_{1}\right\} \end{array} \right] \geqslant 0, \end{aligned}$$
(9)

if there exists a vector function \(x:\left[ t-h_{2},t\right] \longrightarrow \) \(\mathbb {R}^{n}\) such that the integrations in the following are well defined, then

$$\begin{aligned}&-h_{2}\int _{t-h_{2}}^{t}\dot{x}^\mathrm{T}\left( s\right) Z_{1}\dot{x}\left( s\right) \mathrm{d}s\nonumber \\&\quad \leqslant -\varsigma ^\mathrm{T}\left( t\right) \Psi _{12}^\mathrm{T}\Phi \Psi _{12}\varsigma \left( t\right) , \end{aligned}$$
(10)

where

$$\begin{aligned} \varsigma ^\mathrm{T}\left( t\right)= & {} \left[ \begin{array}{cccccc} x^\mathrm{T}\left( t\right)&x^\mathrm{T}\left( t-h_{1}\right)&x^\mathrm{T}\left( t-h_{2}\right)&\varsigma _{1}^\mathrm{T}\left( t\right)&\varsigma _{2}^\mathrm{T}\left( t\right)&\omega ^\mathrm{T}\left( t\right) \end{array} \right] , \\ \varsigma _{1}\left( t\right)= & {} \frac{1}{h_{1}}\int _{t-h_{1}}^{t}x\left( s\right) \mathrm{d}s,\varsigma _{2}\left( t\right) =\frac{1}{h_{12}} \int _{t-h_{2}}^{t-h_{1}}x\left( s\right) \mathrm{d}s, \\ \Psi _{1}= & {} \left[ \begin{array}{cccccc} I &{}\quad -I &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ I &{}\quad I &{}\quad 0 &{}\quad -2I &{}\quad 0 &{}\quad 0 \end{array} \right] ,\\ \Psi _{2}= & {} \left[ \begin{array}{cccccc} 0 &{}\quad I &{}\quad -I &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad I &{}\quad I &{}\quad 0 &{}\quad -2I &{}\quad 0 \end{array} \right] , \\ \Psi _{12}= & {} \left[ \begin{array}{c} \Psi _{1} \\ \Psi _{2} \end{array} \right] ,X=\left[ \begin{array}{cc} X_{11} &{}\quad X_{12} \\ X_{21} &{}\quad X_{22} \end{array} \right] . \end{aligned}$$

3 Main results

Theorem 1

For given scalars \(\alpha \), \(0\le \lambda _{i}<1\), \( h_{2}>h_{1}>0\), matrices \(W_{1}^\mathrm{T}=W_{1}=-\bar{W}_{1}^\mathrm{T}\bar{W} _{1}\leqslant 0\), \(W_{2}\) and \(W_{3}=W_{3}^\mathrm{T}>0\), if there exist real matrices \(\Lambda _{i}>0\), \(P_{i}>0\), \(Q_{1i}>0\), \(Q_{2i}>0\), \(T>0\), \( Z_{1}>0 \), \(Z_{2}>0\) and Y of appropriate dimensions such that the following matrix inequalities hold for each \(i\in \mathcal {S}\)

$$\begin{aligned} \Omega _{i}\triangleq & {} \left[ \begin{array}{cc} \Omega _{11i} &{}\quad \Omega _{12i} \\ *&{}\quad \Omega _{22i} \end{array} \right] <0, \end{aligned}$$
(11)
$$\begin{aligned} \Phi\triangleq & {} \left[ \begin{array}{cc} \mathrm {diag}\left\{ Z_{1},3Z_{1}\right\} &{}\quad X \\ *&{}\quad \mathrm {diag}\left\{ Z_{1},3Z_{1}\right\} \end{array} \right] \ge 0, \end{aligned}$$
(12)
$$\begin{aligned} \Pi _{1}\triangleq & {} \left[ \begin{array}{cc} -Z_{2} &{}\quad -Y \\ *&{}\quad -Z_{2} \end{array} \right] <0, \end{aligned}$$
(13)
$$\begin{aligned} \Xi _{1,i}\triangleq & {} \underset{j\in \mathcal {S}}{\sum }\pi _{ij}\left( \triangle \right) \left( Q_{1j}+Q_{2j}\right) -T<0, \end{aligned}$$
(14)
$$\begin{aligned} \Xi _{2,i}\triangleq & {} \underset{j\in \mathcal {S}}{\sum }\pi _{ij}\left( \triangle \right) Q_{2j}-T<0, \end{aligned}$$
(15)

where

$$\begin{aligned} \Omega _{11i}\triangleq & {} \left[ \begin{array}{ccccc} \Omega _{11i}^{11} &{}\quad \Omega _{11i}^{12} &{}\quad \Omega _{11i}^{13} &{}\quad 6H^\mathrm{T}Z_{1} &{}\quad 2H^\mathrm{T}\left( X_{12}+X_{22}\right) \\ *&{}\quad \Omega _{11i}^{22} &{}\quad \Omega _{11i}^{23} &{}\quad \Omega _{11i}^{24} &{}\quad 6Z_{1}-2\left( X_{12}-X_{22}\right) \\ *&{}\quad *&{}\quad \Omega _{11i}^{33} &{}\quad -2\left( X_{21}^\mathrm{T}-X_{22}^\mathrm{T}\right) &{}\quad 6Z_{1} \\ *&{}\quad *&{}\quad *&{}\quad -12Z_{1}+h_{1}\Xi _{1,i} &{}\quad -4X_{22} \\ *&{}\quad *&{}\quad *&{}\quad *&{}\quad -12Z_{1}+h_{12}\Xi _{2,i} \end{array} \right] , \\ \Omega _{12i}\triangleq & {} \left[ \begin{array}{cccc} P_{i}^\mathrm{T}\tilde{B}_{i} &{}\quad P_{i}^\mathrm{T}\tilde{D}_{i} &{}\quad P_{i}^\mathrm{T}\tilde{C} _{i}+HA_{i}^\mathrm{T}\left( h_{2}^{2}Z_{1}+h_{12}^{2}Z_{2}\right) B_{i}-\tilde{S} _{i}^\mathrm{T}W_{2} &{}\quad \tilde{S}_{i}^\mathrm{T}\bar{W}_{1}^\mathrm{T} \\ Z_{2}-Y &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ Z_{2}-Y^\mathrm{T} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{array} \right] , \\ \Omega _{22i}\triangleq & {} \left[ \begin{array}{cccc} \Omega _{22i}^{11} &{}\quad \lambda _{i}L_{i}^\mathrm{T}\Lambda _{i} &{}\quad L_{i}^\mathrm{T}D_{fi}^\mathrm{T}W_{2} &{}\quad -L_{i}^\mathrm{T}D_{fi}^\mathrm{T}\bar{W}_{1}^\mathrm{T} \\ *&{}\quad \left( \lambda _{i}-1\right) \Lambda _{i} &{}\quad D_{fi}^\mathrm{T}W_{2} &{}\quad -D_{fi}^\mathrm{T}\bar{W}_{1}^\mathrm{T} \\ *&{}\quad *&{}\quad \Omega _{22i}^{33} &{}\quad D_{i}^\mathrm{T}\bar{W}_{1}^\mathrm{T} \\ *&{}\quad *&{}\quad *&{}\quad -I \end{array} \right] , \end{aligned}$$

with

$$\begin{aligned} \Omega _{11i}^{11}\triangleq & {} -4H^\mathrm{T}Z_{1}H+H^\mathrm{T}\left( Q_{1i}+Q_{2i}\right. \\&\left. +\,h_{2}T+h_{2}^{2} A_{i}^\mathrm{T}Z_{1}A_{i}+h_{12}^{2}A_{i}^\mathrm{T}Z_{2}A_{i}\right) H\\&+\,\mathrm{sym}\left( \tilde{A}_{i}^\mathrm{T}P_{i}\right) +\underset{j\in \mathcal {S}}{\sum }\pi _{ij}\left( \triangle \right) P_{j}, \\ \Omega _{11i}^{12}\triangleq & {} -2H^\mathrm{T}Z_{1}-H^\mathrm{T}\left( X_{11}+X_{21}+X_{12}+X_{22}\right) , \\ \Omega _{11i}^{13}\triangleq & {} H^\mathrm{T}\left( X_{11}+X_{21}-X_{12}-X_{22}\right) , \\ \Omega _{11i}^{22}\triangleq & {} -8Z_{1}+\mathrm{sym}\left( X_{11}-X_{21}+X_{12}-X_{22}\right) \\&-Q_{1i}-Z_{2}, \\ \Omega _{11i}^{23}\triangleq & {} -2Z_{1}+\left( -X_{11}+X_{21}+X_{12}-X_{22}\right) +Y, \\ \Omega _{11i}^{24}\triangleq & {} 6Z_{1}+2\left( X_{21}^\mathrm{T}+X_{22}^\mathrm{T}\right) ,\\ \Omega _{11i}^{33}\triangleq & {} -4Z_{1}-Q_{2i}-Z_{2}, \\ \Omega _{22i}^{11}\triangleq & {} -2Z_{2}+Y^\mathrm{T}+Y+\lambda _{i}L_{i}^\mathrm{T}\Lambda _{i}L_{i}, \\ \Omega _{22i}^{33}\triangleq & {} B_{i}^\mathrm{T}\left( h_{2}^{2}Z_{1}+h_{12}^{2}Z_{2}\right) B_{i}+\alpha I-W_{3}\\&-\mathrm{sym}\left( D_{i}^\mathrm{T}W_{2}\right) , \\ h_{12}\triangleq & {} h_{2}-h_{1},H\triangleq \left[ \begin{array}{cc} I&\quad 0 \end{array} \right] . \end{aligned}$$

Then the closed-loop system \(\left( \tilde{\Sigma }\right) \) is stochastically stable and strictly \(\left( W_{1},W_{2},W_{3}\right) -\alpha - \)dissipative.

Proof

For the filtering error system \(\left( \tilde{\Sigma }\right) \), the Lyapunov–Krasovskii function for analyzing stability is constructed as

$$\begin{aligned} V\left( x_{t},i,t\right) =\overset{3}{\underset{s=1}{\sum }}V_{s}\left( x_{t},i,t\right) , \end{aligned}$$
(16)

where

$$\begin{aligned} V_{1}\left( x_{t},i,t\right)= & {} \tilde{x}^\mathrm{T}\left( t\right) P_{i}\tilde{x} \left( t\right) , \\ V_{2}\left( x_{t},i,t\right)= & {} \int _{t-h_{1}}^{t}x^\mathrm{T}\left( s\right) Q_{1i}x\left( s\right) \mathrm{d}s\\&+\int _{t-h_{2}}^{t}x^\mathrm{T}\left( s\right) Q_{2i}x\left( s\right) \mathrm{d}s\\&+\int _{-h_{2}}^{0}\int _{t+\beta }^{t}x^\mathrm{T}\left( s\right) Tx\left( s\right) \mathrm{d}s\mathrm{d}\beta , \\ V_{3}\left( x_{t},t\right)= & {} h_{2}\int _{-h_{2}}^{0}\int _{t+\beta }^{t} \dot{x}^\mathrm{T}\left( s\right) Z_{1}\dot{x}\left( s\right) \mathrm{d}s\mathrm{d}\beta \\&+\,h_{12}\int _{-h_{2}}^{-h_{1}}\int _{t+\beta }^{t}\dot{x}^\mathrm{T}\left( s\right) Z_{2}\dot{x}\left( s\right) \mathrm{d}s\mathrm{d}\beta , \end{aligned}$$

with \(P_{i}>0\), \(Q_{1i}>0\), \(Q_{2i}>0\), \(T>0\), \(Z_{1}>0\) and \(Z_{2}>0\).

Taking the time derivative along the trajectory of system \(\left( \tilde{ \Sigma }\right) \) yields

$$\begin{aligned} \mathcal {L}V\left( x_{t},i,t\right)= & {} \mathcal {L}V_{1}\left( x_{t},i,t\right) +\mathcal {L}V_{2}\left( x_{t},i,t\right) \\&+\,\mathcal {L}V_{3}\left( x_{t},t\right) , \end{aligned}$$

where

$$\begin{aligned} \mathcal {L}V_{1}\left( x_{t},i,t\right)= & {} \mathrm{sym}\left( \overset{\cdot }{ \tilde{x}}^\mathrm{T}\left( t\right) P_{i}\tilde{x}\left( t\right) \right) \nonumber \\&+\,\tilde{x}^\mathrm{T}\left( t\right) \underset{j\in \mathcal {S}}{\sum }\pi _{ij}\left( \triangle \right) P_{j}\tilde{x}\left( t\right) , \end{aligned}$$
(17)
$$\begin{aligned} \mathcal {L}V_{2}\left( x_{t},i,t\right)= & {} x^\mathrm{T}\left( t\right) \left( Q_{1i}+Q_{2i}+h_{2}T\right) x\left( t\right) \nonumber \\&-x^\mathrm{T}\left( t-h_{1}\right) Q_{1i}x\left( t-h_{1}\right) \nonumber \\&-x^\mathrm{T}\left( t-h_{2}\right) Q_{2i}x\left( t-h_{2}\right) \nonumber \\&+\int _{t-h_{1}}^{t}x^\mathrm{T}\left( s\right) \Xi _{1,i}x\left( s\right) \mathrm{d}s\nonumber \\&+\int _{t-h_{2}}^{t-h_{1}}x^\mathrm{T}\left( s\right) \Xi _{2,i}x\left( s\right) \mathrm{d}s, \end{aligned}$$
(18)
$$\begin{aligned} \mathcal {L}V_{3}\left( x_{t},t\right)= & {} \dot{x}^\mathrm{T}\left( t\right) \left( h_{2}^{2}Z_{1}+h_{12}^{2}Z_{2}\right) \dot{x}\left( t\right) \nonumber \\&-h_{2}\int _{t-h_{2}}^{t}\dot{x}^\mathrm{T}\left( s\right) Z_{1}\dot{x}\left( s\right) \mathrm{d}s \nonumber \\&-h_{12}\int _{t-h_{2}}^{t-h_{1}}\dot{x}^\mathrm{T}\left( s\right) Z_{2}\dot{x} \left( s\right) \mathrm{d}s. \end{aligned}$$
(19)

Using Jensen’s inequality, it can see that

$$\begin{aligned} \int _{t-h_{1}}^{t}x^\mathrm{T}\left( s\right) \Xi _{1,i}x\left( s\right) \mathrm{d}s\leqslant & {} h_{1}\varsigma _{1}^\mathrm{T}\left( t\right) \Xi _{1,i}\varsigma _{1}\left( t\right) , \nonumber \\ \end{aligned}$$
(20)
$$\begin{aligned} \int _{t-h_{2}}^{t-h_{1}}x^\mathrm{T}\left( s\right) \Xi _{2,i}x\left( s\right) \mathrm{d}s\leqslant & {} h_{12}\varsigma _{2}^\mathrm{T}\left( t\right) \Xi _{2,i}\varsigma _{2}\left( t\right) . \nonumber \\ \end{aligned}$$
(21)

And in light of Lemma 2, it is straightforward that

$$\begin{aligned} -h_{2}\int _{t-h_{2}}^{t}\dot{x}^\mathrm{T}\left( s\right) Z_{1}\dot{x}\left( s\right) \mathrm{d}s\leqslant -\varsigma ^\mathrm{T}\left( t\right) \Psi _{12}^\mathrm{T}\Phi \Psi _{12}\varsigma \left( t\right) . \end{aligned}$$

On the other hand, from Lemma 1, the following inequality holds

$$\begin{aligned}&-h_{12}\int _{t-h_{2}}^{t-h_{1}}\dot{x}^\mathrm{T}\left( s\right) Z_{2}\dot{x} \left( s\right) \mathrm{d}s \nonumber \\&\leqslant \left[ \begin{array}{c} \left( x\left( t-h_{1}\right) -x\left( t-\tau \left( t\right) \right) \right) \\ \left( x\left( t-\tau \left( t\right) \right) -x\left( t-h_{2}\right) \right) \end{array} \right] ^\mathrm{T}\left[ \begin{array}{cc} -Z_{2} &{}\quad -Y \\ *&{}\quad -Z_{2} \end{array} \right] \nonumber \\&\quad \left[ \begin{array}{c} \left( x\left( t-h_{1}\right) -x\left( t-\tau \left( t\right) \right) \right) \\ \left( x\left( t-\tau \left( t\right) \right) -x\left( t-h_{2}\right) \right) \end{array} \right] \nonumber \\&\leqslant \left[ \begin{array}{c} x\left( t-h_{1}\right) \\ x\left( t-h_{2}\right) \\ x\left( t-\tau \left( t\right) \right) \end{array} \right] ^\mathrm{T}\left[ \begin{array}{ccc} -Z_{2} &{}\quad Y &{}\quad Z_{2}-Y \\ *&{}\quad -Z_{2} &{}\quad Z_{2}-Y^\mathrm{T} \\ *&{}\quad *&{}\quad -2Z_{2}+Y^\mathrm{T}+Y \end{array} \right] \nonumber \\&\quad \left[ \begin{array}{c} x\left( t-h_{1}\right) \\ x\left( t-h_{2}\right) \\ x\left( t-\tau \left( t\right) \right) \end{array} \right] . \end{aligned}$$
(22)

In view of (6), we define

$$\begin{aligned} R(t)\overset{\Delta }{=}\lambda _{i}y^\mathrm{T}\left( t_{k}h\right) \Lambda _{i}y\left( t_{k}h\right) -e_{k}^\mathrm{T}\left( t\right) \Lambda _{i}e_{k}\left( t\right) >0, \nonumber \\ \end{aligned}$$
(23)

and it is easy to yield that

$$\begin{aligned}&\left[ \begin{array}{cc} x^\mathrm{T}\left( t-\tau \left( t\right) \right)&\quad e_{k}^\mathrm{T}\left( t\right) \end{array} \right] \left[ \begin{array}{cc} \lambda _{i}L_{i}^\mathrm{T}\Lambda _{i}L_{i} &{}\quad \lambda _{i}L_{i}^\mathrm{T}\Lambda _{i}\\ *&{} \left( \lambda _{i}-1\right) \Lambda _{i} \end{array} \right] \nonumber \\&\quad \left[ \begin{array}{c} x\left( t-\tau \left( t\right) \right) \\ e_{k}\left( t\right) \end{array} \right] \geqslant 0. \end{aligned}$$
(24)

Recall now that Definition 1 of the dissipation, we denote

$$\begin{aligned}&T\left( W_{1},W_{2},W_{3},t\right) \triangleq -e^\mathrm{T}\left( t\right) W_{1}e\left( t\right) \nonumber \\&\quad -\,\mathrm{sym}\left( e^\mathrm{T}\left( t\right) W_{2}\omega \left( t\right) \right) -\omega ^\mathrm{T}\left( t\right) W_{3}\omega \left( t\right) \nonumber \\&\quad +\,\alpha \omega ^\mathrm{T}\left( t\right) \omega \left( t\right) . \end{aligned}$$
(25)

Then, relying on the conditions (23) and (25), and substituting (20)–(24) to (18), (19), (23 ), it holds that

$$\begin{aligned}&\mathcal {E}\{\mathcal {L}V\left( x_{t},i,t\right) +R(t)+T\left( W_{1},W_{2},W_{3},t\right) \}\nonumber \\&\quad \le \mathcal {E}\{\xi ^\mathrm{T}(t)\bar{\Omega } _{i}\xi (t)\}, \end{aligned}$$
(26)

where

$$\begin{aligned} \xi ^\mathrm{T}(t)\triangleq & {} [\tilde{x}^\mathrm{T}\left( t\right) ,x^\mathrm{T}(t-h_{1}),x^\mathrm{T}(t-h_{2}),\varsigma _{1}^\mathrm{T}\left( t\right) ,\\&\varsigma _{2}^\mathrm{T}\left( t\right) ,x^\mathrm{T}\left( t-\tau \left( t\right) \right) ,e_{k}^\mathrm{T}\left( t\right) ,\omega ^\mathrm{T}\left( t\right) ], \\ \bar{\Omega }_{i}\triangleq & {} \left[ \begin{array}{cc} \bar{\Omega }_{11i} &{}\quad \bar{\Omega }_{12i} \\ *&{} \bar{\Omega }_{22i} \end{array} \right] ,\\ \bar{\Omega }_{11i}\triangleq & {} \left[ \begin{array}{ccccc} \Omega _{11i}^{11}-\tilde{S}_{i}^\mathrm{T}W_{1}\tilde{S}_{i} &{} \Omega _{11i}^{12} &{} \Omega _{11i}^{13} &{} 6H^\mathrm{T}Z_{1} &{} 2H^\mathrm{T}\left( X_{12}+X_{22}\right) \\ *&{} \Omega _{11i}^{22} &{} \Omega _{11i}^{23} &{} \Omega _{11i}^{24} &{} 6Z_{1}-2\left( X_{12}-X_{22}\right) \\ *&{} *&{} \Omega _{11i}^{33} &{} -2\left( X_{21}^\mathrm{T}-X_{22}^\mathrm{T}\right) &{} 6Z_{1} \\ *&{} *&{} *&{} -12Z_{1}+h_{1}\Xi _{1,i} &{} -4X_{22} \\ *&{} *&{} *&{} *&{} -12Z_{1}+h_{12}\Xi _{2,i} \end{array} \right] , \\ \bar{\Omega }_{22i}\triangleq & {} \left[ \begin{array}{ccc} \Omega _{22i}^{11}-L_{i}^\mathrm{T}D_{fi}^\mathrm{T}W_{1}D_{fi}L_{i} &{} \lambda _{i}L_{i}^\mathrm{T}\Lambda _{i}-L_{i}^\mathrm{T}D_{fi}^\mathrm{T}W_{1}D_{fi} &{} L_{i}^\mathrm{T}D_{fi}^\mathrm{T}W_{2}+L_{i}^\mathrm{T}D_{fi}^\mathrm{T}W_{1}D_{i} \\ *&{} \left( \lambda _{i}-1\right) \Lambda _{i}-D_{fi}^\mathrm{T}W_{1}D_{fi} &{} D_{fi}^\mathrm{T}W_{2}+D_{fi}^\mathrm{T}W_{1}D_{i} \\ *&{} *&{} \Omega _{22i}^{33}-D_{i}^\mathrm{T}W_{1}D_{i} \end{array} \right] , \\ \bar{\Omega }_{12i}\triangleq & {} \left[ \begin{array}{ccc} P_{i}^\mathrm{T}\tilde{B}_{i}+\tilde{S}_{i}^\mathrm{T}W_{1}D_{fi}L_{i} &{} P_{i}^\mathrm{T}\tilde{D} _{i}+\tilde{S}_{i}^\mathrm{T}W_{1}D_{fi} &{} P_{i}^\mathrm{T}\tilde{C}_{i}+HA_{i}^\mathrm{T}\left( h_{2}^{2}Z_{1}+h_{12}^{2}Z_{2}\right) B_{i}-\tilde{S}_{i}^\mathrm{T}W_{2}-\tilde{S} _{i}^\mathrm{T}W_{1}D_{i} \\ Z_{2}-Y &{} 0 &{} 0 \\ Z_{2}-Y^\mathrm{T} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{array} \right] , \end{aligned}$$

Then, according to condition (11) and Schur complement, it follows from (26) that,

$$\begin{aligned} \bar{\Omega }_{i}<0, \end{aligned}$$

relying on the conditions (23), one has

$$\begin{aligned} \mathcal {E}\left\{ \mathcal {L}V\left( x_{t},i,t\right) +T\left( W_{1},W_{2},W_{3},t\right) \right\} <0. \end{aligned}$$
(27)

Under the zero initial condition, it is readily concluded that for any \( \gamma \geqslant 0\)

$$\begin{aligned}&\mathcal {E}\left\{ \int _{0}^{\gamma }T\left( W_{1},W_{2},W_{3},t\right) \mathrm{d}t\right\} \\&\quad \leqslant \mathcal {E}\left\{ \int _{0}^{\gamma }\left( \mathcal {L} V\left( x_{t},i,t\right) +T\left( W_{1},W_{2},W_{3},t\right) \right) \mathrm{d}t\right\} \leqslant 0. \end{aligned}$$

Thus, one can yield that

$$\begin{aligned}&\mathcal {E}\left\{ \int _{0}^{\gamma }[e^\mathrm{T}\left( t\right) W_{1}e\left( t\right) +\mathrm{sym}\left( e^\mathrm{T}\left( t\right) W_{2}\omega \left( t\right) \right) \right. \\&\quad \left. +\,\omega ^\mathrm{T}\left( t\right) W_{3}\omega \left( t\right) ]\mathrm{d}t\right\} \geqslant \alpha \int _{0}^{\gamma }\left[ \omega ^\mathrm{T}\left( t\right) \omega \left( t\right) \right] \mathrm{d}t. \end{aligned}$$

It results that the condition (7) is assured for any nonzero \( \omega \left( t\right) \in \mathcal {L}_{2}\left[ 0,\infty \right) \). Furthermore, when \(\omega (t)=0\), according to (27), there exists a scalar \(a>0\) such that

$$\begin{aligned} \mathcal {L}V\left( x_{t},i,t\right) \leqslant -a\tilde{x}^\mathrm{T}\left( t\right) \tilde{x}(t). \end{aligned}$$

Then, following the similar line as the proof of Theorem 1 in [34], and applying Dynkin’s formula and Gronwall–Bellman lemma, we have

$$\begin{aligned} \mathcal {E}\left\{ \int _{0}^{\infty }\tilde{x}^\mathrm{T}\left( t\right) \tilde{x} (t)\mathrm{d}t\right\} <\infty . \end{aligned}$$

In this way, the considered system \(\left( \tilde{\Sigma }\right) \) with \( \omega (t)=0\) is stochastically stable. Thus, in view of Definition 1 , the system \(\left( \tilde{\Sigma }\right) \) is strictly \(\left( W_{1},W_{2},W_{3}\right) -\alpha -\)dissipative, which completes the proof of Theorem 1.

Remark 3

Note that the conditions in (11), (14) and (15) are not easy to be solved. The main reason is that they are dependent on the time-varying terms \(\sum _{j\in \mathcal {S}}\pi _{ij}\left( \triangle \right) \), and then not line matrix inequalities-based. In practice, the transition rate \(\pi _{ij}\left( \triangle \right) \) of semi-Markov process can be partly available [7]. Based on this consideration, as same as that in [7], \(\pi _{ij}\left( \triangle \right) \) is assumed to be in the bound of \(\left[ \pi _{ij}^{d},\pi _{ij}^{u}\right] \). As a result, an assumption on the \(\pi _{ij}\left( \triangle \right) \) can be naturally presented:

$$\begin{aligned} \pi _{ij}\left( \triangle \right) =\sum _{k=1}^{\mathcal {M}}\chi _{k}\pi _{ij,k},\quad \sum _{k=1}^{\mathcal {M}}\chi _{k}=1,\qquad \chi _{k}\ge 0, \nonumber \\ \end{aligned}$$
(28)

and

$$\begin{aligned} \pi _{ij,k}=\left\{ \begin{array}{cc} \pi _{ij}^{d}+\left( k-1\right) \frac{\pi _{ij}^{u}-\pi _{ij}^{d}}{\mathcal {M }-1}, &{}\quad i\ne j,\; j\in \mathcal {S}, \\ \pi _{ij}^{u}-\left( k-1\right) \frac{\pi _{ij}^{u}-\pi _{ij}^{d}}{\mathcal {M }-1}, &{}\quad i=j,\; j\in \mathcal {S} \end{array} \right. \nonumber \\ \end{aligned}$$
(29)

Having obtained the performance results, we are now ready to solve the event-triggered filtering problem. Note that from (11), the filter parameters are coupled with the matrices \(P_{i}\). A co-design scheme will be presented, and the dissipative filter parameters and the event-triggered matrix will be determined simultaneously based on Theorem 1.

Theorem 2

For given scalars \(\alpha \), \(0\le \lambda _{i}<1\), \( h_{2}>h_{1}>0\), matrices \(W_{1}^\mathrm{T}=W_{1}=-\bar{W}_{1}^\mathrm{T}\bar{W} _{1}\leqslant 0\), \(W_{2}\) and \(W_{3}=W_{3}^\mathrm{T}>0\), if there exist real matrices \(\Lambda _{i}>0\), \(G_{i}>0\), \(V_{i}>0\), \(Q_{1i}>0\), \(Q_{2i}>0\), \(T>0 \), \(Z_{1}>0\) and \(Z_{2}>0\) of appropriate dimensions such that (12)–( 13) and the following conditions hold for each \(i\in \mathcal {S}\)

$$\begin{aligned} \hat{\Omega }_{i,k}\triangleq & {} \left[ \begin{array}{cc} \hat{\Omega }_{11i,k} &{} \hat{\Omega }_{12i} \\ *&{} \hat{\Omega }_{22i} \end{array} \right] <0, \end{aligned}$$
(30)
$$\begin{aligned} \hat{P}_{i}\triangleq & {} \left[ \begin{array}{cc} G_{i} &{}\quad V_{i} \\ V_{i} &{}\quad V_{i} \end{array} \right] >0, \end{aligned}$$
(31)
$$\begin{aligned} \Xi _{1,i,k}\triangleq & {} \underset{j\in \mathcal {S}}{\sum }\pi _{ij,k}\left( Q_{1j}+Q_{2j}\right) -T<0,k=1,2,\ldots ,\mathcal {M}, \nonumber \\ \end{aligned}$$
(32)
$$\begin{aligned} \Xi _{2,i,k}\triangleq & {} \underset{j\in \mathcal {S}}{\sum }\pi _{ij,k}Q_{2j}-T<0,k=1,2,\ldots ,\mathcal {M}, \end{aligned}$$
(33)

where

$$\begin{aligned} \hat{\Omega }_{11i,k}\triangleq & {} \left[ \begin{array}{cccccc} \hat{\Omega }_{11i,k}^{11} &{} \hat{\Omega }_{11i,k}^{12} &{} \hat{\Omega } _{11i}^{13} &{} \hat{\Omega }_{11i}^{14} &{} 6Z_{1} &{} 2\left( X_{12}+X_{22}\right) \\ *&{} \mathrm{sym}\left( \hat{A}_{fi}\right) +\underset{j\in \mathcal {S}}{\sum }\pi _{ij,k}V_{j} &{} 0 &{} 0 &{} 0 &{} 0 \\ *&{} *&{} \Omega _{11i}^{22} &{} \Omega _{11i}^{23} &{} \Omega _{11i}^{24} &{} 6Z_{1}-2\left( X_{12}-X_{22}\right) \\ *&{} *&{} *&{} \Omega _{11i}^{33} &{} -2\left( X_{21}^\mathrm{T}-X_{22}^\mathrm{T}\right) &{} 6Z_{1} \\ *&{} *&{} *&{} *&{} -12Z_{1}+h_{1}\Xi _{1,i,k} &{} -4X_{22} \\ *&{} *&{} *&{} *&{} *&{} -12Z_{1}+h_{12}\Xi _{2,i,k} \end{array} \right] , \\ \hat{\Omega }_{12i}\triangleq & {} \left[ \begin{array}{cccc} \hat{B}_{fi}L_{i} &{} \hat{B}_{fi} &{} \hat{\Omega }_{12i}^{13} &{} C_{i}^\mathrm{T}\bar{W} _{1}^\mathrm{T} \\ \hat{B}_{fi}L_{i} &{} \hat{B}_{fi} &{} V_{i}B_{i}+\hat{C}_{fi}^\mathrm{T}W_{2} &{} -\hat{C }_{fi}^\mathrm{T}\bar{W}_{1}^\mathrm{T} \\ Z_{2}-Y &{} 0 &{} 0 &{} 0 \\ Z_{2}-Y^\mathrm{T} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \end{array} \right] , \\ \hat{\Omega }_{22i}\triangleq & {} \left[ \begin{array}{cccc} \Omega _{22i}^{11} &{} \lambda _{i}L_{i}^\mathrm{T}\Lambda _{i} &{} L_{i}^\mathrm{T}\hat{D} _{fi}^\mathrm{T}W_{2} &{} -L_{i}^\mathrm{T}\hat{D}_{fi}^\mathrm{T}\bar{W}_{1}^\mathrm{T} \\ *&{} \left( \lambda _{i}-1\right) \Lambda _{i} &{} \hat{D}_{fi}^\mathrm{T}W_{2} &{} - \hat{D}_{fi}^\mathrm{T}\bar{W}_{1}^\mathrm{T} \\ *&{} *&{} \Omega _{22i}^{33} &{} D_{i}^\mathrm{T}\bar{W}_{1}^\mathrm{T} \\ *&{} *&{} *&{} -I \end{array} \right] , \end{aligned}$$

with

$$\begin{aligned} \hat{\Omega }_{11i,k}^{11}\triangleq & {} -4Z_{1}+Q_{1i}+Q_{2i}+h_{2}T+h_{2}^{2}A_{i}^\mathrm{T}Z_{1}A_{i}\\&+\,h_{12}^{2}A_{i}^\mathrm{T}Z_{2}A_{i}+2A_{i}^\mathrm{T}G_{i}+ \underset{j\in \mathcal {S}}{\sum }\pi _{ij,k}G_{j}, \\ \hat{\Omega }_{11i,k}^{12}\triangleq & {} \hat{A}_{fi}+A_{i}^\mathrm{T}V_{i}\underset{ j\in \mathcal {S}}{+\sum }\pi _{ij,k}V_{j}, \\ \hat{\Omega }_{11i}^{13}\triangleq & {} -2Z_{1}-\left( X_{11}+X_{21}+X_{12}+X_{22}\right) , \\ \hat{\Omega }_{11i}^{14}\triangleq & {} X_{11}+X_{21}-X_{12}-X_{22}, \\ \hat{\Omega }_{12i}^{13}\triangleq & {} G_{i}^\mathrm{T}B_{i}+A_{i}^\mathrm{T}\left( h_{2}^{2}Z_{1}+h_{12}^{2}Z_{2}\right) B_{i}-C_{i}^\mathrm{T}W_{2}. \end{aligned}$$

Then the resulting filtering error system \(\left( \tilde{\Sigma }\right) \) is strictly \(\left( W_{1},W_{2},W_{3}\right) -\alpha -\)dissipative. In this case, the filtering gains \(A_{fi}\), \(B_{fi}\), \(C_{fi}\), and \(D_{fi}\) can be given by

$$\begin{aligned} A_{fi}\triangleq & {} SV_{i}^{-1}\hat{A}_{fi}S^{-1},B_{fi}\triangleq SV_{i}^{-1} \hat{B}_{fi},\nonumber \\ C_{fi}\triangleq & {} \hat{C}_{fi}S^{-1},D_{fi}\triangleq \hat{D} _{fi}. \end{aligned}$$
(34)

Proof

First, since \(\pi _{ij}\left( \triangle \right) =\sum _{k=1}^{ \mathcal {M}}\chi _{k}\pi _{ij,k},\sum _{k=1}^{\mathcal {M}}\chi _{k}=1,\) \(\chi _{k}\ge 0,\) one can obtain that

$$\begin{aligned} \sum _{k=1}^{\mathcal {M}}\chi _{k}\Xi _{1,i,k}= & {} \sum _{k=1}^{\mathcal {M} }\chi _{k}\underset{j\in \mathcal {S}}{\sum }\pi _{ij,k}\left( Q_{1j}+Q_{2j}\right) -\sum _{k=1}^{\mathcal {M}}\chi _{k}T \\= & {} \underset{j\in \mathcal {S}}{\sum }\sum _{k=1}^{\mathcal {M}}\chi _{k}\pi _{ij,k}\left( Q_{1j}+Q_{2j}\right) -T\\= & {} \underset{j\in \mathcal {S}}{\sum }\pi _{ij}\left( \triangle \right) \left( Q_{1j}+Q_{2j}\right) -T=\Xi _{1,i}, \end{aligned}$$

which implies that \(\Xi _{1,i}<0\) is satisfied if condition (32) holds. As a similar way, we can find that \(\Xi _{2,i}<0\) is also guaranteed if condition (33) holds. Next, let us prove that conditions (30)–(31) can ensure that condition (11) is satisfied. To this purpose, we suppose that exist matrices \(P_{i}\) with the form of

$$\begin{aligned} P_{i}=\left[ \begin{array}{cc} P_{1i} &{}\quad P_{2i} \\ P_{2i}^\mathrm{T} &{}\quad P_{3i} \end{array} \right] , \end{aligned}$$

and set \(G_{i}\overset{\Delta }{=}P_{1i}\), \(V_{i}\overset{\Delta }{=} P_{2i}P_{3i}^{-1}P_{2i}^\mathrm{T}\), \(P_{3i}S\overset{\Delta }{=}P_{2i}^\mathrm{T}.\) It is readily concluded that

$$\begin{aligned} \hat{P}_{i}=\left[ \begin{array}{cc} G_{i} &{}\quad V_{i} \\ V_{i} &{}\quad V_{i} \end{array} \right] =\left[ \begin{array}{cc} P_{1i} &{}\quad P_{2i}S \\ S^\mathrm{T}P_{2i}^\mathrm{T} &{}\quad S^\mathrm{T}P_{3i}S \end{array} \right] >0. \end{aligned}$$

Clearly, \(P_{i}>0.\) Furthermore, define \(J\overset{\Delta }{=}\mathrm{diag}\{I,S^\mathrm{T}, \underset{8}{\underbrace{I,\ldots ,I}}\},\) and pre- and post-multiplying both sides of (11) with J and its transpose, respectively, it follows from (28) that condition (11) holds if condition (30) is assured. According to Theorem 2, it can be concluded that the resulting filtering error system \(\left( \tilde{\Sigma }\right) \) is strictly \(\left( W_{1},W_{2},W_{3}\right) \)-\(\alpha \)-dissipative. This completes the proof.

4 Numerical examples

In this section, two examples are given to illustrate the effectiveness and improvement of the proposed design technique. In the first example, we consider a modified networked semi-Markov jump system, whose parameters are borrowed from [27]. By addressing the same issue, the less conservative results will be presented than those in [27]. In the second example, our aim is to illustrate the applicability of the proposed theoretical results, and for this end, the state estimation problem of the networked mass-spring system demonstrated in Fig. 2 will be taken into account.

Fig. 2
figure 2

A mass-spring system in Example 2

Full size image

Example 1

In this example, we used the Markov jump system \(\left( \tilde{\Sigma }\right) \) with the following parameters [27]

$$\begin{aligned} A_{1}= & {} \left[ \begin{array}{ccc} -3 &{}\quad 1 &{}\quad 0 \\ 0.3 &{}\quad -2.5 &{}\quad 1 \\ -0.1 &{}\quad 0.3 &{}\quad -3.8 \end{array} \right] ,B_{1}=\left[ \begin{array}{c} 1 \\ 0 \\ 1\end{array}\right] ,\\ L_{1}= & {} \left[ \begin{array}{ccc} 0.8&\quad 0.3&\quad 0 \end{array} \right] ,C_{1}=\left[ \begin{array}{ccc} 0.5&\quad -0.1&\quad 1 \end{array} \right] , \\ A_{2}= & {} \left[ \begin{array}{ccc} -2.5 &{}\quad 0.5 &{}\quad -0.1 \\ 0.1 &{}\quad -3.5 &{}\quad 0.3 \\ -0.1 &{}\quad 1 &{}\quad -2 \end{array} \right] ,B_{2}=\left[ \begin{array}{c} -0.5 \\ 0.2 \\ 0.3 \end{array} \right] ,\\ L_{2}= & {} \left[ \begin{array}{ccc} -0.5&\quad 0.2&\quad 0.3 \end{array} \right] ,C_{2}=\left[ \begin{array}{ccc} 0&\quad 1&\quad 0.6 \end{array} \right] . \end{aligned}$$

In order to compare our results with that in [27], we first set \(D_{1}=D_{2}=0\), \(D_{f1}=D_{f2}=0\), \(h_{1}=0.01\)s and dissipative-based parameters \(\bar{W}_{1}=-1\), \(W_{2}=0\), \(W_{3}=0.26\), \(\alpha =0.1\). Then, the designed filter reduces to the \(H_{\infty }\) filter with the same \( H_{\infty }\) performance level in [27]. Let semi-Markov chain \(\beta \left( t\right) \) reduces to Markov chain with the transition matrix \( \Pi =\left[ \begin{array}{cc} -0.5 &{}\quad 0.5 \\ 0.3 &{}\quad -0.3 \end{array} \right] \). As stated in Remark 4 in [27], we also set \(S=I,\) and the next example has the same assumption. Table 1 lists the maximum \( h_{2}\) for the different thresholds \(\lambda _{i}\).

Table 1 Comparisons of maximum \(h_{2}\) for different methods in Example 2
Full size table

From Table 1, we can easily get two facts: on the one hand, the value of \( h_{2}\) reduces with the increasing of \(\lambda _{i}\). On the other hand, our method can tolerate bigger time-delay \(h_{2}\) than [27], which means the proposed method is superior to [27].

Example 2

As mentioned earlier, we consider a networked mass-spring system demonstrated in Fig. 2 in this example. Referring to [3], where \(x_{1}\) and \(x_{2}\) are two positions of massed \(M_{1}\) and \(M_{2}\), \(K_{c},K_{1},K_{2},K_{3},K_{4}\) are the stiffness of the springs, and c denotes the viscous friction coefficient between the masses and the horizontal surface. And the plant noise is defined by \(\omega (t).\) Denoting \(x^\mathrm{T}(t)=[x_{1}^\mathrm{T}(t),x_{2}^\mathrm{T}(t),\overset{\cdot }{x} _{1}^\mathrm{T}(t),\overset{\cdot }{x}_{2}^\mathrm{T}(t)]\), the state-space realization of the continuous-time semi-Markov jump system is described by the system (4) with the following parameters:

$$\begin{aligned} A_{i}= & {} \left[ \begin{array}{cccc} 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ \frac{-K_{c}-K_{i}}{M_{1}} &{}\quad \frac{K_{i}}{M_{1}} &{}\quad \frac{-c}{M_{1}} &{}\quad 0 \\ \frac{K_{i}}{M_{2}} &{}\quad \frac{-K_{i}}{M_{2}} &{}\quad 0 &{}\quad \frac{-c}{M_{2}} \end{array} \right] ,B_{i}=\left[ \begin{array}{c} 0 \\ 0 \\ \frac{1}{M_{1}} \\ 0 \end{array} \right] , \\ C_{i}= & {} \left[ \begin{array}{cccc} 0&\quad 1&\quad 0&\quad 0 \end{array} \right] ,D_{i}=0,\\L_{i}= & {} \left[ \begin{array}{cccc} 1&\quad 0&\quad 0&\quad 0 \end{array} \right] ,i=1,2,3,4, \end{aligned}$$

where \(M_{1}=1\) kg, \(M_{2}=0.5\) kg, \(K_{c}=1\) N/m, \(K_{1}=1\) N/m, \( K_{2}=1.04 \) N/m, \(K_{3}=1.09\) N/m, \(K_{4}=1.13\) N/m and \(c=0.5\) kg/s. In this example, suppose that the event-triggered thresholds are \(\lambda _{1}=0.1\), \(\lambda _{2}=0.3\), \(\lambda _{3}=0.2\), \(\lambda _{4}=0.3\), the transition rates of semi-Markov chain \(\beta \left( t\right) \) in the model are \(\pi _{12}(\triangle )\in [0,0.1]\), \(\pi _{13}(\triangle )\in [0.1,0.2]\), \(\pi _{14}(\triangle )\in [0.1,0.2]\), \(\pi _{21}(\triangle )\in [0.15,0.2]\), \(\pi _{23}(\triangle )\in [0.05,0.1]\), \(\pi _{24}(\triangle )\in [0.2,0.3]\), \(\pi _{31}(\triangle )\in [0.1,0.3]\), \(\pi _{32}(\triangle )\in [0.1,0.3]\), \(\pi _{34}(\triangle )\in [0,0.1]\), \(\pi _{41}(\triangle )\in [0.05,0.1]\), \(\pi _{42}(\triangle )\in [0.05,0.1],\) \(\pi _{43}(\triangle )\in [0.1,0.2]\), (\(i\ne j\)), which will be represented with a two-vertex polytope in view of Remark 3. The other parameters are chosen that \(\bar{W}_{1}=-1\), \(W_{2}=5\), \(W_{3}=15\), \(\alpha =0.1\), \(h_{1}=0.01\)s and \(h_{2}=1\)s. By solving the conditions in Theorem 2, we can get the event-triggered parameters \(\Lambda _{1}=2.3932\), \(\Lambda _{2}=1.2039\), \(\Lambda _{3}=1.7218\), \(\Lambda _{4}=1.1336\), and the filter gains are given as

$$\begin{aligned} A_{f1}= & {} \left[ \begin{array}{cccc} -0.9327 &{}\quad 0.1442 &{}\quad 3.1068 &{}\quad 0.0689 \\ 0.0565 &{}\quad -0.8701 &{}\quad -0.7473 &{}\quad 0.8222 \\ -2.9663 &{}\quad 1.2111 &{}\quad -1.2710 &{}\quad 0.0950 \\ 0.2283 &{}\quad -0.8048 &{}\quad -0.3641 &{}\quad -0.6526 \end{array} \right] ,\\ B_{f1}= & {} \left[ \begin{array}{c} -0.0425 \\ -0.0217 \\ -0.0080 \\ -0.0233 \end{array} \right] , \\ C_{f1}= & {} \left[ \begin{array}{cccc} -0.0354&\quad -0.4499&\quad 0.2886&\quad 0.0468 \end{array} \right] ,\\ D_{f1}= & {} 0.0027, \\ A_{f2}= & {} \left[ \begin{array}{cccc} -0.1020 &{}\quad 0.0126 &{}\quad 0.3001 &{}\quad 0.0028 \\ 0.0060 &{}\quad -0.0891 &{}\quad -0.0823 &{}\quad 0.0886 \\ -0.2860 &{}\quad 0.1195 &{}\quad -0.1291 &{}\quad 0.0043 \\ 0.0274 &{}\quad -0.0868 &{}\quad -0.0299 &{}\quad -0.0729 \end{array} \right] ,\\ B_{f2}= & {} \left[ \begin{array}{c} -0.0030 \\ -0.0014 \\ -0.0005 \\ -0.0017 \end{array} \right] , \\ C_{f2}= & {} \left[ \begin{array}{cccc} -0.0264&\quad -0.4093&\quad 0.2580&\quad 0.0573 \end{array} \right] ,\\ D_{f2}= & {} 0.0017,\\ A_{f3}= & {} \left[ \begin{array}{cccc} -0.0493 &{}\quad 0.0076 &{}\quad 0.1634 &{}\quad 0.0018 \\ 0.0019 &{}\quad -0.0458 &{}\quad -0.0435 &{}\quad 0.0450 \\ -0.1562 &{}\quad 0.0666 &{}\quad -0.0670 &{}\quad 0.0037 \\ 0.0132 &{}\quad -0.0438 &{}\quad -0.0181 &{}\quad -0.0351 \end{array} \right] ,\\ B_{f3}= & {} \left[ \begin{array}{c} -0.0019 \\ -0.0010 \\ -0.0004 \\ -0.0010 \end{array} \right] , \\ C_{f3}= & {} \left[ \begin{array}{cccc} -0.0379&-0.4287&0.2762&0.0596 \end{array} \right] ,\\ D_{f3}= & {} 0.0023, \\ A_{f4}= & {} \left[ \begin{array}{cccc} -0.0321 &{} 0.0061 &{} 0.1135 &{} 0.0010 \\ 0.0006 &{} -0.0307 &{} -0.0286 &{} 0.0295 \\ -0.1083 &{} 0.0464 &{} -0.0454 &{} 0.0040 \\ 0.0087 &{} -0.0289 &{} -0.0143 &{} -0.0215 \end{array} \right] ,\\ B_{f4}= & {} \left[ \begin{array}{c} -0.0012 \\ -0.0006 \\ -0.0002 \\ -0.0006 \end{array} \right] , \\ C_{f4}= & {} \left[ \begin{array}{cccc} -0.0428&-0.4576&0.3056&0.0535 \end{array} \right] ,\\ D_{f4}= & {} 0.0023. \end{aligned}$$

On investigating the performance of the designed dissipative filter, we assume the initial condition \(x_{0}=\left[ \begin{array}{cccc} 1.5&-0.5&0.8&-1 \end{array} \right] ^\mathrm{T}\), \(x_{f0}=\left[ \begin{array}{cccc} 0&0&0&0 \end{array} \right] ^\mathrm{T}\) and the external disturbance is

$$\begin{aligned} \omega \left( t\right) =\left\{ \begin{array}{ll} \frac{1}{t^{2}+1}, &{}\quad 0\leqslant t\leqslant 5s \\ -\frac{1}{t^{2}+1}, &{}\quad 10\leqslant t\leqslant 15s \\ 0, &{}\quad \text {otherwise} \end{array} \right. . \end{aligned}$$
Fig. 3
figure 3

Semi-Markov jump mode in Example 2

Full size image
Fig. 4
figure 4

Release instants and intervals with an event-triggered scheme in Example 2

Full size image

Giving a possible time sequences of the mode jumps for \(\beta \left( t\right) \) as in Fig. 3, the event-triggering release instants and intervals are shown in Fig. 4, and the state responses of closed-loop system are depicted in Fig. 5. Figure 6 shows the filtering error, where the curve demonstrates the effectiveness of our method. In addition, on the time interval [0, 50s] and the sampling period \(h=0.12\,\mathrm{s}\), only 137 sample data are sent to the ZOH through a communication network, which means that the transmission rate of sampled data packets (SDPs) defined as the number of successfully transmitted SDPs/the total number of SDPs is 32.9%, and it is obvious to save the resource utilization via ETS by 67.1% of the total communication resources.

Fig. 5
figure 5

State responses with an event-triggered scheme in Example 2

Full size image
Fig. 6
figure 6

Filter error with an event-triggered scheme in Example 2

Full size image

5 Conclusions

In this paper, the problem of co-designing a combined event-triggered communication scheme and dissipative filtering for networked control systems with semi-Markov jumping parameters has been investigated. An new event-triggered mechanism has been introduced to reduce the utilization of network bandwidth. Based on the Lyapunov–Krasovskii methodology and stochastic analysis, some sufficient conditions for the stochastic stability and the strictly dissipativity property of the resulting filtering error system have been established. Then, the explicit expression of the desired filter has been presented by solving a convex optimization problem. Finally, the effectiveness and superiority of our method have been demonstrated by a mass-spring system and a numerical example. It is noteworthy that all data package is assumed to be received in real time, which is difficult to achieve in practice. Therefore, when event-triggered scheme is adopted, how to relax such an assumption on the network communication is a significative question. Besides, the method presented in this paper is expected to be extended into more complex systems, for example, singular semi-Markov jump systems, nonlinear semi-Markov jump systems.