1 Introduction

Chatter is a self-excited vibration that can occur in many cutting processes, such as turning [1–4], milling [5–7], drilling [8–10], boring [1, 11, 12], and grinding [13, 14]. It often leads to the cutting process to unstable, poor surface, low machining precision, tool wear, and so on. For these reasons, it has been and still is a very important and popular topic in academic research.

As we all know, there are three different types of mechanical vibrations in cutting process as proposed by Tobias, they are free, forced, and self-excited vibrations [15, 16]. Free vibrations are allowed to vibrate freely when the mechanical system is displaced from its equilibrium. Forced vibrations occur due to external harmonic excitations. Self-excited vibrations are generally classified into two categories, including primary chatter and secondary chatter [17]. Primary chatter is caused by friction between cutting tool and workpiece, or mode coupling. Secondary chatter is caused by the regeneration of the wavy surface on the workpiece. Regenerative vibration is the most destructive among all other vibrations. Therefore, the majority of researchers have investigated regenerative vibration mechanism and found various techniques to avoid or control it. Free and forced vibrations can be avoided, reduced, even eliminated while the causes of the vibration are identified. It is difficult to research and understand self-excited vibrations because of its complexity of the principle and phenomenon.

Chatter was first identified as a limitation of machining productivity by Taylor [18], who carried out extensive study on metal cutting processes as early as in the 1800s. It is caused by unstability in the cutting process, which was first introduced by Tobias and Fishwick [19], they observed that dynamic chip thickness due to vibration affect cutting force dynamically. The first mathematical theory of nonlinear chatter was developed by Hanna and Tobias in the 1974 [20]. The dynamic model is a second-order differential equation with nonlinear stiffness and nonlinear time delay terms. Nayfeh et al. found periodic, quasi-periodic, and chaotic motions with an increase in the width of cut in the cutting process [21]. Nayfeh et al. [22] have investigated the cutting system dynamics and stability of cutting tool on a lathe due to the regenerative mechanism. In the past, many researchers considered the regenerative vibration effect and several other nonlinear elements. The main nonlinearities considered in the cutting models are the structural nonlinearity, higher-order nonlinearities in the cutting force [23], the nonlinear friction coefficient [24], the nonlinear effect of worn cutting tool [25], and the other possible causes of nonlinear chatter.

Despite extensive research on cutting chatter and the stability of cutting systems, there are not many works have been done on the dynamics of the cutting systems [4, 7, 23, 25–30]. So far, almost no dynamics study has been found on the vibration of the cutting tool with the thermal distortion in the turning system. It is well known that the thermal distortion has a great effect on the machining precision [31]. Therefore, this work is mainly focused on investigating dynamic behaviors of the cutting tool affected by the thermal distortion.

Fig. 1
figure 1

Schematic diagram of a single degree of freedom orthogonal model for turning process, where m is the equivalent mass of the cutting tool, c is the equivalent damping, and k is the nonlinear stiffness of the turning system

Full size image

2 The model

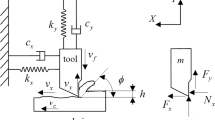
A model about a single degree of freedom orthogonal turning process with a flexible cutting tool and relatively rigid workpiece is shown in Fig. 1 [3, 20, 22, 32], where the cutting tool is considered one-dimensional oscillator with nonlinear stiffness and the thermal distortion both in axial and in radial direction. The motive equation without considering the thermal distortion can be modeled in the radial direction as:

$$\begin{aligned} m\ddot{x}+c\dot{x}+kx+\alpha x^{3}=k_f b(x(t-T)-x(t)) \end{aligned}$$
(1)

where x is the displacement of cutting tool in radial direction, m is the equivalent mass of the cutting tool, c is the equivalent damping, k is the equivalent stiffness, \(\alpha \) is nonlinear constant coefficient of stiffness function, \(k_f\) is the cutting coefficient in radial direction, b is the chip width, T is the time delay, which connected with the spindle speed, and \(x(t-T)-x(t)\) is the dynamic chip thickness due to the cutting tool vibration.

The thermal distortion of the cutting tool at t time can be approximately described as [33]

$$\begin{aligned} \xi =\xi _{\max } (1-e^{-t/t_c }) \end{aligned}$$
(2)

where \(\xi _{\max }\) is the largest thermal distortion of the cutting tool, and \(t_c\) is a constant coefficient associated with cutting conditions.

The dynamic equation of the turning system considered the thermal distortion of the cutting tool both in axial and radial direction can be expressed by

$$\begin{aligned} m\ddot{x}+c\dot{x}+kx+\alpha x^{3}=k_f (b+\xi )(x(t-T)-x(t)+\xi ) \end{aligned}$$
(3)

Equation (3) with substitution (2) can be converted to the form

$$\begin{aligned}&m\ddot{x}+c\dot{x}+kx+\alpha x^{3}=k_f (b+\xi _{\max } (1-e^{-t/t_c }))\nonumber \\&\quad (x(t-T)-x(t)+\xi _{\max } (1-e^{-t/t_c })) \end{aligned}$$
(4)

Rearranging the motive Eq. (4) can obtain

$$\begin{aligned}&\ddot{x}+2\mu \omega _0 \dot{x}+\omega _0 ^{2}x+\beta \omega _0 ^{2}x^{3}\nonumber \\&\quad =p\omega _0 ^{2}(b+\xi _{\max } (1-e^{-t/t_c }))\nonumber \\&\qquad (x(t-T)-x(t)+\xi _{\max } (1-e^{-t/t_c })) \end{aligned}$$
(5)

where \(\mu =c/2m\omega _0 \) is the dimensionless damping ratio, \(\omega _0 =\sqrt{k/m}\) is the natural frequency, and \(\beta =\alpha /m\omega _0 ^{2}\) is the cubic nonlinear spring constant, the above parameters are determined by the natural properties of the cutting tool, \(p=k_f /m\omega _0 ^{2}\), by defining the dimensionless variables marking with tilde as follow

\(x=l\tilde{x}, t=\tilde{t}/\omega _0 , T=\tilde{T}/\omega _0 , t_c =\tilde{t}_c /\omega _0 , p=l\tilde{p}, b=l\tilde{b}, \xi _{\max } =l\tilde{\xi }_{\max } , \beta =l^{2}\tilde{\beta }, l=2\pi R, R\) is the radius of the workpiece. Substituting the above dimensionless variables into Eq. (5) and rearranging, the motive equation can be represented by

$$\begin{aligned}&\ddot{\tilde{x}}+2\mu \dot{\tilde{x}}+\tilde{x}+\tilde{\beta }\tilde{x}^{3}=\tilde{p}(\tilde{b}+\tilde{\xi }_{\max } (1-e^{-\tilde{t}/\tilde{t}_c }))\nonumber \\&\quad (\tilde{x}(\tilde{t}-\tilde{T})-\tilde{x}(\tilde{t})+\tilde{\xi }_{\max } (1-e^{-\tilde{t}/\tilde{t}_c })) \end{aligned}$$
(6)

We remove the tilde for ease of notation and obtain the dimensionless equation of motion can be written in the form

$$\begin{aligned}&\ddot{x}+2\mu \dot{x}+x+\beta x^{3}=p(b+\xi _{\max } (1-e^{-t/t_c}))\nonumber \\&\quad (x(t-T)-x(t)+\xi _{\max } (1-e^{-t/t_c })) \end{aligned}$$
(7)

3 Nonlinear dynamic analysis and numerical simulation

In order to investigate the chatter characteristics of the nonlinear turning system, the numerical results are used to generate time history, phase portrait, Poincaré section, and power spectrum. These figures are used as qualitative tools to explore the nonlinear dynamic behaviors of the cutting tool, such as the periodic, multi-periodic, quasi-periodic, and chaotic motions. For the Poincaré section, we collected all of the points of intersection of the trajectory with the surface of section \(\dot{x}=0\) when \(\ddot{x}<0\). In the following numerical simulations, the time delay T is chosen as the bifurcation parameter.

At the beginning, the bifurcation diagram of the cutting tool displacement can be obtained when the bifurcation parameter T changed from 1.5 to 10. Then, the bifurcation theory is utilized to globally analyze the dynamic responses of the cutting tool. The dynamics system (7) initial conditions and the other parameters are chosen as follow: \(x(0)=2, \dot{x}(0)=0, \mu =0.05, \beta =0.25, p=1, b=0.25, \xi _{\max } =1, t_c =200\), and \(x(t-T)=2\) when \(t\in (-T,0)\).

Fig. 2
figure 2

Bifurcation diagram of the cutting tool displacement x versus time delay T when the largest thermal distortion \(\xi _{\max } =1, T\) form 1.5 to 10

Full size image

The bifurcation diagram as shown in Fig. 2, the horizontal axis represents the time delay T, and the vertical axis represents the displacement of the cutting tool in the radial direction. It is clear that there exist periodic, quasi-periodic, and chaotic motions. We can be observed from the bifurcation diagram in Fig. 2 that with the increase in the time delay T, the motions of the cutting tool to present the following bifurcation pattern: periodic-1, quasi-periodic, and chaotic motions.

Fig. 3
figure 3

The periodic-1, quasi-periodic, and chaotic motions are obtained when the largest thermal distortion \(\xi _{\max } =1\), time delay \(T=3,5,7\), respectively. a1, b1, c1, d1, e1 are time history on the plane \(\{t,x\}\), phase portrait in three-dimensional space \(\{x,\dot{x},x(t-T)\}\), phase portrait on the plane \(\{x,\dot{x}\}\), Poincaré section on the plane \(\{x,x(t-T)\}\), and power spectrum, when \(\xi _{\max } =1, T=3\); a2, b2, c2, d2, e2 are time history on the plane \(\{t,x\}\), phase portrait in three-dimensional space \(\{x,\dot{x},x(t-T)\}\), phase portrait on the plane \(\{x,\dot{x}\}\), Poincaré section on the plane \(\{x,x(t-T)\}\), and power spectrum, when \(\xi _{\max } =1, T=5\); a3, b3, c3, d3, e3 are time history on the plane \(\{t,x\}\), phase portrait in three-dimensional space \(\{x,\dot{x},x(t-T)\}\), phase portrait on the plane \(\{x,\dot{x}\}\), Poincaré section on the plane \(\{x,x(t-T)\}\), and power spectrum, when \(\xi _{\max }=1, T=7\)

Full size image
Fig. 4
figure 4

Bifurcation diagrams of the cutting tool displacement x versus time delay T. a when the largest thermal distortion \(\xi _{\max } =2\), time delay T form 1.5 to 10; b when the largest thermal distortion \(\xi _{\max } =3\), time delay T form 1.5 to 10

Full size image

Based on the bifurcation diagram as shown in Fig. 2, we choose several typical values of the time delay T to obtain the time histories, phase portraits, Poincaré sections, and power spectra of the periodic, quasi-periodic, and chaotic motions in the following simulations, respectively. Fig. 3a1, b1, c1, d1, e1 shows the cutting tool response when the time delay \(T=3\). The time history, as shown in Fig. 3a1, indicates a stable periodic motion. The three-dimensional phase portrait is presented in Fig. 3b1. The phase portrait as shown in Fig. 3c1 is a small closed curve. Poincaré section in Fig. 3d1 consists of one point, confirming the periodic-1 nature of the cutting tool motion and its power spectrum is presented in Fig. 3e1 consists of a fundamental peak that means periodic motion.

When the time delay T increased to 5, the response of cutting tool is presented in Fig. 3a2, b2, c2, d2, e2. The time history is shown in Fig.3a2 that indicates a modulated motion. The messy trajectory is located in a bounded region in Fig. 3b2, c2 that indicate a complex aperiodic motion, but Poincaré section in Fig. 3d2 means that the motion is quasi-periodic because it consists of a large number of points falling on a closed curve. The fundamental frequency now consists of a fundamental peak, and some smaller asymmetric side bands in Fig. 3e2 indicate a periodic motion of the cutting tool.

The response of cutting tool is chaotic motion when the time delay T increased to 7 in Fig. 3a3, b3, c3, d3, e3. The time history is shown in Fig. 3a3 that indicates complex aperiodic motion. A wider range of messy curve that indicates complex aperiodic motions as shown in Fig. 3b3, c3. The dense bounded nature of Poincaré section in Fig. 3d3 indicates chaotic motion. The power spectrum is presented in Fig. 3e3 that has some peaks and a continuous background around the natural frequency of the cutting tool, confirming that the motion is chaotic motion. As shown in Fig. 3, the dynamic response of the cutting tool is similar to a Duffing’s system with time delay excitation [31].

Fig. 5
figure 5

The periodic-7 and periodic-2 motions are obtained when the largest thermal distortion \(\xi _{\max } =2\), time delay \(T=4\), and \(\xi _{\max } =3\), time delay \(T=2.3\), respectively. a1, b1, c1, d1, e1 are time history on the plane \(\{t,x\}\), phase portrait in three-dimensional space \(\{x,\dot{x},x(t-T)\}\), phase portrait on the plane \(\{x,\dot{x}\}\), Poincaré section on the plane \(\{x,x(t-T)\}\), and power spectrum when \(\xi _{\max }=2, T=4\); a2, b2, c2, d2, e2 are time history on the plane \(\{t,x\}\), phase portrait in three-dimensional space \(\{x,\dot{x},x(t-T)\}\), phase portrait on the plane \(\{x,\dot{x}\}\), Poincaré section on the plane \(\{x,x(t-T)\}\), and power spectrum when \(\xi _{\max } =3, T=2.3\)

Full size image
Fig. 6
figure 6

Time histories of the cutting tool when \(T=1.8\), a \(\xi _{\max } =1\); b \(\xi _{\max }=2\); c \(\xi _{\max }=3\)

Full size image
Fig. 7
figure 7

Time histories of the cutting tool when \(T=5\), a \(\xi _{\max } =1\); b \(\xi _{\max }=2\); c \(\xi _{\max }=3\)

Full size image

In the following numerical simulations, we consider the influence of the other largest thermal distortion \(\xi _{\max }\) on the nonlinear dynamic behaviors of the cutting tool. The largest thermal distortion \(\xi _{\max }\) chosen as 2 and 3, comparing with the \(\xi _{\max } =1\), they are the relative medium and large largest thermal distortion of the cutting tool, respectively. The others parameters are the same as shown in Fig.2. The bifurcation diagrams are presented in Fig. 4a, b.

As shown in Fig. 4a, b, the complicated nonlinear dynamics, including periodic, multi-periodic, quasi-periodic, and chaotic motions, can be observed from the bifurcation diagrams. The bifurcation diagram in Fig. 4a indicates the motions of the cutting tool to present the following bifurcation pattern with the increase in the time delay T, periodic-1, quasi-periodic, periodic-7, and chaotic motions. The bifurcation diagram in Fig. 4b means the following bifurcation pattern: periodic-1, periodic-2, quasi-periodic, and chaotic motions. It is noted that the nonlinear dynamic responses of the cutting tool are very sensitive to the change in the largest thermal distortion. In addition, the displacement of the cutting tool became larger with the increase in the largest thermal distortion that is shown in Figs. 2 and 4.

In the subsequent studies, the time history, phase portraits, Poincaré section, and the power spectrum to be adopted to continue to investigate the multi-periodic motion of the cutting tool. From the bifurcation diagram Fig. 4a, it is clear that there exists a multi-periodic motion. When the bifurcation parameter time delay \(T=4\), the time history of the cutting tool is presented in Fig. 5a1. The three-dimensional phase portrait and the phase portrait are a closed curve that indicates a stable periodic motion as shown in Fig. 5b1, c1. In addition, Poincaré section consists of the seven points in Fig. 5d1, meaning the periodic-7 motion of the cutting tool. The power spectrum in Fig. 5e1 indicates that the motion is periodic motion.

It is obvious that the periodic-2 motion occurs, as shown in Fig. 4b. When time delay \(T=2.3\), the time history is shown in Fig. 5a2 that indicates a stable periodic motion and the three-dimensional phase portrait is presented in Fig. 5b2. The phase portrait is displayed in Fig. 5c2 that consists of a closed curve. Poincaré section consists of the two points in Fig. 5d2, confirming the periodic-2 motion of the cutting tool and its power spectrum in Fig. 5e2 consists of a fundamental peak and some smaller asymmetric side bands that mean the motion is periodic motion.

From the above numerical results, it is obvious that nonlinear dynamic responses of the cutting tool are influenced by the largest thermal distortion. As the largest thermal distortion increases, the displacement of the cutting tool became larger gradually. In addition, the motions of the cutting tool present different bifurcation patterns with the difference of the largest thermal distortion.

4 Stability analysis of different thermal distortion

In this section, time history of the cutting tool is utilized to investigate the stability characteristics of the nonlinear turning system. Based on the aforementioned phenomenon, we choose different time delay T and the largest thermal distortion \(\xi _{\max }\) to obtain the time histories of the cutting tool. When the time delay T is 1.8 and 5, the largest thermal distortion \(\xi _{\max }\) is 1, 2, and 3, respectively. The dynamics system (7) initial conditions and the other parameters are chosen as same in Fig. 2. The time histories of cutting tool are shown in Figs. 6 and 7.

As shown in Figs. 6 and 7, it is clear that the stability of the cutting tool is influenced by the largest thermal distortion. The cutting system loses stability earlier with the increase in the largest thermal distortion.

5 Conclusions

This paper studies the dynamics of the regenerative orthogonal turning process by adopting a single degree of freedom model with the nonlinear stiffness and thermal distortion of the cutting tool. Based on the regenerative model, the dynamics motion of the cutting tool that considered the thermal distortion both in the axial and in radial direction is modeled. The numerical method is used to investigate the influence of the largest thermal distortion on the dynamic behavior of the cutting tool. In addition, time histories, phase portraits, Poincaré sections, and power spectra are used as qualitative tools to explore the periodic, multi-periodic, quasi-periodic, and chaotic motions of the cutting tool. We found that nonlinear dynamic responses of the cutting tool are influenced by the largest thermal distortion. The bifurcation phenomenon of the motion of the cutting tool present different bifurcation patterns with different of the largest thermal distortion. There are many other parameters that can also influence dynamic response of the cutting tool [22, 30]. Therefore, thermal distortion of the cutting tool is one of the significant factors to which should pay attention. Furthermore, the largest thermal distortion can affect chatter system stability. As the increase in the largest thermal distortion, the chatter system loses stability earlier and the displacement of the cutting tool became larger. Therefore, the cutting tool should be chosen that the largest thermal distortion as small as possible.