1 Introduction

Grinding craft is a historic powerful machining process which has been widely used in surface finish for its high precision. However, the grinding performance is still restricted by some unsolved problems [1], such as chatter vibrations. Called regenerative chatter, this is a kind of vibration with high frequency usually occurring in the machining process. The onset of the chatter in the grinding process will cause bad surface finish and poor precision, which are both the main objectives of this craft [2]. To clarify the mechanism of the chatter and suppress this vibration, many researches had been performed by mechanical engineers at universities or in industry [3]. There was a time when the negative damping was regarded as the source of the chatter, but nowadays, it is widely accepted that the chatter is a self-excited vibration induced by the force-displacement interactions [4]. Similar to the metal cutting and milling processes, the interaction between the workpiece and the tool involves the so-called regenerative effects. When the machine is started, the surface of the workpiece generated by the tool on the pass becomes the upper surface of the chip on the subsequent pass [5], and the same phenomenon also exists on the surface of the tool when it comes to the grinding process [6]. To study the relation between the regenerative effect and the onset of the chatter, many excellent researches were carried out.

In 1946, Arnold did a lot of experimental works to observe the chatter in turning process, and then he first described the regenerative effects in his report [7]. After the regenerative theory had been accepted, some researchers started to introduce this concept into the researches on grinding chatter. Besides experimental works [8, 9], some theoretical and numerical researches also had been done to study the regenerative chatter in the grinding process. Hahn did the first theoretical study on the chatter in a grinding process [10], in which the wheel was assumed to be wear-resistant and only the regeneration on the workpiece surface was considered. This study was performed theoretical by Laplace transform and Nyquist diagram, and the stability information of the grinding process was obtained. Taking a further step, Thompson proposed a new method to analyze the stability of the steady-state response of the grinder in a grinding process with doubly regenerative effects [11]. His method involved a so-called amplitude growing rate which was adopted as an index to predict the grinding stability. Based on this theory, he successively published a series of papers [12–15] to discuss the effects of different factors, such as grinding stiffness, wave filtering, and the rotational speeds of the workpiece and the grinding wheel, on the grinding stability. However, the expression of the regenerative force considered in his model was assumed to be a sinusoid function. This assumption may cause the loss of the interactive information, thus the relation between system parameters and dynamic behaviors cannot be revealed thoroughly. Since the chatter-free or the stable smooth grinding process is always needed to obtain a good surface quality, it is important to clarify the effects of the parameter values on the dynamic motions of the grinding process and avoid the choice of the bad values which may incur the chatter vibrations. To this end, Yuan et al. proposed a nonlinear five-DOF system to model and study the grinding process [16]. The normal and shear contact force considered in this model were assumed to be proportional to the total penetration of the grindstone. Although the phenomenon that the rotation speed can affect the system behaviors was found in their work, the information revealed by their results was still limited since the employed method is only numerical simulations. Three years later, they carried out a theoretical study on this topic [17], but only the regeneration on the workpiece surface was considered for simplicity, because it is hard to analyze a system with two distinct time delays introduced by the doubly regenerations. Thus, the results of this work may still not be persuadable enough since the regeneration also exists on the wheel surface. Recently, Liu et al. did some researches on the stability and chatter motions in a transverse grinding process [18, 19]. The stability information was obtained by Liu through a numerical method which is based on the labeling of a bound region in the complex plane [18], and then he cooperated with Chung to study the nonlinear chatter motions [19] through a so-called perturbation-incremental scheme [20–22].

It is known that theoretically analyzing the linear stability of systems with multiple delays is next to impossible. Although Campbell did some excellent works on theoretically estimating the stability boundary of a system with multiple delays [23], but the results were not accurate enough for further chatter motion prediction and the analysis method was not easy to be applied in other analysis. Instead of theoretical analysis, the stability information can also be obtained via numerically calculating the right most eigenvalues [18]. When one group of the critical eigenvalues and parameters where the real parts of the right most eigenvalues equal zero [18, 19] is obtained, the continuation algorithm [24] can be employed to find the profile of the chatter-free region in the parameter space. Moreover, this algorithm had already been integrated into a freely available software package DDEBIFTOOL [25, 26], which can be used to analyze the stability and predict the periodic motions of delayed differential equations (DDEs).

In this paper, a cylindrical plunge grinding process is described by a dynamic model, where the expression of the regenerative force between the workpiece and the wheel is based on Liu’s work [18]. To find the parameter range in which the grinding process is chatter-free, we firstly study the linear stability of the trivial equilibrium of the model which is corresponding to the smooth grinding process. This analysis is accomplished by a numerical method which involves eigenvalues analysis and continuation algorithm. Through this, the linear critical boundaries in the parameter space are found, thus the profile of the chatter-free region is clearly presented. Then the nonlinear bifurcation analysis is carried out to predict the chatter motions when the values of system parameters are leaving the chatter-free region. It is interesting that both supercritical and subcritical Hopf bifurcations are found on one boundary curve. It is known that the subcritical one will cause the coexistence of stable equilibrium and periodic motion with large amplitude, and then the dynamic behaviors of the system will be affected by the initial conditions. Thus, there exits a range of the parameters, in which the grinding process might be either chatter-free or chatter. We call this zone the conditional chatter-free region. In engineering, this region is also unavailable since the chatter might be incurred by any misoperation. To locate this, the Bautin bifurcation analysis is carried out numerically with the help of DDEBIFTOOL [25, 26]. Finally, we point out that the results from not only the linear analysis but also the nonlinear analysis must be considered in designing a chatter-free grinding process.

2 Dynamic model for cylindrical plunge grinding process

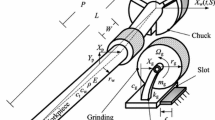
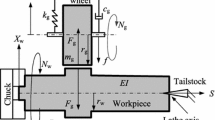
In machining processes, the material in the part surface is gradually removed by tools to help people to make things. For example, this operation is performed by abrading the part surface with a wheel in the grinding process. Mostly, the grinding craft is adopted when the demand for surface quality is high for its high precision, thus the chatter vibration in this operation is strictly avoided. To this end, the dynamic motion of the grinding process is studied by considering the dynamic model which is shown in Fig. 1. In this model, the workpiece is regarded as a damped hinged-hinged slender Euler–Bernoulli beam rotating at an angular speed ω w , and the grinding wheel a damped spring mass system rotating at another angular speed ω g and moving toward the workpiece at a speed of f per revolution.

Fig. 1
figure 1

Schematic of cylindrical plunge grinding process

Full size image

At the top-right of Fig. 1, the details of the contact zone are magnified to illustrate the regenerative effects on the surfaces of both the workpiece and the wheel. The force between the workpiece and the wheel is proportional to the current penetrations of both the wheel and the workpiece owing to the doubly regenerative effects. The depth of the wheel penetration into the workpiece ε g is the difference between the current and previous positions of the wheel x g (t)−x g (t−τ g )+f, and the depth of the workpiece penetration ε w is x w (t)−x w (t−τ w ). It is noticed that f is the initial feed from the moving of the grinding-wheel-rack and x g (t) is the position of the wheel with respect to the rack. Then the contact force is expressed as multiplying these penetrations by a so-called grinding stiffness k c which stands for the combined effects of many physical factors, such as the contact width, the material of the workpiece, and the feed.

The dynamic motions of the grinding process is governed by

$$ \everymath{\displaystyle} \begin{array} {l} m_{g}\ddot{x}_{g} + c_{g}\dot{x}_{g} +k_{g}x_{g} = N,\\[9pt]\rho A\frac{\partial^{2}x_{w}}{\partial t^{2}} + c_{w}\frac{\partial x_{w}}{\partial t} + EI\frac{\partial^{4}x_{w}}{\partial s^{4}}\\[9pt]\quad {}- \frac{EA}{2L}\frac{\partial^{2}x_{w}}{\partial s^{2}}\int_{0}^{L}\biggl( \frac{\partial x_{w}}{\partial s} \biggr)^{2}\, ds = - N\delta ( s - l ),\\[12pt]\left \{ \begin{array} {l} x_{w} ( t,0 ) = 0,\quad \frac{\partial^{2}x_{w}}{\partial s^{2}} (t,0 ) = 0,\\[8pt]x_{w} ( t,L ) = 0,\quad \frac{\partial^{2}x_{w}}{\partial s^{2}} ( t,L ) = 0, \end{array}\right .\\\end{array}$$
(1)

where N is the normal regenerative force between the workpiece and the wheel [18], and it is given by

(2)

where k c is the grinding stiffness. Given the boundary conditions, the displacement of the workpiece is expanded in sine series

$$ x_{w}( t,s ) = \sum_{i = 1}^{\infty} x_{i}( t ) \sin \biggl( \frac{i\pi s}{L}\biggr).$$
(3)

In engineering, the first mode of the beam is the most important one because it is prone to be promoted, thus only the dynamic behaviors of the first mode will be discussed in the following analysis. Substituting Eqs. (2) and (3) into Eq. (1), applying Galerkin projection and keeping the first, one can obtain

$$ \begin{array} {l} m_{g}\ddot{x}_{g} +c_{g}\dot{x}_{g} + k_{g}x_{g}\\[9pt]\quad = k_{c}\biggl[ f + \bigl( x_{1}( t ) -x_{1}( t - \tau_{w} ) \bigr)\sin\biggl( \frac{l\pi}{L}\biggr)\\[9pt]+ \bigl( x_{g}( t - \tau_{g} ) - x_{g}( t ) \bigr)\biggr],\\[9pt]\frac{\rho AL}{2}\ddot{x}_{1} + \frac{c_{w}}{2L}\dot{x}_{1}+ \frac{EI\pi^{4}}{2L^{3}}x_{1} - \frac{EA\pi^{4}}{8L^{3}}x_{1}^{3}\\[9pt]\quad = - k_{c}\biggl[ f + \bigl( x_{1}( t ) -x_{1}( t - \tau_{w} ) \bigr)\sin\biggl( \frac{l\pi}{L}\biggr)\\[9pt]\qquad {}+ \bigl( x_{g}( t - \tau_{g} ) - x_{g}( t) \bigr) \biggr]\sin\biggl( \frac{l\pi}{L} \biggr). \end{array}$$
(4)

Defining a new state vector \(\mathbf{y} = ( y_{1},y_{2},y_{3},y_{4} ) =( \frac{x_{g}}{H} - p,\frac{x_{1}}{H} -q,\frac{\dot{x}_{g}T}{H},\frac{\dot{x}_{1}T}{H} )\), where (p,q) is the equilibrium point of Eq. (4), and introducing the nondimensional parameters listed as

$$ \renewcommand{\arraystretch}{2}\everymath{\displaystyle}\begin{array} {l} \xi_{1} =\frac{c_{g}}{m_{g}}\sqrt{ \frac{m_{g}}{k_{g}}} ,\quad \kappa_{1} =\frac{k_{c}}{k_{g}},\quad \tau_{1} = \frac{\tau_{g}}{T},\quad \gamma =\frac{2m_{g}}{L\rho A},\\\xi_{2} = \frac{c_{w}}{L^{2}\rho A\sin (\frac{l\pi}{L} )}\sqrt{\frac{m_{g}}{k_{g}}} , \quad \\\kappa_{2} = \frac{EI\pi^{4}m_{g}}{L^{4}\rho Ak_{g}\sin ( \frac{l\pi}{L} )}+ \frac{3E\pi^{4}q^{2}m_{g}}{4L^{4}\rho k_{g}\sin ( \frac{l\pi}{L} )},\\\tau_{2} =\frac{\tau_{w}}{T},\\\mu_{2} = \frac{3EH^{2}\pi^{4}m_{g}q}{4L^{4}\rho k_{g}\sin ( \frac{l\pi}{L} )},\quad \mu_{3} =\frac{EH^{2}\pi^{4}m_{g}}{4L^{4}\rho k_{g}\sin ( \frac{l\pi}{L} )}\\\end{array}$$
(5)

and

where \(T = \sqrt{m_{g}/k_{g}}\) and H=0.001(m), one can transform Eq. (4) into

$$ \mathbf{\dot{y}} ( t ) = \mathbf{Ay} ( t ) + \mathbf{D}_{1}\mathbf{y} ( t - \tau_{1} ) + \mathbf{D}_{2}\mathbf{y} ( t -\tau_{2} ) + \mathbf{f},$$
(6)

where

$$ \begin{array}{l}\mathbf{A} = \left ( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c}0 & 0 & 1 & 0 \\0 & 0 & 0 & 1 \\- 1 - \kappa_{1} & \kappa_{1} & - \xi_{1} & 0 \\\gamma\kappa_{1} & - \gamma\kappa_{1} - \kappa_{2} & 0 & - \xi_{2}\\\end{array} \right ),\\[30pt]\mathbf{f} = \left ( \begin{array}{c} 0 \\ 0 \\ 0\\ - \mu_{2}x_{2}^{2} - \mu_{3}x_{2}^{3} \\\end{array} \right ),\\[30pt]\mathbf{D}_{1} = \left ( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c}0 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \\\kappa_{1} & 0 & 0 & 0 \\- \gamma\kappa_{1} & 0 & 0 & 0\\\end{array} \right ),\\[30pt]\mathbf{D}_{2}= \left ( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c}0 & 0 & 0& 0 \\ 0 & 0 & 0 & 0 \\ 0 & - \kappa_{1} & 0 & 0 \\ 0 & \gamma\kappa_{1}& 0 & 0 \\\end{array} \right ).\\\end{array}$$
(7)

For simplicity, we let q=1, or we can adjust f to this end if not.

3 Linear chatter criterion

It is seen from Fig. 1 that the trivial equilibrium point y=(0,0,0,0) represents the smooth grinding process, and its stability varies corresponding to the grinding stability. Thus, the stability of the grinding process can be perceived through analyzing the trivial equilibrium point. It is known that the equilibrium is linearly stable only when the real parts of all the eigenvalues are negative. Then there must be eigenvalues with real parts being zero on the boundary of the chatter-free region in which the smooth grinding process is stable. Moreover, the critical eigenvalues are pure imaginary when the chatter vibration is going to take place.

The characteristic equation is computed

$$ \bigl \vert \lambda\mathbf{I} - \mathbf{A} - \mathbf{D}_{1}\exp ( - \lambda\tau_{1} ) - \mathbf{D}_{2}\exp ( - \lambda \tau_{2} ) \bigr \vert = 0,$$
(8)

where | • | is the determinant of •. Substituting Eq. (7) and λ=±iω into Eq. (8) and separating the real and imaginary parts, we obtain

(9)

and

(10)

Since Eqs. (9) and (10) are transcendental and there is no proper theoretical method to solve such equations, we adopt a numerical scheme to achieve the same goal, locating the chatter-free region.

When a good initial guess is given, one can obtain a numerical solution of Eqs. (9) and (10) via Newton–Raphson iteration. Since groups of numerical solutions are needed to present the boundary of the chatter-free region, we perform the iteration repeatedly, and the scheme used to give the initial guesses at each step is the continuation algorithm [25, 26], which is plotted in Fig. 2.

Fig. 2
figure 2

Continuation algorithm

Full size image

To clarify the effect of the regenerative force on the grinding stability, we fixed the values of other physical parameters, except the grinding stiffness k c and the rotation speeds of the workpiece ω w and the wheel ω g , which are related to the regenerative force. As an example, a set of the parameters is given and stated in Table 1, and then the continuation algorithm is started. Following the algorithm presented in Fig. 2, the linear critical boundaries of the chatter-free region is obtained and plotted in Fig. 3, where different critical surfaces are distinguished by its grey level. It is shown that the grinding process is stable when the values of the system parameters are located under these surfaces, and the grinding chatters with different frequencies are about to occur when the values cross each chatter boundary.

Fig. 3
figure 3

Linear critical boundaries in the parameter space

Full size image
Table 1 Fixed parameters in this research
Full size table

To illustrate the chatter and chatter-free regions, one selected section (τ 1=11.81) is plotted in Fig. 4. When the value of the system parameters is located in the grey region, the trivial equilibrium point is linearly stable, and the corresponding smooth grinding process is stable, namely it is chatter-free. In the other respect, the grinding stability will be lost and the chatter vibration will occur when the parameters are leaving the grey region for the white one. It also can be seen from Fig. 4 that the grinding stability is independent of the rotation speeds of the workpiece ω w and the wheel ω g (where ω w =2π/τ w =2π/Tτ 2 and ω g =2π/τ g =2π/Tτ 1) as long as the grinding stiffness is small. Namely, a weak regenerative force is not enough to promote the chatter vibrations in this process. However, the rotation speeds ω w and the ω g must vary accordingly when one grind some hard material, where the large contact force is needed, or the value of the system parameter would be in the white regions, and thus chatter happens.

Fig. 4
figure 4

Linear critical boundaries with τ 1=11.81

Full size image

4 Nonlinear chatter motions

With the value of the system parameters leaving the grey region for the white one, the stability of the smooth grinding process will be lost, and then the chatter occurs. As examples, the chatter motions are predicted with the value of the system parameters varying in the directions of the arrows A and B plotted in Fig. 4, respectively. The numerical prediction is obtained with the help of DDEBIFTOOL [25, 26], and the results are plotted in Fig. 5.

Fig. 5
figure 5

Bifurcation diagrams and time domains, where points are the stable solutions and circles are the unstable solutions. (1) Supercritical Hopf bifurcation along arrow A, (2) Subcritical Hopf bifurcation along arrow B, (3) Chatter motion of the wheel at point I, (4) Chatter motion with large amplitude at point II, (5) Stable smooth grinding process at point III

Full size image

It is seen from Fig. 5 that the ways from the chatter-free to the chatter along each arrow are different. Mathematically, they are supercritical and subcritical Hopf bifurcations respectively [27]. Figure 5(1) shows the supercritical one through which grinding process from chatter-free to the chatter continuously, and Fig. 5(2) presents the subcritical one cause a jump from the chatter-free to the chatter with a large amplitude when the system parameter cross the boundary. In Fig. 5, there are other three subfigures, Figs. 5(3), 5(4), and 5(5) illustrating the time domains of the wheel displacement with different system parameters. It is shown in Figs. 5(4) and 5(5) that there still exist some chatter vibrations with large amplitudes in some chatter-free regions, which are located through the preceding linear stability analysis. We call this zone the conditional chatter-free region, in which the dynamic behaviors of the system is also related to the initial conditions of the grinding process.

5 Conditional chatter-free region

In industry, the conditional chatter-free region must be avoided too since the chatter might be incurred by any misoperation of the manipulator. Thus, it is important to locate this region so that the grinding process can evade any kind of chatter.

Mathematically, the switching point between the supercritical Hopf bifurcation and the subcritical one is called the Bautin bifurcation point, and it is the start of the conditional chatter-free region. To find this point, the method of multiple scales [28] (MMS) is employed to compute the normal form [29] of the critical situation.

To perform the MMS, the critical eigenvectors must be obtained, and it is governed by

$$ \begin{array}{l}\mathbf{rM} = \mathbf{sN}, \\[3pt]\mathbf{sM} = - \mathbf{rN}, \\ \end{array}$$
(11)

and

$$ \begin{array}{l}\mathbf{Mp} = \mathbf{Nq}, \\[3pt]\mathbf{Mq} = - \mathbf{Np}, \\ \end{array}$$
(12)

where M+i N=iω I−A−D 1exp(−iωτ 1)−D 2exp(−iωτ 2c ) is the critical characteristic matrix, r+i s=(1,r 2+is 2,r 3+is 3,r 4+is 4) and p+i q=(1,p 2+iq 2,p 3+iq 3,p 4+iq 4)T are the critical left and right eigenvectors respectively.

Considering the critical situation where the values of the system parameters are on the boundary and introducing two time scales T 0=t, T 1=εt and T 2=ε 2 t, one has

(13)

where τ 2c and κ 1c represents the critical values of τ 2 and κ 1 on the boundary of the chatter-free region. The delayed terms in Eq. (13) are expanded in terms of Taylor’s series

$$ \renewcommand{\arraystretch}{1.5}\everymath{\displaystyle}\begin{array} {l} y_{1}( t - \tau_{1} )\\\quad = y_{10}( T_{0} - \tau_{1},T_{1},T_{2}) \\\qquad {}+ \varepsilon\biggl( - \tau_{1}\frac{\partial}{\partial T_{1}}y_{10}(T_{0} - \tau_{1},T_{1},T_{2} ) \\\qquad {}+y_{11}( T_{0} - \tau_{1},T_{1},T_{2}) \biggr)\\\qquad {} + \varepsilon^{2}\biggl( - \tau_{1}\frac{\partial}{\partial T_{2}}y_{10}( T_{0} - \tau_{1},T_{1},T_{2})\\\qquad {} + \frac{1}{2}\tau_{1}^{2}\frac{\partial^{2}}{\partial T_{1}}y_{10}(T_{0} - \tau_{1},T_{1},T_{2} ) \biggr)\\\qquad {} + \varepsilon^{2}\biggl( - \tau_{1}\frac{\partial}{\partial T_{1}}y_{11}( T_{0} - \tau_{1},T_{1},T_{2}) \\\qquad {}+ y_{12}( T_{0} - \tau_{1},T_{1},T_{2}) \biggr),\\y_{2}( t - \tau_{2} )\\\quad = y_{20}( T_{0} - \tau_{2c},T_{1},T_{2}) \\\qquad {}+ \varepsilon\biggl( - \tau_{2}\frac{\partial}{\partial T_{1}}y_{20}(T_{0} - \tau_{2c},T_{1},T_{2} )\\\qquad {} +y_{21}( T_{0} - \tau_{2c},T_{1},T_{2}) \biggr)\\\qquad {}+ \varepsilon^{2}\biggl( - \tau_{2c}\frac{\partial}{\partial T_{2}}y_{20}( T_{0} - \tau_{2c},T_{1},T_{2})\\\qquad {} + \frac{1}{2}\tau_{2c}^{2}\frac{\partial^{2}}{\partial T_{1}}y_{20}( T_{0} - \tau_{2c},T_{1},T_{2}) \biggr)\\\qquad {}+ \varepsilon^{2}\biggl( - \tau_{2c}\frac{\partial}{\partial T_{1}}y_{21}(T_{0} - \tau_{2c},T_{1},T_{2} ) \\\qquad {}+y_{22}( T_{0} - \tau_{1},T_{1},T_{2}) \biggr).\\\end{array}$$
(14)

Substituting Eqs. (13) and (14) into Eq. (6), and collecting the coefficients of ε 1, ε 2, and ε 3, one has

$$ \renewcommand{\arraystretch}{1.5}\everymath{\displaystyle} \begin{array} {@{}l} \frac{\partial y_{10}}{\partial T_{0}} ( T_{0},T_{1},T_{2}) - y_{30} ( T_{0},T_{1},T_{2} ) = 0,\\\frac{\partial y_{20}}{\partial T_{0}} ( T_{0},T_{1},T_{2} ) -y_{40} ( T_{0},T_{1},T_{2} ) = 0,\\\frac{\partial y_{30}}{\partial T_{0}} ( T_{0},T_{1},T_{2} ) +\kappa_{1c}y_{20} ( T_{0} - \tau_{2c},T_{1},T_{2})\\\quad {}+ \xi_{1}y_{30} ( T_{0},T_{1},T_{2}) - \kappa_{1}y_{10} ( T_{0} - \tau_{1},T_{1},T_{2})\\\quad {}- \kappa_{1}y_{20} ( T_{0},T_{1},T_{2})\\\quad {} + ( 1 + \kappa_{1} )y_{10} ( T_{0},T_{1},T_{2}) = 0,\\\frac{\partial y_{40}}{\partial T_{0}} ( T_{0},T_{1},T_{2} ) - \gamma \kappa_{1c}y_{20} ( T_{0} - \tau_{2c},T_{1},T_{2})\\\qquad {} + \xi_{2}y_{40} ( T_{0},T_{1},T_{2}) + \gamma\kappa_{1c}y_{10} ( T_{0} -\tau_{1},T_{1},T_{2} )\\\qquad {}- \gamma\kappa_{1c}y_{10} ( T_{0},T_{1},T_{2})\\\qquad {}+ ( \gamma\kappa_{1} + \kappa_{2c} )y_{20}( T_{0},T_{1},T_{2} ) = 0,\\\end{array}$$
(15)
$$ \renewcommand{\arraystretch}{1.8}\everymath{\displaystyle} \begin{array} {l} \frac{\partial y_{11}}{\partial T_{0}} ( T_{0},T_{1},T_{2}) - y_{31} ( T_{0},T_{1},T_{2} )\\\quad = - \frac{\partial y_{10}}{\partial T_{1}} ( T_{0},T_{1},T_{2} ),\\\frac{\partial y_{21}}{\partial T_{0}} ( T_{0},T_{1},T_{2} ) -y_{41} ( T_{0},T_{1},T_{2} )\\\quad = - \frac{\partial y_{20}}{\partial T_{1}} ( T_{0},T_{1},T_{2} ),\\\frac{\partial y_{31}}{\partial T_{0}} ( T_{0},T_{1},T_{2} )\\\qquad {} + \kappa_{1c}y_{21} ( T_{0} -\tau_{2c},T_{1},T_{2} ) + \xi_{1}y_{31}( T_{0},T_{1},T_{2} )\\\qquad {} - \kappa_{1c}y_{11} ( T_{0} -\tau_{1},T_{1},T_{2} )\\\qquad {} - \kappa_{1c}y_{21} ( T_{0},T_{1},T_{2})\\\qquad {}+ ( 1 + \kappa_{1c} )y_{11} ( T_{0},T_{1},T_{2})\\\quad = \kappa_{1c}\tau_{2c}\frac{\partial x_{20}}{\partial T_{1}} (T_{0} - \tau_{2c},T_{1},T_{2} )\\- \frac{\partial y_{30}}{\partial T_{1}} ( T_{0},T_{1},T_{2} ) -\kappa_{1c}\tau_{1}\frac{\partial x_{10}}{\partial T_{1}} ( T_{0} -\tau_{1},T_{1},T_{2} ),\\\frac{\partial y_{41}}{\partial T_{0}} ( T_{0},T_{1},T_{2} ) - \gamma \kappa_{1c}y_{21} ( T_{0} - \tau_{2c},T_{1},T_{2})\\\qquad {} + \xi_{2}y_{41} ( T_{0},T_{1},T_{2}) + \gamma\kappa_{1c}y_{11} ( T_{0} -\tau_{1},T_{1},T_{2} )\\- \gamma\kappa_{1c}y_{11} ( T_{0},T_{1},T_{2}) + ( \gamma\kappa_{1c} + \kappa_{2} )y_{21} (T_{0},T_{1},T_{2} )\\\quad = - \gamma\kappa_{1c}\tau_{2c}\frac{\partial y_{20}}{\partial T_{1}} (T_{0} - \tau_{2c},T,T_{21} )\\\qquad {} - \frac{\partial y_{40}}{\partial T_{1}} ( T_{0},T_{1},T_{2})\\\qquad {} + \gamma\kappa_{1c}\tau_{1}\frac{\partial y_{10}}{\partial T_{1}} (T_{0} - \tau_{1},T_{1},T_{2} )\\\qquad {}- \mu_{2}y_{20} ( T_{0},T_{1},T_{2})^{3},\\\end{array}$$
(16)

and

(17)

When the values of the system parameters are on the boundary, the nontrivial solution corresponding to the chatter motion is given by

(18)

where cc is the complex conjugation of the preceding terms and ω, which is also the imaginary part of the critical eigenvalues, is the frequency of the chatter motion.

Substituting Eq. (18) into Eq. (16) yields

(19)

where ST 1 is the so-called resonance terms which produce the secular terms and given by

(20)

A particular solution of Eq. (19) is given

which satisfies

$$ ( \mathbf{M} + i\mathbf{N} )\mathbf{y}_{1}^{*}= \mathbf{ST}_{1},$$
(21)

to eliminate the resonance terms. Based on Fredholm alternative, ϕ(T 1) is the solution of Eq. (21) only when the solvability condition

$$ ( \mathbf{r} + i\mathbf{s} ) \cdot\mathbf{ST}_{1} = \mathbf{0},$$
(22)

is satisfied [28]. Equation (19) can be solved directly after the secular terms ST 1 is eliminated, and the solution is

(23)

where

To solve Eq. (17), the above process is repeated in the following analysis. Substituting Eqs. (18) and (23) into Eq. (17) yields

(24)

where

(25)

where

$$\Delta_{3} = \frac{ ( p_{2} - \mathrm{i}q_{2} ) ( p_{2} +\mathrm{i}q_{2} )^{2} ( \Delta_{2} ( 4\mu_{2}^{2} -3\kappa_{2}\mu_{3} ) - 2\kappa_{2}\mu_{2}^{2} ( ( -2\mathrm{i}\xi_{1}\omega + 4\omega^{2} - 1 ) - \kappa_{1} (1 - \mathrm{e}^{ - \mathrm{i}2\omega \tau _{1}} ) ))}{\Delta_{2}\kappa_{2}}.$$

As Eq. (19), there is also a solvability condition for Eq. (25) as:

$$ ( \mathbf{r} + i\mathbf{s} ) \cdot\mathbf{ST}_{2} = \mathbf{0}.$$
(26)

Solving \(\frac{\partial B( T_{1},T_{2} )}{\partial T_{1}}\) and \(\frac{\partial B( T_{1},T_{2} )}{\partial T_{2}}\) from Eqs. (22) and (26), one can obtain the amplitude equation

(27)

where

and

Using the nonlinear transform

$$ B( T_{1},T_{2} ) = \frac{1}{2}\alpha(T_{1},T_{2} )\exp \bigl( \mathrm{i}\beta(T_{1},T_{2} ) \bigr).$$
(28)

We transform Eq. (27) into

$$\everymath{\displaystyle}\begin{array}{l}\alpha'( T_{1},T_{2} )= \frac{1}{4}\frac{\Lambda_{1}\Lambda_{3} + \Lambda_{2}\Lambda_{4}}{\Lambda_{3}^{2}+ \Lambda_{4}^{2}}\alpha( T_{1},T_{2} )^{3},\\[15pt]\alpha( T_{1},T_{2} )\beta'(T_{1},T_{2} ) = \frac{1}{4}\frac{\Lambda_{2}\Lambda_{3} - \Lambda_{1}\Lambda_{4}}{\Lambda_{3}^{2} + \Lambda_{4}^{2}}\alpha(T_{1},T_{2} )^{3}. \\ \end{array}$$
(29)

It is known that the Bautin bifurcation point needs the first Lyapunov coefficient of the normal form to be zero [30], and this condition is given by

$$ \frac{\Lambda_{1}\Lambda_{3} + \Lambda_{2}\Lambda_{4}}{\Lambda_{3}^{2} + \Lambda_{4}^{2}} = 0.$$
(30)

Numerically solving Eqs. (9), (10), (11), (12), and (30) simultaneously, the Bautin point is found, and the result is stated in Table 2.

Table 2 Parameters, eigenvalues and eigenvectors at Bautin point
Full size table

From the Bautin point to a larger value of τ 2 (smaller value of ω w ), we successively carry out the numerical Hopf bifurcation analysis for each given τ 2 and record the ranges of κ 1 which is in the conditional chatter-free zone. Finally, all the results are plotted in Fig. 6. It is seen that the regions over the solid curve and below the dashed one are still chatter and chatter-free, respectively, but there is a conditional chatter-free zone between the two curves, where coexist the stable smooth grinding process and the chatter vibrations with large amplitudes.

Fig. 6
figure 6

Bautin bifurcation diagram

Full size image

It should be declared that the situation of losing contact between the workpiece and the wheel is not considered in this model, but large amplitude does not have a direct connection with that situation. As discussed by Chung and Liu [19], it can be seen that the loss of contact will happen when the dynamic penetration ε w +ε g exceeds the initial feed f, namely,

(31)

The occurrence of losing contact and the piecewise nonlinearity from this will be discussed in further works.

6 Conclusion

The dynamic behaviors of a cylindrical plunge grinding process are investigated in this study. The mechanism that the regenerative force induces the chatter vibration is clarified by stability analysis involving the combination of the eigenvalues analysis and the continuation algorithm. Finally, the dynamic motions of the chatter are predicted in DDEBIFTOOL [25, 26], and the conditional chatter-free region is found. The conclusions are summarized as follows:

  1. (1)

    The regenerative chatter vibration can be incurred by the contact force between the workpiece and the wheel only when the regenerative interaction is strong enough, namely the grinding stiffness is large. To avoid the chatter vibration, one can decrease the regenerative force by choosing a soft grinding wheel, decreasing the wheel width or slowing down the feed speed.

  2. (2)

    The chatter vibration may arise in the ways of supercritical and subcritical Hopf bifurcations, in which the changes of the dynamic behaviors are continuous and dramatic, respectively.

  3. (3)

    There is a conditional chatter-free region in which there coexist stable smooth grinding process and chatter vibrations with large amplitudes. This phenomenon shows that the design of grinding process must be based on the results from not only the linear analysis but also the nonlinear analysis.