Three kinds of periodic wave solutions and their limit forms for a modified KdV-type equation

Abstract

A modified KdV-type equation is studied by using the bifurcation theory of dynamical system. By investigating the dynamical behavior with phase space analysis, all possible explicit exact traveling wave solutions including peakon solutions, kink and anti-kink wave solutions, blow-up wave solutions, smooth periodic wave solutions, periodic cusp wave solutions, and periodic blow-up wave solutions are obtained. When the first integral varies, we also show the convergence of the periodic wave solutions, such as the smooth periodic wave solutions converge to the kink and anti-kink wave solutions, the periodic cusp wave solutions converge to the peakon solution, the periodic blow-up wave solutions converge to the blow-up wave solution, the blow-up wave solutions converge to the blow-up wave solution, and the periodic blow-up wave solutions converge to the periodic blow-up wave solution.

1 Introduction

Traveling waves appear in many distinct physical structures in solitary wave theory, such as smooth periodic waves, periodic cusp waves, periodic blow-up waves, periodic loop solitons, periodic compactons, solitary waves, kink and anti-kink waves, blow-up waves, peakons, cuspons, compactons, loop solitons, and many others [1–9]. Many powerful methods have been presented for finding the traveling wave solutions of nonlinear partial differential equations, such as the Bäcklund transformation [10], Darboux transformation [11], inverse scattering method [12], Hirota bilinear method [13], Lie group analysis method [14–16], tanh method [17], ansatz method [18, 19], bifurcation theory of dynamical system [20, 21], exp-function method [22, 23], symbolic computation method [24–26], and other methods [27–30].

It is well known that the KdV equation and its generalizations are probably the most popular nonlinear evolution equations of physical interest, which not only stem from realistic physical phenomena, but can also be widely applied to a lot of physically significant fields such as plasma physics, fluid dynamics, crystal lattice theory, nonlinear circuit theory, and astrophysics. A modified KdV-type equation is given by [31–36]

$$\begin{aligned}&uu_{xxt}-u_xu_{xt}-4u^3u_t+4uu_{xxx}\nonumber \\&\quad -4u_xu_{xx}-16u^3u_x=0, \end{aligned}$$

(1)

where u is a real-valued scalar function, t is time, and x is a spatial variable. Equation (1) was proposed in [31] and was derived in [32] by using a spectral problem and the Lenard gradients as stated before. In [31], Geng and Xue obtained soliton solutions and quasiperiodic solutions. Wazwaz [33] found a variety of traveling wave solutions such as kink, soliton, peakon, periodic wave solutions. Some solitary wave, periodic, and rational solutions are presented in [34]. Bogning [35] obtained all possible solutions of shape “Sech” for Eq. (1) by the Bogning–Djeumen Tchaho–Kofané method. The optical soliton solutions are obtained in [36] by using the ansatz method. Unfortunately, the dynamical behavior of the traveling wave system for Eq. (1) is not studied yet; the blow-up wave solution and the periodic blow-up wave solution are also not found in the literatures.

In this paper, we aim to investigate the dynamical behavior of the traveling wave system and the limit forms of the periodic wave solutions for Eq. (1), and give all possible explicit exact parametric representations of various traveling waves using the bifurcation theory of dynamical system [2, 3, 20, 21].

2 Preliminaries

To investigate the traveling wave solution of Eq. (1), let

$$\begin{aligned} u(x,t)=\phi (\xi ),\quad \xi =x-ct, \end{aligned}$$

(2)

where $c\ (\not =0,4)$ is the wave speed. Substituting (2) into Eq. (1) yields

$$\begin{aligned} (4-c)\phi \phi ^{\prime \prime \prime }-(4-c)\phi ^{\prime }\phi ^{\prime \prime }-4(4-c)\phi ^3\phi ^{\prime }=0, \end{aligned}$$

(3)

where “$\prime$” is the derivative with respect to $\xi .$

Integrating (3) once with respect $\xi ,$ we have

$$\begin{aligned} (4-c)\phi \phi ^{\prime \prime }-(4-c)\left( \phi ^{\prime }\right) ^2-(4-c)\phi ^4=g, \end{aligned}$$

(4)

where g is the integral constant.

Letting $y=\frac{\hbox {d}\phi }{\hbox {d}\xi },$ we get the following planar dynamical system:

$$\begin{aligned} \frac{\hbox {d}\phi }{\hbox {d}\xi }=y,\quad \frac{\hbox {d}y}{\hbox {d}\xi }=\frac{g+(4-c)\phi ^4+(4-c)y^2}{(4-c)\phi }. \end{aligned}$$

(5)

Using $\hbox {d}\xi =\phi \hbox {d}\tau ,$ it carries (5) into the Hamiltonian system

$$\begin{aligned} \frac{\hbox {d}\phi }{\hbox {d}\tau }=\phi y,\quad \frac{\hbox {d}y}{\hbox {d}\tau }=\frac{g}{4-c}+\phi ^4+y^2 \end{aligned}$$

(6)

with the following first integral:

$$\begin{aligned} H(\phi ,y)=\phi ^{-2}\left( y^2-\phi ^4+\frac{g}{4-c}\right) =h. \end{aligned}$$

(7)

For a fixed h, the level curve $H(\phi ,y)=h$ defined by (7) determines a set of invariant curves of system (6) which contains different branches of curves. As h is varied, it defines different families of orbits of system (6) with different dynamical behaviors.

Obviously, system (6) has two equilibrium points at $(\pm \phi _{1,0})$ in $\phi$-axis and has two equilibrium points at $(0,\pm Y_{s})$ in y-axis when $g(c-4)>0,$ where $\phi _1=\root 4 \of {\frac{g}{c-4}},Y_{s}=\sqrt{\frac{g}{c-4}},$ has only one equilibrium point at (0, 0) when $g=0,$ and has no any equilibrium point when $g(c-4)<0.$

From (7), we have

$$\begin{aligned} h_1=H(-\phi _1,0)=H(\phi _1,0)=-\frac{2g}{\sqrt{g(c-4)}}. \end{aligned}$$

(8)

If let $M(\phi _{e},y_{e})$ be the coefficient matrix of the linearized system of system (6) at equilibrium point $(\phi _{e},y_{e}),$ then

$$\begin{aligned} J(\phi _{e},y_{e})=\text {det}\left( M(\phi _{e},y_{e})\right) =2y_{e}^{2}-4\phi _{e}^{4}. \end{aligned}$$

(9)

For an equilibrium point $(\phi _e,y_e)$ of system (6), we know that $(\phi _e,y_e)$ is a saddle point if $J(\phi _e,y_e)<0,$ a center point if $J(\phi _e,y_e)>0,$ a cusp if $J(\phi _e,y_e)=0$, and the Poincar$\acute{\text {e}}$ index of $(\phi _e,y_e)$ is zero.

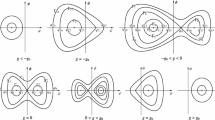
Since both system (5) and system (6) have the same first integral (7), then two systems above have the same topological phase portraits. Therefore, we can obtain the phase portraits of system (5) from that of system (6). By using the properties of equilibrium points and the bifurcation theory of dynamical system, we can show the phase portraits of system (5) are as drawn in Fig. 1.

Fig. 1

Phase portraits of system (5). Parameters: a $g(c-4)>0.$ b $g=0.$ c $g(c-4)<0$

The reminder of this paper is organized as follows. In Sect. 3, we state our main results for Eq. (1). In Sect. 4, we give the derivations for our main results. A short conclusion is drawn in Sect. 5.

3 Main results

In this section, we state our main results. To relate conveniently, let

$$\begin{aligned} \gamma _{1,2}= & {} \frac{\sqrt{2(c-4)\left( -h(c-4)\pm \sqrt{(c-4)(h^2(c-4)-4g)}\right) }}{2|c-4|},\\ \delta _1= & {} \text {max}\{\gamma _1,\gamma _2\},\delta _2=\text {min}\{\gamma _1,\gamma _2\}, T=\frac{1}{\delta _1}\left| \text {sn}^{-1}(1,k_1)\right| ,\\ k_1= & {} \frac{\delta _2}{\delta _1},\quad k_2=\frac{\delta _2}{\sqrt{\delta _1^2+\delta _2^2}},\quad k_3=\frac{\delta _1}{\sqrt{\delta _1^2+\delta _2^2}},\\ \phi _{*}= & {} \root 4 \of {-\frac{g}{c-4}}, \omega _1=\phi _{*}\sqrt{2},\quad \omega _2=\sqrt{\delta _1^2+\delta _2^2},\\ \phi _1= & {} \root 4 \of {\frac{g}{c-4}}, \quad n=0,\pm 1,\pm 2,\ldots , \end{aligned}$$

and $\text {sn}(\cdot ,k),\text {cn}(\cdot ,k),\text {ns}(\cdot ,k)$ are the Jacobian elliptic functions with the modulus k [37, 38].

Proposition 3.1

If $g(c-4)>0,$ then we have the following results:

For $h=h_1,$ Eq. (1) has two kink and anti-kink wave solutions

$$\begin{aligned} u_{1,2}(x,t)=\pm \phi _1\tanh \left( \phi _1(x-ct)\right) , \end{aligned}$$

(10)

has two peakon solutions

$$\begin{aligned} u_{3,4}(x,t)=\pm \phi _{1}\tanh \left( \phi _1|x-ct|\right) , \end{aligned}$$

(11)

and has two blow-up wave solutions

$$\begin{aligned} u_{5,6}(x,t)=\pm \phi _{1}\coth \left( \phi _1|x-ct|\right) . \end{aligned}$$

(12)

For $h\in (-\infty ,h_1),$ Eq. (1) has some smooth periodic wave solutions

$$\begin{aligned} u_{7,8}(x,t)=\pm \delta _{2}\text {sn}\left( \delta _1(x-ct),k_1\right) , \end{aligned}$$

(13)

has some periodic cusp wave solutions

$$\begin{aligned}&u_{9,10}(x,t)=\pm \delta _{2}\left| \text {sn}\left( \delta _1(x-ct-2nT),k_1\right) \right| \nonumber \\&\quad \text {for}\ (2n-1)T<x-ct<(2n+1)T, \end{aligned}$$

(14)

and has some periodic blow-up wave solutions

$$\begin{aligned} u_{11,12}(x,t)=\pm \delta _1\left| \text {ns}\left( \delta _1(x-ct),k_1\right) \right| . \end{aligned}$$

(15)

Moreover, as $h\rightarrow h_1,$ the smooth periodic wave solutions $u_7(x,t),u_8(x,t)$ converge to the kink and anti-kink wave solutions $u_1(x,t),u_2(x,t)$, respectively, the periodic cusp wave solutions $u_9(x,t),u_{10}(x,t)$ converge to the peakon solutions $u_3(x,t),u_4(x,t)$, respectively, and the periodic blow-up wave solutions $u_{11}(x,t),u_{12}(x,t)$ converge to the blow-up wave solutions $u_5(x,t),u_6(x,t)$, respectively.

Proposition 3.2

If $g=0,$ then we have the following results:

For $h=0,$ Eq. (1) has two blow-up wave solutions

$$\begin{aligned} u_{13,14}(x,t)=\pm \frac{1}{|x-ct|}. \end{aligned}$$

(16)

For $h\in (-\infty ,0),$ Eq. (1) has some periodic blow-up wave solutions

$$\begin{aligned} u_{15,16}(x,t)=\pm \sqrt{-h}\left| \csc \left( \sqrt{-h}(x-ct)\right) \right| . \end{aligned}$$

(17)

Moreover, as $h\rightarrow 0,$ the periodic blow-up wave solutions $u_{15}(x,t),u_{16}(x,t)$ converge to the blow-up wave solutions $u_{13}(x,t),u_{14}(x,t)$, respectively.

For $h\in (0,+\infty ),$ Eq. (1) has some blow-up wave solutions

$$\begin{aligned} u_{17,18}(x,t)=\pm \sqrt{h}\text {csch}\left( \sqrt{h}|x-ct|\right) . \end{aligned}$$

(18)

Moreover, as $h\rightarrow 0,$ the blow-up wave solutions $u_{17}(x,t),u_{18}(x,t)$ converge to the blow-up wave solutions $u_{13}(x,t),u_{14}(x,t)$, respectively.

Proposition 3.3

If $g(c-4)<0,$ then we have the following results:

For $h=0,$ Eq. (1) has two periodic blow-up wave solutions

$$\begin{aligned} u_{19,20}(x,t)= & {} \pm \phi _{*}\left| \text {ns}\left( \omega _1(x-ct),\frac{\sqrt{2}}{2}\right) \right| \nonumber \\&\times \sqrt{1+\text {cn}^2\left( \omega _1(x-ct),\frac{\sqrt{2}}{2}\right) }. \end{aligned}$$

(19)

For $h\in (-\infty ,0),$ Eq. (1) has some periodic blow-up wave solutions

$$\begin{aligned} u_{21,22}(x,t)= & {} \pm \left| \text {ns}\left( \omega _2(x-ct),k_2\right) \right| \nonumber \\&\times \sqrt{\delta _1^2+\delta _2^2\text {cn}^2\left( \omega _2(x-ct),k_2\right) }. \end{aligned}$$

(20)

Moreover, as $h\rightarrow 0,$ the periodic blow-up wave solutions $u_{21}(x,t),u_{22}(x,t)$ converge to the periodic blow-up wave solutions $u_{19}(x,t),u_{20}(x,t)$, respectively.

For $h\in (0,+\infty ),$ Eq. (1) has some periodic blow-up wave solutions

$$\begin{aligned} u_{23,24}(x,t)= & {} \pm \left| \text {ns}\left( \omega _2(x-ct),k_3\right) \right| \nonumber \\&\times \sqrt{\delta _2^2+\delta _1^2\text {cn}^2\left( \omega _2(x-ct),k_3\right) }. \end{aligned}$$

(21)

Moreover, as $h\rightarrow 0,$ the periodic blow-up wave solutions $u_{23}(x,t),u_{24}(x,t)$ converge to the periodic blow-up wave solutions $u_{19}(x,t),u_{20}(x,t)$, respectively.

Fig. 2

Profile of $u_1(\xi )$ and the limiting precess of $u_7(\xi )$ tends to $u_1(\xi )$ when $h\rightarrow h_1.$ Parameters: a $h=h_1\approx -1.264911064.$ b $h=-1.5.$ c $h=-1.269.$ d $h=-1.26493$

Fig. 3

Profile of $u_2(\xi )$ and the limiting precess of $u_8(\xi )$ tends to $u_2(\xi )$ when $h\rightarrow h_1.$ Parameters: a $h=h_1\approx -1.264911064.$ b $h=-1.5.$ c $h=-1.269.$ d $h=-1.26493$

4 The derivations to main results

The derivation on Proposition 3.1. When $g(c-4)>0,$ system (6) has four equilibrium points $(\pm \phi _1,0)$ and $(0,\pm Y_s)$; the $(\pm \phi _1,0)$ are two saddle points, and the others are complex equilibrium points. From Fig. 1a, we see that the graph defined by $H(\phi ,y)=h_1$ consists of two heteroclinic orbits connecting with the saddle points $(\pm \phi _1,0)$, four heteroclinic orbits which two of them connecting with the saddle point $(\phi _1,0)$ and passing through the complex equilibrium points $(0,\pm Y_s)$ and two others connecting with the saddle point $(-\phi _1,0)$ and passing through the complex equilibrium points $(0,\pm Y_s),$ and two open curves connecting with the saddle points $(\phi _1,0)$ and $(-\phi _1,0),$ respectively. In $(\phi ,y)$-plane, their expressions are, respectively,

$$\begin{aligned} y= & {} \pm \left( \phi _1^2-\phi ^2\right) ,\quad -\phi _1<\phi <\phi _1,\end{aligned}$$

(22)

$$\begin{aligned} y= & {} \pm \left( \phi _1^2-\phi ^2\right) ,\quad 0\le \phi <\phi _1,\end{aligned}$$

(23)

$$\begin{aligned} y= & {} \pm \left( \phi _1^2-\phi ^2\right) ,\quad -\phi _1<\phi \le 0,\end{aligned}$$

(24)

$$\begin{aligned} y= & {} \pm \left( \phi ^2-\phi _1^2\right) ,\quad \phi _1<\phi <+\infty ,\end{aligned}$$

(25)

$$\begin{aligned} y= & {} \pm \left( \phi ^2-\phi _1^2\right) ,\quad -\infty<\phi <-\phi _1. \end{aligned}$$

(26)

From Fig. 1a, we also see that the graph defined by $H(\phi ,y)=h\ \left( h\in (-\infty ,h_1)\right)$ consists of one periodic orbit passing through the points $(\pm \delta _2,0),$ two heteroclinic orbits connecting with the the complex equilibrium points $(0,\pm Y_s)$ and passing through the the points $(\pm \delta _2,0),$ respectively, and two open curves passing through the point $(\pm \delta _1,0),$ respectively. In $(\phi ,y)$-plane, their expressions are, respectively,

$$\begin{aligned} y= & {} \pm \sqrt{(\delta _1^2-\phi ^2)(\delta _2^2-\phi ^2)},\quad -\delta _2\le \phi \le \delta _2,\end{aligned}$$

(27)

$$\begin{aligned} y= & {} \pm \sqrt{(\delta _1^2-\phi ^2)(\delta _2^2-\phi ^2)},\quad 0\le \phi \le \delta _2,\end{aligned}$$

(28)

$$\begin{aligned} y= & {} \pm \sqrt{(\delta _1^2-\phi ^2)(\delta _2^2-\phi ^2)},\quad -\delta _2\le \phi \le 0,\end{aligned}$$

(29)

$$\begin{aligned} y= & {} \pm \sqrt{(\phi ^2-\delta _1^2)(\phi ^2-\delta _2^2)},\quad \delta _1\le \phi <+\infty ,\end{aligned}$$

(30)

$$\begin{aligned} y= & {} \pm \sqrt{(\phi ^2-\delta _1^2)(\phi ^2-\delta _2^2)},\quad -\infty <\phi \le -\delta _1.\nonumber \\ \end{aligned}$$

(31)

Substituting (22) into the $\frac{\hbox {d}\phi }{\hbox {d}\xi }=y$ and integrating it along the heteroclinic orbits, we have

$$\begin{aligned} \int _{\phi }^{0}\frac{\hbox {d}s}{\phi _1^2-s^2}=\pm \xi . \end{aligned}$$

(32)

From (32) and (2), we obtain the kink and anti-kink wave solutions as (10).

Substituting (23) and (24) into the $\frac{\hbox {d}\phi }{\hbox {d}\xi }=y$ and integrating them along the heteroclinic orbits, respectively, we have

$$\begin{aligned} \int _{0}^{\phi }\frac{\hbox {d}s}{\phi _1^2-s^2}= & {} |\xi |,\end{aligned}$$

(33)

$$\begin{aligned} \int _{\phi }^{0}\frac{\hbox {d}s}{\phi _1^2-s^2}= & {} |\xi |. \end{aligned}$$

(34)

From (33), (34) and (2), we obtain the peakon solutions as (11).

Substituting (25) and (26) into the $\frac{\hbox {d}\phi }{\hbox {d}\xi }=y$ and integrating them along the open curves, respectively, we have

$$\begin{aligned} \int _{\phi }^{+\infty }\frac{\hbox {d}s}{s^2-\phi _1^2}= & {} |\xi |,\end{aligned}$$

(35)

$$\begin{aligned} \int _{-\infty }^{\phi }\frac{\hbox {d}s}{s^2-\phi _1^2}= & {} |\xi |. \end{aligned}$$

(36)

From (35), (36) and (2), we obtain the blow-up wave solutions as (12).

Substituting (27) into the $\frac{\hbox {d}\phi }{\hbox {d}\xi }=y$ and integrating it along the periodic orbit, we have

$$\begin{aligned} \int _{\phi }^{0}\frac{\hbox {d}s}{\sqrt{(\delta _1^2-s^2)(\delta _2^2-s^2)}}=\pm \xi . \end{aligned}$$

(37)

From (37) and (2), we obtain the smooth periodic wave solutions as (13).

Substituting (28) and (29) into the $\frac{\hbox {d}\phi }{\hbox {d}\xi }=y$ and integrating them along the heteroclinic orbits, respectively, we have

$$\begin{aligned} \int _{0}^{\phi }\frac{\hbox {d}s}{\sqrt{(\delta _1^2-s^2)(\delta _2^2-s^2)}}=|\xi |,\end{aligned}$$

(38)

$$\begin{aligned} \int _{\phi }^{0}\frac{\hbox {d}s}{\sqrt{(\delta _1^2-s^2)(\delta _2^2-s^2)}}=|\xi |. \end{aligned}$$

(39)

From (38), (39) and (2), we obtain the periodic cusp wave solutions as (14).

Fig. 4

Profile of $u_3(\xi )$ and the limiting precess of $u_9(\xi )$ tends to $u_3(\xi )$ when $h\rightarrow h_1.$ Parameters: a $h=h_1\approx -0.8528028654.$ b $h=-1.2.$ c $h=-0.86.$ d $h=-0.85281$

Fig. 5

Profile of $u_4(\xi )$ and the limiting precess of $u_{10}(\xi )$ tends to $u_4(\xi )$ when $h\rightarrow h_1.$ Parameters: a $h=h_1\approx -0.8528028654.$ b $h=-1.2.$ c $h=-0.86.$ d $h=-0.85281$

Substituting (30) and (31) into the $\frac{\hbox {d}\phi }{\hbox {d}\xi }=y$ and integrating them along the open curves, respectively, we have

$$\begin{aligned} \int _{\phi }^{+\infty }\frac{\hbox {d}s}{\sqrt{(s^2-\delta _1^2)(s^2-\delta _2^2)}}=|\xi |,\end{aligned}$$

(40)

$$\begin{aligned} \int _{-\infty }^{\phi }\frac{\hbox {d}s}{\sqrt{(s^2-\delta _1^2)(s^2-\delta _2^2)}}=|\xi |. \end{aligned}$$

(41)

From (40), (41) and (2), we obtain the periodic blow-up wave solutions as (15).

Letting $h\rightarrow h_1,$ we have

$$\begin{aligned}&\delta _1\rightarrow \phi _1,\delta _2\rightarrow \phi _1,k_1\rightarrow 1,\text {sn}(\cdot ,k_1)\rightarrow \tanh (\cdot ),\\&\quad \text {ns}(\cdot ,k_1)\rightarrow \coth (\cdot ),T\rightarrow +\infty . \end{aligned}$$

Therefore, as $h\rightarrow h_1,$ the smooth periodic wave solutions $u_7(x,t),u_8(x,t)$ converge to the kink and anti-kink wave solutions $u_1(x,t),u_2(x,t)$, respectively, the periodic cusp wave solutions $u_9(x,t),u_{10}(x,t)$ converge to the peakon solutions $u_3(x,t),u_4(x,t)$, respectively, and the periodic blow-up wave solutions $u_{11}(x,t),u_{12}(x,t)$ converge to the blow-up wave solutions $u_5(x,t),u_6(x,t)$, respectively.

The derivation of Proposition 3.1 is completed.

Example 4.1

If $c=6.5,g=1.0,$ then $h_1\approx -1.264911064.$ Taking $h=-1.5,$ we have $\delta _1\approx 1.073830940$ and $\delta _{2}\approx 0.5889712325.$ Taking $h=-1.269,$ we have $\delta _{1}\approx 0.8278855590$ and $\delta _{2}\approx 0.7639407710.$ Taking $h=-1.26493,$ we have $\delta _{1}\approx 0.7974495647$ and $\delta _2\approx 0.7930978445.$ The profiles of $u_1(x,t)$ and $u_2(x,t)$ are shown in Figs. 2a and 3a, respectively, the limiting process of $u_7(x,t)$ is similar to that in Fig. 2b–d, and the limiting process of $u_8(x,t)$ is similar to that in Fig. 3b–d.

Example 4.2

If $c=-1.5,g=-1.0,$ then $h_1\approx -0.8528028654.$ Taking $h=-1.2,$ we have $\delta _1\approx 1.010997469$ and $\delta _2\approx 0.4217631059.$ Taking $h=-0.86,$ we have $\delta _1\approx 0.6967884370$ and $\delta _2\approx 0.6119525095.$ Taking $h=-0.85281,$ we have $\delta _1\approx 0.6543311085$ and $\delta _2\approx 0.6516600344.$ The profiles of $u_3(x,t)$ and $u_4(x,t)$ are shown in Figs. 4a and 5a, respectively, the limiting process of $u_9(x,t)$ is similar to that in Fig. 4b–d, and the limiting process of $u_{10}(x,t)$ is similar to that in Fig. 5b–d.

Example 4.3

If $c=3.5,g=-0.5,$ then $h_1=-2.0.$ Taking $h=-3.0,$ we have $\delta _1\approx 1.618033989$ and $\delta _2\approx 0.6180339884.$ Taking $h=-2.1,$ we have $\delta _1\approx 1.17053672, \delta _2\approx 0.8543089529.$ Taking $h=-2.000005,$ we have $\delta _1\approx 1.001118658$ and $\delta _2\approx 0.9988825912.$ The profiles of $u_5(x,t)$ and $u_6(x,t)$ are shown in Figs. 6a and 7a, respectively, the limiting process of $u_{11}(x,t)$ is similar to that in Fig. 6b–d, and the limiting process of $u_{12}(x,t)$ is similar to that in Fig. 7b–d.

Fig. 6

Profile of $u_5(\xi )$ and the limiting precess of $u_{11}(\xi )$ tends to $u_5(\xi )$ when $h\rightarrow h_1.$ Parameters: a $h=h_1=-2.0.$ b $h=-3.0.$ c $h=-2.1.$ d $h=-2.000005$

Fig. 7

Profile of $u_6(\xi )$ and the limiting precess of $u_{12}(\xi )$ tends to $u_6(\xi )$ when $h\rightarrow h_1.$ Parameters: a $h=h_1=-2.0.$ b $h=-3.0.$ c $h=-2.1.$ d $h=-2.000005$

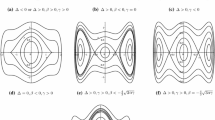
The derivation on Proposition 3.2. When $g=0,$ system (6) has only one equilibrium point (0, 0),  and the (0, 0) is a cusp. From Fig. 1b, we see that the graph defined by $H(\phi ,y)=0$ consists of two open curves connecting with the cusp (0, 0),  the graph defined by $H(\phi ,y)=h\ \left( h\in (-\infty ,0)\right)$ consists of two open curves passing through the points $(\pm \sqrt{-h},0),$ respectively, and the graph defined by $H(\phi ,y)=h\ \left( h\in (0,+\infty )\right)$ consists of two open curves connecting with the cusp (0, 0). In $(\phi ,y)$-plane, their expressions are, respectively,

$$\begin{aligned} y= & {} \pm \phi ^2,\quad 0<\phi <+\infty ,\end{aligned}$$

(42)

$$\begin{aligned} y= & {} \pm \phi ^2,\quad -\infty<\phi <0,\end{aligned}$$

(43)

$$\begin{aligned} y= & {} \pm \phi \sqrt{\phi ^2+h},\quad \sqrt{-h}\le \phi <+\infty ,\end{aligned}$$

(44)

$$\begin{aligned} y= & {} \pm \phi \sqrt{\phi ^2+h},\quad -\infty <\phi \le -\sqrt{-h},\end{aligned}$$

(45)

$$\begin{aligned} y= & {} \pm \phi \sqrt{\phi ^2+h},\quad 0<\phi <+\infty ,\end{aligned}$$

(46)

$$\begin{aligned} y= & {} \pm \phi \sqrt{\phi ^2+h},\quad -\infty<\phi <0. \end{aligned}$$

(47)

Substituting (42) and (43) into the $\frac{\hbox {d}\phi }{\hbox {d}\xi }=y$ and integrating them along the open curves, respectively, we have

$$\begin{aligned} \int _{\phi }^{+\infty }\frac{\hbox {d}s}{s^2}= & {} |\xi |,\end{aligned}$$

(48)

$$\begin{aligned} \int _{-\infty }^{\phi }\frac{\hbox {d}s}{s^2}= & {} |\xi |. \end{aligned}$$

(49)

From (48), (49) and (2), we obtain the blow-up wave solutions as (16).

Substituting (44) and (45) into the $\frac{\hbox {d}\phi }{\hbox {d}\xi }=y$ and integrating them along the open curves, respectively, we have

$$\begin{aligned} \int _{\phi }^{+\infty }\frac{\hbox {d}s}{s\sqrt{s^2+h}}= & {} |\xi |,\end{aligned}$$

(50)

$$\begin{aligned} \int _{-\infty }^{\phi }\frac{\hbox {d}s}{s\sqrt{s^2+h}}= & {} -|\xi |. \end{aligned}$$

(51)

From (50), (51) and (2), we obtain the periodic blow-up wave solutions as (17).

Substituting (46) and (47) into the $\frac{\hbox {d}\phi }{\hbox {d}\xi }=y$ and integrating them along the open curves, respectively, we have

$$\begin{aligned} \int _{\phi }^{+\infty }\frac{\hbox {d}s}{s\sqrt{s^2+h}}= & {} |\xi |,\end{aligned}$$

(52)

$$\begin{aligned} \int _{-\infty }^{\phi }\frac{\hbox {d}s}{s\sqrt{s^2+h}}= & {} -|\xi |. \end{aligned}$$

(53)

From (52), (53) and (2), we obtain the blow-up wave solutions as (18). Letting $h\rightarrow 0,$ we have

$$\begin{aligned} \sqrt{-h}\csc \left( \sqrt{-h}|\xi |\right)= & {} \frac{1}{|\xi |}\left( \frac{\sqrt{-h}|\xi |}{\sin \left( \sqrt{-h}|\xi |\right) }\right) \rightarrow \frac{1}{|\xi |},\\ \sqrt{h}\text {csch}\left( \sqrt{h}|\xi |\right)= & {} \frac{1}{|\xi |}\left( \frac{2\sqrt{h}|\xi |}{\text {e}^{\sqrt{h}|\xi |}{-}\text {e}^{-\sqrt{h}|\xi |}}\right) \rightarrow \frac{1}{|\xi |}\\&\times \left( \frac{2}{\text {e}^{\sqrt{h}|\xi |}+\text {e}^{-\sqrt{h}|\xi |}}\right) \rightarrow \frac{1}{|\xi |}. \end{aligned}$$

Therefore, as $h\rightarrow 0,$ the periodic blow-up wave solutions $u_{15}(x,t),u_{16}(x,t)$ converge to the blow-up wave solutions $u_{13}(x,t),u_{14}(x,t)$, respectively, and the blow-up wave solutions $u_{17}(x,t),u_{18}(x,t)$ converge to the blow-up wave solutions $u_{13}(x,t),u_{14}(x,t)$, respectively.

The derivation of Proposition 3.2 is completed.

Example 4.4

The profiles of $u_{13}(x,t)$ and $u_{14}(x,t)$ are shown in Fig.  8a, b, respectively. The limiting process of $u_{15}(x,t)$ is similar to that in Fig. 9a–d, and the limiting process of $u_{16}(x,t)$ is similar to that in Fig. 10a–d. The limiting process of $u_{17}(x,t)$ is similar to that in Fig. 11a–d, and the limiting process of $u_{18}(x,t)$ is similar to that in Fig. 12a–d.

Fig. 8

Profiles of $u_{13}(\xi )$ and $u_{14}(\xi ).$ Parameters: a $h=0.$ b $h=0$

Fig. 9

Limiting precess of $u_{15}(\xi )$ tends to $u_{13}(\xi )$ when $h\rightarrow 0.$ Parameters: a $h=-3.0.$ b $h=-1.0.$ c $h=-0.20.$ d $h=-0.0001$

Fig. 10

Limiting precess of $u_{16}(\xi )$ tends to $u_{14}(\xi )$ when $h\rightarrow 0.$ Parameters: a $h=-3.0.$ b $h=-1.0.$ c $h=-0.20.$ d $h=-0.0001$

Fig. 11

Limiting precess of $u_{17}(\xi )$ tends to $u_{13}(\xi )$ when $h\rightarrow 0.$ Parameters: a $h=1.0.$ b $h=0.2.$ c $h=0.02.$ d $h=0.0001$

Fig. 12

Limiting precess of $u_{18}(\xi )$ tends to $u_{14}(\xi )$ when $h\rightarrow 0.$ Parameters: a $h=1.0.$ b $h=0.2.$ c $h=0.02.$ d $h=0.0001$

Fig. 13

Profiles of $u_{19}(\xi )$ and $u_{20}(\xi ).$ Parameters: a $h=0.$ b $h=0$

The derivation on Proposition 3.3. When $g(c-4)<0,$ system (6) has no any equilibrium point. From Fig. 1c, we see that the graph defined by $H(\phi ,y)=0$ consists of two open curves passing through the points $(\pm \phi _{*},0),$ respectively, the graph defined by $H(\phi ,y)=h\ \left( h\in (-\infty ,0)\right)$ consists of two open curves passing through the points $(\pm \delta _1,0),$ respectively, and the graph defined by $H(\phi ,y)=h\ \left( h\in (0,+\infty )\right)$ consists of two open curves passing through the points $(\pm \delta _2,0),$ respectively. In $(\phi ,y)$-plane, their expressions are, respectively,

$$\begin{aligned} y= & {} \pm \sqrt{(\phi ^2-\phi _{*}^2)(\phi ^2+\phi _{*}^2)},\quad \phi _{*}\le \phi <+\infty ,\end{aligned}$$

(54)

$$\begin{aligned} y= & {} \pm \sqrt{(\phi ^2-\phi _{*}^2)(\phi ^2+\phi _{*}^2)},\quad -\infty <\phi \le -\phi _{*},\nonumber \\ \end{aligned}$$

(55)

$$\begin{aligned} y= & {} \pm \sqrt{(\phi ^2-\delta _1^2)(\phi ^2+\delta _2^2)},\quad \delta _1\le \phi <+\infty ,\end{aligned}$$

(56)

$$\begin{aligned} y= & {} \pm \sqrt{(\phi ^2-\delta _1^2)(\phi ^2+\delta _2^2)},\quad -\infty <\phi \le -\delta _1,\nonumber \\ \end{aligned}$$

(57)

$$\begin{aligned} y= & {} \pm \sqrt{(\phi ^2-\delta _2^2)(\phi ^2+\delta _1^2)},\quad \delta _2\le \phi <+\infty ,\end{aligned}$$

(58)

$$\begin{aligned} y= & {} \pm \sqrt{(\phi ^2-\delta _2^2)(\phi ^2+\delta _1^2)},\quad -\infty <\phi \le -\delta _2.\nonumber \\ \end{aligned}$$

(59)

Substituting (54) and (55) into the $\frac{\hbox {d}\phi }{\hbox {d}\xi }=y$ and integrating them along the open curves, respectively, we have

$$\begin{aligned} \int _{\phi }^{+\infty }\frac{\hbox {d}s}{\sqrt{(s^2-\phi _{*}^2)(s^2+\phi _{*}^2)}}= & {} |\xi |,\end{aligned}$$

(60)

$$\begin{aligned} \int _{-\infty }^{\phi }\frac{\hbox {d}s}{\sqrt{(s^2-\phi _{*}^2)(s^2+\phi _{*}^2)}}= & {} |\xi |. \end{aligned}$$

(61)

From (60), (61) and (2), we obtain the periodic blow-up wave solutions as (19).

Fig. 14

Limiting precess of $u_{21}(\xi )$ tends to $u_{19}(\xi )$ when $h\rightarrow 0.$ Parameters: a $h=-11.0.$ b $h=-7.0.$ c $h=-4.0.$ d $h=-0.001$

Fig. 15

Limiting precess of $u_{22}(\xi )$ tends to $u_{20}(\xi )$ when $h\rightarrow 0.$ Parameters: a $h=-11.0.$ b $h=-7.0.$ c $h=-4.0.$ d $h=-0.001$

Fig. 16

Limiting precess of $u_{23}(\xi )$ tends to $u_{19}(\xi )$ when $h\rightarrow 0.$ Parameters: a $h=20.0.$ b $h=10.0.$ c $h=4.0.$ d $h=0.001$

Fig. 17

Limiting precess of $u_{24}(\xi )$ tends to $u_{20}(\xi )$ when $h\rightarrow 0.$ Parameters: a $h=20.0.$ b $h=10.0.$ c $h=4.0.$ d $h=0.001$

Substituting (56) and (57) into the $\frac{\hbox {d}\phi }{\hbox {d}\xi }=y$ and integrating them along the open curves, respectively, we have

$$\begin{aligned} \int _{\phi }^{+\infty }\frac{\hbox {d}s}{\sqrt{(s^2-\delta _1^2)(s^2+\delta _2^2)}}= & {} |\xi |, \end{aligned}$$

(62)

$$\begin{aligned} \int _{-\infty }^{\phi }\frac{\hbox {d}s}{\sqrt{(s^2-\delta _1^2)(s^2+\delta _2^2)}}= & {} |\xi |. \end{aligned}$$

(63)

From (62), (63) and (2), we obtain the periodic blow-up wave solutions as (20).

Substituting (58) and (59) into the $\frac{\hbox {d}\phi }{\hbox {d}\xi }=y$ and integrating them along the open curves, respectively, we have

$$\begin{aligned} \int _{\phi }^{+\infty }\frac{\hbox {d}s}{\sqrt{(s^2-\delta _2^2)(s^2+\delta _1^2)}}= & {} |\xi |, \end{aligned}$$

(64)

$$\begin{aligned} \int _{-\infty }^{\phi }\frac{\hbox {d}s}{\sqrt{(s^2-\delta _2^2)(s^2+\delta _1^2)}}= & {} |\xi |. \end{aligned}$$

(65)

From (64), (65) and (2), we obtain the periodic blow-up wave solutions as (21).

Letting $h\rightarrow 0,$ we have

$$\begin{aligned}&\delta _1\rightarrow \phi _{*},\delta _2\rightarrow \phi _{*},\omega _2=\sqrt{\delta _1^2+\delta _2^2}\rightarrow \omega _1,\\&k_{2}=\frac{\delta _2}{\sqrt{\delta _1^2+\delta _2^2}}\rightarrow \frac{\sqrt{2}}{2}, k_{3}=\frac{\delta _1}{\sqrt{\delta _1^2+\delta _2^2}}\rightarrow \frac{\sqrt{2}}{2}. \end{aligned}$$

Therefore, as $h\rightarrow 0,$ the periodic blow-up wave solutions $u_{21}(x,t),u_{22}(x,t)$ converge to the periodic blow-up wave solutions $u_{19}(x,t),u_{20}(x,t)$, respectively, and the periodic blow-up wave solutions $u_{23}(x,t),u_{24}(x,t)$ converge to the periodic blow-up wave solutions $u_{19}(x,t),u_{20}(x,t)$, respectively.

The derivation of Proposition 3.3 is completed.

Example 4.5

If $c=4.5,g=-2.0,$ then $\phi _{*}\approx 1.414213562.$ Taking $h=-11.0,$ we have $\delta _1\approx 3.369324851,\delta _2\approx 0.5935907300.$ Taking $h=-7.0,$ we have $\delta _1\approx 2.744290230,\delta _2\approx 0.7287858905.$ Taking $h=-4.0,$ we have $\delta _1\approx 2.197368226,\delta _2\approx 0.9101797215.$ Taking $h=-0.001,$ we have $\delta _1\approx 1.414390350,\delta _2\approx 1.414036797.$ The profiles of $u_{19}(x,t)$ and $u_{20}(x,t)$ are shown in Fig. 13a, b, respectively. The limiting process of $u_{21}(x,t)$ is similar to that in Fig. 14a–d, and the limiting process of $u_{22}(x,t)$ is similar to that in Fig. 15a–d. Taking $h=20.0,$ we have $\delta _1\approx 4.494222850,\delta _2\approx 0.4450157637.$ Taking $h=10.0,$ we have $\delta _1\approx 3.222602180,\delta _2\approx 0.6206164732.$ Taking $h=4.0,$ we have $\delta _1\approx 2.197368227,\delta _2\approx 0.9101797210.$ Taking $h=0.001,$ we have $\delta _1\approx 1.414390350,\delta _2\approx 1.414036796.$ The limiting process of $u_{23}(x,t)$ is similar to that in Fig. 16a–d, and the limiting process of $u_{24}(x,t)$ is similar to that in Fig. 17a–d.

5 Conclusion

In this paper, we have obtained many new results for a modified KdV-type Eq. (1) by employing the bifurcation method of dynamical system. The results have been given in propositions 3.1–3.3. The method can be applied to many other nonlinear evolution equations, and we believe that many new results wait for further discovery by this method.