Global dynamical aspects of a generalized Chen–Wang differential system

Abstract

We study theoretically the global chaotic behavior of the generalized Chen–Wang differential system

$$\begin{aligned} \dot{x} = y, \quad \dot{y} = z,\quad \dot{z} = -y - b x^2 - x z + 3 y^2 + a, \end{aligned}$$

where $a,b \in {\mathbb {R}}$ are parameters and $b\ne 0$. This polynomial differential system is relevant because is the first polynomial differential system in ${\mathbb {R}}^3$ with two parameters exhibiting chaotic motion without having equilibria. We first show that for $a>0$ sufficiently small it can exhibit up to three small amplitude periodic solutions that bifurcate from a zero-Hopf equilibrium point located at the origin of coordinates when $a=0$. We also show that the system exhibits two limit cycles emerging from two classical Hopf bifurcations at the equilibrium points $({\pm }\sqrt{2a}, 0,0)$, for $a>0, b=1/2$. We also give a complete description of its dynamics on the Poincaré sphere at infinity by using the Poincaré compactification of a polynomial vector field in ${\mathbb {R}}^3$, and we show that it has no first integrals neither in the class of analytic functions nor in the class of Darboux functions.

1 Introduction and statement of the main result

In chaos theory, it is important to study the stability of the equilibria of an autonomous dynamical system. Most of the well-known chaotic systems, like the Lorenz and Chen systems, are of the hyperbolic type, with their equilibria being unstable and the number of equilibria no more than three. Wang and Chen [29] showed that there is an intrinsic relationship between the global dynamical behavior and the number and stability of an equilibria of a chaotic system. To do that they constructed simple chaotic polynomial differential systems that can have any preassigned number of equilibria. They even presented the following very interesting chaotic system with no equilibria:

$$\begin{aligned} \dot{x}= & {} y,\nonumber \\ \dot{y}= & {} z,\\ \dot{z}= & {} -y-x^2 - x z + 3 y^2 + a,\nonumber \end{aligned}$$

(1)

where $a\in \mathbb {R}$ is a parameter. They observed that when $a>0$ system (1) has two equilibria $({\pm }\sqrt{a},0,0)$, when $a=0$ the two equilibria collides at the origin (0, 0, 0) and for $a<0$ system (1) has no equilibria but still generates a chaotic attractor (see for more details again [29]). In [19] the authors showed the existence of a zero-Hopf bifurcation for $a=0$. Generically, a zero-Hopf bifurcation is a two-parameter unfolding of a 3-dimensional autonomous differential system with a zero-Hopf equilibrium. The unfolding can exhibit different topological type of dynamics in the small neighborhood of this isolated equilibrium as the two parameters vary in a small neighborhood of the origin. This, together with the well-known fact that, the existence of parameters in a differential equation may cause chaotic motion, motivates the study of system (1) with one additional parameter.

Fig. 1

The chaotic attractor of system (2) when $a=-0.05$ and $b=1.01$: 2D views on the xy-plane, yz-plane, xz-plane, and the 3D view

Fig. 2

The chaotic attractor of system (2) when $a=0.01$ and $b=1.01$: 2D views on the xy-plane, xz-plane, yz-plane and the 3D view

Considering the characteristics of the Chen–Wang system (the fact that it exhibits chaotic motion with two, one or zero equilibria), the most natural way to generalize system (1) is by considering the following polynomial differential system

$$\begin{aligned} \begin{aligned} \dot{x}&= y,\\ \dot{y}&= z,\\ \dot{z}&= -y-bx^2 - x z + 3 y^2 + a, \end{aligned} \end{aligned}$$

(2)

where $a,b\in \mathbb {R}$ are parameters with $b\ne 0$. This system has two equilibria $({\pm }\sqrt{a/b},0,0)$ when $ab>0$, the two equilibria collides at the origin (0, 0, 0) when $a=0$ and for $ab<0$ system (2) has no equilibria but still generates a chaotic attractor. Performing numerical simulations to system (2) with a and $b \ne 0$ sufficiently small, a strange attractor appears independently on the existence or non-existence of equilibrium points, as shown in Figs. 1 and 2.

Although such a system has either zero, one or two equilibrium points and each solution converges locally to the equilibrium point (when it exists), such system is chaotic. This interesting phenomenon is worth further studying from the theoretically point of view in order to understand the complex global dynamical behavior of a chaotic system with two parameters. This paper is part of this effort to describe such global properties for a quadratic three-dimensional vector field. For related studies on other three-dimensional quadratic vector fields with chaotic behavior see for instance [8, 14, 16–18, 22–24].

The first two results of this paper study the so-called classical Hopf and zero-Hopf bifurcation. A classical Hopf (resp. zero-Hopf) bifurcation in ${\mathbb {R}}^3$ takes place in an equilibrium point with eigenvalues of the form ${\pm }\omega i$ and $\lambda \ne 0$ (resp. $\lambda =0$). The classical Hopf bifurcation theory is quite well understood (see [15]); however, the zero-Hopf bifurcation theory is not that well understood but has been analyzed in [11–13, 15, 26]. In particular, in these papers it is shown that some complicated invariant sets of the unfolding could bifurcate from the isolated zero-Hopf equilibrium under convenient conditions, showing that in some cases the zero-Hopf bifurcation could imply a local birth of “chaos”, see for instance [1–3, 7, 26].

The first result in this paper is the following.

Theorem 1

System (2) has a classical Hopf bifurcation at the equilibrium points $p_{\pm }=({\pm }\sqrt{2a}, 0,0)$ when $a>0$ and $b=1/2$. The first Lyapunov constant is

$$\begin{aligned} l_1(p_{\pm })= \mp \frac{5 \sqrt{2a}}{6 (1 + 2a) (2 + a)}. \end{aligned}$$

The point $p_{+}$ is a weak focus of system (2) restricted to the central manifold of $p_{+}$ and the limit cycle that emerges from $p_{+}$ is stable. The point $p_{-}$ is also a weak focus of system (2) restricted to the central manifold of $p_{-}$ and the limit cycle that emerges from $p_{-}$ is unstable.

Theorem 1 is proved in Sect. 3 where for computing $l_1(p_{\pm })$ we use a result in [15]. We note that the Chen–Wang system (1) [which is system (2) with $b=1$] does not exhibit a classical Hopf bifurcation for any value of a (see Theorem 2 in [19]).

Theorem 2

System (2) has a zero-Hopf bifurcation at the equilibrium point localized at the origin of coordinates when $a=0$. For $a>0$ sufficiently small and $b>0, b\ne 1/2$ the following statements hold:

• 1. If $b \le 4$ system (2) has two small periodic solutions of the form $\gamma _{\pm }=(x_{\pm }(t,a),y_{\pm }(t,a), z_{\pm }(t,a))$, where

  $$\begin{aligned} \begin{aligned} x_{\pm }(t,a)&={\pm } \sqrt{a}+ O(a),\\ y_{\pm }(t,a)&=O(a),\\ z_{\pm }(t,a)&=O(a). \end{aligned} \end{aligned}$$

  The periodic solution $\gamma _{+}$ has a 3-dimensional unstable manifold (a generalized cylinder) when $b< 1/2$ and two 2-dimensional invariant manifolds (one stable and one unstable, both being cylinders) when $b>1/2$. The periodic solution $\gamma _{-}$ has a 3-dimensional stable manifold (a generalized cylinder) when $b< 1/2$ and two 2-dimensional invariant manifolds (one stable and one unstable, both being cylinders) when $b>1/2$.

• 2. If $b>4$ system (2) has three small periodic solutions: $\gamma _{\pm }$ given in the statement above and $\varphi =(x(t,a), y(t,a),z(t,a))$ with

  $$\begin{aligned} \begin{aligned} x(t,a)=&-\frac{\sqrt{2a}}{\sqrt{b-4}}+ O(a),\\ y(t,a)=&\frac{\sqrt{2a}}{\sqrt{b-4}}+ O(a),\\ z(t,a)=&\frac{\sqrt{2a}}{\sqrt{b-4}}+ O(a). \end{aligned} \end{aligned}$$

  The solution $\varphi$ is a linearly stable periodic solution.

The proof of Theorem 2 is done using averaging theory described in Sect. 4. We remark that the Chen–Wang system (1) exhibits only the two small limit cycles $\gamma _{\pm }$ given in statement 1 in Theorem 2 (see again Theorem 2 in [19]).

Now we continue the study of the global dynamics of system (2) by studying its behavior at infinity. For that we shall use the Poincaré compactification for a polynomial vector field in ${\mathbb {R}}^3$. Note that the polynomial vector field associated to system (2) can be extended to an analytic system defined on a closed ball of radius 1, whose interior is diffeomorphic to ${\mathbb {R}}^3$ and its invariant boundary, that two-dimensional sphere

$$\begin{aligned} {\mathbb {S}}^2=\{(x,y,z): x^2+y^2+z^2=1\} \end{aligned}$$

plays the role of the infinity of ${\mathbb {R}}^3$. This ball is called the Poincaré ball since the technique for doing this extension is the well-known Poincaré compactification for a polynomial vector field in ${\mathbb {R}}^3$, see [5, 27] for more details. In Sect. 2 we give a summary of this technique for the case of polynomial vector fields in ${\mathbb {R}}^3$ in order to make the paper self-contained. The boundary of the Poincaré ball is called the Poincaré sphere. Using this compactification technique, we obtain the following result.

Theorem 3

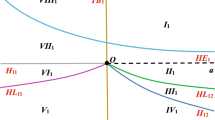
For all values of $a \in \mathbb {R}$ and $b \in \mathbb {R}\setminus \{0\}$, the phase portrait of system (2) on the Poincaré sphere is topologically equivalent to the one shown in Fig. 3.

Fig. 3

Global phase portrait of system (2) on the Poincaré sphere at infinity

Theorem 3 is proved in Sect. 5. Note that the dynamics at infinity does not depend on the value of the parameter a because it appears in the constant terms of system (2). It depends on the parameter b but the global phase portraits at the sphere for different values of b are topologically equivalent.

As we shall see in Sect. 5 the Poincaré compactification reduces the space ${\mathbb {R}}^3$ to the interior of the unit ball centered at the origin of the coordinates and the infinity of ${\mathbb {R}}^3$ to its boundary ${\mathbb {S}}^2$. From Fig. 3 the equilibria at infinity fill up the two closed curves ${\mathbb {S}}^2 \cap {\mathcal {H}}$ where ${{\mathcal {H}}}=\{(x,y,z):H(x,y,z)=0\}$ with $H(x,y,z)=-bx^2+3y^2-xz$.

The Poincaré sphere at infinity is invariant by the flow of the compactified systems. The unique way that an orbit can reach the infinity is by tending to it asymptotically when $t \rightarrow \pm \infty$ and through a critical element. In our case we have two lines filled of equilibria and so that there are many ways in which the orbits can reach the infinity. In this sense, since the dynamics are very sensitive to initial conditions it does not seem that a numerical approach would allow us to understand how the solutions reach the infinity when $t\rightarrow \pm \infty$. A better way to understand how the solutions approach the infinity is if there exist what is called an invariant algebraic surface.

The existence of an invariant algebraic surface provides information about the limit sets of all orbits of a given system (see Sect. 2.4 for its definition). More precisely, if system (2) has an invariant algebraic surface S, then for any orbit $\gamma$ not starting on S either $\alpha (\gamma ) \subset S$ and $\omega (\gamma ) \subset S$, or $\alpha (\gamma ) \subset {\mathbb {S}}^2$ and $\alpha (\gamma ) \subset {\mathbb {S}}^2$, where ${\mathbb {S}}^2$ is the sphere of the infinity (for more details see Theorem 1.2 of [4]) and, $\alpha (\gamma )$ and $\omega (\gamma )$ are the $\alpha$-limit and $\omega$-limit of $\gamma$, respectively (for more details on the $\omega$- and $\alpha$-limit sets see for instance Section 1.4 of [9]). This property is the key result which allows to describe completely the global flow of our system when it has an invariant algebraic surface and, consequently, how the dynamics approach the infinity. Guided by this we will study the existence of invariant algebraic surfaces for system (2).

The characterization of the existence of first integrals is another mechanism that allow us to understand the dynamics and its chaotic behavior (for the definition of first integral see Sect. 2.4). More precisely, the existence of two first independent first integrals will describe completely the dynamics of our system since it will provide the global phase portrait, or in other words its qualitative behavior. The knowledge of a unique first integral can reduce in one dimension the study of the dynamics of our system. In the following result, we study the existence of invariant algebraic surfaces and of first integrals in the class of functions known as Darboux functions.

Theorem 4

The following statements holds for system (2)

• (a) It has neither invariant algebraic surfaces, nor polynomial first integrals.

• (b) All the exponential factors are $\exp (x)$, $\exp (y)$, and linear combinations of these two. Moreover the cofactors of $\exp (x)$ and $\exp (y)$ are y and z, respectively.

• (c) It has no Darboux first integrals.

Note that Theorem 4 states the non-existence of Darboux first integrals. This does not avoid the existence of first integrals in another class of functions, so in the next result we study the existence of first integrals in the class of analytic functions. As usual $\mathbb {Q}^+$ will denote the set of positive rational numbers and $\mathbb {R}^+$ will denote the set of positive real numbers.

Theorem 5

For $a=0$ and $b\ne 1/2$ or $a/b \in \mathbb {R}^+ \setminus \mathbb {Q}^+$, system (2) has no local analytic first integrals at the singular points $({\pm } \sqrt{a/b},0,0)$, and consequently it has no global analytic first integrals.

The paper is organized as follows. In Sect. 2 we present some preliminaries. In Sect. 3 we prove Theorem 1. Theorem 2 is proved in Sect. 4. The dynamics at infinity is studied in Sect. 5. In Sect. 6 we prove Theorem 4 and Theorem 5 is proved in Sect. 7.

2 Preliminaries

2.1 Classical Hopf bifurcation

Assume that a system $\dot{x} = F(x)$, $x\in {\mathbb {R}}^3$ has an equilibrium point $p_0$. If its linearization at $p_0$ has a pair of conjugate purely imaginary eigenvalues and the other eigenvalue has non vanishing real part, then we have a classical Hopf bifurcation. In this scenario we can expect to see a small-amplitude limit cycle bifurcating from the equilibrium point $p_0$. For this to happens we need to compute the so-called first Lyapunov coefficient $l_1(p_0)$ of the system near $p_0$. When $l_1(p_0) < 0$ the equilibrium point is a weak focus of the system restricted to the central manifold and the limit cycle emerging from $p_0$ is stable. In this case we say that the Hopf bifurcation is supercritical. When $l_1(p_0) > 0$ the equilibrium point is also a weak focus of the system restricted to the central manifold but the limit cycle emerging from $p_0$ is unstable. In this second case we say that the Hopf bifurcation is subcritical. To compute $l_1(p_0)$, we will use the following result on page 180 of the book [15].

Theorem 6

Let $\dot{x}= F(x)$ be a differential system having $p_0$ as an equilibrium point. Consider the third-order Taylor approximation of F around $p_0$ given by

$$\begin{aligned} F(x)=Ax + \frac{1}{2!} B(x, x) + \frac{1}{3!} C(x, x, x) + O(|x|^4). \end{aligned}$$

Assume that A has a pair of purely imaginary eigenvalues ${\pm } \omega i$ and these eigenvalues are the only eigenvalues with real part equal to zero. Let q be the eigenvector of A corresponding to the eigenvalue $\omega i$, normalized so that $\overline{q}\cdot q= 1$, where $\overline{q}$ is the conjugate vector of q. Let p be the adjoint eigenvector such that $A^T p = -\omega i p$ and $\overline{p} \cdot q = 1$ ($A^T$ is the transpose of the matrix A). If $\text{ Id }$ denotes the identity matrix, then

$$\begin{aligned} \begin{aligned} l_1(p_0)&=\frac{1}{2 \omega } \text{ Re } (\overline{p}\cdot C(q,q,\overline{q}) - 2 \overline{p}\cdot B(q, A^{-1}B\\&\quad \times (q,\overline{q})) +\overline{p}\cdot B(\overline{q}, (2\omega i \text{ Id }- A)^{-1}B(q,q))). \end{aligned} \end{aligned}$$

2.2 Averaging theory

We present a result from the averaging theory that we shall need for proving Theorem 2. For a general introduction to the averaging theory see the book of Sanders et al. [25].

We consider the initial value problems

$$\begin{aligned} \dot{\mathbf {x}}=\varepsilon F_1(t,\mathbf {x})+\varepsilon ^2 F_2(t,\mathbf {x},\varepsilon ),\quad \mathbf {x}(0)=\mathbf {x}_0, \end{aligned}$$

(3)

and

$$\begin{aligned} \dot{\mathbf {y}}=\varepsilon g({\mathbf{y}}),\quad \mathbf {y}(0)=\mathbf {x}_0, \end{aligned}$$

(4)

with $\mathbf {x}$ , $\mathbf {y}$ and $\mathbf {x}_0$ in some open subset ${\varOmega }$ of ${\mathbb {R}^n}$, $t\in [0,\infty )$, $\varepsilon \in (0,\varepsilon _0]$. We assume that $F_1$ and $F_2$ are periodic of period T in the variable t, and we set

$$\begin{aligned} g(\mathbf {y})=\dfrac{1}{T}\int _{0}^{T}F_1(t,\mathbf {y})dt. \end{aligned}$$

(5)

We will also use the notation $D_\mathbf {x}g$ for all the first derivatives of g, and $D_\mathbf {xx}g$ for all the second derivatives of g.

For a proof of the next result see [28].

Theorem 7

Assume that $F_1$, $D_\mathbf {x}F_1$ ,$D_\mathbf {xx}F_1$ and $D_\mathbf {x}F_2$ are continuous and bounded by a constant independent of $\varepsilon$ in $[0,\infty )\times \ {\varOmega }\times (0,\varepsilon _0]$, and that $y(t)\in {\varOmega }$ for $t\in [0,1/\varepsilon ]$. Then the following statements holds:

• 1. For $t\in [0,1/\varepsilon ]$ we have $\mathbf {x}(t)- \mathbf {y}(t)= O(\varepsilon )$ as $\varepsilon \rightarrow 0$.

• 2. If $p \ne 0$ is a singular point of system (4) such that

  $$\begin{aligned} detD_\mathbf {y}g(p) \ne 0, \end{aligned}$$

  (6)

  then there exists a periodic solution $\mathbf {x}(t,\varepsilon )$ of period T for system (3) which is close to p and such that $\mathbf {x}(0,\varepsilon )-p= O(\varepsilon )$ as $\varepsilon \rightarrow 0$.

• 3. The stability of the periodic solution $\mathbf {x}(t, \varepsilon )$ is given by the stability of the singular point.

2.3 Poincaré compactification

Consider in ${\mathbb {R}}^3$ the polynomial differential system

$$\begin{aligned} \begin{aligned} \dot{x}&= P_1(x,y,z),\\ \dot{y}&= P_2(x,y,z),\\ \dot{z}&= P_3(x,y,z), \end{aligned} \end{aligned}$$

or equivalently its associated polynomial vector field $X=(P_1, P_2, P_3)$. The degree n of X is defined as $n=\text{ max } \{\mathrm{deg}(P_i): i=1,2,3\}$. Let

$$\begin{aligned} {\mathbb {S}}^3 = \{y=(y_1,y_2,y_3,y_4):||y||=1\} \end{aligned}$$

be the unit sphere in ${\mathbb {R}}^4$ and

$$\begin{aligned} {\mathbb {S}}_{+}=\{y\in {\mathbb {S}}^3:y_4 > 0\}\quad \text {and} \quad {\mathbb {S}}_{-}=\{y\in {\mathbb {S}}^3:y_4 < 0\} \end{aligned}$$

be the northern and southern hemispheres of ${\mathbb {S}}^3$, respectively. The tangent space of ${\mathbb {S}}^3$ at the point y is denoted by $T_y{\mathbb {S}}^3$. Then the tangent plane

$$\begin{aligned} \begin{aligned}&T_{(0,0,0,1)}{\mathbb {S}}^3\\&\quad = \left\{ (x_1,x_2,x_3,1)\in {\mathbb {R}}^4: (x_1,x_2,x_3) \in {\mathbb {R}}^3\right\} \end{aligned} \end{aligned}$$

can be identified with ${\mathbb {R}}^3$.

Consider the identification ${\mathbb {R}}^3= T_{(0,0,0,1)}{\mathbb {S}}^3$ and the central projection

$$\begin{aligned} f_{\pm }:T_{(0,0,0,1)}{\mathbb {S}}^3 \rightarrow {\mathbb {S}}_{\pm } \end{aligned}$$

defined by

$$\begin{aligned} f_{\pm }(x)={\pm } \frac{ (x_1,x_2, x_3, 1)}{ {\varDelta }(x)}, \end{aligned}$$

where

$$\begin{aligned} {\varDelta }(x)=\bigg (1 + \sum _{i=1}^3 x_i^2\bigg )^{1/2}. \end{aligned}$$

Using these central projections ${\mathbb {R}}^3$ is identified with the northern and southern hemispheres. The equator of ${\mathbb {S}}^3$ is ${\mathbb {S}}^2=\{y\in {\mathbb {S}}^3:y_4=0\}$.

The maps $f_{\pm }$ define two copies of X on ${\mathbb {S}}^3$, one $Df_{+} \circ X$ in the northern hemisphere and the other $Df_{-} \circ X$ in the southern one. Denote by $\overline{X}$ the vector field on ${\mathbb {S}}^3 \setminus {\mathbb {S}}^2={\mathbb {S}}_{+} \cup {\mathbb {S}}_{-}$, which restricted to ${\mathbb {S}}_{+}$ coincides with $Df_{+} \circ X$ and restricted to ${\mathbb {S}}_{-}$ coincides with $Df_{-} \circ X$. Now we can extend analytically the vector field $\overline{X}(y)$ to the whole sphere ${\mathbb {S}}^3$ by $p(X)=y_4^{n-1}\overline{X}(y)$. This extended vector field p(X) is called the Poincaré compactification of X on ${\mathbb {S}}^3$.

As ${\mathbb {S}}^3$ is a differentiable manifold in order to compute the expression for p(X), we can consider the eight local charts $(U_i,F_i)$, $(V_i, G_i)$, where

$$\begin{aligned} U_i=\left\{ y\in {\mathbb {S}}^3:y_i > 0\right\} \quad \text {and} \quad V_i=\left\{ y\in {\mathbb {S}}^3:y_i < 0\right\} \end{aligned}$$

for $i=1,2,3,4$. The diffeomorphisms $F_i:U_i \rightarrow {\mathbb {R}}^3$ and $G_i:V_i \rightarrow {\mathbb {R}}^3$ for $i=1,2,3,4$ are the inverse of the central projections from the origin to the tangent hyperplane at the points $({\pm } 1,0,0,0)$, $(0,{\pm } 1,0,0)$, $(0,0,{\pm } 1,0)$ and $(0,0,0,{\pm } 1)$, respectively.

Now we do the computations on $U_1$. Suppose that the origin (0, 0, 0, 0), the point $(y_1,y_2,y_3,y_4) \in {\mathbb {S}}^3$ and the point $(1,z_1,z_2,z_3)$ in the tangent hyperplane to ${\mathbb {S}}^3$ at (1, 0, 0, 0) are collinear. Then we have

$$\begin{aligned} \frac{1}{y_1}=\frac{z_1}{y_2}=\frac{z_2}{y_3}=\frac{z_3}{y_4} \end{aligned}$$

and, consequently

$$\begin{aligned} F_1(y)=(y_2/y_1, y_3/y_1, y_4/y_1)=(z_1,z_2,z_3) \end{aligned}$$

defines the coordinates on $U_1$. As

$$\begin{aligned} DF_1(y)= \begin{pmatrix} -y_2/y_1^2 &{}\quad 1/y_1 &{}\quad 0 &{}\quad 0\\ -y_3/y_1^2 &{}\quad 0 &{}\quad 1/y_1&{}\quad 0 \\ -y_4/y_1^2 &{}\quad 0 &{}\quad 1/y_1 &{}\quad 0 \end{pmatrix} \end{aligned}$$

and $y_4^{n-1}=(z_3/{\varDelta }(z)^{n-1})$, the analytical vector field p(X) in the local chart $U_1$ becomes

$$\begin{aligned} \frac{z_3^n}{{\varDelta }(z)^{n-1}} \big ( -z_1 P_1 + P_2, -z_2 P_1 + P_3, z_3 P_1\big ), \end{aligned}$$

where $P_i=P_i(1/z_3, z_1/z_3, z_2/z_3)$.

In a similar way, we can deduce the expressions of p(X) in $U_2$ and $U_3$. These are

$$\begin{aligned} \frac{z_3^n}{{\varDelta }(z)^{n-1}} \big ( -z_1 P_2 + P_1, -z_2 P_2 + P_3, z_3 P_2\big ), \end{aligned}$$

where $P_i=P_i(z_1/z_3, 1/z_3, z_2/z_3)$, in $U_2$ and

$$\begin{aligned} \frac{z_3^n}{{\varDelta }(z)^{n-1}} \big ( -z_1 P_3 + P_1, -z_2 P_3 + P_2, z_3 P_3\big ), \end{aligned}$$

with $P_i=P_i(z_1/z_3, z_2/z_3, 1/z_3)$, in $U_3$.

The expression for p(X) in $U_4$ is $z_3^{n+1}(P_1,P_2,P_3)$ and the expression for p(X) in the local chart $V_i$ is the same as in $U_i$ multiplied by $(-1)^{n-1}$, where n is the degree of X, for all $i=1,2,3,4$.

Note that we can omit the common factor $1/({\varDelta }(z))^{n-1}$ in the expression of the compactification vector field p(X) in the local charts doing a rescaling of the time variable.

From now on we will consider only the orthogonal projection of p(X) from the northern hemisphere to $y_4=0$ which we will denote by p(X) again. Observe that the projection of the closed northern hemisphere is a closed ball of radius one denoted by B, whose interior is diffeomorphic to ${\mathbb {R}}^3$ and whose boundary ${\mathbb {S}}^2$ corresponds to the infinity of ${\mathbb {R}}^3$. Moreover, p(X) is defined in the whole closed ball B in such way that the flow on the boundary is invariant. The vector field induced by p(X) on B is called the Poincaré compactification of X and B is called the Poincaré sphere.

All the points on the invariant sphere ${\mathbb {S}}^2$ at infinity in the coordinates of any local chart $U_i$ and $V_i$ have $z_3=0$.

2.4 Integrability theory

We start this subsection with the Darboux theory of integrability. As usual ${\mathbb {C}}[x,y,z]$ denotes the ring of polynomial functions in the variables x, y and z. Given $f \in {\mathbb {C}}[x, y,z]\setminus \mathbb {C}$ we say that the surface $f(x,y,z)=0$ is an invariant algebraic surface of system (2) if there exists $k \in {\mathbb {C}}[x, y,z]$ such that

$$\begin{aligned} y \frac{\partial f}{\partial x} + z \frac{\partial f}{\partial y}+ (-y - b x^2 - x z + 3 y^2 + a)\frac{\partial f}{\partial z} = k f. \end{aligned}$$

(7)

The polynomial k is called the cofactor of the invariant algebraic surface $f=0$, and it has degree at most 1. When $k=0$, f is a polynomial first integral. When a real polynomial differential system has a complex invariant algebraic surface, then it has also its conjugate. It is important to consider the complex invariant algebraic surfaces of the real polynomial differential systems because sometimes these forces the real integrability of the system.

Let $f,g \in {\mathbb {C}}[x,y,z]$ and assume that f and g are relatively prime in the ring ${\mathbb {C}}[x,y,z]$, or that $g=1$. Then the function $\exp (f/g)\not \in \mathbb {C}$ is called an exponential factor of system (2) if for some polynomial $L \in {\mathbb {C}}[x,y,z]$ of degree at most 1 we have

$$\begin{aligned}&y \frac{\partial \exp (f/g)}{\partial x} + z \frac{\partial \exp (f/g)}{\partial y}+ (-y - b x^2 - x z\nonumber \\&\quad + 3 y^2 + a) \frac{\partial \exp (f/g)}{\partial z} =L\, \exp (f/g). \end{aligned}$$

(8)

As before we say that L is the cofactor of the exponential factor $\exp {(f/g)}$. We observe that in the definition of exponential factor if $f,g \in {\mathbb {C}}[x,y,z]$ then the exponential factor is a complex function. Again when a real polynomial differential system has a complex exponential factor surface, then it has also its conjugate, and both are important for the existence of real first integrals of the system. The exponential factors are related with the multiplicity of the invariant algebraic surfaces, for more details see [6], Chapter 8 of [9], and [20, 21].

Let U be an open and dense subset of ${\mathbb {R}}^3$, we say that a nonconstant function $H :U \rightarrow {\mathbb {R}}$ is a first integral of system (2) on U if H(x(t), y(t), z(t)) is constant for all of the values of t for which (x(t), y(t), z(t)) is a solution of system (2) contained in U. Obviously H is a first integral of system (2) if and only if

$$\begin{aligned} y \frac{\partial H}{\partial x} + z \frac{\partial H}{\partial y}+ (-y - b x^2 - x z + 3 y^2 + a)\frac{\partial H}{\partial z} = 0, \end{aligned}$$

for all $(x,y,z)\in U$.

A first integral is called a Darboux first integral if it is a first integral of the form

$$\begin{aligned} f_1^{\lambda _1} \cdots f_p^{\lambda _p} F_1^{\mu _1}\cdots F_q^{\mu _q}, \end{aligned}$$

where $f_i=0$ are invariant algebraic surfaces of system (2) for $i=1,\ldots , p$, and $F_j$ are exponential factors of system (2) for $j= 1, \ldots , q$, $\lambda _i, \mu _j \in {\mathbb {C}}$.

The next result, proved in [9], explain how to find Darboux first integrals.

Proposition 1

Suppose that a polynomial system (2) of degree m admits p invariant algebraic surfaces $f_i = 0$ with cofactors $k_i$ for $i = 1, . . . ,p$ and q exponential factors $\exp (g_j/h_j)$ with cofactors $L_j$ for $j = 1, . . . ,q$. Then, there exist $\lambda _i$ and $\mu _j \in {\mathbb {C}}$ not all zero such that

$$\begin{aligned} \displaystyle {\sum _{i=1}^p \lambda _i K_i + \sum _{j=1}^q \mu _j L_j=0}, \end{aligned}$$

(9)

if and only if the function

$$\begin{aligned} f_1^{\lambda _1} \cdots f_p^{\lambda _p} \left( \exp \left( \frac{g_1}{h_1} \right) \right) ^{\mu _1} \cdots \left( \exp \left( \frac{g_q}{h_q}\right) \right) ^{\mu _q} \end{aligned}$$

is a Darboux first integral of system (2).

The following result whose proof is given in [20, 21] will be useful to prove statement (b) of Theorem 4.

Lemma 1

The following statements hold.

• (a) If $\exp (f/g)$ is an exponential factor for the polynomial differential system (2) and g is not a constant polynomial, then $g=0$ is an invariant algebraic surface.

• (b) Eventually $\exp (f)$ can be an exponential factor, coming from the multiplicity of the infinity invariant plane.

Let as before U be an open and dense subset of ${\mathbb {R}}^3$. An analytic first integral is a first integral H which is an analytic function in U. Moreover, if $U={\mathbb {R}}^3$ then H is called a global analytic first integral of system (2). If now we choose U as a neighborhood of a singular point p and $H :U \rightarrow {\mathbb {R}}$ is an analytic first integral in U, then H is called a local analytic first integral of system (2) at p.

3 Classical Hopf bifurcation

In this section we study the classical Hopf bifurcation of system (2) using Theorem 6. First we will show that system (2) exhibits a classical Hopf bifurcation if and only if $b=1/2$ and $a=k^2/2$, for any real $k\ne 0$.

System (2) has two equilibrium points $p_{\pm }=({\pm } \sqrt{a/b},0,0)$ when $a/b>0$, which collide at the origin when $a=0$. The proof is made computing directly the eigenvalues at each equilibrium point. The characteristic polynomial of the linear part of system (2) at the equilibrium point $p_\pm$ is

$$\begin{aligned} p(\lambda )= 2 \sqrt{a} \sqrt{b} - \lambda + \frac{\sqrt{a}}{\sqrt{b}} \lambda ^2 - \lambda ^3. \end{aligned}$$

(10)

Note that a / b must be non negative. As $p(\lambda )$ is a polynomial of degree 3, it has either one, two (then one has multiplicity 2), or three real zeros. Imposing the condition

$$\begin{aligned} p(\lambda )=(\lambda -k)(\lambda ^2+\beta ^2) \end{aligned}$$

(11)

with $k,\beta \in \mathbb {R}$, $k\ne 0$ and $\beta >0$ we obtain a system of three equations that correspond to the coefficients of the terms of degree 0, 1 and 2 in $\lambda$ of the polynomial in (11). This system has only the solution $a=k^2/2, b=1/2, \beta =1$. This implies that system (2) exhibits a classical Hopf bifurcation if and only if $b=1/2$ and $a=k^2/2$, for any real $k\ne 0$ and the equilibrium points are $p_{\pm }=({\pm } k,0,0)=({\pm }\sqrt{2a},0,0)$.

We expect to have small-amplitude limit cycle branching from each of the fixed points $p_{+}$ and $p_{-}$. For this we will compute the first Lyapunov coefficient $l_1(p_{\pm })$ of system (2) near of $p_{\pm }$.

Proof of Theorem 1

System (2) is invariant under the symmetry $(x,y,z,t) \rightarrow (-x,y,-z,-t)$ and so it is enough to compute $l_1(p_{-})$. The linear part of system (2) at the equilibrium points $p_{-}$ is

$$\begin{aligned} A=\begin{pmatrix} 0 &{}\quad 1 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 1 \\ k &{}\quad -1 &{}\quad k \end{pmatrix}. \end{aligned}$$

The eigenvalues of A are ${\pm } i$ and k. In order to prove that we have a Hopf bifurcation at the equilibrium point $p_{-}$ it remains to prove that the first Lyapunov coefficient at $l_1(p_{-})$ is different from zero. For this we need to compute the bilinear and trilinear forms B and C associated with the second- and third-order terms of system (2). Since the system is quadratic we have that the trilinear function C is zero. The bilinear form B evaluated at two vectors $u=(u_1,u_2,u_3)$ and $v=(v_1, v_2, v_3)$ is given by

$$\begin{aligned} B(u,v)=\bigg (0,0,\frac{1}{2}(-u_1 v_1-u_3 v_1 + 6 u_2 v_2- u_1v_3)\bigg ). \end{aligned}$$

The inverse of the matrix A is

$$\begin{aligned} A=\begin{pmatrix} \dfrac{1}{k} &{}\quad -1 &{}\quad \dfrac{1}{k} \\ 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 \end{pmatrix}. \end{aligned}$$

The inverse of the matrix $2i\text{ Id } - A$ is

$$\begin{aligned} A=\begin{pmatrix} -\dfrac{3+2ki}{-6i+3k} &{}\quad -\dfrac{1}{3} &{}\quad \dfrac{1}{-6i+3k} \\ \dfrac{k}{-6i+3k} &{}\quad -\dfrac{2i}{3} &{}\quad \dfrac{2i}{-6i+3k} \\ \dfrac{2ki}{-6i+3k} &{}\quad \dfrac{1}{3} &{}\quad -\dfrac{4}{-6i+3k} \end{pmatrix}. \end{aligned}$$

The normalized eigenvector q of A associated with the eigenvalue i normalized so that $\overline{q}\cdot q=1$, where $\overline{q}$ is the conjugated of q, is

$$\begin{aligned} q=-\bigg (\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}} i,-\frac{1}{\sqrt{3}}\bigg ). \end{aligned}$$

The normalized adjoint eigenvector p such that $A^{T}p=-ip$, where $A^{T}$ is the transpose of the matrix A, so that $\overline{p}\cdot q=1$ is

$$\begin{aligned} p=-\bigg (\frac{\sqrt{3}k}{2(i+k)},\frac{\sqrt{3}}{2}i,-\frac{\sqrt{3}i}{2(i+k)}\bigg ). \end{aligned}$$

The first and second terms of $l_1(p_{-})$ are zero. The third term is $20/(9(2+2ki)(k-2i))$. Applying the formula in Theorem 6 we obtain

$$\begin{aligned} l_1(p_{-})= \frac{5 \sqrt{2a}}{6 (1 + 2a) (2 + a)}. \end{aligned}$$

Since $l_1(p_{-})$ is positive we have a subcritical Hopf bifurcation at $p_{-}$ so there exists an unstable limit cycle.

$\square$

4 Zero-Hopf bifurcation

In this section we study the zero-Hopf bifurcation of system (2) using Theorem 7. We will show that system (2) exhibits a zero-Hopf bifurcation if and only if $a=0$ and $b \ne 0$. The characteristic polynomial $p(\lambda )$ of the linear part of this system at the equilibrium points $p_{\pm }$ is given in (10).

Imposing the condition

$$\begin{aligned} p(\lambda )=\lambda (\lambda ^2+\beta ^2) \end{aligned}$$

with $\beta \in \mathbb {R}$, $\beta >0$ we obtain a system of three equations that correspond to the coefficients of the terms of degree 0, 1 and 2 in $\lambda$ of the polynomial in (11). This system has only the solution $a=0$. So, system (2) exhibits a zero-Hopf bifurcation at the origin if and only if $a=0$.

Proof of Theorem 2

We want to study if a small periodic orbit bifurcates from the origin when a is sufficiently small using the averaging theory of first order. In order to apply this theory first, we must do changes of variables to write system (2) as a periodic differential system in the independent variable of the system and moreover, the system must depend on a small parameter, see Eq. (3) in Sect. 2.2. The first thing to do is to write the linear part at the origin of system (2) with $a=0$ into its real Jordan normal form that is

$$\begin{aligned} \begin{pmatrix} 0&{}\quad -1 &{}\quad 0 \\ 1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix}. \end{aligned}$$

To do this we apply the linear change of variables

$$\begin{aligned}&(x,y,z) \rightarrow (u,v,w), \text{ where } \quad x=-u+w, \\&\quad y=v,\, z=u. \end{aligned}$$

In the new variables (u, v, w) system (2) becomes

$$\begin{aligned} \begin{aligned} \dot{u}&= a - v + (1-b)u^2+(2b-1)u w+ 3v^2-bw^2,\\ \dot{v}&= u,\\ \dot{w}&= a +(1-b)u^2+(2b-1)uw +3v^2-bw^2. \end{aligned} \end{aligned}$$

(12)

Writing system (12) in cylindrical coordinates $(r,\theta , w)$, i.e. doing the change of variables

$$\begin{aligned} u=r \cos \theta , \quad v= r \sin \theta , \quad w=w, \end{aligned}$$

in system (12) we get

$$\begin{aligned} \dot{r}= & {} \cos \theta \big (a - b w^2 + (2 b-1) r w \cos \theta \nonumber \\&-\,(b-1)r^2 \cos ^2 \theta + 3 r^2 \sin ^2 \theta \big ),\nonumber \\ \dot{\theta }= & {} 1+\frac{1}{2}\Big (\frac{1}{r} 2(bw^2-a) - 2 (2 b-1) w \cos \theta \nonumber \\&+\, r (b-4 + (2 + b) \cos (2\theta ))\Big ) \sin \theta ,\nonumber \\ \dot{w}= & {} a- b w^2 + (2 b-1) r w \cos \theta -(b-1) r^2 \cos ^2 \theta \nonumber \\&+\,3 r^2\sin ^2\theta . \end{aligned}$$

(13)

Doing the rescaling of the variables through the change of coordinates

$$\begin{aligned}&(r,\theta ,w) \rightarrow (R,\theta , W), \quad \text{ where } \quad r= \sqrt{a} R, \, \\&\quad w= \sqrt{a} W. \end{aligned}$$

system (13) becomes

$$\begin{aligned} \dot{R}= & {} \sqrt{a} \cos \theta \big ( 1-b W^2 + (2b-1) R W \cos \theta \nonumber \\&-(b-1) R^2 \cos \theta + 3 R^2 \sin ^2 \theta \big ),\nonumber \\ \dot{\theta }= & {} 1 - \dfrac{1}{2R}\sqrt{a}\big (2+4R^2 - b R^2 - 2 b W^2 \nonumber \\&+ 2 (2b-1) R W \cos \theta -(b+2)R^2\cos (2\theta )\big )\sin \theta , \nonumber \\ \dot{W}= & {} \sqrt{a}\big (1-b W^2 + (2b-1) R W \cos \theta \nonumber \\&-(b-1) R^2\cos ^2 \theta + 3R^2 \sin ^2 \theta \big ). \end{aligned}$$

(14)

This system can be written as

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}R}{\mathrm{d}\theta }&= \sqrt{a} F_{11}(\theta , R, W) + O(a), \\ \frac{\mathrm{d}W}{\mathrm{d}\theta }&= \sqrt{a} F_{12}(\theta , R, W) + O(a), \end{aligned} \end{aligned}$$

(15)

where

$$\begin{aligned} \begin{aligned} F_{11}(\theta , R, W)&= \frac{1}{2} \cos \theta (2- (b-4)R^2 - 2 b W^2\\&\quad + 2 (2b-1) R W \cos \theta \nonumber \\&\quad - (b+2) R^2 \cos (2\theta )),\\ F_{12}(\theta , R, W)&= 1-b W^2+ (2b-1) R W \cos \theta \\&\quad +(1-b)R^2 \cos ^2\theta + 3 R^2 \sin ^2\theta . \end{aligned} \end{aligned}$$

Using the notation of the averaging theory described in Sect. 2.2, we have that if we take $t=\theta$, $T=2 \pi$, $\varepsilon =\sqrt{a}$, $\mathbf{x}=(R, W)^{T}$ and

$$\begin{aligned}&F_1(t,\mathbf{x})= F_{1}(\theta ,R, W)= \begin{pmatrix} F_{11}(\theta ,R, W)\\ F_{12}(\theta ,R, W) \end{pmatrix}, \\&\varepsilon ^2 F_2(t,\mathbf{x})= O(a), \end{aligned}$$

it is immediate to check that the differential system (15) is written in the normal form (3) for applying the averaging theory and that it satisfies the assumptions of Theorem 7.

Now we must compute explicitly the integral in (5) related with the periodic differential system in order to reduce the problem of finding periodic solutions to a problem of finding the zeros of a function. For doing this, we compute the integral in (5) with $\mathbf{y}= (R,W)^{T}$, and denoting

$$\begin{aligned} g(\mathbf{y})=g (R,W)= \begin{pmatrix} g_{11}(R, W)\\ g_{12}(R, W) \end{pmatrix}, \end{aligned}$$

we obtain

$$\begin{aligned} \begin{array}{l} g_{11}(R,W)= \dfrac{1}{2}(2b-1)R W, \\ g_{12}(R,W)=\dfrac{1}{2} (2- (b-4) R^2 - 2bW^2). \end{array} \end{aligned}$$

Since $g_{11} \not \equiv 0$ we must have $b \ne 1/2$. In this case system $g_{11}(R,W)=g_{12}(R,W)=0$ has the real solutions $(W, R)= ({\pm }1/\sqrt{b}, 0)$ and $(W, R)= (0, \sqrt{2}/\sqrt{b-4})$. Note that in order to have the first two real solutions $b>0$ and for the third one, $b>4$.

The Jacobian (6) is

$$\begin{aligned}&\left| \begin{array}{cc} \dfrac{1}{2} (2b-1) W &{}\quad \dfrac{1}{2} (2b-1) R \\ (4-b) R &{}\quad -2bW \end{array} \right| \\&\quad = \dfrac{2b-1}{2}((b-4)R^2-2 b W^2). \end{aligned}$$

Evaluated at the solutions $(W,R)=({\pm } 1/\sqrt{b}, 0)$ takes the value $1-2b\ne 0$ and evaluated at the solution $(W, R)= (0, \sqrt{2}/\sqrt{b-4})$ takes the value $2b-1 \ne 0$. Then, by Theorem 7, it follows that for any $a>0$ sufficiently small and $b>0$ system (14) has a periodic solution $\mathbf{x}(t,\varepsilon )=(R(\theta ,a), W(\theta , a))$ such that (W(0, a), R(0, a)) tends to $({\pm } 1/\sqrt{b}, 0)$ when a tends to zero. Moreover when $b>4$, again by Theorem 7 it follows that for any $a>0$ sufficiently small system (14) has a periodic solution $\mathbf{x}(t,\varepsilon )=(R(\theta ,a), W(\theta , a))$ such that (W(0, a), R(0, a)) tends to $(0, \sqrt{2}/\sqrt{b-4})$ when a tends to zero. The eigenvalues of the Jacobian matrix at the solution $(-1/\sqrt{b}, 0)$ are $(1-2b)/(2\sqrt{b}), 2\sqrt{b}$ and the eigenvalues of the Jacobian matrix at the solution $(1/\sqrt{b}, 0)$ are $-2\sqrt{b},(2b-1)/(2\sqrt{b})$. This shows that the first periodic orbit has a 3-dimensional stable manifold (a generalized cylinder) when $b< 1/2$ and two 2-dimensional invariant manifolds (one stable and one unstable, both being cylinders) when $b>1/2$. The second periodic orbit has a 3-dimensional unstable manifold (a generalized cylinder) when $b< 1/2$ and two 2-dimensional invariant manifolds(one stable and one unstable, both being cylinders) when $b>1/2$. The eigenvalues of the Jacobian matrix at the solution $(0, \sqrt{2}/\sqrt{b-4})$ are $i \sqrt{2b-1}, - i\sqrt{2b-1}$, so this third periodic solution is a linearly stable periodic solution.

Going back to the differential system (13), we get that such a system for $a>0$ sufficiently small and $b>0$ has two periodic solutions of period approximately $2\pi$ of the form

$$\begin{aligned}&r(\theta )=O(a), \\&w(\theta ) = {\pm } \sqrt{a}+ O(a). \end{aligned}$$

These two periodic solutions become for the differential system (12) into two periodic solutions of period also close to $2\pi$ of the form

$$\begin{aligned}&u(t)= O(a), \\&v(t)= O(a), \\&w(t)= {\pm } \sqrt{a}+ O(a). \end{aligned}$$

for $a>0$ sufficiently small. Finally, we get for the differential system (2) the two periodic solutions

$$\begin{aligned}&x(t)= {\pm } \sqrt{a}+ O(a), \\&y(t)= O(a), \\&z(t)= O(a), \end{aligned}$$

of period near $2\pi$ when $a>0$ is sufficiently small. Clearly these periodic orbits tend to the origin of coordinates when a tends to zero. Therefore, they are small-amplitude periodic solutions starting at the zero-Hopf equilibrium point.

When $b>4$ again going back to the differential system (13), we get that such a system for $a>0$ sufficiently small has also a periodic solution of period approximately $2\pi$ of the form

$$\begin{aligned}&r(\theta )=\sqrt{2a}/\sqrt{b-4}+O(a), \\&w(\theta ) = O(a). \end{aligned}$$

This periodic solution become for the differential system (12) into one periodic solution of period also close to $2\pi$ of the form

$$\begin{aligned}&u(t)=\sqrt{2a}/\sqrt{b-4}+O(a) , \\&v(t)= \sqrt{2a}/\sqrt{b-4}+O(a), \\&w(t)= \sqrt{2a}/\sqrt{b-4}+O(a), \end{aligned}$$

for $a>0$ sufficiently small. Finally we get for the differential system (2) the periodic solution

$$\begin{aligned}&x(t)= \sqrt{2a}/\sqrt{b-4}+O(a) , \\&y(t)= \sqrt{2a}/\sqrt{b-4}+O(a) , \\&z(t)= \sqrt{2a}/\sqrt{b-4}+O(a) . \end{aligned}$$

of period near $2\pi$ when $a>0$ is sufficiently small. Clearly this periodic orbit tends to the origin of coordinates when a tends to zero. Therefore it is also a small-amplitude periodic solution starting at the zero-Hopf equilibrium point. This concludes the proof of Theorem 2. $\square$

5 Compactification of Poincaré

We make an analysis of the flow of system (2) at infinity by analyzing the Poincaré compactification of the system in the local charts $U_i, V_i$ for $i=1,2,3$. We will separate it in different subsections.

5.1 Compactification in the local charts $U_1$ and $V_1$

From the results of Sect. 2.3, the expression of the Poincaré compactification p(X) of system (2) in the local chart $U_1$ is given by

$$\begin{aligned} \begin{aligned} \dot{z}_1&= (z_2-z_1^2)z_3,\\ \dot{z}_2&= -b-z_2+3z_1^2-z_1z_3 + a z_3^2-z_1 z_2 z_3,\\ \dot{z}_3&=-z_1 z_3^2. \end{aligned} \end{aligned}$$

(16)

For $z_3=0$ (which correspond to the points on the sphere ${\mathbb {S}}^2$ at infinity) system (16) becomes

$$\begin{aligned} \begin{aligned} \dot{z}_1&= 0,\\ \dot{z}_2&= -b - z_2+ 3 z_1^2. \end{aligned} \end{aligned}$$

This system has the parabola of equilibria given by $-b-z_2+3z_1^2=0$. Considering the invariance of $z_1z_2$-plane under the flow of (16), we can completely describe the dynamics on the sphere at infinity, which is shown in Fig. 4. Indeed, for $z_2 \ne -b+3z_1^2$ this system is equivalent to

$$\begin{aligned} \begin{aligned} \dot{z}_1&= 0,\\ \dot{z}_2&= 1. \end{aligned} \end{aligned}$$

(17)

whose the solution are given by parallel straight lines. The set $\{-b-z_2+ 3 z_1^2=0\}$ determines a parabola the equilibria.

Fig. 4

Phase portrait of system (2) on the Poincaré sphere at infinity in the local chart $U_1$

The flow in the local chart $V_1$ is the same as the flow in the local chart $U_1$ because the compacted vector field p(X) in $V_1$ coincides with the vector field p(X) in $U_1$ multiplied by $-1$. Hence, the phase portrait on the chart $V_1$ is the same as the one shown in the Fig. 4 reserving in an appropriate way the direction of the time.

5.2 Compactification in the local charts $U_2$ and $V_2$

Using again the results given in Sect. 2, we obtain the expression of the Poincaré compactification p(X) of system (2) in the local chart $U_2$ as

$$\begin{aligned} \begin{aligned} \dot{z}_1&= (1-z_1 z_2) z_3,\\ \dot{z}_2&= 3-z_3-b z_1^2-z_1z_2+ a z_3^2-z_2^2 z_3,\\ \dot{z}_3&=-z_2 z_3^2. \end{aligned} \end{aligned}$$

(18)

System (18) restricted to $z_3=0$ becomes

$$\begin{aligned} \begin{aligned} \dot{z}_1&= 0,\\ \dot{z}_2&= 3-bz_1^2-z_1 z_2. \end{aligned} \end{aligned}$$

(19)

System (19) has the hyperbola of equilibria given by $3 - bz_1^2-z_1 z_2=0$. Considering the invariance of $z_1z_2$-plane under the flow of (18), we can completely describe the dynamics on the sphere at infinity, which is shown in Fig. 3. As in the first chart, this system for $3-bz_1^2-z_1z_2\ne 0$ is equivalent to system (17) and the set $\{3-bz_1^2-z_1 z_2=0\}$ determines an hyperbola of equilibria.

Fig. 5

Phase portrait of system (2) on the Poincaré sphere at infinity in the local chart $U_2$

Fig. 6

Phase portrait of system (2) on the Poincaré sphere at infinity in the local chart $U_3$

Again the flow in the local chart $V_2$ is the same as the flow in the local chart $U_2$ shown in Fig. 5 by reserving in an appropriate way the direction of the time.

5.3 Compactification in the local charts $U_3$ and $V_3$

The expression of the Poincaré compactification p(X) of system (2) in the local chart $U_3$ is

$$\begin{aligned} \dot{z}_1= & {} z_1^2 + z_2 z_3 + b z_1^3 - 3 z_1 z_2^2+ z_1 z_2 z_3 - a z_1 z_3^2,\nonumber \\ \dot{z}_2= & {} z_3+z_1 z_2 + b z_1^2 z_2-3 z_2^3 + z_2^2 z_3 - a z_2 z_3^2,\nonumber \\ \dot{z}_3= & {} z_3 \left( z_1+bz_1^2 - 3 z_2^2 + z_2 z_3 - a z_3^2\right) . \end{aligned}$$

(20)

Observe that system (20) restricted to the invariant $z_1z_2$-plane reduces to

$$\begin{aligned} \begin{aligned} \dot{z}_1&= -z_1 \left( -z_1 - bz_1^2 + 3 z_2^2\right) ,\\ \dot{z}_2&= - z_2 \left( -z_1 - bz_1^2 + 3 z_2^2\right) . \end{aligned} \end{aligned}$$

The solution of this system behaves as in Fig. 6 which corresponds to the dynamics of system (2) in the local chart $U_3$. Indeed for $-z_1 -b z_1^2+3 z_2^2 \ne 0$ the system is equivalent to

$$\begin{aligned} \begin{aligned} \dot{z}_1&=- z_1 ,\\ \dot{z}_2&=- z_2, \end{aligned} \end{aligned}$$

(21)

whose origin is an improper node. The set $\{z_1 + bz_1^2 - 3 z_2^2=0\}$ determines two parabolas of equilibria (see again Fig. 6). The flow at infinity in the local chart $V_3$ is the same as the flow in the local chart $U_3$ reversing appropriately the time.

Proof of Theorem 3

Considering the analysis made before and gluing the flow in the three studied charts, taking into account its orientation shown in Fig. 7, we have a global picture of the dynamical behavior of system (2) at infinity. The system has two closed curves of equilibria, and there are no isolated equilibrium points in the sphere. We observe that the description of the complete phase portrait of system (2) on the sphere at infinity was possible because of the invariance of these sets under the flow of the compactified system. This proves Theorem 3. We remark that the behavior of the flow at infinity does not depend on the parameter a and the global phase portrait at the sphere for different values of b are topologically equivalent. $\square$

Fig. 7

Orientation of the local charts $U_i$, $i=1,2,3$ in the positive endpoints of coordinate axis x, y, z, used to drawn the phase portrait of system (2) on the Poincaré sphere at infinity (Fig. 3). The charts $V_i$, $i=1,2,3$ are diametrically opposed to $U_i$, in the negative endpoints of the coordinate axis

6 Darboux integrability

In this section we prove Theorem 4. To do it we state and prove some auxiliary results. As usual we denote by ${\mathbb {N}}$ the set of positive integers.

Lemma 2

If $h=0$ is an invariant algebraic surface of system (2) with non-zero cofactor k, then $k = k_0- m x$ for some $k_0 \in {\mathbb {C}}$ and $m \in {\mathbb {N}} \cup \{0\}$.

Proof

Let h be an invariant algebraic surface of system (2) with non-zero cofactor k. Then $k = k_0 + k_1 x + k_2 y + k_3 z$ for some $k_0, k_1, k_2, k_3 \in {\mathbb {C}}$. Let n be the degree of h. We write h as sum of its homogeneous parts as $h = \sum _{i=1}^{n} h_i$ where each $h_i$ is a homogenous polynomial of degree i. Without loss of generality, we can assume that $h_n \ne 0$ and $n \ge 1$.

Computing the terms of degree $n + 1$ in (7), we get that

$$\begin{aligned} (-b x^2 - x z + 3 y^2)\frac{\partial h_n}{\partial z}= (k_1 x + k_2 y + k_3 z)h_n. \end{aligned}$$

Solving this linear partial differential equation we get

$$\begin{aligned} h_n(x,y,z)= & {} C_n (x,y) \exp \left( -\frac{k_3 z}{x}\right) \nonumber \\&\times (b^2 x +x z- 3 y^2)^{p(x,y)}, \end{aligned}$$

where $C_n$ is an arbitrary function in the variables x and y and, $p(x,y)=-k_1+k_3b- \dfrac{k_2 y}{x}- \dfrac{3 k_3 y^2}{x^2}$. Since $h_n$ must be a homogeneous polynomial, we must have $k_3=k_2=0$ and $k_1=-m$ with $m \in {\mathbb {N}} \cup \{0\}$. This concludes the proof of the lemma. $\square$

Lemma 3

If $h=0$ is an invariant algebraic surface of system (2) with cofactor $k = k_0- m x$ for some $k_0 \in {\mathbb {C}}$ and $m \in {\mathbb {N}} \cup \{0\}$, then $k_0=m=0$.

Proof

We introduce the weight change of variables

$$\begin{aligned} x=X, \,\,\, y=\mu ^{-1} Y, \,\,\, z= \mu ^{-1}Z, \,\,\, t= \mu T, \end{aligned}$$

with $\mu \in {\mathbb {R}}\setminus \{0\}$. Then system (2) becomes

$$\begin{aligned} \begin{aligned} X'&= Y,\\ Y'&= \mu Z,\\ Z'&=3 Y^2 - \mu Y - \mu ^2 b X^2-\mu X Z + \mu ^2 a, \end{aligned} \end{aligned}$$

(22)

where the prime denotes derivative with respect to the variable T.

Set

$$\begin{aligned} F(X,Y,Z)= & {} \mu ^n f(X, \mu ^{-1}Y, \mu ^{-1}Z)\\= & {} \sum _{i=1}^n \mu ^i F_i(X,Y,Z), \end{aligned}$$

where $F_i$ is the weight homogeneous part with weight degree $n-i$ of F and n is the weight degree of F with weight exponents $s=(0,-1,-1)$. We also set $K(X,Y,Z)=k(X, \mu ^{-1}Y, \mu ^{-1}Z)= k_0 - m X$.

From the definition of an invariant algebraic surface we have

$$\begin{aligned}&(3 Y^2 -\mu Y -\mu ^2 b X^2-\mu X Z + \mu ^2 a )\sum _{i=0}^{n} \mu ^{i} \frac{\partial F_i}{\partial Z}\nonumber \\&\qquad + Y \sum _{i=0}^{n} \mu ^{i} \frac{\partial F_i}{\partial X} + \mu Z \sum _{i=0}^n \mu ^{i} \frac{\partial F_i}{\partial Y} \nonumber \\&\quad = (k_0 - m X) \sum _{i=0}^{n} \mu ^{i} F_i. \end{aligned}$$

(23)

Equating in (23) the terms with $\mu ^0$ we get

$$\begin{aligned} Y \frac{\partial F_0}{\partial X} + 3 Y^2 \frac{\partial F_0}{\partial Z}=(k_0 - m X)F_0, \end{aligned}$$

(24)

where $F_0$ is a weight homogeneous polynomial of degree n.

Solving (24) we readily obtain, by direct computation, that

$$\begin{aligned} F_0(X,Y,Z)=G(Y,Z)\exp \left( \frac{X ( 2 k_0 -m X)}{2Y}\right) , \end{aligned}$$

where G is an arbitrary function in the variables Y and Z. Since $F_0$ must be a polynomial, we must have $k_0=m=0$. Otherwise $F_0=0$ which implies that $F=0$ is not an invariant algebraic surface of system (22), and so $f=0$ is not an invariant algebraic surface of system (2), a contradiction. This completes the proof of the lemma. $\square$

Proof of Theorem 4(a)

Let $f=0$ be an invariant algebraic surface of degree $n\ge 1$ of system (2) with cofactor k(x, y, z). It follows from Lemmas 2 and 3 that $k\equiv 0$. We write f as sum of its homogeneous parts as $f=\sum _{i=0}^{n} f_i$ where $f_i=f_i(x,y,z)$ is a homogeneous polynomial of degree i.

Computing the terms of degree $n + 1$ in (7) we get that

$$\begin{aligned} (-b x^2 - x z + 3 y^2)\frac{\partial f_n}{\partial z}= 0. \end{aligned}$$

Solving this linear differential equation we get that

$$\begin{aligned} f_n(x,y,z)=g(x,y), \end{aligned}$$

(25)

where $g=g(x,y)$ is a homogeneous polynomial of degree n in the variables x and y.

Computing the terms of degree n in (7) we obtain

$$\begin{aligned} ( 3 y^2- b x^2 - x z)\frac{\partial f_{n-1}}{\partial z} +\frac{\partial f_{n}}{\partial x} y + \frac{\partial f_{n}}{\partial y} z+ \frac{\partial f_{n}}{\partial z}(-y) =0. \end{aligned}$$

Solving the partial differential equation above we get

$$\begin{aligned} \begin{aligned} f_{n-1}(x,y,z)\,=\,&K(x,y)+ \frac{z}{x} \frac{\partial g}{\partial y}\\&+ \frac{1}{x^2} \log [x(b x+z)-3y^2]\\&\cdot \Big ( - (b x^2-3 y^2) \frac{\partial g}{\partial y}+xy \frac{\partial g}{\partial x}\Big ), \end{aligned} \end{aligned}$$

where K is an arbitrary function in the variables x and y. Since $f_{n-1}$ must be a homogeneous polynomial of degree $n-1$ we must have

$$\begin{aligned} - (b x^2-3 y^2) \frac{\partial g}{\partial y}+xy \frac{\partial g}{\partial x}=0. \end{aligned}$$

(26)

Solving this partial differential equation we get

$$\begin{aligned} g = g\Big (\frac{2y^2-b x^2}{2 x^6}\Big ). \end{aligned}$$

Taking into account that g must be a homogeneous polynomial of degree n we get $g=0$.

From (25) $f_n=0$, i.e. f is a constant, which is a contradiction with the fact that $f=0$ is an invariant algebraic surface. This completes the proof of Theorem 4(a). $\square$

Proof of Theorem 4(b)

Let $E=\exp (f/g)\notin \mathbb {C}$ be an exponential factor of system (2) with cofactor $L=L_0 + L_1 x + L_2 y + L_3 z$, where $f,g \in {\mathbb {C}}[x,y,z]$ with $(f,g)=1$. From Theorem 4(a) and Lemma 1, $E=\exp (f)$ with $f=f(x,y,z) \in {\mathbb {C}}[x,y,z]\setminus {\mathbb {C}}$.

It follows from Eq. (8) that f satisfies

$$\begin{aligned} \begin{aligned}&(3 y^2 - y - b x^2- x z + a) \frac{\partial f}{\partial z} + y \frac{\partial f}{\partial x} + z \frac{\partial f}{\partial y} \\&\quad =L_0 + L_1 x + L_2 y + L_3 z, \end{aligned} \end{aligned}$$

(27)

where we have simplified the common factor $\exp (f)$.

We write $f=\sum _{i=0}^n f_i(x,y,z)$, where $f_i$ is a homogeneous polynomial of degree i. Assume $n>1$. Computing the terms of degree $n+1$ in (27) we obtain

$$\begin{aligned} (- b x^2 - x z + 3 y^2)\frac{\partial f_n}{\partial z}= 0. \end{aligned}$$

Solving it and using that $f_n$ is a homogeneous polynomial of degree n we get $f_n(x,y,z)=g_n(x,y)$, where $g_n(x,y)$ is a homogeneous polynomial of degree n. Computing the terms of degree n in (27) we obtain

$$\begin{aligned} (3y^2- b x^2 - x z)\frac{\partial f_{n-1}}{\partial z} +\frac{\partial g_{n}}{\partial x} y + \frac{\partial g_{n}}{\partial y} z = 0. \end{aligned}$$

(28)

Solving (28) we get

$$\begin{aligned}\begin{aligned} f_{n-1}&=g_{n-1}(x,y)+\frac{z}{x}\frac{\partial g_n}{\partial y}\\&\quad + \frac{1}{x^2}\left( (3 y^2- b x^2) \frac{\partial g_n}{\partial y}+ x y \frac{\partial g_n}{\partial x}\right) \\&\quad \times \log \left( b x^2+x z-3 y^2\right) , \end{aligned} \end{aligned}$$

where $g_{n-1}(x,y)$ is an arbitrary function in the variables x and y. Since $f_{n-1}$ must a homogeneous polynomial of degree $n-1$, we must have that (26) holds. Taking into account that $g_n$ must be a homogeneous polynomial of degree n, we get $g_n=0$. This implies that $f_n=0$, so $n=1$.

We can write $f=a_1 x + a_2 y + a_3 z$ with $a_i \in \mathbb {C}$. Imposing that f must satisfy (27) we get $f=a_1 x + a_2 y$ with cofactor $a_1 y+a_2 z$. This concludes the proof of Theorem 4(b). $\square$

Proof of Theorem 4(c)

It follows from Proposition 1 and statements (a) and (b) of Theorem 4 that if system (2) has a Darboux first integral, then there exist $\mu _1,\mu _2 \in {\mathbb {C}}$ not both zero such that (9) holds, that is, such that

$$\begin{aligned} \mu _1 y + \mu _2 z= 0. \end{aligned}$$

But this is not possible. In short, there are no Darboux first integrals for system (2) and the proof of Theorem 4(c) is completed. $\square$

7 Analytic integrability

First we prove Theorem 5 when $a=0$ and $b\ne 1/2$. We shall need the following auxiliary result whose proof follows easily by direct computations.

Lemma 4

The linear part of system (2) with $a=0$ at the origin has the two independent polynomial first integrals $x+z$ and $y^2 + z^2$.

Proof of Theorem 5

with $a=0$ and $b\ne 1/2$. We assume that $H=H(x,y,z)$ is a local analytic first integral at the origin of system (2) with $a=0$ and $b\ne 1/2$. We write it as $H=\sum _{k \ge 0} H_k(x,y,z)$ where $H_k$ is a homogeneous polynomial of degree k for $k \ge 0$. We will show by induction that

$$\begin{aligned} H_k =0 \quad \text {for all } k \ge 1. \end{aligned}$$

(29)

Then we will obtain that $H=H_0$. Hence H will be constant in contradiction with the fact that H is a first integral and thus system (2) will not have a local analytic first integral at the origin.

Now we will prove (29). Since H is a first integral of system (2) with $a=0$ and $b\ne 1/2$ it must satisfy

$$\begin{aligned} y \frac{\partial H}{\partial x} + z \frac{\partial H}{\partial y} - (y + b x^2 + x z - 3 y^2 - a)\frac{\partial H}{\partial z}=0. \end{aligned}$$

(30)

The terms of degree one in the variables x, y, z of system (30) are

$$\begin{aligned} y \frac{\partial H_1}{\partial x} + z \frac{\partial H_1}{\partial y} - y\frac{\partial H_1}{\partial z}=0. \end{aligned}$$

(31)

Therefore $H_1$ is either zero, or a polynomial first integral of degree one of the linear part of system (2) with $a=0$. By Lemma 4 we get that $H_1=c_0(x+z)$ with $c_0 \in \mathbb {R}$. Now computing the terms of degree two of Eq. (30) in the variables x, y, z we get

$$\begin{aligned} y \frac{\partial H_2}{\partial x} + z \frac{\partial H_2}{\partial y} - y\frac{\partial H_2}{\partial z}=c_0(b x^2 +x z -3 y^2) . \end{aligned}$$

(32)

Evaluating (32) on $y=z=0$, we have that $c_0=0$, and thus $H_1=0$. This proves (29) for $k=1$.

Now we assume that (29) holds for $k=1,\ldots ,l-1$, and we will prove it for $k=l$. By the induction hypothesis, computing the terms of degree l in (30) we get that

$$\begin{aligned} y \frac{\partial H_l}{\partial x} + z \frac{\partial H_l}{\partial y} - y\frac{\partial H_l}{\partial z}=0. \end{aligned}$$

Then $H_l$ is either zero, or a polynomial first integral of degree l of the linear part of system (2) with $a=0$. It follows from Lemma 4 that it must be of the form

$$\begin{aligned}&H_l=H_l(F_0,F_1) \quad \text {where} \quad F_0=x+z, \\&\quad F_1=y^2 +z^2. \end{aligned}$$

Now computing the terms of degree $l+1$ in (30) we obtain

$$\begin{aligned} \begin{aligned}&y \frac{\partial H_{l+1}}{\partial x} + z \frac{\partial H_{l+1}}{\partial y} - y\frac{\partial H_{l+1}}{\partial z}\\&\quad =(b x^2 +x z -3 y^2)\Big (\frac{\partial H_l}{\partial F_0} + 2 z \frac{\partial H_l}{\partial F_1}\Big ). \end{aligned} \end{aligned}$$

(33)

If we introduce the notation ${\widehat{H}}_{l+1}={\widehat{H}}_{l+1} (F_0,F_1,z) = H_{l+1}(x,y,z)$ with $x=F_0-z$ and $y=\sqrt{F_1-z^2}$ we get

$$\begin{aligned} \begin{aligned} \frac{\partial H_{l+1}}{\partial x}&= \frac{\partial {\widehat{H}}_{l+1}}{\partial F_0}\frac{\partial F_0}{\partial x} = \frac{\partial {\widehat{H}}_{l+1}}{\partial F_0}, \\ \frac{\partial H_{l+1}}{\partial y}&= \frac{\partial {\widehat{H}}_{l+1}}{\partial F_1}\frac{\partial F_1}{\partial y} = 2 y \frac{\partial {\widehat{H}}_{l+1}}{\partial F_1}, \\ \frac{\partial H_{l+1}}{\partial z}&=\frac{\partial {\widehat{H}}_{l+1}}{\partial F_0}\frac{\partial F_0}{\partial z} + \frac{\partial {\widehat{H}}_{l+1}}{\partial F_1}\frac{\partial F_1}{\partial z} + \frac{\partial {\widehat{H}}_{l+1}}{\partial z} \\&= \frac{\partial {\widehat{H}}_{l+1}}{\partial F_0} + 2 z \frac{\partial {\widehat{H}}_{l+1}}{\partial F_1} + \frac{\partial {\widehat{H}}_{l+1}}{\partial z}. \end{aligned} \end{aligned}$$

Then the left-hand side of Eq. (33) becomes

$$\begin{aligned} \begin{aligned}&y \frac{\partial {\widehat{H}}_{l+1}}{\partial F_0} + 2 y z \frac{\partial {\widehat{H}}_{l+1}}{\partial F_1} - y \frac{\partial {\widehat{H}}_{l+1}}{\partial F_0} - 2 y z \frac{\partial {\widehat{H}}_{l+1}}{\partial F_1} \\&\quad - y \frac{\partial {\widehat{H}}_{l+1}}{\partial z} = - \sqrt{F_1-z^2} \frac{\partial {\widehat{H}}_{l+1}}{\partial z} \end{aligned} \end{aligned}$$

and so (33) can be written as

$$\begin{aligned} \begin{aligned} - \sqrt{F_1-z^2} \frac{\partial {\widehat{H}}_{l+1}}{\partial z}&= \big ( b(F_0-z)^2 + z (F_0-z)\\&\quad - 3 (F_1-z^2) \big )\Big (\frac{\partial H_l}{\partial F_0} + 2 z \frac{\partial H_l}{\partial F_1}\Big ). \end{aligned} \end{aligned}$$

(34)

Since $H_l =H_l(F_0,F_1)$ solving (34) we have

$$\begin{aligned} \begin{aligned} {\widehat{H}}_{l+1}&= {\widehat{H}}_{l+1} (F_0,F_1,z) \\&= \frac{1}{2} \frac{\partial H_l}{\partial F_0} \left( ((2 - 4 b)F_0 + (2 + b)z)\sqrt{F_1 - z^2}\right. \\&\quad \left. -\,(2bF_0^2 + (b-4)F_1)\arctan \left( \frac{z}{\sqrt{F_1-z^2}} \right) \right) \\&\quad +\, \frac{1}{6}\frac{\partial H_l}{\partial F_1}\left( \sqrt{F_1 - z^2}(-10F_1 + 3F_0z + 4z^2\right. \\&\quad \left. +\, 2b\left( 3F_0^2 + 2F_1 - 3F_0z + z^2\right) \right) \\&\quad \left. +\, 3(2b-1)F_0F_1\arctan \left( \frac{z}{\sqrt{F_1-z^2}} \right) \right) \\&\quad +\, K(F_0,F_1), \end{aligned} \end{aligned}$$

where K is a function in the variables $F_0$ and $F_1$. Since $H_{l+1}$ must be a polynomial and $b\ne 1/2$, we get that $\partial H_l/\partial F_0=\partial H_l/\partial F_1=0$. Then since $H_l$ has degree l, we have that $H_l=0$ which proves (29) for $k=l$. This proves (29) and consequently Theorem 5 is proved when $a=0$ and $b\ne 1/2$. $\square$

Now we shall prove Theorem 5 with $a/b \in \mathbb {R}^+ \setminus \mathbb {Q}^+$. Before doing that, we shall need some preliminary results. Note that system (2) is reversible with respect to the involution $R(x,y,z)=(-x,y,-z)$. Therefore, in order to prove Theorem 5, it is enough to study only the non-existence of analytic first integrals around the singularity $(-\sqrt{a/b},0,0)$.

We consider $a/b \in \mathbb {R}^+ \setminus \mathbb {Q}^+$, and we make the change of variables $(x,y,z)\rightarrow (X,Y,Z)$ given by

$$\begin{aligned} X= x+ \sqrt{\frac{a}{b}}, \quad Y=y, \quad Z=z \end{aligned}$$

That is, we translate the singular point $(-\sqrt{a/b} ,0,0)$ to the origin. Then system (2) becomes

$$\begin{aligned} \begin{aligned} \dot{x}&= y,\\ \dot{y}&= z,\\ \dot{z}&= -y -2 \sqrt{\frac{a}{b}} x - \sqrt{\frac{a}{b}} z- x^2 - x z + 3 y^2, \end{aligned} \end{aligned}$$

(35)

where we have written again (x, y, z) instead of (X, Y, Z).

Lemma 5

The cubic equation

$$\begin{aligned} u^3-\sqrt{\frac{a}{b}} u^2 +u-2\sqrt{\frac{a}{b}} =0 \end{aligned}$$

(36)

has one simple real root $\lambda$ and two complex roots $\alpha {\pm } i \beta$ with $\lambda ,\alpha ,\beta \in \mathbb {R}$, satisfying

$$\begin{aligned} \begin{aligned}&2 \alpha +\lambda =\sqrt{\frac{a}{b}}, \qquad \alpha ^2 +\beta ^2 + 2 \alpha \lambda = 1 \quad \text{ and } \\&\lambda (\alpha ^2 + \beta ^2) =2 \sqrt{\frac{a}{b}}. \end{aligned} \end{aligned}$$

(37)

Proof

Since the discriminant of the cubic Eq. (36) is less than zero (note that $a/b>0$), it is obvious that it has one simple real root $\lambda$ and two complex roots $\alpha {\pm } i \beta$ with $\lambda ,\alpha ,\beta \in \mathbb {R}$. Moreover, using that

$$\begin{aligned}&u^3-\sqrt{\frac{a}{b}} u^2 +u-2\sqrt{\frac{a}{b}} \\&\quad = (u-\lambda )(u-\alpha - i \beta )(u-\alpha + i \beta ), \end{aligned}$$

we can check that conditions (37) hold.

We have the following easy result, whose proof was given in [10].

Lemma 6

The linear differential system

$$\begin{aligned} \begin{pmatrix} \dot{x} \\ \dot{y} \\ \dot{z} \end{pmatrix} = \begin{pmatrix} \alpha &{}\quad -\beta &{} 0 \\ \beta &{}\quad \alpha &{} 0 \\ 0 &{} 0 &{}\quad \lambda \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} \end{aligned}$$

(38)

has two independent first integrals of the form:

$$\begin{aligned} \begin{aligned} H_1&= \frac{(x^2 + y^2)^\lambda }{z^{2 \alpha }} \quad \text {and} \\ H_2&= (x^2 + y^2)^\beta \exp \big (2 \alpha \arctan (y/x) \big ). \end{aligned} \end{aligned}$$

where $\lambda , 2 \alpha$ and $\beta$ are positive integers.

Lemma 7

The linear differential system

$$\begin{aligned} \begin{aligned} \dot{x}&= y,\\ \dot{y}&= z,\\ \dot{z}&= -y -2 \sqrt{\frac{a}{b}} x - \sqrt{\frac{a}{b}} z, \end{aligned} \end{aligned}$$

(39)

with $a/b \in \mathbb {R}^+ \setminus \mathbb {Q}^+$ has no polynomial first integrals.

Proof

Note that the characteristic polynomial of system (39) is Eq. (36). So, by Lemma 5, the real Jordan matrix of the linear differential system (39) is the one given in (38). Then from Lemma 6 our linear differential system has a polynomial first integral if and only if one of the following two conditions hold: either $\lambda = 2 \alpha m$, or $\alpha =0$ and $\beta =m$ with $m \in \mathbb {Z}$ (here $\mathbb {Z}$ is the set of integer numbers). In the first case, using that $\lambda , \alpha , \beta$ must satisfy (37) and that $a \ne 0$ we obtain the four solutions $(\alpha ,\beta ,a/b)$ equal to

$$\begin{aligned} \begin{aligned}&\left( \alpha _-,\beta _{\pm }, \frac{(m-1)^2(m-2)}{m^2}\right) \quad \text{ and }\\&\left( \alpha _+,\beta _{\pm },\frac{(m-1)^2(m-2)}{m^2}\right) , \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \alpha _{\pm }= {\pm } \frac{\sqrt{m-2}}{2m} \quad \text {and} \quad \beta _{\pm }= {\pm } \frac{\sqrt{8m^2 -9 m +2}}{2m}. \end{aligned}$$

None of them are possible due to the fact that a / b is not a rational number.

For the second case, again using that $\lambda , \alpha , \beta$ must satisfy (37) we obtain the solution

$$\begin{aligned} \lambda =\sqrt{\frac{a}{b}}, \quad m^2 =-1, \quad \lambda m^2 = 2 \sqrt{\frac{a}{b}}, \end{aligned}$$

which is obviously not possible. This completes the proof.

Proof of Theorem 5

with $a/b\in \mathbb {R}^+ \setminus \mathbb {Q}^+$. We assume that $H=H(x,y,z)$ is a local analytic first integral at the origin of system (35) with $a/b\in \mathbb {R}^+ \setminus \mathbb {Q}^+$. We write it as $H=\sum _{k \ge 0} H_k(x,y,z)$ where $H_k$ is a homogeneous polynomial of degree k for $k \ge 0$. We will show by induction that

$$\begin{aligned} H_k =0 \quad \text {for all }k \ge 1. \end{aligned}$$

(40)

Then we will obtain that H is constant in contradiction with the fact that H is a first integral. This will imply that system (2) has no local analytic first integrals at the origin.

Now we shall prove (40). Since H is a first integral of system (35) it must satisfy

$$\begin{aligned}&y \frac{\partial H}{\partial x} + z \frac{\partial H}{\partial y}\nonumber \\&\quad = \left( y +2 \sqrt{\frac{a}{b}} x + \sqrt{\frac{a}{b}} z + b x^2 + x z - 3 y^2\right) \frac{\partial H}{\partial z}.\nonumber \\ \end{aligned}$$

(41)

The terms of degree one in the variables x, y, z of system (41) are

$$\begin{aligned} y \frac{\partial H_1}{\partial x} + z \frac{\partial H_1}{\partial y} - \left( y +2 \sqrt{\frac{a}{b}} x + \sqrt{\frac{a}{b}} z\right) \frac{\partial H_1}{\partial z}=0. \end{aligned}$$

Therefore $H_1$ is either zero, or a polynomial first integral of degree one of system (39). By Lemma 7 this last case is not possible and $H_1=0$. This proves (40) for $k=1$.

Now we assume that (40) holds for $k=1,\ldots ,l-1$ and we will prove it for $k=l$. By the induction hypothesis, computing the terms of degree l in (41) we get that

$$\begin{aligned} \begin{aligned}&y \frac{\partial H_l}{\partial x} + z \frac{\partial H_l}{\partial y}= \\&\quad =\Big (y +2 \sqrt{\frac{a}{b}} x + \sqrt{a} z+ b x^2 + x z - 3 y^2\Big )\frac{\partial H_l}{\partial z}. \end{aligned} \end{aligned}$$

Then $H_l$ is either zero, or a polynomial first integral of degree l of system (39). Again, by Lemma 7 this last case is not possible and $H_l=0$, which proves (40) for $k=l$. Consequently Theorem 5 is proved when $a/b \in \mathbb {R}^+ \setminus \mathbb {Q}^+$. $\square$

8 Discussions

Most chaotic systems that appear in the literature have at least one equilibria. In this paper we study system (2). This system is relevant because is the first polynomial differential system in ${\mathbb {R}}^3$ with two parameters generating a chaotic attractor (at least numerically) without having equilibria for some values of the parameters. It is then worth further studying its globally chaotic behavior from the theoretical point of view.

In this direction, we have shown that for $a>0$ sufficiently small it can exhibit up to three small-amplitude periodic solutions that bifurcate of a zero-Hopf equilibrium point located at (0, 0, 0) when $a=0$ and two limit cycles emerging from two classical Hopf bifurcations at the equilibrium points $({\pm } \sqrt{2a}, 0,0)$, for $a>0, b=1/2$. We have also given a complete description of its dynamics on the Poincaré sphere at infinity, and we have studied its integrability by showing that the system has no first integrals neither in the class of analytic functions nor in the class of Darboux functions.

In order to study its chaotic behavior we can pursue, at least, in two directions not covered in this paper: try to obtain first integrals in some bigger classes of functions such as the Liouvillian, meromorphic or even better $C^1$ functions, and try to study (either analytically or numerically) how the solutions of system (2) reach the infinity characterized in Theorem 3 . Due to the fact that system (2) can exhibit up to two finite equilibria, and that it does not have invariant algebraic surfaces, this last point seems to be very complicated right now.