1 Introduction

Cables are extensively used in various engineering fields, such as suspension/stay cable bridges, power transmission lines, and mooring cables. Due to its elasticity, initial sag, nonlinear axial stretching, and complex boundary connections, cable’s dynamic behaviors are very rich and extensive investigations into cable’s dynamics have been undertaken by many researchers in the past few decades [1, 2].

Irvine and Caughey [3, 4] established a linear cable model and finished linear modal analysis. Triantafyllou [5] conducted extensive researches into mooring cables. Based upon the single-degree-of-freedom (sdof) cable model, Hagedon et al. [6], Luongo et al. [7], and Benedettini et al. [8] investigated free and forced oscillations of elastic cables. Furthermore, mode interactions are key for cable’s nonlinear dynamics. Benedettini et al. [9] investigated modal coupling between in-plane and out-plane motions. By Galerkin discretization, Rao et al. [10], Perkins [11], Lee et al. [12], and Srinil et al. [13] conducted extensive investigations into cable’s planar and/or non-planar 2:1 resonant interactions; Pakdemirli et al. [14] examined cable’s 1:1 resonant interaction; Lacarbonara et al. [15, 16] established a general framework for cable’s 2:1, 1:1, and 3:1 resonant interactions; Zhao and Wang [17] conducted further investigations into cable’s 3:1 internal resonance. And internal resonance modeling and analysis for various structure members can be found in reference [18].

Besides complex mode interactions and nonlinear multimodal dynamic behaviors, cable’s various loading/excitation sources are also key factors for structural design, such as wind loadings [19], rain-wind loadings, and seismic loadings. One more important excitation source, though not so obvious, is moving support-induced excitations, or termed cable-flexible support interactions [20] broadly.

Actually, our motivations for investigations into cable–support interactions are twofold. Firstly, in suspension/stay cable bridge’s cable–tower system, power transmission cable–tower system and marine mooring cable-floating platform system, an important boundary excitation source of elastic cables is the support’s oscillation, which might arise from seismic loadings or sea surface wave loadings; secondly, for the cable–deck or cable–arch system in structural/bridge engineering, the main boundary excitation for cables is deck’s (beam structures) or arch’s oscillations, which might be caused by moving vehicles through vehicle–bridge interactions.

A preliminary step for modeling cable–support interaction is treating supports in motion as moving boundary conditions for cables [21–24]. In this case, the coupling is assumed to be one way, and the support acts as a boundary excitation only. This assumption would be reasonable if the inertia/mass of the support is much larger than that of cables. Using Galerkin discretization, Perkins [11] investigated suspended cable’s two-to-one resonance under longitudinal/tangential support’s motion, and Benedettini et al. [25] established a four-degree-of-freedom discrete cable model for modal couplings under vertical/out-plane support motions. Thereafter, most other work was dedicated to stay/inclined cable’s nonlinear vibrations caused by connected deck/tower’s motion [26–35].

Cai and Chen [26] investigated nonlinear responses of a inclined cable subject to parametric/external resonances numerically. Lilien and Pinto da Costa [27] investigated stay cable’s motions due to parametric excitations. Pintoda Costaetal [28] studied the oscillations of stay cables due to periodic motions of the girder/pylon. Berlioz and Lamarque [29] investigated an inclined cable’s motion under the boundary motions theoretically and experimentally. Georgakis and Taylor [30] investigated the nonlinear dynamics of cable stays induced by sinusoidal deck’s motion. Wang and Zhao [31] investigated inclined cable’s nonlinear multimodal responses with deck’s sinusoidal motion. Gonzalez-Buelga et al. [32] and Macdonald et al. [33] presented modal stability analysis for inclined cable subjected to support excitations. Kang et.al [34] investigated primary/subharmonic resonant responses of stay cable–beam system. Essentially, these support-induced cable dynamics, or roughly cable–support interactions, can actually be categorized into three basic prototype models: cables with vertical, out-plane, and longitudinal support motions.

In the previous investigations into cable–support interactions, the main possible limitations include: (1) Cable’s mode shape functions are usually simplified into or replaced by taut string’s mode functions with cable’s initial sag effect neglected [29–31, 34, 35]. (For reference [35], more strictly, the exact cable mode functions were used for evaluating the model’s large linear terms, while the simpler taut string’s mode functions were used for the small nonlinear terms); (2) almost all the dynamic models are discrete due to Galerkin discretization (by finite modes or even one mode); (3) In the absence of consensus, the ambiguous support-induced quasi-static motion modes [25, 34, 35] were superposed on cable’s elastic/flexible mode (with fixed boundaries).

For the first limitation, approximate taut string modes used for short stay cables might be proper. However, for a long flexible suspended cable, the initial sag cannot be neglected and the induced quadratic interaction is the dominant nonlinearity.

For the second, as pointed out in references [36–38], directly reduced models, i.e., by directly attacking the original continuous partial differential equations through the multiple scale method, would be more appropriate/accurate than the (classical low-order Galerkin) discretized models, especially for characterizing cable’s quadratic nonlinearity effect [37].

For the third, our key observation/assumption herein is that the scale of support motion, in most engineering cases, is much smaller than that of the cable, and the support motion’s influence on cable’s linear modal analysis (fast dynamics) can thus be neglected temporally through proper scaling. The small amplitude support motion can be treated as a boundary modulation term for cable’s reduced (slow) dynamics. Such scale separation idea (boundary modulation) is similar to the nonlinear normal mode analysis for continuous structures with weak geometric nonlinearities [15], especially those with weak boundary nonlinearities [18, 39]. For example, Shaw and Pierre [39], and also Nayfeh [18], neglected nonlinear boundary springs’ influence on a beam’s linear modal dynamics and treated them as boundary modulations of beam’s reduced/slow dynamics, when analyzing nonlinear normal modes of beams. Our assumption can also be validated by the fact that stay cable–deck (beam) systems exhibit many localized modes that mainly involve the transversal cable dynamics only, even full coupling between cable and deck beam/support is assumed a priori [40]. This means that the cable and deck/support can indeed be decoupled for linear modal (fast) dynamics (decoupled in zero-order approximation in terms of multiple scale method) for possible parameters.

Thus, with the idea of boundary resonance in mind, we aim to establish a boundary modulation formulation for cable’s support-excited mode interactions using multiple scale expansions in the direct form.

2 Problem statement

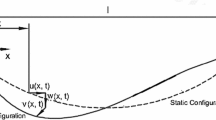
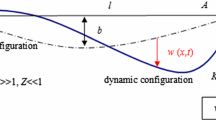
Consider the in-plane motion of a suspended elastic cable, which is fixed at support O and coupled to a vertically oscillating support at A, as depicted in Fig. 1. Assuming the cable stretches in a quasi-static manner, one can derive the following non-dimensional governing equations for cable’s in-plane vertical motion [17–25]:

$$\begin{aligned} \ddot{w}+2c\dot{w}-{w}''-\alpha \left( {{w}''+{y}''} \right) \int _0^1 {\left( {{y}'{w}'+\frac{1}{2}{w}'^{2}} \right) } \hbox {d}x=0\nonumber \\ \end{aligned}$$
(1)

where w(x, t) denotes the cable’s in-plane vertical displacement. The overdot indicates the differentiation with respect to the non-dimensional time t; the prime indicates the differentiation with respect to the non-dimensional coordinate x. The longitudinal kinetic condensation technique has been utilized in Eq. (1), owing to fact that the longitudinal dynamic timescale is much small (thus fast) than the vertical/transversal one. The non-dimensional stiffness \(\alpha ={ EA }/H=8{ EA }/mgl^{2}\), where E is the Young’s modulus, A is the area of the cross section, H is the cable tension’s horizontal component, m is the mass per unit length, g is the gravitational acceleration. The sag-to-span ratio is \(f=b/l\), and the non-dimensional cable’s initial sag is \(y(x)=4 fx(1-x)\), where b is the sag, l is the span.

Fig. 1
figure 1

Illustration of a suspended cable with a vertically oscillating support

Full size image

The fixed boundary condition at \(x=0\) and the time-varying boundary condition at \(x=1\) induced by the oscillating support A are

$$\begin{aligned} \begin{array}{ll} w\left( {x,t} \right) =0,&{}\quad \hbox { at }x=0\\ w\left( {x,t} \right) =z\left( t \right) =Z_0 \cos \varOmega t,&{} \quad \hbox { at } x=1 \end{array} \end{aligned}$$
(2)

In real engineering structures such as suspended/stay cable bridges and mooring cables in marine engineering, vibration of towers/decks or floating- platforms is always responsible for this moving boundary condition in Eq. (2) (seismic loadings/moving vehicles and sea surface wave loadings might cause oscillations of towers/decks and marine platforms, respectively.). It is noted that no other external excitation is applied in Eq. (1), and the only excitation is the support-induced boundary excitation.

For a complete understanding cable’s nonlinear multimodal dynamics, mode interaction’s modeling and analysis is key. For quadratic nonlinearities, triad mode resonance and its degenerate case, i.e., two-to-one resonance, are fundamental. And they satisfy the following resonance relations [18]

$$\begin{aligned} \begin{array}{ll} \pm \omega _1 \pm \omega _2 \pm \omega _3 =0,&{}\quad \hbox { triad resonance} \\ \omega _2 =2\omega _1, &{}\quad 2{:}1 \hbox { resonance }\\ \end{array} \end{aligned}$$
(3)

where cable’s eigenfrequencies are denoted by \(\omega _{1}, \omega _{2}, \omega _{3}\), and these linear modal analysis results are cited in “Appendix 1.” Any three/two eigenfrequencies satisfying the resonance relations in Eq. (3) are called a resonant cluster/pair in the present paper.

Based upon the Newton–Raphson algorithm and the resonance relation in Eq. (3), one can find typical mode resonance points in cables by sweeping the elasto-geometric parameter \(\lambda ^{2}= EA /mgl(8 b/l)^{3}\). For example, we find out possible triad resonant interactions, say

$$\begin{aligned} \omega _1 +\omega _3 -\omega _7 \approx 0 \end{aligned}$$
(4)

with the elasto-geometric parameter \(\lambda _{1}=13.88\) or \(\lambda _{2 }=23.67\). And, \(\omega _1 +\omega _3 -\omega _5 \approx 0\) with \(\lambda _{3 }=5.96\). Also, \(\omega _5 \approx 2\omega _1\) [16] with \(\lambda _{4 }=9.26\) or \(\lambda _{5 }=17.00\), and \(\omega _7 \approx 2\omega _3\) [16] with \(\lambda _{6 }=10.15\). Here \(\omega _k, \;k=1,3,5,7\) denote the eigenfrequency of cable’s k-th in-plane mode.

3 Asymptotic modeling by the multiple scale method

For the sake of brevity, following Lacarbonara [15], we rewrite Eq. (1) in a compact form

$$\begin{aligned}&\dot{w}-u=0 \nonumber \\&\dot{u}+2cu+L[w]-N_2 [w]-N_3 [w]=0 \end{aligned}$$
(5)

where linear operator L, quadratic and cubic nonlinear terms \(N_{2},\, N_{3}\) are defined as

$$\begin{aligned}&L[w]=-{w}''-\alpha {y}''\int _0^1 {\left( {{y}'{w}'} \right) } \hbox {d}x,\nonumber \\&N_2 [w]=\alpha {w}''\int _0^1 {\left( {{y}'{w}'} \right) } \hbox {d}x+\alpha {y}''\int _0^1 {\left( {{{w}'^{2}}/2} \right) } \hbox {d}x,\nonumber \\&N_3 [w]=\alpha {w}''\int _0^1 {\left( {{{w}'^{2}}/2} \right) } \hbox {d}x \end{aligned}$$
(6)

And the boundary conditions are

$$\begin{aligned} \begin{array}{lll} w\left( {x,t} \right) =0, &{} u\left( {x,t} \right) =0&{}\quad \hbox { at }x=0 \\ w\left( {x,t} \right) =z\left( t \right) ,&{}u\left( {x,t} \right) =\dot{z}\left( t \right) &{}\quad \hbox { at } x=1 \\ \end{array} \end{aligned}$$
(7)

An uniform asymptotic expansion of w is assumed as

$$\begin{aligned} w\left( {x,t} \right)= & {} \varepsilon w_1 \left( {T_0, \;T_1 } \right) +\varepsilon ^{2}w_2 \left( {T_0, \;T_1 } \right) \cdots \nonumber \\ u\left( {x,t} \right)= & {} \varepsilon u_1 \left( {T_0, \;T_1 } \right) +\varepsilon ^{2}u_2 \left( {T_0, \;T_1 } \right) \cdots \end{aligned}$$
(8)

where \(T_{i}= \varepsilon ^{i} t\), and \(\varepsilon \) is a small bookkeeping parameter. To make damping, nonlinearity, and the non-homogenous boundary condition in Eq. (7) be balanced at the same order, \(\varepsilon ^{2}\), the damping c and the support motion can be rescaled as \(c\rightarrow \varepsilon c,\;Z_0 \rightarrow \varepsilon ^{2}Z_0 \). Substituting Eq. (8) into Eq. (5), equating coefficients of like powers of \(\varepsilon \), we obtain

Order \(\varepsilon \):

$$\begin{aligned}&D_0 w_1 -u_1 =0 \nonumber \\&D_0 u_1 +L\left[ {w_1 } \right] =0 \end{aligned}$$
(9)

with homogenous boundary conditions

$$\begin{aligned} w_1 =0, u_1 =0 \quad at\;x=0\;,1 \end{aligned}$$
(10)

Order \(\varepsilon ^{2}\):

$$\begin{aligned}&D_0 w_2 -u_2 =-D_1 w_1 \nonumber \\&D_0 u_2 +L\left[ {w_2 } \right] =-D_1 u_1 -2cu_1 +N_2 \left[ {w_1 } \right] \end{aligned}$$
(11)

with non-homogeneous second-order boundary conditions

$$\begin{aligned}&w_2 =0,\qquad \;u_2 =0 \quad \hbox {at}\;\,x=0\; \nonumber \\&w_2 =\frac{Z_0 }{2}\hbox {e}^{{i} \varOmega T_0 }+cc,\,\;\nonumber \\&u_2 ( {x,t} )={i} \varOmega \frac{Z_0 }{2}\hbox {e}^{{i} \varOmega T_0 }+cc.\quad \hbox {at}\;x=1 \end{aligned}$$
(12)

It is noted that the scaling rule \(Z_0 \rightarrow \varepsilon ^{2}Z_0 \) is important for the above perturbation analysis, i.e., decoupling the oscillating boundary from cable’s linear modal (fast) dynamics on order \(\varepsilon \) and thus simplifying the original problem significantly. As mentioned before, such scale separation technique is also used by Shaw [39] and Nayfeh [18] for deriving nonlinear normal modes of beams with (pure) nonlinear resonant boundary conditions.

3.1 Generic triad mode interaction under boundary resonance

The solutions of the first-order problem in Eq. (9) are assumed as

$$\begin{aligned} w_1= & {} \sum _{k=1}^3 {A_k \left( {\;T_1 } \right) \phi _k \left( x \right) \hbox {e}^{{i} \omega _k T_0 }} +cc, \nonumber \\ u_1= & {} \sum _{k=1}^3 {\mathrm{i} \omega _k A_k \left( {T_1 } \right) \phi _k \left( x \right) \hbox {e}^{{i} \omega _k T_0 }} +cc \end{aligned}$$
(13)

where \(\phi _k\) and \(\omega _k\) are cable’s symmetric in-plane mode and eigenfrequency. With a slight abuse of notations, here \(\omega _1,\;\omega _2, \omega _3 \) represent an arbitrary triad resonant cluster, say, \(\omega _1, \omega _3, \omega _7\) or \(\omega _1, \omega _3, \omega _5 \) mentioned in Sect. 2. Their detailed mathematical forms are presented in “Appendix 1”, and cc is short for complex conjugate.

Substituting Eq. (13) into the second-order problem in Eq. (11), we obtain

$$\begin{aligned}&D_0 w_2 -u_2 =-\sum _{k=1}^3 {D_1 A_k \phi _k \left( x \right) \hbox {e}^{{ i} \omega _k T_0 }} +cc, \end{aligned}$$
(14)
$$\begin{aligned}&D_0 u_2 +L[ {w_2 } ]=-\sum _{k=1}^3 {i} \omega _k \left( {D_1 A_k +2cA_k } \right) \phi _k ( x )\hbox {e}^{{i} \omega _k T_0 }\nonumber \\&\quad +\,A_1 A_2 \hbox {e}^{{i} \left( {\omega _1 +\omega _2 } \right) T_0 }\varPi _{12} +A_3 \bar{{A}}_1 \hbox {e}^{{i} \left( {\omega _3 -\omega _1 } \right) T_0 }\varPi _{31}\nonumber \\&\quad +\,A_3 \bar{{A}}_2 \hbox {e}^{{i} \left( {\omega _3 -\omega _2 } \right) T_0 }\varPi _{32} +\hbox {NST.}+cc \end{aligned}$$
(15)

The nonlinear coefficients \(\varPi _{12}, \varPi _{31}, \varPi _{32}\) in Eq. (15) are defined in “Appendix 2”, and NST is short for non-secular/resonant terms. The non-homogeneous 2nd-order problems in Eqs. (14), (15) and (12) should satisfy certain solvability conditions for non-trivial solutions. The problem is self-adjoint, and the adjoint homogeneous solutions are \({\varvec{q}}^{\dagger }=\left[ {{i} \omega _k, 1} \right] \phi _k \left( x \right) \hbox {e}^{-{i} \omega _k T_0 }\), which should be ‘orthogonal’ to the right-hand sides (RHS) of Eqs. (14) and (15).

In most cases, i.e., with homogeneous boundary conditions, resonant/secular terms, distributed in the whole structure domain, are usually caused by external/parametric excitations or internal resonances. However, the present non-homogenous boundary conditions in Eq. (12) might also be resonant, although this resonance appears to be ‘localized’ at the boundary. More care would be needed to derive the solvability conditions for the support-induced resonant responses. The main difficulties lie in that the adjoint solutions \({\varvec{q}}^{\dagger }\) is NOT strictly orthogonal to the LHS/RHS of Eqs. (14) and (15). Actually, it turns out that certain nonzero ‘boundary terms’ (BT) would arise in the process of integration by parts.

Introducing internal and external detuning parameters, i.e., \(\sigma _{1}\) and \(\sigma _{2}\), we write the resonance relations and the primary excitation frequency \(\varOmega \) as

$$\begin{aligned} \omega _3 =\omega _1 +\omega _2 +\varepsilon \sigma _1, \quad \varOmega =\omega _p +\varepsilon \sigma _2, \;p=1,2,3\nonumber \\ \end{aligned}$$
(16)

We multiply the right-hand-sides of Eqs. (14) and (15) by the adjoint solutions \({\varvec{q}}^{\dagger }=\left[ {{i} \omega _k, 1} \right] \phi _k \left( x \right) \hbox {e}^{-{i} \omega _k T_0 }\) and integrate in the domain \([0,1]\times [0,\uptau _{0}]\), where \(\uptau _{0}\) is the typical period of \(w_{2}\) and \(u_{2}\) with respect to \(T_{0}\) [18, 38]. We thus obtain the right-hand-sides (RHS) as

$$\begin{aligned}&\hbox {RHS}=\left\{ {-2{i} \omega _1 \left( {D_1 A_1 +\mu _1 A_1 } \right) +\varGamma _1 \bar{{A}}_2 A_3 \hbox {e}^{{i} \sigma _1 T_1 }} \right\} \tau _0 \delta _{1k} \nonumber \\&\quad + \left\{ {-2{i} \omega _2 \left( {D_1 A_2 +\mu _2 A_2 } \right) +\varGamma _2 \bar{{A}}_1 A_3 \hbox {e}^{{i} \sigma _1 T_1 }} \right\} \tau _0 \delta _{2k} \nonumber \\&\quad + \left\{ {-2{i} \omega _3 \left( {D_1 A_3 +\mu _3 A_3 } \right) +\varGamma _3 A_1 A_2 \hbox {e}^{-{i} \sigma _1 T_1 }} \right\} \tau _0 \delta _{3k}\nonumber \\ \end{aligned}$$
(17)

where the Kroneck delta \(\delta _{jk} =1, \;j=k;\;\delta _{jk} =0,\;j\ne k\), and the triad resonance coefficients \(\varGamma _{\mathrm{k}}\) and the dampings \(\mu _{\mathrm{k}}\) in Eq. (17) can be written as

$$\begin{aligned} \varGamma _1= & {} \left\langle {\phi _1, \varPi _{32} \left( x \right) } \right\rangle , \;\varGamma _2 =\left\langle {\phi _2, \varPi _{31} \left( x \right) } \right\rangle , \nonumber \\ \varGamma _3= & {} \left\langle {\phi _3 ,\varPi _{12} \left( x \right) } \right\rangle , \;\mu _k =\left\langle {c\left( x \right) ,\;\phi _k ^{2}} \right\rangle \end{aligned}$$
(18)

if introducing the inner product for any two smooth functions \(\upvarphi _{1}(x)\) and \(\upvarphi _{2}(x)\)

$$\begin{aligned} \left\langle {\varphi _1, \varphi _2 } \right\rangle =\int _0^1 {\bar{{\varphi }}_1 \left( x \right) \;\varphi _2 \left( x \right) \hbox {d}x} \end{aligned}$$
(19)

Noting Eq. (16), we rewrite the resonant boundary conditions in Eq. (7) as

$$\begin{aligned} \begin{array}{ll} w_2 =\frac{Z_0 }{2}\hbox {e}^{{i} \varOmega T_0 }+cc.=\hbox {e}^{{i} \omega _p T_0 }\frac{Z_0 }{2}\hbox {e}^{{i} \sigma _2 T_1 }+cc.&{}\quad \, \hbox {at} \, x=1\; \\ u_2 \left( {x,t} \right) ={i} \omega _p \frac{Z_0 }{2}\hbox {e}^{{i} \omega _p T_0 }\hbox {e}^{{i} \sigma _2 T_1 }+cc. &{}\quad \hbox {at} \, x=1 \end{array} \end{aligned}$$
(20)

Multiplying the left-hand sides of Eqs. (14) and (15) by the adjoint solutions \({\varvec{q}}^{\dagger }=\left[ {{i} \omega _k, 1} \right] \phi _k \left( x \right) \hbox {e}^{-{i} \omega _k T_0 }\) and integrating in the domain \([0,1]\times [0,\tau _{0}]\), we obtain the more subtle left-hand-sides (LHS), explicitly

$$\begin{aligned} \hbox {LHS}= & {} \int _0^{\tau _0 } \int _0^1 \left\{ {i} \omega _k \phi _k \hbox {e}^{-{i} \omega _k T_0 }\left( {D_0 w_2 -u_2 } \right) \right. \nonumber \\&\left. +\,\phi _k \hbox {e}^{-{i} \omega _k T_0 }(D_0 u_2 +L\left[ {w_2 } \right] ) \right\} \hbox {d}x\hbox {d}T_0 \nonumber \\ \quad= & {} \int _0^{\tau _0 } \int _0^1 \left\{ -D_0 \left( {{i} \omega _k \phi _k \left( x \right) \hbox {e}^{-{i} \omega _k T_0 }} \right) w_2\right. \nonumber \\&\left. -\,\left( {{i} \omega _k \phi _k \left( x \right) \hbox {e}^{-{i} \omega _k T_0 }} \right) u_2 \right\} \hbox {d}x\hbox {d}T_0 \nonumber \\&+\,\int _0^{\tau _0 } \int _0^1 \left\{ -D_0 \left( { \phi _k \left( x \right) \hbox {e}^{-{i} \omega _k T_0 }} \right) u_2\right. \nonumber \\&\left. +\,L\left[ {\phi _k \left( x \right) \hbox {e}^{-{i} \omega _k T_0 }} \right] w_2 \right\} \hbox {d}x\hbox {d}T_0 + \hbox {BT} \nonumber \\ \quad= & {} -\int _0^{\tau _0 } \int _0^1 \underbrace{\left[ {\overline{D_0 \left( { \phi _k \left( x \right) \hbox {e}^{{i} \omega _k T_0 }} \right) -{i} \omega _k \phi _k \left( x \right) \hbox {e}^{{i} \omega _k T_0 }} } \right] }_{=0}\nonumber \\&\quad \cdot \, u_2 \hbox {d}x\hbox {d}T_0 \nonumber \\&+\,\int _0^{\tau _0 } \int _0^1 \underbrace{\left[ {\overline{D_0 \left( {{i} \omega _k \phi _k \left( x \right) \hbox {e}^{{i} \omega _k T_0 }} \right) +L\left[ {\phi _k \left( x \right) \hbox {e}^{{i} \omega _k T_0 }} \right] } } \right] }_{=0}\nonumber \\&\quad \cdot \, w_2 \hbox {d}x\hbox {d}T_0 + \hbox {BT} \nonumber \\= & {} \hbox {BT}\ne 0 \end{aligned}$$
(21)

where integration by parts is used, and the over-bar means complex conjugate manipulations. As marked by the brace, the last two integrals are exactly equal to zero as the braced integrands are actually the first-order linear dynamics denoted by Eq. (9). In this integration process, those nonzero ‘boundary terms’ arising from the non-homogeneous resonant boundary conditions, i.e., Eq. (20), are denoted by BT. And, it is these ‘boundary terms’ (BT) that incorporate those resonant boundary conditions into cable’s reduced dynamics/modulation equations. If the boundary conditions are non-resonant or homogeneous (the support is fixed), extensively treated in references, the boundary terms would be zero, i.e., BT \(=\) 0.

The above nonzero boundary terms BT herein can be obtained as follows. Recall the cable’s linear integral-differential operator

$$\begin{aligned} L[w]=-{w}''-\alpha {y}''\int _0^1 {\left( {{y}'{w}'} \right) } \hbox {d}x \end{aligned}$$
(22)

Thus the boundary terms BT are obtained by inspecting into

$$\begin{aligned}&\int _0^{\tau _0 } {\int _0^1 {\phi _k \left( x \right) \hbox {e}^{-{i} \omega _k T_0 }L\left[ {w_2 } \right] } \hbox {d}x\hbox {d}T_0 } \nonumber \\&\, =\int _0^{\tau _0 } {\int _0^1 {\phi _k \left( x \right) \hbox {e}^{-{i} \omega _k T_0 }\left[ {-{w}''_2 -\alpha {y}''\int _0^1 {\left( {{y}'{w}'_2 } \right) } \hbox {d}x} \right] } \hbox {d}x\hbox {d}T_0 } \nonumber \\&\, =-\int _0^{\tau _0 } \left[ \left. {\left( {\phi _k \left( x \right) {w}'_2 } \right) } \right| _0^1 -\left. {\left( {{\phi }'_k \left( x \right) w_2 } \right) } \right| _0^1\right. \nonumber \\&\left. \quad +\int _0^1 {\left[ {{\phi }''_k \left( x \right) w_2 } \right] } \hbox {d}x \right] \hbox {e}^{-{i} \omega _k T_0 }\hbox {d}T_0 \nonumber \\&\quad -\, \alpha \int _0^{\tau _0 } \left\{ \left[ {\left. {\left( {\phi _k \left( x \right) {y}'} \right) } \right| _0^1 -\int _0^1 {{\phi }'_k \left( x \right) {y}'\hbox {d}x} } \right] \right. \nonumber \\&\left. \quad \cdot \left[ {\left. {\left( {{y}'w_2 } \right) } \right| _0^1 -\int _0^1 {\left( {{y}''w_2 } \right) } \hbox {d}x} \right] \right\} \hbox {e}^{-{i} \omega _k T_0 }\hbox {d}T_0 \nonumber \\&\quad =\int _0^{\tau _0 } {\left. {\left( {{\phi }'_k \left( x \right) w_2 } \right) } \right| _0^1 \hbox {e}^{-{i} \omega _k T_0 }\hbox {d}T_0 }\nonumber \\&\qquad +\,\, \alpha \int _0^{T_0 } {\left. {\left( {{y}'w_2 } \right) } \right| _0^1 \int _0^1 {{\phi }'_k {y}'} \hbox {d}x} \hbox {e}^{-{i} \omega _1 T_0 }\hbox {d}T_0 \nonumber \\&\qquad -\,\int _0^{\tau _0 } {\int _0^1 {\left( {\phi _k \hbox {e}^{-{i} \omega _k T_0 }} \right) ^{\prime \prime }\cdot } w_2 \hbox {d}x} \hbox {d}T_0\nonumber \\&\qquad -\,\int _0^{\tau _0 } {\int _0^1 {\left[ {\alpha {y}''\int _0^1 {\left( {\phi _k \hbox {e}^{-{i} \omega _1 T_0 }} \right) ^{\prime }{y}'\hbox {d}x} } \right] \cdot w_2 } \hbox {d}x} \hbox {d}T_0 \nonumber \\&\, =\underbrace{\left[ {{\phi }'_k \left( 1 \right) +\alpha {y}'\left( 1 \right) \int _0^1 {{\phi }'_k {y}'} \hbox {d}x} \right] \frac{Z_0 }{2}\hbox {e}^{{i} \sigma _2 T_1 }\tau _0 \delta _{kp} }_{BT}\nonumber \\&\quad +\int _0^{\tau _0 } {\int _0^1 {L\left[ {\phi _k \left( x \right) \hbox {e}^{-{i} \omega _k T_0 }} \right] w_2 } \hbox {d}x\hbox {d}T_0 } \end{aligned}$$
(23)

The linear mode function \(\phi _k \) satisfies \(\phi _k \left( 0 \right) =\phi _k \left( 1 \right) =0\), and this is used in the third equality. Furthermore, the non-homogeneous resonant boundary conditions in Eq. (20) are used in the last equality above.

Introducing boundary resonance dynamic coefficients \(\varLambda _k \)

$$\begin{aligned} \varLambda _k ={\phi }'_k \left( 1 \right) +\alpha {y}'\left( 1 \right) \int _0^1 {{y}'{\phi }'_k \left( x \right) \hbox {d}x}, \quad k=1,2,3\nonumber \\ \end{aligned}$$
(24)

Thus, the nonzero boundary terms BT or LHS can be written as

$$\begin{aligned} \hbox {LHS}=\hbox {BT}=\varLambda _k \frac{Z_0 }{2}\hbox {e}^{{i} \sigma _2 T_1 }\tau _0 \delta _{kp} \end{aligned}$$
(25)

where the Kronecker delta \(\delta _{kp} =1, \;k=p;\;\delta _{kp} =0,\;k\ne p\). One notes that the non-homogeneous resonant boundary conditions in Eq. (20) are of vital importance for deriving Eq. (25). We point out that the boundary dynamic coefficients \(\varLambda _k \) are closely related with the first-order derivative of the modal function, i.e.,\({\phi }_k'\) and also the cable’s initial sag y(x). Further discussion on the boundary coefficient \(\varLambda _k \) are detailed in Sect. 4.

Note that the LHS denoted in Eq. (25) is NOT equal to zero, leading to a new boundary modulation term for the amplitudes \(A_{\mathrm{k}}\). This is due to the ‘boundary resonant terms’ in Eq. (20). In nonlinear structure dynamic analysis, most resonant/secular sources originate from the RHS of perturbed equations, say Eq. (11), not LHS, such as internal resonance, primary external resonance, and parametric resonance terms. Thus, this represents another different resonant interaction mechanism in cable dynamics, and we call this as ‘(localized) boundary resonance’ between the cable and support, in comparison with ‘(distributed) bulk resonance’ treated by most previous work, i.e., external/parametric excitations, or internal resonance, occurring in the whole interior domain of cables.

Finally, letting LHS \(=\) RHS, we obtain the cable’s reduced dynamics (modulation equations) with boundary resonance due to support’s motion z(t)

$$\begin{aligned} D_1 A_1= & {} -\mu _1 A_1 -{i} \frac{\varGamma _1 }{2\omega _1 }\bar{{A}}_2 A_3 \hbox {e}^{{i} \sigma _1 T_1 }+{i}\frac{\varLambda _1 }{4 \omega _1 }Z_0 \hbox {e}^{{i} \sigma _2 T_1 }\delta _{1p}\nonumber \\ \end{aligned}$$
(26)
$$\begin{aligned} D_1 A_2= & {} -\mu _2 A_2 -{i} \frac{\varGamma _2 }{2\omega _2 }\bar{{A}}_1 A_3 \hbox {e}^{{i} \sigma _1 T_1 }+{i}\frac{\varLambda _2 }{4 \omega _2 }Z_0 \hbox {e}^{{i} \sigma _2 T_1 }\delta _{2p}\nonumber \\ \end{aligned}$$
(27)
$$\begin{aligned} D_1 A_3= & {} -\mu _3 A_3 -{i} \frac{\varGamma _3 }{2\omega _3 }A_1 A_2 \hbox {e}^{-{i} \sigma _1 T_1 }+{i} \frac{\varLambda _3 }{4\omega _3 }Z_0 \hbox {e}^{{i} \sigma _2 T_1 }\delta _{3p}\nonumber \\ \end{aligned}$$
(28)

Our remark here is that the above boundary resonant interactions, in essence, are one-way coupling between the cable and support, i.e., the support’s motion amplitude \(Z_{0}\) is constant and not affected by the cable’s tension. Our future work would be to extend the present boundary modulation formulation/approach to the two-way coupling /interaction between the cable and (elastic) support, i.e., cable’s motion would induce modulations of support’s motion z(t).

The boundary resonant modulation equations in Eqs. (26)–(28) appear to be similar to those with external excitations. Roughly, the effect of vertical boundary resonant excitations is equivalent to the externally forced resonance. In mathematical forms, this is true. However, such remark is not rigorous enough from a physics viewpoint. The boundary resonance induced excitation amplitude \(\varLambda _k Z_0 \) include cable’s boundary modal information, i.e., \({\phi }'_k \left( 1 \right) \), and even the initial deformation/sag, i.e., y(x), which are not embodied in the case of externally forced resonance.

From the above derivations, it might also be tempting to assume that only principal /primary boundary resonance is possible. This is partially right. Actually, the limitation of our present boundary resonant modulation formulation is that the cable’s resonant boundary condition in Eq. (20) is independent of cable’s displacements (thus linear). Nonlinear boundary conditions are possible, which would induce other nonlinear boundary resonance/modulation patterns. For example, a nonlinear boundary resonance pattern for beams with nonlinear boundary springs was derived by Shaw and Pierre [39] and Nayfeh [18].

3.2 Degenerate two-to-one mode interaction under boundary resonance

For 2:1 internal resonance, the solutions of the first-order problem in Eq. (9) are assumed as

$$\begin{aligned} w_1= & {} \sum _{k=1}^2 {A_k \left( {T_1 } \right) \phi _k \left( x \right) \hbox {e}^{{i} \omega _k T_0 }} +cc, \nonumber \\ u_1= & {} \sum _{k=1}^2 {{i} \omega _k A_k \left( {T_1 } \right) \phi _k \left( x \right) \hbox {e}^{{i} \omega _k T_0 }} +cc \end{aligned}$$
(29)

where \(\phi _k\) and \(\omega _k\) are cable’s symmetric in-plane mode and eigenfrequency, and \(\omega _1, \;\omega _2 \) constitute an arbitrary 2:1 resonant pair.

Substituting Eq. (29) into the second-order problem in Eq. (11), we obtain

$$\begin{aligned}&D_0 w_2 -u_2 =-\sum _{k=1}^2 {D_1 A_k \phi _k \left( x \right) \hbox {e}^{{i} \omega _k T_0 }} +cc,\nonumber \\ \end{aligned}$$
(30)
$$\begin{aligned} D_0 u_2 +L\left[ {w_2 } \right]= & {} -\sum _{k=1}^2 {i} \omega _k \left( {D_1 A_k +2cA_k } \right) \nonumber \\&\times \,\phi _k \left( x \right) \hbox {e}^{{i} \omega _k T_0 }\nonumber \\&+\,A_1 A_1 \hbox {e}^{{i} 2\omega _1 T_0 }\varPi _1 \nonumber \\&+\,A_2 \bar{{A}}_1 \hbox {e}^{{i} \left( {\omega _2 -\omega _1 } \right) T_0 }\varPi _{21} +\hbox {NST.}+cc\nonumber \\ \end{aligned}$$
(31)

The nonlinear coefficients \(\varPi _{1}, \varPi _{21}\) are defined in “Appendix 2”. Introducing internal and external detuning parameters, i.e., \(\sigma _{1}\) and \(\sigma _{2}\), we write the resonance relations and the primary excitation frequency \(\varOmega \) as

$$\begin{aligned} \omega _2 =2\omega _1 +\varepsilon \sigma _1, \quad \varOmega =\omega _p +\varepsilon \sigma _2, \;p=1,2 \end{aligned}$$
(32)

Thus the corresponding resonant boundary conditions in Eq. (7) can be rewritten as

$$\begin{aligned} \begin{array}{ll} w_2 =\frac{Z_0 }{2}\hbox {e}^{{i} \varOmega T_0 }+cc.=\hbox {e}^{{i} \omega _p T_0 }\frac{Z_0 }{2}\hbox {e}^{{i} \sigma _2 T_1 }+cc.&{}\quad \hbox {at} \,x=1 \\ u_2 \left( {x,t} \right) ={i} \omega _p \frac{Z_0 }{2}\hbox {e}^{ {i} \omega _p T_0 }\hbox {e}^{{i} \sigma _2 T_1 }+cc. &{}\quad \hbox {at} \,x=1 \\ \end{array} \end{aligned}$$
(33)

In the similar manner detailed in Sect. 3.1, multiplying Eqs. (30) and (31) by the adjoint solutions \({\varvec{q}}^{\dagger }=\left[ {{i} \omega _k, 1} \right] \phi _k \left( x \right) \hbox {e}^{-{i} \omega _k T_0 }\) and integrating in the domain \([0,1]\times [0,\tau _{0}]\), letting LHS=RHS, we obtain the cable’s 2:1 modulation equations with ‘boundary resonant excitations’ due to support’s vertical motions

$$\begin{aligned} D_1 A_1= & {} -\mu _1 A_1 -{i} \frac{\varGamma _1 }{2\omega _1 }\bar{{A}}_1 A_2 \hbox {e}^{{i} \sigma _1 T_1 }+{i}\frac{\varLambda _1 }{4 \omega _1 }Z_0 \hbox {e}^{{i} \sigma _2 T_1 }\delta _{1p}\nonumber \\ \end{aligned}$$
(34)
$$\begin{aligned} D_1 A_2= & {} -\mu _2 A_2 -{i} \frac{\varGamma _2 }{2\omega _2 }A_1 A_1 \hbox {e}^{-{i} \sigma _1 T_1 }+{i}\frac{\varLambda _2 }{4 \omega _2 }Z_0 \hbox {e}^{{i} \sigma _2 T_1 }\delta _{2p}\nonumber \\ \end{aligned}$$
(35)

where the triad resonance coefficients \(\varGamma _{\mathrm{k}}\) and the dampings \(\mu _{\mathrm{k}}\) are

$$\begin{aligned} \varGamma _1= & {} \left\langle {\phi _1, \varPi _{21} \left( x \right) } \right\rangle , \quad \varGamma _2 =\left\langle {\phi _2, \varPi _1 \left( x \right) } \right\rangle , \nonumber \\ \mu _k= & {} \left\langle {c\left( x \right) ,\;\phi _k ^{2}} \right\rangle \end{aligned}$$
(36)

and the boundary resonance coefficients

$$\begin{aligned} \varLambda _k ={\phi }'_k \left( 1 \right) +\alpha {y}'\left( 1 \right) \int _0^1 {{y}'{\phi }'_k \left( x \right) \hbox {d}x}, \quad k=1,2 \end{aligned}$$
(37)

In a similar manner, for higher precisions, we can also seek a 2nd-order multiple scale expansion of the support-induced cable 2:1 resonant dynamics. Assuming \(c\rightarrow \varepsilon ^{2}c,\;Z_0 \rightarrow \varepsilon ^{3}Z_0\), and \(\varOmega =\omega _p +\varepsilon ^{2}\sigma _2, \) following the basic expansion procedures detailed above, and using the method of reconstitution [38], we derive the associated modulation equations as

$$\begin{aligned} \frac{\hbox {d}A_1 }{\hbox {d}t}= & {} -\mu _1 A_1 -{i} \frac{\varGamma _1 }{2\omega _1 }\bar{{A}}_1 A_2 \hbox {e}^{{i} \sigma _1 t}-{i} \frac{K_{11} }{2\omega _1 }A_1 \left| {A_1 } \right| ^{2}\nonumber \\&- \,{i} \frac{K_{12} }{2\omega _1 }A_1 \left| {A_2 } \right| ^{2}+{i}\frac{\varLambda _1 }{4 \omega _1 }Z_0 \hbox {e}^{{i} \sigma _2 t}\delta _{1p} \end{aligned}$$
(38)
$$\begin{aligned} \frac{\hbox {d}A_2 }{\hbox {d}t}= & {} -\mu _2 A_2 -{i} \frac{\varGamma _2 }{2\omega _2 }A_1 A_1 \hbox {e}^{-{i} \sigma _1 t}-{i} \frac{K_{22} }{2\omega _2 }A_2 \left| {A_2 } \right| ^{2}\nonumber \\&- \,{i} \frac{K_{21} }{2\omega _2 }A_2 \left| {A_1 } \right| ^{2}+{i}\frac{\varLambda _2 }{4 \omega _2 }Z_0 \hbox {e}^{{i} \sigma _2 t}\delta _{2p} \end{aligned}$$
(39)

where the 2nd-order nonlinear coefficients \(K_{11} ,K_{12}, K_{21}, K_{22} \) can be obtained in the similar way proposed by Lacarbonara [15] and here the differentiation rule \(\partial /{\partial t}=D_0 +\varepsilon D_1 +\varepsilon ^{2}D_2 \) and \(\varepsilon =1\) has been substituted.

4 Discussions on the boundary resonance coefficient \(\varLambda _k\)

Noting \(\lambda ^{2}=64\alpha f^{2}\) and using integration by parts, we can simplify the boundary coefficient \(\varLambda _k\) into

$$\begin{aligned} \varLambda _k= & {} {\phi }'_k \left( 1 \right) +\alpha {y}'\left( 1 \right) \left\{ {\left. {{y}'\phi _k \left( x \right) } \right| _0^1 -\int _0^1 {{y}''_k \phi _k \left( x \right) \hbox {d}x} } \right\} \nonumber \\= & {} {\phi }'_k \left( 1 \right) +\alpha {y}'\left( 1 \right) \left( {8f\int _0^1 {\phi _k \left( x \right) \hbox {d}x} } \right) \nonumber \\= & {} \underbrace{{\phi }'_k \left( 1 \right) }_{\varLambda _{k1} }-\underbrace{0.5\lambda ^{2}\int _0^1 {\phi _k \left( x \right) \hbox {d}x} }_{-\varLambda _{k2} -\mathrm{sag} \,\mathrm{effect}}\nonumber \\= & {} \varLambda _{k1} +\varLambda _{k2} \end{aligned}$$
(40)

4.1 Cable’s sag effect

We note that the boundary coefficients \(\varLambda _k \) consists of two parts: The first is the boundary value of the mode function’s first-order derivative, i.e., \(\varLambda _{k1} \), and the second part is a combined/hybrid effect of both the mode function and the initial sag, i.e., \(\varLambda _{k2} \). Therefore, from Eq. (40) we conclude that:

  1. (a)

    For the same elasto-geometric coefficient \(\lambda \): The boundary coefficient’s degenerate form is \(\varLambda _k =\varLambda _{k1} ={\phi }'_k \left( 1 \right) \) for cable’s asymmetrical modes. And for symmetric modes \(\phi _k \left( x \right) \), we can see that the initial deformation y(x) would induce another nonzero sag-related term, i.e., \(\varLambda _{k2}\);

  2. (b)

    For the same symmetric mode function \(\phi _k \left( x \right) \): Note that the boundary coefficient \(\varLambda _k \left( \lambda \right) \) depends on \(\lambda \) in a complicated way, rather than the apparent quadratic way. This is because the mode function \(\phi _k \left( x \right) \) itself is also related to the elasto-geometric coefficient \(\lambda \). We illustrate the boundary coefficient \(\varLambda _k \) for the first four in-plane symmetric modes in the following.

From Fig. 2, four main characteristics can be observed:

  1. (1)

    For each boundary coefficient, there is a maximum \(\left| {\varLambda _k } \right| \) (absolute value) at \(\lambda _m \), and the coefficient is dominated by the sag-induced effect, i.e., \(\varLambda _{k2}\), in the vicinity of this maximum;

  2. (2)

    The boundary coefficient’s first part, i.e., \(\varLambda _{k1}\), turns positive from negative as \(\lambda \) is increased. Thus there is always a \(\lambda \) where \(\varLambda _{k1}\) is exactly equal to zero and the boundary excitation effect is caused only by the sag-induced term, i.e., \(\varLambda _{k2}\);

  3. (3)

    For small elasto-geometric parameters \(\lambda \), the sag-induced \(\varLambda _{k2}\) is small, and the boundary coefficient is can be approximated by \(\varLambda _{k1} \approx {\phi }_k' \left( 1 \right) \). Roughly, this domain can be described as \(0\le \lambda \le \lambda _0 \), where \(\lambda _0 \) denotes the crossing point of \(\varLambda _{k1} \) and \(\varLambda _{k2} \). We point out this observation is in accordance with the fact that the boundary coefficient’s degenerate form is \(\varLambda _k =\varLambda _{k1} ={\phi }_k' \left( 1 \right) \) for really taut strings with \(\lambda \rightarrow 0\).

  4. (4)

    Furthermore, both \(\lambda _m \) and \(\lambda _0\) introduced above get larger as the order of mode functions increases, i.e, the domain where \(\varLambda _{k1} \approx {\phi }_k' \left( 1 \right) \) expands. This means that if boundary resonance occurs at modes of higher orders, the initial sag’s effect on the boundary modulation becomes less important for many small and even intermediate sagged cables.

Fig. 2
figure 2

Boundary resonance coefficient \(\varLambda _k \) associated with the first four symmetric modes

Full size image

4.2 Multiple support motions

The approach used to derive the above boundary coefficient \(\varLambda _k\) at \(x=1\) is general in the mathematical sense. Therefore, in a similar manner, we can obtain the corresponding boundary coefficient at \(x\,=\,0\), explicitly

$$\begin{aligned} \left. {\varLambda _k } \right| _{x=0}= & {} -{\phi }'_k \left( 0 \right) -\alpha {y}'\left( 0 \right) \int _0^1 {{y}'{\phi }'_k \left( x \right) \hbox {d}x} \nonumber \\= & {} -{\phi }'_k \left( 0 \right) -\alpha {y}'\left( 0 \right) \left( {8f\int _0^1 {\phi _k \left( x \right) \hbox {d}x} } \right) \nonumber \\= & {} \underbrace{-{\phi }'_k \left( 0 \right) }_{\varLambda _{k1} }-\underbrace{0.5\lambda ^{2}\int _0^1 {\phi _k \left( x \right) \hbox {d}x} }_{-\varLambda _{k2} -\text {sag effect}} \end{aligned}$$
(41)

Considering that \({\phi }_k' \left( 0\right) =-{\phi }_k' \left( 1 \right) \) for symmetric mode functions, and \({\phi }_k' \left( 0 \right) ={\phi }_k' \left( 1 \right) \) for antisymmetric ones, we therefore conclude

$$\begin{aligned} \begin{array}{ll} \left. {\varLambda _k } \right| _{x=0} =\left. {\varLambda _k } \right| _{x=1}, &{}\quad \quad \phi _k \hbox { is symmetric} \\ \left. {\varLambda _k } \right| _{x=0} =-\left. {\varLambda _k } \right| _{x=1}, &{}\quad \quad \phi _k \hbox { is antisymmetric} \\ \end{array} \end{aligned}$$
(42)

4.3 Cable–support (flexible) dynamic interaction

We believe that the proposed concept of boundary resonance coefficient paves the way for coupled modeling of cable-flexible support dynamic interaction in an asymptotic sense. Noting that the cable and the support can be loosely considered as ‘boundary’ for each other. Therefore, similar to the support-induced boundary coefficient for the cable, one can also, with proper extensions, establish the cable-induced boundary coefficient for the flexible support, through deriving the solvability conditions. And the cable and the flexible support would be coupled naturally on the slow time scale, more explicitly, coupled by the modulation equations, through two sets of boundary coefficients.

5 Dynamic analysis and nonlinear responses for illustrative examples

In this section, we would present the dynamic analysis for the support-induced cable system. The modulation equations established in precedent sections can be considered as cable’s reduced dynamic models and our following analysis would be based upon these models. For the sake of simplicity, we rewrite the modulation equations through polar transformations [18]. All the approximate analytical results based upon these reduced models would also verified by direct numerical simulations using the finite-difference method.

5.1 Modulation equations for triad mode resonant interaction

Introducing the following transformations

$$\begin{aligned} A_k \left( {T_1 } \right) =\frac{1}{2}a_k \left( {T_1 } \right) \hbox {e}^{{i}\beta _k (T_1 )},\quad k=1,2,3 \end{aligned}$$
(43)

If the boundary resonance is applied to the two low-frequency modes of the resonant cluster, only single-mode solutions would exist. This is similar to that of externally forced resonance [18]. Thus setting \(p=3\) in Eqs. (26)–(28), we mainly restrict our attentions to triad mode coupled solutions in the following numerical study. For the generic triad resonance, substituting the transformation in Eq. (43) into the Eqs. (26)–(28), we obtain the amplitude equations

$$\begin{aligned} a_1 ^{\prime }= & {} -\mu _1 a_1 +\frac{\varGamma _1 }{4\omega _1 }a_2 a_3 \sin \left( {\gamma _1 } \right) \end{aligned}$$
(44)
$$\begin{aligned} a_2^{\prime }= & {} -\mu _2 a_2 +\frac{\varGamma _2 }{4\omega _2 }a_1 a_3 \sin \left( {\gamma _1 } \right) \end{aligned}$$
(45)
$$\begin{aligned} a_3 ^{\prime }= & {} -\mu _3 a_3 -\frac{\varGamma _3 }{4\omega _3 }a_1 a_2 \sin \left( {\gamma _1 } \right) -\frac{\varLambda _3 }{2\omega _3 }Z_0 \sin \left( {\gamma _2 } \right) \nonumber \\ \end{aligned}$$
(46)

and the (relative) phase equations

$$\begin{aligned} {\gamma }_1'= & {} \sigma _1 +\frac{\varGamma _1 }{4\omega _1 }\frac{a_2 a_3 }{a_1 }\cos \left( {\gamma _1 } \right) +\frac{\varGamma _2 }{4\omega _2 }\frac{a_1 a_3 }{a_2 }\cos \left( {\gamma _1 } \right) \nonumber \\&-\frac{\varGamma _3 }{4\omega _3 }\frac{a_1 a_2 }{a_3 }\cos \left( {\gamma _1 } \right) +\frac{\varLambda _3 }{2\omega _3 }\frac{Z_0 }{a_3 }\cos \left( {\gamma _2 } \right) \end{aligned}$$
(47)
$$\begin{aligned} {\gamma }_2'= & {} \sigma _2 +\frac{\varGamma _3 }{4\omega _3 a_3 }a_1 a_2 \cos \left( {\gamma _1 } \right) -\frac{\varLambda _3 }{2\omega _3 }\frac{Z_0 }{a_3 }\cos \left( {\gamma _2 } \right) \nonumber \\ \end{aligned}$$
(48)

where \(\gamma _1 =\beta _3 -\beta _2 -\beta _1 +\sigma _1 T_1,\) and \(\gamma _2 =\sigma _2 T_1 -\beta _3 \). Thus, we obtain the autonomous modulation equations in the polar form, i.e., Eqs. (44)–(48). After solving these equations, we derive cable’s first-order triad resonant asymptotic responses as

$$\begin{aligned} w\left( {x,\;t} \right)= & {} \varepsilon \left\{ a_1 \cos \left( {\tilde{\omega }_1 t+\nu _1 } \right) \phi _1 \left( x \right) \right. \nonumber \\&\left. +\, a_2 \cos \left( {\tilde{\omega }_2 t+\nu _2 } \right) \phi _2 \right. \left( x \right) \nonumber \\&\left. {+\, a_3 \cos \left( {\varOmega t-\gamma _2 } \right) \phi _3 \left( x \right) } \right\} +O( {\varepsilon ^{2}} )\cdots \nonumber \\ \end{aligned}$$
(49)

where \(\tilde{\omega }_1 =\omega _1 +\varepsilon \beta _1 ^{\prime },\tilde{\omega }_2 =\omega _2 +\varepsilon \beta _2 ^{\prime },\tilde{\omega }_1 +\tilde{\omega }_2=\varOmega , \;\nu _1 +\nu _2 =-\gamma _1 -\gamma _2 \), and \(\varepsilon \) can be absorbed into \(a_i\), or equivalently be set \(\varepsilon =1\) in the numerical simulation.

Setting \({a}_1' ={a}_2' ={a}_3' =0\) in Eqs. (44)–(46) and \({\gamma }_1' = {\gamma }_2' =0\) in Eqs. (47) and (48), we can obtain equilibrium solutions by the Newton–Raphson algorithm (combined with the homotopic algorithm [41]). By sweeping the detuning parameter \(\sigma _{2,}\) frequency response diagrams are then constructed through the numerical continuation software package XPP-AUTO [42], with the pseudo-arclength method embedded. The equilibrium solutions’ stability is determined by checking that the real part of each eigenvalue of the linearized system matrix is negative or not.

5.2 Modulation equations for two-to-one resonant interaction

A reasonable multiple scale expansion, or equivalently a reliable reduced dynamic model(i.e., modulation equations) requires that the cable’s response amplitudes and the detuning parameters for resonant interactions/excitations should be small. Therefore, for reduced model’s higher precision, we would use the 2:1 resonant modulation equations derived by the 2nd-order expansions in the following, i.e., Eqs. (38) and (39). Setting \(p=1\) in Eqs. (38) and (39), and using the polar transformation

$$\begin{aligned} A_k \left( t \right) =\frac{1}{2}a_k \left( t \right) \hbox {e}^{{i}\beta _k (t)},\quad k=1,2 \end{aligned}$$
(50)

we obtain the amplitude equations

$$\begin{aligned} a_1 ^{\prime }= & {} -\mu _1 a_1 +\frac{\varGamma _1 }{4\omega _1 }a_1 a_2 \sin \left( {\gamma _3 } \right) -\frac{\varLambda _1 }{2\omega _1 }Z_0 \sin \left( {\gamma _4 } \right) \nonumber \\\end{aligned}$$
(51)
$$\begin{aligned} a_2 ^{\prime }= & {} -\mu _2 a_2 -\frac{\varGamma _2 }{4\omega _2 }a_1^2 \sin \left( {\gamma _3 } \right) \end{aligned}$$
(52)

and the (relative) phase equations

$$\begin{aligned} {\gamma }'_3= & {} \sigma _3 +\frac{\varGamma _1 }{2\omega _1 }a_2 \cos \left( {\gamma _3 } \right) -\frac{\varGamma _2 }{4\omega _2 }\frac{a_1^2 }{a_2 }\cos \left( {\gamma _3 } \right) \nonumber \\&-\frac{\varLambda _1 }{\omega _1 }\frac{Z_0 }{a_1 }\cos \left( {\gamma _4 } \right) -\frac{K_{22} }{8\omega _2 }a_2^2 -\frac{K_{21} }{8\omega _2 }a_1^2 +\frac{K_{11} }{4\omega _1 }a_1^2\nonumber \\&+\frac{K_{12} }{4\omega _1 }a_2^2 \end{aligned}$$
(53)
$$\begin{aligned} {\gamma }_4'= & {} \sigma _4 +\frac{\varGamma _1 }{4\omega _1 }a_2 \cos \left( {\gamma _3 } \right) -\frac{\varLambda _1 }{2\omega _1 }\frac{Z_0 }{a_1 }\cos \left( {\gamma _4 } \right) \nonumber \\&+\frac{K_{11} }{8\omega _1 }a_1^2 +\frac{K_{12} }{8\omega _1 }a_2^2 \end{aligned}$$
(54)

where \(\gamma _3 =\beta _2 -2\beta _1 +\sigma _1 t\), and \(\gamma _4 =\sigma _2 t-\beta _1 \). Thus we obtain the autonomous modulation equations in the polar form, i.e., Eqs. (51)–(54). After solving these equations for \(a_{1},\, a_{2}, \gamma _{3}\), and \(\gamma _{4}\), we derive cable’s 2nd-order asymptotic responses as

$$\begin{aligned}&w\left( {x,\;t} \right) =\varepsilon \left\{ a_1 \cos \left( {\varOmega t-\gamma _4 } \right) \phi _1 \left( x \right) \right. \nonumber \\&\left. \quad +\, a_2 \cos \left( {2\varOmega t+\gamma _3 -2\;\gamma _4 } \right) \phi _2 \left( x \right) \right\} \nonumber \\&\quad +\, \frac{1}{2}\varepsilon ^{2}\left\{ {a_1^2 \left[ {\cos \left( {2\varOmega t-2\gamma _4 } \right) \varPsi _{11} \left( x \right) +\chi _{11} \left( x \right) } \right] } \right. \nonumber \\&\quad +\, a_2^2 \left[ {\cos \left( {4\varOmega t+2\gamma _3 -4\gamma _4 } \right) \varPsi _{22} \left( x \right) +\chi _{22} \left( x \right) } \right] \nonumber \\&\quad +\, a_2 a_1 \left[ {\cos \left( {3\varOmega t+\gamma _3 -3\gamma _4 } \right) \varPsi _{21} \left( x \right) } \right. \nonumber \\&\quad +\, \left. {\cos \left( {\varOmega t+\gamma _3 -\gamma _4 } \right) \chi _{21} \left( x \right) } \right] +\left. \cdots \right\} +O( {\varepsilon ^{3}} )\cdots \nonumber \\ \end{aligned}$$
(55)

where the 2nd-order shape functions \(\varPsi _{11}, \varPsi _{22} ,\varPsi _{21}, \chi _{11}, \chi _{22}, \chi _{21} \) are determined by in a similar way of Lacarbonara [15], which is not repeated here. And \(\varepsilon =1\) is used in the numerical simulation.

Similar to Sect. 5.1, setting \({a}_1' ={a}_2' =0\) in Eqs. (51) and (52) and \({\gamma }_3' ={\gamma }_4' =0\) in Eqs. (53) and (54), the equilibrium solutions are obtained by the Newton–Raphson algorithm. And the frequency response diagrams are then constructed by the pseudo-arclength method included in AUTO.

5.3 Numerical validations: finite-difference method

To validate the approximate analytical results of the reduced model obtained by the multiple scale method, based upon the finite-difference method, we use a time-stepping program coded by C++ to simulate the cable’s dynamic responses directly. We note that the finite-difference method was also used to study cable’s nonlinear dynamics by the authors in references [20, 43]. Briefly, using the second-order finite-difference scheme,

$$\begin{aligned}&\frac{\partial \left( \,\right) }{\partial x}\approx \frac{\left( \, \right) _{i+1} -\left( \, \right) _{i-1} }{2\Delta x},\quad \frac{\partial ^{2}\left( \,\right) }{\partial x^{2}}\approx \frac{\left( \, \right) _{i+1} -2\left( \,\right) _i +\left( \, \right) _{i-1} }{\Delta x^{2}}, \nonumber \\&\frac{\partial \left( \,\right) }{\partial t}\approx \frac{\left( \, \right) _{j+1} -\left( \,\right) _{j-1} }{2\Delta t},\quad \frac{\partial ^{2}\left( \,\right) }{\partial t^{2}}\approx \frac{\left( \,\right) _{j+1} -2\left( \, \right) _j +\left( \,\right) _{j-1} }{\Delta t^{2}},\nonumber \\ \end{aligned}$$
(56)

we present the discretized version of the cable dynamics in Eq. (1) as

$$\begin{aligned}&w_{i,j+1} =\frac{1}{\left( {1+c\Delta t} \right) \Delta x^{2}}\left\{ \left( {1+\alpha S\Delta t^{2}} \right) w_{i-1,j}\right. \nonumber \\&\quad \left. -\left( {1-c\Delta t} \right) \Delta x^{2}w_{i,j-1} \right. \nonumber \\&\quad \left. +\left( {2\Delta x^{2}-2\Delta t^{2}-2\alpha S\Delta t^{2}} \right) w_{i,j} \right. \nonumber \\&\left. \quad +\left( {\Delta t^{2}+\alpha S\Delta t^{2}} \right) w_{i+1,j} -8\alpha fS\Delta t^{2}\Delta x^{2} \right\} \end{aligned}$$
(57)

where S is the integral term in the cable equation and is obtained by the Simpson’s integral rule

$$\begin{aligned}&S=\int _0^1 {\left( {{y}'{w}'+\frac{1}{2}{w}'^{2}} \right) \hbox {d}x}\nonumber \\&\quad \approx \frac{\Delta x}{3}\left\{ {s_0 +2\sum _{i=1}^{n/2-1} {s_{2i} } +4\sum _{i=1}^{n/2} {s_{2i-1} } +s_n } \right\} \nonumber \\&s_i \buildrel \Delta \over = 4f\left( {1-2\Delta x i} \right) \frac{w_{i+1} -w_{i-1,j} }{2\Delta x}\nonumber \\&\quad +\frac{1}{2}\left( {\frac{w_{i+1} -w_{i-1,j} }{2\Delta x}} \right) ,i=0,1,\cdots n \end{aligned}$$
(58)

And the support-induced boundary excitation, Eq. (2), i.e., is discretized as

$$\begin{aligned} w_{0,j} =0,\quad w_{n,j} =Z_0 \cos \left( {\varOmega \;t_j } \right) ,\quad t_j =j \Delta t \end{aligned}$$
(59)

We split the cable into 1000 segments, i.e., the space step \(\Delta x=0.001\), and set the time step \(\Delta t=0.0001\). To make the responses reach steady, the total simulation time T is chosen long enough and we have to admit that the simulation is really time-consuming (The number of time steeping \(N=T/\Delta t\) ranges from 4e6 to 1.5e7 in our simulation, depending on the guessed initial conditions each time.). After the cable’s steady responses are obtained, we compare the numerical results to the approximate analytical ones by two complemental approaches.

The first approach is to extract modal amplitudes and frequencies from the numerical multimodal time history responses using the fast Fourier transformation technique (FFT) and then compare the extracted modal quantities with those frequency response diagrams based upon the modulation equations.

The second approach is to reconstruct cable’s time history responses using the approximate analytical modal results from the modulation equations. And these reconstructed time history responses are then compared with those responses obtained directly by the finite- difference program.

5.4 Results and discussions

We calculate the cable’s triad and two-to-one resonant coefficients and corresponding boundary coefficients in Tables 1 and 2, respectively. (Note that \(\varLambda _{3}\) in Table 1 is actually the boundary coefficient associated with \(\omega _{7}\), as the triad resonant modes \(\omega _{1},\, \omega _{3}, \omega _{7}\) have been denoted by \(\omega _{1},\, \omega _{2}, \omega _{3}\) in our theoretical formulations.)

Table 1 Cable’s triad resonance coefficients and boundary resonance coefficients \((\alpha =760)\)
Full size table
Table 2 Cable’s boundary resonance coefficient and 2:1 resonant nonlinear coefficients \((\alpha =760,\, \lambda =9.26, \,\sigma _{1}=0.005)\)
Full size table

In the following figures, both the approximate analytical results from the multiple scale method(MSM) and the finite-difference method(FDM) are presented. The stable and unstable equilibrium solutions from MSM are denoted by solid and dotted lines, respectively. And the results from FDM are represented by filled circles.

Frequency responses for triad mode resonance, with detuning parameter \(\sigma _{1}=-0.0005({\sim }0)\) and \(-0.05({<}0)\), are illustrated in Figs. 3 and 4, respectively. In both cases, the single-mode equilibrium solutions lose stability and bifurcate into stable triad mode coupled solution at points PF1 and PF2, i.e., pitchfork bifurcations. These stable triad coupled solutions turn unstable through saddle-node bifurcations at SN1 and SN4, and regain stability finally at SN2 and SN3, again through saddle-node bifurcations. It is noted that the frequency response diagram is nearly symmetric for \(\sigma _{1}=-0.0005\sim 0\), while bending to the left or the left for \(\sigma _{1}=-0.005<0\). Our further numerical simulations(not shown) also indicate that the frequency response diagram would bend to the right, if a positive detuning parameter is chosen, say \(\sigma _{1}=0.005>0\).

Fig. 3
figure 3

Typical frequency responses for triad mode interactions with boundary resonance: \(\sigma _{1}=-0.0005,\,Z_{0}=0.000008,\, \mu _{i}=0.02\)

Full size image
Fig. 4
figure 4

Typical frequency responses for triad mode interactions with boundary resonance \(\sigma _{1}= -0.05,\, Z_{0}=0.000008,\, \mu _{i}=0.02\)

Full size image

Also shown in Figs. 3 and 4 are modal quantities extracted from the results of the finite-difference method(FDM), denoted by filled circles. We note that in the main parameter domain, the agreement between our approximate analytical results(using MSM) and those from FDM is satisfactory. Note that in both Figs. 3 and 4, the left-most \((\sigma _{2}=-0.045)\) numerical results from FDM are attractive to cable’s single-mode solution, rather than the triad coupled one.

Furthermore, in Figs. 5 and 6, typical time history responses obtained by FDM and those reconstructed from MSM’s results are also compared. For Fig. 5, both the response amplitude and corresponding power spectrum, coincide very well, except for the phases of time history responses.

Fig. 5
figure 5

Typical time history responses and power spectrum for triad interaction under boundary resonance: \(\sigma _{1}=-0.0005,\, \sigma _{2}=0.0,\, Z_{0}=0.000008,\, \mu _{i}=0.02\)

Full size image
Fig. 6
figure 6

Typical time history responses and power spectrum for triad interaction under boundary resonance: \(\sigma _{1}= -0.05, \,\sigma _{2}= 0.045,\, Z_{0}=0.000008,\, \mu _{i}=0.02\)

Full size image

We point out that there is no need to be bothered by the phase issue and actually the phase difference of time responses can be expected. This is because different initial conditions used by the simulation program, would lead to different phases of the steady responses, even though whose amplitude and spectrum are the same. This is also pointed out by Srinil and Regea [43]. Even more, physically, it is impossible to compare these two kinds of time responses at the same or synchronized time, as the MSM-reconstructed one is a born steady response, while the finite-difference program should run for a long enough time to damp the transient before reaching steady responses. Therefore, in our paper, for the illustration purpose, the duration time for the MSM-reconstructed response is fixed as [0, 10], and that for the FDM-produced response is chosen carefully after the transient has been damped out, with a fixed length of 10, say [890, 900] in Fig. 5 and [1490, 1500] in Fig. 6.

We note that the agreement in Fig. 6 is less satisfactory. Actually, we have to admit that, for both modal quantities and time history responses, as the detuning parameters \(\sigma _{1}\) and \(\sigma _{2}\) deviates from zero by a considerable amount, say \(\sigma _{1}= -0.05\) and \(\sigma _{2}= 0.045\) in Fig. 6, (recall that the multiple scale expansion requires both \(\sigma _{1}\) and \(\sigma _{2}\) to be small), our reduced models get more challenged, this is indicated in Figs. 4 and 6. A higher-order multiple scale expansion would improve such a situation. Therefore, in the following study for 2:1 resonance, we would use the reduced model derived by a second-order multiple scale expansion.

The frequency responses for two-to-one resonance under boundary/support motions are illustrated in Figs. 7, 8, 9 and Fig. 10, with the support motion amplitudes \(Z_{0}=1.5\hbox {e}{-}5\), 2.0e\(-\)5, and 7.0e\(-\)5, respectively.

For \(Z_{0}=1.5\hbox {e}{-}5\), the response is relatively simple. The responses in the considered parameter domain are all stable and no bifurcation is found. The agreement between our approximate results(denoted by MSM) and those numerical results from FDM is very good, in the sense of both the modal quantities and the time history responses, as depicted in Figs. 7 and 8, validating our reduced models based on the boundary modulation concept and multiple scale expansion.

Fig. 7
figure 7

Typical frequency responses for triad mode interactions with boundary resonance \(\sigma _{1}= -0.005, \,Z_{0}=0.000015, \,\mu _{i}=0.02\)

Full size image
Fig. 8
figure 8

Time history responses and power spectrum for triad interaction under boundary resonance \(\sigma _{1}=-0.005, \sigma _{2}=0.00,\, Z_{0}=0.000015, \,\mu _{i}=0.02\)

Full size image

For \(Z_{0}=2.0\hbox {e}{-}5\), different from the previous case, bifurcation and instability arise in the frequency response. We note form Fig. 9 that the response turns unstable through a saddle-node bifurcation at SN1 and then regains stability at SN2, again, through a saddle-node bifurcation. Also shown in Fig. 9 are the extracted modal quantities using results of the FDM, which confirm our approximate analytical results by the MSM.

Fig. 9
figure 9

Typical frequency responses for 2:1 interaction with low-frequency boundary resonance: \(\sigma _{1}=0.005, \,Z_{0}=0.00002, \,\mu _{i}=0.02\)

Full size image

Furthermore, in Fig. 10, we present the time history responses and power spectrum, for both those reconstructed from the MSM, and those obtained directly by the FDM, which again agree with each other very well.

Fig. 10
figure 10

Typical time history responses and power spectrum for 2:1 interaction under boundary resonance: \(\sigma _{1}=0.005,\,\sigma _{2}= -0.03,\, Z_{0}=0.00002, \,\mu _{i}=0.02\)

Full size image

Besides that, although the above frequency response diagrams characterize the dominated two-to-one resonant responses, another interesting feather concerning the response component of zero-frequency is neglected, which is contained in the time history responses of Fig. 10. We note that this is captured by both our approximate analytical method and the finite-difference method. We point out that this component corresponds to the drift term in the 2nd-order solutions of the cable’s responses, which would not occur if only a first-order expansion was sought.

As the support motion amplitude increases further, say, \(Z_{0}=7.0\hbox {e}{-}5\), the frequency response diagram becomes more complex and more bifurcations arise. Explicitly, from Fig. 11, we note that the response becomes unstable through a saddle-node bifurcation at SN1 and then regains stability at the response peak through another saddle-node bifurcation; then, the response is reduced, and loses stability at the saddle-node bifurcation point SN2 and regains stability finally at SN3, again through a saddle-node bifurcation.

Fig. 11
figure 11

Typical frequency responses for 2:1 interaction with low-frequency boundary resonance: \(\sigma _{2}=0.005, \,Z_{0}=0.00007, \,\mu _{i}=0.02\)

Full size image

Also, in both Figs. 11 and 12, the agreement between our approximate analytical results(denoted by MSM) and those numerical results from FDM is satisfactory, in the sense of both the modal quantities and the time history responses, which validates again our reduced models established by the multiple scale expansion and boundary modulations.

Fig. 12
figure 12

Typical time history responses and power spectrum for 2:1 interaction under boundary resonance: \(\sigma _{1}=0.005, \,\sigma _{2}= -0.05, \,Z_{0}=0.00007, \,\mu _{i}=0.02\)

Full size image

However, one more warning is that, we have not verified the MSM’s results larger than \(a_{1}=2\hbox {e}{-}3\), or above the dash-dot line, as indicated in Fig. 11 (The corresponding \(a_{2}\) branch is also not verified.).

Firstly, we have to admit that it is difficult to find stable solutions larger than \(a_{1}=2\hbox {e}{-}3\). This is because the numerical solutions are always attracted to the lower branch in the simulations, rather than the upper branch. Note that two branches of stable solutions of the modulation equations exist in this domain.

Secondly, noting SN1 occurs at \(\sigma _{2}=-0.105<-0.1\), we can therefore find a unique stable solutions at \(\sigma _{2}=-0.1\) using the FDM. However, the agreement turns out to be unsatisfactory. Our explanation is that the solution amplitude is too large to admit a reasonable multiple scale expansion. In other words, although our reduced models (modulation equations) are derived in a correct way, their accuracy is not reliable in the domain with large response amplitudes. Recall that our multiple scale expansion is reasonable in an asymptotic sense, requiring both the response amplitudes \(a_{1},\, a_{2}\), and the detuning parameters \(\sigma _{1},\, \sigma _{2}\) to be small. Therefore, for the present example, we do not recommend our reduced model in the domain \(a_{1}>2\hbox {e}{-}3\).

6 Summary and conclusions

Based upon the boundary resonant modulation concept, cable’s triad and two-to-one mode interactions under support motions are solved in a unified way, through attacking the continuous dynamic equations directly by the multiple scale method. Boundary resonance coefficients are introduced to characterize this boundary effect, and their analytical forms are presented. It is found that, both cable’s mode function and initial sag affect this boundary coefficient. After obtaining modulation equation’s equilibrium solutions (corresponding to cable’s periodic oscillation), frequency response diagrams are constructed by the numerical continuation method, with stability and bifurcation properties determined. All these approximate analytical results are verified by the finite- difference method, therefore validating our reduction approach based upon resonant boundary modulations.