1 Introduction

Cable structures play an important role in many engineering fields, such as civil, ocean, and electrical engineering. In the last decades, the span length of cable-supported structures has considerably increased. For example, the span lengths of some cable-stayed bridges are over 1000 m due to new materials and building technologies used in bridge erection [1]. However, cables are susceptible to support motion and often exhibit large amplitude vibration due to their large flexibility, and relatively small mass and damping. These features may make cable stress undue, produce fatigue, and also make people uncomfortable. Therefore, understanding the dynamics of cable structures and developing mitigation method of vibration are very important.

The dynamic behavior of cables is very complicated and has attracted increasing attention in mathematics, mechanics, and engineering. Much work has been conducted in terms of nonlinear in-plane vibrations of cables subjected to forced and/or parametric excitation in the past. Earlier studies [2–5] were mainly focused on forced vibrations. Yamaguchi and Migata [2] studied in-plane dynamic behavior of a cable under harmonic excitations. Benedettini and Rega [3] obtained an approximate solution of the in-plane vibration in primary resonance under harmonic excitation. Rega and Benedettini [4, 5] studied the superharmonic resonances and subharmonic resonances of an elastic cable subjected to a planar forced excitation. Recently, some studies [6–9] have been conducted with stay cables under combined parametric and forced excitations. The cables of cable-stayed bridges subjected to combined parametric and forced excitations (support motion) were studied theoretically by Uhrig [6]. Lilien and Pinto Da Costa [7] predicted that parametric excitation was probable due to the presence of low frequencies in the girder and the cable stays. Warnitchai et al. [8] proposed a nonlinear dynamic model with quadratic and cubic nonlinear couplings for a cable under small support motion. The global and local modes were firstly used to study the quasi-static motions and modal motions in their work. The chaotic dynamics and global bifurcations of a suspended elastic cable under combined parametric and forced excitations were investigated by Zhang and Tang [9]. Recently, the dynamic behaviors of stay cables in cable-beam structure members and cable-stayed bridges have also been studied experimentally and analytically [10–16]. Berlioz and Lamarque [10] devoted to the theoretical and experimental investigations of a stay cable subjected to axial motion, and used experimental observation to validate the theoretical models for primary resonance and subharmonic resonance. Feng and Gao [11] theoretically explored the nonlinear vibration for coupled structure of cable-stayed beam. Ren and Gu [12] investigated the parametric vibration of stayed cable-bridge deck systems, taking into account of cable sag, gravity component in string direction and variation of cable tension along the cable. Subsequently, Fujino et al. [13] developed a 3-dof model of cable-stayed-beam and studied its auto parametric resonance. Costa et al. [14] dealt with the oscillations of bridge stay cables by using theoretical model and laboratory tests. Furthermore, Berlioz and Lamarque [15, 16], Rega et al. [17, 18] studied the nonlinear dynamic behavior of a stay cable by experiment, which was confirmed by theoretical results of 1-, 2- and 4-dof models. Although there are many works published, the dynamics of stay cable, especially the nonlinear dynamics, is still not well understood and there are few papers which provided the suggestion for mitigation of large vibration of stay cable from the point of view of nonlinear dynamic theory.

In the present work, we study the in-plane nonlinear dynamics of a stay cable, especially, its first order symmetric in-plane mode (single-mode model) induced by support motion. The effects of initial tension force, material, stay angle and structural damping of cable, excitation frequency, and amplitude on the dynamic behavior of the stay cable subjected to combined parametric and forced excitations are examined on the condition of subharmonic resonance. Base on the dynamic analysis of the stay cable, some meaningful suggestions for vibration mitigation are also given.

2 Governing equations

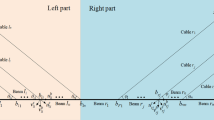
The geometrical configuration of the cable-beam considered is shown in Fig. 1(a). The static configuration of the cable can be described by a parabolic profile y(x c )=4fx c (l−x c )/l 2 [19], which is attained under the influence of gravity. A Cartesian coordinate system Ox c y c is chosen to describe the motion of the stay cable, with the origin O placed at the right support of the cable. The dynamic model of the cable-beam structure is shown in Fig. 1(b).

Fig. 1
figure 1

Cable-beam structure configuration: (a) static state, and (b) dynamic model

Full size image

For brevity, we assume that the bending, torsion and shear rigidities, and material nonlinearity of the cable are neglected. In addition, it is assumed that the motion of the beam can be simplified as a harmonic excitation to the cables. Thus, applying Hamilton’s principle, we can obtain the equations governing the global motion of the cable. These equations can be written as [20–22]

(1)
(2)

where u c and v c are axial and in-plane transverse displacements of the cable measured from the static equilibrium at point x c and time t. The dot indicates the differentiation with respect to time t. Equations (1) and (2) describe the general vibration of the stay cable, which is defined by the Young’s modulus E c , cross sectional area A c , mass per unit length m c , static cable tension H, coordinate x c , and structural damping coefficients c u and c v .

From Fig. 1, it can be seen that the boundary conditions on the axial and in-plane transverse displacements u c and v c can be given by

(3a)
(3b)

Assume that the vertical excitation to the stay cable, induced by the motion of the beam, is given by

$$ Z(t) = B\cos \omega _{b}t. $$
(4)

There exist the following connection conditions between the stay cable and vertical excitation:

(5a)
(5b)

For real stay cables, the dynamic displacement components u c and v c are of order \(O(\bar{\varepsilon} f^{2} / l)\) and \(O(\bar{\varepsilon} f)\), respectively, where \(\bar{\varepsilon}\) is a small parameter of the order of the response amplitude. The interactions between the transverse displacement v c and the longitudinal displacement u c are negligible. Thus, the longitudinal inertia forces \(m_{c}\ddot{u}_{c}\) and damping force \(c_{u}\dot{u}_{c}\) can be neglected in Eq. (1). For such a case, Eq. (1) can be written as

$$ \frac{\partial u_{c}}{\partial x_{c}} + \frac{\mathrm{d}y}{\mathrm{d}x_{c}}\frac{\partial v_{c}}{\partial x_{c}} + \frac{1}{2} \biggl( \frac{\partial v_{c}}{\partial x_{c}} \biggr)^{2} = e(t). $$
(6a)

After some simple manipulations and integrating both sides of Eq. (6a), one can obtain

$$ u_{c}(0,t) - u_{c}(l_{c},t) + \int _{0}^{l_{c}} \biggl[ y'v'_{c} + \frac{1}{2} \bigl(v'_{c} \bigr)^{2} \biggr] = l_{c}e(t). $$
(6b)

Substituting Eqs. (3a, 3b) and (5a) into Eq. (6b), we have

$$ e(t) = \frac{Z(t)}{l_{c}}\cos \theta + \frac{1}{l_{c}}\int _{0}^{l_{c}} \biggl[ y'v'_{c} + \frac{1}{2} \bigl(v'_{c} \bigr)^{2} \biggr]\, dx_{c}. $$
(6c)

Equating Eqs. (6a) and (6b) leads to

(6d)

Now, we determine the differential form of Eq. (2) using the Galerkin method. According to the method, the in-plane transverse displacement v c is approximated through the method of separation of variables. Thus, one assumes that

$$ v_{c}(x_{c},t) = Z(t)\sin \theta (1 - x_{c} / l_{c}) + \sin (\pi x_{c} / l_{c})Q(t), $$
(7)

where Q(t) denotes the temporal behavior of v c . Note that in this equation, we have taken into account the parametric excitation of first order symmetric in-plane mode of the stay cable, and the connection condition (5b) between the stay cable and vertical excitation.

Substituting Eqs. (4), (6d), and (7) into Eq. (2), we can obtain a nonlinear ordinary differential equation

(8)

where l has been used to replace l c for brevity.

The nondimensional variables are defined as following:

(9)

Substituting them into Eq. (8) yields

(10)

where

In Eq. (10), the effect of c v on the parametric excitation has been neglected because it is very small for the vertical excitation. This equation contains both quadratic and cubic nonlinearities. Generally speaking, the quadratic nonlinearity results in softening characteristics and the cubic nonlinearity induces hardening characteristics of a cable [4]. The above equation shows that the quadratic nonlinearity term is a 3=24αλ/π and the cubic nonlinearity term is a 4=π 2 α/4. Quadratic nonlinearity vanishes in the case of a very taut cable (λ→0). It should be noted that ω 0 is the first order natural frequency of a cable only if the cable is extremely stretched (λ=0) and the excitation amplitude is very small (B≈0). a 3 and a 4 can also be expressed as 3ρgEA 2 lsinθ/(πH 2) and π 2 EA/4H, respectively. It can be seen from these expressions that the initial tension force H and the material constant E (elastic modulus) have an important influence on the quadratic and cubic nonlinearities. In addition, the inclination angle θ plays a significant role in quadratic term. The effect of these parameters on the nonlinear dynamics will be studied quantitatively by the multiple scales perturbation method in the following sections.

3 Perturbation analysis

In this section, the method of multiple time scales is used to obtain the modulation equations governing the nonlinear vibration of the stay cable. Let T i =ε i τ, where ε is a small bookkeeping parameter. Using the following scaling scheme,

Equation (10) can be written as

(11)

Considering T i =ε i τ, we have the differential operators

(12)

where D i =∂/∂T i .

The solutions of Eq. (11) can be expanded in the following form in terms of the small positive parameter ε:

(13)

To determine q j (j=0,1,2), we substitute Eqs. (12) and (13) into Eq. (11) and let the coefficients of ε 1, ε 2, and ε 3 be zero, respectively. Thus, one obtains

Order ε 1

$$ D_{0}^{2}q_{0} + \omega _{c}^{2}q_{0} = 0. $$
(14)

Order ε 2

$$ D_{0}^{2}q_{1} + \omega _{c}^{2}q_{1} = - f_{3}q_{0}^{2} - f_{5}\cos \varOmega \tau - f_{6}\cos 2\varOmega \tau. $$
(15)

Order ε 3

(16)

The solution of Eq. (14) for the first-order in-plane motion can be expressed as

$$ q_{0} = A(T_{2})\exp (i\omega _{c}T_{0}) + \mathit{cc}, $$
(17)

where \(\exp (i\omega _{c}T_{0}) = e^{i\omega _{c}T_{0}}\), and cc represents the complex conjugate of other terms at the right- hand side of Eq. (17).

Substituting Eq. (17) into Eq. (15) gives

(18)

where \(\varGamma _{1} = (\varOmega ^{2} - \omega _{c}^{2})^{ - 1}\), \(\varGamma _{2} = (4\varOmega ^{2} - \omega _{c}^{2})^{ - 1}\), \(\bar{A}\) is the complex conjugate of A, and cc indicates the complex conjugate of the preceding terms at the right-hand side of Eq. (18).

Substituting Eqs. (17) and (18) into Eq. (16) yields

(19)

It has been well known that in a cable-stayed bridge, the motions of the stay cable may be large when the excitation frequency is close to the natural frequency of the stay cable (primary resonance) or to the twice of the natural frequency (subharmonic resonance). Using Eq. (19), we can obtain the amplitudes for the cases with the primary resonance and subharmonic resonance for the case considered here as follows.

Case 1

Primary resonance (Ω≈ω c )

To express the proximity of Ω to ω c , we introduce a detuning parameter σ, which gives

$$ \varOmega = \omega _{c} + \varepsilon ^{2}\sigma. $$
(20)

Substituting Eq. (20) into Eq. (19) and eliminating the secular terms in Eq. (19), we can obtain the solvability condition

(21)

To solve Eq. (21), A is expressed in the polar form, that is

$$ A = \frac{1}{2}a\exp (i\beta ), $$
(22)

where \(i = \sqrt{ - 1}\), a and β are the amplitude and phase angle of A, and they are the functions of T 2.

Substituting Eq. (22) into Eq. (21) yields

(23)

where θ=σT 2−β, and the prime (′) indicates the differentiation with respect to T 2.

Separating the real and imaginary parts of the left hand side of Eq. (23), and after some simple manipulations, the following averaged equations are obtained:

(24)
(25)

The above equations are the reduced equations for the planar motion of the stay cable, which is directly excited by both forced excitation and parametric excitation while the primary resonance occurring. For steady state, a′=θ′=0. The corresponding nonlinear algebraic equations can be solved numerically to obtain the fixed-point of response of the system. For single planar motion, the steady solution of Eqs. (24) and (25) can be obtained using the continuation technique [23].

Case 2

Subharmonic resonance (Ω≈2ω c )

In this case, there exists the following relation:

$$ \varOmega = 2\omega _{c} + \varepsilon ^{2}\sigma, $$
(26)

where σ is the detuning parameter.

Substituting Eq. (26) into Eq. (19) and eliminating the secular terms, we obtain the following complex equation describing the variation of complex amplitude A with the scale T 2:

(27)

Substituting Eq. (26) into Eq. (31) yields

(28)

where θ=σT 2−2β.

Equating the real and imaginary parts to zero, the following two equations are obtained:

(29)
(30)

Equations (29) and (30) are the reduced equations governing the planar motion of the stay cable excited by the combined parametric and forced excitations when the subharmonic resonance occurs.

Letting a′=θ′=0, and then solving Eqs. (29) and (30), we can obtain the solution of the system at the steady state

$$ a = 0\quad \mbox{or}\quad a = \sqrt{\frac{\sigma \omega _{c} \pm 2\sqrt{\chi ^{2} - \mu _{c}^{2}\omega _{c}^{2}}}{2\kappa}}, $$
(31)

where \(\kappa = 3f_{4} / 8 - 5f_{3}^{2} / 12\omega _{c}^{2}\), and χ=(f 1/4+Γ 1 f 3 f 5/2). From Eq. (31), it can be seen that the response amplitude of the cable depends on the detuning parameter, excitation amplitude, damping and initial tension.

4 Stability of steady state response

Due to the nonlinearity, the response may be multivalued for an excitation amplitude or frequency. However, not all solutions must be stable. Therefore, it is necessary to examine the stability of the steady state solution. By directly perturbing the reduced equations, one can determine the stability of the nontrivial steady state solutions. But as the reduced equations have the coupled term \(a\theta '_{1}\), the stability of the trivial state cannot be determined by directly perturbing equations. To overcome this difficulty, we introduce the following transformations:

$$ r = a\cos \theta,\qquad s = a\sin \theta. $$
(32)

Thus, directly perturbing the reduced equations in the Cartesian form, one can determine the stability of the trivial steady state solutions as the couple term is uncoupled.

For brevity, only the stability problem for the subharmonic resonance is discussed here. The primary resonance can be tackled using the similar procedure. Substituting Eq. (32) into Eqs. (29) and (30), the following equations can be obtained:

(33a)
(33b)

To determine the stability, one perturbs the steady state solution. Let

(34a)
(34b)

where r 10 and s 10 are the steady state solutions, Δr 1 and Δs 1 represent the perturbation values. Substituting Eqs. (34a), (34b) into Eqs. (33a), (33b) and retaining linear terms in the perturbation, one obtains

$$ \bigl\{ \Delta r'_{1},\Delta s'_{1} \bigr\} ^{\mathrm{T}} = [\mathbf{J}_{C}]\{ \Delta r_{1}, \Delta s_{1}\} ^{\mathrm{T}}, $$
(35)

where T denotes the transpose of a matrix, and [J c ] is the Jacobian matrix whose eigenvalues can be used to determine the stability and bifurcation type of the system.

5 Numerical examples and discussion

The numerical investigations are carried out to understand the nonlinear dynamic response of the stay cable subjected to parametrical and forced excitations. The frequency-response curves and excitation-response curves in the primary resonance and subharmonic resonance are considered. The effects of the initial tension force, damping and inclination angle of stay cable, and the excitation frequency and amplitude on the in-plane behavior of the stay cable are discussed.

5.1 Subharmonic resonance of steel cables

In a cable-stayed bridge, the lengths of cables are different. So, we select a short cable (C1) and a relatively long cable (C2) as specimens. Their parameters are shown in Table 1. The steady state responses of the system subjected to the primary resonance are obtained by solving Eqs. (24) and (25) numerically using the continuation technique [24] and the Newton–Raphson scheme. The relevant frequency-response curves and excitations-response curves are obtained from Eq. (31) when the subharmonic resonance is considered. In the numerical computation, the small bookkeeping parameter ε is set to 1. In the following figures, the solid and broken lines stand for the stable and unstable branches, respectively.

Table 1 Parameters of steel cables
Full size table

Figure 2 shows the excitation-response curves of cable C2 under the primary resonance and subharmonic resonance, respectively. It can be seen that there exists a considerable difference between the two excitation-response curves. When the excitation frequency is close to 2.0, the subharmonic resonance can be observed for a very small excitation quantity. The response amplitude reaches 0.0056 when the excitation is 0.000034. As the excitation is gradually increased, the response amplitude rises rapidly. With the increasing of excitation amplitude, the range of excitation frequency required for the onset of subharmonic resonance enlarges as well, which is dangerous for the safety of stay cable. For instance, as the excitation amplitude increases from 0.0002 to 0.0025, the frequency range increases to 1.85–2.15 from 1.988–2.012, as shown in Figs. 2a and b. However, when the excitation frequency is near to 1.0, the primary resonance can occur only if the excitation amplitude reaches 0.00865, and the response amplitude is fairly small relative to that induced by the subharmonic resonance. With the increase of excitation, the response amplitude increases very slowly. This indicates that the primary resonance is not easy to occur in actual engineering. Therefore, the subharmonic resonance of stay cable is more dangerous than the primary resonance, and will be discussed in more detail in the following.

Fig. 2
figure 2

Excitation-response curves of cable C2 when σ=0.01 and H=8700 kN. (a) and (b) show the frequency-response curves of the subharmonic resonance for z=0.0002 and z=0.0025, respectively

Full size image

To understand the effect of initial tension force on the dynamic behaviors of the stay cable, Fig. 3 displays the frequency-response curves of cables C1 and C2 under the subharmonic resonance with different initial tension force. It can be observed that cable C2 exhibits a mildly softening behavior and the response amplitude is relatively large when the initial tension force is H c2 (=7700 kN, given in Table 1). When the initial tension force is increased to 125 % H c2, the frequency-response curve bends to the right and exhibits a severely hardening behavior. When the initial tension force is decreased to 25 % H c2, the frequency-response curve does not change the direction of bending, but the response amplitude falls sharply. Cable C1 has the similar variation trend with the change of initial tension force. The cable exhibits a hardening behavior initially, and changes to a severely softening one when the initial tension force is decreased to 25 % of its initial value. These results indicate that for different initial tension force, the dynamic behavior of cables in a cable-stayed bridge will be different. Unreasonable initial tension force may result in a mildly softening/hardening behavior and a large vibration. Therefore, in the design of stay cable, it is very important to control the initial tension, which can be done by adjusting the cable inclination angle and spacing.

Fig. 3
figure 3

Frequency-response curves for different initial tension force H when ξ=0.001 and z=0.0001: (a), cable C1 and (b), cable C2

Full size image

Furthermore, Fig. 3 gives the sophisticated bifurcation diagram when the excitation frequency ratio Ω is used as a control parameter. For all considered initial forces, there exist supercritical and subcritical pitchfork bifurcations. For example, for the case with the initial forces H c1 of cables C1, as seen in Fig. 3a, the supercritical pitchfork bifurcation occurs at Ω=1.996, while the subcritical pitchfork bifurcation occurs at Ω=2.004. When Ω<1.996 only one stable trivial solution exists. When Ω is in the interval 1.996<Ω<2.004, there are a stable nontrivial branch (i.e., the supercritical parabolic branch) and an unstable trivial branch. When Ω>2.004, there coexist a stable trivial branch, a stable supercritical parabolic branch and an unstable subcritical parabolic branch. Corresponding to the subcritical pitchfork bifurcation point (at Ω=2.004), there is a critical point C on the supercritical parabolic branch, which divides the supercritical parabolic branch into two sections. The lower section is the response amplitude of large cable vibration under subharmonic resonance in the absence of initial deflection, which is dangerous to cable because it is easy to occur. The upper section is the response amplitude of excessive cable vibration under subharmonic resonance on the condition that the initial deflection is greater than or equal to the corresponding response amplitude. The excessive vibration may occur when the stay cable is simultaneously excited by support motion and other excitation such as wind. For such cases, to control the excessive vibration, parametrical vibration, and wind vibration should be treated simultaneously.

Figure 4 plots the frequency-response curves with different inclination angles of cables C1 and C2. It can be seen that the interval between the supercritical and subcritical pitchfork bifurcation points shrinks with the inclination angle increasing from 55∘ to 65∘. The influence of inclination angle on the dynamic behavior for short cable C1 is not susceptible as seen in Fig. 4a, whereas it is sensitive for long cable C2 as shown in Fig. 4b. With increasing inclination angle, the response amplitude of the cable decreases. In particular, when Ω=2, the response amplitudes are 0.0607, 0.0169, and 0.0113 at θ=55∘, 60∘ and 65∘, respectively. The decrease of response amplitude is due to the fact that the increase of the quadratic nonlinearity term in the governing equation. Therefore, we can moderately change the stay angle of long cable to suppress the large cable vibration in the design of the inclination angle of stay cable.

Fig. 4
figure 4

Frequency-response curves for different stay angle θ when ξ=0.001 and z=0.0001: (a), cable C1, and (b), cable C2

Full size image

Figure 5 considers the effect of damping coefficient on the dynamic behaviors of the stay cable under the subharmonic resonance. For the two cables, when the damping coefficient ξ is relatively low, the excitation amplitude z required for the occurrence of subharmonic resonance is quite low. For example, when ξ=0.0001, z is 0.000022 for cable C1. The response amplitude is almost 200 times greater than the excitation amplitude. When the damping coefficient increases to 0.01, the threshold value of excitation amplitude increases to 0.0008 for cable C1. This indicates that increasing damping can reduce the possibility of the occurrence of subharmonic resonance. Therefore, damping is a factor that can be used to reduce cable vibration, which is similar to that obtained by Costa et al. [14]. However, the efficiency of damping for mitigating vibration of long cable C2 falls. In fact, for the long cable C2, increasing the damping coefficient from 0.0001 to 0.01 causes the threshold value of excitation amplitude to increase to 0.0004 only. Furthermore, when the excitation amplitude is relatively large, increasing damping cannot prevent the large amplitude vibrations induced by the subharmonic resonance. When the damping coefficient increases from 0.0001 to 0.01, for z=0.001 the response amplitude of the short cable C1 decreases only a little, and that of the long cable C2 has almost no change.

Fig. 5
figure 5

Excitation–response curves for different damping coefficient ξ when σ=0.01: (a), cable C1, and (b), cable C2

Full size image

It is well known that with the span of cable-stayed bridge increasing, the efficiency of damping for mitigating cable vibration is increasingly important. However, only small damping can be added if the attachment point is close to bridge deck. For long cables, the relative attachment point becomes increasingly smaller, and passive damping may become insufficient for reducing vibration of stay cable. Here, we propose a suggestion that the structural damping might be increased by adding some visco-elastic polymer when the cable is manufactured.

Furthermore, it can be observed in Fig. 5 that the saddle node bifurcations occur at points P1, P2, and P3 when the system has different damping levels. For given σ and ξ, the jump phenomena occur at one of these points. As the excitation amplitude z reaches a small threshold value, the subharmonic resonance occurs and the response amplitude a s of the stay cable increases abruptly from zero. Taking ξ=0.01 as an example, as z is gradually increased from zero, the trivial solution loses its stability at z=z 2 due to a symmetry-breaking bifurcation. Here, locally, there are no other stable solutions for z>z 2, forcing the system to jump in a fast dynamic transient to D, then the response amplitude continues to increase with the growing of excitation amplitude as shown in Fig. 5a. Additionally, if z is gradually decreased from infinity, the response amplitude decreases until point P3, and then the system is forced to jump from P3 to zero. There coexist a stable nontrivial branch, a stable trivial branch and an unstable nontrivial branch in the interval z 1<z<z 2. It is interesting that point D in the stable nontrivial branch corresponding to excitation amplitude z 2 divides the stable nontrivial branch into two parts. The lower part is called large vibration, which depends on the initial deflection, where as the initial deflection is greater than or equal to the corresponding response amplitude the large vibration will occur. However, the upper section is called excessive vibration, and it mainly depends on excitation amplitude in the absence of initial deflection. Therefore, it is worth noting that the lower section corresponding to the intermediate region z 1<z<z 2 is dangerous area since the lower excitation amplitude can stimulate large vibration, and the upper section also should be controlled by mitigating the amplitude of deck motion because the occurrence of subharmonic resonance is not related to the initial deflection of cable.

5.2 Effect of material properties

Although carbon fiber reinforced polymers (CFRP) are increasingly making their way into the field of bridge engineering [25], there is no literature studying the nonlinear dynamic behavior of the new material cable. Here, we consider two kinds of CFRP cables, one (CFRP1) is a material with high strength (2550 MPa) and low Young’s modulus (160 GPa), the other (CFRP2) is of high strength (3550 MPa) and high Young’s modulus (400 GPa). Their other main parameters are the same as those of the steel cables, being listed in Table 2. In the following figures, like the above figures, the solid and broken lines stand for the stable and unstable branches, respectively. Similar to the steel cables, the dynamic behaviors of the CFRP cables are determined using the aforementioned nonlinear dynamic theory.

Table 2 Parameters of CFRP cables
Full size table

Figure 6 shows frequency-response curves for steel, CFRP1 and CFRP2 cables. For the short cable as shown in Fig. 6a, compared with the steel cable, CFRP1 exhibits almost similar behavior, especially in response amplitude. CFRP2 cable has a slightly lower excitation frequency region and a vibration with higher response amplitude. Overall, the new material is not competitive in reducing the cable vibration for the short cable. However, the influence of material on the dynamic behavior of the long stay cable under the subharmonic resonance is relatively large, as shown in Fig. 6b. When CFRP 1 or CFRP2 cable is used to replace the steel cable, the softening character is changed to hardening one and the response amplitude has a large decline. The reason for the decline is the decreasing of the quadratic nonlinearity term in the governing Eq. (10). From the expression of the quadratic nonlinear term a 3=3ρgEA 2 lsinθ/(πH 2), it is clear that, although the Young’s modulus has an almost 100 % increase, from 210 GPa to 400 GPa, the density of the CFRP cable declines to almost 20 % of the steel cable, and the area of the cross section of the cable falls 50 %, simultaneously. This makes the system trend to have a severely hardening behavior. Therefore, CFRP cable has a better dynamic behavior than that of steel cable at this point, and is therefore a good alternative of steel cable for large span bridge.

Fig. 6
figure 6

Frequency-response curves for three kinds of materials when ξ=0.001 and z=0.0001: (a), cable C1, and (b), cable C2

Full size image

Figures 7 and 8 show the excitation-response curves for different material cables. For the CFRP cables, the saddle node bifurcation occurs, similar to the steel cable. For a given damping coefficient ξ=0.001 as shown in Fig. 7a, the response amplitude of the cable jumps suddenly from zero to 0.00834 when the excitation amplitude reaches 0.00075. Further increasing the excitation amplitude leads to a continuous increasing of response amplitude. In the interval between 0.00015 and 0.00075, there coexist a stable nontrivial branch, a stable trivial branch and an unstable nontrivial branch. The two types of CFRP cables have similar dynamic behaviors. Comparing with the steel cable, the short CFRP cables have slightly higher response amplitudes, and there is almost no difference for the long one. Additionally, from Fig. 7a and Fig. 8a, it is obvious that when the damping coefficient is increased to 0.01 from 0.0001, the excitation amplitude threshold value for the subharmonic resonance for the CFRP cables is larger than that for the steel cable, which would contribute to the cable vibration mitigation. However, compared Fig. 7b and Fig. 8b with Fig. 5b, it can be seen that the CFRP cables in the efficiency of damping for reducing subharmonic resonance may not be good as the steel cable. This means that the effect of damping on the large vibration or excessive vibration of CFRP cables under parametric excitation may not be sensitive and should be paid more attention.

Fig. 7
figure 7

Excitation-response curves for CFRP1 when σ=0.01: (a), cable C1, and (b), cable C2

Full size image
Fig. 8
figure 8

Excitation-response curves for CFRP2 when σ=0.01: (a), cable C1, and (b), cable C2

Full size image

6 Conclusions

In the present paper, the non-linear in-plane dynamics of a stay cable subjected to a planar vertical excitation is investigated. The effects of the key parameters such as initial tension force, inclination angle, damping, material of cable, and excitation amplitude and frequency are examined. Some conclusions are drawn as follows.

  • For a stay cable under parametric and forced excitation, primary resonance is more difficult to occur than subharmonic resonance. The excitation amplitude threshold value for primary resonance is relatively larger than that for subharmonic resonance regardless the influence of excitation frequency.

  • The variation of cable tension may lead to the change of the behavior of the cable: from mildly to severely softening or hardening. On the other hand, unreasonable tension force would cause excessive vibration. Therefore, in the design of stay cable, it is very important to control the initial tension force. The unreasonable tension range can be avoided by adjusting cable’s inclination angle and spacing.

  • The large and excessive vibration of stay cable and the corresponding conditions are firstly classified in the present paper. Actually, most of the published works are focused on the large vibration, few of them on the excessive vibration. Through the present work, we note that both of them regarding the vibration mitigation should be paid attention. The stay angle exhibits a considerable effect on the dynamic behavior for large span cable due to the fact that it is sensitive to the quadratic nonlinearity term of the governing equation. Hence, changing the inclination angle of stay cable can contribute to reducing the large vibration.

  • Damping is a factor that can be used to reduce cable vibration, especially, for short stay cables. Increasing damping can reduce the possibility of the occurrence of subharmonic resonance. The efficiency of damping in vibration mitigation for long cables falls. Therefore, we suggest adding some visco-elastic polymer in the manufacture process of cable to increase its damping level.

  • Based on the analysis of the dynamic behavior of the cables with different material properties, CFRP cable should be a good alternative of steel cable for large span bridge. It has a lower sag, a behavior of severely hardening character, and therefore a better dynamic property (namely, a smaller response amplitude).

Based on the results reported in this paper, the nonlinear dynamics of stay cable is affected by many factors. Hence, the vibration mitigation of stay cable under vertical excitation should be conjunct with the control of spacing, inclination, damping and material of stay cable, wind induced vibration and deck motion.