1 Introduction

Methods of minimizing the vibrations consist of avoiding resonance using vibration isolation mountings, and dynamic vibration absorbers [1]. Up to now, there are a number of strategies to control the response of a system such as passive control, active control, semi-active control and hybrid control [2–6]. To achieve perfect performance of a target system, the structures or mechanical systems should be designed to suit different types of loading, such as particularly dynamic and transient loads, and to obtain high static stiffness resulting in a small static deflection and a small dynamic stiffness resulting in a low natural frequency [7, 8]. A large number of papers have been devoted to studying, improving and testing these relatively simple devices in vibration suppression and isolation.

Eissa and Sayed [2] analyzed the vibration control problem of a nonlinear spring–pendulum system subject to harmonic excitation. An active control via negative displacements feedback was performed to solve pendulum vibration problem. Robertson et al. [9] analyzed a magnetic spring for the purposes of load bearing with low stiffness. Gatti et al. [10] investigated the dynamic behaviors of a coupled system which includes a nonlinear hardening system driven harmonically by a shaker. The shaker is presented as a linear system, and the nonlinear part is modeled as Duffing oscillator. Resonant interaction of the system parameters and coexisting steady states are proved analytically and numerically. More recently, Hortan et al. [11] have studied the dynamics of pendulum driven through its pivot moving in both horizontal and vertical directions. They derived approximate analytical expressions representing the position of the saddle-node bifurcation. Liu et al. [12] investigated vibration transmissibility of a passive nonlinear isolator which is constructed by parallel adding a negative stiffness corrector to a linear spring. Their research shows that the nonlinear characteristic, such as softening and hardening stiffness behaviors, depends on the magnitude of the excitation level. Subsequently, an experimental rig [13] is set up to validate their analytical results. Wu et al. [14] proposed a novel magnetic spring with negative stiffness, which possesses the characteristic of high-static-low-dynamic stiffness (HSLDS).

Moreover, a novel configuration of passive stiffness can also comprise a negative stiffness isolator. Le and Ahn [15, 16] designed a vibration isolation structure to improve the vibration isolation effectiveness of a vehicle seat under low excitation frequencies. For easy application, they also give a procedure to minimize the bending of the frequency response curve and reduce the dimensionality of the system. Carrella et al. [7, 8] investigated an isolator, which consisted of mechanical springs providing a positive stiffness, and magnets in an attracting configuration providing a negative stiffness. The isolator can be performed with high-static-low-dynamic stiffness. Zhou and Liu [17] developed a novel vibration isolator with HSLDS characteristics. The natural frequency of the isolator was validated experimentally, and the effectiveness of the isolator for vibration isolation was tested. Tang and Brennan [18] studied another type of HSLDS isolator, which is comprised by a vertical spring and two horizontal springs. Their work validated the advantage of the HSLDS isolator.

Many works have been devoted to the harmonic vibration problem of the compressed air generator [19, 20]. In the present work, the nonlinear vibration characteristic of a compressed air generator, with the similar negative stiffness of that studied by Tang and Brennan [18], is investigated. The main motivation of this work is to investigate the dynamic behavior of a compressed air generator and to provide a new strategy to reduce the vibration of it in practice. Our proposed model is simplified as a suspension mass connected to a vertical spring and two horizontal springs, and a pendulum is added as an unbalance mass of compressor. In this paper, the incremental harmonic balance method (IHBM) in combination with an arc length continuation technique is used to obtain the periodic motion of the present model subject to external harmonic excitation. The stability of the periodic motion is investigated with Floquet theory. The performance of the vibration system with different excitation frequencies and stiffness ratios is investigated. A numerical integration is also adopted to validate the results obtained by IHBM.

2 System model

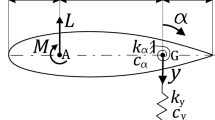
The simple schematic model of a compressed air generator is shown in Fig. 1. In this work, the compressed air generator is simplified as a suspension mass M. The unbalanced mass m due to the generator is modeled as one pendulum hangs from the suspension mass [21]. The unbalanced mass m is connected to the massless rod whose length is \(l_2 \). We define \(\theta \) as the angle displacement of the pendulum. Here, one should note that this angle displacement is very small in practice, but in our model it is not limited as its amplitude is determined by the amplitude of the external excitation. The suspension mass is constrained along the horizontal and vertical directions by two massless rods and springs with total stiffness \(k_x \) and \(k_y \). Here we assume that the spring in the Y direction is always kept vertical. The motion of mass M in the X direction will not affect the deflection of vertical spring. The length of the two rods is both \(l_1 \). Correspondingly, we define x and y as the displacement of the suspension mass along the horizontal and vertical directions, respectively.

Fig. 1
figure 1

Schematic model of pendulum model

Full size image

Let us first consider the suspension mass M. The kinetic energy \(T_M \) yields

$$\begin{aligned} T_M =\frac{1}{2}M\left( {\dot{x}^{2}+\dot{y}^{2}} \right) \end{aligned}$$
(1)

The potential energy becomes

$$\begin{aligned} V_M= & {} Mgy+\frac{1}{2}k_y y^{2}+\frac{1}{2} \left( \frac{1}{2}k_x \left( {x-\tilde{x}} \right) ^{2}\right. \nonumber \\&\left. +\frac{1}{2}k_x \left( {x-\tilde{x}} \right) ^{2} \right) \end{aligned}$$
(2)

here the deformation \(\tilde{x}\) of spring along horizontal direction can be obtained as

$$\begin{aligned} \tilde{x}=l_1 -\sqrt{l_1^2 -y^{2}} \end{aligned}$$
(3)

Similarly, the kinetic energy of mass m can be expressed as

$$\begin{aligned} T_m =\frac{1}{2}m\left[ {\left( {\dot{x}+l_2 \dot{\theta }\cos \theta } \right) ^{2}+\left( {\dot{y}+l_2 \dot{\theta }\sin \theta } \right) ^{2}} \right] \end{aligned}$$
(4)

The potential energy of mass m becomes

$$\begin{aligned} V_m =mgy-mgl_2 \cos \theta \end{aligned}$$
(5)

Combining Eqs.(1) and (4), the total kinetic energy of the system is given by

$$\begin{aligned} T= & {} T_M +T_m =\frac{1}{2}M\left( {\dot{x}^{2}+\dot{y}^{2}} \right) \nonumber \\&+\frac{1}{2}m\left[ {\left( {\dot{x}+l_2 \dot{\theta }\cos \theta } \right) ^{2}+\left( {\dot{y}+l_2 \dot{\theta }\sin \theta } \right) ^{2}} \right] \end{aligned}$$
(6)

The total potential energy of the system becomes

$$\begin{aligned} V= & {} V_M +V_m =Mgy+\frac{1}{2}k_y y^{2} \nonumber \\&+\frac{1}{2}k_x \left( {x-l_1 +\sqrt{l_1^2 -y^{2}}} \right) ^{2}\nonumber \\&+mgy-mgl_2 \cos \theta \end{aligned}$$
(7)

The governing equations are derived by Lagrange equation that is

$$\begin{aligned} \frac{d}{dt}\left( {\frac{\partial \left( {T-V} \right) }{\partial \dot{q}_i }} \right) -\frac{\partial \left( {T-V} \right) }{\partial q_i }=Q_i \end{aligned}$$
(8)

Appling the Lagrange equation, we can obtain the governing equations as

$$\begin{aligned}&\left( {M+m} \right) \ddot{x}+l_2 m\ddot{\theta }\cos \theta -l_2 m\dot{\theta }^{2}\sin \theta \nonumber \\&\qquad +\,k_x \left( {x-l_1 +\sqrt{l_1^2 -y^{2}}} \right) =Q_x \end{aligned}$$
(9)
$$\begin{aligned}&\left( {M+m} \right) \ddot{y}+l_2 m\ddot{\theta }\sin \theta +\left( {M+m} \right) g \nonumber \\&\qquad +\,l_2 m\dot{\theta }^{2}\cos \theta \nonumber \\&\qquad +\,k_y y-k_x y\frac{x-l_1 +\sqrt{l_1^2 -y^{2}}}{\sqrt{l_1^2 -y^{2}}}=Q_y \end{aligned}$$
(10)
$$\begin{aligned}&m\cos \theta \ddot{x}+m\sin \theta \ddot{y}+l_2 m\ddot{\theta }+mg\sin \theta =Q_\theta \end{aligned}$$
(11)

There are two kinds of excitation for a compressed air generator. One is road roughness which can excite the train bogie. It is generally applied to the base. Another excitation generates when the compressed air generator works. In present work, a simple excitation is considered and assuming the external force is only applied on the suspension mass along vertical direction, namely

$$\begin{aligned} Q_x =0, \quad Q_y =A_0 \sin \Omega t, \quad Q_\theta =0. \end{aligned}$$
(12)

Moreover, the dissipation effects of the vertical and horizontal dampers being in the forms of viscous damping, we thus obtain

$$\begin{aligned}&\left( {M+m} \right) \ddot{x}+l_2 m\ddot{\theta }\cos \theta -l_2 m\dot{\theta }^{2}\sin \theta \nonumber \\&\qquad +\,c_x \dot{x}+k_x \left( {x-l_1 +\sqrt{l_1^2 -y^{2}}} \right) =0 \end{aligned}$$
(13)
$$\begin{aligned}&\left( {M+m} \right) \ddot{y}+l_2 m\ddot{\theta }\sin \theta +\left( {M+m} \right) g\nonumber \\&\qquad +\,l_2 m\dot{\theta }^{2}\cos \theta +c_y \dot{y}+k_y y\nonumber \\&\qquad -\,k_x y\frac{x-l_1 +\sqrt{l_1^2 - y^{2}}}{\sqrt{l_1^2 -y^{2}}} =A\sin \Omega t\end{aligned}$$
(14)
$$\begin{aligned}&m\cos \theta \ddot{x}+m\sin \theta \ddot{y}+l_2 m\ddot{\theta }+\,c_\theta \dot{\theta }\nonumber \\&\qquad +\,mg\sin \theta =0 \end{aligned}$$
(15)

here,

$$\begin{aligned} c_x= & {} 2\zeta \left( {M+m} \right) \omega _x ,\quad \omega _x =\sqrt{{k_x }/{\left( {M+m} \right) }},\nonumber \\ c_y= & {} 2\zeta \left( {M+m} \right) \omega _x , \quad c_\theta =2\zeta ml_1 \omega _x^2 . \end{aligned}$$

Letting

$$\begin{aligned} x=l_1 X, \quad y=l_1 Y, \quad \tau =\omega \omega _x t, \end{aligned}$$
(16)

Eqs. (9)–(11) can be written in dimensionless forms

$$\begin{aligned}&\omega ^{2}\ddot{X}+\lambda m_1 \omega ^{2}\ddot{\theta }\cos \theta -\lambda m_1 \omega ^{2}\dot{\theta }^{2}\sin \theta \nonumber \\&\qquad +\,2\zeta \omega \dot{X}+\left( {X-1+\sqrt{1-Y^{2}}} \right) =0 \end{aligned}$$
(17)
$$\begin{aligned}&\omega ^{2}\ddot{Y}+m_1 \lambda \omega ^{2}\ddot{\theta }\sin \theta +m_1 \lambda \omega ^{2}\dot{\theta }^{2}\cos \theta +2\zeta \omega \dot{Y} \nonumber \\&\qquad +\left( {\kappa -1} \right) Y-Y\frac{X-1}{\sqrt{1-Y^{2}}}=f_0 +f_1 \sin t \end{aligned}$$
(18)
$$\begin{aligned}&\omega ^{2}\cos \theta \ddot{X}+\omega ^{2} \sin \theta \ddot{Y}+\lambda \omega ^{2}\ddot{\theta }+ 2\zeta \omega \dot{\theta }\nonumber \\&\qquad -\,f_0 \sin \theta =0 \end{aligned}$$
(19)

Here, \(m_1 =m/{\left( {M+m} \right) },\lambda ={l_2 }/{l_1 },\kappa ={k_y }/{k_x },f_0 ={-g}/{l_1 \omega _x^2 },f_1 =A/{\left( {M+m} \right) l_1 \omega _x^2 },\omega =\Omega /{\omega _x }\). Noted that, without loss of generality, the symbol t is still used for indicating time, and \(\dot{X}\) and \(\ddot{X}\) are derivatives with respect to time t. Equations (17)–(19) can be written in a matrix form as

$$\begin{aligned} \omega ^{2}\mathbf{M}\ddot{\mathbf{q}} +\omega \mathbf{C}\dot{\mathbf{q}}+\mathbf{Kq}+NF\left( \mathbf{q},\dot{\mathbf{q}} \right) =\mathbf{F} \end{aligned}$$
(20)

here,

$$\begin{aligned}&\mathbf{q}=\left[ {q_1 ,q_2 ,q_3 } \right] ^{T}=\left[ {X,Y,\theta } \right] ^{T} \end{aligned}$$
(21)
$$\begin{aligned}&\mathbf{M}=\left[ \begin{array}{ccc} 1&{} 0&{} {\lambda m_1 \cos \theta } \\ 0&{} 1&{} {\lambda m_1 \sin \theta } \\ {\cos \theta }&{} {\sin \theta }&{} \lambda \end{array} \right] , \end{aligned}$$
(22)
$$\begin{aligned}&\mathbf{C}=\left[ \begin{array}{ccc} {2\zeta }&{} 0&{} 0 \\ 0&{} {2\zeta }&{} 0 \\ 0&{} 0&{} {2\zeta } \end{array} \right] , \end{aligned}$$
(23)
$$\begin{aligned}&\mathbf{K}=\left[ \begin{array}{ccc} 1&{} 0&{} 0 \\ 0&{} {\kappa -1}&{} 0 \\ 0&{} 0&{} 0 \\ \end{array} \right] \end{aligned}$$
(24)
$$\begin{aligned}&F_\mathrm{nonl} =\left[ \begin{array}{c} {-\lambda m_1 \omega ^{2}\dot{\theta }^{2}\sin \theta +\sqrt{1-Y^{2}}-1} \\ {m_1 \lambda \omega ^{2}\dot{\theta }^{2}\cos \theta -Y\frac{X-1}{\sqrt{1-Y^{2}}}} \\ {-f_0 \sin \theta } \\ \end{array} \right] \end{aligned}$$
(25)
$$\begin{aligned}&\hbox {F}=\left[ \begin{array}{c} 0 \\ {f_0 +f_1 \sin t} \\ 0 \\ \end{array} \right] \end{aligned}$$
(26)

As indicated in Eqs. (17–19), the stiffness ratio \(\kappa \) and \(f_0 \) have a significant effect on the rigidity of the pendulum model, which may shift the natural frequency with coupling of the nonlinear stiffness function. For example, in Eq. (18), the nondimensional restoring force due to coupling spring is given by

$$\begin{aligned} G\left( Y \right) =\left( {\kappa -1} \right) Y-Y\frac{X-1}{\sqrt{1-Y^{2}}}. \end{aligned}$$
(27)

In static analysis, X can be set as a constant parameter. Then, the nondimensional stiffness in the vertical direction can be obtained as

$$\begin{aligned} \frac{\hbox {d}G\left( Y \right) }{dY}= & {} \left( {\kappa -1} \right) -\frac{X-1}{\sqrt{1-Y^{2}}}\nonumber \\&-Y^{2}\frac{X-1}{\left( {1-Y^{2}} \right) \sqrt{1-Y^{2}}} \nonumber \\= & {} \kappa -X+O\left( {Y^{2}} \right) \end{aligned}$$
(28)

Then, the linearized natural frequency is \(\sqrt{\kappa -X}\), which is coupled with horizontal displacement. The rest is nonlinear and negative stiffness configured by the linear spring [22]. Here, one should note that the total pendulum system is not as simple as above description. The dynamic stiffness and norm natural frequency will remarkably shift from \(\sqrt{\kappa -X}\). To hand this isolation, it is necessary to explore the nonlinear characteristics of the overall system and determine their stabilities to optimize the system parameters. Hence, in the following subsection, the nonlinear characteristic of the pendulum model relative to stiffness \(\kappa \) and \(f_0 \) are investigated theoretically.

3 IHBM and continuation

In this section, the IHBM is formulated to solve Eq. (20). However, the effective mass matrix \(\mathbf{M}\) is not a constant which is related to the position of pendulum. It is convenient to transform the dynamic model into the following form:

$$\begin{aligned} \omega ^{2}\ddot{\mathbf{q}}+\omega \mathbf{M}^{-1} \mathbf{C}\dot{\mathbf{q}}+\mathbf{M}^{-1}\mathbf{Kq}+\mathbf{M}^{-1} F_\mathrm{nonl} \left( \mathbf{q},\dot{\mathbf{q}} \right) \!=\!\mathbf{M}^{-1}\mathbf{F} \end{aligned}$$
(29)

As mentioned in Ref. [23], the first step of the IHBM is a Newton–Raphson procedure. Let \(q_{j0} \) and \(\omega _0 \) denote a state of vibration, and the neighboring state can be expressed by adding the corresponding increments to them as follows

$$\begin{aligned} q_j =q_{j0} +\Delta q_j , \quad \omega =\omega _0 +\Delta \omega , \quad j=1,2,3,\nonumber \\ \end{aligned}$$
(30)

or in matrix form

$$\begin{aligned} \mathbf{q}\left( t \right) =\mathbf{q}_0 \left( t \right) +\Delta \mathbf{q}\left( t \right) , \quad \omega =\omega _0 +\Delta \omega \end{aligned}$$
(31)

Substituting Eqs. (30) or (31) into Eq. (20) and neglecting the higher-order incremental terms, one obtains the following linearized incremental equation

$$\begin{aligned} \omega _0^2 \Delta \ddot{\mathbf{q}}+ \tilde{\mathbf{C}}\Delta \dot{\mathbf{q}}+ \tilde{\mathbf{K}}\Delta \mathbf{q}=\mathbf{R}_1 -\mathbf{R}_2 \Delta \omega \end{aligned}$$
(32)

here the subscript 0 of \(\left[ \right] _{0} \) means that the function locates at \(\mathbf{q}_0 \left( t \right) , \dot{\mathbf{q}}_{0} \left( t \right) ,\ddot{\mathbf{q}}_{0} \left( t \right) \), and

$$\begin{aligned}&\tilde{\mathbf{C}}=\left[ \frac{\partial \omega \mathbf{M}^{-1} \mathbf{C}\dot{\mathbf{q}}}{\partial \dot{\mathbf{q}}} \right] _0 +\left[ \frac{\partial \mathbf{M}^{-1}F_{nonl} \left( {\mathbf{q},\dot{\mathbf{q}}} \right) }{\partial \dot{\mathbf{q}}} \right] _0 \end{aligned}$$
(33)
$$\begin{aligned}&\tilde{\mathbf{K}}=\left[ \frac{\partial \mathbf{M}^{-1} \mathbf{Kq}}{\partial \mathbf{q}} \right] _0 + \left[ \frac{\partial \omega \mathbf{M}^{-1}\mathbf{C} \dot{\mathbf{q}}}{\partial \mathbf{q}} \right] _0 \nonumber \\&\qquad \quad +\left[ \frac{\partial \mathbf{M}^{-1}F_{nonl} \left( {\mathbf{q},\dot{\mathbf{q}}} \right) }{\partial \mathbf{q}} \right] _0 -\left[ \frac{\partial \mathbf{M}^{-1}\mathbf{F}}{\partial \mathbf{q}} \right] _0 \end{aligned}$$
(34)
$$\begin{aligned}&\mathbf{R}_1 =\mathbf{M}^{-1} \left( \mathbf{q}_0 \right) \mathbf{F}- \left[ \omega _0^2 \ddot{\mathbf{q}}_0 +\omega _0 \mathbf{M}^{-1}\left( \mathbf{q}_0 \right) \mathbf{C}\dot{\mathbf{q}}_0 \right. \nonumber \\&\qquad \quad \left. +\,\mathbf{M}^{-1}\left( \mathbf{q}_0 \right) \mathbf{Kq}_0 +\mathbf{M}^{-1} \left( \mathbf{q}_0 \right) F_{nonl} \left( \mathbf{q}_0 ,\dot{\mathbf{q}}_0 \right) \right] , \nonumber \\&\mathbf{R}_2 =2\omega _0 \ddot{\mathbf{q}}_0 + \left[ \frac{\partial \mathbf{M}^{-1}\mathbf{Kq}}{\partial \omega } \right] _0 \nonumber \\&\qquad \quad +\left[ \frac{\partial \omega \mathbf{M}^{-1} \mathbf{C}\dot{\mathbf{q}}}{\partial \omega } \right] _0 +\left[ \frac{\partial \mathbf{M}^{-1}F_{nonl} \left( {\mathbf{q},\dot{\mathbf{q}}} \right) }{\partial \omega } \right] _0 .\nonumber \\ \end{aligned}$$
(35)

The second step of IHBM is the harmonic balance procedure. Letting

$$\begin{aligned}&q_{j0} \left( t \right) =\sum _{k=1}^{n_c } {a_{jk} \cos \left( {k-1} \right) t} +\sum _{k=1}^{n_s } {b_{jk} \sin kt} \nonumber \\&\qquad \qquad =\mathbf{C}_s \mathbf{A}_j , \nonumber \\&\Delta q_{j0} \left( t \right) =\sum _{k=1}^{n_c } {\Delta a_{jk} \cos \left( {k-1} \right) t} +\sum _{k=1}^{n_s } {\Delta b_{jk} \sin kt} \nonumber \\&\qquad \qquad \quad =\mathbf{C}_s \Delta \mathbf{A}_j \end{aligned}$$
(36)

where

$$\begin{aligned}&\mathbf{C}_s =\left[ {1,\cos t,\ldots ,\cos \left( {n_c -1} \right) t,\sin t,,\ldots ,\sin n_s t} \right] , \nonumber \\&\mathbf{A}_j =\left[ {a_{j1} ,a_{j2} ,\ldots ,a_{jn_c } ,b_{j1} ,b_{j2} ,\ldots ,b_{jn_s } } \right] ^{T}, \nonumber \\&\Delta \mathbf{A}_j =\left[ \Delta a_{j1} ,\Delta a_{j2} , \cdots ,\Delta a_{jn_c } ,\Delta b_{j1} ,\Delta b_{j2} ,\right. \nonumber \\&\qquad \quad \left. \ldots ,\Delta b_{jn_s } \right] ^{T}. \end{aligned}$$
(37)

Therefore, the vectors of the unknowns and their increments can be expressed as

$$\begin{aligned} \begin{aligned}&\mathbf{q}_0 =\mathbf{SA},\Delta \mathbf{q}=\mathbf{S}\Delta \mathbf{A}, \\&\mathbf{A}=\left[ {\mathbf{A}_1 ,\mathbf{A}_2 ,\ldots ,\mathbf{A}_m } \right] ^{T}, \\&\Delta \mathbf{A}=\left[ {\Delta \mathbf{A}_1 ,\Delta \mathbf{A}_2 ,\ldots ,\Delta \mathbf{A}_m } \right] ^{T}, \\&\mathbf{S}=\hbox {diag}\left[ {\mathbf{C}_s ,\mathbf{C}_s ,\ldots ,\mathbf{C}_s } \right] \end{aligned} \end{aligned}$$
(38)

Then, substituting Eq. (38) into Eq. (32) and applying the Galerkin procedure for one cycle, one can obtain the following set of linear equations in terms of \(\Delta \mathbf{A}\) and \(\Delta \omega \):

$$\begin{aligned} K_{mc} \Delta \mathbf{A}=\bar{\mathbf{R}}-\bar{\mathbf{R}}_{mc} \Delta \omega \end{aligned}$$
(39)

where

$$\begin{aligned} \begin{aligned}&\mathbf{K}_{mc} =\int _0^{2\pi } {\mathbf{S}^{T} \left( \omega _0^2 \mathbf{S}''+ \tilde{\mathbf{C}}{\mathbf{S}}'+\tilde{\mathbf{K}}\mathbf{S} \right) } d\tau , \\&\bar{\mathbf{R}} =\int _0^{2\pi } {\mathbf{S}^{T}\mathbf{R}_1 } d\tau ,\bar{{\mathbf{R}}}_{mc} =\int _0^{2\pi } {\mathbf{S}^{T}\mathbf{R}_2 } d\tau \end{aligned} \end{aligned}$$
(40)

In Eq. (39), the number of the incremental unknowns is greater than the number of equations available due to the existence of \(\Delta \omega \). In this paper, frequency \(\omega \) is specified as a control increment, and then \(\Delta \omega =0\), while other increments are solved from Eq. (39). The initial values are setting to zeros in the first iteration process. The Newton–Raphson iteration is repeated until the norm of the corrected vector \( \bar{\mathbf{R}}\) is acceptably small (\(10^{-5}\)). Then, the periodic solution is obtained. It is worth mentioning that the analytical expressions of the matrices and the vector in Eq. (40) are not available due to the existence of nonlinear restoring force. Numerical integration for the nonlinear parts is processed, the numerical integration error is controlled and this strategy is validated in our analysis by comparing with the exact results with Runge–Kutta method.

In addition, in the nonlinear problem, it cannot be avoided that the unstable dynamic response or unstable periodic solution such as snapback phenomena [24–26] or jump phenomena [27, 28] in gear dynamics. A common way is to introduce the continuation method, which can overcome this problem and is adopted by many researchers to solve the nonlinear problem recently, such as Grolet and Thouverez [29], Dou and Jensen [30]. Ritto-Corrêa and Camotim [25] reviewed several established continuation methods and discussed their implementation issues. In the present work, a modified Crisfield’s method proposed in [25] is used to solve Eq. (39).

4 Stability of periodic solution

Once the periodic solution is determined, its stability can be investigated by using the Floquet theory [31]. It is the same as Eq. (31), we can obtain the perturbed equation from Eq. (32) by letting \(\mathbf{R}_1 =0, \mathbf{R}_2 =0\) and \(\Delta \omega =0\), and in the form

$$\begin{aligned} \omega _0^2 \Delta \ddot{\mathbf{q}}+\tilde{\mathbf{C}}\Delta \dot{\mathbf{q}}+\tilde{\mathbf{K}}\Delta \mathbf{q}=0 \end{aligned}$$
(41)

This equation is a linear ordinary differential equation with periodic coefficients in \(\tilde{\mathbf{C}}\) and \(\tilde{\mathbf{K}}\). Theoretically, the stability of the periodic solution \(\mathbf{q}_0 \) corresponds to the stability of the solution of Eq. (41).

Eq. (41) can be rewritten as

$$\begin{aligned} \dot{\mathbf{Z}}=\hbox {Q}\left( t \right) \mathbf{Z} \end{aligned}$$
(42)

where

$$\begin{aligned} \mathbf{Z}=\left[ {\Delta \mathbf{q},\Delta \dot{\mathbf{q}}} \right] ^{T}, \quad \mathbf{Q}=\left[ \begin{array}{cc} \mathbf{0}&{} \mathbf{I} \\ {{-\tilde{\mathbf{K}}}/{\omega _0^2 }}&{} {{-\tilde{\mathbf{C}}}/{\omega _0^2 }} \end{array} \right] , \end{aligned}$$
(43)

\(\mathbf{0}\) is a null matrix, and \(\mathbf{I}\) is a unit matrix. Since each component of \(\mathbf{q}_0 \) is a periodic function of t with a period \(T={2\pi }/\omega \), each element of \(- \tilde{\mathbf{K}}/{\omega _0^2 }\) and \(-\tilde{\mathbf{C}}/{\omega _0^2 }\) is also periodic function with the same period T, namely \(\mathbf{Q}\left( {t+T} \right) =\mathbf{Q}\left( t \right) \). Directly, there is a fundamental matrix solution \(\mathbf{Y}\) which satisfies the matrix equation

$$\begin{aligned} \dot{\mathbf{Y}}=\hbox {Q}\left( t \right) \mathbf{Y}, \end{aligned}$$
(44)

and it is same for

$$\begin{aligned} \mathbf{Y}\left( {t+T} \right) =\mathbf{PY}\left( t \right) , \end{aligned}$$
(45)

where \(\mathbf{P}\) is called the monodromy or Floquet transition matrix. Its eigenvalues are called the Floquet multipliers. If any of the Floquet multipliers has a module greater than one, then the solution is unstable; otherwise, it is stable. Some of the most commonly used algorithms are discussed and compared by Peletan in Ref. [32]. In this paper, the monodromy matrix is calculated by ‘2n-pass’ numerical integration.

5 Numerical simulation and discussion

5.1 Nonlinear characteristic with low stiffness

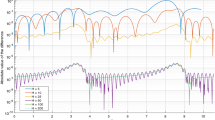
In the low stiffness case, the stiffness ratio \(\kappa \) is 1.5 and others are \(f_0 =-0.1, f_1 =0.1, \zeta =0.05, m_1 =0.09\) and \(\lambda =1\). The external excitation frequency \(\omega \) is set as the control parameter. The harmonic component number \(n_c =3\) and \(n_s =2\) is selected. The dynamic response diagrams, root mean square (rms), versus the excitation frequency \(\omega \) are shown in Fig. 2a–c. In these figures, the solid line ‘-’ denotes the IHBM solutions, and two different color lines are for two continuation curves with different initial values. The numerical integrated solutions denoted by cycle ’o’ are also superposed in the figures. It is shown that the IHBM solution matches the numerical solution perfectly except for these in the shaded regions. The maximum Lyapunov exponent is calculated for these system parameters as shown in Fig. 2d. It can be observed that the maximum error between IHBM and numerical solutions appears within the chaotic region because the maximum Lyapunov exponents crossed the zeros axis on the positive side. In addition, the peaks of the dynamic response in the X direction and rotation displacement of pendulum are almost the same and around 1. However, the peak of the dynamic response in the Y direction is located at \(\sqrt{\kappa }=\sqrt{1.5}\approx 1.2\), which matches the analytical result as calculated in Eq. (28). The occurrence of chaotic motion could be recognized as the result of a resonance in the Y direction. In the chaotic region, the pendulum is not suitable for the assumption of a small amplitude vibration, as shown in Fig. 3. In these figures, the phase portrait for \(\omega =1.1\) and \(\omega =1.25\) corresponding to periodic and chaotic motion is listed. It is observed that the pendulum will rotate circularly and deteriorate stability of the overall system. A detailed control strategy will be discussed in Sect. 5.2.

Fig. 2
figure 2

Response diagram for the low stiffness case \(\kappa =1.5\): a rms at X direction versus \(\omega \), b rms in the Y direction versus \(\omega \), c rms of pendulum rotation displacement \(\theta \) and d corresponding maximum Lyapunov exponents

Full size image
Fig. 3
figure 3

Phase portrait at a \(\omega =1.1\) and b \(\omega =1.25\)

Full size image

In detail, we will focus our interest in the excitation region from 1.1 to 1.5, and the analytical solution calculated by IHBM and continuation is shown in Fig. 4. In this figure, there exists a period double bifurcation at point ‘a’, where one of the Floquet multipliers corresponding to point ‘a’ leaves the unit circle in the \(-\)1 direction. With the increase in the excitation frequency of the system, the period 1 motion bifurcates into a period 2 motion. Subsequently, a series of period double bifurcation occurs around point ‘b’ and the system comes into chaotic motion. For further increase in the excitation frequency, the transit chaotic motion will degenerate into period 1 motion and a new period double bifurcation route into chaos, denoted by ‘c’ as shown in Fig. 4, is detected. Then, the remaining continuation curve will lose its stability denoted by dashed line. By changing the initial value of IHBM, we can obtain a new continuation curve as shown in Fig. 4. A quasiperiodic motion region is detected in Fig. 4 denoted by (quasi-p). With the decrease in the excitation frequency, a saddle-node bifurcation occurs where the Floquet multipliers leave unit circle through \(-\)1. A corresponding numerical bifurcation diagram and Maximum Lyapunov exponent are shown in Fig. 5. It can be observed that the saddle-node bifurcation may be the reason for the degeneration of a chaotic motion into a periodic motion around point ‘d’. In the quasi-p region, the maximum Lyapunov exponent moves around the zeros line, which correspond to quasiperiodic motion.

5.2 Influence of stiffness

In the second case, the stiffness ratio is also set as a control parameter to evaluate the dynamic response of the pendulum vibration system based on the IHBM. The harmonic components for Eq. (36) can be simplified to be \(A_1 =\sqrt{a_{12}^2 +b_{11}^2 },A_2 =\sqrt{a_{13}^2 +b_{12}^2 },A_{jk} =\sqrt{a_{1,k+1}^2 +b_{1,k}^2 }\;\;({j=1,2,3,k=1,2,\ldots ,N_s })\) corresponding to excitation frequency \(\omega \). The other parameters are taken as the same as previously. The harmonic components of the dynamic response about \(\kappa =1.5\) and \(\kappa =2.0\) are shown in Fig. 6, respectively. It can be observed that the appearance of the resonance peaks near \(\omega =0.5\) and \(\omega =1.0\) is induced by the horizontal spring. In other words, the horizontal spring has a significant influence on the pendulum system and the vibration response can be isolated or reduced by optimizing it. In addition, the snap or jump phenomena is detected when \(\kappa =2.0\) around the peak , which means that this resonance peak is excited and related with the vertical spring. The chaotic motion also appears around this region. The response diagrams with different stiffness ratio, \(\kappa =2\), 4, 5 and 7, are shown in Fig. 7. These figures indicate the relationship between the stiffness of the vertical spring and the resonance peak. Furthermore, when the stiffness ratio is larger than 3, the chaotic motion will not appear in the pendulum model. The above results suggest that, in the low-frequency region, the vibration amplitude is determined by the spring in the X direction, but the spring in the vertical direction determines whether the system presents chaotic motion.

Fig. 4
figure 4

Bifurcation diagram with IHBM and continuation, the solid line indicating stable motion and the dashed line indicating unstable motion

Full size image
Fig. 5
figure 5

Bifurcation diagram and max. Lyapunov exponent

Full size image
Fig. 6
figure 6

Harmonic component of dynamic response a \(\kappa =1.5\) and b \(\kappa =2.0\)

Full size image
Fig. 7
figure 7

Response diagram a rms in the X direction versus \(\omega \), b rms in the Y direction versus \(\omega \), c rms of pendulum rotation displacement \(\theta \), with different stiffness ratios.

Full size image

Therefore, to reduce the vibration intensity and improve the stability of the pendulum system, there are at least two strategies to be adopted. Firstly, one can add a firm suspension to increase the stiffness in the vertical direction. The cost of this method may be relatively high, and it is suitable in the design phase. In addition, the vibration will be easily transmitted to the frame with higher suspension stiffness. On the other hand, reducing the stiffness in the horizontal direction can also achieve the purpose of increasing the stiffness ratio.

6 Conclusions

The nonlinear dynamic characteristic of a suspension model simplified from a compressed air generator hang under a vehicle is studied. In the simple model, the suspension mass connected to a vertical spring and two horizontal springs can be configured as a geometrical negative stiffness isolator. The unbalanced mass is modeled as a pendulum. IHBM and arc length continuation technique are used to obtain the response diagram of the present model subject to external harmonic excitation. The stability and bifurcation route are also distinguished with the Floquet theory. The results show that the periodic response of the vibration model computed by the IHBM matches well with the numerical integration solutions. The bifurcation points also match well with the numerical results. The period doubling bifurcation route to chaos is observed. The stiffness ratio between the vertical spring and horizontal springs has a significant influence on the dynamic response. When the vertical stiffness is close to the stiffness in the horizontal direction, the resonance will occur with the emergence of the chaotic motion. Reducing the stiffness in the horizontal direction to increase the stiffness ratio can improve the dynamic response of the vibration system but one cannot remove the horizontal spring because it will change the negative stiffness configuration.