1 Introduction

Synchronization of chaotic or hyperchaotic dynamics has received a lot of attention in the last decades [1, 2]. This interest is increased by practical applications in different fields, particularly in secure/private communications [3–5]. Many different methods have been presented for the synchronization of chaotic systems with linear or nonlinear feedback control [6, 7], adaptive control [8], passive control [9], impulsive control [10] or observer approach [11]. Due to its great potential in secure/private communications domain, the generation of hyperchaos has recently become a focal topic for research [12, 13].

It should be noted that most of the works on the secure/private communications based on the synchronization of chaotic or hyperchaotic systems have been devoted to dynamical systems in continuous time [14, 15], whereas in many cases, the systems are preferred to be in real time and in discrete time. Another disadvantage of the classical chaotic or hyperchaotic systems is the use of complex electronic systems made of analog electronic components that involve op-amps, resistors, capacitors and diodes. Often, this complexity leads to a tedious implementation [16]. The new trend is therefore to derive discrete models which faithfully represent the dynamics of such systems. This is mainly due to two reasons. The first is that, in practice, measurements are usually carried out at specific time intervals. Secondly, digital simulations can be performed easily and quickly either on a microcontroller [17–21] or on a FPGA board [22].

In secure/private domain, it is known that, for the chaos-based cryptosystem, the keys are usually the chaotic system parameters. So, from a control theory point of view, the possibility to reconstruct the keys for chaos-based cryptosystem is equivalent to the possibility to identify the parameters of the chaotic system [4]. Consequently, a robust and reliable chaos-based cryptosystem should be designed such that its parameters be not identifiable. In this paper, solutions are provided to propose an new robust secure data transmission based on hyperchaotic synchronization. Here, the transmitter is a discrete hyperchaotic modified-Henon system and the receiver is a discrete step-by-step observer. At the level of transmitter, the states of the discrete-time hyperchaotic system are added to the message to be transmitted. Then, the embedded message is introduced by the inclusion method in the dynamics of the discrete-time system to make its structure more complex. By using this strategy, the number of parameters is increased. Therefore, the system becomes robust against known-plaintext attacks.

In this work, we have chosen to show the experimental feasibility of our approach. Here, we have realized an implementation of a secure digital data transmission system based on the synchronization of chaotic systems using two Arduino Uno boards. To the best of our knowledge, in the discrete case, this type of implementation has not been done in the literature; there are only implementations of chaotic oscillators using microcontrollers [19, 20], and FPGAs [22]. The choice of the Arduino Uno board is motivated by the advantages that it offers. It exhibits good performances of throughput and cost in terms of resources used. In addition, the use of an Arduino simplifies the amount of hardware and software development necessary to get a system running. On the software side, Arduino provides a number of libraries to make programming the microcontroller easier. The simplest of these are functions to control and read the I/O pins rather than having to fiddle with the bus/bit masks normally used to interface with the Atmega I/O (This is a fairly minor drawback). Also, note that, board programming microcontrollers are far more simpler compared to older existing implementations [19, 20, 22]. In our work, transmission scheme is constructed around two Arduino Uno boards, one of them acting as a transmitter and the other as a receiver. Each board is connected to an individual computer what permits to visualize the experimental results of the transmitter and the receiver.

The work is organized as follows: In Sect. 2, the principle of the proposed method is presented by studying the transmitter and the receiver of the transmission system. In Sect. 3, we expose the simulation results. In Sect. 4, we study the robustness of the proposed transmission scheme. Section 5 exposes the experimental results of the proposed transmission scheme into Arduino board. Finally, we give some concluding remarks.

2 Description of the private transmission chain

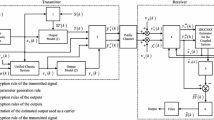
In this work, a communication system based on the hyperchaotic digital dynamical system is designed. The global scheme of the proposed system for private digital communications is shown in Fig. 1. The developed method is presented as follows:

Fig. 1
figure 1

Transmission chain

Full size image

2.1 Presentation of the transmitter

The discrete-time hyperchaotic system is the modified-Henon’s map (see for example [23]). A simplified version of the discrete system that we propose is:

$$\begin{aligned} \left\{ \begin{array}{ll} x_1(k+1)=a-x_2^{2}(k)-bx_3(k) \\ x_2(k+1)=x_1(k) \\ x_3(k+1)=x_2(k)\\ \end{array} \right. \end{aligned}$$
(1)

where \(x=[x_1\ \ x_2\ \ x_3]^{T} \in \mathbb {R}^{3}\) denotes the state vector. Chaotic behavior of System (1) is obtained with parameters values \(a =1.76\) and \(b=0.1\). Initial conditions \(x_1(0)=1\), \(x_2(0)=0.1\) and \(x_3(0)=0.1\) are chosen inside the strange attractor basin.

The chaotic attractor is shown in Fig. 2, and the states responses are shown in Figs. 3, 4 and 5. In private communications, one of the main purposes is to increase security. To do this, it is interesting to modify System (1).

Fig. 2
figure 2

Chaotic attractor of modified-Henon system

Full size image
Fig. 3
figure 3

State \(x_1\) response of modified-Henon system

Full size image
Fig. 4
figure 4

State \(x_2\) response of modified-Henon system

Full size image
Fig. 5
figure 5

State \(x_3\) response of modified-Henon system

Full size image

As shown in Fig. 1, the message \(m(k)\) to be sent is encrypted using an encryption function which depends on states \(x_1(k)\) and \(x_3(k)\) generated by System (1). Finally, in order to preserve the chaotic behavior, the encrypted message is introduced in the third dynamics component of System (1). Thus, we obtain:

$$\begin{aligned} \left\{ \begin{array}{ll} x_1(k+1)=a-x_2^{2}(k)-bx_3(k) \\ x_2(k+1)=x_1(k) \\ x_3(k+1)=x_2(k)+m_{c}(k) \end{array} \right. \end{aligned}$$
(2)

where \(m_{c}(k)\) is chosen equal to:

$$\begin{aligned} m_{c}(k)= & {} m(k)+cx_1(k)+dx_3(k)+ex_1^{2}(k)+fx_3^{2}(k) \nonumber \\&+\, gx_1(k)x_3(k)+hx_1^{2}(k)x_3(k) \end{aligned}$$
(3)

with \(c, d, e, f, g\) and \(h\) being the new coefficients of discrete-time hyperchaotic System (1). To preserve the chaotic behavior of System (1), these parameters are chosen with special care. In our case, we must respect the following values: \(c\le 0.01\), \(d\le 0.01\), \(e\le 0.01\), \(f\le 0.01\), \(g\le 0.01\) and \(h\le 0.01\).

2.2 Presentation of the receiver

In this part, System (2) with output \(y(k)=x_2(k)\) is considered. For the reception, based on the works of Belmouhoub et al. [24] and Djemaï et al. [25], we design a delayed discrete observer for System (2) with sampling period \(T\). In the following, some results on a delayed discrete observer are given.

2.2.1 Some results of the observability matching condition and left invertibility property

Consider the following nonlinear system:

$$\begin{aligned} \left\{ \begin{array}{ll} x(k+1)=f(x(k))+p(x(k))w(k) \\ y(k) =h(x(k)) \end{array} \right. \end{aligned}$$
(4)

where \(w(k)\) represents an unknown input, which can be a perturbation, a fault, or in our case, a message. The vector fields \(f,p: U\subset \mathbb {R}^{n}\rightarrow \mathbb {R}^{n}\) and \(h: U \subset \mathbb {R}^{n}\rightarrow \mathbb {R}\) are assumed to be real-analytic. The output of System (4) is transmitted to the receiver, which should generate an output vector that converges asymptotically toward the input vector of the transmitter. This constitutes the left inversion problem. It is possible to design a delayed discrete observer for System (4). For this, it is necessary to satisfy some assumptions which are given below:

Assumption 1

  1. A1

    The states and the unknown perturbation are bounded,

  2. A2

    span \(\{dh,d(f\circ h),..., d(f^{n-1}\circ h)\}\) is of rank \(n\),

  3. A3

    \(((dh)^{T},d(f\circ h)^{T},..., d(f^{n-1}\circ h)^{T}).p=(0,...,0,\theta )^{T}\)

where \(\theta \) is a nonzero function almost everywhere in \(U \subset \mathbb {R}^{n}\rightarrow \mathbb {R}\). Assumption A3 is called observability matching condition, it guaranties the left invertibility property, i.e., the possibility of recovering all the states and the message \(w(k)\) from \(y(k)\) and its iterations (see [25] for more details).

In the following, we study the choice of the output signal in order to guaranty the observability of the system. Then, we explain that the message inclusion verifies the left invertibility of System (2).

2.2.2 The proposed delayed discrete observer

Let us consider System (2) which can be rewritten in the form of System (4). In what follows, we check the validity of Assumptions A1, A2 and A3.

  • All states and the message \(m(k)\) of the System (2) are bounded. This ensures that Assumption A1 is verified.

  • Observability of System (2)

    We study the weak local observability of System (2). We calculate the observability matrix in the neighborhood of the equilibrium point \((0,0,0)\) of System (2) as below:

    $$\begin{aligned} O=\left( \begin{array}{l} dh \\ d(f\circ h) \\ d(f^{2}\circ h) \\ \end{array} \right) =\left( \begin{array}{l@{\quad }l@{\quad }l} 0 &{} 1 &{} 0 \\ 1 &{} 0 &{} 0 \\ 0 &{} -2x_2 &{} -b \\ \end{array}\right) \end{aligned}$$
    (5)

    Since \(b\ne 0\), we find that \(rank(O)=3\). This means that System (2) is locally weakly observable. Assumption A2 is verified. Then, the observer given below allows to reconstruct all states of System (2). This motivates the choice of output \(y(k)=x_2(k)\).

  • Observability matching condition of System (2)

    In our case, we have:

    $$\begin{aligned} p(x)=\left( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right) \end{aligned}$$
    (6)

    Now, we calculate \(O.p\) as below

    $$\begin{aligned} Op(x)= & {} \left( \begin{array}{ccc} 0 &{} 1 &{} 0 \\ 1 &{} 0 &{} 0\\ 0 &{} -2x_2&{} -b \\ \end{array} \right) \left( \begin{array}{c} 0 \\ 0 \\ 1 \\ \end{array} \right) \nonumber \\ Op(x)= & {} \left( \begin{array}{c} 0 \\ 0 \\ \theta =-b \end{array} \right) \end{aligned}$$
    (7)

    Note that the value of \(\theta \) is not equal to zero. Then, the observability matching condition given in Assumption A3 is verified. This explains the choice of inserting method of the message \(m(k)\) into the third dynamics of System (2). Then, the proposed delayed discrete-time observer with a sampling time \(T\) given below allows to reconstruct all states and the transmitted message \(m(k)\) of System (2).

  • Reconstruction of state \(\hat{x}_1\):

    From the second equation of System (2), we have:

    $$\begin{aligned} \hat{x}_2(k+1)=\hat{x}_1(k) \end{aligned}$$

    By applying one step delay on the output, we deduce state \(\hat{x}_1\) as it follows:

    $$\begin{aligned} \hat{x}_1(k-1)=y(k)=x_\mathrm{1o}(k-1) \end{aligned}$$
    (8)

  • Reconstruction of state \(\hat{x}_3\):

    From the first equation of System (2), we have also:

    $$\begin{aligned} \hat{x}_3(k)=\frac{a-\hat{x}_1(k+1)-\hat{x}_2^{2}(k)}{b} \end{aligned}$$

    Now, let us apply two steps delays on the output. Using Eq. (8), we obtain the state \(\hat{x}_3\) as it follows:

    $$\begin{aligned} \hat{x}_3(k-2)=\frac{a-y(k)-y^{2}(k-2)}{b}=x_{3}\mathrm{o}(k-2)\nonumber \\ \end{aligned}$$
    (9)

  • Reconstruction of message \(\hat{m}(k)\):

    From the third equation of System (2), we have:

    $$\begin{aligned} \hat{m}(k)= & {} \hat{x}_3(k+1)-\hat{x}_2(k)-c\hat{x}_1(k)\nonumber \\&-\,d\hat{x}_3(k)-e\hat{x}_1^{2}(k) -f\hat{x}_3^{2}(k)\nonumber \\&-\,g\hat{x}_1(k)\hat{x}_3(k)-h\hat{x}_1^{2}(k)\hat{x}_3(k) \end{aligned}$$
    (10)

    Using Eqs. (8–10) and by applying three steps delay, we obtain:

    $$\begin{aligned}&\hat{m}(k-3)=\frac{a-y(k)-y^{2}(k-2)}{b}\nonumber \\&\quad -y(k-3)-cy(k-2) \nonumber \\&\quad - d\left( \frac{a-y(k-1)-y^{2}(k-3)}{b}\right) -ey^{2}(k-2) \nonumber \\&\quad - f\left( \frac{a-y(k-1)-y^{2}(k-3)}{b}\right) ^{2} \nonumber \\&\quad - gy(k-2)\left( \frac{a-y(k-1)-y^{2}(k-3)}{b}\right) \nonumber \\&\quad - hy^{2}(k-2)\left( \frac{a-y(k-1)-y^{2}(k-3)}{b}\right) \nonumber \\&= m_{0}(k-3) \end{aligned}$$
    (11)

Subsequently, the observer equations are given by Eqs. (8–11).

3 Simulation results

In the following, we present the simulation results for the synchronization of System (2) exposed in Sect. 2.1 and its observer exposed in Sect. 2.2. The additional parameters \(c, d, e, f,g\) and \(h\) of the transmission scheme are chosen as: \(c=d=e=f = g =h =0.001\), and the message to send is a square signal with amplitude equal to \(0.1\). In our simulation, we have chosen the period \(T\) equal to \(0.04\) s.

Fig. 6
figure 6

States time responses: \(x_1\) (transmitter) and \(x_\mathrm{10}\) (receiver)

Full size image
Fig. 7
figure 7

Synchronization error on the state \(x_1\)

Full size image
Fig. 8
figure 8

States time responses: \(x_3\) (transmitter) and \(x_\mathrm{{3o}}\) (receiver)

Full size image
Fig. 9
figure 9

Synchronization error on the state \(x_3\)

Full size image
Fig. 10
figure 10

Messages: \(m\) (transmitter) and \(m_{o}\) (receiver)

Full size image
Fig. 11
figure 11

Synchronization error on the message \(m\)

Full size image

Simulation results for recovering the two states \(x_1, x_3\) and the message \(m\) of the transmitter are shown in Figs. 6, 8 and 10, respectively. Figures 7, 9 and 11 give the synchronization errors (between transmitter and receiver) on states \(x_1, x_3\) and message \(m\), respectively. As explained before, the reconstruction of the two states is shown step-by-step, i.e., the first reconstructed state is \(x_1\) and the second one is \(x_3\). Finally, the message signal \(m\) is reconstructed after synchronization of these states.

This allows us to establish that error \(e_1=x_1-\hat{x}_1\) vanishes after \(T=0.04\) s which corresponds to the delay of one step according to Eq. (8) (see Fig. 7). Error \(e_3=x_3-\hat{x}_3\) vanishes after \(2T= 0.08\) s, which corresponds to a delay of two steps on the output according to Eq. (9) (see Fig. 9). Finally, the message error \(e_m=m-\hat{m}\) vanishes after \(3T= 0.12\) s which corresponds to the delay of three steps according to the Eq. (10) (see Fig. 11).

With regard to the obtained results, we can highlight the advantage of delayed step-by-step observer. The major advantage of this observer is the exact reconstruction after a short delay, without any error, of the states and the messages as shown in Figs. 7, 9 and 11. It should be noted that other observers undergo the disadvantages of reconstruction errors. Moreover, the convergence of the latter observers is asymptotic [13, 26].

Fig. 12
figure 12

Original message and decrypted message in the presence of noise for SNR\(=20\) dB

Full size image

4 Performances of the proposed transmission scheme

In this section, two important tests will be presented. The first test concerns the robustness of the transmission scheme against channel noise. In the second test, we test the robustness of the transmission scheme against the parameter mismatch of its chaotic systems.

4.1 Robustness against transmission noise

In this part, we study the impact of noise on the quality of the recovered message. The message considered in this part is the square signal described before. In the following, we consider an additive white Gaussian noise (AWGN) noted \(\eta (t)\) with zero mean and standard deviation equal to one, disrupting the transmitted signal. Figures 12, 13 and 14, respectively, depict the recovered message for different signal-to-noise ratio (SNR) 20, 30 and 40 dB. Through these results, we notice that the message is well recovered from a SNR \(=40\) dB. This last value of SNR is chosen since in Alvarez et al. [26], it is mentioned that for a practically viable chaotic cryptography scheme, the recommended value of the SNR is \(40\) dB.

Fig. 13
figure 13

Original message and decrypted message in the presence of noise for SNR \(=30\) dB

Full size image
Fig. 14
figure 14

Original message and decrypted message in the presence of noise for SNR \(=40\) dB

Full size image

4.2 Key analysis

In what follows, we test the robustness of the proposed transmission scheme. To do this, we evaluate the level of the system security of this scheme by testing the sensitivity of System (2) versus the variation of its parameters.

It should be emphasized that the most important property of cryptographic systems is the existence of a secret key which defines the level of security of the cryptosystem. From a cryptographical viewpoint, the initial conditions and the parameters of chaotic systems may be used to define a secret key for the chaos-based communication systems.

Fig. 15
figure 15

State \(x_1\) of the modified-Henon system for small changes (\(10^{-15}\)) of parameter \(p_1=a\)

Full size image
Fig. 16
figure 16

State \(x_1\) of the modified-Henon system for small changes (\(10^{-15}\)) of parameter \(p_4=d\)

Full size image
Table 1 Sensitivity to parameters
Full size table

In our work, we suppose that the initial conditions and the structure of System (2) are exactly known by a non-authorized intruder. We assume that \(P_i: = (P_1 = a; p_2 = b; P_3 = c; P_4 =d; P_5 = e; P_6 = f; P_7 = g ,P_8 = h )\) are the secret key. Here, our goal is to determine the size s of the key space \(Ks = [P_1,P_2, P_3, P_4, P_5, P_6, P_7, P_8]\) which represents the finite set of all possible keys permitting to evaluate the level of security produced by the secret key. Then, we have to define the range of variation and the sensitivity of each parameter \(P_i\) (for \(i=1,\ldots ,8\)). Assume that the size \(r\) of the interval of variation of each parameter \(P_i\) that leads to chaotic behaviors of hyperchaotic System (2) is equal to \(10^{-1}\). In order to evaluate the sensitivity \(S_i\) (for \(i=1,\ldots ,8\)) of each parameter \(P_i\), numerical simulations are conducted. The aim is to determine the smallest parameter variation that gives us two different chaotic behaviors or two different attractors when the rest of parameters are fixed. Figures 15 and 16, respectively, illustrate for example the sensitivity of System (2) to small changes of its parameters \(a\) and \(d\). Table 1 summarizes these different resulting values. Note that in our case, the size of the key space is:

$$\begin{aligned} r=\prod \nolimits _{i=1}^{8}(N_{i})=10^{(7\times 14)+(1\times 13)}=10^{111}. \end{aligned}$$

Relying on nowadays available computational power, a key space of size \(O(2^{100})\) is generally required. Note that in our case, we have \(r=10^{111}\gg 2^{100}\), which means that the key space produced enhances a largely satisfactory level of security from a cryptographical viewpoint.

5 Experimental results

5.1 Setup description

In this subsection, we present the proposed transmission scheme with hyperchaotic discrete-time oscillator. The latter is realized by using an open-source Arduino Uno prototyping platform made up of an Atmel AVR processor (microcontroller). This realization is based on flexible, easy-to-use hardware and software Arduino platform. The latter has \(14\) digital input/output pins, six analog inputs, a \(16 MHz\) crystal oscillator, a USB connection, a power jack, an ICSP header and a reset button as shown in Fig. 17. In our work, we use two Arduino Uno boards. The first acts as a transmitter and the second as a receiver. The connection between the transmitter and the receiver is provided by a cable. We use two individual computers intended to facilitate the visualization of different experimental results of transmitter and receiver. This task is performed by the addition of two graphic interfaces written in JAVA, which offers many advantages in real time.

Fig. 17
figure 17

Arduino Uno prototyping platform

Full size image

Note that the microcontroller used on the Arduino Uno board is a microcontroller ATMega328 [28]. It belongs to the 8 bits-AVR family.

Note also that the Arduino Uno board can be programmed in various ways [27]. In our work, we choose the Integrated Development Environment (IDE) software method which is given below.

Figure 18 gives a view of the experimental hardware implementation and measurements of the modified-Henon’s hyperchaotic signals.

Fig. 18
figure 18

Photo of the experimental setting for hardware implementation and measurements of the modified-Henon’s hyperchaotic signals

Full size image
Fig. 19
figure 19

The connection of the Arduino Uno board

Full size image

5.2 Experimental results of the transmitter

The principle part of the program to be implemented, which is known as “sketch,” is uploaded into the microcontroller using IDE software. The Arduino Uno is connected to the computer through the USB port and programmed using the language “Wiring” which is similar to C and \(C^{++}\) as shown by Fig. 19. The principle part of the program implementation of the transmitter (2) is given below:

figure a

Figures 20 and 21 exhibit the experimental results of the chaotic attractor and the states responses, respectively, of the modified-Henon system.

Fig. 20
figure 20

Experimental result of the chaotic attractor of modified-Henon system

Full size image
Fig. 21
figure 21

Experimental results of the states and the transmitted message at the level of the transmitter

Full size image

5.3 Experimental results of the receiver

In what follows, we assume that the channel is perfect and that no distortion of the transmission message has taken place.

The principle part of the program implementation of the observer (see Eqs. 8–11) into Arduino board is given below:

figure b

Figure 22 shows the experimental results of the states and the reconstructed message at the level of the receiver.

Fig. 22
figure 22

Experimental results of the states and the reconstructed message at the level of the receiver

Full size image

Figures 23, 24 and 25, respectively, show the experimental results of the phase portrait \(x_\mathrm{1O}\) versus \(x_1\), the phase portrait \(x_\mathrm{2O}\) versus \(x_2\) and the phase portrait \(x_\mathrm{3O}\) versus \(x_3\).

Fig. 23
figure 23

Experimental result of the phase portrait \(x_\mathrm{1O}\) versus \(x_1\)

Full size image
Fig. 24
figure 24

Experimental result of the phase portrait \(x_\mathrm{2o}\) versus \(x_2\)

Full size image
Fig. 25
figure 25

Experimental result of the phase portrait \(x_\mathrm{3O}\) versus \(x_3\)

Full size image

6 Conclusion

In this paper, we have presented a new transmission scheme based on discrete hyperchaotic dynamical system with high level of security. The proposed transmission scheme uses a classical unidirectional synchronization method based on a delayed step-by-step observer, where its principal advantages lie in its simplicity of implementation and its robustness to measurement noise. The robustness of the transmission system with respect to parameters variation and robustness against transmission noise has been studied. Simulations have been carried out to illustrate the effectiveness of the proposed scheme. Experimental results are presented to check the validity of the proposed technique. Note that the real-time implementation of the transmission scheme signals obtained is almost identical in shape to those of the simulations ones and then validated. In addition, the implemented solution exhibits good performances of throughput and cost in terms of resources consumptions. In future works, we plan to exploit our transmission scheme in order to transmit a digital image.