Keywords

1 Introduction

Available dynamical characteristic chaotic systems are classified into two clusters. The reported systems with (i) hidden attractors or (ii) self-excited attractors [1,2,3,4,5,6,7,8] are the two main cluster. Finding and advancement of the systems with hidden attractors is more challenging as compared to the other part. This is because in hidden attractors the knowledge of location of equilibrium point does not help in creation of the attractors [1,2,3,4,5,6,7,8]. Lorenz [9], Chen [10], Lu [11], chaotic system and systems in [12,13,14,15,16,17] are the types of self-excited attractors. Systems having stable equilibrium point [18, 19] or no equilibrium point [20, 21] are the main types of hidden attractors. Newly the chaotic/hyperchaotic systems with infinite equilibria also belong to the choice of the hidden attractors [22,23,24,25,26,27]. The study of the chaotic/hyperchaotic systems having such nature is significant. This is so because in such system unexpected and undesired behaviours can be observed [6, 28, 29].

Hidden attractors are seen in various types of chaotic/hyperchaotic system as discussed in the literature [30, 31]. Dynamical systems with stable equilibrium point hidden attractors are comparatively less available in the literature as compared with no equilibrium point system of hidden attractors. We know that the hyperchaotic systems are more complex as compared with the chaotic systems [24, 32]. Thus, development of hyperchaotic system is more important. The available dynamical system (chaotic/hyperchaotic) systems having stable nature of equilibria are given in the Table 1. Table 1 reflects that hyperchaotic systems having stable nature of the equilibrium points are very few in the literature. It is noted from the available literature and the Table 1 that there is still some scope for developing the system with stable equilibria. Considering the above discussion, this paper needs to report a new hyperchaotic system. The important feature in the new system is that it has a stable equilibrium point.

Table 1 The dynamical systems (hyperchaotic/chaotic) having stable nature of equilibria
Full size table

The remaining paper goes like this. Section 2 presents the dynamics of the proposed new system having hyperchaotic behaviour and stable equilibria. Numerical analysis of the reported system is discussed in Sect. 3. Application of the new system is discussed in the Sect. 4 of the paper. Results and discussion of the application is presented in Sect. 5 of the paper. And in the last the paper is concluded in the Sect. 6 of the paper.

2 A New Dynamical Hyperchaotic System Having Stable Nature of Equilibrium Point

In the present section, the dynamics of a new system is presented which is considered in the work. The new proposed system is developed from the Lorenz-stenflo system [19] by using state feedback control. The dynamics of the reporting system is presented in (1).

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = a\left( {x_{2} - x_{1} } \right) + bx_{2} x_{3} + x_{3} x_{4} } \hfill \\ {\dot{x}_{2} = - bx_{1} x_{3} + cx_{2} + x_{4} } \hfill \\ {\dot{x}_{3} = 4 + x_{1} x_{2} - dx_{3} } \hfill \\ {\dot{x}_{4} = - ex_{2} } \hfill \\ \end{array} } \right. $$
(1)

In system (1), \( a, b, c, d, e \) are the parameters and \( x_{1} , x_{2} , x_{3} , x_{4} \) are considered as the state. The system in (1) is obtained from the Lorenz-stenflo system using state feedback control and perturbing one term.

The system in (1) is invariant when \( \left( {x_{1} , x_{2} , x_{3} , x_{4} } \right) \to \left( { - x_{1} , - x_{2} , x_{3} , - x_{4} } \right) \). Therefore, the proposed system dynamics has regularity around the \( x_{3} \) axis.

The new hyperchaotic system proposed in the paper is a dissipative dynamical system. This is proved by finding the divergence of the new system and is given in (2).

$$ \nabla v = \frac{{\partial \dot{x}_{1} }}{{x_{1} }} + \frac{{\partial \dot{x}_{2} }}{{x_{2} }} + \frac{{\partial \dot{x}_{3} }}{{x_{3} }} + \frac{{\partial \dot{x}_{4} }}{{x_{4} }} = - a - c - d = - \left( {a + c + d} \right) $$
(2)

It is seen from (2) that the divergence is negative because \( a, c, d \) are the positive constants. Thus the volume in the phase space of the new system decays exponentially with the rate \( \left( {a + c + d} \right) \). Therefore it may be said that there can be attractors in system (1).

Equilibrium point of the new considered system is found out by putting the derivate of each state variable to zero. The system in (1) has only equilibrium point at \( E = \left( {0,\, 0, \, - \frac{d}{4},\,0} \right). \) Eigenvalues of the new system is found out using the Jacobian matrix given in (3).

$$ J_{1} = \left[ {\begin{array}{*{20}c} { - a} & {a + b\left( {x_{3} } \right)^{*} } & {b\left( {x_{2} } \right)^{*} + \left( {x_{4} } \right)^{*} } & {\left( {x_{3} } \right)^{*} } \\ { - \left( {x_{3} } \right)^{*} } & {17} & { - \left( {x_{1} } \right)^{*} } & 1 \\ {\left( {x_{2} } \right)^{*} } & {\left( {x_{1} } \right)^{*} } & { - d} & 0 \\ 0 & { - e} & 0 & 0 \\ \end{array} } \right] $$
(3)

Table 2 presents the eigenvalues of the system given in (1). It is specious from Table 2 that the new system has all the eigenvalues with stable nature. Thus, the new system may have hidden attractors.

Table 2 Equilibrium point and eigenvalues of system (1) with \( a = 35,\, b = 30, \,c = 17, \,d = 0.78, \,e = 14 \)
Full size table

3 Dynamical Analysis of System (1)

Dynamical behaviour of the considered new proposed system is shown in the present section using some of the numerical method.

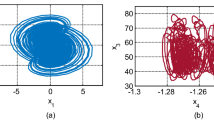
The new system has hyperchaotic behaviour with \( a = 35,\, b = 30, \,c = 17, \,d = 0.78,\, e = 14 \). Finite-time LEs for these sets of parameters are \( L_{i} = \left( {1.014,\, 0.218, \,0,\, - 19.686 } \right). \) Hyperchaotic attractors of the new system with \( a = 35,\, b = 30, \,c = 17, \,d = 0.78, \,e = 14 \) are revealed in Fig. 1. Poincaré map across \( x_{1} = 0 \) plane of the new system is presented in Fig. 2. The dynamical behaviour/characteristics of the new system is investigated by plotting the finite-time Lyapunov spectrum (LS). The finite-time LS is plotted by finding the Lyapunov exponents with the fixed initial conditions \( x\left( 0 \right) = \left( {0.2,\, 0.1, \,5, \,0.1} \right)^{T} \) and observation time T = 20,000 time unit. The LEs are calculated by the method of Wolf et al. algorithm [51] in MATLAB simulation environment. The finite-time Lyapunov spectrum with varying e keeping other parameter fixed in Fig. 3. Presence of the two positive natures of the Lyapunov exponents in Fig. 3 indicates the existence of hyperchaotic behaviour in the new system.

Fig. 1
figure 1

Hyperchaotic attractors with \( a = 35,\, b = 30,\, c = 17,\, d = 0.78, \,e = 14 \) for system (1)

Full size image
Fig. 2
figure 2

Poincaré map across \( x_{1} = 0 \) in: a \( x_{2} - x_{3} \) plane and b \( x_{3} - x_{4} \) plane of the new system

Full size image
Fig. 3
figure 3

Finite time LS with \( a = 35, \,b = 30, \,c = 17,\, d = 0.78 \) and \( x\left( 0 \right) = \left( {0.2, 0.1, 5, 0.1} \right)^{T} \) for the new system

Full size image

4 Secure Communication Using the System in (1)

Here, an application using the new proposed system is illustrated. The application is shown in the field of secure communication by masking and retrieving of information signals.

In last decade chaotic/hyperchaotic systems are commonly being applied for secure communication [52,53,54]. The chaotic signals are being used in various ways in the secure communication. One common way is for encryption and decryption of a message signal. The main reason for this is that chaotic signals have apparently noise like nature and unpredictable behaviour [52,53,54,55].

In the paper the secure communication using the new system in (1) is presented by considering as like the system acting as a master and system acting like as a slave system. Suppose the system acting like as a master and the system acting like as a slave system are given in (4) and (5), respectively

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = a\left( {x_{2} - x_{1} } \right) + bx_{2} x_{3} + x_{3} x_{4} } \hfill \\ {\dot{x}_{2} = - bx_{1} x_{3} + cx_{2} + x_{4} } \hfill \\ {\dot{x}_{3} = 4 + x_{1} x_{2} - dx_{3} } \hfill \\ {\dot{x}_{4} = - ex_{2} } \hfill \\ \end{array} } \right. $$
(4)
$$ \left\{ {\begin{array}{*{20}l} {\dot{y}_{1} = a\left( {y_{2} - y_{1} } \right) + by_{2} y_{3} + y_{3} y_{4} + u_{1} } \hfill \\ {\dot{y}_{2} = - bmy_{3} + cy_{2} + y_{4} + u_{2} } \hfill \\ {\dot{y}_{3} = 4 + my_{2} - dy_{3} + u_{3} } \hfill \\ {\dot{y}_{4} = - ey_{2} } \hfill \\ \end{array} } \right. $$
(5)

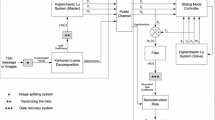
where \( m = x_{1} + s \) and s is the message signal and \( u_{1} ,\, u_{2} ,\,u_{3} \) control inputs which are needed to be designed. Here, the message (m) is added with state \( x_{1} \). When the system acting like a master (4) has states synchronised with the system acting like the system as a slave (5) systems i.e., \( y_{i} = x_{i} \), then at the receiver end the message signal \( \tilde{s} \) is retrieved as \( \tilde{s} = m - y \approx s \). Here it is considered that the SNR of the message signal \( (m) \) is less than the masking signal \( x_{1} \). The application is completely illustrated and sketched in Fig. 4.

Fig. 4
figure 4

Complete communication scheme [52]

Full size image

The synchronisation errors among the system acting like as a master (4) and the system acting like as a slave system (5) are given in (6).

$$ \left\{ {\begin{array}{*{20}l} {\dot{e}_{1} = a\left( {e_{2} - e_{1} } \right) + be_{2} y_{3} + bx_{2} e_{3} + e_{3} y_{4} + x_{3} e_{4} + u_{1} } \hfill \\ {\dot{e}_{2} = - e_{1} y_{3} - x_{1} e_{3} + ce_{2} + e_{4} + u_{2} } \hfill \\ {\dot{e}_{3} = e_{1} y_{2} + x_{1} e_{2} - de_{3} + u_{3} } \hfill \\ {\dot{e}_{4} = - ee_{2} } \hfill \\ \end{array} } \right. $$
(6)

Next question is to narrate the stabilisation of the error dynamics given in (6). It is required to bring the error dynamics to zero. The answer for the question and the required task is performed by designing a suitable SMC. Here proportional integral SMC is designed for this purpose.

The mathematical structure of the PI sliding surface is presented in (7).

$$ \left\{ {\begin{array}{*{20}l} {s_{1} = e_{1} + \mathop \smallint \limits_{0}^{t} \left( {k_{1} e_{1} } \right)d\tau } \hfill \\ {s_{2} = e_{2} + \mathop \smallint \limits_{0}^{t} \left( {k_{2} e_{2} - ce_{4} } \right)d\tau } \hfill \\ {s_{3} = e_{3} + \mathop \smallint \limits_{0}^{t} \left( {k_{3} e_{3} } \right)d\tau } \hfill \\ \end{array} } \right. $$
(7)

where \( k_{1} \) and \( k_{2} \) are the user defined positive parameters. It is needed that when dynamics goes through the sliding variable, it requires to satisfies \( \dot{s}_{i} = 0. \) Now the equivalent mode dynamics [56] is be written as (8).

$$ \left\{ {\begin{array}{*{20}l} {\dot{e}_{1} = - k_{1} e_{1} } \hfill \\ {\dot{e}_{2} = - \left( {k_{2} e_{2} - ee_{4} } \right)} \hfill \\ {\dot{e}_{3} = - \left( {k_{3} e_{3} } \right)} \hfill \\ {\dot{e}_{4} = - ee_{2} } \hfill \\ \end{array} } \right. $$
(8)

The stabilisation of the error dynamics defined in (8) is shown by choosing a Lyapunov function candidate as \( V_{1} \left( e \right) = \frac{1}{2}\left( {e_{1}^{2} + e_{2}^{2} + e_{3}^{2} + e_{4}^{2} } \right) \). The \( \dot{V}_{1} \left( e \right) \) along with (8) is written in (9).

$$ \left\{ {\begin{array}{*{20}l} {\dot{V}_{1} \left( e \right) = e_{1} \dot{e}_{1} + e_{2} \dot{e}_{2} + e_{3} \dot{e}_{3} + e_{4} \dot{e}_{4} } \hfill \\ { = e_{1} \left( { - k_{1} e_{1} } \right) + e_{2} \left( { - \left( {k_{2} e_{2} - ee_{4} } \right)} \right) + e_{3} \left( { - \left( {k_{3} e_{3} } \right)} \right) + e_{4} \left( { - ee_{2} } \right)} \hfill \\ \end{array} } \right. $$

After arranging some terms, we get

$$ \dot{V}_{1} \left( x \right) = - k_{1} e_{1}^{2} - k_{2} e_{2}^{2} - k_{3} e_{3}^{2} - k_{4} e_{4}^{2} $$
(9)

where \( k_{1} , k_{2} , k_{3} , k_{4} \) are the positive constant. It is apparent from (9) that it is negative definite. Therefore, the sliding motion is asymptotically stable.

SMC controllers proposed are designed in (10).

$$ \left\{ {\begin{array}{*{20}c} {u_{1} = - ae_{2} - be_{2} y_{3} - bx_{2} e_{3} - e_{3} y_{4} - x_{3} e_{4} - k_{1} e_{1} - \rho_{1} \tanh \left( {\sigma_{1} } \right) } \\ {u_{2} = e_{1} y_{3} + x_{1} e_{3} - ce_{2} - (1 - e)e_{4} - k_{2} e_{2} + sy_{3} - \rho_{2} \tanh \left( {\sigma_{2} } \right) } \\ {u_{3} = - e_{1} y_{2} - x_{1} e_{2} - k_{3} e_{3} - sy_{2} - \rho_{2} \tanh \left( {\sigma_{2} } \right) } \\ \end{array} } \right. $$
(10)

Theorem 1

The error in (6) converges to \( \sigma_{i} = 0 \) if it is controlled by (10) and also ensure synchronisation between the system as the master (4) and the system as the slave (5) system.

Proof

Suppose Lyapunov candidate function as \( V_{2} \left( s \right) = \frac{1}{2}\left( {s_{1}^{2} + s_{2}^{2} + s_{3}^{2} } \right) \). The time derivative of \( V_{2} \left( s \right) \) along with (7) can be written as

$$ \left\{ \begin{aligned} & \dot{V}_{2} (S) = S_{1} \dot{S}_{1} + S_{2} \dot{S}_{2} + S_{3} \dot{S}_{3} \\ & = s_{1} \left( {\dot{e}_{1} + k_{1} e_{1} } \right) + s_{2} \left( {\dot{e}_{2} + k_{2} e_{2} - ce_{4} } \right) + s_{3} \left( {\dot{e}_{3} + k_{3} e_{3} } \right) \\ & = s_{1} \left( {a\left( {e_{2} - e_{1} } \right) + be_{2} y_{3} + bx_{2} e_{3} + e_{3} y_{4} + x_{3} e_{4} + u_{1} + k_{1} e_{1} } \right) \\ & \quad \quad + s_{2} \left( { - e_{1} y_{3} - x_{1} e_{3} + ce_{2} + e_{4} + u_{2} + k_{2} e_{2} - ce_{4} } \right) + \\ & \quad \quad \quad \quad \quad s_{3} \left( {e_{1} y_{2} + x_{1} e_{2} - de_{3} + u_{3} + k_{3} e_{3} } \right) \\ \end{aligned} \right. $$
(11)

Now inserting the control laws (10) in (11) we get,

$$ \begin{aligned} & \dot{V}_{2} \left( s \right) = - \sigma_{1} s_{1} \tanh \left( {s_{1} } \right) - \sigma_{2} s_{2} \tanh \left( {s_{2} } \right) - \sigma_{3} s_{3} \tanh \left( {s_{3} } \right) \\ & < - \rho_{1} \left| {s_{1} } \right| - \rho_{2} \left| {s_{2} } \right| - \rho_{3} \left| {s_{3} } \right| < 0 \\ \end{aligned} $$
(12)

where \( \rho_{1} , \rho_{2} , \rho_{3} \) are the positive constants. Thus, we can say that \( \dot{V}_{2} \left( s \right) < 0 \) for \( s \ne 0 \). Therefore sliding surfaces \( s_{1} ,s_{2} \) and \( s_{3} \) converge to \( s_{1} = 0 \), \( s_{2} = 0 \) and \( s_{3} = 0 \), [56] respectively. Hence, error dynamics given in (7) stabilises at origin. Therefore, the master (4) and the slave (5) systems states are synchronised. Therefore the message signal is encrypted and decrypted successfully using the proposed approach.

5 Results and Discussion for Secure Communication Using the New Hyperchaotic System

This section discussed the secure communication using the new hyperchaotic system. The application is shown by encryption and decryption of a sinusoidal signal and sound like signal. Simulation of the master and slave hyperchaotic systems is done with the initial conditions \( x\left( 0 \right) = \left( {0.2, \,0.1, \,5,\, 0.1} \right)^{T} \), \( x\left( 0 \right) = \left( {0.5,\, 0.5, \,2, \,0.5} \right)^{T} \), respectively. The values of the constants used for the SMC are \( k_{1} = k_{2} = k_{3} = 2,\, \rho_{1} = 5, \,\rho_{2} = 2, \,\rho_{3} = 2. \)

For masking, a sinusoidal signal in the form \( s = \sin \left( {2\pi 10t} \right) \) and a speech signal available in MATLAB named with “handle.mat” are used.

Results of the secure communication with the sinusoidal signal are shown from Figs. 5, 6, 7 and 8. Synchronisations of the system considered as the master system and system considered as the slave systems having synchronised states are shown in Fig. 5. It is apparent from Fig. 5 that the states of the master and slave systems are synchronised properly. The time behaviours of the designed sliding surfaces and the designed control inputs are shown in the Figs. 6 and 7 respectively. The nature of the carrier, masked and the transmitted signals along with recovered signal are presented in Fig. 8. Figure 8 discussed that the transmitted message signal is recovered properly.

Fig. 5
figure 5

Synchronised states of (4) and (5) systems with sinusoidal signal

Full size image
Fig. 6
figure 6

Behaviour of the sliding surface designed for the synchronisation with sinusoidal signal

Full size image
Fig. 7
figure 7

Behaviour of the designed inputs used for the synchronised system as master (4) and slave (5) systems with sinusoidal signal

Full size image
Fig. 8
figure 8

Responses of the carrier, masked and the transmitted sinusoidal message signal along with recovered sinusoidal message signal

Full size image

Now a sound signal is used for the secure communication. The synchronisation errors between the master and slave systems having synchronised states are shown in Fig. 9. It is apparent from Fig. 9 that master and slave systems are synchronised properly in smaller synchronising time. Behaviour of the transmitted message signal, masked signal and recovered message signal in case sound wave is shown in Fig. 10. It is seen from Fig. 10 that the transmitted message signal is recovered properly. Thus, the concept of application in secure communication using the proposed system is validated.

Fig. 9
figure 9

Synchronisation error between the synchronised states of master (4) and slave (5) systems with considered sound wave message signal

Full size image
Fig. 10
figure 10

Responses of the transmitted sound wave message signal, masked signal and recovered message signal

Full size image

6 Conclusions

In the present work, a new hyperchaotic system is reported. Presence of an equilibrium point having stable nature in the new system makes it to be considered under hidden attractors dynamical system. Dynamical properties in the new system is shown using some numerical methods like phase portrait, Poncaré map and Lyapunov spectrum. The applications of the new system are shown in secure communication by masking of a sinusoidal signal and a sound wave. A PI-SMC is designed for the application. Results using the MATLAB simulation validate the numerous dynamical characteristics and application of the new system.